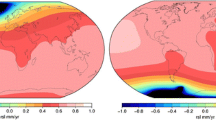
Abstract
The widely used 15-year Gravity Recovery and Climate Experiment (GRACE) data sets do not conserve global total mass. They have a spurious decreasing trend of ~ 280 Gt/year. Various regions contribute differently to the global total mass loss error, with the Greenland Ice Sheet (GrIS) generating ~ 10% of the error alone. Atmospheric parameters from reanalysis datasets drive a well-tested ice model to generate mass variation time series over the GrIS for 2002–2015. Because shorter timescale spikes of ~ 10–30 Gt in GRACE measurements are physically based, only the overall trend of ~ 30 Gt/year requires correcting. A more accurate mass loss rate estimate for 2002–2015 is ~ 120 Gt/year, considerably below previous estimates. With the water redistribution to lower latitudes and other effects from a warming climate, the nontidal Earth moment of inertia (MOI) also increases. After rectification, the GRACE measured mass redistribution shows a steady, statistically robust (passed a two-tailed t-test at p = 0.04 for dof = 15) rate of MOI increase reaching ~ 10.1 × 1027 kg m2/year, equivalent to a 10.91 μs/year increase in the length of a day, during 2002–2017.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent decades, the net top-of-atmosphere energy imbalance reached 1 W/m2 (Hu and Bates 2018; Trenberth and Fasullo 2013). With the increased energy accumulation in the Earth’s climate system, the thermodynamic structure of the atmosphere has been substantially altered. Consequently, the hydrological cycle, the oceanic circulation and the cryosphere dynamics all have been changed. According to the IPCC Special Report on Ocean and Cryosphere in a Changing Climate (2019), the upper (0–200 m depth) ocean heat content had increased at a rate of 8–18 × 1021 J/year. Polar ice sheets respond to this climate change by increased creeping and other related total mass shedding mechanisms (Ren and Leslie 2011). As mountain glaciers retreat (Ren and Karoly 2006), significant portions of solid water become liquid water and are redistributed into global oceans or drained into reservoirs, such as soil moisture and groundwater. The kinetic energy of winds is very unevenly distributed spatially and is concentrated in polar and subtropical jet streams. Subtropical jet stream changes have an important influence on the angular momentum of the Earth system (Lee et al. 2019). Polar jet streams influence mid-latitude weather systems, with the storm tracks being essentially a surface expression of the jet stream. Of great importance is that the mid-latitude meridional temperature gradients are being modified by anthropogenic climate change (Vallis et al. 2015; Ren 2010) and the jet streams are expected to further adjust in response to these changes (Francis and Vavrus 2012, 2015; Haarsma et al. 2013). While kinetic energy eventually dissipates in the boundary layer, lasting effects on Earth result from the associated mass redistribution (e.g., precipitation), which will affect the Earth’s moment of inertia (MOI).
The high latitude Greenland Ice Sheet (GrIS) is a leading contributor to global sea level rise (Box et al. 2006; Shepherd and Wingham 2007; Rahmstorf 2010; Shepherd et al. 2012, 2018; Hanna et al. 2013; Vaughan et al. 2013; Bamber et al. 2018), accounting for ~ 0.7 mm/year. In a future warming climate, faster ice creeping from reduced ice viscosity, enhances dynamic mass loss (Ren et al. 2011a; Ren and Leslie 2011; Rignot and Kanagaratnam 2006). However, estimates of future changes in net mass balance are highly debatable as studies suggest GrIS snowfall will increase as the climate warms (Ettema et al. 2009; Merz et al. 2013; Fyke et al. 2014; Hanna et al. 2018). There also are studies of precipitation and circulation relationships over the GrIS, under present climate conditions (Box et al. 2006; Cassano et al. 2001; Fettweis et al. 2013) and in a warming climate. Doyle et al. (2015) found that summer storms accelerated ice flow, with consequences for the GrIS in a future warmer climate.
The Gravity Recovery and Climate Experiment (GRACE), launched in 2002, provides large scale, coherent changes in the Earth’s mass field. It monitored temporal variations of the Earth’s gravity field with monthly temporal resolution (Bentley and Wahr 1998; Famiglietti and Rodell 2013; Ren 2014a; Voss et al. 2013; IMBIE Team 2018). Horizontal mass redistribution in the atmosphere, the oceans, the hydrosphere, the cryosphere or the lithosphere, all are captured by GRACE measurements. Here, we first correct a readily identifiable error in GRACE measurements, for 2002–2017, which provides rectified datasets suitable for studies in a wide range of disciplines. Then, as one application, the total Earth MOI variations and the various contributors are analyzed using the Scalable Extensible Geofluid Modeling framework for ENvironmenTal issues (SEGMENT, Ren 2014b; Ren et al. 2008, 2012) modeling system. The SEGMENT is the basic modeling system in this study. It has successfully been applied to both the Antarctic Ice Sheet (AIS, Ren et al. 2012) and the GrIS (Ren et al. 2011a, b) for ice sheet total mass balance, to world mountain regions for landslides and debris flow studies (e.g., Ren 2014b), and to various faults for earthquake mechanism studies (Ren and Fu 2019). The primary aim of this study is to quantify the total Earth MOI contributions from its various components. Identifying the persistent contributors during this 15-year period assists in the estimation of the climate-driven MOI evolution, in the transient climate change period.
2 Method and data
The focus of this study is the MOI fluctuations caused by near surface, climate sensitive mass transport phenomena, such as those from the altered hydrological cycle, atmospheric expansion, and cryospheric mass balances. Multiple data sources and an advanced modeling system are used to provide estimates of the changes in the Earth’s total MOI, and in the contributions from the individual MOI components.
2.1 GRACE measurements
Because mass changes integrate spatially, GRACE rapidly measures net mass balance over vast regions, including polar ice sheets, thereby providing mass change rates by repeated measurements over the observation period. Measuring the gravity anomaly at monthly temporal frequency and ~ 3° spatial resolution (Vishwakarma et al. 2018), GRACE is ideal for measuring the evolution of the Earth’s MOI. Here, data are obtained from the Jet Propulsion Laboratory (JPL) global mascon solution (Watkins et al. 2015), at grace.jpl.nasa.gov, after atmospheric vapor corrections and application of other time-invariant harmonic filters.
Monthly averaged global gravity field data from GRACE then are estimated in the form of spherical harmonics (i.e., Stokes coefficients). For many applications involving mass fluxes, the traditional procedure of direct using of spherical harmonics has its limitations (Luthcke et al. 2013; Save et al. 2016; Tapley et al. 2019). Mass concentration blocks (mascons) basis functions typically are used to better estimate mass fluctuations from GRACE measurements. The JPL mascon used in this study (Watkins et al. 2015) applied explicit partial derivatives with analytical expression for mass concentration to relate the intersatellite range-rate measurements to the individual mascons. Specifically, it is solved on 3 × 3 degrees equal area elements, although the final products are interpolated to 0.5 by 0.5 degrees grids. Water equivalent mass flux data are used here. For this purpose, a separate scale factor dataset is used, derived from the community land surface model predicted terrestrial water storage changes. The scale factors, which also are on 0.5 by 0.5 degrees grids, are multiplied to the mascons to eventually obtain the mass grids in units of equivalent water depth. The post glacial rebound (PGR) effects, also called glacial isostatic adjustment (GIA), are removed from the mascon solution using model predictions. Except for the RL05 release of CSR mascons, an ellipsoidal Earth model usually is adopted for mascon solutions (Table 1).
Mascon solutions are used in this study because they have fewer leakage errors, which is usually achieved by the separation of land and ocean signals. Further processing involves representation mascon solutions into finer grids. Spheric harmonic treatments and filtering operations are spatial operations (Wahr et al. 1998; Swenson and Wahr 2006; Duan et al. 2009; Longuevergne et al. 2010; Frappart et al. 2011; Wouters et al. 2014), and do not affect global total mass conservation. The monthly datasets are the ‘original raw data sets’ which provide mass grids, in units of equivalent water depth; hence, the mass unit gigatonnes (Gt, or 109 tonnes) is equivalent to the volume unit km3.
Although the Earth’s total mass should be constant, it is not well conserved in the GRACE measurements from the JPL website (Humphrey et al. 2016; Wiese et al. 2018), as shown in Fig. 1a. It also is not conserved in both the CSR and GSFC/NASA mascon solutions. Globally, it is accepted that the negative trend in raw GRACE data is spurious, with no physical meaning. For regional areas, however, physically meaningful information is contaminated by this artificial signal because, globally, the spurious error is clear whereas, at regional scales, it is not clearly separated from the physical signals. In addition to systematic measurement errors, the GRACE data are contaminated by noise. Here, the empirical mode decomposition (EMD) of Wu et al. (2007, 2016) determines the spurious trend, and detrends the raw GRACE data. EMD identifies signals of differing inertia (e.g., intrinsic trends and natural variabilities on various time scales). The advantages of EMD over traditional Fourier based decomposition are detailed in Wu et al. (2016). EMD also identifies error sources for cyclical signals and generic trends in raw GRACE data.
Panel a shows the raw GRACE measurements (only area weighting, or a static spatial operation, is applied to the 1-degree gridded data) of mass variations for the northern (a global belt of 0°–60° N) and southern (0°–60° S) hemispheres, and for the entire globe. Data are from the JPL public website https://grace.jpl.nasa.gov. Panels b–f are decomposed signals, ranging from white noise to slowly varying signals. Global mass conservation is a basic physical requirement. However, this quantity is not conserved in the raw GRACE data, and the associated unrealistic trend should be removed for many applications. Whereas the total global mass loss is spurious (e.g., from errors due, for example, to the ageing of the GRACE satellites), the mass loss trend in both the Northern and Southern Hemisphere, and in regional areas (not shown), all are physical phenomena contaminated by errors
In summary, the approach of this study is to: (1) rectify the raw GRACE measurements by removing the artificial (non-physical) decreasing trend; (2) use the rectified mass variations to train SEGMENT-Ice driven by reanalysis data; and (3) employ the optimized SEGMENT-Ice modeling system for MOI decomposition into its various components. Hence, it is critical to determine the global distribution of GRACE satellite errors: i.e., how much each grid point on Earth contributes to the global total error. From Fig. 2, mass variations are globally uneven. For a 5 mm water equivalence criterion, over 50% of the Earth’s surface experiences no mass variations of that magnitude. Strong mass field fluctuations occur in several regions with clear precipitation and/or plate convergence, including the Amazon region, central and southern Africa, monsoonal India, the Bay of Bengal, and south-central Greenland. In these regions, mass fluctuation amplitudes reach 20 cm. It is a dynamic situation in that mass deficit centers can become mass gain centers over time. However, regionally, mass fluctuation magnitudes basically are stable. The absolute error contributing to global total mass fluctuation time series, rather than spread evenly from all global areas, may be proportional to the magnitudes of regional mass fluctuations. A weighting scheme partitions total spurious mass loss into regional areas: \(w_{i,j} = A_{i,j} /\sum {A_{i,j} }\). Here Ai,j is the magnitude of raw GRACE mass variation time series over the grid (i,j), summed over the globe (i = 1, 360; j = 1,180 for 1° degree raw data). GrIS contributes ~ 10% of global total mass variation. This scheme filters GrIS measurements, producing a de-trended mass variation time series, further used for SEGMENT-Ice verification and future GrIS mass loss projections. This linear error ascription is supported by Humphrey et al. (2016), despite differing approaches to detrending and decomposing time series.
Global distribution of gravity anomalies in the year 2006. Most areas have no significant mass changes (color shades, in equivalent cm water depth; using 0.5 cm as the threshold). Strong mass field fluctuations are concentrated in several regions with precipitation and/or apparent plate convergences, including the Amazon region, central and southern Africa, the monsoonal region of India and the Bay of Bengal, and south-central Greenland. It is dynamic, as mass deficit centers can become centers of mass gain. However, for a fixed region, magnitude mass fluctuations are relatively stable. The errors in the GRACE data might not be affected by geography. The absolute error introduced in the global total mass fluctuation time series, rather than being contributed evenly, may be proportional to regional mass fluctuation magnitudes. The fluctuation magnitudes, weighted by the representing area, distribute total errors over global regions. This approach filters GrIS mass variation measurements to obtain de-trended time series which are further used for ice model verification and for projections of GrIS mass loss
2.2 Earth’s moment of inertia (I)
The MOI (I) is defined as:
where \(\phi \) is latitude, \(\theta \) is longitude, \(\rho \) is density, and \(R\) is Earth’s radius. As the earth has an angular velocity of \(\omega =7.29\times {10}^{-5}\) rad/s and a moment of inertia I \(\approx \) 8.04 × 1037 kg m2, it therefore has a rotational energy (\({0.5I\omega }^{2}\)) of ~ 2.138 × 1029 J. The coordinates follow the right-hand rule and all variables are in SI units. The total MOI variations are decomposed into various contributors, for increased understanding long-term trends and short-term variations. Hence, contributions from the polar ice sheets (GrIS and AIS), mountain glaciers (MG), atmospheric expansion (Atm), and precipitation driven hydrological cycles (groundwater and soil moisture, SM) all are included. Estimation formulae for the respective contributors are indicated, below.
-
a.
MOI estimates from GRACE gravity anomaly measurements (\({I}_{total}\)):
$${I}_{total}=\sum_{\begin{array}{c}i=1\\ j=1\end{array}}^{\begin{array}{c}j=ny\\ i=nx\end{array}}{W}_{i,j}\Delta {h}_{i,j}{\rho }_{w}{R}^{2}{\mathrm{cos}}^{2}{\phi }_{i,j}$$(2)where subscripts i, j are integer indices of the latitudinal and longitudinal count of the horizontal global grids, W is grid area, \(\Delta h\) is the water equivalent depth (GRACE measurements are in cm, converted into meters), and \({\rho }_{w}\) is water density. The Earth’s MOI is in kg m2.
-
b.
MOI estimates from the elevated atmospheric mass center of the Earth’s atmosphere (\({I}_{atm}\)):
$${I}_{atm}=\sum_{\begin{array}{c}i=1\\ j=1\end{array}}^{\begin{array}{c}j=ny\\ i=nx\end{array}}{\sum_{k=1}^{nz}\Delta {p}_{i,j,k}W}_{i,j}({R+z)}^{2}{\mathrm{cos}}^{2}{\phi }_{i,j}/g$$(3)where subscribe k is integer count of atmospheric vertical levels, \(p\) is atmospheric pressure, \(z=z(p)\) is the geopotential height, and g is gravitational acceleration.
-
c.
MOI from polar ice sheets and mountain glaciers (Iice):
Essentially the same expression as Eq. (2) is followed except that h is now simulated by an advanced ice sheet modeling system SEGMENT-Ice (Ren et al. 2011b). Some technical details are described in the Appendix.
-
d.
MOI from hydrological cycle as a remainder (\({I}_{pr}\)):
Essentially the same expression as Eq. (2) is followed except that h is now simulated by an advanced land surface modeling scheme in SEGMENT-Landslide (Ren et al. 2011c).
Atmospheric variables which are used as inputs to SEGMENT are obtained from a reanalysis dataset. Anomalies (ΔIʹs) of all components are calculated by subtracting from each annual value the value of year 2002.
2.3 Reanalysis data and SEGMENT modeling system
The calculation of the MOI components is obtained either directly from atmospheric parameters (e.g., the expansion of Earth atmospheric columns and thus the elevation of their centers of mass) or is obtained using atmospheric parameters as forcing of the SEGMENT modeling system. For example, driven by atmospheric parameters, the SEGMENT system is used to simulate groundwater fluctuations and ice mass loss from the cryosphere. Atmospheric parameters in this study are from reanalysis datasets. The five reanalysis products used here are the European Centre for Medium-Range Weather Forecasts interim reanalysis [ERA-Interim reanalysis, Dee et al. (2011)], ERA5, the NCEP/NCAR reanalysis (Kalnay et al. 1996), the NASA’s Modern Era Retrospective analysis for Research and Applications (MERRA; Suarez et al. (2008), and the JRA-55 reanalysis (Kobayashi et al. 2015), at respectively horizontal resolutions of 0.75°, 0.25°, 2.5°, 0.625° × 0.5° and 1.25°. The use of five independently produced reanalysis datasets allows the quantification of the sensitivity of our results to uncertainties in the state of the atmospheric forcing. Six-hourly data from 1980 to 2017 are used, which fully covers the period of GRACE measurements (2002–2017). The reason for restricting the temporal coverage to the remote sensing era is due to the large uncertainty in the Southern Hemisphere, due to the lack of observational data coverage (Le Marshall et al. 2013). Time series of globally integrated surface pressure are examined to guarantee the total mass conservation is met by each reanalysis dataset. Other details of the data used in this study are in Table 1.
The total GrIS mass loss results from complex, interlinked processes, that require a physical modelling system for quantitative estimates of mass loss trends. The SEGMENT-Ice modeling system is a numerical treatment of the physical processes of ice dynamics and has been used in other cryosphere studies (Ren et al. 2011a, 2013a; Ren and Leslie 2011). The conservation equations of mass, momentum and energy simulate the ice motion and mass variations. Model settings and spin-up are those in Ren et al. (2011b) and Ren and Leslie (2011). Model tuning uses corrected GRACE measurements for the 2002–2015. Reanalysis data sets provide the atmospheric parameters driving SEGMENT-Ice for the GRACE measurement period. SEGMENT-Ice was used for both GrIS (Ren et al. 2011b) and the AIS (Ren et al. 2013b), and it allows multiple compositions, multiple phases, and multiple rheologies. The SEGMENT-Ice design also includes known physical mechanisms of ocean-land ice-atmospheric interactions, and new mechanisms can readily be implemented as they become available. For example, it has a granular bed-sliding enhancement mechanism (Ren et al. 2013a; Ren and Leslie 2011), calving mechanisms (Ren and Leslie 2014), and unique fatigue mechanisms explaining random, unexpected terminal glacier surges.
3 Results
The Earth’s global mass should be time-invariant. However, Fig. 1a shows a decreasing global total mass trend of ~ 280 Gt/year. To diagnose this trend, the EMD technique (Wu et al. 2016) decomposes the total, noisy, signal into six components. Except for the first component, white noise, in Fig. 1 (not shown), all other five components have physical meanings. Components 2, 3 and 4 respectively indicate seasonal, inter-annual, and multiple year cyclical signals. Component 5 shows an overall trend of ~ 200 Gt/year. The cause of this ‘apparent’ mass loss is unclear but has no physical meaning. Possibly it is due to satellite aging or arises from other technical issues (Watkins et al. 2015). Using the weight function described above, ~ 30 Gt/year of the global mass loss can be credited to the GrIS. After this trend correction, the mass loss rate during 2003–2015 is ~ 120 Gt/year from the GrIS, which still is larger than estimates from InSAR and other measurements, but below that of Velicogna et al. (2005). From Fig. 1a, the global total mass time series also has annular cycles. This cyclical part of the spurious error is largely attributable to tropical regions between 30° S and 30° N, primarily the Amazon region. The in-phase variation of global and Southern Hemispheric belt time series in Fig. 1a is not coincidental. In comparison, the GrIS is insignificant (two orders of magnitude smaller) and is not removed from the GrIS mass loss time series. For other regions of interest, removal of this portion of the spurious signal requires the information in Fig. 1b, c. Removing the overall trend is critical for estimating the GrIS contribution to eustatic sea levels, as shown in Fig. 1f. The two hemispheric belts, benefitting from the net mass loss from the AIS and the GrIS, should experience a net mass gain, as indicated by the most slowly varying components. Unfortunately, due to spurious noise, mass gain trends are insignificant during the observation period (Fig. 1f), for both hemispheric belts. After trend removal, the global signal time series of component 5 are almost zero, whereas for both the Northern and Southern Hemisphere it increased steadily. The Northern Hemisphere (0°–60° N) increase is larger, suggesting that the GrIS net mass loss exceeds the AIS loss (Fig. 1f).
The total mass balance includes dynamic mass balance, due to ice flow convergence/divergence, and surface mass balance, from precipitation and melting. The surface mass balance has strong seasonal variability. The GrIS melting season is May–October. Accumulation occurs year-round but net accumulation is mainly in the frozen season, typically from several snowstorms. Thus, there is steep annual mass accumulation in November–March, followed by a gradual decrease (Fig. 3). The melting season spikes in 2005 and 2007 were snow precipitation from hurricane remnants (TCs Wilma and Noel) reaching high latitudes. Other spikes, primarily in the frozen accumulation season, are largely from polar snowstorms arriving from the south-east, preceded by strong, easterly Fohn winds. The total mass has a significant decreasing trend of ~ 150 Gt/year before correction and ~ 120 Gt/year after rectification (solid and dotted lines in Fig. 3). This is below the estimates of ~ 200 Gt/year of Velicogna and Wahr (2006), and below the ~ 180 Gt/year of Chen et al. (2006). Notably, the seasonal mass variability is small.
GRACE measurements of the 2002–2015 GrIS mass loss before (black solid line) and after (red dotted line) correction of the spurious decreasing trend. The long blue dashed line is the SEGMENT-Ice simulated mass loss rate for the same period, driven by atmospheric parameters provided by the ERA5 reanalysis
SEGMENT-Ice, driven by WRF-ARW model projections, provided encouraging simulations of the GrIS mass loss (Fig. 3). Summer mass loss spikes are captured well, as in year 2005, and are due to the south-east sector of the GrIS being affected by Atlantic TCs approaching Greenland (e.g., TC Wilma 2005; Fettweis et al. 2013). In addition to being a mechanism for the vertical and poleward transport of atmospheric momentum and energy, TCs transport moisture from the tropical oceans to extra-tropical regions (Emanuel and Jagger 2010; Knutson et al. 2010, 2013). Water vapor transported poleward by TC remnants is precipitated as snow over the ice sheets and glaciers and is critical in maintaining the global eustatic sea level. For example, TCs Wilma (2005) and Noel (2007) both match observational spikes. Because snow precipitation from TC remnants is ‘warm’ precipitation (i.e., snowfall warmer than surface ice and, for the ablation zone, some liquid precipitation), the accumulated mass is not persistent, enhancing the dynamic ice loss. The net results are spike-followed-by-trough signals in the decomposed time series (order 2 time series in Fig. 1) of monthly GRACE measurements. Comparing simulated and observed total mass loss, the spikes of 10–30 Gt from GRACE measurements are realistic, thereby requiring an adjustment only in the unrealistic trend possibly from GRACE satellite aging. SEGMENT-Ice parameters were optimized using GRACE measurements. Upon convergence, the root-mean-squared error over the 13-year period is below ~ 20 Gt. Hence, the model simulations and observations are acceptably close.
Different mascon solutions have different definitions (spatial resolution, converging schemes, and even the shape of mascon boxes). For example, the CSR mascon solutions are related to the range-rate observations via partial derivatives with respect to a spherical harmonic expansion that is truncated to degree and order 120. Mass anomalies in each mascon are computed from satellite range rate observations through their partial derivatives (e.g., Save et al. 2016). The CSR resolutions also are estimated directly on a geodetic grid of the size equivalent to equatorial 1°, then to the finer resolution of 0.5° as used here. In contrast, the JPL mascon solutions were solved on 3° elements and represented on 0.5° grids. The global total mass balance is well preserved by both mascon solutions. However, the spatial distribution patterns of the mass flux are different, as are the MOIs. The global total MOI trend estimated using CSR mascon solutions is shown in Fig. 4. Importantly, both solutions suggest a steady, statistically robust rate of MOI increase, passing a two-tailed t-test with p = 0.04 for dof = 15, that reaches ~ 10.1 × 1027 kg m2/year, which is equivalent to a 10.91 \(\upmu \)s/year increase in the length of a day, during 2002–2017. In particular, the short-term spikes associated with hydrological patterns linked with major earthquakes [e.g., the 2006 spike associated with the Nepal earthquakes, Ren and Fu (2019)] agree very well. Repeating the above analyses using the CSR mascon solutions suggest, qualitatively, the same conclusions as those from the JPL mascon solutions. Interestingly, the mascon solution from the GSFC, produced a MOI evolution curve closely resembling those from CSR and JPL mascon solutions. The total MOI trend identified by the three mascon solutions is similar, and hence is suggestive of a robust signal.
The MOI annual means obtained from the GRACE measurements and the estimated contributing components are estimated (Fig. 5). The linear trends during 2002–2017 for the five contributors: the AIS, GrIS, Atm (atmosphere expansion), MG and SM are, respectively, 5.06 × 1027 kg m2/year, 4.8 × 1027 kg m2/year, 1.1 × 1027 kg m2/year, 1.94 × 1027 kg m2/year, and 0.4 × 1027 kg m2/year. Only the SM has a p-value > 0.1 and fails the Student-t test. Other contributors all have p-values less than 0.1. Specifically, the AIS and GrIS have p-values of ~ 0.035. Hence, except for the SM, other components all contribute steadily to increasing the MOI. In absolute terms, the AIS is the largest contributor. Through the increased creeping of the ice sheet, the AIS loses a similar amount of ice to oceans to the GrIS (Ren et al. 2011b, 2013a, b; Chen et al. 2006; Velicogna and Wahr 2006). However, because it is located at higher latitudes than the GrIS, its mass loss to oceans signifies more salient increase of Earth’s moment of inertia. The GrIS is the second largest contributor to the increased MOI, of about an order of magnitude larger than mountain glaciers and that from elevated center of mass of Earth atmosphere. Polar amplification is more salient in the Northern Hemisphere than in the Southern Hemisphere, primarily because the relatively low temperature over Antarctica has not yet activated an albedo feedback (e.g., Charney et al. 1977; Charney and Shukla 1981). When this feedback mechanism is activated in the future due to, for example, increased ground surface exposure from ice cover retreats (or simply from seasonal ice surface melting), the AIS possibly will play an increased role in modulating the Earth’s MOI.
Four contributor components (Atm atmosphere, MG Mountain glaciers, GrIS Greenland Ice Sheet, AIS Antarctic Ice Sheet) estimated independently using reanalysis or from the SEGMENT model with reanalysis atmospheric parameters as input. Shading around the curves represent the uncertainty from the five reanalysis sources. All four curves passed a t-test (two-tailed t-test with dof = 15), with labeled linear trends (i.e., the k values in units of 1027 kg m2/year) and p-values. Anomalies of all components are obtained by subtracting the year 2002 value from each annual value. The global total MOI variation curve is based on JPL mascon solutions (identical to the solid curve in Fig. 4 so not plotted here)
Although the contribution from atmospheric warming is the smallest of the four (Fig. 5), the upward trend is steady and started well before 2002 (Fig. 6). For the entire meteorological remote sensing era (1979-present), there is essentially no significant negative contribution. The MOI fluctuations associated with the expansion of the oceans, although present in the GRACE measurements, is not separated out in this study. The magnitude reported by Landerer et al. (2007) is a good reference as it is on the same order of magnitude (− 0.6 \(\upmu \)s/year). Similarly, Gross (2000) concluded that the atmospheric fluctuations (surface pressure redistribution) are only about one-half of those caused by ocean bottom pressure fluctuations in affecting the MOI. Although their results revealed the equal importance of atmospheric fluctuations and sea level rise, the upward lift of the center of mass of the Earth’s atmosphere (to higher altitudes and away from the axis of rotation; Fig. 6, reaching 1.6 m/year rate at present at polar regions) likely was overlooked. However, this vertical expansion appears to be significant, contributing 0.17 \(\upmu \)s/year alone. Horizontally, the mass re-distribution tendency from the polar regions to the mid-latitudes, due to enhanced mid-latitude high level jets (Lee et al. 2019), is the main driver of the MOI increase. During the GRACE observational period, it has a rate of ~ 0.33 \(\upmu \)s/year, close to the estimates of Gross (2000). If only the ocean expansion is considered, it opposes the atmospheric effects on the MOI, and they effectively cancel each other. As the climate warms, the regional disparity in mass accumulation may play an increasingly important role in affecting the Earth’s MOI. For example, the intensified Antarctic Circumpolar Current, through Coriolis effects, forces ocean water away from the AIS to lower latitudes. The mass accumulation trend over the Southern Ocean hence contributes to an increased MOI. Notably, it opposes the ocean expansion reported by Landerer et al. (2007).
A unique feature of the contribution from the soil moisture and groundwater (Fig. 7) is that its annual variation is in phase with the total MOI as indicated by the GRACE measurements. Consequently, it is the most dynamic contributor to fluctuations in the MOI. For a regional area, enhanced mass can be a result of increased precipitation or enhanced soil moisture/groundwater retention ability. The root mechanism still is not clear, but a plausible explanation is that most of the major earthquakes during this period occurred at lower latitudes (Fig. 7). The energy released then enhanced precipitation distribution in lower latitudes. This might explain the spikes. Comparison of Figs. 4 and 7 indicates that each spike (from earthquakes) elevated the MOI to a new, higher value. For example, the moderate 2004 spike related to the Indian Ocean earthquake (Sumatra Earthquake 2004), would have caused the length of day to shorten by 3 \(\upmu \)s and restored slightly, as the response of upper mantle material. The 2008 Wenchuan, 2011 Tōhoku, 2012 Aceh, and 2015 Nepal earthquakes all can be seen in the MOI time series. Without these spikes, the trend of the soil moisture contribution would be slightly decreased, agreeing with a polar shift of precipitation as the climate warms (Dore 2005; Solomon et al. 2007; Putnam and Broecker 2017). There is post-seismic evidence of enhanced water retention capability of the aquifers, through various hydrologic processes induced by earthquake-induced changes in hydrologic and mechanical properties of the crust (e.g., Ingebritsen and Manga 2019). Recently, Zhang et al. (2019) found that earthquakes can increase aquifer and aquitard permeabilities by fracturing/compaction, implying an enhanced groundwater retention. Accordingly, the mass disturbance is ~ 1.1–4.7 km3 for the 2010 Chilean earthquake. However, the spike in the GRACE curve is > 10 km3, suggesting that there are other indirect effects on the fluid sphere from tectonic earthquakes. Over the 15-year GRACE period, the presence of negative MOI contributions that are large enough to cancel the increasing MOI trend from the other components is not supported by the GRACE observations.
MOI variations caused by groundwater/soil moisture fluctuations during 2002–2017. Major earthquakes occurred at low- and mid-latitudes correspond well with spikes in the MOI fluctuations. The shading indicates the spread using different reanalysis atmospheric parameters to drive the SEGMENT modeling system
4 Discussion and conclusions
Despite its design lifetime of 8–9 years, the GRACE mission has provided almost 15-years of quality data. Errors in raw GRACE total mass variations have been identified and corrected. The primary error source is satellite aging. Using the error-corrected data, the total mass loss rate from the GrIS during the 2002–2015 is ~ 120 Gt/year, which is ~ 20% less than in previous studies but is much closer to other geodetic measurements.
The rectified GrIS total mass loss time series were well-simulated by the SEGMENT-Ice model, including small but important spikes produced by snowfalls from tropical cyclone remnants. These seemingly noisy spikes of ~ 10–30 Gt in the GRACE measurements thus are realistic. Hence, only correcting the overall trend is required. Model parameters are optimized with corrected GRACE data and are used to determine the total non-tidal MOI fluctuations for 2002–2017. The modeling system quantifies the contributions from various components. In this study, we found that the mass shed from the polar ice sheets, mountain glaciers retreats, and the atmospheric fluctuations (i.e., the horizontal re-distribution and uplift of the mass center of the atmosphere) all contribute to increasing the Earth’s MOI and hence to a small, but identifiable, slowing of the Earth’s rotation rate. Components of the GRACE time series were analyzed and the abrupt changes in the MOI correspond well with major earthquakes. Instead of the relocation of crust and upper mantle material, it is the associated groundwater, or precipitation redistribution, that dominate the MOI fluctuations. This may be another facet of the relation between droughts and major earthquakes (Ren and Fu 2019). Notably, the dynamic nature of permeability, as revealed by co-seismic and post-seismic hydrologic phenomena (Ingebritsen et al. 2006), has implications for groundwater systems in the fault vicinity. With advances in earthquake hydrogeology, quantitative detection of the earthquake contribution to the MOI changes is expected. Hitherto, sea level rise and mass redistribution effects on the MOI have been actively studied (Adhikari and Ivins 2016; Munk 2002; Seoane et al. 2012; Mitrovica et al. 2006). However, other components have not yet been studied extensively (e.g., the land hydrological cycle), or remain overlooked (e.g., the expansion of Earth’s atmosphere). Although we do not claim a complete decomposition of the total MOI trend, other mechanisms represented in the residual term likely have secondary roles in the Earth’s MOI evolution during the GRACE observational period.
It was found that there is a statistically significant (p = 0.039) total increase in the Earth’s MOI, during the GRACE 15-year period. This steady increase in MOI has five major contributors. The two leading contributions are from the AIS and GrIS, with trends in both passing two-tailed t-tests at p = 0.035 (dof = 15). Considered jointly, the linear trend of the polar ice sheets reaches 8.7 × 1027 kg m2/year (equivalent to a 9.4 \(\upmu \)s/year increase in the length-of-a-day). In the foreseeable future, this is the dominant term for MOI changes, as the climate warms. Among the climate warming contributors only the changes in rainfall redistribution has a statistically non-significant trend (p = 0.604). The mass redistribution caused by the hydrological cycle also is the most dynamic, contributing to fluctuation spikes in the global MOI. The ice sheet contribution is steady and is a persistent trend in the recent MOI evolution during the GRACE observational period. Compensating mechanisms, such as the GIA, operate on a much longer time scale. The increasing MOI trend is likely to continue in the transient climate warming period (the upcoming several hundred years), before the GIA and other possible negative factors dominate. Except for the wavier hydrological cycles, other contributing components are responses to a warming climate in synergy, rather than opposing each other. The Earth’s MOI variations during the 15-year GRACE period of reliable observational data form a basis for identifying climate change impacts on the Earth’s MOI and provide more precise insights into fluid and solid mass transport near the Earth’s surface.
Change history
25 November 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00382-021-06049-4
References
Adhikari S, Ivins E (2016) Climate-driven polar motion: 2003–2015. Sci Adv 2(4):e1501693. https://doi.org/10.1126/sciadv.1501693
Bamber J, Wesyaway R, Marzeion B, Wouters B (2018) The land ice contribution to sea level during the satellite era. Environ Res Lett 13:063008
Bentley C, Wahr J (1998) Satellite gravity and the mass balance of the Antarctic ice sheet. J Glaciol 44:206–213
Box J et al (2006) Greenland ice sheet surface mass balance variability (1988–2004) from calibrated Polar MM5 output. J Clim 19:2783–2800
Cassano J, Box J, Bromwich D, Li L, Steffen K (2001) Verification of Polar MM5 simulations of Greenland’s atmospheric circulation. J Geophys Res 106:33867–33890
Charney JG, Shukla J (1981) Predictability of monsoons. In: Lighthill SJ, Pearce RP (eds) Monsoon dynamics. Cambridge University Press, Cambridge
Charney JG, Quirk WJ, Chow S, Kornfield J (1977) A comparative study of the effects of albedo change on drought in semi-arid regions. J Atmos Sci 34:1366
Chen J, Wilson C, Tapley B (2006) Satellite gravity measurements confirm accelerated melting of Greenland ice sheet. Science 313:1958–1960
Dee D et al (2011) the ERAInterim reanalysis: configuration and performance of the data assimilation syatem. Q J R Meteorol Soc 137:553–597
Dore M (2005) Climate change and changes in global precipitation patterns: what do we know? Environ Int 31(8):1167–1181
Doyle S et al (2015) Amplified melt and flow of the Greenland ice sheet driven by late-summer cyclonic rainfall. Nat Geosci 8:647–653
Duan X, Guo J, Shum C, van der Wal W (2009) On the postprocessing removal of correlated errors in GRACE temporal gravity field solutions. J Geod 83:1095–1106
Emanuel K, Jagger T (2010) On estimating hurricane return periods. J Appl Meteor Clim 49:837–844
Ettema J, van den Broeke M, van Meijgaard E, van de Berg W, Bamber J, Box J, Bales R (2009) Higher surface mass balance of the Greenland ice sheet revealed by high-resolution climate modeling. Geophys Res Lett 36:L12501
Famiglietti J, Rodell M (2013) Water in the balance. Science 340:1300–1301
Fettweis X, Hanna E, Lang C, Belleflamme A, Erpicum M, Gallee H (2013) Important role of the mid-tropospheric atmospheric circulation in the recent surface melt increase over the Greenland ice sheet. Cryosphere 7:241–248
Francis J, Vavrus S (2012) Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys Res Lett 39(6):L06801
Francis J, Vavrus S (2015) Evidence for a wavier jet stream in response to rapid Arctic warming. Environ Res Lett 10:014005
Frappart F, Ramillien G, Famiglietti J (2011) Water balance of the Arctic drainage system using GRACE gravimetry products. Int J Remote Sens 32:431–453
Fyke J, Eby M, Mackintosh A, Weaver A (2014) Impact of climate sensitivity and polar amplification on projections of Greenland Ice Sheet loss. Clim Dyn 43:2249–2260
Gross R (2000) The excitation of the Chandler wobble. Geophys Res Lett 27:2329–2332
Haarsma R, Selten F, van Oldenborgh G (2013) Anthropogenic changes of the thermal and zonal flow structure over Western Europe and Eastern North Atlantic in CMIP3 and CMIP5 models. Clim Dyn. https://doi.org/10.1007/s00382-013-1734-8
Hanna E et al (2013) Ice-sheet mass balance and climate change. Nature 498:51–59
Hanna E, Fettweis X, Hall R (2018) Brief communication: recent changes in summer Greenland blocking captured by none of the CMIP5 models. Cryosphere 12:3287–3292
Hu A, Bates S (2018) Internal climate variability and projected future regional steric and dynamic sea level rise. Nat Commun 9(1):1068. https://doi.org/10.1038/s41467-018-03474-8
Humphrey V, Gudmundsson L, Seneviratne S (2016) Assessing global water storage variability from GRACE: trends, seasonal cycle, subseasonal anomalies and extreme. Surv Geophys 37:357–395
IMBIE Team (2018) Mass balance of the Antarctic Ice Sheet from 1992–2017. Nature 558:219–222
Ingebritsen S, Manga M (2019) Earthquake hydrogeology. Water Resour Res 55:5212–5216
Ingebritsen S, Sanford W, Neuzil C (2006) Groundwater in geologic processes, 2nd edn. Cambridge University Press, Cambridge
Kalnay E et al (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:437–471
Knutson T, McBride J, Chan J, Emanuel K, Holland G, Landsea C, Held I, Kossin J, Srivastava A, Sugi M (2010) Tropical cyclones and climate change. Nat Geosci 3:157–163
Knutson T et al (2013) Dynamical downscaling projections of twenty-first-century Atlantic hurricane activity: CMIP3 and CMIP5 model-based scenarios. J Clim 26:6591–6617
Kobayashi S et al (2015) The JRA-55 reanalysis: general specifications and basic characteristics. J Meteorol Soc Jpn Ser II 93:5–48
Landerer F, Jungelaus JH, Marotzke J (2007) Ocean bottom pressure changes lead to decreasing length-of-day in a warming climate. Geophys Res Lett 34:L06307
Le Marshall J, Lee J, Jung J, Gregory P, Roux B (2013) The considerable impact of earth observations from space on numerical weather prediction. Aust Meteorol Oceanogr J 63:497–500
Lee SH, Williams PD, Frame THA (2019) Increased shear in the North Atlantic upper-level jet stream over the past four decades. Nature. https://doi.org/10.1038/s41586-019-1465-z
Longuevergne L, Scanlon B, Wilson C (2010) GRACE hydrological estimates for small basins: evaluating processing approaches on the High Plains Aquifer, USA. Water Resour Res 46:W11517
Luthcke S, Sabaka T, Loomis B et al (2013) Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution. J Glaciol 59:613–631
Merz N, Raible C, Fischer H, Varma V, Prange M, Stocker T (2013) Greenland accumulation and its connection to the large-scale atmospheric circulation in ERA-Interim and paleoclimate simulations. Clim past 9:2433–2450
Mitrovica JX, Wahr J, Matsuyama I, Paulson A, Tamisiea M (2006) Reanalysis of ancient eclipse, astronomic and geodetic data: a possible route to resolving the enigma of global sea-level rise. Earth Planet Sci Lett 243:390–399
Munk W (2002) Twentieth century sea level: an enigma. Proc Natl Acad Sci 99:6550–6555
Putnam A, Broecker W (2017) Human-induced changes in the distribution of rainfall. Sci Adv 3(5):e1600871. https://doi.org/10.1126/sciadv.1600871
Rahmstorf S (2010) A new view on sea level rise. Has the IPCC underestimated the risk of sea level rise? Nat Rep Clim Change 4:44–45
Ren D (2010) Effects of global warming on wind energy availability. J Renew Sustain Energy 2:052301. https://doi.org/10.1063/1.3486072
Ren D (2014a) The devastating Zhouqu Storm-triggered debris flow of August 2010: Likely causes and possible trends in a future warming climate. J Geophys Res 119(7):3643–3662
Ren D (2014b) Storm-triggered landslides in warmer climates. Springer, New York. https://doi.org/10.1007/978-3-319-08518-0. Library of Congress Control Number: 2014947106. ISBN 978-3-319-08517-3
Ren D, Fu R (2019) How droughts influence earthquakes. Adv Environ Stud 1:1. https://doi.org/10.36959/742/220
Ren D, Karoly D (2006) Comparison of glacier-inferred temperatures with observations and climate model simulations. Geophys Res Lett 33:L23710. https://doi.org/10.1029/2006GL027856
Ren D, Leslie L (2011) Three positive feedback mechanisms for ice sheet melting in a warming climate. J Glaciol 57:206
Ren D, Leslie L (2014) Effects of waves on tabular ice-shelf calving. Earth Interact 18:1–28
Ren D, Leslie LM, Karoly D (2008) Mudslide risk analysis using a new constitutive relationship for granular flow. Earth Interact 12:1–16
Ren D, Fu R, Leslie LM, Karoly DJ, Chen J, Wilson C (2011a) A multirheology ice model: formulation and application to the Greenland ice sheet. J Geophys Res 116:D05112. https://doi.org/10.1029/2010JD014855
Ren D, Fu R, Leslie L, Chen J, Wilson C, Karoly D (2011b) The Greenland ice sheet response to transient climate change. J Clim 24:3469–3483
Ren D, Fu R, Leslie LM, Dickinson R (2011c) Predicting storm-triggered landslides. Bull Am Meteor Soc 92:129–139. https://doi.org/10.1175/2010BAMS3017.1
Ren D, Leslie LM, Lynch M (2012) Verification of model simulated mass balance, flow fields and tabular calving events of the Antarctic ice sheet against remotely sensed observations. J Clim Dyn. https://doi.org/10.1007/s00382-012-1464-3
Ren D, Leslie L, Lynch M (2013a) Verification of model simulated mass balance, flow fields and tabular calving events of the Antarctic ice sheet against remotely sensed observations. Clim Dyn 40:2617–2636
Ren D, Leslie L, Lynch M (2013b) Antarctic ice sheet mass loss estimates using Modified Antarctic Mapping Mission surface flow observations. J Geophys Res 118:2119–2135
Rignot E, Kanagaratnam P (2006) Changes in the velocity structure of the Greenland Ice Sheet. Science 311:986–990
Save H, Bettadpur S, Tapley B (2016) High resolution CSR GRACE RL05 mascons. J Geophys Res Solid Earth 121:7547–7569
Seoane J, Takkouch B, Varela-Centelles P, Tomas I, Seoane-Romero J (2012) Impact of delay in diagnosis on survival to head and neck carcinomas: a systematic review with meta-analysis. Clin Otolaryngol 37:99–106
Shepherd A, Wingham D (2007) Recent sea level contributions of the Antarctic and Greenland Ice Sheets. Science 315:1529–1532
Shepherd A et al (2012) A reconciled estimate of ice-sheet mass balance. Science 338:1183–1189
Shepherd A, Ficker H, Farrell S (2018) Trends and connections across the Antarctic cryosphere. Nature 558:223–232
Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Mille HL (2007) IPCC fourth assessment report: climate change 2007: Climate change 2007: working group I: the physical science basis. Cambridge Univ Press, Cambridge
Suarez M et al (2008) The GEOS-5 Data Assimilation System—documentation of versions 5.0.1, 5.1.0, and 5.2.0, NASA/TM-2008-104606, 27
Swenson S, Wahr J (2006) Post-processing removal of correlated errors in GRACE data. Geophys Res Lett 33:L08402
Tapley et al (2019) Contributions of GRACE to understanding climate change. Nat Clim Change 9:358–369
Trenberth K, Fasullo J (2013) An apparent hiatus in global warming? Earth’s Future 1:19–32
Vallis G, Zurita-Gotor P, Cairns C, Kidston J (2015) Response of the large-scale structure of the atmosphere to global warming. Q J R Meteorol Soc 141:1479–1501
Vaughan D et al (2013) Ch. 4, In climate change. In: Stocker TF et al (eds) The physical science basis. IPCC, Cambridge Univ Press, Cambridge
Velicogna I, Wahr J (2006) Acceleration of Greenland ice mass loss in spring 2004. Nature 443:329–331
Velicogna I, Wahr J, Hanna E, Huybrechts P (2005) Short term mass variability in Greenland, from GRACE. Geophys Res Lett 32:L05501
Vishwakarma B, Devaraju B, Sneeuw N (2018) What is the spatial resolution of GRACE satellite products for hydrology? Remote Sens 10:852
Voss K, Famiglietti J, Lo M, de Linage C, Rodell M, Swenson S (2013) Groundwater depletion in the Middle East from GRACE with implications for transboundary water management in the Tigris-Euphrates-Western Iran region. Water Resour Res 49:904–914
Wahr J, Molenaar M, Bryan F (1998) Time variability of the Earth’s gravity field: hydrological and oceanic effects and their possible detection using GRACE. J Geophys Res 103:30205–30230
Watkins M, Wiese D, Yuan D, Boening C, Landerer F (2015) Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons: improved Gravity Observations from GRACE. J Geophys Res Solid Earth 120:2648–2671
Wiese D, Yuan D, Boening C, Landerer F, Watkins M (2018) JPL GRACE mascon ocean, ice, and hydrology equivalent water height release 06 Coastal Resolution Improvement (CRI) Filtered Version 1.0. Ver. 1.0. PO.DAAC, CA, USA
Wouters B, Bonin J, Chambers D, Riva R, Sasgen I, Wahr J (2014) GRACE, time-varying gravity, earth system dynamics and climate change. Rep Prog Phys 1:1. https://doi.org/10.1088/0034-4885/77/11/116801
Wu Z, Huang N, Long S, Peng C (2007) On the trend, detrending, and variability of nonlinear and nonstationary time series. PNAS 104:14889–14894
Wu Z, Feng J, Qiao F, Tan Z (2016) Fast multidimensional ensemble empirical mode decomposition for the analysis of big spatio-temporal datasets. Phil Trans R Soc A. https://doi.org/10.1098/rsta.2015.0197
Zhang H, Shi Z, Wang G, Sun X, Yan R, Liu C (2019) Large earthquake reshapes the groundwater flow system: insight from the water level response to Earth tides and atmospheric pressure in a deep well. Water Resour Res 55:4207–4219
Acknowledgements
We thank Dr. Z. Wu (Florida State University) for suggesting the EMD data analysis techniques, and Professors Zhaomin Wang (BAS and Hohai University) for constructive comments. The 1° monthly GRACE data are available from JPL, at https://grace.jpl.nasa.gov. We also thank one anonymous reviewer for the suggestion of providing the code to readers.
Author information
Authors and Affiliations
Contributions
Lead author DR designed the study, performed the analysis and wrote the paper. LML, AH and YH all provided essential assistance in the writing and revision stages.
Corresponding authors
Ethics declarations
Conflict of interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
This supplementary material contains two parts: (1) Simulating the GrIS total mass balance using SEGMENT-Ice; and (2) Matlab code examining in global GRACE mascon solution from JPL.
1.1 Simulating the GrIS total mass balance using SEGMENT-Ice
The GrIS ice is replenished dynamically in that, at any geographical location, the thickness (and hence the surface elevation) fluctuates as a result of net surface mass balance (snow precipitation adjusts the surface and melt/sublimation at the ice-bedrock interface) and the dynamic mass balance ice resulting from flow divergence/convergence. Generally, ice creeps from the central region to the peripheral regions, where it either melts or drains to the ocean through the inlets. The oldest ice apparently is located at the bottom of the central region (for GrIS, ~ 50 km north of the Summit) and is of age ~ 110 kyr. The model simulation domain contains the entire ice domain plus 1 km thick bedrock with assumed viscosity of 1019 Pa s. Thus, the deformation to the bedrock elevations is estimated from the ice weight. The current geometry of the GrIS primarily is a result of snow precipitation climatology (direct precipitation and the turbulent wind-caused re-distribution, especially at the early stage of snow accumulation over the GrIS). Ice flow fields are an integral component of the ice model. With time marching, the ice velocities are updated together with the mass and thermal fields. There is a long-term glacial residual, which is small but negative, in total mass balance. For simulating mass changes of the GrIS over the next several centuries, this glacial residual is assumed to be constant. Spin-up simulations, using paleo-climate records of precipitation and analytical surface air temperature, arguably provide only the general GrIS mass, flow and thermal configuration.
Remote sensing observations, especially for the most recent decade, make available surface ice flow measurements (e.g. NASA’s Making Earth System Data Records for Use in Research Environments, MEaSUREs, http://nsidc.org/data/measures/; Ren et al. 2013a, b) and gravity field fluctuations (e.g. Gravity Recovery and Climate Experiment, GRACE, http://www.csr.utexas.edu/grace/science/gravity_measurement.html; Ren et al. 2011a). This information can provide further constraints on 3D ice temperature fields. We used an adjoint-based 4DVar scheme to fully extract the information. Unfortunately, the satellite era also coincides with a salient climate warming period. The topmost tens of meters of ice already has felt the warming and crept faster than under natural variability. To account for the effects from recent warming, it is assumed that the mean net snow precipitation over 1960–1990 perfectly balances the dynamic mass balance term everywhere over the GrIS (after adjusting for glacial residuals). Technical details of SEGMENT-Ice can be found in Ren et al. (2013a). Application to the GrIS are detailed in Ren et al. (2011a, b, c).
1.2 Matlab code examining total mass conservation in GRACE mascon solution from JPL
%Examination of trends in global GRACE data from JPL.
%Load JPL scale factor for CRI solution.
scaleFile = 'CLM4.SCALE_FACTOR.JPL.MSCNv01CRIv01.nc';
scale_factor = ncread(scaleFile,'scale_factor');
%The scale factor applies to land areas only.
%Give ocean data a weight of 1: scale_factor(isnan(scale_factor)) = 1;
%Load JPL GRACE data.
%fileName = 'GRCTellus.JPL.200204_201706.GLO.RL05M_1.MSCNv02.nc';
fileName = 'GRCTellus.JPL.200204_201706.GLO.RL05M_1.MSCNv02CRIv02.nc';
lwe_thickness = ncread(fileName,'lwe_thickness');
%Mass change data (cm).
lat_bounds = ncread(fileName,'lat_bounds');
lon_bounds = ncread(fileName,'lon_bounds');
time = ncread(fileName,'time');
%Days since Jan. 1, 2002.
% Compute area of grid cells.
earthradius = almanac('earth','radius');
area = zeros(size(lwe_thickness,1),size(lwe_thickness,2));
for i = 1:(size(lon_bounds,2)-1)
for j = 1:(size(lat_bounds,2)-1)
UL_lat = lat_bounds(1,j);
UL_lon = lon_bounds(1,i);
UR_lat = lat_bounds(1,j);
UR_lon = lon_bounds(2,i);
LR_lat = lat_bounds(2,j);
LR_lon = lon_bounds(2,i);
LL_lat = lat_bounds(2,j);
LL_lon = lon_bounds(1,i);
xShape = [UL_lat, UR_lat, LR_lat, LL_lat, UL_lat];
yShape = [UL_lon, UR_lon,LR_lon, LL_lon, UL_lon];
area(i,j) = areaint(xShape,yShape,earthradius);
end
end
total_area = sum(area(:));
% Create timeseries of global mass (with and without area weighting).
total_timeseriesWt = zeros(1,size(lwe_thickness,3));
total_timeseriesNoWt = total_timeseriesWt;
for i = 1:size(lwe_thickness,3) thickness_day = lwe_thickness(:,:,i);
%Apply scale factor to daily mass change and weight by area.
thickness_dayWt = thickness_day.*scale_factor.*area/total_area;
thickness_dayNoWt = thickness_day.*scale_factor;
total_timeseriesWt(i) = nansum(thickness_dayWt(:));
total_timeseriesNoWt(i) = nansum(thickness_dayNoWt(:));
end
%Plotting
set (0,'DefaultFigureRenderer','painters');
timePlot = datenum(2002,1,1) + time;
Figure (1)
set(gcf,'color','w')
plot(timePlot,total_timeseriesNoWt,'r-')
datetick
xlabel('Time')
ylabel('Total Mass Change (cmWE) (not weighted)')
set(gca,'fontsize',18)
title('JPL GRACE Global Mass Timeseries, No Weighting')
Figure (2)
set(gcf,'color','w')
plot(timePlot,total_timeseriesWt,'r-')
datetick
xlabel('Time')
ylabel('Total Mass Change (cmWE) (weighted)')
set(gca,'fontsize',18)
title('JPL GRACE Global Mass Timeseries, Area Weighting')
% This output indicates also that any spatial operation cannot explain the spurious trend.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ren, D., Leslie, L.M., Huang, Y. et al. Correction of GRACE measurements of the Earth’s moment of inertia (MOI). Clim Dyn 58, 2525–2538 (2022). https://doi.org/10.1007/s00382-021-06022-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-021-06022-1