Diurnal cycle of precipitation and near-surface atmospheric conditions over the maritime continent: land–sea contrast and impacts of ambient winds in cloud-permitting simulations

Abstract

A set of cloud-permitting-scale numerical simulations during January–February 2018 is used to examine the diurnal cycle (DC) of precipitation and near-surface variables (e.g., 2 m temperature, 10 m wind and convergence) over the Indo-Pacific Maritime Continent under the impacts of shore-orthogonal ambient winds (SOAWs). It is found that the DC of these variables and their variabilities of daily maxima, minima, and diurnal amplitudes vary over land, sea, and coastal regions. Among all variables, the DC of precipitation has the highest linear correlation with near-surface convergence (near-surface temperature) over coastal (noncoastal) regions. The correlations among the DCs of precipitation, wind, and heating are greater over the ocean than over land. Sine curves can model accurately the DCs of most variables over the ocean, but not over land. SOAWs act to influence the DC mainly by affecting the diurnal amplitude of the considered variables, with DC being stronger under more strengthened offshore SOAWs, though variable dependence and regional variability exist. Composite analysis over Sumatra reveals that under weak SOAWs, shallow clouds are dominant and cause a pre-moistening effect, supporting shallow-to-deep convection transition. A sea breeze circulation (SBC) with return flow aloft can develop rapidly. Cold pools are better able to trigger new updrafts and contribute to the upscale growth and inland migration of deep convection. In addition, warm gravity waves can propagate upward throughout the troposphere, thereby supporting a strong DC. In contrast, under strong SOAWs, both shallow and middle-high clouds prevail and persist throughout the day. The evolution of moistening and SBC is reduced, leading to weak variation in vertical motion and rainwater confined to the boundary layer. Large-scale winds, moisture, and convection are discussed to interpret how strong SOAWs affect the DC of Sumatra.

1 Introduction

The diurnal cycle is the fundamental mode of precipitation variability over the Indo-Pacific Maritime Continent (MC) region, which features complex land–sea areas and plays a significant role in fueling the global atmospheric circulation (Yang and Slingo 2001; Kikuchi and Wang 2008; Yamanaka et al. 2018). The diurnal variation is strongest over land, but its amplitude over the ocean is not negligible (Gray and Jacobson 1977; Nesbitt and Zipser 2003; Janowiak et al. 2005). Diurnal oscillations are also observed over other surfaces and/or in near-surface meteorological parameters, such as wind speed (Yu et al. 2009; Kilpatrick et al. 2017; Short et al. 2019), wind convergence (Dai and Deser 1999; Wood et al. 2009), and air temperature (Gentemann et al. 2003; Stuart-Menteth et al. 2003; Ruzmaikin et al. 2017; Sharifnezhadazizi et al. 2019). Understanding of the diurnal cycles of these fields and their interactions in numerical models is of great importance in weather forecasts and climate predictions (Qian 2008; Baranowski et al. 2019).

Due to the complicated land–sea distribution, the diurnal cycle of precipitation and near-surface variables over the Indo-Pacific MC region features evident land–sea contrasts. For example, the diurnal maximum of precipitation over land usually occurs in the late afternoon or evening, while over the ocean the maximum is observed mostly in the early morning (Yang and Slingo 2001; Kikuchi and Wang 2008; Vincent and Lane 2017; Wei et al. 2020). Previous studies also found “non-sinusoidal” diurnal variation, in which the duration from the diurnal minimum to maximum is shorter than that from the diurnal maximum to minimum (e.g., Murakami 1983; Kondragunta and Gruber 1994; Masselink and Pattiaratchi 2001; Ling et al. 2019). This implies that the harmonic analysis method used in some studies that considers only sine waves 1 or 2 (e.g., Deser 1994; Yang and Slingo 2001; Love et al. 2011; Peatman et al. 2014) may extract a distorted diurnal cycle (Slingo et al. 2004; Ling et al. 2019). Strong boundary layer mixing probably serves as a key factor in producing non-sinusoidal or asymmetric diurnal cycles in surface variables over land (e.g., Svensson et al. 2011; Lee 2018). Due to the complexity of the “non-sinusoidal” diurnal variation over the MC, the land–sea and mountain-valley contrasts, along with other mechanisms, such as the gravity wave (GW) theory (e.g., Mapes et al. 2003; Love et al. 2011; Yokoi et al. 2017; Ruppert and Zhang 2019) are used to explain the diurnal cycle over the MC. It is suggested that warm (cold) GWs responding to surface heating (nocturnal precipitation evaporation) may play a role in regulating diurnal precipitation. Cold pool (or density current) dynamics (e.g., Feng et al. 2015) could also contribute to the transition from shallow to deep convection (Khairoutdinov and Randall 2006) via additional lifting effects over updraft regions (Cheng et al. 2018). Some previous studies have also used “moist instability” to explain the diurnal cycle of convection (e.g., Chaboureau et al. 2004; Birch et al. 2016; Ruppert and Johnson 2016; Ruppert 2016; Katsumata et al. 2018). In general, sufficient lower tropospheric moistening is suggested to be important in supporting diurnal deep convective initiation and development by strengthening moist instability (e.g., Chaboureau et al. 2004). Typically, daytime cumulus invigoration plays a key role in cloud-layer moistening in suppressed regimes (Ruppert and Johnson 2015, 2016). Despite the diversity of the mechanisms reviewed here for interpreting the diurnal cycle over the MC, these mechanisms are not necessarily independent of each other. Furthermore, despite much progress made by these previous studies, there are still many fundamental science questions to be addressed. For example, what are the bulk characteristics of the diurnal cycle in precipitation and near-surface variables over the entire MC? How and to what extent are the diurnal variations of these variables correlated with each other?

The characteristics of the diurnal cycle also depend on large-scale ambient winds. For example, Helmis et al. (1995) suggested that offshore background flow is more likely to create a strong sea breeze front (SBF) and thus convective initiation over the Saronic Gulf. Using observations from several land–sea sites over a high-latitude region, Barthelmie et al. (1996) showed that the prevailing wind direction can influence the diurnal cycle of near-surface wind speed. Atkins and Wakimoto (1997) demonstrated that the offshore flow regime has the strongest impact on sea breeze events. Recently, Li et al. (2017) developed a new technique to examine the cross-coastal processes associated with the diurnal cycle of rainfall along all coastlines of the MC. They discovered that the prevailing wind direction could affect the location of land rainfall and the depth of the land–sea breeze, where a shallow land–sea breeze circulation was simulated under offshore prevailing winds.

Besides the prevailing direction, the speed of ambient winds may also influence the diurnal cycle over the MC. Qian et al. (2010), for example, found that under strongly synoptic wind speed conditions, the diurnal amplitude of rainfall becomes larger and the diurnal maximum occurs later. By contrast, Sobel et al. (2011) pointed out that it was just the weaker ambient winds over the MC than over the Caribbean that led to a stronger diurnal cycle of precipitation over the MC. Using idealized model experiments, Wang and Sobel (2017) indicated that the prevailing wind speed controls the dynamic flow regimes over small tropical islands. Sea breezes and deep convection dominate when wind speed is very weak, and rainfall achieves its maximum. Moderate increases in wind speed lead to topographic waves, which interfere with deep convection because of their alternating ascent and descent and decrease rainfall compared to weak winds. Rao et al. (2019) suggested that higher wind speed conditions over south China can support a higher occurrence of convection and also stronger diurnal variation, although they did not directly examine the diurnal amplitude of precipitation. More recently, Zhu et al. (2020) showed that both sea breeze circulations and afternoon rainfall over Hainan Island could become stronger under weaker ambient wind speed at the lower level. However, whether their conclusion is applicable for the MC is still not clear. Therefore, how do the diurnal characteristics depend on the ambient winds and land–sea contrasts over the MC?

Since global reanalysis products are commonly available at coarser resolution (e.g., ~ 25 km horizontally or greater), previous studies indicated that cloud-permitting model simulation that resolves cloud and convective processes at a spatial scale of several kilometers is a good way to study the diurnal cycle in the tropics (Sato et al. 2009; Love et al. 2011; Argüeso et al. 2016, 2019; Hassim et al. 2016; Vincent and Lane 2016; Wei et al. 2020). Specifically, a recent study by Wei et al. (2020) and Wei and Pu (2021) indicated a set of cloud-permitting-scale numerical simulations could reasonably represent the diurnal variations of precipitation and winds over the MC region. In this study, with the same set of cloud-permit scale simulations, we conduct a comprehensive analysis of the diurnal cycle of precipitation and near-surface variables over the MC, with the following objectives. (a) To reveal the land–sea contrast in the diurnal characteristics of precipitation and near-surface temperature, winds, and convergence over the whole MC region; and (b) to explore the impacts of ambient winds (both speed and direction) on the key characteristics of diurnal variation in the variables mentioned above. A new “coastline-following” method will be developed to examine the diurnal cycle of different variables as a function of distance from the coastline. Diurnal cycle variation over Sumatra under the influence of ambient winds will be investigated using composite analysis. Mechanisms discovered in previous studies, including land–sea breezes, moist instability, cold pool dynamics, and GWs will also be examined in detail.

The rest of this paper is structured as follows. In Sect. 2, we introduce the data and methodology. In Sect. 3, we diagnose the bulk characteristics of the diurnal cycle over the entire MC region using cloud-permitting-scale numerical simulations. Section 4 introduces the impacts of both the speed and direction of ambient winds on the diurnal cycle of key variables over representative land and sea areas of the MC. Composite analysis of the diurnal cycle over Sumatra under the influence of ambient winds is given in Sect. 5. The paper ends with a summary and discussion in Sect. 6.

2 Data and methodology

2.1 Brief description of WRF numerical simulations

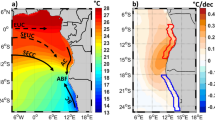
The data used in this study come from a set of cloud-permitting-scale numerical simulations by the advanced research version of the Weather Research and Forecasting (WRF) model version 4.0 (Skamarock 2019). The 3-km nested domain d03 is shown in Fig. 1a and covers the entire Indo-Pacific MC region. A set of physical parameterization schemes specific to tropical regions is used to perform the hindcast simulations. Model integration was conducted for 36 h initiated at 0000 UTC every day from January 1st to February 28th 2018, and the first 12 h were considered the spin-up period. More details about model configuration, simulations, and validation against satellite observations can be found in Wei et al. (2020), in which the model results also show high correspondence with satellite observations with consistent regional variation in diurnal characteristics of precipitation and offshore/onshore propagation in the diurnal phases.

Fig. 1

a WRF domain d03. Shading shows the distance from the coastline (DFC, km) over the Indo-Pacific Maritime Continent region. The DFC is negative for land grid points and positive for ocean (i.e., offshore) grid points. Zero DFC (i.e., coastline) is highlighted by black contours. Green contours enclose the regions with terrain higher than 500 m. The three black rectangles mark the target study areas, namely, Sumatra (8° S–0, 97° E–105° E), Borneo (1° S–8° N, 109° E–117° E), and New Guinea (6° S–1° N, 138° E–146° E). b Domain zoomed into the Sumatra box. Shading is the terrain height (m), and the black parallel lines show transects used in the composite analysis near Sumatra. c Ambient winds information (01/Jan–28/Feb 2018) over the (a) Sumatra, (b) Borneo, and (c) New Guinea boxes. A gray area shows the time evolution of shore-orthogonal wind velocity (m s⁻¹). A positive (negative) value denotes the offshore (onshore) direction. Arrows are the box-averaged wind vectors (i.e., u and v) varying with time. The colors indicate the (blue) onshore, (red) offshore, and (black) shore-parallel flow regimes. The dashed black line in (a) represents the mean plus one standard deviation of the strength of the shore-orthogonal wind velocity.

2.2 Methodology

To examine the land–sea contrast characteristics of the diurnal cycle in the MC region, a “coastline-following” method is developed here to calculate the distance from the coastline (DFC) for each d03 model grid point. The first step of this method is to automatically extract the latitude and longitude coordinates of the coastline. For each land mask point m(x_i, y_j) ≡ m_i,j, we calculate (m_i+1,j − m_i−1,j)/2, and (m_i,j+1 − m_i,j−1)/2, and if either one of them equals ± 0.5, we define the point (x_i, y_j) to be a coastal point. We use forward differencing in place of central differencing at boundary points. The second step of our method is the direct extraction of the land or sea points enclosing a curve that follows the coastline in parallel. For example, to obtain the first contour on the inland side of the coastline, we select the grid points closest to the coastal points in a background area of 9 × 9 km². Then nested loops are used to derive other inland contours or contours over the sea. Based on the method, one can recognize that the grid points in each “coastline-following” contour will have the same DFC. We define the DFC as negative for land grid points and positive for ocean (i.e., offshore) grid points. Figure 1a shows the map of DFCs over the Indo-Pacific MC region, where the “coastline-following” features can be seen clearly. In this way, the diurnal cycle as a function of DFCs in the whole MC can be investigated.

Note that our method is different from that of Li et al. (2017), who identified the coastline by selecting the coastal points for which the offshore direction was well defined, namely, for which there was more landmass on the land side than on the ocean side. We have comped our methods with Li et al. (2017), and the results suggested that both can well extract the coastline points over the Indo-Pacific MC region. In addition, we directly extract the offshore and onshore grid points at high resolution grids, while Li et al. (2017) interpolated two- and/or three-dimensional fields along the offshore/onshore directions they calculated.

To understand the coupling among convection, wind dynamics, and thermodynamics at a diurnal time scale, four variables are examined, including precipitation (Precip), 2 m temperature (T2), 10 m wind speed (Wind10), and 10 m convergence (Con10). Six parameters are extracted from the diurnal variation, which include diurnal maximum (R_max) and its timing (τ_max), diurnal minimum (R_min) and its timing (τ_min), diurnal amplitude (R_d = R_max/2 − R_min/2), and duration time (τ_d) from R_min to R_max. The calculation formula for τ_d is τ_max − τ_min (τ_max > τ_min) or τ_max − τ_min + 24 (τ_max < τ_min). The definition of R_d is similar to that of Kikuchi and Wang (2008) and Ling et al. (2019) and fully considers the contributions of semi-diurnal and even higher-frequency components. To our best knowledge, the parameters of R_min, τ_min, and τ_d have not been thoroughly examined so far in previous studies. In contrast to R_max, R_min can be treated as a non-diurnal quantity. Diurnal growth begins from the non-diurnal R_min, and if we take Precip as an example, then τ_min should correspond to the initial trigger time of diurnal rain. Furthermore, analyzing R_min can help us understand the relative contribution of R_max and R_min in determining R_d. Using τ_min, one can easily derive τ_d, through which the extent of using sine waves 1 or 2 to estimate the full diurnal variation over land versus sea areas can be investigated.

Referring to previous studies (e.g., Ichikawa and Yasunari 2006, 2008; Zhu et al. 2020), we define ambient winds as daily mean horizontal winds at 850 hPa averaged over selected land/sea areas, including Sumatra (8° S–0, 97° E–105° E), Borneo (1° S–8° N, 109° E–117° E), and New Guinea (6° S–1° N, 138° E–146° E); these areas are shown in Fig. 1a as black rectangles. The daily mean of, say day i (i runs from 1 to 59), is defined as the mean from 12 to 24 UTC on day i and 0 to 12 UTC on day i + 1. We choose these three areas because (i) they feature much stronger diurnal variation over both land and ocean during boreal winter (e.g., Kikuchi and Wang 2008; Vincent and Lane 2017; Wei et al. 2020), and (ii) a nearly straight coastline exists so that we can easily derive onshore and offshore ambient winds based on zonal and meridional winds. We prescribe shore-orthogonal ambient wind (SOAW) speeds to be positive (negative) in the offshore (onshore) direction. Linear correlation is first used to detect the general dependence of the diurnal cycle on SOAWs. The significance of the correlation coefficients (CCs) is evaluated based on the Student’s t test at the 90 and 95% confidence levels. For the convenience of discussion, SOAWs are also classified into three flow regimes (Atkins and Wakimoto 1997), namely offshore, onshore, and shore-parallel flow regimes. The shore-parallel flow regime occurs when the absolute value of the SOAW is smaller than 10% of the total wind speed. Vice versa, the offshore (onshore) flow regime is defined when the SOAW is positive (negative).

3 Bulk characteristics of the diurnal cycle over the MC

We first conduct statistical analysis of probability density functions (PDFs) to examine the bulk characteristics of the diurnal cycle of the four variables identified above during January–February 2018. To reveal the impacts of land–sea contrast and also the differences between coastal and noncoastal areas, the PDFs are calculated separately over the following DFC ranges: noncoastal land (− 200 to − 100 km), coastal land (− 100 to 0 km), coastal sea (0–100 km), and noncoastal sea (100–200 km).

3.1 Diurnal amplitude, maximum, and minimum

Figure 2 shows the R_d PDF in different DFC ranges. For Precip (Fig. 2a) over noncoastal regions, the occurrence frequency of very small R_d (~ 0.2 mm h⁻¹) is large, exceeding that of intermediate R_d (~ 2–3 mm h⁻¹). By contrast, over coastal regions, the intermediate R_d of Precip occurs the most frequently. The land features more occurrence of strong (> 3.2 mm h⁻¹) R_d and less occurrence of weak (< 3.2 mm h⁻¹) R_d as compared with the ocean. The separation of PDF curves results in different mean values of R_d, in which the coastal land is the strongest and the noncoastal ocean is the weakest. The biggest land–sea contrast is seen in T2 (Fig. 2b). The R_d PDFs over land are much wider than those over the ocean, indicating that the air temperature near the ocean surface usually undergoes weak diurnal variation. Despite the similar coastal-noncoastal contrast of T2 with Precip over the sea, the R_d of land T2 is usually stronger over noncoastal than coastal areas, which is contrary to the land Precip. For Wind10 (Fig. 2c), the distribution of R_d over land shows an evident positive skewness, implying that the land usually has small diurnal variation in near-surface wind speed. In contrast, the ocean R_d has a relatively symmetric distribution, featuring larger mean values than land. Note that R_d over noncoastal land also has a secondary peak centered at ~ 3.3 m s⁻¹, which leads to a larger mean R_d as compared with coastal land, while over the sea, the diurnal variation of Wind10 in coastal regions is stronger. For Con10, the R_d PDF features a curve resembling the normal distribution over both land and sea (Fig. 2d). The contrasts between land and sea and also between coastal and noncoastal areas are seen mainly in the tails of the PDF curves. The land has more occurrence of large R_d and less occurrence of small R_d as compared with the ocean, and similar results hold for the contrast between coastal and noncoastal regions.

Fig. 2

Probability density function (PDF, %) of R_d of a Precip (mm h⁻¹), b T2 (K), c Wind10 (m s⁻¹), and d Con10 (day⁻¹) in the DFC ranges of [− 100, 0], [− 200, − 100], [0, 100], and [100, 200] km. Dotted lines denote the mean values of R_d averaged in different DFC ranges (the colors correspond to those of the PDF curves)

In general, the above results from Fig. 2 reveal that for Precip and Con10, the diurnal variations over land or coastal regions are usually stronger than those over the sea or noncoastal regions, consistent with previous studies (e.g., Mori et al. 2004; Kikuchi and Wang 2008; Birch et al. 2015; Li et al. 2017). For T2 and Wind10, however, the situations are somewhat complicated. For T2, the uniqueness is the stronger diurnal variation over noncoastal regions than over coastal regions. Wind10 is special because it has weaker diurnal variation over land than ocean and also the noncoastal regions have larger mean diurnal amplitude than coastal regions. These results are consistent with Li et al. (2017) and Short et al. (2019).

The statistical distributions of R_d are further diagnosed with the bivariate PDFs between R_d and R_max (Fig. 3) and between R_d and R_min (Fig. 4). CCs and PDFs of R_max and R_min are also attached in each subplot. For Precip, R_min is usually close to zero (Fig. 4a1–d1), and so R_d ≈ R_max/2, explaining the very high linear correlation between these variables in Fig. 3a1–d1. For T2, the correlation with R_max (Fig. 3a2–d2) is stronger than that with R_min (Fig. 4a2–d2), suggesting the dominant role of daytime warming in setting up the diurnal cycle of T2. Except for coastal land, R_min in other DFC ranges shows dramatic positive correlations with R_d. Therefore, a nonlinear relationship between R_d and R_max or R_min in T2 may exist, as reflected by the exponential growth–like PDFs, especially over the sea (Figs. 3c2–d2, 4c2–d2). For Wind10, nighttime strength is often small over land due to friction, but not over the sea where friction has less of an effect. Thus R_min is often near zero over land (Fig. 4a3–b3), which implies that R_d ≈ R_max/2 for the diurnal cycle of land near-surface wind. As a result, the land R_d shows a high linear correlation with R_max (Fig. 3a3–b3), while over the ocean linear correlation becomes weak (Figs. 3c3–d3, 4c3–d3) and a nonlinear relation may hold. For Con10, R_d shows a high linear correlation with both R_max (Fig. 3a4–d4) and R_min (Fig. 4a4–d4), which simply reflects that under mass conservation in the tropics, R_max ≈ − R_min for Con10. This is especially true over the sea (Fig. 4a4–b4) where linear aggregation of scattered points is less noisy as compared with that over land (Fig. 3a4–b4).

Fig. 3

Bivariate PDF between R_d and R_max of Precip (mm h⁻¹) in the DFC range of a1 [− 200, − 100] km, b1 [− 100, 0] km, c1 [0, 100] km, and d1 [100, 200] km. The PDF of R_max for precipitation is attached along the vertical axis. The correlation coefficient between R_d and R_max is also added. a2–d2, a3–d3, and a4–d4 are the same as a1–d1, but for T2 (K), Wind10 (m s⁻¹), and Con10 (day⁻¹), respectively

Fig. 4

Same as Fig. 3, but for R_min

To understand the covariation among different variables, we further show the bivariate PDF of R_d between any two variables among Precip, T2, Wind10, and Con10 in Fig. 5. Figure 5a1 shows that the R_d of Precip has a significant negative correlation with that of T2, indicating that over noncoastal land strong diurnal variation of precipitation often corresponds to weak diurnal variation of near-surface temperature. The significance of CC at the 90% confidence level is evaluated based on Monte Carlo tests. In coastal land, the R_d of Precip shows a significant positive correlation with that of Con10 (Fig. 5b3), suggesting the crucial role of near-surface wind convergence in supporting a strong precipitation diurnal cycle over coastal land. In addition, the R_d of Wind10 and Con10 is also positively correlated over land (Fig. 5a6, b6), since they are both related to land–sea or mountain-valley breezes. Otherwise, there is no clearly visible relationship for R_d in other groups of two variables over land. Interestingly, over the ocean, the R_d of all groups of two variables among Precip, T2, Wind10, and Con10 shows strong positive correlations, and all CCs can pass the 0.1 significance test, indicating that the amplitudes of the diurnal cycles of precipitation, wind, and temperature covary over the ocean of the MC. Furthermore, each of these correlations is greater over noncoastal than coastal seas, suggesting that the covariation of the diurnal cycles of different variables is more profound in the far offshore ocean.

Fig. 5

Bivariate PDF of R_d between each two-variable combination of Precip (mm h⁻¹), T2 (K), Wind10 (m s⁻¹), and Con10 (day⁻¹) in the DFC ranges of a1–a6 [− 200, − 100] km, b1–b6 [− 100, 0] km, c1–c6 [0, 100] km, and d1–d6 [100, 200] km. Correlation coefficients are also added. Asterisk denotes that the correlation coefficient is significant at the 90% confidence level, evaluated based on Monte Carlo tests

3.2 Timing of diurnal maximum and minimum

The bulk characteristics of τ_max and τ_min are examined to gain further understanding of the complex relationship among convection, wind dynamics, and thermodynamics at the diurnal time scale over land/sea areas of the MC. Figure 6a shows that τ_max of Precip can occur at virtually any time of day, reflecting the regional variability of the diurnal cycle over the MC. For coastal land, τ_max occurs mostly at LST 12–21, with the peak at LST 15. For noncoastal land, τ_max occurs mostly at LST 15–21, with the peak at LST 18, which is 3 h later than that over coastal land, consistent with the onshore propagation of diurnal Precip once it is triggered near the coastline. Using Tropical Rainfall Measuring Mission (TRMM) satellite observations, Li et al. (2017) suggested that coastal (noncoastal) land has maximum Precip occurring mostly at LST 17–18 (20–21) over the MC, which is 3 h later than our model simulations. Wei et al. (2020) found that TRMM featured R_max occurring 3 h later than other satellite Precip products over MC islands. This fact partially compensates for the earlier bias of our model results. Over the ocean, τ_max occurs mostly at LST 3–9 (3–12) for the coastal (noncoastal) sea. For τ_min, we may understand it as the initial triggering time of Precip. As seen from Fig. 6e, the diurnal land Precip is triggered mostly at LST 9; while the triggering time for ocean Precip is widely distributed and ranges from LST 12 to 21.

Fig. 6

Histogram of τ_max (LST) of a Precip, b T2, c Wind10, and d Con10 over the DFC ranges of [− 100, 0] km, [− 200, − 100] km, [0, 100] km, and [100, 200] km. e–h Same as a–d, but for τ_min (LST). i–l Same as a–d, but for τ_d (hours). Solid (dotted) lines denote the mean value of τ_d averaged over land (ocean)

From the histogram of T2 τ_min, we can see that the diurnal land warming begins simultaneously with sunrise at LST 6 (Fig. 6f) and reaches maximum warmth mostly after 6 (9) h for coastal (noncoastal) areas (Fig. 6b), which leads τ_max of Precip by 3 h and is consistent with the convective triggering mechanism of land warming. Over the ocean, the minimum T2 occurs mostly at LST 6–9, which corresponds well with τ_max of Precip. This suggests that the oceanic diurnal Precip is associated mainly with the cooling effect of such as density currents (Feng et al. 2015).

The statistical distribution of τ_min of Wind10 in Fig. 6g indicates that the diurnal land Wind10 begins to increase mostly at LST 6, consistent with the beginning of diurnal land warming and suggesting that the strengthening of near-surface wind speed over land is mainly thermally induced. This is also in accordance with the mixing of faster winds aloft down to the surface, as the boundary layer begins to mix after sunrise (e.g., Svensson 2011; Lee 2018). The land Wind10 generally reaches its peak at LST 15–18 (Fig. 6c) which is 3 h later than the peak warming of T2 at LST 12–15 over land (Fig. 6b), again suggesting the critical role of thermal forcing. By contrast, over the ocean the initial increase in Wind10 at mostly LST 12–18 (Fig. 6g) tends to be simultaneous with the initial cooling of T2, with occurrence at LST 15–21 (Fig. 6b). Oceanic Wind10 develops to its strongest at the time of the coldest T2, i.e., at about LST 6–9, and in this time range, Precip also reaches its maximum (Fig. 6a). The good relation among precipitation and near-surface winds and temperature over the sea is consistent with the high linear correlation of R_d in these fields shown in Fig. 5.

The coupling mechanism over the ocean can also be confirmed by τ_max of Con10, which occurs mostly at LST 3–12 (Fig. 6d), consistent with the preferred τ_max of Precip and Wind10 and also τ_min of T2. Over land, τ_max of Con10 begins ~ 3 h earlier than τ_max of Precip, suggesting that the near-surface wind convergence likely serves as a forcing mechanism of diurnal precipitation over land, in accordance with Kilpatrick et al. (2017).

3.3 Duration from diurnal minimum to maximum

The bulk characteristics of τ_d over the MC are shown in Figs. 6i–l. Over land, τ_d of Precip is mostly 9 h, implying that the recovery time (hereafter, τ_d⁻) to R_min from R_max is usually as long as 15 h. This asymmetry between τ_d and τ_d^˗ suggests that the diurnal variation of land Precip is often “non-sinusoidal.” By contrast, over the ocean the peak occurrence of τ_d is at 12 h, implying that the oceanic Precip usually features a “sinusoidal” diurnal variation. For T2 over land, τ_d peaks at 6 h with the implication of 18-h τ_d^˗ (Fig. 6j), which well explains the “non-sinusoidal” diurnal variation of land Precip. For T2 over the ocean, τ_d features peak occurrence at 9–12 h and a mean value of 10.5 h, consistent with the “sinusoidal” diurnal cycle of ocean Precip. For τ_d of Wind10, the peak occurrence at 9 h over land also implies a “non-sinusoidal” diurnal variation, while over the ocean τ_d of Wind10 is very changeable, with an almost equivalent frequency of occurrence at 6–18 h (Fig. 6k). For Con10, there is no evident difference between different bins of τ_d (Fig. 6l), which suggests that there is no preferred occurrence frequency of τ_d for Con10 over either land or ocean.

The land–sea contrast of the peak occurrence of τ_d/τ_d^˗ revealed from the above is likely the result of asymmetric heating and cooling over land, and more symmetric heating and cooling over the ocean (Svensson 2011). Because of the usually “sinusoidal” diurnal variation over the ocean, it would be valid to examine the ocean diurnal cycle using harmonic analysis with only sine wave 1 considered (e.g., Wei et al. 2020), while over land the assumption of 12-h symmetry may not be able to provide a good fit of the diurnal cycle (Ling et al. 2019) due to the prevalence of “non-sinusoidal” diurnal variation. Taking into account the asymmetric diurnal wind cycle over the Australian coastal regions, Short (2020) fit the hourly data using the modified, asymmetric sinusoidal curves and obtained good effects.

4 Impacts of shore-orthogonal ambient winds

4.1 Ambient wind information

We first examine the ambient winds over the selected areas of Sumatra, Borneo, and New Guinea shown in Fig. 1c. Over Sumatra, the westerly winds are dominant in the lower troposphere throughout the two months, thereby causing mostly onshore ambient winds (Fig. 1c(a)). Over Borneo, both onshore and offshore ambient winds occur frequently (Fig. 1c(b)), which may result from the regulation of synoptic-scale activity, such as the Borneo Vortex (Chang et al. 2003, 2005; Anip 2012). Over New Guinea, a regular variation of ambient winds is seen (Fig. 1c(c)): in January, the prevailing easterly lower-tropospheric wind causes persistent onshore ambient winds; by contrast, in February the lower troposphere is dominated by westerly wind, thereby causing mostly offshore ambient winds. The turnover of the prevailing direction of lower-tropospheric zonal wind over New Guinea between January and February 2018 is likely determined by the crossing of MJO through the MC (Wei et al. 2020; Li et al. 2020).

4.2 Variable dependence, land–sea contrast, and regional variability in the impacts of ambient winds

To diagnose the influence of SOAWs on the diurnal cycle of precipitation and near-surface variables, Fig. 7 sketches the strategy and procedures. Two attributes of the diurnal cycle, R_d and τ_max, are examined. Considering that the impact of ambient winds on the diurnal cycle may be variable dependent, we thus describe our results variable by variable. For each variable, the land–sea and coastal-noncoastal contrasts of the impacts of ambient winds are also investigated by considering the linear correlations in different DFC ranges. In addition, the regional variability of ambient wind impacts is examined by intercomparison of the results over different selected areas. Table 1 shows the CCs between SOAWs and R_d of Precip, T2, Wind10, and Con10 averaged in the DFC ranges of [− 200, − 100] km, [− 100, 0] km, [0, 100] km, and [100, 200] km over Sumatra, Borneo, and New Guinea. Table 2 is the same as Table 1, but for τ_max. Scatter diagrams for SOAW and R_d of the four variables in different DFC ranges over different areas have also been examined but not shown, as they are consistent with the results in Table 1.

Fig. 7

Sketch to demonstrate the mechanisms of the impacts of shore-orthogonal ambient winds on the diurnal cycle over the Indo-Pacific Maritime Continent region. Please see detailed descriptions in Sect. 4

Table 1 Linear correlation coefficients between R_d of the four variables considered in this study (i.e., Precip, T2, Wind10, and Con10) and the shore-orthogonal ambient winds over Sumatra, Borneo, and New Guinea from WRF simulations and considered in different DFC ranges, i.e., noncoastal land ([− 200, − 100] km), coastal land ([− 100, 0] km), coastal sea ([0, 100] km), and noncoastal sea ([100, 200] km)

Table 2 Same as Table 1, and except for T2 over the sea, we consider τ_max of variables

4.2.1 Precipitation

Over Sumatra, as seen in Table 1, R_d of Precip depends significantly on the SOAWs over land, while over the sea, the CCs are weak and insignificant. The linear dependence with positive CCs suggests that stronger onshore winds weaken the diurnal variation in Precip over the land of Sumatra. Also noted are the slightly higher CCs over the coastal than over the noncoastal lands, though R_d of Precip is generally weaker over the former than the latter. Over Borneo, R_d of Precip over both the land and sea has significant positive CCs with the SOAWs, and the highest CCs occur over the coastal sea. Over New Guinea, R_d of Precip and SOAWs are also positively correlated over coastal regions, while over the noncoastal land with mostly mountaintops (Fig. 1) a significant negative CC is obtained, indicating that strong offshore winds act to suppress the strength of the Precip diurnal cycle. In fact, the strong offshore flow regime during February 2018 corresponds to a period of active large-scale MJO deep convection (Li et al. 2020; Wei et al. 2020), which may suppress the daytime convergence induced by valley breezes and thus R_d of Precip over mountaintops (Rauniyar and Walsh 2011; Wei et al. 2020). In contrast, some other studies have shown a weak intraseasonal variation of the diurnal wind cycle over the MC under the modulation of MJO (e.g., Vincent and Lane 2017; Short et al. 2019), suggesting that further explorations are needed to prove the conjecture above.

For τ_max of Precip (Table 2), its linear dependence on the SOAWs is generally small and insignificant. The exceptions are over New Guinea, where a significant positive CC is seen over the coastal land while a negative CC appears over the coastal sea. The above results reflect the land–sea and coastal-noncoastal contrasts, and also the regional variability concerning the impact of SOAWs on the Precip diurnal cycle. In addition, focusing on each island over a specific DFC range, the CC of τ_max is always smaller than the CC of R_d in Precip, which suggests that SOAWs tend to influence the diurnal cycle of Precip mainly by regulating R_d.

4.2.2 2 m temperature

In contrast to Precip, R_d of T2 over the land of Sumatra shows significant negative CCs with SOAWs, which is in accordance with Fig. 5a1 showing the correspondence of strong R_d of Precip with weak R_d of T2 over land. Over the coastal sea near Sumatra, however, the strength of T2 diurnal variation is positively correlated with SOAWs. Over Borneo, the ambient wind influence on R_d of T2 is the strongest over coastal sea and second strongest over noncoastal sea with significant positive CCs. In contrast, over land the CCs are weak and cannot pass the 10% significance t test. Positive CCs between R_d of T2 and SOAWs are seen over all areas of New Guinea, but only those over the coastal regions are significant.

Regional variability and land–sea contrast of the impacts of SOAWs are also seen for τ_max of T2 (Table 2). For example, over Sumatra τ_max of T2 over the coastal sea decreases with strengthening onshore winds. Over New Guinea, a significant CC between τ_max of T2 and SOAWs is also seen over the coastal sea, but it is negative, suggesting that stronger offshore winds will lead to smaller τ_max of T2. Over Borneo, the strongest CC of − 0.2 appears over the coastal land but cannot pass the 10% significance t test. Besides, the generally weaker CCs in Table 2 as compared with those in Table 1 focusing on T2 suggest that SOAWs influence the R_d of T2 more than its τ_max.

4.2.3 10 m wind speed

For Wind10, the positive CCs between R_d and SOAWs are robust across the three islands, as seen in Table 1, suggesting that the diurnal variation of near-surface wind speed will become stronger with increasing SOAWs, although the land–sea and coastal-noncoastal contrast, and also the magnitudes of CCs are region dependent. For instance, over Sumatra significant CCs over noncoastal land are larger than those over coastal land/sea areas. Over Borneo, the CCs over the land become weak and insignificant at the 90% confidence level. In contrast, over the sea significant CCs appear and are especially large over the coastal sea. Over New Guinea, the CCs over all land/sea areas can pass the 10% significance t test, and the largest CC occurs over the coastal land.

The τ_max of Wind10 also shows significant linear correlation with SOAWs in some DFC ranges over each of the three islands. For example, over the noncoastal land of Sumatra, the significant positive CC of 0.5 is even larger than the CC of R_d. The τ_max of Wind10 over other DFC ranges of Sumatra is also positively correlated with SOAWs, but the 10% significance t test is passed only over the sea areas. A significant CC of 0.23 between τ_max of Wind10 and SOAWs also exists over the noncoastal sea of Borneo. Over New Guinea, a significant positive CC of 0.24 between the two variables is seen over noncoastal land, which is weaker than the negative CC of − 0.34 over coastal land.

4.2.4 10 m convergence

The linear correlation between R_d and SOAWs for Con10 is similar to that for Precip. In general, a positive (negative) CC for Con10 can be found when there is a positive (negative) CC for Precip. This is consistent with the positive correlation between R_d of Precip and that of Con10 shown in Fig. 5a3–d3 focusing on the entire MC region. For the τ_max of Con10, as seen in Table 2, significant negative CCs occur over the coastal land of Borneo, and also over the coastal land/sea areas of New Guinea. In other regions of the three boxes, no significant CC exists, however. Over New Guinea, especially over the coastal land, the CC of τ_max is higher than that of R_d, suggesting that SOAWs influence the diurnal cycle of Con10 over this region mainly by regulating τ_max. Otherwise, the CCs of R_d are always higher than those of τ_max and thus R_d is the major pathway by which SOAWs influence the Con10 diurnal variation.

4.3 Summary of ambient wind impacts on the diurnal cycle over the three selected land/sea areas

Overall, through the variable-by-variable diagnostic analysis above, we confirmed the characteristics of the SOAWs regulation (i.e., positive versus negative correlation) and the ambient wind impact (i.e., magnitude of linear correlation) on the diurnal cycle over the MC are distinct over land and sea, and also vary with the geographic region and variables.

Robust conclusions are found over the sea. In particular, R_d of all variables over the sea becomes larger with increasing SOAWs, suggesting that strengthening offshore ambient winds support strong diurnal variation over the MC ocean. This seems to be in accordance with Short et al. (2019), who using merged observations found a positive CC between the perturbation diurnal surface wind speed and background offshore wind velocity over the sea regions of the MC. In addition, the ambient wind impacts are stronger over coastal than noncoastal seas. The robust positive CC between ocean R_d and SOAWs is also consistent with the well-correlated diurnal variation of all variables over the seas of the whole MC derived from Fig. 5.

The intercomparison of different seas suggests that the linear dependence of R_d over the sea northwest of Borneo on the SOAWs is stronger than that over the seas near Sumatra and New Guinea. Regional variability is also found for the land–sea contrast of SOAW impacts on the diurnal cycle. Over Sumatra, the land CCs are higher than those over sea for each variable, while the opposite is true over Borneo. The weaker variation of the diurnal cycle over the land than the sea northwest of Borneo under the influence of large-scale environmental conditions (such as MJO) is also documented by previous studies (e.g., Kanamori et al., 2013; Wei et al. 2020). Over New Guinea, SOAW impacts are stronger over coastal than noncoastal regions, while the land–sea contrast is somewhat weaker than that over Sumatra and Borneo.

Variable-dependent characteristics of SOAW impacts are clearly revealed over land. For Precip, a positive correlation between R_d and SOAWs can be found in general except over the noncoastal land of New Guinea, where a negative CC exists possibly due to the influence of MJO deep convection clouds. For T2, negative CCs are found over the land of Sumatra, while over other land regions, positive CCs of weak magnitude are seen. For R_d of Wind10 and Con10, which are both related to the land–sea breeze circulation, there is usually a positive correlation with SOAWs.

The variation in SOAW impacts on the diurnal cycle with geographic region, variables, and DFC ranges over the MC is even more profound for τ_max. Moreover, compared with R_d, the CCs of τ_max are generally weak and insignificant, which is consistent with previous studies showing the insignificant influence of large-scale wind conditions on the diurnal phase of Precip over the MC (e.g., Tian et al. 2006; Suzuki 2009). Therefore, SOAWs act to influence the diurnal cycle over the MC mainly by regulating R_d rather than the timing of the diurnal phases of precipitation and near-surface meteorological variables considered in this study.

5 Composite diurnal cycle under the impacts of ambient winds over Sumatra

To further understand the variation of the diurnal cycle under the impacts of Strong and Weak ambient winds, composite analysis is performed focusing on the sea breeze phase (i.e., LST 8–19) over Sumatra. The sea breeze phase of LST 8–19 is defined based on our WRF model run. Strong Wind days are those in which the SOAW is stronger than its mean plus one standard deviation, while Weak Wind days are those with SOAW weaker than the mean minus one standard deviation. Over the Sumatra box from January 1 to February 28 2018, the Strong Wind days identified in this study consist of only onshore flow regimes (Fig. 1c(a)).

5.1 Clouds, circulation, and convection

Figures 8 and 9 show the composite diurnal variation of rainwater, vertical velocity, and cloud fraction averaged over transects shown in Fig. 1b under Weak and Strong Winds, respectively. Weak Wind is characterized by a large (small) fraction of low (middle and high) clouds, especially over the ocean. Strong diurnal variation in the cloud fraction is seen primarily over the coastal land with steep topography. The low cloud fraction increases from LST 8–9 (Fig. 8a) to 10–11 (Fig. 8b) in the DFC range of [− 50, 0] km, and rainwater increases locally along with the formation of ascending motion. At noon, with a further increase in shallow clouds, the convection becomes deeper and rainwater increases (Fig. 8c), and middle and high clouds begin to grow. During the afternoon and evening (Fig. 8d–f), the shallow cloud fraction shrinks while the middle and high cloud fractions grow continuously and expand toward the land interior. The vertical motion transfers from a deep convection mode to a stratiform mode. The content of rainwater reaches its maximum in the early afternoon and then decays before finally merging with the other body of rainwater from the northeastern plain. Overall, the development of deep convective middle/high clouds is preceded by shallow clouds, which suggests the crucial role of shallow clouds in preconditioning the occurrence of land deep convection and rainfall under Weak Wind. Under Strong Wind (Fig. 9), all cloud types occupy a large fraction (~ 70%), except for the coastal sea where shallow clouds are less (~ 10%). As expected from the linear correlation, the diurnal variation becomes much weaker as compared with that under Weak Wind. For instance, the cloud fractions undergo a small change and the convection is shallow and weak near the coastline. Rain occurs mainly over the ocean where stratiform-mode vertical motion persists.

Fig. 8

Composite diurnal variations of rainwater (shading, g kg⁻¹), vertical velocity (contours, m s⁻¹), and cloud fraction (bottom lines, %) under Weak Wind, averaged over transects shown in Fig. 1. Solid (dashed) contours denote ascent (descent), with a contour interval of 0.1 m s⁻¹. The red, blue, and green lines denote low cloud, middle cloud, and high cloud, respectively. The threshold height values of the three cloud fractions are 300, 2000, and 6000 m, respectively

Fig. 9

Same as Fig. 8, but for Strong Wind

Figure 10 shows the composite diurnal cycle of wind speed, shore-orthogonal wind velocity, and wind vectors at 10 m. Under Weak Wind, the near-surface winds undergo strong diurnal variation in speed (Fig. 10a) and direction (Fig. 10c, e). The orientation of the anticlockwise hodograph in 10 m wind vectors is perpendicular with the southwest coastline of Sumatra, suggesting the dominant role of the land–sea breeze in determining the diurnal variation of Wind10 under Weak Wind (Fig. 10a). Under Strong Wind, however, the change in 10 m wind direction is limited (Fig. 10d, f), which suggests small diurnal variation in 10 m winds and is in accordance with the linear correlation analysis (Table 1). The orientation of the hodographs shows a small angle with the coastline of Sumatra, which is especially evident over the far offshore region beyond 200 km (not shown). Despite the evident diurnal cycle in shore-orthogonal wind velocity under Strong Wind (Fig. 10b), this does little to explain the total Wind10 variation.

Fig. 10

Composite diurnal cycle of 10 m wind speed (shading, m s⁻¹) and shore-orthogonal wind velocity (contours, m s⁻¹) under a Weak and b Strong Wind. Solid (dashed) contours denote offshore (onshore) winds, with a contour interval of 1 m s⁻¹. Zero anomalies are highlighted by thick solid contours. Hodographs of 10 m wind vectors (m s⁻¹) averaged under Weak Wind in the DFC ranges of c [0, 200] km and e [− 200, 0] km. Red and blue dots denote the wind vectors at 12 and 0 UTC, respectively. d and f are the same as c and e, respectively, but for Strong Wind

To better understand the diurnal variation in winds, we show the sub-daily evolution of a vertical wind section in Fig. 11 averaged over transects of Sumatra. The wind vectors in Fig. 11 consist of shore-orthogonal wind velocity and vertical velocity. To quantify the degree of diurnal variation under different ambient winds, we calculate the hourly ratio between shore-orthogonal wind velocity and total wind speed, displayed as shading in Fig. 11. The positive (red shading) and negative (blue shading) ratios in Fig. 11 reflect the onshore and offshore directions, respectively. Note that a high-magnitude ratio will indicate a small angle between the shore-orthogonal wind vector and the total ambient wind vector, given a certain location and time. Under Weak Wind, the land–sea breeze represented by the shore-orthogonal wind velocity can well explain the total wind speed variation throughout almost the entire troposphere. The sea breeze starts at LST 10–11 (Fig. 11b) and becomes stronger and deeper at noon (Fig. 11c). It then expands rapidly over the sea area (Fig. 11d–f). Both the SBF and return flows aloft can be seen clearly, forming a deep sea breeze circulation. In contrast, under Strong Wind, only a small part of the troposphere has wind speed variation related to the shore-orthogonal wind velocity (Fig. 11g–l). Typically, the depth of the anomalous return flow aloft and its counterpart in the lower level is shallower than that under Weak Wind. Remember that the ascent is also shallow and weak under Strong Wind (Fig. 9), which means that the diurnal wind variation in the lower levels tends to decouple with that in the upper level, and therefore there is only weak or even no sea breeze circulation formed under Strong Wind.

Fig. 11

Pressure-DFC sections of vertical circulation (i.e., shore-orthogonal wind velocity and vertical wind velocity) (vectors, m s⁻¹) and the contribution of shore-orthogonal wind velocity to the total wind speed (shading in %), averaged over Weak (a–f) and Strong (g–l) Wind days, and over the Sumatra transects shown in Fig. 1. DFC is the distance from the coastline (km).

5.2 Moist thermodynamics

5.2.1 Moist static energy

Figure 12 shows the composite anomalous diurnal variation of the moist static energy (MSE) and water vapor mixing ratio averaged over transects of Sumatra. Under Weak Wind after sunrise, both the land and ocean surfaces begin to be moistened (Fig. 12a). The moistening of the land surface, especially near the coastline, is more rapid than that of the ocean surface (Fig. 12b). The more efficient pre-moistening effect near the coastline is due mainly to the growth of shallow clouds. In the afternoon, the near-coastline moistening becomes stronger and even penetrates into the tropopause (Fig. 12c, d). Due to the consumption of rainwater, the moisture content decreases in the late afternoon (Fig. 12e, f). The oceanic boundary layer is moistened continuously from LST 10–11 to 18–19. The diurnal variation of MSE bears a strong resemblance with the water vapor mixing ratio. Exceptions are near the land surface and tropopause, where the role of other sources of MSE (such as turbulent flux, radiation flux, and temperature variation) is dominant. Under Strong Wind (Fig. 12g–l), moistening efficiency is weak and moisture growth is constrained below 800 hPa over land, corresponding well to the shallow ascent and weak rainwater variation shown in Fig. 9. In addition, drying rather than moistening prevails over the oceanic boundary layer during LST 10–11 to 18–19 under Strong Wind. Similar variations are also noted for MSE. In brief, the contrasting diurnal variations of circulation and convection under Strong and Weak Wind are well explained by the moist thermodynamics of MSE.

Fig. 12

Composite anomalous diurnal cycle of moist static energy (shading, J Kg⁻¹) and water vapor mixing ratio (contours, g kg⁻¹) averaged over transects shown in Fig. 1 under a–f Weak and g–l Strong Wind. Solid (dashed) contours denote positive (negative) anomalies, with a contour interval of 0.3 g kg⁻¹. Zero anomalies are highlighted by thick solid contours

To give a further explanation of surface MSE variation, we show the anomalous diurnal cycles of latent heat flux (LH) and shortwave radiation (SW) in Fig. 13. As we can see, the diurnal variations of both LH and SW are stronger under Weak than under Strong Wind (see the difference between Weak Wind and Strong Wind in Fig. 13c, f), corresponding well to the contrast in surface MSE diurnal variation shown in Fig. 12. The strong diurnal variation of LH under Weak Wind may be due to the strong diurnal variation of Wind10, with stronger surface winds producing greater evaporation. Furthermore, the dominance of shallow clouds under Weak Wind leads to more daytime absorption of SW at the surface, thereby leading to strong diurnal variation of SW. Also note the more rapid reduction of LH and SW after LST 14 near the coastline under Weak Wind, as compared with that under Strong Wind. This can be attributed mainly to the formation of precipitating middle and high clouds near the coastline under Weak Wind (Fig. 8d, e), which effectively causes near-surface cooling and suppresses SW absorption at the surface.

Fig. 13

Composite anomalous diurnal cycle of latent heat (LH) flux (W m⁻²) averaged over transects shown in Fig. 1 under a Weak and b Strong Wind. c Difference between a and b. d–f Same as a–c, but for net surface shortwave (SW) radiation (W m⁻²). The black dashed line denotes the coastline, i.e., zero distance from the coastline (DFC, km)

5.2.2 Cold pool

The strong diurnal variation of convection under Weak Wind, such as the transition from shallow to deep convection and the inland propagation of precipitating clouds, could also be related to cold pool dynamics (Khairoutdinov and Randall 2006; Feng et al. 2015). To evaluate the effects of the cold pool, Figs. 14 and 15 show the hourly variations of 1000-hPa MSE under Weak and Strong Wind cases, which occur on February 27–28 and January 12–13, 2018, respectively. The associated 10 m wind vectors and 1000-hPa vertical velocity are also shown in Figs. 16 and 17.

Fig. 14

Hourly variation of moist static energy (MSE, J g⁻¹) at 1000 hPa over Sumatra under Weak Wind (i.e., February 27–28, 2018)

Fig. 15

Same as Fig. 14, but for Strong Wind (i.e., January 12–13, 2018)

Fig. 16

Same as Fig. 14, but for 1000-hPa vertical velocity (shading, m s⁻¹) and 10 m wind (vectors, m s⁻¹)

Fig. 17

Same as Fig. 15, but for 1000-hPa vertical velocity (shading, m s⁻¹) and 10 m wind (vectors, m s⁻¹)

Under Weak Wind at LST 13 (Fig. 14), the near-surface MSE is characterized by a small-scale eddy structure, in which the in-eddy MSE is low while the eddy edge has high MSE, as is typical of cold pools (Khairoutdinov and Randall 2006). The cold pools are especially strong over high topography, where extensive precipitating downdrafts form (Fig. 8). Updrafts can be seen clearly over the cold pool edges (Fig. 16). With time, these cold pools grow upscale and the near-surface MSE becomes large due to the intersection of adjacent cold pools (Feng et al. 2015). The upscale growth of cold pools originating from the precipitating clouds near the high topography is especially significant. For example, the leading edge (or density currents) of cold pools is characterized by strong gust fronts, where strong updrafts and MSE exist. The inland migration of gust fronts coincides well with the inland expansion of rainwater and middle-high cloud fractions, suggesting the crucial role of cold pool updraft dynamics (Cheng et al. 2018).

Under Strong Wind, however, the cold pools are visible only over the mountain ranges with small amplitude (Fig. 15). The near-surface MSE diurnal variation is limited. These phenomena correspond to the weak diurnal variation of vertical velocity and rainwater under the prevailing middle and high clouds. Moreover, these small cold pools cannot grow upscale or propagate inland, as shown under Weak Wind. Without the strong effect of cold pool updraft dynamics, the ascent is constrained near the coastline and cannot migrate into the land interior (Fig. 17). This partially explains the weak amplitude of diurnal MSE near the surface under Strong Wind as shown in Fig. 12 g–l.

In other words, the Strong Wind environment cannot support the upscale growth and inland propagation of cold pools, and therefore a strong diurnal cycle accompanying the transition from shallow to deep convection cannot be seen. Here, to make some possible explanations from the perspective of large-scale conditions. We checked the composite outgoing longwave radiation (OLR) and 850-hPa horizontal winds for all days (i.e., January to February 2018), Weak Wind days, and Strong Wind days, respectively from the WRF simulations (Fig. 18). ERA5 reanalysis products are also employed to validate the WRF simulation. As expected from the definition, Weak Wind days feature very small wind speed over the whole Sumatra box (Fig. 18b, e), as compared with the all-days composition (Fig. 18a, d). Interestingly, the convective activity (denoted by OLR) is very strong over land but suppressed over the sea. By contrast, on Strong Wind days, vigorous deep convection occurs mainly over the far offshore region. The convection over land, however, becomes less active (Fig. 18c, f). The different convective activity over land implies that the low-level atmosphere over the land of Sumatra is drier under Strong Wind than Weak Wind. This is also clearly reflected in Figs. 14 and 15, where the Strong Wind case features a very dry boundary layer over the land of Sumatra. The importance of a moist environment in supporting cold pool formation, growth, and propagation has been highlighted in previous studies. For example, Zuidema et al. (2017) showed that cold pools are most effective at influencing mesoscale organization when the atmosphere is moist in the lower free troposphere. Haerter and Schlemmer (2018) suggested that in a drier boundary layer, there is less moisture available that can be reorganized along cold pool boundaries. Also seen in Fig. 18 is that the ambient winds over land are so strong under Strong Wind that a large gradient of temperature and thus cold pools cannot form effectively, as compared with the calm land condition of Weak Wind.

Fig. 18

Composite large-scale background state of outgoing longwave radiation (shading, W m⁻²) and wind velocity (vector, m s⁻¹) for (left) all days, (middle) Weak Wind days, and (right) Strong Wind days during January–February 2018 from a–c ERA5 reanalysis and d–f WRF simulations. The red rectangle denotes the Sumatra box

5.2.3 Gravity waves (GWs)

GWs are another mechanism used to explain diurnal cycles (Mapes et al. 2003; Love et al. 2011; Yokoi et al. 2017). Wei et al. (2020) adopted GWs to explain the diurnal cycle of precipitation under the modulation of MJO over the Indo-Pacific MC region. They revealed that the cold GWs near Sumatra responding to nocturnal precipitation evaporation are weaker in the active convection phase of MJO that those in the suppressed phase of MJO. In this study, we take a further look at the diurnal variation in temperature under different ambient wind forcings. Figure 19 shows the composite anomalous diurnal cycle of temperature averaged over transects (shown in Fig. 1b) under Weak and Strong Winds. It is apparent that the atmospheric boundary layer warms rapidly after sunrise, and anomalous warming is manifested as outward and upward expansion, characterizing the propagation of warm GWs (Mapes et al. 2003). Cold anomalies appear early, at LST 16–17, due to the evaporation of rainwater near the coastline. Despite these common features, the degree of the outward and upward extension of warm GWs is distinct under the impacts of different ambient winds. Typically, warm GWs under Weak Wind can fill the entire troposphere, while under Strong Wind the evolution of GWs is limited. The effective upward propagation of GWs can also explain the deep structure of MSE under Weak Wind. In Fig. 12c, for example, the moistening near the coastline can reach only 700 hPa, while the positive MSE has a top approaching 400 hPa. This deep structure of MSE, which is related to the deep ascent and strong rainwater, can be attributed to the upward propagation of warm GWs. Overall, the results here suggest that the strong diurnal variation of convection and circulation under Weak Wind is also related to strong warm GWs. This is in accordance with previous studies highlighting the important role of GWs in explaining the diurnal cycle near Sumatra (Yokoi et al. 2017; Wei et al. 2020).

Fig. 19

Composite anomalous diurnal cycle of temperature (K) averaged over transects shown in Fig. 1 under a–f Weak and g–l Strong Wind

The identification of certain GW characteristics from Fig. 19 is necessary to justify the above interpretation. Following Holton (2004), the dispersion relationship of internal GWs can be expressed as

$$\sigma =N{k({k}^{2}+{m}^{2})}^{-1/2}+\overline{s }k,$$

(1)

where $\sigma$ is the intrinsic frequency, $k$ and $m$ denote the horizontal and vertical wavenumbers, $\overline{s }$ is the background wind speed, and $N$ is the Brunt–Väisälä frequency. Therefore, the horizontal propagation speed of GWs, $c$, is derived as follows:

$$c\equiv \frac{\sigma }{k}=N{m}^{-1}{\left(1+{k}^{2}/{m}^{2}\right)}^{-\frac{1}{2}}+\overline{s }.$$

(2)

In the scenario of atmospheric GW propagation, the vertical wavelength, ${\lambda }_{z}$ (~ O(10) km), should be far smaller than the horizontal vertical wavelength, ${\lambda }_{x}$ (~ O(10³) km), which means that $k\ll m$. Thus, Eq. (2) may be reduced to

$$\widehat{c}=\frac{N{\lambda }_{z}}{2\pi }+\overline{s },$$

(3)

noting that $m=2\pi /{\lambda }_{z}$. Because the temperature variation under Strong Wind is limited (Fig. 19g–l), we choose to analyze the Weak Wind scenario. Seen from Fig. 19c–e, there is generally one maximum between 400 and 900 hPa, which corresponds to an n = 3 GW mode with a vertical wavelength of two-thirds of the tropopause height (Lane and Zhang 2011; Tulich et al. 2007; Tulich and Mapes 2008). Similar to Vincent and Lane (2016), we could obtain an outward propagation speed of ~ 15.9 m s⁻¹ if we assume an $N$ of 0.01 s⁻¹ and ${\lambda }_{z}$ of 10 km. Under the Weak Wind scenario, the SOAW speed $\overline{s }$ is about 2 m s⁻¹ (Fig. 1c), yielding an estimation of c as 13.9 m s⁻¹. From Fig. 19c, d, the warm temperature anomaly over the sea propagates ~ 100 km offshore in about 2 h, indicating a phase speed of 13.8 m s⁻¹, which is consistent with the estimation based on the GW theory. The above justification suggests the importance of GWs in explaining the contrasting evolution of the diurnal cycle under Strong and Weak Wind over Sumatra.

6 Summary and concluding remarks

Using a set of cloud-permitting-scale numerical simulations together with a “coastline-following” method, the bulk characteristics of the diurnal cycle in Precip, T2, Wind10, and Con10 as a function of DFCs over the Indo-Pacific MC region were investigated. The diurnal cycle of each variable was examined using six characteristic parameters, including diurnal amplitude (R_d), diurnal maximum (R_max) and its timing (τ_max), diurnal minimum (R_min) and its timing (τ_min), and duration from diurnal minimum to maximum (τ_d). Among the six parameters, the last three have rarely been investigated in previous studies. For Precip, T2, and Con10, the land–sea contrast is consistent, and the land features a stronger R_d than the sea. For Wind10, the sea area statistically has a stronger R_d as compared with the land. In addition, we also detected different coastal-noncoastal contrast characteristics for the diurnal cycle of different variables. Over the sea, all variables have stronger R_d in the coastal area than in the noncoastal area. However, over land, the R_d of T2 and Wind10 in the coastal area is weaker than that in the noncoastal area. By contrast, for Precip and Con10, R_d in the coastal land is stronger than R_d in the noncoastal land. The relative contribution of R_max and R_min in determining R_d is also variable dependent. For T2, although R_max largely determines R_d, an exponential growth–like bivariate PDF between R_max and R_d is clear over the sea, reflecting the nonlinear character of R_max in determining R_d of oceanic T2. For Wind10, the land R_d is explained mainly by R_max, while for ocean R_d, both R_max and R_min play a role. For Con10, R_d is well correlated with R_max and R_min regardless of the land/sea and coastal/noncoastal contrasts.

The diurnal cycle of precipitation over coastal land is closely related to the near-surface convergence induced by the land–sea breeze, while over noncoastal land the diurnal precipitation is more related to the near-surface temperature variation. The linear correlations between the amplitude of the diurnal cycles of precipitation, wind, and temperature near the surface are stronger over the ocean than over land. Non-sinusoidal diurnal variation occurs mostly over land, while sinusoidal diurnal variation is dominant over the ocean. Some previous studies have always preferred to extract diurnal variation using sine wave 1 harmonic analysis regardless of whether it is over land or ocean (e.g., Yang and Slingo 2001; Love et al. 2011; Peatman et al. 2014), which may cause misleading conclusions (Slingo et al. 2004; Ling et al. 2019). Further work is needed to prove this perspective.

The impacts of ambient winds on the diurnal cycle have been recognized previously. Many studies have highlighted the vital role of wind speed (i.e., strong versus weak) or direction (i.e., offshore versus onshore), while few studies have considered their joint effect (Short et al. 2019). Specifically, most previous studies have focused on the middle- and high-latitude regions, while less attention has been paid to the tropics, especially the Indo-Pacific MC region. Aided by the “coastline-following” technique, we further investigated the dependence of diurnal characteristics on SOAWs as a function of DFCs. In general, we unraveled the variable dependence, land–sea contrast, and regional variability in the impacts of SOAWs on the diurnal cycles. The key points from the analysis are summarized as follows.

For all variables considered in this study, the ocean diurnal amplitude increases with the strengthening of offshore ambient winds. The most significant impacts of SOAWs on the ocean diurnal cycle occur over the coastal region. The intercomparison of different seas suggests that the linear dependence of R_d on the SOAWs over the sea northwest of Borneo is stronger than that over the sea near Sumatra and New Guinea. Over Sumatra, the land CCs are higher than those over the sea for each variable, while the opposite is true over Borneo. Over New Guinea, the SOAW impacts are stronger over coastal than noncoastal regions, while the land–sea contrast is somewhat weaker than that over Sumatra and Borneo. Variable-dependent characteristics of SOAW impacts are clearly reflected over land. Furthermore, compared with R_d, the CCs of τ_max are generally weak and insignificant, which suggests that SOAWs act to influence the diurnal cycle over the MC mainly by affecting R_d rather than the timing of the diurnal phases of precipitation and near-surface meteorological variables considered in this study.

To understand diurnal variation under the influence of SOAWs, we performed a composite analysis focusing on Sumatra. The results suggest that: (1) Under Weak Wind, shallow clouds are dominant and cause a pre-moistening effect over the coastal regions, supporting the transition from shallow to deep convection. The middle and high clouds along with rainwater undergo strong diurnal variation. Sea breeze circulation (SBC) with return flow aloft can develop rapidly. In contrast, under Strong Wind, both shallow and middle-high clouds prevail and persist with small diurnal variation over both land and sea. Meanwhile, the evolution of moistening in the column is limited, leading to very weak variation in vertical motion and rainwater. Stronger surface MSE in the afternoon is attributed mainly to the larger growth of LH and SW under the relatively cloud-free environment of Weak Wind, as compared with the cloudy Strong Wind environment. (2) Under Weak Wind, cold pools form effectively. Gust fronts cause enhanced MSE at the surface and strong ascent in the boundary layer, which plays an important role in supporting the triggering and upscale growth of deep convection. The precipitation-induced cold pools over high topography can grow extensively and migrate slowly toward the land interior through interactions with the leading updrafts (Cheng et al. 2018). These processes, however, are absent under Strong Wind. (3) Warm GWs responding to the surface heating under Weak Wind can propagate upward and outward throughout the troposphere, thereby supporting strong diurnal variation in convection and circulation. In contrast, Strong Wind days have only limited evolution of GWs, corresponding well to the weak diurnal variation.

Note that the above explanations arise from a mesoscale view, which is virtually distinct from the root causes of large-scale dynamic and thermodynamic conditions. In this regard, we also discussed the contrast in diurnal variations over Sumatra under different SOAWs by diagnosing the ambient winds, moisture, and convection. Strong Wind days feature windy conditions, a dry lower troposphere and boundary layer, and suppressed convection over the land of Sumatra. These large-scale environmental conditions do not favor the formation, upscale growth, and inland propagation of cold pools, and therefore strong diurnal variation with a shallow-to-deep convection transition cannot be supported. In contrast, on Weak Wind days, the land of Sumatra is calm, moist, and active in deep convection. These conditions together create a favorable environment for the occurrence and maintenance of strong diurnal variation. Since this study focuses mainly on the exploration of mesoscale circulation and convection, the analysis of large-scale dynamics and thermodynamics is limited and preliminary. More work should be conducted to address this issue in the future.

Future work will also emphasize more comprehensive numerical simulations with sensitivity studies to further examine the physical and dynamic connections among near-surface atmospheric variables on a diurnal scale and their interaction with large-scale and mesoscale environments. Their dependence on and interactions with the large-scale background, such as MJO, BSISO, etc., should also be examined in detail. Moreover, the discussions and conclusions drawn from the composition of strong ambient winds in this study correspond to the influence of strong onshore winds. Long-term simulation over Sumatra that covers both onshore and offshore flow regimes is needed in the future to explore the asymmetric influences of strong ambient winds.