1 Introduction

Extra-tropical windstorms are one of the costliest natural hazards affecting Europe and cyclones that follow the Shapiro–Keyser (SK) conceptual model (Shapiro and Keyser 1990) account for a large proportion of the most damaging windstorms (Hewson and Neu 2015). Within Shapiro–Keyser storms, there are three main sources of extreme surface wind gusts; the warm and cold jets that accompany the warm conveyor belt (WCB) (Harrold 1973) and the cold conveyor belt (CCB) (Carlson 1980; Browning and Roberts 1994), and the sting jet, if present (Browning 2004; Baker 2009; Schultz and Browning 2017; Clark and Gray 2018). According to Hewson and Neu (2015), the highest and most damaging surface wind gusts are generally due to the sting jet when it is present, followed in order by the CCB and WCB. Previous storms known to have produced sting jets include the most damaging windstorm to hit the UK, the Great Storm of’87 (Browning 2004; Clark et al. 2005), as well as windstorms Ulli and Friedhelm (Fox et al. 2012), Tini (Slater et al. 2017; Volonté et al. 2018), and Ellen (Met Éireann 2020). The latter four storms each warranted a red level warning, the highest level to be issued by forecasting agencies due to the high likelihood of extreme impacts occurring. Reported impacts include large numbers (> 150,000) of households without electricity (Perils 2012) as well as high insured losses such as US$0.2bn for Windstorm Ulli and US$6.7 billion for the Great Storm of 1987 (Roberts et al. 2014). In this article, we quantify the contribution of such windstorms to wind risk using current and future climate simulations produced by a convection-permitting climate model (CPM), and compare these with a 25 km global climate model (GCM) to assess the added-value offered by a CPM in the representation of extreme wind speeds.

The WCB and CCB are low-level jets that occur within the warm and cold sectors, respectively, of extra-tropical cyclones, and both can lead to extremely damaging surface wind gusts (Hewson and Neu 2015). A sting jet is a meso-scale slantwise airstream that occurs in a SK cyclone. It descends from the mid-troposphere, within the cloud head of the cyclone, into what is known as the frontal fracture region or dry slot (Weldon and Holmes 1991), in front of (or eastward of) the CCB (Clark and Gray 2018). This descent is distinct from a dry intrusion which descends from near tropopause level to the mid-troposphere. The sting jet exhibits a number of features that makes it particularly hazardous. Firstly, the dry slot is generally characterised by weak stability conditions that are favourable to high momentum air from the SJ being transferred down towards the surface (Clark et al. 2005; Hewson and Neu 2015; Clark and Gray 2018). And secondly, the sting jet accelerates during its descent within the free atmosphere unopposed by friction, bringing high momentum air towards the surface (Slater et al. 2015). This descent can then be further accelerated by evaporative cooling (Browning 2004; Clark et al. 2005; Browning et al. 2015; Rivière et al. 2020; Eisenstein et al. 2020) and the release of a slantwise instability, known as conditional symmetric instability (Clark et al. 2005; Gray et al. 2011; Baker et al. 2014; Coronel et al. 2016; Volonté et al. 2018; Eisenstein et al. 2020). As a result, the presence of a sting jet may yield wind speeds that can far exceed those expected when viewing isobars of a synoptic chart. Such characteristics, the small footprint and the short timescale of a sting jet, compared to a CCB or WCB (1–12 h vs. 12–36 h: Hewson and Neu 2015), presents challenges for forecasters who can sometimes only identify the presence of a sting jet in real-time (Fox et al. 2012).

To adequately simulate sting jets using a numerical model, both high horizontal and vertical resolution are required. The minimum requirements suggested are horizontal grid spacings below 10–15 km and vertical grid spacings of around 250 m in the mid-troposphere, and smaller spacings below (Clark et al. 2005; Clark and Gray 2018). Besides the small spatial scale of a sting jet, high-resolution is required in order to realise the instabilities that can accelerate a sting jet during its descent. For instance, Volonté et al. (2018) compare a sting jet’s descent in a high-resolution model with that in a global model with reduced horizontal and vertical resolution. Although both simulations produce a sting jet, the sting jet’s descent in the high-resolution simulation coincided with the release of conditional symmetric instability and increases in wind speed, while no such instability release was found in the lower resolution model. Subsequently, the maximum sting jet wind speeds at 850 hPa were underestimated by 12 ms−1 compared to the high-resolution model (48 vs. 60 ms−1). Similarly, Coronel et al. (2016) found that reducing both the horizontal and the vertical resolution results in reduced wind speeds and no sting jet forming. However, there was little difference when only reducing the horizontal resolution (4 vs 20 km). In other comparisons where only vertical resolution was decreased, studies reported a reduction in sting jet strength (Clark et al. 2005) and in the area of intense wind speeds (Martínez-Alvarado et al. 2010). In contrast, Slater et al. (2015) reported no sensitivity to either horizontal (10 vs. 20 km) or vertical resolution in idealised simulations, though possible changes in the sting jet due to the release of slantwise instabilities were not included in the simulation (Clark and Gray 2018). Overall, the effect of resolution appears to vary and may depend on characteristics such as the size of the sting jet and the contribution of conditional symmetric instability release. In cases where the latter is significant, it is evident that high vertical and horizontal resolution is required.

Quantifying the contribution of sting jets to wind extremes, relative to the CCB or WCB, remains an understudied topic. This is partly because observations of wind speeds are sparse and may miss cores of very strong wind speeds produced by sting jets, while high-resolution simulations are restricted to case studies due to the large costs they incur. Within such case studies, Smart and Browning (2014) find the sting jet produced higher wind gusts than the CCB, but over a much smaller footprint and shorter timescale, while Martínez-Alvarado et al. (2014) show that the sting jet and CCB may occur alongside making it difficult to disentangle their relative contributions. Furthermore, sting jets are a difficult phenomenon to identify due to their small spatial and short temporal scales. Confirming the presence of a sting jet requires the computation of trajectories (Martínez-Alvarado et al. 2014) which needs output on many pressure levels at time intervals of around an hour (Eisenstein et al. 2020). Such an approach is not feasible on climatological timescales due to the huge storage costs involved. As an alternative, Schultz and Sienkiewicz (2013) use frontogenesis to diagnose sting jets in lower resolution simulations, though this approach has not been automated. It is therefore important to develop a low-cost automated approach that can be applied to high-resolution climate simulations.

The likelihood of sting jets occurring in windstorms has so far been indirectly inferred using a large-scale precursor known as downdraught slantwise convective available potential energy (DSCAPE) (Martínez-Alvarado et al. 2012) which indicates the presence of slantwise instabilities or the environmental conditions that are conducive to sting jets. When applied to ERA-Interim (Martínez-Alvarado et al. 2012; Hart et al. 2017), and a 10-year climate simulation (Martínez-Alvarado et al. 2018), the diagnostic was present in roughly 0.1 storms per month that pass over Northwest Europe. This was found to increase to 0.5 cyclones per month in a future climate simulation under the RCP8.5 scenario. Within these studies, Hart et al. (2017) and Martínez-Alvarado et al. (2018) characterised storm severity using the maximum 850 hPa wind speed. They found that DSCAPE storms (that develop explosively) account for more than 40% of storms with maximum wind speeds > 40 ms−1 in a present climate while the frequency of these storms that exceed 35 ms−1 was found to increase by 140% in a future simulation. The presence of DSCAPE can thus indicate potentially damaging windstorms and is currently used in operational forecasting to do so (Gray et al. 2020). DSCAPE points to the high risk of a sting jet developing in these storms, although the models it is applied to are too coarse resolution to adequately capture sting jets and resulting wind speeds. Thus, the high-resolution climate simulations analysed in this study should provide a better opportunity to understand the contributions of sting jets to extreme wind speeds in windstorms.

The aim of this study is twofold: to develop a low-cost method to identify sting jets in high-resolution climate simulations; and to assess the added-value offered by a high resolution (2.2 km) convection permitting climate model (CPM), compared to a 25 km GCM, for wind extremes in extra-tropical windstorms with a focus on those that produce a sting jet. The added-value will be assessed through a comparison with observed wind gusts as well as by identifying systematic differences between the CPM and GCM that would indicate improved process representation in the CPM. In particular, we would like to understand if the likelihood of extreme wind speeds due to sting jets are underestimated in the GCM compared to the CPM, and what implication this may have for impacts due to wind extremes in a current and future climate.

2 Data and methods

2.1 Model simulations

Table 1 provides a summary of the simulations used in this study. Three simulations from a high-resolution convection permitting regional climate model (CPM) are analysed in this study: a hindcast driven by the ERA-Interim reanalysis dataset (ERAI) (Dee et al. 2011) at the lateral boundaries (March 1999–February 2018), as well as a control simulation with current climate forcing (1998–2007) and a future climate simulation with RCP8.5 climate forcing (2091–2100), driven by a 25 km N512 HadGEM3 global climate model (GCM), each 10 years in length. The CPM simulations are carried out with the UK Met Office Unified Model (UM) at a 2.2 km horizontal grid spacing over a European domain shown in Fig. 1a, and have previously been assessed in terms of their improved representation of precipitation (Berthou et al. 2020), as well as future projections of precipitation (Chan et al. 2020). The CPM uses 70 terrain following vertical levels with a 40 km top. The lowest level is 2.5 m above the ground and vertical level spacings increase quadratically with height. This gives grid spacings of 40, 140, 300, and 590 m at heights of approximately 100 m, 1, 5, and 16 km above sea level. The CPM therefore satisfies both horizontal and vertical resolution requirements for the representation of sting jets as outlined in Clark and Gray (2018). A detailed summary on the model physics can be found in Berthou et al. (2020). The GCM providing the lateral boundaries is run at a 25 km resolution with 85 vertical levels with an 85 km top, further details on the model physics may be found in Williams et al. (2018) and Stratton et al. (2018).

Table 1 Summary of the simulations used in the analysis
Full size table
Fig. 1
figure 1

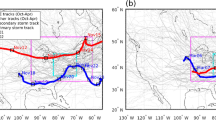
Demonstration of the methodology used to extract the warm seclusion of a Shapiro–Keyser cyclone (Storm Anatol). a \({\theta }_{w}\) at 850 hPa; b \({\theta }_{w}\) at 850 hPa within a region enclosed by red box in a; c a latitudinal cross-section of \({\theta }_{w}\) at 850 hPa taken along the red line in b, S and N denote south and north respectively, the dotted red line denotes the \({\theta }_{w}^{thresh}\) while the solid red line denotes the threshold applied to identify seclusion points (\({\theta }_{w}^{thresh}+2K\)). d The extracted seclusion feature, \({\theta }_{w}\) at 850 hPa, overlain by MSLP. Only cyclones occurring north of the grey line in a are considered in the analysis

Full size image

2.2 Wind data, analysis and metrics

We analyse wind speeds in the northern part of the domain only (grid cells north of the grey line in Fig. 1a), as the sting jet algorithm is not suitable to be applied to the south of this line (see Sect. 2.4.2. for further information). We also mask the outer 100 grid cells to prevent contamination from the downscaling method. All months of the year are included in this analysis, as sting jets are not limited to one season.

2.2.1 Surface wind gusts over land

We assess the CPM’s representation of surface wind gusts over land compared to ERA-Interim (ERAI) and observations, using the hindcast simulation. Surface wind gusts are not studied for the control and future climate simulations as wind gust output was not available from the GCM climate simulations nor for the entirety of the CPM climate simulations. The maximum 3-s wind gust is output from the CPM hindcast simulation on a 3-hourly basis, that is, the maximum gust within a 3-hourly interval, as does ERAI. Observed surface wind gusts are obtained from the Met Office Integrated Data Archive System (MIDAS) weather station observations. These are reported as the maximum gust over a mixture of 1-, 3-, and 6-hourly intervals, depending on the given station. We include observed gusts for 15 storms from the XWS (eXtreme WindStorms) catalogue (Roberts et al. 2014) during the period of 2001–2014. Storms prior to 2001 are not assessed as wind gust output from CPM hindcast is not available before then. The XWS catalogue comprises the most extreme windstorms to hit Europe in the period 1979–2012, and later extended to 2014, which were selected through a combination of consultation with insurance companies and an analysis of windstorm metrics to find the most important windstorms over this period. One storm in this period, Storm Dagmar/Patrick, was excluded as it did not occur within the CPM domain. Additionally, Storms Christian, Tini, and Xaver which occurred after their initial analysis period, were also included. In total, 15 storms are assessed.

2.2.2 850 hPa wind speeds

As wind gusts are not available for the CPM and GCM control and future climate simulations, all analysis of wind speeds in the climate change simulations is done using 3-hourly instantaneous wind speeds at 850 hPa. Winds at 850 hPa are not directly comparable to surface wind gusts but they give an indication of the maximum surface wind gusts achievable in a storm, as argued by Hart et al. (2017).

  • Analysis of storm severity over land

The severity of storms is characterised as the 95th percentile of all 850 hPa wind speeds that exceed 25 ms−1 within the storm footprint (\({SF}_{95}\)). This is calculated by incorporating grid cells that occur within 500 km of the cyclone centre. Only land grid cells are incorporated so that the metric is impact relevant. A threshold of 25 ms−1 was chosen as this is recognised as the surface wind gust level at which damages due to wind start to occur (Roberts et al. 2014). This metric provides an indication of the extremity of wind speeds over a relevant area of the storm (5% of the area where winds exceed 25 ms−1). It is chosen instead of the maximum wind speed that has been used in previous studies with coarser resolution models (e.g. Zappa et al. 2013; Hart et al. 2017; Martínez-Alvarado et al. 2018), as the maximum wind speed from a single grid cell at 2.2 km resolution may not always be representative of the overall storm severity.

  • Identification of warm and cold sector winds

850 hPa wind speeds are classified into cold and warm sector wind speeds to identify winds related to the warm conveyor belt in the warm sector of storms and the cold conveyor belt and sting jet in the cold sector of storms. We include both land and ocean grid cells in this analysis as sting jets often occur over the ocean. Following Hart et al. (2017), the cold and warm sectors of a storm are separated at 3-hourly intervals using a temperature threshold at 850 hPa (\({T}_{850}\)) that represents the frontal boundary between the warm and cold sector. Wet bulb potential temperature (\({\vartheta }_{w}\)) is more commonly used but we do not have this output available at 3-hourly intervals. \({T}_{850}\) is firstly regridded to the 25 km GCM grid and the threshold is identified in each storm, at the time of minimum MSLP within the CPM domain, as the mean \({T}_{850}\) from grid cells that exceed the 99th percentile of \(\Vert {T}_{850}\Vert\) within a 1000 km radius of the cyclone centre, where \(\Vert {T}_{850}\Vert\) is the norm of the temperature gradient vector at each grid cell. Grid cells at elevations above 500 m are masked before calculating the 99th percentile of \(\Vert {T}_{850}\Vert\). The resulting threshold obtained from the application of this method is demonstrated by the thick blue line in Fig. 2a.

Fig. 2
figure 2

Demonstration of the methodology to extract a sting-jet in Storm Anatol over the North Sea. a Wind speeds at 850 hPa overlain by cloud defined as RH at 500 hPa > 80%, the blue line is the temperature threshold contour which indicates the position of frontal boundaries and the boundary of the cyclone’s warm sector b extracted gradient reversal feature, red/blue indicates positive (+ ve)/negative (− ve) vertical gradient, c example series of vertical gradients extracted along streamline shown as gold line in b, d the extracted sting-jet wind feature at 850 hPa which is all points within a 4 m s−1 contour of the maximum wind speed from blue area in b

Full size image

2.3 Storm identification

Cyclone positions have been identified at 3-hourly intervals. They were initially tracked at a 6-hourly resolution (00, 06, 12, 18 h) in ERA-Interim and in the 25 km GCM using the Hoskins and Hodges (2002) tracking algorithm, which identifies and tracks cyclones using 850 hPa relative vorticity, regridded to a T42 grid (~ 300 km) resolution. As sting jets may occur over timescales shorter than 6 h, cyclone positions at 3-hourly timesteps between the 6-hourly timesteps (i.e. 03, 09, 15, 21 h) were subsequently identified. These positions were identified as the point with maximum relative vorticity at 850 hPa within a search-region whose extent was bounded using storm coordinates at the previous and following 6-hourly timestep (e.g. 00 and 06 h are used to define search region for storm position at 03 h). The longitude and latitude coordinates of the storm at the 6-hourly timesteps are used to define the northern, southern, eastern and western bounds of the search region. Each corner of the search-region is then extended outwards by two grid points to account for storms that remain relatively stationary over a 6-h period, which would result in a very small search region.

2.3.1 Diagnosing warm seclusion of Shapiro–Keyser cyclones

Shapiro–Keyser (SK) cyclones are identified at a 6-hourly timescale (00, 06, 12, 18 h) using wet-bulb potential temperature (\({\vartheta }_{w}\)) at 850 hPa and mean sea level pressure (MSLP). SK Cyclones develop a warm seclusion during Stage IV of the SK conceptual model (Catto 2016), which occurs as a result of a bent-back front that encloses or wraps around a core of relatively warmer air. An example of such a feature is provided in Fig. 1. This exemplifies the secluded warm air feature, coincident with the MSLP core, which is surrounded by colder air to the north, south and west. The boundaries between the warm and cold air mark the position of the bent-back front which appears as a cold front to the south, and warm front to the north of the cyclone’s core in the SK conceptual model. Methods are available to identify the position of frontal boundaries (e.g. Hewson 1998; Berry et al. 2011) based on temperature gradients between adjacent grid points in coarse resolution datasets. However, at 2.2 km resolution, grid spacings are too small to detect a frontal boundary whose temperature gradients occur over larger spatial scales. Furthermore, such approaches will not distinguish between fronts associated with a warm seclusion and those not. We therefore develop an approach that is better suited to this resolution that will identify the warm seclusion feature.

A latitudinal cross-section through the storm along the red line in Fig. 1b, depicts the warm seclusion as a sharp peak in \({\vartheta }_{w}\) in Fig. 1c. Similarly, a longitudinal cross-section would show a sharp increase in \({\vartheta }_{w}\) in the west–east direction (not shown). The warm seclusion diagnostic is based on the identification of such peaks in \({\vartheta }_{w}\) that coincide with the MSLP core of the cyclone. Specifically, a warm seclusion is identified if the MSLP core of the cyclone coincides with an area where \({\vartheta }_{w}\) is at least 2 K warmer than surrounding areas. The steps of the identification procedure are outlined below:

  1. 1.

    Extract a region around cyclone centre which extends 1000 km to the north, south, east and west (red box in Fig. 1a).

  2. 2.

    Within each latitudinal row of the resulting matrix, identify the presence of a peak in \({\vartheta }_{w}\). A peak in \({\vartheta }_{w}\) refers to a consecutive number of points when \({\vartheta }_{w}\) is greater than a threshold \({\vartheta }_{W}^{Thresh}\), which is equal to \({\vartheta }_{w}\) at the beginning of a peak (see Fig. 1c). The beginning of a peak is identified at point \(i\) when \({{\vartheta }_{w}}_{i}>{{\vartheta }_{w}}_{i-1}\) and a peak is only identified if an end point is found which indicates a reversal in the latitudinal \({\vartheta }_{w}\) gradient that is indicative of a warm seclusion. Only points within a peak that exceed \({\vartheta }_{W}^{Thresh}\)+ 2 K, are considered as potential warm seclusion points. The thresholds \({\vartheta }_{W}^{Thresh}\) and \({\vartheta }_{W}^{Thresh}\) + 2 K are indicated in Fig. 1c. The selection of 2 K is a subjective choice based on experience and analysis of the known events in Table 2, though it is similar to the 1.5 K threshold used to identify the warm core of Medicane cyclones (Tous et al. 2016).

  3. 3.

    The previous step is repeated in the longitudinal direction (west to east).

  4. 4.

    The MSLP core is identified in the same way, although a trough in MSLP is identified rather than a peak. Once the presence of a MSLP trough is detected, the minimum MSLP is found (\({MSLP}_{min}\)) and the MSLP core is identified as all points within the trough less than \({MSLP}_{min}\) + 6 hPa. This threshold is also a subjective choice guided by experience and analysis of known events.

  5. 5.

    A warm seclusion is identified if the number of potential warm seclusion points, that satisfy both 2 and 3, within the MSLP core exceeds 500 points. The number 500 was selected from experience to remove very small and incoherent cases that can occur due to a noisy field at 2.2 km. To give some perspective, at 2.2 km, 500 points would cover an area of around 2200 km2, which as a circle, would have a radius of approximately 26 km, which is far below the average radius of a cyclone core.

Table 2 Performance of automated approach for sting jets identified in case studies and in Hewson and Neu (2015) (HN 2015)
Full size table

2.3.2 Sting jet diagnostic

The identification of sting jets in this analysis was limited by the number of pressure levels available in the output. Five pressure levels (300, 500, 700, 850 and 925 hPa) were available, of which only two were useful to identify the slantwise descent of a sting jet. The only existing automated method to detect sting jets in high-resolution simulations, known as back-trajectory analysis (Martínez-Alvarado et al. 2014) requires output on many pressure levels at time intervals of at least one hour (Eisenstein et al. 2020). Although this is a powerful method, its application is not feasible on a climatological timescale due to its large storage and computational costs. This motivates the need for a low-cost method with low data requirements. In this study, sting jets are identified within the subset of diagnosed Shapiro–Keyser cyclones, at a 3-hourly timescale using wind speeds at 700 and 850 hPa as well as relative humidity (RH) at 500 hPa.

A sting jet occurs in the cold sector of a cyclone where it descends from the mid-troposphere (~ 600 hPa) to the top of the boundary layer (~ 850 hPa) or lower, emerging from the edge of an extrusion of cloud on the northeast side of the cyclone called the cloud head (Bottger et al. 1975) into a region of low relative humidity known as the dry slot. In doing so it produces areas of low RH within the cloud head from where it has descended as well as a distinct region of strong winds at the level it descends to in front of the cloud head (Clark and Gray 2018). The diagnostic presented here is based on identifying the three characteristics described above, namely the slanted descent of a sting jet, the reduction in RH and the distinct feature of high wind speeds in front of the cloud head around the southern flank of the cyclone. To remain consistent with previous analyses of sting jets that use RH to indicate the cloud head (e.g. Volonté et al. 2018; Eisenstein et al. 2020), relative humidity is defined with respect to ice, RHice.

The slanted descent is identified by a reversal of the vertical gradient of horizontal wind speed (\(\nabla v\)) between winds at 700 hPa (\({ws}_{700}\)) and 850 hPa (\({ws}_{850}\)), along streamlines at 850 hPa.

$$\nabla v={ws}_{700}-{ws}_{850}$$

If present, a sting jet will produce a transition from positive to negative gradients along a streamline, (see Fig. 2b, c) that originates from an area of high RHice (cloud head) into an area of low RHice (dry slot) as can be seen from the comparison of RHice and the location of the gradient reversal feature in Fig. 2a, b respectively. The transition is identified by extracting streamlines (e.g. gold dashed line in Fig. 2b) along wind directions at the 850 hPa level, which are used to provide an approximation of the actual sting jet trajectory, as if it were projected from above on to the 850 hPa level. The streamlines are initiated from points (e.g. gold dot in Fig. 2c) with negative gradients in the cold sector of the storm whose wind speed at 850 hPa also exceeds the local 98th percentile of the winter season December, January, and February (DJF). This is calculated separately for the hindcast, while the 98th percentile value for the control is applied to both the control and future simulations.

At each grid cell along the streamline, the vertical gradient of horizontal wind speed (\(\nabla v\)) is extracted along with RHice at 500 hPa and wind speed at 850 hPa. Only streamlines to the south of a cyclone are considered, which are those whose backward direction is towards the west. Each streamline will have a maximum length of ~ 200 km. This is a subjective choice, Clark et al. (2005) show for one storm that the length of the sting jet feature was around 150 km, though this can vary between different storms (Hewson and Neu 2015). For a sting jet to be identified, several criteria should be met along a given streamline:

  1. 1.

    Moving backwards along a streamline, a continuous sequence of negative gradients, beginning from the initial point of the streamline, should be followed by a continuous sequence of positive gradients. An example of this transition along a streamline is provided in Fig. 2c. Each positive and negative sequence must be at least 20 grid cells in length and occur within 10 grid cells of one another to account for possible fluctuations in the vertical gradient.

  2. 2.

    The median RHice at 500 hPa within the positive gradient points should be greater than 80%, indicating the descent originates from within the cloud head. The threshold of 80% is applied as this has been used in previous sting jet analyses to indicate the location of cloud (Eisenstein et al. 2020; Volonté et al. 2018; Coronel et al. 2016). RHice at 500 hPa was chosen instead of at 700 hPa, as the algorithm was found to perform better.

  3. 3.

    The median RHice at 500 hPa within the negative sequence should be, in absolute terms, at least \({\Delta }_{RH}\) = 50% lower than that within the sequence of positive gradients. Together, the RHice criteria indicates the emergence of the sting jet from the cloud head region into the dry slot of the cyclone. The value of 50% was chosen to optimise the algorithm’s performance, as described further below.

  4. 4.

    The maximum 850 hPa wind speed of the negative sequence should be at least \({\Delta }_{WS}\) = 6 ms−1 higher than the maximum wind speed from the positive sequence. Along with the RHice criteria, this indicates a distinct wind feature ahead the cloud head. Similarly to RHice, 6 ms−1 was chosen to optimise the algorithm’s performance (see Sect. 2.4.2.).

  5. 5.

    The above procedure is applied to each point in the cyclone’s cold sector with a negative vertical gradient which exceeds the DJF 98th percentile described above. The number of these points that satisfy 1–4 should exceed 50 points. This is an arbitrary selection to remove randomly identified events that occur due to the noisy nature of a 2.2 km grid.

2.4 Performance and limitations of algorithm

The performance of the algorithm has been tested for 14 known or speculated storms (see Table 2) that produced sting jets within the time period of the hindcast simulation (1999–2018). Some of these have been confirmed as having sting jets through backward trajectory analysis (Clark and Gray 2018), while others have been subjectively identified through visual analysis (Hewson and Neu 2015). The algorithms to detect a warm seclusion and a sting jet were applied to each time step of these storms. Each storm produced a warm seclusion which was detected by the algorithm, as indicated in Table 2, and we find this to be a robust feature in storms that is relatively easy to detect. As such, we have high confidence in the automated detection of warm seclusions. To assess the sting jet algorithm’s performance, we firstly subjectively identify if the simulation has produced a sting jet in each of the 14 storms.

2.4.1 Subjective identification of sting jets

Two subjective assessments were carried out independently by the first author and a Chief Operational Meteorologist at the UK Met Office, Dan Suri. The two assessments are used to minimise any unconscious bias and increase our confidence in the robustness of the subjective assessment. The first author used criteria recommended by Hewson and Neu (2015) in which a sting jet is visually identified if the wind maxima at 850 hPa occurs just ahead of the cloud head close to the cyclone’s core on the equatorward side, as shown in Fig. 2a. The algorithm is also based on these criteria. As detailed in Table 2, nine storms were found to exhibit these characteristics. The second subjective assessment by Dan Suri used the above information but also looked at surface wind gusts (where available) for evidence that a sting jet had reached the surface. Eleven of the fourteen storms presented evidence of a sting jet according to these criteria. To highlight the inherent subjectivity of this approach, and the difficulty in identifying if a sting jet has occurred or not, Dan Suri categorised each of these eleven storms according to the degree of certainty (high, medium, or low) he had that the identified feature was produced by a sting jet (see Table 2). Five fall into the high confidence category, three in medium, and three in low.

All nine storms identified by the lead author are included in the eleven storms identified by Dan Suri, and the timings of the identified sting jets are generally the same, except for Storm Xynthia (Table 2). The remaining two storms not included in this eleven by the first author (Storms Tini and Gudwin/Erwin), presented no evidence of a distinct wind feature ahead of the cloud head but did show signs of a sting jet in surface wind gusts. It is possible that sting jets may be missed in 3-hourly instantaneous output but seen in the 3-hourly maximum wind gusts if they occur over a short period in between. It is also possible that the definition used for the cloud head may not be optimal for all storms and result in missed cases. Furthermore, in reality Storm Tini developed a sting jet in the western side of the domain (Volonté et al. 2018), and so the CPM domain may be too small to capture this storm, particularly due to the large jump in resolution between ERA-Interim and the CPM which results in a wide spin-up zone. However, there is a large overlap between the two assessments and so we are confident that the criteria used by the first author, which is also used by the algorithm, provides a good indicator of a sting jet. The timings shown here are also consistent with those reported in the literature shown in Table 2 of Clark and Gray (2018). Two exceptions are storms Gudrun/Erwin and Christian where sting-jets are detected later than in Baker (2009) and Browning et al. (2015). However, we do not expect exact correspondence between timings in the model and observations given that information on the observed state is only fed at the lateral boundaries of the CPM domain.

2.4.2 Optimisation and performance of sting jet algorithm

As the criteria used by the algorithm is the same as that used in the subjective assessment by the lead author, the performance of the algorithm is optimised against the nine storms identified by the lead author. The parameters \({\Delta }_{RH}\) and \({\Delta }_{WS}\) were selected to optimise the algorithm’s performance by maximising the number of correctly identified sting jets whilst minimising the number of false alarms and missed events. A number of combinations of \({\Delta }_{RH}\) (− 20 to − 70%) and \({\Delta }_{WS}\) (2–10 ms−1) were tested, and the optimum parameter values found were \({\Delta }_{RH}=-50\%\) and \({\Delta }_{WS}=6m{s}^{-1}\). The performance of the algorithm with the chosen parameters is summarised in Table 2. The algorithm identified 6 of the 9 events and had 1 false alarm. The number of missed events increases from 3 to 5 compared to the Forecaster’s assessment. However, it only identified 7 of the 22 sting jet time steps from across all storms but had just 3 false alarms. These results indicate that the algorithm with the prescribed parameters has skill in identifying storms where the indicators of sting jets are present, namely the distinct wind feature at 850 hPa ahead of the cloud head. However, it has less skill in identifying all such timesteps in those storms.

The main source of the missed cases lies with the criteria applied to RHice along the extracted streamlines. The comparison of the median RHice in the positive and negative sequence of the gradient reversal feature (Fig. 2b, c) is problematic as it requires the positive and negative sequences to lie mostly within an area of high and low RH respectively, which is not always the case. Comparing the maximum and minimum RH in the positive and negative sequences respectively increases the number of hits to 17 of the 22 timesteps but is also accompanied by a large number of false alarms (23) which is not acceptable. We therefore decided to compare the median RH to remain conservative and are confident that the storms identified with this approach are done so for the right reasons. Other missed cases such as Storms Egon and Jeanette had no gradient reversal present. It is possible that no sting jet is actually present in these storms, or that the sting jet descends close to or over the cold conveyor belt which is indicated in a case study analysis of Storm Egon (Eisenstein et al. 2020). This occurrence may remove the positive gradient between 850 and 700 hPa, leading to a missed case. Furthermore, in cases where the occurrence of strong evaporative cooling prevents drying during descent, a wind feature may not be seen ahead of the cloud head leading to a missed event, though this potential shortcoming may depend on the pressure level used to define the cloud head.

Some further quality control was carried out to investigate the overall performance for all storms. The algorithm was found to produce many false alarms in the Mediterranean and surrounding areas with complex orography as it identifies subsidence in downslope winds on the lee side of mountains as well as events such as the Mistral in the south of France that produces subsiding air and extreme wind speeds downstream of the Rhone valley. We therefore decided to remove the Mediterranean and surrounding areas with complex orography from the analysis as we found little evidence of sting jets there in the simulations and it would be difficult to distinguish between the abovementioned features and sting jets without applying arbitrary criteria. As such, the sting jet algorithm is not applied to cyclones south of the grey line in Fig. 1a.

The low data requirements, compared to the 3-dimensional fields needed for back-trajectory analysis, are a large advantage of this approach, which creates the possibility to automate the analysis of sting jets in high-resolution climate simulations and to allow the further exploitation of such simulations that are continually increasing in number (Schär et al. 2020). There is also potential for it to be applied operationally to help the forecasting community with high-impact weather warnings. However, the low-cost advantage of the method does come with caveats, in that several parameters are required with arbitrary thresholds due to the low number of pressure levels available. In future applications, improvements might be achieved through increasing the number of pressure levels output from simulations between 900 and 500 hPa, or potentially through applying an online diagnostic while the model is running which would remove the need for large volumes of output. It would also be helpful to use case study simulations of known sting jets to fine tune the method and guide the selection of required output from high-resolution climate simulations. Despite the caveats though, we are confident that the algorithm with the specified criteria is identifying storms for the right reasons and can be used to extract information related to sting jets from these simulations.

3 Results

3.1 Comparison with observed wind gusts

We compare cumulative distribution functions (CDFs) of observed maximum 3-s wind gusts for 15 storms from the XWS catalogue to those produced by the hindcast simulation and ERAI (Fig. 3). Only wind gusts from stations/grid-points below an elevation of 500 m are considered. CDFs are firstly constructed for each storm from the maximum gust at each grid cell or station that occurred within 500 km of a cyclone centre (Fig. 3b–p). These CDFs are then pooled for the CPM, ERAI and observations and shown in Fig. 3a. The CPM generally produces higher wind gusts than ERAI and compares better with observations both on the native grid and when regridded to the ERA Interim grid. Compared to the observations, the CPM underestimates wind gusts above 25 ms−1. This feature is also seen in Roberts et al. (2014) and Haas and Pinto (2012), who compared observed wind gusts to those simulated by a limited-area model run at coarser resolutions of 25 and 7 km respectively. In Roberts et al. (2014), possible reasons for this underestimation included weaker pressure gradients in the model and the non-representation of convective gusts.

Fig. 3
figure 3

Comparison of wind gust CDFs between observed (black lines), ERA Interim (blue line), and the CPM on its native grid (solid red line) and regridded to the ERA Interim grid (~ 75 km) (dashed red line). CDFs are constructed by pooling wind gusts over land from stations/grid-points below a 500 m elevation for a all 15 windstorms from the XWS Catalogue (Roberts et al. 2014), and for b–p each individual windstorm. Storms are ordered according to their reported insured losses (if available) according to the XWS catalogue

Full size image

However, when comparing CDFs on an event-by-event basis we see the CPM compares quite well with the observations in some events. In other events, the CPM can both overestimate and underestimate wind gusts, and so no systematic bias is seen in this respect. For those events where the CPM underestimates observed gusts, CPM simulated gusts are either similar to or better than ERAI (e.g. Fig. 3b, e, g, h). This suggests that the CPM’s performance may be limited by the use of lateral boundary conditions from ERAI which tends to underestimate the minimum MSLP in windstorms due to its resolution (Hewson and Neu 2015). This bias is not necessarily corrected through dynamical downscaling, potentially contributing to underestimation of wind gusts by the CPM.

It is important to note that we do not expect one-to-one correspondence between simulated and observed gusts on an event-by-event basis, although we would expect the overall climatology of gusts to be captured. This is because the CPM only receives information on the observed state of the atmosphere at the lateral boundaries of the Europe-wide model domain, and within this domain it evolves freely. Furthermore, station observations at a given point in space are not directly comparable to gridded model data, as modelled gusts represent an areal mean for a grid cell that may tend to make the model gusts too low. On the other hand, observations may also miss peak wind gusts as they are sparsely distributed in space. There are no gridded products of observed wind gusts and so this is the best comparison we can make. Overall, the results provide an indication that the CPM can represent maximum wind gusts within extra-tropical cyclones, providing an improvement over ERAI.

3.2 Assessment of storm frequency and severity

Storms are categorised into three storm types; non-Shapiro–Keyser storms (\(nSK\)), Shapiro–Keyser storms without a sting jet (\({SK}_{N{-}SJ}\)), and those that produce a sting jet (\({SK}_{SJ}\)). The total number of cyclones within each category for the three simulations is provided in Table 3. The hindcast is split into two 10-year periods (Hindcast 1: March 1999–February 2009; Hindcast 2: March 2008–February 2018) to provide an indication of decadal variability. The frequency of cyclones in the hindcast and control are similar, though there are more \({SK}_{SJ}\) cyclones in the control. The absolute difference in the number of \({SK}_{SJ}\) cyclones (14 and 17 vs. 26) is rather large. Reasons for this are unclear but could be related to natural variability or differences in boundary conditions and downscaling ratios (75–2 km for ERAI, and 25–2 km for the GCM). The number of \({SK}_{SJ}\) cyclones in the control and future simulations is the same, although, due to the overall reduction of SK cyclones in the future simulation, the proportion of SK cyclones with sting jets is slightly higher in the future (4.7 vs. 4.3%). Compared to Hart et al. (2017) and Martínez-Alvarado et al. (2018) who report climatologies of 0.1 and 0.5 DSCAPE cyclones per month over Northwest Europe in present and future climates respectively, our present-day estimates are similar to these at 0.1 and 0.2 \({SK}_{SJ}\) cyclones per month in the hindcast and control, though our future estimate is lower at 0.2 \({SK}_{SJ}\) cyclones per month.

Table 3 Total number of cyclones within each storm type
Full size table

The severity of storms is characterised by \({SF}_{95}\) (see Sect. 2.2.2.). CDFs of \({SF}_{95}\) for each storm type are provided in Fig. 4. The conditional CDF for \({SK}_{N{-}SJ}\) storms is shifted to higher values compared to \(nSK\) storms, while the CDFs of \({SK}_{SJ}\) storms are shifted to even higher values in each of the three simulations, indicating an increased probability of extreme wind speeds when a sting jet occurs. The absolute contributions of each storm type to exceedances of \({SF}_{95}\) above high thresholds is provided in Fig. 5. Each bar represents the number of storms exceeding a given threshold, while the colours indicate the frequency contribution of each storm type. The hindcast is split into the same two 10-year periods in Table 3 to give an indication of natural variability in \({SF}_{95}\). The number of storms with \({SF}_{95}\) exceeding 35 ms−1 in each period differs by around 10 storms. This difference varies depending on the threshold. The control simulation has more storms exceeding 35 ms−1 than both hindcast periods, but the numbers exceeding higher thresholds are quite comparable. The proportional contributions from each storm type in the hindcast and control are also similar. \({SK}_{N{-}SJ}\) cyclones account for the majority of the most extreme windstorms at all thresholds, while \(nSK\) storms show a large contribution at lower thresholds, but their contribution diminishes at higher thresholds. \({SK}_{SJ}\) storms have a small representation at each bin, although their proportional contribution increases with increasing threshold. In the future simulation, there are increased exceedances for all storm types, although the changes are mostly driven by increased contributions from \({SK}_{N{-}SJ}\) and \({SK}_{SJ}\) storms as shown by numbers above each bar in Fig. 5c. For instance, above 40 ms−1, the number of storms increases from 10 to 28, with 44 and 39% of that increase accounted for by \({SK}_{N{-}SJ}\) and \({SK}_{SJ}\) respectively. Overall, even with the difficulties found in identifying sting jets themselves, the methodology developed here is identifying storms that have a chance of developing sting jets (i.e. \(SK\) storms) which are generally the most impactful storms and dominate future increases in extreme threshold exceedances.

Fig. 4
figure 4

Comparison of storm metric SF95 CDFs between the three storm types within the hindcast (1999–2018) (a), control (b), and future (c) simulations. Solid lines represent non-SK storms, dotted lines represent SK where sting-jets are not detected, while dashed lines represent sting-jet storms

Full size image
Fig. 5
figure 5

Stacked bar plot of storm metric SF95 for the hindcast (a), control (b), and future (c) simulations. Each bin shows the number of events exceeding the given threshold. Two bins are shown for the hindcast at each threshold, one for the 1999–2008 period and another for the 2009–2018 period. The proportion of events belonging to each of the three storm types in each bin is indicated by the colour (grey: \(nSK\), light blue: \({SK}_{N{-}SJ}\), dark blue: \({SK}_{SJ}\)). The numbers in panel c show the absolute increase in number of storms in each category for that bin

Full size image

3.3 Sting jet storms: sources of wind extremes

The results above relate to overall storm severity (i.e. all extreme winds within a \({SK}_{sj}\) storm footprint and not just the sting jet itself). We now examine the contribution of the sting jet feature to the overall distribution of wind speeds relative to the warm and cold conveyor belts (WCB and CCB) for storms in which a sting jet was identified (Fig. 6). Contributions from the sting jet, CCB and WCB are extracted by firstly separating wind speeds into warm and cold sector winds. All warm sector wind speeds are classified as WCB, while cold sector wind speeds are classified as a sting jet at timesteps when a sting jet was detected and CCB otherwise. It is possible that a CCB may be present at the same time as a sting jet, and so sting jet and CCB winds refer to cold sector winds in the presence or absence of a sting jet. Furthermore, it worth noting that winds due to a dry intrusion or convection may also be included within cold sector wind types. Wind speeds are then pooled across all storms within each wind type (i.e. SJ, CCB or WCB).

Fig. 6
figure 6

Proportional contributions of the sting-jet (SJ—dark blue), cold conveyor belt (CCB—light blue) and warm conveyer belt (WCB—red) to the pooled distributions of wind speeds from all sting-jet storms in the hindcast (a), control (b), and future (c) simulations. The dotted lines represent the proportional contribution of each wind type to the given bin

Full size image

It is clear from Fig. 6 that the CCB is the main driver of extreme 850 hPa wind speeds, a finding that is in line with Hart et al. (2017). It accounts for more than 40% of winds greater than 35 ms−1 and this proportion increases at higher thresholds. The WCB has a similar contribution at 35 ms−1, but this decreases with increasing threshold. Contributions from sting jet winds are generally lower than the CCB and WCB, but increase at higher thresholds. The low estimate for sting jet winds at 850 hPa is partly due to its relatively smaller spatial and temporal scales compared to the CCB and WCB, but it is also likely to be underestimated given the number of timesteps on which sting jets are missed (Table 3). Furthermore, it is possible that its contribution to extreme surface gusts would be greater than at 850 hPa as it can more readily transfer momentum from aloft towards the surface than the CCB and WCB.

3.4 Comparison with GCM

The comparison between the CPM and GCM aims to highlight systematic differences that would indicate potential added-value of the CPM through better process representation. For this comparison, CPM 850 hPa wind speeds are regridded to the 25 km grid of the GCM. Hereafter, the CPM on its native grid and that regridded to the 25 km GCM grid will be referred to as CPMn and CPMr respectively. The metric \({SF}_{95}\) is then calculated for the CPMr and GCM. Compared to CPMr, the GCM underestimates the frequency of storms exceeding high values of \({SF}_{95}\) in both the control and future simulations (Fig. 7a, b). In terms of future changes, the changes are higher in the GCM than CPMr for storms with \({SF}_{95}\) < 40 ms−1 but are higher in the CPMr for storms with \({SF}_{95}\) > 40 ms−1 (Fig. 7f). The CPMn has similar or slightly higher changes than the GCM at all thresholds (Fig. 7c). Overall, the future changes in the CPM and GCM are similar which indicates that changes in \({SF}_{95}\) are dominated by large-scale changes in storms captured in the GCM that are inherited by the CPM. This is a similar finding to Leckebusch et al. (2006), though Donat et al. (2011) report differences between RCMs when driven by the same GCM, and so this result may differ depending on the RCM or CPM used. However, there is a difference in future changes of 3 storms at high thresholds (> 42 ms−1) which accounts for 33% of changes in the CPM. Over longer simulations, an accumulation of this difference may become significant if maintained, and it would be interesting to explore this as longer high-resolution climate simulations become available.

Fig. 7
figure 7

a, b Show the number of storms where \({SF}_{95}\) exceeds a range of thresholds in the CPM on its native grid (solid line) and CPMr (CPM regridded to the 25 km GCM grid—dotted line) and the GCM (dashed line), in the control and future respectively, while the future change for each simulation is provided in c. d and e show the absolute difference in \({SF}_{95}\) between CPMr and GCM storms (for CPMr storms with \({SF}_{95}\) exceeding 35 m s−1) in each of the three storm categories, in the control and future, while f shows the absolute difference in future changes between CPMr and GCM

Full size image

To compare \({SF}_{95}\) within each storm type (i.e. \(nSK\), \({SK}_{N{-}SJ}\) or \({SK}_{SJ}\)), we apply the classification obtained from CPMn that is used for results in Sect. 3.3. Hence, we do not identify the presence of a warm seclusion or sting jet on the 25 km grid, but classify a GCM storm, for instance, as \({SK}_{SJ}\) if a warm seclusion and a sting jet is identified in that given storm within CPMn output. In fact, the given storm may not have a sting jet in the GCM, due to the coarser resolution, but we have not been able to assess this as the performance of the algorithm when applied to a 25 km grid was not acceptable, indicating that the algorithm requires high-resolution input. Thus, potential added-value of the CPM in capturing the actual sting jet feature is not considered here, and instead we focus purely on the overall extreme wind distribution and any evidence of added-value in this. The distribution of absolute differences in \({SF}_{95}\) between each storm in the CPMr and GCM is presented as boxplots in Fig. 7d, e. \({SF}_{95}\) is generally higher for CPMr storms than GCM storms, and the differences seen are consistent across each storm type. However, the differences are more relevant in \({SK}_{N{-}SJ}\) and \({SK}_{SJ}\) storms as wind speeds are generally higher in these storms (Fig. 5).

Next, we look to understand the source of the \({SF}_{95}\) differences between CPMr and GCM for \({SK}_{N{-}SJ}\) and \({SK}_{SJ}\) storms. To do so, we pool all 850 hPa wind speeds that occur within 500 km of a cyclone centre for both storm types in each simulation separately. The percentage difference between CPMr and GCM is then calculated for the difference in absolute number of 850 hPa wind speed exceedances of specified thresholds (Fig. 8) within four categories: (1) all 850 hPa wind speeds within 500 km of a cyclone centre (ALL); (2) warm conveyor belt winds (WCB); (3) cold conveyor belt winds (CCB); and (4) sting jet winds (SJ). Winds are classified as WCB if they occur within the warm sector of a cyclone, identified separately in CPMr and GCM, while cold sector winds are classified as sting jet on timesteps when a sting jet was identified in the CPMn, and CCB otherwise. Thus, winds occurring at timesteps before a sting jet is detected will be assigned as CCB, even though CCB winds occur later than SJ winds in reality, though we do not expect this to detract from the results as cold sector winds at this point in the storm are unlikely to be extreme. The approach of assigning wind speeds to sting jet assumes that the stage at which a sting jet develops (between stage 3 and 4 in the Shapiro–Keyser conceptual model (Clark and Gray 2018), occurs simultaneously in the CPM and GCM, though it may not occur in the GCM at all. Storms can deviate in the CPM domain from the GCM, but qualitatively we do not observe large differences in the position of storms between GCM and CPM, and so we deem this a reasonable assumption to make. It should also be noted that CCB, which occurs after a sting jet, also account for windstimesteps occurring before a sting jet is detected are assigned as CCB.

Fig. 8
figure 8

% difference in number of grid cells exceeding 850 hPa wind speed thresholds between CPMr and GCM in \({SK}_{N{-}SJ}\) (top row) and \({SK}_{SJ}\) storms (bottom row), in the control (a, c) and future (b, d) simulations. Differences are shown for each wind type SJ (navy), CCB (blue) and WCB (red) alongside the total difference in all wind speeds together (ALL: black). Points along lines indicate differences are significantly different from zero according to a 95% uncertainty interval. The uncertainty interval is constructed via non-parametric bootstrapping in which we randomly sample storms 1000 times with replacement to create 1000 event sets. Each event set has the same number of \({SK}_{N{-}SJ}\) or \({SK}_{SJ}\) storms as detected in the control and future simulations. Within each event set, wind speeds are pooled according to SJ, CCB, WCB and all together (ALL) in the CPMr and GCM and the % differences are calculated. This provides a null distribution of % differences for each threshold, with 1000 points, from which we calculate the upper and lower bounds of the 95% uncertainty interval as the 97.5th and 2.5th percentiles

Full size image

The GCM underestimates extreme wind speeds at 850 hPa compared to the CPMr (black line in Fig. 8) in both CPM-classified \({SK}_{N{-}SJ}\) (Fig. 8a, b) and \({SK}_{SJ}\) storms (Fig. 8c, d) within the control and future simulations. These differences increase with increasing threshold, where the underestimation can be between 20 and 40% for thresholds between 35 and 45 ms−1. Many of these differences are also deemed significantly different from zero, as indicated by points along each line (see figure caption for details on the construction of the uncertainty interval). The meaning of significance in this case is an indication that the given difference is robust across the event set and is insensitive to the occurrence of single events or minor differences in the areal extent of extremes in storms. The differences between CPMr and GCM are generally higher for the control simulation, particularly for \({SK}_{SJ}\) storms (Fig. 8c). In contrast, the differences are robust for \({SK}_{N{-}SJ}\) storms in the control and future simulations (Fig. 8a, b), which have a much larger sample size.

Differences seen between CPMr and GCM are likely due to an underestimation of wind speeds related to the sting jet and CCB, as can be deduced through comparison of the relevant lines in Fig. 8 with the black line representing ALL wind speeds, particularly for \({SK}_{N{-}SJ}\) storms (Fig. 8a, b). The largest differences in \({SK}_{SJ}\) storms come from sting jet winds (Fig. 8c, d), though significant differences are not seen for the future simulation (Fig. 8d), and so this finding may not be as robust as differences seen for CCB winds in \({SK}_{N{-}SJ}\) storms. In contrast, the GCM tends to overestimate WCB winds though differences are smaller (< 20%) and only significant for lower thresholds below 35 ms−1. Overall, the results suggest that the CPM and GCM are similar in their representation of WCB winds, while the GCM largely underestimates cold sector wind speeds at 850 hPa related to the sting jet and CCB, particularly for the extremes. It is therefore likely that the CPM will provide more reliable information on potential future changes in extreme 850 hPa wind speeds, which may result in the GCM underestimating changes in frequency of the most severe windstorms as indicated by the differences in future changes in \({SF}_{95}\) > 42 ms−1 (Fig. 7f). The underestimation at 850 hPa may also lead to an underestimation in extreme surface wind gusts, though we cannot show this as wind gust output was not available from these simulations. Such an underestimation in wind gusts may have large implications if using GCM output for use in impact models, as the expected impact, or insured loss, increases with cube of the wind speed. Consequently, a small underestimation in extreme wind speeds can yield a disproportionately larger underestimation in expected impacts (Klawa and Ulbrich 2003).

4 Summary and conclusions

We have investigated wind extremes within extra-tropical windstorms using high-resolution convection-permitting model (CPM) simulations over Europe. This paper assesses the added-value of the CPM compared to a 25 km GCM and proposes a novel, low-cost, automated methodology that detects cyclones which develop warm seclusions, namely Shapiro–Keyser cyclones (using wet bulb potential temperature and MSLP) and sting jets within those cyclones (using wind speeds on different pressure levels and relative humidity).

The added value of the CPM was firstly assessed by comparing simulated surface wind gusts from the hindcast simulation with those from ERA-Interim and observations. Secondly, we looked for systematic differences between the CPM and 25 km GCM that would indicate added-value. The CPM is generally able to replicate the observed CDF of maximum wind gusts during 15 extreme windstorms from the XWS catalogue (Roberts et al. 2014), and offered an improvement compared to ERA Interim wind gusts. As wind gust output was not available for the climate simulations, we compared the CPM and GCM using 850 hPa wind speeds. The GCM underestimates the frequency of extreme winds speeds compared to the CPM, and this underestimation is largely attributed to a better representation of cold-conveyor belts (CCBs) and sting jets in the CPM. For the CCB, the CPM will capture tighter thermal and MSLP gradients close to the cyclone centre that will result in higher wind speeds. While this is also important for sting jets, the CPM can also realise the release of slantwise instabilities that accelerate a sting jet’s descent, unlike the GCM, and improve the downward transfer of momentum inside the boundary layer (Rivière et al. 2020). Consequently, we expect that a similar underestimation by the GCM would be seen for surface wind gusts.

The automated detection methodology was applied to a hindcast, control and future climate simulation. Shapiro–Keyser cyclones were found to account for the majority of extreme windstorms in each simulation, while those that develop a sting jet account for a smaller number. The method was found to be effective in detecting Shapiro–Keyser cyclones and sting jets in historical windstorms, and we have high confidence in the identification of warm seclusions. We are also confident that the algorithm used to detect sting jets is identifying events for the right reasons, though we have seen that it is prone to missing some sting jet occurrences (and in particular does not identify all the time-steps within a given storm where a sting jet is present). The low-cost advantage of the method comes with caveats in that several parameters are required with thresholds to be defined. Specific benefits and shortcomings of the method are discussed in the main text. In the future, it would be helpful to use case study simulations of known sting jets to fine tune the method and guide the selection of required output from high-resolution climate simulations. Nevertheless, here we have demonstrated that it is possible to diagnose sting jets with significantly reduced information compared to that required for more precise methods such as back-trajectory analysis (Martínez-Alvarado et al. 2014; Volonté et al. 2018; Eisenstein et al. 2020). This advantage allows for the analysis of sting jets in high-resolution climate simulations and may be valuable to forecasters (depending on performance) to help with the detection of sting jets in output from deterministic weather prediction models.

A large increase in the frequency of extreme windstorms was found in the future simulation. This is mostly accounted for by Shapiro–Keyser cyclones as well as those in which sting jets are detected. Although the 10-year simulations assessed here are relatively short, the response of the future climate simulation is similar to previous studies (Leckebusch et al. 2007; Pinto et al. 2007, 2012; Gastineau and Soden 2009; Donat et al. 2011; Zappa et al. 2013; Vautard et al. 2019), and an increase of extreme windstorms seems a robust response to anthropogenic climate change across many studies (Feser et al. 2015). However, assessments of multi-model ensembles reveal a large spread in the simulated response from different models indicating a significant role of internal variability (Donat et al. 2011; Zappa et al. 2013). While a moister, warmer environment due to anthropogenic climate change is expected to lead to more favourable conditions for sting jets (Martínez-Alvarado et al. 2018), the overall influence of anthropogenic climate change on the frequency of extreme windstorms remains uncertain and requires further investigation (Catto et al. 2019; Zappa 2019).

The CPM and GCM are similar in their future change response, although there is a hint that the GCM underestimates changes in the most extreme windstorms compared to the CPM. Overall, we can see that changes in the frequency of extreme windstorms are dominated by large-scale changes in storms captured in the GCM and inherited by the CPM. However, since the CPM provides local added detail and an improved representation of sting jets and cold conveyor belts, the projections of changes to extreme wind speeds are expected to be more reliable from the CPM. Further work is needed to confirm whether there are robust differences in future changes at convection permitting scale and this will be investigated using longer high-resolution simulations from additional CPMs (e.g. Coppola et al. 2020) when they become available.

This study has implications for stakeholders and downstream impact modellers. In particular, the improved performance of the hindcast in representing surface wind gusts indicates that the CPM will provide better input data for impact models. Indeed, Dunn et al. (2018) demonstrate an improvement in modelling wind impacts to electrical infrastructure when moving to higher resolution simulations. We expect that the GCM will underestimate surface wind gusts driven by CCBs and sting jets compared to the CPM, and importantly also their future changes. Consequently, impact models will likely require output from high-resolution simulations or bias corrected GCM output (e.g. Haas and Pinto 2012; Roberts et al. 2014). Although, for these to be reliable, large-scale features such as storm tracks must be adequately represented and the assumptions of the bias correction must be valid for future intense cyclones (Maraun et al. 2017).