Abstract
Southern hemisphere subtropical anticyclones are projected to change in a warmer climate during both austral summer and winter. A recent study of CMIP 5 & 6 projections found a combination of local diabatic heating changes and static-stability-induced changes in baroclinic eddy growth as the dominant drivers. Yet the underlying mechanisms forcing these changes still remain uninvestigated. This study aims to enhance our mechanistic understanding of what drives these Southern Hemisphere anticyclones changes during both seasons. Using an AGCM, we decompose the response to CO2-induced warming into two components: (1) the fast atmospheric response to direct CO2 radiative forcing, and (2) the slow atmospheric response due to indirect sea surface temperature warming. Additionally, we isolate the influence of tropical diabatic heating with AGCM added heating experiments. As a complement to our numerical AGCM experiments, we analyze the Atmospheric and Cloud Feedback Model Intercomparison Project experiments. Results from sensitivity experiments show that slow subtropical sea surface temperature warming primarily forces the projected changes in subtropical anticyclones through baroclinicity change. Fast CO2 atmospheric radiative forcing on the other hand plays a secondary role, with the most notable exception being the South Atlantic subtropical anticyclone in austral winter, where it opposes the forcing by sea surface temperature changes resulting in a muted net response. Lastly, we find that tropical diabatic heating changes only significantly influence Southern Hemisphere subtropical anticyclone changes through tropospheric wind shear changes during austral winter.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Subtropical Anticyclones (SA)s are semi-permanent high-pressure systems that are crucial components of the large-scale atmospheric circulation in both hemispheres. Climatologically, SAs in the Southern Hemisphere (SH) influence the hydrological cycle and precipitation in the SH subtropics and midlatitudes (Sturman and Tapper 1996; Tyson and Preston-Whyte 2000; Reboita et al. 2010). For example, recent changes in the area and strength of SH SAs have been linked to regional drought extremes (e.g. Burls et al. 2019). To understand how the weather and climate of SH subtropical and midlatitude regions will change in response to global warming, understanding how the SH SAs will respond is crucial. In this article, we use the word “change” to describe the difference between a model’s future projection (a warmer climate due to external forcings) and the respective control run (e.g. piControl, Historical) of the same climate model.
In simulations conducted by the models participating in the Coupled Model Intercomparison Project (CMIP), it is well documented that the subtropical to midlatitude atmospheric circulation is significantly affected in both hemispheres under future warming (Li et al. 2012, 2013; Shaw and Voigt 2015; He et al. 2017; Song et al. 2018a, Fahad et al. 2020) (Fig. 1a, b). The mechanisms that drive SA changes in the Northern Hemisphere (NH) have been explored in a number of studies (Li et al. 2012; Shaw and Voigt 2015, 2016; He et al. 2017; Song et al. 2018a). The SH SAs have however received less attention, with open questions surrounding our understanding of what drives the simulated changes in the SH SAs during both the austral summer and winter season.
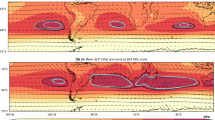
The CMIP6 MMM change, SSP585 (2050–2099)—Historical (1950–1999), in a DJF (austral summer) SLP, b JJA (austral winter) SLP, c DJF (austral summer) diabatic heating, & d JJA (austral winter) diabatic heating (SLP unit: hPa, diabatic heating units: k/day). The 1020 hPa Historical SLP isobar is contoured in black and the future projection SSP585 isobar is contoured in red. Contour plots are stippled when there is at least 75% agreement across the CMIP6 models on the sign of the SLP and diabatic heating change respectively. The CMIP6 CESM2 SSP585—Historical SST is shown for e DJF (austral summer) & f JJA (austral winter). The vertical structure of the zonal mean (15S°–15N°) heating of the CAM6 added heating experiment (CAM Q) forcing file (units: k/day) for g DJF (austral summer) & h JJA (austral winter). The CAM Q heating perturbation for the forcing file is taken from the CMIP6 CESM2 coupled run experiments (SSP585—Historical)
The SH SAs are projected to extend in the area and intensify along the poleward flank of the subtropics during both the austral summer (December–January–February or DJF) and winter (June–July–August or JJA) season (Li et al. 2013; Fahad et al. 2020). Li et al. (2013) found that all three SAs in the SH, namely the South Pacific SA (SPSA), South Atlantic SA (SASA), and South Indian SA (SISA) extend in area and strength due to increased land-sea thermal contrast due to intensified cooling over the ocean. This local diabatic heating mechanism is consistent with Wu and Liu (2003), which show a longwave, latent, and sensible heating pattern in the subtropical region drives changes in the climatological area and strength of the summertime SH SAs’.
Later, He et al. (2017) argued that changes in upper troposphere static stability have a significant influence on changes in the summertime SH SAs under global warming conditions. Using CMIP5 output He et al. (2017) analyzed changes in subsidence, low-level divergence, and rotational wind from 10°–40° S focusing on the difference between future RCP8.5 projections (years 2050–2099) and historical (years 1950–1999). He et al. (2017) found that while the SPSA increases in strength; the SASA and SISA weaken in future climate during local summer even though decreased heating over the subtropical ocean supposedly acts to intensify the SH SAs. He et al (2017) argue that increased tropical upper troposphere static stability in a future climate lead to mean advection of stratification changes (MASC) that act to decrease the strength of the SASA and SISA during local summer (Ma et al. 2012; He et al. 2017). In the case of the SPSA, the contribution from the MASC mechanism is relatively small and the local diabatic heating decreases primarily acts to increase the SPSA’s strength in future climate. Using a linear baroclinic model, He et al. (2017) show that the changes in SH SAs are consistent with prescribed changes in the heating and tropospheric static stability. The inconsistency of the austral summer SASA and SISA change in future climate between Li et al. (2013) and He et al. (2017) is due to the choice of domains to define the SH SAs. Li et al. (2013) defined the centers of the SAs as where the 925 hPa stream function is at a maximum over the subtropical Ocean, whereas He et al. (2017) regionally averaged between 10° and 40° S, this latter definition focuses largely over the equatorward flank of the SAs where the MASC mechanism has a larger effect.
Analyzing the CMIP5 and CMIP6 models, Fahad et al. (2020) show that Sea Level Pressure (SLP) and 925 hPa wind associated with SAs intensifies in the center and along the poleward flank in the SH comparing historical (years 1950–1999) to future projections (RCP8.5 for CMIP5 and SSP585 for CMIP6) (years 2050–2099). Fahad et al. (2020) defined the 1020 hPa isobar area as the center of the SH SAs, and 25°–45° S as the latitudinal extent of the domain for the austral summer (DJF), and 20–40° S as the latitude domain for the austral winter (JJA). Findings of SH SAs change in the future climate compared to the historical multi-model mean (MMM) are consistent between Li et al. (2013) and Fahad et al. (2020) for austral summer. However, Fahad et al. (2020) show that reduced baroclinic eddy growth in the future climate acts to intensify SAs along their poleward flank in both seasons. Potential temperature changes affecting atmospheric stability and wind shear change via the westerly wind jet can influence the subtropical SLP associated with anticyclones through baroclinicity change (Lu et al. 2008; Fahad et al. 2020; Zhou et al. 2021). The metric for the Philipps criterion (Phillips 1954) can be decomposed into the changes in baroclinic instability due to static stability changes and wind shear changes respectively. Static stability increases, as a result of potential temperature increase in the upper troposphere, act to reduce baroclinic eddy growth by creating a more stable atmosphere. Whereas increased wind shear is associated with a more unstable atmosphere acting to intensify baroclinic eddy growth and low-pressure systems (Fahad et al. 2020; Lu et al. 2008). Fahad et al. (2020) found that a decrease in the Phillips criterion metric, and hence the conditions promoting the baroclinic eddy growth, was strongly correlated with static stability changes across the CMIP5 and CMIP6 multi-model ensemble.
The climatological influence of the tropical diabatic heating, especially heating over the Inter Tropical Convergence Zone (ITCZ) and the South Pacific convergence zone (SPCZ) on SAs in both hemispheres are documented in several studies (Hoskins 1996; Chen et al. 2001; Nigam and Chan 2009; Fahad et al. 2021). Tandon et al. (2013) applied thermal forcings in different latitude from tropics to midlatitude to investigate how different regions of heating influence Hadley expansion and the largescale circulation of midlatitude. Future changes in NH SAs are reported by Song et al. (2018a, b) to be related to the change in the tropical precipitation (and latent heating) resulting from a delay in the boreal spring to summer seasonal cycle of tropical rainfall and heating under global warming conditions. Changes in the onset of the rainfall band over the tropical ocean affect the Hadley circulation in the NH leading to a change in the zonal mean component of NH SAs (Song et al. 2018a, b. With the exception of the MASC mechanism (Ma et al. 2012; He et al. 2017), the influence of tropical diabatic heating changes under global warming conditions on SH SAs has received much less attention compared to their NH counterparts.
Focusing on the midlatitude atmospheric circulation, several studies have investigated the relative importance of the fast atmospheric response due to the direct radiative forcing component of CO2 versus the slower atmospheric response due to the indirect forcing component related to the patterns of Sea Surface Temperature (SST) warming (Shaw 2014; Simpson et al. 2014; Grise and Polvani 2014; Staten et. al. 2018; Shaw and Voigt 2015). For the summertime NH atmospheric circulation change in a warming climate, Shaw and Voigt (2015) show that the North Pacific SA responses to an increase in the direct radiative forcing from the elevated atmospheric CO2 concentrations oppose those from the indirect SST warming. Using an atmospheric general circulation model forced with prescribed SSTs, Shaw and Voigt (2015) found the North Pacific SA increases in strength during boreal summer due to increased direct radiative forcing, however, this weakens in strength due to the SST warming patterns. In coupled model simulations these opposing responses to direct radiative forcing and indirect SST warming lead to a small net change of the North Pacific SA’s strength under future warming. There is also a similar tug-of-war response between these two forcings found on upper troposphere atmospheric circulation in the North Pacific (Shaw and Voigt 2015). Song et al. (2018a, b) show that the boreal spring North Pacific SA response to global warming is dominated by indirect SST warming more than in boreal summer.
As with the influence of tropical diabatic heating, the response of the SH SAs to direct CO2 radiative forcing (fast atmospheric forcing), and indirect SST warming (slow oceanic forcing) has received much less attention compared to their NH counterparts. This study aims to determine which of these two forcings primarily drives changes in the SH SAs. Using the Community Earth System Model version 2 (CESM2) coupled ocean–atmosphere experiments from CMIP6, and prescribed SST Community Atmospheric Model 6 (CAM6) numerical experiments, we explore how the direct CO2 radiative forcing versus indirect SST warming patterns drive the SH SAs during both austral summer and winter. We further investigate the relative contribution of these two forcing mechanisms to future changes in tropical diabatic heating and how changes in the tropical diabatic heating alone act as a remote forcing on the SH SAs. The sections of this study are structured as follows: Sect. 2 describes the experimental design, numerical model configurations, and data analyzed from different experiments. Results from the analysis are presented in Sect. 3. Finally, in Sect. 4, the discussion and conclusions from the results are documented.
2 Methodology
In this study, we both analyze climate simulations performed as part of CMIP6 and perform a suit numerical experiments using CAM6 with prescribed climatological SST and sea-ice component sets (model compset F2000climo). A list of numerical experiments performed and/or analyzed in this study is presented in Table 1. CAM6 is the atmospheric component of CESM2.0 (Danabasoglu et al. 2020). A 1.9° × 2.5° model resolution is used for the active atmosphere (CAM6) and land (CLM5) components, with data ocean and sea ice components. 30 ensemble members of a one-year control run (CAM Control) are carried out with prescribed climatological SST and sea-ice cover derived from a 50-year mean of the CMIP6 CESM2 Historical simulation (years 1950–1999) (i.e. every ensemble member was forced with this climatological mean SST). Every year of this 30-member ensemble is initialized with a random selection of January 1st initial conditions taken from a previously spun-up CESM2 Historical simulation. Details on the natural and external forcing used to force the CMIP6 CESM2 Historical simulation are documented in Eyring et al. (2016).
To isolate the influence of the SST changes in a future warm climate, a 30-ensemble-member, prescribed-SST run (CAM SST) is performed using a 50-year climatological mean SST from the CESM2 SSP585 experiment (years 2050–2099). The SSP585 experiment in CMIP6 is forced with the high radiative forcing projections for the end of the century (Matthes et al. 2017). The ensemble members of the CAM SST experiment are initialized using initial conditions from the CAM Control experiment for both DJF (initialized on November 01 of that year and run until February of the next year) and JJA (initialized on May 01 of that year and run until the end of August). Similarly, a 30-ensemble-member, increased CO2 concentration experiment (CAM CO2) is done with the same boundary conditions as CAM Control except for the CO2 concentration. In the CAM CO2 experiment, the CO2 is increased from the CAM Control run value of 370–740 ppm. This CO2 concentration increase is equivalent to an approximate average of the CESM2 SSP585 CO2 concentration for the years 2050–2090 compared to the years 1950–1999 of the CESM2 Historical simulation (Matthes et al. 2017). Finally, the CAM SSTCO2 experiment is done in which the CO2 concentration is increased (global mean ~ 740 ppm) with prescribed SSP585 climatological SST (years 2050–2099). The purpose of the CAM SSTCO2 experiment is to investigate the response of SH SAs to the combined CO2 and SST forcing. The one-year, 30-ensemble-member approach is taken so that it is consistent with the design required for the diabatic heating experiments (as described in the next paragraph), as well as limit the influence of slow surface heating within the land component. To assess the influence of temporal adjustment on the SLP response within the respective experiments, the CAM SST, CAM CO2, and CAM SSTCO2 experiments have also alternatively been done as continuous 30-years simulations instead of a series of one-year branch the results of which are shown in the supplementary information and briefly discussed in the final section as a point of comparison.
To isolate the influence of tropical diabatic heating, a 30-ensemble member set of branched tropical added heating experiments (CAM Q) are run with the prescribed climatological SST and sea-ice cover derived from a 50-year mean of the CMIP6 CESM2 Historical simulation (years 1950–1999) (Fig. 1e, f). The CAM Q ensemble members are initialized using initial conditions from the CAM Control experiment for both DJF (initialized on November 01 of that year and run until February of the next year) and JJA (initialized on May 01 of that year and run until the end of August). Heating is only added over the tropical oceans between 15° S and 15° N, where diabatic heating changes in the future are significant (Fig. 1c, d), with a Gaussian decay applied at the edges of this domain. The added heating technique is similar to that of Swenson et al. (2019) and Fahad et al. (2021). The added heating experiments (CAM Q) are performed using an iterative process to identify the amount of added heating that needs to be imposed in order to reproduce the diabatic heating difference between the SSP585 (years 2050–2099) and the Historical (years 1950–1999) CESM2 CMIP6 simulations. 20% of the tropical diabatic heating difference between SSP585 and the Historical CESM2 CMIP6 simulations is added iteratively until the 1-year 30-ensemble-member climatological mean across the branched CAM Q experiments minus the 1-year 30-ensemble-member climatological mean across the branched CAM Control experiments converges toward a field similar to that seen between the SSP585 (years 2050–2099)—Historical (years 1950–1999) coupled experiments. The iteration of added heating run CAM Q is done 6 times for both DJF and JJA for every year starting from CAM Control initial conditions. The final iteration of the run was used for the analysis where the diabatic heating of CAM Q converged to the solution so that the difference between CAM Q—CAM Control is similar to the CMIP6 CESM2 SSP585—Historical simulation. The vertical structure of the added heating in the experiment CAM Q is shown in Fig. 1g, h. The vertical mean spatial structure of the heating is the difference between CESM2 SSP585 (years 2050–2099) and Historical (years 1950–1999) simulations (Figs. 4b & 9b).
As a complement to our CAM6 model simulations, we analyze sets of CESM2 experiments that form part of two CMIP6 projects: the Cloud Feedback Model Intercomparison Project (CFMIP) (Webb et al. 2017) and the Atmospheric Model Intercomparison Project (AMIP) (Gates et al. 1999), see Table 1. From CFMIP, experiment PiSST is compared with the experiment piSST4xCO2, A4SST, and Abrupt4XCO2. The piSST experiment is a 30-year AGCM run with monthly varying SST, sea-ice, and atmospheric constituents taken from the CMIP6 piControl experiment. The 30 years chosen from the piControl are parallel to the Abrupt4XCO2 experiment’s years 111–140. The piSST4xCO2 experiment is the same as piSST except for the CO2 concentration is quadrupled compared to the piSST. The A4SST experiment is the same as piSST, except for SST is taken from the coupled CMIP6 Abrupt4XCO2 experiments (years 111–140 monthly varying SST output). Finally, 30 years (years 111–140) of the Abrupt4XCO2 CMIP6 experiment are analyzed to compare with these experiments. The AMIP experiments are forced by time-varying observed SST and sea ice concentration with present-day atmospheric composition for the years 1979–2014. For this study 30 years of AMIP data are analyzed (years 1979–2008). The AMIP4xCO2 experiment is the same as AMIP, except for CO2 concentration is quadrupled. Similarly, the AMIP4k experiment is the same as AMIP except for increased SST warming 4 kelvins uniformly everywhere. The list of CMIP6 models used in the analysis is shown in the supplementary Table S1.
The CESM2 total diabatic heating is taken directly from the model’s output. Additionally, the vertically integrated diabatic heating is calculated as a sum of net radiation going into the atmospheric column, latent heating, and sensible heating similar to Fahad et al. (2020) to compare it with the model output.
The Phillips criterion metric (C) (1954) is used to evaluate the conditions promoting baroclinic eddy growth, defined as in Lu et al. (2008) and Fahad et al. (2020):
The Phillips criterion C increases with increased baroclinic eddy growth. Here H is the geometric height of the column—lower level (the average between 850 and 1000 hPa) to 500 hPa, \(\Theta\) is reference potential temperature. Similar to Lu et al. (2008) and Fahad et al. (2020), the criterion changes are decomposed into changes due to static stability (Cs) and zonal wind shear (Cw) as:
Here δ is the difference between future warmed climate projection and control simulation. The subscript h represents the historical climate. Here the vertical level 850 hPa and 500 hPa are chosen as baroclinic eddy growth is primarily influenced by the lower tropospheric baroclinicity (Held and O’Brien 1992).
3 Results
3.1 Projected changes in the southern hemisphere subtropical anticyclone’s during Austral summer
The CMIP6 MMM SLP change (SSP585—Historical) during austral summer (DJF) shows an increase in the center and along the poleward flanks of the SH SAs (Fig. 1a). The area of each SA’s center is defined as the area where SLP is ≥ the 1020 hPa isobar increases and extends toward the pole in the future climate SSP585 (years 2050–2099) compared to Historical (years 1950–1999) simulation. The SLP change (SSP585—Historical) in CESM2 coupled model run is largely similar to the CMIP6 MMM (Fig. 2b).
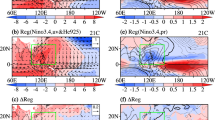
CAM6 numerical experiments. DJF (austral summer) mean SLP (unit: hPa) climatological mean of a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, (e) Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. The 1023 hPa Control SLP isobar is contoured in black and the future projection isobar is contoured in red (CMIP6 CESM2 SSP585 is in red contoured in b, and corresponding future forcing projection is contoured in red for c–f). Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample
The vertically averaged (1000 hPa–200 hPa) diabatic heating increases in the tropics in both the CMIP6 MMM and CESM2, especially over the tropical Pacific (Figs. 1c and 3b). The total diabatic heating increase in the tropical Pacific Ocean is ~ 0.6 k/day in the CMIP6 MMM, and ~ 1.0 k/day in the CESM2 during austral summer in the SSP585 scenario compared to the Historical experiment. A cooling zone (~ − 0.5 K/day) is also present near the subtropics of both hemispheres (near 10° N and 10° S, 120° W) in the SSP585 scenario compared to the Historical experiment.
CAM6 numerical experiments. DJF (austral summer) mean diabatic heating (unit: k/day) climatological mean for a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample
The results from the CAM6 sensitivity experiments indicate that the SST change in the coupled SSP585 experiment is the dominant forcing that drives the SH austral summer SLP change in the subtropics and midlatitudes (Fig. 2). The SLP changes associated with the SPSA and SISA in the coupled CESM2 SSP585—Historical experiment (Fig. 2b) are largely reproduced in the CAM SST experiment forced only by SSP585 SST (Fig. 2d). In contrast, direct radiative forcing by CO2 increase appears to be a secondary influence on the SPSA and SISA SLP changes during DJF (Fig. 2e). For the SASA on the other hand, CO2 forcing appears to be primarily responsible for the increase in SLP along its poleward flank (Fig. 2e). Both mechanisms combined (Fig. 2f) largely reproduce the SLP changes seen within the coupled simulation (Fig. 2b). In order to gain further insight into the mechanisms driving the SLP changes in CAM SST and CO2 experiments, we will now turn to (1) the CAMQ experiment as it isolates the role of tropical diabatic heating and (2) an assessment of the conditions that promote baroclinic instability.
The CAM6 experiment forced only by SSP585 SST captures the tropical heating change (CAM SST—CAM Control) seen in the CESM2 SSP585 coupled run (CESM2 SSP585—Historical), indicating that the tropical diabatic heating change seen in the SSP585 CESM2 coupled run is primarily forced by the SST change rather than direct radiative forcing (Fig. 3b–d). However, the diabatic heating sensitivity experiment (CAM Q) reveals that a remote response of the SH SA to tropical heating changes does not appear to be the dominant mechanism responsible for the increase in SH subtropical SLP during local summer (Fig. 2c). The prescribed tropical diabatic heating in the CAM Q experiment (Fig. 3c) warms the upper troposphere and increases atmospheric static stability in the tropics (Fig. 5c) but this does not lead to a strengthening of the SH SAs, if anything the SH SAs decrease in this experiment, specifically the SPSA (Fig. 2c). He et al. (2017) attributes the reduced DJF SLP seen along the equatorward flanks of SH SAs in global warming experiments to the zonal-mean increase in tropical static stability via the “positive mean advection of stratification change (MASC)” mechanism of Ma et al. (2012). We speculate that this mechanism is responsible for the weakening of the SH SAs in the CAM Q experiment. Our experiments indicate that it is the absence of SST changes in the CAM Q experiment that limits subtropical and mid-latitude static stability changes (Figs. 5 and S1), and as discussed in the following paragraph, it is increased subtropical and mid-latitude static stability in the CAM SST experiment that leads to increased subtropical and midlatitude SLP by reducing the condition that promote baroclinic eddy growth (Lu et al. 2008).
The Phillips criterion metric for baroclinic eddy growth (C) decreases in the center, and poleward flank of the SH SAs in the CESM2 coupled run (Fig. 4b). This decrease indicates more stable atmospheric conditions through tropospheric potential temperature changes (Fig. 5b), suppressing baroclinic instability and increasing SLP in the center, and poleward flank of the SH SAs (Fig. 2b). When considering the decomposition of the Phillips criterion metric into the relative contribution of static stability changes, Cs, (Fig. S1) and zonal wind shear changes, Cw, (Fig. S2) both contribute to the more stable conditions along the poleward flanks via increased subtropical and midlatitude static stability (Fig. 5) and a poleward shift in the midlatitude jet (Fig. S3), respectively. Prescribed SSP585 SST is the dominant driver of this suppressed eddy growth, specifically for the poleward flanks of the SPSA and SISA (Fig. 4d), with both static stability and wind shear changes making important contributions (Figs. S1 vs S2). Whereas suppressed eddy growth in response to direct CO2 radiative forcing plays the dominant role along the poleward flank of the SASA (Fig. 4e), with the eddy growth changes in this experiment largely driven by wind shear changes associated with a poleward shift in the westerly wind jet (Figs. S1 vs S2 and S3).
CAM6 numerical experiments. DJF (austral summer) climatological mean of the Phillips Criterion metric C for a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e increased CO2 (CAM CO2)—CAM Control, and f increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from the 30-year sample. The 1023 hPa Control SLP isobar is contoured in black and the future projection isobar is contoured in red (CMIP6 CESM2 SSP585 is in red contoured in b, and corresponding future forcing projection is contoured in red for c–f). Negative C values indicate a reduction in the conditions supporting baroclinic eddy grow, which in turn supports high SLP
CAM6 numerical experiments. DJF (austral summer) mean potential temperature (unit: Kelvin) climatological mean of a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample
Once again when comparing the CAM Q (Fig. 4c) and CAM SST (Fig. 4d) we see that tropical diabatic heating alone cannot explain the subtropical to midlatitude reduction in the conditions that promote baroclinic eddy growth. This comparison points to a role for SST changes outside of the tropics in giving rise to the Cw changes (Fig. S2b vs c), and in particular, the large potential temperature changes and Cs changes (Figs. 5c vs d & S1b vs c), seen along the poleward flank of the SAs within the CAM SST experiment when compared to the CAM Q experiment. Similarly, these SST changes give rise to a much large reduction in midlatitude baroclinicity through static stability change (potential temperature change) in CAM SST than CAM CO2 (Figs. 4d vs e, S1c vs S1d) that in turn leads to a larger reduction in C along the poleward flank of the SPSA and SISA. Consistent with the SLP change, the DJF baroclinic eddy growth change associated with SH SAs is well simulated in the CAM6 experiments when forced with both CO2 concentration increase and SSP585 SST warming (Fig. 4f).
Results from the CFMIP and AMIP experiments conducted using CESM2/CAM6 paint a consistent picture. The CFMIP Abrupt4XCO2—piSST shows SH subtropical SLP changes and tropical diabatic heating changes that are similar to those seen in CESM2 SSP585—Historical but intensified (Figs. 2b vs 6b, and 3b vs 6f). SST acts as the primary driver of these SH DJF SA SLP and tropical diabatic heating changes (Fig. 6c, g), whereas the CO2 increase acts as a secondary forcing during austral summer (Fig. 6d, h). We likewise see that SST acts as the primary driver of DJF SH SA SLP and tropical diabatic heating changes in the AMIP experiments (Fig. S4). Due however to the fact that the SST forcing in AMIP4k is increased uniformly by 4 Kelvin the SLP and tropical diabatic heating changes in the AMIP4k—AMIP are not as representative of the full (Abrupt 4xCO2-AMIP) diabatic heating change as seen in the other sets of experiments (e.g. CAM SST—CAM Control in representing SSP585-Historical, and CFMIP A4SST—piSST in representing Abrupt4xCO2—piSST). This is due to the fact that the uniform SST warming does not capture the influence of warming patterns on the atmospheric circulation changes. In contrast, the CAM SST and A4SST numerical experiments have prescribed the full SST field from their respective global warming scenario experiment.
CFMIP CESM2 DJF (austral summer) 30-year mean of SLP (unit: hPa) for a Pi Control (piSST), b Abrupt4XCO2—piSST, c PiCO2 with Abrupt SST (A4SST)—piSST, d piSST with 4XCO2 (piSST4XCO2)—piSST, and diabatic heating SLP (unit: k/day) for a Pi Control (piSST), b Abrupt4XCO2—piSST, c Pi with Abrupt SST (A4SST)—piSST, d piSST with 4XCO2 (piSST4XCO2)—piSST. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample. The 1023 hPa Control SLP isobar is contoured in black and the future projection isobar is contoured in red
3.2 Projected changes in the southern hemisphere subtropical anticyclone’s during austral winter
During austral winter (JJA) the projected SSP585 (2050–2099)—Historical (1950–1999) SH subtropical SLP changes in the CMIP6 MMM and CESM2 coupled model runs are the most intense over the South Pacific and South Indian Oceans (Figs. 1b and 7b). One evident difference between these two is that the SASA SLP doesn’t change significantly in the CESM2 coupled model run, whereas the SASA SLP increases to some extent in the CMIP6 MMM. The pattern of vertically averaged (1000–200 hPa) diabatic heating change in the SSP585 over the tropics is broadly similar between the CMIP6 MMM, and the CESM2 coupled run, only more intensified in CESM2 (Figs. 1d and 8b).
CAM6 numerical experiments. JJA (austral winter) mean SLP (unit: hPa) climatological mean of a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. The 1023 hPa Control SLP isobar is contoured in black and the future projection isobar is contoured in red (CMIP6 CESM2 SSP585 is in red contoured in b, and corresponding future forcing projection is contoured in red for c–f). Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample
CAM6 numerical experiments. JJA (austral winter) mean diabatic heating (unit: k/day) climatological mean of a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample
The vertically averaged JJA diabatic heating primarily increases over the tropical Pacific Ocean and decreases near the eastern tropical Pacific Ocean and eastern tropical Indian Ocean in future warmed climates. The total diabatic heating increase in the tropical Pacific Ocean is ~ 1.0 K/day in the CMIP6 MMM and ~ 1.3 K/day in the CESM2. The cooling over the eastern Pacific Ocean (near 10° N, 90° W) is ~ − 1.0 K/day in the CMIP6 MMM ~ -– 1.3 K/day in the CESM2 in the SSP585 scenario compared to the Historical experiment.
The CAM6 sensitivity experiment forced with SSP585 SST simulates SLP changes (CAM SST—CAM Control) over the subtropical South Indian Ocean and Southwestern Pacific Ocean that are similar to those seen in the CESM2 (SSP585—Historical) coupled run (Fig. 7b, d). There are some key differences between these two runs in the South Indian Ocean where maximum SLP changes are centered around Southern Africa in CAM SST—Control (Fig. 7d), while the maximum SLP changes are centered near Australia in SSP585—Historical (Fig. 7b). The major differences between these runs occur in the Eastern South Pacific and South Atlantic where they show roughly the opposite response (Fig. 7b, d). The center of the SPSA increases in strength in the SSP585 CESM2, whereas it decreases in the CAM6 sensitivity experiment forced with only SSP585 SST (CAM SST—CAM Control).
The direct CO2 radiative forcing plays a secondary role in the SH subtropical SLP change associated with SAs in the austral winter similar to austral summer (Fig. 7e). There are no significant changes in the area of SH SAs due to only the CO2 increase. However, the intensity of SISA increases in the south-western flank, the SPSA intensifies (particularly in the western flank), and SASA intensifies in the far south-western flank, whereas the SASA weakens over the south-eastern flank (Fig. 7e). Interestingly, a combination of both CO2 increases and SSP585 SST forcing simulates an SPSA SLP increase in austral winter similar to the CESM2 coupled model run (Fig. 7f, b).
Similar to austral summer, the tropical diabatic heating change in the austral winter is largely forced by the tropical SST change (Fig. 8b–d). Unlike in DJF, the CAM6 numerical experiment forced only by tropical diabatic heating changes (CAM Q) produces SH subtropical SLP changes similar to the CAM6 experiment forced by SSP585 SST (CAM SST) (Fig. 7c, d). This result points out that remote tropical diabatic heating plays a more prominent role in the SH subtropical SLP response during austral winter. Evaluating the Phillips criterion metric for the CAM Q experiment (Fig. 9c) demonstrates that baroclinicity changes are associated with these SLP changes, which are in turn predominantly due to wind shear changes (Fig. S6b vs S5b). These wind shear changes are due to a poleward jet shift in response to the tropical heating (Fig. S7). We reiterate however that the tropical diabatic heating change is in turn largely forced by the tropical SST change (Fig. 8b, d) and hence the similarities between the CAM Q and CAM SST experiments for JJA.
CAM6 numerical experiments. JJA (austral winter) climatological mean of Phillips Criterion metric C of a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample. The 1023 hPa Control SLP isobar is contoured in black and the future projection isobar is contoured in red (CMIP6 CESM2 SSP585 is in red contoured in b, and corresponding future forcing projection is contoured in red for c–f)
CO2 also drives a poleward jet shift reducing subtropical baroclinic eddy growth. Therefore, the combined forced run (CAM SSTCO2) with a tropical diabatic heating increase due to tropical SST increase and a CO2 increase captures a response in the SISA and SASA that is most similar to the coupled CESM2 run (Fig. 7).
The added heating experiment (CAM Q) shows no substantial potential temperature change (static stability change) in the SH subtropics due to this increase in tropical diabatic heating (Figs. S5b, 10c). However, the JJA added heating experiment (CAM Q) shows much more muted, poleward-shifted, and zonally asymmetric Phillips Criterion changes due to static stability changes (Fig. S4b). While the Phillips Criterion changes due to static stability changes in the SST experiment (CAM SST) have more of a subtropical and midlatitude signature and are negative throughout (Fig. S4c). This result implies that the subtropical baroclinic eddy growth changes due to static stability changes in the fully coupled SSP585-Historical (Fig. S4a) are primarily due to SH forced tropospheric warming and static stability changes in response to the SST warming patterns (Figs. 7d, S5c, and 10d), as opposed to static stability changes forced by tropical upper tropospheric diabatic heating (Figs. 7c, S5b, and 10c). As noted above, tropical diabatic heating (Fig. 8c), due to tropical SST changes (Fig. 8d, noting its similarity with Fig. 8c), does however act as a remote forcing on baroclinic eddy growth but primarily by influencing the zonal wind shear (Figs. 9, S6, and S7).
CAM6 numerical experiments. DJF (austral summer) mean potential temperature (unit: Kelvin) of a CAM Control, b CESM2 SSP585—Historical, c tropical added heating (CAM Q)—CAM Control, d prescribed SSP585 SST (CAM SST)—CAM Control, e Increased CO2 (CAM CO2)—CAM Control, and f Increased CO2 with prescribed SSP585 SST (CAM SSTCO2)—CAM Control. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample
Results from the CFMIP and AMIP experiments broadly show a similar response of SH subtropical SLP change due to direct CO2 radiative forcing and indirect SST warming (Figs. 11 and S8). However, the opposite response of the SASA SLP change due to these two forcings is more robust in the CFMIP and AMIP experiments. The indirect SST warming forces the SASA SLP to decrease, whereas the direct CO2 radiative forcing acts to increase the SASA SLP. This tug of war response between these two forcings is similar to the response of North Pacific SA change during boreal summer in a warming climate (Shaw and Voigt 2015). This is potentially due to a remote connection between Asian boreal summer (JJA) monsoon heating and the strength of the SASA during austral winter (JJA) (Richter et al. 2008). The direct CO2 radiative forcing increases diabatic heating over the Asian monsoon and intensifies SASA SLP during JJA during JJA (austral winter) (Fig. 11d, h). In contrast, indirect SST warming decreases diabatic heating over the Asian monsoon and weakens the SASA due to indirect SST warming (Fig. 11c, g). The opposing responses of the Asian monsoon to these two forcings are consistent with the findings of Shaw and Voigt (2015).
CFMIP CESM2 JJA (austral winter) 30 years mean of SLP (unit: hPa) for a Pi Control (piSST), b Abrupt4XCO2—piSST, c Pi with Abrupt SST (A4SST)—piSST, d piSST with 4XCO2 (piSST4XCO2)—piSST, and diabatic heating SLP (unit: k/day) for a Pi Control (piSST), b Abrupt4XCO2—piSST, c Pi with Abrupt SST (A4SST)—piSST, d piSST with 4XCO2 (piSST4XCO2)—piSST. Figures are stippled at 95% significance computed using a difference of means 2-sided t-test from 30 years sample. The 1023 hPa Control SLP isobar is contoured in black and the future projection isobar is contoured in red
Contrasting the CFMIP and AMIP experiments indicates the importance of the patterns of SST warming and the associated changes in tropical diabatic heating on the SH SLP change during austral winter. In the CFMIP experiments, the tropical diabatic heating increases similar to CESM2 coupled model runs (SSP585—Historical) forced by SST warming (Fig. 11). However, in the AMIP experiments, the SST warming is uniformly 4 Kelvin added and has a weak tropical diabatic heating change (Supplementary Fig. S8). As a result, the SH SLP response due to only SST forcings is different in the austral winter between CFMIP and AMIP experiments (Supplementary Fig. S8). For example, the SASA decreases in strength in the CFMIP prescribed SST experiment, whereas, there is an increase in SASA SLP in the AMIP 4 K warming experiment (Fig. 11c and S8c). There is also a significant SPSA SLP increase in the CFMIP compared to AMIP in the forced SST run.
4 Conclusions and discussion
This study aims to understand the mechanisms that drive changes in the SH SAs under global warming, focusing on both the austral summer and winter seasons. The influence of direct radiative forcing due to increased atmospheric CO2 concentrations and indirect SST warming as a result of feedbacks is analyzed separately through CAM6 sensitivity experiments. Moreover, to study the remote influence of tropical diabatic heating changes in the future climate, we have performed a set of CAM6 added heating experiments forced with a tropical heating change similar to that within the couple CESM2 projection (SSP585—Historical). As a complement to our CAM6 experiments, a set of CESM2 experiments performed as part of the CMIP6 CFMIP and AMIP runs have been analyzed.
The key findings are summarized as follows:
-
(1)
Indirect SST warming in the future climate (years 2050–2099) is the dominant forcing driving SH subtropical SLP changes during both the austral summer and winter seasons. During both seasons the warming pattern leads to more stable atmospheric conditions through enhanced upper tropospheric warming, suppressing baroclinic instability and increasing SLP in the center, and poleward flank of the SH SAs. Both increased static stability and reduced zonal wind shear associated with a poleward shift in the westerly jet contribute to the suppression of baroclinic instability in the center, and poleward flank of the SH SAs.
-
(2)
Indirect SST warming is also the dominant forcing driving increased tropical diabatic heating. During austral summer this tropical heating alone has a limited impact on the static stability, wind shear and hence baroclinicity of the subtropical to midlatitude atmosphere therefore playing a limited role in driving SH SA changes. During austral winter tropical heating contributes to SH SA changes via its impact on the westerly jet, zonal wind shear and hence baroclinic instability. This result is consistent with the previous studies that show climatologically tropical diabatic heating during austral winter influences the SH SAs, westerly jet streams, and storm tracks (Yand and Webster 1990a, b).
-
(3)
The direct radiative forcing from increasing CO2 plays a secondary role in the SH subtropical SLP change during both seasons. Exceptions to this are the future SPSA SLP change in austral summer and SASA SLP change in austral winter where the response to direct CO2 radiative forcing plays a key role as summarized in summary paragraphs 4 & 5 below. The increased CO2 in the troposphere primarily forces a poleward shift in the westerly jet, with zonal wind stress changes that in turn forces decreased baroclinic eddy growth in the subtropical region associated with SH SAs.
-
(4)
A combination of direct radiative forcing due to CO2 increase and indirect SST warming acts as forcing to increase the austral summer (DJF) SLP associated with the SPSA. The role of direct CO2 radiative forcing and indirect SST warming found in this study is generally consistent with Grise and Polvani (2014), who show that direct CO2 radiative forcing acts as a secondary forcing to influence the SH jet streams in a warming climate.
-
(5)
In austral winter (JJA) the response of the SASA to the direct radiative CO2 forcing is the opposite of its response to indirect SST warming. Indirect SST warming acts to decrease the strength of the SASA, whereas CO2 radiative forcing acts to increase the strength of the SASA. This is due to the opposing response of Asian monsoon diabatic heating, and the resulting low-level circulation, to direct CO2 radiative forcing and indirect SST warming during JJA. As a result of this “tug of war”, the SASA net SLP change (SSP585—Historical) in the CESM2 coupled model runs, and CMIP6 MMM is very small compared to the other two SH subtropical oceans during austral winter (JJA). A similar tug of war phenomena between these two forcings is also reported for the boreal summer (JJA) North Pacific SA in previous studies (Shaw and Voigt 2015).
As mentioned in the Methods Section, as an alternative to the short seasonal runs the CAM SST, CAM CO2, and CAM SSTCO2 experiments have also been performed as continuous 30-year-long runs with fixed climatological prescribed SST for every year. The results from these runs are consistent with the short seasonal runs (Supplementary Figs. S9, S10, S11, & S12). Furthermore, the prescribed SST and CO2 experiments from CFMIP and AMIP projects cross-validate our short CAM6 numerical simulations forced with prescribed variable climatological SST and CO2 forcings.
In conclusion, SAs are key elements of largescale atmospheric circulation in both hemispheres. SH SAs are projected to increase in the area and strength in future warmed climates during both seasons. The indirect SST warming in the future is the dominant mechanism that drives the baroclinic eddy growth reduction in the SH subtropics and leads to an increase of SLP associated with SH SAs. Tropical diabatic heating increases mostly over the tropical Pacific Ocean driven by tropical SST warming during both seasons. The tropical diabatic heating increase has a significant influence on SH SAs during austral winter. The direct radiative forcing due to CO2 increase plays a secondary role to influence SH SAs during both seasons.
Availability of data and material
CMIP6 data are available online (https://esgf-node.llnl.gov/projects/cmip6/). CESM2 CAM6 experiments data will be available upon request.
Code availability
Codes will be available upon request.
References
Burls NJ, Blamey RC, Cash BA et al (2019) The Cape Town “Day Zero” drought and Hadley cell expansion. Npj Clim Atmos Sci 2:27. https://doi.org/10.1038/s41612-019-0084-6
Chen P, Hoerling MP, Dole RM (2001) The origin of the subtropical anticyclones. J Atmos Sci 58:1827–1835. https://doi.org/10.1175/1520-0469(2001)058%3c1827:TOOTSA%3e2.0.CO;2
Danabasoglu G, Lamarque J-F, Bacmeister J et al (2020) The community earth system model version 2 (CESM2). J Adv Model Earth Syst. https://doi.org/10.1029/2019MS001916
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci Model Dev 9(5):1937–1958
Fahad AA, Burls NJ, Strasberg Z (2020) How will southern hemisphere subtropical anticyclones respond to global warming? Mechanisms and seasonality in CMIP5 and CMIP6 model projections. Clim Dyn 55:703–718. https://doi.org/10.1007/s00382-020-05290-7
Fahad AA, Burls NJ, Swenson ET, Straus DM (2021) The influence of south pacific convergence zone heating on the South Pacific Subtropical Anticyclone. J Clim 34(10):3787–3798. https://doi.org/10.1175/JCLI-D-20-0509.1
Gates WL, Boyle JS, Covey C, Dease CG, Doutriaux CM, Drach RS, Fiorino M, Gleckler PJ, Hnilo JJ, Marlais SM, Phillips TJ (1999) An overview of the results of the atmospheric model intercomparison project (AMIP I). Bull Am Meteorol Soc 80(1):29–56
Grise KM, Polvani LM (2014) The response of midlatitude jets to increased CO 2: Distinguishing the roles of sea surface temperature and direct radiative forcing. Geophys Res Lett 41:6863–6871. https://doi.org/10.1002/2014GL061638
He C, Wu B, Zou L, Zhou T (2017) Responses of the summertime subtropical anticyclones to global warming. J Clim 30:6465–6479. https://doi.org/10.1175/JCLI-D-16-0529.1
Held IM, O’Brien E (1992) Quasigeostrophic turbulence in a three-layer model: effects of vertical structure in the mean shear. J Atmos Sci 49:1861–1870. https://doi.org/10.1175/1520-0469(1992)049%3c1861:QTIATL%3e2.0.CO;2
Hoskins B (1996) On the existence and strength of the summer subtropical anticyclones. Bull Am Meteorol Soc 77:1287–1292
Li W, Li L, Ting M, Liu Y (2012) Intensification of Northern Hemisphere subtropical highs in a warming climate. Nat Geosci 5:830–834. https://doi.org/10.1038/ngeo1590
Li W, Li L, Ting M et al (2013) Intensification of the Southern Hemisphere summertime subtropical anticyclones in a warming climate. Geophys Res Lett 40:5959–5964. https://doi.org/10.1002/2013GL058124
Lu J, Chen G, Frierson DMW (2008) Response of the zonal mean atmospheric circulation to El Niño versus global warming. J Clim 21:5835–5851. https://doi.org/10.1175/2008JCLI2200.1
Ma J, Xie SP, Kosaka Y (2012) Mechanisms for tropical tropospheric circulation change in response to global warming. J Clim 25:2979–2994. https://doi.org/10.1175/JCLI-D-11-00048.1
Matthes K, Funke B, Andersson ME, Barnard L, Beer J, Charbonneau P, Versick S (2017) Solar forcing for CMIP6 (v3.2). Geosci Model Dev 10(6):2247–2302
Nigam S, Chan SC (2009) On the summertime strengthening of the Northern Hemisphere Pacific sea level pressure anticyclone. J Clim 22:1174–1192. https://doi.org/10.1175/2008JCLI2322.1
Phillips NA (1954) Energy Transformations and Meridional Circulations associated with simple Baroclinic Waves in a two-level, Quasi-geostrophic Model. Tellus 6:273–286. https://doi.org/10.3402/tellusa.v6i3.8734
Reboita MS, Gan MA, da Rocha RP, Ambrizzi T (2010) Precipitation regimes in South America: a bibliography review. Rev Bras Meteorol 25:185–204
Richter I, Mechoso CR, Robertson AW (2008) What determines the position and intensity of the South Atlantic anticyclone in austral winter?—An AGCM study. J Clim 21:214–229. https://doi.org/10.1175/2007JCLI1802.1
Shaw TA (2014) On the role of planetary-scale waves in the abrupt seasonal transition of the Northern Hemisphere general circulation. J Atmos Sci 71:1724–1746. https://doi.org/10.1175/JAS-D-13-0137.1
Shaw TA, Voigt A (2015) Tug of war on summertime circulation between radiative forcing and sea surface warming. Nat Geosci 8:560–566. https://doi.org/10.1038/ngeo2449
Shaw TA, Voigt A (2016) Understanding the links between subtropical and extratropical circulation responses to climate change using aquaplanet model simulations. J Clim 29:6637–6657. https://doi.org/10.1175/JCLI-D-16-0049.1
Simpson IR, Shaw TA, Seager R (2014) A diagnosis of the seasonally and longitudinally varying midlatitude circulation response to global warming. J Atmos Sci 71:2489–2515. https://doi.org/10.1175/JAS-D-13-0325.1
Song F, Leung LR, Lu J, Dong L (2018a) Seasonally dependent responses of subtropical highs and tropical rainfall to anthropogenic warming. Nat Clim Change 8:787–792. https://doi.org/10.1038/s41558-018-0244-4
Song F, Leung LR, Lu J, Dong L (2018b) Future Changes in Seasonality of the North Pacific and North Atlantic Subtropical Highs. Geophys Res Lett 45:11959–11968. https://doi.org/10.1029/2018GL079940
Staten PW, Lu J, Grise KM et al (2018) Re-examining tropical expansion. Nat Clim Change 8:768–775. https://doi.org/10.1038/s41558-018-0246-2
Sturman AP, Tapper NJ (1996) The weather and climate of Australia and New Zealand. Oxford University Press, USA
Swenson ET, Straus DM, Snide CE, Al Fahad A (2019) The role of tropical heating and internal variability in the California response to the 2015/16 ENSO event. J Atmos Sci 76:3115–3128. https://doi.org/10.1175/JAS-D-19-0064.1
Tandon NF, Gerber EP, Sobel AH, Polvani LM (2013) Understanding Hadley cell expansion versus contraction: Insights from simplified models and implications for recent observations. J Clim 26(12):4304–4321
Tyson PD, Preston-Whyte RA (2000) Weather and climate of southern Africa. Oxford University Press
Webb MJ, Andrews T, Bodas-Salcedo A et al (2017) The Cloud Feedback Model Intercomparison Project (CFMIP) contribution to CMIP6. Geosci Model Dev. https://doi.org/10.5194/gmd-10-359-2017
Wu G, Liu Y (2003) Summertime quadruplet heating pattern in the subtropics and the associated atmospheric circulation. Geophys Res Lett. https://doi.org/10.1029/2002GL016209
Yang S, Webster PJ (1990a) The effect of summer tropical heating on the location and intensity of the extratropical westerly jet streams. J Geophys Res. https://doi.org/10.1029/jd095id11p18705
Yang S, Webster PJ (1990b) The effect of summer tropical heating on the location and intensity of the extratropical westerly jet streams. J Geophys Res Atmos 95(D11):18705–18721
Zhou W, Leung LR, Song F, Lu J (2021) Future changes in the great plains low-level jet governed by seasonally dependent pattern changes in the North Atlantic Subtropical High. Geophys Res Lett 48(4):e2020GL090356
Acknowledgements
This study was supported by the National Science Foundation (NSF; AGS-1613318, AGS-1338427, AGS-1844380), the National Aeronautics and Space Administration (NASA; NNX14AM19G), and the National Oceanic and Atmospheric Administration (NOAA; NA14OAR4310160). N.J.B. is supported by the Alfred P. Sloan Foundation as a Research Fellow. We acknowledge high-performance computing and analysis support from Cheyenne provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the NSF (https://doi.org/10.5065/D6RX99HX). We also acknowledge ECMWF for use of the Era-Interim reanalysis dataset downloaded from https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest/Competing interests
No conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fahad, A.A., Burls, N.J. The influence of direct radiative forcing versus indirect sea surface temperature warming on southern hemisphere subtropical anticyclones under global warming. Clim Dyn 58, 2333–2350 (2022). https://doi.org/10.1007/s00382-021-06006-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-021-06006-1