1 Introduction

Deep moist convection is frequent during spring and summer over the Pannonian Basin region, located within Central and Eastern Europe (Taszarek et al. 2019; Seres and Horváth 2015). Severe thunderstorms are a leading source of hazardous weather affecting human health, agriculture, infrastructure, and aviation (Bentley et al. 2002; Ashley 2007; Púčik et al. 2019; Taszarek et al. 2020b). It is therefore essential to assess the spatiotemporal distribution of convective phenomena during historical and future climate periods, which can be accomplished using observations, reanalysis products, and numerical model output (Brooks 2013; Tippett et al. 2015; Brooks et al. 2019). A straightforward climatological analysis of convective weather events is difficult due to dataset limitations regarding human reports (Groenemeijer and Kühne 2014; Czernecki et al. 2016), remote sensing techniques (Punge et al. 2014, 2017; Taszarek et al. 2019; Fluck et al. 2021), and the relatively coarse resolution of model simulations with parameterized convection (Weisman et al. 1997; Prein et al. 2015). As an alternative, proxy parameters have been used to identify environmental conditions favorable for the occurrence of deep convection (e.g., Rasmussen and Blanchard 1998; Brooks et al. 2003; Púčik et al. 2015; Taszarek et al. 2020a). Convective environmental parameters can be calculated from radiosonde measurements and model data as well.

Global atmospheric reanalyses provide spatially and temporally consistent upper air data for convective research that agree well with radiosonde measurements over the United States (Gensini et al. 2014a; Li et al. 2020) and Australia (Allen and Karoly 2014). For Europe, Taszarek et al. (2018) (hereafter TA18) evaluated the pressure level version of the ERA-Interim reanalysis of the European Centre for Medium-Range Weather Forecasts (ECMWF) using observed soundings. Recently, Taszarek et al. (2020c) (hereafter TA20) extended their work to the new generation ERA5 model level dataset. These studies compared several thermodynamic parcel parameters, moisture, temperature, and wind variables, along with composite indices derived from collocated observed and reanalysis profiles. The hybrid sigma-pressure level version of the ERA5 reanalysis used in the current study has been proven to skillfully depict mid-latitude convective environments (Li et al. 2020; TA20). TA20 suggested that a high vertical resolution in the boundary layer is beneficial for the accurate computation of buoyancy parameters. However, they did not present a direct comparison of results obtained from the pressure level and native ERA5 data.

General circulation models and regional dynamical downscaling have been used worldwide to investigate future changes in convective environments (Trapp et al. 2007, 2009, 2019; Diffenbaugh et al. 2013; Gensini and Mote 2014; Allen et al. 2014a; Seely and Romps 2015; Púčik et al. 2017; Rasmussen et al. 2020; Childs et al. 2020; Glazer et al. 2020). Given the continuous nature of model fields and the high quality of data assimilation systems, many studies verified simulation results for the reference period with reanalysis data (Marsh et al. 2007; Diffenbaugh et al. 2013; Pistotnik et al. 2016; Glazer et al. 2020). Several studies also used severe thunderstorm report characteristics for validation (Trapp et al. 2011; Robinson et al. 2013; Allen et al. 2014b, Gensini and Mote 2014). Despite their spatial and temporal scarcity, direct aerological measurements accommodate a straightforward assessment of modeled convective variables. A few studies employed radiosonde observations for climate model verification (Seely and Romps 2015; Walawender et al. 2017; Li et al. 2020; Rasmussen et al. 2020). Frequently utilized environmental proxy parameters include convective available potential energy, convective inhibition, and 0–6 km vertical wind shear.

The WRF model has been applied extensively to produce decades-long historical simulations for general climatological evaluation over Europe (Heikkilä et al. 2011; Warrach-Sagi et al. 2013; Kotlarski et al. 2014; Marteau et al. 2015; Marta-Almeida et al. 2016; Kryza et al. 2017). Lately, we adapted the WRF regional climate model (RCM) for the Carpathian Basin by conducting short-term sensitivity tests to achieve an optimal physical-dynamical configuration (Varga and Breuer 2020). Dynamical downscaling with WRF at convection-permitting horizontal grid sizes of 4 km or less is common among severe weather researchers in the United States (Trapp et al. 2011; Robinson et al. 2013; Gensini and Mote 2014; Trapp et al. 2019; Childs et al. 2020; Rasmussen et al. 2020). Most regional climate simulations, however, are still available on 10-km or coarser grids (Gensini et al. 2014b; Mohr et al. 2015; Púčik et al. 2017; Vautard et al. 2020). Convection-parameterizing WRF configurations have not yet been evaluated in detail in terms of convective environmental climatology.

This study adopts the analysis methodology of TA18 and TA20 in verifying model-derived convective environmental parameters using radiosonde data but complements those papers in two ways. First, we present a direct comparison of results obtained from the pressure level and the native ERA5 reanalysis. Second, we include WRF regional climate simulations at 50 and 10 km grid spacing. The objective is to evaluate the mean climatological distribution of convective proxies calculated from ERA5 and WRF against sounding observations and investigate the effects of refined vertical (in case of ERA5) and horizontal (in case of WRF) resolution. The results aim to contribute to a better understanding of model performance and its driving processes, which is essential to increase the fidelity in historical reconstructions and future projections of convection-related phenomena. Most of the regional models used in climate change research must parameterize convection. However, the number of studies verifying proxy variables from such simulations with in-situ observations is limited. We present an evaluation of severe weather indices from a convection-parameterizing configuration of the WRF regional climate model using radiosonde measurements as a reference.

The paper is organized as follows. Section 2 describes the observational and model-based datasets used in this study. Section 3 presents the analysis methods. Section 4 discusses the results. The work is summarized in Sect. 5.

2 Data

2.1 Observations

To evaluate the performance of ERA5 and WRF from a general climatological perspective, we compared model-derived surface air temperature at 2 m, total precipitation, and global radiation (direct plus diffuse downward shortwave radiation flux at the surface) with the ensemble mean of the 0.1° regular grid E-OBS v22.0e daily observational dataset, produced by the Royal Netherlands Meteorological Institute (KNMI) within the European Climate Assessment and Dataset (ECA&D) framework (Haylock et al. 2008; van den Besselaar et al. 2011; Cornes et al. 2018). E-OBS is based on in-situ ground measurements, and the global radiation database additionally incorporates a satellite product. Despite its known limitations regarding the interpolation method over complex terrain and areas with low station network density, E-OBS is extensively used for climate model verification (Hofstra et al. 2009; Herrera et al. 2019; Kotlarski et al. 2019).

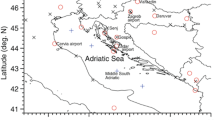
Reference convective environmental parameters (Table 1) were calculated from upper air sounding measurements. We downloaded 1200 UTC radiosonde data for 19 synoptic stations located in the wider Pannonian Basin region (Fig. 1) from the University of Wyoming website (https://www.weather.uwyo.edu/upperair/sounding.html, last access 7 May 2021). We focus on this region because of the geographical coverage of the 10 km WRF simulation (Sect. 2.3). The 1200 UTC soundings better represent the atmospheric conditions around the diurnal peak of convective activity in the area than their 0000 UTC counterparts (Seres and Horváth 2015; TA18; Taszarek et al. 2020a). Observations at 0600 UTC and 1800 UTC are very limited in number, so we excluded them from the analysis. All soundings available in the 26-year period went through comprehensive quality control (QC) similar to that of TA18 and TA20. This includes discarding each profile with less than ten records (unless located at the 850 hPa, 700 hPa, 500 hPa, and 300 hPa main isobaric levels), a parameter entirely missing, the highest level below 6 km or the lowest level above 6 km, unrealistic gradients (“spikes”) in the temperature or humidity profile, a decrease in height or an increase in pressure with altitude, an excessively large distance between consecutive levels, or the height of the first level not matching the station elevation. We also imposed some physical constraints on the parameters, e.g., we disposed of cases with 850–500 hPa lapse rate > 10 °C/km, DLS > 70 m/s, MLS > 45 m/s, LLS > 35 m/s, CIN < − 1000 J/kg, CAPE > 6500 J/kg, PW > 60 mm, or mean mixed-layer mixing ratio > 20 g/kg. These limits were adopted from TA18 with slight adjustments based on the ERA5 dataset (so that all reanalysis pseudo-profiles satisfied the QC assumptions). Approximately 145,000 (≈ 80 %) daily observations passed QC for the 1985–2010 period, and ≈ 12,000 profiles could be used in each month for calculating the 26-year mean annual cycles across the 19 stations (see Table S1 of the supplementary material). We excluded sounding stations in the investigation area with less than 50% of all 1200 UTC measurements remaining after the quality check. Although a perfect QC is not possible, a visual inspection of the calculated parameter time series implies a satisfactory performance of the selection procedure (e.g., there are no conspicuous outstanding values that seem unrealistic).

Table 1 Convective environmental parameters used in this study
Full size table
Fig. 1
figure 1

Investigation area with terrain height from the 0.1° E-OBS dataset. Red points mark the sounding stations used for the analysis with the respective WMO identification numbers

Full size image

2.2 ERA5 reanalysis

The role of the 0.25° ERA5 global atmospheric reanalysis of the ECMWF (Copernicus Climate Change Service (C3S) 2017; Hersbach et al. 2020) was twofold in this study. First, it provided initial and boundary conditions (ICBCs) for the 50 km WRF regional climate simulation at 6-hourly intervals. For this purpose, we used all 37 pressure levels available. Second, we calculated convective proxy parameters from both its pressure level (ERA5PL) and model level (ERA5ML) version. We extracted profiles from 29 constant pressure levels from 1000 hPa up to 50 hPa, which is the top of the WRF model atmosphere. The native ERA5 dataset consists of 137 hybrid sigma-pressure levels in the vertical, 20 of which are located in the lowest 1 km. ERA5 is based on cycle Cy41r2 (2016) of the Integrated Forecasting System (IFS) and applies state-of-the-art 4DVAR data assimilation that also ingests radiosonde observations.

2.3 WRF simulations

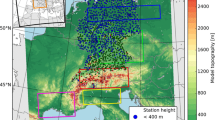
The non-hydrostatic mesoscale Advanced Research WRF (ARW) version 4.2 (Skamarock et al. 2019) was set up with two one-way nested domains on a Lambert conformal projection (Fig. 2). First, a simulation at 50 km grid spacing (WRF50) was produced driven by the ERA5 reanalysis (Sect. 2.2). Then, WRF50 was further downscaled to a 10 km mesh (WRF10). The model runs start on 1 July 1984 at 0000 UTC and end on 1 January 2011 at 0000 UTC. We considered the first 6 months as spin-up time and hence discarded them from the analysis. We performed a continuous integration (i.e., no reinitialization) without spectral nudging, which contrasts many previous studies examining model-derived convective environments (e.g., Robinson et al. 2013; Trapp et al. 2019; Rasmussen et al. 2020). This methodology poses a potential limitation on the results as the RCM fields might significantly drift from reality, a problem that presumably exacerbates with the length of the simulation (Molina et al. 2020). However, the statistical performance of the WRF runs utilized here shows no degradation with simulation time. The vertical grid of both WRF simulations comprises 61 hybrid levels (so-called “full” levels) that are terrain-following in the lower parts of the atmosphere and transform into constant pressure surfaces aloft, with a 50 hPa top layer. The resolution becomes denser towards the surface and at the tropopause. With 23 levels in the lowest 1 km, the near-surface resolution of WRF50 and WRF10 is comparable to that of ERA5ML. A schematic of the model layer distribution is shown in Fig. S1 of the Supplementary Material. Geopotential was unstaggered (averaged between adjacent “full” levels so that it refers to the 60 layer centers or “mass” points) before the computations to match the spatial location of temperature, pressure, moisture, and the horizontal wind components. Identical physical parameterization schemes were used in the two simulations (Table 2), the selection of which was based on our previous sensitivity study and further fine-tuning experiments (Varga and Breuer 2020).

Table 2 Configuration of the WRF regional climate simulations
Full size table
Fig. 2
figure 2

Geographical coverage and terrain height of the WRF model domains

Full size image

3 Methods

3.1 General climatology

From the 3-hourly WRF and ERA5 output (the latter downloaded at this time increment to match the WRF interval), we calculated daily mean surface (2 m) temperature, total precipitation, and global radiation. For the comparison, we interpolated the E-OBS measurements and the model-derived values to a 0.5° regular grid, the resolution of which is close to that of the coarsest dataset used in this study (WRF50). For temperature and radiation, either bilinear (in the case of E-OBS and ERA5) or inverse distance squared (in the case of WRF) weighting; for precipitation, optimal spatial kriging interpolation (Kottek and Rubel 2007) was used. We evaluate model performance in terms of the spatial distribution of the mean seasonal error. The investigation area extends from 4.125° E to 29.125° E and 42.375° N to 51.625° N (Fig. 1).

3.2 Convective environments

Vertical profiles of pressure, geopotential, temperature, humidity, wind speed, and wind direction (u and v components) were used to calculate convective environmental proxies. These include parcel thermodynamic parameters, bulk wind shear, moisture, temperature, and composite variables (Table 1). The parameter selection was based on previous studies (e.g., Pistotnik et al. 2016; TA18; TA20; Li et al. 2020). We chose WMS (the product of theoretical maximal vertical velocity and deep-layer shear) because of its relatively good performance among composite indices in terms of correlation coefficients between observations and reanalyses (TA20). ERA5 and WRF pseudo-soundings were extracted from the geographically nearest grid point to each station location. We inserted surface height and pressure, temperature and humidity at 2 m, and horizontal wind components at 10 m as an additional record for ERA5 and WRF.

Observed and model-derived profiles were first interpolated to a vertical resolution of 1 hPa from the surface up to the 50 hPa level. Then, convective environmental variables were determined in a uniform way for every dataset. Initial properties of mixed-layer parcels reflect the mean atmospheric state of the lowest 500 m. Virtual temperature correction was applied in all cases (Doswell and Rasmussen 1994). In the climatological analysis, we only considered 1200 UTC model pseudo-profiles with a matching observation of good quality (i.e. if the observation for the given day and station passed QC).

We verify the time series of daily 1200 UTC convective parameters from ERA5 and WRF by computing the mean error (ME), mean absolute error (MAE), root-mean-square error (RMSE), and the Pearson and Spearman correlation coefficients (PCORR and SCORR) using radiosonde observations as reference. The mean annual cycle of environmental proxies from the different datasets is also presented. We focus on the mean climatology, so zero CAPE cases are also included. We repeated the experiment taking only unstable environments into account, which resulted in larger climatological values for thermodynamic parameters but identical conclusions.

A serious limitation of this study is that the grid cell averaged quantities may not represent the values observed at the sounding sites. This issue arises from the low resolution of the model fields and elevation differences (for the geographical coordinates and terrain height of the stations and the corresponding grid cells, see Table S2 of the Supplementary Material). For spatially heterogeneous parameters such as CAPE and CIN, this representativity problem might be especially significant. The model formulation and the parameterization of various physical processes in ERA5 and WRF, including deep convection and boundary layer turbulence, introduce uncertainties in the accuracy of the simulated variables and thus the diagnosed indices. TA20 notes that the quality and quantity of radiosonde measurements have improved over time, which also impacts reanalysis products. This issue is not supposed to affect our results because we do not analyze long-term trends and apply a thorough quality check on the radiosonde profiles participating in the comparison.

4 Results and discussion

4.1 General climatology

ERA5 reproduces the mean summer (JJA) climatological parameters over Central Europe with low errors relative to the E-OBS dataset in the 26-year period (Fig. 3). Temperature, precipitation, and global radiation biases mostly remain below 1 °C, 0.5 mm/day, and 10 W/m2, respectively. Errors of the regional climate simulations are larger than those of the reanalysis. WRF50 and WRF10 overestimate summer mean temperature by 2–4 °C and global radiation by 30–50 W/m2 in the investigation area. Precipitation is underestimated by 1 mm/day or more over the southern, southwestern parts of the domain. The largest dry biases are located southeast of the Alps, over Slovenia. A precipitation overestimation reaching 1.5 mm/day in ERA5 and 3 mm/day in the WRF simulations can be found over the climatologically wettest Eastern Alpine mountain ranges. The wet bias is presumably related to the insufficient representation of orography in the models (Wang et al. 2009; Wang and Kotamarthi 2014). However, observational uncertainty is also large over complex terrain in the gridded E-OBS product (Hofstra et al. 2009; Herrera et al. 2019; Kotlarski et al. 2019). Reduction of the horizontal grid spacing in WRF from 50 to 10 km slightly improves model performance, except for precipitation over the Eastern Alps and the Carpathians. In the other seasons (DJF, MAM, SON), precipitation is overestimated, and temperature and global radiation errors are lower than those in summer (Figs. S2–4. of the Supplementary Material).

Fig. 3
figure 3

Mean summer (JJA) temperature, precipitation, and global radiation from E-OBS and biases of ERA5, WRF50, and WRF10 in the 1985–2010 period

Full size image

The dry bias and the overestimation of global radiation and temperature in summer in the WRF simulations might be attributed to several interrelated factors, e.g., a deep convection parameterization that is not active enough, excessive turbulent transfer between the land surface and the atmosphere, too low soil moisture content, soil type and land use misclassifications and related parameter inaccuracies, and the inadequate representation of cumulus clouds in the radiation calculations (Breuer et al. 2012; García-Díez et al. 2015; Katragkou et al. 2015; Jach et al. 2020; Varga and Breuer 2020). Although the exact mechanisms are difficult to disentangle, errors in the simulation of general climatological parameters certainly affect the accuracy of modeled convective environmental proxies.

4.2 Convective environments

Convective environmental parameters are remarkably well depicted by the ERA5 reanalysis. For the WRF simulations, correlation coefficients are lower, and errors are higher when computed for the entire period (Table 3).

Table 3 Pearson’s and Spearman’s correlation coefficient (PCORR and SCORR), mean error (ME), mean absolute error (MAE), and root-mean-square error (RMSE) of parameters from ERA5ML, WRF50, and WRF10
Full size table

Differences between the pressure and model level ERA5 datasets are negligible for most statistical indices; therefore, only ERA5ML is presented. The only exception is the mean error of mixed-layer convective available potential energy, which will be discussed later. ERA5 correlation coefficients exceed 0.95 for LI, DLS, PW, and MLR85. The lowest PCORR numbers are found for SB CIN (0.45) and ML CIN (0.55). Reanalysis-derived CAPE values correlate relatively well with the observations (coefficients ≈ 0.7–0.8 as opposed to ≈ 0.3–0.5 in the case of the WRF simulations). Looking at WRF50 and WRF10, correlation coefficients are the highest for LI and PW (> 0.8) and the lowest for CIN (≈ 0.2–0.3). Surface-based CAPE correlates better with the sounding measurements than its mixed-layer version; however, the opposite is true for CIN. TA18 also found that the correlation of SB CAPE is better than ML CAPE in ERA-Interim. Out of the wind shear parameters, PCORR and SCORR numbers are the highest for DLS (0.95 in ERA5 and ≈ 0.7 in the WRF runs) and the lowest for LLS (≈ 0.7–0.8 in ERA5 and ≈ 0.5–0.55 in the WRF runs), which is in line with the findings of TA18 and is likely caused by the degradation of model performance in the boundary layer. LI is a better represented thermodynamic variable than CAPE as its Pearson correlation coefficient is larger by ≈ 0.2 in ERA5 and by ≈ 0.36–0.48 in the WRF simulations. The lifted index is less impacted by the various sources of model errors as it uses environmental and parcel temperature only from one atmospheric level. However, LI is related to CAPE and has also been proven to be a skillful thunderstorm predictor that can be used in climate change studies (Púčik et al. 2017). The 26-year mean error (bias) of ERA5 is effectively zero for PW and MLR85. The only non-negligible difference between the pressure level and the native ERA5 dataset occurs for the mean error of ML CAPE, which is 7.8 J/kg in ERA5ML and 18.9 J/kg in ERA5PL. As formerly suggested by TA18 and TA20, the higher near-surface vertical resolution in ERA5ML improves thermodynamic parameter calculations. In terms of the average 1985–2010 statistical indices, the performance of other proxies from ERA5 is not affected by the vertical interpolation to pressure levels. MAE and RMSE values of the WRF simulations are always larger than those of ERA5. Looking at the mean error, the superiority of the reanalysis is not always evident (e.g., the MLS bias of both WRF50 and WRF10 is lower than that of ERA5, and bias magnitudes are close to each other for several parameters). The sign of the mean error in ERA5 and the WRF runs is opposite for ML CIN, SB CIN, and DLS. WRF10 displays slightly (0.02–0.05) higher PCORR and SCORR numbers compared to WRF50; however, a reduction of the grid increment does not universally yield lower error values for the whole 26-year period.

Fig. 4
figure 4

Annual cycle of ML CAPE (top), ML CIN (middle), and ML LI (bottom) from radiosonde observations (OBS), the native (ERA5ML) and the pressure level (ERA5PL) ERA5 reanalysis, and the 50-km (WRF50) and 10-km (WRF10) WRF regional climate simulations. Reference: daily 1200 UTC radiosonde measurements in the 1985–2010 period. Boxes and whiskers represent the interannual variability. The data series are spatially averaged across the station locations

Full size image

The mean annual cycle of mixed-layer parcel thermodynamic variables is adequate in ERA5. In the WRF simulations, monthly mean MLCAPE values peak in June instead of July, and parameter magnitudes differ substantially from the radiosonde observations in several months (Fig. 4). Both WRF runs overestimate ML CAPE by 100–200 J/kg from May to August; meanwhile, the suppression of convective processes is too strong in the RCM (ML CIN is 10–20 J/kg higher than observed). The errors of ERA5 are considerably lower; monthly mean ML CAPE is overestimated by 20–50 J/kg in ERA5PL and by less than 20 J/kg in ERA5ML during the convectively most active period (from April to September). On a monthly basis, using the native instead of the pressure level reanalysis reduces the mean error of ML CAPE by ≈ 20–30 J/kg. Contrary to WRF, ML CIN is underestimated in ERA5 by ≈ 5 J/kg (i.e., the convective inhibition is too weak). The overestimated CAPE and underestimated CIN values indicate excessively unstable conditions in the reanalysis, which might at least partially explain its slight positive summer precipitation biases (Fig. 3). ML LI is underestimated by about 0.5 °C in ERA5 and 1–2 °C in the WRF simulations from May to August. The interannual spread of ML CAPE and ML CIN is larger in WRF50 and WRF10 compared to the observations and the reanalysis. CAPE and CIN errors can to some extent be interpreted through the vertical positioning of the lifted condensation level (LCL), the level of free convection (LFC), and the equilibrium level (EL) in the model-based datasets (Fig. S5). The positive ML CAPE bias in the RCM simulations is facilitated by the EL altitudes being displaced upwards compared to the observations (i.e., the layer of positive buoyancy is thicker than in reality, which to a lesser extent also holds for ERA5). The overestimated summer surface temperature in WRF (Fig. 3) ensures that parcels ascending from the lower parts of the boundary layer are significantly warmer than their environment throughout a large vertical distance, resulting in overestimated EL heights and CAPE values. The overestimation of convective inhibition in the WRF runs might also be implied by the location of the LCL and the LFC being too high up in the atmosphere. A possible physical reason for this is the excessively dry and warm air near the surface (from where the mixed-layer parcel originates) that has too low relative humidity. However, it must be noted that the limited number of the vertical model levels and their spatial distribution potentially contribute to the incorrect depiction of the LCL, LFC, and EL heights and thus the parcel instability parameters.

Fig. 5
figure 5

Mean error of ML CIN from the pressure level (ERA5PL) and the native (ERA5ML) ERA5 reanalysis, and the 50-km (WRF50) and 10-km (WRF10) WRF regional climate simulations. Reference: daily 1200 UTC radiosonde measurements in the 1985–2010 period. Positive values indicate underestimation of convective inhibition

Full size image

Comparing the two regional climate simulations, the overestimation of monthly mean ML CIN in WRF10 is larger by 5–10 J/kg than in WRF50 (Fig. 4). Therefore, the performance of the high-resolution run is seemingly worse compared to its coarser counterpart. It can be seen from the spatial distribution of the 26-year mean error (bias) that the differences between the two WRF simulations occur over the southwestern parts of the investigation area, where WRF50 displays too weak convective inhibition on average (Fig. 5). The CIN underestimation in WRF50 originates from a false error compensation, as revealed by comparing the topographic height of the corresponding model grid points with the actual station elevations (Table S2). For example, the terrain height of Payerne (06610) is 491 m in reality but 975 m in WRF50; the elevation of Udine (16044) is 94 m in reality but 654 m in WRF50. As monthly mean LFC heights are not markedly different between the two RCM simulations (Fig. S5), the higher surface elevations in WRF50 potentially result in an underestimation of CIN as the atmospheric layer below the LFC is thinner. TA18 pointed out that using a limited number of vertical levels for CIN calculations leads to a weaker convective inhibition. ML CAPE is also affected by error compensation in WRF50 over Northern Italy (Fig. S6). Parcels initiating from higher-altitude grid points possess different meteorological characteristics and rise through different layer depths, which overall leads to reduced CAPE and CIN values in WRF50 compared to WRF10. To summarize, the better agreement of the 50-km run with the observations does not arise from an improved model performance but the misrepresentation of terrain elevation. The high-resolution run (WRF10) is not impacted by such error compensations as terrain heights are closer to reality using a 10-km grid. This highlights the representativity issue emerging from the nearest grid point methodology and underlines the necessity of a refined horizontal resolution in such studies. We note that for each station location affected, ≈ 500–550 observed soundings were used per month to derive mean LFC heights in summer in the case of the observations, ERA5PL, ERA5ML, and WRF10. In the case of WRF50, however, LFC could only be inferred from ≈ 300–400 profiles as candidate parcels were presumably too cold and dry to reach sufficient altitudes. These zero-CIN and zero-CAPE cases also influence the error statistics but excluding them from the analysis leads to qualitatively similar conclusions. Considering that LFC values are close to the observations in ERA5 (Fig. S5), its higher surface elevations (Table S2) might also contribute to the negative CIN bias, apart from possible physical reasons (e.g., an overestimation of air humidity from above the parcel launch altitude to the LFC).

The overestimation of ML CIN by WRF10 is the largest for stations located in the Mediterranean region, where a precipitation underestimation is apparent in summer (Fig. 3). This is also evident from the spatial distribution of the MAE of mixed-layer convective inhibition that peaks around 30 J/kg for sounding sites in Northern Italy and Southeastern France (Fig. S7). The underestimation of precipitation in the warm season over Northern Italy has been demonstrated previously with various WRF configurations and other regional climate models (e.g., Kotlarski et al. 2014; García-Díez et al. 2015; Katragkou et al. 2015). CIN overestimation indicates an excessive suppression of convection that might contribute to the dry bias over the southwestern parts of the investigation domain. According to TA18, CIN values below − 50 J/kg greatly reduce the probability of thunderstorm formation. Precipitation underestimation is more severe in WRF50 than in WRF10, but this is not reflected in the CIN errors because of the false compensations by topographic discrepancies pointed out earlier.

Fig. 6
figure 6

As in Fig. 4 but for SB CAPE (top), SB CIN (middle), and SB LI (bottom)

Full size image

The monthly mean bias patterns of the surface-based instability parameters are similar to those of the mixed-layer indices (Fig. 6). Error magnitudes increase in ERA5 but decrease in both WRF simulations when parcel properties are taken from the surface. The reanalysis overestimates mean SB CAPE from May to August by 130–190 J/kg. The RCM runs also display positive errors of 100–250 J/kg during the rest of the year; however, they are closer to the observations than ERA5 from July to September with biases of ≈ 50 J/kg. The larger overestimation of SB CAPE compared to ML CAPE has also been noted by TA18 for ERA-Interim. SB CIN is underestimated in ERA5 and overestimated in WRF50 and WRF10 by about 5–10 J/kg. Like SB CAPE, SB LI is better captured from July to September by the WRF simulations than by ERA5 with errors around 0.5 °C in the former and around 1 °C in the latter. The CAPE overestimation in ERA5 originates from an upward displacement of the EL (Fig. S8), which implies that the parcel is too warm and thus positively buoyant over a too large vertical extent. The altitude of the LCL, LFC, and EL is on average overestimated in both WRF climate simulations because of the excessively dry and warm atmospheric conditions, especially near the surface. Despite its upward displacement, the depth of the positively buoyant layer in the WRF runs is close to the observed in late summer and early autumn, which results in low CAPE errors.

Fig. 7
figure 7

As in Fig. 4 but for DLS (top), MLS (middle), and LLS (bottom)

Full size image

The mean annual cycles of wind shear variables in the models display maxima in winter and minima in summer, consistent with observations (Fig. 7). The magnitude of the underestimation in ERA5 is the smallest for DLS (< 0.5 m/s) and the largest for LLS (≈ 1–2 m/s). The decreasing error with increasing layer depth agrees with the results of TA18 for ERA-Interim. Monthly mean shear parameters calculated from the pressure level and the native ERA5 dataset are indistinguishable. Contrary to the reanalysis, the WRF simulations overestimate DLS by 1.5–3 m/s and MLS by 0.5–1 m/s in spring and summer. This positive difference during the warm seasons, accompanied by a negative bias in winter, leads to a less pronounced annual cycle (i.e., a reduced intra-annual amplitude). LLS is negatively biased in the examined model-based datasets, although the underestimation in ERA5 is not considerable in winter. This results in a larger LLS annual cycle amplitude in the reanalysis compared to the observation. Differences between the 50-km and 10-km climate simulations are negligible on a monthly scale. The interannual spread is well captured. In the case of ERA5, too weak upper-level winds might lead to the underestimation of shear indices. This assumption is plausible because reanalysis wind velocities are strictly constrained by the assimilation of synoptic observations near the surface. Indeed, TA20 demonstrated an increasingly negative mean wind speed error from the surface up to the 700 hPa level in ERA5 over Europe and the USA. On the other hand, Minola et al. (2020) revealed a positive average 10 m wind speed bias in the reanalysis for inland stations in Sweden, which could similarly result in the underestimation of vertical shear. The tendency of WRF to generate excessively strong near-surface winds has also been documented before (Jiménez and Dudhia 2012; Li et al. 2018). In terms of the mid-level shear, the climate model performs marginally (by 0.1–0.6 m/s) better than the reanalysis from April to October.

Fig. 8
figure 8

Mean error of MLS from the pressure level (ERA5PL) and the native (ERA5ML) ERA5 reanalysis, and the 50-km (WRF50) and 10-km (WRF10) WRF regional climate simulations. Reference: daily 1200 UTC radiosonde measurements in the 1985–2010 period

Full size image

The improvement in the WRF simulations compared to ERA5 is also apparent from the spatial distribution of the mean MLS error computed for the 26-year period (Fig. 8). The errors are on average ≈ 0.3 m/s and ≈ 0.5 m/s lower in WRF50 and WRF10, respectively than in ERA5. Stations in Northern Italy stand out with an overestimation that contrasts the negative bias for other sites, which again raises concerns about the representativity issue. However, the error reduction is not confined to locations with large topographic discrepancies and is also widely present in WRF10, where surface elevations do not deviate significantly from reality.

Fig. 9
figure 9

As in Fig. 8 but for the Pearson correlation coefficient of DLS

Full size image

The Pearson correlation coefficient of the 0–6 km wind shear computed for the entire period is above 0.9 in the ERA5 reanalysis for all station locations (Fig. 9). PCORR numbers in the WRF simulations decrease from ≈ 0.75 over the northwestern to ≈ 0.6–0.65 over the southeastern parts of the investigation area. This pattern is also observable for MLS (Fig. S9) and indicates a deterioration of model performance away from the western boundaries as the constraining effect of the driving data weakens. The large-scale circulation of the RCM deviates from that of the ERA5 reanalysis towards the domain interior. This issue impacts the 50-km simulation initially, but the pattern is passed on to the 10-km domain without alteration. It is a long-known fact that the forcing fields have a substantial impact on the RCM solution (Giorgi 2019). The larger the domain, the less control the input data exerts on the nested model (Laprise et al. 2008). Moreover, it is reasonable to assume that the large-scale features of WRF diverge more from ERA5 during the summer when local processes become dominant. This is possibly related to the contrasting MLS and DLS biases in WRF and ERA5 from April to September, but the underlying mechanisms require further investigation.

Fig. 10
figure 10

As in Fig. 4 but for PW (top) and MLR85 (bottom)

Full size image

As we have seen in the case of the statistical indices computed for the entire period (Table 3), the mean bias of PW and MLR85 is close to zero in the ERA5 reanalysis, which is also true on a monthly basis (Fig. 10). WRF10 reproduces the annual cycle of PW with negligible errors during the rest of the year; however, a slight (1–2 mm) overestimation is detectable in spring and June. The interannual spread is well represented by all datasets. Climatological PW values in WRF50 are consistently 1–2 mm lower than in WRF10, which again emerges from the higher altitude of the grid points at coarser resolution. Locations with the largest topographic discrepancies are the most affected by the dry bias (Fig. S10). It is noteworthy that even ERA5 and WRF10 demonstrate an underestimation of PW for stations in orographically complex regions. The amount of water vapor in the atmosphere decreases with increasing altitude. Therefore, the computation of precipitable water is sensitive to terrain height; the total moisture content of an air column will be less if the surface elevation is higher.

The WRF model overestimates mean 850–500 hPa lapse rates by 0.2–0.3 °C/km from June to October (Fig. 10). Contrary to the observations and the reanalysis, monthly mean MLR85 values in the RCM runs do not peak in April and May but remain almost unchanged from April until August. The temporal occurrence of the positive MLR85 bias coincides with the excessive near-surface dryness of the WRF simulations in summer (Fig. 3). The lapse rate overestimation reaches its maxima over the southern parts of the investigation area, where negative precipitation errors are the most severe (Fig. S11). The decrease of temperature with altitude is steeper in a dry atmosphere.

Fig. 11
figure 11

As in Fig. 4 but for ML WMS (top) and SB WMS (bottom)

Full size image

Composite severe weather indices incorporate multiple individual variables, the errors of which can amplify or negate each other. Therefore, discrepancies of the annual cycle of model-derived WMS resemble the deviations of CAPE and DLS. The native ERA5 dataset represents monthly mean ML WMS remarkably well with low (< 5–10 m2/s2) errors but overestimates SB WMS by 30–60 m2/s2 (Fig. 11). ERA5PL and ERA5ML perform similarly in the case of the surface-based index, but ML WMS is higher by 15–20 m2/s2 in the pressure level reanalysis leading to an overestimation compared to the observations. As DLS biases are negligible in ERA5 (Fig. 7), WMS error characteristics are mostly determined by CAPE differences. The superiority of ERA5ML underlines the importance of a higher vertical resolution in mixed-layer instability calculations. The overestimation of WRF-derived WMS reaches 80–90 m2/s2 for mixed-layer and 110–140 m2/s2 for surface-based parcels from May to June, and the positive bias persists throughout the year. Excessive CAPE and DLS in the RCM runs both contribute to the positive errors of the composite index. The slight improvement of SB WMS in the WRF simulations compared to ERA5 from July to September originates from the more accurate SB CAPE values, the effect of which is mitigated by the overestimated DLS.

5 Summary and conclusions

In this study, we utilized 1200 UTC radiosonde observations to evaluate the mean climatological distribution of convective environmental parameters derived from the ERA5 reanalysis and WRF regional climate simulations. Sounding data from 19 synoptic stations located in the wider Pannonian Basin region were used as a reference in the 1985–2010 period. Collocated model profiles were inferred from both the pressure level and the native ERA5 dataset as well as two WRF runs with different grid spacings of 50 and 10 km. The objective was to assess the performance of the reanalysis and the climate model and investigate the effects of a refined vertical and horizontal resolution. The main findings contribute to a better understanding of model behavior and are summarized below.

The ERA5 reanalysis represents convective environmental parameters remarkably well with correlation coefficients higher than 0.9 for multiple variables and low error characteristics computed for the 26-year period (e.g., the mean bias of precipitable water and the mid-tropospheric lapse rate is close to zero). The agreement is lower for parcel thermodynamic parameters (CAPE, CIN, WMS) and low-level wind shear. The annual cycles are correctly depicted by the reanalysis, but convective instability is overestimated because of concurrent CAPE overestimation and CIN underestimation. ERA5 displays an underestimation of vertical wind shear, the magnitude of which decreases with increasing layer depth (i.e., biases are the largest for the 0–1 km and lowest for the 0–6 km wind shear). The native ERA5 improves on its pressure level version in terms of the ML CAPE (the mean bias is reduced by 11 J/kg for the entire period and 20–30 J/kg in some months). Therefore, as formerly suggested by Taszarek et al. (2018) and Taszarek et al. (2020c), it is recommended to use the full hybrid-sigma ERA5 dataset for mixed-layer instability (especially CAPE) calculations. On the other hand, climatological values derived from the pressure and the model level reanalysis were indistinguishable in the case of surface-based thermodynamic variables as well as temperature, wind, and moisture indices explored in this study. The advanced data assimilation and numerical modeling techniques applied in the production of ERA5 make it a highly suitable tool for convective research purposes over the Central European region. We propose that the reanalysis might be used with some confidence as a surrogate to observations when verifying spatially continuous model parameters that are sparsely measured (e.g., because of their dependence on upper-level information). Reanalysis data have been used before to evaluate convective environmental variables from climate models (Marsh et al. 2007; Diffenbaugh et al. 2013; Pistotnik et al. 2016; Glazer et al. 2020). However, caution must be taken for parameters that are strongly dependent on near-surface conditions (e.g., surface-based instability indices, CIN, and LLS). It is unclear whether the high quality of atmospheric pseudo-profiles is maintained away from the sounding stations where measurements are not available for assimilation.

The WRF runs reproduce the main features of the annual cycle of proxy parameters but with lower correlation coefficients and higher errors than ERA5. Both convective available potential energy and convective inhibition are excessive in the simulations compared to the sounding data; therefore, it would be difficult to draw a conclusion about the overall potential for thunderstorm formation in WRF. CAPE and CIN biases emerge from temperature and moisture errors as well as model formulation aspects (e.g., limited horizontal and vertical resolution and the downscaling methodology). Contrary to ERA5, deep-layer shear is overestimated by the WRF runs in spring and summer; meanwhile, mid-level shear biases are reduced in comparison with the reanalysis. Most of the differences between the 50-km and the 10-km WRF simulations originate from the misrepresentation of topography in the coarse-resolution run. The surface elevation of a few grid points in WRF50 is considerably higher than the corresponding station altitude. The upward displacement of the surface leads to different atmospheric conditions aloft. Consequently, precipitable water is underestimated at those locations and false error compensations occur for thermodynamic parameters (e.g., the overestimation of CAPE and CIN is mitigated). This highlights the limitations of the nearest grid point method in the case of coarse model data and encourages horizontal resolution improvement for such applications. In the present analysis, a grid spacing of 10 km was sufficient to eliminate topographical discrepancies and their detrimental effects on the simulated variables. Due to its relative simplicity, WRF captures the lifted index better than CAPE, which makes it an appropriate instability index for studying convective environments under current and future climatic conditions. This is important because the vertical resolution of currently available regional climate model output is limited, which prevents the accurate calculation of CAPE (Púčik et al. 2017).

The evaluation of convective proxies contributed to a better understanding of RCM behavior and performance in terms of the general climatological variables. The CIN overestimation in the WRF simulations is indicative of an excessive suppression of convective activity that to some extent explains the summer precipitation shortage over the southern parts of the investigation area. The near-surface dryness of the WRF simulations might be reduced with different deep convection, planetary boundary layer, and land-surface parameterizations. Future sensitivity tests are required to find a more suitable configuration. The correlation coefficient of deep-layer (0–6 km) and mid-level (0–3 km) wind shear decreases from the northwestern to the southeastern parts of the study region. Such deterioration is not observed in ERA5 and suggests that the large-scale circulation of the RCM increasingly diverges from that of the driving reanalysis away from the western boundaries. As the main purpose of dynamical downscaling is the addition of fine-scale details, it might be beneficial to prevent the deviation of the synoptic features in the RCM by decreasing the size of the 50-km domain (especially in the west–east direction) or applying spectral nudging (Molina et al. 2020).