Abstract
Land surface and atmosphere are interlocked by the hydrological and energy cycles and the effects of soil water-air coupling can modulate near-surface temperatures. In this work, three paired experiments were designed to evaluate impacts of different soil moisture initial and boundary conditions on summer temperatures in the Mediterranean transitional climate regime region. In this area, evapotranspiration is not limited by solar radiation, rather by soil moisture, which therefore controls the boundary layer variability. Extremely dry, extremely wet and averagely humid ground conditions are imposed to two global climate models at the beginning of the warm and dry season. Then, sensitivity experiments, where atmosphere is alternatively interactive with and forced by land surface, are launched. The initial soil state largely affects summer near-surface temperatures: dry soils contribute to warm the lower atmosphere and exacerbate heat extremes, while wet terrains suppress thermal peaks, and both effects last for several months. Land-atmosphere coupling proves to be a fundamental ingredient to modulate the boundary layer state, through the partition between latent and sensible heat fluxes. In the coupled runs, early season heat waves are sustained by interactive dry soils, which respond to hot weather conditions with increased evaporative demand, resulting in longer-lasting extreme temperatures. On the other hand, when wet conditions are prescribed across the season, the occurrence of hot days is suppressed. The land surface prescribed by climatological precipitation forcing causes a temperature drop throughout the months, due to sustained evaporation of surface soil water. Results have implications for seasonal forecasts on both rain-fed and irrigated continental regions in transitional climate zones.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
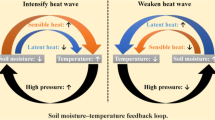
Important feedback mechanisms of the land surface to the atmosphere arise when three elements co-exist within the land–air system (Dirmeyer and Halder 2017). The first is sensitivity, that enables the response of one state or flux to variations in another; the second is variability, in other words the potential of the forcing component to change in time; the third is memory (Koster and Suarez 2001), namely the persistence of anomalies. The first two elements are commonly combined in a single mechanism called coupling, which identifies the reciprocal interaction between land surface and atmosphere (Dirmeyer 2001; Koster et al. 2006; Seneviratne et al. 2006b). Land memory, that is the inertia of the system accumulated from foregoing conditions, is the factor that affects predictability at the subseasonal and seasonal scales (Guo et al. 2011).
The land surface components with the greatest effect on the planetary boundary layer are vegetation (Zemp et al. 2017), snow (Xu and Dirmeyer 2011) and soil moisture (Santanello et al. 2011), with the latter being recognized as crucial for the understanding of rainfall and temperature variability. While the soil moisture-precipitation interaction has been investigated for decades (Walker and Rowntree 1977; Shukla and Mintz 1982; Eltahir 1998), the coupling between soil moisture and temperature has only received attention in the last 15 years (Seneviratne et al. 2010), pushed by the Global Land–Atmosphere Coupling Experiment (GLACE, Koster et al. (2006)).
Soil moisture feedback to the atmosphere plays an important role in shaping summer temperatures and eventually in modulating duration and intensity of heat waves (Lorenz et al. 2010). For instance, it is well established that the lack of soil moisture has strongly reduced latent cooling and thereby amplified and prolonged the surface temperature anomalies during the 2003 European heat wave (Fischer et al. 2007). Hirschi et al. (2011) examined the observational relationships among spring soil moisture and summer hot weather for central and southeastern Europe, concluding that dry soil conditions intensified the distribution of temperature extremes in the eastern Mediterranean basin. Mueller and Seneviratne (2012) showed that surface moisture deficits are a relevant factor for the occurrence of hot extremes in many areas of the world, suggesting that effects of soil moisture–temperature coupling are geographically more widespread than commonly assumed. More recently, Vogel et al. (2017) found that soil moisture influence is strongest in transitional climate regimes, where evapotranspiration is dependent on soil moisture, while the water availability and variability are large enough to remarkably affect the surface heat fluxes.
The key variable that allows for the establishment and maintenance of coupling processes is evapotranspiration, which enters both the land energy and water balance equations (Seneviratne et al. 2010). Evapotranspiration is the sum of bare ground evaporation and vegetation transpiration. In models, ground evaporation is usually estimated as a non-linear function of surface soil moisture (Jefferson and Maxwell 2015), and this simple representation often causes its underestimation (Chang et al. 2018). Plant transpiration requires more complex formulations with non-linear dependencies on multiple environmental factors, including root-zone soil moisture, stomatal conductance and atmospheric \(\text {CO}_{2}\) concentration (Franks et al. 2018). Soil moisture restrictions may limit evapotranspiration, affecting the partitioning of surface energy defined by the Bowen ratio, that is the ratio between sensible and latent heat flux. Changes in this relationship help explain a large fraction of the variability of temperature (Miralles et al. 2012). Depending on regions and seasons, evapotranspiration is either energy-limited or soil-moisture limited. Non-linearities may be particularly strong in transitional regimes where and when soil moisture limitation plays a major role (Berg and Sheffield 2018).
Soil moisture memory is the factor influencing predictability, and when it is combined with coupling the cumulative effect onto atmosphere can become remarkable. Since the cardinal work of Fennessy and Shukla (1999), the role played by land surface processes, and in particular soil moisture, has gained growing attention in the seasonal prediction community. Soil moisture is among the slowest-evolving land state variables, and its anomalies may impart a considerable fraction of predictability in mid-latitudes at sub-seasonal to seasonal time-scale (Guo and Dirmeyer 2013). This effect is negligible in winter when land is generally decoupled from the atmosphere, but it emerges strongly in late spring, summer and fall (Dirmeyer 2003). Materia et al. (2014) have found the contribution of land surface initialization crucial to boost summer forecast skill in the Mediterranean region, while Prodhomme et al. (2016) showed that knowledge of soil initial anomalies has a positive impact on temperature skill, and for some extreme events of the past (e.g. the Russian heat wave in 2010), neglecting the land initial state would compromise the correctness of any seasonal prediction.
In this study, we aim to investigate the response of summer temperatures to extreme soil conditions, and clarify the role of coupling between land surface and atmosphere in a water-limited environment. The strongly idealized experimental setup adopted here allows to better identify the physical processes behind the atmospheric response to land surface state, with the intention of facilitating interpretation of results. The analysis is performed over the Mediterranean transitional climate regime region, that is the area where evapotranspiration is largely limited by soil moisture, whose geographical definition and strength of land-atmosphere coupling is still uncertain (Seneviratne et al. 2010).
The transitional climate region of the Mediterranean used in this study is described in Sect. 2, together with models and data used and the experimental design. Section 3 shows the main outcomes of our study, while a discussion including limitations and unexpected outcomes is sketched in Sect. 4. Section 5 summarizes the most important results of our study.
2 Methods
2.1 Models and data
Two global coupled models (GCMs) participate in the experiments: the CMCC Seasonal Prediction System version 3 (Sanna et al. (2016), hereinafter CMCC), and the Centre National de Recherches Météorologiques Coupled Model version 6 (Voldoire et al. (2019), hereinafter CNRM). Regional climate models would better address additional aspects linked to a higher horizontal resolution. However, the employed sensitivity experiments are designed in the wider framework of the European Research Area for Climate Services (ERA4CS) MEDSCOPE project (https://www.medscope-project.eu/), aimed at improving our comprehension of the remote and local mechanisms driving climate variability and predictability in the Mediterranean. Land surface is only one of these drivers, and its anomalies may also have remote impacts for the establishment of stationary wave events that have been shown to affect areas distant from the source region (Teng et al. 2019; Wang et al. 2019). This aspect has not been tackled in this work.
The spectral element dynamical core of the CMCC-SPS3 makes use of the Community Atmospheric Model version 5.3 (CAM5.3, Neale et al. (2010)) and the Community Land Model version 4.5 (CLM4.5, Oleson et al. (2013)) with a horizontal resolution of about 110 km and an integration time-step of 30 min. CAM5.3 is run on 46 vertical levels up to 0.3 hPa, while CLM4.5 soil column is constituted of 15 depth levels. Soil moisture is distributed over the first ten layers down to about 2.5 m. The soil moisture prescription applied in SXP-CP, SXP-DP and SXP-WP adjusts to the regional scale the methodology described in Hauser et al. (2017).
The transport of water throughout the soil is governed by gravity, infiltration, surface and sub-surface runoff, gradient diffusion, root absorption for transpiration, and interactions with groundwater (Oleson et al. 2013). The soil texture properties, such as clay and sand soil fraction, are retrieved from the soil dataset of the International Geosphere-Biosphere Programme (IGBP, Task (2000)). Soil organic matter data merge the ISRIC-WISE dataset (Batjes 2012) and the Northern Circumpolar Soil Carbon Database (Hugelius et al. 2013). CLM4.5 soil (snow-free) albedo varies with twenty color classes (see Table 3.3 in Oleson et al. (2013)). The soil colors are prescribed so to best reproduce observed MODIS local solar noon surface albedo values at the CLM grid cell (Lawrence and Chase 2007).
CLM4.5 uses a Satellite Phenology configuration, where leaf area index (LAI) is prescribed to a monthly climatology developed from the 1-km MODIS-derived dataset of Myneni et al. (2002). The plant functional types (PFTs) distribution is prescribed to that of year 2000: global vegetated areas are divided into fifteen PFTs, that cover tropical, temperate and boreal forests, needleleaf and broadleaf trees and shrubs, grasslands and crops (see Table 2.1 in Oleson et al. (2013)). Each of these categories is characterized by specific optical, morphological and photosynthetic parameters that modulate plant transpiration (Peano et al. 2019). The root fraction in each soil layer is computed by means of a two-parameters equation (Zeng 2001), and it depends on the plant functional type (see Table 8.3 in Oleson et al. (2013)).
The atmospheric component of CNRM-CM6 is ARPEGE-Climat V6.3 (Roehrig et al. 2020) with a linear triangular truncation Tl127 and a corresponding reduced Gaussian grid at a horizontal resolution about \(1.4\,^\circ\) at the equator. It holds 91 vertical levels up to 0.01 hPa, while the boundary layer is described with about 15 levels below 1500 m.
The land surface scheme ISBA-CTRIP (Decharme et al. 2019) accounts for 14 soil layers down to 12-m depth, with a diffusive vertical propagation for soil temperature and water. The soil textural properties, such as clay and sand, and the soil organic carbon content are obtained by the Harmonized World Soil Database (HWSD) at a 1-km resolution (http://webarchive.iiasa.ac.at/Research/LUC/External-World-soil-database/HTML/). The snow-free land albedo is derived from a 10-year analysis of the MODIS product (Carrer et al. 2014). Mean seasonal cycles at a 10-day time step for visible and near-infrared vegetation, as well as vegetation-free albedos, are retrieved at 1-km resolution by using a Kalman Filter-based method.
ISBA uses a prescribed LAI annual cycle, combining the Collection 5 MODIS LAI product at 1-km spatial resolution and the Normalized Difference Vegetation Index from the ECOCLIMAP-II database (Faroux et al. 2013). The plant functional types are twelve (see Table 1 in Decharme et al. 2019, with land cover properties specified according to the 1-km resolution ECOCLIMAP-II database (Faroux et al. 2013). The depth of the roots (see Figure 2c in Decharme et al. (2019)) is specified for each land cover unit, according to Canadell et al. (1996).
Maps of land cover, represented by PFTs, can be found for both models in the supplementary materials (Fig. S1).
When run offline, land models must be constrained by a set of atmospheric variables that force a response in terms of soil moisture, surface temperatures and fluxes, etc. Rainfall, solar radiation, sea-level pressure, near-surface temperature, specific humidity and wind from the NOAA 20th century reanalysis dataset (NOAA-20CR version 2c, Compo et al. (2011)) are imposed to this aim at a 3-hourly time interval (except for CMCC precipitation and radiation that are accumulated every 6 h). The reanalyses are generated by assimilating only surface pressure and using monthly SST and sea ice distributions as boundary conditions within a deterministic Ensemble Kalman Filter.
2.2 Experimental design
For both GCMs, a series of sensitivity experiments (SXPs) is set up as idealized present climate runs in atmosphere-land mode, and compared to a control experiment (EXP-B0) consistent in nature. The oceanic boundary condition is constituted by climatological sea surface temperatures (SSTs, HadISST v2.2 Titchner and Rayner (2014)) for the 1981–2010 period, and the radiative forcing is fixed to the observed value of the year 2000, a standard configuration of CAM5.3 used to evaluate present climate representations (Gettelman et al. 2019). These choices are meant to secure a minimum anthropogenic background trend for our approach, ensuring a discussion that only implies natural variability. Figure 1 illustrates the experimental setup.
The EXP-B0 control is run continuously for 50 years, in order to sample the models internal atmospheric variability: since the SSTs and the radiative forcing are the same every year, each of the fifty experimental year may be seen as one independent ensemble member. This number of members is in line with most literature that aims to assess the contribution of internal atmospheric variability to heat and dry near-surface conditions (e.g. Chen and Zhou (2018); Baek et al. (2021)), therefore atmosphere variance can be considered well represented. In CMCC, a 20-year spin-up is allowed in order to bring the multi-layer soil moisture to an equilibrium state. In CNRM, 60 years were run starting from a random land-surface restart, in which soil moisture was already at equilibrium. Given that, a spin-up was not necessary, however the first ten years have been discarded. Soil water fraction for the spin-up years may be found in the Supplementary Materials (Fig. S2).
The SXPs are three pairs of sensitivity experiments that are run to evaluate the summer atmospheric response to distinct soil water conditions: very dry, very wet, close to norm.
Schematic representation of the experimental design. a Shows the workflow to obtain the sensitivity experiments (SXPs). b Explains the characteristics of the land-only runs (LORs) and SXPs: the top box illustrates the LORs, used to produce the initial conditions (May \(1{\text {st}}\) on year 1) for the SXPs. The runs are extended until October \(31{\text {st}}\) to obtain the prescribed daily (over a 31-day running mean) land conditions for the prescribed SXP-CP, SXP-DP, SXP-WP, represented in the bottom-right box. The coupled land-atmosphere SXP-CI, SXP-DI, SXP-WI are illustrated in the bottom-left box. Redrawn starting from Ardilouze et al. (2020)
To obtain the initial conditions for all the SXPs, and also the boundary conditions for a group of them, three 18-month-long land-only runs (LORs) are launched, forced by atmospheric reanalyses (see Sect. 2.1). The LORs start on May 1st of year 0 from an in-balance land condition, and end on October 31st of year 1. To ensure an extensive sampling of the atmospheric variability and be consistent with EXP-B0, every LOR is composed of fifty ensemble members. The members are generated through a perturbation of the NOAA-20CR daily atmospheric forcing, constituted by 2 m-temperature, 10 m-wind, specific humidity, surface pressure, solar radiation, precipitation. A different forcing year is randomly selected between 1913 and 2012, to constrain each of the LORs starting from May 1st. Among the set of forcing variable, only precipitation over the enlarged Mediterranean region (EMR, \(28^{\circ }\,\text {N} - 50^{\circ }\,\text {N} / 10^{\circ }\,\text {W} - 45^{\circ }\,\text {E}\), see Fig. 2) is modified in order to obtain dry, wet, and close to norm conditions. Therefore, the dry LOR (LOR-D) receives zero precipitation in all its members; the wet LOR (LOR-W) receives climatological precipitation + 3 standard deviation; the close-to-norm LOR (LOR-C) receives climatological precipitation. The other forcing fields are unchanged from NOAA-20CR, and differ in every ensemble member.
After 12 simulated months, on May 1st (year 1), the obtained land surface states are used as initial conditions for the above-mentioned three pairs of corresponding atmosphere-land runs, that last 6 months (until October 31st): dry (SXP-DI/DP), wet (SXP-WI/WP), and close-to-norm (SXP-CI/CP). The suffixes “I” and “P” stand for interactive and prescribed experiments. In the three interactive SXPs (SXP-DI/WI/CI), land surface and atmosphere fully interact with each other. In the three prescribed SXPs (SXP-DP/WP/CP), land surface forces the atmosphere, therefore land state is identical for each member, regardless of the inter-ensemble atmospheric variability. Outside the EMR, land surface of all the SXPs is unchanged with respect to that of EXP-BO. The three paired-experiment are here described in detail (see also Table 1):
-
Experiment SXP-CI: starting from the “C” LOR (land initial state generated by a full year of climatological precipitation over the EMR), a 6-month atmosphere-land experiment is run until October 31st, with atmosphere and land surface fully interacting with each other.
-
Experiment SXP-CP: same as SXP-CI, but land and atmosphere are decoupled for the entire 6-month SXP. Land surface is in fact prescribed daily to a close-to-norm state, that is the one produced by the LOR-C in the last 6 months of integration (May 1–Oct 31 year 1). The land prescribed condition is smoothed by a 31-day running mean filter, to limit the risk of unwanted high frequency atmospheric response caused by day-to-day spikes in the prescribed surface soil moisture.
-
Experiment SXP-DI: starting from the “D” LOR (land initial state generated by a full year of zero precipitation over the EMR), a 6 month atmosphere-land experiment is run until October 31st, with atmosphere and land surface fully interacting with each other.
-
Experiment SXP-DP: same as SXP-DI, but land and atmosphere are decoupled for the entire 6-month SXP. Land surface is in fact prescribed daily to a “dry” state, that is the one produced by the “D” LOR in the last 6 months of integration (May 1–Oct 31 year 1, 31-day averaged).
-
Experiment SXP-WI: starting from the “W” LOR (land initial state generated by a full year of precipitation = 3\(\sigma\) beyond the observed climatology), a 6 month atmosphere-land experiment is run until October 31st with atmosphere and land surface fully interacting with each other.
-
Experiment SXP-WP: same as SXP-WI, but land and atmosphere are decoupled for the entire 6-month SXP. Land surface is in fact prescribed daily to a “wet” state, that is the one produced by the “W” LOR in the last 6 months of integration (May 1–Oct 31 year 1, 31-day averaged).
Most of these experiments are also described and used in the Ardilouze et al. (2020) companion study, which analyzes the precipitation response to soil water extreme conditions. The large perturbation for initialization of the dry and wet experiments was necessary to reach very low water content in the soil, close to the wilting point (SXP-DI) and field capacity (SXP-WI) by the beginning of the summer. The same configuration is then maintained for an additional 6-month-period in SXP-DP and SXP-WP.
2.3 Definition of Mediterranean transitional region
The Mediterranean region is located in a transitional regime between arid and temperate climates (Di Castri 1991). In the wider Mediterranean sector, the summer soil moisture exerts a strong constraint over evapotranspiration, and thus it is a major driver of atmospheric variability (Lionello et al. 2006).
Schwingshackl et al. (2017) affirm that about 30–60% of the global land area is in the transitional regime during half of the year, but we used a stricter definition for the identification of the Mediterranean transitional climate regime (MedTCR) region. We start from the definition of land–atmosphere coupling described through the Terrestrial Coupling Index by Dirmeyer (2011). The TCI is computed as the product of the standard deviation of the latent heat flux and the correlation between variation in soil moisture and in latent heat flux. A positive concurrent correlation between soil moisture and latent heat flux (or evapotranspiration) is representative of a situation where water limits evaporation more than energy. Hence, soil moisture, and not radiation, is the principal control on latent heat flux, and a soil moisture decrease causes reduced evapotranspiration. A negative correlation suggests that soil moisture is responding to the fluxes (hence decreasing while evapotranspiration/latent heat increases), then energy is the limiting factor.
The TCI has the same sign as correlation at any location, but the magnitude is modulated by the variability in surface fluxes: this helps highlight regions where the potential feedback to the atmosphere is meaningful. Conversely, a low TCI indicates that the actual interaction is ineffective to modulate surface climate (e.g. hot deserts, where where soil water is so scarce that his contribution to the boundary layer is often insignificant (Dirmeyer and Halder 2017)).
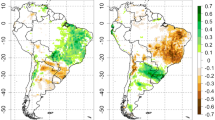
Representation of the multi-step procedure to obtain the Mediterranean transitional climate regime region (MedTCR). The procedure is applied to the EXP-B0 ensemble means: left panels display results for the CMCC model, right panels for the CNRM model. a and b Show the Terrestrial Coupling Index TCI. Grid points where TCI \(\le\) 67th percentile are maske out in c and d, that show the difference between cold season (November–April) and warm season (May–October) precipitation (mm). Grid points where this difference is negative are masked out in e and f, that show the difference between annual precipitation and potential evapotranspiration (mm). Grid points where this difference is negative are masked out in g and h, that represent the MedTCR, bounded within the area where land surface conditions were changed in the sensitivity experiments
Figure 2 shows the multi-step approach used to obtain the Mediterranean transitional climate regime region for the two climate models. Figure 2a and b show the TCI for the CMCC and CNRM models, respectively. Values shown are the warm season averages of daily TCI in the EXP-B0 ensemble means. Major differences can be easily spotted between the two models: in the CMCC simulation, the area where soil controls evapotranspiration is confined to the Mediterranean boundaries and arid areas, while in CNRM almost all of continental Europe shows positive TCI values, indicating that evapotranspiration is water limited. Such a dispersion among different models is not surprising: Boé and Terray (2008) found remarkable differences in the representation of summer evapotranspiration over Europe in the CMIP3 models, linked to the way these models represent the respective role of soil moisture and surface radiative energy on evapotranspiration. More recently, soil moisture-evapotranspiration links have been analyzed for CMIP5 models (Berg and Sheffield 2018), showing that uncertainty is still very high on the outer margins of regions characterized by positive coupling, extending into regions of energy-limited evapotranspiration. In addition, Knist et al. (2017) show that regional climate models participating in EURO-CORDEX tend to overestimate the coupling strength in the transition zone that covers large parts of central Europe.
The top panels are useful to identify grid-points featured by land–air coupling of significant magnitude: only areas where the TCI \(\le 67{\text {th}}\) percentile, with respect to the TCI spatial distribution over the entire domain, are retained for the definition of the MedTCR. Values that do not reach this threshold are masked out in the following panels.
Figure 2c and d highlight the difference between cold season (November–April) and warm season (May–October) rainfall simulated by the two models’ SXP-B0. In fact, a single rain season during the cold half of the year is the main characteristic of the Mediterranean climate (Lionello et al. 2006). This is not the case for Central Europe in CNRM, North Africa in CMCC (although here rainfall amounts are very small all throughout the year) and the Caucasus Mountains in both simulations, therefore these regions are masked out in the following panels.
Figure 2e and f show the difference between annual precipitation and potential evapotranspiration. This diagnostic is important to detect regions featured by a desert climate according to Koppen (1936) classification (i.e. regions characterized by annual mean precipitation lower than potential evapotranspiration), which are meant to be excluded by this analysis, and negative grid points are masked out in the following panels.
The identified transitional climate regime covers, in both models, an area similar to that estimated by observational and quasi-observational measures (Miralles et al. 2012). The MedTCR region is delimited by the EMR box (Fig. 2g, h), and all the analyses in this work are performed using these grid cells. It is to be noted that only grid cells with 100% land fraction are retained from the models’ land sea mask, to avoid calculation of fluxes over fractions of ocean.
3 Results
3.1 Soil moisture memory
We evaluated the soil moisture memory using the Koster and Suarez (2001) approach, revised by Seneviratne and Koster (2012), that uses lagged autocorrelation to assess the persistence of soil moisture anomalies.
where \(\rho\) is the correlation coefficient between the soil water fraction on day 1 \(w_{{d1}}\) and day d*. Figure 3 shows, for both models, the soil moisture decorrelation time series, that is the autocorrelation of soil moisture between its value on May \(1{\text {st}}\) and in every day until October \(31{\text {st}}\). Soil moisture memory is arbitrarily considered lost when the autocorrelation drops below the 5% confidence level. Within this definition, it ranges between about 20 and 140 days, which is in line with many studies: for example, Dirmeyer et al. (2009) finds similar numbers for the Mediterranean summer, although slightly smaller due to the choice of a stricter p-value.
In the interactive experiments, memory is longer when initial conditions are close to normal (correlations are significant for about 4 months or more in SXP-B0 and SXP-CI experiments), indicating that a small perturbation persists longer than a large one in the MedTCR region. This finding agrees with other AGCM multi-model studies (e.g. Seneviratne et al. (2006a)), but conflicts with observational studies (Orth and Seneviratne 2012) that found increased memory in extremely dry and wet soil states. Both models also show extended memory when dry conditions are artificially maintained during the summer (SXP-DP), and in general prescribed soil moisture persists for longer time with respect to interactive soil moisture, whose amount is modulated by the variability of precipitation, 10 m-wind, solar radiation, etc.
Ensemble mean of Tmax, averaged for the entire warm season (May \(1{\text {st}}\)–Oct \(31{\text {st}}\)) in the MedTCR for the CMCC model (left panels) and CNRM model (right panels). On each panel’s title, the corresponding sensitivity experiment is specified. EXP-B0 control runs are shown in g and p
3.2 Long-term mean and interannual variability of daily maximum temperatures
The spatial variability of temperature response to the different land surface initial and boundary conditions is displayed in Fig. 4. An ensemble mean averaged over the entire warm season is shown. The control runs display many similarities between the CMCC and CNRM model, although the latter appears slightly warmer in eastern Europe. Among the common grid points, those in Southern Spain and European Russia are the hottest, while those in northern Spain and France are the coldest. It is to be noted that the two GCMs’ MedTCRs include almost identical areas in the European Mediterranean. However, the CMCC’s transitional region considers part of Middle East (eastern Turkey and northern areas of Syria, Iraq and Iran), which is discarded by CNRM; on the other hand, CNRM’s MedTCR incorporates northwestern Africa, which is not included in CMCC.
In general, the wet experiments are the coldest, with the prescribed SXP-WPs (Fig. 4f, o) showing lower Tmax values than the interactive SXP-WI (Fig. 4e, n). The dry experiments are the warmest, with the prescribed SXP-DPs (Fig. 4b, i) showing higher Tmax values than the interactive SXP-DIs (Fig. 4a, h). The close-to-norm experiments exhibit Tmax values in between, and closer to the EXP-B0. However, the SXP-CPs (Fig. 4d, m) are clearly colder than the corresponding SXP-CIs (Fig. 4c, l). The Middle-East grid points, included only in the CMCC MedTCR, show very pronounced variability among the experiments: the forced Tmax differ by about \(10\;^{\circ }\text {C}\) in the two extreme SXPs (Fig. 4b, f). In Northwestern Africa, incorporated only in the CNRM MedTCR definition, forced Tmax in the dry (Fig. 4i) and wet (Fig. 4o) runs are only about \(4\;^{\circ }\text {C}\) apart.
By removing land-atmosphere coupling, we expect to decrease the internal model variability as a consequence of the elimination of an important degree of freedom. In the adopted experimental framework, internal variability may be represented with the ensemble spread, i.e. as the standard deviation of all members with respect to the ensemble mean. Since each member is the result of perturbed atmospheric forcing pertaining to a specific historical calendar year, we can assume that its mathematical description represents the interannual variability of the system:
where \(\tau\) is the average daily maximum temperature anomaly of each ensemble member, \(Tmax_{m,d}\) is the daily maximum temperature of each ensemble member, \(\langle Tmax_{d}\rangle _{m}\) is the daily climatology of Tmax calculated across the ensemble members, M and D are the total number of members (50) and days (184), respectively. \(\sigma\) is the ensemble spread, that is the standard deviation across the members, and the subscript indicates that this operation is done for each of the sensitivity experiments.
Figure 5 illustrates the ratio between the ensemble spread of the prescribed SXP to the corresponding coupled SXP. The figure shows that Tmax interannual variability in all the prescribed SXPs is considerably lower than interannual variability in the corresponding coupled experiments. The climatological and wet SXPs appear more sensitive to the land-atmosphere coupling, with respect to the dry SXPs. This could be due to the fact that rain is scarce in MedTCR during most of the warm season, therefore the SXP-DI atmospheric forcing marginally affects soil water for a long time, similarly to SXP-DP where the soil water response is artificially blocked. This hypothesis finds confirmation north and east of the MedTCR domain (not shown), where average early summer rain is more abundant, and the ensemble spread ratio SXP-DP/SXP-DI is similar to that of the other experiments.
3.3 Daily maximum temperature seasonal evolution
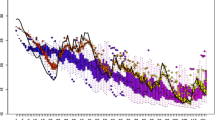
The seasonal evolution of daily maximum temperatures (Tmax) for the two models is shown in Fig. 6, while that of the extreme maximum temperatures (Tmax90, calculated as the mean of members temperature exceeding the \(90{\text {th}}\) percentile) is illustrated in Fig. 7. Mean monthly Tmax and Tmax90 values are shown in Tables 2 and 3, respectively.
The graphs depict the 50-member ensemble mean on a 31-day running average, for all the SXPs and B0 simulations. Top panels (Figs. 6a, b and 7a, b) refer to the experiments where land surface is bounded to create the initial conditions, and then released to respond to atmospheric variability (SXP-DI, -CI, -WI). Bottom panels (Figs. 6c, d and 7c, d) show the experiments where land surface is constrained throughout the entire season, therefore not responding to the atmosphere.
The CMCC model (Figs. 6a, c and 7a, c) shows a more pronounced seasonal cycle with respect to CNRM (Figs. 6b, d and 7b, d). This results in higher summer \({\text {Tmax}}_{\text {B0}}\) and \({\text {Tmax90}}_{\text {B0}}\), but colder temperatures in May and October. Also, CMCC MedTCR is generally more sensitive to soil moisture anomalies, being warmer than CNRM in the dry experiments and colder in the wet experiments. As pointed out in Sect. 3.2, the distribution of the MedTCR grid points is different in CMCC and CNRM: the fact that CMCC includes part of Middle East and does not consider Northwest Africa, included in CNRM, may explain the stronger CMCC Tmax response. In fact, inland Middle East climate is rather continental, with a more pronounced interannual and seasonal variability than Northwestern Africa (see also Fig. 4).
3.3.1 Wet sensitivity experiments
In the two wet experiments, the annual maximum temperature is always recorded in July and August, but is delayed compared to EXP-B0. Saturated soils, in fact, release humidity to the atmosphere for long time, inhibiting the emergence of the warmest days until the beginning of August, which is thirteen (CMCC) and ten (CNRM) days later than in EXP-B0 (not shown).
The fingerprint of the initial extreme soil water anomaly affects near-surface temperatures throughout the entire summer. \({\text {Tmax}}_{\text {WI}}\) is about \(1.2\;^{\circ }\text {C}\) cooler than \({\text {Tmax}}_{\text {B0}}\) for CMCC, and \(0.6\;^{\circ }\text {C}\) cooler for CNRM during the summer (June–July–August mean—JJA, Fig. 6a, b and Table 2). A saturated soil favors strong evapotranspiration in the region, since a large amount of water is available for evaporation during the solar radiation peak. We assume that land-air coupling is dramatically reduced, since the land surface state, and soil moisture in particular, does not respond to varying solar radiation, near-surface temperature, etc. Therefore, evapotranspiration is totally energy-limited (Seneviratne et al. 2010), and the Bowen ratio reduction contributes to cool off the overlying atmosphere for months. In both models, this effect lasts until early September, when \({\text {Tmax}}_{\text {WI}}\) becomes indistinguishable from \({\text {Tmax}}_{\text {B0}}\).
Both CMCC and CNRM show important cooling in SXP-WP (Fig. 6c, d), more pronounced in mid summer, with \({\text {Tmax}}_{\text {WP}}\) colder than EXP-B0 by, respectively, \(3.6\;^{\circ }\text {C}\) and \(2.5\;^{\circ }\text {C}\) (average over JJA). The continuously wet terrain keeps the Bowen ratio low, not allowing Tmax to rise as much as in the control experiment.
Wet spring soils account for a reduction of hot extremes (Fig. 7), with the average JJA hottest temperatures decreased by about \(1.4\;^{\circ }\text {C}\) for CMCC (Fig. 7a), and about \(0.7\;^{\circ }\text {C}\) for CNRM (Fig. 7b), compared to EXP-B0. Fig. 7a, b suggests that the impact of wet initial conditions on temperature extremes is even slightly more durable than on mean Tmax.
The SXP-WP shows an even stronger cooling response of Tmax extremes, with both models hardly reaching \(30\;^{\circ }\text {C}\) and a summer Tmax90 reduction of 3–5\(\;^{\circ }\text {C}\) with respect to EXP-B0. Basically, the effect of maintaining a saturated terrain during the entire summer is to suppress hot days in both models.
3.3.2 Dry sensitivity experiments
In both models, \({\text {Tmax}}_{\text {DI}}\) is warmer than \({\text {Tmax}}_{\text {B0}}\) until the end of the meteorological summer, with temperatures becoming indistinguishable in the two simulations by early September (Fig. 6a, b and Table 2). The fingerprint of the initial extreme soil water anomaly is remarkable throughout the entire summer: early in the season, the dry soil is not replenished by the rare precipitation falling across the MedTCR, and higher temperatures are favored by the unbalanced partitioning of the surface energy towards sensible turbulent fluxes (Fischer et al. 2007). The temperature difference between SXP-DI and EXP-B0 is \(1.3\;^{\circ }\text {C}\) for CMCC and \(2.1\;^{\circ }\text {C}\) for CNRM in early season (May, see Table 2), reduces to values around 1–1.5\(\;^{\circ }\text {C}\) throughout the summer, and become insignificant in September. Therefore, exceptionally dry soil moisture in late spring impacts the atmosphere atop for four months, with warmer average daytime conditions.
The warming is more persistent in SXP-DP: \({\text {Tmax}}_{\text {DP}}\) is consistently about 1.5–2\(\;^{\circ }\text {C}\) higher than \({\text {Tmax}}_{\text {B0}}\) in CMCC and CNRM (Fig. 6c, d and Table 2). Mean Tmax is overall higher in the prescribed SXP-DP for CMCC (Fig. 6c), meaning the artificial maintenance of extreme soil conditions determines an intensification of the PBL thermal response, and for both models from late summer onwards. The CNRM \({\text {Tmax}}_{\text {DP}}\) response is instead very similar to the \({\text {Tmax}}_{\text {DI}}\) response until mid August (Fig. 6b, d and Table 2). In both models, differences between \({\text {Tmax}}_{\text {DI}}\) (Fig. 6a, b) and \({\text {Tmax}}_{\text {DP}}\) (Fig. 6c, d) become remarkable after the end of the summer: while in the coupled SXPs Tmax becomes indistinguishable from EXP-B0, in the prescribed runs it gets considerably warmer than the baseline. When precipitation should restart replenishing the ground, in early autumn, the lack of water refill due to the SXP-DP constraint causes reduced evapotranspiration, and so the Tmax difference between SXP-DP and EXP-B0 increases again in autumn.
The main characteristics described for the mean Tmax are also found in Tmax90 (Fig. 7), but the stronger differences between SXPs and B0 suggest that a dry soil affects extreme temperatures more markedly. Dry initial state generates extreme temperatures that are \(2.1\;^{\circ }\text {C}\) (CMCC) to \(3\;^{\circ }\text {C}\) (CNRM) warmer than EXP-B0 in May, and on average 1.1–1.6\(\;^{\circ }\text {C}\) higher in the summer (Table 3).
In CMCC, \({\text {Tmax90}}_{\text {DP}}\) is very close to \({\text {Tmax90}}_{\text {DI}}\) in the first weeks (cf. Fig. 7a, c), then \({\text {Tmax90}}_{\text {DP}}\) becomes warmer. In CNRM, \({\text {Tmax90}}_{\text {DI}}\) is warmer than \({\text {Tmax90}}_{\text {DP}}\) until the end of August (cf. Fig. 7c, d), meaning that high temperatures are more intense when land and atmosphere interact with each other. If very hot atmospheric conditions are in place and compound with strong solar radiation, the amplified evaporative demand further dries the soil (Vicente-Serrano et al. 2020) in SXP-DI, while the prescribed land surface (SXP-DP) is not altered. When land and atmosphere interact, a self-intensification of heat waves is then observed in a soil moisture-limited region such as the Mediterranean in summer. This result finds confirmation in a recent review by Miralles et al. (2019).
As in Fig. 4, but for Tmax \(90{\text {th}}\) percentile
As for Tmax, differences between \({\text {Tmax90}}_{\text {DI}}\) (Fig. 7a, b) and \({\text {Tmax90}}_{\text {DP}}\) (Fig. 7c, d) become remarkable after the end of the summer: while in the coupled SXPs Tmax90 is indistinguishable from EXP-B0, in the prescribed runs the difference between \({\text {Tmax90}}_{\text {DP}}\) and \({\text {Tmax90}}_{\text {B0}}\) increases in September–October. The impact on Tmax and Tmax90 is further reinforced by an increase in sensible heat flux, due to a marked precipitation reduction (Ardilouze et al. 2020).
Probability distribution functions for a CMCC and b CNRM Tmax in the SXP-DI (dark yellow curves), SXP-DP (brown curves) and EXP-B0 (grey curves) experiments. CMCC: \({\text {Tmax}}_{\text {B0}}/{\text {Tmax90}}_{\text {B0}} = 28.3\;^{\circ }\text {C}/35.9\;^{\circ }\text {C}\); \({\text {Tmax}}_{\text {DI}}/{\text {Tmax90}}_{\text {DI}} = 29.3\;^{\circ }\text {C}/36.9^{\circ }\text {C}\); \({\text {Tmax}}_{\text {DP}}/{\text {Tmax90}}_{\text {DP}} = 30.4\;^{\circ }\text {C}/37.4\;^{\circ }\text {C}\). CNRM: \({\text {Tmax}}_{\text {B0}}/{\text {Tmax90}}_{\text {B0}} = 27.6\;^{\circ }\text {C}/34.3\;^{\circ }\text {C}\); \({\text {Tmax}}_{\text {DI}}/{\text {Tmax90}}_{\text {DI}} = 29.0\;^{\circ }\text {C}/35.5^{\circ }\text {C}\); \({\text {Tmax}}_{\text {DP}}/{\text {Tmax90}}_{\text {DP}} = 29.2\;^{\circ }\text {C}/35.0\;^{\circ }\text {C}\)
We show the probability distribution functions for summer (JJA) Tmax in SXP-DI, SXP-DP and EXP-B0, in order to quantify the different thermal response in the two models (Fig. 8). For both models, the three PDFs are different according to a Kolmogorov-Smirnov test, which rejects the null hypothesis at the 1% significance level. In CMCC, mean \({\text {Tmax}}_{\text {DI}}\) and mean \(\text {Tmax}_{\text {DP}}\) are \(0.8\;^{\circ }\text {C}\) and \(1.8\;^{\circ }\text {C}\) higher than \(\text {Tmax}_{\text {B0}} = 28.7\;^{\circ }\text {C}\) (Fig. 8a, see the figure caption for exact values). The same ranking is shown for mean Tmax in CNRM (Fig. 8b). However, in CNRM \(\text {Tmax}_{\text {DP}}\) is only slightly warmer (\(0.2\;^{\circ }\text {C}\)) than \(\text {Tmax}_{\text {DI}}\).
Extreme temperatures are significantly higher in the coupled experiment for CNRM (\(\text {Tmax90}_{\text {DI}} - \text {Tmax90}_{\text {DP}} = 0.6\;^{\circ }\text {C}\), Fig. 8b). This means that land–air coupling contributes to amplify heat extremes in the MedTCR. Instead, in CMCC \(\text {Tmax90}_{\text {DP}}\) > \(\text {Tmax90}_{\text {DI}}\), but the delta between the two is decreased with respect to mean Tmax: \(0.6\;^{\circ }\text {C}\) versus \(1\;^{\circ }\text {C}\). In this case, the impact of a constantly dry surface on the maintenance of torrid temperatures is stronger than that of an interacting land, but the two-way land-atmosphere coupling contributes to shrink the \(\text {Tmax90}_{\text {DP/DI}}\) gap with respect to mean Tmax. The different behaviour of CMCC and CNRM may be ascribed to the regional difference in the definition of MedTCR.
Seasonal evolution of evaporative fraction in the SXP-DI (full lines) and SXP-DP (dashed lines): light red (purple) lines show evaporative fraction for CMCC (CNRM). The top panel shows results for mean fluxes, the bottom panel for the composites of fluxes associated with Tmax exceeding the \(90{\text {th}}\) percentile
To explain this feature, we look at the evaporative fraction (EVF, Fig. 9), used to characterize the energy partition over land:
where LHF and SHF are the latent and sensible heat fluxes, respectively. In exceptionally dry situations, such as those designed in SXP-DI and SXP-DP, the main contributor to the energy balance is SHF, since evapotranspiration is strongly reduced due to the scarcity of soil water. In agreement with Fig. 6, \(\text {EVF}_{\text {DP}}\) (Fig. 9a) is clearly lower than \(\text {EVF}_{\text {DI}}\) in CMCC, while the two almost overlap in CNRM until late summer.
Figure 9b shows composites of surface fluxes associated with maximum temperatures > Tmax90, for both experiments and models. \(\text {EVF}_{\text {DI}}\) is, in both models, smaller than \(\text {EVF}_{\text {DP}}\) at the beginning of the hot season. This means that sensible heat flux initially has a more prominent role. In fact, the very dry soil featuring SXP-D* experiments at the season start is not the driest in every respect: if the environmental conditions are favorable (i.e. very hot and dry), the soil in SXP-DI can get even drier, because evapotranspiration increases in response to higher atmospheric evaporative demand. Instead, in SXP-DP land conditions are prescribed, therefore evapotranspiration does not change regardless of the strong forcing radiation and high temperatures. Therefore, \(\text {Tmax90}_{\text {DI}}\) may reach even higher values then \(\text {Tmax90}_{\text {DP}}\) in the beginning of summer. Basically, a drying soil is able to sustain and persist heat wave conditions that start at the end of the spring, likely causing an extension in their duration. This effects slowly fades away with scattered summer rain that waters the SXP-DI soils. Nevertheless, \(\text {SHF}_{\text {DI}}\) remains predominant in CNRM until the end of summer. Instead, in CMCC the turbulent surface fluxes in the two SXPs almost overlap by late May.
3.3.3 Climatological sensitivity experiments
No significant differences are found between \(\text {Tmax}_{\text {CI}}\) and \(\text {Tmax}_{\text {B0}}\) in either models for the entire warm season. \(\text {Tmax}_{\text {CI}}\) response to a soil wetness generated by climatological precipitation is very similar to the baseline, as long as land and atmosphere interact with each other (top panels in Figs. 6, 7 and Tables 2, 3). When soil is prescribed, both \(\text {Tmax}_{\text {CP}}\) and \(\text {Tmax90}_{\text {CP}}\) are remarkably colder than \(\text {Tmax}_{\text {B0}}\) for the entire season (Figs. 6c, d and 7c, d and Tables 2, 3).
Seasonal evolution of latent and sensible heat fluxes (blue and red lines, respectively, in \(\text {W/m}^{\text {2}}\)), soil moisture (green lines, in \(\text {m}^{\text {3}}/\text {m}^{\text {3}}\)) and precipitation (gray histograms, in mm) in the SXP-CI/CP and EXP-B0. The top panels shows results for the CMCC-SPS3 model, the bottom panels for the CNRM-CM6 model. Note that NOAA-20C precipitation is different in c–f, because it is averaged over two MedTCR that are not the same in the two models
Since the precipitation forcing comes from NOAA-20CR, we tested whether a large discrepancy between modeled and reanalysis precipitation was the cause of reduced Tmax. In fact, if NOAA-20CR rainfall was much larger than modeled rainfall, the generated soil moisture would be increased, possibly reducing mean and extreme maximum temperatures. This is the case for CMCC, whose precipitation is significantly lower than NOAA-20CR precipitation in spring (Fig. 10b, c). Hence, SXP-CP shows increased soil moisture fraction with respect to EXP-B0, particularly until mid summer. On the other hand, CMCC SXP-CI shows a fraction of moisture in the soil column comparable to that of SXP-CP (Fig. 10a, c), even if the model precipitation is considerably lower. The partition between latent and sensible heat in SXP-CI is instead more similar to that in EXP-B0, with a dominant role of SHF over LHF from late June to mid October (Fig. 10b). This explains why \(\text {Tmax}_{\text {CI}}\) \(\approx\) \(\text {Tmax}_{\text {B0}}\) and \(\text {Tmax90}_{\text {CI}} \approx \text {Tmax90}_{\text {B0}}\). \(\text {Tmax}_{\text {CP}}\) and \(\text {Tmax90}_{\text {CP}}\) are instead considerably colder, affected by an energy partition more favorable to LHF for longer time.
Regarding CNRM, Fig. 10 shows that modeled \(\text {Precip}_{\text {B0}}\) and \(\text {Precip}_{\text {CI}}\) are comparable, and so are the generated soil moistures. \(\text {Precip}_{\text {CP}}\) is larger than average \(\text {Precip}_{\text {B0}}\) in spring, but the total soil moisture is considerably lower (Fig. 10f). In particular, when the rain season restarts after the summer drought, the soil moisture recovery in SXP-CP is much slower than SXP-CI and EXP-B0.
As for CMCC, \(\text {LHF}_{\text {CP}}\) dominates over \(\text {SHF}_{\text {CP}}\) (\(\text {SHF}_{\text {CP}}> \text {LHF}_{\text {CP}}\) from early July to mid September, Fig. 10c) almost two month longer than in SXP-CI (\(\text {SHF}_{\text {CI}} > \text {LHF}_{\text {CI}}\) from late June to mid October, Fig. 10a). The surface fluxes partition, again, clarifies why \(\text {Tmax}_{\text {CP}} < \text {Tmax}_{\text {CI,B0}}\).
The energy partition is little dependent on the total soil moisture. Rather, the vertical distribution of water within the soil column (Fig. 11) explains the different evaporative fractions featuring the sensitivity experiments: surface soil moisture, which can easily evaporate and then cause intensified latent heat flux, appears as the main contributor to the decrease in near-surface temperatures observed in Figs. 6c, d and 7c, d.
The way soil moisture is generated in SXP-CI (Figs. S3 and S4 in supplemental material), sheds light on the reason of such a difference in the energy partition, with respect to SXP-CP. In the prescribed experiment, the average precipitation forcing (see vertical histograms in Fig. 10c–f), imposed every third hour to produce the land surface state in SXP-CP, is not intense enough to water the deeper soil layers. Most part of the precipitated water evaporates before infiltrating, not contributing to the deeper soil moisture. In EXP-B0 and SXP-CI instead, scattered but stronger rainfall (Figs. S3 and S4) waters the soil in depth, and terrain gets replenished at the end of the dry season.
Therefore, surface soil water is more abundant in the prescribed experiment than in the coupled ones, because it is affected by constant but small precipitation amounts (Fig. 10c, f). On the other hand, this surface water is subject to almost immediate evaporation, driven by the high temperatures characterizing the MedTCR warm semester. Therefore, only a minor portion of it infiltrates through the soil, and deeper layer moisture is decreased in SXP-CP with respect to SXP-CI (Fig. 11d–h). What is uncovered in the simulation is similar to what is observed over areas of intense agriculture, that are very widespread in Europe, where expanding irrigation practices have led to regional cooling (Yang et al. 2020), and will probably contribute to alleviate hot extremes in a warming climate (Thiery et al. 2020). In the coupled experiments, most rainfall penetrates into the terrain, replenishing its water amount. The evaporation of this water is much slower and contributes less to near-surface cooling.
4 Discussion
The experimental setup was partly inspired by that of Lorenz et al. (2010), who used very strong soil perturbations to assess the impact of soil moisture on heat wave persistence. They also made use of the wilting point and field capacity thresholds to constrain soil water. At a first sight, the degree of model perturbation may appear unrealistically strong for the dry and wet experiments. Modeled initial soil moisture is in fact obtained after a one-year-run with zero precipitation (dry runs) and precipitation increased by 3 standard deviations (wet runs). However, this choice relies on evapotranspiration thresholds that are physically sound and applicable in a similar way to different GCMs, regardless of the different parameterizations featured in their land surface schemes.
Only such a large perturbation allows to reach amounts of soil moisture close to the wilting point and field capacity by the beginning of the summer. A 1-year run to obtain these extreme conditions was due because the two models’ soil water is scarcely sensitive to precipitation, and it is hard to say whether this low responsiveness is accurate, since observational-based studies still struggle to establish strength and location of the soil moisture response to rain (Ford et al. 2018). Observational studies report reaching soil moisture contents below the wilting point after few months of very little rain (e.g. Ramos and Martínez-Casasnovas (2010)). The time to reach field capacity is strongly dependent on soil hydraulic properties, such as porosity, permeability, etc. (Twarakavi et al. 2009), which are crudely parameterized in GCMs, therefore often distant from the observed world.
On the other hand, the strong perturbation may disclose a few criticalities that the Mediterranean region will face in a future warming world. Considerable changes in soil moisture regimes are projected by the end of the century, and these changes strongly affect, among others, the Mediterranean climate, in particular for temperature (Seneviratne et al. 2013). The response of temperature to soil moisture-induced variations in evaporative cooling is remarkable, with strongest effects on extremes. In the quasi-totality of CMIP5 projections, the expected drying signal in southern Europe is highly linked to warmer temperatures and increased solar radiation (Ruosteenoja et al. 2018).
The climatological experiments raise a question on the appropriateness of these runs, because the choice of daily average precipitation as a constraint for soil water does not reflect any plausible weather condition. A more realistic distribution of daily precipitation forcing across the season would assure a definite answer on the reason behind the distinct temperature response between SXP-CI and SXP-CP: is the cooling caused by artificial block of the interactive mechanisms between soil and atmosphere, or the way rainfall is prescribed plays a dominant role in reducing the forced Tmax? This question cannot find a definite answer on the basis of this study. The design of the climatological runs could then pave the way for the outline of future sensitivity experiments involving precipitation. Besides, this argument could probably also be extended to other contexts and experiments, such those following the AMIP protocol. The use of monthly average SSTs as boundary conditions is largely unable to capture, e.g., the threshold exceedance needed for triggering deep convection and establishing specific teleconnection mechanisms.
On the other hand, the strongly idealized climatological setup made clear that surface water, rather than soil moisture in general, is a major actor in the land-air coupling process. This outcome adds a tiny piece to the complicated puzzle of soil moisture-atmosphere interactions, rarely considered in previous literature on the topic.
Finally, in this study we did not consider the minimum temperature response to changes in land surface conditions, although this topic is highly relevant (Thomas et al. 2020), and could be of major importance for its impact on health and energy. However, the processes regulating nighttime temperatures are strongly linked to other players, such as the boundary layer stability, cloudiness and long-wave radiation. Therefore, we felt that this analysis would not fit in the present paper.
5 Conclusions
This work investigates the temperature response to soil water conditions in the transitional climate region of the Mediterranean (MedTCR), that is the region where soil moisture, and not radiation, is the main constraint to evapotranspiration. Maximum daily temperatures (Tmax), which are the main focus of the study, are therefore largely modulated by the availability of soil moisture. A novel set of six sensitivity experiments was used to investigate this effect: coupled (i.e. land and atmosphere interact with each other) and forced (i.e. atmosphere is constrained by a land surface unresponsive to the atmospheric forcing) runs are launched with arid, saturated and average soil moisture initial conditions.
Dry soils favor the onset of persisting higher summer temperatures, while anomalously wet soils alleviate temperature peaks. Dry and wet conditions at the beginning of the Mediterranean summer exert a significant impact on both MedTCR mean and extreme Tmax. The imprint of land initial state lasts for about four months, meaning that land surface memory, combined with the large sensitivity of near-surface temperature to a highly-varying component, such as the soil moisture, may play an important role in the predictability at the seasonal time-scale (Dirmeyer and Halder 2017).
If wet conditions are artificially maintained for the entire warm semester (SXP-WP), extreme temperatures (\(\text {Tmax}_{\text {90}}\)) may not develop at all, hardly reaching \(30^\circ\), that is 3–5\(\;^{\circ }\text {C}\) lower than the average \(\text {Tmax}_{\text {90}}\) for the area. When aridity is imposed and maintained by means of a prescribed dry soil (SXP-DP), warmer temperatures persist through September and October. Normally, these months are characterized by a sharp recovery in precipitation, and consequent evaporation contributes to buffer the air-land boundary warming. When the soil is artificially kept dry, the cooling effect is suppressed and the lower atmosphere becomes more than \(1\;^{\circ }\text {C}\) warmer compared to the case of an interactive soil.
When a hot-weather-favorable atmospheric pattern is in place at the beginning of the season, the conditions for persisting and intensified heat waves are supported by an interacting land surface. In fact, soil can respond to the increased atmospheric evaporative demand and become drier, sustaining heatwaves for longer. This effect is long-lasting in the CNRM model, while in the CMCC model it vanishes after few weeks, when the prescribed dry soil starts inducing a stronger temperature response than the interactive soil.
In the climatological simulations, the evolution of near-surface temperatures in the coupled experiment is almost indistinguishable from the baseline, following very similar initial conditions and homologous land-atmosphere interaction. In the prescribed SXP-CP, the lower atmosphere is considerably colder than the baseline, especially in terms of extreme temperatures. The average precipitation is imposed on a 3-hourly time basis to generate the prescribed land conditions in SXP-CP, and its amount is so small that most part of it evaporates before infiltrating, not contributing to the deeper soil moisture. This sustained evaporation continuously cools the boundary layer and dampens temperature highs.
The moisture amount in the surface soil layer, rather than its total fraction in the soil column, plays a fundamental role in the modulation of temperature extremes. Surface water is very effective because its fast evaporation modifies the evaporative fraction locally, increasing the latent heat flux. If a sustained source of surface water is maintained during the course of the Mediterranean dry season, through e.g. crop irrigation, local temperatures would be lower and extreme values strongly moderated. This aspect should be contemplated in post-processed evaluations of seasonal forecast outlooks, in regions characterized by a high agricultural density. Dynamical predictions, in fact, do not usually consider the effect of irrigation on near-surface temperatures, as long as farming practices are not resolved or parameterized in the GCMs, possibly resulting in biased forecasts.
References
Ardilouze C, Materia S, Batté L et al (2020) Precipitation response to extreme soil moisture conditions over the Mediterranean. Clim Dyn. https://doi.org/10.1007/s00382-020-05519-5
Baek SH, Smerdon JE, Cook BI, Williams AP (2021) Us pacific coastal droughts are predominantly driven by internal atmospheric variability. J Clim 34(5):1947–1962. https://doi.org/10.1175/JCLI-D-20-0365.1
Batjes NH (2012) Isric-wise derived soil properties on a 5 by 5 arc-minutes global grid (ver. 1.2). In: Technical report, ISRIC-World Soil Information
Berg A, Sheffield J (2018) Soil moisture-evapotranspiration coupling in CMIP5 models: relationship with simulated climate and projections. J Clim 31(12):4865–4878
Boé J, Terray L (2008) Uncertainties in summer evapotranspiration changes over Europe and implications for regional climate change. Geophys Res Lett 35:L05702
Canadell J, Jackson R, Ehleringer J, Mooney H, Sala O, Schulze ED (1996) Maximum rooting depth of vegetation types at the global scale. Oecologia 108(4):583–595
Carrer D, Meurey C, Ceamanos X, Roujean JL, Calvet JC, Liu S (2014) Dynamic mapping of snow-free vegetation and bare soil albedos at global 1 km scale from 10-year analysis of modis satellite products. Remote Sens Environ 140:420–432
Chang LL, Dwivedi R, Knowles JF, Fang YH, Niu GY, Pelletier JD, Rasmussen C, Durcik M, Barron-Gafford GA, Meixner T (2018) Why do large-scale land surface models produce a low ratio of transpiration to evapotranspiration? J Geophys Res Atmos 123(17):9109–9130
Chen X, Zhou T (2018) Relative contributions of external sst forcing and internal atmospheric variability to july-august heat waves over the yangtze river valley. Clim Dyn 51(11):4403–4419
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ, Yin X, Gleason BE, Vose RS, Rutledge G, Bessemoulin P et al (2011) The twentieth century reanalysis project. Q J R Meteorol Soc 137(654):1–28
Decharme B, Delire C, Minvielle M, Colin J, Vergnes JP, Alias A, Saint-Martin D, Séférian R, Sénési S, Voldoire A (2019) Recent changes in the isba-ctrip land surface system for use in the cnrm-cm6 climate model and in global off-line hydrological applications. J Adv Model Earth Syst 11(5):1207–1252
Di Castri F (1991) An ecological overview of the five regions of the world with mediterranean climate. Biogeography of Mediterranean invasions. Cambridge University Press, Cambridge, pp 3–15
Dirmeyer PA (2001) An evaluation of the strength of land-atmosphere coupling. J Hydrometeorol 2(4):329–344
Dirmeyer PA (2003) The role of the land surface background state in climate predictability. J Hydrometeorol 4(3):599–610
Dirmeyer PA (2011) The terrestrial segment of soil moisture–climate coupling. Geophys Res Lett 38:L16702
Dirmeyer PA, Halder S (2017) Application of the land-atmosphere coupling paradigm to the operational coupled forecast system, version 2 (cfsv2). J Hydrometeorol 18(1):85–108
Dirmeyer PA, Schlosser CA, Brubaker KL (2009) Precipitation, recycling, and land memory: an integrated analysis. J Hydrometeorol 10(1):278–288
Eltahir EA (1998) A soil moisture-rainfall feedback mechanism: 1. Theory and observations. Water Resour Res 34(4):765–776
Faroux S, Kaptué Tchuenté A, Roujean JL, Masson V, Martin E, Moigne PL (2013) Ecoclimap-ii/Europe: a twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci Model Dev 6(2):563–582
Fennessy MJ, Shukla J (1999) Impact of initial soil wetness on seasonal atmospheric prediction. J Clim 12(11):3167–3180
Fischer EM, Seneviratne SI, Vidale PL, Lüthi D, Schär C (2007) Soil moisture–atmosphere interactions during the 2003 European summer heat wave. J Clim 20(20):5081–5099
Ford TW, Quiring SM, Thakur B, Jogineedi R, Houston A, Yuan S, Kalra A, Lock N (2018) Evaluating soil moisture-precipitation interactions using remote sensing: a sensitivity analysis. J Hydrometeorol 19(8):1237–1253
Franks PJ, Bonan GB, Berry JA, Lombardozzi DL, Holbrook NM, Herold N, Oleson KW (2018) Comparing optimal and empirical stomatal conductance models for application in earth system models. Glob Change Biol 24(12):5708–5723
Global Soil Data Task (2000) Global soil data products CD-ROM contents (IGBP-DIS). https://doi.org/10.3334/ORNLDAAC/565. http://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=565
Gettelman A, Hannay C, Bacmeister J, Neale R, Pendergrass A, Danabasoglu G, Lamarque JF, Fasullo J, Bailey D, Lawrence D et al (2019) High climate sensitivity in the community earth system model version 2 (cesm2). Geophys Res Lett 46(14):8329–8337
Guo Z, Dirmeyer PA, DelSole T (2011) Land surface impacts on subseasonal and seasonal predictability. Geophys Res Lett 38:L24812
Guo Z, Dirmeyer PA (2013) Interannual variability of land-atmosphere coupling strength. J Hydrometeorol 14(5):1636–1646
Hauser M, Orth R, Seneviratne SI (2017) Investigating soil moisture–climate interactions with prescribed soil moisture experiments: an assessment with the community earth system model (version 1.2). Geosci Model Dev 10(4):1665–1677
Hirschi M, Seneviratne SI, Alexandrov V, Boberg F, Boroneant C, Christensen OB, Formayer H, Orlowsky B, Stepanek P (2011) Observational evidence for soil-moisture impact on hot extremes in southeastern Europe. Nat Geosci 4(1):17–21
Hugelius G, Tarnocai C, Broll G, Canadell J, Kuhry P, Swanson D (2013) The northern circumpolar soil carbon database: spatially distributed datasets of soil coverage and soil carbon storage in the northern permafrost regions. Earth Syst Sci Data 5(1):3–13
Jefferson JL, Maxwell RM (2015) Evaluation of simple to complex parameterizations of bare ground evaporation. J Adv Model Earth Syst 7(3):1075–1092
Knist S, Goergen K, Buonomo E, Christensen OB, Colette A, Cardoso RM, Fealy R, Fernández J, García-Díez M, Jacob D et al (2017) Land-atmosphere coupling in euro-cordex evaluation experiments. J Geophys Res Atmos 122(1):79–103
Koppen WD (1936) Das geographische system der klimat. In: Koppen WD (ed) Handbuch der klimatologie. Gebrüder Borntraeger, p 46
Koster RD, Suarez MJ (2001) Soil moisture memory in climate models. J Hydrometeorol 2(6):558–570
Koster RD, Sud Y, Guo Z, Dirmeyer PA, Bonan G, Oleson KW, Chan E, Verseghy D, Cox P, Davies H et al (2006) Glace: the global land–atmosphere coupling experiment. Part i: overview. J Hydrometeorol 7(4):590–610
Lawrence PJ, Chase TN (2007) Representing a new modis consistent land surface in the community land model (CLM 3.0). J Geophys Res Biogeosci 112:G01023
Lionello P, Malanotte-Rizzoli P, Boscolo R (2006) Mediterranean climate variability. Elsevier
Lorenz R, Jaeger EB, Seneviratne SI (2010) Persistence of heat waves and its link to soil moisture memory. Geophys Res Lett 37:L09703
Materia S, Borrelli A, Bellucci A, Alessandri A, Di Pietro P, Athanasiadis P, Navarra A, Gualdi S (2014) Impact of atmosphere and land surface initial conditions on seasonal forecasts of global surface temperature. J Clim 27(24):9253–9271
Miralles DG, Gentine P, Seneviratne SI, Teuling AJ (2019) Land-atmospheric feedbacks during droughts and heatwaves: state of the science and current challenges. Ann N Y Acad Sci 1436(1):19
Miralles DG, van den Berg M, Teuling AJ, De Jeu RAM (2012) Soil moisture-temperature coupling: a multiscale observational analysis. Geophys Res Lett 39:L21707
Mueller B, Seneviratne SI (2012) Hot days induced by precipitation deficits at the global scale. Proc Natl Acad Sci 109(31):12398–12403
Myneni RB, Hoffman S, Knyazikhin Y, Privette J, Glassy J, Tian Y, Wang Y, Song X, Zhang Y, Smith G et al (2002) Global products of vegetation leaf area and fraction absorbed par from year one of modis data. Remote Sens Environ 83(1–2):214–231
Neale R, Chen C, Gettelman A, Lauritzen P, Park S, Williamson D, Conley A, Garcia R, Kinnison D, Lamarque J, et al (2010) Description of the ncar community atmosphere model (CAM 5.0). In: NCAR Tech Note NCAR/TN-486+ STR, vol 1, issue (1), pp 1–12
Oleson K, Lawrence D, Bonan G, Drewniak B, Huang M, Koven C, Levis S, Li F, Riley W, Subin Z, et al (2013) Technical description of version 4.5 of the community land model (clm)(ncar technical note no. ncar/tn-503+ str). In: Citeseer, National Center for Atmospheric Research, PO Box 3000
Orth R, Seneviratne S (2012) Analysis of soil moisture memory from observations in Europe. J Geophys Res Atmos 117:D15115
Peano D, Materia S, Collalti A, Alessandri A, Anav A, Bombelli A, Gualdi S (2019) Global variability of simulated and observed vegetation growing season. J Geophys Res Biogeosci 124(11):3569–3587
Prodhomme C, Doblas-Reyes F, Bellprat O, Dutra E (2016) Impact of land-surface initialization on sub-seasonal to seasonal forecasts over Europe. Clim Dyn 47(3–4):919–935
Ramos M, Martínez-Casasnovas J (2010) Effects of precipitation patterns and temperature trends on soil water available for vineyards in a mediterranean climate area. Agric Water Manag 97(10):1495–1505
Roehrig R, Beau I, Saint-Martin D, Alias A, Decharme B, Guérémy JF, Voldoire A, Abdel-Lathif AY, Bazile E, Belamari S et al (2020) The cnrm global atmosphere model arpege-climat 63: description and evaluation. J Adv Model Earth Syst 12:e2020MS002-7
Ruosteenoja K, Markkanen T, Venäläinen A, Räisänen P, Peltola H (2018) Seasonal soil moisture and drought occurrence in Europe in cmip5 projections for the 21st century. Clim Dyn 50(3):1177–1192
Sanna A, Borrelli A, Athanasiadis P, Materia S, Storto A, Navarra A, Tibaldi S, Gualdi S, et al (2016) CMCC-SPS3: the CMCC seasonal prediction system 3. In: CMCC Research Paper (RP0285)
Santanello JA Jr, Peters-Lidard CD, Kumar SV (2011) Diagnosing the sensitivity of local land–atmosphere coupling via the soil moisture–boundary layer interaction. J Hydrometeorol 12(5):766–786
Schwingshackl C, Hirschi M, Seneviratne SI (2017) Quantifying spatiotemporal variations of soil moisture control on surface energy balance and near-surface air temperature. J Clim 30(18):7105–7124
Seneviratne SI, Koster RD (2012) A revised framework for analyzing soil moisture memory in climate data: derivation and interpretation. J Hydrometeorol 13(1):404–412
Seneviratne SI, Koster RD, Guo Z, Dirmeyer PA, Kowalczyk E, Lawrence D, Liu P, Mocko D, Lu CH, Oleson KW et al (2006a) Soil moisture memory in agcm simulations: analysis of global land–atmosphere coupling experiment (glace) data. J Hydrometeorol 7(5):1090–1112
Seneviratne SI, Lüthi D, Litschi M, Schär C (2006b) Land–atmosphere coupling and climate change in Europe. Nature 443(7108):205–209
Seneviratne SI, Corti T, Davin EL, Hirschi M, Jaeger EB, Lehner I, Orlowsky B, Teuling AJ (2010) Investigating soil moisture–climate interactions in a changing climate: a review. Earth Sci Rev 99(3–4):125–161
Seneviratne SI, Wilhelm M, Stanelle T, van den Hurk B, Hagemann S, Berg A, Cheruy F, Higgins ME, Meier A, Brovkin V et al (2013) Impact of soil moisture-climate feedbacks on cmip5 projections: first results from the glace-cmip5 experiment. Geophys Res Lett 40(19):5212–5217
Shukla J, Mintz Y (1982) Influence of land-surface evapotranspiration on the earth’s climate. Science 215(4539):1498–1501
Teng H, Branstator G, Tawfik AB, Callaghan P (2019) Circumglobal response to prescribed soil moisture over North America. J Clim 32(14):4525–4545
Thiery W, Visser AJ, Fischer EM, Hauser M, Hirsch AL, Lawrence DM, Lejeune Q, Davin EL, Seneviratne SI (2020) Warming of hot extremes alleviated by expanding irrigation. Nat Commun 11(1):1–7
Thomas NP, Bosilovich MG, Marquardt Collow AB, Koster RD, Schubert SD, Dezfuli A, Mahanama SP (2020) Mechanisms associated with daytime and nighttime heat waves over the contiguous united states. J Appl Meteorol Climatol 59(11):1865–1882
Titchner HA, Rayner NA (2014) The met office hadley centre sea ice and sea surface temperature data set, version 2: 1. Sea ice concentrations. J Geophys Res Atmos 119(6):2864–2889
Twarakavi NKC, Sakai M, Šimůnek J (2009) An objective analysis of the dynamic nature of field capacity. Water Resour Res 34:W10410
Vicente-Serrano SM, McVicar TR, Miralles DG, Yang Y, Tomas-Burguera M (2020) Unraveling the influence of atmospheric evaporative demand on drought and its response to climate change. Wiley Interdiscip Rev Clim Change 11(2):e632
Vogel MM, Orth R, Cheruy F, Hagemann S, Lorenz R, van den Hurk BJ, Seneviratne SI (2017) Regional amplification of projected changes in extreme temperatures strongly controlled by soil moisture-temperature feedbacks. Geophys Res Lett 44(3):1511–1519
Voldoire A, Saint-Martin D, Sénési S, Decharme B, Alias A, Chevallier M, Colin J, Guérémy JF, Michou M, Moine MP et al (2019) Evaluation of cmip6 deck experiments with cnrm-cm6-1. J Adv Model Earth Syst 11(7):2177–2213
Walker J, Rowntree P (1977) The effect of soil moisture on circulation and rainfall in a tropical model. Q J R Meteorol Soc 103(435):29–46
Wang H, Schubert SD, Koster RD, Chang Y (2019) Phase locking of the boreal summer atmospheric response to dry land surface anomalies in the northern hemisphere. J Clim 32(4):1081–1099
Xu L, Dirmeyer P (2011) Snow-atmosphere coupling strength in a global atmospheric model. Geophys Rese Lett 38:L13401
Yang Q, Huang X, Tang Q (2020) Irrigation cooling effect on land surface temperature across china based on satellite observations. Sci Total Environ 705(135):984
Zemp DC, Schleussner CF, Barbosa HM, Hirota M, Montade V, Sampaio G, Staal A, Wang-Erlandsson L, Rammig A (2017) Self-amplified amazon forest loss due to vegetation-atmosphere feedbacks. Nat Commun 8(1):1–10
Zeng X (2001) Global vegetation root distribution for land modeling. J Hydrometeorol 2(5):525–530
Acknowledgements
This work has been performed in the framework of the MEDSCOPE (MEDiterranean Services Chain based On climate PrEdictions) ERA4CS project (grant agreement no. 690462) funded by the European Union. Chloe Prodhomme was supported by the Spanish Juan de la Cierva (IJCI-2016-30802) program. Support for the Twentieth Century Reanalysis Project version 2c dataset is provided by the U.S. Department of Energy, Office of Science Biological and Environmental Research (BER), and by the National Oceanic and Atmospheric Administration Climate Program Office.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This paper is a contribution to the MEDSCOPE special issue on the drivers of variability and sources of predictability for the European and Mediterranean regions at subseasonal to multi-annual time scales. MEDSCOPE is an ERA4CS project co-funded by JPI Climate. The special issue was coordinated by Silvio Gualdi and Lauriane Batté.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Materia, S., Ardilouze, C., Prodhomme, C. et al. Summer temperature response to extreme soil water conditions in the Mediterranean transitional climate regime. Clim Dyn 58, 1943–1963 (2022). https://doi.org/10.1007/s00382-021-05815-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-021-05815-8