Abstract
The impact of the observed sea surface temperature (SST) frequency in the model initialization on the prediction of the boreal summer intraseasonal oscillation (BSISO) over the Western North Pacific (WNP) is investigated using the Beijing Climate Center Climate System Model. Three sets of hindcast experiments initialized by the observed monthly, weekly and daily SST data (referred to as the Exp_MSST, Exp_WSST and Exp_DSST, respectively) are conducted with 3-month integration starting from the 1st, 11th, and 21st day of each month in June–August during 2000–2014, respectively. The results show that the useful prediction skill of BSISO index reaches out to about 10 days in the Exp_MSST, and further increases by 1–2 days in the Exp_WSST and Exp_DSST. The skill differences among various hindcast experiments are especially apparent during the forecast time of 6–20 days. Focusing on the strong BSISO cases in this period, the BSISO activity and its related moist static energy (MSE) characteristics over the WNP are further diagnosed. It is found that from the Exp_MSST to the Exp_WSST and Exp_DSST, the enhanced BSISO prediction skill is associated with the more realistic variations of intraseasonal MSE and its tendency. Among the various budget terms that dominate the MSE tendency, the surface latent heat flux and MSE advection are evidently improved, with reduction of mean biases by more than 21% and 10%, respectively. Therefore, the better reproduced MSE variation may contribute to the more skillful BSISO forecast through improving the surface evaporation as well as atmospheric convergence and divergence that related to the BSISO activity. Our findings suggest the necessity of increasing the observed SST frequency (i.e., from monthly to weekly or daily) in the initialization process of coupled models to enhance the actual BSISO predictability, since some current subseasonal forecast operations and researches still use relatively low-frequency SST observations for the model initialization.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The boreal summer intraseasonal oscillation (BSISO) is an essential mode of atmospheric variability with a period of 10–60 days over the Asian summer monsoon region (Yasunari 1980; Zhu and Wang 1993). The BSISO correlates with the monsoon dynamics (Yasunari 1979; Lau and Chan 1986), tropical cyclone activity (Liebmann et al. 1994; Weng and Hsu 2017) and the El Niño-Southern Oscillation (Ding and Wang 2005; Lin 2019) and can result in severe weather and climate events (such as rainfall extremes and heat waves) over the Western North Pacific (WNP) region (Mao et al. 2010; Ren et al. 2013; Hsu et al. 2016, 2017). Due to its recurrent nature (Van den Dool and Saha 1990) and association with the tropical and extratropical atmospheric circulations (Ding and Wang 2005), the BSISO acts as a leading source of subseasonal predictability over the WNP (Waliser et al. 2003; Vitart et al. 2012; Hsu et al. 2017; Fang et al. 2019).
Despite great progress in the climate model development, the capability in BSISO simulation and prediction is still limited (Waliser et al. 2003; Sobel et al. 2008; Fang et al. 2016). Most current models show deficiency in simulating the spatial structure, amplitude, evolution and northward propagation of BSISO (Sabeerali et al. 2013; Hu et al. 2017; Neena et al. 2017). In the latest Subseasonal to Seasonal (S2S) Prediction Project, most state-of-the-art operational models exhibit useful BSISO forecast skill of about 2 weeks in advance (Jie et al. 2017). This skill is much lower than the potential BSISO predictability limit of about 5 weeks (Ding et al. 2011). Using the hindcasts by several models in the Intraseasonal Variability Hindcast Experiment (ISVHE) project, Lee et al. (2015) also found that the multi-model mean actual prediction skill is clearly lower than the theoretical predictability of BSISO, indicating that there is large room to improve the BSISO prediction.
The prediction of intraseasonal oscillation is found to be sensitive to many factors, such as physical parameterization (e.g., Liu et al. 2019), model resolution (e.g., Vitart 2017), ensemble generation (e.g., Rashid et al. 2011), air-sea interaction (e.g., Fu et al. 2008) and initial conditions (e.g., Liu et al. 2017; Bo et al. 2020). Among these factors, SST initial condition and its impact have drawn much attention. The atmosphere-only model is comparable to its coupled counterpart in the predictability and prediction skill of intraseasonal oscillation if specified with daily SST forecasted by the coupled run (Fu et al. 2008, 2013). Abhilash et al. (2014) found that the bias-corrected SST has great influence on the BSISO prediction at the 10–20-day extended range scale. Wang et al. (2015) noted that the uncertainty of observed SST data could exert important impact on the prediction of tropical intraseasonal oscillation beyond the forecast time of 5 days. Liu et al. (2017) and Bo et al. (2020) also showed that the prediction skill of intraseasonal oscillation can be increased by the updated SST initial conditions beyond the forecast time of 5 days. Some studies further explored that the mean state, temporal and spatial resolution of SST included in the model initialization could affect the prediction of intraseasonal oscillation (e.g., Wang et al. 2009; Seo et al. 2014; Zhang et al. 2019).
Previous studies mostly based on the atmosphere-only models have suggested that adopting the SST observations with relatively higher temporal frequency during the model initialization can improve the model performance in capturing the intraseasonal variability. Simulations with daily SST forcing show improvements against those with monthly SST forcing in terms of periodicity, intensity and propagation of intraseasonal oscillation (Fu and Wang 2004; Fu et al. 2003; Klingaman et al. 2008; Pegion and Kirtman 2008). Stan (2018) revealed that the inclusion of 1–5-day frequency of SST forcing is essential to the accurate simulation of intraseasonal oscillation. Zhang et al. (2019) noted that the experiments with prescribed daily SST forcing exhibit higher prediction skill of BSISO than those with seasonal SST forcing. Kim et al. (2008) and Boisséson et al. (2012) also found that the forecast skill of tropical intraseasonal oscillation is higher when forcing model with daily or weekly SST than with monthly SST.
To investigate the impacts of observed SST frequency in the model initialization on the subseasonal prediction, previous studies focused more on the intraseasonal oscillation during boreal winter than in boreal summer. Additionally, most of these studies used atmosphere-only models rather than coupled models. Given the importance of ocean-atmosphere coupling to the representation of intraseasonal oscillation, it is worth further exploring the effect of SST initial condition on the BSISO prediction using multi-component coupled models. Meanwhile, exploring the influence of observed SST frequency in the model initialization is also a demand for the practice in dynamical climate forecasts. This is because the initialization of forecast model needs to determine the temporal frequency of SST data when adopting nudging scheme or the size of time window for assimilation analysis. In this context, this study conducts a series of hindcast experiments using a coupled model to address the following questions: (1) Whether and to what extent increasing the frequency of SST observations in the model initialization process could improve the prediction skill of BSISO over the WNP? (2) What are the possible pathways for the impact of observed SST frequency in the model initialization on the BSISO forecast?
The rest of this paper is organized as follows. The model, data, experimental design and methods are described in Sect. 2. Section 3 provides the evaluation of model performance in the long-term free run simulation of BSISO. Section 4 examines the BSISO prediction skills in the hindcast experiments initialized by the SST observations with different temporal frequencies, and Sect. 5 gives the diagnostics of moist static energy budget for BSISO forecasts in various experiments. The summary and discussion are provided in Sect. 6.
2 Model, data, experimental design, and methods
2.1 Model
The model used in this study is the Beijing Climate Center Climate System Model version 2 (BCC-CSM2) with moderate resolution. It is a fully coupled model with atmosphere, land, ocean and sea ice components. The atmospheric component is the BCC Atmospheric General Circulation Model version 2 with a horizontal resolution of T106 (approximately 110 km) and 56 vertical hybrid sigma/pressure layers (Wu et al. 2019). The land component is the BCC Atmosphere and Vegetation Interaction Model Version 2 with T106 triangular truncation (Li et al. 2019). The ocean and sea ice components adopt the Modular Ocean Model Version 4 (Griffies et al. 2005) and the Sea Ice Simulator (Winton 2000) from the National Oceanic and Atmospheric Administration (NOAA) Geophysical Fluid Dynamics Laboratory (GFDL) respectively, with a horizontal resolution of 1/3°–1° at tripolar grid.
The BCC-CSM2 is one of the members in the Coupled Model Intercomparison Project Phase 6 (CMIP6). More details about BCC-CSM2 and its application in climate projection are documented in Wu et al. (2019). Several earlier versions of this model have been widely used in the S2S and seasonal-to-interannual climate predictions (e.g., Huang et al. 2013; Liu et al. 2015, 2017, 2019; Fang et al. 2019; Bo et al. 2020).
2.2 Data
To initialize the model for climate prediction, the following datasets from 2000 to 2014 are used: (1) the 6-hourly atmospheric winds, temperature, humidity, and surface pressure fields from the National Center for Environmental Prediction’s Final Operational Global Analysis (NCEP-FNL; Kalnay et al. 1996), which are available at https://rda.ucar.edu/datasets/ds083.2/; and (2) the daily SST from NOAA Optimum Interpolation Sea Surface temperature (OISST) dataset (Reynolds et al. 2007), which can be obtained from https://www.ncdc.noaa.gov/oisst.
In addition, we use several datasets during 2000–2014 to evaluate the model results as follows: (1) the daily outgoing longwave radiation (OLR) from NOAA (Liebmann and Smith 1996), which is available at https://catalog.data.gov/dataset/noaa-daily-outgoing-longwave-radiation-olr; (2) the daily precipitation from the Global Precipitation Climatology Project (GPCP; Adler et al. 2003), which can be downloaded at https://www.ncdc.noaa.gov/cdr/atmospheric/precipitation-gpcp-daily; and (3) the daily wind, temperature, geopotential height, specific humidity, longwave and shortwave radiative heating, surface latent heat and surface sensible heat fields from the European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5 (ERA5; Hersbach et al. 2020), which are available at https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5.
2.3 Experimental design
To conduct the S2S prediction, the model initial conditions are firstly obtained by three sets of initialization experiments based on a nudging strategy. As shown in Fig. 1, during the initialization process, the atmospheric component is nudged toward 6-hourly NCEP-FNL atmospheric reanalysis, while the ocean component is nudged toward monthly/weekly/daily SST observations derived from the daily OISST data (i.e., raw OISST data is averaged over time window with monthly, weekly, or daily interval). The SST observations with different frequencies (i.e., daily, weekly and monthly) used for the three sets of initialization experiments in 2001 are shown as an example in Fig. 2. It is obvious that the SST with high frequency displays larger variability than that with low frequency (Fig. 2a). This SST difference in the initialization experiments may have distinct impacts on the predictions of rainfall and circulation. For example, for the forecast case starting from 1 August 2001, the use of higher-frequency SST observations in the initialization experiment clearly improves the skill of rainfall prediction at long forecast time (Fig. 2b). The initialization experiments nudged by monthly, weekly, or daily SST observations are all integrated from 1 January 2000 to 31 December 2014 to output compatible model initial conditions at each day for the hindcast experiments shown below. More detailed descriptions of the initialization scheme can be found in Liu et al. (2017).
a Time series of the SST observations (unit: °C) with different frequencies regionally averaged over the area (10–20 °N, 130–140 °E) during June–August 2001 in the initialization process of various initialization experiments. b Time series of the precipitation (unit: mm day− 1) regionally averaged over the area (10–20 °N, 130–140 °E) in observations and hindcasts starting from 1 August 2001. The decimals shown in the brackets are temporal correlation coefficients (COR) and root mean square errors (RMSE) between the observations and hindcasts during the forecast time of 1–20 day
We then carry out three sets of hindcast experiments named Exp_MSST, Exp_WSST and Exp_DSST, respectively, and the initial conditions of each hindcast experiment is derived from the output of the corresponding initialization experiments with monthly, weekly, or daily SST observations. The hindcasts are conducted with 3-month forecast integration starting from the 1st, 11th, and 21st day of each month in June–August during 2000–2014. To reduce the uncertainty of initial condition, a simple ensemble scheme based on lagged average forecasting strategy is adopted in each forecast case, with four ensemble members using the initial conditions at 00:00 UTC of the forecast day, 18:00 UTC, 12:00 UTC and 06:00 UTC of the previous day, respectively. The ensemble scheme in current study is similar to the previous studies (e.g., Xiang et al. 2015; Liu et al. 2017; Bo et al. 2020). Therefore, there are 135 forecast cases with four ensemble members in each hindcast experiment. The following analysis is based on the ensemble mean forecast from each hindcast experiment.
In addition, a 15-year free run simulation is conducted to examine the model capability in simulating the BSISO characteristics. Both the simulation and prediction mentioned above adopt the greenhouse-gas external forcing that are identical to those in the CMIP5 historical simulation.
2.4 Methods
To extract the BSISO signal over the WNP, the real-time multivariate BSISO indices are applied following previous studies (e.g., Lin 2012; Lee et al. 2013). The observed BSISO indices are defined as the first two principle component time series (PC1 and PC2) of Empirical Orthogonal Function (EOF) modes of combined intraseasonal anomalies of OLR and 850-hPa zonal wind (U850), which are zonally averaged along 90–150 °E during 1 May to 30 September over 2000–2014 (Lin 2012, 2019). Before the EOF analysis, the observed intraseasonal anomalies are obtained by removing the seasonal cycle climatology and the anomaly averaged over the preceding 120 days. Similarly, the forecasted intraseasonal anomalies are computed by removing the forecasted climatology and the anomaly averaged over the previous 120 days, with corresponding observed anomalies appended before the initial date of forecast. Then the predicted BSISO indices are calculated by projecting the forecasted intraseasonal anomalies onto the observed EOF modes. The bivariate anomaly correlation (BAC) and bivariate root mean square error (RMSE) are computed to measure the prediction skill of BSISO indices against the observations (e.g., Lin et al. 2008; Rashid et al. 2011).
To investigate the physical processes regulating the BSISO convection, the moist static energy (MSE) budget is utilized following previous studies (e.g., Kiranmayi and Maloney 2011; Maloney 2009). The column-integrated MSE (\(\langle{m}\rangle\)) is defined as
where T, Z and q are air temperature (unit: K), geopotential height (unit: gpm) and specific humidity (unit: kg kg− 1), respectively; Cp is heat capacity of dry air at constant pressure (1004 JK− 1 kg− 1), g is gravitational acceleration (9.8 ms− 2), and Lv is the latent heat of condensation (2.5\(\times\)106 Jkg− 1). Angled brackets represent the mass-weighted vertical integration from 1000 to 100 hPa. Following Neelin and Held (1987), the MSE budget equation is defined as
where V is the horizontal wind vector (unit: ms− 1), \({\upomega }\) is vertical pressure velocity (unit: Pa s− 1), and p is pressure (unit: Pa); \(\partial \langle m\rangle /\partial t\) (unit: Wm− 2) is the tendency of \(\langle{m}\rangle\) (unit: Jm− 2); \(- \langle{V\cdot \nabla m}\rangle\) and \(-\langle \omega \cdot \partial m/\partial p\rangle\) (unit: Wm− 2) are the horizontal and vertical advection of \(\langle{m}\rangle\), respectively; \(LW\) and \(SW\) represent the longwave and shortwave radiative heating, and their column-integrated values (i.e., \(\langle{LW}\rangle\) and \(\langle{SW}\rangle\)) (unit: Wm− 2) are derived from the differences of net fluxes between the bottom and top of atmosphere, respectively; \(LH\) and \(SH\) (unit: Wm− 2) denote the surface latent heat and sensible heat fluxes, respectively. As discussed in previous studies (e.g., DeMott et al. 2016; Gao et al. 2019), the MSE budget terms affect the maintenance (\(\langle{m}\rangle\)) and propagation (\(\partial \langle m\rangle /\partial t\)) of BSISO convection.
3 Evaluation of BSISO characteristics in the free run
In this section, we evaluate the model performance in capturing the basic feature of BSISO over the WNP region in a 15-year free run simulation. Figure 3 shows the spatial distribution of climatological mean precipitation and 850-hPa wind during June–August. The model can basically capture the position of observed maximum centers of summer precipitation and low-level wind, but with clear biases in the amplitude (Fig. 3a, b). Large wet biases occur at the west coast of Indian Subcontinent and Indo-China Peninsula, associated with the overestimated westerlies over these regions (Fig. 3c). These wet biases can also be found in the older versions of the BCC model and other climate models (e.g., Kim et al. 2008; Liu et al. 2014; Liu et al. 2015; Hu et al. 2017). Additionally, small wet biases and weak easterly wind biases appear in the east of Maritime Continent. Such wind biases are contrary to the westerly biases found in the earlier versions of the BCC model (e.g., Liu et al. 2015; Jie et al. 2017).
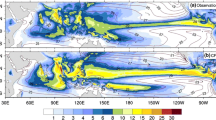
The spatial distribution of standard deviation of intraseasonal precipitation and U850 anomalies during June–August is given in Fig. 4. In the observation, the precipitation field shows two strong variance centers near the Indian Subcontinent and the WNP (Fig. 4a), whereas the U850 field displays a relatively different pattern with maximum variability over the WNP and a secondary maximum over the tropical Indian Ocean (Fig. 4f). The simulated variances of precipitation and U850 generally agree well with the observations. However, for both precipitation and U850 fields, the magnitude of variance is clearly overestimated, especially over the Indian Subcontinent, Indo-China Peninsula and east of the Philippines in the tropical WNP. The overestimated intraseasonal variances of precipitation and U850 over these regions also exist in the earlier versions of the BCC model (e.g., Liu et al. 2014; Hu et al. 2017), probably due to the deficiencies in parameterizations of convection and cloud physical process over the tropics.
Spatial distribution of standard deviation of intraseasonal precipitation (left panel) and 850-hPa zonal wind (right panel) anomalies from (a, f) observations, (b, g) free run simulations and (c–e, h–j) hindcasts in June–August during 2000–2014. The results in c–e and h–j are derived from the 3-month-integration forecasts starting from 1 June in each year during 2000–2014. The decimals shown in brackets are the pattern correlation coefficients between the observations and simulations or hindcasts
Figure 5 depicts the spatial structure of the leading two EOF modes of the combined intraseasonal anomaly fields of OLR and U850. In the observation, the EOF1 mode is characterized by a deep convection center around 15 °N, whereas the EOF2 mode exhibits a dipole structure with enhanced convection near 20 °N and suppressed convection near 10 °N. For both the EOF1 and EOF2 modes, easterly (westerly) zonal wind anomalies prevail to the north (south) of the strong positive convection center. The two EOF modes are in a close quadrature relationship with a joint contribution of about 46 % to the total variance. The leading two EOF modes of simulations generally resemble the observations, whereas the simulated EOF2 mode shows an erroneous strong convection around 5°S. In addition, the total explained variance of the EOF1 and EOF2 modes in the simulation is about 30 %, which is lower than that in the observation. Note that these biases of BCC-CSM2 are slightly larger than those of its earlier version BCC-CSM1.2 (Bo et al. 2020), and the reason for the degradation is worth further investigation but beyond the scope of this study.
Figure 6 further shows the composite intraseasonal anomalies of precipitation and 850-hPa wind during the BSISO lifecycle, which is divided into eight phases according to different angles between PC1 and PC2 (Lin 2012; Lee et al. 2013), and the composite is performed when the BSISO amplitude is larger than 1. In the observation, the BSISO rainband is tilted northwest-southeastward and exhibits an obvious northward propagating feature (Fig. 6a). The BSISO convection initiates over the equatorial eastern Indian Ocean in phase 1, migrates northward to the Bay of Bengal and northeastward to the Gulf of Thailand and equatorial western Pacific in phase 2, develops rapidly over the South China Sea and east of the Philippines in the tropical WNP in phase 3, further moves northward to the subtropical WNP during phases 4–6, and finally dissipates over the south China during phases 7–8. Meanwhile, zonally-elongated anomalous cyclonic (anti-cyclonic) circulation appears to the north of the enhanced (suppressed) convection. The composite intraseasonal anomaly of OLR in each BSISO phase is generally consistent with that of precipitation (figure not shown).
Composite intraseasonal anomalies of precipitation (shaded) and 850-hPa wind (vector) as a function of BSISO phase in June–August during 2000–2014 from the observations (left panel) and free run simulations (right panel). The composite is performed using the days when BSISO amplitude is larger than 1. The decimals shown in brackets are the pattern correlation coefficients of intraseasonal precipitation anomalies between observations and free run simulations
The model can reasonably reproduce the northward movement of convection and circulation anomalies from equatorial Ocean to south China but with some biases in the location and amplitude of convection center (Fig. 6b) compared to the observations (Fig. 6a). The BSISO rainband over WNP is located more northward in simulation than in observation. This may be related to the faster-than-observed northward propagation of BSISO signal, which also exists in the earlier versions of the BCC model (e.g., Fang et al. 2019; Bo et al. 2020). The amplitude of enhanced (suppressed) convection center over the WNP is underestimated when the BSISO is in phases 3–6 (phases 7, 8, 1 and 2) (Fig. 6). The underestimated precipitation anomalies are also evident in the tropical Indian Ocean. In addition, near the west coast of Indo-China Peninsula, the precipitation anomalies are overestimated in most phases, especially phases 5 and 8, corresponding to the much overestimated intraseasonal variance of precipitation over the same areas (Fig. 4b). It is also noted that the wind direction over Bay of Bengal in phase 3 in the model is almost reversed compared to observations, denoting apparent circulation biases in some areas.
The lifecycle composites of intraseasonal SST anomaly for different BSISO phases are given in Fig. 7. Along with the evolution of BSISO convection, the SST anomaly also shows an evident northward propagation. Over the tropical WNP region, significant positive (negative) SST anomalies are found in phases 1, 2 and 8 (4–6) when the BSISO convection is suppressed (enhanced). The model results generally agree with the observations. However, the simulated SST anomaly center over the WNP extends more northward with reduced magnitude than the observation, corresponding to the feature of simulated BSISO convection (Fig. 6). Additionally, the pattern correlation of SST anomalies between the simulation and observation over the Asian-Pacific region (10 °S–40 °N, 60 °E–180 °E) is nearly zero in phase 7, apparently lower than those of about 0.4–0.6 in other phases. This indicates that the model can hardly capture the intraseasonal variation of SST when the BSISO convection over the tropical WNP is at the transition from wet to dry spell.
4 Forecast skill of BSISO
The predicted standard deviations of summer intraseasonal precipitation and U850 in the three sets of hindcast experiments are also given in Fig. 4. For both precipitation and U850 fields, there is no significant differences among the three sets of hindcast experiments, though the Exp_WSST and Exp_DSST produce slightly stronger variance than the Exp_MSST over the tropical WNP especially near the Philippines. Similar to the feature in the free run simulation (Fig. 4b, g), the large variance centers over the Indian Landmass, Indo-China Peninsula and tropical WNP are overestimated in all sets of hindcast experiments (Fig. 4c–e, h–j). This indicates that the overestimation of summer intraseasonal variance in the predictions may arise from the systematic errors of model itself, and it can hardly be reduced by only using the high-frequency observed SST data in the model initialization process.
The overall prediction skill, measured by BAC and RMSE between the observed and predicted BSISO indices, as a function of forecast time is given in Fig. 8. Taken the BAC = 0.5 or RMSE = 1.414 as the threshold of useful prediction skill (e.g., Lin et al. 2008; Rahid et al. 2011), the Exp_MSST can predict the BSISO up to around 10 days in advance. With relatively higher-frequency observed SST data included in the model initialization, the Exp_WSST and Exp_DSST further improve the useful BSISO prediction skill by about 1–2 days compared to the Exp_MSST. The useful skill of BSISO prediction in the Exp_WSST and Exp_DSST is comparable to that in the hindcast experiments of Bo et al. (2020), who also used high-frequency OISST SST observations to initialize the earlier version of the BCC model (i.e., BCC-CSM1.2). This emphasizes the importance of SST initial conditions for the BSISO prediction. In addition, compared to the BCC-CSM1.2 in previous studies (Jie et al. 2017; Bo et al. 2020), the model in this study degrades the BSISO spatial modes in the simulation but achieves similar skills in the BSISO prediction as before. This suggests that the model performance in the simulation of intraseasonal oscillation does not necessarily determine the skill of subseasonal prediction, consistent with the findings of Klingaman et al. (2015) and Liu et al. (2019).
The forecast skill as a function of the forecast time. Shown are the a bivariate anomaly correlation (BAC) and b bivariate root mean square error (RMSE) of BSISO index, and the mean pattern anomaly correlation coefficients (PCC) of intraseasonal anomalies of c precipitation and d 850-hPa zonal wind zonally averaged over the WNP (10 °S–40 °N, 90–150 °E) between observations and predictions of each hindcast experiment. The dashed lines in (a) and (b) represent skill values of 0.5 and 1.414, respectively. PCCs larger than 0.23 are significant at the 95% confidence level
In addition, during the first 5-day (i.e., 1-pentad) forecast time, the three sets of hindcast experiments exhibit comparable prediction skills (Fig. 8a). However, during the forecast time of 6–20 days (i.e., 2–4 pentads), the Exp_WSST and Exp_DSST show slightly higher skill than the Exp_MSST. This indicates that the atmospheric initial condition plays a dominant role in the BSISO prediction within the first pentad, beyond which the impact of SST initial condition gradually emerges. This is consistent with the previous studies (e.g., Wang et al. 2015; Liu et al. 2017; Bo et al. 2020). Similar results can be obtained from the pattern anomaly correlation coefficients (PCCs) between the observed and predicted intraseasonal precipitation and 850-hPa zonal wind fields over the WNP. From the Exp_MSST to the Exp_WSST and Exp_DSST, the PCCs of these two atmospheric variables are slightly increased during the forecast time of 2–4 pentads (Fig. 8c, d). In fact, about 53% of forecast cases show overall enhanced PCCs during that time. In some particular forecast cases, the mean PCC of precipitation (U850) can even be increased by more than 0.3 (0.5) (figure not shown). Note that the overall BAC, RMSE and PCCs of U850 in the Exp_DSST are slightly lower than that in the Exp_WSST beyond the forecast time of 5 days. This suggests that the closest-to-observed daily SST does not necessarily produce the optimal forecast results, possibly due to the high uncertainty of forecast under the complex interaction between model error and initial condition error.
Previous studies have demonstrated that the intraseasonal oscillation is more predictable in the strong-amplitude events than in the weak-amplitude events (e.g., Xiang et al. 2015; Fang et al. 2019). To further examine the prediction skill and skill differences among the three sets of hindcast experiments, strong and weak cases are selected according to the BSISO amplitude during the forecast time of 6–20 days. The strong BSISO cases are identified if the occurrences of the BSISO with amplitude larger than 1 are at least 10 days during the forecast time of 6–20 days, otherwise the weak BSISO cases are detected. Among the total 153 forecast cases, we identified 76 strong cases and 59 weak cases. The BAC skills for the strong and weak cases are given in Fig. 9. For the strong cases, the Exp_WSST and Exp_DSST increase the BAC by a maximum of about 0.1 during the forecast time of 6–20 days relative to the Exp_MSST, similar to the results of BAC for all cases (Fig. 8a). However, for the weak cases the three sets of hindcast experiments display relatively similar skills within the forecast time of 6–20 days. This indicates the superiority of high-frequency SST data to the low-frequency SST data in the model initialization is especially apparent in the prediction of strong BSISO events.
5 Possible mechanisms
It is supposed that the MSE and its tendency at intraseasonal time scale can basically represent the maintenance and propagation of BSISO convection (DeMott et al. 2016; Gao et al. 2019). Thus, to investigate the possible physical processes related to the impacts of observed SST frequency in the model initialization on the BSISO prediction, we conduct an MSE budget diagnostic in this section. The diagnostic is based on the composite analysis of some strong BSISO cases, in which the three sets of hindcast experiments exhibit apparent skill differences as shown in the previous section.
Examination on the forecast cases in this study shows that the BSISO, with a relatively short periodicity of about 10–60 days, evolves fast in the phase space (i.e., phase 1–8) and hardly stays in one particular phase for a long time (figure not shown). This indicates that the BSISO exhibits relatively quick propagation of convection anomaly over the WNP during the forecast time of 1–20 days. Thus, to better reveal the impact of SST initial conditions on the BSISO evolution, the BSISO cases are divided into different categories according to the main characteristics of wet and dry phases. Here the wet (dry) phase denotes the phases 3–6 (phases 7, 8, 1 and 2), in which wet (dry) spell prevails over the tropical WNP. During the forecast time of 1–20 days, the strong BSISO cases evolving from dry to wet (wet to dry) phases are referred to as DW (WD) cases, while those staying persistently in wet or dry phase are referred to as PW or PD cases. The numbers of the DW, WD, PW and PD cases involved in the following composite analysis are 15, 15, 18 and 18, respectively. These four categories of cases account for 90% of the total 76 strong BSISO cases selected in Sect. 4. They all exhibit long duration of wet or dry anomalies over the tropical WNP during the forecast time of 6–20 days when the forecast skills are clearly different among the hindcast experiments.
The composite BSISO trajectories for the above four categories of cases during the forecast time of 1–20 days are given in Fig. 10. In the observation, the DW (WD) cases exhibit enhanced (suppressed) convection propagating from equatorial ocean to east of Philippines, corresponding to the evolution of BSISO from phase 1 to phase 5 (phase 5 to phase 1). The PW cases propagate from phase 3 to phase 6 with wet spell over the tropical WNP, while the PD cases decay in phase 8 and then develop in phases 1–2 with dry spell over the tropical WNP. By comparison, the Exp_WSST and Exp_DSST better reproduce the evolution of all four categories of BSISO cases beyond the forecast time of 5 days relative to the Exp_MSST, with closer-to-observed BSISO amplitude and phase variation. This is consistent with the results of prediction skill shown in Figs. 8 and 9.
The forecast skill as a function of the forecast time. The bivariate anomaly correlation (BAC) of BSISO index between observations and predictions of each hindcast experiment for strong and weak cases are shown in (a) and (b), respectively. The dashed lines in (a) and (b) represent skill values of 0.5
Composite trajectories for the strong BSISO cases with a dry-to-wet (DW), b wet to dry (WD), c persistent-wet (PW) and d persistent-dry (PD) phase variation. The black big dots denote the location at the previous day of forecast starting date, and small dots represent the location at each day since the forecast starting date
For the DW cases, Fig. 11 depicts the composite time-latitude distributions of intraseasonal anomalies of precipitation, U850, column-integrated MSE and its tendency averaged along 110–140 °E. During the forecast time of 1–20 days, the observation shows a northward propagation of wet anomalies from equator to subtropical WNP and an obvious transition from dry to wet (wet to dry) anomalies over the tropical (equatorial) western Pacific. The Exp_MSST basically captures the variation feature of BSISO convection. However, it underestimates the intensity of enhanced (suppressed) convection over the tropical (equatorial) western Pacific beyond the forecast time of 5 days. Compared with the Exp_MSST, the Exp_WSST and Exp_DSST can more reasonably predict the northward propagation and intensity of precipitation anomalies over the WNP beyond the 5-day forecast time. Correspondingly, the predictions of easterly (westerly) wind anomalies prevailing over the areas north (south) to the deep convection center are also improved. Despite the differences in the location and peak time of the BSISO precipitation and circulation centers, the observed intraseasonal anomalies of column-integrated MSE and its tendency show northward propagation associated with the evolution of BSISO convection. The variation feature of intraseasonal MSE and MSE tendency is also better reproduced in the Exp_WSST and Exp_DSST than in the Exp_MSST. These results indicate that adopting higher-frequency SST observation in the model initialization process tends to produce a more skillful forecast of the intraseasonal anomalies of precipitation, circulation, MSE and MSE tendency that are closely related to the BSISO characteristics.
Figure 12 further gives the composite time-latitude distributions of intraseasonal anomalies of various budget terms contributing to the column-integrated MSE tendency averaged along 110–140 °E for the DW cases. The terms include horizonal and vertical advection of MSE, net longwave and shortwave radiative heating, surface latent and sensible heat flux. At the intraseasonal time scale, the observed vertical and horizontal MSE advection, longwave radiation flux and latent heat flux show strong anomalies propagating northward, indicating large contribution to the MSE tendency. In contrast, the shortwave radiation flux and sensible heat flux are quite weak, contributing little to the MSE tendency. Although featured by similar biases in the magnitude, location and peak time of anomaly center for the above terms, the three sets of hindcast experiments could differ remarkably in some budget terms. From the Exp_MSST to the Exp_WSST and Exp_DSST, the prediction of latent heat flux is remarkably improved in the magnitude and propagation. This improvement is also evident for the terms of horizontal and vertical MSE advection. Moreover, the prediction of longwave radiation is slightly improved, whereas the predictions of shortwave radiation flux and sensible heat flux are hardly improved. Although the differences among the three sets of hindcast experiments are very significant in some forecast cases (figure not shown), the composite differences of MSE budgets terms between different predictions are only statistically significant over several small areas. This is possibly due to the sharply smoothed BSISO evolution features by composite of various cases with different position and intensity of dry/wet anomaly center.
Same as in Fig. 11, but for the intraseasonal anomalies of column-integrated horizontal advection (\(- V\cdot \nabla m\)), vertical advection (\(-\omega \cdot \partial m/\partial p\)), net longwave radiation (\(LW\)), net shortwave radiation (\(SW\)), surface latent (\(LH\)), and surface sensible heat (\(SH\)). Stippling denotes where the differences between the Exp_WSST/Exp_DSST predictions and the Exp_MSST predictions are significant at the 90% confidence level according to the Student’s t test
For the DW cases, the composite time variations of intraseasonal anomalies of precipitation, MSE, MSE tendency and its budget terms regionally averaged over the core region (10–20 °N, 110–140 °E) are given in Fig. 13. In this region, the observed precipitation anomalies turn from negative to positive at the beginning of forecast, peaks around the 15th forecast day and remains strong subsequently. The MSE shows similar variation feature, but its tendency peaks around the 6th forecast day and then decays rapidly. This indicates that the intraseasonal MSE is highly in phase with the BSISO precipitation and intensive moistening appears about 1 week ahead of the convection center, consistent with the findings of previous studies (e.g., DeMott et al. 2016; Gao et al. 2018). Meanwhile, the various observed MSE budget terms differ in the magnitude and the occurrence time of peaking and transiting between negative and positive states. During the 1–5th forecast day when the dry anomalies occur, the horizontal and vertical advection act as apparent sources to recharge the MSE, whereas the latent heat flux and longwave radiation flux serve as apparent sinks to discharge the MSE. This recharge-discharge process is reversed when the BSISO precipitation is persistently enhanced during the 6–20th forecast day. The three sets of hindcast experiments can generally capture the variation feature of precipitation, MSE and MSE budget terms, but with obvious biases in the magnitude. By comparison, with less root mean square errors against the observations, the Exp_WSST and Exp_DSST outperform the Exp_MSST in predicting the precipitation, MSE, and MSE tendency especially beyond the forecast time of 5 days. For the MSE budget terms, compared with the Exp_MSST, the Exp_MSST and Exp_DSST exhibit much closer-to-observed magnitude of latent heat flux, as well as somewhat improved horizonal and vertical MSE advection during the 6–20-day forecast time. Nevertheless, the three sets of hindcast experiments display relatively small differences of longwave radiation flux, shortwave radiation flux and sensible heat flux. This indicates that the realistic representation of latent heat flux as well as horizontal and vertical MSE advection may largely contribute to the above-mentioned closer-to-observed evolution of the DW cases in the Exp_WSST and Exp_DSST than in the Exp_MSST.
Composite time variations of intraseasonal anomalies of several variables for the strong BSISO cases with dry-to-wet (DW) phase variation. a Precipitation, and column-integrated b MSE, c MSE tendency, d horizontal advection (\(- V\cdot \nabla m\)), e vertical advection (\(-\omega \cdot \partial m/\partial p\)), f net longwave radiation (\(LW\)), g net shortwave radiation (\(SW\)), h surface latent (\(LH\)), and i surface sensible heat (\(SH\)) regionally averaged over the area (10–20 °N, 110−140 °E). The decimals shown beside the legends are root mean square errors between the observations and predictions of each hindcast experiment during the forecast time of 1–20 day
In addition, for the WD, PW and PD cases, the composite time-latitude cross sections of intraseasonal anomalies of precipitation averaged along 110–140 °E are shown in Fig. 14a. For the WD cases, the Exp_WSST and Exp_DSST can better capture the magnitude of dry anomalies over the tropical WNP beyond the 5-day forecast time than the Exp_MSST. For the PW cases, different from the observation in which the wet anomalies over the WNP maintains within the forecast time of 20 days, the Exp_MSST shows wet anomalies over the tropical WNP before the forecast time of about 15 days, but exhibit an erroneous transition from wet to dry anomalies beyond that time. The deficiency of the unrealistic transition is reduced in the Exp_WSST and Exp_DSST. For the PD cases, the magnitude and variation of dry anomaly over the WNP during the forecast time of 6–20 days are also somewhat improved from the Exp_MSST to the Exp_WSST and Exp_DSST. These results suggest that using relatively higher-frequency SST observations for the model initialization could result in improved prediction of the magnitude and propagation of BSISO convection over the tropical WNP whenever the BSISO is persistently active/break or evolves between wet and dry phases over that region.
From the Exp_MSST to the Exp_WSST and Exp_DSST, the intraseasonal MSE tendency and most budget terms averaged along 110–140 °E are overall more skillfully predicted during the forecast time of 6–20 days for the WD, PW, and PD cases (figure not shown). The improvement is especially evident in the prediction of latent heat flux that related to the BSISO convection (Fig. 14b). This is similar to the results of DW cases in Figs. 12 and 13, further confirming that the improved forecast of BSISO characteristics is associated with the more realistic description of latent heat flux. This stresses the key role of the intraseasonal latent heat flux on the development of BSISO convection over the WNP, possibly through triggering instability of atmospheric boundary layer prior to the convection center as demonstrated by Wang et al. (2018).
Furthermore, aiming at the forecast time of 6–20 days when the differences of BSISO prediction among the three hindcast experiments are notable, Fig. 15 gives the temporal mean intraseasonal MSE tendency and its budget terms averaged over the region (10–20 °N, 110–140 °E) for various cases. During the forecast time of 6–20 days, for the DW and PW (WD and PD) cases, the observed MSE tendency is largely compensated (offset) by the latent heat flux and longwave radiation flux and offset (compensated) by the horizontal and vertical advection of MSE, but is little attributed to the shortwave radiation flux and sensible heat flux. The Exp_MSST considerably underestimates the amplitude of the four dominant MSE budget terms (i.e., horizontal advection, vertical advection, latent heat flux, and longwave radiation flux). The Exp_WSST and Exp_DSST can reduce the biases, especially in the latent heat flux, consistent with previous results in Figs. 12, 13 and 14. The latent heat flux is underestimated by about 5 Wm− 2, 6 Wm− 2, 12 Wm− 2, and 5 Wm− 2 in the Exp_MSST for the DW, WD, PW and PD cases, respectively. It is further improved in the Exp_WSST and Exp_DSST, with reduction of biases by more than 87 %, 51 %, 21 %, and 66 % for the above four different types of BSISO cases, respectively. Also, from the Exp_MSST to the Exp_WSST and Exp_DSST, the biases of vertical MSE advection are reduced by about 14–30% for the DW and PD cases, and those of horizontal MSE advection are decreased by about 10–41% for all four categories of cases. In addition, the longwave radiation is slightly improved for most cases.
Composite temporal mean intraseasonal anomalies of column-integrated MSE tendency and various MSE budget terms (unit: Wm− 2) averaged over the region (10–20 °N, 110−140 °E) during the forecast time of 6–20 days. The MSE budget terms include horizontal advection (\(- V\cdot \nabla m\)), vertical advection (\(-\omega \cdot \partial m/\partial p\)), net longwave radiation (\(LW\)), net shortwave radiation (\(SW\)), surface latent (\(LH\)), and surface sensible heat (\(SH\)). The results are for the strong BSISO cases with a dry-to-wet (DW), b wet-to-dry (WD), c persistent-wet (PW), and d persistent-dry (PD) phase variation
The above results suggest that the inclusion of higher-frequency observed SST in the model initialization can lead to improvement in the BSISO-related MSE variations, possibly by changing the surface evaporation (related to the surface latent heat flux) and atmospheric convergence and divergence (related to the MSE advection). This improvement may further result in more skillful forecast of BSISO over the WNP.
6 Summary and discussion
Based on the prediction of three sets of hindcast experiments with BCC-CSM2 initialized by SST observations of different temporal frequencies, this study examines the impact of observed SST frequency in the model initialization on the prediction of BSISO over the WNP.
A 15-year free run simulation shows that the model itself can reasonably reproduce the spatial structure of the BSISO variability and BSISO mode, the northward propagation of intraseasonal anomalies of precipitation, circulation and SST over the WNP, as well as the convection-circulation phase relationship. However, it still shows clear biases in simulating the amplitude and location of BSISO activity center. These deficiencies may limit the forecast skill of BSISO over the WNP to some extent.
The useful prediction skill of real-time BSISO indices is up to 10 days in the Exp_MSST, and further increases to 11–12 days in the Exp_WSST and Exp_DSST. Among the three sets of hindcast experiments, the BSISO prediction skills are very similar within the first few days of forecast but exhibit clear differences beyond the forecast time of 5 days, indicating that the impacts of SST initial conditions gradually become more noticeable as the forecast time increases. Compared to the Exp_MSST, the Exp_WSST and Exp_DSST slightly enhance the overall prediction skill during the forecast time of 6–20 days, in terms of the BAC and RMSE of BSISO indices and the PCCs of intraseasonal precipitation and U850 anomalies over the WNP. This suggests that adopting higher-frequency SST observations in the model initialization process tends to improve the prediction of BSISO feature over the WNP. The BSISO skill differences among the three sets of hindcast experiments are dependent on the amplitude of BSISO. From the Exp_MSST to the Exp_WSST and Exp_DSST, the prediction skill is clearly enhanced for the strong BSISO cases, but it is almost unchanged for the weak BSISO cases. About 90% of the strong BSISO cases are characterized by long duration of dry or wet anomaly over the tropical WNP during the forecast day of 6–20 days. For these cases, the Exp_WSST and Exp_DSST can more skillfully capture the BSISO magnitude and phase variation than the Exp_MSST.
Further composite analysis on the strong BSISO cases indicates that the three sets of hindcast experiments show remarkable differences in the predicted BSISO-related MSE and MSE tendency during the forecast time of 6–20 days when the differences of BSISO prediction skill among the three hindcast experiments are evident. Diagnostic of MSE budget indicates that the Exp_WSST and Exp_DSST can generally better reproduce the amplitude and propagation of intraseasonal MSE, MSE tendency and most of its budget terms than the Exp_MSST. Especially, from the Exp_MSST to the Exp_WSST and Exp_DSST, for various BSISO cases during the forecast time of 6–20 days, the mean biases of latent heat flux and MSE advection over the WNP are reduced by about 21–87% and 10–41%, respectively. This suggests that using higher-frequency SST observations for the model initialization can lead to more realistic prediction of BSISO-related MSE variations, and thus enhance the BSISO prediction skill possibly through changing the surface evaporation (related to the latent heat flux) and atmospheric convergence and divergence (related to the MSE advection).
This study demonstrates that the forecast experiments with daily or weekly SST observations used in the model initialization process can enhance the BSISO prediction skill during the forecast time of 6–20 days compared to those with monthly SST observations. However, this skill enhancement in this study is less significant than that in Kim et al. (2008) and Boisséson et al. (2012), probably because of the different model settings. In contrast to atmosphere-only model with prescribed SST field used in previous studies, the coupled climate system model used in this study may suffer from a deteriorating SST forecast with increasing forecast time, partly because of the model drift in ocean-atmosphere coupling process. This may to some extent limit the forecast skill at long forecast time. In addition, although we suppose it is necessary to increase the frequency of SST observations in the model initialization process, the highest-frequency SST observation in this study is not optimal for the BSISO prediction. This implies the huge uncertainty of S2S prediction, which is largely affected by the errors in both initial conditions and model itself. It is of course that the above results are perhaps somewhat uncertain because of the model-dependent forecast errors, the difference in SST observations, and the limited number of hindcast cases, as well as the considerable residuals of MSE budget shown in this study and many other studies (e.g., Kiranmayi and Maloney 2011; Sobel et al. 2014). To improve the S2S prediction of the BCC model as well as other models, more efforts should be made to optimize the model initial conditions, in addition to a sustained endeavor to upgrade the model physical parameterizations.
Change history
05 July 2021
A Correction to this paper has been published: https://doi.org/10.1007/s00382-021-05844-3
References
Abhilash S, Sahai AK, Borah N et al (2014) Does bias correction in the forecasted SST improve the extended range prediction skill of active-break spells of Indian summer monsoon rainfall? Atmos Sci Lett 15:114–119
Adler RF, Huffman GJ, Chang A et al (2003) The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979–present). J Hydrometeorol 4:1147–1167
Bo Z, Liu X, Gu W, Huang A et al (2020) Impacts of atmospheric and oceanic initial conditions on boreal summer intraseasonal oscillation forecast in the BCC model. Theor Appl Climatol 142(1):393–406
Boisséson Ed, Balmaseda M, Vitart F, Mogensen K (2012) Impact of the sea surface temperature forcing on hindcasts of Madden-Julian Oscillation events using the ECMWF model. Ocean Sci 8:1071–1084
DeMott CA, Benedict JJ, Klingaman N et al (2016) Diagnosing ocean feedbacks to the MJO: SST-modulated surface fluxes and the moist static energy budget. J Geophys Res Atmos 121:8350–8373
Ding Q, Wang B (2005) Circumglobal teleconnection in the Northern Hemisphere summer. J Clim 18:3483–3505
Ding R, Li J, Seo KH (2011) Estimate of the predictability of boreal summer and winter intraseasonal oscillations from observations. Mon Weather Rev 139:2421–2438
Fang Y, Wu P, Wu T et al (2016) An evaluation of boreal summer intra-seasonal oscillation simulated by BCC_AGCM2.2. Clim Dyn 48:3409–3423
Fang Y, Li B, Liu X (2019) Predictability and prediction skill of the boreal summer intra-seasonal oscillation in BCC_CSM model. J Meteorol Soc Jpn 97:295–311
Fu X, Wang B (2004) The boreal-summer intraseasonal oscillation simulated in a hybrid coupled atmosphere-ocean model. Mon Weather Rev 132:2628–2649
Fu X, Wang B, Li T, McCreary JP (2003) Coupling between northward-propagating, intraseasonal oscillations and sea surface temperature in the Indian Ocean. J Atmos Sci 60:1733–1753
Fu X, Yang B, Bao Q, Wang B (2008) Sea surface temperature feedback extends the predictability of tropical intraseasonal oscillation. Mon Weather Rev 136:577–597
Fu X, Lee JY, Hsu PC et al (2013) Multi-model MJO forecasting during DYNAMO/CINDY period. Clim Dyn 41:1067–1081
Gao Y, Klingaman NP, DeMott CA, Hsu PC (2019) diagnosing ocean feedbacks to the BSISO: SST-modulated surface fluxes and the moist static energy budget. J Geophys Res Atmos 124:146–170
Griffies S, Gnanadesikan A, Dixon KW et al (2005) Formulation of an ocean model for global climate simulations. Ocean Sci 1:45–79
Hersbach H, Bell B, Berrisford P et al (2020) The ERA5 global reanalysis. Q J R Meteorol Soc 146:1999–2049
Hsu PC, Lee JY, Ha KJ (2016) Influence of boreal summer intraseasonal oscillation on rainfall extremes in southern China. Int J Climatol 36:1403–1412
Hsu PC, Lee JY, Ha KJ, Tsou CH (2017) Influences of boreal summer intraseasonal oscillation on heat waves in monsoon Asia. J Clim 30:7191–7211
Hu W, Duan A, He B (2017) Evaluation of intra-seasonal oscillation simulations in IPCC AR5 coupled GCMs associated with the Asian summer monsoon. Int J Climatol 37:476–496
Huang A, Zhang Y, Wang Z et al (2013) Extended range simulations of the extreme snow storms over southern China in early 2008 with the BCC_AGCM2.1 model. J Geophys Res Atmos 118:8253–8273
Jie W, Vitart F, Wu T, Liu X (2017) Simulations of the Asian summer monsoon in the sub-seasonal to seasonal prediction project (S2S) database. Q J R Meteorol Soc 143:2282–2295
Kalnay E, Kanamitsu M, Kistler R et al (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:437–472
Kim HM, Hoyos CD, Webster PJ, Kang IS (2008) Sensitivity of MJO simulation and predictability to sea surface temperature variability. J Clim 21:5304–5317
Kiranmayi L, Maloney ED (2011) Intraseasonal moist static energy budget in reanalysis data. J Geophys Res Atmos 116:D21117
Klingaman NP, Inness PM, Weller H, Slingo JM (2008) The importance of high-frequency sea surface temperature variability to the intraseasonal oscillation of Indian monsoon rainfall. J Clim 21:6119–6140
Klingaman NP, Jiang X, Xavier PK, Petch J, Waliser D, Woolnough SJ (2015) Vertical structure and physical processes of the Madden-Julian oscillation: synthesis and summary. J Geophys Res Atmos 120:4671–4689
Lau KM, Chan PH (1986) Aspects of the 40–50-day oscillation during the northern summer as inferred from outgoing longwave radiation. Mon Weather Rev 114:1354–1367
Lee JY, Wang B, Wheeler MC, Fu X, Waliser DE, Kang IS (2013) Real-time multivariate indices for the boreal summer intraseasonal oscillation over the Asian summer monsoon region. Clim Dyn 40:493–509
Lee SS, Wang B, Waliser DE, Neena JM, Lee JY (2015) Predictability and prediction skill of the boreal summer intraseasonal oscillation in the Intraseasonal Variability Hindcast Experiment. Clim Dyn 45:2123–2135
Li W, Zhang Y, Shi X, Zhou W, Huang A, Mu M, Qiu B, Ji J (2019) Development of land surface model BCC_AVIM2.0 and its preliminary performance in LS3MIP/CMIP6. J Meteorol Res 33(5):851–869
Liebmann B, Smith CA (1996) Description of a complete (interpolated) outgoing longwave radiation dataset. Bull Am Meteorol Soc 77:1275–1277
Liebmann B, Hendon HH, Glick JD (1994) The relationship between tropical cyclones of the western Pacific and Indian Oceans and Madden-Julian oscillation. J Meteorol Soc Jpn 72:401–412
Lin H (2012) Monitoring and predicting the intraseasonal variability of the East Asian–Western North Pacific summer monsoon. Mon Weather Rev 141:1124–1138
Lin H (2019) Long-lead ENSO control of the boreal summer intraseasonal oscillation in the East Asian-western North Pacific region. NPJ Clim Atmos Sci 2(1):1–6
Lin H, Brunet G, Derome J (2008) Forecast skill of the Madden–Julian oscillation in two Canadian atmospheric models. Mon Weather Rev 136:4130–4149
Liu X, Wu T, Yang S et al (2014) Relationships between interannual and intraseasonal variations of the Asian-western Pacific summer monsoon hindcasted by BCC_CSM1. 1 (m). Adv Atmos Sci 31:1051–1064
Liu X, Wu T, Yang S et al (2015) Performance of the seasonal forecasting of the Asian summer monsoon by BCC_CSM1. 1(m). Adv Atmos Sci 32:1156–1172
Liu X, Wu T, Yang S et al (2017) MJO prediction using the sub-seasonal to seasonal forecast model of Beijing Climate Center. Clim Dyn 48:3283–3307
Liu X, Li W, Wu T et al (2019) Validity of parameter optimization in improving MJO simulation and prediction using the sub-seasonal to seasonal forecast model of Beijing Climate Center. Clim Dyn 52:3823–3843
Maloney ED (2009) The moist static energy budget of a composite tropical intraseasonal oscillation in a climate model. J Clim 22:711–729
Mao J, Sun Z, Wu G (2010) 20–50-day oscillation of summer Yangtze rainfall in response to intraseasonal variations in the subtropical high over the western North Pacific and South China Sea. Clim Dyn 34:747–761
Neelin JD, Held IM (1987) Modeling tropical convergence based on the moist static energy budget. Mon Weather Rev 115:3–12
Neena JM, Waliser D, Jiang X (2017) Model performance metrics and process diagnostics for boreal summer intraseasonal variability. Clim Dyn 48:1661–1683
Pegion K, Kirtman BP (2008) The impact of air–sea interactions on the simulation of tropical intraseasonal variability. J Clim 21:6616–6635
Rashid HA, Hendon HH, Wheeler MC, Alves O (2011) Prediction of the Madden–Julian oscillation with the POAMA dynamical prediction system. Clim Dyn 36:649–661
Ren X, Yang XQ, Sun X (2013) Zonal oscillation of western pacific subtropical high and subseasonal SST variations during Yangtze persistent heavy rainfall events. J Clim 26:8929–8946
Reynolds RW, Smith TM, Liu C et al (2007) Daily high-resolution-blended analyses for sea surface temperature. J Clim 20:5473–5496
Sabeerali C, Ramu Dandi A, Dhakate A et al (2013) Simulation of boreal summer intraseasonal oscillations in the latest CMIP5 coupled GCMs. J Geophys Res Atmos 118:4401–4420
Seo H, Subramanian AC, Miller AJ, Cavanaugh NR (2014) Coupled impacts of the diurnal cycle of sea surface temperature on the Madden-Julian oscillation. J Clim 27:8422–8443
Sobel A, Maloney E, Bellon G, Frierson D (2008) The role of surface fluxes in tropical intraseasonal oscillations. Nat Geosci 1:653–657
Sobel A, Wang S, Kim D (2014) Moist static energy budget of the MJO during DYNAMO. J Atmos Sci 71:4276–4291
Stan C (2018) The role of SST variability in the simulation of the MJO. Clim Dyn 51:2943–2964
Van den Dool H, Saha S (1990) Frequency dependence in forecast skill. Mon Weather Rev 118:128–137
Vitart F (2017) Madden-Julian oscillation prediction and teleconnections in the S2S database. Q J R Meteorol Soc 143:2210–2220
Vitart F, Robertson AW, Anderson DL (2012) Subseasonal to seasonal prediction project: Bridging the gap between weather and climate. WMO Bull 61:23–28
Waliser D, Stern W, Schubert S, Lau K (2003) Dynamic predictability of intraseasonal variability associated with the Asian summer monsoon. Q J R Meteorol Soc 129:2897–2925
Wang W, Chen M, Kumar A (2009) Impacts of ocean surface on the northward propagation of the boreal summer intraseasonal oscillation in the NCEP climate forecast system. J Clim 22:6561–6576
Wang W, Kumar A, Fu X, Hung MP (2015) What is the role of the sea surface temperature uncertainty in the prediction of tropical convection associated with the MJO? Mon Weather Rev 143:3156–3175
Wang T, Yang X, Fang J, Sun X, Ren X (2018) Role of air-sea interaction in the 30–60-day boreal summer intraseasonal oscillation over the western north Pacific. J Clim 31:1653–1680
Weng CH, Hsu HH (2017) Intraseasonal oscillation enhancing C5 typhoon occurrence over the tropical western North Pacific. Geophys Res Lett 44:3339–3345
Winton M (2000) A reformulated three-layer sea ice model. J Atmos Oceanic Technol 17:525–531
Wu T, Song L, Li W et al (2014) An overview of BCC climate system model development and application for climate change studies. J Meteorol Res 28:34–56
Wu T, Lu Y, Fang Y et al (2019) The Beijing Climate Center Climate System Model (BCC-CSM): The main progress from CMIP5 to CMIP6. Geosci Model Dev 12:1573–1600
Xiang B, Zhao M, Jiang X et al (2015) The 3–4-week MJO prediction skill in a GFDL coupled model. J Clim 28:5351–5364
Yasunari T (1979) Cloudiness fluctuations associated with the northern hemisphere summer monsoon. J Meteorol Soc Jpn 57:227–242
Yasunari T (1980) A quasi-stationary appearance of 30 to 40-day period in the cloudiness fluctuations during the summer monsoon over India. J Meteorol Soc Jpn 58:225–229
Zhang Y, Hung MP, Wang W, Kumar A (2019) Role of SST feedback in the prediction of the boreal summer monsoon intraseasonal oscillation. Clim Dyn 53:3861–3875
Zhu B, Wang B (1993) The 30–60-day convection seesaw between the tropical Indian and western Pacific Oceans. J Atmos Sci 50:184–199
Acknowledgements
This study was jointly supported by the National Key R&D Program of China under Grant 2016YFA0602100, the National Natural Science Foundation of China under Grant 42075161, 41975081, 41675090, and 41875004, the Postgraduate Research and Practice Innovation Program of Jiangsu Province of China under Grant KYCX190038, the bilateral research project GZ1259 of the Sino-German Center for Research Support, CAS “Light of West China” Program, the Jiangsu University “Blue Project” outstanding young teachers training object, and the Fundamental Research Funds for the Central Universities and the Jiangsu Collaborative Innovation Center for Climate Change. We appreciate the four anonymous reviewers for their constructive and insightful suggestions to improve the manuscript greatly.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhu, X., Liu, X., Huang, A. et al. Impact of the observed SST frequency in the model initialization on the BSISO prediction. Clim Dyn 57, 1097–1117 (2021). https://doi.org/10.1007/s00382-021-05761-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-021-05761-5