Interannual variability in the subduction of the South Atlantic subtropical underwater

Abstract

The South Atlantic subtropical underwater (STUW) is a high-salinity water mass formed by subduction within the subtropical gyre. It is a major component of the subtropical cell and affects stratification in the downstream direction due to its high salinity characteristics. Understanding the interannual variability in STUW subduction is essential for quantifying the impact of subtropical variability on the tropical Atlantic. Using the output from the ocean state estimate of the Consortium for Estimating the Circulation and Climate of the Ocean (ECCO), this study investigates the interannual variability in STUW subduction from 1992 to 2016. We find that heat fluxes, wind stress, and wind stress curl cause interannual variability in the subduction rate. Heat fluxes over the subduction area modulate the sea surface buoyancy and regulate the mixed layer depth (MLD) during its deepening and shoaling phases. Additionally, the wind stress curl and zonal wind stress can modulate the size of the subduction area by regulating the probability of particles entrained into the mixed layer within 1 year of tracing. This analysis evaluates the influence of subtropical wind patterns on the South Atlantic subsurface high-salinity water mass, highlighting the impact of heat and wind on the interannual changes in the oceanic component of the hydrological cycle.

Introduction

The South Atlantic subtropical underwater (STUW, also called salinity maximum water) is a high-salinity water mass (36.23 ~ 37.09 g/kg in absolute salinity) located within the South Atlantic subtropical and tropical gyres. The density of the STUW ranges from 24.65 to 25.63 $\text{kg}/{\text{m}}^{3}$, which is lower than that of the South Atlantic subtropical mode water (> 26 $\text{kg}/{\text{m}}^{3}$, Sato and Polito 2014).

The formation and transportation of STUW occur in subtropical cells (STCs, Malanotte-Rizzoli et al. 2000; Zhang et al. 2003), which involve a shallow overturning system associated with the water properties of subtropical to tropical gyres. Newly formed STUW is transported to the tropical ocean (Donners et al. 2005) and creates barrier layers along the route (Araujo et al. 2011). The majority of the South Atlantic STUW is transported to the equator and dissipates within the tropical ocean (Liu and Qu 2020), and it potentially plays a role in shaping the local salinity distribution and barrier layer thickness and influencing the tropical climate (Balaguru et al. 2012; Breugem et al. 2008). Furthermore, STUW has been reported to travel into the Northern Hemisphere via mesoscale rings (Silva et al. 2008), thereby affecting the water properties in remote locations. Due to the broad-scale impact of the South Atlantic STUW, this water mass deserves further inspection.

STUW is formed by subduction of sea surface salinity maximum water (SSS-max) within the subtropical gyre in the global ocean. Subduction consists of two components: vertical pumping and lateral induction (Qiu and Huang 1995). Worthington (1976) reported that vertical pumping from the wind leads to the formation of STUW. Recent analysis shows that lateral induction, induced by mass fluxes across the slope of the mixed layer, enhances the production of STUW (Qu et al. 2016). Early studies investigated STUW subduction on a climatological scale due to a lack of salinity data. For example, O’Connor et al. (2005) provide the global distribution of the climatological STUW subduction rate from observational data over two periods (1988–1998 and 1987–1995). Because of the rapid growth in the number of salinity profiles since 2000, more research has focused on the interannual variability or the long-term trend in STUW subduction in the global ocean. The subduction of the South Pacific STUW can be attributed to changes in the South Equatorial Current (SEC), Ekman transport, and Ekman pumping from 2011 to 2017 (Bingham et al. 2019). The interannual variability in STUW subduction in the North Pacific is associated with eddy diffusion and surface freshwater fluxes from 2003 to 2011 (Katsura et al. 2013). Qu et al. (2016) reported that surface buoyancy associated with winds controls the interannual variability in North Atlantic STUW subduction. Thus, there is not a single unified process that can explain the interannual variability in STUW subduction globally.

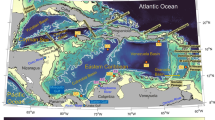
In this analysis, our priority lies in the interannual variability of STUW subduction in the South Atlantic Ocean. The South Atlantic STUW has received little examination by previous studies on STUW globally (O’Connor et al. 2005) because of the sparsity of salinity observations. An increased number of salinity profiles in the central South Atlantic from Argo floats have become available in recent decades. Liu and Qu (2020) were the first to identify the basin-wide structure and property distribution of the South Atlantic STUW from climatological and seasonal perspectives. The STUW is thick in the center of the subtropical gyre (Fig. 1d) and shallow to the north of 10°S. STUW can be transported across the equator. Most of the STUW reemerge back into the mixed layer of the western and central tropical South Atlantic. The STUW can be divided into two types based on its relative location to the 21°S zonal line (Liu and Qu 2020). The STUW on the northern side of 21°S is generally located within the permanent thermocline, and STUW on the southern side of 21°S is generally located within the seasonal thermocline, persisting from October to the next June. The 21°S zonal line in the South Atlantic demarcates where the western subtropical and tropical gyre bifurcate (Cabré et al. 2019).

Fig. 1

a Distribution of the STUW core depth, b climatological mean MLD, c difference between the MLD and STUW core depths, and d STUW thickness. Positive values in c denote that the STUW core depth is deeper than the mixed layer. The units for the STUW core depth are m

In this analysis, we take a further step to examine the interannual variability in STUW subduction. This analysis investigates the interannual variability in the STUW subduction rate using the Eulerian method from Liu and Qu (2020), which is a modified version of Eq. (2) in Qiu and Huang (1995). This method has been shown to provide reliable estimates of climatological maps of the subduction rate in the South Atlantic (Liu and Qu 2020).

This analysis investigates the interannual variability in STUW subduction and attributes it to changes in ocean processes and the associated atmospheric forcing. We quantified the variability of the subducted STUW volume in Sect. 3. The interannual variability in the STUW subduction rate is investigated in Sect. 4, and its causes are discussed in Sect. 5. A discussion is included in Sect. 6. Section 7 summarizes the paper.

Data and method

Datasets

This study calculates the STUW volume and subduction rate using a model estimate: an ocean state estimate of the Consortium for Estimating the Circulation and Climate of the Ocean (ECCO, Forget et al. 2015; Fukumori et al. 2017). ECCO v4r4 provides monthly averaged estimates from 1992 to 2017. This analysis requires tracing water particles forward for 1 year. Thus, the calculation of the STUW production-related results cover 1992 to 2016. The horizontal resolution of the estimates varies between 1/3° in the tropics and 1° at high latitudes. The ECCO estimate assimilates a large volume of in situ measurements, including most of the Argo floats. Furthermore, the ECCO estimate is dynamically consistent. Therefore, a derivation of STUW production is feasible without considering the underlying data sampling.

Subduction rate

The subduction rate denotes the volume of water irreversibly inserted from the mixed layer to the permanent thermocline. The monthly subduction rate is determined based on the approach from Eq. (2) in Qiu and Huang (1995) and Yu et al. (2017) in Eulerian coordinates. The subduction rate (m/s) can be calculated as follows:

$${Sub}_{i}=-\frac{1}{\Delta t}{\int }_{{t}_{\text{i}}}^{{t}_{i}+\Delta t}\left[\left(\frac{\partial h}{\partial t}+{{\varvec{u}}}_{b}\nabla h\right)+{w}_{b}\right]dt$$

(1)

where $h$ denotes the mixed layer depth (MLD), which is defined as the depth at which the density is higher than its value at the sea surface by 0.125 $\text{kg}/{\text{m}}^{3}$ (Monterey and Levitus 1997). ${{\varvec{u}}}_{b}$ and ${w}_{b}$ are the horizontal and vertical velocities (Qiu and Huang 1995) at the bottom of the mixed layer, respectively. ${t}_{\text{i}}$ denotes a certain month (from January to December). $\Delta t$ is 1 month. It should be noted that the monthly subduction rate ${Sub}_{i}$ is an integral of all particles (released from the STUW outcropping area) that are subducted in month ${t}_{\text{i}}$ and remain below the mixed layer through month ${t}_{\text{i}}$ of the next year. If a water particle re-enters the mixed layer within 1 year, then the subduction rate at the original release point is counted as 0. The location where water particles remain permanently for 1 year after release is considered the subduction area.

$\frac{\partial h}{\partial t}+{{\varvec{u}}}_{b}\nabla h$ in Eq. (1) is analogous to $\frac{{\text{Dh}}}{{\text{Dt}}}$ in the Lagrangian approach (Kwon et al. 2013; Woods 1985). In Eulerian coordinates, ${{\varvec{u}}}_{b}\nabla h$ denotes lateral induction, expressing the water volume exiting from the MLD from the tilting of the mixed layer. $\frac{\partial h}{\partial t}$ denotes the temporal variability of the mixed layer, and it is calculated by the following equation:

$${\left(\frac{\partial h}{\partial t}\right)}_{i}=\frac{{h}_{i+1}-{h}_{i-1}}{2\Delta t}$$

(2)

The last term on the right-hand side of Eq. (1) denotes vertical pumping. The annual mean subduction rate is defined as the average of the monthly subduction rate in each year.

To derive the STUW subduction rate, velocity fields from ECCO are used (Forget et al. 2015). The velocities from ECCO effectively reproduce the velocities from estimates derived from both undrogued and drogued drifters (Liu and Qu 2020), especially near the western boundary. Details about the ECCO v4r4 estimates can be found in Fukumori et al. (2017) and references therein. To account for the eddy effect on the mean flow, the eddy-induced residual circulation, parameterized by the Gent and McWilliams scheme in the ECCO model, has been added to the mean circulation. The eddy-induced velocity in ECCO is denoted by the bolus velocity.

The calculation of subduction in this analysis requires tracing water particles for 1 year after their release. The total number of released particles is determined by the size of the outcropping area (i.e., formation area) in a specific month. The trajectories of water particles are calculated using a Lagrangian method by integrating the three-dimensional velocity fields from ECCO. The daily velocity, which is interpolated from the monthly mean values, is used in the calculation. The details for the methods of Lagrangian tracing are provided in Liu and Qu (2020).

South Atlantic subtropical underwater

STUW definition and its spatial distribution

The practical salinity and potential temperature from the ECCO products in the following sections are converted to the conservative temperature and the absolute salinity (McDougall and Barker 2011). We adopt the criteria used by Liu and Qu (2020) and define STUW on the basis of an absolute salinity range of 36.23–37.09 g/kg and a conservative temperature range of 20.35–24.89 $^\circ \text{C}$, corresponding to a potential density range of 24.65–25.63 $\text{kg}/{\text{m}}^{3}$. The advantage of this definition is its ability to quantify an integral property of the STUW, such as volume, over the entire subtropical gyre. The STUW outcropping area can be defined as the overlapping area between the near-surface isohalines, isotherms, and isopycnals constrained by the above criteria. The STUW volume can be defined as the overlapping space among the three criteria. The STUW core depth (Fig. 1a) is defined as the depth of the 25.14 $\text{kg}/{m}^{3}$ isopycnal. The climatological annual mean STUW core depth is shallow (< 50 m) in the southeastern South Atlantic subtropical gyre, where STUW outcrops. The STUW core depth is deep (> 100 m) in the western South Atlantic tropical gyre. According to Liu and Qu (2020), the STUW can be divided into two parts by its vertical distribution relative to the mixed layer. The STUW on the tropical or northern side of the subtropical gyre (Fig. 1c) is persistent throughout the entire year because the STUW penetrates the permanent thermocline. The STUW on the southern or southeastern side of the subtropical gyre resides above the permanent thermocline (Fig. 1c). This analysis focuses on the components of the STUW that penetrate the permanent thermocline. To remove the STUW volume within the surface layers, we define the upper limit of the vertical integral of the STUW volume as the mean mixed layer depth (55 m) within the spatial extent of the STUW (Fig. 1a), and the southern limit in the horizontal direction for volume integration is 25 $^\circ$ S.

STUW volume

One of the basic properties of the STUW is its volume. The climatological mean STUW volume is (2.50 ± 0.22) ·10¹⁴ m³. The error bar represents one standard deviation of the annual mean values from 1992 to 2017. We analyzed the interannual variability in the STUW volume anomalies by removing the climatological mean values. Over the period 1992–2017, the annual mean STUW volume did not display any significant linear trend (Fig. 2). Positive STUW volume anomalies occurred from late 2002 to 2011. Negative anomalies occurred over 1992–2001 and 2012–2017. The maximum STUW volume anomalies occurred in 2009, with a magnitude of 0.4·10¹⁴ m³. The minimum STUW volume anomalies occurred in 1992 during 1992–2001 (− 0.4·10¹⁴ m³) and in 2012 during 2011–2017 (− 0.35·10¹⁴ m³). In this study, 55 m is used as the upper limit for the calculation of the STUW volume. We have also tested the sensitivity of our results using the seasonal MLD or a constant MLD as the upper boundary. The interannual variability of the STUW volume remains the same. Thus, our results are insensitive to the choice of the upper limit for the integral of the volume. Furthermore, sensitivity tests using a slightly different upper boundary or the southern boundary are also examined. We find out that that slight changes in the choice of the upper boundary or the southern boundary for the calculation of the STUW volume do not impact the outcome of this analysis.

Fig. 2

Time series of the STUW volume anomalies calculated by ECCO from 1992 to 2017

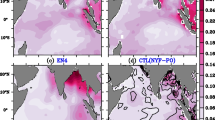
One caveat of interannual variability of STUW volume in Fig. 2 is the uncertainty raised by low sampling number of salinity and temperature. The STUW is a high-salinity water mass, which is determined by salinity, temperature, and density criteria defined in Liu and Qu (2020). The accurate representation of the STUW properties (e.g., volume) depends highly on the underlying number of salinity/temperature profiles. However, the number of temperature and salinity profiles is low over the central subtropical South Atlantic before 2009 (figures not shown here). Thus, we emphasize that caution should be taken regarding the results before 2009. In contrast, the STUW volume derived from well-known datasets (e.g., EN4, IAP, SODA, ORAS5, and GLORYS12v1) shows consistent variations with the results derived from ECCO r4v4 after 2009 (Supplementary Figure S1). Thus, the results after 2009 are more robust in this study.

Changes in the STUW subduction area and rate

The subduction area is defined as the region with particles released from the bottom of the mixed layer within the outcropping area (Fig. 3) that are traced for 1 year. If the water particle is persistent below the mixed layer after 1 year, the release point of the water particle is considered the subduction area. The spatiotemporal variations in the horizontal extent of the STUW subduction area and rate at each grid point are examined (Figs. 3 and 4). The STUW ($24.65<\upsigma <25.63\text{ kg}/{\text{m}}^{3}$) mainly subducts in the central subtropical gyre (northwestern flanks of the STUW outcropping area), consistent with subduction regions of the surface water ($\upsigma <25.5\text{kg}/{\text{m}}^{3}$) and light South Atlantic Central Water ($25.5<\upsigma <26.2\text{kg}/{\text{m}}^{3}$) derived from Donners et al. (2005). The subduction area only exists in the northern part of the outcropping area (Fig. 3). It can be attributed to two causes. STUW particles released from the outcropping area generally show two routes (Fig. 5). STUW particles on the northern side of the subduction area are transported toward the equator, where the mixed layer is relatively shallow. These particles are preferentially subducted due to a shallower mixed layer downstream. However, the particles released on the southern side of the outcropping area are generally transported southward, where the mixed layer is deeper (e.g., to the south of 21°S). There is a high possibility that those particles will be carried by the subsurface current and entrained back into the mixed layer downstream within 1 year. This result is consistent with those from Liu and Qu (2020), which shows that the STUW on the northern flank of the subtropical gyres (21°S) resides under the permanent thermocline, and the STUW on the southern flank of the subtropical gyre is located within the seasonal thermocline. The other reason is attributed to the spatial distribution of the mixed layer (shown in Fig. 11 from Liu and Qu 2020). A large portion of relatively cold and salty water originating from the Indian Ocean has contributes to the South Equatorial Current (Fig. 5), which leads to a denser surface in the center of the subtropical South Atlantic. Those locations are generally associated with a deeper MLD (Fig. 5). However, in the southwestern STUW outcropping area, relatively warm water is at the sea surface, leading to a shallower MLD. STUW particles released from a shallower depth are hard to be subducted.

Fig. 3

Spatial distribution of the annual subduction rate from 1992 to 2016. The black contours denote the outcropping area in each year. The units for the subduction rate are m/month

Fig. 4

Time series of a the area-integrated annual subduction rate (blue line) and subduction area (orange line) anomalies, b the monthly subduction rate, c the monthly subduction area, and d the subduction rate components due to vertical pumping and lateral induction. The lateral induction is separated into two components: $\frac{\partial h}{\partial t}$ and ${{\varvec{u}}}_{b}\nabla h$ [Eq. (1)]. The subduction rate is the integral of the subduction at each grid point within the subduction area. The units for the area-integrated subduction rate and area are $\text{Sv}$ and ${10}^{12}{\text{m}}^{2}$, respectively

Fig. 5

A schematic diagram illustrating the position of the outcropping area (magenta contour) and winter MLD (background shading). The black lines with arrows denote the streamlines of the subsurface flows averaged between 55 and 200 m

The climatological mean value for the subduction area over winter-spring months (averaged from September to December) is $8.33\times {10}^{11}{\text{m}}^{2}$, which is approximately 18% compared to the size of the STUW outcropping area ($4.66\times {10}^{12}{\text{m}}^{2}$) during the same period. The difference in the size of these two areas suggests that dynamic processes (e.g., subsurface advection of the water particles) play an active role in regulating STUW production.

The subduction rate at each grid point (units are m/s) shows a consistent distribution from 1992–2016 (Fig. 3). A higher subduction rate can generally be found on the southeastern flank of the subduction area (i.e., the central part of the outcropping area, Fig. 3). This result agrees well with the horizontal distribution of the subduction rate derived from the Hybrid Coordinate Ocean Model (Mill and de Moraes Paiva 2013). The horizontal distributions of the subduction rate are consistent with the horizontal pattern of the mixed layer (Liu and Qu 2020). The magnitude of the subduction rate over most of the grid points is generally less than 20 m/s to the north of 15°S, which is a result of the shallower mixed layer in the northern subtropical gyre. A lower subduction rate also occurs between 15°S and 30°S in some years. For example, in 1994, 2003, 2006, and 2011, the subduction rate was generally between 10 and 25 m/s. The magnitude of the subduction rate was generally greater than 40 m/s to the south of 20°S in 1992, 1998, 2005, 2007, 2010, 2012, 2014, and 2015. The subduction rate with a magnitude of over 40 m/s shows the maximum spread in 2010 and 2015, leading to peaks in the area-integrated STUW subduction over the entire subtropical gyre from 1992 to 2016 (Fig. 4a).

The total STUW subduction rate (area-integrated subduction rate, with units of Sv) is calculated by integrating the subduction rate at each grid over the subduction area in every month of each year. The annual mean area-weighted subduction rate is 3.2 Sv, with a standard deviation of 0.67 Sv from 1992 to 2016. The minimum STUW subduction rate occurred in 1993, during which the STUW subduction rate at most of the grid points within the subduction area was low. The minimum subduction rate can be attributed to the relatively shallow MLD in winter 1993 and relatively deep MLD in spring 1993, which leads to a smaller difference in the mixed layer anomalies. A more detailed analysis into the cause of the subduction rates will be shown later. The maximum subduction rate occurred in 2002, agreeing with the results of the maximum subduction area in 2002 (Fig. 4a).

From 1992 to 2016, the subduction area and rate generally showed consistent variations (Fig. 4a). In this analysis, the subduction rate is a spatial integral of the regions with positive subduction rates at each grid point. By definition, the subduction area and rate should have a positive correlation. However, in some years, discrepancies between the subduction rate and area exist. For example, in 1993, 2006, and 2014, the time series of the annual mean subduction rate shows troughs. During the same years, the annual mean subduction area does not show a local minimum. To further understand the difference and similarity in the interannual variability of the subduction area and rate, the annual subduction area is split into monthly components (Eq. (1)) and compared with each other to assess the interannual variabilities (Fig. 4b and c). The correlation between the subduction area and rate varies between seasons. In September 1992–2016, the correlation coefficient between the time series of the subduction area and rate was 0.58, satisfying the 95% confidence level. In October, November, and December, the correlation coefficients between the subduction area and rate were 0.73, 0.88, and 0.98, respectively. All correlations satisfy the 95% confidence level. Thus, the two time series are mostly alike during November and December, and discrepancies exist during September and October. In other words, the subduction area plays a more important role in regulating the subduction rate toward the austral spring.

The differences/similarities in the interannual variability between the subduction area and rate are further assessed by comparing the peaks in different months. The maximum subduction area and rate generally never occurred during September, October, and November in the same year, suggesting that the subduction rate at each grid point plays an important role in determining the area-integrated subduction rate. However, the minimum subduction area and rate occurred during October and November in the same year, indicating that the subduction rate was highly dependent on the size of the subduction area in some years during 1992–2016.

Considering the variable subduction area, the contribution of each term in Eq. (1) to the total annual mean subduction rate is displayed in Fig. 4d. The temporal variability of the mixed layer ($\frac{\partial h}{\partial t}$) plays the most dominant role in the interannual variability in the subduction rate. It contributes approximately 88% to the interannual variation in the total subduction rate. In contrast, the remaining component contributes only 12% to the interannual variance in the subduction rate. Thus, the temporal variability in the MLD controls interannual changes in the STUW subduction rate.

To test the sensitivity of our results to the definition of the MLD, we also calculated the subduction rate using different definitions of the MLD, which includes density thresholds with a magnitude of 0.125 kg/m³ and 0.03 k/m³ and temperature thresholds with a magnitude of 0.2 °C and 0.5 °C. All of the subduction rates defined using different MLDs are consistent over most of the period from 1992–2016 (Supplementary Figure S2). As a result, our results are not sensitive to different definitions of the MLD.

Mechanism for STUW subduction

Causes of the interannual variability in the subduction rate within a constant subduction area

In this section, we explore possible causes of the interannual variability in the STUW subduction rate. As illustrated in the previous section, the temporal variability in the mixed layer ($\partial h/\partial t$) plays an important role in the interannual variability of the subduction rate (Fig. 4d). In this section, we consider the contribution of the interannual changes in the temporal rate of the mixed layer to changes in the subduction rate. The area-weighted $\partial h/\partial t$ anomalies in each month of each year from 1992–2016 were calculated within the climatological subduction area to remove the possible nonlinear effects caused by interseasonal and interannual variations in the subduction area.

Based on Eq. (2), the changes in the temporal rate of the mixed layer anomalies can be attributed to the different variabilities in the MLD anomalies between austral winter and austral spring. The large difference in the MLD anomalies between austral winter and spring is generally associated with positive MLD anomalies in austral winter and negative MLD anomalies in austral spring. We emphasize that the averaged MLD anomalies over the entire winter-spring season do not imply changes in subduction, but the seasonal difference in the MLD anomalies accounts for changes in subduction. For example, the MLD during austral winter (from August to September) in 2009 was shallower than that in 2011 (Fig. 6), but the MLD in 2009 exhibited greater seasonal differences (positive value) than that in 2011 (Fig. 4d). This accounts for the stronger subduction in 2009 than in 2011. In 2011, a deeper MLD during November–December resulted in negative anomalies of the MLD difference (Fig. 6). These results are consistent with the smaller subduction rate observed in 2011. It should be noted that if a forward difference is applied in the calculation for $\partial h/\partial t$, the magnitude of $\partial h/\partial t$ changes, but the interannual variations remain the same. Positive MLD anomalies in winter and negative anomalies in spring sometimes do not indicate a strong subduction rate. Therefore, other processes must be at work during these years.

Fig. 6

Time series of the MLD anomalies within the STUW subduction area from 1992 to 2016 in each month. The units for the anomalies are m

The deepening and shoaling of the MLD represent conversion between turbulent kinetic energy (TKE) and potential energy input by surface fluxes (Niiler 1975). During austral winter (July, August and September), the MLD deepens (Fig. 7a) due to surface convection (i.e., buoyancy loss) and TKE input by wind stirring. The buoyancy fluxes are extracted from the ocean surface and lead to the convective mixing by increasing the potential energy at the sea surface. During spring, the MLD shoals (Fig. 7a) due to warming (Fig. 7b) at the ocean surface (net surface heat flux > 0). The MLD is maintained by the TKE balance between the effects of wind stirring and stabilization due to surface buoyancy input. In summary, the driving forcing for the MLD varies depending on the season. In the next section, we investigate the causes of the interannual variability of the MLD during winter and spring, seperately.

Fig. 7

Seasonal cycle of a heat flux and b MLD within the climatological STUW subduction area. The units for the heat flux are ${\text{Wm}}^{-2}$, and the units for MLD are m

The cause of MLD anomalies in winter

The MLD is an expression of the strength of convection during winter. The convection induced MLD is defined as (Marshall and Schott 1999):

$${H}_{conv}={\left[\frac{2{\int }_{{t}_{1}}^{{t}_{2}}{B}_{0}dt}{{N}^{2}}\right]}^{1/2}$$

(3)

where ${t}_{1}$ is April, ${t}_{2}$ is September, and ${N}^{2}$ is the averaged Brunt-Vaisala frequency between the maximum MLD over austral winter and the mean MLD over austral summer. ${B}_{0}$ represents the buoyancy flux and is calculated as follows:

$${B}_{0}=-\frac{g\alpha }{{C}_{p}{\rho }_{0}}{Q}_{net}+g\beta {S}_{m}\left(E-P\right)$$

(4)

where a positive ${B}_{0}$ indicates a buoyancy loss, and a negative value indicates a buoyancy gain. The variable $g$ is the acceleration of gravity, $\alpha$ is the thermal expansion coefficient, ${C}_{p}$ is the heat capacity, ${Q}_{net}$ is the net heat flux, $\beta$ is the haline contraction coefficient, ${\rho }_{0}$ is the constant reference density (1027 kg/m³), ${S}_{m}$ is the mixed layer salinity, and $E-P$ is the surface freshwater flux.

The TKE input can be estimated using the depth scale of the turbulent Ekman boundary layer (Rossby and Montgomery 1935). The turbulent Ekman depth is calculated as follows:

$${H}_{EKD}\sim \frac{{u}^{*}}{\left|f\right|}$$

(5)

where ${u}^{*}$ is the friction velocity, which is quantified as follows:

$${u}^{*} =\bigg({\frac{\left|{\tau }_{a}\right|}{\stackrel{-}{\rho }}\bigg)}^{1/2}$$

(6)

where ${\tau }_{a}$ is the wind stress magnitude.

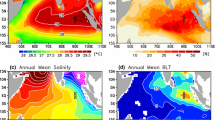
The MLD anomalies (Fig. 8a and b) generally show consistent changes with the convective MLD (${H}_{conv}$, Fig. 8c and d) in August and September. The correlation coefficients between the convective MLD and the MLD are 0.88 and 0.81 for August and September, respectively. The p-values of the two correlation coefficients are smaller than 0.05, indicating that the correlation is significant. The root-mean-square errors (RMSEs) between the two types of MLDs are 11.35 m and 20.65 m for August and September, respectively. The time series of the turbulent Ekman depth (${H}_{EKD}$, Fig. 8e) shows a large difference with MLD in August (Fig. 8a). The correlation is not significant between the MLD and turbulent Ekman depth. In September, the correlation between the two types of depths is significant. However, the correlation coefficient between the two types of depths in September is 0.62, which is smaller than that of the convective MLD. Thus, convection plays a more important role in regulating the winter MLD than turbulence induced by wind stress. According to Eq. (3), convection is determined by buoyancy and stratification. We also compared the magnitude of the heat and freshwater fluxes and found that heat fluxes show stronger variations than the freshwater fluxes (figures not shown here). Thus, heat fluxes control the buoyancy fluxes in August and September. In summary, heat fluxes and stratification play the leading role in the interannual variability of the MLD during August and September, respectively.

Fig. 8

Time series of the normalized MLD anomalies in a August and b September. c, d are the same as a, b except for the normalized convective MLD. e, f are the same as a, b except for the turbulent Ekman depth. The Pearson’s correlation coefficients (${r}^{2}$) and root-means-squared error are displayed on the top in c–f. The normalized anomalies are unitless

Cause of the MLD anomalies in Spring

According to Morioka et al. (2011), the MLD in the subtropical South Atlantic during austral spring and summer can be determined based on the Monin–Obukhov depth. The Monin–Obukhov depth can be calculated as follows (Nurser et al. 1999):

$${H}_{mo}=\left({m}_{0}{{u}^{*}}^{3} +\frac{\alpha g}{{\rho }_{0}{c}_{p}}{\int }_{-{H}_{m0}}^{0}q\left(z\right)dz\right)/\frac{\alpha g}{2{\rho }_{0}{c}_{p}}({Q}_{net}+qd)$$

(7)

where ${q}_{d}$ is the penetrating shortwave radiation (Paulson and Simpson 1977), and ${m}_{0}$ is 0.5. The contribution of heat fluxes and wind stress to the variation of the Monin–Obukhov depth can be examined by decomposing it into three components as follows:

$$\delta \left({H}_{mo}\right)\left[=\delta \left(\frac{{m}_{0}{u}_{*}^{3}+{q}_{*}}{{Q}_{*}}\right)\right]=\frac{\delta ({m}_{0}{u}_{*}^{3})}{\overline{{Q}_{*}}}+\frac{\delta {q}_{*}}{\overline{{Q}_{*}}}-\frac{\delta {Q}_*\left(\overline{{m}_{0}{u}_{*}^{3}}+\overline{{q}_{*}}\right)}{{\overline{{Q}_{*}}}^{2}}+Res$$

(8)

where ${Q}_{*}=\frac{\alpha g}{2\rho {c}_{p}}({Q}_{net}+{q}_{d})$, and ${q}_{*}=\frac{\alpha g}{\rho {c}_{p}}{\int }_{-{H}_{clim}}^{0}q(z)dz$. ${H}_{clim}$ is the climatological seasonal cycle of the MLD.

The Monin–Obukhov depth shows a good correlation with the MLD in October, November, and December, with magnitudes of 0.88, 0.8, and 0.89, respectively (Fig. 9). All correlations are significant. The RMSE of the Monin–Obukhov depth is large in October, with a magnitude of 84.43 m. During November and December, the RMSEs are relatively small, with magnitudes of 52.98 m and 37.15 m, respectively. Although the RMSE is large, the Monin–Obukhov depth still shows a consistent change with the MLD, indicating that the Monin–Obukhov depth can express the interannual variability of the MLD during its shoaling phase. Next, we compare the contribution of heat fluxes (the second and third terms in Eq. (8)) and wind stress to changes in the Monin–Obukhov depth. The time series of the heat flux terms match well with those of the Monin–Obukhov depth in October, November, and December. Furthermore, the STDs of the heat fluxes in October, November, and December are 17 m,13 m, and 7 m, respectively. The STDs of the wind stress term are 6 m, 3 m, and 2 m. The STDs of the residual term are 7 m, 4 m, and 2 m. Thus, the STDs of the heat fluxes have a larger magnitude than the sum of the wind stress term and the residual term. As a result, the Monin–Obukhov depth is controlled by the variability in the heat fluxes in October, November, and December.

Fig. 9

Time series of the normalized MLD anomalies in a October, b November, and c December. d–f) are the same as a–c except for the normalized Monin–Obukhov depth. The Pearson’s correlation coefficients (${r}^{2}$) and root-mean-squared error are displayed on the top in d–f. g–i The time series of components of Monin–Obukhov depth.The black line denotes the wind stress, the red line denotes the heat flux, which contains the second and the third terms on the right-hand side of Eq. (8), and the green line denotes the residual term. The three terms are divided by the STDs of the Monin–Obukhov depth in October, November, and December, respectively. The normalized anomalies are unitless

Causes of the subduction zone variations

The previous section showed that changes in the subduction area were consistent with the interannual variability in the subduction rate in most years. For example, the low subduction rate observed in 2012 is attributed to the small size of the subduction area in September and November 2012 (Fig. 4b).

This analysis determines the total subduction area based on the number of released water particles remaining within the permanent thermocline for 1 year. Under this definition, two possible variables could affect the size of the subduction area: (1) the total number of particles released from the outcropping area and (2) modulation of the total number of particles that penetrate the permanent thermocline due to variability in three-dimensional advection and the MLD downstream.

The total number of particles released from the outcropping area from 1992–2016 was 647,225, with an average of 24,893 ± 2546 particles released in each year. The number of particles used in tracing during each year depends on the size of the outcropping area because particles are released regularly every 0.25° × 0.25° within the outcropping area. A comparison between the normalized subduction area and the normalized outcropping area is displayed in Fig. 10. During September 1992–2016, the outcropping area showed changes consistent with but slightly different than the subduction area. For example, the maximum in the outcropping area occurred in 2009, whereas the maximum in the subduction area occurred in 2003. The correlation coefficients of the two time series are 0.69, satisfying the 95% confidence level. During October, November, and December, the two time series do not have any significant correlation. Significant discrepancies exist between the outcropping area and the subduction area during October, November, and December from 1992–2016. Hence, the size of the STUW outcropping area does not play the leading role in controlling the size of the subduction area from October-December.

Fig. 10

Normalized outcropping area and subduction area in a September, b October, c November and d December during the period 1992–2016. The normalized anomalies are unitless

Next, we explore the relationship between the downstream dynamics (including the spatial/temporal pattern of the MLD and three-dimensional velocities) and the size of the subduction area. Generally, the route of the particles alone, derived from the three-dimensional velocities, cannot determine whether the particles are entrained back to the mixed layer or penetrate the thermocline after one year of tracing. The MLD downstream must be taken into consideration. However, the South Atlantic STUW is a unique water mass according to Liu and Qu (2020). STUW outcropping area sits on the SEC, which bifurcates when encountering the western South Atlantic coast. Thus, the STUW particles after release from the outcropping area are transported in two directions (Fig. 11a). The STUW particles headed northward are preferably subducted because the MLD in the northern flank (north of 21°S, according to Liu and Qu 2020) of the outcropping area is shallow (Fig. 1). These particles are counted as being subducted because they reach as deep as the permanent thermocline. In contrast, the STUW particles headed southward (south of 21°S, according to Liu and Qu 2020) are preferably transported to the seasonal thermocline because the MLD is deep in the southern side of the outcropping area. Whether the STUW particles are subducted or entrained into the seasonal thermocline is determined by the meridional direction of the particles’ route. Thus, the unique characteristics of the STUW transport allow us to assess the meridional velocities alone to identify the downstream flows’ contribution to the subduction area.

Fig. 11

Schematic diagram of the STUW particle routes in a the climatological November averaged from 1992 to 2016 and b November 2012. The red lines in a, and b denote STUW particles transported to the equator after formation, and the blue lines denote STUW particles transported to the poleward section of the subtropical gyre. The dotted lines in a, and b denote the difference in the direction of the transportation, although the release point is the same. c The climatological mean of the subsurface (averaged between 50 and 150 m, with a 1 m interval) meridional velocity (m/s) averaged over 1992–2016. d The meridional velocity anomalies are derived from the velocity averaged from November 2011 to October 2012 minus the climatological annual mean meridional velocity. The percentage of the subducted particles to the total released particles in a and b denote the percentage of STUW particles subducted into the permanent thermocline divided by the total number of released particles. The number next to the upper (lower) arrow denotes the percentage of the particles dissipated with the seasonal thermocline or above (i.e., not subducted particles) to the north (south) of the 21°S zonal line divided by the total number of released particles. The sum of the percentage of subducted particles and not subducted particles equals one, reflecting the total number of released particles

In this section, we analyze the causes of the subduction area in November 2012 as an example to illustrate the possible impact of the downstream velocity on the variability in the number of subducted particles. November 2012 is selected because it shows one of the lowest percentages (5%) of subducted particles during 1992–2016 (Supplementary Figure S3), as derived from the number of subducted STUW particles divided by the total number of released particles during each month of every year. In Fig. 11, a schematic diagram of the STUW particle route and the effect of the meridional velocities on the route is displayed. From a climatological mean perspective, the STUW particles head toward the northwest immediately after being released because the climatological subsurface meridional velocity averaged between 50 and 150 m is directed northward (Fig. 11c). Then, the route of the particles encounters the western coast of South America and bifurcates into two components: the northern one and the southern one. 84% of the released STUW particles are entrained into the mixed layer, and 16% of them are subducted into the permanent thermocline. 59.92% of the non-subducted STUW particles (i.e., 50.63% of the total released number of particles in Fig. 11a) are transported to the south of 21°S. From November 2012 to October 2013, abnormal poleward meridional velocity anomalies occurred at 40°W and 22°S–30°S and 20°W and 20°S (Fig. 11d). The non-subducted particles increase to 95%. 64% (i.e., 61.13% of the total released number) of them are transported to the south. However, particles headed to the north of the 21°S zonal line do not show a large difference between the climatological mean value (32.92% in Fig. 11a) and November 2012 (33.53% in Fig. 11b). Thus, the southward meridional velocity anomalies lead to more particles heading to the south of 21°S. This further results in an increase in the percentage of particles being entrained back to the mixed layer (deeper MLD to the south of 21°S) and fewer particles get subducted.

Discussion

Relationship between STUW subduction and volume

Based on the above results, the persistence time can be calculated by dividing the climatological STUW volume by the annual mean subduction rate. The persistence time in this study is 2.04 ~ 3.13 years, consistent with the reemergence time (2.2 years) of water masses (σ < 25.5 $\text{kg}/{\text{m}}^{3}$) reported by Donners et al. (2005). However, according to Liu and Qu (2020), approximately 75% of STUW subducted particles lose the characteristics of STUW within 1 year. Therefore, mixing plays a vital role during water transport.

For a given water mass, the relationship between subduction and STUW volume can be inferred from the volume budget equation. The STUW volume budget can be modified from equations represented by Nurser et al. (1999) as follows:

$$\frac{\partial V}{\partial t}=Sub+D$$

(9)

where $D$ represents the volume exchange by mixing in the STUW downstream. The left-hand term represents the rate of changes in the STUW volume, and the first right-hand term represents subduction. The normalized subduction rate and rate of changes in the STUW volume are consistent only during some of the years from 1992–2016 (Fig. 12). For example, both the subduction rate and rate of changes in the STUW volume show negative anomalies in 1996, 1999, 2009, 2011, 2012, and 2014 and positive anomalies in 1998, 2001, 2002, 2005, 2007, and 2008. However, in the remaining years, the two time series show the opposite signs. Thus, in over 50% of the period between 1992 and 2016, the changes in subduction are not consistent with changes in the rate of changes in the volume. The difference between those two variables is attributed to mixing. Previous studies have shown that mixing plays a role in modulating the STUW in the North Atlantic (Schmitt and Blair 2015). We suspect that mixing plays a similar role in regulating the South Atlantic STUW. The released STUW particles in the South Atlantic could lose their characteristics downstream by mixing (Liu and Qu 2020). Due to the high salinity characteristics, the STUW can enhance mixing by inducing salt finger convection (Johnson et al. 2016). An increase in transport by mixing along the STUW route is also possible. The surrounding waters along the advection route could also be converted to STUW by mixing and advection. A calculation of STUW transport considering mixing should be performed, but it is beyond the scope of this analysis.

Fig. 12

Annual mean subduction rate (black line), rate of volume change (red line), and the residual term (i.e., the mixing term $D$, blue line) from 1992 to 2016. The units for the anomalies are ${\text{m}}^{3}/\text{month}$

A possible cause for the poleward transport of STUW particles from 2012 to 2013

There are two causes for the possible increases in the poleward transport of the STUW particles: the southward meridional velocities over the outcropping area and the southward velocities in the downstream area. The former is possibly attributed to the zonal wind stress because the imprint of the wind stress on the flow is relatively shallow (i.e., Ekman layer is shallow). The latter is due to wind stress curl because the Sverdrup velocities are generally dominant below the Ekman layer. The zonal wind stress anomalies from November 2012 to October 2013 show a westward direction over the northern flanks of the subduction area, leading to a possible poleward meridional velocity (Fig. 13a). Simultaneously, the wind stress curl over some locations of the STUW downstream displays negative anomalies (Fig. 13b). Due to the Sverdrup balance, the negative wind stress curl induced poleward flow in most of the subtropical South Atlantic region. Comparing Fig. 11 with Fig. 13, the changes in the zonal wind stress, wind stress curl, and meridional velocity anomalies do not show an exact match over the subtropical South Atlantic. A possible reason is that the SEC (the main flow in the regions shown in Fig. 11c) is fed by Agulhas leakage (Beal et al. 2011; Biastoch et al. 2008; Kolodziejczyk et al. 2014). Therefore, the interannual variability in the strength of horizontal transport by Agulhas leakage might play a role in modulating the properties of the SEC (e.g., its strength and locations). Other possible causes, such as Rossby waves or eddies (which is also included in Fig. 11d), might also be in play. A further analysis of the cause of the abnormal meridional velocities is beyond the scope of this study.

Fig. 13

a Zonal wind stress and b wind stress curl anomalies derived from values averaged from November 2012 to October 2013 minus the climatological annual mean values. The solid line in a denotes the rough coverage of the subduction area, and the dotted line in b denotes the horizontal extent of the STUW downstream. The units for zonal wind stress are N/m², and the units for wind stress curl are ${10}^{-7}$ N/m³

Summary

The South Atlantic STUW is a high-salinity water mass between the 24.65 $\text{kg}/{\text{m}}^{3}$ to 25.63 $\text{kg}/{\text{m}}^{3}$ isopycnal surfaces in the subtropical and tropical South Atlantic. The STUW associated with the subtropical gyre is generally located above the mixed layer, and the STUW associated with the tropical gyre is mostly situated within the permanent thermocline. Based on the results from ECCO v4r4 estimates, the interannual variability in the South Atlantic STUW subduction rate was evaluated from 1992 to 2016. The annual mean area-integrated subduction rate is 3.2 ± 0.67 Sv.

The causes of interannual variability in the area-integrated subduction rate (over the subduction area) can either be explained by changes in the subduction area or by changes in the subduction rate at each grid point. The changes in the subduction rate at each grid point can be attributed to changes in the temporal variability of the mixed layer anomalies. We further determined that the temporal variability in the mixed layer can be attributed to a change in heat fluxes at the surface during austral winter and spring, repsectively.

Interannual changes in the subduction area can explain most of the changes in the subduction rate from 1992–2016. In this study, we used the subduction area in November 2012 as an example to illustrate the causes of the changes in the subduction area. A large decrease in the subduction area occurred in November 2012. This decrease in the subduction area was due to abnormal poleward flow between November 2012 and October 2013. The poleward flow led to increases in the number of particles transported southward, where the mixed layer was deeper than the STUW core depth (Fig. 1c). Thus, this increase in the number of STUW particles transported southward led to an increased number of particles being entrained into the mixed layer instead of penetrating the permanent layer, resulting in a shrinkage of the subduction area. Further analysis showed that the poleward velocity near the transport route of the STUW may have been linked to negative wind stress curl and negative zonal wind stress anomalies observed during the same period. Thus, changes in the wind and its curl over the STUW formation and downstream region can also play an important role in modulating the STUW subduction rate.

The STUW volume shows inconsistent variations with the subduction rate during more than 50% of the period between 1992 and 2016. The difference between the interannual variability in volume and subduction might be caused by mixing (Johnson et al. 2016), which could either convert surrounding waters into high-salinity water or dissipate the STUW downstream. Further analysis is needed to identify the causes of the interannual changes in the South Atlantic STUW volume, including the effect of mixing on the STUW after subduction.

The subduction rate showed a decadal signal (Fig. 4a): generally positive during 2001–2010 and mostly negative before 2001 and after 2010. We compared the subduction rate time series with some well-known climate indices: the Atlantic Meridional Mode, the South Atlantic Subtropical Dipole, the Pacific Decadal Oscillation, the Interdecadal Pacific Oscillation, the Southern Annual Mode, and the North Atlantic Oscillation, and we did not find consistency between the climate modes and subduction rate (by comparing the correlation and shapes of the time series during the 1992–2016, Supplementary Figure S4). Thus, we suspect that multiple climate modes or other climate modes might be at work simultaneously to modulate the decadal changes in the subduction rate. Further analysis is needed to identify the key processes modulating the decadal variability of the subduction rate.