1 Introduction

One of the key areas where progresses are expected in this decade is that of forecasts of weather regimes (WRs) from two to four weeks, a time range until recently considered a ”predictability desert” (Vitart et al 2012). WRs are one of the main tools to simplify the continuum of atmospheric circulation in a relatively small number of classes (typically 4–10) per season or year (Vautard 1990; Michelangeli et al 1995).

As WRs represent long-lasting and recurrent weather conditions over extended regions, they are useful to predict large-scale events with a strong impact on society, such as droughts (Lavaysse et al 2018), heat waves (Alvarez-Castro et al 2018), cold spells (Ferranti et al 2018) and wind power fluctuations (Grams et al 2017). WRs characterize climate variability over extra-tropical regions, and are mainly studied in Europe (Plaut and Simonnet 2001; Casado et al 2009; Toreti et al 2010; Polo et al 2013; Couto et al 2015) and North America (Solman and Menéndez 2003; Coleman and Rogers 2007; Roller et al 2016). In the last decade, WRs were identified also in less studied areas, like Asia (Gerlitz et al 2018; Wang et al 2019), Australia (Wilson et al 2013) and Africa (Fauchereau et al 2009).

WRs are usually defined by employing unsupervised machine learning algorithms that cluster similar daily atmospheric circulation fields as geopotential height, sea level pressure or wind speed direction (Hannachi et al 2017). WR classifications in the Northern Hemisphere are often performed for the boreal winter (DJF) or extended winter (NDJFMA), when they are more effective predictors of local climate (Vrac et al 2014; Thornton et al 2017). However, WRs can also be obtained for summer (JJA) (Cassou et al 2005; Yiou et al 2008; Guemas et al 2010; Quesada et al 2012), for spring and autumn, but in these two last seasons the usefulness of WRs in characterizing climate variability in the Euro-Atlantic region has been less explored. Annual classifications that analyze all the days of the year together (Neal et al 2016; Grams et al 2017), or separately for each month of the year (Cortesi et al 2019) also proved useful for applications. In principle, weekly WR classifications might be considered too, however their statistical significance is limited by the reduced data sampling, and no large differences are expected from one week to the next one.

The implicit assumption underlying any WR classification is that WRs are able to capture most part of the variability of atmospheric circulation in the clustering period (Philipp et al 2010). This assumption is important because an excessive simplification of the representation of the atmospheric flows might also modify both the impact of the regimes on surface variables of users’ interest and the skill of forecast systems in simulating the regimes. However, if the clustering period increases to include more than a few months, as in the case of the extended seasonal classifications or of the annual classifications, circulation variability in the study domain increases too. It is important to know if the WRs defined for periods larger than a season are a good characterization of the circulation variability for the whole period they represent, or if they simplify it excessively, lacking some important atmospheric flow. This is particularly relevant if the number of WRs does not increase accordingly with the period expansion. For example, while four WRs characterize winter (DJF) circulation quite well, they might be not be so good characterizing circulation of extended winter (NDJFM, ONDJFM or NDJFMA) or of the whole cold season from October to April (Ferranti and Corti 2011).

The first objective of this study is to settle this assumption by comparing the spatial patterns of two extended WR classifications of six months each (respectively from October to March and from April to September, hereby ”extended WRs”), with those of a reference WR classification defined with a rolling window of 13 weeks each (hereby ”reference WRs”), that is roughly the length of three months or of a season. The spatial patterns of the reference WRs for two consecutive weeks are not significantly different from one week to the following, as most of the period is in common. Thus, they cannot be considered a proper WR classification. However, their main usefulness is that the evolution along the year of their WR patterns represents a way to characterize the annual cycle of atmospheric circulation. Significant differences between the extended WR patterns and those of the reference WRs would indicate that the extended WR classifications simplify too much circulation variability.

The second objective of this study is to assess the forecast skill in simulating the weekly frequencies of the extended WR classifications in the particular case of the sub-seasonal forecasts, comparing it with the skill of the reference WRs. To the best of our knowledge, this is the first time sub-seasonal forecast skill in simulating WR frequencies is assessed outside winter season. The only available validation for the Euro-Atlantic region at the time of writing is focused on the winter season (Vitart 2014). The present work extends it to the rest of the year, making it possible to understand the annual evolution of the forecast skill. Skillful forecasts are crucial for developing products for many sectors of the society, particularly renewable energies, agriculture, insurance and health. WRs, in fact, can be used as proxies for surface climate variables of user relevance (Beerli 2017; Soret et al 2019; Terrado et al 2019; Bloomfield et al 2020) in the areas where they have a significant impact on these variables. Particularly, improving the prediction of WR weekly frequencies of occurrence should be considered one of the most important possible advancements for the exploitation of forecast systems in a climate services context.

This article is organized as follows: Sect. 2 is dedicated to the description of the data and the methodology to compute both observed and forecasted WRs and to assess the skill of the sub-seasonal forecast system. Results are presented in Sect. 3, while Sect. 4 discusses them. Finally, conclusions are drawn in Sect. 5.

2 Data and methodology

The procedure to pre-process data, define WRs and evaluate forecast skill requires numerous steps. To better illustrate them, three schematics were provided synthesising the steps required: the first one for the two extended WR classifications, respectively from October to March and from April to September (Fig. 1), the second one for the reference WRs (Fig. 2), and the third one for describing how weekly WR frequencies were concatenated to measure forecast skill (Fig. 3). Each of the following sub-sections describes a specific part of these schematics.

Fig. 1
figure 1

Summary of the methodology to classify the two extended WR classifications from October to March and from April to September (1979–2018) and to validate the sub-seasonal forecast skill of simulating the frequencies of occurrence of these WRs for the reforecast period 1998–2017. Both ERA-Interim and ECMWF-Ext-ENS daily SLP anomalies are referred to their common period

Full size image
Fig. 2
figure 2

Summary of the methodology to classify the reference WRs (1979–2018) and to validate the sub-seasonal forecast skill of simulating the frequencies of occurrence of these WRs for the reforecast period 1998–2017. The schematic is similar to that in Fig. 1, except that the clustering is applied to the observed SLP anomalies of 13 consecutive calendar weeks, in a rolling window approach: the same method was repeated for all the 52 calendar weeks of the year, one by one, generating a different set of 4 WRs for each week

Full size image
Fig. 3
figure 3

Graphical representation of the values employed to measure the Pearson correlations and the BSS for a chosen WR and forecast week. The interannual time series (1998–2017) of 20 pairs of observed and forecasted weekly WR frequencies are concatenated for five consecutive start dates to form a single time series of 100 pairs of values. Correlation or BSS is then measured for this longer time series and its value is assigned to the start date in the middle (in this case, the 15th of January)

Full size image

2.1 Data and pre-processing

This work utilizes both observed and forecasted daily mean fields of sea level pressure (SLP). Daily means of SLP were considered in this study instead of the more popular geopotential height (Hafez and Almazroui 2014), because SLP does not present any significant long-term trend in the Euro-Atlantic domain. Thus, it is less affected by global warming than geopotential height and may provide more information about the impact of atmospheric circulation on surface variables of users’ interest. SLP observations proceed from ERA-Interim reanalysis dataset (Dee et al 2011), with a regular Gaussian N128 grid (512 \(\times\) 256 points). Sensitivity of WRs to the observational dataset in the northern extratropics is quite low (Carvalho et al 2014; Stryhal and Huth 2017; Cortesi et al 2019).

Forecasts were provided by the European Centre for Medium-Range Weather Forecasts (ECMWF). They consist of a set of past forecasts (reforecasts) for 1998–2017 from their Extended range Ensemble forecast system (ECMWF-Ext-ENS) released in 2018. The ECMWF-Ext-ENS is an operational forecast system based on a fully coupled global earth system model (Vitart et al 2008). This particular version of the system is made up of two different cycles: CY43R1, operational from July 2017 to June 2018, and CY45R1 from June 2018 to June 2019. Thus, though only reforecasts of 1998–2017 are employed in this work, they belong to two different model versions, the ones used to produce forecasts of 2018.

Sub-seasonal forecasts are probabilistic to better represent the chaotic nature of the earth system. Several independent simulations (ensemble members) are provided to represent the uncertainties; each one originates from slightly perturbed initial conditions and/or different physical parameters (Doblas-Reyes et al 2009). In the case of the reforecasts of ECMWF-Ext-ENS, they consist of 11 ensemble members, 10 of which perturbed and 1 unperturbed, while the ensemble size of the forecasts is larger, 51. Both reforecasts and forecasts are issued on Monday and Thursday each week, for a total of 104 bi-weekly start dates in a year (Molteni et al 2011). Only reforecasts data of the 11 members of the 52 Mondays start dates were used in this study. ECMWF-Ext-ENS provides reforecasts up to 46 days with a spatial resolution of \(0.2^\circ\) until day 15 and of \(0.4^\circ\) afterwards.

SLP fields were extracted for the Euro-Atlantic region (\(27^\circ\)N–\(81^\circ\)N, \(85.5^\circ\)W–\(45^\circ\)E), the same of Cortesi et al (2019) during the 40-years period 1979-2018 (for ERA-Interim) or the 20-years period 1998–2017 (for ECMWF-Ext-ENS reforecasts). For both datasets, daily-mean SLP were computed as the average of 6-hourly raw data (00, 06, 12 and 18 UTC). ERA-Interim data was extracted for the longest period available for this reanalysis, in order to obtain the most statistically robust WRs possible (Hannachi et al 2017).

Sub-seasonal forecast systems usually present biases which depend on the forecast time, the so-called ’model drift’ (Alves et al 2004). To minimize the effect of the biases on the weather regime analysis, daily anomalies were computed separately for the reanalysis and the reforecasts with respect to their own daily climatology for period 1998–2017. To remove the influence of the annual cycle of SLP (still visible even if WRs are defined for a 6-month period) and to minimize the high short-term variability of its climatology, daily data was filtered point by point with a LOESS polynomial regression with a degree of smoothing \(\alpha\) = 0.15 (Mahlstein et al 2015) applied to all members, that was found to provide optimal smoothed climatologies. SLP anomalies were weighted by the cosine of the latitude, in order to ensure equal area weighting at each grid point. Most WR studies employ principal components analysis (PCA) to filter out noise, by reducing the dimensionality of the k-means before the clustering (Philipp et al 2010). In this work, data were not filtered, so the full range of SLP values was preserved, as in Cassou et al (2005).

2.2 WR classifications

All observed WRs were classified by clustering daily SLP anomalies extracted for 1979–2018 with the k-means clustering algorithm (Hartigan and Wong 1979) with 50 random starts and a maximum of 200 iterations. The k-means clustering algorithm minimizes the sum over all clusters of the within-cluster SLP variance. Its main caveat is that the optimal number of clusters N is not defined a priori. For both extended and reference classifications, the number of WRs N = 4 was chosen in this work as it corresponds to the more robust regime partition during winter season in the Euro-Atlantic region (Michelangeli et al 1995; Ferranti et al 2015; Neal et al 2016; Matsueda and Palmer 2018; Torralba 20010). Four is also a good compromise for forecasting purposes: using a higher number of WRs would decrease the differences between their spatial patterns, also decreasing the overall forecast skill. All days were assigned to one and only one WR, leaving no days unassigned.

Some authors also introduce a WR specific of the days in the transition period between one WR sequence and the following, when the WR patterns are often a mix of the two WRs (Conil and Hall 2006; Grams et al 2017). This particular WR is usually indicated as the ‘unclassified’ type and it tends to group together days with weak anomalies, so the other WRs are more related to extreme events and are more useful in impact studies, as they exert a greater influence on the target variable. This work, however, is not focused on the impact of WRs, so the ’unclassified’ WR was not introduced.

The two extended (6 months long) WR classifications were defined by clustering daily SLP anomalies from October to March and from April to September respectively in two distinct sets of 4 WRs each. The spatial patterns of each WR were obtained by averaging the daily SLP anomalies of all days of the extended season belonging to the chosen WR. Spatial patterns of seasonal WR classifications can also be adjusted week by week by using the daily projections of a given week, i.e: by averaging SLP anomalies of all days of the extended season for a chosen WR and week. In this way, the spatial patterns of the SLP anomalies of the extended WRs can be compared to those of the reference WRs (Figs. 4 vs. 5). Last day of last calendar week of March 2018 falls on Sunday the 1st of April, that does not belong to the October to March wintertime period, so SLP data of the 1st of April was not included when averaging SLP anomalies of that week.

Fig. 4
figure 4

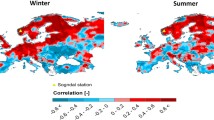
Main figure: projection of the spatial patterns of the SLP anomalies (in hPa) of the Euro-Atlantic extended WRs on each calendar week. Horizontal labels indicate the 52 weeks of the year, while vertical labels show the four WRs. The two thick black vertical lines separate the projections of the two different sets of wintertime and summertime extended WRs shown at bottom right, explaining the abrupt shift visible between the patterns separated by the two black lines. Bottom right: spatial patterns of the SLP anomalies of the extended WR anomalies without projecting. WRs were defined by clustering the daily SLP anomalies of October–March (first column) and April–September (second column) separately using ERA-Interim (1979–2018). Average frequency of occurrence (in %) of each WR is indicated in the bottom left corner of each pattern

Full size image
Fig. 5
figure 5

Spatial patterns of the SLP anomalies (in hPa) of the Euro-Atlantic reference WRs for each calendar week of the year (1979–2018), as shown by the horizontal labels. Vertical labels indicate the four WRs. Average frequency of occurrence (in %) of each WR is indicated in the bottom left corner of each pattern. Reference WRs were defined by clustering daily SLP anomalies in a rolling window of 13 weeks each. Weeks in figure indicate the central weeks of each rolling window. Red boxes show the patterns resembling Atlantic Low regime, while blue boxes show patterns similar to NAO+ but with an anomaly dipole slightly shifted southward

Full size image

Reference WRs were classified by clustering daily SLP anomalies (excluding leap days) in a rolling window of 13-weeks, starting from the 1st of January and shifting the window of one week at time. Thus, a different set of 4 WRs was obtained for each calendar week of the year, for a total of 52 sets of WRs. Last day of the year does not fall in any calendar week, so it was not included in the clustering. The rolling window of 13 weeks months has a similar length of that of the seasonal WR classifications, but with much smoother transitions from 1 week to the following. In winter weeks, spatial patterns of the reference WRs shown in Fig. 5 were reordered to match the more traditional WRs identified by various authors in the winter season: NAO+, NAO-, blocking and Atlantic ridge Cassou et al (2004). Spatial patterns of the other weeks were reordered in a subjective way to match the winter ones as much as possible and to minimize the discontinuities between one week and the following, with the aim of better representing the evolution of atmospheric variability of SLP through the year.

The method to assign to each day of the year one probabilistic simulated WR from the deterministic observed WRs was firstly proposed by Ferranti et al (2015) and is the same for both the extended WR classifications and the reference WRs. One and only one simulated WR was assigned to each day d in 1998–2017 and to each ensemble member m of the ECMWF-Ext-ENS, by measuring the minimum root mean squared difference (RMSD) between the reforecasted daily SLP anomaly field F(d,m) and the four observed WR spatial patterns O(k):

$$\begin{aligned} WR (d, m) = arg\,min_{k=1,\ldots , 4} RMSD_{k} (d, m) \end{aligned}$$
(1)

being:

$$\begin{aligned} RMSD_{k} (d, m) = \sqrt{ \frac{\sum _{i=1}^{N} (F_{i} (d, m) - O_{i} (k))^2}{N} } \end{aligned}$$
(2)

with k = 4 the number of WRs and N = 14,322 the number of points that form the Euro-Atlantic spatial domain.

Then, the observed WR of the pattern with the lowest of the four RMSDs was assigned to that day and member, becoming its simulated WR. In order to measure the RMSD between the observed and simulated grid, reforecasted SLP fields had to be previously bilinearly interpolated to a coarser grid with the same resolution of ERA-Interim. It is worth noting that due to the choice of this assignation method, the spatial patterns of the SLP anomalies of the WRs obtained for the sub-seasonal reforecasts are by construction very close to the observed ones, with spatial correlations between them almost always higher than 0.8 for both the WR classifications (not shown). The reasons for taking the observed WRs as reference are explained in detail in Sect. 4.

2.3 WR verification

The predictability of the ECMWF-Ext-ENS in forecasting WRs was evaluated by four metrics, two deterministic and two probabilistic ones, and by the analysis of extremely persistent WR events. The two deterministic metrics are the Pearson correlation coefficient and the mean absolute error, while the two probabilistic metrics are the Brier skill score and the fair continuous ranked probability skill score.

For verification purposes, reforecasts were grouped in four forecast weeks, the same ones defined by Vitart (2004) and Weigel et al (2008) for the ECMWF-Ext-ENS: week 1 (days 5–11), week 2 (days 12–18), week 3 (days 19–25) and week 4 (days 26–32). Days from 32 to 46 were not considered, as at these high forecast times model sub-seasonal skill is still low and it is better to aggregate data in periods larger than a week (Vitart 2014).

the Pearson correlation coefficient was measured between the predicted and observed frequencies of occurrence of the WRs. A paired t-test was utilized to measure the significance of the correlations. For each forecast week, the frequency of occurrence of the WRs was measured by counting the percentage of days and members that were assigned to each regime. For example, if WR 1 would be assigned by all 11 members during the first 3 days of the week, while the other WRs would be assigned during the 4 subsequent days, then the frequency of WR 1 would be 42.9% (3/7). Validation of correlation skill was performed in a leave-one-out cross-validation framework, by removing the SLP data of one year at time when classifying the WRs, and measuring the correlation values of the WR frequencies for all the years (except the excluded one) before moving to the following year. The mean absolute error (MAE) is the mean of the absolute values of the differences between the forecasted values and the observed ones and tells how big of an error can be expected from the forecasts on average (Wilks 2011). In this case, it is applied to the WR weekly frequencies of occurrence:

$$\begin{aligned} MAE_{r}(s,w) = \frac{\sum _{i=1}^{N} |F_{ir} (s,w) - O_{ir}(s,w)|}{N} \end{aligned}$$
(3)

being r the WR number, N = 20 the number of reforecast weeks of start date s and forecast week w from 1998 to 2017, \({O_{ir}(s,w)}\) the observed weekly frequency of occurrence of WR r for start date s and forecast week w, and \({F_{ir}(d,m)}\) the reforecasted weekly WR frequency of the ensemble mean for the same WR r, start date s and forecast week w. Thus, the MAE is a non-negative number, equal to 0 in case of perfect forecasts.

The multi-category Brier skill score (BSS) is widely used to verify categorical probabilistic forecasts of WRs (Chessa and Lalaurette 2001; Fil and Dubus 2005; Kober et al 2014; Matsueda and Palmer 2018):

$$\begin{aligned} BSS = 1 - \frac{BS}{BS_{ref}} \end{aligned}$$
(4)

the Brier score (BS) is the extension of the root mean square error to dichotomous or multi-category events (Wilks 2011):

$$\begin{aligned} BS = \frac{1}{N}\sum _{i=1}^{N}\sum _{j=1}^{R}(F_{ir}-O_{ir})^{2} \end{aligned}$$
(5)

being R and N respectively the number of WRs (4) and the number of events (in this work, the 20 weeks from 1998 to 2017 associated to the same start date and forecast week). \({F_{ir}}\) and \({O_{ir}}\) are respectively the forecasted and observed weekly frequency probabilities of WR r in week i (counting all days and members). The reference forecast \({BS_{ref}}\) is the observed climatological weekly frequency of the WRs. The maximum value of BSS is 1 for a perfect probabilistic forecast, while positive values of BSS indicate that the ECMWF-Ext-ENS are an improvement over the reference forecasts.

The fair continuous ranked probability skill score (FCRPSS) is a probabilistic skill score that allows the predictive assessment of the full probability distribution (Jolliffe and Stephenson 2011). It is based on the continuous ranked probability score (CRPS), a score that represent the extension of the MAE to probabilistic events (Wilks 2011). CRPS can be expressed as:

$$\begin{aligned} CRPS = \int _{-\infty }^{\infty } |F(y) - F_{0}(y)|^{2} \ dy \end{aligned}$$
(6)

where F(y) is the cumulative density function of the predictions and \({F_{0}(y)}\) is the cumulative step function that jumps from 0 to 1 at the point where the forecast variable (y) equals to the observation (x):

$$\begin{aligned} F_{0}=\left\{ \begin{array}{rl} 0, &{} y < x\\ 1, &{} y \ge x \end{array}\right. \end{aligned}$$

The CRPS measures the difference between the predicted and observed cumulative distributions and it can be converted into a skill score (CRPSS), measuring, in case of the WR frequencies, the performance of a forecast relative to the observed weekly climatological frequency of the WRs:

$$\begin{aligned} CRPSS = 1 - \frac{CRPS}{CRPS_{clim}} \end{aligned}$$
(7)

The CRPSS ranges between \(-\infty\) to 1. CRPSS values below 0 are defined as unskillful, those equal to 0 indicate that the forecast is similar to the climatological forecasts of weekly WR frequencies, and CRPSS > 0 that the predictions are better than weekly WR climatology. CRPSS = 1 indicates a ‘perfect’ frequency forecast. Finally, since the CRPS and CRPSS are biased to finite ensemble size, additionally ensemble-size corrected ’fair’ skill score FCRPSS is also calculated (Ferro 2014).

To increase the statistical robustness, the four metrics were measured after concatenating the interannual time series of the frequencies of occurrence of five consecutive Monday start dates in a single time series, with a rolling window approach. For example, for a chosen WR and forecast week, the weekly frequencies of the first 5 Monday start dates of the year were concatenated together and the result of their validation was associated to the central week of the sequence, the third Monday of January. In this way, the number of frequency pairs to measure Pearson correlations increases five times (100 pairs instead of 20, see Fig. 3). Selecting less than 5 start dates increases the noise, making results more difficult to interpret. In case of Pearson correlations, the time series of the frequencies corresponding to each start date and forecast week were standardized with their mean and standard deviation before concatenating them. This step is important because correlations could artificially increase when concatenating time series of different mean and standard deviation.

The uncertainty in the measure of the four metrics was estimated by bootstrapping WR time series (with replacement) 1000 times, thus measuring 1000 different values for each metric, start date and forecast week. Their 10th, 25th, 50th, 75th and 90th percentiles are the values shown in the box and whisker plots, along with the values of the original, non-bootstrapped data. In this way, it is possible to understand if the difference between the extended and reference WRs of the same metric and start date, or between those of two adjacent start dates, is also statistically significant. For example, significant differences at the 10% of confidence are found when the top line of a box and whisker plot (which indicates the 90% percentile) is below the bottom line of another box and whisker plot (indicating the 10% percentile), or vice versa.

Finally, the analysis of extreme WR events was conducted firstly by detecting all periods during 1998–2017 with an extremely high WR persistence (3 weeks or more with the same WR), and by counting the percentage of members and day in that period that predicted the observed WR, considering the forecasts issued for a single start date previous to the period with high persistence. This analysis is not feasible for the reference classification, as each calendar week has a different set of WRs, so it is presented only for the two extended classifications.

3 Results

3.1 Yearly evolution of the WRs

Spatial patterns of the SLP anomalies of the two extended WR classifications and their projections on each calendar week are shown in Fig. 4. Weekly projections were compared with the reference weekly WRs in Fig. 5, representative of the annual cycle of the WR patterns. Average WR frequencies of occurrence for 1998–2017 are also shown as % inside the maps.

WR patterns for the extended seasons are divided in two separate classifications of four WRs each, the first one during wintertime (October–March) and the second one during summertime (April–September). Wintertime WR patterns are similar to the four WR patterns traditionally identified in the Euro-Atlantic region in winter (Cassou et al 2004; Ferranti and Corti 2011). Wintertime patterns of WR 1 and WR 2 shown at bottom right of Fig. 4 represent the two opposite phases of the NAO (Trigo et al 2004). WR 3 is called blocking (BL), as its pattern shows a strong positive anomaly centred over Scandinavia (Tyrlis and Hoskins 2008). WR 4 is called Atlantic ridge (AR), and it is characterized by a strong positive anomaly over the Atlantic Ocean and a weak negative anomaly over Scandinavia, resembling the negative phase of the East Atlantic pattern (Barnston and Livezey 1987).

Summertime WR patterns at bottom right of Fig. 4 were reordered to try to match the wintertime WR patterns: WR 1 resembles NAO+, WR 2 NAO-, WR 3 BL, while WR 4 pattern is different from all wintertime ones and was paired with wintertime AR. Globally, summertime WR patterns present slightly less intense centroids than wintertime ones, with SLP anomalies usually within the range of \(\pm 6\) hPa in summertime and exceeding \(\pm 6\) hPa in wintertime. Their projected weekly WR patterns shown in the rest of Fig. 4 have even a wider range of values, as they are measured by averaging a smaller sample of daily SLP anomalies than the non-projected patterns. A clear annual cycle of pattern intensities can be observed in Fig. 4, with winter weeks being the ones with the most intense patterns, and summer weeks with the less intense ones.

Transitions between the projected patterns of two consecutive weeks in Fig. 4 almost always exhibit a quite continuous evolution of the SLP anomaly fields, with small differences in the strength and position of the patterns and their centroids. Only two important discontinuities are observed, each one in correspondence to the two weeks separating wintertime and summertime extended WR classifications, the first discontinuity between weeks 26 March–1 April and 2–8 April, and the second one between 24–30 September and 1–7 October. The patterns of the first week of April and October are the projection of the other set of extended WRs, hence the abrupt shifts observed. In both cases, WR 4 is the one exhibiting the biggest differences of its spatial patterns from 1 week to the following, as its positive centroids become negative ones and vice-versa. These two discontinuities are easy to explain, as the projected regimes are directly obtained from the non-projected ones, so their spatial differences just reflect the differences between the wintertime and summertime WR patterns shown at bottom right of Fig. 4. Taken individually, the weekly projected patterns quite closely resemble the non-projected ones for October–March or April–September (pattern correlations of 0.90 or higher). Hence, also their variability from one week to the following is very low.

Reference WRs in Fig. 5 present more discontinuities from one week to the following than extended WRs in Fig. 4. The most stable patterns through the year are those of reference WR 3 (resembling blocking) and WR 4 (similar to Atlantic ridge). Blocking pattern may be that with the least variability, because it is the only WR not associated with the preferred location of the eddy-driven, midlatitude western jet stream (Woollings et al 2010). WR 2 resembles NAO- and its patterns are constant only from October to April. Patterns of WR 1 are the more discontinuous. From December until the beginning of March, they closely resemble those of NAO+. However, in March and April WR 1 patterns evolve to resemble that of the Atlantic low (AL) regime, as shown by the red boxes in Fig. 5. AL regime was identified by (Cassou et al 2005) during summer (JJA) season and it is characterized by a deep anomalous trough covering the northern part of the Atlantic Ocean, while weaker positive anomalies extend over continental Europe. AL pattern bears some resemblance to the positive phase of the East Atlantic teleconnection pattern (Barnston and Livezey 1987).

Another striking discontinuity is observed between week 9–15 April and week 16–22 April, when reference WR 1 evolves to a pattern different from both NAO+ and AL. In subsequent May weeks, its patterns shift again, resembling those of extended WR 4 in summertime. In June and July weeks, reference WR 1 shifts to resemble a weak NAO+ with the dipole displaced slightly southward (blue boxes in Fig. 5. After July, WR 1 patterns remain quite stable until the end of year, with the negative centroid growing in strength, particularly during the weeks of 27 August–2 September, of 15–28 October and of 19–25 November. All these pattern shifts are the expression of the high variability of the SLP field through the year.

The differences shown for reference WR 1 and WR 2 are particularly important, because AL regime is not present in any of the two extended WR classifications in Fig. 4. The most similar pattern to AL is that of extended WR 4 from April to September, that presents a similar negative centroid over the North Atlantic Ocean. However, its positive anomalies are shifted much more northward than AL, so it cannot be truly considered the same WR. Thus, even if AL regime is present only in a few weeks of the annual cycle, it is not reproduced by the weekly projections of both extended WR classifications. Probably, AL regime appears as one of the four WRs of Cassou et al (2005) because the WRs were defined on a much shorter clustering period (JJA) than in the present work (April to September). Another discontinuity is also evident between weeks 8–14 and 15–21 October for WR 1, WR 2 and WR 4. However, in this case it is mainly due to a different vertical ordering of the reference and extended WRs for the 2 weeks, so most of the discontinuities are only apparent. WRs were not reordered in this case, so their patterns after the 14th of October closely match those in Fig. 4, making it easier to compare them.

The most striking differences between the spatial patterns shown in Figs. 4 and 5 are due to the appearance of AL regime in some March and April weeks of WR 1 (Fig. 5), as explained above and illustrated by the red boxes of Fig. 5. In these weeks, pattern correlations between WR 1 in Figs. 4 and 5 drop below 0.75. Other differences are observed in June and July weeks, when the north-south dipole of NAO+ anomalies shifts southward, always in case of reference WR 1 (see blue boxes in Fig. 5), and pattern correlations with the correspondent patterns in Fig. 4 decrease to 0.60. In August and part of September, reference and extended WR 2 patterns are also quite distinct from each other. However, in these cases differences are only apparent, due to a distinct vertical ordering of the four WRs in the two figures. Differences disappear if both the extended and reference WRs are reordered in the same sequence, in this case swapping WR 2 with WR 4. Reordering WRs in Fig. 5 to prioritize matching those in Fig. 4 is possible, but it would introduce more discontinuities in the patterns of Fig. 5. In this work, priority was given to minimize discontinuities from 1 week to the following, so when the same week is compared between Figs. 4 and 5, it may be necessary to reorder the WRs before the comparison.

Fig. 6
figure 6

Average weekly frequencies of occurrence (in %) of the WRs (1979–2018) of the extended (top) and reference (bottom) classifications. The two vertical dotted lines separate the periods of the two extended classifications (October–March and April–September)

Full size image

Figure 6 shows the annual evolution of the average weekly frequencies of occurrence of the WRs. Frequencies of the two extended classifications range from 12 to 42%, while those of the reference classification span a much shorter range (18–33%). This is due to the shorter period employed by the k-means clustering: the two extended classifications span 6 months of data each, while the reference one 13 weeks only, that is approximately half the length of the period of each of the two extended classifications. A shorter clustering period means that the k-means is applied to a smaller number of days, so the variability of WR average frequencies has to decrease. On the contrary, the seasonal variability of average weekly WR frequencies is very high for the two extended classifications, as the weekly WR frequencies are not filtered out, making it difficult to identify any clear seasonal cycle. WR 1 exhibits higher-than-average frequencies in July and August weeks, while WR 2 clearly has lower-than-average frequencies in the same months. WR 3 of the reference classification shows higher-than-average frequencies in August and September weeks, roughly in the same period WR 4 presents lower-than-average frequencies.

3.2 Pearson correlations

The first metric verified is the Pearson correlation between predicted and observed interannual (1998–2017) weekly frequency of occurrence, separately for each WR and forecast week. Correlations were averaged over all start dates and shown in Fig. 7, while values for each start date are shown in the box-and-whisker plots of Figs. 8, 9, 10 and 11 (one WR per figure), both for the extended WRs and the reference WRs. The horizontal gray line corresponds to r = 0.5. Above this correlation, the potential value of forecast products based on WRs for different user applications is obvious. Below it, their usefulness is not so clear.

Fig. 7
figure 7

Pearson correlations between observed and forecasted weekly frequencies of each of the four WRs averaged over all start dates. X-axis shows the WRs and the forecast weeks, while y-axis indicates the average correlation values. Color bars represent the average correlations over all start dates of the year, while small crosses and circles show average correlations over all start dates of October–March and April–September, respectively

Full size image
Fig. 8
figure 8

Box-and-whisker plots of cross-validated, bootstrapped Pearson correlations between observed and forecasted weekly frequencies of WR 1 for 1998–2017. Start dates are shown in full on the horizontal axis at the bottom of the figure. The other horizontal axes only show the first letter of the month of the start date. Colors represent forecast days: black for 5–11 days, yellow for 12–18 days, blue for 19–25 days and red for 26–32 days. Light colors indicate the correlations for the reference WR 1, while dark colors show the correlations of WR 1 of the two extended classifications. The two gray dotted vertical lines indicate the separation between the October–March and April–September start dates. The two horizontal gray lines show correlations of 0 and 0.5. If the correlation value of the non-bootstrapped weekly frequencies is also significantly different from zero for a paired t-test (p-value \(< 0.05\)), then it is shown with a small round point inside the plot. Non-significant values are not shown

Full size image

Overall, considering all WRs, start dates and classifications, ECMWF-Ext-ENS predicts the frequencies of occurrence of the extended WRs with similar correlations to that of the reference WRs. Correlations are highest during the first forecast week (5–11 days, black boxes), when their average values is r = 0.73 (Fig. 7). Average correlation values of the second forecast week (12–18 days, yellow boxes) are half those of the first forecast week: only r = 0.30. Both the third forecast week (19–25 days, blue boxes) and the fourth forecast week (26–32 days, red boxes) present average correlations close to r = 0.1 or even negative ones, like WR 3 in the third forecast week. The small skill increase observed in the fourth forecast week (26–32 days) of WR 3 (Fig. 7) is just noise, as the correlation values of all start dates are not significant (all red boxes in Fig. 10). Beyond the first forecast week, in fact, many correlations are not significantly different from zero. Overall, correlations are usually highest from October to March (Fig. 7, crosses) and lowest from April to September (Fig. 7, circles). Beyond the first forecast week, average correlations of WR 1, 2 and 4 during October–March can even double their value during April–September. On the contrary, the first forecast week has more constant correlations through the year than the other forecast weeks, and they rarely decrease below r = 0.5, even in summer.

Fig. 9
figure 9

As Fig 8, but for WR 2

Full size image
Fig. 10
figure 10

As Fig 8, but for WR 3

Full size image
Fig. 11
figure 11

As Fig 8, but for WR 4

Full size image

Notably, there are some start dates that stand out with correlations close to r = 0.5 also in the third and fourth forecast weeks, and for both extended WRs and reference WRs. A peak in correlations is often observed for WR 1 and WR 2 (similar to NAO+ and NAO- respectively) during many January and February start dates. For these start dates, correlation values can raise up to r = 0.5–0.7 in the case of the second forecast week, or r = 0.4–0.5 for the two subsequent forecast weeks. This peak is more pronounced in case of WR 2 (NAO-), that is also the WR with the highest average correlations, for both WR classifications (Figs. 7 and 9). WR 2 also achieves values of r > 0.5 during late November and December start dates of the second forecast week. These results are in agreement with both Vigaud et al (2018) and Ferranti et al (2015), that identified the NAO- regime as the one with the highest winter skill, in terms of anomaly correlation of the ensemble mean. Each peak is also followed by a steep decrease in the subsequent March start dates, up to very low values (close to zero) that characterize many April start dates. On the contrary, WR 3 (similar to blocking) is the one with lowest average correlations (Fig. 7), consistent with previous studies (Tibaldi and Molteni 1990; Pelly and Hoskins 2003). Its average correlations are also very similar during both wintertime and summertime start dates (Fig. 7). WR 3 rarely achieve correlations above r = 0.5. Moreover, correlations of WR 3 beyond the first forecast week present a minimum between December and January, that is not observed in case of the other WRs. It is the only WR that show negative average correlations, in case of the third forecast week. Maximum values of WR 3 are observed in March and June start dates, but after the first forecast week they rarely reach the value of r = 0.5. Finally, forecast skill of WR 4 (Atlantic ridge) is quite similar to that of WR 1. Its maximum values for the second forecast week are quite stable through all the October–February start dates and achieve the value of r = 0.5 in most of them. Correlations of the third forecast week never reach the value of r = 0.5, that is observed instead for some February start dates of the fourth forecast week.

Correlations of the extended and reference WR classifications globally follow a similar temporal evolution along the start dates of the year. However, some discrepancies can be found. Correlations of extended WR 1 are significantly higher than its reference WR 1 during three June and July start dates of the first forecast week, six start dates of the second one (Fig. 8), two August start dates of the third forecast week, and five April, May and August start dates of fourth forecast weeks. They are significantly lower than its reference WR only in case of four June and October start dates of the fourth forecast week. The more pronounced differences are observed in June and July start dates of the second forecast week. For these start dates, the higher forecast skill of extended WR 1 might be caused by the differences between the spatial patterns of the two WRs: the negative centroid of the reference WR 1, in fact, is shifted slightly southward compared to that of extended WR 1 (pattern correlation of 0.50), which is more similar to the traditional pattern of NAO+ (cfr. Fig. 4 with the patterns in the blue boxes of Fig. 5). The reason for such a southward shift is the different clustering period employed by the two WR classifications.

The presence of spatial patterns similar to those of the AL regime in the annual cycle of the reference WRs was identified in Sect. 2.3 for some March and April start dates. However, AL regime is absent from both extended WR classifications in Fig. 4. Thus, it raises the question if AL frequencies might be better simulated by forecast systems than those of the extended WR 1 (NAO+) observed in its place. AL regime appears during some March and April start dates, particularly from 19 March to 15 April. For these four start dates, correlations of the first and second forecast weeks of the extended WR 1 (NAO+) are almost always higher than those of the reference WR 1 (AL), even through not significantly. Considering all start dates and forecast week, predictability of extended WR 1 (NAO+) is similar or higher than that of AL regime, but not significantly higher. In summary, ECMWF-Ext-ENS simulates the weekly frequencies of NAO+ and AL regimes equally well.

3.3 Mean absolute error

Figures 12, 13, 14 and 15 show that for all WRs, start dates and forecast weeks, the MAE of the frequencies of occurrence of the WRs is always lower than 0.4. MAE is lowest (better) during the first forecast week and highest (worse) during the fourth forecast week. Differently from Pearson correlations, MAE is not better from October to March and worse from April to September: instead, its temporal evolution is more uniform through the year. For this reason, results for the MAE are discussed with less details than in case of the Pearson correlations.

Fig. 12
figure 12

Box-and-whisker plots of cross-validated, bootstrapped MAE of the weekly frequency of occurrence (y-axis) of WR 1 for 1998–2017. Start dates are shown in full on the horizontal axis at the bottom of the figure. The other horizontal axes only show the first letter of the month of the start date. Colors represent forecast days: black for 5–11 days, yellow for 12–18 days, blue for 19–25 days and red for 26–32 days. Light colors indicate the correlations for the reference WR 1, while dark colors show the correlations of WR 1 of the two extended classifications. The two gray dotted vertical lines indicate the separation between the October–March and April–September start dates

Full size image
Fig. 13
figure 13

As Fig 12, but for WR 2

Full size image

January, February and March start dates are still those with the lowest MAE, but they don’t show a clear minimum in correspondence to the start dates with the maximum Pearson correlations, like those observed for WR 1 and WR 2 (Figs. 1, 2). This may be due to the fact that for these WRs, the period when the Pearson correlations are highest coincides with the period of the year when their average observed WR frequency is also highest, so the MAE is expected to be high in these periods.

Fig. 14
figure 14

As Fig 12, but for WR 3

Full size image
Fig. 15
figure 15

As Fig 12, but for WR 4

Full size image

The MAE of October, November and December start dates is often as bad as that of the summer (JJA) start dates, and can be even worse, particularly in case of WR 4. On the contrary, the start dates of March and September are usually those with the best (lowest) MAE. Finally, differences between the extended and reference WRs are usually non-significant, with a few isolated exceptions, like some August and September start dates of WR 3, and some March and June start dates of WR 3 and WR 4.

3.4 Brier skill score

BSS gives information about the mean squared error of the probabilistic forecasts, as described at Sect. 2.3 and presented in Fig. 16. BSS indicates when the weekly WR frequency forecasts of ECMWF-Ext-ENS are an improvement over the reference weekly observed climatological WR forecasts (positive values of BSS) and when they are not (negative values).

Fig. 16
figure 16

Box-and-whisker plots of cross-validated and bootstrapped BSS of the weekly frequencies of occurrence of the WRs for 1998–2017. Start dates are shown in full on the horizontal axis at the bottom of the figure. The other three horizontal axes only show the first letter of the month of the start date. Colors represent forecast days: black for 5–11 days, yellow for 12–18 days, blue for 19–25 days and red for 26–32 days. Light colors indicate the BSS for the reference WRs, while dark colors show the BSS of WRs for the two extended classifications. The two gray dotted vertical lines indicate the separation between October–March and April–September start dates. The two horizontal gray lines show correlations of 0 and 0.5

Full size image
Fig. 17
figure 17

Box-and-whisker plots of cross-validated, bootstrapped FCRPSS of the weekly frequency of occurrence of WR 1 for 1998–2017. Start dates are shown in full on the horizontal axis at the bottom of the figure. The other horizontal axes only show the first letter of the month of the start date. Colors represent forecast days: black for 5–11 days, yellow for 12–18 days, blue for 19–25 days and red for 26–32 days. Light colors indicate the correlations for the reference WR 1, while dark colors show the correlations of WR 1 of the two extended classifications. The two gray dotted vertical lines indicate the separation between the October–March and April–September start dates. The two horizontal gray lines shows FCRPSS of 0 and 0.5. Positive FCRPSS values indicate when ECMWF-Ext-ENS beats reference climatological forecasts

Full size image

While ECMWF-Ext-ENS WR forecasts of the first forecast week (5–11 days) are always better than the climatological WR forecasts, it is evident from Fig. 16 that in subsequent forecast weeks, climatological WR forecasts almost always beat those of ECMWF-Ext-ENS. Moreover, BSS is always smaller than 0.3. Only during some start dates of January, February and March of the second forecast week (12–18 days), ECMWF-Ext-ENS WR forecasts are better than the climatological WR forecasts, reaching their maximum peak values around BSS = 0.2 in February start dates. Consistently, these are also the same start dates when the peak of Pearson correlations is observed for the WRs in Fig. 8, 9, 10 and 11. Thus, though ECMWF-Ext-ENS sometimes shows moderate-to-good Pearson correlations also beyond the first forecast week for some WRs, it rarely represents an improvement over simple climatological forecasts. April to October start dates, in particular, are almost always characterized by negative values of the BSS.

Notably, in case of the BSS the differences between extended and reference WR classifications are very small and always non-significant, thus also for this metric the ECMWF-Ext-ENS simulates the weekly frequencies of the two sets of WRs (including NAO+ and AL) equally well.

3.5 Fair continuous ranked probability skill score

FCRPSS is the extension of the BSS to the continuous case and it is defined in Sect. 2.3. Results are presented separately for each WR, in Figs. 17, 18, 19 and 20. Positive values of FCRPSS indicate that the weekly WR frequency forecasts of ECMWF-Ext-ENS are an improvement over the reference weekly observed climatological WR forecasts, and vice-versa for negative values.

Fig. 18
figure 18

As Fig 17, but for WR 2

Full size image
Fig. 19
figure 19

As Fig 17, but for WR 3

Full size image
Fig. 20
figure 20

As Fig 17, but for WR 4

Full size image

As or the other metrics, also FCRPSS is highest during the first forecast week (5–11 days). However, it decreases only slightly in subsequent forecast weeks, remaining positive even in the fourth forecast week (26–32 days). Thus, in case of FCRPSS the model is able to beat simple climatological forecasts. A few exceptions can be found during some start dates of March, April and September. Thdse results are very different from those of the BSS, whose values are almost always negative after the first forecast week. This is an interesting example of how a model can be considered globally better than climatology for one skill score and worse for another.

CRPSS is highest during October–March and lowest during April–October, and it often exhibits one or two peaks, usually from December to March start dates, depending on the WR: WR 1 shows two maximum in the first forecast week, and a single maximum in February for subsequent weeks. WR 2 exhibits a maximum around December and another one around the end of February. WR 3 also presents a peak at the end February, but the maximum are less pronounced than those of WR 2. Finally, WR 4 show a maximum at the end of February and another one in November.

Overall, FCRPSS of extended WRs are slightly higher than the FCRPSS of reference WRs, but differences are almost always non-significant at 90% confidence (as described at Sect. 2.3). A few exceptions can be found, as in case of some March start dates of WR 1 at forecast time 19–25 days, when the FCRPSS of extended WR 1 is always significantly higher than FCRPSS of reference WR 1.

3.6 Predictability of extremely persistent events

A total of eleven periods with an extreme WR persistence (three weeks of more) were observed during 1998–2017 by the two extended classifications (see Fig. 21). The majority of them belong to WR 2 (5 periods, reddish boxes), and the minority to WR 3 (one period only, gray box). During 2009–2016, five long-lasting WR events occurred, all of them associated with WR 2 (similar to NAO-), as also identified by Matsueda and Palmer (2018). Right side of Fig. 21 shows the predictability of ECMWF-Ext-ENS in forecasting the WR frequency of these periods from the hindcasts initialized in the start date previous to the start of the periods (black triangles). Predictability of the climatological WR forecasts is also shown as a benchmark (black lines).

Fig. 21
figure 21

Visualization of the 11 periods of extreme WR persistence (3 weeks of more) observed during 1998–2017 by the extended WR classifications. Vertical axis shows the year where the period is observed, and horizontal axis the month. Each rectangle corresponds to a different period. Its width is proportional to the duration of the period (also written inside the box). The color of the box specifies the WR the period belongs to. The two numbers below the box indicate the start and end day of the period. The black triangle before each box indicates the start date employed to measure the predictability of the period in the box, and the number above its calendar day. Right bars: percentage (%) of days and members during the period to the left that predicted the observed WR. Dark vertical lines show the % of days during the same period with the same observed WR predicted by the benchmark model based on the WR weekly climatological frequencies

Full size image

ECMWF-Ext-ENS beats the climatological forecasts for nine of the eleven periods, including two of the three summertime periods. This is an important achievement, considering that the BSS is negative in summer weeks beyond forecast days 5–11 (see Fig. 16). Predictability can be even twice or more that of the climatological forecasts (years 2001, 2009, 2010, 2011). By contrast, the maximum predictability measured is 62,9% in 2009–2010, so the system is able to correctly forecast a maximum of 6.3 days out of 10 consecutive ones belonging to the same WR. This is also a confirmation that the systems typically underestimate WR persistence (Strommen and Palmer 2019).

It is interesting to compare these results with those of Matsueda and Palmer (2018), that found that the longer the NAO- events persist, the higher the predictability of medium-range forecasts (up to 16 days) initialized on NAO-. In case of sub-seasonal forecasts, this relation is not so clear, as the highest predictability was measured for a 25-days NAO- (WR 2) period (from 14 of December 2009 to 7 January 2010, see Fig. 21), that is much shorter than the longest NAO- period observed of 39 days (from 12 of December 2019 to 19 of January 2010). However, in case of sub-seasonal, forecasts were not initialized on NAO-, and predictability also depends on the number of days between the Monday start date and the beginning of the period (the distance from the triangles to the boxes in Fig. 21), which is different for each period: it varies from a minimum of 4 days to a maximum of 10. In order to compare the predictability of two different periods, they should begin after the same number of days from the start dates shown in Fig. 21. Thus, predictability of different periods can be rightfully compared only for periods whose distance from their start date in Fig. 21 is the same, as in case of periods in years 2006 and 2016, or in years 2012 and 2017 (last row of Fig. 21). For this reason, it is not possible to clearly identify which of the four WRs is better forecasted by ECMWF-Ext-ENS, though WR 2 (NAO-) seems a good candidate, as all its five periods in Fig. 21 are better forecasted by the system than by climatological forecasts. However, the low number of WRs and periods that can be compared (e.g: there is only one period for WR 1) prevents drawing any definitive conclusion.

Fig. 22
figure 22

Left: number of observed WR periods as a function of their duration (in days), normalized by the total number of periods of target WR, for the October–March extended classification. A WR period is defined as a sequence of days all belonging to the same WR (period duration is truncated at 20 days in the figure). WR persistence (in days) is the mean of the durations of all WR periods and it is shown in parenthesis. Right: as left, but for the April–September extended classification

Full size image

The high number of periods of WR 2 might be due to its high observed persistence (Fig. 22), particularly in the October–March period, when its persistence is the highest of all the four WRs (5.3 days), while during April–September it is the second highest (4.2 days). On the contrary, WR 4 is the one with the lowest observed persistence and it is only present with two periods in Fig. 22.

4 Discussion

This work is not aimed at presenting the reference WRs as an alternative classification to the more popular seasonal, extended seasonal or yearly WR classifications. It just employs them to describe the evolution of atmospheric variability of SLP through the year. It is important to stress that the reference WRs do not represent a proper WR classification, as the spatial patterns of the WRs of two consecutive weeks are not significantly different between them and thus the two sets of WRs cannot be considered physically different from each other. In fact, due to the 13-weeks rolling window approach, most of the SLP data used for clustering WRs of two consecutive weeks is shared and only 2 of the 13 weeks are different (the first one and the last one of the rolling window).

Results of other verifications of the medium-range WR forecasts are not directly comparable to the present one, due to differences in the aggregation of forecast data (e.g: daily instead of weekly, as in Ferranti et al (2015)), or in the seasonality (e.g: yearly instead of seasonal clustering, as in Neal et al (2016)), or in the circulation variable used to classify WRs (e.g: geopotential height instead of SLP, as in Matsueda and Palmer (2018)), or in the spatial domain for the k-means clustering (e.g: North America instead of Euro-Atlantic region, as in Vigaud et al (2018) and in Wang and Robertson (2019)). Notwithstanding, a few correspondences were found regarding the higher Pearson correlations of WR 2 (NAO-) and the lower ones of WR 3 (blocking). Future work will try to find out if the better/worse predictability of NAO-/blocking frequencies may be also related to a higher/lower persistence, and if the source of WR skill may be associated to ENSO, MJO or SSWs.

The choice of the assignation method to classify simulated WRs was conditioned on the requirement to generate WR patterns similar to the observed ones. If k-means clustering is applied separately to forecasts instead of using the RMSD criterion, as for instance in Fil and Dubus (2005); Dawson and Palmer (2015); Vigaud et al (2018); Matsueda and Palmer (2018), the forecasted WRs do not always adequately represent the observed WR patterns, as also evidenced by different authors (Fereday et al 2008; Neal et al 2016; Torralba 2019). The analysis of simulated WRs is more appropriate to understand the physical properties of the system, and the biases leading to different WR patterns than the observed WRs. Thus, it is useful to model developers. On the contrary, by assigning to each forecasted daily SLP anomaly its closest observed WR with the RMSD criterion, by default their spatial patterns are always the closest possible to the observed ones, so it is more interesting from the forecast verification perspective. This is the main reason why this last method was preferred. The work of Vigaud et al (2018), in particular, is the most similar to this study, as they also consider 4 WRs from October to March as forecasted by ECMWF-Ext-ENS, albeit for a different variable (geopotential height at 500 hPa), period (1995–2014), region (North America), and applying k-means also to cluster forecasted WRs. Nonetheless, it is interesting to notice that despite all these differences, they too detected that NAO- is the WR with the highest winter skill, in terms of anomaly correlation of the ensemble mean. Moreover, they found that skill in forecasting daily regime sequences and weekly regime frequencies is largely limited to two weeks.

WR classifications are not very sensitive to spatial resolution. For example, Michelangeli et al (1995) employed data with \(10^\circ\) resolution from the National Oceanic and Atmospheric Administration (NOAA) to classify WRs over the Euro-Atlantic domain. For this reason, ERA-Interim reanalysis (resolution of \(0.70^\circ\)) was chosen in this work as reference instead of more modern reanalyses like ERA5 (Hersbach 2016), which has a higher resolution (\(0.28^\circ\)). However, when a daily SLP reforecast field is assigned to an observed WR, ECMWF-Ext-ENS data has to be interpolated into the same grid of the coarser reanalysis, in order to measure the RMSD (see Sect. 2.3). Regridding introduces an error that is difficult to quantify, so Pearson correlations measured in this study are probably slightly worse than the ones that would be obtained without interpolating.

In this work, the forecast skill was assessed by two deterministic and two probabilistic metrics. However, other metrics can also be employed to better understand the performance of the subseasonal forecast systems, such as the reliability diagram, the ROC score or the ranked probability skill score. They might be introduced too in a future work. Probabilistic metrics, in particular, are a powerful tool in verification, as they assess not only mean values, but the full range of forecast values.

Finally, it is important to highlight that in order to increase the statistical robustness of the four metrics, five consecutive Monday start dates were concatenated (see Sect. 2.3). This affects the metrics measured, which returns a different value of that measured for a single start date, as recently discussed in Manrique-Suñén et al (2020). Moreover, validating only the 11 reforecast members instead of the 51 available in the operational forecasts of ECMWF-Ext-ENS introduces another difference from the ”real” forecast skill measured by the metrics. For some metrics, this difference can be minimized by employing their ’fair’ version, as in case of the FCRPSS. At present, the short length of the reforecasts and their small number of members characterize not only ECMWF-Ext-ENS, but all sub-seasonal forecast systems. Considering also all Thursday start dates available in ECMWF-Ext-ENS would alleviate this issue, by restricting the concatenation of 5 consecutive start dates to a period of 15 days instead of 1 month. Nonetheless, forecast systems with more than 20 years of reforecasts are still needed. Their production consumes many computational resources, but with a long enough set of reforecasts, the use of a moving window to validate them wouldn’t be necessary anymore, and verification scores’d be much more useful to forecasters and for developing applications. However, extending too much the reforecasts has the disadvantage of including more effect of climate change (Lavaysse et al 2020). Lagged ensembles (with one start date for each day) may offer an alternative way to solve this issue, as it is possible to increase the sample size by concatenating several start dates within the same week (Chen et al 2013).

5 Conclusions

The aim of this study was to highlight the limits of extended WR classifications in characterizing atmospheric circulation variability, and to validate sub-seasonal forecast skill in predicting the frequencies of WRs beyond the winter season. To this end, two extended WR classifications of four WRs each were classified, both based on k-means clustering of daily SLP fields from October to March and from April to September 1979–2017 respectively. Their spatial patterns were projected on each calendar week of the year and were compared with those of the WRs representing the annual cycle. Sub-seasonal reforecasts of the ECMWF-Ext-ENS were employed to validate its forecast skill in predicting the weekly frequencies of occurrence of the WRs, in term of four metrics: Pearson correlations, MAE, BSS and FCRPSS. For the first time, the evolution of the forecast skill of each WR outside winter period was presented and described in detail.

Comparison of the WR spatial patterns revealed that though the patterns of the two extended classifications can be projected on any week, this does not mean that they are always able to reproduce the annual cycle. The weekly projected patterns, in fact, are much more similar to those of October–March or April–September than to the weekly patterns of the annual cycle. The main difference is represented by patterns resembling AL regime, that are observed in the annual cycle for some March and April weeks, but not in the weekly projected patterns of the two extended WR classifications. For these weeks, patterns resembling NAO+ are observed in the extended WRs instead of AL regime. This is reasonable, as SLP anomalies are more variable outside winter, so it is more difficult for the extended WR classifications to capture SLP variability in spring without increasing the number of WRs. However, the forecast skill of ECMWF-Ext-ENS in simulating the Pearson correlations of the weekly frequency of occurrence of AL regime for March and April start dates is roughly similar to that of predicting NAO+ for the same start dates. Hence, even if the extended WR classifications are not always able to fully reproduce the regime patterns of the annual cycle, their predictability is not affected by such oversimplification. Furthermore, in case of the second forecast week of extended WR 1, forecast skill of many June and July start dates is significantly higher than that of reference WR 1, and may also achieve values close to r = 0.5.

WR frequency validation identified a peak of Pearson correlations for many start dates of January and February, the principal period of the year when correlations beyond the first forecast week can achieve value of r \(=\) 0.5 or higher. Such a window of opportunity is more pronounced for WR 2, resembling NAO-. During the other start dates of the year, correlations after the first forecast week are almost always below r = 0.5, with a few exceptions mainly in March, July, October and November start dates. Probabilistic WR forecasts assessed by the BSS show that beyond the first forecast week, ECMWF-Ext-ENS rarely performs better than simple climatological WR forecasts: it beats them only during some January, February and March start dates of the second forecast week (12–18 days). However, in case of the FCRPSS, or when long periods of persistent WRs are considered, the situation is the opposite: predictability of ECMWF-Ext-ENS is often higher than that of the climatological forecasts, even during summer.

The predominance of start dates with low correlations, high MAE and/or negative BSS actually represents the principal obstacle to the development of any forecast product for climate services purposes. Skill improvement might be achieved employing multi-model ensembles, for example combining the reforecasts available in the Sub-seasonal to Seasonal Project (S2S) described by Vitart et al (2017). Future work will explore the multi-model approach in the WR context, comparing the forecast skill of ECMWF-Ext-ENS in simulating key variables in the renewable energy sector, like wind speed and capacity factor.