1 Introduction

The location and intensity of the South Pacific Convergence Zone (SPCZ) affect the climate of the South Pacific (Brown et al. 2012). The SPCZ is a large cloud band with low-level convergence and precipitation (Vincent et al. 2011; Kiladis et al. 1989; Brown et al. 2013a; Salinger et al. 1995; Vincent 1994; Trenberth 1976; Charles et al. 2014; Brown et al. 2012) that extends southeastward from New Guinea across the dateline (Vincent 1994; Vincent et al. 2011; Brown et al. 2012) (see Fig. 1). Small changes to its location affect the climate of many South Pacific islands (Brown et al. 2012; Vincent et al. 2011). These islands are subject to a large precipitation gradient across the SPCZ that influences the location of tropical cyclogenesis, or intense rainfall shortages or deluges (Cai et al. 2012; Vincent et al. 2011; Folland et al. 2002; Australian Bureau of Meteorology and CSIRO 2011; Salinger et al. 1995, 2014). The effects of the SPCZ also extend to north-eastern regions of Australia (Kidwell et al. 2016).

Variations in the SPCZ location, slope and intensity affect water availability and hence productivity of subsistence crops for many islanders (Cai et al. 2012). Agricultural practices in the South Pacific are heavily dependent on rainfall due to the absence of extensive irrigation (Barnett 2011) and a reliable seasonal forecast for the South Pacific could improve agricultural management practices (He and Barnston 1996). In northeast Australia (NEA) rainfall influences sugar cane productivity (Everingham et al. 2008). This growing industry is leading to more nitrogen fertilisers being used in the Wet Tropics, Burdekin and Mackay–Whitsunday areas (Kroon et al. 2016). The health of the Great Barrier Reef (GBR) is being impacted by nutrient run-off (Kroon et al. 2016; Brodie et al. 2013; Great Barrier Reef Marine Park Authority 2014), and accurate seasonal rainfall forecasts could play an important role in governing how nitrogen fertilisers are used (Thorburn et al. 2011, 2013). Given that the SPCZ’s effects can extend to NEA (Kidwell et al. 2016), accurate forecasts of the SPCZ are therefore of great importance.

Fig. 1
figure 1

Map of SPCZ region. The dotted red line and black triangle represent the SPCZ and mean latitude position of the maximum rainfall averaged over 23 DJF seasons based on Global Precipitation Climatology Project (GPCP) data respectively

Full size image

The interannual variability of the SPCZ is affected by El Niño Southern Oscillation (ENSO) (Kidwell et al. 2016; Widlansky et al. 2012; Lorrey et al. 2012; Folland et al. 2002; Trenberth 1997). The SPCZ generally moves northeast in an El Niño and southwest in a La Niña phase (Kidwell et al. 2016; Folland et al. 2002; Trenberth 1976; Vincent et al. 2011). Warm water travels to the east in an El Niño as the SPCZ shifts eastward (van der Wiel et al. 2015b), shifting the precipitation to the east. Similarly, the SPCZ shifts south-west as the Warm Pool moves to the west in a La Niña (van der Wiel et al. 2015b), shifting the precipitation closer to NEA. In eastern areas of Australia, the likelihood of drought is commonly understood to be linked to El Niño conditions, and floods for La Niña (Cai et al. 2010; McBride and Nicholls 1983; Ropelewski and Halpert 1987; Philander 1990).

On a decadal basis, the climatic impact on South Pacific nations by SPCZ movements is detailed by Salinger et al. (2014). They show that even small movements can have extensive effects in the South Pacific, bringing increases or decreases in annual rainfall of Island nations depending on which side of the SPCZ the countries lie (Salinger et al. 2014). Between 1981–2011 the SPCZ was displaced south-west, and this resulted in up to a 450 mm/decade increase (360 mm/decade decrease) in rainfall if the nation was positioned south west (north east) of the SPCZ (Salinger et al. 2014). The SPCZ is an important climate driver which strongly affects South Pacific Islands on a decadal scale, with effects extending to tropical cyclogenesis and rainfall shortages or deluges (Salinger et al. 2014).

The modulation of the SPCZ by large-scale climate drivers poses challenges for coupled ocean–atmosphere models to accurately represent the slope of the SPCZ (van der Wiel et al. 2015b; Brown et al. 2013a). The Coupled Model Intercomparison Project phase 5 (CMIP5) (Taylor et al. 2012) models better simulate the northward displacement of the SPCZ with El Niño and southward displacement with La Niña compared with the Coupled Model Intercomparison Project phase 3 (CMIP3) (Meehl et al. 2007), although it is generally too ‘zonal’ in orientation (Brown et al. 2013a). This poor simulation of the SPCZ orientation could be due to persistent biases in the models’ sea surface temperature (SST) fields, resulting in an overly westward location of the edge of the Western Pacific Warm Pool (Brown et al. 2011, 2013a; Cai et al. 2009).

An earlier study by Charles et al. (2014) examined the seasonal performance of the Australian Bureau of Meteorology’s operational seasonal forecast Predictive Ocean–Atmosphere Model for Australia (POAMA) (Wang et al. 2004) in predicting the SPCZ. This study showed POAMA could accurately forecast the SPCZ’s displacement with ENSO variability, but it struggled to replicate the SPCZ’s variability in orientation. Using the ensemble mean, December–January–February (DJF) forecasts from November 1st (1-month lead time) over a 1980–2010 hindcast period for mean SPCZ latitude had a correlation with the Climate Prediction Centre Merged Analysis of Precipitation (CMAP) (Xie and Arkin 1997) dataset of 0.69, while forecasts for the SPCZ slope had a correlation of 0.4.

In August 2018 the Australian Bureau of Meteorology introduced ACCESS-S1 as its new operational coupled model-based seasonal forecasting system. This study is conducted to validate ACCESS-S1’s capability to predict seasonal variations of the SPCZ with reference to its associated summer rainfall in the South West Pacific Region and NEA. Significant economic costs to countries in the Pacific can arise because of their heightened vulnerability to severe weather (Griffiths et al. 2003; McCarthy et al. 2001). Using longer lead times for forecasts is of greater benefit to Pacific Island nations because of the advance warning they could have for such events. This analysis focuses primarily on seasonal DJF forecasts with a 1-month leadtime (initialised on November 1st) following the analysis completed by Charles et al. (2014), although other leadtimes are also assessed. Given the relationship between ENSO and the SPCZ (Kidwell et al. 2016; Widlansky et al. 2012; Lorrey et al. 2012), we hypothesise that the improved ability of ACCESS-S1 over POAMA to predict ENSO in autumn and winter (Hudson et al. 2017) will lead to improved SPCZ representation.

2 Data and methods

2.1 ACCESS-S1 seasonal climate prediction system

ACCESS-S1 is a modified version of the UK Met Office (UKMO) Global Seasonal forecast system version 5, Global Coupled model configuration 2 (GloSea5-GC2) with 11 ensemble members in the 23-year hindcast period (1990–2012) (Hudson et al. 2017; MacLachlan et al. 2015). As part of the GC2 model, ACCESS-S1 uses the Unified Model Global Atmosphere 6.0 (GA6.0) (Walters et al. 2017; Williams et al. 2015), Global Land 6.0 (GL6.0) (Best et al. 2011; Walters et al. 2017; Williams et al. 2015), Global Ocean 5.0 (GO5.0) (Madec 2008; Megann et al. 2014; Williams et al. 2015) and Global Sea Ice 6.0 (GSI6.0) ( Hunke and Lipscomb 2010; Rae et al. 2015; Williams et al. 2015) models for its atmosphere, land surface, ocean and sea ice simulations respectively (Hudson et al. 2017; Williams et al. 2015). GA6.0 is deployed with an atmospheric mid-latitude horizontal resolution of approximately 60 km (N216), with 85 vertical levels (Hudson et al. 2017; Williams et al. 2015). The relevant parameterizations used in GA6.0 (Walters et al. 2017) which impact tropical convection and rainfall include a mass flux convection scheme (Gregory and Rowntree 1990), convective available potential energy (CAPE) closure (Fritsch and Chappell 1980), prognostic cloud fraction and condensate (PC2) scheme (Wilson et al. 2008) and an atmospheric boundary layer parameterization scheme (Lock et al. 2000) with upgrades as per (Brown et al. 2008). The ocean horizontal resolution is \(0.25^{\circ }\), with 75 vertical levels (Hudson et al. 2017; Williams et al. 2015). The following initial conditions are used to create the hindcast dataset: ERA-Interim reanalysis (Dee et al. 2011) for the atmosphere (Hudson et al. 2017; MacLachlan et al. 2015), Forecast Ocean Assimilation Model (FOAM) (Blockley et al. 2014) for the ocean and sea ice (Hudson et al. 2017), and climatological data for the soil moisture (Hudson et al. 2017; MacLachlan et al. 2015). Further details of the ACCESS-S1 model can be found in Hudson et al. (2017). We note that the hindcast period (1980–2010) used by Charles et al. (2014) for the POAMA model differs to that of ACCESS-S1, however the results from this analysis will still be used to compare with POAMA given our inability to readily create more hindcast data.

For this assessment, precipitation and SST from hindcasts initialised on September 1, October 1, November 1, and December 1 (3, 2 1 and 0-month lead times) are used to assess the seasonal variation of the SPCZ from December through to February (DJF) for 1990/1991 to 2012/2013 seasons (23 seasons in total). The ensemble mean is used throughout this study, however each of the 11 ensemble members are considered in the analysis shown in Fig. 8 and Table 2. For any given season, mean DJF precipitation and SST values were obtained by averaging (over time) the monthly December, January and February mean values.

2.2 Observation data

The observed precipitation data used in this study are Global Precipitation Climatology Project (GPCP) (Adler et al. 2003) and Tropical Rainfall Measuring Mission (TRMM) (GES DISC 2011). The TRMM dataset has a finer resolution [\(0.25^{\circ } \times 0.25^{\circ }\) (GES DISC 2011)] compared to GPCP [\(2.5^{\circ } \times 2.5^{\circ }\) (Adler et al. 2003)] and is only available from 1998; hence GPCP is used for most of the analysis. Sea surface temperature observations were determined by adding anomaly SST observations to the climatology, using Optimum Interpolation Sea Surface Temperature Version 2 (Reynolds et al. 2002) as the original dataset. For any given season, mean DJF precipitation and SST observations were obtained by averaging the monthly December, January and February mean observations. The hindcasts are compared with observational Global Precipitation Climatology Project (GPCP) (Adler et al. 2003) precipitation data in Fig. 3, which shows ACCESS-S1 (regridded to the GPCP resolution) minus GPCP precipitation data.

Niño3 and Niño4 anomaly data (used in Fig. 13) were obtained from the National Weather Service Climate Prediction Centre (Climate Prediction Center 2020b). Seasonal values were computed by taking the average Niño3 or Niño4 anomaly values across DJF months.

2.3 Verification metrics

Verification of ACCESS-S1’s ability to forecast DJF rainfall (with 0–3-month lead time) in the South Pacific region was first completed by assessing the skill of the probability above median precipitation hindcasts in the 1990–2012 period. For each year in the hindcast period, the probability above median forecast was determined by calculating the percentage of ensemble members (total of 11) that were above the median rainfall of the remaining 22 years (with 11 ensemble members in each year). Verification of these probability above median forecasts was done using two metrics: the recently developed user-oriented Weighted Percent Correct (WPC) (Wang et al. 2019) and the Brier Skill Score (BSS) (Brier 1950).

WPC is now widely used for the Bureau of Meteorology’s operational climate prediction products (for example, see the Bureau’s Seasonal Climate Outlook: http://www.bom.gov.au/climate/outlooks/#/rainfall/skill/seasonal/0), which has replaced the previously used Percent Correct (PC) metric. The WPC is defined by Wang et al. (2019) as:

$$\begin{aligned} \text {Weighted Percent Correct} = \frac{\sum (\text {HCR} \times \mid \text {Observed anomaly} \mid )}{\sum (\mid \text {Observed anomaly} \mid )} \end{aligned}$$
(1)

where HCR represents whether the model correctly forecasts the observed outcome (\(\text {HCR}=1\)) or not (\(\text {HCR}=0\)) (Wang et al. (2019)). Any WPC value greater than approximately 50% is considered to have skill (Wang et al. (2019)). Further details of how the PC and WPC are calculated are given by Wang et al. (2019).

One shortfall of the WPC metric is that it does not measure the reliability of the forecast because it converts a probabilistic chance above median forecast into a binary categorical result (Wang et al. 2019). The uncertainty, reliability and resolution in the forecast are elements which constitute the Brier Score (BS) (Wang et al. 2019; Murphy 1973), which is used to calculate the Brier Skill Score (BSS) as shown in Eq. 2 (Wang et al. 2019; Wilks 2010; Mason 2004; Wilks 1995; Toth et al. 2003). Hence, the BSS can be more conservative than the WPC (Wang et al. 2019), where a perfect BS is equal to zero (Brier 1950; Wilks 2010; Stefanova and Krishnamurti 2002), and a perfect BSS equal to 1 (Stefanova and Krishnamurti 2002; Palmer et al. 2000) (see Eq. 2). Since a BSS equal to (or less than) 0 is considered to not have any skill (Palmer et al. 2000), our analysis focuses on positive BSS scores. Further details about the BS and how it can be broken up into its uncertainty, reliability and resolution constituents are given by Brier (1950) and Murphy (1973) respectively.

$$\begin{aligned} \text {Brier Skill Score} = 1 - \frac{\text {Brier Score}}{\text {Reference Brier Score}} \end{aligned}$$
(2)

Verification of rainfall anomalies over the 1990–2012 hindcast period was computed using the Root Mean Square Error (RMSE) and Correlation metrics. The forecast anomaly was computed by subtracting the full DJF forecast model climatology (computed over 23 years) from the ensemble mean for each separate DJF forecast. These spatial timeseries of forecast rainfall anomalies were then compared to the observed rainfall anomalies over the same time period.

To further understand how well the model is able to predict interannual variations of rainfall and SSTs in the SPCZ region and along the SPCZ itself, standard deviations were computed across all DJF and ENSO seasons for precipitation and SSTs (Figs. 6 and 7). Absolute SST temperatures (as defined above) were used in this analysis.

2.4 Defining the SPCZ region

The axis of maximum SPCZ precipitation is defined as the location of maximum precipitation for each longitudinal coordinate from \(155^{\circ }\hbox {E}\) to \(140^{\circ }\hbox {W}\), between \(0^{\circ }\hbox {S}\) to \(30^{\circ }\hbox {S}\) for values above 6 mm/day, and the mean SPCZ position as the average of these latitudinal coordinates, following Charles et al. (2014), Brown et al. (2011, 2012, 2013a) and Vincent et al. (2011) (note that Brown et al. (2011) did not use this 6 mm/day threshold criteria). In Fig. 2a, the mean SPCZ position is plotted as a black triangle. The SPCZ slope metric is defined by the gradient of the line of best fit of these precipitation maximum points using least squares (Charles et al. 2014; Brown et al. 2011, 2012; Vincent et al. 2011), shown by the red line in Fig. 2a.

Following Vincent et al. (2011) and Charles et al. (2014), latE and latW indices are defined as the average SPCZ latitude from \(5^{\circ }\hbox {S}\) to \(30^{\circ }\hbox {S}\) between \(190^{\circ }\hbox {E}\) and \(210^{\circ }\hbox {E}\) and \(160^{\circ }\hbox {E}\) and \(180^{\circ }\hbox {E}\), respectively. LatE and latW positions are shown by the red dots (Fig. 2a) and are plotted at the central longitudinal point in their respective ranges. The shifts in latE and latW values over the 23 DJF seasons are shown by the red error bars. This Figure can be compared directly to Figure 1 in Charles et al. (2014).

Fig. 2
figure 2

GPCP observed (left) and ACCESS-S1 (right) precipitation DJF climatologies initialised on November 1 for 1990–2012 a all seasons, b El Niño, c La Niña and d neutral years. The black triangle represents the mean SPCZ latitude, and the two red circles are the latE and latW indices. The red line is fitted using least squares of the latitudes of maximum precipitation (for rainfall greater than 6 mm/day) from \(0^{\circ }\hbox {S}\) to \(30^{\circ }\hbox {S}\) for longitudes of \(155^{\circ }\hbox {E}\) to \(140^{\circ }\hbox {W}\) (Charles et al. 2014; Brown et al. 2011; Vincent et al. 2011). Error bars show the range of latE and latW values obtained in the 23 seasons

Full size image
Fig. 3
figure 3

DJF ACCESS-GPCP precipitation bias for hindcasts initialised on November 1. The SPCZ and mean latitude is shown by the dotted red line and black triangle respectively, using GPCP data

Full size image

2.5 ENSO years

El Niño (La Niña) DJF seasons are defined by National Oceanic and Atmospheric Administration (NOAA) (Climate Prediction Center 2020a) as those where the average Niño 3.4 SST deviation is more (less) than \(+0.5^{\circ }\hbox {C}\) (\(-0.5^{\circ }\hbox {C}\)), and which are part of at least 5 successive overlapping 3-month periods which meet this criteria, using NOAA/CPC ERSSTv5 data (Huang et al. 2017; Climate Prediction Center 2020a) (neutral years are those otherwise). This study uses the following lists defined in Vincent et al. (2011) and Charles et al. (2014), with the addition of the 2011/12 and 2012/13 seasons [defined according to NOAA (Climate Prediction Center 2020a)]. El Niño years (seven in total) are 1991/92, 1994/95, 1997/98, 2002/03, 2004/05, 2006/07, 2009/10, La Niña years (nine in total) are 1995/96, 1998/99, 1999/00, 2000/01, 2005/06, 2007/08, 2008/09, 2010/11, 2011/12, and neutral years (eight in total) are 1990/91, 1992/93, 1993/94, 1996/97, 2001/02, 2003/04, 2005/06, 2012/13 (Huang et al. 2017; Vincent et al. 2011; Charles et al. 2014). El Niño and La Niña DJF climatologies are shown in Fig. 2b, c.

3 Results

3.1 Simulation of SPCZ rainfall

The average of the mean SPCZ latitude for each season in the model is \(11.59^{\circ }\hbox {S}\), which is only \(0.24^{\circ }\) different from the GPCP observations as shown in Table 1 and represented by the black triangle in Fig. 2a. The eastern (LatE) and western (LatW) arms of the SPCZ are denoted by red circles in the Figures. The eastern and western endpoints of the SPCZ (latE and latW) are \(2.14^{\circ }\) and \(0.24^{\circ }\) further equatorward compared to the observations respectively (Table 1). The \(4.5^{\circ }\) difference in slope makes the SPCZ predicted by ACCESS-S1 more zonally oriented than the observations.

In addition to differences in SPCZ location, the model produces too much rain throughout the DJF period. The model forecasts mean rainfall values of 7.38 mm/day in the SPCZ region, compared to 5.59 mm/day in the GPCP observed data. This has implications over the Solomon Islands, Samoa and French Polynesia where the model is generally over-predicting rainfall (Fig. 3). As illustrated in Fig. 3, this bias is relatively small in the region along the equator between the SPCZ and Inter Tropical Convergence Zone (ITCZ).

The model also shows strongly positive bias in over-predicting tropical rainfall in the Indian Ocean. This is a known problem in the UK Met Office (UKMO) Unified Model (Bush et al. 2015; Levine and Martin 2018; Jin et al. 2019); see Bush et al. (2015) for analysis of this bias using Global Atmosphere 3.0 (GA3.0) models at N96 resolution, Levine and Martin (2018) for GA3.0 analysis at N512 resolutions and Jin et al. (2019) for analysis of GA6.0 at N96 and N216 resolutions.

3.2 ACCESS-S1 precipitation verification

Figure 4a shows a large area of high WPC on either side of the SPCZ with a minimum or no skill zone located along most of the SPCZ. There are areas of low skill along the SPCZ which persist even at short forecast lead times. Figure 4b shows the corresponding Brier Skill Score. The model has good skill along the equator in areas where seasonal SST anomalies vary relatively significantly.

Verification of the rainfall anomaly forecasts are shown in Fig. 5a, b. These show similar behaviour to the probabilistic metrics, with high values of RMSE (and low correlation) observed close to the SPCZ. As an aside, the Bureau of Meteorology prefers issuing probabilistic versus anomaly forecasts for long range outlooks, as the computing of forecast anomalies collapses all uncertainty information contained in the ensemble spread.

Figure 6 shows that the standard deviations of DJF total precipitation for both the observations and ACCESS-S1 (initialised on November 1) are, in general, smaller along the climatological SPCZ compared to its surrounding area for all, El Niño, La Niña and neutral years. In other words, the interannual variation of precipitation along the SPCZ is relatively small. We also note that there is minimal interannual SST variation along the SPCZ (Fig. 7), indicating that this area is not affected by ENSO events as much as areas either south, or especially north of the SPCZ (as indicated by its larger standard deviations) are. Hence, rainfall in the area north (and to a lesser extent, the south) of the SPCZ is more influenced by ENSO than along the SPCZ itself. This perhaps explains why forecast skill is poor along the SPCZ, as its ENSO-driven variations seem relatively small.

Given that the BSS can be more conservative than the WPC (Wang et al. 2019), we notice that the area of positive BSS is smaller than that with WPC higher than 50%. Comparing Figs. 2a and 6a with Fig. 4, we observe the areas with relatively large interannual rainfall variability are mostly within the areas of high skill, suggesting ACCESS-S1-based forecasts have high value. The hindcast assessment shows good skill over many Island nations such as Vanuatu, New Caledonia and Fiji, which affirms the value of climate forecasts in these countries. Although the skill is relatively low in the region along the SPCZ (affecting countries such as Samoa), the climatology itself could be used as the best forecast because it is within the SPCZ area where precipitation is relatively constant from year to year.

Fig. 4
figure 4

ACCESS-S1 precipitation verification skill scores for a weighted percent correct (WPC) and b Brier skill score for DJF months with 0–3 month lead times over the 1990–2012 hindcast period using GPCP as the observations dataset. The SPCZ and mean latitude is shown by the dotted red line and black triangle respectively, using GPCP data

Full size image
Fig. 5
figure 5

ACCESS-S1 precipitation anomaly verification skill scores for a root mean square error (RMSE) and b correlation for DJF months with 0–3 month lead times over the 1990–2012 hindcast period using GPCP as the observations dataset. The SPCZ and mean latitude is shown by the dotted red line and black triangle respectively, using GPCP data

Full size image
Fig. 6
figure 6

GPCP observed (left) and ACCESS-S1 (right) precipitation DJF standard deviation, using the ensemble mean, for 1990–2012 a all seasons, b El Niño, c La Niña and d neutral years. The ACCESS-S1 data is initialised on November 1. The black triangle represents the mean SPCZ latitude, and the two red circles are the latE and latW indices. SPCZ lines, mean latitude, latE and latW indices are found using GPCP (left) and ACCESS-S1 (right) data

Full size image
Fig. 7
figure 7

GPCP observed (left) and ACCESS-S1 (right) SST DJF standard deviation, using the ensemble mean, for 1990–2012 a all seasons, b El Niño, c La Niña and d neutral years. The ACCESS-S1 data is initialised on November 1. The black triangle represents the mean SPCZ latitude, and the two red circles are the latE and latW indices. SPCZ lines, mean latitude, latE and latW indices are found using GPCP (left) and ACCESS-S1 (right) data

Full size image

3.3 Simulation of the SPCZ position and orientation

Figure 2a shows the meridional variability of the SPCZ with error bars (red vertical lines on LatE and LatW markers on the diagonal SPCZ line) showing the range of SPCZ orientations throughout the hindcast period for hindcasts initialised on November 1. While illustrating the model has little movement in the western arm of the SPCZ, this figure also suggests that it has particular difficulty in predicting the eastern arm’s interannual variability that is evident in the observations.

Fig. 8
figure 8

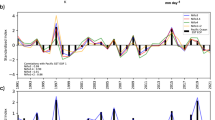
Time series of a eastern component of SPCZ (latE), b western component of SPCZ (latW), c mean SPCZ latitude and d slope of SPCZ for the ACCESS-S1 compared to observations from GPCP and TRMM across DJF months from 1990–2012. ACCESS-S1 data is the mean metric value for the 11 ensembles initialised on November 1, and dotted lines are one standard deviation from the mean. El Niño and La Niña years are shown by the pink and purple shaded years, respectively

Full size image

Figure 2b–d repeat this analysis for El Niño, La Niña and neutral years respectively. While the model simulates the mean location of the SPCZ well, it is the interannual variability that holds the most value for decision-making in the southwestern Pacific region (since this variability can profoundly affect the seasonal rainfall received by many Island nations). As shown by the error bars, the model fails to replicate the extent of the interannual movements of the SPCZ, particularly in the eastern arm. This is shown in Fig. 2a for all years, of which the most significant discrepancy occurs in the neutral years (Fig. 2d), where the model consistently predicts a less-sloping SPCZ. Figure 8 further highlights these interannual differences in observed SPCZ metrics, computed with both available observation datasets. This reveals that while the largest latE difference occurs in a neutral season (1993/94), this is an extreme anomaly compared to other neutral years.

Time series of annual variations of the eastern and western components as well as the mean position of the SPCZ are shown in Fig. 8a–c, respectively, for hindcasts initialised on November 1. Yearly movements of the SPCZ in DJF (Fig. 8) also highlight the biases described in Fig. 2a. The mean SPCZ (Fig. 8c) and the eastern arm (LatE; Fig. 8a) latitudes are relatively constant in the model forecasts compared to the observations, particularly from 1998 to 2008. The observations generally have large movements in the mean SPCZ latitudes that correspond to El Niño (northward shift) and La Niña (southward shift) years but the model underestimates the amplitude of this variability. The correlations between model and observations for each of these latitudinal metrics are 0.76, 0.85 and 0.81 for the latE, latW and mean SPCZ latitude, respectively, given in the 3rd column of Table 2. These correlation values are an improvement, compared to corresponding POAMA values in Charles et al. (2014) (6th column of Table 2). The correlation of the slope of the SPCZ (Fig. 8d) is lower (0.54 in Table 2), but is nonetheless an improvement over POAMA. The relatively constant SPCZ slope in the model is reflected in its relatively low standard deviation (\(4.01^{\circ }\)) in Table 2. SPCZ metrics for ACCESS-S1 for other leadtimes are also shown in Table 2. There is very little variation with forecast leadtime, which is consistent with the precipitation results discussed earlier in Sect. 3.2.

Comparing ACCESS-S1 results shown in Table 1 and 2 with CMIP3 (Table 2 from Brown et al. (2011)) and CMIP5 models (Table 2 from Brown et al. (2013a)), we note that ACCESS-S1 can generally better predict the SPCZ slope. The average SPCZ slope across the CMIP3 models was \(-0.05 ^{\circ }\hbox {N}/^{\circ }\hbox {E}\), compared to \(-0.29 ^{\circ }\hbox {N}/^{\circ }\hbox {E} (-0.25 ^{\circ }\hbox {N}/^{\circ }\hbox {E})\) observed with the CMAP (GPCP) dataset over 1979–1999 DJF seasons (Brown et al. 2011). Similarly, the average SPCZ slope across the CMIP5 models was \(-0.09 ^{\circ }\hbox {N}/^{\circ }\hbox {E}\), compared to \(-0.28 ^{\circ }\hbox {N}/^{\circ }\hbox {E}\) (\(-0.25 ^{\circ }\hbox {N}/^{\circ }\hbox {E}\)) observed with the CMAP (GPCP) dataset over 1980–2005 DJF seasons (Brown et al. 2013a). Furthermore, the CMIP5 (average of all models) mean SPCZ latitude standard deviation was \(2.1^{\circ }\), compared to \(3.1^{\circ }\) (\(3.2^{\circ }\)) observed with the CMAP (GPCP) dataset (Brown et al. 2013a). These results highlight that the CMIP3 and CMIP5 models generally have a tendency to predict a zonal SPCZ, as found by Brown et al. (2011, 2013a).

Table 1 Mean LatE, latW, SPCZ latitude and slope metrics in ACCESS-S1 (initialised on November 1) and GPCP for ENSO years
Full size table

To estimate the uncertainty due to sampling a relatively short timeseries, a block bootstrap resampled time series method was used to determine the 5th and 95th percentiles, using a block length of 5 years and 5000 samples (Charles et al. 2014; Efron 1981). Table 2 highlights a large ensemble spread for latE values (compared to latW), while further illustrating that ACCESS-S1 forecasts the western arm of the SPCZ more accurately than the eastern. This coincides with the biases noted earlier in Table 1. The 5th and 95th percentile values for the slope further expose this error with values of 0.02 and 0.76, respectively for a 1-month lead time. To estimate the sensitivity of these results to forecast lead time, these metrics were also computed for forecasts with a 0-month, 2-month and 3-month lead time, initialised on December 1, October 1 and September 1 respectively.

The relatively larger spread of slope values (compared to LatE and LatW) illustrates the compounded inaccuracy of the model’s ability to predict the slope as a result of poorly predicting LatE, and to a lesser extent LatW. This spread (for all lead times shown in Table 2) is however smaller than POAMA, showing that ACCESS-S1 has improved model performance over its predecessor.

Table 2 LatE, latW, mean latitude and slope values correlated with observed GPCP data for ACCESS-S1 DJF 1990–2012 seasons with a 0-month (1st column), 1-month (2nd column), 2-month (3rd column) and 3-month (4th column) lead time, and POAMA DJF 1980–2010 seasons with a 1-month lead time (5th column)
Full size table

Standard deviations of the latE, latW, mean SPCZ latitude and slope values (across all hindcast DJF seasons and 11 ensemble members) are shown in the square brackets in Table 2. Standard deviations reflect the interannual spread of the mean latE, latW, mean SPCZ latitude and slope values across all 11 ensembles. This further emphasises the ability of ACCESS-S1 to more accurately predict the SPCZ in the western region, which has a lower standard deviation for all lead times shown, compared to the eastern.

The results from Table 2 which show lead time has little effect on the skill of SPCZ seasonal forecasts is somewhat counter-intuitive. Persistent model biases may result in predicting an overly-zonal SPCZ, which may be independent of lead time at seasonal timescales.

To investigate further, fields for December, January and February rainfall and SSTs were analysed for the 1993/94 season which had a particularly large slope (see Fig. 8d). These results are shown for a 1-month lead time forecast (i.e. initialised November 1st) in Fig. 9. ACCESS-S1 was able to accurately predict the slope in December (Fig. 9a), but with increasing lead time the slope becomes more zonal (January and then February). This suggests that ACCESS-S1 can predict the slope inside a one month lead time, but this accuracy decreases with increasing forecast lead time. Figure 9d–f show forecast and observed SSTs for the same period. While the forecasts show evidence of a ‘cold tongue bias’ (Cai et al. 2009, 2010; Davey et al. 2002; Cai et al. 2003) (i.e. the equatorial SSTs between around 150–110 \(^{\circ }\)W become noticeably cooler than the observations by February), the forecast zonal SST gradients from 10 \(^{\circ }\)S are consistent with the observations throughout the season. During December, the forecast and observed location of LatE is very similar, close to the 29.5 \(^{\circ }\)C isotherm. As the SSTs cool during the rest of the season, the size of the 29.5 \(^{\circ }\)C isotherm diminishes. This relative cooling of the waters near the SPCZ is forecast accurately in this specific case. However, the forecast position of LatE remains within the 28.5 \(^{\circ }\)C isotherm. In contrast, the entire observed SPCZ moves further south during the season, with LatE lying well outside the 28.5 \(^{\circ }\)C isotherm. For this case study of DJF 1993/94, the ACCESS-S1 ocean model has provided a good seasonal forecast of SSTs in the vicinity of the SPCZ. While the atmospheric model was able to replicate the correct slope for the first month of the forecast, it returned to a more zonal configuration orientation later in the season. The atmospheric model shows an inability to initiate convection south of the 28.5 \(^{\circ }\)C isotherm.

Fig. 9
figure 9

1993/94 season observed (left) and modelled (right) monthly Figures for a–c precipitation and d–f sea surface temperatures initialised on November 1st. SST isotherms are at 1 \(^{\circ }\)C intervals. SPCZ lines, mean latitude, latE and latW indices are found using GPCP (left) and ACCESS-S1 (right) data for each respective month in the 1993/94 DJF season

Full size image

To further investigate sub-seasonal performance and the effect of forecast lead time, the SST plots of Fig. 9 are repeated for forecasts initialised on 1st December 1993, 1st January 1994 and 1st February 1994 and shown in Fig. 10. For 1st December forecasts, the forecast SPCZ slope stays relatively constant throughout December and January but becomes zonal in February. For 1st January forecasts, the forecast SPCZ slope matches the observations well, but it is positioned too far north. This is replicated for the forecast initialised on February 1st 1994. While the model produces a sloping SPCZ, it has a smaller slope than the observed SPCZ and is located too far north. These shorter-lead forecasts remove the noticeable equatorial cold-tongue bias (as seen in longer-lead forecasts) in the forecast SST fields which eliminates this as a potential factor in SPCZ forecasting errors.

Fig. 10
figure 10

1993/94 season observed (left) and modelled (right) monthly Figures for sea surface temperatures for a–c forecasts initialised on 1st December 1993, d–e forecasts initialised on 1st January 1994 and (f) forecast initialised on 1st February 1994. SST isotherms are at 1 \(^{\circ }\)C intervals. SPCZ lines, mean latitude, latE and latW indices are found using GPCP (left) and ACCESS-S1 (right) data for each respective month in the 1993/94 DJF season

Full size image

In conclusion, this analysis shows that the ACCESS-S1 atmospheric model can produce a sloping SPCZ at short lead times. With increasing model time steps, the forecast SPCZ returns to a more zonal orientation. In this specific season (1993/94) the SPCZ shifted further south during the season. No forecast was able to replicate this movement, even with a lead-zero forecast for February 1994.

Contours of forecast and observed SSTs are shown in Fig. 11 for various seasonal forecasts with a 1-month lead time. In addition to the 1993/94 forecasts, two La Niña seasons (1998/99 and 2008/09) show similar outcomes. The observed location of LatE lies south of the observed 28.5\(^{\circ }\)C isotherm for the entire season, while the forecast position of LatE remained inside the forecast 28.5 \(^{\circ }\)C isotherm. Indeed, ACCESS-S1 forecast a stronger slope for the 2004/05 El Niño season (Fig. 11e) than for the 1998/99 La Niña (Fig. 11d). This is confirmed in Fig. 8d. A noticeable feature of the 2004/05 El Niño was the extent and duration of the 29.5 \(^{\circ }\)C isotherm. The strong zonal SST asymmetries within the SPCZ warm pool may have been a factor in creating an accurate SPCZ forecast (van der Wiel et al. 2015b). The fact that the observed SPCZ showed no southward shift also helped, as Figs. 9 and 10 show that the model cannot accurately forecast a southward shift of the SPCZ.

Therefore, the available evidence suggests the atmospheric model used within ACCESS-S1 is unable to sustain convection south of the 28.5 \(^{\circ }\)C isotherm which results in poor seasonal forecasts of SPCZ location (especially in La Niña seasons). This explains the independence of forecast lead time on the seasonal SPCZ forecasts, as there are atmospheric model processes which work at sub-seasonal scales which prevent convection occurring at the correct latitude, even with an accurate SST forecast.

Fig. 11
figure 11

Observed (left) and modelled (right) DJF sea surface temperature isotherms at \(1^{\circ }\hbox {C}\) intervals for 1990–2012 a all seasons, b 1993/94, c 1997/98, d 1998/99, e 2004/05 and f 2008/09 selected seasons. SPCZ lines, mean latitude, latE and latW indices are found using GPCP (left) and ACCESS-S1 (right) data

Full size image

3.4 Factors affecting the SPCZ

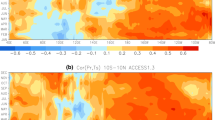
Factors affecting the SPCZ location and orientation include the sea surface temperature gradient (van der Wiel et al. 2015b; Folland et al. 2002; Kiladis et al. 1989; Widlansky et al. 2011), Madden Julian Oscillation (MJO) (Lorrey et al. 2012; Madden and Julian 1971) and ENSO (Kidwell et al. 2016; Widlansky et al. 2012; Lorrey et al. 2012). The minimum sea surface temperature required for active convection in the tropics is approximately 28 \(^{\circ }\)C (Evans and Webster 2014) which has typically been used for the Oceanic Warm Pool boundary (Hoyos and Webster 2012). The edge of the Western Pacific Warm Pool has previously been defined with isotherms between 28–29 \(^{\circ }\)C (Cravatte et al. 2009; Wyrtki 1989; Picaut and Delcroix 1995; McPhaden and Picaut 1990), and this analysis employs a 28.5 \(^{\circ }\)C isotherm to define its edge as consistent with (Clarke et al. 2000). Figures 11a and 12 show there to be mostly a minimal difference in the SSTs between the model and observations for all 1990–2012 DJF seasons, however it does predict some of the equatorial region to be too cold. Many climate models have a cold tongue bias (Cai et al. 2009, 2010; Davey et al. 2002; Cai et al. 2003), however Fig. 11a illustrates that ACCESS-S1 predicts the 28.5 \(^{\circ }\)C isotherm quite closely to the observed. While it is possible that the cold tongue bias may interfere with the atmospheric circulation in the region to the north of the SPCZ, van der Wiel et al. (2015b) showed the SPCZ’s orientation (and intensity) is affected by the extent of how zonally symmetric the SSTs are. More zonally-asymmetric SSTs will contribute to a less-zonal SPCZ and higher rainfall in the SPCZ region (van der Wiel et al. 2015b). Furthermore, ACCESS-S1 has good forecast skill for rainfall in the region of the cold tongue, which suggests the atmospheric model can react to cooler SSTs at the equator during the DJF period. Additionally, data from shorter-lead forecasts shown in Fig. 10 showed the forecasts of SPCZ location were poor without the equatorial cold tongue present. Given the model’s accuracy in predicting the SSTs over all years (as well as some extreme ENSO seasons shown in Fig. 11c, f), we hypothesise that the model’s difficulty in predicting the SPCZ’s orientation is more affected by atmospheric processes as opposed to oceanic ones.

Fig. 12
figure 12

Observed (left) and modelled (right) location of the Warm Pool edge as shown by the red and blue contours, based on a 28.5 \(^{\circ }\)C isotherm for El Niño and La Niña 1990–2012 DJF months. The ACCESS-S1 hindcasts are initialised on November 1. SPCZ lines, latE and latW indices are found using GPCP (left) and ACCESS-S1 (right) data

Full size image

Work by Matthews (2012) and van der Wiel et al. (2015a) showed that the movement of refracted Rossby waves into the Pacific is linked to the precipitation belt forming the SPCZ. However section 4.1.2 and Figure 4 of van der Wiel et al. (2015b) showed that zonal asymmetries in SSTs must exist for ‘sloping’ precipitation to occur from these refracted Rossby waves.

Fig. 13
figure 13

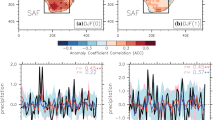
DJF observed a SPCZ mean latitude and b slope are compared with Niño3 and Niño4 anomalies. Niño3 and Niño4 anomalies have correlation values of 0.72 and 0.80 with the SPCZ mean latitude, compared with 0.03 and \(-0.21\) with the SPCZ slope respectively. El Niño and La Niña years are shown by the pink and purple shaded years respectively

Full size image

To further understand the relationship between observed SPCZ and ENSO, Fig. 13a illustrates a strong correlation between the SPCZ mean latitude and Niño3 (0.72) and Niño4 (0.80) indices. The SPCZ slope however appears to have little or no correlation with the Niño3 (0.03) and Niño4 (\(-0.21\)) indices (Fig. 13b). Even though the correlation is weakened with the SPCZ slope, there is a relationship between the Warm Pool movement (represented by Niño3 and Niño4 indices) and the SPCZ’s location. This is illustrated well in the 1997/98 season, which was a strong El Niño event and had a very zonal SPCZ orientation (Fig. 11c). In large El Niño events the Warm Pool shifts to the east, which is correlated with the SPCZ shifting northwards (in line with van der Wiel et al. 2015b).

4 Discussion and conclusions

This study evaluated the ability of the Australian Bureau of Meteorology’s new seasonal forecasting model, ACCESS-S1, to forecast the position and variability of the SPCZ. ACCESS-S1 has capability in predicting the mean SPCZ location for DJF months for up to three month lead times; however its ability to predict the slope is less reliable. ACCESS-S1 has notable model biases, but it nevertheless proves to be an improvement on the previous POAMA seasonal climate prediction system.

These results show that ACCESS-S1 forecasts have more capability in predicting SPCZ metrics than POAMA as recorded in Charles et al. (2014). While this improvement is welcome, ACCESS-S1 still requires improvement in capturing the variability in SPCZ slope and its location with the movement of the 28.5 \(^{\circ }\)C isotherm in order to better predict local rainfall. This study has shown discrepancies in the SPCZ mean latitude, LatW and LatE, of which latE inconsistencies (between ACCESS-S1 and observations) are particularly noticeable in La Niña years. The results show the model fails to correctly represent atmospheric processes which create deep convection and heavy rainfall south of the Warm Pool’s boundary at the 28.5 \(^{\circ }\)C isotherm. Understanding these processes and its representation in the model should be the focus of further development of the seasonal prediction system. ACCESS-S1 had particular difficulty predicting the eastern arm’s movement outside the warm pool in the 1993/94 and 2008/09 seasons (Fig. 11b, f), which suggests that further improvements to the model could be made if the warm pool’s interaction with the SPCZ is better understood.

The ability to predict cloud movements also play an important role in the reliability of such climate prediction systems because of their relationship with sea surface temperatures (Yu and Mechoso 1999; Lintner and Neelin 2008; Ma et al. 1996). Improved cloud parameterisation competency may help reduce the existing errors in modelling the relationship between the ocean and atmosphere (Yu and Mechoso 1999; Lintner and Neelin 2008; Ma et al. 1996).

In terms of applications in Australia, the extent of how well the sugarcane industry does in a given season relies (in part) on how accurately rainfall can be predicted in growing areas (Everingham et al. 2008). The Wet Tropics, Burdekin and Mackay–Whitsunday floodplain areas near the coast are primarily used for sugarcane crops, and the use of nitrogen-containing fertilisers is increasing as a result of the growing industry (Kroon et al. 2016). There are substantial interannual rainfall fluctuations in the GBR region (Thorburn et al. 2013; Petheram et al. 2008), resulting in uncertainty of how successful a given cropping season will be (Thorburn et al. 2013; Everingham et al. 2007). This has given rise to farmers excessively using nitrogen fertilisers in the GBR catchment area (Thorburn et al. 2013; Thorburn and Wilkinson 2013). The seasonal rainfall outlook has value because an accurate forecast could help better understand how fruitful a cropping season will be (Thorburn et al. 2013; Everingham et al. 2007, 2008), which could lead to better nitrogen fertiliser practices (Thorburn et al. 2011, 2013). Thorburn et al. (2013) suggested this to be a worthwhile topic of research in the future.

Due to the dependency South Pacific Island nations have on rainfall for agricultural production (Barnett 2011), 3-month seasonal forecasts could provide great value for decision making for many of these countries (He and Barnston 1996). We have shown that the performance of the forecast in this region relies (in part) on how well the position and orientation of the SPCZ are simulated. Errors in SPCZ slope prediction will have consequences for seasonal forecasts for countries in the southwest Pacific. Here we have demonstrated that while the zonal movements of the SPCZ are replicated in the model, the slope of the SPCZ is not. This is particularly concerning for extreme years (such as the 2008/09 season shown in Fig. 11f), which could have important ramifications for agricultural planning. Weaknesses in the model simulations would mean that the direct model output would have advised islands such as Samoa and French Polynesia of higher rainfall than they actually experienced in 2008/09. In addition to errors in SPCZ slope, ACCESS-S1 also forecasts higher rainfall than the observed (average difference of 1.8 mm/day in the SPCZ region). Biases in the orientation of the SPCZ suggest that taking direct rainfall (or rainfall anomalies) from ACCESS-S1 for the nearest grid point might not give the best forecasts. This is especially true for islands which are situated near the ‘avenue of uncertainty’ of skill that was shown in Fig. 4.

For the sugar cane industry in NEA, seasonal rainfall can be predicted by statistical methods using the phase of ENSO (Everingham et al. 2008). As demonstrated here the NEA rainfall does not have much skill when compared to forecasts for some Pacific Island nations such as New Caledonia and Vanuatu (see Fig. 4). This may contribute to the challenges of developing seasonal rainfall forecasts for sugar industries located in the NEA region. We suggest that the appropriate way forward is to develop a hybrid approach in seasonal rainfall forecasting, combining the prediction of climate drivers from the dynamical model with the statistical relationships between those drivers and local rainfall. One pathway to circumventing these biases and developing forecasts was suggested by Brown et al. (2013b) for fully coupled global climate models, which use the models to predict changes to the strength and relative movements of the SPCZ. A bias correction applied to the slope and position of the SPCZ could be applied to specific Pacific Islands.

While the model cannot produce a skilful seasonal forecast of SPCZ slope, it may provide useful quantitative forecasts of SPCZ slope anomalies. Figure 14 shows the ACCESS-S1 seasonal slope anomaly for hindcasts initialised on November 1 (multiplied by two) against the observed slope anomaly.

Fig. 14
figure 14

DJF observed and forecast slope anomalies initialised on November 1. The ACCESS-S1 slope anomalies are multiplied by a factor of two. El Niño and La Niña years are shown by the pink and purple shaded years respectively

Full size image

Whether the atmospheric model used in ACCESS-S1 can capture the large-scale mid-latitude wave dynamical influences in the SPCZ region is a good question. The definitive verification paper for GA6.0 is Walters et al. (2017). They cite Mittermaier et al. (2016) who verified mid-latitude GA6.0 forecasts in Numerical Weather Prediction configurations at N512 and N768 resolutions for 144-h forecasts. Using synoptic tracking algorithms, the results of Mittermaier et al. (2016) showed that GA6.0 forecasted lows that are larger and deeper, and highs that are stronger and smaller.

Whether the results of Mittermaier et al. (2016) suggest a seasonal forecast model can replicate the mid-latitude Rossby wave behaviour depends, at least in part, on how significant numerical diffusion is at lower resolutions and longer lead times. Fig. 9a proved that GA6.0 at N216 resolution can replicate the atmospheric dynamics required to produce a strongly sloping SPCZ. However, this occurred for a month when forecast SSTs were very high in the eastern arm of the SPCZ (greater than 29.5 \(^{\circ }\)C). Figures 9d and 10 showed the model can produce a sloping SPCZ within the 28.5 \(^{\circ }\)C isotherm but with increasing model time steps it reverts to a more zonal orientation. Figure 11e shows that a good seasonal forecast of the SPCZ slope is possible when SSTs are very high (greater than 29.5 \(^{\circ }\)C) and the observed precipitation lies within the Warm Pool. The available evidence suggests the model can replicate the Rossby-wave dynamics which create the SPCZ slope, however it cannot sustain this slope at seasonal time frames.

How to attribute these shortcomings of the atmospheric model is a difficult question. Numerical diffusion at longer lead times may eventually dampen the strength of the refracted mid-latitude Rossby waves, or biases in the model’s convection initiation may dominate Rossby wave-related processes at longer timescales. A combination of factors may be an issue. The inability to forecast southward shifts in SPCZ latitude may be related to atmospheric biases in the overall global circulation, which could be related to tropical convection. Franklin et al. (2013) evaluated computed cloud formation in ACCESS1.3, a CMIP climate model that used a modified version of GA1.0 at N96 resolution (Bi et al. 2013; Franklin et al. 2013; Hewitt et al. 2011) against space-based cloud observations. Franklin et al. (2013) found that the model failed to generate enough deep convective cloud over SSTs between 25–28 \(^{\circ }\)C. The model simulated a change from shallow to deep convection at SSTs above 27 \(^{\circ }\)C, 1 \(^{\circ }\)C higher than the observations (at 26 \(^{\circ }\)C) (Franklin et al. 2013).

While the deep convective scheme used in GA1.0 (Hewitt et al. 2011) is different to that of GA6.0 (Walters et al. 2017), these statements are consistent with our forecast precipitation behaviour compared to observations, i.e. ACCESS-S1 often doesn’t produce enough maximum rain (associated with deep tropical convection) south of the equator in the SPCZ and the change from shallow to deep convection occurs at higher SSTs than in reality.

Future challenges to improving predictability in this region require further investigations into the mechanisms that determine atmospheric convection at longer lead times. While an ENSO teleconnection to the latitudinal movements of the SPCZ seems to exist within the ACCESS-S1 system, seasonal prediction of its slope is much harder to forecast.