Abstract
Mountain glaciers are key indicators of climate change. Their response is revealed by the environmental equilibrium-line altitude (ELA), i.e. the regional altitude of zero mass balance averaged over a long period of time. We introduce a simple approach for distributed modelling of the environmental ELA over the entire European Alps based on the parameterization of ELA in terms of summer temperature and annual precipitation at a glacier. We use 200 years of climate records and forecasts to model environmental ELA from 1901 to 2100 at 5 arcmin grid cell resolution. Historical environmental ELAs are reconstructed based on precipitation from the Long-term Alpine Precipitation reconstruction (LAPrec) dataset and temperature from the Historical Instrumental climatological Surface Time series of the greater Alpine region (HISTALP). The simulations of future environmental ELAs are forced with high-resolution EURO-CORDEX regional climate model projections for the European domain using three different greenhouse gas emissions scenarios (Representative Concentration Pathways, RCP). Our reconstructions yielded an environmental ELA across the European Alps of 2980 m above sea level for the period 1901−1930, with a rise of 114 m in the period 1971−2000. The environmental ELA is projected to exceed the maximum elevation of 69%, 81% and 92% of the glaciers in the European Alps by 2071−2100 under mitigation (RCP2.6), stabilization (RCP4.5) and high greenhouse gas emission (RCP8.5) scenarios, respectively.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The European Alps (hereafter referred to as “the Alps”) have warmed twice as much as the global average between the late 19th and the early twenty-first century (Auer et al. 2007; Ceppi et al. 2012), and a trend of faster warming at higher mountain elevations is predicted to continue until the mid-twenty-first century regardless of the choice of future climate scenario (IPCC 2018). Beyond the mid-twenty-first century, atmospheric warming in mountains will be stronger under a high greenhouse gas emission scenario (RCP8.5) and will stabilise at mid-twenty-first century levels under a low greenhouse gas emission scenario (RCP2.6) (IPCC 2018). While temperature trends in the Alps are clear, precipitation trends in the Alps show high spatial variability (Auer and Böhm 1994) with precipitation increasing in the NE and decreasing in the SW part of the Alps over the past decades (Brunetti et al. 2006; Auer et al. 2007). Taking into account the entire Alps, only slight shifts in average precipitation (Auer et al. 2007) and decrease in snowfall were recorded over the past decades (IPCC 2014). Summer precipitation reduction associated with increased convective rainfall is projected (Giorgi et al. 2016), whereas future trends in annual precipitation are uncertain (IPCC 2014).
The 4395 glaciers currently still present in the Alps with a total area of 1806 ± 60 km2 (Paul et al. 2020) are projected to lose a substantial part of their volume in the coming century and many of them are expected to disappear by 2100 regardless of which emission scenario is used (Haeberli and Hoelzle 1995; Zemp et al. 2006, 2007). Current regional and global estimates of the future evolution of glaciers in the Alps are based on models of variable complexity and rely on different climate projections. These models generally suggest a glacier volume loss of about 65–80% between the early twenty-first century and 2100 under a low greenhouse gas emission scenario (RCP2.6), 80–90% under a moderate greenhouse gas emission scenario (RCP4.5) and an almost complete disappearance of glaciers (volume loss 90−98%) under a high greenhouse gas emission scenario (RCP8.5) (Marzeion et al. 2012; Radić et al. 2014; Huss and Hock 2015; Zekollari et al. 2019).
Although the contribution of glaciers in the Alps to sea-level rise is low and is projected to account for less than 0.3 mm sea-level equivalent for the period 2010−2100 (Huss and Hock 2015), their relatively large volume loss could have a profound impact on river runoff, as already suggested in some earlier publications from the twentieth century (Collins 1987; Chen and Ohmura 1990a, b). Several studies have reported an increase in average winter runoff over the past decades in glacier-dominated Alpine basins and a decrease in summer runoff (Bosshard et al. 2013; Bocchiola 2014; Addor et al. 2014; Bard et al. 2015), with peak water discharge from the majority of Alpine glaciers already surpassed (Huss and Fischer 2016; Huss and Hock 2018). Similar trends in the amount and seasonality of river runoff are projected to continue over the twenty-first century and are expected to affect downstream water management, related hazards and ecosystems. There are also socio-economic risks related to rapid changes in mountain glaciers, such as the decline of tourism (Spandre et al. 2019; Steiger et al. 2019), deterioration of drinking water quality (Hodson 2014), impact on livelihoods (Haeberli and Whiteman 2015; Carrivick and Tweed 2016) and hydro-electric power generation (Farinotti et al. 2019).
One way to quantify the response of glaciers to changing climate is by monitoring their equilibrium-line altitude (ELA) (e.g. Lie et al. 2003; Zemp et al. 2007; McGrath et al. 2017). ELA is defined as the spatially-averaged altitude of the set of points on the surface of the glacier where the climatic mass balance is zero at a given point in time (Cogley et al. 2011). Although the ELA is generally understood as annual ELA, many different variations and approximations of the ELA exist in the literature (e.g. Lie et al. 2003; Zemp et al. 2007; Braithwaite and Raper 2009). Most of the previous studies on ELA report either the steady state equilibrium-line altitude (ELA0) of glaciers, calculated from direct glaciological mass balance measurements or the local topographic equilibrium-line altitude, also referred to as the effective ELA (hereafter referred to as “effELA”), which accounts for the effect of topography (Anderson et al. 2018). In contrast, the environmental ELA (hereafter referred to as “envELA”) is the regional altitude of zero glacier mass balance without the effects of shading, avalanching, snow drifting, glacier geometry or debris-cover (Anderson et al. 2018), averaged over a period that is long enough to be climatic, usually several decades. The envELA represents the theoretical altitude at which a glacier can form.
In this paper, we adopt the terminology of Anderson et al. (2018), who distinguished between the envELA and effELA. We investigate the past envELA over the entire Alps and project its evolution under different future climate forcing scenarios using a simple parameterization of the ELA in terms of summer temperature and annual precipitation initially proposed by Ahlmann (1924) and recently updated by Ohmura and Boettcher (2018) based on the theory of mass and energy conservation. Our approach has the advantage that it does not require detailed input data from various sources as in more sophisticated models, nor the parameterization of ice flow dynamics driven by the mass balance (e.g. Huss and Hock 2015; Zekollari et al. 2020).
We use 200 years of climate records and forecasts over the period 1901−2100 for the distributed modelling of the envELA at 5 arcmin grid cell resolution over the entire Alps. Historical envELAs are reconstructed based on the Long-term Alpine Precipitation reconstruction (LAPrec) dataset (Isotta et al. 2019) and temperature datasets from the Historical Instrumental climatological Surface Time series of the greater Alpine region (HISTALP) (Auer et al. 2007). Previous simulations of ELA changes over the Alps were mostly based on earlier greenhouse gas emission scenarios (e.g. Zemp et al. 2007) or relied on global climate series with low spatial resolution (e.g. Huss and Hock 2015). In contrast, our model is forced with high-resolution CORDEX regional climate model (RCM) simulations for the European domain (EURO-CORDEX, Jacob et al. 2014), which provide a better description of local climatic conditions. The envELA patterns are validated against existing end-of-mass-balance-year ELAs from the WGMS FoG database over the entire Alps for the period 1948−2017 (WGMS 2019). The projected envELA pattern under various climate scenarios is additionally validated for the period 2006−2019 using annual highest end-of-summer snow line altitudes (SLAs) derived from Landsat data for a subset area of the Alps using a previously developed semi-automated remote sensing method (Racoviteanu et al. 2019).
Our goal is to use modelled envELAs as a proxy for climate change in the Alps. Specifically, our work is motivated by the following research questions:
-
How many glaciers in the Alps currently lie below the envELA?
-
What is the projected envELA rise in the Alps under different climate forcing scenarios?
-
How many glaciers in the Alps are likely to disappear (when envELA is above their maximum altitude) by the end of the twenty-first century under different climate forcing scenarios?
-
What is the spatial pattern of the envELA across the Alps?
2 Data and methods
2.1 Climate data
Our study area is defined between the latitude ~ 43° and 48° N and longitude ~ 4° to 17° E (Fig. 1) and covers the entire currently glacierised area of the Alps. We selected the long-term Alpine precipitation reconstruction (LAPrec) dataset (Auer et al. 2007; Isotta et al. 2014, 2019) and temperature historical instrumental climatological surface time series of the greater Alpine region (HISTALP) (Auer et al. 2007) (Table 1) to reconstruct the envELA back to 1901. We used EURO-CORDEX simulations (Jacob et al. 2014; https://www.euro-cordex.net/) to produce projections of the future envELA evolution by 2100.
Study area defined as the Alpine Convention perimeter (https://www.alpconv.org/en/home/). Glacierised areas in ~ 2003 are from Randolph Glacier Inventory (RGI v6.0) (RGI Consortium 2017). Grid cells at 5 arcmin spatial resolution cover locations of every glacier polygon centroid and represent a basis for the Alpine environmental ELA distributed modelling. Rectangle shows the subset extent used for remote sensing ELAs
LAPrec is a new gridded monthly precipitation dataset of the Alps on a regular 5 km grid that is spatially referenced in ETRS89/ETRS-LAEA (European Terrestrial Reference System 1989-Lambert Azimuthal Equal Area). LAPrec integrates information from two data sources: the HISTALP station data archive (Auer et al. 2007) which extends over the full period of interest, and the high-resolution station-based spatial analysis EURO4M-APGD (Isotta et al. 2014), which spans the period 1971−2008 and incorporates more than 5500 rain-gauge measurements on average per day. This is one of the densest in-situ observation networks over a high-alpine topography worldwide. Two variants of LAPrec exist. The longer version starts in 1871 and uses 85 almost continuous series, whereas the shorter version starts in 1901 and uses 164 almost continuous series. Both versions end in 2017. We decided to use the LAPrec1901 version due to its higher reliability (Isotta et al. 2019).
The original measurements used for LAPrec1901 have not been corrected for precipitation gauge undercatch and as a result are expected to generally underestimate precipitation, especially in winter months and at high elevations (e.g. Sevruk 1985; Adam and Lettenmaier 2003). In order to account for this effect, we added a gauge correction to the LAPrec1901 dataset by first estimating a mean monthly undercatch correction from the global precipitation data set of Legates and Willmott (1990) (UDel Version 3.01) (Table 1), spanning the period 1900 to 2010, and then using it to correct the monthly precipitation values in the LAPrec1901.
The HISTALP gridded dataset comprises monthly homogenized records of mean air temperature for topography height on a regular grid with a spatial resolution of 5 arcmin. The dataset was created by merging high resolution gridded climate means (1961−1990) for each month (Hiebl et al. 2009) and long-term monthly data from 140 stations (Chimani et al. 2013). The time period covered is 1780−2014.
For the climate model simulations, twelve sets of driving GCM and corresponding RCM experiments carried out in the frame of EURO-CORDEX at 0.11° resolution and three different emission scenarios for the variables near surface air temperature (tas) and precipitation (pr) are considered (Table 2) (Jacob et al. 2014; https://www.euro-cordex.net/). EURO-CORDEX RCM simulations are forced with different scenarios, denoted by Representative Concentration Pathways (RCPs) (van Vuuren et al. 2011; IPCC 2014). RCPs are identified by their approximate total radiative forcing in year 2100 relative to 1750. The three considered RCPs in this study include the RCP2.6 low end scenario leading to a very low forcing level (2.6 W m−2), the RCP4.5 stabilization scenario (4.5 W m−2), and the RCP8.5 high end scenario with maximum greenhouse gas emissions (8.5 W m−2). For RCP2.6, the radiative forcing peaks at 3 W m−2 before 2100 and then declines to 2.6 W m−2 by 2100; for RCP4.5 it stabilizes by 2100, and for RCP8.5, it does not peak by year 2100. Historical runs for the selected models were used for systematic bias correction. We compared the monthly precipitation totals and mean monthly temperature of the observed and simulated datasets over the period 1976−2005 (Fig. S1) and estimated a bias correction following the procedure described in Huss and Hock (2015). The bias is then assumed to remain constant in time also during the projection period and is used to bias-correct temperature and precipitation on a monthly basis from 2006 to 2100. For precipitation, we use a linear scaling bias correction method in which, for each month m of a year y of the projection period, precipitation is corrected as:
where \(\overline{{P}_{m, LAPrec1901 (1976-2005)}}\) is the average monthly precipitation total from the LAPrec1901 dataset over the period 1976−2005, \({P}_{m,EURO-CORDEX (1976-2005)}\) is the average monthly precipitation total for the EURO-CORDEX historical simulation dataset over the period 1976−2005, and \({P}_{m,y EURO-CORDEX (2006-2100)}\) is the monthly precipitation total for every year of the EURO-CORDEX RCM simulation for the period 2006−2100.
Variance scaling after Huss and Hock (2015) was used to bias-correct temperature by which, for each month m in a year y, we apply the following equation:
where \(\overline{{T}_{m, 25}}\) is the centred running mean of monthly temperature in a 25-year period for y, \({T}_{m,y EURO-CORDEX (2006-2100)}\) is the mean monthly temperature for every year of EURO-CORDEX RCM simulation for the period 2006−2100, \({\sigma }_{HISTALP,m (1976-2005)}\) is the standard deviation of monthly temperatures of the HISTALP dataset over the period 1976−2005, \({\sigma }_{EURO-CORDEX,m (1976-2005)}\) is the standard deviation of monthly temperatures of EURO-CORDEX historical simulations over the period 1976−2005, \(\overline{{T}_{m HISTALP \left(1976-2005\right)}}\) is the monthly average of HISTALP over the period 1976−2005 and \({T}_{m EURO-CORDEX (1976-2005)}\) is the monthly average of EURO-CORDEX historical simulation over the period 1976−2005. In this way, the EURO-CORDEX temperature series are adjusted to account for differences in year-to-year variability between the historical (HISTALP) and projected (EURO-CORDEX) time series.
Because the historical and simulated datasets do not use the same horizontal grid, we interpolated all EURO-CORDEX RCM simulations and LAPrec historical data onto the HISTALP equidistant grid of 5 arcmin (~ 6 × 9 km) resolution. Both downscaling (for EURO-CORDEX datasets) and upscaling (for LAPrec dataset) interpolation was performed using the distance-weighted average remapping method in the Climate Data Operators software (CDO, https://code.zmaw.de/projects/cdo), which uses the four nearest neighbour values for each grid cell from the original field. According to Torma et al. (2015), the distance-weighted average method produces the most consistent spatial patterns among several interpolation methods (e.g. bilinear, bicubic, field conserving) applied to the Alps area. The interpolation was done as a first-step operation on the original field before any further computation (undercatch correction, bias correction, calculation of yearly precipitation sum and mean summer temperature).
The final 200-year time series of temperature and precipitation fields, comprising 105 years of historical data (1901−2005) and 95 years of bias-corrected projections (2006−2100), were used in the distributed modelling of envELA.
2.2 Environmental ELA distributed modelling
For the sake of comparison with other glacier-related modelling studies (e.g. Huss and Hock 2015; Huss et al. 2017; Zekollari et al. 2019), glacierised areas were obtained from the Randolph Glacier Inventory (RGI) v6.0 (RGI Consortium 2017), which provides a snapshot of glacier extents at the end of the summer 2003 (more than 96% of those glaciers in the Alps that are included in the RGI) for the Alpine area. During that year, there were 3892 glaciers covering an area of 2089 km2 and altitudinal range of 1269−4776 m above sea level (asl). Each individual glacier polygon centroid was rasterized to the resolution of HISTALP dataset (5 arcmin) and then used as a mask area for the calculation of envELAs.
The envELA for every “glacierised” grid cell was computed over the period 1901−2100 using the new precipitation/temperature diagram of Ohmura and Boettcher (2018). This precipitation/temperature curve is based on data from 104 glaciers worldwide and takes the form of a fourth-order polynomial. However, for wide applications such as ours, the approximation of the P/T relationship via a quadratic function, that was derived by Ohmura and Boettcher (2018), is more practical:
where \({P}_{a}\) is annual precipitation (mm) and \({\mathrm{T}}_{sum}\) is summer (JJA) air temperature (°C). This equation was applied to every 5 arcmin grid cell comprising the glacier centroids. First, the value of \({\mathrm{T}}_{sum}\) was obtained using the gridded LAPrec/RCM precipitation dataset (\({P}_{a}\)). Then, the height difference (ΔHTsum) between the simulated \({\mathrm{T}}_{sum}\) and HISTALP/RCM \({\mathrm{T}}_{sum}\) was computed by applying a summer environmental lapse rate of 0.65 °C 100–1 m representative for the greater Alpine region (Rolland 2003; Rubel et al. 2017) to the digital elevation model (DEM) that underlies the HISTALP climatology. Finally, the envELA was calculated by subtracting ΔHTsum from DEM (Fig. 2). In contrast to a generally clear relationship between temperature and altitude, the variations in precipitation with elevation are very complex and less robust (Frei and Schär 1998). The spatial variation in precipitation gradients with elevation has been found to vary from 2 mm m−1 at the northern and southern foothills of the Alps and in the outer regions, to 0−0.6 mm m−1 in the inner regions and southern slopes, while small negative gradients have also been detected (Schwarb et al. 2000). Because of these uncertainties, no additional adjustments to the precipitation of each grid cell were made except the one related to the equation’s standard error of 648 mm, which served to determine the envELA error.
In our computations of the envELA, we assume that the glacier centroid masks remain constant throughout the model simulation. In other words, we are essentially computing the lowest boundary of climatic glacierisation, which is dependent solely on climatic factors, i.e. annual precipitation and mean summer temperature.
2.3 Model validation
We validated the envELA time series pattern over two time periods using two ELA datasets representing the effELA as per the terminology used in this study: a) a dataset of glacier-wide end-of-mass-balance-year equilibrium-line altitudes from the WGMS FoG database (WGMS 2019) and b) annual end-of-summer SLAs derived from Landsat time series.
In the first validation exercise, we compared the envELA gridded data (5 arcmin spatial resolution) with point values from the WGMS dataset (a), both averaged over the entire study area for the historical climatological time series (1948−2017). The WGMS dataset used here (hereinafter referred to as “wgmsELA”) consists of 1255 ELA values spread over 70 years (1948−2017) for 62 glaciers, well distributed geographically and climatologically over the Alps (Fig. 1). Since time spans for individual glaciers in the WGMS FoG database were variable, we excluded those ELAs that were outside the glacier altitude range reported in the database, as well ELAs before the year 1948 and after the year 2017 with a too small annual sample size. However, to match the end of the envELA historical time series (1901−2005), only wgmsELAs for the period 1948−2005 were taken into account in the model performance analysis.
In the second validation exercise, we compared the envELAs derived from climate projections for the period 2006−2019 with the end-of-summer SLAs (b), both averaged over the subset area covering the western Alps (Fig. 1), where adequate images Landsat cloud-free were available. SLAs were extracted using a previously developed automated method (Racoviteanu et al. 2019) and Landsat data 5, Enhanced Thematic Mapper Plus (ETM +) and Operational Land Imager (OLI) (30 m spatial resolution), freely obtained from the USGS. We used level 2 (surface reflectance) data, which is orthorectified, analysis-ready imagery. We selected all the cloud-free images during the ablation season for each year (July to September) (a total of 50 images for the western Alps). Out of these, only 36 images were suitable for the calculation of the highest SLAs. Assuming that for mid-latitude mountain glaciers, superimposed ice can be considered negligible, the end-of-summer remote sensing SLA is an accurate approximation of the glacier ELA (hereafter referred to as “rsELA”) (Braithwaite 1984; Rabatel et al. 2005, 2013). The performance of the rsELAs over the subset region was checked visually using Landsat colour composites, as well as against manually-derived ELAs for 43 glaciers in the French Alps by Rabatel et al. (2013) for the period 2003−2010. The rsELAs were checked for errors due to shadows in the accumulation area of glaciers, and manually corrected when necessary. Uncertainties in the rsELAs were calculated as root mean square error (RMSEz) on the basis of DEM (EU-DEM v1.1 2017) accuracy, buffer size used to derive snowlines and differences with manually edited ELAs.
3 Results
3.1 Past climate and future projections
Here we present the analysis of mean summer temperature and annual precipitation, which are used as inputs for the envELA computations. The climate results are presented as average values over the area inside the Alpine Convention perimeter (Fig. 1) unless otherwise stated.
The increase in mean summer temperature is evident in the 50-year segment from 1901 to 1950, then a stable to slight cooling in the subsequent 25-year section until the mid-1970s, followed by a trend towards a strong warming in the last 25 years of the twentieth century. Mean summer temperature in the Alps in the period 1901−1930 was 13 °C, whereas it was 0.1 °C higher in the period 1911−1940, 0.5 °C higher in the periods 1921−1950, 1931−1960 and 1941−1970, only 0.2 °C higher in the period 1951−1980 and 0.4 °C higher in the period 1961–1990. In the period 1971−2000, mean summer temperature was 13.9 °C, which is the highest in the twentieth century. The coolest summer during the historical period (1901−2005) was recorded in 1913 with an average temperature of 11.7 °C and the warmest in 2003, when the average temperature over the Alps was 17.7 °C. Mean summer temperature anomalies (2071−2100 vs. 1971−2000) range from + 1 °C to + 2 °C under RCP2.6, from + 2 °C to + 4 °C under RCP4.5 and from + 4 °C to + 7 °C under RCP8.5. Projections also suggest that the warming will be stronger in the western Alps with respect to the eastern and this anomaly is particularly evident under RCP4.5 and RCP8.5 (Fig. 3).
a Summer air temperature in the period 1971–2000 for HISTALP historical datasets. Absolute change in summer temperature in 2071–2100 relative to reference period (1971–2000) for b RCP2.6, c RCP4.5 and d RCP8.5 scenarios. e 11-year centred running mean region-averaged summer air temperature of HISTALP temperature dataset (1901–2005) and bias-corrected EURO-CORDEX multi model mean (2006–2100) for RCP2.6 RCP4.5 and RCP8.5 simulations (Table 1)
No clear temporal and spatial trend in precipitation exists for the historical period (1901−2005). The only evident dry period was recorded near 1950 in correspondence with an increase of summer temperature. However, this period was also characteristic of increased transport of convective moisture at high elevations (Auer et al. 2007). The driest year during the historical period (1901−2005) was recorded in 1921 with 965 mm of precipitation and the wettest in 1960, when the average precipitation over the Alps was 1906 mm. Annual precipitation is projected to increase (2071−2100 vs. 1971−2000) by 5−10% in the eastern part and only by 0−5% in the western part of the Alps under RCP2.6. Projections suggest that under RCP4.5 and RCP8.5, the annual precipitation will decrease by 14% in the S-SW and increase by 22% in N-NE (Fig. 4).
a Annual precipitation in the period 1971–2000 for LAPrec historical datasets. Percent change in annual precipitation in 2071–2100 relative to reference period (1971–2000) for b RCP2.6, c RCP4.5 and d RCP8.5 scenarios. e 11-year centred running mean region-averaged annual precipitation totals of LAPrec1901 precipitation dataset (1901–2005) (corrected for gauge undercatch) and bias-corrected EURO-CORDEX multi model mean (2006–2100) for RCP2.6, RCP4.5 and RCP8.5 simulations (Table 1)
As for the climate across glaciated areas (see ELA calculation grid cells in Fig. 1), the summer mean temperature in the period 1901−1930 was 6.8 °C and 7.6 °C in the period 1971−2000. Projections suggest that the temperature will rise by 1.6 °C under RCP2.6, 2.8 °C under RCP4.5 and 5.4 °C under RCP8.5 by the end of the twenty-first century (1971−2000 mean vs. 2071−2100 mean). The mean annual precipitation in the period 1931−1960 was 1541 mm and 1592 mm in the period 1971−2000. About 4% increase in precipitation for all three emission scenarios is projected by 2071−2100 compared with 1971−2000.
3.2 Past and future environmental ELA evolution
Our reconstructions of past envELAs suggest that in the first 30-years of the twentieth century (1901−1930) the mean ELA over the Alps was 2980 m asl and stayed almost the same (2977 m asl) in the period 1911−1940. The subsequent period (1921−1950) showed a dramatic rise in envELA by 101 m with respect to 1901−1930, whereas the envELA stabilized during the periods 1931−1960 and 1941−1970 at 3063 m asl and 3066 m asl, respectively. The envELA in the period 1951−1980 rose only by 19 m with respect to the period 1901−1930 and by 60 m in the subsequent 30-year period (1961−1990). In the period 1971−2000, the mean envELA was 3094 m asl and rose by 1.6 m yr−1 between 1901−1930 and 1971−2000. In the last 30-years (1991−2020), the mean envELA was 3234 m asl (Fig. 5). This was calculated as average of the mean ELA for the period 1991−2005 (calculated from HISTALP and LAPrec datasets) and mean ELA for all three RCPs for the period 2006−2020 (calculated from RCMs dataset).
The envELA evolution (11-year centred running mean) for historical period (1901–2005) and various EURO-CORDEX RCM simulations (2006–2100) for a RCP2.6, b RCP4.5 and c RCP8.5. The red thick line corresponds to envELA computed with HISTALP and LAPrec historical datasets. Other thick lines are the RCM means for individual scenario and thin lines are individual RCM simulations (12 per RCP) (Fig. S2). The transparent bands correspond to the standard error of Eq. 3 (i.e. 648 mm). The numbers marked are 30-year mean envELAs (in m asl) for the periods 1901–1930, 1991–2020 and 1971–2100
Our projections, which are based on the multi model mean of 12 EURO-CORDEX RCM simulations (Table 2), suggest that the envELA will rise at a very similar rate across scenarios by 2050, whereas in the second half of the twenty-first century, the envELA is largely determined by the RCP. The mean envELA for the first half of the twenty-first century (2001−2050) is projected to reach 3283 m asl under RCP2.6, 11 m higher under RCP4.5 and 36 m higher under RCP8.5. For the second half of the century (2051−2100) the mean envELA is projected to rise to 3293 m under RCP2.6, 172 m higher under RCP4.5 and 457 m higher under RCP8.5. In contrast to envELA evolution under RCP2.6 and RCP4.5, a substantial part of the rise will take place in the second part of the twenty-first century under RCP8.5, and while the envELA seems to stabilize by 2100 under RCP2.6 and RCP4.5, it will continue to rise under the RCP8.5. By the end of the century (2071−2100), the mean envELA in the Alps rises to 3288 m asl under RCP2.6, 3484 m asl under RCP4.5 and 3880 m asl under RCP8.5 (Fig. 6). According to our calculations, the envELA in the Alps will rise by 194 m, 390 m and 786 m by the end of the century (2071−2100) under RCP2.6, RCP4.5 and RCP8.5, respectively, compared with the reference period 1971−2000, which amounts to a rise of 1.9, 3.9 and 7.9 m yr−1.
a Average envELA in the period 1971–2000. b envELA rise between 2071–2100 for RCP 2.6 relative to reference period (1971–2000). c envELA rise between 2071–2100 for RCP 4.5 relative to reference period (1971–2000). d envELA rise between 2071–2100 for RCP 8.5 relative to reference period (1971–2000). Black dots represent the remaining glaciers with envELAs below their maximum elevation. e Number and percentage of glaciers that will remain (lower part)/disappear (upper part) by 2071–2100 according RCP 2.6, RCP 4.5 and RCP 8.5
3.3 Environmental ELA variation across the Alps
Here we present past and future environmental ELA patterns across the Alps (west to east, and south to north). Figure 7 shows that the envELA rises from west to east with one anomaly between 7° and 9°E, where the envELA is on average lower due to higher precipitation amounts with respect to nearby sectors. The mean 1971−2000 envELA in the easternmost sector (Fig. 7e) was 2567 m asl, about 742 m lower than in the westernmost sector (Fig. 7a). The relative difference between the two periods when the envELA dropped during the twentieth century (around 1915 and 1960), is 50−130 m greater in the eastern Alps (between 9° and 15°E) compared to the western Alps (between 5° and 9° E). This corresponds to a larger change in precipitation in the east (3−6%) compared to the west (0−2%) (1910−1920 mean vs. 1950−1960 mean). While sectors in the east show a gradual rise in envELA since around 1960, the western sectors exhibit a steady envELA between the 1960s and 1980s, with only a slight drop towards 1980. The rise in envELA towards the end of the twenty-first century is more pronounced in the west compared to the east under all scenarios, but especially under RCP8.5 (+ 9 m year−1 in the westernmost sector vs. + 7 m year−1 in the easternmost sector). This is related to a negative precipitation anomaly and a higher positive temperature anomaly in the western Alps, the latter being especially evident under RCP8.5 (Figs. 3 and 4). We projected a rise in envELA for the periods 1971−2000 vs. 2071−2100 in the westernmost sector of + 899 m under RCP8.5, compared to + 695 m in the easternmost sector (Table S1).
(a–e) The envELA evolution (11-year centred running mean) by longitude (every 2° between 5° and 15°E) for various EURO-CORDEX RCM simulations. Thin lines are individual RCM simulations (36 in total). Thick lines are the RCP means and the transparent bands correspond to multi model standard deviation. The red line corresponds to the envELA computed with HISTALP and LAPrec historical datasets. f Map of division of sections by longitude
Regarding the envELA variation by latitude, our model suggests that the envELA rises from north to south (Fig. 8, Table S2), with the mean 1971−2000 envELA of 2861 m asl in the northernmost sector (Fig. 8d), which is 520 m lower compared to the southernmost sector (Fig. 8a). We found different past ELA evolution patterns between the northern and southern sectors. Glaciers in the northernmost sector (Fig. 8d) had two envELA peaks of similar magnitude at around 1930 and just before 1950, while other sectors (Fig. 8a–c) showed only one prominent peak around 1950. The latter corresponds to a decrease of 10−12% in annual precipitation and an increase in summer temperature of + 0.4−0.5 °C at that time (1941−1950 mean vs. 1901−2005 mean), whereas the drop in annual precipitation and an increase in summer temperature in the northernmost sector was 5% and + 0.2 °C, respectively. While northern sectors (Fig. 8c–d) show gradual rise in the envELA since around 1965, the southern sectors (Fig. 8a-b) exhibit a slight drop in the envELA between 1955 and 1980. We project a faster rise in the envELA in the south compared to the north by the end of the twenty-first century (2071−2100 mean), under all scenarios. While the rise is very similar for all sectors under RCP2.6 (1.8−2.3 m year−1), there are larger differences among sectors under RCP4.5 (3.3−4.8 m year−1) and especially under RCP8.5 (6.9−9.5 m year−1). This is primarily related to the precipitation anomaly, namely an increase in precipitation by more than 5% under RCP4.5 and more than 10% under RCP8.5 in the north and an increase by less than 5% or even decrease by more than 5% under RCP4.5 and RCP8.5 in the south (Fig. 4).
a–d The envELA evolution (11-year centred running mean) by latitude (every 1° between 44° and 48°N) for various EURO-CORDEX RCM simulations. Thin lines are individual RCM simulations (36 in total). Thick lines are the RCP means and the transparent bands correspond to multi model standard deviation. The red line corresponds to envELA computed with HISTALP and LAPrec historical datasets. e Map of division of sections by latitude
3.4 Model performance
The mean envELA for the period 1948−2005 was 3089 m asl, which is 110 m higher than the wgmsELA over the same time period (2979 ± 183 m asl). For the reference period 1971−2000, the mean envELA was 3094 m asl, 74 m higher with respect to the wgmsELA over the same time period (3020 ± 193 m asl). Despite a relatively low coefficient of determination (r2 of 0.47), the envELA reproduces fairly well the time series pattern of the wgmsELA for the period 1948−2005 (Fig. 9a) with a root-mean-square error (RMSE) of 190 m and a median absolute deviation (MAD) of 140 m.
a Comparison between the envELA averaged over the grid cells as defined in Fig. 1 and average regional wgmsELA for 62 glaciers for the period 1948−2017. The last 12 years (2006−2017) of the envELA (dashed line) represent average of all three RCPs envELAs. Thick lines correspond to 11-year centred running mean, thin lines represent yearly variations, and transparent bands correspond to the standard error of Eq. 3 (i.e. 648 mm) for the envELA and sample standard deviation for wgmsELA. (b) Comparison between the rsELA derived from Landsat images and envELA derived from climate projections under three different scenarios (RCP2.6, RCP4.5 and RCP8.5) for the period 2006−2019 over the rsELA extent as defined in Fig. 1
For the time period over which we validated with the rsELA (2006−2019), the mean envELA averaged over the subset area of the western Alps was 3314 ± 252 m asl, 3288 ± 244 m asl and 3315 ± 242 m asl (uncertainties are reported as multi-model mean standard deviations) under RCP2.6, RCP4.5 and RCP8.5, respectively. The rsELA derived from the Landsat time series, averaged over this subset area over the same time period was 3165 ± 44 m asl. The year to year variability shows that the overall temporal pattern of the rsELA for the period 2006−2019 is best reproduced by the envELA derived under RCP2.6 (RMSE of 168 m, MAD of 127 m and r2 of 0.24) (Fig. 9b). Under this scenario, the mean envELA is on average 149 m higher than the rsELA over the 2006−2019 period. A comparison of the rsELA with manually derived ELAs (based on end-of-ablation season SLAs) from 43 glaciers in the French Alps over the period 2003–2010 (Rabatel et al. 2005) yielded an RMSE of 41 m based on year-to-year comparison, which is within the uncertainty calculated for the rsELA; the temporal pattern of the rsELA is reproducing well the manually derived ELAs.
4 Discussion
4.1 Environmental versus effective ELA
The results presented here concern the envELA over an entire mountain range, based purely on climate data, which represents the first study of this kind. In contrast, the effELA that is here represented by both wgmsELA and rsELA, and was used to validate the envELA, takes into account the topoclimatic effects as well. Consequently, the envELA is ~ 75−150 m higher than the regional effELA when averaged over a longer climate period, e.g. 15−30 years. The difference between envELA and wgmsELA might also be related to the fact that the glaciers selected for measuring annual glacier mass balance by the WGMS are those with easier access and thus tend to be located on lower altitudes, consequently having on average lower ELAs. While the envELA is consistently higher than effELA, the time series pattern is in general well reproduced (Fig. 9). However, when comparing year-by-year values, we note some “extreme” values in the envELA with respect to the regional effELA. In the year 2003, the envELA is the highest recorded over the historical period 1901−2005 (Fig. 9a) and overestimates the regional wgmsELA by 668 m. The 2003 envELA is 4.1 standard deviations above the 30-year mean (1988−2017), whereas the regional wgmsELA deviates only by 2.0 standard deviations. This anomaly is related to the 2003 summer heatwave in Europe (Fink et al. 2004), when average summer temperatures were far above the long-term mean and were accompanied by annual precipitation deficits of up to 300 mm (Parry et al. 2007). Since the envELA is computed as a direct function of these two climate variables, it may immediately react to these climate anomalies. This is not the case for effELA, which is a result of the snow accumulation and metamorphism from previous years as well. Winter accumulation in steep alpine terrain can be heavily dominated by avalanches and wind-blown snow supply (Winstral et al. 2002; Dadic et al. 2010; Purdie et al. 2015). As a consequence of both of these drivers the additional accumulation on a glacier can be more than two times the winter precipitation (Kuhn 1995; Lie et al. 2003), which will enhance snow thickness locally and lower the effELA. Small glaciers are particularly susceptible to these two phenomena and their ELA can become progressively decoupled from climate (Dahl and Nesje 1992; Colucci 2016; Scotti and Brardinoni 2018). However, a reliable estimate and small deviation from the effELA can be achieved once the envELA is averaged over a longer climate period.
4.2 Model uncertainties
Model uncertainties are mainly related to the description of cloud and precipitation processes and to possible dependencies on elevation (e.g. Frei and Schär 1998), which are not included here. In addition, the input for the envELA model is annual and not winter precipitation, since the former represents annual accumulation better because precipitation in summer is often solid at high altitudes (Ohmura and Boettcher 2018). However, even at high altitudes a small portion (on average 9% at ELA according to Ohmura and Boettcher (2018)) of the total annual precipitation will fall in liquid form. Even though part of the liquid precipitation might remain in the snow and firn layers as superimposed ice, this amount represents a potential loss that would be unaccounted for as a contribution to the accumulation. Model uncertainties related to precipitation are relevant for both historical and future envELAs, whereas an even bigger source of uncertainty for the latter is probably the ensemble spread (for both temperature and precipitation) within each RCP.
4.3 Link between environmental ELA and historical observations of glacier fluctuations
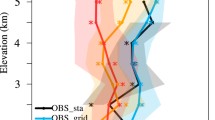
The envELA is a direct, undelayed signal of climate change, whereas glacier length, and to some extent the effELA, lag their equilibrium response to a climate trend. The lag in geometric glacier response has been estimated at 50 ± 28 years for glaciers in the Alps longer than 1 km (Zekollari et al. 2020). Glaciers shorter than 1 km and ice bodies of the smallest size (i.e. ice patches and glacierets with an area of 0.1−0.5 km2), which account for almost 90% of all glaciers in the Alps (RGI Consortium 2017), are likely to respond much faster under changing climate (Kuhn 1995; Huss and Fischer 2016). These ice bodies are often so small that can repeatedly lie entirely in the ablation or accumulation zone on an annual basis. Despite the lag in glacier response, the envELA variation can be correlated, to some extent, with the front variation (e.g. Colucci 2016) and effELA of individual glaciers (Fig. 10), but quantitative comparison of the first two is not presented here. Although the majority of large valley glaciers in the Alps have retreated continuously since around 1865 (Painter et al. 2013), there are three documented advances of smaller mountain glaciers in the 1890s, 1920s and 1970−80 s (Zemp et al. 2008). The two advances in the twentieth century can be recognized from the drop in the envELA around that time. The first drop in the envELA is recorded from the beginning of our studied period until around 1915, when the envELA was the lowest on record in the twentieth century. This is followed by a substantial and constant rise until the 1950s, when the envELA starts to decline again. A similar rising pattern in the effELA until the 1950s can be recognized for the Claridenfirn and Silvretta glaciers (Fig. 10). The second drop takes place for about 10 years and is followed by ~ 25-year period of stable values. While the effELAs of most of the glaciers presented in Fig. 10 follow the envELA curve and display in general stable values for the period between 1960 and 1985, when many Alpine glaciers were relatively close to equilibrium (Zekollari et al. 2020), few others (e.g. Allalin, Hohlaub, Schwarzberg) exhibit a substantial drop in the effELA in the 1970−80 s, when many smaller mountain glaciers slightly readvanced in the 1980s (Zemp et al. 2006, 2008). After that period, a rise in the envELA occurs until the end and beyond the historical period. Over this period, glaciers showed an area reduction of about 22% mainly occurring after 1985 (Zemp et al. 2006). Around 2010, glacier retreat in the Alps started to catch up and outpace the climate warming signal (Zekollari et al. 2020). The main processes leading to glacier decline are disintegration and down-wasting (Paul et al. 2004). Only glaciers of the smallest size show any sort of equilibrium, mostly in areas with high mean annual precipitation (e.g. Colucci and Žebre 2016; Scotti and Brardinoni 2018).
The wgmsELAs of 14 glaciers located in the sectors a between 7° and 9°E longitude and b 9° and 11°E longitude. Lighter lines equate to northern located glaciers and darker lines to southern located glaciers. In red is the envELA averaged over that same sector. All ELAs are presented as 11-year centred running means
4.4 Comparison with modern and future ELA projections from other studies
Results from previous global studies (Huss and Hock 2015; Huss et al. 2017) rely on a method in which geometry changes are parameterised; they suggest that the regionally averaged ELA was at 3147 m asl in 2010 in Central Europe and at ~ 2900−3000 m asl in the period 1980−2000 in the Alps. The same studies projected a rise in ELA by ~ 100−500 m depending on the emission scenario by the end of the twenty-first century. Our model suggests that the envELA in the Alps in 2010 was on average at 3190 m asl and between 3023 and 3291 m asl for the different RCPs, the mean 1980−2000 envELA was 3131 m asl, while the envELA is projected to rise by 91−683 m (1981−2010 mean vs. 2071−2100 mean). According to the regional study by Zemp et al. (2007) the mean ELA of all Alpine river basins over the period 1971−1990 was 2951 m asl, 107 m lower than our envELA for the same period. This difference can be attributed to a different empirical relationship between temperature and precipitation and higher (3 arc sec) spatial resolution used in the ELA distributed modelling in the work of Zemp et al. (2007). Unlike the study of Huss and Hock (2015), 35 glaciers in Pyrenees, Apennines and Balkans are not taken into account in our calculations. These glaciers are located at very low altitudes, where the topoclimatic effect plays a dominant role in their existence (e.g. Hughes 2010; Serrano et al. 2011; Colucci and Žebre 2016; Gachev et al. 2016), contributing to the lower regional ELA calculated by Huss and Hock (2015). In addition, in Huss and Hock (2015), the ELA is considered as a regional effELA, and this generally underestimates the envELA. Dissimilarities might also be attributed to different climatological time series used for the ELA calculations. Huss and Hock (2015) projections are based on 14 individual GCM time series from the Coupled Model Intercomparison project Phase 5 (CMIP5) (Taylor et al. 2012), while ours relay on 12 EURO-CORDEX RCM simulations of higher resolution. However, the trend of our future envELA (Figs. 5 and S3) agrees well with the results of Huss and Hock (2015), who projected a slight decrease in the rate of ELA rise beyond 2050 under RCP2.6 and stabilization under RCP4.5, and a nearly linear rise throughout the projection period under RCP8.5 (Fig. S9 in Huss and Hock (2015)).
4.5 Implications for future glacier state
Most glaciers in the Alps are in disequilibrium with current climate (e.g. Christian et al. 2018) and part of their future mass loss is committed even without further warming (e.g. Bahr et al. 2009; Mernild et al. 2013; Marzeion et al. 2017, 2018; Santin et al. 2019). In 2001, the committed volume loss was 34% of the total ice volume at that time, increasing to 42% in 2010 (Zekollari et al. 2020). A glacier volume loss of about 65–80% under RCP2.6, 80–90% under RCP4.5 and 90–98% under RCP8.5 is projected for the period between the early twenty-first century and 2100 by different models (Marzeion et al. 2012; Radić et al. 2014; Huss and Hock 2015; Zekollari et al. 2019). Here, we assume that a glacier becomes unviable and likely to disappear when the envELA lies above its maximum altitude, meaning on average no accumulation area on a glacier for at least a 30-year period. At the date of the Randolph Glacier Inventory v6.0 (RGI Consortium 2017) (~ 2003), 51% of all glaciers in the Alps were already placed completely below the mean envELA over the period 1974−2003 (3113 m asl). Our projections suggest that under RCP2.6, RCP4.5 and RCP8.5, the envELA will exceed the maximum elevation of 69%, 81% and 92% of the glaciers in the Alps by the end of the twenty-first century (2071−2100 mean), respectively (Fig. 6e). Therefore, glacier retreat and disappearance in the Alps will potentially have a considerable impact on river runoff and hydrology.
5 Conclusions
Using a simple model, we explored 200-years of the environmental ELA evolution over the entire Alps. Our results are in line with available observations and qualitatively in line with previous work employing more sophisticated models that include glacier dynamics. We find that the environmental ELA between the beginning and end of the twentieth century (1901−1930 mean vs. 1971−2000 mean) rose by 114 m mainly due to an increase of 0.8 °C in summer temperature, whereas the annual precipitation stayed largely unchanged. Our results suggest that projected summer warming of 1.6 °C, 2.8 °C and 5.4 °C under the RCP2.6, RCP4.5 and RCP8.5 scenarios, respectively, will likely drive significant environmental ELA rises of about 194 m, 390 m and 786 m by the end of the twenty-first century (2071−2100 mean) for glaciers in the Alps compared with the period 1971−2000. A slight increase (~ 4%) in annual precipitation for all three emission scenarios, derived from a winter increase and a summer decrease, will only have a minor effect on the average environmental ELA over the entire Alps. However, local precipitation anomalies will drive different changes in environmental ELA over different regions of the Alps, suggesting in general a faster environmental ELA rise in the west and south with respect to the east and north. These future projected levels of the environmental ELA will result in the unviability and possible subsequent disappearance of between 69 and 92% of all glaciers in the Alps by the end of the twenty-first century. This will have substantial implications for water resources in the region, particularly during the summer season.
This is the first study to investigate the environmental ELA of the entire Alps over such a long period and provides a strong basis to better understand regional differences in glacier response to a changing climate. Our modelling approach needs a minimum set of input data and can thus be easily applied to larger areas and longer time periods. This approach can be particularly useful in Quaternary science for quick and robust palaeo-ELA reconstructions. However, there is still potential to improve the simulations, for example by incorporating solar radiation as the third variable in the model and increasing the spatial resolution of the input data.
Availability of data and material
The data that support the findings of this study are included in this published article (and its supplementary information files). The modelled past (1901–2005) and future (2006–2100 multi-model mean for RCP2.6, RCP4.5 and RCP8.5) environmental ELA evolution for every glacierised grid cell is provided in the Supplementary material as netCDF files (.nc).
References
Adam JC, Lettenmaier DP (2003) Adjustment of global gridded precipitation for systematic bias. J Geophys Res Atmos 108:4257. https://doi.org/10.1029/2002JD002499
Addor N, Rössler O, Köplin N et al (2014) Robust changes and sources of uncertainty in the projected hydrological regimes of Swiss catchments. Water Resour Res 50:7541–7562. https://doi.org/10.1002/2014WR015549
Ahlmann HW (1924) Le niveau de glaciation comme fonction de l’accumulation d’humidité sous forme solide. Méthode Pour le Calcul de L’humidité Condensée Dans la Haute Montagne et Pour L’étude de la Fréquence des Glaciers. Geogr Ann 6:223–272. https://doi.org/10.2307/519625
Anderson RS, Anderson LS, Armstrong WH et al (2018) Glaciation of alpine valleys: the glacier—debris-covered glacier—rock glacier continuum. Geomorphology 311:127–142. https://doi.org/10.1016/j.geomorph.2018.03.015
Auer I, Böhm R (1994) Combined temperature-precipitation variations in Austria during the instrumental period. Theor Appl Climatol 49:161–174. https://doi.org/10.1007/BF00865531
Auer I, Böhm R, Jurkovic A et al (2007) HISTALP—historical instrumental climatological surface time series of the Greater Alpine Region. Int J Climatol 27:17–46. https://doi.org/10.1002/joc.1377
Bahr DB, Dyurgerov M, Meier MF (2009) Sea-level rise from glaciers and ice caps: A lower bound. Geophys Res Lett. https://doi.org/10.1029/2008GL036309
Bard A, Renard B, Lang M et al (2015) Trends in the hydrologic regime of Alpine rivers. J Hydrol 529:1823–1837. https://doi.org/10.1016/j.jhydrol.2015.07.052
Bocchiola D (2014) Long term (1921–2011) hydrological regime of Alpine catchments in Northern Italy. Adv Water Resour 70:51–64. https://doi.org/10.1016/j.advwatres.2014.04.017
Bosshard T, Kotlarski S, Zappa M, Schär C (2013) Hydrological climate-impact projections for the Rhine River: GCM–RCM uncertainty and separate temperature and precipitation effects. J Hydrometeorol 15:697–713. https://doi.org/10.1175/JHM-D-12-098.1
Braithwaite RJ (1984) Can the mass balance of a glacier be estimated from its equilibrium-line altitude? J Glaciol 30:364–368. https://doi.org/10.3189/S0022143000006237
Braithwaite RJ, Raper SCB (2009) Estimating equilibrium-line altitude (ELA) from glacier inventory data. Ann Glaciol 50:127–132. https://doi.org/10.3189/172756410790595930
Brunetti M, Maugeri M, Nanni T et al (2006) Precipitation variability and changes in the greater Alpine region over the 1800–2003 period. J Geophys Res Atmos. https://doi.org/10.1029/2005JD006674
Carrivick JL, Tweed FS (2016) A global assessment of the societal impacts of glacier outburst floods. Glob Planet Change 144:1–16. https://doi.org/10.1016/j.gloplacha.2016.07.001
CDO (2020) CDO. https://code.zmaw.de/projects/cdo
Ceppi P, Scherrer SC, Fischer AM, Appenzeller C (2012) Revisiting Swiss temperature trends 1959–2008. Int J Climatol 32:203–213. https://doi.org/10.1002/joc.2260
Chen J, Ohmura A (1990a) Estimation of Alpine Glacier Water Resources and their Change Since the 1870s. IAHS Publ (Hydrology Mt Reg I-Hydrological Meas Water Cycle) 193:127–135
Chen J, Ohmura A (1990b) On the influence of Alpine glacieis on runoff. IAHS Publ (Hydrology Mt Reg I-Hydrological Meas Water Cycle) 193:117–125
Chimani B, Matulla C, Böhm R, Hofstätter M (2013) A new high resolution absolute temperature grid for the Greater Alpine Region back to 1780. Int J Climatol 33:2129–2141. https://doi.org/10.1002/joc.3574
Christian JE, Koutink M, Roe G (2018) Committed retreat: controls on glacier disequilibrium in a warming climate. J Glaciol 64:675–688. https://doi.org/10.1017/jog.2018.57
Cogley JG, Hock R, Rasmussen LA, et al (2011) Glossary of Glacier Mass Balance and Related Terms. IHP-VII Technical Documents in Hydrology No. 86. IACS Contribution No. 2.
Collins D (1987) Climatic fluctuations and runoff from glacierised Alpine basins. In: The Influence of Climate Change and Climatic Variability on the Hydrologie Regime and Water Resource, Proceedings of the Vancouver Symposium, IAHS Publ. no. 168. pp 77–89
Colucci RR (2016) Geomorphic influence on small glacier response to post-Little Ice Age climate warming: Julian Alps, Europe. Earth Surf Process Landforms 41:1227–1240. https://doi.org/10.1002/esp.3908
Colucci RR, Žebre M (2016) Late Holocene evolution of glaciers in the southeastern Alps. J Maps 12:289–299. https://doi.org/10.1080/17445647.2016.1203216
Dadic R, Mott R, Lehning M, Burlando P (2010) Wind influence on snow depth distribution and accumulation over glaciers. J Geophys Res Earth Surf. https://doi.org/10.1029/2009JF001261
Dahl SO, Nesje A (1992) Paleoclimatic implications based on equilibrium-line altitude depressions of reconstructed Younger Dryas and Holocene cirque glaciers in inner Nordfjord, western Norway. Palaeogeogr Palaeoclimatol Palaeoecol 94:87–97. https://doi.org/10.1016/0031-0182(92)90114-K
EU-DEM v1.1 (2017) Copernicus Land Monitoring Service - EU-DEM. European Environment Agency (EEA)
Farinotti D, Round V, Huss M et al (2019) Large hydropower and water-storage potential in future glacier-free basins. Nature 575:341–344. https://doi.org/10.1038/s41586-019-1740-z
Fink AH, Brücher T, Krüger A et al (2004) The 2003 European summer heatwaves and drought–synoptic diagnosis and impacts. Weather 59:209–216. https://doi.org/10.1256/wea.73.04
Frei C, Schär C (1998) A precipitation climatology of the Alps from high-resolution rain-gauge observations. Int J Climatol 18:873–900. https://doi.org/10.1002/(SICI)1097-0088(19980630)18:8%3c873::AID-JOC255%3e3.0.CO;2-9
Gachev E, Stoyanov K, Gikov A (2016) Small glaciers on the Balkan Peninsula: State and changes in the last several years. Quat Int 415:33–54. https://doi.org/10.1016/J.QUAINT.2015.10.042
Giorgi F, Torma C, Coppola E et al (2016) Enhanced summer convective rainfall at Alpine high elevations in response to climate warming. Nat Geosci 9:584–589. https://doi.org/10.1038/ngeo2761
Haeberli W, Hoelzle M (1995) Application of inventory data for estimating characteristics of and regional climate-change effects on mountain glaciers: a pilot study with the European Alps. Ann Glaciol 21:206–212
Haeberli W, Whiteman C (2015) Snow and ice-related hazards, risks, and disasters. Elsevier, Amsterdam
Hiebl J, Auer I, Böhm R et al (2009) A high-resolution 19611990 monthly temperature climatology for the greater Alpine region. Meteorol Zeitschrift 18:507–530. https://doi.org/10.1127/0941-2948/2009/0403
Hodson AJ (2014) Understanding the dynamics of black carbon and associated contaminants in glacial systems. WIREs Water 1:141–149. https://doi.org/10.1002/wat2.1016
Hughes PD (2010) Little ice age glaciers in the balkans: low altitude glaciation enabled by cooler temperatures and local topoclimatic controls. Earth Surf Process Landforms 35:229–241. https://doi.org/10.1002/esp.1916
Huss M, Fischer M (2016) Sensitivity of very small glaciers in the Swiss Alps to future climate change. Front Earth Sci 4:1–17. https://doi.org/10.3389/feart.2016.00034
Huss M, Hock R (2015) A new model for global glacier change and sea-level rise. Front Earth Sci 3:54. https://doi.org/10.3389/feart.2015.00054
Huss M, Hock R (2018) Global-scale hydrological response to future glacier mass loss. Nat Clim Chang 8:135–140. https://doi.org/10.1038/s41558-017-0049-x
Huss M, Bookhagen B, Huggel C et al (2017) Toward mountains without permanent snow and ice Earth ’ s Future. Earrth’s Futur 5:418–435. https://doi.org/10.1002/eft2.207
IPCC (2014) Climate change 2013—the physical science basis: working group i contribution to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
IPCC (2018) Summary for Policymakers. In: Masson-Delmotte V, Zhai P, Pörtner H, et al. (eds) Global Warming of 1.5°C. An IPCC Special Report on the impacts of global warming of 1.5°C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change,. World Meteorological Organization, Geneva, Switzerland, p 32
Isotta FA, Frei C, Weilguni V et al (2014) The climate of daily precipitation in the Alps: development and analysis of a high-resolution grid dataset from pan-Alpine rain-gauge data. Int J Climatol 34:1657–1675. https://doi.org/10.1002/joc.3794
Isotta F, Frei C, Chimani B, Hiebl J (2019) LAPrec—user guide and technical report. In: A gridded precipitation dataset for the Alpine region that extends back into the 19th century.
Jacob D, Petersen J, Eggert B et al (2014) EURO-CORDEX: new high-resolution climate change projections for European impact research. Reg Environ Chang 14:563–578. https://doi.org/10.1007/s10113-013-0499-2
Kuhn M (1995) The mass balance of very small glaciers. Zeitschrift für Gletscherkd und Glazialgeol 31:171–179
Legates DR, Willmott CJ (1990) Mean seasonal and spatial variability in gauge-corrected, global precipitation. Int J Climatol 10:111–127. https://doi.org/10.1002/joc.3370100202
Lie Ø, Dahl SO, Nesje A (2003) A theoretical approach to glacier equilibrium-line altitudes using meteorological data and glacier mass-balance records from southern Norway. The Holocene 13:365–372. https://doi.org/10.1191/0959683603hl629rp
Marzeion B, Jarosch AH, Hofer M (2012) Past and future sea-level change from the surface mass balance of glaciers. Cryosph 6:1295–1322. https://doi.org/10.5194/tc-6-1295-2012
Marzeion B, Champollion N, Haeberli W et al (2017) Observation-based estimates of global glacier mass change and its contribution to sea-level change. Surv Geophys 38:105–130. https://doi.org/10.1007/s10712-016-9394-y
Marzeion B, Kaser G, Maussion F, Champollion N (2018) Limited influence of climate change mitigation on short-term glacier mass loss. Nat Clim Chang 8:305–308. https://doi.org/10.1038/s41558-018-0093-1
McGrath D, Sass L, O’Neel S et al (2017) Hypsometric control on glacier mass balance sensitivity in Alaska and northwest Canada. Earth’s Futur 5:324–336. https://doi.org/10.1002/2016EF000479
Mernild SH, Lipscomb WH, Bahr DB et al (2013) Global glacier changes: a revised assessment of committed mass losses and sampling uncertainties. Cryosph 7:1565–1577. https://doi.org/10.5194/tc-7-1565-2013
Ohmura A, Boettcher M (2018) Climate on the equilibrium line altitudes of glaciers: theoretical background behind Ahlmann’s P/T diagram. J Glaciol 64:489–505. https://doi.org/10.1017/jog.2018.41
Painter TH, Flanner MG, Kaser G et al (2013) End of the Little Ice Age in the Alps forced by industrial black carbon. Proc Natl Acad Sci 110:15216–15221. https://doi.org/10.1073/pnas.1302570110
Parry ML, Canziani OF, Palutikof JP et al (2007) Cross-chapter case study climate change 2007: impacts adaptation and vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, pp 843–868
Paul F, Kääb A, Maisch M et al (2004) Rapid disintegration of Alpine glaciers observed with satellite data. Geophys Res Lett 31:L21402. https://doi.org/10.1029/2004GL020816
Paul F, Rastner P, Azzoni RS et al (2020) Glacier shrinkage in the Alps continues unabated as revealed by a new glacier inventory from Sentinel-2. Earth Syst Sci Data 12:1805–1821. https://doi.org/10.5194/essd-12-1805-2020
Purdie H, Rack W, Anderson B et al (2015) The impact of extreme summer melt on net accumulation of an avalanche fed glacier, as determined by ground-penetrating radar. Geogr Ann Ser A, Phys Geogr 97:779–791. https://doi.org/10.1111/geoa.12117
Rabatel A, Dedieu J-P, Vincent C (2005) Using remote-sensing data to determine equilibrium-line altitude and mass-balance time series: validation on three French glaciers, 1994–2002. J Glaciol 51:539–546. https://doi.org/10.3189/172756505781829106
Rabatel A, Letréguilly A, Dedieu J-P, Eckert N (2013) Changes in glacier equilibrium-line altitude in the western Alps from 1984 to 2010: evaluation by remote sensing and modeling of the morpho-topographic and climate controls. Cryosph 7:1455–1471. https://doi.org/10.5194/tc-7-1455-2013
Racoviteanu AE, Rittger K, Armstrong R (2019) An automated approach for estimating snowline altitudes in the karakoram and eastern himalaya from remote sensing. Front Earth Sci 7:220. https://doi.org/10.3389/feart.2019.00220
Radić V, Bliss A, Beedlow AC et al (2014) Regional and global projections of twenty-first century glacier mass changes in response to climate scenarios from global climate models. Clim Dyn 42:37–58. https://doi.org/10.1007/s00382-013-1719-7
RGI Consortium (2017) Randolph glacier inventory—a dataset of global glacier outlines: Version 6.0: Technical Report, Global Land Ice Measurements from Space
Rolland C (2003) Spatial and seasonal variations of air temperature lapse Rates in Alpine Regions. J Clim 16:1032–1046. https://doi.org/10.1175/1520-0442(2003)016%3c1032:SASVOA%3e2.0.CO;2
Rubel F, Brugger K, Haslinger K, Auer I (2017) The climate of the European Alps: Shift of very high resolution Köppen–Geiger climate zones 1800–2100. Meteorol Zeitschrift 26:115–125. https://doi.org/10.1127/metz/2016/0816
Santin I, Colucci RR, Žebre M et al (2019) Recent evolution of Marmolada glacier (Dolomites, Italy) by means of ground and airborne GPR surveys. Remote Sens Environ 235:111442. https://doi.org/10.1016/j.rse.2019.111442
Schwarb M, Frei C, Schär C, Daly C (2000) Mean annual precipitation throughout the European Alps 1971–1990. In: Hydrological Atlas of Switzerland, Plates 2.6. Federal Office for Water and Geology, Bern
Scotti R, Brardinoni F (2018) Evaluating millennial to contemporary time scales of glacier change in Val Viola, Central Italian Alps. Geogr Ann Ser A Phys Geogr 100:319–339. https://doi.org/10.1080/04353676.2018.1491312
Serrano E, González-Trueba JJ, Sanjosé JJ, Del Río LM (2011) Ice patch origin, evolution and dynamics in a temperate high mountain environment: the Jou Negro, Picos de Europa (NW Spain). Geogr Ann Ser A Phys Geogr 93:57–70. https://doi.org/10.1111/j.1468-0459.2011.00006.x
Sevruk B (1985) Systematischer Niederschlagsmessfehler in der Schweiz. In: Der Niederschlag in der Schweiz. Beiträge zur Geol der Schweiz - Hydrol 31:65–75
Spandre P, François H, Verfaillie D et al (2019) Climate controls on snow reliability in French Alps ski resorts. Sci Rep 9:8043. https://doi.org/10.1038/s41598-019-44068-8
Steiger R, Scott D, Abegg B et al (2019) A critical review of climate change risk for ski tourism. Curr Issues Tour 22:1343–1379. https://doi.org/10.1080/13683500.2017.1410110
Taylor K, Ronald S, Meehl G (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Torma C, Giorgi F, Coppola E (2015) Added value of regional climate modeling over areas characterized by complex terrain—precipitation over the Alps. J Geophys Res Atmos 120:3957–3972. https://doi.org/10.1002/2014JD022781
van Vuuren DP, Edmonds J, Kainuma M et al (2011) The representative concentration pathways: an overview. Clim Change 109:5. https://doi.org/10.1007/s10584-011-0148-z
WGMS (2019) Fluctuations of glaciers database. World Glacier Monitoring Service, Zurich
Winstral A, Elder K, Davis R (2002) Spatial snow modeling of wind-redistributed snow using terrain-based parameters. J Hydrometeorol 3:524–538. https://doi.org/10.1175/1525-7541(2002)003%3c0524:SSMOWR%3e2.0.CO;2
Zekollari H, Huss M, Farinotti D (2019) Modelling the future evolution of glaciers in the European Alps under the EURO-CORDEX RCM ensemble. Cryosph 13:1125–1146. https://doi.org/10.5194/tc-13-1125-2019
Zekollari H, Huss M, Farinotti D (2020) On the Imbalance and Response Time of Glaciers in the European Alps. Geophys Res Lett 47:e2019GL085578. https://doi.org/10.1029/2019GL085578
Zemp M, Haeberli W, Hoelzle M, Paul F (2006) Alpine glaciers to disappear within decades? Geophys Res Lett. https://doi.org/10.1029/2006GL026319
Zemp M, Hoelzle M, Haeberli W (2007) Distributed modelling of the regional climatic equilibrium line altitude of glaciers in the European Alps. Glob Planet Change 56:83–100. https://doi.org/10.1016/j.gloplacha.2006.07.002
Zemp M, Paul F, Hoelzle M, Haeberli W (2008) Glacier fluctuations in the European Alps 1850–2000: an overview and spatiotemporal analysis of available data. In: Orlove B, Wiegandt E, Luckman BH (eds) The darkening peaks: Glacial retreat in scientific and social context. University of California Press, pp 152–167
Funding
This work has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie Grant Agreements Nos. 793403 and 663830.
Author information
Authors and Affiliations
Contributions
RRC and MŽ conceived the idea and led this work. MŽ performed the computations. AER processed the Landsat images and computed the annual snowlines. RRC, FG and NFG supervised the findings of this work. MŽ designed the figures and wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Žebre, M., Colucci, R.R., Giorgi, F. et al. 200 years of equilibrium-line altitude variability across the European Alps (1901−2100). Clim Dyn 56, 1183–1201 (2021). https://doi.org/10.1007/s00382-020-05525-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05525-7