Abstract
Sea levels of different atmosphere–ocean general circulation models (AOGCMs) respond to climate change forcing in different ways, representing a crucial uncertainty in climate change research. We isolate the role of the ocean dynamics in setting the spatial pattern of dynamic sea-level (ζ) change by forcing several AOGCMs with prescribed identical heat, momentum (wind) and freshwater flux perturbations. This method produces a ζ projection spread comparable in magnitude to the spread that results from greenhouse gas forcing, indicating that the differences in ocean model formulation are the cause, rather than diversity in surface flux change. The heat flux change drives most of the global pattern of ζ change, while the momentum and water flux changes cause locally confined features. North Atlantic heat uptake causes large temperature and salinity driven density changes, altering local ocean transport and ζ. The spread between AOGCMs here is caused largely by differences in their regional transport adjustment, which redistributes heat that was already in the ocean prior to perturbation. The geographic details of the ζ change in the North Atlantic are diverse across models, but the underlying dynamic change is similar. In contrast, the heat absorbed by the Southern Ocean does not strongly alter the vertically coherent circulation. The Arctic ζ change is dissimilar across models, owing to differences in passive heat uptake and circulation change. Only the Arctic is strongly affected by nonlinear interactions between the three air-sea flux changes, and these are model specific.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sea-level rise presently is and will continue to be an important consequence of anthropogenically forced climate change. Global mean thermosteric sea-level rise, due to thermal expansion of a warming ocean, accounts for 30–55% of the global mean sea-level rise (GMSLR) projected for the years 2081–2100 (Church et al. 2013). The remainder results mostly from ocean mass gain due to melting land ice (glaciers and ice sheets). Regional sea-level changes are much more complicated, involving ocean and climate dynamics as well as solid-Earth processes, typically not included in coupled climate models. The latter can make up 50% or more of regional sea-level change pattern by the end of the 21st Century (Slangen et al. 2012; Stammer et al. 2013).
As part of the Coupled Model Intercomparison Project (CMIP), atmosphere–ocean general circulation models (AOGCMs) simulate anthropogenic sea-level change related to changes in climate dynamics by starting from a near-equilibrium (i.e. well spun-up) preindustrial control state (piControl) and running forward with time-varying forcing agents (greenhouse gases, anthropogenic aerosol, etc.). In these models, ocean dynamic sea level, ζ, is defined at each location and time as
where η is the local sea-surface height relative to a surface on which the geopotential has a uniform constant value, and η̅ is its global mean over the ocean area. η is termed ‘sterodynamic sea level’ according to recent terminology conventions (Gregory et al. 2019). By definition, the global mean of ζ is zero, but locally it is not zero due to ocean circulation and horizontal density gradients. Using CMIP terminology, ζ is the variable ‘zos’ (Griffies et al. 2016). The sterodynamic sea-level change (Δη) that an individual location experiences may differ substantially from the global mean thermosteric sea-level rise (GMSLR, \(\stackrel{-}{\Delta \eta }\)), because of changes in ocean circulation and density. This present work focuses on the spatial pattern in ocean dynamic sea-level change
projected to occur over the coming century due to anthropogenic greenhouse gas forced climate change. Accordingly, Δζ is calculated from CMIP output as the difference between the ‘zos’ fields in a forcing experiment relative to a control state (see Sects. 2.2 and 2.3 for details). In results from AOGCMs from CMIP’s fifth phase (CMIP5), the spatial standard deviation of the multi-model mean Δζ projected under scenario RCP4.5 by 2081–2100 is 0.06 m, which is 30% of the multi-model mean GMSLR due to thermal expansion (Gregory et al. 2016). Thus, in some locations, Δη is more than twice its global mean, because of ocean dynamic sea-level change. Moreover, different AOGCMs predict diverse spatial patterns and magnitudes of sea-level change (Slangen et al. 2014). The global mean of the inter-model standard deviation of Δζ in the same projections is also about 0.06 m; in other words, the systematic uncertainty in predicting the pattern of dynamic sea-level change is of first order, being about the same magnitude as the pattern itself (see also Fig. 3). It is this spread among AOGCMs that we seek to investigate: one of the largest uncertainties affecting regional impacts of anthropogenic sea-level and climate change this century and beyond.
Part of the spread among AOGCMs comes from their different representations of forcing agents, especially anthropogenic aerosol (Melet and Meyssignac 2015). The idealized scenario of increasing the concentration of CO2 by 1% per year, called ‘1pctCO2’ is simpler to interpret than more complex experiments with differing time profiles of numerous types of climate forcing (Eyring et al. 2016). After seven decades, 1pctCO2 reaches a similar magnitude of radiative forcing to RCP 4.5 by the end of the twenty-first century.
Developing a more complete understanding of the climate response to idealized 1pctCO2 forcing provides insight into how we expect the climate to respond to moderate greenhouse gas and aerosol emissions by the end of this century. However, even when AOGCMs are forced with this simple, idealized setup, they produce a range of climate response, primarily because of their differing climate sensitivities (i.e. the degree of surface warming that results per radioactive forcing). Differences in the representation of cloud feedback mechanisms in atmosphere models accounts for the greatest uncertainty in climate sensitivity (Ceppi et al. 2017). The control climate, which is different for each model, also contributes to the spread (Bouttes and Gregory 2014), e.g. via the strength of the ice coverage and water vapour feedbacks (Hu et al. 2017), and sea-surface temperature (SST) biases (He and Soden 2016). These and other factors affect the spatial patterns and magnitudes of the air-sea fluxes of heat, freshwater, and momentum, which are the drivers of Δζ. Unpacking the influence of oceanic processes from atmospheric processes is therefore difficult in experiments like 1pctCO2.
Previous work has investigated how the diversity in the changes of air-sea fluxes of heat, freshwater and momentum contribute to the spread in projections of sea-level change. A typical approach is to force a single model with ensembles of boundary conditions like SST (Huber and Zanna 2017) or air-sea flux change (Bouttes and Gregory 2014) to mimic the spread of fully coupled simulations. These studies find that forcing individual models with a variety of boundary conditions produces a large spread of ocean responses, in terms of sea-level change (Bouttes and Gregory 2014), ocean heat uptake (OHU) and circulation change (Huber and Zanna 2017). While these studies demonstrate that models are sensitive to surface fluxes, the uncertainty that results from the diversity of ocean model structure in coupled models has not yet been assessed.
The change of the Atlantic Meridional Overturning Circulation (AMOC) strength in response to climate change is model specific, and is believed to be a key factor setting the pattern of North Atlantic sea-level change (Yin et al. 2009; Hawkes 2013; Bouttes et al. 2014). Globally, ocean heat uptake has been related to the degree of AMOC weakening (Xie and Vallis 2012; Rugenstein et al. 2013; Kostov et al. 2014). However, more recently, the correlation between OHU and AMOC strength was shown to arise because both are affected by mesoscale eddy transfer (Saenko et al. 2018), where OHU is more intense and deep reaching with decreasing mesoscale eddy transfer. The ocean components of most CMIP5 and CMIP6 models are not able to resolve mesoscale eddies, so their effects are parameterized in different ways across models. It is therefore plausible that the differing representations of mesoscale and other unresolved phenomena are likely to contribute to the spread of sea-level projections among AOGCMs, through their influence on seawater properties (e.g. temperature, salinity and density) and ocean transports of heat and salt.
The Flux-Anomaly-Forced Model Intercomparison Project (FAFMIP) outlines a protocol for forcing different AOGCMs with perturbations to their air-sea fluxes—heat, freshwater, and momentum—to systematically explore the oceanic response to CO2-forced climate change (Gregory et al. 2016). The key goal of FAFMIP is to replicate the oceanic response to 1pctCO2 forcing, while excluding the model spread due to changes in air-sea fluxes. Initial FAFMIP results have highlighted the importance of the heat flux perturbation in setting much of the global pattern of Δζ, and that both the wind stress and heat flux perturbations set the Southern Ocean dipole (Gregory et al. 2016).
Building on previous findings, we present in this study: (1) new sea-level results based on AOGCM simulations forced with simultaneous rather than separate flux perturbations, (2) an intercomparison of the roles of temperature and salinity-driven density changes, and (3) further examination of the decomposition of ocean heat content (OHC) changes due to changes in temperature and transport. Our study also includes new CMIP6 simulations and paves the way for possible forthcoming FAFMIP analyses.
This paper is structured as follows: an explanation of the configuration of model experiments and analysis methods is given in Sect. 2. In Sect. 3.1, the sea-level responses to FAFMIP and 1pctCO2 forcing are compared, followed by a comparison of the 1pctCO2 sea-level response from CMIP5 and CMIP6 in Sect. 3.2. The response of AOGCMs to individually applied surface flux perturbations (heat, freshwater and momentum) is assessed in Sect. 3.3, while nonlinear interactions between these flux perturbations are described in Sect. 3.4. A decomposition of ocean heat uptake based on a subset of the AOGCMs is presented in Sect. 3.5. Results are discussed in Sect. 4 and the conclusions are laid out in Sect. 5. An appendix with further notes on the decomposition of ocean heat uptake is included in "Appendix".
2 Methods
2.1 Perturbation of air-sea fluxes
The FAFMIP protocol presents a method that mimics the effect of 1pctCO2 forcing on the ocean but applies identical perturbations to each model (Gregory et al. 2016). The perturbations are the multi model mean changes in the air-sea fluxes of heat, freshwater, and momentum from 1pctCO2 simulations averaged over the 61st-80th years of forcing relative to the piControl state. This period covers the time where CO2 concentration reaches double its preindustrial values (at year 70). The suite of CMIP5 AOGCMs available at the time to derive the required surface flux perturbations for the FAFMIP protocol comprises 13 members; CNRM-CM5, CSIRO-Mk3-6-0, CanESM2, GFDL-ESM2G, HadGEM2-ES, MIROC-ESM, MIROC5, MPI-ESM-LR, MPI-ESM-MR, MPI-ESM-P, MRI-CGCM3, NorESM1-ME, and NorESM1-M. It was decided that all perturbations should be derived from a common set of models to allow for consistent comparison of model-mean sea-level change and the associated spread (Gregory et al. 2016). Further details about FAFMIP and the protocol, including the perturbation files can be found at https://www.fafmip.org.
Time-dependent CO2 and other forcing causes a varying magnitude of sea-level change, while the spatial pattern is relatively time-invariant (Hawkes 2013; Perrette et al. 2013; Slangen et al. 2014; Bilbao et al. 2015). This phenomenon of ‘pattern scaling’ means that time-dependent forcing is not necessary for our investigation of the spatial structure. Therefore, in the interest of simplicity the FAFMIP flux perturbations are applied as a constant forcing for the full 70 years of each experiment, with no time-variation except for the annual cycle.
2.2 Experiments
FAFMIP perturbations to the fluxes of heat, water and momentum (Fig. 1) were applied in five different experiments, as listed below. All perturbations were applied at the air-sea interface in direct contact with seawater surface, such that sea ice is not directly affected. However, there will be indirect effects on sea ice due to the redistribution of heat and freshwater in response to all the perturbations. The heat and freshwater fluxes are defined positive downward into the ocean, and the momentum flux perturbations are positive eastward and northward. FAFMIP experiments were run by nine modelling groups using 13 AOGCMs (Table 1).
Annual means of downward flux perturbations applied in FAFMIP experiments at the ocean surface for heat, water, eastward momentum, and northward momentum, a–d respectively. Perturbations are the multi model mean surface flux anomalies from simulations forced with 1% per year rising CO2 concentrations averaged over years 61–80
Experiment 1 In FAF-passiveheat, the heat flux perturbation (Fig. 1a) is applied to a ‘passive added temperature’ tracer, Ta. FAF-passiveheat is a control (similar to piControl), since its climate is not perturbed and experiences only internal variability while the extra tracer allows for the passive uptake of the heat perturbation to be quantified. Ta is initially set to 0 everywhere and the forcing, F, is applied at the surface like a heat flux (none of it penetrates below the surface, like shortwave radiation does). It is transported within the ocean via the same schemes that each model uses to advect and diffuse temperature, T, without affecting the evolution of the ocean state at all because it is passive. Since the perturbation has positive and negative values locally, Ta can be positive and negative. While the input of the passive added heat tracer via the prescribed surface heat flux is identical across models, the geographic patterns of its distribution in the ocean will differ across models, depending on each model’s preindustrial circulation and parameterized tracer transports. The FAF-passiveheat experiment makes it possible to consistently compare the unperturbed tracer uptake across models, which is necessary for a decomposition of the heat uptake in each model when forced with transient climate change (Sect. 2.4).
Experiment 2 In FAF-heat, the heat flux perturbation F is applied as a forcing to ocean temperature, T. (Note that we call it a “forcing” because it is an external perturbation to the climate system, but it is not a radiative forcing, such as is given by CO2 increase.) The perturbation is strongly positive in the North Atlantic and in the Southern Ocean (Fig. 1a). Relative to annual mean climatological heat fluxes, the perturbation reduces the North Atlantic (north of the equator) basin-mean upward heat flux by about 50% (the precise amount varies between models). In the Southern Ocean south of 45° S, the perturbation is roughly 160% of the climatological flux and of opposite sign, switching the basin into a region of net ocean heat uptake. To avoid the atmosphere’s tendency to eliminate the SST anomaly through an opposing air-sea flux, a further passive tracer is used, called the redistributed temperature tracer, Tr which is initialized to equal T at the start and is transported within the ocean in the just the same ways as T but is not forced by the surface heat flux perturbation. The atmosphere is decoupled from the SST of T, and instead sees the surface field of Tr (Fig. 2). The result is that the perturbation gets added to the ocean, where it accumulates and modifies seawater density, and changes ocean transport, but the atmosphere does not absorb any of the added heat and is only modified by changes to surface Tr that arise indirectly through the changing ocean circulation. In FAF-heat, fields of Tr and T quickly diverge from each other by a value approximately equal to Ta. Sub-grid scale schemes (e.g. boundary layer schemes; neutral diffusion; parameterized eddy advection) have nonlinear effects on the transport of temperature that we ignore, meaning that T is assumed equal to Tr + Ta (Gregory et al. 2016). In FAF-passiveheat, Tr (if introduced and treated in the same way) would be identical to T, because no forcing is applied to T. By comparing the distribution of Ta in FAF-heat (whose circulation changes) against FAF-passiveheat (whose circulation follows the steady state) it is possible to identify regions where the changing circulation stores added heat ‘actively’ (i.e. unlike a passive tracer).
Treatment of surface heat flux perturbation in FAF-heat and FAF-all, redrawn from (Gregory et al. 2016). Q is the net surface heat from the atmosphere and sea ice into the ocean and F is the flux perturbation. The SST used to calculate the surface heat flux to atmosphere and sea ice is coupled to a redistributed temperature tracer Tr, which does not feel F
Experiment 3 The water flux perturbation is derived from the CMIP5 ‘wfo’ diagnostic, which is the sum of precipitation, evaporation, river inflow and water fluxes between floating ice and seawater. There is no perturbation applied over land. The freshwater flux perturbation applied in FAF-water has a very small global annual average, and mainly redistributes freshwater (Fig. 1b). The perturbation is broadly consistent with the “wet gets wetter, dry gets drier” pattern (Held and Soden 2006), reinforcing evaporation in the mid latitudes (by about 10%), and adding freshwater elsewhere (also about 10% reinforcement): namely the equatorial Pacific, the Southern Ocean, the Arctic Ocean, and the high latitude North Pacific and North Atlantic.
Experiment 4 The surface momentum perturbation applied in FAF-stress is mainly characterized by a reinforcement and southward shift of the Southern Ocean westerlies (Fig. 1c). Between 45° and 65° S, the perturbation strengthens the westerlies by about 10%. The perturbation has smaller effects on the zonal and meridional downward momentum fluxes in the mid latitudes (Fig. 1c, d). The perturbation is added to the momentum balance of the ocean surface, such that it does not directly affect sub-grid scale parameterization schemes (e.g. planetary boundary closures) that depend on wind stress or ice stress.
Experiment 5 All three perturbations are applied together in the FAF-all experiment. This experiment serves two purposes: to assess how well the perturbations mimic the effect of CO2 forcing as in 1pctCO2, and to determine the extent to which the perturbations counteract or amplify each other’s effects on sea level when applied simultaneously. If the flux perturbations interact with each other when applied together in FAF-all, then the FAF-all sea-level response will not equal the sum of the sea-level responses to the individual perturbations. This aspect of the FAFMIP design was not tested by Gregory et al. (2016), since no results for FAF-all were available at the time from the five pre-CMIP6 models analysed.
2.3 Calculation of change due to perturbations
∆ζ can be derived from CMIP output as the difference in the ‘zos’ field from a forced experiment relative to the ‘zos’ field in an unforced control state. Although ‘zos’ is usually defined to have a zero global area mean (Griffies et al. 2016), for some models it was necessary to subtract the nonzero area mean. This study is focused on the regional sea-level changes expected by the end of the twenty-first century. Because exponentially increasing CO2 concentration, such as in 1pctCO2, gives a radiative forcing which increases linearly in time, and the FAFMIP perturbations correspond to 1pctCO2 forcing at year 70, 70 years of time invariant FAFMIP forcing integrates to approximately the same as a 100-year time integral of 1pctCO2 forcing. ∆ζ is therefore calculated from the final decade (years 61–70) of the perturbation experiments (FAF-stress, -water etc.), and from years 91–100 of 1pctCO2 experiments for comparison. This approach means the amplitudes of ∆ζ will be approximately similar, but in any case, the spatial pattern of ∆ζ is the object of interest in this study.
Decadal fields of ζ are calculated to reduce (but cannot not totally eliminate) the effect of unforced interannual variability, reflecting our interest in understanding the climate response to forcing by the end of this century. A change (i.e. ∆ζ) is deemed significant for our purposes if its magnitude is more than twice the decadal standard deviation (a 95% interval for a normal distribution) of variability determined at that location in the relevant control simulation (i.e. piControl for 1pctCO2 and FAF-passiveheat for all other experiments). Decadal mean fields of ζ are calculated for each decade of control simulation, and the threshold for significance is taken to be double the standard deviation across the decadal averages. Insignificant ∆ζ features (within ± 2 standard deviations) are set to 0 for plotting purposes.
The steric sea-level responses to each perturbation can be decomposed into the thermosteric (∆ζT) and halosteric (∆ζS) components:
The thermosteric sea-level change (resulting from temperature change), ∆ζT (3), is the depth integral (from the surface, η, to the full ocean depth, H, with a layer thickness \(\Delta\)z) of the change in temperature (∆T, °C) multiplied by the seawater thermal expansion coefficient (α, °C−1) with the global mean thermosteric sea-level change, \({l}_{\theta }\), removed. We focus on the thermosteric component with its global mean removed to because the spatial pattern of change is the quantity of interest for this study, not the global mean change. The temperature change is the difference in potential temperature from the forced experiment relative to the control (FAF-passiveheat) averaged over the final decade. A similar Eq. (4) can be constructed for the halosteric component of sea-level change, using the change in salinity (S) and the haline contraction coefficient of seawater (β, dimensionless). Since saline water of a given mass has a smaller volume than the same mass of freshwater, a minus sign converts contraction to expansion, which is more readily comparable with ∆ζ and ∆ζT. The halosteric change typically has a near-zero global mean because total ocean salinity changes are small, making only a very small or negligible contribution to the global mean sea-level change (Gregory et al. 2019). α and β were calculated using the mean temperature, salinity and pressure fields of the final decade of the control simulation using standard nonlinear equations of state (McDougall and Barker 2011).
A sensitivity test (not shown) found that the calculation of ∆ζT and ∆ζS is not strongly affected by the choice of decade used to derive α and β; the effect of the temperature and salinity changes on α and β are small and it is the spatial patterns of \(\Delta T\) and \(\Delta S\) that set ∆ζT and ∆ζS. Note that the dynamic sea-level change will differ from the steric change (the sum of ∆ζT and ∆ζS) in locations where there is a large barotropic redistribution of density such as the subpolar North Atlantic and the Arctic (Lowe and Gregory 2006; Yin et al. 2010). The dynamic and steric sea-level changes will also differ in locations such as shelf seas, where the change in mass loading of the full water column (a non-steric effect) can be large (Landerer et al. 2007; Yin et al. 2010).
We quantify the part of dynamic sea-level change that is non-steric, \(\Delta {\zeta }_{N}\), as
In plots of \(\Delta \zeta_{N}\), we subtract the area mean to reveal the spatial pattern of non-steric sea-level change, since spatial anomalies are the quantity of interest for this work. According to recent terminology conventions (Gregory et al. 2019), \(\Delta \zeta\) is related to other components of sea-level change through
where \(\Delta B\) is the change due to the inverse barometer effect, \(\Delta {R}_{m}\) is the manometric sea-level change (due to change in ocean mass per unit area), \(\Delta\Gamma\) is the change due gravitational, rotational and deformational (GRD) effects from the redistribution of mass over the surface of the planet, \({l}_{b}\) is the barystatic change (due to addition of water to the ocean, mostly from land ice). The difference between the dynamic sea-level change and the steric change in the real world is
However, in the AOGCMs considered in this study (Table 1) \(\Delta\Gamma\) and \({l}_{b}\) are zero because these processes are not represented. \(\Delta B\) is not readily quantifiable from these models, but is assumed to be small and average to near zero over long time periods since it is of most relevance on meteorological rather than climate timescales (Ponte 2006; Gregory et al. 2019). Therefore, maps of \(\Delta {\zeta }_{N}\) relative to its global area mean in these models reveals the spatial pattern of \(\Delta {R}_{m}\), the manometric sea-level change. This sea-level component is broadly analogous to the ‘barotropic component’ of sea-level change discussed in previous literature, although they are calculated differently (e.g. see Lowe and Gregory 2006).
2.4 Decomposition of ocean heat content change
We can decompose OHC change into components due to changes in ocean temperature and in transport. Following Gregory et al. (2016), we let \(\Phi\) represent the transport operator that encompasses all processes that affect heat transport, including resolved and parameterized advection, diffusion, and convection. That is, \(\Phi \left(T\right)=-\nabla \bullet \left({\varvec{u}}T+{\varvec{P}}\right)\), the convergence of temperature due to the three dimensional resolved velocity field \({\varvec{u}}\) and parameterized subgrid-scale tracer transport processes \({\varvec{P}}\). In \(\Phi (T)\) parentheses around \(T\) indicates the action of ocean tracer transport on the temperature within the parentheses. At steady state, the ocean has an unperturbed temperature, \(\stackrel{-}{T}\), and an unperturbed three-dimensional transport, \(\stackrel{-}{\Phi }\), where overlines indicate a long time average over the control run. The convergence of unperturbed temperature transport, \(\stackrel{-}{\Phi }\left(\stackrel{-}{T}\right),\) is zero in the steady state, except at the surface where it balances the surface heat flux.
Forced climate change modifies the surface fluxes. It alters the ocean temperature by an amount T′, relative to the unperturbed state by the addition of heat, and the transport by \({\Phi }^{^{\prime}}\) through changing both the wind driven and density driven transports. As a result, the convergence \(\Phi (T)\) of heat is modified as well and is no longer zero. Hence, interior temperature changes according to
where \([\stackrel{-}{\Phi }+{\Phi }^{^{\prime}}](\stackrel{-}{T}+{T}^{^{\prime}})\) is symbolically the action of both the unperturbed and perturbed transport acting on the unperturbed and perturbed temperature. Note also that \(\stackrel{-}{\Phi }(\stackrel{-}{T})= 0\).
Thus we distinguish three different causes of temperature change that arise from the convergence of: \(\stackrel{-}{\Phi }\left({T}^{^{\prime}}\right)\), transport of the added heat by the unperturbed transport processes; \({\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)\), changes in the ocean transport redistributing unperturbed heat; and \({\Phi }^{^{\prime}}\left(T{^{\prime}}\right)\), perturbation in the transport that redistributes the added heat (8).
If the oceans absorbed the added heat from anthropogenic climate change like a passive tracer that does not affect ocean circulation or other transport processes, then OHU would be driven entirely by the first term, \(\stackrel{-}{\Phi }\left({T}^{^{\prime}}\right)\). This term is therefore the “passive uptake of added heat”. In reality, the ocean circulation and subgrid scale processes are affected by temperature change and other surface flux changes, so the other terms play a part. The second term is a pure redistribution, whose global volume integral is small (but not precisely zero because \(\stackrel{-}{T}\) can be fluxed to the atmosphere). The final term is of second order in perturbation quantities, but it is not always negligible.
Consider the following illustrative situation in a convective zone of the Labrador Sea, where climate change causes increased heat flux into the ocean, and the ocean temperature gets warmer at around 250 m depth. Positive \(\stackrel{-}{\Phi }\left({T}^{^{\prime}}\right)\) describes the change in temperature that results from the unperturbed circulation and subgrid processes that passively transport the additional heat downwards. However, these transport processes are weakened by the input of \({T}^{^{\prime}}\) because the air-sea heat input strengthens stratification and weakens downward heat transport by convection. The weakened downward transport carries less additional heat than in the passive case; and \({\Phi }^{^{\prime}}\left(T{^{\prime}}\right)\) is weakly negative because \({\Phi }^{^{\prime}}\) is negative. Finally, weakened downward transport means that less heat from lower latitudes gets brought northward and downward, causing strongly negative \({\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)\).
FAFMIP experiments and diagnostics allow for the three contributions to the change in the convergence of heat to be distinguished. We can express the change in ocean heat content (∆h, Jm−2) due to each contribution by converting the appropriate temperature (T) field using a reference heat capacity for seawater (cp0 = 4000 J kg−1 K−1), a reference density (ρ0 = 1026 kg m−3) and the ocean grid cell vertical thickness (\(\Delta\)z, m). Differencing particular experiments and temperature fields (T, Ta, or Tr) yields different components of OHC change. Further notes on the time evolution of Tr, Ta and T, describing how different temperature change terms are grouped in the decomposition are included in the “Appendix”.
The OHC change due all three convergences of temperature in (8), Δh, is
where ∆T, is the difference of the model’s temperature field (T) between the final decades of FAF-heat and FAF-passiveheat (9). In FAF-heat, the heat flux changes the transport processes (\({\Phi }^{^{\prime}}\) ≠ 0) and the temperature (\(T{^{\prime}}\) ≠ 0) and, thus there is a change in heat content due to all three types of temperature convergence.
The OHC change due to passive uptake of additional heat, \(\Delta h\left[ {\overline{\Phi }\left( {T^{\prime}} \right)} \right]\) is
where the notation \(\Delta h[\dots ]\) symbolically represents the change in OHC due to the convergence of temperature enclosed by the square brackets. Since passive temperature is initially 0, its decadal mean change by the end of simulation is simply \({\stackrel{-}{T}}_{a}\), the time mean Ta from FAF-passiveheat for the years 61–70.
The OHC change due to the redistribution of unperturbed temperature, \(\Delta h\left[ {{{\Phi^{\prime}}}\left( {\overline{T}} \right)} \right]\) is
where ∆Tr is the difference between FAF-heat redistributed temperature, Tr, and FAF-passiveheat T, averaged over the final decade.
The OHC change due to the perturbation in the transport redistributing the added heat, \(\Delta h\left[ {{{\Phi^{\prime}}}\left( {T^{\prime}} \right)} \right]\) is
where \(\Delta {T}_{a}\) is the difference of Ta between FAF-heat and FAF-passiveheat (12).
2.5 Models analysed
Different suites of models are analysed in different parts of this work, subject to the availability of output fields. The first analysis required sea-surface height above geoid, ζ, ocean temperature, and seawater salinity, available from 13 FAFMIP AOGCMs (Table 1), although less than the full set of output for all experiments was available for CESM2, GISS-E2-R-CC and MIROC6. The ocean heat budget decomposition in Sect. 3.5 required 3-D fields of redistributed and added temperature, available for ten FAFMIP models (the exceptions being CESM2, GISS-E2-R-CC and MIROC6). A comparison of the sea-level response to 1pctCO2 forcing was also performed for a suite of 19 CMIP5 models and 16 CMIP6 models listed in Table 2. The ‘zos’ fields of MIROC5, CAMS-CSM1-0 and GISS-E2-1-G required correction for the inverse barometer effect due to sea ice loading, following (Griffies et al. 2016).
From the 13 models that have performed FAFMIP experiments, five are from the CMIP5 era, seven from CMIP6, and one (HadCM3) is pre-CMIP5. All ocean model components of models feature similar horizontal resolution (roughly 1-by-1 degree of latitude), and so unresolved features such as mesoscale eddies are parameterized. Even the finest of these ocean grids (MPI-ESM1-2-HR, about 0.4-by-0.4 degrees of latitude) is ‘eddy-permitting’ and not ‘eddy-resolving’, as it can resolve some large ocean eddies, but it still employs an eddy flux parameterization to represent unresolved mesoscale and sub-mesoscale processes. While horizontal resolution is broadly similar across models, details such as the vertical grids or refined resolution near the equator are model-specific.
3 Results
3.1 FAF-all versus 1pctCO2
This section explores the diversity in Δζ in FAF-all versus 1pctCO2, to demonstrate the extent to which patterns of Δζ are generated by ocean processes rather than by the patterns and magnitude of all fluxes.
The spatial pattern of the sea-level response to all flux perturbations applied simultaneously (FAF-all, Fig. 3a) is similar to the pattern that results from 1pctCO2 forcing (Fig. 3c). The agreement between responses to 1pctCO2 and FAF-all forcing is an intended feature of the experimental design and shows that the mean pattern of CO2-forced sea-level change can be reproduced when the models are forced instead with perturbations to their surface fluxes. The spatial standard deviation of ∆ζ is a useful scalar that summarizes the magnitude (or heterogeneity) of the spatial pattern of dynamic sea-level change. The spatial standard deviation of ∆ζ is 0.082 m for FAF-all; larger than 0.059 m for 1pctCO2, indicating a stronger spatial pattern in FAF-all.
Ocean dynamic sea-level response Δζ to greenhouse gas forcing in 1pctCO2 runs (above) and FAF-all runs (below) for 11 AOGCMs: ACCESS-CM2, CanESM2, CanESM5, GFDL-ESM2M, HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MIROC6, MPI-ESM-LR, MPI-ESM1-2-HR and MRI-ESM2-0. Mean across models (above) and standard deviation across models (below)
The three prominent features of regional sea-level change identified in previous work (Church et al. 2013; Slangen et al. 2014; Gregory et al. 2016) are apparent here: (1) the Southern Ocean meridional gradient with positive Δζ north of 55° S and negative Δζ at higher latitudes, (2) the meridional dipole of positive Δζ in the northern North Atlantic against weakly negative Δζ in the southern North Atlantic, and (3) positive Δζ in the Arctic.
The large positive Δζ in the North Atlantic is greater in magnitude in FAF-all than 1pctCO2. This is due to the “North Atlantic redistribution feedback”, wherein the heat flux perturbation (which is strongly positive in the North Atlantic) causes the AMOC to decline (Winton et al. 2013; Gregory et al. 2016). The weakening of the AMOC reduces the northward heat transport, thus redistributing the OHC, leading to cooler SST at high latitudes, and reinforcing ocean heat uptake there (by reducing the heat loss from the ocean to the atmosphere). This occurs because the atmosphere is coupled to the redistributed temperature, Tr, and therefore “sees” a cooling in the North Atlantic due to redistribution, but does not respond to the added heat, which it cannot see. Because of this feedback, the heat input into the North Atlantic is about double what it would be in a 1pctCO2 simulation. By comparing FAF-heat experiments with two corresponding pairs of an AOGCM and an OGCM, Todd et al. (2020) find, however, that the AMOC weakening is greater by only about 10% in the AOGCM case due to the feedback. Their finding is consistent with our results, where the total OHC change in FAF-heat is about 10% greater (due to the redistribution feedback) than the time- and area-integral of the imposed perturbation. The feedback is a complicating feature of the simulation design, but does not diminish the utility of the experiments, because the imposed heat flux perturbation is the same for all models. The degree of AMOC weakening (and ocean heat transport change) shown by each model reflects the sensitivity of each model to common forcing, regardless of whether it resulted directly from the forcing or through the redistribution feedback.
When the different AOGCMs are forced with identical surface flux perturbations in FAF-all, the spread in sea-level response (Fig. 3d) is similar to the spread that results from 1pctCO2 forcing (Fig. 3b). The largest spread of sea-level change among the 11 models (measured as the standard deviation across models) is focused on the same three regions in FAF-all as in 1pctCO2—the Arctic, the Southern Ocean, and the North Atlantic—and is of similar magnitude. The area mean of inter-model standard deviation is 0.045 m in 1pctCO2, and 0.046 m in FAF-all. This evidence indicates that much of the spread in projections of the dynamic sea-level response to climate forcing arises due to differences in ocean model formulation, rather than in the surface flux forcing from the diverse atmosphere models. This conclusion is different from that of Huber and Zanna (2017), who found that the parametric uncertainty of a given model is too small to explain the spread of ocean responses to climate change. The dynamic sea-level responses of the individual AOGCMs to FAF-all forcing are included in the “Appendix” (Fig. 13 in “Appendix”).
3.2 Sea-level response to 1% per year CO2 forcing in CMIP5 and CMIP6
There is strong similarity between the sea-level responses to 1pctCO2 forcing from the much larger CMIP5/6 ensembles (Fig. 4a, c) and the sea-level responses to our smaller suite of FAFMIP models (Fig. 3), especially in the North Atlantic, Arctic, and Southern oceans. This similarity indicates that the FAFMIP-participant models form a representative subset of the wider CMIP5 and CMIP6 ensembles. It also suggests that the findings of FAFMIP are likely to be applicable to a wider range of models than the 13 FAFMIP models analysed here.
Multi model mean projections of ∆ζ (left) from 1pctCO2 forcing experiments averaged over years 91–100 for 19 CMIP5 models (a), 16 CMIP6 models (c). Standard deviation of the model spread (right). Models used are described in Table 2
The 1pctCO2 response in the two different CMIP eras is similar (Fig. 4a, c), in agreement with recent findings (Lyu et al. 2020). The similarity of responses of models from the different eras indicates that models from across the eras may be analysed together as one ensemble, rather than separately. The current generation of AOGCMs show diverse sea-level responses in the Arctic, Southern Ocean, North Atlantic and North Pacific (Fig. 4d), much like the previous generation (Fig. 4b), indicating a continuing need to focus on these regions.
The CMIP5 ensemble uses ten different ocean components (ignoring version differences) among its 19 members (Table 2). In the 16 different CMIP6 AOGCMs shown, there are eight different ocean model components. In the CMIP6 ensemble, six models use a version of NEMO (Nucleus for European Modelling of the Ocean), three use POP (Parallel Ocean Program), two use MOM (Modular Ocean Model), and the remaining five use an ocean component unique to the ensemble. Hence, there is a greater diversity of ocean components in terms of the number of unique ocean models in CMIP5. For all the CMIP6 models that use NEMO, the horizontal ocean resolution of the ORCA1 grid used is the same (roughly 1°-by-1° of latitude, with a refinement to 1/3° at equator), although different AOGCMs use different numbers of ocean vertical levels, which has effects on Southern Ocean OHU (Stewart and Hogg 2019). One might argue that there is a decrease in the diversity of representations of ocean processes in this ensemble of CMIP6 models, but the increasing use of common ocean components has apparently not reduced the spread of sea-level projections in response to 1pctCO2 forcing in the CMIP6 era versus CMIP5 (Fig. 4b, d). Sea-level projections from the CMIP6 ensemble were checked for similarities among models sharing a similar ocean component, but no clear correlation exists (not shown). One might therefore expect that diversity in air-sea fluxes (rather than in ocean models) causes the spread (e.g., Huber and Zanna 2017). However, the increased use of common ocean components does not necessarily mean that water properties and ocean transport processes are represented in the same way across models. NEMO and other ocean components support a potentially enormous variety of configurations through customisable combinations of different parameterisations and schemes, and spin-up procedures. Parameter choices of, for example, coefficients of vertical diffusivity and eddy mixing are important for setting OHU in the Pacific and Southern Oceans (Huber and Zanna 2017). The convergence of structure in ocean components does not directly translate into convergent representations of ocean heat uptake.
3.3 Ocean response to perturbations in individual fluxes
Comparison of the multi model mean ∆ζ from FAF-all with the sea-level response to individual perturbations allows us to determine which features result from changes to each flux. The spatial pattern of sea-level change from the heat flux forcing (Fig. 5c) most closely matches the response to all perturbations simultaneously applied (Fig. 3c). For FAF-heat, the spatial standard deviation is 0.080 m, which is close to that of FAF-all (0.082 m). The spatial standard deviation is 0.021 m for FAF-stress and 0.018 m for FAF-water. This indicates that the heat flux contributes the most to the sea-level change in FAF-all and 1pctCO2, in agreement with previous work (Bouttes and Gregory 2014; Gregory et al. 2016). The wind stress perturbation causes part of the pattern of ∆ζ, but its influence is mostly confined to the Southern Ocean (Fig. 5a). There, strengthened and poleward-shifted westerlies steepen the meridional sea-level gradient across the ACC (Frankcombe et al. 2013). The freshwater perturbation contributes the least sea-level change of the three perturbations, but it sets part of the spatial pattern of ∆ζ in the Southern and Arctic Oceans (Fig. 5e). Recall that the three key locations for which models show diverse predictions of ∆ζ in 1pctCO2 and FAF-all were the Arctic, the eastern subpolar North Atlantic and the Southern Ocean south of Australia and New Zealand (Fig. 3c, d). There is coincident diversity in the FAF-heat responses (Fig. 5d), which suggests that spread in FAF-all is due primarily to the heat flux perturbation. The dynamic sea-level responses of each AOGCM to each individually applied flux perturbation are shown in the “Appendix” (Fig. 13–16).
Maps of multi model ensemble mean ocean dynamic sea-level response to individually-applied flux perturbations (left) and standard deviation across 13 AOGCMs (right) for the wind stress (FAF-stress, top), heat flux (FAF-heat, middle), and water flux (FAF-water, bottom) experiments. AOGCMs used: ACCESS-CM2, CanESM2, CanESM5, CESM2 (FAF-stress and FAF-water only), GFDL-ESM2M, GISS-E2-R-CC (FAF-stress and FAF-water only), HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MIROC6, MPI-ESM-LR, MPI-ESM1-2-HR and MRI-ESM2-0
3.3.1 Wind stress
The wind stress perturbation creates a gradient of ∆ζ across the Southern Ocean (Fig. 5a). The intensified Southern Ocean westerlies drive a northward positive meridional ∆ζ gradient with a zonal mean of 0.05–0.025 m from 75° to 35° S. South of 60° S, ∆ζ diverges depending on the model (Fig. 5b). The models disagree on whether the wind stress perturbation causes negative or weakly positive depth integrated OHC change south of 60° S (Fig. 6g), which is not yet well understood but merits further investigation. The wind stress perturbation tends to weakly warm the surface ocean, cool the shallow subsurface and warm the deeper ocean (Fig. 6d, j). Part of the discrepancy between models occurs because although this area-integrated picture is qualitatively common to models, the depth at which each OHC change inflection occurs is model-specific. In agreement with Gregory et al. (2016), while the local OHC change due to the wind stress perturbation can be large (Fig. 6a, g, j) its global integral is small; two orders of magnitude smaller than the heat flux perturbation (not shown). Other work finds that the Southern Ocean OHC response to wind stress change is sensitive to the location of the zero wind stress curl, which may be a source of some of the spread reported here (Stewart and Hogg 2019).
Multi model ensemble mean integrated ocean heat content (OHC) change for FAF-stress (left), FAF-heat (middle), FAF-water (right) for 12 AOGCMs: ACCESS-CM2, CanESM2, CanESM5, CESM2 (FAF-stress and FAF-water only), GFDL-ESM2M, GISS-E2-R-CC (FAF-stress and FAF-water only), HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MPI-ESM-LR, MPI-ESM1-2-HR and MRI-ESM2-0. Depth integrated OHC change (a–c), area integrated OHC change (d–f), zonally and depth integrated OHC change (g–i), zonally integrated OHC change (j–l). Dashed lines in d–i indicate ± 2 standard deviations of ensemble spread. 1 GJ = 109 J, 1 ZJ = 1021 J, 1 EJ = 1018 J
The maps of ∆ζT, ∆ζS and ∆ζN show that the wind forced sea-level change in the Southern Ocean is almost entirely thermosteric (Fig. 7c), as suggested by Gregory et al. (2016). The perturbation causes heat to accumulate between 55° and 30° S while higher latitudes cool (Fig. 6a, g). This is consistent with a wind driven enhancement of the residual meridional overturning documented elsewhere (Liu et al. 2018). The halosteric change in the Southern Ocean is much smaller and opposes the thermosteric change (Fig. 7e). The wind-forced ∆ζT change is largest in the Atlantic and Indian sectors of the Southern Ocean, and the models generally agree on the pattern and magnitude of this feature, although the details of the magnitude near the South American coast are model dependent, (Fig. 7d). The non-steric component dominates the sea-level change in the Antarctic shallow shelf seas (Fig. 7g). Elsewhere, in the Pacific sector and Weddell Sea, the AOGCMs predict different magnitudes of negative ∆ζ (Fig. 7a, b) and this spread is thermosteric (Fig. 7d).
Multi model ensemble mean dynamic sea-level response to momentum flux forcing (a) and the standard deviation across models (b) for 13 AOGCMs: ACCESS-CM2, CanESM2, CanESM5, CESM2, GFDL-ESM2M, GISS-E2-R-CC, HadCM3, HadGEM2-ES, HadGEM-GC31-LL, MIROC6, MPI-ESM1-2-HR, MPI-ESM-LR and MRI-ESM2-0. Multi model mean momentum flux-forced thermosteric (c), halosteric (e), and non-steric (g) contributions, and the standard deviation across models (d, f, h) where the area mean has been subtracted from (g)
In some models, but not all, the wind stress perturbation drives sea-level change in the Arctic East Siberian Sea and northwestern Atlantic (Fig. 5b). GISS-E2-R-CC predicts widespread, large positive ∆ζ in the Arctic, while CanESM5, MPI-ESM1-2-HR and HadCM3 predict a gradient of ∆ζ that is negative at the pole and increases southwards (Fig. 14). HadGEM3-GC31-LL shows positive ∆ζ at the pole. The other models predict near zero ∆ζ in the Arctic. The spread in the North Atlantic is due to the responses of HadGEM2-ES, MPI-ESM-LR, MPI-ESM1-2-HR and GFDL-ESM2M, which predict weakly positive ∆ζT and ∆ζS here, while the other models show ∆ζ ≈ 0 (Fig. 14).
3.3.2 Heat flux
The heat flux perturbation drives the most change in sea level, both in terms of magnitude and area of effect (Fig. 5c). The perturbation causes positive OHC change over most of the ocean area (Fig. 6b) in the upper 1000 m (Fig. 6e, k). Note that even though the heat flux perturbation adds large amounts of heat to the global ocean, it is possible for the net OHC change in some locations to be weakly negative; either because of negative values of the perturbation flux or via the redistribution of heat by changing ocean transport. The models agree that the largest OHC change occurs in south of 30° S, and the changes elsewhere are more model dependent (Fig. 6h). In the upper 300 m, the ensemble spread of the area integrated OHC change is on the order of half the mean change (Fig. 6e). This spread indicates that the strength of the mechanisms by which heat is transported away from the surface is different among models. The largest values of ∆ζ are in the North Atlantic. The most intense perturbation to the heat flux per unit area is directed here. As described earlier in Sect. 3.1, the North Atlantic redistribution feedback means that the magnitude of North Atlantic sea-level response is greater in FAF-heat and FAF-all than in 1pctCO2 experiments.
In general, the pattern of ∆ζ is similar across most models, and the magnitude of the change varies between models (Fig. 5). The fact that the hotspots of inter-model spread (Fig. 5d) are coincident with most of the strongest ∆ζ features reflects this. The multi-model mean map of ∆ζ (Fig. 5c) therefore reflects a pattern that is very similar to each individual model’s response, rather than the mean of several very different patterns. Most models show the maximum ∆ζ between 45° and 65° N in the western North Atlantic (Fig. 15). All models predict the Atlantic dipole of positive ∆ζ north of 45° N and weakly negative ∆ζ near Cape Hatteras in the western basin around 35° N. The weak dynamic sea-level drop occurs at the center of the subtropical gyre, consistent with the decline of the dynamic sea-level gradient across the Gulf Stream. In the eastern basin off the west Saharan-African coast most models predict a “tropical arm” of positive ∆ζ that diminishes westward (Fig. 5c), which is weak in HadGEM2-ES and absent in GFDL-ESM2M (which shows near zero ∆ζ, Fig. 15e, h). Most models predict a small region of negative ∆ζ north of Iceland. MPI-ESM-LR and MRI-ESM2-0 instead predict positive ∆ζ north of Iceland and negative/neutral ∆ζ to the south of Iceland (Fig. 15k, m). HadGEM2-ES and MPI-ESM1-2-HR exhibit regions of negative/neutral ∆ζ both south and north of Iceland (Fig. 15h, l).
The steric sea-level rise in the Atlantic subpolar gyre, north of 45° N, is due predominantly to positive ∆ζS (i.e. freshening), opposed by weaker negative ∆ζT (Fig. 8c). North of 45° N, there is positive ∆ζS and weaker negative ∆ζT,, in agreement with previous work (Bouttes et al. 2014; Saenko et al. 2015). This is consistent with a reduced northward flux of heat and salt as a result of a weakened AMOC. The models disagree on the magnitude of ∆ζ, particularly to the south of Iceland (Fig. 8b) and most of this spread is due to diversity in predictions of thermosteric change, but the halosteric response is also uncertain across models (Fig. 8d, f). The sea-level change on the shelves of the subpolar North Atlantic has a strong non-steric component (Fig. 8g), consistent with an increase of on-shelf ocean mass (Yin et al. 2010).
Multi model ensemble mean dynamic sea-level response to heat flux forcing (a) and the standard deviation across models (b) for 11 AOGCMs: ACCESS-CM2, CanESM2, CanESM5, GFDL-ESM2M, HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MIROC6, MPI-ESM-LR, MPI-ESM1-2-HR, MRI-ESM2-0. Multi model mean heat flux-forced thermosteric (c), halosteric (e), and non-steric (g) contributions, and the standard deviation across models (d, f, h) where the area mean has been subtracted from (g)
The thermosteric and halosteric effects change sign south of 45° N and the thermal effect dominates, but they compensate more closely, and so ∆ζ is smaller than further north. The 45° N latitude line coincides with the divide between the North Atlantic subpolar and subtropical gyres formed by the northern boundary of the North Atlantic Current. The opposing changes either side of the divide are consistent with a change in the inter-gyre exchange of heat and salt: a warmer and saltier subtropical gyre and a cooler and fresher subpolar gyre. Further south, most models predict positive ∆ζ in the eastern basin off the West African coast (Fig. 8a). There is also considerable inter-model spread in the thermosteric and halosteric contributions (Fig. 8d, f). Interestingly, five models predict a mixture of thermo- and halosteric contributions (ACCESS-CM2, CanESM2, CanESM5, HadGEM3-GC31-LL, MPI-ESM1-2-HR), four models predict the tropical arm as being purely halosteric (HadCM3, MIROC6, MPI-ESM-LR and MRI-ESM2-0), one model predicts a purely thermosteric effect (HadGEM2-ES), and one model shows no positive ∆ζ feature here at all (GFDL-ESM2M) (not shown).
In the North Pacific, all models respond to the heat flux perturbation with a North–South dipole in ∆ζ that changes sign around 35° N (Fig. 8c). This meridional dipole has the opposite sign to that of the North Atlantic. In the western basin, the pattern is essentially the same across models, and its extent eastward is model dependent (Fig. 15). The dipole is mostly thermosteric (Fig. 8c), owing to a stronger accumulation of heat per unit area north of 35° N in the region east of Newfoundland than further south (Fig. 6b). This is sea-level change is consistent with a steepening of the across-current sea-level slope, and an intensification of the Kuroshio western boundary current (Chen et al. 2019).
The lower latitudes of the Arctic around the East Siberian and Beaufort Seas show positive ∆ζ in response to the heat flux perturbation, while ∆ζ is negative at higher latitudes. The only exception to this is HadCM3 (Fig. 15), which predicts strongly negative ∆ζ everywhere in the Arctic, contributing strongly to the large inter-model spread there (Fig. 8b). The Arctic shows a strong non-steric component of ∆ζ (Fig. 8g), corresponding to a shift of mass from the highest latitudes onto the shelves. The patterns of Arctic sea-level change in 1pctCO2 and FAF-all are very similar (Fig. 3), suggesting that the coupling of sea ice to redistributed temperature rather than regular temperature in FAFMIP experiments (Sect. 2.2) does not introduce unintended effects on ocean transport. Nevertheless, the diverse representations of sea ice in AOGCMs generally remains a key source of uncertainty in the projection of future polar climate change (Meredith et al. 2019).
The Southern Ocean sea-level change in response to heat flux forcing is smallest at the highest latitudes (negative ∆ζ), changing sign to positive ∆ζ between 40° and 55° S (Fig. 8a). All models predict a maximum of ∆ζ off the South African coast that extends eastward. The spatial pattern of negative ∆ζ across much of the Southern Ocean is predicted by all models. CanESM2, HadGEM3-GC31-LL, MPI-ESM-LR and GFDL-ESM2M (and to a lesser extent, HadCM3 and ACCESS-CM2) show positive ∆ζ in the sector between 130° and 160° E, south of Australia and New Zealand (not shown). This inter-model variation is also identifiable in the spread of sea-level responses in FAF-all (Fig. 3d) and is thermosteric (Fig. 8d).
The Southern Ocean Δζ zonal gradient in FAF-heat is the result of both thermosteric and halosteric effects (Fig. 8a, c, e). Gregory et al. (2016) pointed out that the gradient of Δζ across the Southern Ocean arises primarily because more heat accumulates in the mid latitudes (around 45° S) than further south (Fig. 9a). However, if sea-level change were simply proportional to OHU, then Δζ would show a prominent maximum at 45° S and decline until 25° S. Instead, Δζ increases northward to about 45° S, with only a slight decline further North (Fig. 9b, solid black line). The waters further North are warmer and therefore have greater thermal expansivity, which, in addition to the convergence of heat between 30–45° S, creates a thermosteric maximum around 40° S (Fig. 9b, red dotted line). However, at the same latitude, the changing salinity causes a halosteric effect that opposes the thermosteric effect and the meridional gradient of Δζ plateaus, instead of peaking at 40° S and declining to the north (Fig. 9b, cyan dashed line). Note that the deviation between the steric sea-level change (Fig. 9b, cyan dashed line) and the dynamic change (Fig. 9b, solid black line) north of 40° N indicates a considerable barotropic component of the change due to the redistribution of ocean mass (Lowe and Gregory 2006; Yin et al. 2010; Bouttes and Gregory 2014 and Fig. 8g).
Comparison of the multi model ensemble mean zonally- and depth-integrated OHC change in response to heat flux forcing (a) and zonal mean dynamic sea-level change (b) for 11 AOGCMs, showing Δζ (black solid line), the thermosteric component ΔζT (red dotted line) and the sum of thermo- and halosteric components (cyan dashed line). AOGCMs used: ACCESS-CM2, CanESM2, CanESM5, GFDL-ESM2M, HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MIROC6, MPI-ESM-LR, MPI-ESM1-2-HR, MRI-ESM2-0
3.3.3 Freshwater flux
Interestingly, the sea-level response to freshwater forcing is strongly thermosteric as well as halosteric (Fig. 10c, e). The North Atlantic is sensitive to opposing, nearly compensating thermal and haline effects. The sea-level change in the Arctic is mostly halosteric, whereas the Southern Ocean shows a mostly thermosteric response. The sea-level change on the Antarctic shelves is non-steric (Fig. 10g).
Multi model ensemble mean dynamic sea-level response to freshwater flux perturbation (a) and the standard deviation across models (b) for 13 AOGCMs: ACCESS-CM2, CanESM2, CanESM5, CESM2, GFDL-ESM2M, GISS-E2-R-CC, HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MIROC6, MPI-ESM-LR, MPI-ESM1-2-HR and MRI-ESM2-0. Multi model mean freshwater flux-forced thermosteric (c), halosteric (e), and non-steric (g) contributions, and the standard deviation across models (d, f, h) where the area mean has been subtracted from (g)
The locations where the models disagree on the sea-level response to freshwater forcing are not always coincident with the locations of largest sea-level change (Fig. 10a, b), particularly in the North Atlantic and the Arctic. This indicates that different models predict different features (Fig. 16), rather than all models responding with similar patterns of different magnitude. The models predict diverse patterns of sea-level change in the subpolar North Atlantic (Fig. 10b) because they disagree on the eastward extent of the sea-level change (Fig. 16). Presumably, simulated North Atlantic currents have differing sensitivities to freshwater forcing.
The sea-level changes closest to the Antarctic coast are predicted with some agreement across models (Fig. 10b). The inter-model spread around 50°–60° S south of Australia arises due to different thermosteric responses to freshwater forcing (Fig. 10d). A poleward contraction of the ACC here would explain the positive Δζ (Fig. 10a) but the inter model spread suggests that not all models predict this (Figs. 10b, 16a, b, d, f, h, j).
In the Arctic, the freshwater forcing is widespread and positive, due to a mixture of increased river runoff and precipitation. This causes freshening, which in turn causes halosteric sea-level rise (Fig. 10e). However, the models disagree on the spatial extent of the halosteric sea-level rise (Fig. 10f).
3.4 Linearity of sea-level responses to flux perturbations
Here we explore how sea level responds to flux perturbations applied individually versus simultaneously. If the sea-level response to all perturbations is linear, then the sum of the responses when the perturbations are applied individually Δζsum,
should equal the response when the fluxes are applied together, Δζall. The differences between Δζsum and Δζall represent the nonlinear sea-level response to simultaneous flux forcing and is explored for 11 AOGCMs (Table 1, excluding CESM2 and GISS-E2-CC). The significance of nonlinear features is tested against the variability of the seven decades of FAF-passiveheat, calculated as the standard deviation of seven decadal averages, which we assume is representative of the internally generated variability in the other experiments as well. The quantity Δζsum − Δζall is calculated using four independent simulations (FAF-heat, -stress, -water, -all), each with its own unforced variability. The difference Δζsum − Δζall can therefore be affected by the unforced variability of four different simulations, so the standard deviation of the difference is twice the standard deviation of unforced decadal variability (from FAF-passiveheat). For a Δζsum − Δζall feature to be judged significant at the 5% level, it must be larger than four times the unforced standard deviation. Locations where Δζsum − Δζall is not significant are set to 0 for each model, before being averaged in Fig. 11 to reveal only significant differences. The features removed through this process are small in spatial extent and magnitude, and are particular to each model (not shown). The flux perturbations show significant nonlinear interaction in the Arctic and subpolar North Atlantic (Fig. 11a). Across the Arctic, Δζsum − Δζall is negative, meaning most models predict a stronger dynamic sea-level change in FAF-all than the individual flux perturbation experiments suggest.
For most of the global ocean, Δζsum − Δζall is small and therefore Δζsum approximates the patterns of Δζall. However, small values of multi-model mean Δζsum − Δζall are not necessarily indicative of agreement between models that the responses to perturbations sum linearly. In the western North Pacific and Southern Ocean south of Australia and New Zealand (Fig. 11b) some models show some nonlinear interactions between the flux perturbations. South of Australia and New Zealand, Δζwind is small, so the interaction is between the freshwater and heat fluxes. It could be that local details of the change in sea-ice cover in response to heat flux forcing are model specific, causing the momentum forcing to have different results in FAF-all versus FAF-stress where no heat perturbation is applied. More detailed investigation into each model’s results is necessary to explore this.
In the northwest Pacific, in the Kuroshio separation region, the AOGCMs show various sensitivities to the three individual forcings (not shown). For ACCESS-CM2, GFDL-ESM2M, MIROC6 and MPI-ESM-LR, the Δζsum − Δζall dipole is positive to the south and negative to the north, indicating that simultaneously applied flux perturbations do not produce the same degree of intensification of the across-current slope as when the perturbations are applied individually. For CanESM5, the dipole is reversed. For the other models there is no strong nonlinear sea-level response.
HadGEM2-ES, MPI-ESM1-2-HR, and GFDL-ESM2M show strong nonlinear interactions between forcings in the North Atlantic, as these models are sensitive to all three perturbations here (not shown). The spread in the North Atlantic indicates that the AMOC response to the flux perturbations (and also the nonlinear interactions between them) is model-specific.
3.5 Decomposition of ocean heat uptake
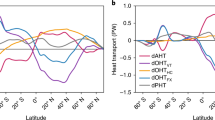
As shown above, ocean dynamic sea-level change is largely thermosteric, and reflects changes in OHC. Here, we decompose the OHC change (see Sect. 2.4 and “Appendix” for details) of ten AOGCMs (Table 1, excluding CESM2, GISS-E2-R-CC, MIROC6) into contributions from changes in ocean transports and the uptake of the imposed perturbation. Most of the heat added to the oceans in FAF-heat is stored in the Southern Ocean, between 30° S and 60°S (Figs. 6h, 12a), particularly in the Indo–Pacific sectors. The North Atlantic shows the highest rate of heat uptake per unit area, but the small total area of the basin means its contribution the global total OHU is smaller than that of the much larger Southern Ocean (Fig. 6h). The Arctic also shows moderate rates of heat storage per unit area (Fig. 12a), but this basin stores less heat than other latitudes because of its small total area (Fig. 6h).
Decomposition of depth-integrated ocean heat uptake in ten AOGCMs (ACCESS-CM2, CanESM2, CanESM5, GFDL-ESM2M, HadCM3, HadGEM2-ES, HadGEM3-GC31-LL, MPI-ESM-LR, MPI-ESM1-2-HR and MRI-ESM2-0) in FAF-heat, left panels show the multi-model ensemble mean and right panels show the standard deviation across models for the total ocean heat uptake mean (a) and spread (b). Components of heat uptake (c, e, g) are shown as a percentage of the total (a). Passive uptake of added heat, \(\Delta \mathrm{h}[\stackrel{-}{\Phi }({\mathrm{T}}{{^{\prime}}})]\), mean (c) and spread (d). Pure redistribution of unperturbed heat, \(\Delta \mathrm{h}[{\Phi }{{^{\prime}}}(\stackrel{-}{\mathrm{T}})]\) mean (e) and spread (f). Redistribution of added heat by the perturbed transport, \(\Delta \mathrm{h}[{\Phi }{{^{\prime}}}\left({\mathrm{T}}{{^{\prime}}}\right)]\), mean (g) and spread (h)
In the Southern Ocean, passive heat uptake in the Southern Ocean (Fig. 12c) is close to 100% of the total heat uptake (Fig. 12a). The OHC change due to the perturbed transport (Fig. 12e, g) is much smaller than the total passive uptake, but is locally important and strongly negative near the Ross and Weddell gyres. Further, there is relatively little spread of \(\Delta h[\stackrel{-}{\Phi }({T}^{^{\prime}})]\) across models (Fig. 12d). This means that these AOGCMs agree that heat uptake by the Southern Ocean is mostly passive, in agreement with recent findings (Bronselaer and Zanna 2020). The perturbed transport has secondary influence on heat uptake in the Southern Ocean. Both \(\Delta h\left[\stackrel{-}{\Phi }\left({T}^{^{\prime}}\right)\right]\) and \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) are important components in the Indian sector (Fig. 12c, e), and the spread here is not due to passive uptake (Fig. 12d). South of Australia and New Zealand, where the total OHC change differs across models (Fig. 12b) the spread comes from \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) (Fig. 12f), which could suggest a model-dependent reduction of upwelling.
OHU in the North Atlantic is characterized by positive passive heat uptake that is partially opposed by the perturbed transport (Fig. 12c, e, g). Strong negative \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) and \(\Delta h[{\Phi }^{^{\prime}}\left({T}^{^{\prime}}\right)]\) mean that the effect of transport change here is large, cooling the basin. Furthermore, this transport change manifests differently in different models (Fig. 12f, h). Indeed, the large spread in total heat uptake south of Iceland (Fig. 12b) results mostly from the redistribution of unperturbed temperature (Fig. 12f), with \(\Delta h[{\Phi }^{^{\prime}}\left({T}^{^{\prime}}\right)]\) and \(\Delta h[\stackrel{-}{\Phi }({T}^{^{\prime}})]\) also playing smaller roles.
Moderate heat storage per unit area by the Arctic Ocean is commonly predicted across AOGCMs, but there are large differences between them (Fig. 12a, b). Here, the total OHC change has contributions from all three components: \(\Delta h[\stackrel{-}{\Phi }({T}^{^{\prime}})]\) and \(\Delta h[{\Phi }^{^{\prime}}\left({T}^{^{\prime}}\right)]\) are strongly positive while \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) is negative. Similarly, the spread of OHU has roots in all three components (Fig. 12d, f, h), highlighting that the mechanisms of Arctic heat uptake are highly model dependent. Since the heat flux perturbation into the Arctic is quite weak, the OHC change results from the oceanic transport of heat. Some of the added heat is brought into the basin by the unperturbed transport, (Fig. 12c). The negative values of \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) (Fig. 12e), indicate reduced poleward transport of unperturbed heat, possibly due to the weakened AMOC (although reduced heat transport through the Bering Strait cannot be ruled out). The widespread positive \(\Delta h[{\Phi }^{^{\prime}}\left({T}^{^{\prime}}\right)]\) in the Arctic (Fig. 12g) could be explained by the following mechanism: the heat flux perturbation causes a weakened Atlantic overturning, which causes added heat to flow northwards into the Arctic from the North Atlantic and/or North Pacific instead of being subducted and transported equatorward. Further work should explore whether such a mechanism is at work.
The equatorial Atlantic shows moderate area-weighted OHU (Fig. 12a). The equatorial Atlantic OHU is mostly driven by\(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\), (Fig. 12e) and passive heat storage is important in the west, (Fig. 12c). The local heat flux perturbation is near zero (Fig. 1a) and so the heat content change here is mostly a consequence of \(\Phi\)′, rather than T′. These results echo previous work, which also identify an important role of active transport change in the low latitudes (e.g. Garuba and Klinger 2018). This is one of the few locations where the redistribution of unperturbed heat has a large positive depth integral. Elsewhere in the tropics, although \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) is a large component, the total heat storage per area is smaller (Fig. 12a). In the western basin, \(\Delta h[{\Phi }^{^{\prime}}\left({T}^{^{\prime}}\right)]\) is weakly negative, in contrast with the eastern. This could be consistent with a weakened poleward transport of heat causing an accumulation of unperturbed and added heat, and a coincident reduced westward equatorial transport of added heat. Reduced upwelling of unperturbed temperature as a part of the weakened poleward transport of unperturbed heat could explain the accumulation of \(\Delta h[{\Phi }^{^{\prime}}\left(\stackrel{-}{T}\right)]\) here. Changes in the subtropical and subpolar gyre circulation (and the exchange of heat between them) as suggested by previous authors could also play a role that has not yet been explored. A complete explanation is currently lacking but warranted (Boeira Dias et al. 2020).
4 Discussion
4.1 Diversity of sea-level response to common air-sea flux perturbation
The largest and most widespread features of dynamic sea-level change in response to 1pctCO2 forcing have been shown to result mostly from the change in air-sea heat flux. Further, the inter-model uncertainty of the pattern of Δζ results from model-specific ocean transport responses to standardized air-sea flux changes, rather than diversity in the flux changes themselves. For the most part, the spread in response to heat flux perturbation relates to different models responding with a similar pattern of sea-level change, whose magnitude differs across models. The North Atlantic hosts a large diversity of Δζ across models, but although the geographic pattern is different across models, the sea-level changes have similar dynamical origins. We find that the North Atlantic inter-model variance is mostly due to the redistribution of preindustrial heat being different in each model, probably in turn due to the spread in predicted weakening of the AMOC. The spread of Δζ also has smaller contributions from uptake of added heat by both the perturbed and unperturbed transport. Part of the spread of North Atlantic sea-level change arises because added heat penetrates into the deep ocean in deep convection sites that are geographically different among models (Bouttes et al. 2014), but this reason is found to be secondary in our analysis. Other authors pointed out that ocean heat uptake is sensitive to model-specific factors such as SST biases (He and Soden 2016), mesoscale eddy transfer (Exarchou et al. 2015; Saenko et al. 2018), stratification (Huber and Zanna 2017) and the isopycnal diffusion scheme (Exarchou et al. 2015). These factors may explain why the models that we have examined show similar horizontal patterns of heat uptake with differing magnitudes even though these models are forced with identical heat inputs.
Previous work has highlighted that individual models when forced with different surface fluxes can produce diverse ocean responses in terms of sea level (Bouttes and Gregory 2014) and ocean heat uptake (Huber and Zanna 2017). Indeed, the uncertainty in surface fluxes is key challenge for climate modelling. By forcing different AOGCMs with common flux perturbations the spread of sea-level projections can be more directly attributed to the diversity of ocean model formulation than in prior studies. Huber and Zanna (2017) tested the parametric uncertainty of a single a model (i.e. the sensitivity of ocean heat uptake to the choice of parameter values), finding it to be small. Parametric uncertainty is only a subset of the total uncertainty due to the different representation of ocean processes in models (Zanna et al. 2018). Therefore, while previous work shows that accurate representation of surface fluxes is essential in climate simulations, our findings add that the use of ocean models with differing structures is also a key uncertainty. Nevertheless, there is clearly still more to learn about the link between the diversity caused by differences in surface fluxes versus differing ocean models. For instance, differences in ocean model design may lead to differences in steady state properties (e.g. stratification strength, mean temperature, overturning strength etc.), which in turn affect the steady state air-sea fluxes as well as the system’s sensitivity to change. On the other hand, one could argue that changes in air-sea fluxes that result from the ocean response to common flux forcing are the result of each ocean component’s unique sensitivity to forcing. While previous studies and the present study have separated the spread due to ocean models and the spread due to air-sea flux change in different ways, clearly they affect each other and this connection is not yet fully understood.
4.2 Role of individual and simultaneous flux perturbations causing key regional sea-level changes
One of the key features of the sea-level response to heat flux forcing was the contrast in meridional dipoles in the North Pacific and North Atlantic (Gregory et al. 2016). In the North Atlantic, the meridional dipole is positive to the north, while in the North Pacific, it is positive to the south. The opposite dipoles are consistent with recent work investigating why the Kuroshio current is predicted to strengthen in AOGCM simulations of climate change, whereas the Gulf Stream weakens (Chen et al. 2019). Those authors described how the air-sea heat flux that results from a warming climate causes stronger warming to the east of the Kuroshio than to the west, steepening the across-current density slope. In the North Atlantic, the heat flux change causes a reduction of northward salinity transport that freshens the high latitudes, reducing the across-current slope and weakening the current. This is consistent with the dynamic sea-level changes that result from FAF-heat. The thermosteric change tends to steepen the across-current slope of the Gulf Stream, but this is counteracted by the larger opposing effect of haline contraction. Our results show that the intensity and pattern of Kuroshio strengthening is similar across models, but the change in the North Atlantic is more uncertain across models (Fig. 12f). The Gulf Stream dipole, unlike the Kuroshio dipole, is likely to be affected by the AMOC weakening, and so will be different for each model. Further, Bouttes and Gregory (2014) reported that the sea-level change in the western North Pacific was caused by both the wind stress and heat flux perturbations. In our ensemble, not every model’s Kuroshio and extension regions were sensitive to wind forcing.
The water flux perturbation shows the smallest changes of all three perturbations when applied alone, but it nevertheless has important local effects in parts of the Southern Ocean, Arctic and subpolar North Atlantic. However, the importance of the water flux change may be underestimated by considering experiments in which only one flux is varied because of nonlinear interactions between flux perturbations. Other work has described how the sea-level responses to individually applied flux perturbations combine approximately linearly (Bouttes and Gregory 2014), which we also find is true to first order. However, we have identified that the nonlinear interaction between the three forcings is model dependent, which cannot be understood from a multi-model mean perspective. Models such as GFDL-ESM2M and MRI-ESM2-0 show strong nonlinear amplification of the sea-level response in the North Atlantic when all fluxes are perturbed simultaneously. Further, other work has shown that perturbing freshwater fluxes increases the uptake of heat by the subpolar Atlantic (Garuba and Klinger 2018).
The Southern and Arctic Oceans host many local features of dynamic sea-level change that are model specific. Coupled models (including the ones analysed here) show markedly different sea-ice extents and sensitivities to forcing (Turner et al. 2013). It seems likely that at least some of the model spread in projections of ∆ζ stems from the fact that sea-ice thermodynamics are model specific. The Weddell Gyre and its heat budget are thought to be sensitive to regional wind forcing (Jullion et al. 2010; Saenko et al. 2015). The spread of ∆ζ and ∆ζT in response to FAF-stress in the western Weddell Gyre indicates that some models show a significant thermosteric response to intensified westerlies. Inter-model differences in Arctic dynamic sea-level change and heat uptake have very different mechanisms for each model. The diversity of Arctic climate responses forcing is not necessarily limited to the representation of the oceans, but perhaps also poor representation of ice albedo and cloud feedbacks (Karlsson and Svensson 2013), biases in the unperturbed state (Franzke et al. 2017) or other factors that have not been explored.
The east Atlantic “tropical arm” of positive ∆ζ in response to heat flux forcing is halosteric, but is not predicted by all models. The analysis of ocean heat content therefore yields little information about the cause of the feature. The feature bears strong resemblance to the tropical arm SST anomalies characteristic of the Atlantic Multidecadal Variability (Yuan et al. 2016), however, our ∆ζ feature is the result of 70 years of integration of step forcing rather than variability, and is a vertical integral signal rather than purely SST. Nevertheless, the similarity between that pattern of variability and the forced response we present suggests common driving mechanisms may be responsible. In the context of the AMV, the tropical arm is thought to arise in response to midlatitude warm SST anomalies that weaken the tropical trade winds, which reduce low cloud and dust loading, thereby warming tropical SST (Yuan et al. 2016). Observations and some models show that the tropical SST arm coincides with freshening in the upper 50 m (Kavvada et al. 2013), which is consistent with the positive ∆ζS response to FAF-heat. The origin of the freshening in our simulations is not known, and the roles of input from the subpolar Atlantic, the Mediterranean or elsewhere are not ruled out. Whether this is driven by the atmospheric response to forcing, the thermohaline circulation or a mixture of effects is not clear, but merits further investigation.
4.3 Caveats, unmodeled processes and further outlook
FAFMIP experiments were designed to provide insight into the causes of model spread in greenhouse gas-forced climate change experiments, particularly the 1pctCO2 experiment. The design aimed to mimic the magnitude of 100 years of 1pctCO2 forcing, but the North Atlantic redistribution feedback (wherein the perturbation weakens the AMOC, causing an advection-driven cooling and increasing the air-sea heat flux into the North Atlantic, see Sects. 2.2 and 3.1) causes the total heat input into the North Atlantic to be larger than the just the imposed perturbation (Gregory et al. 2016). Todd et al. (2020) investigated the strength of this unwanted feedback by forcing ocean-only models (which have no redistribution feedback) with the same heat flux perturbation as this study, and compared the ocean heat transport response with the response of coupled AOGCMs (which do have the feedback). Those authors find that the feedback causes an additional 10% AMOC weakening versus the change that occurs in fully coupled AOGCMs. The feedback affects the North Atlantic heat uptake and transport, but has limited impact elsewhere and its effect on global ocean heat uptake is smaller than the perturbation of interest. In the AOGCMs we examine, global total heat uptake is about 10% greater than the area- and time-integral of the imposed perturbation. Therefore, the forced changes in the North Atlantic presented in this work are larger than one would expect from 100 years of 1pctCO2 forcing. Nevertheless, the fact that the imposed perturbation is common to all models matters more than the precise magnitude, when investigating the sensitivity of ocean model responses to common forcing.
Previous work investigating ‘pattern scaling’ has shown that the spatial structure of sea-level change remains similar across a range of magnitudes of forcing (Hawkes 2013; Perrette et al. 2013; Slangen et al. 2014; Bilbao et al. 2015). The spatial patterns of change and the underlying drivers presented here are therefore likely to be qualitatively applicable to greenhouse gas-forced experiments. Nevertheless, the sensitivity of the ocean response to different heat inputs into the North Atlantic is an open area of research, and will be further investigated in future work. Additional FAFMIP experiments, which apply heat inputs like those presented here, except with differing magnitudes in the North Atlantic, are already underway, and will be presented in future work.
FAFMIP experiments do not account for the input of freshwater by the melting of the Greenland and Antarctic ice sheets. Over the North Atlantic area (50°–70° N, 70° W–30° E), the freshwater perturbation integrates to a freshwater input of 0.007 Sv (1 Sv = 106 m3 s−1). This is comparable in magnitude to the input of 0.006 Sv (0.00065 m year−1 or 0.01625 m of global mean sea-level rise) of meltwater from the Greenland Ice Sheet (GIS) over 1993–2018 (Frederikse et al. 2020), albeit applied for a much longer duration. Recent projections (Oppenheimer et al. 2019) of the GIS contribution to global mean sea-level rise by the year 2100 relative to 2000 across the full range of emissions scenarios are 0.063 to 0.119 m (0.00063–0.00119 m year−1), which corresponds to a freshwater input of about 0.007–0.013 Sv. This rough comparison suggests that the rate of addition of meltwater from the GIS alone is 1–1.8 times stronger than the local water flux perturbation in the North Atlantic. The water flux perturbation in the Southern Ocean (south of 45° S) integrates to 0.115 Sv. The Antarctic Ice Sheet (AIS) loss contribution to recent historical global mean sea-level rise is smaller than that of the GIS, at 0.00032 m year−1 or 0.008 m over 1993–2018, approximately 0.003 Sv (Frederikse et al. 2020). The AIS, unlike the GIS, is dominated by marine melting (Paolo et al. 2015; Wouters et al. 2015), a coupled atmosphere-ice sheet-ocean process that cannot yet be fully interactively represented in climate models (Oppenheimer et al. 2019). As such, projections of the AIS contribution to future global mean sea level remain highly uncertain, although recent estimates of the AIS have an across-scenario range of 0.040–0.120 m by the year 2100 relative to 2000 (Oppenheimer et al. 2019), equivalent to 0.0004–0.0012 m year−2 or 0.004–0.013 Sv. The AIS contributions are therefore on the order of 0.03–0.1 times the perturbation imposed over the Southern Ocean. The water flux perturbation studied here was sufficient to produce features of regional sea-level change 0.05–0.1 m greater than the global mean in the Northwestern Atlantic and the coastal Southern Ocean. The missing GIS and AIS meltwater contributions (which are locally of a similar order to the freshwater perturbation that we imposed) could plausibly enhance the local freshwater-forced sea-level changes by an amount the order of 0.01–0.1 m, especially in the northwestern Atlantic. Note that this rough estimate of unmodeled meltwater contributions is not intended as a quantitative account, but instead serves to highlight a need for experiments that include these effects (Nowicki et al. 2016).
Gravitational, rotational and deformational (GRD) processes associated with ice mass loss to the oceans, which typically impose a negative feedback on sea-level rise by elevating retreating glaciers away from marine heat, are also not accounted for in this study. However, the magnitude of these effects is too small to reduce the rate of AIS melting over the twenty-first century sea-level rise, and become more important after the year 2250 (Larour et al. 2019; Oppenheimer et al. 2019). More generally though, GRD processes are vital in the determination of local relative sea-level change through the 21st Century and beyond (Mitrovica et al. 2011; Oppenheimer et al. 2019). The complex interaction between atmosphere–ocean-ice sheet-GRD processes makes it difficult to speculate about the net effects of all processes, and highlights a need to interactively simulate all such elements of the system.
Echoing findings from the previous generation of coupled atmosphere–ocean climate models, the regions showing the largest dynamic sea-level changes at the end of the twenty-first century also show the largest inter-model uncertainty (Church et al. 2013, Figs., 3, 4). Regions with both large projected changes and large uncertainty are the northwestern Atlantic, the Arctic, parts of the Southern Ocean and the northwest Pacific. This uncertainty highlights an ongoing need to better understand the reasons for diverse predictions of ocean transport change in these regions. This inter-model spread cannot presently be readily reduced by excluding models, since it is not trivial to determine the relative robustness of each AOGCM projection. Accordingly, the upper and lower limits of future sea-level scenarios should be constructed with the consideration that the dynamic sea level in these regions could be larger or smaller than the multi-model ensemble mean suggests. There is an increasing understanding that the diversity of cloud feedbacks is an important cause of the variations of climate sensitivity across different AOGCMs (Zelinka et al. 2020). Establishing realistic representations of cloud feedbacks in AOGCMs is therefore a key step to reduce the spread future climate and sea-level projections. Regarding ocean components, Lyu et al. (2020) have recently attributed the spread of sea-level projections to biases in model mean states, and so the reduction of such biases remains an important goal for climate projection.
5 Conclusions
This work documents how FAFMIP experiments are useful tools to derive a new understanding of the drivers of dynamic sea-level change in idealized greenhouse gas forcing experiments. Notably, these latest FAFMIP results show that:
-
Most of the spread of predictions of dynamic sea-level change in response to idealised greenhouse gas forcing by AOGCMs can be reproduced by forcing models with common air-sea flux perturbations. These findings show that the diverse representation of the ocean component in climate models is a key uncertainty in sea-level projection under greenhouse gas forcing.
-
The increased air-sea heat flux associated with greenhouse gas forced climate change sets the broad spatial pattern of dynamic sea-level change. The dynamic sea-level changes that result from the changing freshwater flux and wind stress have important effects locally but are smaller contributors to the global change.
-
The main effect of the wind-stress change is to rearrange the distribution of heat in the Southern Ocean, which steepens the meridional sea-level gradient.
-
The sea-level response to the change in surface freshwater flux is mostly confined to the Arctic and the Southern Ocean south of Australia and New Zealand, although models disagree on whether North Atlantic is affected significantly.
-
The Southern Ocean absorbs a large portion of the added heat perturbation, where models agree that most of this heat is taken up like a passive tracer, without strongly affecting the local transport.
-
The flux perturbations create nonlinear dynamic sea-level responses when applied simultaneously, especially in the Arctic and the North Atlantic, but the details are different across models.
FAFMIP simulations provide new avenues to probe the sea-level response to greenhouse gas forcing, and ocean heat-content change generally. The results presented here represent a step highlighting where AOGCMs give diverse predictions of sea-level change because of their different ocean models. Many details of local processes that cause the sea-level changes described here remain to be fully explored. We have highlighted that a key source of spread of AOGCM predictions of sea-level change in the North Atlantic is because the change of local transport is highly model dependent; subsequent work should uncover what characteristics of ocean models cause this. AOGCMs give diverse predictions about Arctic heat uptake, owing to the interaction between passive and active heat uptake processes that call for more detailed examination. Further process-based analysis of FAFMIP simulations will shed new light on the key areas of uncertainty highlighted here.
References
Bentsen M et al (2013) The Norwegian earth system model, NorESM1-M—Part 1: description and basic evaluation of the physical climate. Geosci Model Dev 6:687–720
Bi D et al (2020) Configuration and spin-up of ACCESS-CM2, the new generation Australian Community Climate and Earth System Simulator Coupled Model. J South Hemisph Earth Syst Sci (in review)
Bilbao RAF, Gregory JM, Bouttes N (2015) Analysis of the regional pattern of sea level change due to ocean dynamics and density change for 1993–2099 in observations and CMIP5 AOGCMs. Clim Dyn 45:2647–2666. https://doi.org/10.1007/s00382-015-2499-z
Boeira Dias F, Fiedler R, Marsland SJ, Domingues CM, Rintoul SR, McDonagh EL, Mata MM, Savita A (2020) Ocean heat storage in response to changing ocean circulation processes. J. Clim 33:9065–9082
Boucher O et al (2020) Presentation and evaluation of the IPSL-CM6A-LR climate model. J Adv Model Earth Syst 12:1–52 (e2019MS002010)
Bouttes N, Gregory JM (2014) Attribution of the spatial pattern of CO2-forced sea level change to ocean surface flux changes. Environ Res Lett 9:34004
Bouttes N, Gregory JM, Kuhlbrodt T, Smith RS (2014) The drivers of projected North Atlantic sea level change. Clim Dyn 43:1531–1544
Bronselaer B, Zanna L (2020) Heat and carbon coupling reveals ocean warming due to circulation changes. Nature 584:227–233
Ceppi P, Brient F, Zelinka MD, Hartmann DL (2017) Cloud feedback mechanisms and their representation in global climate models. Wiley Interdiscip Rev Clim Chang 8:e465
Chen C, Wang G, Xie S-P, Liu W (2019) Why does global warming weaken the Gulf stream but intensify the Kuroshio? J Clim 32:7437–7451
Church JA et al (2013) Sea Level Change. In: Stocker TF et al (eds) Climate Change 2013: The Physical Science Basis Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, pp 1137–1216
Collier MA et al (2011) The CSIRO-Mk3. 6.0 Atmosphere-Ocean GCM: participation in CMIP5 and data publication. In: International Congress on Modelling and Simulation–MODSIM. pp 2691–2697. https://doi.org/10.36334/modsim.2011.F5.collier
Danabasoglu G et al (2020) The community earth system model version 2 (CESM2). J Adv Model Earth Syst 12:e2019MS001916
Dufresne J-L et al (2013) Climate change projections using the IPSL-CM5 earth system model: from CMIP3 to CMIP5. Clim Dyn 40:2123–2165
Dunne JP et al (2012) GFDL’s ESM2 global coupled climate–carbon earth system models. Part I: physical formulation and baseline simulation characteristics. J Clim 25:6646–6665
Exarchou E, Kuhlbrodt T, Gregory JM, Smith RS (2015) Ocean heat uptake processes: a model intercomparison. J Clim 28:887–908. https://doi.org/10.1175/JCLI-D-14-00235.1
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci Model Dev. https://doi.org/10.5194/gmd-9-1937-2016
Frankcombe LM, Spence P, Hogg AM, England MH, Griffies SM (2013) Sea level changes forced by Southern Ocean winds. Geophys Res Lett 40:5710–5715
Franzke CLE, Lee S, Feldstein SB (2017) Evaluating Arctic warming mechanisms in CMIP5 models. Clim Dyn 48:3247–3260
Frederikse T et al (2020) The causes of sea-level rise since 1900. Nature 584:393–397
Garuba OA, Klinger BA (2018) The role of individual surface flux components in the passive and active ocean heat uptake. J Clim 31:6157–6173
Gettelman A et al (2019) The Whole Atmosphere Community Climate Model Version 6 (WACCM6). J. Geophys. Res, Atmos
Giorgetta MA et al (2013) Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the coupled model intercomparison project phase 5. J Adv Model Earth Syst 5:572–597
Gordon C, Cooper C, Senior CA, Banks H, Gregory JM, Johns TC, Mitchell JFB, Wood RA (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Dyn Clim. https://doi.org/10.1007/s003820050010
Gregory JM et al (2016) The Flux-Anomaly-Forced Model Intercomparison Project (FAFMIP) contribution to CMIP6: Investigation of sea-level and ocean climate change in response to CO2 forcing. Geosci Model Dev 9:3993–4017. https://doi.org/10.5194/gmd-9-3993-2016
Gregory JM et al (2019) Concepts and terminology for sea level: mean, variability and change, both local and global. Surv Geophys 40:1251–1289
Griffies SM et al (2011) The GFDL CM3 coupled climate model: characteristics of the ocean and sea ice simulations. J Clim 24:3520–3544
Griffies SM et al (2016) OMIP contribution to CMIP6: Experimental and diagnostic protocol for the physical component of the Ocean Model Intercomparison Project. Geosci Model Dev 9:3231–3296. https://doi.org/10.5194/gmd-9-3231-2016
Hawkes PJ (2013) Sea level change. Cambridge University Press, Cambridge, pp 895–900
He B et al (2020) CAS FGOALS-f3-L model dataset descriptions for CMIP6 DECK experiments. Atmos Ocean Sci Lett. https://doi.org/10.1080/16742834.2020.1778419
He J, Soden BJ (2016) The impact of SST biases on projections of anthropogenic climate change: a greater role for atmosphere-only models? Geophys Res Lett. https://doi.org/10.1002/2016GL069803
Held IM, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19:5686–5699
Hu X, Taylor PC, Cai M, Yang S, Deng Y, Sejas S (2017) Inter-model warming projection spread: inherited traits from control climate diversity. Sci Rep. https://doi.org/10.1038/s41598-017-04623-7
Huber MB, Zanna L (2017) Drivers of uncertainty in simulated ocean circulation and heat uptake. Geophys Res Lett 44:1402–1413
Jullion L, Jones SC, Naveira Garabato AC, Meredith MP (2010) Wind-controlled export of Antarctic Bottom Water from the Weddell Sea. Geophys Res Lett. https://doi.org/10.1029/2010GL042822
Karlsson J, Svensson G (2013) Consequences of poor representation of Arctic sea-ice albedo and cloud-radiation interactions in the CMIP5 model ensemble. Geophys Res Lett 40:4374–4379
Kavvada A, Ruiz-Barradas A, Nigam S (2013) AMO’s structure and climate footprint in observations and IPCC AR5 climate simulations. Clim Dyn 41:1345–1364
Kelley et al (2020) GISS-E21: configurations and climatology. J Adv Model Earth Syst 12:e2019MS002025
Kiss AE et al (2020) ACCESS-OM2 v1. 0: a global ocean-sea ice model at three resolutions. Geosci Model Dev 13:401–442
Kostov Y, Armour KC, Marshall J (2014) Impact of the Atlantic meridional overturning circulation on ocean heat storage and transient climate change. Geophys Res Lett 41:2108–2116
Kuhlbrodt T et al (2018) The low-resolution version of HadGEM3 GC3.1: development and evaluation for global climate. J Adv Model Earth Syst 10:2865–2888
Landerer FW, Jungclaus JH, Marotzke J (2007) Ocean bottom pressure changes lead to a decreasing length-of-day in a warming climate. Geophys Res Lett. https://doi.org/10.1029/2006GL029106
Larour E, Seroussi H, Adhikari S, Ivins E, Caron L, Morlighem M, Schlegel N (2019) Slowdown in Antarctic mass loss from solid Earth and sea-level feedbacks. Science 364:eaav7908
Li L et al (2013) The flexible global ocean-atmosphere-land system model, Grid-point Version 2: FGOALS-g2. Adv Atmos Sci 30:543–560
Liu W, Lu J, Xie S-P, Fedorov A (2018) Southern Ocean heat uptake, redistribution, and storage in a warming climate: the role of meridional overturning circulation. J Clim 31:4727–4743
Lowe JA, Gregory JM (2006) Understanding projections of sea level rise in a Hadley Centre coupled climate model. J Geophys Res Ocean 111:1–12. https://doi.org/10.1029/2005JC003421
Lyu K, Zhang X, Church JA (2020) Regional dynamic sea level simulated in the CMIP5 and CMIP6 models: mean biases, future projections, and their linkages. J. Clim 33:6377–6398
Martin GM et al (2011) The HadGEM2 family of Met Office Unified Model climate configurations. Geosci Model Dev. https://doi.org/10.5194/gmd-4-723-2011
Mauritsen T et al (2019) Developments in the MPI-M Earth System Model version 1.2 (MPI-ESM1. 2) and its response to increasing CO2. J Adv Model Earth Syst 11:998–1038
McDougall TJ, Barker PM (2011) Getting started with TEOS-10 and the Gibbs Seawater (GSW) oceanographic toolbox. SCOR/IAPSO WG 127:1–28
Melet A, Meyssignac B (2015) Explaining the spread in global mean thermosteric sea level rise in CMIP5 climate models. J Clim 28:9918–9940
Meredith MP et al (2019) Polar regions. In: Pörtner H-O et al (eds) IPCC special report on the ocean and cryosphere in a changing climate. pp 203–320, in press. Available: https://www.ipcc.ch/srocc/
Mitrovica JX, Gomez N, Morrow E, Hay C, Latychev K, Tamisiea ME (2011) On the robustness of predictions of sea level fingerprints. Geophys J Int 187:729–742
Nowicki SMJ et al (2016) Ice sheet model intercomparison project (ISMIP6) contribution to CMIP6. Geosci Model Dev 9:4521
Oppenheimer M, Glavovic BC, Hinkel J, van de Wal R, Magnan AK, Abd-Elgawad A, Cai R, CifuentesJara M, DeConto RM, Ghosh T, Hay J, Isla F, Marzeion B, Meyssignac B, Sebesvari Z (2019) Sea level rise and implications for low-lying islands, Coasts and Communities. In: Pörtner H-O, Roberts DC, Masson-Delmotte V, Zhai P, Tignor M, Poloczanska E, Mintenbeck K, Alegriá A, Nicolai M, Okem A, Petzold J, Rama B, Weyer NM (eds) IPCC special report on the ocean and cryosphere in a changing climate. pp 321–445, In press. Available: https://www.ipcc.ch/srocc/
Paolo FS, Fricker HA, Padman L (2015) Volume loss from Antarctic ice shelves is accelerating. Science 348:327–331
Park S, Shin J, Kim S, Oh E, Kim Y (2019) Global Climate Simulated by the Seoul National University Atmosphere Model Version 0 with a Unified Convection Scheme (SAM0-UNICON). J Clim 32:2917–2949
Perrette M, Landerer F, Riva R, Frieler K, Meinshausen M (2013) A scaling approach to project regional sea level rise and its uncertainties. Earth Syst Dyn. https://doi.org/10.5194/esd-4-11-2013
Ponte RM (2006) Low-frequency sea level variability and the inverted barometer effect. J Atmos Ocean Technol 23:619–629
Rugenstein MAA, Winton M, Stouffer RJ, Griffies SM, Hallberg R (2013) Northern high-latitude heat budget decomposition and transient warming. J Clim 26:609–621
Saenko OA, Yang D, Gregory JM, Spence P, Myers PG (2015) Separating the influence of projected changes in air temperature and wind on patterns of sea level change and ocean heat content. J Geophys Res Ocean 120:5749–5765
Saenko OA, Yang D, Gregory JM, Spence P, Myers PG (2018) Impact of mesoscale Eddy transfer on heat uptake in an Eddy-parameterizing ocean model. J Clim 31:8589–8606
Schmidt GA et al (2014) Configuration and assessment of the GISS ModelE2 contributions to the CMIP5 archive. J Adv Model Earth Syst 6:141–184
Séférian R et al (2019) Evaluation of CNRM earth-system model, CNRM-ESM 2–1: role of earth system processes in present-day and future climate. J Adv Model Earth Syst 11:4182–4227
Slangen ABA, Katsman CA, Van de Wal RSW, Vermeersen LLA, Riva REM (2012) Towards regional projections of twenty-first century sea-level change based on IPCC SRES scenarios. Clim Dyn 38:1191–1209
Slangen ABA, Carson M, Katsman CA, Van de Wal RSW, Köhl A, Vermeersen LLA, Stammer D (2014) Projecting twenty-first century regional sea-level changes. Clim Change 124:317–332
Stammer D, Cazenave A, Ponte RM, Tamisiea ME (2013) Causes for contemporary regional sea level changes. Ann Rev Mar Sci 5:21–46
Stewart KD, Hogg AM (2019) Southern Ocean heat and momentum uptake are sensitive to the vertical resolution at the ocean surface. Ocean Model 143:101456
Swart NC et al (2019) The Canadian Earth System Model version 5 (CanESM5.0.3). Geosci Model Dev Discuss. https://doi.org/10.5194/gmd-2019-177
Tatebe H et al (2019) Description and basic evaluation of simulated mean state, internal variability, and climate sensitivity in MIROC6. Geosci Model Dev 12:2727–2765
Todd A et al (2020) Ocean-only FAFMIP: understanding regional patterns of Ocean Heat Content and dynamic sea level change. J Adv Model Earth Syst 12:e2019MS002027
Turner J, Bracegirdle TJ, Phillips T, Marshall GJ, Hosking JS (2013) An initial assessment of Antarctic sea ice extent in the CMIP5 models. J Clim 26:1473–1484
Voldoire A et al (2013) The CNRM-CM5. 1 global climate model: description and basic evaluation. Clim Dyn 40:2091–2121
Voldoire A et al (2019) Evaluation of CMIP6 DECK experiments with CNRM-CM6-1. J Adv Model Earth Syst 11:2177–2213. https://doi.org/10.1029/2019MS001683
Volodin EM, Dianskii NA, Gusev AV (2010) Simulating present-day climate with the INMCM4. 0 coupled model of the atmospheric and oceanic general circulations. Izv Atmos Ocean Phys 46:414–431
Watanabe M et al (2010) Improved climate simulation by MIROC5: mean states, variability, and climate sensitivity. J Clim 23:6312–6335
Watanabe S et al (2011) MIROC-ESM 2010: Model description and basic results of CMIP5-20c3m experiments. Geosci Model Dev 4:845
Winton M, Griffies SM, Samuels BL, Sarmiento JL, Frölicher TL (2013) Connecting changing ocean circulation with changing climate. J Clim 26:2268–2278
Wouters B, Martin-Español A, Helm V, Flament T, van Wessem JM, Ligtenberg SRM, Van den Broeke MR, Bamber JL (2015) Dynamic thinning of glaciers on the Southern Antarctic Peninsula. Science 348:899–903
Xie P, Vallis GK (2012) The passive and active nature of ocean heat uptake in idealized climate change experiments. Clim Dyn 38:667–684
Xin Y, Dai Y, Li J, Rong X, Zhang G (2019) Coupling the common land model to echam5 atmospheric general circulation model. J Meteorol Res 33:251–263
Yang D, Saenko OA (2012) Ocean heat transport and its projected change in CanESM2. J Clim. https://doi.org/10.1175/JCLI-D-11-00715.1
Yin J, Schlesinger ME, Stouffer RJ (2009) Model projections of rapid sea-level rise on the northeast coast of the United States. Nat Geosci 2:262–266
Yin J, Griffies SM, Stouffer RJ (2010) Spatial variability of sea level rise in twenty-first century projections. J Clim 23:4585–4607
Yuan T, Oreopoulos L, Zelinka M, Yu H, Norris JR, Chin M, Platnick S, Meyer K (2016) Positive low cloud and dust feedbacks amplify tropical North Atlantic Multidecadal Oscillation. Geophys Res Lett 43:1349–1356
Yukimoto S et al (2012) A new global climate model of the Meteorological Research Institute: MRI-CGCM3—model description and basic performance. J Meteorol Soc Japan Ser II 90:23–64
Yukimoto S et al (2019) The Meteorological Research Institute Earth System Model version 2.0, MRI-ESM2.0: description and basic evaluation of the physical component. J Meteorol Soc Japan Ser II 97:931–965. https://doi.org/10.2151/jmsj.2019-051
Zanna L, Brankart JM, Huber M, Leroux S, Penduff T, Williams PD (2018) Uncertainty and scale interactions in ocean ensembles: From seasonal forecasts to multidecadal climate predictions. Q J R Meteorol Soc 145:160–175. https://doi.org/10.1002/qj.3397
Zelinka MD, Myers TA, McCoy DT, Po-Chedley S, Caldwell PM, Ceppi P, Klein SA, Taylor KE (2020) Causes of higher climate sensitivity in CMIP6 models. Geophys Res Lett 47:e2019GL085782
Acknowledgements
We acknowledge the World Climate Research Programme's Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modelling groups for producing and making available their model output. We thank the Earth System Grid Federation (ESGF) for archiving the data and providing access, and the multiple funding agencies who support CMIP6 and ESGF. This work was supported in part by grant NE/R000727/1 from the UK Natural Environment Research Council as a contribution to the WCRP’s Grand Challenge on Regional Sea Level Change and Coastal Impacts. OG and AH were supported by the Regional and Global Model Analysis (RGMA) component of the Earth and Environmental System Modeling (EESM) program of the U.S. Department of Energy's Office of Science Biological and Environmental Research (BER), as a contribution to the HiLAT-RASM and CATALYST projects. OG also acknowledges helpful discussions with Phil Rasch. Contributions from JJ, AK, SO and DS were supported in part through the Deutsche Forschungs Gemeinschaft (DFG) as part of the SPP 1889 on “Regional sea level change and society”. ACCESS-CM2 simulations were supported by NCMAS and NCI-STRESS2020 grants through the National Computing Infrastructure National Facility at the Australian National University. FBD and A. Savita were supported by a Tasmanian Graduate Research Scholarship and CSIRO-UTAS Quantitative Marine Science top-up. A. Savita, SJM and PD were supported by projects jointly funded through CSIRO and the Earth Systems and Climate Change Hub of the Australian Government’s National Environmental Science Programme. CMD was supported by the Australian Research Council (FT130101532 and DP160103130) and UK’s Natural Environment Research Council (NE/P019293/1). A. Savita, FBD, PD,SJM, CMD are thankful for the support from the Consortium for Ocean-Sea Ice Modelling in Australia (COSIMA). TS and MI were supported by the Integrated Research Program for Advancing Climate Models (TOUGOU) Grant Number JPMXD0717935457 and JPMXD0717935561 the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, respectively. A. Shao was supported by the Marine Environmental Observation Prediction & Response (MEOPAR) network. This work was supported by grant ly62 from the National Computational Infrastructure.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Time evolution of temperature tracers
Consider the time evolution of Tr, Ta and T, adapted from Eqs. (8) to (10) in (Gregory et al. 2016).
where \(\Phi\) is the transport operator and \(\Phi^{\prime}\overline{T}\) is symbolically \(- \nabla \, \cdot \,\left( {{\varvec{u}}^{\prime } \overline{T} + {\varvec{P}}^{\prime } } \right)\), where u is the three dimensional resolved velocity field, P is the action of parameterized subgrid-scale tracer transport processes and parentheses around \(\overline{\Phi } + \Phi^{\prime}\) indicates the action of both the unperturbed and perturbed circulation on the temperature noted after the parentheses. Equation (16) implies that
i.e. that the anomaly T′ can be decomposed into added and redistributed parts. Initially, all the terms are zero. When we switch on the heat forcing, F, the initial tendencies are
Therefore after some time dt, we have
because T′ is now non-zero, densities change, so \(\Phi^{\prime}\) becomes non-zero, and
where \(dT_{a} = Fdt\). So we can symbolically identify four terms contributing to \(\frac{{\partial T^{\prime } }}{\partial t}\) by (16). F is of zeroth-order size, and each d means of the next order in small quantities. The leading order terms in each category are listed in Table 3.
After another timestep, more terms then appear.
Since Tr is now non-zero, we have
ignoring the fact that \({\Phi }^{^{\prime}}\) will have changed since T′ has, and also ignoring Q′ in (14). The order of these terms after two timesteps is described in Table 4.
All other terms are of a smaller order. Thus the perturbation T′ is still dominated by Ta′. Symbolically, \(\stackrel{-}{\Phi }\left({\Phi }{{^{\prime}}}(T)\right)\) and \(\stackrel{-}{\Phi }\left(\stackrel{-}{\Phi }\left(d{T}_{a}\right)\right)\) are both \(\stackrel{-}{\Phi }({{\rm T}{^{\prime}}})\) terms, but both an order of magnitude smaller than \(\stackrel{-}{\Phi }\left(d{T}_{a}\right)\), which was already present from the previous timestep. Note that the anomalous surface heat flux due to the redistribution feedback Q′ will appear in \({\Phi }{{^{\prime}}}(\stackrel{-}{T})\), even though it is not a convergence of temperature, Eq. (14).
1.2 Responses of individual AOGCMS to flux-anomaly forcing
Maps of ocean dynamic sea-level response to simultaneously applied flux perturbations (FAF-all) for each AOGCM (a–m), with the ensemble mean (n) and standard deviation (o). Output for this experiment was not available for CESM2 (b) or GISS-E2-R-CC (f). The divergent color bar (bottom left) applies to a–n, the sequential color bar (bottom right) applies to o
Maps of ocean dynamic sea-level response to the heat flux perturbation (FAF-heat) for each AOGCM (a–m), with the ensemble mean (n) and standard deviation (o). Output for this experiment was not available for CESM2 (b) or GISS-E2-R-CC (f). The divergent color bar (bottom left) applies to a–n, the sequential color bar (bottom right) applies to o
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Couldrey, M.P., Gregory, J.M., Boeira Dias, F. et al. What causes the spread of model projections of ocean dynamic sea-level change in response to greenhouse gas forcing?. Clim Dyn 56, 155–187 (2021). https://doi.org/10.1007/s00382-020-05471-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05471-4