1 Introduction

Terrestrial precipitation can originate from evaporated moisture in remote continental or oceanic regions, which is then advected through long-distance transport, or from local terrestrial sources. The input of the latter is termed precipitation recycling (PR) (Dirmeyer and Brubaker 2007; Dominguez et al. 2006; Eltahir and Bras 1996; Gimeno et al. 2012; van der Ent et al. 2010). Quantifying the respective contributions to terrestrial precipitation from oceanic moisture transport and the land surface is critical for understanding the water cycle and land-atmosphere coupling strength.

As the highest and widest plateau on Earth and with an average elevation over 4000 m, the Tibetan Plateau (TP) has attracted worldwide attention, not only because of its impacts on Asian and global climate due to its unique topography, but also because of its abundant water resources, despite its remote location from the oceans. It is called the “water tower” of Asia, from where nine major rivers, such as the Yangtze, Yellow, Indus, Ganges, Brahmaputra, Irrawaddy, Salween, Tarim, and Mekong originate (Cuo and Zhang 2017; Gao et al. 2018a; Xu et al. 2008). The abundant precipitation over the TP feeds 1.65 billion people and nearby ecosystems; therefore, understanding the contribution of various moisture sources to the regional precipitation is critical for understanding variations and sustainability of TP water resources.

In the TP, contrasting PR ratios have been reported in the literature, which are summarized in Table 1. The computed PR ratios in the TP can be divided into groups depending on the calculation method used: the isotopic method, PR models and Lagrangian models.

Table 1 Summary of studies on PR ratio in or around the TP
Full size table

The isotopic method is based on observations of the stable oxygen isotope (δ18O) and hydrogen isotope (δD) ratios in precipitation. Using isotopic analysis, Yang et al. (2004) determined the contribution of moisture from different sources to rainfall in the central TP during June and September 1998. They found that 32.06% had its origin in oceanic moisture, 46.86% was from local recycling, and 21.8% from other continental evaporation sources. Also using isotopic data, Kurita and Yamada (2008) reported that PR could range from 30 to 80% in a given precipitation event in the central TP. Results using the isotope method, which derive from observations, could be treated as baseline reference. However, those studies are usually based on short-term observations at a specific location, and are therefore limited to small spatial and temporal scales. To investigate the long-term variability of the PR ratio at large spatial scale, researchers turn to PR analytical models.

PR models are formulations based on moisture conservation equations that are applied to gridded climate datasets to obtain the PR ratio. The simplest method consists in comparing precipitation with the net water-vapor influx into a region. Using this strategy, Curio et al. (2015) argued that the PR ratio could reach up to 63% in the TP, but this estimate is subject to a large uncertainty, because precipitation can be much higher than the net moisture influx and still originate entirely from advection if water vapor from local surface evaporation is not involved in the condensation process (Fitzmaurice 2007; Insua-Costa and Miguez-Macho 2018). Several more elaborate PR models have been proposed since the 1970s, when Budyko (1974) introduced the very idea of PR using a one-dimensional model, which was later improved by Brubaker et al. (1993) by extending it to the two horizontal dimensions. The main assumption in these simplified models is that moisture from local evapotranspiration and that advected from remote location are well mixed in the air column. This implies that the moisture fraction from either origin in precipitation is the same as that in the air, which allows formulating water budget equations that can be solved for the recycling ratio. All analytical recycling models can be considered as generalizations of Budyko’s model and invoked the well-mixed atmosphere assumption until very recently. The well-mixed assumption tends to either underestimate or overestimate regional PR ratios, depending on the precipitation mechanism (Fitzmaurice 2007), because of errors in regions experiencing strong shear (Dominguez et al. 2020). In addition, these PR models usually operate with mean values of water vapor, at least monthly, and ignore changes during shorter periods (i.e., sub-monthly and daily) as well as the water storage term. Studies in the TP using the aforementioned analytical models tend to yield PR ratios smaller than 20% (Dominguez et al. 2006). For example, the PR estimate for the TP is 20.83% when using the method of Brubaker et al. (1993) and ERA-Interim data (Guo and Wang 2014), and 20% in the Yellow River and 7.3% in the Yangtze River Basin of China (Kang et al. 2005), when using the model of Eltahir and Bras (1996) and NCEP/NCAR reanalysis.

Later on, analytical Budyko-based PR models relaxed some of the assumptions in the earlier models. For example, Dominguez et al. (2006) developed an analytical dynamic two-dimensional, semi-Lagrangian recycling model (DRM), which retains the well-mixed atmosphere assumption, but is based on the time-dependent water-balance equation and can calculate daily recycling ratios. Using the DRM model, Hua et al. (2015) estimated the PR ratio for the TP to be about 25% for the annual mean, and approaching 30% in summer. van der Ent et al. (2010) using the WAM model, which is also based on the temporal-dependent water-budget equation, identified the TP as a global hotspot for PR. The recycling ratios across the TP found by van der Ent et al. (2010) were around 5% when computed at the small scale of 1.5° side cells, the resolution of the ERA-I interim data used in the analysis. This is a relatively high value (it is less than 1% at this scale over most regions) for such small areas for computation, and it would probably be greatly increased when considering the TP as a whole for the calculation. Zhang et al. (2017) using the same WAM model and ERA-Interim data estimated a PR ratio of 18% over a large area covering the west and central TP.

Lagrangian models tracking fluid particles in space and time, commonly used in air pollutant or aerosol dispersion studies, are also often employed in the analysis of sources and sinks of atmospheric moisture (Drumond et al. 2008; Nieto et al. 2006; Stohl et al. 2005; Stohl and James 2004; Wernli and Davies 1997), thus providing estimates of the PR ratio. They generally operate on gridded global datasets, similarly to the aforementioned analytical PR models. Using the FLEXPART model, Stohl et al. (2005) and Chen et al. (2012) studied the origin and fate of moisture over the TP in summer, concluding that the moisture departing from the TP is a significant source modulating precipitation in East Asia, and that recycling over the TP is an important part of this process. One shortcoming of the FLEXPART model is that it treats P–E (precipitation minus evapotranspiration) as a whole and cannot separate the contribution of either variable individually. Dirmeyer and Brubaker (2007) proposed a quasi-isentropic backward trajectory model, considering moisture storage variation and allowing for a high-resolution temporal calculation that can trace transient precipitation events. This temporal detail contrasts with the use of time-averaged data in the bulk models, but due to the complexity of this model, it has been seldomly used. Recently, Xu and Gao (2019) employed this method and found approximately 30–40% PR ratios over the TP.

The wide-range of estimated PR ratios using different methods and scales highlights the uncertainty in the water cycle and land-atmosphere coupling strength over the TP. All of the above-mentioned PR models are a posteriori tracking (Curio et al. 2015; Dominguez et al. 2020; Guo and Wang 2014; Hua et al. 2015; van der Ent et al. 2013; Zhang et al. 2017), operating on gridded climate datasets such as GCMs outputs or reanalysis data. Their accuracy is compromised because they neglect the vertical heterogeneity in water vapor transport and assume it to be small when compared with that of the mean horizontal transport at the time resolution of the input data.

The latest-generation PR-estimation analysis tool, known as the water-vapor tracing (WVT) method is an Eulerian water–vapor tagging approach embedded in climate models. It is free from the well-mixed assumption, and tracks evaporation sources precisely within the framework of the climate-model solution. The basis of the moisture tagging technique is to replicate for moisture tracers the prognostic equation for total moisture. It is run in an online mode, and hence computationally expensive. The method was introduced in general circulation models in the 1980s (Bosilovich and Schubert 2002; Bosilovich et al. 2003; Goessling and Reick 2013; Joussaume et al. 1984; Koster et al. 1986; Noone and Simmonds 2002; Numaguti 1999; Werner et al. 2001), and has been successively implemented in regional models starting in 2009 (Arnault et al. 2016; Insua-Costa and Miguez-Macho 2018; Knoche and Kunstmann 2013; Sodemann et al. 2009). The WVT method, when coupled with a global model, allows for investigations at the planetary scale; but it is prone to large biases because of the GCMs’ incapability to represent subgrid-scale complex topography and land characteristics (Insua-Costa and Miguez-Macho 2018; Knoche and Kunstmann 2013; Winschall et al. 2014). WVTs in regional climate models, which employ a much finer resolution and significantly improve the representation of small-scale features of the hydrology cycle, are the better alternative for diagnosing precipitation moisture sources, particularly for extreme-precipitation episodes.

In this study, we used WVTs embedded into the Weather Research and Forecasting (WRF) (Insua-Costa and Miguez-Macho 2018) to investigate the PR ratio over the TP. The purpose of this study is to quantify the PR ratio over the TP, in terms of annual mean and seasonal cycle. In addition, the impacts of different treatments of inland lakes on the calculation of the PR ratio are assessed. The relationship between PR ratio and precipitation is examined, by comparing a normal year with a dry year and 2 wet years. The contributions of evapotranspiration to six moisture species (water vapor, cloud water, rain water, ice, snow, graupel) are also explored. The paper is structured as follows. In Sect. 2, we describe the WVT model and WRF model configurations, data, and methodology. Section 3 evaluates precipitation. The PR ratio is analyzed in Sect. 4, in terms of annual, monthly mean, diurnal cycle. Section 5 investigates the land-surface treatment impacts on the PR ratio. The quantified PR ratio and its relationship with precipitation are examined in Sect. 6. In Sect. 7, we discuss results and draw conclusions.

2 Models, experiments and methods

2.1 Description of models

This study used the WVT model incorporated into the WRF regional model, known as the WRF-WVT (Insua-Costa and Miguez-Macho 2018). The WVT model implements a state-of-the-art understanding of moisture movement and transformation as it travels through the atmosphere, mirroring prognostic moisture equation and parameterizations in WRF. Detailed descriptions can be found in Insua-Costa and Miguez-Macho (2018). Six moisture types are tagged using the following equation:

$$\frac{{\partial q_{n} }}{{\partial t}} = - {\text{v}} \cdot \nabla q_{n} {\text{ + }}v_{q} \cdot \nabla ^{2} q_{n} + \left( {\frac{{\partial q_{n} }}{{\partial t}}} \right)_{{PBL}} + \left( {\frac{{\partial q_{n} }}{{\partial t}}} \right)_{{microphysics}} + \left( {\frac{{\partial q_{n} }}{{\partial t}}} \right)_{{convection}}$$
(1)

where qn refers to different moisture types considered, namely, water vapor, cloud, rain, snow, ice, and graupel. The first two terms on the right-hand side in Eq. (1) represent the tendencies due to advection and molecular diffusion, respectively; and the other terms correspond to tendencies resulting from parameterized turbulent transport, microphysics and convection. The latter three terms account for sub-grid physical processes affecting atmospheric moisture, such as phase change and precipitation, or redistribution by convection and turbulent diffusion. The set of equations for tagged moisture is analogous to that for full moisture in the model, and both are solved in a coupled mode, meaning that conditions for turbulent mixing, convection and phase changes in the tracer equations are determined by full moisture, instead of tracer values. The WVT method is highly accurate, and errors in water–vapor source estimates and PR ratio originate almost entirely from errors in the WRF model solution, rather than from the WVT method itself.

2.2 WRF configuration

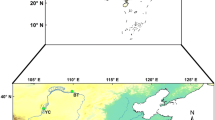
The WRF model version 3.4 was used with a simulation domain (Fig. 1) of 30-km grid spacing and 35 vertical levels. The chosen parameterization options include the Yonsei University [YSU; (Hong et al. 2006)] PBL scheme, the WRF Single-Moment 6-class [WSM6; (Hong and Lim 2006)] microphysics scheme, the Kain–Fritsch (Kain 2004) convection scheme, the NCAR Community Atmospheric Model (CAM; (Collins et al. 2004)] shortwave scheme and longwave scheme, and the Noah land surface model (Noah LSM) with frozen soil and snow-cover prediction (Chen and Dudhia 2001; Chen et al. 1996).

Fig. 1
figure 1

Simulation domain: a topography (shading; in meters) and b dominant land use/cover type. In (a), topography higher than 2500 m is marked as the Tibet Plateau in which the evapotranspiration is tagged. In (b), 1: Urban and Build-up Land; 2: Cropland and Pasture; 7: Grasslan 8: Shrublan 9: Mixed Shrubland/Grassland 11: Forest; 16: Water bodies; 19: Barren or Sparsely vegetation; 24: Snow/ice; 28: Lakes

Full size image

2.3 Experiments and datasets

The 2001 water year (from October of the previous year to September of the following) was taken as a normal year to study the normal PR condition over the TP, because the surface air temperature and precipitation in 2001 were close to the climatology in 1979–2011 (Gao et al. 2014). Spatial variations of the PR ratio in 2001 were examined in terms of annual and seasonal means. To explore the relationship of the PR ratio with precipitation amount, 3 more water years–1 dry year (1994) and 2 wet years (2003 and 2008)—were simulated and analyzed. Initial and boundary conditions were obtained from ERA-Interim reanalysis (Dee and Uppala 2009; Dee et al. 2011) and updated every six hours. This reanalysis product has been shown to be the best forcing among the reanalysis products available for describing the water cycle over the TP (Gao et al. 2014, 2015a, 2015c).

The default run was conducted first to assess the accuracy of simulated precipitation critical for the PR ratio calculation (Insua-Costa and Miguez-Macho 2018). A preliminary examination of the results from this control run revealed a significant overestimation of precipitation (Fig. 2b); a bias that we linked to deficiencies in WRF lake treatment due to unrealistic lake water temperatures. To assess the impact of lake treatment on precipitation and PR ratio, three extra experiments were designed (Table 2).

Table 2 The lake treatments in four experiments
Full size table
Fig. 2
figure 2

Spatial distributions of a observed and biases of simulated annual mean precipitation (units: mm/day) for b the default, c no-lake, d lake-I, and e lake-II experiments for 2001 in the TP. Number at the left-bottom corner is a observed annual mean precipitation averaged over the TP, or b–e absolute (relative) biases of annual mean precipitation compared with (a)

Full size image

The default experiment uses the SST in the closest oceanic grid cell as lake temperature. Experiment no-lake replaced inland water bodies using the dominant land cover type (grassland) over the TP. Experiment Lake-I used surface-skin temperature following the approach of Liu et al. (2016) for TP lake water temperature. Experiment Lake-II used an adjusted surface-skin temperature based on in-situ lake-temperature in the TP. Wen et al. (2016) showed that the observed differences between surface-skin temperature and surface-air temperature ranged from 4 to 9 °C from June to December on average, whereas it is about 1 °C higher in May than in June according to observations in Lake Ngoring in the TP. Therefore, we increased the surface-skin temperature used in Lake-I by 5, 4, 5, 6, 7, 8, 9 °C, for May, June, July, August, September, October, and November, respectively in Lake-II. Lakes are frozen from December to April of the following year; so, no change was made during these months.

The four experiments followed identical configuration except for the specification of lake surface-skin temperature in the TP. Differences among the four experiments are listed in Table 2. One-year (2001) run of all four experiments was analyzed in terms of precipitation validation and impacts of lake treatment on the PR ratio. The best experiment after validation was chosen to carry out the dry and wet year simulations.

The PR ratio was calculated using 3-h WRF outputs as well as using monthly mean outputs, because previous PR ratio studies usually used monthly mean reanalysis data. No significant differences between monthly mean results using monthly outputs and those using 3-h outputs were detected (not shown). Therefore, in the following analysis the 3-h outputs were used in PR ratio calculations. In addition to the total PR ratio computation, the PR ratio was further partitioned into its large-scale and convective precipitation contributions, which were analyzed separately. The relationship between the PR ratio and precipitation was examined through the temporal correlation efficiency.

Observations used in evaluating simulated precipitation are obtained from the China monthly 0.5º × 0.5º precipitation dataset version 2. It was generated by an optimum interpolation method based on a climatological background field, which can substantially reduce analysis error arising from the heterogeneity of precipitation (Shen et al. 2010). All the evaluations and analyses were conducted at the horizontal resolution of 0.25°, which is that of the WRF model grid.

3 Precipitation validation

Figure 2 exhibits the spatial distributions of observed gridded annual mean precipitation and simulation biases of the four experiments. Figure 3 shows monthly variabilities of observed and simulated total, large-scale and convective precipitation averaged over the TP. The default experiment significantly overestimates annual mean precipitation over the lakes and their surrounding areas (Fig. 2b) and also the monthly mean precipitation averaged over the TP (Fig. 3a). The relative bias of annual mean precipitation averaged over the whole TP for the default experiment reaches 148% (Fig. 2b). The three other experiments, however, show lower precipitation, with relative biases of 71%, 63% and 58% averaged over the TP, which largely outperform the default experiment. The only overestimate remains at the south edge of the TP, characterized by steep slopes and abundant moisture transport (Fig. 2e). The seasonal variabilities averaged over the TP in these three experiments are very similar (except for August) and also much closer to the observation than those in the default simulation (Figs. 3a). Lake-II performs slightly better than the other two experiments for August.

Fig. 3
figure 3

Monthly variability of observed and simulated a total, b onvective and c large-scale precipitation (units: mm/day) for the default, no-lake, lake-I, and lake-II experiments averaged over the TP for the water year of 2001

Full size image

Precipitation accumulations are 2–3 mm/day in summer and 0–0.2 mm/day in winter in the TP. The monthly mean bias in winter is around 1 mm/day in the default experiment and about 0.2 mm/day in the other experiments. The simulated convective precipitation in winter is almost zero in all experiments (Fig. 3b) and large-scale precipitation represents total precipitation in winter (Fig. 3c), which implies that precipitation over the TP during this season is generated mainly from large-scale rather than convective dynamics. Thus, precipitation simulation biases in winter mainly come from large-scale processes. In summer, precipitation is more complex, and simulation biases originate from either large-scale or convection process. Since there are no direct measurements of the large-scale and convective partition of precipitation, the corresponding validation cannot be done. Nevertheless, we used the estimation of stratiform and convective precipitation contributions from TRMM 3B42 for an approximative comparison and found that WRF fares well, simulating more convective precipitation than stratiform precipitation in the TP in summer. WRF results are closer to the convective precipitation fraction estimates by TRMM (Zhang and Gao, accepted) than those in global models such as CCSM4, which indicates that WRF is better at simulating convective precipitation than a large-scale GCM.

4 PR ratio in 2001

4.1 Annual mean

Figure 4 displays the spatial distributions of annual mean PR ratios in 2001 from the four experiments. Substantial differences exist between the default and the other three experiments. The maximum of the PR ratio in the default experiment exceeds 0.7 in the central-western TP. However, the other three experiments produced similar PR ratios, with the highest annual mean PR ratios less than 0.5 at the headwaters of the three Rivers (Yellow, Yangtze and Mekong) in the central-eastern TP. Because the PR calculation using the WVT approach is highly dependent on the accuracy of precipitation, the PR ratio in Lake-II in August is likely more accurate than in the other experiments and months.

Fig. 4
figure 4

Spatial distributions of simulated annual mean PR ratio for the water year of 2001 in the TP for a the default, b no-lake, c lake-I, d lake-II experiments

Full size image

4.2 Seasonal cycle

Figure 5 illustrates the monthly variability of total, convective and large-scale PR ratios in 2001 averaged over the TP. Again, the default results are substantially different from those of the other simulations. The default experiment has an annual mean PR ratio of 0.32 averaged over the TP (Fig. S1), with almost no seasonal cycle (Fig. 5), while the annual mean PR ratio averaged over the TP is around 0.20 in the other three experiments with distinct seasonal cycles (Fig. S1)—highest in August and lowest in November (Fig. 5). The winter PR ratio in the default is three times higher than those in the other three experiments. In summer, particularly in August, the PR ratio in the default is close to those in the three experiments, but there are slight differences between no-lake and the other three. Experiment no-lake simulates a lower PR ratio than the others in August. Experiments Lake-I and Lake-II simulate the same August PR ratio as the default. Because Experiment Lake-II outperforms the others in terms of precipitation-skill scores, particularly during summer (Figs. 2e and 3a), it is further analyzed to show the PR ratio seasonal features next.

Fig. 5
figure 5

Seasonal variabilities of simulated a total, b convective and c large-scale monthly PR ratio for the default (black), no-lake (blue), lake-I (green), and lake-II (red) experiments averaged over the TP in 2001

Full size image

Figure 5a shows that the PR ratios are high (low) in summer (winter), with a minimum in November and a maximum in August in Lake-II. The PR ratios from November to February are low, seemingly correlated to the low-amount precipitation and to the dry and frozen soil that suppresses evapotranspiration (Fig. S2). The winter PR ratios over the majority of the TP area are below 0.2, and the ratio rises in March–April prior to the monsoons, which might be related to increased snow sublimation and melting of the snowpack to recharge soils, hence increasing also soil evaporation (Fig. S2). An average PR ratio of 0.2 is observed in the snow-melting period (Fig. 5a). In May, the moisture over the TP starts to increase due to the monsoon onset, but no heavy precipitation occurs yet; meanwhile, soil moisture is relatively low because evaporation in March–April depletes soil-water storage (Fig. S2), leading to a relatively low PR ratio of less than 0.2. During the monsoon season beginning in June, heavy precipitation significantly increases soil moisture, leading to enhanced evapotranspiration and increased average PR ratio (> 0.2). The highest TP-averaged PR ratio is above 0.4 in August, and the minimum PR ratio in November indicated the retreat of the monsoons.

Figure 6 displays the seasonal spatial distribution of total PR ratio in 2001 from experiment Lake-II, showing a westward progression of the maximum PR ratio from winter to summer. The high values of the PR ratio in winter are centered in the source region of the Yellow River Basin in the eastern TP, but in August shift to the central TP in the source region of the Yangtze River Basin. This westward shift corresponds to the evolution of the summer monsoon. Most areas show PR ratios greater than 0.5 with the highest over 0.8 in August, highlighting the important contribution of local evaporation to the total precipitation during this month. Results of 4 years average conclude the same spatial and monthly distribution of PR ratios (Fig. S3).

Fig. 6
figure 6

Spatial distributions of monthly mean PR ratio for experiment lake-II for the water year of 2001

Full size image

4.3 Diurnal cycle

The above-discussed monthly mean results usually eliminate transient variations related to shorter timescales, which we examine next with three hourly data. Figure 7 shows the diurnal cycle of the PR ratio averaged over the TP for February and August in 2001 for experiment Lake-II. The average daily mean of the PR ratio is 0.1 in February and 0.4 in August (Fig. 5a). Three-hourly PR ratios in February range from 0.0 to 0.2, with a daily mean spread of 0.05–0.15; whereas in August the PR ratio ranges from 0.1 to 0.6, with a daily mean spread of 0.35–0.45. The PR ratio is at its highest at 09:00 GTM and at its lowest at 00:00 GTM (17:00 and 08:00 local standard times, respectively) in both months, largely following the diurnal cycle of ET. A substantial difference exists in terms of magnitude and spread between August and February, which are much greater in the earlier, regardless of time of day. Similar differences between summer and winter are found in 4 years average (Fig. S4). The robust diurnal variation in PR ratio demonstrates not only the significantly stronger land-atmosphere interaction, but also a much higher temporal variability in this interaction during summer than in winter in the TP.

Fig. 7
figure 7

Box-whisker diagram of the diurnal cycle of the TP-averaged PR ratio for a February and b August of 2001 for experiment Lake-II. The upper and bottom bounds of the box are 90 and 10 percentiles, respectively; whiskers indicate the maximum and minimum values

Full size image

5 Impact of lake treatment on PR ratio

A fundamental difference was observed in the PR ratio computation between the default experiment and any of the other three experiments (Fig. 8a, b). Unlike the spatial distributions of precipitation and evapotranspiration with increasing gradients from the northwestern to the southeastern TP, the default experiment produces the highest PR ratio in the central-western TP. The majority of those areas of the central TP with high annual mean PR ratio are closely correlated with inland lakes (Figs. 1b and 8a), where WRF in this experiment produces abundant precipitation (Fig. 2b). This high precipitation over the lakes is associated with high surface-skin temperature in winter (Fig. 8c), when lakes are 30 °C warmer than the surrounding land sites. Compared with the default experiment, the other three experiments simulate similar surface-skin temperature patterns in DJF without the extreme high values over the lakes (Fig. 8d), which largely eliminates the bias in precipitation and changes the PR ratio pattern. The issue of excessive precipitation associated with unreasonably high lake temperatures in the default simulation was also discussed in Liu et al. (2016).

Fig. 8
figure 8

Spatial distributions of simulated a, b annual mean PR ratio, and c, d simulated surface skin temperature (units: °C) of DJF in 2001 over the TP for a, c the default and b, d experiment Lake II

Full size image

During summer, with warming land surface, the contrast in surface skin temperature between lakes and surrounding land points is greatly decreased, which correlates with less excessive precipitation around lakes. So it is likely that the stronger surface-temperature contrast between lakes and surrounding land is responsible for the pronounced overestimates in precipitation and PR in winter.

To examine the physical processes undertaken by the evaporative source of moisture, longitude-height cross sections of its fraction in the six moisture types considered in the simulations are shown along 33° N, where all four experiments show the maximum PR ratio in August 2001 (Fig. 9). In general, higher-tagged evaporative moisture fractions are found in the default and in lake-II than in the other two experiments, especially for the ice-phase moisture species. The ice-phase moisture type plays a critical role in precipitation generation despite its small portion in the whole air column, which may explain the similar high TP-averaged PR ratio in these two experiments (Fig. 3a). Experiment Lake-II shows even higher-tagged ice-phase moisture fraction in the eastern TP than the default, yielding also higher PR ratios over the headwaters of the three river basins in the eastern TP.

Fig. 9
figure 9

Longitude-height cross sections along 33º N of evaporative fraction in the six moisture species considered, for the default (1), No-lake (2), Lake-I (3), and Lake-II (4) experiments in August 2001 (a water vapor; b cloud water; c rain water; d cloud ice; e snow; f: raupel). The Y-axis denotes sigma level. Grey means no moisture of the given type at that level

Full size image

The seasonal cycle of evaporative fraction varies across the six moisture types (Fig. 10). The evaporative fractions of the six moisture types are higher in the monsoon season than in the non-monsoon season. Moreover, during the monsoon season, evaporated moisture is more involved in the three ice-phase types than in the three liquid-phase types. During the dry season, the contrary happens, and more evaporated moisture is involved in the liquid-phase types. Evapotranspiration has no impact on cloud water during the winter season because it is greatly diminished. It contributes more to the formation of rain water during the rest of the non-monsoon season. Evaporated moisture reaches higher elevations in the monsoon season than in the non-monsoon season. Water vapor and the three ice-phase types may rise to above 50 hPa in August due to the occurrence of strong convection, whereas they concentrate nearer to ground surface in the non-monsoon season. Four years average shows similar seasonal cycle except for the small magnitudes (Fig. S5). In general, compared with other seasons, two factors thus contribute to the higher PR ratio in summer, and more precisely in August: (1) more frequent fluctuations of high evaporative fraction in the six moisture types, (2) the stronger convection during the monsoon season, which is revealed though the existence of a greater evaporative fraction in the ice-phase moisture type than in the liquid one and a higher altitude that in general the tagged evaporated moisture can reach.

Fig. 10
figure 10

Longitude-height cross sections along 33º N of evaporative fraction in the six moisture species considered for experiment Lake-II in (1) November, (2) February, (3) May, and (4) August 2001 (a water vapor; b cloud water; c rain water; d cloud ice; e snow; f graupel). The Y-axis denotes the sigma level. Grey means no moisture of the given type at that level

Full size image

6 PR ratio relation with precipitation

Using the DRM PR model and JRA-25 reanalysis datasets, Hua et al. (2015) investigated the PR ratio during the summer season across the Chinese mainland. They found a negative correlation of PR ratio with total precipitation (Pt), but a positive correlation with the convection precipitation over large-scale precipitation (Pc/Pnc) in the TP.

To examine the relationship between PR ratio and precipitation, monthly temporal correlations are calculated using 3-h PR ratio and precipitation (Pt), and large-scale precipitation (Pnc), convective precipitation (Pc), large-scale precipitation percentage (Pnc/Pt), convection precipitation percentage (Pc/Pt), and convection precipitation over large-scale precipitation (Pc/Pnc). Correlation coefficients are shown in Fig. 11, illustrating monthly correlations between PR ratio and precipitation-relevant variables in 2001. The correlation of PR ratio with total precipitation varies between positive and negative values. Most of those correlation values do not pass the two-tailed t test at the 99.9% confidence level. The correlation with large-scale precipitation also varies in winter, but it shows more significant negative values in summer. The correlation of the PR ratio with the fraction of large-scale precipitation in the total, Pnc/Pt, is generally negative, except in February. Nine out of the 12 months pass the two-tailed t test at the 99.9% confidence level. In contrast, the majority of the correlations with the three convective precipitation-relevant variables (Pc, Pc/Pt and Pc/Pnc) are positive and significant at the 99.9% confidence level.

Fig. 11
figure 11

Monthly correlation coefficiencies between 3-hourly PR ratio and total precipitation (Pt; thick dash), large-scale precipitation (Pnc), convective precipitation (Pc), large-scale precipitation percentage (Pnc/Pt), convective precipitation percentage (Pc/Pt), and convective precipitation over large-scale precipitation (Pc/Pnc) for the water year of 2001, and consistency with 1994, 2003 and 2008. Correlations passing the statistically significant two-tail student t test at 99.9% confidence level are marked by small black circles. Correlations passing the statistically significant t test for all 4 years are marked by red filled circles, black squares, blue triangles, and green pentagrams

Full size image

To assess the robustness of the significant and positive correlations between PR ratio and convective precipitation-relevant variables in the single year of 2001, 3 more water years (1 dry year of 1994 and the 2 wet years of 2003 and 2008) were simulated and correlations were calculated. If correlations pass the statistically significant t test for all 4 years, they are marked in Fig. 11 by red filled circles, black squares, blue triangles, and green pentagrams, respectively. None of them passed the significant test for all of the months of the 4 years. There are more months passing the significant test in summer than in winter, and all correlations for the monsoon season pass the t-test at the 99.9% confidence level except for Pc/Pnc in August. These correlations for Pc/Pnc in August do not pass the significant t-test consistently among the 4 years even at the 95% confidence level, which implies that they are not solid. However, significant and positive correlations do exist for the PR ratio with Pc and Pc/Pt in the monsoon season.

The negative and significant correlations between PR ratio and Pnc/Pt in MJJASO of 2001 are consistent in MJJA across the 4 years, but the negative correlation of PR ratio with total precipitation is questionable at both monthly and annual scales. Figure 12 shows the monthly mean PR ratios for the four simulated years. These 4 years were selected according to annual precipitation amount: dry year of 1994, normal year of 2001 and wet years of 2003 and 2008; however, no alike sequence is found in annual mean PR ratio. At the monthly scale, no apparent difference is observed in PR ratio across the 4 years, except in summer. In summer, the highest PR ratio corresponds to August of the normal year, rather than to any month in dry or wet years. No correlation could be found between monthly PR ratio and total precipitation. Therefore, the negative correlations between PR ratio and total precipitation at sub-daily scale are not valid at monthly and annual scales.

Fig. 12
figure 12

Monthly variation of the PR ratio for the four simulated years. Annual mean PR ratio for each year is marked in parentheses

Full size image

7 Conclusions and discussion

The advanced WVT method coupled with WRF was used to calculate the PR ratio over the TP. The annual mean, seasonal variability and diurnal cycle of the PR ratio were analyzed to examine the coupling strength between the terrestrial and atmospheric hydrological cycles over the TP. The impact of lake treatment on the PR ratio was also examined. Simulation results from the normal water year of 2001 were used as a reference and then compared with those from dry and wet years to investigate the relationship between PR ratio and precipitation. The following summarizes our findings.

  1. 1

    Averaged over the whole TP, the recycling ratio ranges from 0.1 to 0.4, with the highest value in August and its lowest in November. Spatially, the ratio exhibited high values for the headwaters of the three river basins. In August, the PR ratio rose to more than 0.8 in the headwaters of the Yangtze River Basin. Larger evaporative moisture fractions during the monsoon season, and specifically of the ice-phase types and at higher altitudes, are responsible for the higher PR ratio in the monsoon season than in the non-monsoon season.

  2. 2

    The PR ratio showed a distinct diurnal variation, peaking at 17:00 and having its minimum at 08:00 local standard times, a cycle that remained the same in winter and in summer. The PR ratio magnitude and spread at the diurnal scale were substantially larger in summer than in winter, which indicated stronger land-atmosphere interactions and larger daily variability in summer than in winter.

  3. 3

    Despite the relatively small spatial coverage of the lakes, their treatment exerts substantial impact on the PR ratio estimate from WRF-WVT. The default experiment using the nearest grid cell SST overestimated evaporative moisture fractions, particularly the ice-phase types, which resulted in a significant overestimate of precipitation, and subsequent overestimate of the PR ratio for lake regions. The overestimate in the default run is due to large-scale process precipitation rather than to convective precipitation. The overestimates of PR ratio and precipitation were improved by refining the lake treatment, with relative biases dropping from 148 to 58%.

  4. 4

    Significant positive correlations were found between PR ratio and convection in terms of hourly, daily, seasonal scale, or annual mean. On the contrary, significant negative correlations between 3-hourly PR ratio and total precipitation observed in summer 2001 were not detected consistently in the other seasons or the other years.

Note that although there are advantages in using the WVT method, the accuracy of the obtained PR ratio estimate depends on the performance of the model (WRF in this study) in reproducing the hydrological cycle, particularly precipitation. Substantial overestimates of precipitation have been reported in the TP with GCM simulations (Su et al. 2013). Uncertainties in physical parameterizations, for example, model configuration and forcing, can cause this overestimation (Gao et al. 2008,  2011), 2017. Dynamic downscaling with WRF helped reduce precipitation biases by 35% (Gao et al. 2015c, 2017, 2018b) and improved lake treatment further reduced the errors. Notwithstanding, an overestimation in precipitation still exists over the TP, especially at its southern edge (Fig. 2e), which needs to be improved.

Another factor playing a fundamental role in PR ratio calculations is evapotranspiration, which is significantly constrained by the land-surface model’s performance. Numerous uncertainties in land-surface processes still exist over the TP because of its complex terrain and land characteristics (Zhang et al. 2016). For instance, soil characteristics (Gao et al. 2008; Li et al. 2018), plant roots (Gao et al. 2015b), the snow-albedo feedback mechanism (Gao et al. 2017), as well as the lake treatments tested in this study can greatly influence the interaction between the land surface and atmosphere in terms of moisture. In this study, the Noah LSM was used in the WVT method. Gao et al. (2015d) claimed that Noah-MP outperformed the Noah LSM because of parameterization improvements. Further studies should be undertaken to couple the WVT method with more comprehensive land surface schemes to enhance the evapotranspiration modeling performance and improve the accuracy of the PR ratio estimation.

We note that as in all recycling studies, the PR ratio calculated here with the WVT approach is also scale-dependent, theoretically ranging from zero at a point to one globally. Our results using the WRF-WVT on-line method apply for the selected target region, which is the entire TP, from where evapotranspiration was tagged. Assessing the scale-dependency of the PR ratio over the TP is beyond the scope of this study. Finally, only 4 years simulations were conducted and analyzed here because of limited computational resources. More simulations and analyses are necessary to explore the PR ratio change in response to climate warming.