Abstract
Stratospheric aerosol injection (SAI) is considered as a backup approach to mitigate global warming, and understanding its climate impact is of great societal concern. It remains unclear how differently global monsoon (GM) precipitation would change in response to tropical and Arctic SAI. Using the Community Earth System Model, a control experiment and a suite of 140-year experiments with CO2 increasing by 1% per year (1% CO2) are conducted, including ten tropical SAI and ten Arctic SAI experiments with different injecting intensity ranging from 10 to 100 Tg yr−1. For the same amount of injection, a larger reduction in global temperature occurs under tropical SAI compared with Arctic SAI. The simulated result in the last 40 years shows that, for a 10 Tg yr−1 injection, GM precipitation decreases by 1.1% (relative to the 1% CO2 experiment) under Arctic SAI, which is weaker than under tropical SAI (1.9%). Further, tropical SAI suppresses precipitation globally, but Arctic SAI reduces the Northern Hemisphere monsoon (NHM) precipitation by 2.3% and increases the Southern Hemisphere monsoon (SHM) precipitation by 0.7%. Under the effect of tropical SAI, the reduced GM precipitation is mainly due to the thermodynamic term associated with the tropical cooling-induced decreased moisture content. The hemispheric antisymmetric impact of Arctic SAI arises from the dynamic term related to anomalous moisture convergence influenced by the anomalous meridional temperature gradient.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Global monsoon (GM) precipitation has been viewed as the dominant mode of annual variation in the tropical region, which imposes substantial impacts on the society and living environment of two-thirds of the world’s people (Wang and Ding 2008; Wang et al. 2012). Understanding the dynamics of GM is essentially crucial to agriculture, food security, ecosystem, and social development (Wang et al. 2018). Trenberth et al. (2000) depicted the global monsoon as a global-scale seasonal reversal of atmospheric overturning throughout the tropics. Some previous studies suggest an increase of global monsoon precipitation under the anthropogenic forcings using the results in the Coupled Model Intercomparison Project (CMIP5) (Hsu et al. 2012; Lee and Wang 2014).
Although some studies suggest that global warming will increase the global monsoon precipitation (Hsu et al. 2012; Lee and Wang 2014), this could also have adverse effects, such as more climate extremes events (i.e., Zhang et al. 2018; Li et al. 2018). Meanwhile, the Arctic warming will be largely amplified, named the Arctic amplification (Chapman and Walsh 1993; Holland and Bitz 2003), causing the loss of Arctic sea ice and melting of Greenland, which is a potential threat to the local ecosystem. Geoengineering is considered to be a backup approach to slow down or mitigate global and Arctic warming (National Research Council 2015). Many methods have been proposed in the geoengineering schemes, such as stratospheric aerosol injections (SAI), marine stratocumulus clouds, and increasing the surface albedo (Kravitz et al. 2011; Early 1989; Seitz 2011; Cao et al. 2017). Among these approaches, the injection of stratospheric aerosols seems to be an effective way to slow down future warming (Lenton and Vaughan, 2009), which is partly based on the knowledge of the volcanic impact on global climate (Crutzen 2006; Plazzotta et al. 2018). However, it is still uncertain to what extent the implementation of SAI will affect GM precipitation.
Previous modeling studies typically injected aerosols into the tropics (i.e., Kravitz et al. 2015), which may cool the tropical region and cause the reduction of global and tropical precipitation (Boucher et al. 2013; Ferraro and Griffiths 2016). Recently, the Stratospheric Aerosol Geoengineering Large Ensemble (GLENS) was conducted (Tilmes et al. 2018), where SO2 was injected at 30°N, 15°N, 15°S, and 30°S, and a feedback-control algorithm was used to annually adjusted the amount of injection. Using the results from GLENS, some studies also found the tropical precipitation is suppressed, especially over the Indian, South/North American, and South African monsoon region (i.e., Cheng et al. 2019; Kravitz et al. 2019). Arctic injection might be thought to mitigate Arctic amplification and have a relatively small impact on the tropical climate because the lifetime of Arctic injecting stratospheric sulfate aerosols is shorter and the aerosols cover a relatively small area. Robock et al. (2008) simulated the impacts of tropical and Arctic aerosol injection on climate using an atmosphere–ocean general circulation model. They found both tropical and Arctic injections would decrease the precipitation over the Asian and African monsoon regions. Similarly, Nalam et al. (2018) found that Arctic geoengineering shifts the ITCZ southward and causes the precipitation decrease (increase) over the Northern (Southern) Hemisphere monsoon regions using the Community Atmosphere Model version 4 (CAM4) coupled to a slab ocean model. However, these studies use the different injection intensities for the tropical/global and Arctic SAI experiments, which is hard to reflect the contribution of tropical and Arctic SAI to the climate changes.
The relative contribution of physical processes responsible for the GM precipitation will change due to the anthropogenic warming. Using three atmospheric general circulation models, Hus et al. (2012) found that the thermodynamic effect due to the increased moisture substantially increases global monsoon precipitation, while the dynamic effect associated with the atmospheric circulation change is much weaker. Huang et al. (2013) further found that the wet-get-wetter pattern over the tropical region is dominant by the thermodynamic component using 18 CMIP5 models, which is associated with the climatological ascending motion pumping up the moisture near the surface. Additionally, the global monsoon precipitation is also influenced by other external forcings, such as volcanic eruptions (Liu et al. 2009; Wang et al. 2017). Liu et al. (2016) discovered that the monsoon precipitation in one hemisphere is substantially increased by the other hemispheric volcanic eruptions using the Community Earth System Model (CESM), and this volcano-induced remote enhancement is mainly through circulation changes. Similarly, recent studies using the CESM1-CAM5 and proxy data found a weakened (strengthened) Northern (Southern) Hemisphere monsoon following northern eruptions (Fasullo et al. 2019; Meng et al. 2019). They suggested that the dynamic process associated with atmospheric circulation change plays an essential role in precipitation response. Nevertheless, the changes in thermodynamic and dynamic processes related to GM under the CO2-induced warming with SAI have not been explained.
In this study, we use CESM to analyze the impacts of tropical and Arctic SAI on GM precipitation changes compared to a 140-yr experiment with CO2 increasing by 1% every year (1% CO2). The strength of SAI is larger than previous geoengineering researches because the stronger injection can induce a lager signal of the climate effect. That provides a useful insight for stratospheric geoengineering. Following questions will be aimed to address: (1) What are the different impacts of tropical and Arctic SAI on the global temperature and monsoon precipitation changes? (2) What is the dominant physical process behind the monsoon precipitation response under tropical and Arctic SAI? The following is the paper organization. The experimental design, definition of global monsoon, and method are shown in Sect. 2. Section 3 describes the global temperature changes under tropical and Arctic SAI. Section 4 shows the GM precipitation changes under the SAI. Section 5 analyzes the physical mechanisms behind the GM precipitation changes. Section 6 shows the conclusion and discussion.
2 Model and method
2.1 Experimental design
In this study, the model we used is the CESM, with the CAM4 (Neale et al. 2013) and the Parallel Ocean Program version 2 (POP2). In CAM4, the horizontal resolution of the atmosphere is T31_g37, which is about 3.75° × 3.75°, given the limited computing resources. Many previous studies have validated the performance of CESM (i.e., Otto-Bliesner et al. 2016; Sun et al. 2019b).
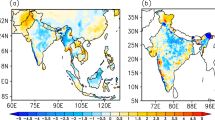
First, we conducted a 2400-year pre-industrial control experiment (Ctrl) (Wang et al. 2015; Sun et al. 2017) in which the external forcing conditions were fixed at 1850 AD. The first 400-years in the Ctrl was a spin–up run, and then the Ctrl was run for 2000 years. Since we focus on the equilibrium responses, the last 2000 years are analyzed. We use the observational data to evaluate the model performance in simulating the climatological precipitation. These data are made by averaging two monthly mean precipitation datasets from 1979–2008: (a) the Climate Prediction Center Merged Analysis Precipitation (CMAP) (Xie and Arkin 1997) and (b) the Global Precipitation Climatology Project (GPCP) version 2 (Adler et al. 2003). The simulated major distribution of the climatological annual mean and local summer precipitation is consistent with that in observations (Fig. 1). The pattern correlation coefficient of the annual mean (local summer) precipitation between the Ctrl and the CMAP-GPCP ensemble mean is 0.87 (0.85). It should be noted that the Ctrl focuses on the 1850 AD climate conditions with a lower CO2 compared to the observations, which could cause some differences between model and observations (Jiang et al. 2015).
Comparison of climatological precipitation between the Ctrl experiment (the last 30 years, left panels) and the observations (1979–2008, right panels). a, b Annual mean precipitation (mm day−1). c, d Local summer precipitation. Local summer represents May to Sep in NH and Nov to Mar in SH. The numbers in the lower-left and lower-right corners in the left panels indicate pattern correlation coefficient (PCC) and normalized root-mean-square-error (NRMSE)
Second, a 140-year 1% CO2 experiment is carried out based on the last year in the Ctrl, where the atmospheric CO2 concentration is increased at a rate of 1% per year beginning in the 1st year. Third, ten 140-year tropical aerosol injection experiments and ten Arctic aerosol injection experiments are conducted, respectively, where the CO2 is increasing by 1% every year and sulfate aerosols are injected into lower stratosphere per year. The intensities of sulfate aerosols (H2SO4) are from 10 to 100 Tg yr−1, which are chosen based on the magnitude of the middle and large volcanic eruptions during the past 1500 years (Gao et al. 2008). Volcanic aerosols are injected at the equator with an altitude of 18–25 km and at the 63.4°N with a height of 10–16 km in the tropical and Arctic SAI experiments, respectively.
Figure 2 shows the sulfate aerosol forcings in the first 5 years. According to the parameterization of stratospheric transport, a 5-years spatiotemporal evolution of sulfate aerosol for one injection is produced (Gao et al. 2008), which is added to the first five years of the constructed forcing. From the second year, we superimpose the same 5-years spatiotemporal evolution of aerosol based on the original one every year (Fig. 2). Then the 140-years sulfate aerosol forcings are constructed and used to force the SAI experiments. The injecting season is March in the SAI experiments. It is because injecting in only part of the year (such as March) can be more efficient than annually-constant injections for the tropical SAI (Visioni et al. 2019). Sun et al. (2019a) also found that the spring Arctic volcanic eruptions can induce more substantial Northern Hemisphere cooling than other seasons.
2.2 Global monsoon definition
The global monsoon domains are delineated by the regions where the local summer precipitation exceeds 55% of the annual total and the annual range exceeds 2 mm day−1 (Wang and Ding 2008; Liu et al. 2009). The annual range denotes the local summer-minus-winter precipitation at each location. For the Northern Hemisphere (NH), summer is May–September and winter is November-March, while for the Southern Hemisphere (SH), summer is November-March and winter is May–September. In this study, the global monsoon area is computed using the GPCP. Using the same GM definition, Liu et al. (2016) checked the simulated GM area by CESM and found the results are similar to the GPCP’s results. The GM precipitation is defined by the weighted-area average local summer precipitation over the monsoon area.
2.3 Moisture budget
To reveal the physical process of the SAI’s impact on GM precipitation, we investigate a column-integrated moisture budget over the monsoon region (Hsu et al. 2012). The moisture tendency equation is written as:
where < > denotes the vertical integration from 1000 to 100 hPa, P is the precipitation, E is the surface evaporation, \(\partial /\partial t\) is the time tendency, \(\nabla\) denotes the gradient operator, V denotes the wind vectors, q represents the specific humidity. \(\partial \langle q\rangle /\partial t\) is the time derivative of vertically integrated moisture, which can be neglected for steady motion. We separate \(V=\overline{V}+V{^{\prime}}\) and \(q=\overline{q}+q{^{\prime}}\), where the overbars represent climatology in the Ctrl, and the primes denote the difference between Tro/Arc and 1% CO2 experiments. Then, the precipitation change can be expressed as
where the first term on the right of (2) represents the thermodynamic term, the second term denotes the dynamic term, and the third term represents the nonlinear term. The thermodynamic and dynamic terms can be further divided into.
where u, v, and w are the zonal wind, meridional wind, and vertical pressure velocity, respectively. The three terms on the right of (3) and (4) represent the zonal, meridional, and vertical components. We use Vh to denote the horizontal wind vectors.
3 Surface temperature changes under tropical and Arctic SAI
Before we discuss the effect of external forcings in the simulation, the internal variability needs to be checked. The result of power spectrum shows that the significant 2–7-yr and 20-yr peaks are found in global mean temperature in the Ctrl, and a 2–10-years periodicity is found in NH/SH mean temperature (Fig. 3a–c). A significant 2–10-years periodicity dominates the GM, NH monsoon (NHM), and SH monsoon (SHM) precipitation, while a 16–18-years peak is also found in NHM/SHM precipitation (Fig. 3d–f). We also conduct the power spectrum analysis in the 1% CO2, Tro, and Arc experiments, and the results are similar to that in the Ctrl. It means that the internal variability has an interannual-decadal (2–20 years) signal.
Power spectrum of annual surface temperature (TS, a–c) and global monsoon precipitation (PR, d–f) in the Ctrl experiment. a–c Annual surface temperature over the Global, NH and SH regions. d–f Local summer precipitation over GM, NHM and SHM regions. The red points are the results exceeding the 95% confidence level
The time series of temperature are smoothed via an 11-year running mean, which could largely reduce the internal variability and better reflect the effect of external forcings (Fig. 4). We find that an increased global mean temperature occurs during 101–140 in the tropical SAI experiments with intensity less than or equal to 40 Tg yr−1, while a decreased global temperature only occurs in the 100 Tg yr−1 Arctic injection experiment and the SH warming is not offset. In the tropical injection experiments, the 101–140 years mean cooling in the NH, is stronger than in the global and SH (Fig. 4, left). When injecting the same strength of aerosols in the Arctic region (Fig. 4, right), the global cooling effect is weaker than under tropical injection, especially for the SH. Using the linear regression analysis, we find that the contribution of tropical SAI to global, NH, SH, and Arctic temperatures during 101–140 is about − 0.6, − 0.7, − 0.4, and − 1.1 °C/(10 Tg yr−1), respectively, while the contribution of Arctic SAI is about − 0.3, − 0.5, − 0.1, and − 1.2 °C/(10 Tg yr−1), respectively. The reduced shortwave radiation at the top of atmosphere (TOA) contributes to the temperature change, which is investigated by previous work (i.e., Robock et al. 2008; Zanchettin et al. 2016). The change in global shortwave radiation at TOA is about − 0.7 W m−2/(10 Tg yr−1) in Arctic SAI, weaker than the − 1.6 W m−2/(10 Tg yr−1) in tropical SAI, which explains the lower efficiency in suppressing global warming under Arctic SAI.
The 11-yr running mean time series of simulated annual surface temperature anomalies (°C) over the global (a, b), NH (c, d), and SH (e, f) regions, relative to the Ctrl experiment. Left represents results in the tropical injection experiments, while right represents results in the Arctic injection experiments. Black lines denote the results in the 1% CO2 experiment. Lines of other colors represent results in the experiments with injection strength from 10 to 100 Tg yr−1
The spatial pattern of annual mean anomalous temperature is shown in Fig. 5. The tropical SAI causes a strong cooling over the tropical and mid-high latitude land region and a relatively weak cooling over the ocean (Figs. 5b–d). The Arctic SAI mainly leads to the NH mid-high latitude cooling, inducing the hemispherical meridional temperature gradient (Fig. 5e–g). Additionally, the large-scale anomaly pattern of global surface temperature does not change under the different injecting intensities.
Annual mean surface temperature (°C) changes during 101–140. a Difference between results in the 1% CO2 experiment and Ctrl experiment. Results in (b–g) denote the differences between the SAI and 1% CO2 experiments. b–d Results in the 20, 50, and 80 Tg yr−1 tropical injection experiments, respectively. e–g Results in the 20, 50, and 80 Tg yr−1 Arctic injection experiments, respectively. The horizontal black line denotes the equator. Only the significant anomalies with confidence level exceeding the 95% (via a two‐tailed Student's t test) are displayed
4 Changes in global monsoon precipitation
Figure 6 shows the time series of monsoon precipitation changes. Precipitation decreases rapidly and reaches the minimum within the first 20 years in both tropical and Arctic injection experiments. Then the precipitation tends to increase due to the effect of CO2 increase. The spatial anomalies of precipitation show that the GM precipitation is increased in the 1% CO2 experiment (Fig. 7a), which is similar to the previous studies (Hsu et al. 2012). Under the tropical SAI, the decreased precipitation significantly occurs in the equatorial regions, and the mid-latitude precipitation is also reduced (Fig. 7b–d). The precipitation in the monsoon region is largely decreased, especially for the Asian, North American, Australian, and South American monsoon precipitation. Under Arctic SAI, the NH tropical monsoon precipitation is substantially suppressed, especially over the Indian and western North African monsoon regions (Fig. 7e–g). Instead, increased precipitation occurs over the SH tropical region, especially over the Australian monsoon region. There is a southward shift of ITCZ in the Arctic SAI experiments, which also occurs under the Arctic geoengineering and high latitude volcanic eruptions suggested by previous researches (Krvitz et al. 2016; Nalam et al. 2018; Pausata et al. 2015). In this study when the strength of SAI changes, the large-scale anomaly pattern of global precipitation will not change.
Same as Fig. 4, but for the monsoon precipitation anomalies (mm day−1)
Local summer precipitation (mm day-1) changes during 101–140. a Difference between results in the 1% CO2 experiment and Ctrl experiment. Results in (b–g) denote the differences between the SAI and 1% CO2 experiments. b– d Results in the 20, 50, and 80 Tg yr−1 tropical injection experiments, respectively. e– g Results in the 20, 50, and 80 Tg yr−1 Arctic injection experiments, respectively. The horizontal black line denotes the equator. The blue thick lines represent the global monsoon region. Only the significant anomalies with confidence level exceeding the 95% (via a two‐tailed Student's t test) are displayed
The combined effect of CO2 and SAI on the change in precipitation during the last 40 years is checked. Comparing with the Ctrl, the last 40-year mean GM precipitation changes within ± one SD of precipitation in the Ctrl in the 20, 30 and 40 Tg yr−1 tropical injection experiments (Fig. 8a). The change in GM precipitation is within ± one SD in the 30–60 Tg yr−1 Arctic injection experiments, and the SHM precipitation is enhanced in each Arctic injection experiment (Fig. 8b). To examine the pure effect of SAI on GM precipitation, we compare the results between the SAI and 1% CO2 experiments. The contributions of tropical SAI to GM, NHM, and SHM precipitation are about − 1.9, − 2.2, and − 1.4%/(10 Tg yr−1), respectively (Fig. 8c), while the contributions of Arctic SAI are about − 1.1, − 2.3, and 0.7%/(10 Tg yr−1), respectively (Fig. 8d). These percentage changes are relative to the last 40 years mean in the 1% CO2 experiment. It means that when injecting aerosols with the same magnitude, the effect of tropical SAI on the suppression of GM precipitation is about 1.7 times that of Arctic injection. Arctic SAI has a relatively strong influence on decreasing the NHM precipitation than that under the impact of tropical SAI, and it tends to enhance the precipitation over the SHM region. Meanwhile, it is found that tropical SAI above 20 Tg yr−1 can cause a decrease in GM precipitation, which exceeds one SD (Fig. 8c). When injecting more than 30 (20) Tg yr−1 aerosols in the Arctic region, the GM (NHM) precipitation will be suppressed (exceed one SD), while a one-SD increase in SHM precipitation occurs when Arctic SAI is up to 30 Tg yr−1 (Fig. 8d).
Change rates (%) in last 40 years mean local summer precipitation over global monsoon region in the tropical (left) and Arctic (right) SAI experiments. a, b Anomalies are relative to the Ctrl experiment. c, d Anomalies are relative to the 1% CO2 experiment. In each monsoon region, bars from left to right represents the 10, 20, 30, …, 100 Tg yr−1 injection experiments, respectively. The horizontal dashed lines denote the one standard deviation of local summer precipitation in the Ctrl
Over the NH submonsoon regions, Arctic SAI has a stronger impact on the suppression of North African and Asian monsoon precipitation but a weaker impact on the decreased North American monsoon precipitation, compared with tropical SAI (Fig. 9a, b). Over the SH submonsoon regions, South African, South American, and Australian monsoon precipitations are all decreased under the effect of tropical SAI (Fig. 9c). In contrast, in the Arctic injection experiment, no significant change in the South African and South American monsoon precipitation is found, and the Australian monsoon precipitation tends to be increased (Fig. 9d). However, on regional scales, the simulated results are with less confidence due to the coarse resolution of the model (discussed in Sect. 6).
Change rates (%) in last 40 years mean local summer precipitation over submonsoon region in the tropical (left) and Arctic (right) SAI experiments, relative to the 1% CO2 experiment. a, b North African monsoon (NAF), Asian monsoon (ASIA), and North American monsoon (NAM) regions. c, d South African monsoon (SAF), Australian monsoon (AUS), and South American monsoon (SAM). In each monsoon region, bars from left to right represents the 10, 20, 30, …, 100 Tg yr−1 injection experiments, respectively. The horizontal dashed lines denote the one standard deviation of local summer precipitation in the Ctrl
5 Physical mechanisms behind the global monsoon precipitation response
We use a method of moisture budget analysis to understand the physical processes of the monsoon precipitation change. Similar to previous studies (Hsu et al. 2012; Huang et al. 2013), the thermodynamic term (0.62 mm day−1) plays an important role in enhancing the global monsoon precipitation in the 1% CO2 experiment (during 101–140). For simplicity, we only show the results in the 30 Tg yr−1 SAI experiments. The uncertainty would be large for the weak terms (i.e., nonlinear and \(-\langle {V}_{h}{^{\prime}}\partial q\rangle\) terms) under the different SAI intensities, but the dominant term in the budget analysis is not changed. In the tropical injection experiment, the negative thermodynamic term (− 0.44 mm day−1) largely suppresses the global monsoon precipitation, while the positive dynamic term tends to increase the precipitation but its intensity is relatively weak (Fig. 10a), which is opposite to the results in the 1% CO2 experiment. The surface evaporation term and nonlinear term slightly decrease the GM precipitation. The mean convergence term (\(-\langle \overline{\omega }{\partial }_{p}{q}^{^{\prime}}\rangle\)) plays a critical role in the negative thermodynamic component (Fig. 10b). Under the effect of Arctic SAI, the thermodynamic and nonlinear terms contribute to the suppression of GM precipitation, while dynamic term tends to increase the GM precipitation.
Changes in local summer precipitation, evaporation (E), dynamic term (Dyn), thermodynamic term (Therm), and nonlinear term (NL) (mm day−1) during 101–140 in the tropical (yellow) and Arctic (red) 30 Tg yr−1 injection experiments, relative to the 1% CO2 experiment. a, b GM region. c, d NHM region. e, f SHM region. Blue dots denote the differences exceeding one standard deviation in the Ctrl.
For the tropical SAI case, the anomalous negative thermodynamic term contributes to the decreased precipitation over both the NHM and SHM regions, which is associated with the moisture change (Fig. 10c, e). The mean convergence term contributes most in this negative thermodynamic term (Fig. 10d, f). In the Arctic SAI experiment, the negative dynamic and thermodynamic terms play an important role in suppressing the NHM precipitation (Fig. 10c), while the positive dynamic term leads to the enhanced SHM precipitation (Fig. 10e), which is related to the circulation change. The anomalous convergence (\(-\langle w{^{\prime}}\bullet {\partial }_{p}\overline{q}\rangle\)) and mean convergence terms (\(-\langle \overline{\omega }{\partial }_{p}{q}^{^{\prime}}\rangle\)) are important in the NHM, while the anomalous convergence term (\(-\langle \omega {^{\prime}}{\partial }_{p}\overline{q}\rangle\)) is dominant in the SHM (Fig. 10d, f). Besides, the thermodynamic and nonlinear terms tend to decrease the SHM precipitation, but their amplitudes are weak.
To understand how SAI affects the important terms, we show the anomalous temperature and atmospheric circulation in the SAI experiments, relative to the 1% CO2 experiment (Fig. 11 and 12). Since the sulfate aerosol is injected into the equatorial stratosphere in the tropical SAI experiment (Fig. 2a), the tropospheric temperature decreases the most at the equator (Fig. 11, left), inducing the anomalous descending motion there, weakening the equatorial precipitation (Fig. 12, left). Tropical SAI also contributes to the strong cooling over the tropical troposphere, substantially reducing the tropical specific humidity, which decreases the mean convergence term (\(-\langle \overline{\omega }{\partial }_{p}{q}^{^{\prime}}\rangle\)) (Fig. 10b). However, the anomalous ascending motions occur over the NH and SH tropical monsoon regions (Fig. 11, left), resulting in the relatively weak positive dynamic term (Fig. 10a).
Latitude-height cross section of the anomalous temperature (°C, shading) and circulation [vectors denote meridional wind (m s-1) and vertical pressure velocity (0.02 Pa s−1)] averaged over 180°W–180°E during 101–140, relative to the 1% CO2 experiment. Left column represents results in the tropical SAI experiments, while right column denotes results in Arctic SAI experiments. a–d Results in MJJAS in the 50 Tg yr−1 injection and 80 Tg yr−1 injection experiments, respectively. e–h same as (a–d), but for the results in NDJFM. The reference magnitude of vectors are shown in the upper right corner of each panel. Only the significant anomalies with confidence level exceeding the 95% (via a two‐tailed Student's t test) are displayed
Anomalous precipitation (mm day-1, shading) and 850 hPa horizontal wind (m s-1, vectors) during 101–140, relative to the 1% CO2 experiment. Left column represents results in the tropical injection experiments, while right column denotes results in Arctic injection experiments. a–d Results in MJJAS in the 50 Tg yr−1 injection and 80 Tg yr−1 injection experiments, respectively. e–h same as (a–d), but for the results in NDJFM. The blue thick lines represent the global monsoon region. The reference magnitude of vectors are shown in the upper right corner of each panel. Only the significant anomalies with confidence level exceeding the 95% (via a two‐tailed Student's t test) are displayed
Arctic SAI induces a strong tropospheric cooling over the NH mid-high latitudes (Fig. 11, right), causing the NH-SH meridional temperature gradient. This anomalous temperature gradient leads to the anomalous descending (ascending) motion over the NH (SH) tropical region and enhances the anomalous cross-equatorial northerlies. Then the negative (positive) dynamic term occurs in the NHM (SHM) (Fig. 10c, e), suppressing (enhancing) the NHM (SHM) precipitation (Fig. 12, right). The anomalous NH tropical cooling also decreases the moisture content, which induces the negative thermodynamic term over the NHM region (Fig. 10c). Over East Asia, the anomalous meridional land-sea thermal contrast are formed (Fig. 5e–g), which induces the northwesterly anomalies (Fig. 12b, d) and weakens the summer monsoon circulation (Fasullo 2012). Meanwhile, the summer temperature is decreased substantially in the Arabian Peninsula under Arctic SAI, causing a large anomalous anticyclone there and resulting in the northerly anomalies over the Indian region, suppressing the Indian summer monsoon precipitation (Fig. 12b, d). Due to the thermal contrast between North Africa and tropical North Atlantic Ocean (Fig. 5e–g), North African monsoon region is dominated by the northeasterly anomalies, weakening the North African monsoon precipitation (Fig. 12b, d).
6 Conclusion and discussion
In this study, the CESM is used to analyze the impacts of tropical and Arctic SAI on global monsoon precipitation changes and understand the mechanism behind that, which intends to provide useful insight for geoengineering. The followings are the major findings:
-
1.
Arctic SAI has a lower efficiency in suppressing global warming compared with tropical SAI. The global temperature reduces by − 0.3 °C/(10 Tg yr−1) during 101–140 in the Arctic SAI experiment, while it reduces by − 0.6 °C/(10 Tg yr−1) under tropical SAI.
-
2.
GM precipitation decreases by 1.1%/10 Tg yr−1 injection during 101–140 under Arctic SAI, which is weaker than under tropical SAI (1.9%/10 Tg yr−1). Tropical SAI tends to suppress precipitation globally, but Arctic SAI reduces the NHM precipitation by 2.3%/10 Tg yr−1, while increases the SHM precipitation by 0.7%/10 Tg yr−1, leading to a significant NH-SH asymmetry in the precipitation change.
-
3.
Moisture budget analysis suggests that in the tropical injection experiment, the negative thermodynamic term plays a dominant role in suppressing the GM precipitation, and the mean convergence term contributes most to this thermodynamic term. Under the effect of tropical SAI, the tropical tropospheric cooling substantially reduces the moisture over the tropics, resulting in the negative thermodynamic term.
-
4.
In the Arctic injection experiment, the negative (positive) dynamic term decreases (increases) the NHM (SHM) precipitation. Under the effect of Arctic SAI, the NH cooling induces the anomalous cross-equatorial northerlies and anomalous descending (ascending) motion over the NH (SH) tropical region, which causes the change in the dynamic term.
Some previous studies checked the impacts of geoengineering on monsoon precipitation changes. Tilmes et al. (2013) suggested a 4.5% decrease in global precipitation, especially over East Asian, Indian, North/South American, and South African land monsoon regions by reducing the solar radiation (3.8%–5.0%). Nalam et al. (2018) prescribed 20 Mt sulfate aerosols uniformly around the globe in an equilibrium experiment and found the decreased local summer precipitation over each monsoon region except for North America and North Africa. These studies show a reduction in GM precipitation, but there are some differences in the regional monsoon. When prescribing 11 Mt sulfate aerosols over 50°N–90°N, there is no significant change in DJF (Dec–Feb) precipitation over the SHM region (Nalam et al. 2018), but we find an increase in SHM precipitation when the Arctic injection is above 30 Tg yr−1. The experiments in Nalam et al. (2018) considered the difference between global and Arctic injection, while this study investigated the impacts of equatorial and Arctic injection with various injecting intensities. Additionally, this study also provides more details in the mechanism of monsoon change. The reduced GM precipitation is mainly due to the thermodynamic term under the effect of tropical SAI, while the hemispheric antisymmetric impact of Arctic SAI arises from the dynamic term. However, since each SAI experiment is only run for one time, internal variability cannot be removed. Future research needs to use more models and experiments to investigate that.
There are some limitations in our simulated results. The coarse resolution in our model may affect the simulated regional monsoon circulation (Song and Zhou 2014). Some studies found that a higher resolution can make the topography more accurate, which reduces the bias in simulating the monsoon (i.e., Li et al. 2015; Mishra et al. 2018). Meanwhile, we are aware that the CAM4 does not consider the influence of aerosols in the troposphere and include some processes, for example, aerosol-cloud interaction, nonorographic gravity waves, termed turbulent mountain stress, and quasi-biennial oscillation (Richter et al. 2010; Marsh et al. 2013), which could influence the rainfall response. Using the CESM1 (WACCM), the precipitation over the North American, western North African, SH monsoon and mid-latitude region is suppressed in the equatorial geoengineering (Kravitz et al. 2019), which is similar to the result in tropical SAI experiments in this study. However, they found the increased precipitation over Indian monsoon and southern China, while the suppressed Indian monsoon and East Asian monsoon were found in our experiments. Although some uncertainties occur in the regional monsoon changes, our simulations capture the global monsoon pattern. Previous studies using the same model found that the simulated volcanic impacts on global monsoon and ENSO were consistent with the observations and reconstructions (Liu et al. 2016, 2018; Sun et al. 2019b), but climate response to volcanic eruption is not a perfect analogue for climate response to SAI.
The bulk aerosol parameters with a log-normal distribution for the sulfate aerosol are used in this model, which is another physical limitation. The aerosol mass is assumed to be a volcanic-like distribution with an effective radius of 0.426 μm and a standard deviation of 1.25 (Neely et al. 2016), similar to the setting about an effective radius of 0.5 μm and a standard deviation of 1.25 in CESM1 (WACCM4) (Marsh et al. 2013). Previous studies found that the aerosol particle size plays an important role in simulating geoengineering responses, and larger particles are less effective at counteracting greenhouse warming (Rasch et al. 2008). Using the particle size with a volcanic-like distribution can be idealized and unrealistic in the study of geoengineering. In the real world, the injection methods of SAI (i.e., high-flying aircraft, stratospheric balloons) are still in the early stage of development, which is hard to simulate the specific processes in models (Lawrence et al. 2018; Kravitz et al. 2015). Since this study mainly focuses on the impacts of different injection locations (equator and Arctic), their relative contributions to GM precipitation and the underlying mechanisms may be reasonable.
References
Adler RF, Huffman GJ, Chang A et al (2003) The version 2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J Hydrometeorol 4:1147–1167
Boucher O, Randall D, Artaxo P et al (2013) Clouds and aerosols. In: Climate change 2013: the physical science basis. contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change (pp. 571–657). Cambridge University Press
Cao L, Duan L, Bala G et al (2017) Simultaneous stabilization of global temperature and precipitation through cocktail geoengineering. Geophys Res Lett 44. https:doi.org/10.1002/2017GL074281
Chapman WL, Walsh JE (1993) Recent variations of sea ice and air temperature in high latitudes. Bull Am Meteorol Soc 74:33–47
Cheng W, MacMartin D, Dagon K et al (2019) Soil moisture and other hydrological changes in a stratospheric aerosol geoengineering large ensemble. J Geophys Res Atmos. https://doi.org/10.1029/2018JD030237
Crutzen PJ (2006) Albedo enhancement by stratospheric sulfur injections: a contribution to resolve a policy dilemma? Clim change 77:211–220
Early JT (1989) Space-based solar shield to offset greenhouse effect. J Br Interplanet Soc 42:567–569
Fasullo JT (2012) A mechanism for land-ocean contrasts in global monsoon trends in a warming climate. Clim Dyn 39:1137–1147
Fasullo JT, Otto-Bliesner BL, Stevenson S (2019) The influences of volcanic aerosol meridional structure on monsoon responses over the last millennium. Geophys Res Lett 46:12350–12359
Ferraro AJ, Griffiths HG (2016) Quantifying the temperature-independent effect of stratospheric aerosol geoengineering on global-mean precipitation in a multi-model ensemble. Environ Res Lett 11:034012
Gao C, Robock A, Ammann C (2008) Volcanic forcing of climate over the past 1500 years: an improved ice core-based index for climate models. J Geophys Res Atmos 113:1–15
Holland M, Bitz C (2003) Polar amplification of climate change in coupled models. Clim Dyn 21:221–232
Huang P, Xie S-P, Hu K et al (2013) Patterns of the seasonal response of tropical rainfall to global warming. Nature Geosci 6:357–361
Hsu P, Li T, Luo JJ, Murakami H, Kitoh A, Zhao M (2012) Increase of global monsoon area and precipitation under global warming: a robust signal? Geophys Res Lett 39:L06701. https://doi.org/10.1029/2012GL051037
Jiang DB, Tian ZP, Lang XM (2015) Mid-Holocene global monsoon area and precipitation from PMIP simulations. Clim Dyn 44:2493–2512
Kravitz B, MacMartin DG, Wang H, Rasch PJ (2016) Geoengineering as a design problem. Earth Syst Dyn 7:469–497
Kravitz B, Robock A, Boucher O et al (2011) The geoengineering model intercomparison project (GeoMIP). Atmos Sci Lett 12:162–167
Kravitz B, Robock A, Tilmes S et al (2015) The geoengineering model intercomparison project phase 6 (GeoMIP6): simulation design and preliminary results. Geosci Model Dev 8:3379–3392
Kravitz B, MacMartin DG, Tilmes S et al (2019) Comparing surface and stratospheric impacts of geoengineering with different SO2 injection strategies. J Geophys Res 124:7900–7918
Lawrence MG, Schafer S, Muri H et al (2018) Evaluating climate geoengineering proposals in the context of the Paris agreement temperature goals. Nat Commun 9:3734
Lee J-Y, Wang B (2014) Future change of global monsoon in the CMIP5. Clim Dyn 42:101–119
Lenton TM, Vaughan NE (2009) The radiative forcing potential of different climate geoengineering options. Atmos Chem Phys 9:5539–5561
Li J, Yu RC, Yuan WH et al (2015) Precipitation over East Asia simulated by NCAR CAM5 at different horizontal resolutions. J Adv Model Earth Syst 7:774–790. https://doi.org/10.1002/2014MS000414
Li DH, Zhou TJ, Zou LW et al (2018) Extreme high-temperature events over East Asia in 1.5 °C and 2 °C warmer futures: analysis of NCAR CESM low-warming experiments. Geophys Res Lett 45:1541–1550
Liu J, Wang B, Ding QH et al (2009) Centennial variations of the global monsoon precipitation in the last millennium: results from ECHO-G Model. J Clim 22:2356–2371
Liu F, Chai J, Wang B et al (2016) Global monsoon precipitation responses to large volcanic eruptions. Sci Rep 6:24331. https://doi.org/10.1038/srep24331
Liu F, Chen X, Sun LY et al (2018) How do tropical, Northern hemispheric and Southern hemispheric volcanic eruptions affect ENSO under different initial ocean conditions? Geophys Res Lett https. https://doi.org/10.1029/2018GL080315
Marsh D, Mills M, Kinnison D et al (2013) Climate change from 1850 to 2005 simulated in CESM1(WACCM). J Climate 26:7372–7391
Mishra SK, Anand A, Fasullo JT et al (2018) Importance of the resolution of surface topography in Indian monsoon simulation. J Clim 31:4879–4898
Meng Z, Zhou TJ, Man WM (2019) Hydroclimate responses over global monsoon regions following volcanic eruptions at different latitudes. J Clim 32:4367–4385
Nalam A, Bala G, Modak A (2018) Effects of Arctic geoengineering on precipitation in the tropical monsoon regions. Clim Dyn 50:3375–3395
National Research Council (2015) Climate intervention: reflecting sunlight to cool earth. National Academies Press, Washington, p 234
Neale RB, Richter J, Park S et al (2013) The mean climate of the community atmosphere model (CAM4) in forced SST and fully coupled experiments. J Clim 26:5150–5168
Neely R, Conley A, Vitt F et al (2016) A consistent prescription of stratospheric aerosol for both radiation and chemistry in the Community Earth System Model (CESM1). Geosci Model Dev 9:2459–2470
Otto-Bliesner BL, Brady EC, Fasullo J (2016) Climate variability and change since 850 CE: an ensemble approach with the community earth system model. B Am Meteorol Soc 97:735–754
Pausata FSR, Chafik L, Caballero R et al (2015) Impacts of high-latitude volcanic eruptions on ENSO and AMOC. Proc Natl Acad Sci 112:13784–13788
Plazzootta M, Séférian R, Douville R et al (2018) Land surface cooling induced by sulfate geoengineering constrained by major volcanic eruptions. Geophys Res Lett https. https://doi.org/10.1029/2018GL077583
Rasch P, Crutzen P, Coleman D (2008) Exploring the geoengineering of climate using stratospheric sulfate aerosols: the role of particle size. Geophys Res Lett 35:L02809. https://doi.org/10.1029/2007GL032179
Richter J, Sassi F, Garcia R (2010) Toward a physically based gravity wave source parameterization in a general circulation model. J Atmos Sci 67:136–156
Robock A, Oman L, Stenchikov GL (2008) Regional climate responses to geoengineering with tropical and Arctic SO2 injections. J Geophys Res 113:D16101
Seitz R (2011) Bright water: Hydrosols, water conservation and climate change. Clim Change 105:365–381
Song FF, Zhou TJ (2014) Interannual variability of East Asian summer monsoon simulated by CMIP3 and CMIP5 AGCMs: Skill dependence on Indian Ocean–western Pacific anticyclone teleconnection. J Climate 27:1679–1697
Sun W, Liu J, Wang ZY (2017) Simulation of centennial-scale drought events over eastern China during the past 1500 years. J Meteor Res 31:17–27
Sun W, Wang B, Liu J et al (2019a) How northern high-latitude volcanic eruptions in different seasons affect ENSO. J Clim 32:3245–3262
Sun W, Liu J, Wang B et al (2019b) A ‘‘La Niña-like’’ state occurring in the second year after large tropical volcanic eruptions during the past 1500 years. Clim Dyn 52:7495–7509
Tilmes S, Richter J, Kravitz B et al (2018) CESM1(WACCM) stratospheric aerosol geoengineering large ensemble project. B Am Meteorol Soc 99:2361–2371
Trenberth KE, Stepaniak DP, Caron JM (2000) The global monsoon as seen through the divergent atmospheric circulation. J Clim 13:3969–3993
Visioni D, MacMartin DG, Kravitz B et al (2019) Seasonal injection strategies for stratospheric aerosol geoengineering. Geophys Res Lett https. https://doi.org/10.1029/2019GL083680
Wang B, Ding QH (2008) Global monsoon: Dominant mode of annual variation in the tropics. Dynam Atmos Oceans 44:165–183
Wang B, Li J, Cane MA et al (2018) Toward predicting changes in the land monsoon rainfall a decade in advance. J Clim 31:2699–2714
Wang B, Liu J, Kim H-J et al (2012) Recent change of the global monsoon precipitation (1979–2008). Clim Dyn 39:1123–1135
Wang PX, Wang B, Cheng H et al (2017) The global monsoon across time scales: Mechanisms and outstanding issues. Earth-Sci Rev 174:84–121
Wang ZY, Li Y, Liu B et al (2015) Global climate internal variability in a 2000-year control simulation with community earth system model (CESM). Chinese Geogr Sci 25:263–273
Xie P, Arkin P (1997) Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull Amer Meteor Soc 78:2539–2558
Zanchettin D, Khodri M, Timmreck C et al (2016) The model intercomparison project on the climatic response to Volcanic forcing (VolMIP): experimental design and forcing input data for CMIP6. Geosci Model Dev 9:2701–2719
Zhang WX, Zhou TJ, Zou LW et al (2018) Reduced exposure to extreme precipitation from 0.5 °C less warming in global land monsoon regions. Nat Commun 9:3158
Acknowledgements
We thank the CMAP and GPCP for the observational data. Comments from three anonymous reviewers improved the quality of this paper. Our study is supported by the National Science Foundation (NSF) of China (41971108), National Key Research and Development Program of China (2016YFA0600401), NSF of China (41420104002, 41671197, and 41971021), and Priority Academic Program Development of Jiangsu Higher Education Institutions (164320H116). This is publication No 11110 of SOEST, No 1463 of IPRC and number 317 of the Earth System Modeling Center.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sun, W., Wang, B., Chen, D. et al. Global monsoon response to tropical and Arctic stratospheric aerosol injection. Clim Dyn 55, 2107–2121 (2020). https://doi.org/10.1007/s00382-020-05371-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05371-7