Abstract
This study investigates how teleconnections linking tropical rainfall anomalies and wintertime circulation in the northern extra-tropics are represented in historical simulations for the period 1950–2010 run by partners of the EU-funded PRIMAVERA project, following the HighResMIP protocol of CMIP6. The analysis focusses on teleconnections from the western/central Indian Ocean in mid-winter and from the NINO4 region in both the early and the late part of winter; this choice is justified by a substantial change in the relationship between ENSO and the North Atlantic Oscillation (NAO) in the two parts of the season. Model results for both coupled integrations and runs with prescribed sea-surface temperature (SST) are validated against data from the latest ECMWF 20th-century re-analysis, CERA20C. Simulations from six modelling groups are considered, comparing the impact of increasing atmospheric resolution in runs with prescribed SST, and of moving from uncoupled to coupled simulations in the high-resolution version of each model. Single runs were available for each model configurations at the time of writing, with one centre (ECMWF) also providing a 6-member ensemble. Results from this ensemble are compared with those of a 6-member multi-model ensemble (MME) formed by including one simulation from each model. Using only a single historical simulation from each model configuration, it is difficult to detect a consistent change in the fidelity of model-generated teleconnections when either atmospheric resolution is increased or ocean coupling is introduced. However, when simulations from six different models are pooled together in the MME, some improvements in teleconnection patterns can be seen when moving from uncoupled to coupled simulations. For the ECMWF ensemble, improvements in the coupled simulations are only apparent for the late-winter NINO4 teleconnection. While the Indian Ocean teleconnection and the late-winter NINO4 teleconnection appear equally robust in the re-analysis record, the latter is well simulated in the majority of both uncoupled and coupled runs, while the former is reproduced with (generally) much larger errors, and a high degree of variability between individual models and ensemble members. Most of the simulations with prescribed SST fail to produce a realistic estimate of multi-decadal changes between the first and the second part of the 60-year record. This is (at least partially) due to their inability to simulate an Indian Ocean rainfall change which, in observations, has a zonal gradient out of phase with SST changes. In coupled runs, at least one model run with both realistic teleconnections and a good simulation of the inter-decadal pattern of Indian Ocean rainfall also shows a realistic NAO signal in extratropical multi-decadal variability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Teleconnections have long been recognised as a fundamental dynamical mechanism linking weather and climate variability in the tropics and the extra-tropics. Although they can be detected throughout the whole yearly cycle, many teleconnection patterns affecting the northern midlatitudes reach their largest amplitude during the northern winter, when the strong vorticity gradients in the subtropical regions intensify the Rossby wave sources associated with tropical convection (Sardeshmukh and Hoskins 1988).
Although connections between variability in specific regions of both tropics and mid-latitudes had been studied since the 1930′s, the interest in teleconnections grew strongly in the early 1980′s, when it was recognised that northern hemisphere patterns detected from covariance/correlation analysis resembled the dynamical response to diabatic heating anomalies in the tropics, especially those related to the El Nino—Southern Oscillation (ENSO) phenomenon (Wallace and Gutzler 1981; Horel and Wallace 1981; Hoskins and Karoly 1981; Shukla and Wallace 1983 among others). In turn, this led to a strong emphasis on teleconnections in studies on seasonal predictability (see review papers in Anderson et al. 1998).
Teleconnections linking tropics and extratropics do not act only on seasonal time scales. In the last decade, a growing interest in sub-seasonal predictions has been accompanied by a large number of studies on teleconnections associated with the Madden–Julian Oscillation (MJO), and especially those linking the MJO and North Atlantic variability (see Cassou 2008; Lin et al. 2009; Vitart and Molteni 2010; Garfinkel et al. 2014; Stan et al. 2017; Vitart 2017). On multi-decadal time scales, interest in teleconnections has been focussed on specific phenomena, such as the link between decadal variability in Indian Ocean temperature and in the North Atlantic Oscillation, advocated by Hurrell et al. (2004) and Hoerling et al. (2004), or the relationship between the tropical and extratropical components of the Pacific Decadal Oscillation (Newman et al. 2016).
Although it is recognised that a correct modelling of teleconnection is essential to relate regional climate change in tropical and extratropical regions, assessments of the fidelity of climate models used for historical and scenario runs in reproducing teleconnections have been comparatively less frequent, and have mostly focussed on ENSO variability (Bellenger et al. 2013; Weare 2013). In this paper, we follow recent works on predictability associated with tropical precipitation anomalies in different tropical regions (Molteni et al. 2015; Scaife et al. 2019) to diagnose teleconnections in historical runs performed following the HighResMIP protocol (Haarsma et al. 2016) of the Coupled Model Intercomparison Project—phase 6 (CMIP6). These simulations, which were delivered as the “Stream-1” contribution to the EU-funded PRIMAVERA project (www.primavera-h2020.eu), cover the period 1950–2014 and have been performed with both ocean–atmosphere coupled models and atmosphere-land models forced by prescribed sea-surface temperature (SST) from the HadISST-2 dataset (Titchner and Rayner 2014).
Assessing the benefits of increased resolution in climate models is one of the main goals of the PRIMAVERA project, and this paper will address one aspect of this topic, namely the impact of higher resolution in the atmospheric/land models. An assessment of the impact of moving from atmosphere/land-only to fully coupled models (including ocean and sea-ice components) will also be presented. However, the paper also aims to address some general questions which are relevant to most current GCMs, independently from their resolution:
-
How do errors in model-simulated teleconnections compare with the observational uncertainty in the teleconnection patterns, and how affected are they by internal variability?
-
Teleconnections from certain tropical regions appear to be simulated with better fidelity and robustness than others; are these differences consistent across models?
-
How do teleconnections detected on interannual time scales relate to interdecadal changes during the 60-year period covered by HighResMIP historical runs, in both observations and model simulations?
Investigating these topics is possibly the most original aspect of this paper, and our findings provide suggestions for future research which go beyond the model-intercomparison aspects of our study.
Validating results on the relationship between tropical rainfall and the extra-tropical circulation on a 60-year time scale requires observational estimates of precipitation over tropical oceans before the satellite era. Rainfall data from the latest 20th-century re-analysis performed at the ECMWF with a weakly-coupled data assimilation system, named CERA20C (Laloyaux et al. 2018), have compared favourably with gridded data over continents in the GPCC dataset (Schneider et al. 2017). In this study, upper-air and precipitation data from CERA20C are used for verification. The latter data have been calibrated against GPCPv2.3 data in the 1981–2010 period, using a regression procedure described in the Appendix.
A description of the model simulations, the observational data, and the statistical methods used in this study are given in Sect. 2. Teleconnections estimated from CERA20C data are presented in Sect. 3, comparing results with those obtained from other data sources and estimating the uncertainty associated with sampling. The focus is on teleconnections from the Indian Ocean and the tropical Pacific, whose importance for Northern Hemisphere extratropical variability has been shown in numerous previous studies. Section 4 presents results from historical simulations from 6 European climate models; here, we assess the impact of increasing atmospheric resolution and of moving from prescribed-SST to coupled simulations. We also compare variability across models and within a single-model ensemble, and discuss differences in the fidelity of simulated teleconnections from different tropical regions and/or in different months. How teleconnections affect multi-decadal changes in tropical and extra-tropical circulation, and the ability of the PRIMAVERA models to reproduce them, is the topic of Sect. 5. Conclusions are presented in Sect. 6, highlighting the need of reasonably-sized ensembles from individual models to increase the statistical confidence in most of our results.
2 Datasets and methodology
2.1 HighResMIP simulations from the PRIMAVERA project
The historical simulations analysed in this paper have been run as a deliverable of the EU-funded project PRIMAVERA (see www.primavera-h2020.eu), and follow the HighResMIP protocol of CMIP-6 (Haarsma et al. 2016). They cover the 1950–2014 period, using CMIP6 historical forcings, and include:
-
a)
runs made with atmosphere-land models, where observed SST and sea-ice concentration are prescribed using a high-resolution (1/4°) dataset derived from HadISST-2 (Titchner and Rayner 2014);
-
b)
runs made with coupled climate models (including atmosphere, land, ocean and sea-ice), started from a spin-up run of at least 50 years with constant 1950 forcings.
Both the coupled and uncoupled models have been run in a low-resolution and a high-resolution version (the actual resolutions being chosen by the individual modelling groups). Table 1 lists the institutions, the model acronyms and the resolution of the atmosphere and ocean components. In this paper, we analyse data from the uncoupled runs at low and high resolution, and from the high-resolution coupled runs. For simplicity, we will refer to the prescribed-SST runs as AMIP-L and AMIP-H respectively, and to the coupled historical high-resolution runs as CHist-H.
The comparison between results from AMIP-L and AMIP-H will address the potential impact of atmospheric resolution, while the impact of ocean/sea-ice coupling will be assessed by comparing AMIP-H with CHist-H. We decided not to include the low-resolution coupled runs in our comparisons for two reasons:
-
Different groups have used different strategies in going from their low-res. to their high-res. coupled runs in PRIMAVERA, ranging from using the same ocean configuration, to using models with different resolutions and different degrees of retuning. Therefore, an assessment of the impact of increasing ocean resolution could not be performed for all models; and because of different retuning strategies (as well as the combination with changes in atmospheric resolution), differences in teleconnections from low-res. to high-res. coupled models cannot be ascribed to a single common factor.
-
There is already ample evidence on the benefit of moving from eddy-parametrised to eddy-permitting, or eddy resolving ocean models in coupled climate simulations (with reference to some of the models used here, see Sein et al. 2018; Docquier et al. 2019; Roberts et al. 2020).
Although the PRIMAVERA project plan required only one single run to be delivered for each configuration, a few institutions have run more than one realization in at least some of their model configurations. In particular, ECMWF has run (at least) six ensemble members for both uncoupled and coupled runs at low and high resolution. Therefore, in Sect. 4, we are able to compare results from 6-member ensembles composed from either single-model or multi-model simulations.
2.2 Observational reference
The historical simulations in HighResMIP cover the period 1950–2014. In order to validate the results of the teleconnection analysis performed on model data, we need observational datasets covering a large proportion of this 65-year period. Since we are mainly interested in the co-variability of tropical rainfall and northern-hemisphere (NH) geopotential height, we need a reliable estimate of rainfall over the tropical oceans spanning several decades and extending back into the pre-satellite era.
Because of combination of model biases and variations in the observing system, rainfall estimates from conventional re-analysis (using a multiplicity of data sources) may exhibit spurious trends and interdecadal differences (see the problems with Sahel rainfall variability in different re-analyses, discussed by Berntell et al. 2018 and Di Giuseppe et al. 2013). In the last 10 years, re-analyses covering at least a century using a restricted set of surface and near-surface data to ensure a higher data continuity have been performed by NOAA (20CR, Compo et al. 2011) and ECMWF (ERA20C, Poli et al. 2016). Although the impact of data discontinuity is reduced in these re-analyses, so is the observational constraint on model-generated field such as rainfall. Recently, ECMWF produced a second century-scale re-analysis using a weakly-coupled data assimilation system (CERA20C, Laloyaux et al. 2018) and a recent version of their coupled model, extending from 1900 to 2010. Rainfall variability over continents from CERA20C was found to be in reasonably good agreement with that estimated from the raingauge-based GPCC dataset (Schneider et al. 2017). CERA20C was therefore a potentially good candidate as a verification dataset for teleconnection patterns from HighResMIP simulations.
A preliminary comparison of tropical rainfall variability in CERA20C and in GPCP v2.3 (Adler et al. 2003) during the 1979–2010 period (not shown) confirmed the overall good quality of CERA20C data, but also showed the impact of model biases on rainfall variability and co-variability, which had been documented in teleconnection studies based on seasonal integrations of the ECMWF coupled model (Molteni et al. 2015). For this reason, it was decided to perform a calibration of CERA20C data against GPCP before using the re-analysis rainfall in the present study.
The calibration process, performed on monthly-mean data, is described in detail in Appendix A. Basically, it consists in a stepwise regression, in which GPCP data at any grid-point are first estimated using a linear regression against CERA20C data at the same point. In a second step, the residual term (by definition orthogonal to the local signal) is regressed against the leading principal components of the global CERA20C rainfall anomalies. This process is performed separately for each calendar month, using regression coefficients computed from a 3-month window over 30 years (1981–2010) in order to ensure continuity and increase statistical significance. For example, February data in the 1950–2010 period are calibrated using regression coefficients computed from January, February and March data in the satellite era.
As shown in the Appendix, in most locations the local term accounts for the majority of the GPCP rainfall variance, but there are regions in the tropics and the subtropics (such as those surrounding the Maritime Continents) where the contribution of the non-local correction is important. For geopotential height, no calibration was necessary for our study, since the model biases of mid-tropospheric fields in the northern extratropics are relatively small and the observational constraint provided by near-surface data is well exploited by the 4D-var assimilation system used in CERA20C.
2.3 Computation of teleconnection patterns and associated metrics
The computation of teleconnection patterns in this study follows the simple methodology adopted by Molteni et al. (2015). If we want to relate the variability of field F1 in a given location (or its gradient in a region) with the variability of field F2 on a global or hemispheric domain, we perform the following two steps.
-
For each time interval in the selected time domain, an index of the teleconnection “source” S(t) is defined either as the area average of anomalies of field F1 in a given longitude-latitude box (eg rainfall anomalies in the NINO4 region), or as a difference of area-averaged anomalies in two regions (as in the NAO index based on 500-hPa height used by Molteni et al. 2015).
-
A teleconnection pattern T(x) is defined as the covariance between anomalies of F2 at any grid point in a chosen spatial domain and the source index S(t), divided by the standard deviation of S(t):
$${\text{T}}\left( {\text{x}} \right) \, = {\text{ cov }}\left[ {{\text{F}}_{{2}} \left( {{\text{x}},{\text{t}}} \right),{\text{ S}}\left( {\text{t}} \right)} \right] \, /\sigma \left[ {{\text{S}}\left( {\text{t}} \right)} \right]$$(1)
In this way, T(x) is a dimensional field representing the anomaly of F2 associated with one positive standard deviation of the index S(t).
In the calculation of teleconnections, anomalies are always defined with respect to the mean in the same period for which the covariances are computed; specifically, 60-winter means are used to compute 60-winter covariances. No detrending or moving averages have been applied.
Suppose that teleconnection patterns with the same index are computed from two different samples, for example form re-analysis and model data, and their difference in a target area A needs to be quantified. A simple metric to quantify this is given by the Euclidean norm (ie, the root-mean-square amplitude over area A) of the difference between the two patterns, divided by the average of their norms:
Note that, in a phase space spanned by the anomalies of field F2, the origin (corresponding to climatology) and the two teleconnection patterns T1 and T2 define a triangle whose sides are measured by the three norms in Eq. 2. Therefore the normalised difference δ is bound to be between 0 and 2, where the upper limit corresponds to an exact anti-correlation in space between the two patterns. This graphical interpretation is also valid when two teleconnection patterns are visualised in a so-called Taylor diagram (Taylor 2001), provided that one of the two patterns is taken as a reference (ie, it defines the x-axis of the diagram).
Finally, we point out that teleconnection patterns defined by Eq. 1 are sensitive to the amplitude of the F2 anomalies. These are preferred to patterns defined by correlations, since one common error in the GCM representation of teleconnections is an (often serious) underestimation of their amplitude with respect to observations. Using the normalised difference in Eq. 2 to quantify errors in teleconnections implies that underestimations in amplitude are reflected by our chosen metric; specifically, model patterns with low amplitude are characterised by large values of δ because of the normalisation by the combined amplitude of observed and model patterns in Eq. 2.
3 Teleconnections in CERA20C
3.1 Selection of regions and periods
In scientific literature, teleconnections have been computed with a variety of techniques and over a large number of space and time domains. This paper does not aim to provide a comprehensive picture of teleconnections in the PRIMAVERA simulations; rather, we will concentrate on teleconnections linking the northern-hemisphere (NH) extra-tropical circulation with diabatic heating anomalies in selected areas of the tropical Indo-Pacific regions, which have been recognised in previous studies as key areas for tropical-extratropical interactions. Specifically, we will focus on two tropical areas where rainfall anomalies have been shown to have significant links to NH anomalies during the boreal winter (Molteni et al. 2015; Scaife et al. 2019), namely the western/central Indian Ocean (WCIO) and the central Pacific at longitudes corresponding to the NINO4 region.
Following the terminology of Sect. 2.3, our “sources” of teleconnections are defined as rainfall anomalies in the following areas:
It should be noted that our definition of the NINO4 region has a wider meridional extent than the traditional definition based on a 5N-5S band; this is done to better capture the extent of rainfall anomalies and to have anomalies defined in regions of equal size.
Molteni et al. 2015 identified these two regions as corresponding to regional maxima in the correlation between seasonal-mean SST and rainfall in individual locations (see their Fig. 1). In other words, in these areas above-average SST is associated with above-average rainfall, with the positive correlation being particularly strong in the NINO4 region. On the other hand, the region in between, covering the eastern tropical Indian Ocean, the Maritime Continents and the western edge of the tropical Pacific, is characterised by much weaker or even negative correlation between SST and rainfall, indicating that SST responds to (rather than forces) changes in radiative and surface heat fluxes induced by anomalies in the Walker circulation. The focus on the WCIO and NINO4 region is therefore justified by their characterization as actual forcing regions for the atmospheric flow.
a Covariance of rainfall anomalies with the first principal component (PC) of monthly-mean rainfall over the Indo-Pacific Ocean in the November-to-March season, from calibrated CERA20C data. Blue box: domain of PC analysis. Red boxes: near-equatorial regions used in the teleconnection study of Molteni et al. 2015, namely the western-central Indian Ocean (WCIO: 40E–90E, 10N–10S) and a meridionally extended NINO4 region (160E–150 W, 10N–10S). b: as in (a) but from a PC analysis in an Indian-West Pacific domain, after subtracting the rainfall component correlated with NINO3.4 SST
The choice of the WCIO and NINO4 regions can also be based on the examination of the leading modes of rainfall variability in the Indo-Pacific region. Figure 1a shows the pattern of the leading empirical orthogonal function of monthly rainfall in the Indo-Pacific region derived from monthly CERA20C data from November to March 1950 to 2010 (precisely, the map is computed as the covariance with the 1st principal component computed in the domain delimited by the blue box). The WCIO and NINO4 regions, shown by the red boxes, stand out as regions of spatially coherent rainfall anomalies.
One could object that the pattern in Fig. 1a is very close to the mean rainfall response to ENSO, and therefore rainfall in both regions are both dependent on the same SST signal. However, if we remove the ENSO SST signal by subtracting the regression of rainfall anomalies onto the NINO3.4 SST, and also limit the EOF computation to the region west of 160E, the covariance with the 1st principal component (see Fig. 1b) still shows a tripolar pattern with nodes and maxima at the same locations, albeit with much reduced amplitude in the central Pacific. This indicates that rainfall variability with the tripolar pattern in Fig. 1b can exist independently of ENSO. In fact, this rainfall pattern resembles one of the EOFs of outgoing longwave radiation (OLR) associated with MJO variability (Lin et al. 2009), as well as the inter-decadal changes in tropical rainfall discussed in Sect. 5.
In many studies on tropical-extratropical teleconnections, data are averaged according to traditional seasonal definitions. However, since here we are specifically concerned with impacts on the North-Atlantic and European regions, we should take into account that the ENSO impact on these regions changes significantly from late fall/early winter to the late part of winter (see Ayarzaguena et al. 2018, King et al. 2018 and references within). Therefore, instead of using the traditional December-to-February (DJF) means, we will compute teleconnections from NINO4 separately from November–December (ND) means and from January–February (JF) means. For consistency, we will use 2-month means also for the WCIO teleconnections; since the WCIO link to the North Atlantic is more consistent through the boreal winter, and reaches its maximum strength in December and January, we will use a DJ mean to display the WCIO teleconnection pattern.
To support the above statements, we show in Fig. 2 correlations of a NAO index with equatorial SST and rainfall anomalies (averaged in overlapping 20 × 20-degree boxes) in the Indo-Pacific domain, for averages in ND, DJ, and JF computed from HadISST-2 and CERA20C data. Here we have used an Atlantic-wide NAO index, also adopted by Molteni and Kucharsky (2019), which is based on 500-hPa height anomalies from 70 to 20 W and better captures the traditional ENSO response over the Atlantic than indices based on eastern Atlantic grid points (see discussion in Sects. 3.2 and 3.3, and Table S1 in Supplementary Material). Both SST and rainfall correlations change sign in the central and eastern Pacific between early and late winter, while the rainfall signal keeps the same sign in the WCIO region (even though the location of the maximum shifts to the east in late winter).
Correlation between an Atlantic-wide NAO index (see Eq. 3a) and anomalies of SST (a) and rainfall (b) averaged in 20 × 20-degree boxes centred on the Equator, from two-month averages in November–December (orange), December-January (green) and January–February (blue). The horizontal grey lines delimit the range beyond which correlation is significant at a 90% confidence level in a two-tail test. Data from CERA20C re-analysis
It is worth noting that NAO correlations with equatorial SST only exceed the 90% confidence level in parts of the eastern Pacific; over the Indian Ocean, only NAO correlations with rainfall anomalies are significant, reaching approximately 0.4 with anomalies centred between 60 and 80E in DJ. The fact that correlations with SST change sign from ND to JF in the western Indian Ocean, while those with rainfall are larger and positive throughout the winter, suggests that the WCIO rainfall anomalies which correlate with the NAO are only weakly constrained by local SST anomalies.
3.2 Northern hemisphere teleconnections with tropical rainfall
Having defined the tropical teleconnections sources and the appropriate time domains, we can now investigate the connections between the tropical rainfall variability and anomalies in the NH circulation and temperature patterns, using CERA20C data for winters 1950/51 to 2009/10. Figure 3 shows teleconnection of 500-hPa height and 850-hPa temperature with tropical rainfall anomalies from WCIO (in DJ) and NINO4 (ND and JF), computed according to Eq. 1.
Left column (a–c): Covariance of 500-hPa geopotential height over the NH with normalised precipitation anomalies in the tropical regions defined in Fig. 1. Top: covariance with WCIO prec. in Dec-Jan; centre: covariance with NINO4 prec. in Nov-Dec; bottom: covariance with NINO4 prec. in Jan-Feb. Right column (d–f): as in left column but for covariances with 850-hPa temperature. Data from CERA20C in winters 1950/51 to 2009/10
The WCIO teleconnection in geopotential height (Fig. 3a) shows a pattern dominated by zonal wavenumbers 2 and 3, with the main negative centres over the Aleutian Islands and Southern Greenland, and a strong projection onto the positive phase of the NAO. The anomalous south-westerly flow towards western Europe is associated with advection of warm Atlantic air over the European continent, resulting in a warm anomaly over most of the continent (Fig. 3d). Warm anomalies are also present over most of North America and North Asia; indeed, Molteni et al. 2015 already discussed the similarity of the WCIO teleconnection with the Cold Ocean—Warm Land (COWL) pattern defined by Wallace et al. (1996).
Consistent with the results in Fig. 2, the NINO4 teleconnection (Fig. 3b, c) has opposite projections onto the NAO in ND and JF, although in both cases the Euro-Atlantic anomalies are shifted (either to the south in ND or to the west in JF) with respect to the canonical NAO pattern. For this reason, the NINO4 impact is better described by the Atlantic-wide index used by Molteni and Kucharski (2019):
than by an index based on boxed centred around Portugal and Iceland:
where Z′ is the 500-hPa height anomaly (see Supplementary Material).
The NINO4 signal in the central and eastern part of North Pacific becomes much stronger in late winter, as well as the temperature impact over North America; this justifies the frequent use of January–March seasonal means in studies of seasonal predictability over North America. Although the late winter response to ENSO is probably the most studied among tropical-extratropical teleconnections, it is worth noting that, in terms of impact on European temperatures, the WCIO teleconnection gives a much stronger signal than the late-winter NINO4 response.
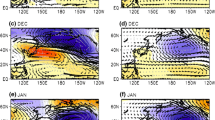
Since one may question the reliability of CERA20C data before the satellite era, the geopotential patterns shown in the left column of Fig. 3 have been recomputed for the second half of the record (1981–2010), and are shown in Fig. 4. This calculation has been done using both CERA20C data (left-column of Fig. 4) and a combination of ERA-interim (Dee et al. 2011) data for height and GPCP2.3 (Adler et al. 2003) for rainfall (right column of Fig. 4). Patterns are very similar to those in the 60-year CERA20C record; one may note a strengthening of the NAO signal in the WCIO teleconnection for the last 30 years, which reinforces the wavenumber-2 component in the hemispheric pattern, and also a stronger late-winter response to NINO4 anomalies in JF.
Covariance of 500-hPa geopotential height over the NH with normalised precipitation anomalies in the tropical regions defined in Fig. 1. Left column (a–c): as in Fig. 3a–c, but for winters 1980/81 to 2009/10. Right column (d–f): as in the left column, but using rainfall data from GPCP v2.3 and 500-hPa height from ERA-Interim
3.3 Measures of statistical significance
In the following, the similarity between observed and modelled teleconnection patterns will be quantified by the normalised rms error defined by Eq. 2. Two NH regions are considered for the model assessment: a North Atlantic/Europe sector (30–85 N, 80 W–40E) and a North Pacific/North America sector (30–85 N, 160E–80 W). For reasons of brevity, only differences in geopotential height patterns will be presented; the teleconnection patterns derived from CERA20C data and shown in the left column of Fig. 3 will be taken as a reference.
In doing a comparison between teleconnections in re-analyses and model data, one should account for the fact that the re-analysis patterns are also affected by errors. These partly originate from limitations in the data assimilation process (especially in surface-driven twentieth century re-analyses) which may induce flow-dependent biases in the data, and partly from the sampling errors that affect the computation of covariances from a limited sample (see Deser et al. 2017 for a detailed analysis on the ENSO teleconnection). In this subsection, we concentrate on the second type of uncertainty, and estimate confidence levels which can be compared with differences between observed and modelled teleconnections.
In order to assess the probability that differences may arise just by sampling events from two populations with the same statistical properties, we used a bootstrap technique to construct 200 alternative 60-year samples from the whole 1950–2010 CERA20C record. To account for the potential effect of radiative forcing trends which are expected to be reproduced in the PRIMAVERA runs, and the consequent change in the mean state (note that in AMIP runs SST trends are prescribed), we impose the condition that the number of years resampled from either the first or the second half of the CERA20C record cannot exceed 2/3 of the total. This means that our bootstrap statistics are appropriate for runs that span the full 60-year record.
For each of the 200 bootstrap samples, we computed teleconnection patterns of 500-hPa height with WCIO and NINO4 rainfall, and derived statistics of the differences with respect to the actual (non-resampled) teleconnection patterns shown in Fig. 3a–c. We also computed such statistics from patterns obtained by merging six 60-year random samples, to be compared with those from six-member ensembles of model simulations. Specifically, we estimated distributions of:
-
local differences at individual grid points;
-
normalised rms differences δ averaged over the European-Atlantic and the Pacific-North American domains defined above.
From these distributions, confidence levels for the hypothesis that difference between model and observed teleconnections exceed those caused to random sampling were estimated. For local differences, a 90% confidence level will be used to highlight regions with significant errors in the model teleconnections patterns shown in Figs. 6, 8, 9, 11 and 12 of Sect. 4. For area-averaged values of δ, 90% and 95% confidence levels are used to assess the significance of the area-averaged errors shown in Fig. 10 of Sect. 4.
As an example, the cumulative distributions D(δ) of normalised differences in the European-Atlantic sector (from individual 60-year samples) are shown in left-column of Fig. 5. A steeper curve can be seen for the differences in WCIO teleconnection than for those in the NINO4 patterns in either early or late winter, indicating that the WCIO pattern over the Atlantic is more robust with respect to sampling errors. The same computation for the Pacific-North American region (not shown) indicates that the late-winter NINO4 teleconnection is the most robust in this sector, with a distribution curve as steep as that of the WCIO Atlantic response.
Left column (a–c): cumulative distribution of the normalised distance δ between teleconnection patterns of 500-hPa, derived from 200 re-sampled datasets of 60 winters and from the original CERA20C 60-winter dataset. Distances are computed over a European-Atlantic domain (80 W–40E, 30 N–85 N). The top/centre/bottom panels correspond to the three teleconnection patterns shown in Fig. 3a–c respectively. Right column (d–f): as in the left column, but for the probability density function of the NAO index (from Eq. 3a, in dam) in the three teleconnection patterns
From the same bootstrap sample, the probability density function (PDF) of NAO indices in the three teleconnection patterns considered above has also been computed, using the definitions given in both Eqs. 3a and 3b. In the right column of Fig. 5, we show PDFs for the Atlantic-wide index already used for the computation of Fig. 2, which is particularly suited to represent the signal in the NINO4 response (see Supplementary Material for a comparison with the more traditional “Portugal-minus-Iceland” index, and a discussion on changes in the NAO statistics at multi-decadal time scales). Note that although the amplitude of the NAO signal has non-negligible sampling variability, the sign of the NAO signal in the three teleconnection patterns is clearly defined when the Atlantic-wide index in Eq. 3a is used. This means we can be confident in the sign of the NAO signal in the teleconnection patterns shown in Fig. 3a–c, at least as far as anomalies in the western and central Atlantic are concerned.
If the Portugal-Iceland index (Eq. 3b) is used, confidence in the positive NAO sign of the WCIO teleconnection is even stronger; for the late-winter NINO4 teleconnection, NAO values remains mostly in the negative range, but positive values up to 2 dam are also possible (see Fig. S1 in Supplementary Material). This reflects a moderate uncertainty in the eastern Atlantic and European part of the NAO signal connected to NINO4 rainfall, especially when compared to the stronger connection with the WCIO region.
4 Teleconnections in historical runs from PRIMAVERA
4.1 Results from the ECMWF ensemble
We start our evaluation of model teleconnection from the 6-member ensembles of AMIP and coupled simulations made with the ECMWF model. For the computation of teleconnections, members are concatenated to provide a record of 61 × 6 years, a single mean is defined for each variable as the average over both time and ensemble members, and variances/covariances are computed with respect to this mean.
Maps of 500-hPa height teleconnections with WCIO and NINO4 rainfall in the AMIP-L, AMIP-H, CHist-H ensembles are compared in Fig. 6; regions where the model patterns differ from the CERA20C teleconnections in Fig. 3a–c at a 90% confidence level (estimated from the variability of re-sampled datasets from CERA20C, as discussed in Sect. 3.3) are indicated by stippling. Taylor diagrams for these patterns, using the observed teleconnections in Fig. 3a–c as a reference, are shown in Fig. 7, where the normalised errors over the Atlantic-European and Pacific-North American sectors are also listed.
Teleconnection patterns (as in left column of Fig. 3) computed from 6-member ensemble historical simulations with the ECMWF model. Left: low-resolution AMIP ensemble (AMIP-L); Centre: high-resolution AMIP ensemble (AMIP-H); right: high-resolution coupled historical ensemble (CHist-H). Stippling denotes regions where differences from the CERA20C teleconnection patterns are significant at a 90% confidence level (estimated by the bootstrap technique described in Sect. 3.3)
Taylor diagrams for the teleconnection patterns from the ECMWF ensembles shown in Fig. 6, computed for the North Atlantic-European domain (top) and the Pacific-North American domain (bottom). Left: AMIP-L; centre: AMIP-H, right: CHist-H. Full circles: WCIO teleconnections in Dec-Jan; open and full squares: NINO4 teleconnections in Nov-Dec and Jan-Feb respectively
As reported in Roberts et al. (2018), for the NINO4 teleconnection in late winter the similarity between model and re-analysis improves going from AMIP-L to AMIP-H and then to CHist-H, particularly over the Atlantic-European area, where the normalised error is 1.41, 0.88 and 0.41 for the 3 model configurations. For the WCIO and early-winter NINO4 teleconnections, the two AMIP ensembles provide comparable results, while the coupled ensemble shows a clear degradation. Over the Atlantic-Europe, the normalised error of the WCIO teleconnection goes from 0.66 in AMIP-L to 0.85 in CHist-H; the error increase is even stronger for the early-winter NINO4 teleconnection, from 0.85 in AMIP-L to 1.75 in CHist-H. The degradation of the WCIO teleconnection going from prescribed SST runs to coupled runs was also found in seasonal re-forecasts made with same ECMWF model cycle (Johnson et al. 2019).
Teleconnection maps and their normalised errors have also been computed for individual ensemble members; the range of errors from single members is indicated in Table 2, for both the Atlantic-European (Table 2a) and the Pacific-North American region (Table 2b). The smallest range in the normalised error is found for the NINO4 teleconnection in JF over the latter region; teleconnections usually show a larger spread over the Atlantic region than over the Pacific, with a ratio of 1:2 to 1:3 between the smallest and the largest error of single members.
To illustrate the actual spread in the full patterns, Fig. 8 shows teleconnections with Indian Ocean rainfall from the 6 members of the ECMWF CHist-H ensemble. While ensemble members 3, 4 and 6 show a positive NAO signal, comparable to that found in the full AMIP ensembles (Fig. 6a, 6d), the first two members show a very weak response over both the North Atlantic and the North Pacific.
Teleconnection of WCIO rainfall with 500-hPa height in Dec.-Jan in the six individual ensemble members of the ECMWF high-resolution coupled ensemble (CHist-H). Stippling indicates areas where differences from the CERA20C pattern in Fig. 3a are significant at a 90% confidence level
At least two alternative explanations can be given for the results shown in Fig. 8. One possibility is that, while coupling affects the average strength of the WCIO teleconnection, atmospheric internal variability in the model generates enough differences in single-member responses to produce a few particularly poor outliers in CHist-H. Another possibility is that differences in ocean mean state and/or variability between different coupled members are the main cause of the differences in teleconnections.
Looking at the range of normalised errors for the WCIO teleconnections over the Atlantic-European region, listed in Table 2a, one finds that members of the CHist-H ensemble show a wider error range than the members of the AMIP-H ensemble (which use the same atmospheric component). This suggests that internal variability in coupled phenomena plays a role in increasing the variability of teleconnection. On the other hand, over the Atlantic-European region the largest error among the AMIP-H members is only about 20% lower than the error the worst CHist-H member, and actually three CHist-H members (no. 3, 4 and 6) have normalised errors which are equal or lower than the smallest error among AMIP-H members.
If we focus on the relationship between WCIO rainfall and NAO variability, we can also quantify the strength and fidelity of the teleconnection by comparing the covariance between the normalised WCIO index and the (dimensional) Portugal-Iceland NAO index defined in Eq. 3b (This is equivalent to computing the NAO index from the teleconnection patterns defined by Eq. 1)
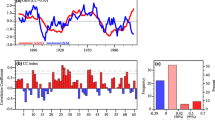
Figure 9a shows the WCIO-NAO covariance for the six members of the AMIP-L, AMIP-H and Chist-H ensembles; the value from CERA20C (36 m) is indicated by a horizontal grey line. There is a wide overlap between the NAO covariances from the members of the three ensembles, with most members showing values between 10 and 25 m. However, each of the AMIP ensembles has one member with a NAO covariance close to observation, while values less than 10 m are only shown by the first two members of CHist-H. The possibility that such low values are related to different ocean variability is explored in Fig. 9b, where the NAO covariance of the CHist-H members is plotted against the interannual standard deviation of the Nino3.4 SST in DJ. It turns out that the two members with very low NAO signal are those with the largest Nino3.4 variability (exceeding the observed value by about 20%), while the three members with largest NAO signal have Nino3.4 variability close to or lower than observed SST.
a Covariance between normalised WCIO rainfall in Dec-Jan and the Portugal-Iceland NAO index in the six members of the AMIP-L (red), AMIP-H (green) and CHist-H (blue) ECMWF ensembles; (b) CHist-H covariance plotted against the standard deviation of Dec-Jan NINO3.4 SST in each ensemble member. The grey line in (a) and the black square in (b) indicate re-analysis values. c Covariance between normalised WCIO rainfall in Dec-Jan and 500-hPa height, from a composite dataset including data from the ECMWF CHist-H ensemble member with the smallest difference between model and observed SST over the eastern eq. Indian Ocean in Oct-Nov. Stippling indicates areas where differences from the CERA20C pattern in Fig. 3a are significant at a 90% confidence level
The reason why a larger ENSO variability leads to a deterioration of the WCIO-teleconnection in the ECMWF coupled model is further explored in the Supplementary Material. Summarizing the results, we found that ENSO variability is associated with a seasonally-persistent meridional shift of rainfall in the central Indian Ocean, rather than a rainfall change which is (in observation and AMIP runs) nearly-symmetric with respect to the Equator (see Figs. S4 and S5). From CERA20C data, it is found that a north–south dipole in rainfall anomaly over the central Indian Ocean has a negligibly small connection with the NAO, while a coherent signal across the equator between 70 and 90E gives an NAO teleconnection very similar to the full WCIO (Fig. S6).
Also, we found that the meridional shift of Indian Ocean rainfall is due to the connection between ENSO and large-amplitude SST anomalies in the eastern equatorial Indian Ocean (EEIO) simulated by the ECMWF model during boreal autumn (see Fig. 4 in Johnson et al. 2019 and Table S2). If, for each year between October and January, data are selected from the single CHist-H member with the autumn SST anomaly in EEIO closer to the observed anomaly, the winter (DJ) WCIO teleconnection computed from this composite dataset shows an NAO covariance of 30 m, almost as large as in the “best” member of AMIP-H (see Fig. 9c and S7).
This aspect of the systematic error in coupled SST-rainfall variability in the Indian Ocean affects all members of CHist, and therefore may explain the overall poor WCIO teleconnections in this ensemble. However, because of the (negative) correlation between SST in the eastern Indian Ocean and the central Pacific in boreal autumn, it has a stronger impact on the teleconnection if a larger-than-average ENSO variability is simulated in individual coupled simulations.
4.2 Results from six European climate models
We now consider simulations performed with the six European climate models listed in Table 1. Most such simulations are only available as single runs rather than ensembles, so for consistency we have used what is referred to as ‘ensemble member 1′ (r1i1p1f1 in HighResMIP notation) for each model configuration. The first member of the ECMWF ensemble is also included in this analysis. For both AMIP and coupled simulations, teleconnection patterns have been computed for each of these models, as well as for a six-member multi-model ensemble (MME) obtained by merging the anomalies from each simulation into a 6 × 60 field dataset. The AMIP-L, AMIP-H and CHist-H MMEs have the same size as the corresponding ECMWF ensembles; however, MME anomalies are computed with respect to the mean of each model run, rather than as differences from the time and ensemble mean. An obvious objection to the MME approach is that there is a large variety of resolutions in the low-resolution and high-resolution groups of PRIMAVERA models (see again Table 1); therefore one should use such MME results only in a comparative way, and avoid drawing conclusions about ‘critical’ levels of resolution.
Normalized errors for 500-hPa height teleconnections over the Atlantic-Europe and Pacific-North America from individual historical runs of the 6 climate models, as well as from the full ECMWF and MME ensembles, are compared in Fig. 10 with the confidence levels derived from the bootstrap re-sampling of the CERA20C record. Red, green and blue mark indicate errors from AMIP-L, AMIP-H and CHist-H simulations respectively. The numbering on the x-axis corresponds to the models’ numbers in Table 1; scores for the ECMWF and MME ensembles are indicated as model 7 and 8 respectively. The 90% and 95% confidence levels are marked by grey lines: marks lower than these lines indicate an error in teleconnection patterns comparable with sampling uncertainty. The following main messages can be derived from Fig. 10.
-
From these scores, there is no systematic evidence of a positive impact of increasing atmospheric resolution, or of going from uncoupled to coupled simulations; results are different for individual models, and also vary depending on the source and verification regions. For example, for the Indian Ocean teleconnection over the Atlantic (Fig. 10a), for three models the best results (i.e. the smallest errors) are obtained by the high-resolution coupled run, for the other three by the low-resolution AMIP.
-
As typical for multi-model ensembles, the errors of the MME teleconnections are lower than those of the majority of individual models. It is worth noting that, in both the ECMWF ensembles and the MMEs, the difference in scores between different model configurations are reduced with respect to the single-member results. However, even multi-model scores do not provide a consistent message with regard to the impact of resolution and coupling, with results depending on the specific teleconnection considered.
-
A quite consistent pattern appears when scores for different teleconnection sources are compared with the confidence levels estimated from the observed interannual variability. As for the ECMWF ensemble discussed above, the vast majority of model simulations reproduce the late-winter response to NINO4 rainfall over the Pacific and North America with good fidelity, while the errors for the Indian Ocean teleconnection over Europe far exceed (in most cases) the confidence levels. Errors for the late-winter response to NINO4 rainfall are much larger over the Atlantic than over the Pacific, but the confidence levels in the former area are also larger, so the actual skill of the models is consistent with the larger uncertainty in the Atlantic response.
-
Comparing different teleconnection sources and verification areas, it appears the worst performance of the coupled ensembles is found for the early-winter NINO4 teleconnection over the Atlantic and Europe (Fig. 10b). In this case, both the ECMWF and the MME coupled ensemble are worse than their respective AMIP simulations. Ayarzaguena et al. (2018) also documented a poor simulation of the early-winter ENSO teleconnection to the North Atlantic and Europe by CMIP-5 coupled models, and suggested a link to deficiencies in the simulation of Caribbean rainfall anomalies in the historical CMIP-5 runs.
Normalised errors of 500-hPa height teleconnection patterns for historical simulations run with six European climate models (no. 1 to 6 on the x-axis; see Table 1), the 6-member ECMWF ensemble (no. 7 on x-axis), and the 6-member multi-model ensemble (no. 8), for the North Atlantic-European domain (left) and the Pacific-North American domain (right). Top, centre and bottom panels correspond to the teleconnection patterns in Fig. 3a–c. Red squares: AMIP-L; green circles: AMIP-H; blue circles: CHist-H simulations. The grey lines show the 90% and 95% percentiles of the error distribution obtained from the bootstrap re-sampling of the CERA20C record (note that lower values, obtained from 6 × 60-year samples, are used for 6-member ensembles)
Figure 11 shows 500-hPa teleconnection maps from the three MMEs, in a similar format as for the ECMWF ensembles in Fig. 6. Comparing Fig. 11g with Fig. 3a, the coupled simulation of the Indian Ocean response shows a wavenumber-2 pattern which resembles the structure of the observed response at hemispheric scale. However, looking at regional domain, the AMIP-H MME has a stronger signal over the North Pacific, while the AMIP-L MME shows the strongest positive NAO signal although its hemispheric pattern is too zonally symmetric. As deduced from the scores in Fig. 10f, both coupled and uncoupled runs do a good job in simulating the late-winter response to NINO4 rainfall. Here, coupling reduces the strength of the North Pacific response, but it increases the agreement with observations over Europe. On the other hand, in all three MMEs the early-winter response to NINO4 rainfall looks like a weaker version of the late-winter response (as in the CMIP-5 analysis by Ayarzaguena et al. 2018; see their Fig. 3), with only a marginal sign of a positive NAO component. In this case, the AMIP-H ensemble shows the smallest error over the Atlantic.
For the six CHist-H simulations, teleconnection maps with Indian Ocean and NINO4 rainfall (the latter in late winter) are shown in Figs. 12 and 13 respectively. For the NINO4 teleconnection (Fig. 13), results are quite consistent over the North Pacific (as indicated by the scores in Fig. 10f), while the response over the North Atlantic and (especially) Europe shows a large amount of variability. The two coupled simulations with the smallest error over the Atlantic-European region (from CMCC and ECMWF) both show a negative NAO signal in the western and central Atlantic, although the flow over western Europe changes from anti-cyclonic in the CMCC pattern (Fig. 13a) to cyclonic in the ECMWF pattern (Fig. 13f).
The response to Indian Ocean rainfall (Fig. 12) shows large inter-model differences over most of the hemisphere, with a clear positive NAO signal in the CNRM, HadGEM and (even more so) in the MPI simulations. This teleconnection appears particularly weak in the single-member ECMWF simulation, but it should be noted (from Fig. 8) that three other members of the ECMWF coupled ensemble show an NAO signal comparable with the coupled MME signal in Fig. 11g. Ensemble simulations for each model configurations would be needed to assess the relative contribution of model formulation and internal variability to the differences among the patterns shown in Figs. 12 and 13.
5 Multi-decadal variability in historical runs with uncoupled and coupled models
In the previous section, the focus of our analysis has been on the simulation of teleconnections on the interannual time scale. However, historical simulations spanning more than 60 years give the opportunity to assess how the PRIMAVERA models perform in reproducing inter-decadal variability. Although a detailed analysis of decadal variability in the PRIMAVERA runs is clearly beyond the scope of this paper, in this section we focus on one specific aspect: the relevance of the Indo-Pacific teleconnections in explaining inter-decadal variability in the wintertime NH circulation, particularly in the North Atlantic and European sector. In doing so, we argue that improving the simulations of interannual-scale teleconnections may have a beneficial effect on the understanding of variability at time scales relevant to the climate change problem.
The inter-decadal variability and apparent long-term trend in the phase and amplitude of the NAO during boreal winter was a strongly debated topic around the end of the twentieth century, following a series of papers by Hurrell and collaborators (Hurrell 1995, 1996; Hurrell and Van Loon 1997; Hurrell et al. 2004; Hoerling et al. 2004) which discussed extratropical impacts and possible dynamical explanations for the shift towards positive NAO values in the last quarter of the century.
Specifically, Hurrell et al. (2004) and Hoerling et al. (2004) used simulations made with AGCMs forced by observed SST to investigate possible tropical sources for the apparent NAO trend, and suggested a link between the (almost monotonic) warming of the Indian Ocean in the second half of the twentieth century and the NAO inter-decadal changes. Although a number of other research groups tried to explain the observed changes over the North Atlantic as a response to SST changes (Sanchez-Gomez et al. 2008; King et al. 2010), AGCM experiments typically explained only 30% to 50% of the observed signal.
The first decade of the twenty-first century saw a partial reversal of the NAO tendency, with negative NAO anomalies becoming prevalent during boreal winters in the so-called “warming hiatus” or “slowdown” (eg Trenberth and Fasullo 2013). Still, significant differences in both the tropical and extratropical circulation during boreal winter can be seen between the first half and the second half of the 60-year period (1951 to 2010) covered by PRIMAVERA experiments and by the CERA20C re-analysis. These are shown in Fig. 14 for SST from the HadISST-2 dataset, and for global precipitation and NH 500-hPa height from CERA20C. For consistency with statistics shown in previous sections, we focus on two-month averages in December-January, which are representative of changes computed over the whole winter season and highlight the relevance of teleconnections from the Indian Ocean.
Interdecadal differences between DJ-mean anomalies in the second and the first 30-year periods of the 1950–2010 record: (a) sea-surface temperature from HadISST-2; (b) precipitation from CERA20C; (c) NH 500-hPa height from CERA20C. The inter-decadal change in the Portugal-Iceland NAO index is listed above c
The maps of SST and 500-hPa changes (Fig. 14a, c respectively) are very similar to those derived from other SST datasets and re-analyses (see eg. Figure 11 in Molteni et al. 2015, covering the last 50 years of the twentieth century). The inter-decadal changes in precipitation from CERA20C (Fig. 14b), however, are substantial and more difficult to validate against actual observations; they strongly resemble the leading EOF of Indian-West Pacific rainfall in boreal winter shown in Fig. 1b.
The 500-hPa height interdecadal changes (Fig. 14c) show a number of features resembling the early or mid-winter teleconnections from the WCIO and NINO4 tropical regions (Fig. 3a, b), specifically the high-latitude negative height anomalies over the North Pacific and the North Atlantic. This is consistent with the positive rainfall changes over these two tropical regions shown in Fig. 14b. However, looking at the SST changes in Fig. 14a, it is worth noting that the SST increase in the tropical Indian Ocean is larger in the eastern than in the western part, while the precipitation changes show an opposite east–west gradient.
We can test if the PRIMAVERA AMIP-type simulations using prescribed SST from HadISST-2 reproduce the observed decadal changes. The (DJ 1980/2009) minus (DJ 1950/1979) differences from the ECMWF and multi-model AMIP-H ensembles are shown in Fig. 15a–d respectively, for both rainfall and 500-hPa height. As typical for AMIP runs, the models tend to generate tropical rainfall patterns mostly in phase with SST gradients, so Indian Ocean rainfall increases in the east and (mostly) decreases in the west along the Equator. In a similar way, the AMIP simulation provide a poor simulation of North Atlantic changes in 500-hPa height, with an NAO response which is either much weaker than the observed pattern (for the MME) or even of opposite sign (for the ECMWF ensemble).
The failure of AMIP ensembles in reproducing the pattern of rainfall changes in the Indian Ocean is caused by the well-known inability of prescribed-SST runs to reproduce the negative correlation between SST and rainfall over the Eastern Indian ocean and around the Maritime Continents (e.g. Wang et al. 2005). Coupled runs, on the other hand, can reproduce the negative feedback on SST from changes in surface solar radiation and latent heat flux, but in multi-decadal historical runs there is no guarantee that tropical SST variability at regional level will be in phase with observations. With this important caveat, we looked at the high-resolution coupled runs from individual models. It turned out that those which showed the best connection between the NAO and WCIO rainfall at interannual scale (namely the CRNM-6, HadGEM-3 and MPI-ES; see Fig. 12) were also showing a positive interdecadal change of the NAO index, while the other three simulations had a NAO change of opposite sign. As a result, the MME mean of the CHist-H runs (not shown) has hardly any signal in either rainfall or NAO on this multi-decadal scale.
The strongest positive NAO signal was found in the HadGEM-3 simulation; the inter-decadal variations in rainfall and 500-hPa height from this run are shown in Fig. 16a, b. In the HadGEM-3 coupled simulation, Indian Ocean rainfall shows a pattern in better agreement with re-analysis than AMIP ensembles, with a positive maximum in the western part of the ocean (mainly south of the Equator) and negative changes between 90 and 150E. This is associated with a positive NAO signal in 500-hPa height, approximately twice as large as in the AMIP MME ensemble.
Interdecadal differences in precipitation (a) and 500-hPa height (b), from the high-resolution coupled simulation with the HadGEM-3 model, for the same periods as in Fig. 14; (c) and (d): as in (a) and (b), but from a composite dataset from the ECMWF CHist-H ensemble, with data selected among the 6 members according to SST anomalies in the Eastern Equatorial Indian Ocean (see Sect. 4.1)
If there is indeed a relationship between the fidelity in simulating the WCIO teleconnection and the strength of the inter-decadal NAO signal, we should expect the “composite member” of the ECMWF CHist-H ensemble described in Sect. 4.1 (whose data are selected according the agreement between model and observed SST in the eastern equatorial Indian Ocean, and which shows a stronger WCIO -NAO teleconnection that any of the actual ensemble members) to also show a significant positive NAO change between the two 30-year periods. As shown in Fig. 16c, d, this is indeed the case: the change in the NAO index is actually larger than in re-analysis, and consistently the rainfall map shows a clear increase in the WCIO region and a decrease in the eastern Indian Ocean.
Although we cannot make statements regarding the robustness and significance of the inter-decadal changes simulated by individual coupled models, the statistics shown here strongly suggest that a correct simulation of the rainfall changes in the Indian Ocean is a pre-requisite for an adequate representation of NAO inter-decadal variability. However, because of the different relationship between SST and rainfall variability in the western and eastern part of the basin, the impact of decadal SST changes can only be properly simulated in coupled models. Carefully designed “pacemaker” experiments may provide a way to assess the impact of the observed changes in tropical rainfall in a coupled-model framework. Alternatively, we may look at large ensembles of multi-decadal simulations (see Kay et al. 2015; Maher et al. 2019), where multiple realizations of the historical climate record provide the opportunity for a proper statistical assessment of the simulated decadal variations and teleconnections (see eg. Bodai et al. 2020).
6 Conclusions
In this study, we have investigated how teleconnections linking tropical rainfall anomalies and wintertime circulation in the northern extra-tropics are represented in historical simulations for the period 1950–2010 run by partners of the EU-funded PRIMAVERA project, following the HighResMIP protocol of CMIP6. The analysis has focussed on teleconnections from the western/central Indian Ocean in mid-winter and from the NINO4 region in both the early and the late part of winter; this choice is justified by a substantial change in the relationship between ENSO and the NAO in the two parts of the season. Model results for both coupled integrations and runs with prescribed sea-surface temperature (SST) were validated against data from the latest ECMWF 20th-century re-analysis, CERA20C (Laloyaux et al. 2018).
Using only a single historical simulation from each model configuration, it is difficult to detect a consistent change in the fidelity of model-generated teleconnections when either atmospheric resolution is increased or ocean coupling at high resolution is introduced. When simulations from six different models are pooled together in a MME, improvements in some of the teleconnection patterns can be seen when moving from uncoupled to coupled simulations, particularly for the “traditional” late-winter teleconnection from central Pacific rainfall. This is also true for six-member ensembles performed with the ECMWF model. On the other hand, the teleconnection from Indian Ocean rainfall and the early-winter teleconnection from the NINO4 region over the North Atlantic and Europe are degraded when going from uncoupled to coupled ensembles.
A relatively consistent signal across models is the difference in performance when teleconnections from different tropical regions and in different months are considered. While, according to a bootstrap re-sampling of CERA20C data, both the Indian Ocean teleconnection in DJ and the NINO4 teleconnection in JF are equally robust, the latter is well simulated in the majority of both uncoupled and coupled runs, while the former is reproduced with (generally) much larger errors, and a high degree of variability between individual models and ensemble members. For the ECMWF coupled model, the degradation of the Indian Ocean teleconnection was found to be connected to an excessively large variability of SST in the eastern equatorial Indian Ocean during autumn, which in turn altered the relationship between ENSO and rainfall anomalies in the central Indian Ocean in the following winter.
Deficiencies in the Indian Ocean teleconnection may have a significant impact on the simulation of decadal variability and climate change over Europe during the cold season, when links between tropical and extratropical variability are of major importance. Decadal changes in tropical rainfall and NH geopotential height computed from CERA20C are consistent with the patterns of inter-annual teleconnections.
We investigated if the fidelity in simulating teleconnections on an inter-annual time scale was reflected in a realistic estimate of multi-decadal changes between the first and the second 30 years covered by the historical runs. For AMIP simulations, this is not the case; the AMIP runs failed to reproduce the observed pattern of Indian Ocean rainfall change which, in observations, has an opposite zonal gradient with respect to SST changes. In coupled runs, some evidence of consistency across time scales was found. At least one model run with both realistic teleconnections and a good simulation of the inter-decadal pattern of Indian Ocean rainfall also shows a realistic NAO signal in extratropical multi-decadal variability. A strong positive change in the NAO pattern was also shown by a “composite member” of the ECMWF coupled ensemble, made by selecting data from members with a realistic SST variability in the eastern Indian Ocean on a yearly basis.
In summary, our assessment of teleconnections in PRIMAVERA models raises a number of issues which go beyond the impact of changes in model configurations. While evidence of the impact of atmospheric resolution and ocean coupling has been limited, our study has highlighted common differences in model performance when teleconnections from different sources and periods are considered. In addition, the analysis of the multi-decadal CERA20C record has confirmed that teleconnections active at interannual time scale also play a major role on multi-decadal scale.
An important limitation in our study has been the availability of a single historical realization for most of the models. Historical ensembles of at least 5 to 10 members for each model configuration would be needed to improve the statistical significance of results presented here, and particularly to allow a meaningful (rather than tentative) analysis of the impact of tropical teleconnections on extra-tropical inter-decadal variability. A few large ensembles of climate simulations are now available to the scientific community (Kay et al. 2015; Maher et al. 2019), and they allow to separate the impact of long-term trends and internal variability at constant forcing. Hopefully, this should encourage future CMIP-type project to put stronger emphasis on the provision of ensemble simulations from the majority (or at least a large number) of participants.
References
Adler RF, Huffman GJ, Chang A, Ferraro R, Xie P et al (2003) The Version 2 Global Precipitation Climatology Project (GPCP) Monthly Precipitation Analysis (1979-Present). J Hydrometeor 4:1147–1167
Anderson DLT, Sarachik ES, Webster PJ, Rothstein LM (1998) The TOGA decade: reviewing the progress of El Niño research and prediction. J Geophys Res 103(C7):14167–14510. https://doi.org/10.1029/98JC00112
Ayarzagüena B, Ineson S, Dunstone NJ, Baldwin MP, Scaife AA (2018) Intraseasonal effects of El Niño-Southern oscillation on North Atlantic climate. J Clim 31:8861–8873. https://doi.org/10.1175/JCLI-D-18-0097.1
Cassou C (2008) Intraseasonal interaction between the Madden-Julian Oscillation and the North Atlantic Oscillation. Nature 255:523–527
Bellenger H, Guilyardi E, Leloup J, Lengaigne M, Vialard J (2013) ENSO representation in climate models: from CMIP3 to CMIP5. Clim Dyn 42:1999–2018
Berntell E, Zhang Q, Chafik L, Körnich H (2018) Representation of multidecadal sahel rainfall variability in 20th century reanalyses. Nat Sci Rep 8:10937. https://doi.org/10.1038/s41598-018-29217-9
Bodai T, Dotros G, Herein M, Lunkeit F, Lucarini V (2020) The forced response of the El Nino-Southern Oscillation-Indian Monsoon teleconnection in ensembles of Earth System Models. J Climate 33:2163–2182. https://doi.org/10.1175/JCLI-D-19-0341.1
Cherchi A, Fogli PG, Lovato T, Peano D, Iovino D et al (2019) Global mean climate and main patterns of variability in the CMCC-CM2 coupled model. J Adv Modeling Earth Syst 11:185–209. https://doi.org/10.1029/2018MS001369
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ et al (2011) The Twentieth century reanalysis project. Quart J Roy Meteorol Soc 137:1–28. https://doi.org/10.1002/qj.776
Dee DP, Uppala M, Simmons AJ, Berrisford P, Poli P et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597. https://doi.org/10.1002/qj.828
Deser C, Simpson IR, McKinnon KA, Phillips AS (2017) The Northern Hemisphere extra-tropical atmospheric circulation response to ENSO: How well do we know it and how do we evaluate models accordingly? J Climate 30:5059–5082. https://doi.org/10.1175/JCLI-D-16-0844.1
Di Giuseppe F, Molteni F, Dutra E (2013) Real-time correction of ERA-Interim monthly rainfall. Geophys Res Lett 40:3750–3755. https://doi.org/10.1002/grl.50670
Docquier D, Grist JP, Roberts MJ, Roberts CD, Semmler T et al (2019) Impact of model resolution on Arctic sea ice and North Atlantic Ocean heat transport. Clim Dyn. https://doi.org/10.1007/s00382-019-04840-y
Garfinkel CI, Benedict JJ, Maloney ED (2014) Impact of the MJO on the boreal winter extratropical circulation. Geophys Res Lett 41:6055–6062. https://doi.org/10.1002/2014GL061094
Gutjahr O, Putrasahan D, Lohmann K, Jungclaus J, von Storch J-S, Brüggemann N, Haak H, Stössel A (2019) Max planck institute earth system model (MPI-ESM1.2) for high-resolution model intercomparison project (HighResMIP). Geosci Model Dev 12:3241–3281. https://doi.org/10.5194/gmd-12-3241-2019
Haarsma RJ, Roberts M, Vidale PL, Senior CA, Bellucci A et al (2016) High resolution model intercomparison project (HighResMIP v1.0) for CMIP6. Geosci Model Dev 9:4185–4208. https://doi.org/10.5194/gmd-9-4185-2016
Haarsma RJ, Acosta M, Bakhshi R, Bretonnière P-A, Caron L-P et al (2020) HighResMIP versions of EC-Earth: EC-Earth3P and EC-Earth3P-HR. Description, model performance, data handling and validation. Model Dev Discuss Geosci. https://doi.org/10.5194/gmd-2019-350
Hoerling MP, Hurrell JW, Xu T, Bates GT, Phillips AS (2004) Twentieth century North Atlantic climate change. Part II: Understanding the effect of Indian Ocean warming. Clim Dyn 23:391–405
Horel JD, Wallace JM (1981) Planetary-scale atmospheric phenomena associated with the Southern Oscillation. Mon Wea Rev 109:813–829. https://doi.org/10.1175/1520-0493(1981)109
Hoskins BJ, Karoly DJ (1981) The steady linear response of a spherical atmosphere to thermal and orographic forcing. J Atmos Sci 38:1179–1196. https://doi.org/10.1175/1520-0469(1981)038
Hurrell JW (1995) Decadal trends in the North-Atlantic oscillation: regional temperatures and precipitation. Science 269:676–679. https://doi.org/10.1126/science.269.5224.676
Hurrell JW (1996) Influence of variations in extratropical wintertime teleconnections on northern hemisphere temperature. Geophys Res Lett 23:665–668. https://doi.org/10.1029/96GL00459
Hurrell JW, Van Loon H (1997) Decadal variations in climate associated with the North Atlantic Oscillation. Climatic Change 36:301–326. https://doi.org/10.1023/A:1005314315270
Hurrell JW, Hoerling MP, Phillips AS, Xu T (2004) Twentieth century North Atlantic climate change Part I: assessing determinism. Clim Dyn 23:371–389
Johnson SJ et al (2019) SEAS5: the new ECMWF seasonal forecast system. Geosci Model Dev 12:1087–1117. https://doi.org/10.5194/gmd-12-1087-2019
Kay JE et al (2015) The community earth system model (CESM) Large ensemble project: a community resource for studying climate change in the presence of internal climate variability. Bull Amer Meteor Soc 96:1333–1349. https://doi.org/10.1175/BAMS-D-13-00255.1
King MP, Herceg-Bulić I, Bladé I, García-Serrano J, Keenlyside N et al (2018) Importance of late fall ENSO teleconnection in the Euro-Atlantic sector. Bull Am Meteor Soc 99:1337–1343
King MP, Kucharski F, Molteni F (1990s) The roles of external forcings and internal variabilities in the Northern Hemisphere atmospheric circulation change from the 1960s to the 1990s. J Clim 23:6200–6220
Laloyaux P, de Boisseson E, Balmaseda M et al (2018) CERA-20C: a coupled reanalysis of the twentieth century. J Adv Model Earth Syst 10:1172–1195. https://doi.org/10.1029/2018MS001273
Lin H, Brunet G, Derome J (2009) An observed connection between the North Atlantic Oscillation and the Madden–Julian Oscillation. J Climate 22:364–380
Maher N, Milinski S, Suarez-Gutierrez L, Botzet M, Dobrynin M et al (2019) The max planck institute grand ensemble: enabling the exploration of climate system variability. J Adv Modeling Earth Syst 11:1–21. https://doi.org/10.1029/2019MS001639
Molteni F, Kucharski F (2019) A heuristic dynamical model of the North Atlantic Oscillation with a Lorenz-type chaotic attractor. Climate Dyn 52:6173–6193. https://doi.org/10.1007/s00382-018-4509-4
Molteni F, Stockdale T, Vitart F (2015) Understanding and modelling extra-tropical teleconnections with the Indo-Pacific region during the northern winter. Clim Dyn 45:3119–3140. https://doi.org/10.1007/s00382-015-2528-y
Newman M et al (2016) The pacific decadal oscillation, revisited. J. Clim 29:4399–4427. https://doi.org/10.1175/JCLI-D-15-0508.1
Poli P, Hersbach H, Dee DP, Berrisford P, Simmons AJ et al (2016) ERA-20C: an atmospheric reanalysis of the twentieth century. J Climate 29:4083–4097. https://doi.org/10.1175/JCLI-D-15-0556.1
Roberts CD, Senan R, Molteni F, Boussetta S, Mayer M, Keeley S (2018) Climate model configurations of the ECMWF Integrated Forecast System (ECMWF-IFS cycle 43r1) for HighResMIP. Geosci Model Dev 11:3681–3712. https://doi.org/10.5194/gmd-11-3681-2018
Roberts CD, Vitart F, Balmaseda MA, Molteni F (2020) The time-scale-dependent response of the wintertime North Atlantic to increased ocean model resolution in a coupled forecast model. J Clim 33:3663–3689. https://doi.org/10.1175/JCLI-D-19-0235.1
Roberts MJ et al (2019) Description of the resolution hierarchy of the global coupled HadGEM3-GC3.1 model as used in CMIP6 HighResMIP experiments. Geosci Model Dev. https://doi.org/10.5194/gmd-2019-148
SanchezGomez E, Cassou C, Hodson DLR, Keenlyside N, Okumura Y, Zhou T (2008) North Atlantic weather regimes response to Indian-western Pacific Ocean warming: a multi-model study. Geophys Res Lett 35:L15706. https://doi.org/10.1029/2008GL034345
Sardeshmukh PD, Hoskins BJ (1988) The generation of global rotational flow by steady idealized tropical divergence. J Atmos Sci 45:1228–1251
Scaife AA, Ferranti L, Alves O, Athanasiadis P, Baehr J et al (2019) Tropical rainfall predictions from multiple seasonal forecast systems. Int J Climatol 39:974–988. https://doi.org/10.1002/joc.5855
Schneider U, Finger P, Meyer-Christoffer A, Rustemeier E, Ziese M, Becker A (2017) Evaluating the hydrological cycle over land using the newly-corrected precipitation climatology from the global precipitation climatology centre (GPCC). Atmosphere 8:52. https://doi.org/10.3390/atmos8030052
Sein DV, Koldunov NV, Danilov S, Sidorenko D, Wekerle C et al (2018) The relative influence of atmospheric and oceanic model resolution on the circulation of the North Atlantic Ocean in a coupled climate model. J Adv Model Earth Syst 10:2026–2041. https://doi.org/10.1029/2018MS001327
Shukla J, Wallace JM (1983) Numerical simulation of the atmospheric response to equatorial Pacific sea surface temperature anomalies. J Atmos Sci 40:1613–1630. https://doi.org/10.1175/1520-0469(1983)040
Stan C, Straus D, Frederiksen J, Lin H, Maloney E, Schumacher C (2017): Review of tropical‐extratropical teleconnections on intraseasonal time scales. Rev Geophys, 55. https://doi.org/10.1002/2016rg000538
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. J Geophys Res 106(D7):7183–7192. https://doi.org/10.1029/2000JD900719
Titchner HA, Rayner NA (2014) The met office hadley centre sea ice and sea surface temperature data set, version 2: 1. Sea ice concentrations. J Geophys Res Atmos 119:2864–2889. https://doi.org/10.1002/2013JD020316
Trenbert KE, Fasullo JT (2013) An apparent hiatus in global warming? Earth’s Future 1:19–32. https://doi.org/10.1002/2013EF000165
Vitart F (2017) Madden-Julian oscillation prediction and teleconnections in the S2S database. Quart J Roy Meteor Soc 143:2210–2220. https://doi.org/10.1002/qj.3079
Vitart F, Molteni F (2010) Simulation of the MJO and its teleconnections in the ECMWF forecast system. Quart J Roy Meteor Soc 136:842–855
Voldoire A, Saint-Martin D, Sénési S, Decharme B, Alias A, Chevallier M et al (2019) Evaluation of CMIP6 DECK experiments with CNRM-CM6-1. J Adv Model Earth Syst. https://doi.org/10.1029/2019MS001683
Wallace JM, Gutzler DS (1981) Teleconnections in the geopotential height field during the northern hemisphere winter. Mon Wea Rev 109:784–812
Wallace JM, Zhang Y, Bajuk L (1996) Interpretation of interdecadal climate trends in Northern Hemisphere surface air temperature. J Climate 9:249–259
Wang B, Ding Q, Fu X, Kang I-S, Jin K, Shukla J, Doblas-Reyes F (2005) Fundamental challenge in simulation and prediction of summer monsoon rainfall. Geophys Res Lett 32:L15711. https://doi.org/10.1029/2005GL022734
Weare BC (2013) El Niño teleconnections in CMIP5 models. Climate Dyn 41:2165. https://doi.org/10.1007/s00382-012-1537-3
Acknowledgements
The simulations and diagnostics described in this paper have been funded by the European Union Horizon 2020 PRIMAVERA project, grant agreement no. 641727. Model output from the PRIMAVERA simulations can be accessed from the archive of the Centre for Environmental Data Analysis (CEDA). Re-analysis data from CERA20C is available from the European Centre for Medium-Range Weather Forecasts (ECMWF).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix: calibration of CERA20C rainfall against GPCP-v2.3
Appendix: calibration of CERA20C rainfall against GPCP-v2.3
Because of the limited amount of observational data used to constrain the model trajectory in the CERA20C re-analysis, it is inevitable that precipitation data generated in the re-analysis display deviations from other observational datasets which reflect the assimilating model biases. In order to ensure a better compatibility between results obtained from CERA20C data and from other reliable datasets over the satellite (post-1979) era, such as the ERA-Interim re-analysis (Dee et al. 2011) and GPCP data (Adler et al. 2003), a linear calibration has been applied to CERA20C precipitation to match closely the GPCP-2.3 monthly data over the 1981–2010 period, corresponding to the second half of the full validation period used in this paper.
Since the calibration process is applied to each calendar month separately (even though overlapping data from adjacent months are used for continuity), in the following we describe the procedure applied to a given calendar month.
Let PC(x,t) be precipitation from CERA20C in a sub-sample including data for calendar months m, m1 = m-1, m2 = m + 1 and years 1981 to 2010 (where December data are used for m1 = 0 and January data for m2 = 13). Here, x is a grid-point coordinate covering the global domain. Let PG(x,t) be the GPCP v2.3 data in the same space and time domain. Also, let PC’(x,t) and PG’(x,t) be the anomalies with the respect to the 30-year mean in each calendar month.
The first step of the procedure uses a linear regression to write PG’(x,t) at each grid-point x as a sum of two components, one proportional to PC’(x,t) at the same grid-point and one orthogonal to PC’(x,t)
The second step uses non-local data (i.e., at grid points different from x) to approximate the orthogonal residual PO’(x,t). To achieve this, principal component analysis is applied to the PC’(x,t) dataset on the global domain, and the first N principal components pk(t) are selected, where k = 1,…,N. Then, at each grid point, PO’(x,t) is regressed against the first N principal components:
where βk (x) are the regression coefficients at grid-point x and P”(x,t) is a residual term.
Eqs. (A1) and (A2) can be rearranged to write the GPCP anomalies as a sum of a regression term and a local residual:
where:
P′R(x,t) represents our calibrated estimate of the GPCP anomalies starting from CERA20C precipitation. Note that each principal component can be computed as the spatial inner product between the corresponding empirical orthogonal function (EOF) and the global rainfall anomaly:
Therefore, a regression estimate P′R(x,t) can also be computed from P′C(x,t) for month m in years 1950 to 1980 if the regression coefficients α(x), βk(x) and the EOFs derived from the 1981–2010 period are used. We chose to use N = 15 EOFs in the estimation of the non-local correction in Eqs. A2 and A4. Note that, while the computation of regression coefficients and EOFs is done from a sample using three consecutive months in the 1981–2010 period, in the production of the final calibrated dataset for the full 1950–2010 period these coefficients are just used for the central month (since the procedure is repeated for each calendar month).
The impact of using non-local data in the calibration can be assessed by comparing the variance of GPCP precipitation explained by local and non-local (i.e. derived from global principal components as in Eq. A2) CERA20C data. These are shown in Fig.
17 for January and July data, together with the correlation coefficient between GPCP and the calibrated CERA20C data defined by Eq. A4 (note that the first step of the calibration process described by Eq. A1 does not change the correlation with GPCP). For both original and calibrated CERA20C data, correlations with GPCP data are higher in the boreal winter than in the boreal summer. For the original data, the largest proportions of variance (exceeding 90% in winter) are explained over the northern continents and the central/eastern equatorial Pacific, while the non-local correction adds relatively large fractions of variance in many subtropical regions, as well as (during boreal winter) in the eastern Indian Ocean and Maritime continents, and in the Southern Ocean.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Molteni, F., Roberts, C.D., Senan, R. et al. Boreal-winter teleconnections with tropical Indo-Pacific rainfall in HighResMIP historical simulations from the PRIMAVERA project. Clim Dyn 55, 1843–1873 (2020). https://doi.org/10.1007/s00382-020-05358-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05358-4