Climate change projections of temperature and precipitation in Chile based on statistical downscaling

Abstract

General circulation models (GCMs) allow the analysis of potential changes in the climate system under different emissions scenarios. However, their spatial resolution is too coarse to produce useful climate information for impact/adaptation assessments. This is especially relevant for regions with complex orography and coastlines, such as in Chile. Downscaling techniques attempt to reduce the gap between global and regional/local scales; for instance, statistical downscaling methods establish empirical relationships between large-scale predictors and local predictands. Here, statistical downscaling was employed to generate climate change projections of daily maximum/minimum temperatures and precipitation in more than 400 locations in Chile using the analog method, which identifies the most similar or analog day based on similarities of large-scale patterns from a pool of historical records. A cross-validation framework was applied using different sets of potential predictors from the NCEP/NCAR reanalysis following the perfect prognosis approach. The best-performing set was used to downscale six different CMIP5 GCMs (forced by three representative concentration pathways, RCPs). As a result, minimum and maximum temperatures are projected to increase in the entire Chilean territory throughout all seasons. Specifically, the minimum (maximum) temperature is projected to increase by more than 2 °C (6 °C) under the RCP8.5 scenario in the austral winter by the end of the twenty-first century. Precipitation changes exhibit a larger spatial variability. By the end of the twenty-first century, a winter precipitation decrease exceeding 40% is projected under RCP8.5 in the central-southern zone, while an increase of over 60% is projected in the northern Andes.

Introduction

Many studies have demonstrated that climate change affects the development of countries and impacts the environment irreversibly. One consequence of climate change is the modification of the statistical distribution of atmospheric patterns (Sanabria et al. 2009). This could largely affect the world’s population, as increasing temperatures and precipitation fluctuations might have an effect on water availability and crop production in the future (Kang et al. 2009). Thus, knowledge of the current and projected future global climate conditions is fundamental for the determination of vulnerabilities and the development of climate change adaptation strategies (Magaña et al. 2000).

General circulation models (GCMs) are the most reliable tools to assess climate evolution under different anthropogenic forcings such as greenhouse gas emissions, and thus provide an estimation of possible future climates based on socio-economic and demographic factors corresponding to different emissions scenarios (Cabré 2011). GCMs are based on physical principles that numerically describe the climate system and can reproduce the observed characteristics of the current climate and past climate changes (Solomon et al. 2007). However, the low spatial resolution of these global models (i.e., 150–300 km) limits their direct use in regional or local impact models, which require higher resolution (Amador and Alfaro 2009).

Statistical downscaling (SD) and dynamical downscaling (DD) are two commonly used approaches to bridge the gap between coarse GCMs and local impacts (Amador and Alfaro 2009). DD is often performed through regional climate models (RCMs), which solve the governing equations of the atmosphere in a limited spatial domain, subject to initial conditions from GCMs (or reanalysis), on a higher resolution than the driving GCMs (e.g., 12–50 km). They are computationally expensive and include certain parameterizations to represent the processes occurring at a higher resolution than the grid space (Amador and Alfaro 2009). SD techniques establish empirical relationships between predictors (large-scale variables) and predictands (local variables; Zorita and von Storch 1999; Amador and Alfaro 2009; Gutiérrez et al. 2013), featuring the advantages of low computation requirements and providing information with the same spatial resolution as the observational input data, that is, as high-resolution grids or local points (Ruiz 2007). However, statistical downscaling assumes that the empirical relationships deduced for the present climate are valid for the future climate (stationarity assumption), requires sufficiently long and high-quality observational series, and provides results only for variables of which one has observed data (Gaertner et al. 2012). Moreover, the set of predictors that best explains the objective variable need to be optimized for each predictand, location, season, etc. (Casanueva et al. 2016). SD could be classified by technique (Wilby and Wigley 1997) into regression method, weather type approaches and stochastic weather generators, and also by approach (Rummukainen 1997) into Perfect prognosis (PP) and Model Output Statistics (MOS). Regression models and weather type approaches establish a relationship between observed large-scale predictors and observed local-scale predictands (Maraun et al. 2010). The perfect prognosis approach is the application of this relationship to predictors from GCM in a weather forecasting context (Maraun et al. 2010). MOS contrary to PP calibrates the statistical relationship between predictor and predictand by using simulated predictors and observed predictand (Maraun et al. 2010).

Climate change projections over Chile can provide essential information for the establishment of mitigation and adaptation policies. In particular, high-resolution projections enable the assessment of possible risks and vulnerabilities related to specific impacts, such as ecosystems (Walther et al. 2002), productive sectors (Jones and Thornton 2003) and vegetation coverage (Breshears et al. 2005). Chile is a very diverse country from an orographic and physical standpoint. Latitude, altitude, and the influence of the Pacific Ocean and continentality are among the major climate drivers in the region, as along with the influence of the Amazon in the northern zone, westerly winds in the southern zone, and the Humboldt current system, which is driven by the South Pacific Subtropical high-pressure cell (Sarricolea 2017a; Gutiérrez et al. 2016). Thus, the application of downscaling methods is particularly challenging in Chile due to its large regional spatio-temporal variabilities, which are evident not only regarding temperature and precipitation but also for region-specific climate impacts.

Downscaling techniques have been applied in Chile for the determination of future climate based on the scenarios of the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (Solomon et al. 2007) through the application of (1) DD for the entire territory (Fuenzalida 2007; Garreaud 2011; Santibañez 2014) and (2) SD for specific regions (Souvignet et al. 2010; Fiebig-Wittmaack et al. 2012). Souvignet et al. (2010) used multiple linear regression with the SDSM (Statistical DownScaling Model) software for the HadCM3 model and A2a and B2a emissions scenarios, considering different predictors for each meteorological station in the Upper-Elqui watershed in Coquimbo. Fiebig-Wittmaack et al. (2012) employed a stochastic weather generator in the Elqui river basin based on the CGCM3 model for SRES A2 and B2 scenarios (Long Ashton Research Station Weather Generator). To our knowledge, SD has been used to produce climate change projections at local or basin levels only, whereas country-level applications have not been attempted. Given the need for high-resolution projections to establish a baseline for subsequent impact-oriented studies, this study aimed to develop climate change projections of minimum/maximum temperature and precipitation in Chile based on statistical downscaling under a perfect prognosis approach of different GCMs under RCP2.6, RCP4.5, and RCP8.5 emissions scenarios.

The paper is organized as follows. Material and methods are described in Sect. 2 and results are presented in Sect. 3. Section 4 includes a discussion of the results and Sect. 5 summarizes the main conclusions.

Materials and methods

Study area and datasets

Study area and Chilean climate

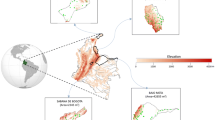
This study was carried out in continental Chile, which is approximately located between latitudes 17° S and 56° S and features a meridional axis of 70° W (Fig. 1a; Gaete et al. 2006). The Chilean territory is divided into 16 administrative regions (Fig. 1b).

Fig. 1

a Reference map of the study area. b Study area and its administrative regions. c–e Spatial distribution of meteorological stations for c precipitation (blue dots), d maximum temperature (red dots), and e minimum temperature (green dots) used as predictands in the downscaling process. Four exemplary stations used for further validations are depicted by red stars

In Chile, longitudinal temperature variations are more pronounced than latitudinal ones because of the marine front. In contrast, precipitation regimes are subject to larger latitudinal variations; even on the same parallel, altitude strongly modulates annual precipitation (Sarricolea et al. 2017a; Uribe et al. 2012).

Temperatures become gradually cooler from north to south (Uribe et al. 2012). The region between 17° S and 26° S (i.e., from the Arica y Parinacota to the Antofagasta administrative regions) corresponds to a cold desert climate with dry summer, where the temperature frequently exceeds 35 °C. The dryness of these regions is always limited to the plains; however, a cloudy coastal desert climate is observed towards the coast between 17° S and 27° S (i.e., from Arica y Parinacota to the Atacama region). Moreover, a dry-winter tundra climate can be observed over 3,000 above the sea level (MASL) in the Andes, with mean annual temperature of 2 °C and cumulative precipitations of up to 100 mm/year occurring mostly in summer. The region between 26° S and 32° S (i.e., the Antofagasta to Coquimbo administrative regions) experiences cold semi-arid climate with dry summers and oceanic influence towards the coast, where temperatures vary from 9 to 20 °C and the mean precipitation is 130 mm/year. A cold semi-arid climate with dry summer is observed in the valleys and the mountains are characterized by a tundra climate with dry summers. The regions between 32° S and 40° S (i.e., the Coquimbo to Araucanía administrative regions) experience Mediterranean climate. There, the climate conditions range from annual mean temperature of 15 °C and a 150–200 mm/annual accumulated precipitation in the Valparaíso region to up to 23 °C in the hottest month in the La Araucanía region, which experiences precipitation of 1000–2500 mm/year. Between 40° S and 44° S (i.e., the Araucanía to Los Ríos regions) the classification corresponds to a marine west coast climate (warm and dry summer, with, a mean annual temperature of 12 °C and mean annual precipitation of 2000 mm). The regions between 44° S and 56° S (i.e., the Los Ríos to Magallanes regions) experience tundra climate, with average temperatures below 0 °C and a mean annual precipitation of 3500 mm in the Magallanes region (Sarricolea et al. 2017a; Inzunza 2019).

Historical temperature trends in central Chile (i.e., from Coquimbo to Ñuble) between 1979 and 2005 showed a decrease of − 0.15 °C per decade in the coastal areas, while slight temperature increases were observed in the central valley; this contrasts with the almost 0.25 °C/decade increases in the mountain range (Garreaud 2011). A slight cooling predominates south of the Biobío region (Garreaud 2011). Seasonal trends between 1979 and 2015 indicated warming in valley and in the Andes region in autumn, particularly for regarding mean and maximum temperatures, whereas the coastal region exhibited cooling temperature trends at all seasons (Burger et al. 2018).

Precipitation between the Maule region and Los Lagos decreased by 100 mm/decade in Valdivia according to Garreaud (2011). Sarricolea et al. (2017b) did not find significant changes between 1972 and 2013 in the coastal and intermediate depression, whereas precipitation decreases were identified in the pre-mountain range and highlands, except in Parinacota in the Arica highlands.

Predictands

Daily precipitation and minimum/maximum temperatures for the period of 1980–2015 were compiled from data provided by Dirección General de Aguas (https://www.dga.cl/Paginas/default.aspx), Dirección Meteorológica de Chile (https://www.meteochile.cl/PortalDMC-web/index.xhtml), Centro de Estudios Avanzados en Zonas Áridas (https://www.ceaza.cl), Red Agrometeorológica del Instituto de Investigaciones Agropecuarias de Chile (https://www.agromet.inia.cl), and Explorador Climático Centro de Ciencias del Clima y la Resiliencia (https://www.explorador.cr2.cl).

Stations with at least 15 out of the total of 35 years of historical records were used. Outliers were processed based on a modification of De Luque (2011) method considering only wet days for precipitation (San Martín et al. 2017). Values below the 25th percentile minus three times the interquartile range and above the 75th percentile plus three times the interquartile range were considered temperature outliers ([P₂₅ – 3*(P₇₅ – P₂₅), P₇₅ + 3*(P₇₅ – P₂₅)]). The same criteria were applied to precipitation, albeit changing the reference percentiles and considering only the wet-day distributions ([P₁ – 3*(P₉₀ – P₁), P₉₀ + 3*(P₉₀ – P₁)]). Outliers were indicated as missing data and stations that recorded data over less than 50% of the 35 year period were eliminated.

After applying the above described criteria, a total of 427 stations distributed across the country were used for precipitation, 129 for minimum temperature, and 131 for maximum temperature assessment (Fig. 1c–e). The different number of stations was due to variations in the number of stations with more than 18 years (i.e., approximately 50% of the 35 years of available daily data) of historical data.

Predictors and preprocessing

Standard atmospheric variables at different height levels were considered as potential predictors for statistical downscaling. In particular, we considered predictor variables used in similar downscaling studies, such as that of Gutiérrez et al (2014) in Perú. Daily data for these variables (Table 1) were retrieved from NCEP/NCAR Reanalysis 1 (Kalnay et al. 1996) for the period 1980–2015. The predictor domain extended from 57.5° S to 15° S and from 92.5° W to 65° W.

Table 1 Predictor variables used from the NCEP/NCAR reanalysis 1 and CMIP5 GCMs for the historical and the RCP2.6, RCP4.5, RCP8.5 scenarios

Single GCMs can adequately simulate current climate, but they may not be as reliable in projecting future climate. It is recommended to use more than one GCM, in order to obtain more accurate results (Cabré 2011) and fully sample different uncertainty sources (Knutti et al. 2010). For these reasons, fifty models from CMIP5 (5th Climate Model Intercomparison Project, Taylor et al. 2012) were firstly considered for this study (more details are given in Online Resource 1) and a subset of 6 GCMs (CMCC-CM, CMCC-CMS, CNRM-CM5, MPI-ESM-MR, MPI-ESM-LR and NorESM1-M; Table 2) was selected based on the data availability of the chosen predictor variables (see Sect. 3.1) for the entire study area, for the historical and RCP scenarios. Some models presented orographic-driven missing data for some predictor variables at low elevation levels over parts of the region of study. Therefore, they were not included in the analysis.

Table 2 Details of the 6 GCM models on the Climate Model Intercomparison Project Phase 5 (CMIP5) project selected for statistical downscaling

Data for the historical scenario were available for all six models; CMCC-CM and CMCC-CMS had data for RCP4.5 and RCP8.5, and the remaining four models had data for the three RCP scenarios (RCP2.6, RCP4.5, and RCP8.5). These data were accessible via the Earth System Grid Federation (ESGF, https://esgf.llnl.gov/) and were retrieved for the historical and the available scenarios (Stocker 2014) in May 2018. The historical scenario extended from 1986 to 2005, and three periods (2016–2035, 2046–2065, and 2081–2100) were used for the RCPs, which was consistent with the periods selected in the IPCC Fifth Assessment Report (Stocker 2014). The original spatial resolution of predictor variables (2.5° × 2.5° in the reanalysis and model-dependent for the GCMs, see Table 2) was regridded onto a common regular 2° × 2° grid using the nearest neighbor method to ensure grid compatibility (San Martín et al. 2017).

Since the statistical downscaling method is trained using reanalysis data and applied to GCM data, NCEP was additionally used to correct systematic biases in the GCMs and to make both datasets comparable. Corrections were applied individually to each predictor variable by removing the bias in the mean annual cycle (monthly means) and adding the reanalysis counterparts (White and Toumi 2013; San Martín et al. 2017).

Several predictor sets were conformed based on those defined by Gutiérrez et al (2013, 2014) and, additionally, considering the correlation between each potential predictor variable and predictand (Maraun et al. 2010). Table 3 summarizes the predictor sets used for minimum/maximum temperature (P1–9) and precipitation (P10–18). Principal component analysis is often used to reduce the high dimensionality of the predictor fields (308 grid boxes, for 1–8 variables). In this work, principal components were derived from each predictor set and the number of principal components explaining 95% of the total variance were used as predictors (Maraun et al. 2010; Casanueva et al. 2013; Gutiérrez et al. 2013).

Table 3 Predictor variables for temperature (P1–P9) and precipitation (P10–P18)

Statistical downscaling method

Figure 2 shows the scheme of the methodology used in the present work. Statistical downscaling was firstly applied testing several predictor configurations for each predictand (Table 3) under the perfect prognosis approach. Under this approach, the statistical method was trained between predictand and predictor (represented by quasi-observations from reanalysis) using daily data, since day-to-day correspondence between predictor and predictand is required (Maraun et al. 2010; San Martín et al. 2017). The obtained relationships were later applied to the output of selected GCM scenarios to generate projections on a local scale (Gutiérrez et al. 2013). The method was trained with reanalysis data and observations from the period 1980–2015 and tested using the 1986–2005 period as the historical scenario and three future periods for the future scenarios; each period consisted for 20 years for convenient comparison. The statistical downscaling method used in this work was the analog method (Zorita and von Storch 1999), which consisted of identifying the atmospheric state of the day to be estimated (described by the predictors) and detecting the most similar situation (in terms of a distance metric, i.e., the Euclidean distance in this case) in a pool of historical records from reanalysis data. The predicted value was the corresponding value for the predictand (observations) on the analog day (Maraun et al. 2010).

Fig. 2

Methodology of the present study

Statistical downscaling and data transformations were performed with the “downscaleR” and “transformeR” R statistical computing packages included in the climate4R bundle (Cofiño et al. 2018; Bedia et al. 2019; Iturbide et al. 2019).

Cross-validation procedure

The k-fold cross-validation methodology (Gutiérrez et al. 2013; San Martín et al. 2017) was applied to employ independent data for the calibration/training and testing/validation of the statistical method for the period 1980–2015, exclusively using predictors from the reanalysis. This method consisted in dividing the data set into k subsets or folds. Each time, one of the k subsets was used for testing and the other k-1 subsets were put together to train the statistical downscaling method. The process was then repeated k times. Herein, k = 6 was chosen, each one conformed by 6 year (36 years in total). The results of the downscaled series for the six folds were merged into one series that was validated against observations. Specifically, predictions at each point or meteorological station were validated using three validation metrics for annual and seasonal series, namely the mean bias (difference between modeled and observed data, as an error measure), temporal correlation (Spearman and Pearson), and the Kolmogorov–Smirnov (K–S) test (San Martín et al. 2017).

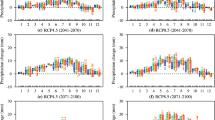
Biases for precipitation and temperature (minimum and maximum) were obtained to estimate the mean error between the downscaled and observed data for all seasons (DJF, MAM, JJA, SON) and the annual series (San Martín et al. 2017). Temporal day-to-day correlation between downscaled and observational data was calculated using the Pearson correlation for temperature and the Spearman correlation for precipitation. For precipitation, the correlation coefficient was obtained from the 10-day aggregated series to avoid the spurious effects of serial autocorrelation on results (San Martín et al. 2017). The K–S test was used to measure the degree of dissimilarity between distributions (10-day aggregated series for precipitation). Evaluation results based on these metrics were considered to select the best predictor set (Figs. 3, 4, 5, 6).

Fig. 3

Mean bias (in absolute value) and temporal correlation of the downscaled predictions calibrated using the different predictor combinations from the reanalysis. a Each box represents the spatially averaged score, for each season and annual series (in rows) and the three predictands (in columns). b Each box represents the spatially averaged score, for each administrative region calculated from the annual time series (in rows) and the three predictands (in columns). Darker colors indicate better performance

Fig. 4

Spatial distribution of the mean bias of the predictions for 1980–2015 using the selected predictor set (P8 for temperature and P11 for precipitation) for a minimum and b maximum temperature and c precipitation, for each season (DJF, MAM, JJA, SON) and annual series (year)

Fig. 5

Same as Fig. 4, but for mean temporal correlation

Fig. 6

Same as Fig. 4, but for log₁₀(p value) of K–S test

Validation of historical simulations

The downscaled projections in the historical scenario were validated against observations for the common period 1986–2005 to test the ability of the analog method to downscale the GCMs (Camargo-Bravo and García-Cueto 2012; Ferrelli et al. 2016). Four meteorological stations representing different climatic zones of Chile, were selected for illustrative purposes, namely Sierra Gorda (in the north of the country, Antofagasta region), Quinta Normal (in the central zone of the country, Metropolitana region), Pichoy Valdivia Ad. (in the south of the country, Los Ríos region), and Villa Maihuales (in the austral zone of the Aysén region). Those stations are marked with stars in Fig. 1.

Climate change signal

Climate change signals (CCSs) were calculated as the difference between the projected scenario and the historical scenario for each variable (precipitation, minimum temperature, and maximum temperature), season, RCP (RCP2.6, RCP4.5, and RCP8.5), and period (2016–2035, 2046–2065, 2081–2100). The signal for precipitation was calculated in a relative form as Eq. 1 (Garreaud, 2011).

Calculation of CCS for precipitation:

$$\frac{projected - historical}{{historical}} \times 100$$

(1)

Results

Evaluation of the downscaling method and predictor selection

Nine predictor sets were defined for maximum and minimum temperature and precipitation (Table 3). The analog method was trained with the different predictors and cross-validated (see Sect. 2.3) in order to select the best-performing predictor set. Biases in the seasonal and annual means, as well as temporal correlation and p values of the K–S test of the seasonal and annual series were obtained for all predictors. The spatially averaged scores of the evaluation metrics are summarized in Fig. 3 for the sake of conciseness. The spatial distribution of the validation metrics for the best-performing predictor is shown in Figs. 4, 5 and 6.

Biases are smaller (absolute values between 0 and 0.3) for predictors conformed by more than one predictor variable, for minimum and maximum temperature (Fig. 3a). For precipitation, all predictors present similar performance in terms of biases (Fig. 3a). Better correlation results are found in austral autumn (MAM) and the annual series, for the three predictands (Fig. 3a). Minimum temperature presents better performance (mean biases between 0 and 0.3 and high correlations), between Atacama and Bío-Bío and between Los Ríos and Magallanes y la Antártica Chilena (values between 0.6 and 0.8, Fig. 3b). Maximum temperature presents worse results for the Maule region (mean bias between 0.6 and 0.9 °C) and Arica and Parinacota (temporal correlation between 0.4 and 0.6). Precipitation shows better results in the northern zone in terms of bias and in the southern zone in terms of spatial correlation (Fig. 3b).

The best performing predictor for temperature is P8, which consists of T_as, T₇₀₀, T₈₅₀, Z₂₅₀ and Z₅₀₀, with the smallest spatially averaged bias in all seasons for minimum temperature (0–0.3 °C in absolute value, Fig. 3a, upper left panel) and in austral summer (DJF) and spring (SON), for maximum temperature 0–0.3 °C (Fig. 3a, upper middle panel). With respect to temporal correlation good performance is obtained in autumn for minimum and maximum temperature and in spring for maximum temperature, with values lying between 0.4 and 0.6. (Fig. 3a, lower left and middle panels).

More precisely, the spatial distribution of biases in minimum temperature shows values of up to − 0.4 °C in summer (DJF) and 0.4–0.8 °C in autumn and winter (JJA) between the Coquimbo and Los Lagos regions (Fig. 4a). Maximum temperature presents better results in summer and spring (biases of 0–0.4 °C across the whole country) than in winter and autumn [biases of − 0.4 to − 0.8 °C between the Coquimbo and Los Lagos regions (Fig. 4b)]. Temporal correlation results for minimum temperature were better in the central zone between the regions of Coquimbo and Bío Bío with values over 0.4, and for maximum temperature with values over 0.6 between the same regions (Fig. 5a, b). The spatial distribution of K–S test presents good results with several exceptions in some locations between the Maule and Ñuble regions (Fig. 6a).

The best predictor for precipitation, P11, consists of T_as, Q₇₀₀, Z₅₀₀ and Z₈₅₀, and shows good results in terms of mean bias and temporal correlation in the spatially averaged scores (Fig. 3a, right panel). Biases in seasonal (or annual) mean precipitation amount to less than 0.3 mm (in absolute value) in summer, autumn, spring and the annual series (Fig. 3a, upper right panel). The best correlation is also obtained for P11, with spatially-averaged values of 0.4–0.6 observed in autumn and winter (Fig. 3a, lower right panel).

According to the spatial distribution of the bias, the largest values are found in winter between the Valparaíso and Los Ríos regions, ranging between − 1.2 and − 1.6 mm (Fig. 4c, JJA). The spatial distribution of correlation shows values of 0.6–1 between the Valparaíso and Los Ríos regions throughout the year (Fig. 5c). The best results of the K–S test are found in winter and spring between the Arica y Parinacota and Valparaíso regions and in summer and autumn between the Arica y Parinacota and Bío-Bío regions (Fig. 6c).

Validation of historical projections

The historical scenario of six GCMs (CMCC-CM, CMCC-CMS, CNRM-CM5, MPI-ESM-MR, MPI-ESM-LR, and NorESM1-M) are downscaled using the best-performing predictor set (Sect. 3.1). Results are compared with observations for the common period 1986–2005 in order to check the ability of the analog method to downscale GCM predictors. Results for four meteorological stations, namely “Sierra Gorda,” “Quinta Normal Santiago,” “Pichoy Valdivia Ad.,” and “Villa Maihuales,” are shown for illustrative purposes (Figs. 7, 8). More details on the spatial distribution of the annual bias between the historical scenario and the observed data can be found in Online Resource 2.

Fig. 7

Mean annual cycle of the projections of the historical scenario and the observations (period 1986–2005) for minimum temperature (a–d) and maximum temperature (e–h) at four exemplary locations, Sierra Gorda, Quinta Normal Santiago, Pichoy Valdivia Ad. and Villa Maihuales

Fig. 8

Same as Fig. 7, but for monthly accumulated precipitation

Overall good performance of the mean annual cycle is found for the four stations representing a variety of different climates. Results for minimum temperature in Sierra Gorda reveal that the historical projections agree approximately with the observed data, except for an overestimation of 1 °C in April, June and July for all GCMs (Fig. 7a). For the Quinta Normal Santiago station, results for the historical projection are rather similar to their observed counterparts, with a largest difference of 1 °C in July for all GCMs (Fig. 7b). In the case of Pichoy Valdivia Ad., biases in monthly means remain below 1 °C (Fig. 7c). In Villa Maihuales, the historical projections underestimate temperature in January, February and October, with the largest differences of approximately 1 °C in February, particularly for MPI-ESM-MR (Fig. 7d).

Results for maximum temperature are very similar to those for minimum temperature. In Sierra Gorda and Quinta Normal Santiago, the historical projections overestimate maximum temperature in March, April, May, June and July (Fig. 7e, f). An overestimation (less than 1.5 and 2 °C, respectively) of maximum temperature is found in Pichoy Valdivia Ad. and Villa Maihuales in June and July (Fig. 7g, h).

Historical projections for monthly accumulated precipitation in Sierra Gorda provide good representation of the observed data (note the different precipitation range among stations on the Y-axis in Fig. 8a). In Quinta Normal Santiago, all models underestimate precipitation between March and August and overestimate from September to November (Fig. 8b). The most remarkable feature in Pichoy Valdivia Ad. is the underestimation in June, which is the wettest month, by all GCMs (Fig. 8c). The largest discrepancies between historical projections and observed data are found in Villa Maihuales, which is the place receiving the highest precipitation amount out of the four locations (Fig. 8d). The overall annual cycle is fairly well represented, with less precipitation in February and maximum values in JJA.

Climate change projections

Minimum temperature

For all GCMs, the near-future (2016–2035) CCS of minimum temperature features an increment of up to 2 °C in austral summer (DJF) and winter (JJA) under RCP8.5 (Fig. 9a, b). For the mid-future (2046–2065) in summer, projections present an increment of 2–4 °C toward the Andes in Arica y Parinacota and Tarapacá regions (17° S–21° S), an increase of 0–2 °C in Antofagasta and Maule regions (24° S–35° S) and from Los Lagos to Magallanes (44° S–56° S) (Fig. 9c). All GCMs showed some decreases up to 2 °C from Maule to Los Ríos regions (35° S–43° S) (Fig. 9c). In winter, increments of minimum temperature are projected to amount to 0–2 °C mostly in the central and southern zones (near 30° S–32° S), whereas CMCC-CM and MPI-ESM-MR show increments of up to 6 °C in certain locations in the central zone toward the Andes (Fig. 9d).

Fig. 9

Climate change signal of minimum temperature under RCP8.5 scenario for (a) 2016–2035, (b) 2046–2065 and (c) 2081–2100 periods (rows), for austral summer (DJF) and winter (JJA)

For the long-term future (2081–2100), the increment in austral winter is remarkably larger than in summer (Fig. 9e, f). In winter, CMCC-CM, CMCC-CMS, MPI-ESM-LR, and MPI-ESM-MR models show increases of 6–8 °C between Arica y Parinacota and Maule regions (17° S–35° S), while CNRM-CM5 and NorESM1-M show increments of 2–6 °C in the same regions (Fig. 9f). In summer, decreases in the minimum temperature of 0–2 °C between the Coquimbo and Los Ríos regions (30° S–44° S) are projected by all considered GCMs, with slightly smaller changes presented by NorESM1-M (Fig. 9e).

Results for RCP2.6 are included in the Supplementary Material (Online Resource 3). Note that larger differences among scenarios arise for the far-future period mainly.

In terms of the annual cycle, the increase of minimum temperature by the end of the twenty-first century is apparent in the four exemplary locations in June, July and August under the three RCP scenarios, increasing with the level of warming (Fig. 10). However, in Quinta Normal Santiago and Pichoy Valdivia (Fig. 10b, c), RCP8.5 projections depict a decrease for January and February. In general, more robust projections among models are obtained in February, August, September, and October, while higher uncertainties arise in June (Fig. 10).

Fig. 10

Mean annual cycle of minimum (a–d) and maximum (e–h) temperature for the observed (1986–2005) and projected (2081–2100) data. Thick lines represent the multi-model ensemble median for three RCPs in different colors. Whiskers represent the full range of models. Results are depicted for 4 representative locations Sierra Gorda, Quinta Normal Santiago, Pichoy Valdivia Ad and Villa Maihuales

Maximum temperature

The climate change signal of maximum temperature under RCP8.5 for the near future (2016–2035) presents increments of up to 2 °C (Fig. 11a, b), similarly to minimum temperature (Sect. 3.3.1). Some localized increments (up to 4 °C) are found in La Araucanía region in DJF (37° S–40° S; NorESM1-M), and between Coquimbo and El Maule regions in JJA (30° S–35° S; MPI-ESM-MR).

Fig. 11

Same as Fig. 9, but for maximum temperature

For mid-future (2046–2065) CCSs are overall slightly larger than for minimum temperature in both seasons (Fig. 11c, d). In summer, projections show an increment of 2–4 °C in Arica y Parinacota and Tarapacá regions toward the Andes (17° S–21° S) and rises of 0–2 °C for the rest of the regions, except for MPI-ESM-MR and NorESM1-M, which presents increases of 4–6 °C between Biobío and La Araucanía regions (37° S–40° S). In winter, most GCMs project an increase of 4–6 °C in the central zone (30° S–37° S), but CNRM-CM5 and NorESM1-M project increments of up to 4 °C.

Changes are markedly larger than the minimum temperature for the long-term future (2081–2100, Fig. 11e, f). In summer, an increase of up to 2 °C from the Atacama to the Coquimbo regions (25° S–30° S) is projected. In the north of the country, toward the Andes, all considered GCMs indicate a maximum temperature increment of 2–6 °C in summer and 6–8 °C in winter for almost all territory (Fig. 11f). The reader is referred to Online Resource 4 for the corresponding RCP2.6 results. Overall, changes under RCP2.6 remain below ± 2 ºC throughout the twenty-first century.

Unlike minimum temperature, the maximum temperature might increase throughout the year for the three RCPs in the selected locations (Fig. 10). Similar to minimum temperatures, larger changes are found in winter (JJA) than in summer (DJF). Consequently, larger model uncertainty is also found in June.

Precipitation

Climate change projections for mean precipitation present larger spatial variability and less robust results among models than the temperature counterparts (Fig. 12). For the near future, the largest changes can be found in the central part, between the Atacama and Biobío regions (25° S–38° S), and in the northern zone to the Andes area specifically in Arica y Parinacota, Tarapacá and Antofagasta regions (17° S–25° S) in DJF (> 40% with CNRM-CM5, MPI-ESM-LR, MPI-ESM-MR and NorESM1-M) and in the northern zone (17° S–25° S) in JJA (> 60% with CMCC-SM, MPI-ESM-LR and MPI-ESM-MR). In the rest of the country, CCS reaches levels of 20% (Fig. 12a, d).

Fig. 12

Same as Fig. 9, but for accumulated precipitation

The GCMs project larger decreases in the mid-future (2046–2065) than in near-future and stronger differences in summer than in winter. In summer, decreases of 60–100% are found between Atacama and Biobío (25° S–38° S) while in winter these differences are seen in the north between the Arica y Parinacota and Coquimbo regions (17° S–30° S, Fig. 12c, d). Changes in CNRM-CM5 shows the opposite sign with differences of over 40% in winter (Arica y Parinacota to Atacama in the Andes).

GCMs are consistent in the results for the long-term future period (2081–2100) for the northern and central zone (from Atacama to Los Ríos, 25° S–43° S) projecting decreases of 60–100% in summer and winter. In the Andes and Austral zone, accumulative precipitation will increase over 40% and 20%, respectively, in summer and winter (NorESM1-M projects decreases of precipitation in the Andes area in winter). However, there are some locations with a projected decrease in the austral zone in summer and in winter (Fig. 12e, f). The reader is referred to Online Resource 5 for the corresponding RCP2.6 results. For the far-future period under RCP2.6, changes in accumulated precipitation are projected to remain below ± 40% in the central region in winter, whereas large changes of more than 80% might occur in summer.

A reduction in monthly accumulated precipitation is projected in Quinta Normal Santiago, Pichoy Valdivia Ad. and Villa Maihuales throughout the year, regardless of the RCP (Fig. 13). In Quinta Normal Santiago and Pichoy Valdivia Ad., changes are larger with the increasing level of warming (i.e., from RCP2.6 to RCP8.5). Meanwhile, RCP-related uncertainty is smaller than differences among GCMs in Villa Maihuales. Large multi-model uncertainties are found for May and June.

Fig. 13

Same as Fig. 10, but for monthly accumulated precipitation

Discussion

Predictor assessment and selection are highly relevant for statistical downscaling, as they are the basis for the generation of climate projections (Hewitson and Crane 1996; Cavazos and Hewitson 2005). Several metrics (namely seasonal bias, correlation, and K–S test) allow for the evaluation of the downscaling method’s performance for current climate predictions when different predictor combinations are used. Evaluation results are sensitive to the predictor set considered (Fig. 3). Moreover, bias and correlation between the predicted values and the corresponding predictand varied both seasonally and geographically (Figs. 4, 5, 6). We acknowledge that considering different predictors for each region and season could bring better evaluation results. Such optimization is, however, not straightforward, since regional climates and seasons are projected to change in a warmer climate.

Still, the region that presented the largest biases in minimum and maximum temperature (values of 0.4–0.8 and 0.8–1.2, respectively) was the Mediterranean zone located between the Coquimbo and La Araucanía regions (Fig. 4a, b). However, this area exhibited a better temporal correlation (over 0.6 in minimum and maximum temperature; Fig. 5a, b). The same results were found for precipitation (Figs. 4c, 5c).

Remaining biases in the evaluation exercise cannot be neglected in the interpretation of future changes. Results of precipitation seasonal bias (Predictor 11) in austral winter in the Valparaíso and Metropolitana regions (Fig. 4) and Quinta Normal Santiago (Fig. 8b) show an underestimation of winter precipitation. Therefore, climate projections of precipitation in that region should be taken with caution and might be underestimated, since model biases might be transferred to the results of downscaling applied to scenarios (Raäisaänen 2007). Likewise, when comparing the historical scenario against the observed data, projections for Sierra Gorda overestimate the minimum temperature in March–September (Fig. 7a) and maximum temperature in March-August (Fig. 7e). Thus, the results of projections under RCP scenarios should be interpreted considering such overestimations (Fig. 10a, e), and the CCS results for minimum and maximum temperature in the northern zone, near the Sierra Gorda, might be overestimated (Figs. 9b, d, f, 11b, d, f).

Validation results of precipitation reveal high spatial and temporal variability (Fig. 8), which together with its nonlinear nature poses a challenge in the downscaling exercise (Maraun et al. 2010). Nonetheless, the models captured rather well the annual cycle of monthly accumulated precipitation. For Quinta Normal Santiago (central zone), the best-performing GCMs along the year are CMCC-CMS and CMCC-CM (Fig. 8b).

For 2081–2100 under the RCP8.5 scenario in the central zone, precipitation could decrease by 80% (Fig. 12f), reducing water availability and affecting its use for hydroelectricity, mining, agribusiness and human consumption (MMA 2015). Under global warming, the subtropical descent is predicted to expand towards the poles, which is referred to as the Hadley expansion (Johanson and Fu 2009; Zhou et al. 2019). In turn, this expansion displaces the subtropical anticyclone of the South Pacific towards the south, where greater atmospheric stability is achieved due to the storm repelling effect of the anticyclone (Johanson and Fu 2009). Another mechanism responsible for the decrease in precipitation is associated with the physiological effect of the increasing atmospheric CO₂ on plant stomata. Under elevated CO₂ concentrations, the stomata open less widely, leading to reduce plant transpiration and evapotranspiration; hence, the transfer of water vapor to the overlying atmosphere is reduced (Cao et al. 2012).

Minimum and maximum temperature, in the period 2081–2100 under the RCP8.5 scenario in the central zone, are projected to increase at 5–6 and 7–8 °C, respectively (Figs. 9f, 11f), which might cause the zero isotherm to move higher. According to Cifuentes and Meza (2008), such displacement can cause a reduction of the Andean area that stores snow and, thus, would affect water availability and decreases water flow. There is clear evidence of the relationship between CO₂ and surface temperature, over the past millennium (Jouzel et al. 2007; Lüthi et al. 2008) and more recent enhanced warming (e.g. Stips et al. 2016). Changes in atmospheric CO₂ concentrations influence climate both directly through the radiative effect of CO₂ and indirectly through its physiological effects (as mentioned earlier). On one hand, greenhouse gases (including CO2) largely absorb the longwave radiation emitted from the earth’s surface (Cubasch et al. 2013). On the other hand, in response to an increase of CO₂ levels, a decrease in canopy transpiration reduces evaporation, triggering changes in atmospheric water vapor and clouds (such as decreasing in low cloudiness; Cao et al. 2012) and affecting surface radiative fluxes (such as increasing shortwave radiation reaching the surface), thus producing changes in temperature and the water cycle (Cao et al. 2010). The intensification or weakening of these mechanisms and responses depends on the concentration of greenhouse gases in the atmosphere, which is represented in the present work through three different emission scenarios (RCP2.6, RCP4.5 and RCP8.5). While the climate system is in a constant state of flux, attaining RCP2.6 will certainly present the smallest impacts for natural ecosystems and human activities.

The decreases of minimum temperature projected during the far future (2081–2100) between Coquimbo and Los Ríos Regions could be the result of an intensification of southern winds along the coast due to a southward expansion of the subtropical anticyclone’s influence zone of the south-east Pacific, a large-scale feature consistent with global warming (Garreaud 2011). Another physical phenomenon that explains this result is Humboldt Current behavior, which is a cold current that could intensify with climate change by cooling the surface waters near the coast of Chile. These colder waters will have a cooling effect (i.e., greater than that of the current) on the air masses entering from the ocean to the continent, neutralizing global warming in the coastal strip (Santibañez et al. 2008; Santibañez 2017).

In the present study, increases of over 6 °C in winter in the central and northern zone based on the RCP8.5 scenario for the far future (2081–2100) are projected. Previously, Garreud (2011) projected increases of 5 °C in the same area, under A2 scenario and for the future period of 2070–2100 with respect to 1961–1990. Our study also shows increases of over 4 °C in the Altiplano region in winter, based on the RCP8.5 scenario for the end of the twenty-first century (2081–2100) and Fuenzalida (2007) obtained increases of 4–5 °C, based on the A2 scenario for the future period 2071–2100 with respect to 1961–1990.

The CCS for precipitation under the RCP8.5 scenario for the near future (2016–2035) shows decreases in summer and increments in winter for the Altiplano region (Fig. 12a, b), increments in the northern zone and toward the Andes in the mid-future (2046–2065; Fig. 12c, d), and increments exceeding 60% in the Altiplano region in the far future (2081–2100) (Fig. 12e, f). Previously, Garreaud (2011) also projected increases in the Altiplano region but stressed that these results were not very robust.

Although the methods used are distinct and the emissions scenarios were different, we reached a certain qualitative agreement with these previous studies. Some discrepancies between this and others studies and even among the different models in this study could be related to predictors that include signs of climate change such as temperature or specific humidity (P8 and P11) which sensitively influence the results of the projections (Brands et al. 2012; Manzanas et al. 2015). Specifically, Ruiz (2007) reported that the effect of the internal variability of a climate system in a given study area could be an important source of uncertainty. Ruiz (2007) also indicated that even without modification of radiative forcing, climate presents variations that are largely attributable to nonlinear dynamics. Moreover, the differences between models are also a large source of uncertainty, as they respond differently to the different forcings (Stocker 2014). According to the IPCC (Stocker 2014), the dispersion between the scenarios within the CMPI5 ensemble is the main source of uncertainty for the global temperature at the end of the twenty-first century. Additionally, the uncertainty is associated with the capacity of the GCM to simulate future climates; in other words, even if the GCM adequately simulates the current climate, it may not be as reliable for future climate projections. To reduce this uncertainty, more than one GCM is generally used (Cabré 2011), which is why six GCMs were used in the present study. We acknowledge that the use of a limited number of models might not provide a representative sample of the entire uncertainty range; thus, a larger ensemble could help to determine whether the projected changes are significant in ligh of model uncertainty (e.g., analyzing signal-to-noise ratios). The next generation of global climate models could potentially improve the present results. Moreover, the reanalysis dataset used to train the statistical downscaling method might also have some impacts on the projections (Brands et al. 2012; Manzanas et al. 2015).

Conclusions

In order to develop reliable climate change projections, large-scale predictors need to be extensively assessed (San Martín et al. 2017). Additionally, all the predictor variables which present a clear link with the predictand should be included, including signal-bearing predictors (Maraun et al. 2010). A comprehensive evaluation should consist of metrics that account for different characteristics, e.g., temporal and distributional features (San Martín et al. 2017). In this work, we analyze correlation, bias, and K–S test results for all seasons and the annual series to facilitate the predictor selection. For Chile, the best predictor for minimum and maximum temperature was formed by T_as, T₇₀₀, T₈₅₀, Z₂₅₀, and Z₅₀₀; the best predictor for precipitation was formed by T_as, Q₇₀₀, Z₅₀₀, and Z₈₅₀.

Here, six CMIP5 models were used to assess future climate, namely CMCC-CM, CMCC-CMS, CNRM-CM5, MPI-ESM-LR, MPI-ESM-MR, and NorESM1-M. The use of more than one GCM is highly recommended to increase different uncertainty sources and to analyze the robustness of the results (Knutti et al. 2010. Any conclusion based on a single GCM should be called into question. Moreover, one should keep in mind model bias in the historical scenario in different sub-areas and seasons of the study area.

Temperature increases (minimum and maximum) are projected under the three scenarios (RCP2.6, RCP4.5, and RCP 8.5) throughout the national territory. Under scenario RCP8.5 for the period of 2081–2100, minimum and maximum temperature in winter might increase about 4–8 and 6–8 °C, respectively. Under RCP8.5 for the period of 2081–2100, precipitation is projected to decrease by over 40% from the northern zone to the southern zone (between the regions of Antofagasta and Aysén) and might increase by 60% in the Altiplano regions (between the regions of Arica y Parinacota and Antofagasta) as well as in the austral zone (Aysén and Magallanes regions).

This work presents state-of-the-art of climate projections for Chile and potential changes in precipitation and temperature if different emissions scenarios are attained in the future. A warmer atmosphere can hold more water vapor, which in turn produces more intense precipitation, including precipitation intensity icreases of 6–7% per degree of warming or even more for sub-hourly precipitation (Schroeer and Kirchengast 2018). Thus the present analysis of extreme events and their intensification related to the increases in moisture due to warming (Trenberth 2011) provides an important baseline for future work.

Knowing how the climate might change could provide basic information for decision making in ecological, economic, social and health areas. The results of the present work can be applied in the impact on ecosystems, agricultural production and the risk of extinction of flora and fauna, and can also be used to reduce threats to food security and water resources.