Abstract
In August 2018, the Indian state of Kerala received an extended period of very heavy rainfall as a result of a low-pressure system near the beginning of the month being followed several days later by a monsoon depression. The resulting floods killed over 400 people and displaced a million more. Here, a high resolution setup (4 km) of the Weather Research and Forecasting (WRF) model is used in conjunction with a hydrological model (WRF-Hydro, run at 125 m resolution) to explore the circumstances that caused the floods. In addition to a control experiment, two additional experiments are performed by perturbing the boundary conditions to simulate the event in pre-industrial and RCP8.5 background climates. Modelled rainfall closely matched observations over the study period, and it is found that this would this would have been about 18% heavier in the pre-industrial due to recent weakening of monsoon low-pressure systems, but would be 36% heavier in an RCP8.5 climate due to moistening of the tropical troposphere. Modelled river streamflow responds accordingly: it is shown the six major reservoirs that serve the state would have needed to have 34% more capacity to handle the heavy rainfall, and 43% had the deluge been amplified by an RCP8.5 climate. It is further shown that this future climate would have significantly extended the southern boundary of the flooding. Thus it is concluded that while climate change to date may well have mitigated the impacts of the flooding, future climate change would likely exacerbate them.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
About 80% of the annual rainfall in India falls during the monsoon season (Parthasarathy et al. 1994) and the Indian population depends on this water for agriculture, hydration, and industry. Any variability in timing, duration and intensity of the monsoon rains have a significant impact on the lives of the people in India. In recent years, several parts of India have experienced devastating flooding events. For example, on 26 July 2005, Mumbai experienced the worst flooding in recorded history when the city received 942 mm of rainfall on a single day (Prasad and Singh 2005). Similarly, on 17 June 2013, the state of Uttarakhand received more than 340 mm of rainfall resulting in disastrous flood and landslides that lead to unparalleled damage to life and property (Dube et al. 2014; Martha et al. 2015). The November 2015 Chennai floods, which resulted in over 500 deaths when Chennai experienced three times the usual rainfall, is another such example (Ray et al. 2019). Each year, flooding in India from extreme rains results in a loss of around $3 billion, which constitutes about 10% of global economic losses (Roxy et al. 2017).
In August 2018, the state of Kerala experienced its worst flooding since 1924. The devastating flood and associated landslides affected 5.4 million people and claimed over 400 lives. The post-disaster assessment commissioned by the Government of Kerala estimated the economic loss to be more than $3.8 million.Footnote 1 These floods, as well as many like the ones listed earlier, occurred during the passage of a monsoon depression. Though depressions are not directly responsible for more than a few percent of the monsoon rainfall over Kerala (Hunt and Fletcher 2019), could their broad scale modulate the westerly moisture flux that is responsible?
Kerala is bounded by Arabian Sea to its west and the Western Ghat mountain range to its east. Around 44 rivers flow through Kerala and there are about 50 major dams distributed mostly across the Western Ghats (Ramasamy et al. 2019) which provide water for agriculture and hydroelectric power generation. Second to the northeastern states, Kerala receives the most monsoon rainfall in India: the average annual rainfall is around 300 cm spread over 6 months, the highest amounts being received in June and July. Between 1 and 19 August 2018, Kerala received 164% more rainfall than normal, most of which fell during the two torrential rainfall episodes of 8–10 August (contemporaneous with a low-pressure area, see Fig. 1) and 14–19 August (contemporaneous with a monsoon depression). During 14–19 August, the Keralan district of Idukki received the most rainfall (\(\sim 700\) mm)—about twice the normal amount. According to Mishra et al. (2018a), the one- and two-day extreme precipitation values that occurred in Kerala on 15–16 August had return periods of 75 and 200 years respectively when compared to a long term record from 1901–2017. Periyar basin, one of the most affected areas, received a 145-year return period rainfall amount (Sudheer et al. 2019).
The first of these two episodes of rain resulted in flooding along the banks of some of the rivers and water was released from only a few dams as the rain fell mostly over their catchment areas. After the first episode of heavy rain, most of the reservoirs in the state were near their Full Reservoir Level (FRL) and most of the soil in the region became saturated. Thus, when the second episode started several days later, the authorities had to open the shutters of almost all the major dams in Kerala. A combination of these torrential rains and opening of the dam shutters resulted in severe flooding in 13 out of the 14 districts in Kerala (Mishra et al. 2018b; CWC 2018). Given the volume of precipitation that fell during this period, could the dams possibly have prevented the floods that followed?
Sudheer et al. (2019) used a hydrological model to explore the role of dams in the Periyar river basin in the 2018 floods. They suggested that emptying the reservoirs in advance would not have avoided the flood as a large bulk of the surface runoff was caused by intermediate catchments which do not have controlled reservoir operations. They found that, in the Periyar river basin, improved reservoir management would have only attenuated the flood by 16–21%. Furthermore, they highlighted that the probability of getting extreme rainfall events in the Periyar river basin in August is only 0.6% and hence a reliable extreme rainfall event forecast coupled with a reservoir inflow forecast is needed to plan mitigation. Mishra et al. (2018b) found that the extreme precipitation and subsequent flooding of the 2018 event was unprecedented over a 66-year record. They suggested that while mean monsoon precipitation has decreased and mean temperature has increased over that period, one- and two-day extreme precipitation and extreme runoff conditions in in August 2018 exceeded the 95th percentile of the long-term mean from 1951–2017.
According to the recent Intergovernmental Panel for Climate Change (IPCC) report (Solomon et al. 2007), wet extremes are projected to become more severe in many areas where mean precipitation is projected to increase, as is flooding in the Asian monsoon region and other tropical areas. Several studies suggest that rainfall extreme events will increase in India under global warming (Goswami et al. 2006a; Rajeevan et al. 2008; Guhathakurta et al. 2011a; Menon et al. 2013; Roxy et al. 2017). Most extreme events over central India are associated with monsoon depressions (Dhar and Nandargi 1995), hence intensification of extreme rainfall events could be related to the change in dynamics of the monsoon depressions (Pfahl et al. 2017). However, due to the coarse resolution of global climate models, it is unknown if the extreme rainfall events in these models are caused by monsoon depressions (Turner and Annamalai 2012). Several observational studies, however suggest that the frequency of monsoon depressions has decreased and the frequency of low-pressure systems has increased in the recent past (Dash et al. 2004; Ajayamohan et al. 2010), implying a weakening trend in monsoon synoptic activity. So, how did climate change affect the 2018 floods, and to what extent would they differ under future climate change?
In this study, we will use high-resolution WRF and the WRF-Hydro simulations to explore the major factors behind the Kerala floods of August 2018. We also simulate the floods under pre-industrial and RCP8.5 background states to determine the effects of past and future climate change. Section 2 explains the model setup, data and methods used in this study. Section 3 deals with the major results from the precipitation and hydrology analysis. Results are concluded and discussed in Sect. 4.
2 Data and methodology
2.1 ERA-Interim
For the initial and lateral boundary conditions in our regional model setup, we use the European Centre for Medium-Range Weather Forecasts Interim reanalysis (ERA-I; Dee et al. 2011). The surface fields, as well as soil temperature and moisture at selected depths are used only for initial conditions; atmospheric variables, which include wind, temperature and moisture defined over pressure levels are used to construct both initial and boundary conditions. All fields are available at 6-h intervals with a horizontal resolution of T255 (\(\sim 78\) km at the equator), with the three-dimensional fields further distributed over 37 vertical levels spanning from the surface to 1 hPa. Data are assimilated into the forecasting system from a variety of sources, including satellites, ships, buoys, radiosondes, aircraft, and scatterometers. Fields deriving purely from the model (i.e. not analysed), for example precipitation and cloud cover, are not used in this study.
2.2 Precipitation data
We need a relatively high-resolution observational rainfall dataset with which to compare our model output. Arguably the most suitable such dataset is the NCMRWF merged product (Mitra et al. 2009, 2013), which combines automatic gauge data from the India Meteorological Department with satellite data from the TRMM multisatellite precipitation analysis (Huffman et al. 2007). This provides a rainfall dataset covering India and surrounding oceans at daily frequency and \(0.25^\circ\) horizontal resolution.
2.3 CMIP5
For this study, we use the 32 freely-accessible CMIP5 models (Taylor et al. 2012) for which monthly pressure level data were available. Where possible, the r1p1i1 ensemble member was chosen as the representative of each model, so as not to unfairly weight the results towards any particular model. The exception was EC-EARTH, for which, due to data availability reasons, member r9p1i1 was used. In this study, we use data from three of the CMIP5 experiments: historical, pre-industrial, and RCP8.5. The historical experiments of all models used here are forced with observed natural and anthropogenic contributions, usually from over the period 1850–2005, from which we take a representative period of 1980–2005, against which all perturbations are computed. The pre-industrial experiment comprises longer simulations with no anthropogenic forcings; these have varying baseline periods depending on the model, so we take the representative period as being the last 25 years of the run. The future scenario used here, RCP8.5, corresponds to an effective net change in radiative forcing in 2100 of \(8.5\,\hbox {W}\,\hbox {m}^{-2}\), equivalent to roughly 1370 ppm \(\hbox {CO}_2\) (Van Vuuren et al. 2011). We again choose the final 25 years (2075–2100) as the representative period for the experiment.
2.4 WRF
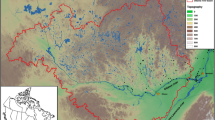
Throughout this study we will make use of version 4.0 of the Advanced Research Weather Research and Forecasting (WRF) model (Skamarock et al. 2008). Two domains (see Fig. 1) were employed for this study: the \(61\times 61\) outer domain had a resolution of 36 km, whereas the \(100\times 181\) inner domain had a resolution of 4 km. We note that though this nesting ratio seems high, previous authors (e.g. Liu et al. 2012; Mohan and Sati 2016) have found that results are insignificant to the ratio, so long as it is an odd number. The inner domain was chosen to encapsulate the entire state of Kerala, as well as the Western Ghats and an area of the Arabian Sea to the west, allowing us to capture offshore convective development as well as the orographic features that play an important role in monsoon rainfall in the state. The larger domain, which covers most of India, was chosen to include the monsoon depression that was contemporaneous with the flooding.
Convection was parameterised in the outer domain, but explicit in the inner—this and the other physics schemes used are outlined in Table 1. Here, we use the combination recommended by NCAR and specified in the WRF User’s Guide for convection-permitting simulations of tropical cyclones; it is very similar to that used by previous authors simulating orographic rainfall in South Asia (e.g. Patil and Kumar 2016; Norris et al. 2017), as well as monsoons in general (e.g. Srinivas et al. 2013; Dominguez et al. 2016). We use 35 eta levels in the vertical with a model lid at 50 hPa. Lateral boundary conditions were supplied at every 6-h timestep from ERA-Interim reanalysis data, as were initial conditions for the first timestep.
2.5 WRF-Hydro
In this study, we use the WRF-Hydro hydrological model (Gochis et al. 2014), coupled to the Noah-MP land surface model (LSM; Gochis and Chen 2003; Niu et al. 2011; Yang et al. 2011). In our configuration, both overland (steepest descent) and channel routing (differential wave gridded) were activated, with the hydrological model running at a resolution of 125 m (timestep: 10 s) and the land surface model running at 4 km (timestep: 1 h). The LSM takes as input hourly output from the WRF model, distributing surface precipitation among its four soil layers (set at 7, 28, 100, and 289 cm to match ERA-Interim) and the surface; WRF-Hydro then channels this moisture accordingly at the higher resolution. The high-resolution input files, containing important geospatial information (e.g. slope direction, river channel mask) were created using the WRF-Hydro GIS preprocessing toolkit and the satellite-derived HydroSHEDS hydrographic dataset (Lehner et al. 2008; Lehner and Grill 2013). These modelled rivers and their basins are shown in Fig. 2.
Because of a lack of relevant reservoir and lake data for the state of Kerala, these features were not implemented in the hydrological model; one major implication of this was that the surface water output from WRF-Hydro was inaccurate (while the natural lakes were correctly represented, the artificial reservoirs were not). Given that some of the reservoirs are substantial (the largest, created by the Idukki dam, is about \(60\,\hbox {km}^2\) in area), we chose to run the LSM and WRF-Hydro offline (i.e. coupled to each other but not to WRF) in order to mitigate incorrect feedbacks caused by mislocated surface water.
Furthermore, the long spin-up time necessary for the hydrological model meant that a cold start in the summer of 2018 would have been inappropriate. As such, we ran WRF with the control experiment parameters from 1 June 2017 to 1 July 2018 (the start date of all experiments), using the output to force WRF-Hydro so that warm restart files were available for the study period.
2.6 Climate perturbation and experimental setup
One of the key foci of this study will be to explore how the 2018 floods would have differed in the absence of anthropogenic climate change and how it would differ in a projected future climate. To this end we use a technique commonly referred to as pseudo-global warming (PGW, e.g. Kimura and Kitoh 2007; Prein et al. 2017; Hunt et al. 2019). Taking an example of modifying 01-08-2018 00Z boundary conditions to reflect RCP8.5 conditions, we describe the methodology below:
- 1.
For a given prognostic variable, say, temperature, compute the CMIP5 multi-model August mean for the historical experiment over the period 1980–2005. Call this \(T_0\).
- 2.
Compute the multi-model August mean for the RCP8.5 experiment over the period 2075–2100. Call this \(T_p\).
- 3.
Take the difference field, \(T_d=T_p - T_0\), then slice and interpolate it to match the dimensions of the boundary condition. Add \(T_d\) to the boundary condition, and repeat for all boundaries for T at this time step.
- 4.
Repeat for all variables (and all time steps) on both lateral and lower boundaries.
In this way, we can keep the important high-magnitude, high-frequency weather information, but see how the impacts adjust when perturbed by a low-magnitude, low-frequency climate signal.
2.7 Storage calibration
Much of this study focuses on reservoirs, and since the hydrological model used can only compute the river discharge (or reservoir inflow) for a given point, we need to be able to convert this to storage, so that it can be compared appropriately with observations. To this end, we propose a simple model to compute the storage, S, at some time \(t_1\), given its value at \(t_0\), the inflow rate as a function of time, \(\phi (t)\), the evacuation rate, \(\eta\), and some shape parameter, \(\alpha\):
The evacuation rate represents the sum of all contributions to drainage from the reservoir—comprising artificial sinks (sluices, spillways) and natural sinks (seepage, evaporation). Strictly speaking, this should be a function of time; however, that information is not freely available for the dams studied in this work and fitting a time dependent variable using model output would be a highly underconstrained problem. Therefore, we make a simplification—separating the contributions into a constant (following the notion that reservoir output is generally intended to be kept constant), \(\eta\) and a factor proportional to the accumulated storage as a function of time (assuming that, e.g., groundwater seepage is proportional to storage,Footnote 2) \(\beta\). For readability, we define \(\alpha = 1-\beta\) and call that the shape factor because it also includes the effects of having a more complex, partitioned reservoir system.
3 Results
3.1 Precipitation
Mean precipitation [\(\hbox {mm h}^{-1}\)] over the inner domain for the period August 6 to August 18 inclusive. From left: the NCMRWF merged product; the control experiment; the difference between the control and pre-industrial experiments; and the difference between the RCP8.5 and control experiments. State boundaries are marked in black, with black crosses representing the major dams shown in Fig. 2
We start our analysis by looking at the primary cause of all floods: precipitation. Figure 3 shows different aspects of the rainfall occurring during and immediately before the floods, covering the period August 6 to August 18 inclusive. The leftmost panel shows the mean rainfall for this period according to the NCMRWF merged precipitation product (see Sect. 2.2). Rainfall is concentrated mostly along the peaks of the Western Ghats, thus the hydrological stress that triggered the flooding came about from an (approximate) amplification of the mean monsoon pattern rather than through rainfall falling in unusual locations. This pattern is in agreement with the assessment of Mishra and Shah (2018) who investigated IMD rainfall dataFootnote 3 for the period. Most of the rainfall falls over land as opposed to ocean indicating the extended presence of a so-called coastal convective phase, as described by Fletcher et al. (2018). Coastal phases stand in contrast to offshore phases, and usually develop under conditions of anomalously strong and moist westerlies—in this case provided by the low pressure systems passing over the peninsula.
Second from left in Fig. 3 is the mean rainfall for our WRF control experiment for the same period (06/08–18/08), showing a broad structure very similar to observations for the period shown in the first panel.Footnote 4 Again, the rainfall is predominantly onshore, concentrated over the orography. At this resolution, though it was suggested by the observational data, we can see that the mean rainfall for this period is heaviest over—or slightly upstream of—the major dams. Upstream of Idamalayar and Parambikulam the mean rate for some areas reached more than \(15\,\hbox {mm}\,\hbox {h}^{-1}\), amounting to an accumulation exceeding 4.5 m for period. This is in accordance with data released by the Central Water Commission,Footnote 5 as is the spatial distribution.
The remaining two panels, on the right hand side of Fig. 3, compare the control experiment mean rainfall with that of the two perturbation experiments. We recall from the methodology that these experiments are—like the control—hindcasts, with their boundary conditions adjusted to simulate how the events leading to the flood may differ if occurring under pre-industrial or RCP8.5 climates. The first of these (second from right) shows the difference in mean rainfall for the period between the control and pre-industrial experiments. It is almost universally drier in the pre-industrial experiment—averaging a mean reduction over the inner domain of about 18% compared to the control. Let us start to unpick this by noting that historical rainfall trends show that the monsoon is drying and that that pattern is amplified over Kerala and the Western Ghats due to weakening monsoon westerlies (Krishnan et al. 2016). This picture is complicated somewhat by previous studies showing that extreme rainfall events embedded within the monsoon have seemingly worsened (e.g. Goswami et al. 2006b), though spatial maps of such trends (Guhathakurta et al. 2011b) suggest that they are very slight along the southwest coast. We will resolve this in the next section by looking at the changes from a moisture flux perspective. Finally, we compare the control and RCP8.5 experiments, as shown in the rightmost panel of Fig. 3. The RCP8.5 perturbed scenario is almost universally wetter than the control over the inner domain (by about 36%), particularly over the southern Keralan Ghats, where the control rainfall is highest and where the major dams are situated. This is in contrast to the pre-industrial experiment which exhibited the most drying over the north of the state with a more mixed signal around the major dams. This non-linearity could indicate that different processes are responsible for the respective changes.
Vertically-integrated moisture flux for the period 2018-08-15 00Z to 2018-08-19 00Z over the outer domain (with Kerala indicated in black). The left panels shows the mean vector field and its magnitude for the pre-industrial and control experiments respectively. The middle panels show the changes to those fields in the control and RCP8.5 experiments respectively considering only changes to specific humidity. The right panels are as the middle panels but for changes to the wind field. The right and middle panels are coloured by the effect their presence has on the total magnitude, note that the colours scales differ between the two pairs of experiments
The moisture flux that impinges upon the Western Ghats is responsible for the vast majority of the monsoon rainfall that falls over Kerala, subject to localised dynamics dependent also on the land-sea contrast (Fletcher et al. 2018). To first order, changes in this moisture flux can be thought of as a sum of contributions from changes to humidity and changes to the wind field, i.e.:
where q and \({\mathbf {u}}\) are the quantities in the perturbation experiment, \({\bar{q}}\) and \(\bar{{\mathbf {u}}}\) are the values in the control experiment, and \(q'\) and \({\mathbf {u}}'\) are the differences between them.
Considering the period when the monsoon depression was most active: Aug 15 to Aug 18 inclusive, we compare these terms between the control experiment and two perturbation experiments in Fig. 4. The first of the two groups, Fig. 4a treats the pre-industrial experiment as the base, with the control experiment acting as the perturbation. The leftmost panel, indicating mean moisture flux for the period, shows clearly the impact of the depression. It dominates the organisation of moisture over the peninsula, with high values of vertically integrated flux and flux convergence both slightly to the south of its centre and over Kerala. The middle panel shows how this pattern would change in the present day considering differences to humidity alone. As the tropical atmosphere has not moistened drastically since the pre-industrial, these changes are slight when compared to the absolute values, adding only a very small positive contribution—amounting to a few percent—to the flux magnitude over Kerala. The right-hand panel is as the middle panel, but instead looking at the contribution from the wind field alone. Immediately, one can see that the depression is surrounded by a significantly weaker circulation causing a reduction in moisture flux over almost all of India, except for a small region near the depression centre caused by track translation. This is expected: previous studies have shown that monsoon low-pressure systems become weaker and less numerous as the climate warms (Prajeesh et al. 2013; Cohen and Boos 2014; Sandeep et al. 2018) as low-level vorticity associated with the monsoon decreases. Despite this, the reduction in flux over Kerala is comparatively weak, though easily more than enough to override the contribution from \(q'\). This is largely in agreement with Sørland et al. (2016) who found that, for an ensemble of ten individual storms, uniform atmospheric temperature increases of 2 K and 4 K yielded mean precipitation increases of 22% and 53% respectively.
The second set of panels, Fig. 4b, shows the contributions to the difference in moisture flux between the control and RCP8.5 experiments. The mean vertically integrated moisture flux for the control experiment appears quite similar to that of the pre-industrial experiment, which we expect from the preceding analysis. The humidity change (middle panel) increases the moisture flux incident on Kerala by over 20% from the control experiment to the RCP8.5 experiment, as well as a universally positive contribution over the whole subcontinent. The expected further weakening of the depression (right-hand panel) is much weaker than in the pre-industrial to control case before, and nowhere near strong enough to counter the large moisture-drive contribution.
In summary, in the control (present-day) experiment, there was marginally less moisture flux over Kerala than in the pre-industrial experiment due to a marked weakening of the monsoon depression; in contrast, there is significantly increased flux over Kerala in the RCP8.5 experiment in spite of slight weakening of the depression, due to a large rise in tropospheric humidity.
3.2 Hydrology
Modelled river discharge (\(\hbox {m}^3\hbox {s}^{-1}\)) for 13–18 August 2018 inclusively as: a the control experiment mean; b the ratio of the control experiment and pre-industrial experiment means; and c the ratio of the RCP8.5 experiment and control experiment means. The seven major dams shown in Fig. 2 are given here by black crosses
Precipitation is only one part of the complex hydrological cascade that leads to flooding. To work towards a more complete picture, we now use the WRF hydrological model (see Sect. 2.5) to explore the response of rivers to the heavy precipitation analysed in the previous section.
Figure 5 shows the mean modelled discharge over from 13-08-2018 00Z to 19-08-2018 00Z for the control experiment and how it compares to the two perturbation experiments. The control mean (Fig. 5a) splits the discharge into decades, with green hues representing the largest rivers (flow rates exceeding \(100\,\hbox {m}^3\,\hbox {s}^{-1}\)), red hues representing the smallest rivers (flow rates below \(10\,\hbox {m}^3\,\hbox {s}^{-1}\)), and yellow covering those in between. All seven of the important dams (and their eponymous reservoirs) lie on major rivers or significant tributaries thereof. Given the complicated partitioning of river basins over Kerala (Fig. 2), these maps provide a useful overview of their response to heavy rainfall during August 2018 and how that response changes when the rainfall responds to the different climates of the pre-industrial and RCP8.5 perturbation experiments.
Figure 5b shows the difference between the mean control discharge and that of the pre-industrial experiment. As the rainfall is generally less in the latter during this period, we see the expected pattern of almost completely reduced streamflow over the domain; the exact reduction varies considerably depending on location (and is indeed an increase in some areas) but averages 16% over the domain. In contrast, Fig. 5c shows that streamflow almost universally increases over the domain in the RCP8.5 experiment when compared to the control. In some places, the change is quite drastic: the mean increase over the domain is 33%, the upper quartile is 77%, and the ninetieth percentile is 97%. In other words, one in ten river points in the domain would have experienced twice the discharge were this event to have happened in an RCP8.5 climate. The domain-averaged changes of −16% and 33% for pre-industrial and RCP8.5 are in strong agreement with the domain-averaged rainfall changes of −18% and 36% respectively.
Idukki reservoir: modelled inflow (blue, grey, red lines for control, pre-industrial, RCP8.5 experiments respectively), modelled storage (orange solid, dotted, dashed lines respectively), and observed storage (black crosses). Nominal reservoir maximum capacity is marked by the dashed grey line towards the right of the figure
The story would be incomplete without some focus on the reservoir/dam system that failed in the lead up to the floods. While a complete treatment of that topic is beyond the scope of this work, we will endeavour to give a thorough analysis with the available data. We start by using the largest reservoir in the state, Idukki, as a case study. Figure 6 shows the modelled inflow and storage for all three experiments, as well as the observed storage from India-WRIS and the nominal capacity of the reservoir. As discussed in Sect. 2.7, to convert modelled inflow to a representative storage we must integrate it over time and include both a sluicing rate and a shape factor. These are reservoir-specific unknowns that we need to fit for using a standard least-squares method. Leveraging part of the long spin up period required by the hydrological model, we calibrated using observational and (control experiment) model data from January to June 2018 inclusive; the low rainfall during the pre-monsoon being particularly useful to establish the correct sluicing rate.
The inflow rates from all three experiments are in line with what we expect from Fig. 5: overall the control experiment is the driest, with slightly more inflow in the pre-industrial experiment and significantly more in the RCP8.5 experiment. The control experiment inflow very closely matches that given in the CWC report (see their Fig. 4). These project accordingly onto the modelled storages, all three of which closely follow the observations until the first LPS (Aug 6 to Aug 10). At that point, the reservoir hit capacity—denoted in Fig. 6 by the dashed horizontal grey line, and the floodgates had to be opened. Our model is not party to that information and continues to assume the constant sluicing rate from the pre- and early monsoon periods, resulting in a divergence between the three model storages and observations. The control experiment provides a useful estimate of how much additional storage would have been required: the nominal maximum capacity is \(1.45\times 10^9\,\hbox {m}^{3}\), the control experiment modelled storage peaked at \(2.04\times 10^9\,\hbox {m}^{3}\) (41% higher), and the RCP8.5 experiment reached a storage of \(2.30\times 10^9\,\hbox {m}^{3}\) (59% higher than maximum capacity, 13% higher than the control). Making the naïve assumption that when modelled storage values exceed the maximum capacity, the difference is converted into floodwater, the control experiment yields a total excess of \(5.89\times 10^8\,\hbox {m}^{3}\) between breaching on August 11th and remission ten days later; the RCP8.5 experiment (breaching one day earlier) yields \(8.52\times 10^8\,\hbox {m}^{3}\), an increase of 45%. It is clear, therefore, that using the dams to mitigate downstream flooding would have been largely impossible; furthermore, were such an event to happen again in an end-of-century RCP8.5 climate, it would be significantly more catastrophic.
Comparison of modelled (orange) and observed storage rates for 2018 with the 2001–2017 climatology (mean in black, with grey swath denoting extrema) for six major reservoirs. Storage at maximum capacity for each is given by the dotted grey line. The three modelled storage values are given by solid, dashed, and dotted lines for the control, pre-industrial, and RCP8.5 experiments respectively
We now generalise this analysis to the major Keralan reservoirs. This is only possible for the six whose storage data are released by India-WRIS, without which we cannot calibrate using Eq. 1. Observed and modelled storages, along with climatological information, are given for these six (Idamalayar, Idukki, Kakki, Kallada, Malampuzha, and PeriyarFootnote 6) in Fig. 7. There are two brief caveats to make before we move into the analysis. Firstly, we have assumed that the reservoir outflow is the sum of a constant sluicing rate and some additional contribution proportional to the inflow; this is a very good approximation for the larger reservoirs (which the reader is invited to verify by inspection of the CWC report) but can be poor in smaller reservoirs where the supply and demand is comparably much more variable. Secondly, as discussed in the previous section, our model has no information on floodgates, so continues to add to the storage of a reservoir even after the maximum capacity (FRL) has been passed. In each case this manifests as a large divergence between modelled and observed storage starting in mid August.
Figure 7 compares these storages for the reservoirs in question. In all cases except Periyar (and to a lesser extent, Kallada), the modelled storage from the control experiment closely follows the observed storage; in all but Kallada, the 2018 observed storage reached its FRL; and in all cases, at some point in July or August, the storage reaches its highest value since records began in 2001. Two reservoirs, Idamalayar and Malampuzha, exhibit seemingly counter-intuitive behaviour: by the end of August, the largest storage values come from the pre-industrial experiment and the smallest from RCP8.5. Inspection of Fig. 3 reveals that although nearly everywhere in the domain receives more rainfall in the RCP8.5 experiment (compared to the control), both these dams are situated downstream of small regions where the reverse is true, seemingly in part due to the absence of some rainfall-triggering event in mid July. Thus, in these unusual cases, it is possible that future climate may mitigate hydrological stress on these reservoirs. The remaining four have storage patterns that more closely reflect the general results presented earlier in this study: the highest storage values are reached in RCP8.5, followed by pre-industrial, with control at the bottom. Averaged over these four reservoirs, the peak storage in the control experiment is 34% higher than the nominal maximum capacity, rising to 43% in pre-industrial conditions and 54% in RCP8.5 conditions. Including the two anomalous reservoirs, these become 37%, 50% and 44% respectively.
Sum of model inflow to all reservoirs (see Fig. 2) separated by river basin. Basins are organised by latitude, with the northernmost being shown at the left hand side. Solid, dashed, and dotted lines represent the control, pre-industrial, and RCP8.5 experiments respectively
Finally, we look at the general impact on the 62 dams/reservoirs shown in Fig. 2, whose inflows are grouped by river basin in Fig. 8; for each basin, the inflow is computed as the sum of inflow to all reservoirs therein. Noting that the basins are arranged by latitude, several important contrasts emerge. Firstly, the relative impact of the first LPS (triggering the peaks between Aug 8 and Aug 10) is less among the more southerly basins; likely because as a weaker system, it would have a smaller region of influence, and thus less impact on the bulk monsoon flow. Secondly, the impact of switching to an RCP8.5 climate becomes drastically more significant in basins situated further south. Over the period Aug 14 to Aug 19 inclusive, the three smaller basins towards the north (Kuttiyadi, Bharatapuzha, and Karuvannur) have mean control inflow of \(26.2\,\hbox {m}^3\,\hbox {s}^{-1}\), rising 25% to \(32.7\,\hbox {m}^3\,\hbox {s}^{-1}\) in the RCP8.5 experiment. For the middle three basins (Chalakkudy, Periyar, and Muvattupuzha), the mean inflow increases 32% from \(563\,\hbox {m}^3\,\hbox {s}^{-1}\) in the control to \(745\,\hbox {m}^3\,\hbox {s}^{-1}\) in RCP8.5. For the southernmost three (Meenachal, Pamba, and Kallada), this changes drastically: rising 98% from \(152\,\hbox {m}^3\,\hbox {s}^{-1}\) to \(302\,\hbox {m}^3\,\hbox {s}^{-1}\). Revisiting Figs. 3 and 4b, we can see why: this area has the largest fractional increase of rainfall in the RCP8.5 experiment (this can be confirmed directly by looking at a ratio map, which we do not show here). This in turn is at least partially caused by a significant increase in moisture flux and moisture flux convergence over the southernmost part of the peninsula, a pattern that is echoed in CMIP5 projections (Sharmila et al. 2015). This has a profound implication: the southern part of Kerala did not flood in 2018 (Mishra and Shah 2018), but the results here suggest that it almost certainly would do were such an event to happen again in an end-of-century RCP8.5 climate.
4 Discussion
During mid-August 2018, unprecedented and widespread flooding resulted in the deaths of over 400 people and the displacement of over a million more in the Indian state of Kerala. The flooding was preceded by several weeks of heavy rainfall over the state, caused mostly due a monsoon depression (13–17 Aug) that immediately followed a monsoon low-pressure system (6–9 Aug). In this manuscript, we explored the underlying causes and hydrological responses, as well as how they would differ under alternative climate scenarios. To achieve this, we used a two-domain setup in the Weather Research and Forecasting Model (WRF) with the outer domain (20 km resolution) covering most of the Indian peninsula and the nested inner domain (4 km resolution, explicit convection) covering its southwest, including the entire state of Kerala and a significant portion of the Arabian Sea. Alongside this, we used the companion hydrological model (WRF-Hydro) at 125 m resolution to simulate river channel response to the varying precipitation forcings. The ‘alternative’ climates (pre-industrial and RCP8.5) were simulated by perturbing the model initial and lateral boundary conditions by their projected difference from the present day, computed using CMIP5 multi-model output.
We found that the simulated rainfall from the control experiment, concentrated over the Western Ghats, closely matched observations for that period. The rainfall over this period was higher in both the perturbation experiments: by about 36% over the inner domain in the RCP8.5 experiment and by about 18% in the pre-industrial. We attributed these changes to two trends that previous studies have established as effects of climate change: the weakening of synoptic activity within the Indian monsoon and the moistening of the tropical troposphere. We found that the former was the dominant driver of moisture flux change between the pre-industrial and the present day (hence lower rainfall in the control than in the pre-industrial experiment), whereas the latter was the strongest driver of change between the present-day and RCP8.5. Given this trade-off between competing factors, we cannot safely infer how the rainfall associated with this event would change in other future climates (e.g. RCP4.5, RCP6.0), and so we leave this task for future work.
Using a high-resolution setup of WRF-Hydro, we showed that the change in domain mean rainfall projected onto approximately equivalent changes in mean river streamflow, though as expected there was substantial spatial and temporal variance: for example, the 90th percentile streamflow over the domain increased by 97% in the RCP8.5 experiment compared to the control. Because the India Water Resource Information Service (India-WRIS) only make certain data publically available (only storage data, and only for six of the largest reservoirs), we used a simple model to convert modelled inflow into reservoir storage to verify our hydrological model. For four of the six reservoirs, before reaching their full reservoir level (FRL), the Pearson correlation coefficient between the observed and modelled storage exceeded 0.99 with the remaining two both exceeding 0.9. Furthermore, inflow values for several reservoirs in the days preceding the flood published in a report by the Central Water Commission agree closely with the model output, confirming the efficacy of the hydrological model.
By comparing the modelled storage, which is not affected by FRL, with the observed storage, which is, we were able to calculate the surplus water for each of the six main reservoirs. On average, over the four reservoirs that most closely represented the rainfall trends, 34% more capacity would have been required to handle all the excess precipitation that fell during August 2018; rising to 43% in the pre-industrial and 54% in RCP8.5. It is clear, therefore, that no matter what approach was taken to opening the dams, the catastrophe was inevitable; furthermore the results presented here suggest that they would be significantly more devastating in an end-of-century RCP8.5 climate. Analysis of river streamflow at all 62 dams in the state showed that climate change would have the strongest impact in the south of the state: mean inflow for Aug 14 to Aug 19 increased 25% between the control and RCP8.5 experiments in the three northernmost river basins, rising to 98% in the three southernmost basins.
Notes
This is only strictly true if reservoir cross-sectional area is constant with height. Of course it isn’t; but for the sake of simplicity, we make this approximation.
Note that the NCMRWF dataset used here is in part derived from IMD rainfall data, so a high pattern correlation is expected.
For a fairer comparison, the model output should be regridded to the resolution of the NCMRWF dataset. However we intend this particular comparison to be qualitative, not quantitative- and have thus retained the higher resolution.
Note that in some literature, this is referred to Mullaperiyar.
References
Ajayamohan RS, Merryfield WJ, Kharin VV (2010) Increasing trend of synoptic activity and its relationship with extreme rain events over central india. J Clim 23(4):1004–1013
Cohen NY, Boos WR (2014) Has the number of Indian summer monsoon depressions decreased over the last 30 years? Geophys Res Lett 41:7846–7853. https://doi.org/10.1002/2014GL061895
CWC (2018) Kerala floods of August 2018. Central Water Commission, New Delhi https://reliefweb.int/sites/reliefweb.int/files/resources/Rev-0.pdf
Dash SK, Kumar JR, Shekhar MS (2004) On the decreasing frequency of monsoon depressions over the Indian region. Curr Sci Bangalore 86(10):1404–1410
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Quart J R Meteor Soc 137(656):553–597. https://doi.org/10.1002/qj.828
Dhar O, Nandargi S (1995) On some characteristics of severe rainstorms of India. Theor Appl Climatol 50(3–4):205–212
Dominguez F, Miguez-Macho G, Hu H (2016) WRF with water vapor tracers: a study of moisture sources for the North American monsoon. J Hydrometeorol 17(7):1915–1927
Dube A, Ashrit R, Ashish A, Sharma K, Iyengar G, Rajagopal E, Basu S (2014) Forecasting the heavy rainfall during Himalayan flooding—June 2013. Weather Clim Extrem 4:22–34
Fletcher JK, Parker DJ, Turner AG, Menon A, Martin GM, Birch CE, Mitra AK, Mrudula G, Hunt KMR, Taylor CM, et al (2018) The dynamic and thermodynamic structure of the monsoon over southern India: New observations from the INCOMPASS IOP. Q J R Meteorol Soc
Gochis DJ, Chen F (2003) Hydrological enhancements to the community Noah land surface model. Tech. rep., NCAR
Gochis DJ, Yu W, Yates DN (2014) The WRF-Hydro model technical description and user’s guide, version 2.0. Tech. rep., NCAR
Goswami BN, Venugopal V, Sengupta D, Madhusoodanan M, Xavier PK (2006a) Increasing trend of extreme rain events over India in a warming environment. Science 314(5804):1442–1445
Goswami BN, Venugopal V, Sengupta D, Madhusoodanan MS, Xavier PK (2006b) Increasing trend of extreme rain events over India in a warming environment. Science 314(5804):1442–1445
Guhathakurta P, Sreejith O, Menon P (2011a) Impact of climate change on extreme rainfall events and flood risk in India. J Earth Syst Sci 120(3):359
Guhathakurta P, Sreejith O, Menon P (2011b) Impact of climate change on extreme rainfall events and flood risk in India. J Earth Syst Sci 120(3):359
Hong SY, Lim JOJ (2006) The WRF single-moment 6-class microphysics scheme (WSM6). Asia-Pac J Atmos Sci 42(2):129–151
Hong SY, Noh Y, Dudhia J (2006) A new vertical diffusion package with an explicit treatment of entrainment processes. Mon Weather Rev 134(9):2318–2341
Huffman GJ, Bolvin DT, Nelkin EJ, Wolff DB, Adler RF, Gu G, Hong Y, Bowman KP, Stocker EF (2007) The TRMM multisatellite precipitation analysis (TMPA): quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J Hydrometeor 8:38–55. https://doi.org/10.1175/JHM560.1
Hunt KMR, Fletcher JK (2019) The relationship between Indian monsoon rainfall and low-pressure systems. Clim Dyn pp 1–13
Hunt KMR, Turner AG, Parker DE (2016) The spatiotemporal structure of precipitation in Indian monsoon depressions. Q J R Meteor Soc 142(701):3195–3210. https://doi.org/10.1002/qj.2901
Hunt KMR, Turner AG, Shaffrey LC (2019) The impacts of climate change on the winter water cycle of the western Himalaya. Clim Dyn Prep
Iacono MJ, Delamere JS, Mlawer EJ, Shephard MW, Clough SA, Collins WD (2008) Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J Geophys Res Atmos 113(D13):
Jiménez PA, Dudhia J, González-Rouco JF, Navarro J, Montávez JP, García-Bustamante E (2012) A revised scheme for the WRF surface layer formulation. Mon Weather Rev 140(3):898–918
Kain JS (2004) The Kain-Fritsch convective parameterization: an update. J Appl Meteorol 43(1):170–181
Kimura F, Kitoh A (2007) Downscaling by pseudo-global-warming method. Final Rep ICCAP RIHN Proj 1–1:43–46
Krishnan R, Sabin TP, Vellore R, Mujumdar M, Sanjay J, Goswami BN, Hourdin F, Dufresne JL, Terray P (2016) Deciphering the desiccation trend of the South Asian monsoon hydroclimate in a warming world. Clim Dyn 47(3–4):1007–1027
Lehner B, Grill G (2013) Global river hydrography and network routing: baseline data and new approaches to study the world’s large river systems. Hydrol Processes 27(15):2171–2186
Lehner B, Verdin K, Jarvis A (2008) New global hydrography derived from spaceborne elevation data. Eos Trans Am Geophys Union 89(10):93–94
Liu J, Bray M, Han D (2012) Sensitivity of the weather research and forecasting (WRF) model to downscaling ratios and storm types in rainfall simulation. Hydrol Process 26(20):3012–3031
Martha TR, Roy P, Govindharaj KB, Kumar KV, Diwakar P, Dadhwal V (2015) Landslides triggered by the June 2013 extreme rainfall event in parts of Uttarakhand state, india. Landslides 12(1):135–146
Menon A, Levermann A, Schewe J (2013) Enhanced future variability during India’s rainy season. Geophys Res Lett 40(12):3242–3247
Mishra V, Shah HL (2018) Hydroclimatological perspective of the Kerala flood of 2018. J Geol Soc India 92(5):645–650
Mishra V, Aaadhar S, Shah H, Kumar R, Pattanaik DR, Tiwari AD (2018a) The Kerala flood of 2018: combined impact of extreme rainfall and reservoir storage. Hydrol Earth Syst Sci Discuss pp 1–13
Mishra V, Aaadhar S, Shah H, Kumar R, Pattanaik DR, Tiwari AD (2018b) The Kerala flood of 2018: combined impact of extreme rainfall and reservoir storage. Hydrol Earth Syst Sci Discuss pp 1–13
Mitra AK, Bohra AK, Rajeevan MN, Krishnamurti TN (2009) Daily Indian precipitation analysis formed from a merge of rain-gauge data with the TRMM TMPA satellite-derived rainfall estimates. J Meteorol Soc Japan Ser II 87:265–279
Mitra AK, Momin IM, Rajagopal EN, Basu S, Rajeevan MN, Krishnamurti TN (2013) Gridded daily Indian monsoon rainfall for 14 seasons: merged TRMM and IMD gauge analyzed values. J Earth Syst Sci 122(5):1173–1182
Mohan M, Sati AP (2016) WRF model performance analysis for a suite of simulation design. Atmos Res 169:280–291
Niu GY, Yang ZL, Mitchell KE, Chen F, Ek MB, Barlage M, Kumar A, Manning K, Niyogi D, Rosero E, et al (2011) The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J Geophys Res Atmos 116(D12)
Norris J, Carvalho LMV, Jones C, Cannon F, Bookhagen B, Palazzi E, Tahir AA (2017) The spatiotemporal variability of precipitation over the himalaya: evaluation of one-year wrf model simulation. Clim Dyn 49(5–6):2179–2204
Parthasarathy B, Munot AA, Kothawale D (1994) All-India monthly and seasonal rainfall series: 1871–1993. Theor Appl Climatol 49(4):217–224
Patil R, Kumar PP (2016) WRF model sensitivity for simulating intense western disturbances over North West India. Model Earth Syst Environ 2(2):1–15
Pfahl S, O’Gorman PA, Fischer EM (2017) Understanding the regional pattern of projected future changes in extreme precipitation. Nat Clim Change 7(6):423
Prajeesh AG, Ashok K, Bhaskar Rao DV (2013) Falling monsoon depression frequency: a Gray-Sikka conditions perspective. Sci Rep 3:1–8. https://doi.org/10.1038/srep02989
Prasad AK, Singh RP (2005) Extreme rainfall event of July 25–27, 2005 over Mumbai, west coast, India. J Indian Soc Remote Sens 33(3):365–370
Prein AF, Rasmussen RM, Ikeda K, Liu C, Clark MP, Holland GJ (2017) The future intensification of hourly precipitation extremes. Nat Clim Change 7(1):48
Rajeevan M, Bhate J, Jaswal AK (2008) Analysis of variability and trends of extreme rainfall events over India using 104 years of gridded daily rainfall data. Geophys Res Lett 35(18):
Ramasamy S, Gunasekaran S, Rajagopal N, Saravanavel J, Kumanan C (2019) Flood 2018 and the status of reservoir-induced seismicity in Kerala, India. Nat Haz pp 1–13
Ray K, Pandey P, Pandey C, Dimri AP, Kishore K (2019) On the recent floods in india. Curr Sci 117(2):204–218
Roxy MK, Ghosh S, Pathak A, Athulya R, Mujumdar M, Murtugudde R, Terray P, Rajeevan M (2017) A threefold rise in widespread extreme rain events over central India. Nat Commun 8(1):708
Sandeep S, Ajayamohan RS, Boos WR, Sabin TP, Praveen V (2018) Decline and poleward shift in Indian summer monsoon synoptic activity in a warming climate. Proc Natl Acad Sci (USA) 115(11):2681–2686
Sharmila S, Joseph S, Sahai AK, Abhilash S, Chattopadhyay R (2015) Future projection of indian summer monsoon variability under climate change scenario: an assessment from CMIP5 climate models. Glob Planet Change 124:62–78
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Wang W, Powers JG (2008) A description of the Advanced Research WRF version 3. NCAR Technical note -475+str
Solomon S, Qin D, Manning M, Averyt K, Marquis M (2007) Climate change 2007-the physical science basis: working group I contribution to the fourth assessment report of the IPCC, vol 4. Cambridge University Press, Cambridge
Sørland SL, Sorteberg A, Liu C, Rasmussen R (2016) Precipitation response of monsoon low-pressure systems to an idealized uniform temperature increase. J Geophys Res Atmos 121(11):6258–6272
Srinivas C, Hariprasad D, Rao DVB, Anjaneyulu Y, Baskaran R, Venkatraman B (2013) Simulation of the Indian summer monsoon regional climate using advanced research WRF model. Int J Climatol 33(5):1195–1210
Sudheer K, Bhallamudi SM, Narasimhan B, Thomas J, Bindhu V, Vema V, Kurian C (2019) Role of dams on the floods of august 2018 in Periyar River Basin, kerala. Curr Sci (00113891) 116(5)
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteor Soc 93(4):485–498
Tewari M, Chen F, Wang W, Dudhia J, LeMone MA, Mitchell K, Ek M, Gayno G, Wegiel J, Cuenca RH (2004) Implementation and verification of the unified NOAH land surface model in the WRF model. In: 20th conference on weather analysis and forecasting/16th conference on numerical weather prediction, American Meteorological Society Seattle, WA, vol 1115
Turner AG, Annamalai H (2012) Climate change and the South Asian summer monsoon. Nat Clim Change 2(8):587
Van Vuuren DP, Edmonds J, Kainuma M, Riahi K, Thomson A, Hibbard K, Hurtt GC, Kram T, Krey V, Lamarque JF et al (2011) The representative concentration pathways: an overview. Clim Change 109(1–2):5
Yang ZL, Niu GY, Mitchell KE, Chen F, Ek MB, Barlage M, Longuevergne L, Manning K, Niyogi D, Tewari M, et al (2011) The community Noah land surface model with multiparameterization options (Noah-MP): 2. Evaluation over global river basins. J Geophys Res Atmos 116(D12)
Acknowledgements
KMRH is funded through the Weather and Climate Science for Service Partnership (WCSSP) India, a collaborative initiative between the Met Office, supported by the UK Government’s Newton Fund, and the Indian Ministry of Earth Sciences (MoES). AM is funded by the INCOMPASS project (NERC Grant numbers NE/L01386X/1 and NE/P003117/1), a joint initiative between the UK-Natural Environment Research Council and the Indian Ministry of Earth Sciences.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hunt, K.M.R., Menon, A. The 2018 Kerala floods: a climate change perspective. Clim Dyn 54, 2433–2446 (2020). https://doi.org/10.1007/s00382-020-05123-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-020-05123-7