1 Introduction

The tropics are expanding at about 0.5\({^\circ }\) per decade in observations (Staten et al. 2018; Grise et al. 2019). The expansion is robust for many different tropical edge metrics, for example the zero crossing of the mass stream function (Solomon et al. 2016; Davis and Birner 2017). Despite the robust expansion of the tropics, there is no robust change in the subtropical jet position (Archer and Caldeira 2008; Davis and Rosenlof 2012; Fu and Lin 2011; Davis and Birner 2013). (A comprehensive introductory discussion can be found in Sect. 2 on tropical expansion, tropical edge metrics and methods used to locate the subtropical jet.) We propose five interpretations for why trends in the subtropical jet position may be smaller than trends in the Hadley cell

  1. 1.

    Current methods for identifying the subtropical jet are not accurate.

  2. 2.

    Natural variability in the subtropical jet is too large to identify trends.

  3. 3.

    The Hadley cell edge is not co-located with the subtropical jet core and can be displaced from one another.

  4. 4.

    The subtropical jet is not well defined in seasons when the Hadley cell trends are strongest.

  5. 5.

    Hadley cell trends are smaller than reported.

In this study we explore the first two interpretations. To test if current methods for locating the subtropical jet are accurate, we aim to develop a new method for identifying the location of the subtropical jet stream using the maximum gradient in potential temperature along the dynamical tropopause. We then use the tropopause gradient method to ask: Is there a poleward trend in the subtropical jet position in either hemisphere? We then test if natural variability in the subtropical jet is too large to reliably detect an expansion of 0.5\({^\circ }\) per decade. To the best of our knowledge no other study has used the peak gradient in potential temperature on the dynamic tropopause as a metric for locating the subtropical jet.

2 Locating the subtropical jet position and tropical expansion

The motivation for this study is to investigate why trends in the subtropical jet are smaller than other tropical edge metrics. We expand the introductory discussion on tropical expansion in Sect. 2.1 and on the current methods for locating the subtropical jet in Sect. 2.2. We then justify the value of a new approach in Sect. 2.3 and describe our motivation for using the tropopause break for locating the subtropical jet in Sect. 2.4.

2.1 Tropical expansion

The observed tropical edge has been shifting poleward since the beginning of satellite observational record (e.g., Davis and Rosenlof 2012). Over a decade ago, Seidel et al. (2008) first observed the poleward expansion of the tropics. Initial estimates suggested an alarming 2°–3\({^\circ }\) per decade (e.g., Seidel and Randel 2007; Hu and Fu 2007; Lucas et al. 2013 for a review). More recent studies estimate a trend of 0.2\({^\circ }\)–0.6\({^\circ }\) per decade (Staten et al. 2018; Grise et al. 2019). There are a number of factors that contribute to the reduction in the more recent trend estimates: a smaller subset of methods used to measure the tropical edge (Waugh et al. 2018; Adam et al. 2018), higher quality modern reanalysis (Long et al. 2017) and longer data records.

Expansion estimates are largest in summer and fall, and in the North Pacific and North Atlantic oceans (Lucas and Nguyen 2015; Grise et al. 2018; Manney and Hegglin 2018). Natural decadal variability is also very important to take into account when investigating trends. For example, the negative phase of the Pacific Decadal Variability (PDO) is correlated with a poleward expansion (Grassi et al. 2012; Mantsis et al. 2017). The length of the data record, hence the time window over which trends are calculated, is very important for understanding the role of natural decadal variability.

There are many different tropical edge metrics [for example see the review of Lucas et al. (2013) and a summary of trends in Fig. 4 of Davis and Rosenlof (2012)]. One of the most common measures of the tropical edge is the middle tropospheric zero crossing of the meridional mass over-turning stream function, however, this metric only captures zonal-mean changes in circulation. Other metrics can be described as upper- and lower-atmospheric metrics. Examples of lower-atmospheric metrics include the latitude of the eddy-driven jet and the latitude where precipitation balances evaporation. Examples of upper-atmospheric metrics include the latitude of the subtropical jet, the tropopause break, and the location where outgoing longwave radiation exceeds 250 W m\(^{-1}\). Some of the tropical edge metrics can be defined at every longitude and these can be used to explore the regional variability.

Trend estimates using the Hadley cell edge show statistically significant poleward trends in observations (Hu and Fu 2007; Johanson and Fu 2009) and similar values in CMIP5 models (Davis and Birner 2017). However, not all tropical edge metrics show significant trends and there is a disconnect between trends in the lower- and upper-atmospheric metrics. The Hadley cell edge is highly correlated with lower-atmospheric metrics, however, only weakly correlated with upper-atmospheric metrics. The Hadley cell edge is correlated with the eddy-driven jet but only very weakly correlated with either the subtropical jet position or tropopause break (Davis and Rosenlof 2012; Solomon et al. 2016; Davis and Birner 2017; Waugh et al. 2018). Interestingly, the subtropical jet strength is correlated with Hadley cell edge in CMIP5 models (Menzel et al. 2019). The weak correlations between the upper-atmospheric metrics and the Hadley cell edge suggest that the upper- and lower-atmospheric metrics measure different aspects of the tropical edge (Davis and Birner 2017) and that the suitability of upper-atmospheric methods needs to be considered (Waugh et al. 2018).

2.2 Current methods for locating the subtropical jet

The subtropical jet can be difficult to locate as it is not continuous, meanders meridionally and has large deviations in both speed and elevation (Archer and Caldeira 2008). This is further complicated by the existence of the eddy-driven jet (also referred to as the polar front jet or mid-latitude jet) and distinguishing the jets is difficult when they are near one-another [see the introduction of Manney et al. (2014) for a more thorough discussion].

Fig. 1
figure 1

Subtropical jet location method comparison between the DB method (Davis-Birner, black) and the latitude of the maximum zonal wind on 250 hPa (U Max, purple) for a representative subset of the data from 2012 to 2018 using monthly ERA-I data. The left panels are the subtropical jet position time series for the a NH and b SH. The right panels are two examples of large differences in the methods used to locate the subtropical jet zonal mean positions for the c NH in May 2018 and d SH in March 2017. These dates correspond to the vertical dashed lines with open circles in left panels. Color contours in the right panels are the zonal wind (ms\(^{-1}\)) on the 350 K surface

Full size image

The existence of the eddy-driven jet prevents the subtropical jet from being identified directly using only the maximum in the upper tropospheric zonal wind. This is highlighted in Fig. 1 which shows the latitude of the maximum 250 hPa u-wind (U Max method, purple line) and the Davis and Birner (2016) method (DB herein, black line, see Sect. 3.3 for the method description). The key difference in the two methods is that DB removes the surface wind to isolate the subtropical jet from the eddy driven jet. In both hemispheres, the U Max method identifies the subtropical jet further poleward than the DB method. In the Northern Hemisphere (NH), the variability of the subtropical jet is similar (up to \(\pm \;10{^\circ }\) about the mean) for the two methods. In the Southern Hemisphere (SH), the U Max method has a similar range of variability to the NH. The DB method has a lot less variability in the SH compared to the NH (\(\pm \;5{^\circ }\) about the SH mean position but with two instances of a much more poleward subtropical jet). The differences in the two methods are highlighted using two examples from the time series in Fig. 1c, d. For the NH case of May 2018, there are two distinct jets seen over the North Pacific and North Atlantic Oceans in the zonal wind contours. In the SH case of March 2017, the dominant feature is the eddy-driven jet. In both examples, the DB method (black) is located closer to the subtropical jet core than the U Max method (purple) as the U Max method identified the eddy-driven jet. This highlights that using only the maximum in an upper level wind method should be avoided.

Locating the subtropical jet is further complicated by its seasonal variability. In winter, the zonal-mean climatological position of the SH subtropical and eddy driven jets are approximately \(30{^\circ }\) S and 55–60\({^\circ }\) S (Gallego et al. 2005), respectively. However, there is a lot of zonal and meridional variability in the mean positions [see Fig. 2 of Lee and Kim (2003), Figs. 2 and 6 of Manney et al. (2014) and Figs. 1–4 of Manney and Hegglin (2018)]. The winter jet streams are often easier to uniquely locate than the summer jet streams, as the circulation is stronger and the jet cores are further separated in latitude. We also note that identifying the winter jet streams are dependent on longitude and some regions are more challenging. For example, the subtropical jet and eddy-driven jets are difficult to uniquely identify over the western Pacific and North America (Manney et al. 2014). In summer, the jets may favor a merged jet structure (more commonly seen in monthly data) where the subtropical jet can not be distinguished from the eddy-driven jet, for example see Fig. 1 of Gallego et al. (2005). This makes the summer subtropical jet ambiguous and difficult to locate (Koch et al. 2006). The same is true in the NH but with additional variability due to the large stationary Rossby wave activity associated with orography and land-sea contrast.

Table 1 Subtropical jet methods
Full size table

Because the subtropical jet is difficult to locate, developing algorithms to accurately capture its behavior is challenging. In Table 1 a number of methods used to locate the subtropical jet are shown. These methods generally isolate a Eulerian surface of maximum upper-level wind and find the wind peak on that surface. However, the implementation of the methods are quite different in terms of their data frequencies (6-hourly, daily or monthly), thresholds (latitudinal bands, vertical levels, minimum wind speeds), wind surfaces (i.e., isobaric, column averaged etc) and approach to locating the subtropical jet. Choosing the data sampling is an important consideration. Monthly data can be inaccurate for zonal-mean zonal-wind metrics that may only find a single wind peak (hence the subtropical jet and eddy driven jets can not be uniquely defined). A single zonal mean peak can arise when the jets are merged, when the jets broadly meander (i.e., large fluctuations in the jet’s latitude) or from weak easterlies that are advected poleward from the tropics (canceling out the westerlies in the zonal mean). Daily and sub-daily data have the advantage of including synoptic variability, however, there are practical challenges due to the size of the data and its availability (in time and vertical resolution).

Most methods for identifying the subtropical jet aim to identify the peak in the zonal-wind on a given surface. This is an intuitive approach as the subtropical jet is a band of strong wind in the upper troposphere. However, there are some limitations with these methods that are described in more detail in Sect. 2.3. The subtropical jet position can also be defined as the latitude of zero eddy momentum flux divergence (Kang and Polvani 2011) or indirectly measured by locating the Hadley cell edge (Maher and Sherwood 2014), though recent evidence in Waugh et al. (2018) indicates that the Hadley cell edge and subtropical jet are poorly correlated when the Davis and Birner (2016) method is used.

2.3 Justification for a new subtropical jet method

There are already many different methods available for locating the subtropical jet (see Table 1). Why do we need another? In the Sect. 1 we listed five interpretations for why the subtropical jet trends might be less than other tropical edge trends. The first interpretation is that current methods are not accurately locating the subtropical jet. To test this idea, we need a very different approach. Current methods for locating the subtropical jet are diagnostic algorithms that search for the location of the maximum wind within a set of constraints. Our first key reason for needing a new method for locating the subtropical jet is to develop a dynamic definition (one that does not search for a wind surface but rather searches for the signature of the subtropical jet on the PV contours) hence providing a contrast to existing methods which will also have different biases compared to existing methods.

Two existing methods that could be described as dynamic definitions for the subtropical jet are the Kang and Polvani (2011) method (herein KP) and Manney and Hegglin (2018) method. The KP method identifies the latitude of upper level (200 hPa) zero eddy momentum flux divergence. While not their original purpose, the KP method can be adapted to generate a subtropical jet time series (see Sect. 3.3). The hybrid dynamic-diagnostic method of Manney and Hegglin (2018) uses the diagnostic Jet and Tropopause Products for Analysis and Characterization (JETPAC) method of Manney et al. (2014) to identify possible jet locations but instead of using a critical latitude to identify the subtropical jet they use a minimum threshold and altitude drop of the thermal tropopause height across the jet.

The second key reason why a new method is needed is that current methods are not without error. There are a few areas that we can improve on (other recent methods also aim to address these problems):

  1. 1.

    taking into account the longitudinal variability,

  2. 2.

    making code publicly available (recreating methods from the literature can be very time consuming and explaining differences when comparing the results becomes guess work),

  3. 3.

    reporting the accuracy of the methods (e.g., how often is the subtropical jet uniquely identified from the eddy-driven jet?),

  4. 4.

    avoiding interpolating data to higher resolutions, and

  5. 5.

    minimizing the number of thresholds.

This last point on thresholds is an important one. Thresholds are used to constrain the algorithm search domain, to help reduce false identifications and overall increase the accuracy of the algorithm. Example thresholds include a pre-defined latitudinal range, minimum wind speed, and minimum jet separation. The sensitivity of the subtropical jet position to these threshold choices is often not described in the literature. Thresholds should be avoided, where possible, as the jet position is sensitive to arbitrary threshold choices (Davis and Rosenlof 2012), and the threshold values may not apply across data sets. Nevertheless, some thresholds may be necessary to identify the subtropical jet and are somewhat physically based, such as wind speed thresholds that reflect the jets definition as a peak in the wind field compared to the background flow.

In summary, there are two key reasons why there is utility in continuing to develop new method: (i) to develop methods with different approaches or perspectives (i.e., a dynamical definition instead of existing diagnostic definitions), and (ii) because current methods have a few areas that can be improved on.

2.4 Motivation for using the tropopause break as a subtropical jet metric

We propose an new approach for locating the subtropical jet based on the maximum gradient in potential temperature along the dynamic tropopause height which changes sharply at the intersection of the circulation cells in the vicinity of subtropical jet core, sometimes referred to as the “tropopause break”. Davis and Rosenlof (2012) used the latitude of the peak meridional gradient of the thermal tropopause height to identify the tropical edge (see their Eq. 2), see also Solomon et al. (2016).

A key motivation for our method is to develop a robust identification of the subtropical jet position on any timescale by using the observation that the subtropical jet maximum is co-located with a maximum in PV gradient on isentropic surfaces. This also implies a region of strong gradient in potential temperature on the dynamic tropopause, defined as surface of constant PV. This is a useful property because the tropopause intersects the full range of isentropic surfaces where the jet might occur and allows for seasonal variation in the potential temperature range of those surfaces.

Koch et al. (2006) showed the subtropical jet core is located where the gradient of the 2 PVU (PV units) contour with height is steepest for the winter period 1979–1993 (see their Fig. 1), this is also seen for two isolated winter months in Fig. 1 of Davis and Rosenlof (2012) and Fig 1c of Methven and Berrisford (2015). In the modified Lagrangian mean framework of Methven and Berrisford (2015), the wind maximum of the subtropical jet must lie precisely at the same place as the maximum PV gradient (on each isentropic surface intersecting the tropopause), as a consequence of the PV inversion property. This structural connection is also found in synoptic observational cross-sections perpendicular to the jet stream (where the jet is relatively straight) for the same reason. However, other studies suggest the subtropical jet and tropopause break do not occur at the same latitude. For example, in Fig. 1 of Waugh et al. (2018) they depict the tropopause break and subtropical jet at different latitudes but highly correlated [0.6 in both hemispheres, though we also note that Davis and Birner (2017) have lower correlations of 0.3 in both hemispheres].

Using MERRA-2 reanalysis data, Manney et al. (2014) showed that the seasonal mean values of PV at the SH subtropical jet core are 2.0–2.1 PVU in all seasons, except summer which is 2.3 PVU, and similar in the NH with 1.6–1.7 in all seasons, except summer which is 2.0 PVU, (see their Table 1). Manney et al. (2014) also show that the eddy-driven jet has larger values of PV, ranging from 2.0-2.6 PVU in the SH and 2.1–3.2 PVU in the NH. The vertical gradient in PV is steepest near the subtropical jet core when the large-scale circulation is strongest (Kunz et al. 2011, see their Fig. 6). Identifying the location of the steepest gradient becomes more subjective when the circulation is weak, making the summer jet more difficult to locate. Other methods also struggle to locate the subtropical jet in summer, especially zonal-mean wind maximum methods that use monthly data. Methods which use daily data and include longitudinal variability may be more skillful in locating the subtropical jet, thought to the best of our knowledge this has not been directly tested.

Table 2 Resolution, time period and references for the reanalysis products used in this study
Full size table

3 Data and methods

We describe the reanalysis products used in this study in Sect. 3.1, introduce the algorithm for the tropopause gradient method in Sect. 3.2, describe two subtropical jet methods we will compare our new method to in Sect. 3.3, and describe the statistical methods used to test the significance of our results in Sect. 3.4.

3.1 Data

We use four reanalysis products in this study. The first product is Climate Forecast System Reanalysis (CFSR/CFSv2) from the National Center for Environmental Prediction. The second product is ERA-Interim (ERA-I) from the European Centre for Medium-Range Weather Forecasts. The third product is the Japanese 55 year Reanalysis product (JRA-55) from the Japan Meteorological Agency. The fourth product is the second generation of the Modern-Era Retrospective Analysis for Research and Applications (MERRA-2) assimilated fields from the National Aeronautics and Space Administration. The horizontal and vertical resolution, time period and references for each product can be found in Table 2.

For CFSR/CFSv2, ERA-I, and JRA-55, data were downloaded on isentropic levels, while MERRA-2 assimilated data was downloaded on isobaric levels and interpolated to isentropic levels. The vertical resolution of the data are shown in Fig. S1. For data storage reasons, horizontal resolutions of approximately \(1.25{^\circ }\times 1.25{^\circ }\) were used, except for CFSR/CFSv2 that was downloaded at \(0.5{^\circ }\times 0.5{^\circ }\).

The results were found to be less sensitive to different horizontal and vertical resolutions than to the inter-reanalysis differences. For example, the seasonal mean change in the subtropical jet position using ERA-I monthly data down-sampled to 2.5\({^\circ }\) is less than \(0.4{^\circ }\), and the two time series computed at 1.25\({^\circ }\) and 2.5\({^\circ }\) are highly correlated (\(r\ge 0.99\)). Similarly using JRA-55 monthly data down-sampled to half the number of vertical levels, the difference in the subtropical jet latitude annual mean is \(0.4{^\circ }\) in the Northern Hemisphere, and no change in the Southern Hemisphere. In both hemispheres, the subtropical jet latitude using full and reduced vertical levels is highly correlated (\(r\ge 0.97\)).

3.2 The tropopause gradient method

The tropopause gradient method is centered on the idea that the subtropical jet core occurs where the gradient in potential temperature along the dynamic tropopause is steepest. The dynamic tropopause is defined as a surface of constant Ertel Potential Vorticity (PV) and a threshold of 2 PVU is commonly used (Davis and Emanuel 1991), see Sect. 2.4 for a discussion on why 2 PVU is suitable. (Throughout this paper we use 2 PVU to describe the dynamic tropopause in both hemispheres, this is only for convenience and note that the dynamic tropopause is − 2 PVU in the SH). The isentropic-coordinate hydrostatic approximation to Ertel PV is calculated is given by Eq. 1:

$$\begin{aligned} PV = -g\left( \zeta _{\theta }+f\right) \left( \frac{\partial \theta }{\partial p}\right) \end{aligned}$$
(1)

where f is the planetary vorticity (\(f=2\varOmega \sin {\phi }\)) and the isentropic relative vorticity (\(\zeta _{\theta }\)) is defined as

$$\begin{aligned}\zeta_{\theta}={\left(\frac{1}{a \cos\phi}\frac{\partial v}{\partial \lambda}- \frac{1}{a}\frac{\partial u}{\partial \phi}\right)}_{\theta}\end{aligned}$$
(2)

where \(\phi \) and \(\lambda \) are latitude and longitude respectively, and all other notation as standard. The tropopause gradient method requires PV and zonal wind (needed for the jet intensity) fields. If PV is not available (either as a model output or reanalysis field), then air temperature and meridional-wind are also required to calculated PV using Eq. 1, each of which are standard outputs. However, this does require sufficient vertical resolution [approximately 400 m in the vertical per 100 km of horizontal resolution depending on the latitude (Birner 2006)] to accurately capture the static stability term. All four reanalyses products used in this study provide potential vorticity (which is the most height dependent component of the method) and most provide fields on isentropic levels (only MERRA-2 did not). As such, the vertical resolution is sufficient to determine the subtropical jet location. If computing potential vorticity directly, care needs to be taken to ensure sufficient vertical levels are provided. If the tropopause gradient method were applied to CMIP5 data, then the vertical resolution of monthly data is sufficient, however, daily data is not (as there are only limited levels available). For future intercomparisons, including CMIP6, data availability is likely to be improved, thus alleviating this concern.

Fig. 2
figure 2

An example of the tropopause gradient method for June 2013 using monthly ERA-I data for a single longitude, 180\({^\circ }\), for the a SH and b NH. The left y-axis is potential temperature (\(\theta \)) and right y-axis (green) its derivative with respect to latitude (\(\partial \theta / \partial \phi \)). The dynamic tropopause potential temperature (\(\theta _2\)) is shown with black “.” marker, the solid blue line is the polynomial fit to \(\theta _2\), the dashed green line is the meridional gradient of the potential temperature of the dynamical tropopause, and the blue solid circle is the identified subtropical jet position. Contours are the isentropic zonal-wind for context only (not part of the algorithm). The zonal wind on the 350 K isentropic surface is shown in c with the identified subtropical jet for each longitude in black. In d the black line is the zonal mean of the subtropical jet latitudes (\(\phi _{NH}=36.8{^\circ }\) N, \(\phi _{SH}=29.2{^\circ }\) S) and the orange line is the zonal mean zonal wind at 350K for context only (not part of the algorithm). The colour bar relates to plots (a–c)

Full size image

The tropopause gradient method for identifying the subtropical jet position is a three step process (see Fig. 2 for an illustration of the method).

  1. 1.

    Step one: identify a surface of constant 2 PVU.

    1. (i)

      If PV data is not supplied, compute PV using Eq. 1.

    2. (ii)

      Interpolate potential temperature to a constant 2 PVU surface—black dots on Fig. 2a.

  2. 2.

    Step two: numerically compute the meridional potential temperature gradient along the 2 PVU surface (\(\theta _{2}\)) using a Chebyshev polynomial of degree 6 between 10\({^\circ }\) and 65\({^\circ }\) in each hemisphere—blue line on Fig. 2a.

  3. 3.

    Step three: isolate the position of the subtropical jet.

    1. (i)

      At each longitude, differentiate \(\theta _2\) along the dynamic tropopause \((\frac{\partial \theta _{2}}{\partial \phi })\)—green line on Fig. 2a.

    2. (ii)

      Locate the relative maximum of the meridional gradient (NH) or relative minimum (SH) (i.e., turning points of the green line in Fig. 2a).

    3. (iii)

      If multiple turning points exist, the jet latitude is selected as the turning point with the largest shear between the 2 PVU contour and the near surface (850hPa, this is similar to DB who remove the surface wind in order to separate the subtropical from the eddy driven jet).

    4. (iv)

      Calculate the zonal mean subtropical jet position (optional).

    5. (v)

      At the subtropical jet latitude and height, identify the zonal wind speed for the subtropical jet intensity.

The purpose of the polynomial fit in step two is not for data interpolation but for accurate differentiation of \(\theta _{2}\), which is required to find the turning points in step three. A Chebyshev polynomial estimate is used here to differentiate the potential temperature on 2 PVU as it is a higher order method than centered finite differences, and can be computed using fast cosine transforms (Kopriva 2009).

The tropopause gradient method is conceptually similar to Davis and Rosenlof (2012), who use the peak meridional gradient in the thermal tropopause to locate the tropopause break that is then used as a tropical edge metric. We believe this is the first study to propose the location of the tropopause break as a method for locating the subtropical jet position.

3.3 Davis and Birner (2016) and Kang and Polvani (2011) methods

We will compare the time series from the tropopause gradient method to two different methods for locating the subtropical jet. The first method is DB that computes a surface of maximum zonal-mean zonal-wind, up to 50 hPa, for each latitude poleward of 10\({^\circ }\). The near-surface (850-hPa) zonal-mean zonal-wind is then subtracted from the surface of maximum wind. In implementing the DB method, we selected the more commonly used 400–100 hPa levels [suggested in Adam et al. (2018) and first implemented in Koch et al. (2006)], rather than all vertical levels up to 50 hPa. We tested the sensitivity of this choice and found it had very little impact. We use a 15\({^\circ }\) latitude limit rather than the 10\({^\circ }\) threshold suggested in DB in order to exclude several spurious low-latitude points.

The second method we will compare the tropopause gradient method to is the KP method that computes the horizontal eddy momentum flux divergence (requires daily data). The subtropical jet is then defined as the 200 hPa zero-crossing latitude in the subtropics. In KP the seasonal climatological zero-crossing latitude is easily located. However, multiple zero-crossing latitudes exist in daily data. To overcome this we adapted their method and imposed a maximum shear condition, consistent with the tropopause gradient method, to isolate the zero-crossing latitude in the vicinity of the subtropical jet (as such, this method is more accurately described as an adapted KP method). Monthly means of the daily subtropical jet latitudes are than compared to the tropopause gradient method in Fig. S4.

3.4 Statistical model

A simple statistical model is used to identify trends in the position of the subtropical jet. The jet position \(\phi _t\) is modeled as

$$\begin{aligned} \phi _t = \mu + \beta t + \sum _{m=1}^2 ( a_m \cos m \omega t + b_m \sin m \omega t ) + x_t \end{aligned}$$
(3)

where \(x_t \sim \mathrm {N} (\alpha x_{t-1}, \sigma ^2 )\) and \(\omega = 2\pi /n\) where 1 / n is the sampling frequency. The parameter \(\mu \) represents the mean jet position, \(\beta \) represents any linear trend in time (t), and \(a_1\), \(b_1\) and \(a_2\), \(b_2\) represent the annual and semi-annual cycles (twice yearly) in the jet position. In order to capture the day-to-day or month-to-month dependence in the jet position, the residual variation \(x_t\) is modeled as an autoregressive process with coefficient \(\alpha \) and variance \(\sigma ^2\). It is common practice to estimate the mean, trend and seasonal cycles without allowing for the time dependence. However, if the trend \(\beta \) is small and the time dependence \(\alpha \) is large, then the trend may be hidden if we do not model the dependence explicitly. Therefore, the parameters \(\mu \), \(\beta \), \(a_1\), \(b_1\), \(a_2\), \(b_2\), \(\alpha \) and \(\sigma ^2\) are estimated simultaneously by numerical maximization of the log-likelihood function (Wilks 2011, Chapter 4.6.1). Approximate confidence intervals for the trend \(\beta \) can be obtained by numerical evaluation of the Hessian matrix (second derivatives) of the resulting estimates (Wilks 2011, Chapter 4.6.4).

4 Validation

Having described the reanalysis products, the tropopause gradient method and the statistical model, we next validate the tropopause gradient method in Sect. 4.1 and compare it with two alternative methods for locating the subtropical jet in Sect. 4.2.

4.1 Validating the tropopause gradient method

The method is illustrated in Fig. 2 using ERA-I monthly data for the austral winter month of June 2013, see also Fig. S2 for the boreal winter case in January 2013. In Fig. 2a, b, the main algorithm steps (see Sect. 3.2) are shown for a single longitude (180\({^\circ }\)): defining potential temperature along the dynamical tropopause (\(\theta _2\), black dots), its polynomial fit (blue line), and the first derivative of the fit (green line).

The zonal wind in colored contours is shown for context (not part of the method) and shows two distinct weak peaks in the winter SH (Fig. 2a, one for each jet stream). The longitudinal variability in the subtropical jets position can be seen in the 350 K isentropic surface of zonal wind in Fig. 2c. The zonal-mean wind (orange line) and the mean latitude of the subtropical jet (black line) are shown in Fig. 2d.

The mean latitude and zonal structure of the SH subtropical jet is well captured by the tropopause gradient method. The zonal mean subtropical jet position is located at 29.2\({^\circ }\) S, sitting on the zonal-mean zonal-wind peak (blue dot in Fig. 2a and black line in Fig. 2d). In Fig. 2a the SH polar night jet is also visible at 55\({^\circ }\) S above 380 K. For climatological jet stream positions see Gallego et al. (2005) and Manney et al. (2014). In the boreal summer, the zonal wind is weaker and the structure of the jets are not as clear, see Fig. 2b, c. Over the North Pacific and North Atlantic oceans there are two unique jets, however, over all the major land masses in the NH the subtropical and eddy-driven jets are merged. In this example, the tropopause gradient method identifies the subtropical jet at 36.8\({^\circ }\) N. This example highlights that care needs to be taken in interpreting the summer season jet positions in which the two jets may be co-located rather than uniquely defined. We also note, that the boreal NH jets can also be difficult to distinguish in different regions such as the West Pacific and North America [Fig. 2 of Lee and Kim (2003)].

4.2 Comparison with other methods

As discussed in the Sect. 2.2, multiple methods exist for finding the location of the subtropical jet. Our goal in Sect. 3.2 was to describe the tropopause gradient method and in Sect. 4.1 demonstrate the success of the new method and its limitations. In this section, our goal is to compare the tropopause gradient method to the DB method, a commonly used subtropical metric, and to observe any similarities with the KP method, another dynamical method for locating the subtropical jet, thought not used directly as a metric in Kang and Polvani (2011). See Sect. 3.3 for the description of both methods.

Fig. 3
figure 3

Time series of the subtropical jet position using the DB method (blue) and the tropopause gradient method (orange) for monthly ERA-I from 1979–2018 for the NH (top) and SH (bottom)

Full size image

The time series of the DB method (blue) and the tropopause gradient method (orange) using monthly ERA-I data are shown in Fig. 3. The tropopause gradient and DB methods are highly correlated with \(r>0.87\) in the NH and \(r>0.68\) in the SH, using ERA-I monthly data. In the NH, both methods have very similar means (Davis-Birner: 33.7\({^\circ }\), Tropopause Gradient: 33.3\({^\circ }\)) but the DB method has more variability than the tropopause gradient method (1\(\sigma \) of 6.5\({^\circ }\) and 5.6\({^\circ }\), respectively). There are 10 instances where the latitude using the tropopause gradient method is more than \(10{^\circ }\) further poleward than the DB method (see Fig. S3). Despite these differences, the DB and tropopause gradient methods are quite similar. In the SH, the time series have larger differences. The DB method is located further equatorward than the tropopause method (28.7\({^\circ }\) S and 32.3\({^\circ }\) S, respectively) and has less variability (1\(\sigma \) of 3.4\({^\circ }\) and 4.5\({^\circ }\), respectively). The tropopause gradient method has a larger seasonal cycle compared to the DB method (the seasonal cycle is present in the difference plot in Fig. S3). Unlike in the NH, the time series does not have consistently large differences in either the poleward or equatorward direction.

Fig. 4
figure 4

Distributions of the subtropical jet latitude using ERA-I monthly data for the method of the DB method (D-B, blue) and tropopause gradient method (STJPV, orange). Thick horizontal lines indicate mean position. Thin horizontal lines indicate 1 standard deviation above and below the mean (\(\pm \;1\sigma \))

Full size image

The seasonal distributions of the DB method and the tropopause gradient methods are shown in Fig. 4. In the NH, the DB method has a long tail of the distribution in summer, where the subtropical jet is more equatorward in the tail despite having a more poleward mean compared to the tropopause gradient method. The other seasons have similar means and distributions using the different methods. In the SH, the winter mean and distributions are similar, however, all other seasons the mean of the tropopause gradient method is more poleward compared to DB.

Next we compare the tropopause gradient method to the KP method, see Fig. S4. The two methods have similar means and distributions in winter and fall. The distributions are smaller in winter-fall compared to summer-spring. The primary differences in the methods are in the NH summer and spring, where the mean using the tropopause gradient is more equatorward compared to the KP method. In the SH, the summer and spring means and distributions are very similar. The tropopause gradient and KP methods are highly correlated with \(r>0.93\) in the NH and \(r>0.88\) in the SH, using ERA-I data.

In this section we have validated the tropopause gradient method, compared it to the established diagnostic method of Davis and Birner (2016) and then compared it to another existing dynamic definition of the subtropical jet using an adapted method from Kang and Polvani (2011). The tropopause gradient method captures the position of the subtropical jet and appears to isolate differences in the subtropical jet and eddy-driven jet. In the NH, the Davis and Birner (2016) and tropopause gradient methods are very similar. In the SH, there are differences in the two methods seasonality, variability, and mean. The two dynamic subtropical jet position methods (tropopause gradient and adapted KP) have similar time series distributions and means in each season. Having validated the method and compared with existing methods, we next explore the sensitivities of the tropopause gradient method to parameter choices, data frequency and different reanalysis products.

5 Sensitivity testing

To test the sensitivity of the tropopause gradient method to the algorithm’s free parameters we explore the parameter space in Sect. 5.1. We then test the sensitivity of the tropopause gradient to the data frequency and reanalysis products used in Sect. 5.2.

5.1 Sensitivity to parameters

The first free parameter of the tropopause gradient method is selecting the appropriate line of constant PV. We start with the 2 PVU surface as this is typically used for defining the dynamical tropopause height (Holton et al. 1995), its slope changes rapidly at the tropical edge (Koch et al. 2006), and the subtropical jet is close to 2 PVU in both hemispheres and in each season (Manney et al. 2014). We explore the parameter space around the 2 PVU contour to test the sensitivity to the surface selected, see Fig. S5 and the first column of Table S1. There is a sensitivity in the subtropical jet time series to the PV surface selected, though this is physically consistent. The seasonal mean subtropical jet position is generally located more poleward for larger PV values. This is expected as the absolute value of PV generally increases with increasing height and poleward latitude, thus isentropic potential vorticity surfaces are nearly parallel in the \(\phi \)–\(\theta \) space. In most seasons, the sensitivity is small, however, it is statistically significant. While there is a sensitivity to the PV surface selected, we choose the 2 PVU surface for consistency with other studies.

The second free parameter is the degree of fit for the Chebyshev polynomial. The polynomial fit of the 2 PVU contour of potential temperature is a possible source of error. However, it is required to compute the derivative of the slope, which is more accurate than using centered finite differences. There is a small sensitivity in the subtropical jet position to the degree of interpolation, see Fig. S6 and the second column of Table S1. The sensitivities are small and only statistically significant in austral summer and spring. Above degree 6 of the Chebyshev polynomial, there is very little sensitivity to degree fit, for this reason we selected 6 as the default degree of interpolation.

The final two free parameters are the minimum and maximum latitudes between which the polynomial fit is performed. The minimum latitude is required as the potential temperature on the 2 PVU surface approaches infinity at the equator and the polynomial fit of potential temperature on the 2 PVU surface is more accurate when the equatorial latitudes are excluded from the fit. A maximum latitude is needed to constrain the longitudinal variability of the subtropical jet position as the dynamical tropopause slope becomes small towards the pole, thus small deviations can lead to a poor polynomial fit. This removes unrealistically poleward positions, which are rare but impact the statistics. The sensitivity of the subtropical jet position to the minimum and maximum latitudes are shown in Fig. S7–S8 and Table S1. There is a small sensitivity to the minimum latitude. A minimum latitude of 10\({^\circ }\) is selected (also used in DB, see Sect. 3.3) as it improves the polynomial fit without encroaching on possible subtropical jet latitudes. The sensitivity to the maximum latitude is small. The maximum latitude threshold has little impact on the mean subtropical jet position but its standard deviation is much improved, see Fig. S9. A maximum latitude of 65\({^\circ }\) is selected as it the largest latitude possible while still having a realistic annual cycle in the standard deviation.

In general the tropopause gradient method is not very sensitive to the free parameters selected. The latitude of the subtropical jet does depend on the PV surface selected, however, this is also true for the definition of the dynamic tropopause. As such, the PV level selected is not a sensitivity per-say but rather a latitudinal offset in the reported subtropical jet position. Having validated the method in Sect. 4 and justified the parameter settings in Sect. 5.1, we herein use the default setting for the tropopause gradient method: a 6th degree polynomial fit of a surface of constant 2 PVU constrained between 10\({^\circ }\)–65\({^\circ }\).

5.2 Sensitivity to data sampling and reanalysis products

The sensitivity of the subtropical jet position to the frequency of data sampling and reanalysis product are shown in the violin plots for the NH in Fig. 5 and SH in Fig. 6 using daily (lighter colours) and monthly (darker colours) data. The horizontal bold lines on the violin plots show the mean and 1 standard deviation above and below the mean (\(\pm \;1\sigma \)). Compared to monthly data, the daily subtropical jet mean positions are located further poleward, see also Table S3–S7 for mean latitudes. This suggests that the synoptic variability in daily data, which is averaged out in the monthly mean, impacts the mean position of the subtropical jet. This is not surprising given that the jet streams have synoptic variability. However, it is interesting to note that the climatological means differ when monthly and daily data are used by 1.7\({^\circ }\) to 5.5\({^\circ }\) (depending on the reanalysis products), and that the means using monthly data are consistently more poleward compared to using daily data.

Fig. 5
figure 5

Distributions of the Northern Hemisphere subtropical jet latitude for all reanalysis products used. For each product, the daily data is lighter and plotted to the left compared to the monthly data. Thick horizontal lines indicate mean position. Thin horizontal lines indicate 1 standard deviation above and below the mean (\(\pm \;1\sigma \)). See Table S3–S7 for annual and seasonal mean subtropical jet latitudes

Full size image
Fig. 6
figure 6

As in Fig. 5 but for the Southern Hemisphere. See Table S3–S7 for annual and seasonal mean subtropical jet latitudes

Full size image

The sensitivity of the subtropical jet position to the reanalysis product can also been seen in Figs. 5 and 6 for ERA-I (orange), MERRA-2 (green), JRA-55 (blue) and CFSR/CFSv2 (maroon). All four reanalysis products have similar distributions and mean positions consistent with Manney and Hegglin (2018) (see their Fig. 5), although we do note that in each season there are some differences in their distributions. This suggests that while the reanalysis products are similar there are small differences in the time series which may be important for assessing trends.

In Sects. 5.1 and 5.2 the tropopause gradient method was stringently tested for sensitivities to the free parameters, data sampling and different data sources. The tropopause gradient method is found to be sensitive to the data frequency and reanalysis product used. As a result, the subtropical mean position and trends are considered in Sect. 6 for each reanalysis product, and for both daily and monthly data.

6 Results

In this section we apply the tropopause gradient method to four different reanalysis products to identify the subtropical jet zonal mean position in Sect. 6.1 and its trends in Sect. 6.2. We explore the robustness of the trends in Sect. 6.3 and identify if natural variability in the subtropical jet can account for it’s small trends in Sect. 6.4.

6.1 Mean position of the subtropical jet.

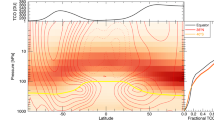
Monthly mean variability in the subtropical jet position is shown in the bottom panel of Fig. 7 for monthly ERA-I data, see also Fig. S10 for daily ERA-I data. In both hemispheres, the most poleward extent of the subtropical jet occurs in summer and fall, as expected. The subtropical jet position is relatively constant through winter and spring in the SH with a more broadly peaked equatorward position. The relationship between the position, height (in \(\theta \)) and intensity of the subtropical jet are shown in the top panel of Fig. 7. Two linear gradients are seen in both hemispheres that relate a more equatorward subtropical jet with a higher altitude, and the steeper of the two slopes occurs for more equatorward position (consistent with winter conditions).

Fig. 7
figure 7

Subtropical jet relationship between the height (theta), latitude and intensity for the SH (top left) and NH (top right). The larger the circle markers the more intense the jet strength. Bottom is the hemispheric monthly mean position with 1 and 2 sigma range for the NH (blue, from 20–50\({^\circ }\) N) and SH (purple, from 20–50\({^\circ }\) S). Plotted using ERA-I monthly data (see also Table S3) for climatological and seasonal mean subtropical jet latitudes..

Full size image
Fig. 8
figure 8

Climatological mean subtropical jet position (with confidence intervals around the mean value) for CFSR/CFSv2 (maroon), ERA-I (orange), JRA-55 (blue), and MERRA-2 (green) for the a NH and b SH. The subtropical jet positions are calculated using monthly and daily data on the native reanalysis grid. See Tables S3–S8 for climatological and seasonal mean subtropical jet latitudes. Confidence intervals are calculated using the statistical model described in Sect. 3.4

Full size image

In Fig. 8 the climatological zonal-mean subtropical jet positions in the NH and SH are shown for each reanalysis product, and for monthly and daily data. The confidence intervals, calculated using the statistical model described in Sect. 3.4, are smaller for the daily data as the sample size is larger. In the NH, CFSR/CFSv2 and ERA-I have very similar annual mean subtropical jet positions using monthly data (33.4\({^\circ }\) and 33.2\({^\circ }\), respectively). JRA-55 and MERRA-2 are also very similar (31.3\({^\circ }\) and 31.4\({^\circ }\), respectively), but occur 2\({^\circ }\) more equatorward than CFSR/CFSv2 and ERA-I. The climatological zonal-mean subtropical jet positions using daily data are similar for three of the reanalysis products (36.5\({^\circ }\)–37.4\({^\circ }\)) and MERRA-2 is 4.0\({^\circ }\) more equatorward (31.4\({^\circ }\)). The SH mean positions using daily and monthly data are very similar to the NH, the only major difference is that the SH means are located a little more equatorward (see Table S2–S9). In both hemispheres, the data frequency has a bigger impact on the mean subtropical jet position than the reanalysis product, except for MERRA-2.

6.2 Trends in the subtropical jet position

The decadal trends in the subtropical jet position are shown in Fig. 9. The trends generated from monthly data have larger confidence intervals (confidence intervals are calculated using the statistical model described in Sect. 3.4). In the NH, only one out of the four reanalysis products has a significant trend when monthly data are used (CFSR/CFSv2 has a 0.31\({^\circ }\) equatorward trend per decade). When daily data are used, all four reanalysis products have statistically significant trends, however, three reanalysis products show poleward trends (ranging from 0.06\({^\circ }\) to 0.10\({^\circ }\)) and CFSR/CFSv2 has an equatorward trend (0.08\({^\circ }\)). Similarly in the SH, two reanalysis products have significant equatorward trends when monthly data are used (ERA-I is 0.37\({^\circ }\) and CFSR/CFSv2 is 0.70\({^\circ }\)) and two without significant trends (JRA-55, MERRA-2). When daily data are used, two products have no significant trends in the SH (JRA-55, MERRA-2), an equatorward trend in CFSR/CFSv2 (0.25\({^\circ }\)) and poleward trend in JRA-55 (0.10\({^\circ }\)).

Fig. 9
figure 9

Decadal trends for the a Northern and b Southern Hemispheres for CFSR/CFSv2 (maroon), ERA-I (orange), JRA-55 (blue), and MERRA-2 (green) using monthly and daily data. Filled circles are significant, for the 95% confidence interval, and empty circles are not significant. Positive latitudes in the NH are for poleward shifted trends and negative values in the SH for poleward shifted trends. See Table S10 for decadal trends in the subtropical jet latitudes. Confidence intervals are calculated using the statistical model described in Sect. 3.4

Full size image

There are large differences in the subtropical jet trends across the reanalysis products: (i) CFSR/CFSv2 has equatorward trends in both hemispheres and data frequencies, (ii) MERRA-2 has no significant trends except a weak NH poleward trend when daily data is used, (iii) JRA-55 has poleward trends in both hemispheres but only with daily data, and (iv) ERA-I has poleward trends in the NH using daily data and an equatorward trend in the SH using monthly data.

As such, there is no robust trend in the subtropical jet position in either hemisphere. This is consistent with Manney and Hegglin (2018), see their Figs. 5 and 9, they also find no robust trend in seasonal trends.

6.3 Attributing differences in the trends

To explore the subtropical jet latitude trends in more detail, we consider the linear decadal trends in the zonal-mean zonal-wind, PV, and temperature (see Figs. 10, 11). In all four reanalysis products, there is a strengthening in the SH zonal wind (colored contours) at the climatological maximum wind (black contours) near the subtropical jet (‘x’ marker) and a weakening in the NH. The trends in the zonal-wind are much stronger in CFSR/CFSv2 than the other products, consistent with larger trends shown in Fig. 9.

Fig. 10
figure 10

Coloured contours are linear decadal trends in zonal mean zonal wind (top) and PV (bottom) for each reanalysis dataset using monthly data. Trends are computed for the common period from 1980–2016 for resolutions as in Table 2. Black contours are the climatological mean. The climatological mean subtropical jet position it shown as an ‘x’ marker. Positive trends in the zonal wind indicate strengthening. A poleward shifted subtropical jet would have weakening on the equatorward flank and a strengthening on the poleward flank (in both NH and SH). Positive trends in PV in the NH indicate an equatorward shifted line of constant PV. In the SH a positive PV trend corresponds to poleward shifting line of constant PV. Trends are computed using standard linear regression

Full size image
Fig. 11
figure 11

As in Fig. 10 but for temperature. Positive trends indicate warming

Full size image

The mid-tropospheric PV in the NH mid-latitudes is decreasing (see bottom panel of Fig. 10), which represents a poleward and upward shift of the dynamical tropopause. This is consistent with the NH subtropical jet trends using daily data. However, in the SH the trends in PV are less consistent between reanalyses products and have more variability vertically. This means that the dynamical tropopause does not simply shift poleward and upward but changes shape and that the steepest gradient of the dynamical tropopause may remain in the same place even though the 2 PVU contour has changed shape. This may explain the inconsistency across reanalysis products.

The PV field is dependent on the vertical derivative of temperature, see Eq. 1, and so we also consider the linear decadal temperature trends (see Fig. 11). Temperature trends are generally similar in three of the products (not CFSR/CFSv2). Lower level stratospheric cooling is seen below 100 hPa in CFSR/CFSv2 and to some extent in JRA-55. Both CFSR/CFSv2 and MERRA-2 have warming trends in the upper troposphere in the tropics and subtropics. The cooling of the stratosphere and warming of the troposphere in response to global warming raise the tropopause (Lorenz and DeWeaver 2007). The lifting of the tropopause with global warming will impact the line of constant 2 PVU. Reanalyses also have inherent inconsistency in their potential vorticity fields, due in part to data sources included at different times which impacts the trends (Lawrence et al. 2018).

To explore the differences in the reanalysis products further, we calculated the Root Mean Square Differences (RMSD) between the monthly tropical (25\({^\circ }\) N–25\({^\circ }\) S) area averaged zonal-mean zonal-wind at 350 K. The RMSD is computed between the ensemble mean (all four reanalysis products) and each individual reanalysis in Fig. 12. The RMSD for CFSR/CFSv2 is much larger than the other products and there is a discontinuity at 2010 (toward the end of CFSR and the start of CFSv2). When the RMSD is recomputed without CFSR/CFSv2, the reanalysis products are similar (not shown). This discontinuity raises doubts about the reliability of the trends in the zonal wind in CFSR/CFSv2 and, as such, we consider CFSR/CFSv2 to be unreliable to calculate trends in the subtropical jet position. See Long et al. (2017) for a discussion on using CFSR/CFSv2 for looking at trends.

Fig. 12
figure 12

The Root Mean Square Difference (RMSD) between the monthly 350 K zonal-wind data for each reanalysis product and the ensemble mean of all four products for the 2000–2018 period

Full size image

6.4 Natural variability in the subtropical jet position

Is the natural variability of the subtropical jet position too large to detect tropical expansion? Statistical tests such as those used in Sects. 6.1 and 6.2 aim to control the rate of false positives (5%), i.e., to be confident that the reported trends were not just a result of internal variability. However, if the signal-to-noise ratio is low, i.e., if the trend is small and the internal variability is large, then we may not be able to reliably detect a trend. In this section we use the statistical model in Eq. 3 to perform a power analysis in order to check whether we can reliably detect small trends (see supplementary material for details). For a given trend, the power is the probability that we correctly reject the null hypothesis of no trend at the \(5\%\) level (Wilks 2011, Chapter 5.1.5). Statistical power is directly related to the rate of false negatives, the higher the power, the lower the false negative rate. In other words, the power quantifies our ability to reliably detect a trend, given the natural variability in the subtropical jet and the amount of data available. A power greater than 0.8 is often used as a threshold value for a reliable test.

Fig. 13
figure 13

Monthly (purple) and daily (burgundy) power for the decadal trends shown on a log x-axis to stretch the differences in the two lines. Plotted lines are the inter-dataset and inter-hemisphere mean, with shading of one standard deviation from the mean, i.e., mean and variability across datasets and hemispheres. When the power exceeds 0.8 (black line) the trend can be reliably be detected

Full size image

In Fig. 13 we plot the statistical power against the logarithmic decadal trend in the subtropical jet position. The daily data have more power than the monthly data because of the increased sample size. The power is similar in both hemispheres and in each reanalysis product. The 0.8 power threshold is exceeded at approximately 0.09\({^\circ }\) per decade for daily data and 0.24\({^\circ }\) per decade for monthly data. This means that we would be able to detect trends in daily data of > 0.09\({^\circ }\) per decade and > 0.24\({^\circ }\) per decade in monthly data. This is well below the current tropical expansion estimates of \(0.5{^\circ }\) per decade, however, it is approximately the same as trends in the subtropical jet in Fig. 9. Excluding CFSR/CFSv2 because of concerns about the reliability of the trends (see Sect. 6.3), the only remaining trends that are significant are the poleward daily trend in both hemispheres for JRA-55 and the equatorward trend in the SH for the monthly ERA-I.

If similar trends were expected in the subtropical jet position as in other tropical edge metrics, the power analysis has shown these could be reliably be distinguished from natural variability. However, the trends in the subtropical jet tend to be much smaller than in other tropical edge metrics. Furthermore, the reanalysis product with the largest trends show problems with the 350 K zonal wind trends compared to the other reanalysis products. As such, we find there are no robust trends in the subtropical jet position in either hemisphere.

7 Conclusions

Trends in the subtropical jet have previously been shown to be smaller than the \(\approx 0.5{^\circ }\) per decade trends found in the Hadley cell edge. We offer five interpretations for why the trends in the subtropical jet are not consistent with other tropical edge measures: (i) current methods for detecting the subtropical jet do not sufficiently capture its position, (ii) natural variability in the subtropical jet time series is too large for it to be a reliable metric for detecting tropical expansion, (iii) the Hadley cell edge is decoupled from the subtropical jet position, (iv) the subtropical jet is not well defined in seasons when the strongest trends are found, and (v) tropical edge trends are smaller than current estimates.

In this study we tested the first two of these interpretations. We propose a new approach—the tropopause gradient method—for locating the subtropical jet using the peak gradient in potential temperature along the dynamic tropopause. Our first goal was to test if the tropopause break could be used to locate the subtropical jet. After extensive testing we have shown the approach is a valid metric of the subtropical jet position. The tropopause gradient method has a number of advantages: thoroughly tested the sensitivity of parameter choices, justified the four thresholds that are required (PV level, degree of fit, min \(\phi \), max \(\phi \)), and not restricted the data sampling. While not unique to this method, the tropopause gradient method also has the advantage that it can be applied to any data set, does not require interpolating the data to artificially increase the data resolution, is not a zonal-mean metric (but can be if desired) and is robust to temporal samping of the data. This gives the method flexibility in its application to different datasets, although it is important to consider the influence of temporal sampling and spatial resolution on the results. We have also made the code publicly available [see acknowledgments for the code location, the only other publicly available code we are aware of is TropD from Adam et al. (2018)]. One disadvantage of the method is that if PV is not provided then three 3-D data fields are required to compute PV, which is non-trivial for daily data.

Having validated the tropopause gradient method, our second goal was to test if trends in the subtropical jet are also smaller than the 0.5\({^\circ }\) per decade found in other tropical edge metrics. The key idea here is that if we apply a very different approach for locating the subtropical jet and also find small subtropical jet position trends, then we can disprove our first interpretation that current methods are not accurate for locating the jet. Using the tropopause gradient method, we find a weak but poleward trend in the subtropical jet in the NH when daily data are used, however, no significant trend is found when monthly data are used. Trends in the SH are not consistent between reanalysis products or the sampling frequency of the data. This is consistent with Manney and Hegglin (2018) who find no robust subtropical jet trends in reanalysis (they do find significant trends in some regions and seasons). We summarise our findings in Fig. 14 for three of the reanalysis products (excluding CFSR/CFSv2, see Sect. 6.3 for justification).

Fig. 14
figure 14

Summary schematic of subtropical jet trends using the tropopause gradient method for the NH (above the line) and SH (below the line). Trends are shown using monthly data (orange triangle) and daily data (blue circle). Solid markers are statistically significant and open markers are not. CFSR/CFSv2 was excluded from the plot, see Sect. 6.3 for justification

Full size image

The second interpretation we tested in this study for why subtropical jet trends are smaller, is that natural variability of the subtropical jet is too large to detect trends. We find that trends could reliably be detect if the subtropical jet had similar magnitude trends to the Hadley cell edge. This is an important new result that dismisses natural variability as a reason for why subtropical jet trends are smaller than other tropical edge metrics. As such, we have ruled out two possible reasons why the subtropical jet trends are small compared to other tropical edge metrics.

The remaining interpretations were not tested in this study. Our third interpretation is that the Hadley cell may be decoupled from the subtropical jet. Waugh et al. (2018) showed that the subtropical jet, measured using the DB method, is poorly correlated with the Hadley cell. Why the Hadley cell is decoupled from the subtropical jet is not know. This is an interesting idea and warrants further investigation. Davis and Birner (2017) hypothesised this disconnect between the Hadley cell edge and the subtropical jet, is due to the Hadley cell edge (and lower-atmospheric metrics) capturing changes in eddy-momentum fluxes while the upper-atmospheric winds capture changes in temperature gradients. Our fourth interpretation is that the seasonal and regional variability are critical for subtropical jet trend estimates which are overlooked in annual zonal mean trends. Specifically, the subtropical jet is not well defined when the subtropical jet trends are the strongest in summer-fall (Grise et al. 2018) and trends in the subtropical jet vary with longitude (Manney and Hegglin 2018). This may also account for why the eddy-driven jet is more correlated with the Hadley cell edge than the subtropical jet. The recovery of ozone in the SH (Polvani et al. 2011) is also another factor to consider when looking at seasonal variability. Our final interpretation is that other tropical edge metrics may not be as large as reported (or that there is no tropical explansion), however, there are many recent studies that support the current tropical expansion estimate of about 0.5\({^\circ }\) per decade. Further investigation is needed to identify why the subtropical jet is not shifting poleward with the Hadley circulation.