Abstract
The equilibrium climate sensitivity (ECS, in K) to \(\hbox {CO}_{2}\) doubling is a large source of uncertainty in projections of future anthropogenic climate change. Estimates of ECS made from non-equilibrium states or in response to radiative forcings other than \(\hbox {2}\times \hbox {CO}_{2}\) are called “effective climate sensitivity” (EffCS, in K). Taking a “perfect-model” approach, using coupled atmosphere–ocean general circulation model (AOGCM) experiments, we evaluate the accuracy with which \(\hbox {CO}_{2}\) EffCS can be estimated from climate change in the “historical” period (since about 1860). We find that (1) for statistical reasons, unforced variability makes the estimate of historical EffCS both uncertain and biased; it is overestimated by about 10% if the energy balance is applied to the entire historical period, 20% for 30-year periods, and larger factors for interannual variability, (2) systematic uncertainty in historical radiative forcing translates into an uncertainty of \({\pm }\,30\, {\rm to} \,45\%\) (standard deviation) in historical EffCS, (3) the response to the changing relative importance of the forcing agents, principally \(\hbox {CO}_{2}\) and volcanic aerosol, causes historical EffCS to vary over multidecadal timescales by a factor of two. In recent decades it reached its maximum in the AOGCM historical experiment (similar to the multimodel-mean \(\hbox {CO}_{2}\) EffCS of 3.6 K from idealised experiments), but its minimum in the real world (1.6 K for an observational estimate for 1985–2011, similar to the multimodel-mean value for volcanic forcing). The real-world variations mean that historical EffCS underestimates \(\hbox {CO}_{2}\) EffCS by 30% when considering the entire historical period. The difference for recent decades implies that either unforced variability or the response to volcanic forcing causes a much stronger regional pattern of sea surface temperature change in the real world than in AOGCMs. We speculate that this could be explained by a deficiency in simulated coupled atmosphere–ocean feedbacks which reinforce the pattern (resembling the Interdecadal Pacific Oscillation in some respects) that causes the low EffCS. We conclude that energy-balance estimates of \(\hbox {CO}_{2}\) EffCS are most accurate from periods unaffected by volcanic forcing. Atmosphere GCMs provided with observed sea surface temperature for the 1920s to the 1950s, which was such a period, give a range of about 2.0–4.5 K, agreeing with idealised \(\hbox {CO}_{2}\) AOGCM experiments; the consistency is a reason for confidence in this range as an estimate of \(\hbox {CO}_{2}\) EffCS. Unless another explosive volcanic eruption occurs, the first 30 years of the present century may give a more accurate energy-balance historical estimate of this quantity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The equilibrium climate sensitivity (ECS), defined as the steady-state global-mean surface air temperature change due to a doubling of the atmospheric carbon dioxide concentration, has been used for decades as a benchmark for the magnitude of climate change predicted by general circulation models (GCMs) in response to \(\hbox {CO}_{2}\) increase. Although an equilibrium climate is not expected in the future, ECS is relevant to future climate change because it correlates with global warming under realistic time-dependent scenarios for the future, which are dominated by \(\hbox {CO}_{2}\) increase (Gregory et al. 2015; Knutti et al. 2017; Grose et al. 2018). Over the past 25 years, GCMs have considerably improved in their simulation of present climate and historical climate change (Reichler and Kim 2008; Flato et al. 2013, where by “historical” we mean since the 19th century), but their ECS has had a persistently wide spread. The range of ECS simulated by GCMs was 1.9–5.2 K (Mitchell et al. 1990) when assessed in the first Assessment Report of the Intergovernmental Panel on Climate Change, and 2.1–4.7 K in the most recent (the Fifth Assessment Report, AR5, Flato et al. 2013).
This uncertainty has stimulated efforts to evaluate the ECS from observed historical climate change. One common approach is to apply the global-mean energy balance of the climate system
where F is the effective radiative forcing (ERF, Myhre et al. 2013, calculated from observed or estimated forcing agents), N is the global-mean net downward radiative flux at the top of the atmosphere (TOA) i.e. the heat flux into the climate system, T is the global-mean surface temperature change with respect to an unperturbed equilibrium in which \(N=F=0\), and \(R=F-N=\alpha T\) is the radiative response of the system to change in T. Note that F is positive downwards, while R is positive upwards.
Our \(\alpha\) in Eq. (1) is the positive-stable climate feedback parameter \(\left( \hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\right)\), with \(\alpha >0\) so that \(R=\alpha T\) resists F. This sign convention is convenient for our purposes. Some papers on this subject use a negative-stable climate feedback parameter \(\lambda\), numerically the same as ours but with \(+\,\lambda T\) instead of \(-\,\alpha T\) in Eq. (1). The advantage of that convention is that those processes which are positive feedbacks in a physical sense e.g. water vapour feedback, tending to amplify T, make positive contributions to the net \(\lambda\), which is negative. The reciprocal of \(\alpha (=-\,\lambda )\) is the climate sensitivity parameter \(\hbox {S}=1/\alpha\) (\(\hbox {K}\,\hbox {W}^{-1}\,\hbox {m}^{2}\)); the larger \(\alpha\), the smaller \(S\). This quantity is always given a positive sign, regardless of the sign convention for \(\alpha\).
The energy balance (Eq. 1) implies that \(\hbox {ECS}=F_{2\times }/\alpha\), where \(F_{2\times }\) is the ERF of \(\hbox {2}\times \hbox {CO}_{2}\), since \(N=0\) in the perturbed equilibrium. Thus a larger \(\alpha\) implies a smaller ECS. When \(\alpha\) is estimated from climate change which has not reached equilibrium (whether historical, future or under idealised scenarios), \(F_{2\times }/\alpha =\hbox {S}F_{2\times }\) is called the “effective climate sensitivity” (EffCS), which equals the ECS only if \(\alpha\) is a constant, as was formerly assumed (e.g. by Gregory et al. 2002, among many others). The usual method to estimate \(\alpha\) in CMIP5 is from Eq. (1), by regression of N against T for the abrupt4xCO2 experiment, in which \(\hbox {CO}_{2}\) is instantaneously quadrupled at \(t=0\) with respect to the control state (Gregory et al. 2004). Recent work shows that historical climate change tends to give a larger median estimate of \(\alpha\), and hence a smaller EffCS, than GCMs do under idealised high-\(\hbox {CO}_{2}\) scenarios, such as abrupt4xCO2, which have ERF of the magnitude typically projected for the 21st century (Forster 2016).
Since the unperturbed equilibrium is not a known historical state, in practice Eq. (1) is applied to the differences (denoted by Δ, in N, F and T) between two historical states (Gregory et al. 2002; Otto et al. 2013)
or by regression in the differential form
Both Eqs. (2) and (3) eliminate the unknown equilibrium state. If data is available throughout the period of interest, regression (Eq. 3) is a more efficient estimator of the slope than differences (Barnes and Barnes 2015). Either way, this is a modified version of the method of Gregory et al. (2004), following Forster and Gregory (2006) and Tett et al. (2007), for the situation where F is time-dependent. Many studies have estimated \(\alpha\) from real-world historical F, N and T using Eqs. (1), (2) or (3) in various ways (examples are cited in the review by Knutti et al. 2017).
ERF F is not an observable quantity, and has to be calculated using models of radiative transfer, calibrated formulae (e.g. supplementary material of Myhre et al. 2013) and atmosphere GCM (AGCM) experiments (Sect. 3.1; Hansen et al. 2005). Therefore historical F is a source of systematic uncertainty in estimating \(\alpha\), especially on account of anthropogenic tropospheric aerosol forcing (Gregory et al. 2002; Myhre et al. 2013; Forster 2016; Skeie et al. 2018).
Historical N is a source of statistical uncertainty in estimating \(\alpha\), due to the combination of two circumstances. First, internally generated i.e. unforced variations in the climate system add statistical “noise” to the externally forced signal in N. Second, the comparative shortness of the observational record of N limits the possibility of reducing the imprecision due to the noise. N can be evaluated reasonably precisely from satellite measurements of the global TOA Earth radiation budget, especially by the Earth Radiation Budget Experiment (ERBE) during 1985–1988 and by the Clouds and Earth’s Radiant Energy System (CERES) since 2000, and of global ocean temperature measurements by Argo floats since 2005 (Allan et al. 2014; Roemmich et al. 2015; Palmer 2017). N can be estimated less precisely from the sparser ocean temperature measurements made by ships back to the 1960s, but hardly at all for earlier decades (Abraham et al. 2013).
An alternative method for estimating \(\alpha\) (Sect. 6.1) has recently been developed, using an AGCM experiment called amip-piForcing, in which observed sea surface temperature (SST) is a boundary condition, to which simulated N responds (Gregory and Andrews 2016; Zhou et al. 2016; Andrews et al. 2018). This method does not involve knowing real historical F and N, and thus avoids the uncertainties associated with these quantities. The amip-piForcing experiment gives a larger \(\alpha\) (smaller EffCS) for historical climate change than experiments using the same AGCMs, incorporated in coupled atmosphere–ocean GCMs (AOGCMs), to simulate the response to \(\hbox {4}\times \hbox {CO}_{2}\). Moreover, amip-piForcing shows substantial decadal historical variation in \(\alpha\).
For any transient climate state, the EffCS and \(\alpha\) quantify the relationship between changes in global-mean R and global-mean T, determined by the response to SST of surface and atmospheric processes which affect TOA radiation. The AOGCM, AGCM and energy-budget analyses provide evidence that \(\alpha\) is not constant in various ways. We can distinguish two kinds of reason for the inconstancy of \(\alpha\). First, \(\alpha\) might depend on the magnitude of global-mean T or F, which could be formalised by making Eq. (1) non-linear in these quantities (Meraner et al. 2013; Good et al. 2012; Gregory et al. 2015; Bloch-Johnson et al. 2015). Second, R and \(\alpha\) may vary because of changes in the pattern of SST, i.e. “pattern effects” (Stevens et al. 2016; Gregory and Andrews 2016; Ceppi and Gregory 2019). Such effects cannot be predicted by Eq. (1), because it deals only with global means, and it becomes nonsensical in limiting cases. For instance, if changing SSTs alter R but not T, \(\alpha\) is infinite and EffCS is zero.
The inconstancy of \(\alpha\) raises the question which is the title of this paper. To address the question, we analyse AOGCM simulations of the historical period. The analysis has two aspects. First, we evaluate how accurately we would be able to estimate the EffCS for \(\hbox {CO}_{2}\) forcing from the historical record if the real world truly behaved like an AOGCM i.e. a “perfect-model” test. The AOGCMs enable this investigation because they provide complete datasets for many alternative realisations of the historical period, whereas the historical period has occurred only once in the real world and the observational dataset of it is incomplete. Second, we investigate the causes of the time-variation of \(\alpha\) in the historical period. We make use of AOGCM experiments that simulate change due to unforced variability alone and to subsets of historical forcings, whereas we cannot control these influences in the real world.
In Sect. 2 we give details of the AOGCM experiments, and in Sect. 3 we derive estimates of F for the AOGCMs. In Sect. 4 we show that, if the AOGCMs are realistic, \(\mathrm {d}R/\mathrm {d}T\) evaluated from historical climate change by Eq. (3) may be an imprecise and biased estimate of the historical \(\alpha\), owing to the statistical effects of unforced variability. In Sect. 5 we show that \(\alpha\) varies during the historical period in response to the changing nature of the forcing, which is not due to \(\hbox {CO}_{2}\) alone. The AOGCMs indicate that the most recent decades should have \(\alpha\) closest to its \(\hbox {CO}_{2}\) value, but in Sect. 6 we present evidence that the historical time-variation of \(\alpha\) in the AOGCMs may be unrealistic in that regard, by comparison with AGCM amip-piForcing experiments. We conclude in Sect. 7 by discussing the answer to the question posed by the paper, in view of the statistical and systematic errors in estimating the \(\hbox {CO}_{2}\)\(\alpha\) from the historical \(\alpha\).
Throughout the paper, uncertainties written with \({\pm }\) in the text and shown by coloured shading in the diagrams are one standard deviation or one standard error (as appropriate). Our notation for different methods of estimating \(\alpha\), discussed throughout the paper, is summarised in Table 1.
2 AOGCM historical experiments
We analyse results from the historical, historicalNat and historicalGHG experiments from 16 AOGCMs of the Coupled Model Intercomparison Project Phase 5 (CMIP5, Table 2). Climate change is calculated with respect to the piControl experiment, which has constant pre-industrial forcing agents. The historical, historicalGHG and historicalNat experiments begin in the latter part of the 19th century from piControl states, and run to 2005 with time-dependent historical changes in forcing agents. The historical experiment includes all changes in atmospheric composition, anthropogenic and volcanic aerosols, solar irradiance and land-use; historicalGHG includes changes only in greenhouse gas concentrations, historicalNat only in the natural forcing agents of volcanic aerosol and solar irradiance.
Unforced interannual variability in T (pooled standard deviation of 0.11 K in the AOGCM piControl experiments) is not negligible compared with the change in T during the historical period (about 0.8 K, depending on definition, Hartmann et al. 2013). Therefore, in order to clarify the forced signal, historical experiments with most AOGCMs have been run as ensembles of various sizes, with each integration in the ensemble beginning from a different state in the piControl experiment. Provided the states are sufficiently separated, the unforced variability in the ensemble members is not correlated, and its temporal standard deviation is a factor \(1/\sqrt{N}\) smaller in the ensemble mean of N integrations than in each individually.
The CMIP5 historical ensembles have no more than 10 members and fewer in most cases (Table 2). We also use a much larger historical ensemble of 100 members carried out with the MPI-ESM1.1 AOGCM, which is an updated version of the CMIP5 AOGCM of Giorgetta et al. (2013). We assume that variations in global climate in the mean of this ensemble are mostly the response to forcing, since unforced variability is reduced by a factor of 10. This makes it very useful in a perfect-model approach, since we can obtain an accurate estimate of its true \(\alpha\), provided we know F, which is the subject of the next section.
Comparison of the AR5 estimate of annual-mean historical ERF F(t), relative to the 1860–1879 time-mean (a period without large volcanic eruptions, approximating pre-industrial), with diagnoses of F(t) from piClim-histall and piClim-control experiments using the ECHAM6.3 and HadGEM2-A AGCMs. The vertical dashed lines indicate the years of major volcanic eruptions
3 Historical radiative forcing
To apply the global-mean energy balance to observed climate change, we need to know historical ERF. Myhre et al. (2013, AR5) estimated F(t) from historical emissions and atmospheric composition, radiative transfer calculations, and a variety of models. The net forcing goes up as greenhouse gas concentrations increase, partly compensated by negative ERF from anthropogenic aerosols (our Fig. 1, their Figure 8.18). There is a large negative spike for a small number of years following each major volcanic eruption, due to reflection of sunlight by aerosol formed from sulphur dioxide injected into the stratosphere. A wide systematic uncertainty range of 1.1–3.3 \(\hbox {W}\,\hbox {m}^{-2}\) is given for the net anthropogenic ERF at 2011 relative to 1750.
In the following sections we diagnose \(\alpha\) from CMIP5 historical experiments using Eq. (1). For that purpose we need to know F in the AOGCMs, which may be substantially different from the real world F, on account of various model errors. The object of this section is to estimate the model F.
3.1 Diagnosis using AGCMs
The historicalF(t) can be diagnosed for an AOGCM by running a pair of experiments with the AGCM alone, having prescribed unchanging climatological pre-industrial sea surface temperature and sea ice concentration. One of the experiments, called piClim-histall, has time-dependent atmospheric composition and land use for the historical period, while the other is a control, called piClim-control, with constant pre-industrial forcings (Hansen et al. 2005; Held et al. 2010; Andrews 2014; Pincus et al. 2016).
If we assume, despite the forcing, that the surface boundary conditions enforce the same surface temperature in the two experiments, \(T=0 \Rightarrow F=N\) for the difference in energy balance Eq. 1 between them. That is, the historical ERF equals the net input N of energy to the climate system due to the forcing agents. Surface temperature is free to change over land, for practical reasons (e.g. Kamae et al. 2019), giving \(T\simeq 10\)% of the equilibrium T (Andrews et al. 2012, red crosses in their Fig. 1). This effect has not been quantified for CMIP5 historical simulations, but it will be possible to quantify it in CMIP6 using the experiments piClim-histall and piClim-control.
We have run the experiments with the ECHAM6.3 and HadGEM2-A AGCMs to obtain F(t) for MPI-ESM1.1 and HadGEM2-ES AOGCMs, which incorporate these AGCMs respectively. The ECHAM6.3 (MPI-ESM1.1) F(t) is very close to the AR5 estimate, whereas the HadGEM2 F increases considerably less (Fig. 1), in part due to strong negative land-use forcing (Andrews et al. 2017). The difference between these two models illustrates the possibly large but unknown spread in CMIP5 F.
3.2 Forcing due to tropospheric and volcanic aerosol
Timeseries of historical global-mean annual-mean surface air temperature, relative to the time-mean of 1900–2005, from observations, from CMIP5 AOGCMs (using the ensemble mean for each AOGCM) and from the step-model emulation of CMIP5 using the \(\hbox {AR5}'\) ERF timeseries with scaling factors (described in the text) applied to volcanic and anthropogenic aerosol ERF. The solid lines show the multimodel mean for the AOGCMs and the emulation of AOGCMs. In a the envelopes show the ensemble standard deviation, and b compares the multimodel means with the observational estimate
To examine the consistency between our set of AOGCMs and the AR5 regarding forcing, we estimate the historical annual-mean T(t) expected in response to the AR5 F(t) with the “step model”, which uses T(t) in response to a step-change in \(\hbox {CO}_{2}\) in each AOGCM as a kernel to be convolved with the forcing timeseries (more detail given in Appendix A). The step-model mean shows more warming during the historical period than the AOGCM mean (Fig. 2a). We suggest that this is because the AR5 F is larger than the AOGCM mean F, due to the negative anthropogenic aerosol forcing being stronger in AOGCMs than in reality, consistent with the expert judgement of Myhre et al. (2013). Alternatively, EffCS may be larger for anthropogenic aerosol forcing than it is for \(\hbox {CO}_{2}\) (i.e. efficacy greater than unity, defined at the start of Sect. 5; Hansen et al. 2005; Shindell 2014; Marvel et al. 2016; but cf. Paynter and Frölicher 2015). The step model implicitly assumes the same EffCS for all forcing agents.
The multimodel standard deviation of the step-model timeseries is 0.08 K (the pink envelope in Fig. 2a, pooled over years), which must be due mostly to the AOGCM spread in climate feedback, because the step model uses the same AR5 F for all AOGCMs. The multimodel standard deviation of the AOGCM historical timeseries is 0.14 K (the grey envelope, pooled over years). If the standard deviation of unforced interannual variability in T in every AOGCM were 0.11 K, which is the pooled estimate from piControl, and if the 64 historical integrations (Table 2) were equally weighted (both of these are fair approximations), unforced variability would make a negligible contribution of \(0.11/\sqrt{64}=0.013\) K to the AOGCM historical multimodel standard deviation. Therefore we suggest that the multimodel standard deviation is larger for the AOGCMs than the step model because of the AOGCM spread in F. Since different choices have been made for numerous aspects of the formulation of AOGCMs, the actual ERF in a given CMIP5 historical run will not necessarily be the same as the AR5 median estimate for the real world.
To estimate the uncertainty in F from AOGCMs, we take \(N\simeq F/3\) for the multimodel mean (Gregory and Forster 2008), whereby Eq. (2) becomes \(\alpha =(F-N)/T\simeq \frac{2}{3} F/T \Rightarrow T\simeq \frac{2}{3} F/\alpha\). Therefore the fractional uncertainty in T will be the sum in quadrature of the fractional uncertainties in \(\alpha\) and historical F, which we assume to be uncorrelated (Forster et al. 2013). For the time-mean of 1986–2005 (the reference period of the AR5 for projections) relative to the time-mean of 1860–1879 (our reference period for ERF in Fig. 1), T has a standard deviation in the step model of about \({\pm } 15\%\). This uncertainty is attributable to \(\alpha\). It is negligible compared with the standard deviation in the AOGCMs in T of \({\pm } 45\%\), which must therefore be nearly entirely attributable to the AOGCM uncertainty in F. By comparison, if the AR5 likely range for F of 1.13–3.33 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) at 2011 relative to 1750 (Myhre et al. 2013) is assumed to represent the 5–95% range of a normal distribution, its standard deviation is \({{\pm }}30\%\).
We have evaluated the root-mean-square (RMS) difference in T(t) for 1900 onwards between the step-model mean and the AOGCM mean as a function of a time-independent scaling factor applied to the AR5 timeseries of anthropogenic aerosol ERF. The smallest RMS difference, meaning the closest mean match of the step models to the AOGCMs (dashed red line in Fig. 2b), is obtained by making the anthropogenic aerosol ERF 50% stronger (more negative) than the AR5 estimate. Consistent with this finding, the estimate by Zelinka et al. (2014) of the anthropogenic aerosol ERF at 2000 relative to 1860 in a set of AR5 AGCMs is \(1.6 {\pm } 0.4\) times larger than the AR5 median estimate.
It may also be noted that the negative spikes of F in volcano years are not as deep in the AGCMs as in the AR5 estimate (Fig. 1). Linear regression of AGCM F against AR5 F for the years with strong volcanic forcing gives 0.78 for ECHAM6.3 and 0.58 for HadGEM2. This is qualitatively consistent with earlier findings that volcanic forcing is about 80% of the AR5 estimate in the mean of CMIP5 AOGCMs (Larson and Portmann 2016), and about 70% in the HadCM3 AOGCM (Gregory et al. 2016), which the latter authors attributed to rapid cloud adjustments not included in the AR5 estimate.
3.3 Estimate of CMIP5 historical forcing
To estimate the historical F(t) in CMIP5 models, in view of the findings of this section, we multiply the AR5 volcanic F by 0.8 and the AR5 anthropogenic aerosol F by 1.5. Henceforth by “\(\hbox {AR5}'\) forcing” we mean the AR5 F with these modifications. The \(\hbox {AR5}'\)F is not a revised estimate for the real world. We note that there there is a model spread of \({\pm } 45\%\), but we do not have estimates for individual CMIP5 models. In CMIP6, the historical F for each model will be diagnosed by the AGCM experiments of Sect. 3.1, which are included in the Radiative Forcing Model Intercomparison Project (RFMIP, Pincus et al. 2016).
4 Using regression to estimate historical climate feedback
During the historical period, the net forcing grows, T rises, and the heat loss R to space increases. The 100-member MPI-ESM1.1 historical ensemble is useful to illustrate this behaviour because it is so large that the noise is fairly small in the ensemble mean, and because we have a diagnosis of F for this model (Sect. 3.1), enabling an accurate estimate of \(R=F-N\). We see that the decadal trends of \(R=F-N\) and T usually have the same sign, both usually being positive, and their interannual variability shows some similarity as well, especially regarding the negative excursions caused by volcanic forcing (Fig. 3). Their agreement on these features means that the ensemble-mean annual-mean R and T are positively correlated (with coefficient of 0.94, Fig. 4). This is consistent with the assumption \(R=\alpha T\) of the energy balance Eq. 1, which motivates the estimation of \(\alpha\) from the covariation of R and T.
In this section, we summarise some statistical issues that affect the accuracy of the estimate. Its findings are important to the interpretation of historical data, but its subject is a digression from the physical investigation. Therefore we have put the detailed discussion and mathematical demonstrations in appendices.
Following many other authors, we obtain \(\alpha\) according to Eq. (3) as the slope from linear regression of R against T. Unforced variability affects N and hence R, making \(\alpha\) statistically uncertain. From the MPI-ESM1.1 historical ensemble, the distribution of \(\alpha\) obtained by regression of R against T in the individual integrations is \(1.38\,{\pm }\,0.08\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (mean and standard deviation). This is consistent with the median of 1.43 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) estimated by Dessler et al. (2018) from the same dataset using differences between the means of the last and the first decades Eq. 2. The standard deviation of slopes from the difference method is 0.14 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), larger than from the regression method, because the latter uses more data, making it a more efficient estimator (Appendix D.1).
The choice of T as independent variable follows our physical intuition that T determines the magnitude of R rather than vice-versa. Using the historical MPI-ESM1.1 ensemble, we show that this choice is preferable also on statistical grounds (Appendix B). We show further that estimates of historical \(\alpha\) made by OLS regression from real-world R and T are biased low, giving an overestimate of historical EffCS, due to noise \(T'\) in T which does not produce proportionate variability \(\alpha T'\) in R (Appendix C).
Evaluating the statistics for all the AOGCMs, we find that the bias is larger in \(\widetilde{\alpha }\) (multimodel mean of 20%) for a 30-year period than in \(\overline{\alpha }\) (10%) for the entire historical period. The bias affects the difference method as well as OLS regression (Appendix D.1). Total least-squares regression is a method that would avoid the bias, but it is not obviously applicable because it depends on information that we do not have (Appendix D.5).
As well as the mean bias, individual integrations give a spread of slopes due to the noise. The consequent uncertainty is larger in \(\widetilde{\alpha }\) than in \(\overline{\alpha }\) (multimodel mean respectively of 0.42 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) or \(\sim\) 30%, and 0.11 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) or \(\sim\) 10%, Appendix C).
For the real world, random error in the observational dataset, due to instrumental uncertainty or sampling, is a possible source of noise in T that is uncorrelated with R, but this is not relevant to the model world, where we have perfect information. In both worlds, unforced variability in the climate system, unrelated to F, is the likely source of bias, through two physical mechanisms (both demonstrated in Appendix D.6).
First, if variability is driven by spontaneous fluctuations in N that have some persistence, and if the response in T to these fluctuations has some thermal inertia, \(\alpha\) will be biased low (the second case considered by Proistosescu et al. 2018). This effect could be caused for example by interannual variability in cloudiness, and hence planetary albedo, produced by regional climate variability; such variations may persist with anomalies of SST, and the heat capacity of the upper ocean sets the timescale of response. The effect causes \(\alpha\) to be underestimated by OLS because the spontaneous fluctuation in N is misattributed to R.
Second, if spontaneous variability in SST produces a response in N with a different \(\alpha\) from the externally forced response, probably because it has a different geographical pattern (Dessler et al. 2018), the OLS slope is contaminated by \(\alpha\) from the variability. Unlike the first mechanism, this one can produce variability in \(\alpha\) in either sense.
5 Time-variation of historical climate feedback related to forcing agents
Time-dependent climate feedback parameter \(\widetilde{\alpha }_{E}\) (the same solid black line in all panels, labelled “CMIP5 E” in panel (a) and “historical” in the other two) for the multimodel mean of the CMIP5 historical experiment, a compared with the mean \(\widetilde{\alpha }_{I}\) of individual CMIP5 models (labelled “CMIP5 I”), and with \(\widetilde{\alpha }_{e}\) and \(\widetilde{\alpha }_{i}\) from the MPI-ESM1.1 ensemble, b compared with \(\widetilde{\alpha }_{E}\) for the multimodel means of the CMIP5 historicalGHG and historicalNat experiments, and with the time-mean (dotted horizontal line) of \(\widetilde{\alpha }\) for 30-year periods in the CMIP5 piControl simulations, c compared with \(\widetilde{\alpha }_{E}\) for the multimodel means of the AGCM amip-piForcing, the CMIP5 historicalNat experiments, and an estimate made from observational datasets for N and T. The lightly coloured regions around the some of the lines are \({\pm }1\) standard error, with \({\pm }1\) standard deviation for CMIP5 I in (a). In b and c the vertical dashed lines indicate the beginning of the three periods of the regression analysis of Fig. 6a, centred on 1930, 1960 and 1990. Note that \(\widetilde{\alpha }\)decreases upwards on the vertical axis, in order that the effective climate sensitivity increases upwards
Regression of annual-mean \(R=F-N\) against Ta for the CMIP5 AOGCM means in historical, historicalGHG and historicalNat experiments in three consecutive periods, centred on 1930, 1960 and 1990, b for the CMIP5 AOGCM means in the historical and historicalNat experiments and the AGCM mean in the amip-piForcing experiment, for the entire historical period and for 1975 onwards (to 2005 for CMIP5, 2011 for amip-piForcing). The periods are distinguished by the choice of symbol for the data points and the style of line for the regression slope. For the historical experiment, the circles mark the years with volcanic ERF \(<-\,0.2\)\(\hbox {W}\,\hbox {m}^{-2}\) in a, and sequences of such years are joined by a solid line in b. The same T-axis is used for all experiments and periods, relative to time-mean of 1979–2005 i.e. the AMIP period omitting 2006–2008, because the CMIP5 historical period ends in 2005. On the R-axis the experiments are shifted so that they can be seen separately and their slopes compared conveniently, and in a the individual periods of historical and historicalNat are also shifted for the same reason
The original motivation for estimating ECS from historical climate change depends on the assumption that \(\alpha\) is constant. If it is not, the historical \(\alpha\) may differ from \(\alpha\) for idealised \(\hbox {CO}_{2}\)-forced climate change (Paynter and Frölicher 2015). In this section, we examine the dependence of \(\alpha\) in AOGCMs on time, and relate this to the changing nature of the forcing, in order to work out how \(\hbox {CO}_{2}\)\(\alpha\) may best be estimated from historical \(\alpha\).
The relationship between forcing and climate response is often discussed in terms of the efficacy, defined as T forced by unit F of the given agent divided by T for unit forcing of \(\hbox {CO}_{2}\) (Hansen et al. 2005). Our discussion is related to this concept, but it is framed in terms of \(\alpha\) because we are interested in the variation of R with T due to climate feedbacks. In contrast, efficacy quantifies the dependence of T on F, which involves ocean heat uptake as well, and its definition therefore requires a choice of scenario and timescale for the temperature response. For example, efficacy may be defined using T after a specified elapsed time in an AOGCM experiment with constant forcing (as by Hansen et al. 2005) or the equilibrium T under constant forcing of an AGCM with a slab ocean.
5.1 Time-variation of climate feedback in the historical experiment
In the MPI-ESM1.1 historical ensemble, we evaluate the time-variation of \(\widetilde{\alpha }_{i}(t)\) and \(\widetilde{\alpha }_{e}(t)\) (see Table 1 for definition) by regression in overlapping 30-year periods e.g. \(\widetilde{\alpha }\) for the 30 years centred on 1st January 1940 is obtained from regression of annual means for 1925–1954. We find that \(\widetilde{\alpha }_{e}(t)\) shows significant decadal variation (solid orange line in Fig. 5a). For example, \(\widetilde{\alpha }_{e}=1.14 \,{\pm }\, 0.30\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) in 1924 and \(2.63\, {\pm }\, 0.36\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) in 1955, whose difference of \(1.49 \,{\pm }\, 0.47\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) is significant at the 1% level. This variation must be evidence of time-dependence which is synchronous across the ensemble of integrations, and therefore attributable to external forcing.
On the other hand, \(\widetilde{\alpha }_{i}(t)\) does not depend significantly on time (dotted orange line in Fig. 5a), judged by comparison with its standard deviation of 0.35 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) due to unforced variability (the standard deviation among the 100 integrations, pooled over years, not shown). This is because unforced variability has a greater effect on individual integrations, and obscures the response to forcing that can be discerned in the ensemble mean.
Since the historical ensembles with CMIP5 models are much smaller than the MPI-ESM1.1 ensemble, to suppress the unforced variability we aggregate the models, by calculating a time-dependent climate feedback parameter, denoted by \(\widetilde{\alpha }_{E}\) (Table 1), from the multimodel-mean R(t) and T(t) of the ensemble means of individual CMIP5 models i.e. treating the models as equally weighted members of a “super-ensemble”. (We use the word “multimodel” instead of just “model” to emphasise that it is a mean over all models, rather than the mean over all integrations of a single model.) We assume that the forced response will have correlated time-dependence among the models, whereas the unforced variability will be uncorrelated. The multimodel mean is used for similar reasons in statistical studies of attribution of climate change to forcing agents (e.g. Jones et al. 2013; Hua et al. 2018).
The small standard error of \(\widetilde{\alpha }_{E}\) (grey envelope in Fig. 5b) means that its time-variation is well-defined and statistically significant. It is moreover rather similar to \(\widetilde{\alpha }_{e}\) of MPI-ESM1.1 (compare solid black and orange lines in Fig. 5a), corroborating the idea that the time-variation is forced, and thus similar among all models. There is a minimum in \(\widetilde{\alpha }_{E}\) around 1930, a maximum during 1945–1974, and the absolute minimum (highest EffCS) occurs after 1980. The time-variation cannot be an artefact arising from the OLS bias because the minima in \(\widetilde{\alpha }\) occur when the rate of warming is largest (around 1930 and after 1980), and hence the bias towards small \(\widetilde{\alpha }\) due to unforced variability is of minimal importance compared with the response to forcing.
The time-variation of \(\widetilde{\alpha }_{E}\) in the CMIP5 historical experiment is similar in amplitude and period to the time-variation of \(\widetilde{\alpha }\) in the AGCM amip-piForcing experiment with observed historical sea-surface temperature (described in Sect. 1; Andrews et al. 2018), but different in time-profile (compare black and blue lines in Fig. 5c). We will study amip-piForcing in Sect. 6, once we have drawn conclusions from the present section concerning the response to forcing in the AOGCMs.
For comparison, we also calculate a multimodel mean, denoted by \(\widetilde{\alpha }_{I}(t)\) (dotted black line in in Fig. 5a), from the \(\widetilde{\alpha }_{i}(t)\) timeseries of the individual models. Like \(\widetilde{\alpha }_{i}\) of MPI-ESM1.1, \(\widetilde{\alpha }_{I}\) has insignificant forced time-variation, judged by comparison with the standard deviation among integrations (grey envelope, calculated for each model ensemble and pooled over models; if also pooled over years, the standard deviation is 0.42 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\)). The lack of significant forced variation is due to the dominance of \(\widetilde{\alpha }\) by unforced variability in individual integrations, while the greater OLS bias (Sect. 4) caused by larger unforced variability explains why \(\widetilde{\alpha }_{I}<\widetilde{\alpha }_{E}\) at all times (compare solid and dotted black lines in Fig. 5a).
5.2 Greenhouse-gas forcing
Since the largest historical forcing is \(\hbox {CO}_{2}\), we consider the possibility that the response to \(\hbox {CO}_{2}\) could somehow cause forced time-variation in \(\widetilde{\alpha }_{E}\). Most CMIP5 models have a tendency for \(\alpha\) to decrease with time under constant \(\hbox {CO}_{2}\) (Armour et al. 2013; Andrews et al. 2015). In our set of CMIP5 AOGCMs, regression of \(-N\) against T for years 1–20 and years 1–140 of abrupt4xCO2 gives multimodel-mean \(\alpha =1.26\) and 1.02 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) respectively. In some AGCMs and AOGCMs, it has been found that \(\alpha\) decreases as \(\hbox {CO}_{2}\) concentration rises (Good et al. 2012; Jonko et al. 2012; Gregory et al. 2015). Either of these effects might explain the long-term decreasing tendency in historical\(\widetilde{\alpha }_{E}\) (Fig. 5b), although not its decadal variation.
To test this hypothesis, we calculate \(\overline{\alpha }_{E}\) in the historicalGHG experiment, whose forcing is predominantly \(\hbox {CO}_{2}\), using the AR5 estimate of greenhouse-gas F(t). We find that R and T in historicalGHG have a high correlation coefficient of 0.99 over the historical period (1871–2005, shown in red in Fig. 6a for the period since 1915), and there is little time-variation in \(\widetilde{\alpha }_{E}\) in the historicalGHG experiment (solid red line in Fig. 5b). Therefore we reject the hypothesis that the long-term decreasing trend in historical\(\widetilde{\alpha }_{E}\) is due to \(\hbox {CO}_{2}\) forcing. After about 1960, historical\(\widetilde{\alpha }_{E}\)decreases strongly. This tendency is opposite to that of historicalGHG\(\widetilde{\alpha }_{E}\), which increases slightly, perhaps due to reduction of OLS bias as the greenhouse-gas forcing grows relative to the unforced variability (Appendices D.3 and D.6).
5.3 Comparison of historicalGHG and abrupt4xCO2 climate feedback
The historicalGHG\(\overline{\alpha }_{E}=1.03\, {\pm }\, 0.01\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (EffCS 3.6 K, Fig. 6a) is close to multimodel-mean \(\alpha =1.02\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) from years 1–140 of abrupt4xCO2 (Sect. 5.2). The correlation coefficient across models between \(\textit{abrupt4xCO2}\ \alpha\) and historicalGHG\(\overline{\alpha }_{e}\) is 0.55 for years 1–20 and 0.68 for years 1–140, both significant at the 10% level. This similarity is expected, since historicalGHG is dominated by \(\hbox {CO}_{2}\) forcing, but because \(\hbox {CO}_{2}\)\(\alpha\) varies with time and perhaps with \(\hbox {CO}_{2}\) concentration, and \(\alpha\) might differ among the various greenhouse gases, we cannot expect a perfect correlation. We suppose that it is larger for years 1–140 because this timescale is more similar to the length of the historicalGHG experiment.
The correlation might also be reduced by our neglect of model-dependence in the greenhouse-gas F(t), which we do not know for any of the models. To take this approximately into account, we recalculate historicalGHG\(\overline{\alpha }_{e}\) using the AR5 greenhouse-gas F scaled for each AOGCM by the ratio of that AOGCM’s abrupt4xCO2 ERF to the multimodel-mean value. The correlation coefficients with \(\textit{abrupt4xCO2}\ \alpha\) are increased to 0.61 for years 1–20 and 0.77 for years 1–140 (Fig. 7a), supporting the conjecture that the model spread in greenhouse-gas forcing is substantial (Andrews et al. 2012; Chung and Soden 2015). The historicalGHG\(\overline{\alpha }_{e}\) is about 10% larger than \(\textit{abrupt4xCO2}\ \alpha\) for years 1–140 in the multimodel mean.
5.4 Volcanic and anthropogenic aerosol forcings
We have seen that the time-dependence of historical\(\widetilde{\alpha }_{E}\) is statistically significant (Sect. 5.1), but not related to greenhouse-gas forcing (Sect. 5.2). Therefore we suppose that it is due to the varying relative importance of the other forcing agents. Such an effect could occur if \(\alpha\) depends on the nature of the forcing. As discussed at the start of Sect. 5, this idea is related to the efficacy of forcing agents. For many agents, including anthropogenic aerosols, \(\alpha\) is found to be close to \(\hbox {CO}_{2}\)\(\alpha\) (efficacy is near unity), provided ERF is used to quantify forcing (Hansen et al. 2002; Shine et al. 2003; Sherwood et al. 2015). For volcanic aerosol, \(\alpha\) may be larger than for \(\hbox {CO}_{2}\) (EffCS smaller, efficacy less than unity; Marvel et al. 2016; Gregory et al. 2016; Ceppi and Gregory 2019).
In this discussion, we frequently consider and contrast three consecutive historical periods, which have different mixtures of forcing, as described in the following paragraphs. We choose them each to be 30 years, like the sliding window used to evaluate \(\widetilde{\alpha }\), because that means the OLS bias will not affect their comparison (Sect. 4).
The time-dependence of \(\widetilde{\alpha }_{E}\) in historicalNat, in which the forcing is dominated by volcanic aerosol (Fig. 1), shows large decadal variation (Fig. 5b). During 1915–1944 there were no large volcanic eruptions, so the variation of T and R and their correlation of 0.41 are all relatively small (green crosses in Fig. 6a) and must be due nearly entirely to unforced variability. For historicalNat during this period regression gives \(\widetilde{\alpha }_{E}=0.7\, {\pm }\, 0.4\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (solid green line), which is not distinguishable from historicalGHG\(\widetilde{\alpha }_{E}=1.0\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (solid red line, Sect. 5.2).
Unlike in historicalNat, T and R have substantial trends in the historical experiment during 1915–1944 (black crosses in Fig. 6a) due to anthropogenic forcing, especially by greenhouse gases (Fig. 1). The historical\(\widetilde{\alpha }_{E}=1.4\, {\pm }\, 0.1\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) of this period (solid black line) is somewhat larger than for greenhouse gas forcing (solid red line). This could be explained by the growth of negative anthropogenic aerosol forcing during this period, with a smaller \(\alpha\) (larger EffCS) than for greenhouse-gas forcing; the combination would produce a larger \(\alpha\) than either alone (Appendix B in supplementary online material of Gregory and Andrews 2016).
For historicalNat for the period since 1945, during which there were three large volcanic eruptions, \(\widetilde{\alpha }_{E}\) is fairly constant (green line in Fig. 5b). The regression of R against T gives \(\alpha =2.5\,{\pm }\,0.2\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for 1945–1974 and \(2.4\,{\pm }\,0.1\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for 1975 onwards, which are very similar (EffCS 1.5 K), and more than twice historicalGHG\(\widetilde{\alpha }_{E}\) (compare the dotted and dashed red lines in Fig. 6a with the dotted and dashed green lines). These results suggest that the climate feedback parameter for volcanic forcing is larger (smaller EffCS) than for greenhouse gases (predominantly \(\hbox {CO}_{2}\)) in CMIP5 AOGCMs on average.
For 1945–1974 (30 years centred on 1st January 1960) historical\(\widetilde{\alpha }_{E}=2.1\,{\pm }\,0.2\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), similar to historicalNat (dotted black and green lines in Fig. 6a), and distinct from historicalGHG (dotted red line). We suggest that historical and historicalNat\(\widetilde{\alpha }_{E}\) are similar during this period because the increase in greenhouse-gas forcing in the historical experiment is offset by the increase in negative anthropogenic aerosol forcing, leaving only a small net anthropogenic forcing trend (Fig. 1), so the strong volcanic forcing from Agung is the greatest influence in both experiments.
For 1975–2005 (a period of 31 years, centred in 1990 and running up to the end of the CMIP5 historical integrations), historical\(\widetilde{\alpha }_{E}=1.2\, {\pm } \,0.1\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) diverges from historicalNat and comes much closer to historicalGHG (black approaches red in Fig. 5b, dashed black and red lines have a similar slope in Fig. 6a). We suggest that the historical and historicalGHG\(\widetilde{\alpha }_{E}\) are similar during this period because the net anthropogenic forcing grows much more rapidly due to greenhouse gas increase, once the aerosol forcing is steady (Fig. 1). Despite the further years of volcanic forcing from El Chichon and Pinatubo, the greenhouse-gas forcing dominates the historicalF and the consequent rise in T (Fig. 3).
In summary, the time-variation of historical\(\widetilde{\alpha }_{E}\) in CMIP5 can be mainly explained by the varying importance of forcings due to greenhouse gases and volcanic aerosol, if \(\alpha\) is larger for the latter. This means the EffCS is higher (\(\alpha\) smaller) when volcanic forcing is relatively less important, around 1940 (when there were no major eruptions) and since 1975 (when greenhouse-gas forcing has rapidly increased). The growth of negative anthropogenic aerosol forcing during the intermediate period meant that the increase in net anthropogenic forcing was less important than the volcanic forcing, so the EffCS was dominated by response to volcanic forcing, and was relatively low. This explanation does not require EffCS for anthropogenic aerosol to differ substantiantially from the \(\hbox {CO}_{2}\) EffCS.
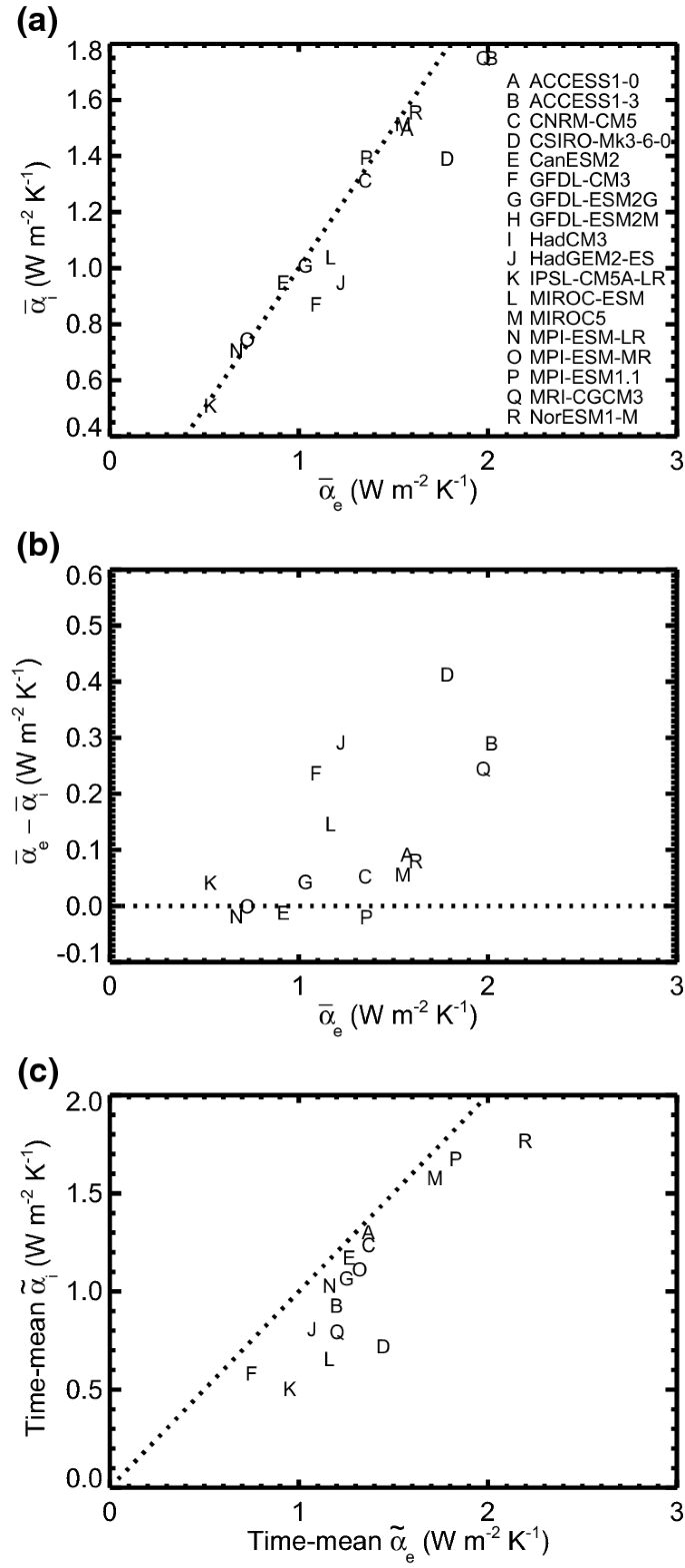
Relationships in CMIP5 AOGCMs between \(\textit{abrupt4xCO2}\ \alpha\) and ahistoricalGHG\(\overline{\alpha }_{e}\), bhistorical\(\overline{\alpha }_{e}\), chistorical\(\widetilde{\alpha }_{e}\) for 1975–2004 (in black), amip-piForcing\(\widetilde{\alpha }_{e}\) for 1925–1954 (in red), d time-mean piControl\(\widetilde{\alpha }\). In a we plot \(\alpha\) for years 1–140 of abrupt4xCO2, and in b–d years 1–20. In a we use the AR5 estimate for historicalGHGF(t), scaled for each AOGCM by its own abrupt4xCO2 ERF (as discussed in the text), and for b, c we use our \(\hbox {AR5}'\) estimate for historicalF(t) for all AOGCMs except HadGEM2-ES and MPI-ESM1.1 (models J and P), for which we use F(t) diagnosed in these models individually (compared in Fig. 1). The dotted line in all panels is 1:1; all models lie to the left of this line in d, indicating that \(\textit{piControl}\ \widetilde{\alpha }<{\textit{abrupt4xCO2}\ \alpha }\)
5.5 Comparison of historical and abrupt4xCO2 climate feedback
Despite the large time-variation of \(\alpha _{E}\) (black in Fig. 5), multimodel-mean R and T are highly correlated (coefficient of 0.94 for 1871–2006, black symbols in Fig. 6b). Moreover, \(\overline{\alpha }_{E}=1.27\,{\pm }\,0.04\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for the entire historical period (dotted black line in Fig. 6b) is very close to the multimodel-mean \(\alpha =1.26\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for years 1–20 of abrupt4xCO2 (Sect. 5.2).
However, for individual AOGCMs, the correlation of \(\overline{\alpha }_{e}\) with \(\textit{abrupt4xCO2}\ \alpha\) is much weaker, and insignificant at the 10% level, at 0.24 for years 1–20 (Fig. 7b) and \(-\,0.02\) for years 1–140. The multimodel standard deviation of the difference between \(\overline{\alpha }_{e}\) and \(\textit{abrupt4xCO2}\ \alpha\) is 37% (0.47 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\)). The likely reason is the large AOGCM spread in F, which we have estimated as \({\pm } \,45\)% (Sect. 3.2), due principally to anthropogenic aerosol. Scaling the greenhouse-gas forcing using the ratio of abrupt4xCO2 ERF, as we did for historicalGHG, raises the correlation coefficients somewhat, to 0.37 and 0.24, but they are are still insignificant at the 10% level, confirming the dominant effect of uncertainty in non-greenhouse-gas forcing.
A more accurate estimate might be obtained from periods which are dominated by \(\hbox {CO}_{2}\) forcing, when historical\(\widetilde{\alpha }\) should be closer to \(\hbox {CO}_{2}\)\(\alpha\) and F is more accurately known. One possibility is the recent decades, when the greenhouse-gas forcing has been increasing rapidly and the anthropogenic sulphate aerosol forcing has been fairly constant (Sect. 5.4; Gregory and Forster 2008; Bengtsson and Schwartz 2013), so historical and historicalGHG\(\widetilde{\alpha }_{E}\) are consequently close (Fig. 5b). For 1975–2004 (30 years centred on 1st January 1990) the correlation of \(\widetilde{\alpha }_{e}\) with \(\textit{abrupt4xCO2}\ \alpha\) is 0.64 (Fig. 7c), a considerably stronger correlation than for \(\overline{\alpha }_{e}\), and the standard deviation of the difference is smaller, at 27%. Scaling the greenhouse-gas forcing using the ratio of abrupt4xCO2 ERF improves the correlation only a little in this case.
For most of the historical period, \(\widetilde{\alpha }_{E}(t)\) is much larger (EffCS smaller) in historical than historicalGHG (the time-mean difference between the black and red lines is 0.75 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) in Fig. 5b), but the multimodel-mean difference between historical\(\overline{\alpha }_{e}\) and \(\textit{abrupt4xCO2}\ \alpha\) is only 2% (0.03 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\)). We can understand this apparent contradiction by considering multimodel-mean R(t) and T(t). The slope during intervals of volcanic forcing (joined by solid orange lines in Fig. 6b) is evidently greater than at other times, consistent with time-varying historical\(\widetilde{\alpha }_{E}(t)\) (Fig. 5b). However, the volcanic forcing is small on the long-term mean, and although the periods affected by volcanic forcing are of several years, they are only temporary digressions from the long-term trend. Hence the large volcanic \(\widetilde{\alpha }\) has little effect on the best-fit slope for the entire historical period (dotted black line in Fig. 6b), which is only a little larger than \(\widetilde{\alpha }_{E}=1.19\,{\pm }\,0.10\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for the last 30 years of the timeseries (dashed black line, the same as in Fig. 6a).
In summary, in the AOGCMs, as an estimate of \(\textit{abrupt4xCO2}\ \alpha\), historical\(\overline{\alpha }_{E}\) has a small positive bias, because of the influence of volcanic forcing, and a large uncertainty, due principally to anthopogenic aerosol forcing. In the real world, we cannot evaluate \(\overline{\alpha }\) accurately because we do not have adequate estimates of F and N for the entire historical period. Response to volcanic forcing has a much stronger effect on the time-dependent \(\widetilde{\alpha }_{E}\) than it does on \(\overline{\alpha }_{E}\). Therefore \(\widetilde{\alpha }_{E}\) from periods that are affected by volcanoes has a large positive bias as an estimate of \(\textit{abrupt4xCO2}\ \alpha\). In the AOGCMs, the bias is smallest in the period since 1975, during which we have the best observations of the real world.
5.6 Comparison of unforced and abrupt4xCO2 climate feedback
In Sect. 5.4 we noted that historicalNat\(\widetilde{\alpha }_{E}\) and historicalGHG\(\widetilde{\alpha }_{E}\) for 1915–1944 are not distinguishable. Since there are no volcanic eruptions during this period, historicalNat has no forcing. Therefore it is of interest to know what \(\widetilde{\alpha }\) to expect from unforced variability alone, which we evaluate from the piControl experiments by regressing R (\(=-\,N\) since \(F=0\)) against T in overlapping 30-year segments. We use 480 \((=16\times 30)\) years from each AOGCM, and exclude ACCESS1.0, for which we have only 250 years.
For the population of \(\widetilde{\alpha }\), taking all segments from all models together, the mean \(\widetilde{\alpha }=0.70\) (dotted horizontal line in Fig. 5b). Neglecting autocorrelation for lags greater than 30 years, the population contains 16 independent values from each of 15 experiments. The population standard deviation is 0.69 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), so the standard error of the time-mean \(\widetilde{\alpha }_{E}\) is \(0.69/\sqrt{16\times 15}=0.044\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (grey envelope around the dotted horizontal line). Hence historical\(\widetilde{\alpha }_{E}(t)\) is always distinct from time-mean piControl\(\widetilde{\alpha }\).
HistoricalGHG and piControl are different in the character of the covariation of R and T, which is highly correlated in the former but not in the latter (correlation coefficient of 0.24 between annual-mean R and T in the piControl population). Nonetheless, their regression slopes are similar. Although historicalGHG\(\widetilde{\alpha }_{E}\) is greater than piControl\(\widetilde{\alpha }\) during nearly all the historical period, their difference is rarely statistically significant (Fig. 5b, 5% two-tailed significance level) before about 1970. This explains the simularity of historicalNat and historicalGHG\(\widetilde{\alpha }_{E}\) during 1915–1945.
For each model we compare the piControl\(\widetilde{\alpha }\) for unforced variability with \(\textit{abrupt4xCO2}\ \alpha\) for \(\hbox {CO}_{2}\) forcing. These quantities have a modest but significant correlation across models (0.55, Fig. 7d), as found by Zhou et al. (2015) for the cloud component. Colman and Power (2018) note both similarities and differences in feedbacks for decadal variability and \(\hbox {CO}_{2}\) forcing. It is clear that \(\textit{abrupt4xCO2}\ \alpha\) is larger than piControl\(\widetilde{\alpha }\) in all models, leading us to infer that historicalGHG\(\widetilde{\alpha }_{e}\) and \(\widetilde{\alpha }_{E}\) are also larger than piControl. In some models, piControl\(\widetilde{\alpha }<0.5\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), implying EffCS exceeding 7 K, and it is negative in one model (MIROC5). Dessler (2013) found similar results for piControl experiments of AOGCMs from the Coupled Model Intercomparison Project Phase 3 (CMIP3). These low values result from a pronounced OLS bias due to noise in T that is not correlated with R (Appendix C). There is a more complex relationship between R and T for internally generated fluctuations, and it is physically incorrect to treat R simply as an instantaneous response to T (Xie and Kosaka 2017; Lutsko and Takahashi 2018; Proistosescu et al. 2018)
6 Time-variation of historical climate feedback related to SST patterns
Previously published work has shown that the variation of \(\alpha\) is mostly determined by the pattern and magnitude of sea surface change in response to radiative forcing (Armour et al. 2013; Andrews et al. 2015; Gregory and Andrews 2016; Haugstad et al. 2017; Ceppi and Gregory 2019). The effect of the agent comes mainly via the surface forcing, which is rapidly modified by climate feedbacks, ocean heat uptake and atmospheric and oceanic dynamical responses. We depend on AOGCMs to project the consequent sea surface changes, but we do not know whether their results are realistic in the characteristics relevant to \(\alpha\).
In this section we compare \(\alpha\) from historical AOGCM simulations, driven by forcing agents, with \(\alpha\) from AGCM simulations driven by sea surface conditions prescribed from observations. AMIP experiments have shown that AGCMs reproduce the time-variation of TOA radiation and other quantities quite well when given realistic surface conditions (Allan et al. 2014). Thus the advantage of the AGCM simulations is their closer resemblance than the AOGCM simulations to the real historical record, while their disadvantage is that they do not allow us to isolate the effects of the individual forcing agents and unforced variability, which have imprinted their effects all together on the observational sea surface conditions.
6.1 Time-variation of climate feedback in the amip-piForcing experiment
a, b Timeseries of ensemble-mean global-mean radiative response R with respect to the time-mean of 1860–1899 in the HadCM3-A experiments (see text for explanation), CMIP5 historical and historicalNat experiments. The timeseries have been smoothed by calculating a 3-year running mean. Linear regressions for R(t) during 1925–1954 and 1975–2004 are shown by dotted and dashed lines respectively for all experiments except historicalNat. c Time-dependent climate feedback parameter \(\widetilde{\alpha }_{e}\) computed with R(t) from the HadCM3-A experiments indicated and T(t) from HadCM3-A amip-piForcingClimI. All panels follow the legend in a
The AGCM experiment named amip-piForcing, using observationally derived time-dependent historical sea-surface boundary conditions from the Atmosphere Model Intercomparison Project (AMIP, Gates et al. 1999; Hurrell et al. 2008), with constant pre-industrial forcing agents (atmospheric composition etc.), has recently been carried out with various AGCMs (Andrews 2014; Gregory and Andrews 2016; Zhou et al. 2016; Silvers et al. 2018; Andrews et al. 2018). In this experiment, \(F=0 \Rightarrow R=-N=\alpha T\). Because amip-piForcing does not have time-varying forcing agents, the evaluation of its \(\overline{\alpha }_{e}\) is not affected by the uncertainty in anthropogenic aerosol ERF, unlike the CMIP5 historical\(\overline{\alpha }_{e}\). In this section we use the amip-piForcing ensembles of ECHAM6.3, HadGEM2-A, GFDL-AM2.1 and GFDL-AM3 (the AGCMs of MPI-ESM1.1, HadGEM2-ES, GFDL-ESM2M and GFDL-CM3; data from Andrews et al. 2018) and HadCM3-A (the AGCM of HadCM3, Gordon et al. 2000, employed for further experiments in this section). The amip-piForcing experiment is included in the Cloud Feedback Model Intercomparison Project of CMIP6 (Webb et al. 2017).
In each of these AGCMs, \(\overline{\alpha }_{e}\) obtained by regression of \(-N\) against T from amip-piForcing for the entire historical period is larger (EffCS smaller) than in the abrupt4xCO2 experiment with the corresponding AOGCM (Andrews et al. 2018). Regression of multimodel-mean R against T for the five AGCMs gives \(\overline{\alpha }_{E}=1.59\,{\pm }\,0.08\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for amip-piForcing (blue crosses and dotted line in Fig. 6b), about 30% larger than both historical\(\widetilde{\alpha }_{E}\) (black crosses and dotted line), and multimodel mean abrupt4xCO2\(\alpha =1.25\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for years 1–20 (Sect. 5.5).
When computed in a 30-year window, \(\widetilde{\alpha }(t)\) shows large decadal variation, but the spread of \(\widetilde{\alpha }\) among the integrations of each AGCM is rather small, because most of the interannual variability is prescribed through the sea surface conditions (SST patterns dominate the effect, and sea ice variations are relatively uninfluential; Gregory and Andrews 2016). In each AGCM, there is consequently little difference between \(\widetilde{\alpha }_{i}(t)\) and \(\widetilde{\alpha }_{e}(t)\), unlike in AOGCMs. Owing to the strong influence of the common surface boundary conditions, the AGCMs furthermore have synchronised time-variations in \(\widetilde{\alpha }\) (Andrews et al. 2018), illustrated by \(\widetilde{\alpha }_{E}\) of the multimodel mean (blue in Fig. 5c), but they have different time-means and vary with roughly constant offsets. Their spread is similar to that of \(\alpha\) in the standard idealised amip-p4K AGCM experiment, which imposes a uniform SST warming of 4 K (Ringer et al. 2014).
The minimum \(\widetilde{\alpha }_{E}\) (maximum EffCS) of amip-piForcing is close to historicalGHG\(\widetilde{\alpha }_{E}\) (1.03 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), Sect. 5.5), and occurs in the middle of the longest interval without major volcanic eruptions, when forced climate change was therefore anthropogenic. This is consistent with the inference that EffCS for greenhouse-gas forcing is higher than for volcanic forcing. For the five AGCMs in our ensemble of amip-piForcing experiments, we have compared \(\widetilde{\alpha }_{e}\) for 1925–1954 with \(\textit{abrupt4xCO2}\ \alpha\) of the corresponding AOGCM (red in Fig. 7c). The rank correlation is perfect, and the (product–moment) correlation coefficient is 0.94, consistent with the dominance of \(\hbox {CO}_{2}\) forcing during this period.
The maximum \(\widetilde{\alpha }_{E}\) (minimum EffCS) of amip-piForcing is attained in the period since 1960, during which it is fairly constant, while CMIP5 historical\(\widetilde{\alpha }_{E}\) is declining (EffCS increasing), due to the dominance of the greenhouse-gas increase over volcanic forcing once anthropogenic aerosol has stabilised (as found above, Sect. 5.4). The large recent \(\widetilde{\alpha }_{E}\simeq 2.5\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) of amip-piForcing is outside the range of all individual CMIP5 historical integrations since 1960 (Marvel et al. 2018) and of all individual CMIP5 piControl integrations, whose maximum \(\widetilde{\alpha }\) are 2.3 and 2.2 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) respectively for 30-year periods, and it is about twice the CMIP5 multimodel-mean \(\textit{abrupt4xCO2}\ \alpha\) (Sect. 5.5).
6.2 Effect of patterns of SST change on radiative response
Since amip-piForcing and historical experiments both reproduce observed T(t) closely, the differences in \(\widetilde{\alpha }=\mathrm {d}R/\mathrm {d}T\) between amip-piForcing and historical, which are particularly large around 1940 and 1990 (Fig. 5c), must be due to differences in R(t). During 1925–1954 (30 years around 1940), \(R=F-N\) in the CMIP5 historical multimodel mean has an increasing trend, but \(R=-N\) in the HadCM3-A amip-piForcing experiment has no trend (black in Fig. 8b and blue in Fig. 8a respectively), consistent with \(\widetilde{\alpha }\) being smaller in amip-piForcing (EffCS larger). By contrast, during 1974–2004 (30 years around 1990), R is increasing about twice as fast in amip-piForcing, which has larger \(\widetilde{\alpha }\) (EffCS smaller).
To investigate how the two sets of sea surface fields (one from CMIP5 AOGCMs, the other from observations) produce the same T(t), but different R(t), we use three further HadCM3-A experiments with constant pre-industrial forcing agents, like amip-piForcing. These experiments have no interannual variation in sea ice concentration, which follows the climatological annual cycle of the AMIP dataset for 1871–1900. The first of the three is the amip-piForcingClimI experiment (Gregory and Andrews 2016), which has the same SST fields as amip-piForcing, and yields very similar R(t) (blue and cyan in Fig. 8a), confirming that the interannual variation is due almost entirely to SST changes (rather than sea ice changes).
The other two experiments follow Zhou et al. (2016). One of them applies the global warming but no change in SST pattern, while the other applies the pattern of change but no global warming. They aim to distinguish the effects on \(\alpha\) from variation of global-mean T and from the changing pattern of SST. The monthly SST fields for 1871–2012 for both experiments are derived from the AMIP SST fields \(T_{S}(x,y,M,Y)\), where x, y are longitude and latitude, M the month within the year and Y the year.
First we calculate the monthly SST climatology \(T_{SC}(x,y,M)\) of the late nineteenth century (1871–1900), which we treat as the unperturbed climate, then we calculate the anomaly \(\delta T_{S}=T_{S}(x,y,M,Y)-T_{SC}(x,y,M)\) of the SST in a given month from the unperturbed climatological mean. In one experiment, a geographically uniform warming \(\delta T_{SU}\) is added to the climatological SST, equal to the global-mean of the anomaly,
where \(G(\cdot )\) denotes a global mean. In the other experiment, the local perturbation \(\delta T_{SD}\) to the climatology is the deviation of the local anomaly from its global mean,
By construction,
and
In the experiment with the uniform perturbation \(\delta T_{SU}\), the time-mean global-mean surface air temperature anomaly is \(T=0.37\) K for 1975–2004 with respect to the 1871–1900 climatology, almost the same as amip-piForcingClimI, and 15% less than \(T=0.44\) K from amip-piForcing because of omitting the effect of the recent decline in Arctic sea-ice.
The zero-mean perturbation \(\delta T_{SD}\) to SST produces negligible global-mean temperature change, but the time-varying changes to the pattern of SST have a strong effect on cloudiness and thus affect N and hence R. During 1975–2004, the trends in R in the HadCM3-A uniform and deviation experiments are positive (\(\mathrm {d}R/\mathrm {d}T>0\)) and about the same size (dotted red and grey lines in Fig. 8a). Each alone is similar to the trend in the CMIP5 historical experiment (dotted black line in Fig. 8b), consistent with our finding above that in amip-piForcing, whose SST perturbation is the sum of the uniform and deviation perturbations, the trend of R is about twice the size as in the historical experiment, making the EffCS smaller in amip-piForcing.
During 1925–1954, the trends in R in the HadCM3-A uniform and CMIP5 historical experiments are positive and similar, but the R in the HadCM3-A deviation experiment has a negative trend. That is, although global-mean T is rising, the changing pattern of SST tends to produce an increasing trend in heat uptake \((\mathrm {d}N/\mathrm {d}T>0, \mathrm {d}R/\mathrm {d}T<0)\) by the climate system. The opposed trends due to the global mean and its pattern lead to the weak net trend of R and make the EffCS larger in amip-piForcing during this period.
Thus R is not a response to T alone, but depends also on the changing patterns of SST. It could be that both the global mean and the patterns have the same causes (unforced or forced), but they do not have a consistent relationship. The time-variation of \(\widetilde{\alpha }\) in amip-piForcingClimI (and therefore amip-piForcing) is mainly due to the patterns of \(\delta T_{SD}\), while \(\widetilde{\alpha }\) for the uniform \(\delta T_{SU}\) is fairly constant through the historical period (Fig. 8c). Assuming that HadCM3-A is typical of AGCMs in amip-piForcing, we suppose that the common time-variation of \(\widetilde{\alpha }\) is due to the patterns, while the fairly time-constant model spread is due to model-dependent climate feedback in response to uniform warming.
6.3 Differences between simulated and observed responses to volcanic forcing
In Sect. 5.4 we concluded that the time-dependence of historical\(\widetilde{\alpha }_{E}\) could be mainly explained by the varying relative importance of forcings due to greenhouse gases and volcanic aerosol, if \(\alpha\) is larger for the latter. In Sect. 6.1 we saw that the time-variation of \(\widetilde{\alpha }_{E}\) is different for amip-piForcing and historical. In Sect. 6.2 we attributed the time-variation in amip-piForcing to the changing patterns of deviation of SST from its global mean. We conjecture that these findings could be linked if volcanic forcing has a pattern effect that gives large \(\widetilde{\alpha }\) in both amip-piForcing and historical, but with different time-dependence.
For information about the effect of volcanoes, we turn to historicalNat. There is greater similarity in time-dependence of \(\widetilde{\alpha }_{E}\) since 1930 between historicalNat and amip-piForcing than between historical and amip-piForcing (Fig. 5c). Although all three have smaller \(\widetilde{\alpha }_{E}\) in the first half of the twentieth century (higher EffCS), the minimum has a similar magnitude and date (around 1940) in amip-piForcing and historicalNat, while historical is increasing by then, having reached its minimum earlier and at a larger value. Moreover, \(\widetilde{\alpha }_{E}\) is minimum (highest EffCS) in recent decades in historical, but maximum (lowest EffCS) and similar in amip-piForcing and historicalNat. During this period in the latter two experiments \(\widetilde{\alpha }_{E}\) is close to 2.3 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (magenta cross in Fig. 5c, EffCS 1.6 K), which is the value calculated from observational estimates for 1985–2011 for T (HadCRUT4 blended land and sea surface temperature, Morice et al. 2012) and N (ERBE and CERES satellite measurements of TOA radiative flux, Allan et al. 2014) with the AR5 F.
Despite the similarity of the timeseries of \(\widetilde{\alpha }_{E}(t)\) in amip-piForcing and historicalNat, their R(t) timeseries look quite different (Fig. 8a, b). In historicalNat, immediately after each major volcanic eruption, there is a large negative spike in R, which then returns to zero over \(\sim\)10 years. The same structure is apparent in R in the historical experiment, where it is superimposed on the positive trend due to global warming. The episodic covariation of volcanically forced T and R gives the large \(\widetilde{\alpha }_{E}\simeq 2.5\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) of historicalNat for the period since 1975 (green in Fig. 6b).
In the same period, while amip-piForcing has a similar \(\widetilde{\alpha }_{E}\) (blue line), it does not show unusually large variations in R at the times of eruptions (Fig. 8a); on the contrary, it has larger excursions at other times, presumably due to unforced variability. The same difference of character can be seen when comparing T from the CMIP5 historical experiment with the observational estimate (Fig. 2). Rapid cooling following major eruptions is clear in CMIP5, but not in observations.
Normalised pattern (\(\hbox {K}\,\hbox {K}^{-1}\), see text for derivation) of SST change 1975–2004 within 65°S–65°N in the a AMIP II observational dataset, b–d multimodel mean of CMIP5 historicalNat, historical and historicalGHG experiments, respectively. The numbers shown in the titles of the panels are the spatial standard deviations of SST variation explained by regression (K, see text for derivation)
The forced response in R to volcanoes in obvious in the historicalNat multimodel mean (green line in Fig. 8b), because the unforced variability has been intentionally suppressed by taking the mean. The negative spikes in R should also be present in amip-piForcing if the CMIP5 simulated forced response is realistic. Because amip-piForcing is driven by the observed record of SST, which is a single realisation of history rather than a mean, we expect that unforced variability will be larger than in the historicalNat multimodel mean, and could cancel out a volcanic spike by chance.
However, it seems unlikely that all the historical major eruptions would have been obscured in this way. The historicalNat multimodel mean R(t) falls below \(-\,0.3\)\(\hbox {W}\,\hbox {m}^{-2}\) following the eruptions of Krakatau, Agung, Santa Maria and Pinatubo (green line in Fig. 8b). The same is true for all four of these eruptions in the majority of the 31 individual historicalNat integrations (Table 2), where we count \(R<-\,0.3\)\(\hbox {W}\,\hbox {m}^{-2}\) in the year of the eruption or in either of the following two years as a volcanic signal. There is no historicalNat integration in which fewer than two of these four eruptions produce such a signal, but none of them does in amip-piForcingR (blue line in Fig. 8a).
An alternative possibility is that unforced variability in R is larger in the real world than in CMIP5 AOGCMs, and dwarfs all variations of the size of the forced volcanic signal. Such large unforced variability would dominate the T–R relationship throughout the historical period, Neither anthropogenic nor natural forced signals would be discernible; instead \(\widetilde{\alpha }_{E}\) would be fairly steady, like in the individual historical integrations (\(\widetilde{\alpha }_{i}\) of MPI-ESM1.1 and \(\widetilde{\alpha }_{I}\) of CMIP5 in Fig. 5a, Sect. 5.1). This is quite unlike what we see in amip-piForcing (Figs. 5c and 6b).
Therefore we suggest that CMIP5 AOGCMs are not realistic in their response to volcanic forcing. In the real world, represented by amip-piForcing, volcanic forcing does not cause a large rapid cooling of T, as it does in CMIP5. Instead, volcanic forcing “sucks” heat from the ocean beneath. The system reacts as though it had a large heat capacity, so that \(T \simeq 0 \Rightarrow R\simeq 0 \Rightarrow N\simeq F<0\), yielding a negative spike in N. We suggest that, in both the real world and CMIP5, the volcanically forced SST pattern gives a large \(\alpha\), but that it lasts for longer in the real world. Following the eruption, the pattern of SST change causes \(R>0\) for a decade or two, perhaps through some persistent response to the subsurface cooling (discussed in Sect. 7). Consequently the volcanic episodes since 1960 are not distinct in the real world, but form a continuous period.
In support of this suggestion, we note that the normalised patterns of SST variation during 1975–2004 in historicalNat and observations have some similarities (Fig. 9a, b), especially regarding features in the North and low-latitude Pacific. On the other hand, the normalised patterns of the historical and historicalGHG experiments (Fig. 9c, d) resemble each other in these regions. For these “normalised patterns”, we exclude areas poleward of \(65^\circ\), where observational SST data is sparse and the comparison with model data is complicated by the treatment of sea-ice. We regress local annual-mean SST over the 30 years against its area-mean within \(65^\circ\) S–\(65^\circ\)N, to obtain a pattern in \(\hbox {K}\,\hbox {K}^{-1}\) with unit mean. Note that any correlated variation of local SST and global mean will contribute to this pattern, both trends and variability. Finally we subtract unity uniformly, and divide by the spatial standard deviation. The result is a field with zero mean and unit standard deviation.
The observed and historicalNat patterns could be consistent with a low EffCS because the warming in the west Pacific in these patterns leads to large upper tropospheric warming, giving large negative lapse-rate feedback, and increased stability in the low-cloud regions, giving small or negative cloud feedback (Zhou et al. 2016; Ceppi and Gregory 2017; Andrews and Webb 2018). Further GCM experiments or analyses are needed to establish how the differences in the observed and CMIP5 SST patterns lead to their various values of \(\alpha\).
Although the pattern of SST change in historicalNat is somewhat similar to observations, it is much less pronounced, as shown by smaller magnitude of SST variation explained by regression in historicalNat (0.025 K) compared with observations (0.100 K). (This number is the spatial standard deviation of the field obtained from multiplying the pattern in \(\hbox {K}\,\hbox {K}^{-1}\) from the regression, before normalisation, by the temporal standard deviation of T. This field quantifies the local temporal variation of SST due to the global-mean temporal variation.) The comparison suggests that the AOGCMs respond with a realistic pattern to volcanic forcing, but too weakly. Consequently the stronger SST variation due to greenhouse-gas forcing (0.044 K) is able to overwhelm the volcanic pattern during 1975–2004 in the CMIP5 historical experiment, making \(\widetilde{\alpha }_{E}\) similar to historicalGHG (Fig. 5c). In the real world, on the other hand, the volcanic response is persistent and dominant, and accounts for the low EffCS of the AMIP period.
7 Summary, discussion and conclusions
7.1 How accurately can \(\hbox {CO}_{2}\) EffCS be estimated from historical EffCS?
Many calculations have been published of the effective climate sensitivity (EffCS), i.e. the equilibrium warming of global-mean surface air temperature for doubled \(\hbox {CO}_{2}\), as estimated from non-equilibrium states or radiative forcings other than \(\hbox {2}\times \hbox {CO}_{2}\). Some calculations use observed climate change during the historical period, others use GCM simulations of climate change with idealised elevated \(\hbox {CO}_{2}\) concentration. For convenience, we refer to these two kinds of estimate as “historical” and “\(\hbox {CO}_{2}\)”. Both historical EffCS and \(\hbox {CO}_{2}\) EffCS have a wide spread (Knutti et al. 2017). We have quantified several reasons for the differences among these estimates, in order to address the question which supplies the title of this work.
First, the estimate of the climate feedback parameter \(\alpha\) using ordinary least-square regression (OLS) of the global-mean top-of-atmosphere radiative response against the global-mean surface temperature change from a single realisation of historical change (such as the real world) is both uncertain and biased towards low values by the presence of unforced variability. The bias causes \(\hbox {EffCS}\propto 1/\alpha\) to be overestimated, in the multimodel mean by about 10% for regression of the entire historical period, and 20% for 30-year periods. It is unimportant in scenarios of strong forcing, such as abrupt4xCO2, but cannot be neglected when considering historical variations.
Second, evaluating historical EffCS is hampered by the systematic uncertainty in the forcing F, which in CMIP5 AOGCMs gives a \({\pm }\, 45\%\) uncertainty in historical EffCS. The present phase of the Coupled Model Intercomparison Project contains new experiments which should greatly reduce the spread in all the model forcings, but an accurate estimate of real-world historical EffCS from the global-mean energy balance depends on reduction of the uncertainty in real-world historical F, assessed as about \({\pm }\,30\)% by the AR5.
Third, \(\alpha\) varies substantially on multidecadal timescales, according both to AOGCM historical experiments, which simulate climate change in response to forcing agents, and to AGCM amip-piForcing experiments, in which observed historical sea surface temperature is prescribed. This means that historical EffCS depends on the period from which it is evaluated. The historical and amip-piForcing experiments indicate that for most of the historical period the EffCS was smaller (\(\alpha\) larger) than \(\hbox {CO}_{2}\) EffCS, by up to a factor of \(\sim 2\) at some times. This bias is in the opposite direction to and therefore not explained by bias in the OLS slope.
The time-variation of \(\alpha\) in the historical experiments can mainly be explained by the varying relative importance of greenhouse gas and volcanic aerosol forcing, provided that the EffCS for volcanic aerosol forcing is smaller than for \(\hbox {CO}_{2}\) forcing (i.e. its efficacy is less than unity), so that historical EffCS falls below \(\hbox {CO}_{2}\) EffCS during volcanically affected periods. As a result, the EffCS from regression of the historical multimodel mean for the entire historical period is about 5% lower than \(\hbox {CO}_{2}\) EffCS.
The time-variation of \(\alpha\) in the amip-piForcing experiments is due to the evolving patterns of SST, and synchronised in all the AGCMs because of their common boundary conditions. The EffCS from regression of the amip-piForcing multimodel mean for the entire historical period is about 30% less than \(\hbox {CO}_{2}\) EffCS, a much greater bias than in the historical multimodel mean.
AOGCM historical and AGCM amip-piForcing experiments agree that the EffCS was relatively high in the period around 1940, when there were no large volcanic eruptions, and both greenhouse-gas and anthropogenic aerosol forcings were increasing in magnitude. The EffCS for this period in amip-piForcing has a range of 2.1–4.6 K, and is highly correlated with AOGCM \(\hbox {CO}_{2}\) EffCS across models. The agreement increases confidence in this range as an estimate of \(\hbox {CO}_{2}\) EffCS.
Since 1960, there have been three large volcanic eruptions. During this period, EffCS falls to its lowest values in amip-piForcing, of around 1.6 K, in agreement with our observational estimate for the 27 years around 1998, and consistent with low EffCS for volcanic forcing. On the other hand, EffCS increases since 1960 in the historical experiment, converges with the historicalGHG EffCS, and is correlated across AOGCMs with the \(\hbox {CO}_{2}\) EffCS. We further discuss the disagreement between historical and amip-piForcing in Sect. 7.2.
Nearly 30 years have now passed since the eruption of Pinatubo, similar to the interval between the eruption of Katmai and 1940, so we might expect that the EffCS has returned to its \(\hbox {CO}_{2}\) value, although another decade of observations may be required to demonstrate it clearly. Because greenhouse-gas forcing is increasing more rapidly now than in the early 20th century, the OLS bias in \(\alpha\) will be less important. We therefore consider that the EffCS of the first 30 years of the present century may give the most accurate energy-balance historical estimate of \(\hbox {CO}_{2}\) EffCS, especially if the uncertainty in F can be reduced, unless another explosive volcanic eruption occurs.
7.2 SST and EffCS since 1975
We have carried out AGCM experiments to show that the observed pattern of SST change during 1975–2004 (the final 30 years of the CMIP5 historical experiments) induces heat loss from the climate system, producing the historically low EffCS that is simulated in amip-piForcing, and suppressing the greenhouse warming. In some respects this pattern (Fig. 9a, b) resembles the Interdecadal Pacific Oscillation, which has been associated with the reduced rate or hiatus of global warming during the early twenty-first century, through the influence of accelerated Pacific trade winds on ocean heat uptake (England et al. 2014; Meehl et al. 2016; Oka and Watanabe 2017; Xie and Kosaka 2017).
The observed pattern of SST change during 1975–2004 has some similarities to the pattern that results during the same period from volcanic forcing in the AOGCM historicalNat experiment, including for instance the contrast between strong warming in the western Pacific and cooling or weak warming in the east, consistent with feedbacks giving a low EffCS (Zhou et al. 2016; Ceppi and Gregory 2017; Andrews and Webb 2018). However, the amplitude is much weaker in historicalNat than in observations. Therefore in the historical experiment the volcanic pattern is overwhelmed by the greenhouse-gas pattern as the latter forcing increases, whereas in the real world the similar but stronger pattern has continued to dominate. This explains why \(\alpha\) for recent decades is larger (EffCS smaller) when estimated from observations or AGCM amip-piForcing experiments than from AOGCM historical experiments.
There are several possible causes of the observed SST pattern, apart from volcanic forcing. It could be forced by anthropogenic aerosol (Smith et al. 2016), which is not distinguished in our analysis of the time-dependence of the EffCS. It could be due to an internal mode of Pacific interannual variability that is stimulated by the response to or recovery from volcanic forcing (Emile-Geay et al. 2008; Maher et al. 2015; Khodri et al. 2017; Hua et al. 2018; Eddebbar et al. 2019), or it could be due entirely to unforced variability.
Whatever the cause, it is striking that \(\alpha\) in amip-piForcing, associated with this pattern, reaches such a large value, given that it is derived from the single realisation of observed climate history. This contrasts with the AOGCMs, in which we found \(\alpha\) evaluated from a single integration to be biased low by the presence of unforced variability (Appendix C), and comparably large values are attained only in the multimodel mean. We speculate that there are coupled atmosphere-ocean feedbacks which reinforce this SST pattern in the real world but are lacking in models (McGregor et al. 2014, 2018; Raedel et al. 2016; Yuan et al. 2018; Liu et al. 2018).
The divergence of historical and amip-piForcing\(\alpha\) indicates either that the AOGCM forced response is unrealistic, or that unforced variability has recently taken the EffCS outside the range it shows in piControl experiments. Either explanation implies a deficiency in AOGCMs, and calls for further investigation.
7.3 Prospects for estimating the climate response to \(\hbox {CO}_{2}\)
There are powerful reasons for wanting to evaluate the \(\hbox {CO}_{2}\) EffCS from existing historical data, rather than waiting until we have accumulated enough further years of greenhouse-gas-forced climate change to enable an accurate energy-budget estimate. For the period since the 1980s, an estimate of EffCS can already be made from the observed energy budget (subject to systematic uncertainty in F), but this may be an underestimate of the \(\hbox {CO}_{2}\) EffCS, due to pattern effects (Sects. 7.1 and 7.2). To avoid this problem, GCMs have been used to obtain relationships between historical and \(\hbox {CO}_{2}\)-forced EffCS that may be used to correct observationally derived estimates of the EffCS (Armour 2017; Andrews et al. 2018). However, such methods suffer from systematic uncertainty owing to their dependence on the SST patterns being correctly represented by GCMs.
In order to make better use of the observed data and to refine or constrain AOGCM projections of the future, we need to study the interactions of the forcings, climate feedbacks and ocean heat uptake with the spatiotemporal patterns of SST change. Although such an analysis is more difficult than appealing to the historical global energy balance, it is necessary because the assumption that a single constant global climate feedback parameter can describe the responses to all forcings on all timescales is clearly inadequate.
References
Abraham JP, Baringer M, Bindoff NL, Boyer T, Cheng LJ, Church JA, Conroy JL, Domingues CM, Fasullo JT, Gilson J, Goni G, Good SA, Gorman JM, Gouretski V, Ishii M, Johnson GC, Kizu S, Lyman JM, Macdonald AM, Minkowycz WJ, Moffitt SE, Palmer MD, Piola AR, Resegetti F, Schuckmann K, Trenberth KE, Velicogna I, Willis JK (2013) A review of global ocean temperature observations: Implications for ocean heat content estimates and climate change. Rev Geophys 51(3):450–483. https://doi.org/10.1002/rog.20022
Allan RP, Liu C, Loeb NG, Palmer MD, Roberts M, Smith D, Vidale PL (2014) Changes in global net radiative imbalance 1985–2012. Geophys Res Lett 41:5588–5597. https://doi.org/10.1002/2014GL060962
Andrews T (2014) Using an AGCM to diagnose historical effective radiative forcing and mechanisms of recent decadal climate change. J Clim 27:1193–1209. https://doi.org/10.1175/JCLI-D-13-00336.1
Andrews T, Webb MJ (2018) The dependence of global cloud and lapse rate feedbacks on the spatial structure of tropical Pacific warming. J Clim 31:641–654. https://doi.org/10.1175/JCLI-D-17-0087.1
Andrews T, Gregory JM, Webb MJ, Taylor KE (2012) Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere-ocean climate models. Geophys Res Lett 39(7):L09,712. https://doi.org/10.1029/2012GL051607
Andrews T, Gregory JM, Webb MJ (2015) The dependence of radiative forcing and feedback on evolving patterns of surface temperature change in climate models. J Clim 28:1630–1648. https://doi.org/10.1175/JCLI-D-14-00545.1
Andrews T, Betts RA, Booth BBB, Jones CD, Jones GS (2017) Effective radiative forcing from historical land use change. Clim Dyn 48:3489–3505. https://doi.org/10.1007/s00382-016-3280-7
Andrews T, Gregory JM, Paynter D, Silvers LG, Zhou C, Mauritsen T, Webb MJ, Armour KC, Forster PM, Titchner H (2018) Accounting for changing temperature patterns increases historical estimates of climate sensitivity. Geophys Res Lett 2018:45. https://doi.org/10.1029/2018GL078887
Armour KC (2017) Energy budget constraints on climate sensitivity in light of inconstant climate feedbacks. Nature Clim Change 2017:1–8. https://doi.org/10.1038/nclimate3278
Armour KC, Bitz CM, Roe GH (2013) Time-varying climate sensitivity from regional feedbacks. J Clim 26:4518–4534. https://doi.org/10.1175/JCLI-D-12-00544.1
Barnes EA, Barnes RJ (2015) Estimating linear trends: simple linear regression versus epoch differences. J Clim 28:9969–9976. https://doi.org/10.1175/JCLI-D-15-0032.1
Bengtsson L, Schwartz SE (2013) Determination of a lower bound on Earth’s climate sensitivity. Tellus B 65(21):533. https://doi.org/10.3402/tellusb.v65i0.21533
Bloch-Johnson J, Pierrehumbert RT, Abbot D (2015) Feedback temperature dependence and equilibrium climate sensitivity. Geophys Res Lett 42:4973–4980. https://doi.org/10.1002/2015GL064240
Cahill N, Kemp AC, Horton BP, Parnell AC (2015) Modeling sea-level change using errors-in-variables integrated Gaussian processes. Ann Appl Stat 9:547–571. https://doi.org/10.1214/15-AOAS824
Ceppi P, Gregory JM (2017) Relationship of tropospheric stability to climate sensitivity and earth’s observed radiation budget. Proc Natl Acad Sci USA 114:13,126–13,131. https://doi.org/10.1073/pnas.1714308114
Ceppi P, Gregory JM (2019) A refined model for the earth’s global energy balance. Clim Dyn https://doi.org/10.1007/s00382-019-04825-x
Chung ES, Soden BJ (2015) An assessment of direct radiative forcing, radiative adjustments, and radiative feedbacks in coupled ocean-atmosphere models. J Clim 28(10):4152–4170. https://doi.org/10.1175/JCLI-D-14-00436.1
Colman R, Power SB (2018) What can decadal variability tell us about climate feedbacks and sensitivity? Clim Dyn 51:3815–3828. https://doi.org/10.1007/s00382-018-4113-7
Dessler AE (2013) Observations of climate feedbacks over 2000–10 and comparisons to climate models. J Clim 26:333–342. https://doi.org/10.1175/JCLI-D-11-00640.1
Dessler AE, Mauritsen T, Stevens B (2018) The influence of internal variability on Earth’s energy balance framework and implications for estimating climate sensitivity. Atmos Chem Phys 18:5147–5155. https://doi.org/10.5194/acp-18-5147-2018
Eddebbar YA, Rodgers KB, Long MC, Subramanian AC, Xie SP, Keeling RF (2019) El Niño-like physical and biogeochemical ocean response to tropical eruptions. J Clim 32(9):2627–2649. https://doi.org/10.1175/JCLI-D-18-0458.1
Emile-Geay J, Seager R, Cane MA, Cook ER, Haug GH (2008) Volcanoes and ENSO over the past millennium. J Clim 21:3134–3148. https://doi.org/10.1175/2007JCLI1884.1
England MH, McGregor S, Spence P, Meehl GA, Timmermann A, Cai W, Gupta AS, McPhaden MJ, Purich A, Santoso A (2014) Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nature Clim Change 4(3):222–227. https://doi.org/10.1038/nclimate2106
Flato G, Marotzke J, Abiodun B, Braconnot P, Chou SC, Collins W, Cox P, Driouech F, Emori S, Eyring V, Forest C, Gleckler P, Guilyardi E, Jakob C, Kattsov V, Reason C, Rummukainen M (2013) Evalutation of climate models. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. In: Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, pp 741–866. https://doi.org/10.1017/CBO9781107415324.020
Forster PM (2016) Inference of climate sensitivity from analysis of the Earth’s energy budget. Annu Rev Earth Planet Sci 2016:44. https://doi.org/10.1146/annurev-earth-060614-105156
Forster PMDF, Gregory JM (2006) The climate sensitivity and its components diagnosed from Earth radiation budget data. J Clim 19:39–52. https://doi.org/10.1175/JCLI3611.1
Forster PM, Andrews T, Good P, Gregory JM, Jackson LS, Zelinka M (2013) Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models. J Geophys Res 118:1–12. https://doi.org/10.1002/jgrd.50174
Frost C, Thompson SG (2000) Correcting for regression dilution bias: comparison of methods for a single predictor variable. J R Statist Soc A 163:173–189. https://doi.org/10.1111/1467-985X.00164
Gates WL, Boyle JS, Covey C, Dease CG, Doutriaux CM, Drach RS, Fiorino M, Gleckler PJ, Hnilo JJ, Marlais SM, Phillips TJ, Potter GL, Santer BD, Sperber KR, Taylor KE, Williams DN (1999) An overview of the results of the Atmospheric Model Intercomparison Project (AMIP I). Bull Am Meteorol Soc 80(1):29–55
Giorgetta MA, Jungclaus J, Reick CH, Legutke S, Bader J, Boettinger M, Brovkin V, Crueger T, Esch M, Fieg K, Glushak K, Gayler V, Haak H, Hollweg HD, Ilyina T, Kinne S, Kornblueh L, Matei D, Mauritsen T, Mikolajewicz U, Mueller W, Notz D, Pithan F, Raddatz T, Rast S, Redler R, Roeckner E, Schmidt H, Schnur R, Segschneider J, Six KD, Stockhause M, Timmreck C, Wegner J, Widmann H, Wieners KH, Claussen M, Marotzke J, Stevens B (2013) Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J Adv Model Earth Syst 5:572–597. https://doi.org/10.1002/jame.20038
Good P, Gregory JM, Lowe JA (2011) A step-response simple climate model to reconstruct and interpret AOGCM projections. Geophys Res Lett 38:L01,703. https://doi.org/10.1029/2010GL045208
Good P, Ingram W, Lambert FH, Lowe JA, Gregory JM, Webb MJ, Ringer MA, Wu P (2012) A step-response approach for predicting and understanding non-linear precipitation changes. Clim Dyn 39:2789–2803. https://doi.org/10.1007/s00382-012-1571-1
Good P, Gregory JM, Lowe JA, Andrews T (2013) Abrupt \({\rm CO}_{2}\) experiments as tools for predicting and understanding CMIP5 representative concentration pathway projections. Clim Dyn 40:1041–1053. https://doi.org/10.1007/s00382-012-1410-4
Gordon C, Cooper C, Senior CA, Banks H, Gregory JM, Johns TC, Mitchell JFB, Wood RA (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16:147–168. https://doi.org/10.1007/s003820050010
Gregory JM, Andrews T (2016) Variation in climate sensitivity and feedback parameters during the historical period. Geophys Res Lett 43:3911–3920. https://doi.org/10.1002/2016GL068406
Gregory JM, Forster PM (2008) Transient climate response estimated from radiative forcing and observed temperature change. J Geophys Res 113(D23):105. https://doi.org/10.1029/2008JD010405
Gregory JM, Stouffer RJ, Raper SCB, Stott PA, Rayner NA (2002) An observationally based estimate of the climate sensitivity. J Clim 15:3117–3121
Gregory JM, Ingram WJ, Palmer MA, Jones GS, Stott PA, Thorpe RB, Lowe JA, Johns TC, Williams KD (2004) A new method for diagnosing radiative forcing and climate sensitivity. Geophys Res Lett 31(L03):205. https://doi.org/10.1029/2003gl018747
Gregory JM, Andrews T, Good P (2015) The inconstancy of the transient climate response parameter under increasing \({\rm CO}_{2}\). Philos Trans R Soc Lond 373(20140):417. https://doi.org/10.1098/rsta.2014.0417
Gregory JM, Andrews T, Good P, Mauritsen T, Forster PM (2016) Small global-mean cooling due to volcanic radiative forcing. Clim Dyn 47:3979–3991. https://doi.org/10.1007/s00382-016-3055-1
Grose MR, Gregory J, Colman R, Andrews T (2018) What climate sensitivity index is most useful for projections? Geophys Res Lett 45:1559–1566. https://doi.org/10.1002/2017GL075742
Hansen J, Sato M, Nazarenko L, Ruedy R, Lacis A, Koch D, Tegen I, Hall T, Shindell D, Santer B, Stone P, Novakov T, Thomason L, Wang R, Wang Y, Jacob D, Hollandsworth-Frith S, Bishop L, Logan J, Thompson A, Stolarski R, Lean J, Willson R, Levitus S, Antonov J, Rayner N, Parker D, Christy J (2002) Climate forcings in Goddard Institute for Space Studies SI2000 simulations. J Geophys Res 2002:107. https://doi.org/10.1029/2001JD001143
Hansen J, Sato M, Rudy R, Nazarenko L, Lacis A, Schmidt GA, Russell G, Aleinov I, Bauer M, Bauer S, Bell N, Cairns B, Canuto V, Chandler M, Cheng Y, Del Genio A, Faluvegi G, Fleming E, Friend A, Hall T, Jackman C, Kelley M, Kiang N, Koch D, Lean J, Lerner J, Lo K, Menon S, Miller R, Romanou A, Shindell D, Stone P, Sun S, Tausnev N, Thresher D, Wielicki B, Wong T, Yao M, Zhang S (2005) Efficacy of climate forcings. J Geophys Res 110(D18):104. https://doi.org/10.1029/2005JD005776
Hansen J, Sato M, Kharecha P, Von Schuckmann K (2011) Earth’s energy imbalance and implications. Atmos Chem Phys 11:13,421–13,449. https://doi.org/10.5194/acp-11-13421-2011
Hartmann DL, Klein Tank AMG, Rusticucci M, Alexander LV, Brönnimann S, Charabi Y, Dentener FJ, Dlugokencky EJ, Easterling DR, Kaplan A, Soden BJ, Thorne PW, Wild M, Zhai PM (2013) Observations: Atmosphere and surface. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate Change 2013: the physical science basis. Contribution of working group I to the Fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press. https://doi.org/10.1017/CBO9781107415324.008
Haugstad AD, Armour KC, Battisti DS, Rose BEJ (2017) Relative roles of surface temperature and climate forcing patterns in the inconstancy of radiative feedbacks. Geophys Res Lett 2017:44. https://doi.org/10.1002/2017GL074372
Held IM, Winton M, Takahashi K, Delworth T, Zeng F, Vallis GK (2010) Probing the fast and slow components of global warming by returning abruptly to preindustrial forcing. J Clim 23:2418–2427. https://doi.org/10.1175/2009JCLI3466.1
Hua W, Dai A, Qin M (2018) Contributions of internal variability and external forcing to the recent Pacific decadal variations. Geophys Res Lett 2018:45. https://doi.org/10.1029/2018GL079033
Hurrell JW, Hack JJ, Shea D, Caron JM, Rosinski J (2008) A new sea surface temperature and sea ice boundary dataset for the Community Atmosphere Model. J Clim 21:5145–5153. https://doi.org/10.1175/2008JCLI2292.1
Jones GS, Stott PA, Christidis N (2013) Attribution of observed historical near surface temperature variations to anthropogenic and natural causes using cmip5 simulations. J Geophys Res 18(10):4001–4024. https://doi.org/10.1002/jgrd.50239
Jonko AK, Shell KM, Sanderson BM, Danabasoglu G (2012) Climate feedbacks in CCSM3 under changing \(\text{ CO }_{2}\) forcing. Part II: variation of climate feedbacks and sensitivity with forcing. J Clim 26:2784–2795. https://doi.org/10.1175/JCLI-D-12-00479.1
Kamae Y, Chadwick R, Ackerley D, Ringer M, Ogur T (2019) Seasonally variant low cloud adjustment over cool oceans. Clim Dyn 52:5801–5817. https://doi.org/10.1007/s00382-018-4478-7
Khodri M, Izumo T, Vialard J, Janicot S, Cassou C, Lengaigne M, Mignot J, Gastineau G, Guilyardi E, Lebas N, Robock A, McPhaden MJ (2017) Tropical explosive volcanic eruptions can trigger El Niño by cooling tropical Africa. Nat Commun 8:778. https://doi.org/10.1038/s41467-017-00755-6
Knutti R, Rugenstein MAA, Hegerl GC (2017) Beyond equilibrium climate sensitivity. Nat Geosci 10:727–736. https://doi.org/10.1038/NGEO3017
Larson EJL, Portmann RW (2016) A temporal kernel method to compute effective radiative forcing in CMIP5 transient simulations. J Clim 29:1497–1509. https://doi.org/10.1175/JCLI-D-15-0577.1
Liu F, Lu J, Garuba O, Leung LR, Luo Y, Wan X (2018) Sensitivity of surface temperature to oceanic forcing via \(q\)-flux Green’s function experiments. Part I: linear response function. J Clim 31:3625–3641. https://doi.org/10.1175/JCLI-D-17-0462.1
Lutsko NJ, Takahashi K (2018) What can the internal variability of cmip5 models tell us about their climate sensitivity? J Clim 31:5051–5069. https://doi.org/10.1175/JCLI-D-17-0736.1
Maher N, McGregor S, England MH, Sen Gupta A (2015) Effects of volcanism on tropical variability. Geophys Res Lett 42:6024–6033. https://doi.org/10.1002/2015GL064751
Marvel K, Schmidt GA, Miller RL, Nazarenko LS (2016) Implications for climate sensitivity from the response to individual forcings. Nature Clim Change 6:386–389. https://doi.org/10.1038/NCLIMATE2888
Marvel K, Pincus R, Schmidt GA, Miller RL (2018) Internal variability and disequilibrium confound estimates of climate sensitivity from observations. Geophys Res Lett 45:1595–1601. https://doi.org/10.1002/2017GL076468
McGregor S, Timmermann A, Stuecker MF, England MH, Merrifield M, Jin FF, Chikamoto Y (2014) Recent Walker circulation strengthening and Pacific cooling amplified by Atlantic warming. Nature Clim Change 4(10):888–892. https://doi.org/10.1038/nclimate2330
McGregor S, Stuecker MF, Kajtar JB, England MH, Collins M (2018) Model tropical atlantic biases underpin diminished pacific decadal variability. Nature Clim Change 8:493–498. https://doi.org/10.1038/s41558-018-0163-4
Meehl GA, Hu A, Santer BD, Xie SP (2016) Contribution of the Interdecadal Pacific Oscillation to twentieth-century global surface temperature trends. Nature Clim Change 6:1005–1008. https://doi.org/10.1038/NCLIMATE3107
Meraner K, Mauritsen T, Voigt A (2013) Robust increase in equilibrium climate sensitivity under global warming. Geophys Res Lett 40:5944–5948. https://doi.org/10.1002/2013GL058118
Mitchell JFB, Manabe S, Meleshko V, Tokioka T (1990) Equilibrium climate change—and its implications for the future. In: Houghton JT, Jenkins GJ, Ephraums JJ (eds) Climate change: the IPCC scientific assessment. Cambridge University Press, chap 5, pp 131–172
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. J Geophys Res 117(D08):101. https://doi.org/10.1029/2011JD017187
Myhre G, Shindell D, Bréon FM, Collins W, Fuglestvedt J, Huang J, Koch D, Lamarque JF, Lee D, Mendoza B, Nakajima T, Robock A, Stephens G, Takemura T, Zhang H (2013) Anthropogenic and natural radiative forcing. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, pp 659–740. https://doi.org/10.1017/CBO9781107415324.018
Oka A, Watanabe M (2017) The post-2002 global surface warming slowdown caused by the subtropical Southern Ocean heating acceleration. Geophys Res Lett 44:3319–3327. https://doi.org/10.1002/2016GL072184
Otto A, Otto FEL, Boucher O, Church J, Hegerl G, Forster PM, Gillett NP, Gregory J, Johnson GC, Knutti R, Lewis N, Lohmann U, Marotzke J, Myhre G, Shindell D, Stevens B, Allen MR (2013) Energy budget constraints on climate response. Nature Geosci 6:415–416. https://doi.org/10.1038/ngeo1836
Palmer MD (2017) Reconciling estimates of ocean heating and Earth’s radiation budget. Curr Clim Change Rep 3:78–86. https://doi.org/10.1007/s40641-016-0053-7
Paynter D, Frölicher TL (2015) Sensitivity of radiative forcing, ocean heat uptake, and climate feedback to changes in anthropogenic greenhouse gases and aerosols. J Geophys Res 120:9837–9854. https://doi.org/10.1002/2015JD023364
Pincus R, Forster PM, Stevens B (2016) The Radiative forcing model intercomparison project (RFMIP): experimental protocol for CMIP6. Geosci Model Dev 9:3447–3460. https://doi.org/10.5194/gmd-9-3447-2016
Proistosescu C, Donohoe A, Armour KC, Roe GH, Stuecker MF, Bitz CM (2018) Radiative feedbacks from stochastic variability in surface temperature and radiative imbalance. Geophys Res Lett 45:5082–5094. https://doi.org/10.1029/2018GL077678
Raedel G, Mauritsen T, Stevens B, Dommenget D, Matei D, Bellomo K, Clement A (2016) Amplification of El Nino by cloud longwave coupling to atmospheric circulation. Nat Geosci 9:106–111. https://doi.org/10.1038/NGEO2630
Reichler T, Kim J (2008) How well do coupled models simulate today’s climate? Bull Am Meteorol Soc 89(3):303–311. https://doi.org/10.1175/BAMS-89-3-303
Ringer MA, Andrews T, Webb MJ (2014) Global-mean radiative feedbacks and forcing in atmosphere-only and coupled atmosphere-ocean climate change experiments. Geophys Res Lett 41:4035–4042. https://doi.org/10.1002/2014GL060347
Roemmich D, Church J, Gilson J, Monselesan D, Sutton P, Wijffels S (2015) Unabated planetary warming and its ocean structure since 2006. Nature Clim Change 5:240–245. https://doi.org/10.1038/NCLIMATE2513
Sherwood S, Bony S, Boucher O, Bretherton C, Forster P, Gregory J, Stevens B (2015) Adjustments in the forcing-feedback framework for understanding climate change. Bull Am Meteorol Soc 96:217–228. https://doi.org/10.1175/BAMS-D-13-00167.1
Shindell D (2014) Inhomogeneous forcing and transient climate sensitivity. Nature Clim Change 4:274–277. https://doi.org/10.1038/NCLIMATE2136
Shine KP, Cook J, Highwood EJ, Joshi MM (2003) An alternative to radiative forcing for estimating the relative importance of climate change mechanisms. Geophys Res Lett 30:2047. https://doi.org/10.1029/2003GL018141
Silvers LG, Paynter D, Zhao M (2018) The diversity of cloud responses to twentieth century sea surface temperatures. Geophys Res Lett 45:391–400. https://doi.org/10.1002/2017GL075583
Skeie RB, Berntsen T, Aldrin M, Holden M, Myhre G (2018) Climate sensitivity estimates–sensitivity to radiative forcing time series and observational data. Earth Sys Dyn 9(2):879–894. https://doi.org/10.5194/esd-9-879-2018
Smith DM, Booth BBB, Dunstone NJ, Eade R, Hermanson L, Jones GS, Scaife AA, Sheen KL, Thompson V (2016) Role of volcanic and anthropogenic aerosols in recent slowdown in global surface warming. Nature Clim Change 6:936–940. https://doi.org/10.1038/NCLIMATE3058
Stevens B, Sherwood SC, Bony S, Webb MJ (2016) Prospects for narrowing bounds on earth’s equilibrium climate sensitivity. Earth’s Future 4:512–522. https://doi.org/10.1002/2016EF000376
Tett SFB, Betts R, Crowley TJ, Gregory J, Johns TC, Jones A, Osborn TJ, Öström E, Roberts DL, Woodage MJ (2007) The impact of natural and anthropogenic forcings on climate and hydrology. Clim Dyn 28(1):3–34. https://doi.org/10.1007/s00382-006-0165-1
Webb MJ, Andrews T, Bodas-Salcedo A, Bony S, Bretherton CS, Chadwick R, Chepfer H, Douville H, Good P, Kay JE, Klein SA, Marchand R, Medeiros B, Siebesma AP, Skinner CB, Stevens B, Tselioudis G, Tsushima Y, Watanabe M (2017) The cloud feedback model intercomparison project (CFMIP) contribution to CMIP6. Geosci Model Dev 10:359–384. https://doi.org/10.5194/gmd-10-359-2017
Xie SP, Kosaka Y (2017) What caused the global surface warming hiatus of 1998–2013? Curr Clim Change Rep 3:128–140. https://doi.org/10.1007/s40641-017-0063-0
Yuan T, Oreopoulos L, Platnick SE, Meyer K (2018) Observations of local positive low cloud feedback patterns and their role in internal variability and climate sensitivity. Geophys Res Lett 2018:45. https://doi.org/10.1029/2018GL077904
Zelinka MD, Andrews T, Forster PM, Taylor KE (2014) Quantifying components of aerosol-cloud-radiation interactions in climate models. J Geophys Res 119(12):7599–7615. https://doi.org/10.1002/2014jd021710
Zhou C, Zelinka MD, Dessler AE, Klein SA (2015) The relationship between interannual and long-term cloud feedbacks. Geophys Res Lett 42:10,463–10,469. https://doi.org/10.1002/2015GL066698
Zhou C, Zelinka MD, Klein SA (2016) Impact of decadal cloud variations on the Earth’s energy budget. Nature Geosci 9:871–875. https://doi.org/10.1038/NGEO2828
Acknowledgements
We are grateful to Luis Kornblueh for proposing the 100-member MPI-ESM1.1 historical ensemble, to the coauthors of Andrews et al. (2018) for the use of their amip-piForcing data, to Andy Dessler, Rob Colman, Jean-Louis Dufresne and other colleagues at CFMIP meetings for useful discussions, to Andy Dessler for useful comments on the manuscript, and to Michel Crucifix and two anonymous reviewers for their thorough, thoughtful and constructive comments. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement 786427, project “Couplet”). Work at the Met Office was supported by the Joint UK BEIS/Defra Met Office Hadley Centre Climate Programme (GA01101). Paulo Ceppi was supported by an Imperial College Research Fellowship. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP, and we thank the climate modeling groups (listed in Table 2 of this paper) for producing and making available their model output.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendices
A The step model
The step model (Good et al. 2011, 2013; Hansen et al. 2011; Gregory et al. 2016) is based on the assumption that the climate responses \(X_{i}(t)\) in the quantities of interest (T and N) to separate forcings \(F_{i}(t)\) combine linearly to give \(X(t)=\sum _{i}\,X_{i}(t)\) in response to the forcings applied together as \(F(t)=\sum _{i}\,F_{i}(t)\). By assuming further that the response to any step-change in forcing depends only on the size of the step and not the nature of the forcing agent, we can estimate the response to historical time-dependent net forcing F(t) due to all agents by treating it as the sum of a set of discrete steps in forcing, such that \(F(t)=\sum _{j=1}^{t}\,[F(j)-F(j-1)]\) where j are successive instants of time (we use a timestep of one year) and \(F(0)=0\). The response of an AOGCM at time t to the forcing increment which occurred at time \(j<t\) is estimated as \(X_{4\times }(t-j+1)[F(j)-F(j-1)]/F_{4\times }\), where \(X_{4\times }\) is the AOGCM’s time-dependent response to the step-change forcing \(F_{4\times }\) in the abrupt4xCO2 experiment, since time t is timestep \(t-j+1\) since the forcing increment \([F(j)-F(j-1)]\) occurred. Hence, adding up the response to all previous increments,
Note that the step-model makes no assumption about the value or time-variation of \(\alpha\), except that it is the same for all magnitudes and kinds of forcing.
Relationships in CMIP5 AOGCM historical experiments between \(\alpha\) evaluated from the ensemble-mean R(t) and T(t), and the ensemble-mean of \(\alpha\) evaluated from R(t) and T(t) in individual integrations, a, b between \(\overline{\alpha }_{i}\) and \(\overline{\alpha }_{e}\), c between time-mean \(\widetilde{\alpha }_{i}\) and time-mean \(\widetilde{\alpha }_{e}\) (see Table 1 for notation). Only those AOGCMs which have more than one ensemble member are included (see Table 2). We use our \(\hbox {AR5}'\) estimate for historicalF(t) for all AOGCMs except HadGEM2-ES and MPI-ESM1.1 (models J and P), for which we use F(t) diagnosed in these models individually (compared in Fig. 1). The dotted line in b is zero on the vertical axis; all models lie very near or above this line, indicating that \(\overline{\alpha }_{e}-\overline{\alpha }_{i}\ge 0\). The dotted line in a, c is 1:1; all models lie very near or to the right of this line in a, indicating that \(\overline{\alpha }_{e}\ge \overline{\alpha }_{i}\) (consistent with b), and in c, indicating that \(\hbox {time-mean}\ \widetilde{\alpha }_{e} \ge \hbox {time-mean}\ \widetilde{\alpha }_{i}\)
B Choice of independent variable for regression
Ordinary least-squares (OLS) linear regression assumes that all variations in the independent variable x cause proportionate variations in the dependent variable y. If there is “noise” in y, meaning fluctuations that are linearly uncorrelated with the “signal”, which is a function of x, the OLS estimate of the slope \(\mathrm {d}y/\mathrm {d}x\) is imprecise, with a standard error that increases with the amplitude of the noise (Appendix D.2), but it is unbiased, meaning that expectation value of the estimate equals the true value. On the other hand, if our data for x contain some noise which does not cause variations in y i.e. the “true” independent x on which y depends is not precisely known (possible sources of such noise are considered in Sect. 4), the OLS estimate of the slope is biased. It is expected to be smaller than the true value, and the bias grows with the amplitude of the noise (Appendix D.3).
Therefore if one of the variables contains noise which is not correlated with the other variable, the former should be chosen as dependent and the latter as independent, in order to obtain an unbiased estimate of the slope. This is the natural choice for a situation where the independent variable is chosen precisely by the experimenter, and the dependent variable is measured with some uncertainty. In our application, N and T are physically both dependent on the prescribed F, so it is not obvious which of \(R=F-N\) or T we should select as the independent variable.
Because random error is small in the MPI-ESM1.1 historical ensemble mean, we expect the bias in the estimated slope to be small, regardless of whether T or R is chosen as the independent variable. The correlation between T and R is less than unity, so the slopes for the two choices are not quite equal (Appendix D.4), but they are close, namely \(1.36\,{\pm }\,0.04\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for regression of ensemble-mean R against ensemble-mean T, denoted by \(\overline{\alpha }_{e}\) (Table 1, solid line in Fig. 4), and \(1.54\,{\pm }\,0.05\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) for T against R (dashed line), where the standard error is inferred from the residual of the fit. Therefore the historical slope for the ensemble mean is \(\overline{\alpha }_{e}=\)1.4–1.5 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), assuming the underlying physical relationship is truly linear.
The mean of the ensemble of slopes obtained by regression of R against T in the individual integrations is \(\overline{\alpha }_{i}=1.38\,{\pm }\,0.01\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) (mean and standard error), not shown in Fig. 4 because it is statistically indistinguishable from \(\overline{\alpha }_{e}\). However, the mean of the slopes from individual members when we regress T against R is quite different (dotted line in Fig. 4, slope of \(2.08\,{\pm }\,0.01\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\)), and looks like a poor fit to the ensemble-mean data. This bias is the expected outcome of OLS regression of y against x when x contains noise which is uncorrelated with y (Appendix D.3). If there is uncorrelated noise in R, linear regression of T against R gives an estimate of \(\mathrm {d}T/\mathrm {d}R\) which is biased low, and hence its reciprocal \(\overline{\alpha }=\mathrm {d}R/\mathrm {d}T\) is biased high.
To minimise the bias, we prefer to choose T as the independent variable for OLS regression (Appendix D.4), assuming that the noise in R is not correlated with T. Certainly, there appears to be more noise in R than in T (Fig. 3), consistent with physical understanding that T is related to the time-integral of N (although a similar bias in the slope could be caused by correlated noise in T and R, Appendix D.6). The results from the MPI-ESM1.1 are consistent with assuming that T contains no noise, but this may not hold for other AOGCMs.
C Error in estimating climate feedback from a single ensemble member
Using the HadGEM2 historicalF (Sec. 3.1), we carry out the calculations of Appendix B for the HadGEM2-ES historical ensemble, which comprises only five members, a typical size for CMIP5 submissions. We obtain \(\overline{\alpha }_{i}=0.94\,{\pm }\,0.10\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\) and \(\overline{\alpha }_{e}=1.22\,{\pm }\,0.14\)\(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), thus \(\overline{\alpha }_{e}>\overline{\alpha }_{i}\), unlike MPI-ESM1.1, in which we found above that \(\overline{\alpha }_{e}\simeq \overline{\alpha }_{i}\). The correlation coefficient between ensemble-mean R and T is 0.59, weaker than for MPI-ESM1.1 due to the smaller ensemble size and consequently greater noise in the ensemble mean.
For the same calculations with the historical experiments of other CMIP5 AOGCMs we use our \(\hbox {AR5}'\) estimate for F(t) (Sect. 3.3), because F has not been diagnosed in these models. Since F is model-dependent, it may differ from the \(\hbox {AR5}'\) estimate, so \(\overline{\alpha }\) from the regression could be inaccurate; that would be a systematic error that affects all the ensemble members of each model equally, rather than a statistical uncertainty affecting them randomly. Within each model ensemble, noise produces a spread of \(\overline{\alpha }\). The geometrical multimodel mean of the ensemble standard deviation of \(\overline{\alpha }\) is 0.11 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), \(\sim\) 10% of the multimodel-mean \(\overline{\alpha }_{e}\).
Across AOGCMs, the correlation cofficient of \(\overline{\alpha }_{i}\) and \(\overline{\alpha }_{e}\) is very high (0.96, Fig. 10a) but \(\overline{\alpha }_{e}>\overline{\alpha }_{i}\) (Fig. 10b), as for HadGEM2-ES, except in the MPI and CanESM2 AOGCMs, in which \(\overline{\alpha }_{e}\simeq \overline{\alpha }_{i}\). This is consistent with the bias of OLS regression whereby the slope is underestimated when there is noise in T that is not correlated with R (Appendix B); because the noise is larger in individual integrations than in the ensemble mean, \(\overline{\alpha }_{i}\) is underestimated more severely than \(\overline{\alpha }_{e}\). Furthermore, the bias tends to be greater for larger \(\overline{\alpha }_{e}\) (Fig. 10b, correlation 0.61), consistent with the same explanation (Appendix D.3). The multimodel-mean underestimate of \(\overline{\alpha }_{i}\) with respect to \(\overline{\alpha }_{e}\) is 10%.
As mentioned in Sect. 1, estimates of \(\alpha\) using observed N can be made only from the more recent \(\sim\)30 years, since interannual variation of N is not well enough known at earlier times. To evaluate the effect of the OLS bias on \(\alpha\) estimated from a 30-year period, denoted by \(\widetilde{\alpha }\) (Table 1), with each AOGCM we regress R against T for 30-year periods starting in every year (i.e. they overlap) in every integration, obtaining a timeseries \(\widetilde{\alpha }(t)\) for each integration (following Gregory and Andrews 2016). From these we calculate the ensemble-mean timeseries, denoted by \(\widetilde{\alpha }_{i}(t)\), and its historical time-mean. The time-mean is the expectation value of \(\widetilde{\alpha }\) for a randomly chosen 30-year period of a single integration. The geometrical multimodel mean of the ensemble standard deviation of \(\widetilde{\alpha }\), pooled over years in each model, is 0.42 \(\hbox {W}\,\hbox {m}^{-2}\,\hbox {K}^{-1}\), 30% of the multimodel-mean time-mean \(\widetilde{\alpha }_{e}\). Similarly, from the ensemble-mean R and T of each model we compute the \(\widetilde{\alpha }_{e}(t)\) for 30-year periods and its historical time-mean.
Across models, the correlation coefficient of the time-means of \(\widetilde{\alpha }_{i}\) and \(\widetilde{\alpha }_{e}\) is high (0.88), but time-mean \(\widetilde{\alpha }_{e}\) is greater in all cases (Fig. 10c), consistent with a greater bias of OLS regression for a randomly chosen 30-year period of a single integration than of the ensemble mean, just as for \(\overline{\alpha }_{i}\) and \(\overline{\alpha }_{e}\), but the effect is more pronounced because the noise is more important for a shorter period. The multimodel-mean underestimate of \(\widetilde{\alpha }_{i}\) with respect to \(\widetilde{\alpha }_{e}\) is 20%. Since the CMIP5 ensembles are fairly small, it is likely that \(\widetilde{\alpha }_{e}\) is also biased, and the underestimate of the true value therefore greater.
D Statistical issues in regression
Illustration of the effect of random noise on ordinary least squares regression. We take the x(t) shown in black in a, with a slope of unity so that \(y=x\), generate many sets of \({\hat{x}}_{i}(t)\) and \({\hat{y}}_{i}(t)\) by adding noise either to y or x, and calculate the distribution of estimated slopes. a Red shows an example with noise in y of standard deviation 0.075 and its regression line, grey envelope is the 5–95% range of regression lines; b distribution of correlation coefficients between \({\hat{x}}_{i}(t)\) and \({\hat{y}}_{i}(t)\) with noise in either x or y; c, d distribution of slopes of regression lines when there is noise in y or x respectively; b–d each show results for noise with three different standard deviations, as indicated by the key in d
In this appendix, we consider various statistical issues related to the estimation of \(\alpha\) as the slope of the regression of R against T. These issues apply more generally than to those specific variables. The general problem is to estimate the slope m in the linear relationship \(y(t)=mx(t)\), where x and y are timeseries of length n with values at times \(t=\tau _{1}, \tau _{2}, \ldots , \tau _{n}\), given the data \({\hat{x}}_{i}\) and \({\hat{y}}_{i}\), which may differ from x and y because of random noise. (To simplify the formulae we have chosen the origin so that the means of x and y are zero.) In the model world, we may have an ensemble of integrations \(i=1,\ldots \,N\), with the same x and y in all but different noise in each. For ensemble member i, we obtain an estimate \({\hat{m}}_{i}=\mathrm {cov}({\hat{x}}_{i},{\hat{y}}_{i})/\mathrm {var}({\hat{x}}_{i})\) of \(m=\mathrm {d}y/\mathrm {d}x\) by ordinary least-squares linear regression (OLS) of \({\hat{y}}_{i}(t)\) against \({\hat{x}}_{i}(t)\). The OLS estimate minimises the root-mean-square (RMS) of the residuals of the \(y_{i}(t)\) from the fitted line in the y-direction. By doing so it maximises the likelihood that the residuals are consistent with independent identically distributed random noise \(\epsilon _{i}(t)\) in y.
1.1 D.1 The difference method is a special case of regression
In the special case of \(n=2\), whatever the noise may be, a straight line can be drawn exactly through the two points \({\hat{x}}=x_{0}\,{\pm }\,\frac{1}{2}{{\Delta }}x\) and \({\hat{y}}=y_{0}\,{\pm }\,\frac{1}{2}{{\Delta }}y\), leaving zero residual. Denoting a mean by \(\mathrm {M}(\cdot )\), we obtain \(\mathrm {M}({\hat{x}})=x_{0}\), \(\mathrm {M}({\hat{y}})=y_{0}\), \({\mathrm{var}}({\hat{x}})={\mathrm{M}}({\hat{x}}^{2})-({\mathrm{M}}({\hat{x}}))^{2}=(\frac{1}{2}{{\Delta }}x)^{2}\), \({\mathrm{cov}}({\hat{x}},{\hat{y}})= {\mathrm{M}}({\hat{x}}{\hat{y}}) -{\mathrm{M}}({\hat{x}}){\mathrm{M}}({\hat{y}}) =\frac{1}{4}{{\Delta }}x\,{{\Delta }}y\). Hence for this case the OLS formula gives \({\hat{m}}=\mathrm {var}({\hat{x}})/\mathrm {cov}({\hat{x}},{\hat{y}})={{\Delta }}y/{{\Delta }}x\), the slope of the line passing through the points. Therefore \({\hat{m}}\) estimated as the slope between the endpoints in \({\hat{x}}\) is a special case of OLS, using a minimal amount of data, and the results derived in this appendix, that \({\hat{m}}\) is uncertain and may be biased on account of noise in x and y, apply to the difference method Eq. 2 just as they do to regression Eq. 3.
1.2 D.2 No bias in \({\hat{m}}\) due to uncorrelated noise in y
The rationale for the use of OLS is that the the independent variable \({\hat{x}}_{i}\) is perfectly known but the dependent variable \({\hat{y}}_{i}\) is noisy,
With these assumptions, \(\mathrm {var}({\hat{x}})=\mathrm {var}(x)\), and
since \(\mathrm {M}(x)=0\). Therefore the OLS slope
is an imprecise estimate of m. However, the expectation value \(E({\hat{m}})=m\), because \(E(\mathrm {M}(x\epsilon ))=0\) if there is no correlation between x and \(\epsilon\); we call the noise “uncorrelated” to indicate that is not correlated with x or y. Thus, the OLS estimate of the slope is not biased by the presence of uncorrelated noise in y.
To illustrate this, we choose a set of \(n=10\) random numbers x(t) in the interval 0–1, and take \(m=1 \Rightarrow y=x\) (x, y and \(y=x\) are shown in black in Fig. 11a). We generate \(N=10^{5}\) instances of \({\hat{y}}_{i}(t)\) from y(t) by adding independent normally distributed \(\epsilon _{i}(t)\) with standard deviation of 0.075. The correlation coefficients of x with \({\hat{y}}_{i}\) have a positively skewed distribution (red in Fig. 11b). We regress each \({\hat{y}}_{i}(t)\) against x(t) to obtain \({\hat{m}}_{i}\) (an example \({\hat{y}}_{i}\) and its regression line are shown in red in Fig. 11a). The distribution of \({\hat{m}}\) is normal, its mean is \(m=1\) and its standard deviation 0.079 (red in Fig. 11c). If we increase the amplitude of noise to 0.100 and 0.125, \({\hat{m}}\) remains unbiased but becomes less precise (standard deviation of 0.105 for green and 0.131 for blue in Fig. 11c), and the correlation is degraded gradually (Fig. 11b).
Although x was chosen randomly, there is no uncorrelated noise in x in this example, because \({\hat{x}}_{i}=x_{i}\). For example, we might have
where x(t) is the response to external forcing and the same in all ensemble members, while \(\xi _{i}(t)\) is unforced variability that is different in each member. Although \(\xi\) might be called “noise in x”, it is perfectly correlated with noise \(m\xi\) in y. If all variations \(x'\) in \({\hat{x}}\), however they are caused, produce corresponding variations \(mx'\) in \({\hat{y}}\), \({\hat{m}}\) will be an unbiased estimate of m. If x and y are T and R, this is the case which Proistosescu et al. (2018) call “ocean-forced”.
1.3 D.3 Bias in \({\hat{m}}\) due to uncorrelated noise in x
If y is not noisy but x contains uncorrelated noise \(\delta _{i}(t)\) in ensemble member i, we have
which differs from Eq. (5) because the variations \(\delta\) in \({\hat{x}}\) do not produce proportionate variations \(m\delta\) in \({\hat{y}}\). In this situation
and
Similiar to Sect. D.2, \(E(\mathrm {M}(x\delta ))=0\) for uncorrelated noise, giving
i.e. the estimate of the slope is not only imprecise, but also biased low if there is uncorrelated noise in x. (We have written this as an approximation because the expectation value of a ratio does not exactly equal the ratio of expectation values.) The slope is underestimated, through the appearance of \(\mathrm {var}(\delta )\) in the denominator, because OLS assumes that all variations in \({\hat{x}}\) cause variations in \({\hat{y}}\). The larger the ratio of noise to signal \(\mathrm {var}(\delta )/\mathrm {var}(x)\), the greater the bias. This bias has been called “regression dilution” (Frost and Thompson 2000).
We illustrate this case with the same x(t) and y(t) as the previous case, but this time we take \({\hat{y}}(t)=y(t)\) and generate N instances of \({\hat{x}}_{i}(t)\) from x(t) by adding independent normally distributed \(\delta _{i}(t)\). The distribution of \({\hat{m}}_{i}\) from regressing y(t) against \({\hat{x}}_{i}(t)\) is negatively skewed and biased low (median 0.95, 5–95% range 0.85–1.09, red in Fig. 11d). For larger noise, the spread and the bias both increase (median 0.92 for green and 0.88 for blue in Fig. 11d). The distribution of correlation coefficients in the three cases are the same as for noise in y, because the formula is symmetrical in x and y.
In our application we are estimating \(m=\alpha\) from \(R=y\) and \(T=x\). The expected magnitude of the bias in \({\hat{\alpha }}\) is therefore
If \(\mathrm {var}(T)\) and \(\mathrm {var}(\delta )\) are independent of \(\alpha\), this formula predicts that the expected bias in \({\hat{\alpha }}\) will increase in proportion to \(\alpha\). In our set of model simulations of the past, \(\mathrm {var}(T)\) is not independent of \(\alpha\), because we expect that a model with a larger \(\alpha\) (smaller EffCS) will produce a smaller historical T increase. This makes \(\mathrm {var}(T)\) smaller, \(1/(\mathrm {var}(T)+\mathrm {var}(\delta ))\) larger, and strengthens the dependence of the expected negative bias \(E({\hat{\alpha }})-\alpha\) upon \(\alpha\).
1.4 D.4 Correct choice of independent variable
If y is independent and perfectly known while x is dependent and noisy, we should instead minimise the RMS deviations of the x from the fitted line in the x-direction, obtaining from ensemble member i an estimate \({\hat{m}}_{i}^{\dag }=\mathrm {cov}({\hat{x}}_{i},{\hat{y}}_{i})/\mathrm {var}({\hat{y}}_{i})\) of the slope \(\mathrm {d}x/\mathrm {d}y\). The product \({\hat{m}}_{i}^{\dag }{\hat{m}}_{i}=(\mathrm {cov}({\hat{x}}_{i},{\hat{y}}_{i}))^{2}/ (\mathrm {var}({\hat{x}}_{i})\mathrm {var}({\hat{y}}_{i}))=r_{i}^{2}\), where \(r_{i}\) is the (product-moment) correlation coefficient between \({\hat{x}}_{i}\) and \({\hat{y}}_{i}\). Thus the lines fitted in the two ways have equal slopes \({\hat{m}}_{i}=1/{\hat{m}}_{i}^{\dag }\) if and only if \({\hat{x}}_{i}\) and \({\hat{y}}_{i}\) are perfectly correlated or anticorrelated (\(r_{i}=\,{\pm }\,1\)).
In the usual situation of imperfect correlation, the choice of independent variable therefore makes a difference to the OLS estimate of the slope. This is because of the bias caused by noise in the independent variable (Sect. D.3). If one of the variables is noisy and the other is not, we must treat the noisy variable as the dependent one to get an unbiased estimate of the slope.
1.5 D.5 Uncorrelated noise in both x and y
If there is independent noise in both x and y, we cannot get an unbiased estimate of m using OLS. This case can be be treated with “orthogonal” or “total least-squares” regression, in which the RMS deviation of the points from the line is minimised in a direction orthogonal to the line, but that requires a prior estimate of the relative size of \(\delta\) and \(\epsilon\), which we do not have. Other methods, called “error in variables”, have been developed for this case (e.g. Cahill et al. 2015).
1.6 D.6 Correlated noise in x and y
Another situation to consider is that of correlated noise in x and y. Suppose that
where \(\mu\) is a constant and \(\xi _{i}\) is noise that is different in each ensemble member. Because \(\xi _{i}\) affects both \({\hat{x}}_{i}\) and \({\hat{y}}_{i}\), the noise \(\hat{x_{i}}(t)-x_{i}(t)=\xi _{i}(t)\) in x and the noise \(\hat{y_{i}}(t)-y_{i}(t)=\mu \xi _{i}(t) + \epsilon _{i}(t)\) in y have a non-zero correlation coefficient \(\mu \,\mathrm {var}(\xi )/\sqrt{\mu ^{2}\mathrm {var}(\xi )+\mathrm {var}(\epsilon )}\). Now by following the method of Appendix D.3 we obtain
assuming x and \(\xi\) are uncorrelated.
This case is more general than, and encompasses, all of those previously considered. If \(\mathrm {var}(\xi )\ll \mathrm {var}(x)\), the noise in x is negligible, and we recover \(E({\hat{m}})=m\). If \(\mu =m\), \(y_{i}(t)=m(x_{i}(t)+\xi _{i}(t))\), as in Eq. (5), in which case we have shown that \(E({\hat{m}})=m\) still (Appendix D.2). If \(\mu =0\), the noise in x and y is decorrelated, and \(E({\hat{m}})=m/(1+\mathrm {var}(\xi )/\mathrm {var}(x))<m\) (as in Appendix D.3). The general formula with \(\mu \ne 0\) applies to two relevant physical situations in which T is x, R is y and m is the climate feedback parameter for forced climate change on multidecadal timescales.
Firstly, suppose there is unforced variability that arises spontaneously in N and causes correlated variability \(T'\) in T. This is the case which Proistosescu et al. (2018) call “radiatively forced”, and we describe it qualitatively in Sect. 4. We can illustrate the effect with a simple model. Suppose that that the spontaneous random variability \({\Phi }(t)\) in N(t) has a stepwise behaviour, such that \({\Phi }(t)={\Phi }_{j}\) for \(\tau _{j} \le t < \tau _{j+1}\), with a step-change in N of \({\Phi }_{j}-{\Phi }_{j-1}\) at \(t=\tau _{j}\). According to the step model (Appendix A), the response of \(T'\) to \({\Phi }\) is
for \(\tau _{j} \le t < \tau _{j+1}\), where \(\Theta (t)\) is the response of T per unit step-change in forcing at \(t=0\). This \(T'\) response will add a further perturbation \(\alpha T'\) to N, assuming the same climate feedback parameter \(\alpha\) applies to both forced and unforced variations. If \(T_{F}(t)\) is the response of T to external forcing F(t), we have \(T=T_{F}+T'\), \(N=F-\alpha T_{F}+{\Phi }_{j}-\alpha T'\) and \(R=F-N=\alpha T_{F}-{\Phi }_{j}+\alpha T'\). We can rewrite this as
with
This has the form of Eq. (8) for correlated noise, with \(x=T_{F}+H\), \(\xi =\Theta (t-\tau _{j}){\Phi }_{j}\), \(y=R\), \(\mu =(\alpha \Theta (t-\tau _{j})-1)/\Theta (t-\tau _{j})= \alpha -1/\Theta (t-\tau _{j})\) and \(m=\alpha\), where H is the response of T to \({\Phi }\) earlier than \(\tau _{j}\).
Physically, the correlation arises because the noise in T is the response to \({\Phi }_{j}\), while the noise in R is the sum of \({\Phi }_{j}\) itself and the response in N to \({\Phi }_{j}\). Since the responses to \({\Phi }_{j}\) in both N and T are proportional to \({\Phi }_{j}\), the noise in R and T is correlated. From \(\mu =m-1/\Theta (t-\tau _{j})\) we obtain \(\mu -m=-1/\Theta (t-\tau _{j})<0\) because for climate stability we must have \(\Theta (t)>0\). Hence \(\mu<m\Rightarrow E({\hat{m}})<m\). The climate feedback parameter will inevitably be underestimated if the correlation is due to spontaneous fluctuations in N. The effect is therefore similar to regression dilution (Appendix D.3) but it is not formally the same.
The correlation is present because both \({\Phi }\) and T have non-zero timescales of change. A zero timescale of response in T means it changes instantly when the energy balance is perturbed, keeping the system always in equilibrium with \(\alpha T=F+{\Phi }\). This requires \(\Theta (t)=1/\alpha\) for all \(t>0\), and hence \(\mu =0\), so the correlation vanishes. With stepwise variation, \({\Phi }\) has persistence with a non-zero timescale. This can be removed by replacing its step-changes at times \(\tau _{j}\) with \(\delta\)-function spikes. In that case \({\Phi }=0\) between these times, and \({\Phi }_{j}\) does not appear in \(R=\alpha (T_{F}+T')\). This is the situation of perfectly correlated noise described by Eq. (5), with \(\xi =T'\), effectively the same as no noise, because signal and noise cannot be distinguished.
Secondly, \(\xi\) could represent unforced variability that arises spontaneously in T on interannual timescales, causing an immediate radiative response in R that may have a climate feedback parameter \(\mu \ne m\). The estimate of m obtained by regression of R against T will be biased in the direction of \(\mu\) by unforced variability. The larger \(\mathrm {var}(\xi )/\mathrm {var}(x)\), the greater the bias. The ratio will be large if unforced variability is large, or if the record is short and hence shows little forced change. Unlike the previous cases, the bias in \({\hat{m}}\) could be in either direction; when \(\mu \lessgtr m\), \(E({\hat{m}})\lessgtr m\).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Gregory, J.M., Andrews, T., Ceppi, P. et al. How accurately can the climate sensitivity to \(\hbox {CO}_{2}\) be estimated from historical climate change?. Clim Dyn 54, 129–157 (2020). https://doi.org/10.1007/s00382-019-04991-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04991-y