Abstract
We investigate the opposing effects of direct radiative forcing and sea surface warming on the atmospheric circulation using a hierarchy of models. In large ensembles of three general circulation models, direct \(\hbox {CO}_2\) forcing produces a wavenumber 5 stationary wave over the Northern Hemisphere in summer. Sea surface warming produces a similar wave, but with the opposite sign. The waves are also present in the Coupled Model Intercomparison Project phase 5 ensemble with opposite signs due to direct \(\hbox {CO}_2\) and sea surface warming. Analyses of tropical precipitation changes and equivalent potential temperature changes and the results from a simple barotropic model show that the wave is forced from the tropics. Key forcing locations are the Western Atlantic, Eastern Atlantic and in the Indian Ocean just off the east coast of Africa. The stationary wave has a significant impact on regional temperature anomalies in the Northern Hemisphere summer, explaining some of the direct effect that \(\hbox {CO}_2\) concentration has on temperature extremes. Ultimately, the climate sensitivity and future changes in the land–sea temperature contrast will dictate the balance between the opposing effects on regional changes in mean and extreme temperature and precipitation under climate change.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is well established that there are differing, and sometimes opposing, effects of radiative forcing versus sea surface temperature (SST) change on the atmospheric circulation (e.g. Mitchell 1983; He and Soden 2015; Shaw and Voigt 2015; Chadwick et al. 2017). Land warming is primarily driven by the SST warming of the oceans, an indirect effect of anthropogenic emissions, rather than the direct response to increasing greenhouse gases (GHGs) over land (Compo and Sardeshmukh 2009). However, global mean temperature increase driven by the SST warming is not the sole driver of changes in temperature and precipitation patterns (Folland et al. 1998; Sexton et al. 2003; Bony et al. 2013; Dong and Sutton 2015; Richardson et al. 2016) or extremes (Kamae et al. 2014a; Seneviratne et al. 2014; Dong et al. 2016; Baker et al. 2018a).
Shaw and Voigt (2015) investigate the large scale circulation responses to direct \(\hbox {CO}_2\) radiative forcing versus SST warming in the Coupled Model Intercomparison Project phase 5 (CMIP5) ensemble, finding that \(\hbox {CO}_2\) forcing leads to positive land–sea equivalent potential temperature (\(\theta _e\)) contrasts, and SST forcing leads to negative land–sea \(\theta _e\) contrasts. In the \(\hbox {CO}_2\) case, the positive land–sea \(\theta _e\) contrasts lead to low-level convergence around Asia, a stronger Asian monsoon cyclone and Pacific anticyclone, and a poleward shift of the Pacific jet stream. The negative land–sea \(\theta _e\) contrasts in the SST case lead to the opposite effects on the circulation. However, Shaw and Voigt (2015) do not look specifically at changes in midlatitude stationary waves in response to the two types of forcing, which may have an important impact on future changes in regional Northern Hemisphere (NH) summer temperatures and heatwave hazard due to the direct effect of \(\hbox {CO}_2\) shown by Baker et al. (2018a).
A key factor in the opposing circulation responses comes from the differing land–sea contrast response to radiative forcing versus SST warming (Kamae et al. 2014b; Shaw and Voigt 2015). The land–sea contrast arises from the non-linearity of the Clausius–Clapeyron relationship between saturation specific humidity and temperature (Joshi et al. 2008). The dynamical precipitation response to direct \(\hbox {CO}_2\) forcing has been associated with the land–sea contrast, leading to an increase in precipitation over tropical land, and a decrease over the oceans due to a weakening of the overturning circulation (Bony et al. 2013). Upper tropospheric heating stabilises the atmosphere which leads to a decrease in convection (He and Soden 2015). However, in response to the heating the land warms and destabilises the atmosphere, leading to an increase in convection over land (Bony et al. 2013).
Changes in convection can cause changes in the upper-level divergence, which can force Rossby waves that can propagate from the tropics into the extratropics (Sardeshmukh and Hoskins 1988). Specifically, changes in the Walker circulation have been shown to affect upper tropospheric divergence and produce a stationary wave with wavenumber 5 over the NH midlatitudes in winter (Haarsma and Selten 2012) which strongly resembles the circumglobal wave guide pattern described by Branstator (2002). The NH summer circulation also has a wave 5 circumglobal wavetrain associated with natural variability (Ding and Wang 2005), which has a forced component arising from the tropics (Ding and Wang 2007; Yasui and Watanabe 2010).
Schubert et al. (2011) suggest that stationary Rossby waves can play an important role in causing NH summer heat extremes and Screen and Simmonds (2014) show the link between extreme weather event frequency in the NH and amplified stationary planetary waves. Studies using reanalysis (Cassou et al. 2005) and model data (Lee et al. 2017) point towards tropical forcing in exciting Rossby waves that cause extremes. One particular theory of how summer stationary waves cause heat extremes is quasiresonant amplification (Petoukhov et al. 2013). However, in this study we test the hypothesis that simple changes in tropical forcing can trigger stationary Rossby waves that can affect heat extremes. Previous studies identify the tropical Atlantic (Cassou et al. 2005), tropical Pacific and Caribbean (Wulff et al. 2017; O’Reilly et al. 2018), Indian monsoon region (Joseph and Srinivasan 1999; Lin 2009) and equatorial Africa (Yasui and Watanabe 2010) as important Rossby wave forcing regions. We aim to diagnose the important forcing locations for the stationary waves seen in response to the SST and \(\hbox {CO}_2\) forcings.
Here we investigate the responses of precipitation and NH stationary waves to these two types of forcings. Using three general circulation models (GCMs) and the CMIP5 ensemble, we develop and test a theory on the midlatitude circulation response to SST warming and direct \(\hbox {CO}_2\) forcing. We hypothesize that the two different forcings produce opposite changes in divergence (and corresponding opposite changes in precipitation) in the tropics, leading to stationary waves in antiphase. These opposite divergence responses arise from the opposite responses of land–sea \(\theta _e\) contrasts and the differing thermodynamic effects of radiative forcing versus SST increases. We then test our hypothesis that the anomalous forcings produce the stationary wave using a simple barotropic model to reproduce the GCM wave response and identify key forcing locations.
Section 2 outlines the methods and models used in the study. Section 3 presents the GCM results leading us to perform the barotropic model experiments which we analyse in Sect. 4. We then investigate the forcing mechanisms in Sect. 5. Section 6 discusses the relevance of the work and the implications of our findings, before we present our conclusions in Sect. 7.
2 Methods
2.1 GCM data
In this study, we use results from large ensembles of three general circulation models (GCMs): HadAM3P, MIROC5 (Watanabe et al. 2010) and CAM4 (Gent et al. 2011). HadAM3P is an atmosphere only, medium resolution GCM developed by the UK Met Office. It is based upon the atmospheric component of HadCM3 (Pope et al. 2000; Gordon et al. 2000). We use an improved version of HadAM3P which has a more sophisticated land-surface scheme (Guillod et al. 2017). We run HadAM3P using the large-ensemble capability provided by the climateprediction.net volunteer computing network (Allen 1999; Guillod et al. 2017), where members of the public run initial condition ensemble GCM simulations. We compare results from HadAM3P (run at \(1.25^{\circ }\times 1.875^{\circ }\) resolution) to MIROC5 and CAM4 (run at \(1.4^{\circ }\times 1.4^{\circ }\) and \(1.9^{\circ }\times 2.5^{\circ }\) resolutions respectively). The models are run as Atmospheric Model Intercomparison Project (AMIP) style ensembles (Taylor et al. 2012) with prescribed SSTs and sea ice. All the ensembles and their setups are summarised in Table 1.
2.1.1 \(1.5\,^\circ \hbox {C}\) experiments
The first set of experiments, the \(1.5\,^\circ \hbox {C}\) experiments, have two ensembles for each model, which use the Half a degree Additional warming, Prognosis and Projected Impacts (HAPPI; http://www.happimip.org) design (Mitchell et al. 2017). These two ensembles use SSTs and other boundary conditions to simulate conditions in a world \(1.5\,^{\circ }\hbox {C}\) warmer than pre-industrial (1861–1880) conditions. Here we use the HAPPI Tier 1 experimental design (Mitchell et al. 2017), which uses the multi-model mean SST patterns; thus, all ensembles and models are run with an identical time varying \(1.5\,^{\circ }\hbox {C}\) SST pattern. The full details are discussed in Mitchell et al. (2017).
The two ensembles differ only in \(\hbox {CO}_{2}\) concentration, but otherwise use the RCP2.6 scenario forcings from the last decade of the twenty-first century. In HadAM3P and MIROC5, \(\hbox {CO}_{2}\) is fixed at 395.8 ppm (hereafter the \(\hbox {LCO}_2\) ensemble) and 550.0 ppm (\(\hbox {HCO}_2\) ensemble), representing the lower and higher likely \(\hbox {CO}_{2}\) concentrations averaged over 2091–2100 in adaptive pathways that succeed in achieving warming below \(1.5\,^{\circ }\hbox {C}\) in 2100 for the assessed ranges of climate response uncertainty (Millar et al. 2017). For CAM4, we use experiments with the \(\hbox {CO}_{2}\) fixed at 379.0 ppm and 423.1 ppm; hence, differences between the CAM4 ensembles still occur due to the difference in \(\hbox {CO}_2\) concentration, but should not be quantitatively compared to the other two models. All \(\hbox {CO}_{2}\) concentrations are prescribed as a global mean atmospheric concentration and the \(\hbox {CO}_{2}\) is well-mixed. All ensemble members are run for 11 years, with the first year discarded to allow the atmosphere to spin up. For HadAM3P there are 98 and 119 members for the \(\hbox {LCO}_2\) and \(\hbox {HCO}_2\) ensembles respectively. Both MIROC5 ensembles have 50 members, and both CAM4 ensembles have 501 members. For the full details of these ensembles, see Baker et al. (2018a). These simulations provide large ensembles from three models in which the \(\hbox {CO}_2\) concentration is varied but the SSTs are held fixed.
2.1.2 Hadley experiments
We run a further three ensembles just using HadAM3P, the Hadley experiments. These ensembles, named NAT, GHG and SST, are designed to isolate the response of the atmosphere to SST forcings and GHG forcings associated with global warming separately. The NAT ensemble has natural SSTs and GHGs which simulates a world with no anthropogenic climate change. The NAT SSTs are calculated by removing the modelled anthropogenic warming from observed SSTs. The anthropogenic warming is calculated as in Haustein et al. (2016): 11 GCM simulations from the CMIP5 archive are averaged and the monthly climatologies (1996–2005) of the HistoricalNat simulations are subtracted from the Historical simulations. The mean of these 11 patterns is used as the SST pattern for the NAT ensemble and pre-industrial atmospheric GHG concentrations (IPCC 1900 forcing) are used to force the NAT ensemble. For further details, see Haustein et al. (2016) and Schaller et al. (2016). The GHG ensemble uses the NAT SSTs, with RCP4.5 GHGs (from 2005–2015). The SST ensemble uses the observed 2005–2015 SSTs from the OSTIA SST dataset (Donlon et al. 2012) and pre-industrial GHGs. The \(\hbox {CO}_2\) concentration of the NAT and SST ensembles is 284.4 ppm, the average \(\hbox {CO}_2\) concentration of the GHG ensemble is 390.4 ppm. Sea ice for the NAT and GHG ensembles is taken from the maximum well-observed sea ice (DJF 1986/1987), for the SST ensemble the 2005–2015 observed OSTIA sea ice is used. Volcanic forcings are set to zero in all three ensembles, and the solar forcing is taken from 2005–2015. All three ensembles are run for 11 years, with the first year discarded. There are 124, 118 and 113 ensemble members for the NAT, GHG and SST ensembles respectively.
2.1.3 CMIP5 experiments
We also make use of AMIP data from the AMIP control, AMIP4K and AMIP4xCO2 simulations (Taylor et al. 2012) from the following CMIP5 models: bcc-csm1-1, CanAM4, CNRM-CM5, FGOALS-g2, HadGEM2-A, IPSL-CM5A-LR, IPSL-CM5B-LR, MPI-ESM-LR and MPI-ESM-MR. All simulations are forced with historical SSTs and greenhouse gases and are run over the 30-year period 1979–2008.
2.2 Barotropic model
In this study we employ the idealised barotropic model from O’Reilly et al. (2018). Following Hoskins and Ambrizzi (1993), the model integrates the barotropic vorticity equation on a sphere:
where \(\mathbf {u}_\varPsi\) is the rotational velocity field, \(\zeta\) is the absolute vorticity (the sum of planetary and relative vorticity components), F is a constant forcing term, \(\lambda\) is a linear damping rate with a timescale of 10 days, and \(\mu =2.4\times 10^{16}\hbox { m}^4\hbox { s}^{-1}\) is a biharmonic diffusion coefficient. The equation is solved using spectral harmonics with a triangular truncation at wavenumber 42 (i.e. T42). The forcing is decomposed into two terms, \(F=\overline{F}+{F}'\), where \(\overline{F}\) is selected to maintain the basic state exactly, which is taken to be the climatological vorticity field at 200 hPa from the relevant dataset.
The model output from HadAM3P, used as the background state in the barotropic model, includes winds on 850, 500 and 200 hPa pressure surfaces. We choose the 200 hPa winds to calculate the climatological vorticity field for the barotropic model; the anomalous tropical forcing (via divergent outflow) is strongest in the upper troposphere (e.g. Krishnamurti et al. 2013); and vorticity gradients, upon which the signal propagates out of the tropics, are also significantly stronger in the upper troposphere. It is necessary that the basic state includes these strong wave guides to achieve a reasonable response, both in amplitude and pattern (O’Reilly et al. 2018).
The anomalous forcing, \({F}'\), is selected to mimic the forcing of the barotropic vorticity equation by divergent outflow in the tropics. Following Sardeshmukh and Hoskins (1988), the linearised Rossby wave source (RWS) anomaly \({S}'\) is given by
where \(\mathbf {u}_\chi\) is the divergent velocity field and \(D=\nabla \cdot \mathbf {u}_\chi\) is the divergence. Here the overbars and the primes denote climatological and anomaly fields respectively. In this study, we force the model with a RWS anomaly due only to anomalous divergence and anomalous transports of mean vorticity. We ignore terms due to anomalous vorticity, as these terms largely correspond to the circulation response we are assessing. The forcing term therefore reduces to:
The model is initialised from the basic state and integrated forward for 25 days. The response becomes quasi-stationary after about two weeks, so the stationary response to forcing is presented as the average over the period 16–20 days.
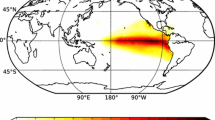
Responses of the different models to \(\hbox {CO}_{2}\) forcing. a HadAM3P \(\hbox {CO}_{2}\), b MIROC5 \(\hbox {CO}_{2}\) and c CAM4 \(\hbox {CO}_{2}\). Contours show the JJA 200 hPa meridional wind response (interval: \(0.2\hbox { ms}^{-1}\) with the zero contour suppressed), colours show the JJA precipitation response. The CAM4 wind and precipitation responses have been multiplied subjectively by 2.5 to be plotted on the same scale as the other two model responses
Responses to GHG and SST forcing. a AMIP4\(\hbox {xCO}_{2}\), b AMIP4K, c HadAM3P GHG and d HadAM3P SST. Contours show the JJA 200 hPa meridional wind response (interval: \(0.4\hbox { ms}^{-1}\) (a, b) and \(0.2\hbox { ms}^{-1}\) (c, d) with the zero contour suppressed), colours show the JJA precipitation response
3 GCM results
The June–July–August (JJA) difference in precipitation (colours) and 200 hPa meridional wind (contours) between ensemble mean \(\hbox {HCO}_2\) and \(\hbox {LCO}_2\) ensembles (\(\hbox {CO}_2\) response) are shown in Fig. 1. The pattern of tropical precipitation change in the \(\hbox {CO}_2\) response for the three models is very similar: a wetting over land and a drying over the oceans. This is associated with a poleward shift of the intertropical convergence zone (ITCZ) over the Sahel region of Western Africa.
We also observe a circumglobal wave pattern over the NH between \(30^\circ \hbox {N}\)–\(70^\circ \hbox {N}\). Whilst the strength of the wave varies spatially in the different models, a wavenumber 5 stationary wave with wave centres in the same locations is observed in all three \(\hbox {CO}_2\) responses. Due to large ensemble sizes and long runs, the responses of the tropical precipitation and meridional wind are both statistically significant (shown for the quantities plotted in Fig. 1 in Fig. S1 and Fig. S2). To quantify the agreement between the model responses, we compute the anomaly correlation coefficients between the responses (shown in Table S1 and Table S2). As the correlation coefficients show, the model responses bear strong quantitative similarities to one another.
Very similar stationary wave and precipitation responses to \(\hbox {CO}_2\) forcing are evident and robust in the difference between the multi-model-mean of the AMIP4\(\hbox {xCO}_2\) and AMIP control ensembles (AMIP4\(\hbox {xCO}_2\) response) (Fig. 2a, individual model responses in Fig. S3). The responses to a uniform SST increase are shown in Fig. 2b (individual model responses in Fig. S4), the difference between the multi-model mean AMIP4K and AMIP control ensembles (AMIP4K response). Here, there is an opposite response in the precipitation over the tropical Atlantic and over the tropical region of Africa compared to the response to \(\hbox {CO}_2\). The stationary wave is still present, but with the wave centres in antiphase to the \(\hbox {CO}_2\) and AMIP4\(\hbox {xCO}_2\) responses.
A similar picture emerges when we consider the difference between the GHG and NAT ensembles (GHG response), and SST and NAT ensembles (SST response) (Fig. 2c, d). The GHG response shows increased precipitation over the tropical region of Africa, and decreased precipitation over the tropical Atlantic. The stationary wave is present, with the same wave centres as the \(\hbox {CO}_2\) and AMIP4\(\hbox {xCO}_2\) responses. In agreement with the AMIP4K response, the SST response is almost diametrically opposed to the \(\hbox {CO}_2\) and AMIP4\(\hbox {xCO}_2\) responses: drying over the tropical regions of Africa and wetting over the tropical Atlantic. The stationary wave is also apparent in the SST response with the same wave centre locations as the AMIP4K response.
Summary of the responses to forcing in the different experiments. a Summary of the CMIP5 AMIP experiments showing difference the between 4\(\hbox {xCO}_{2}\) and AMIP4K ensemble mean responses, b summary of the Hadley experiments showing the difference of GHG and SST ensemble mean responses. Contours show the JJA 200 hPa meridional wind response (interval: \(0.8\hbox { ms}^{-1}\) (a) and \(0.4\hbox { ms}^{-1}\) (b) with the zero contour suppressed), colours show the JJA precipitation response. c Summary of the barotropic modelling experiments. Colours show the difference between the anomalous June RWS forcings in the GHG and SST ensembles. Contours show the difference between the model response when forced with the anomalous GHG RWS and when forced with the anomalous SST RWS (interval: \(0.3\hbox { ms}^{-1}\) with the zero contour suppressed)
Effect of the hemispheric wave on summer temperatures. JJA daily mean temperatures regressed onto the standardized circulation index for a HadAM3P \(\hbox {CO}_{2}\), b MIROC5 \(\hbox {CO}_{2}\), c CAM4 \(\hbox {CO}_{2}\), d HadAM3P GHG and e HadAM3P SST. The hatching shows where the regression is significant at the 5% level using a two-sided Wald Test. Pink and green dots mark the positive and negative meridional wind wave centres respectively used to create the circulation index for each ensemble
To summarise the precipitation and meridional wind changes, we plot the differences between the AMIP4\(\hbox {xCO}_2\) and AMIP4K responses and the differences between the GHG and SST responses in Fig. 3. This emphasises the important features consistent between the responses to direct \(\hbox {CO}_2\) forcing and SST warming, and removes elements of noise. It is clear that the consistent precipitation changes between the CMIP5 experiments and Hadley experiments are located in the tropics over the Atlantic, Africa and Central-West Pacific. The wave 5 pattern and wave centres in the two experiments are also co-located, with slight differences over Europe. The similarity of the wave and precipitation responses across the range of models (quantified in Table S1 and Table S2) illustrates their robustness. Further to this, given the wave and precipitation responses to SST warming arise not only when applying the warming pattern (in the Hadley experiments), but also in the case of uniform warming (AMIP4K response), this suggests that the response is not just due to the spatial location of the SST warming pattern, but is a robust response to broad SST warming. The comparisons also show a similar response arising from both strong forcing (in the case of the CMIP5 experiments) and weak forcing (in the case of the Hadley experiments).
Before examining the origin of the stationary wave, we investigate what impact such a wave has on NH temperature. As shown by Baker et al. (2018a), the ensemble mean JJA temperature response in the \(\hbox {CO}_2\) forced ensembles is a wavelike positive-negative temperature anomaly pattern across the NH in JJA, which is associated with increases in extreme temperature events. We focus on the \(1.5^\circ \hbox {C}\) and Hadley experiment results as we have large ensembles for these models, as opposed to the one realization from each model in the CMIP5 AMIP ensemble. We use a simple linear regression to diagnose the relationship between the temperature anomalies and the stationary wave.
We first define the response of a particular member as the difference between the \(\hbox {HCO}_2\) ensemble member 10-year mean and the \(\hbox {LCO}_2\) ensemble mean across the ensemble members. For each member we create a circulation index by subjectively taking the locations of the maximum clearly defined wave centres in the JJA ensemble mean 200 hPa meridional wind responses (see dots in Fig. 4 for wave centre locations). We sum the positive wave centres (pink dots) and subtract the negative wave centres (green dots) to give a circulation index for each ensemble member response. We then regress the standardized circulation indices for each ensemble member against the ensemble member mean temperature response at each gridpoint.
The regression coefficients are plotted in Fig. 4. They show that members with a strong circulation index response have strong temperature anomalies compared to members with weaker circulation index responses. Regions where the stationary wave is anticyclonic are associated with regions of increased temperature, and cyclonic regions are associated with regions of decreased temperature. Anticyclonic regions are typically characterised by clear skies, which leads to greater incident solar radiation on the Earth’s surface, hence an increase in surface temperature (Bieli et al. 2015). The temperature anomalies are completely opposite for the SST case, which supports the link between the wave and the temperature anomalies further. In the \(\hbox {CO}_2\) cases, the regions of positive temperature anomaly are co-located with the NH regions that see increases in heat extremes under higher \(\hbox {CO}_2\) concentrations in Baker et al. (2018a). This suggests that the direct circulation response to higher \(\hbox {CO}_2\) concentrations governs the regional differences in increases in extremes. It is worth noting that this regression approach likely underestimates the effect of the circulation on temperature as the circulation index is comprised of wave centres across the NH. As we will show in Sect. 4, the wave is actually forced from several different locations which contribute to parts of the wavetrain meaning the full wave is not necessarily present at all longitudes in each ensemble member. This suggests that if a single wave centre were used as the circulation index, there would be a larger local regression coefficient and therefore a larger effect on the local temperature.
A potential mechanism for the emergence of a stationary wave response to forcing is through changes in convection in the tropics forcing a Rossby wave that then propagates into the midlatitudes (Haarsma and Selten 2012). These changes in convection can cause changes in upper-level divergence (with associated precipitation changes) which can be captured by changes in the RWS. One robust precipitation change is the decrease in precipitation in the tropical Western Atlantic and Caribbean Sea for the \(\hbox {CO}_2\) forced cases (Figs. 1, 2a, c), and an increase in the SST forced cases (Fig. 2b, d). A second robust change is the increase in precipitation in the tropical regions of Africa for the \(\hbox {CO}_2\) forced cases (Figs. 1, 2a, c), and a decrease in the SST forced cases (Fig. 2b, d). The reasons behind these observed changes will be explored in Sect. 6, for now we just seek to highlight these regions as potentially important regions where changes in the divergence lead to changes in the RWS. Another potential mechanism that could explain the stationary wave is by changes in the zonal mean westerlies in the sub-tropical upper troposphere (Simpson et al. 2016). The zonal mean westerly changes can cause changes in the midlatitude waveguides, affecting the propagation of Rossby waves. To investigate both these effects, we choose to focus on the wave response further in HadAM3P given the data available from the Hadley experiments for both GHG and SST forcing cases plus the fact that HadAM3P exhibits the clearest wave response (see Fig. 1).
4 Barotropic model results
4.1 Full response
To investigate the wave pattern, we perform a series of experiments with the barotropic model. We choose a barotropic model as it is the simplest model where we can investigate both wave forcing from the tropics by applying an anomalous RWS, and also the effect of the background state on wave propagation by applying either the control background state or SST/GHG forced background state. The impact of changing the background state on wave propagation can be explained via the linear theory of barotropic Rossby waves in a zonal flow (Simpson et al. 2016), and so this effect is captured in the barotropic model. The RWS from the full model which acts as wave forcing can be backed out simply from the full model wind response field. The main disadvantages of the barotropic model are that it only has one level and so no vertical profile. This requires a choice of level as background state, and this choice is not always obvious (O’Reilly et al. 2018). Despite this, we employ the barotropic model as a tool to provide potential insight into the stationary wave pattern.
As outlined in Sect. 2.2, we compute the RWS (neglecting anomalous vorticity terms). We do this using the NAT ensemble mean as the 200 hPa climatological fields (overbar variables in Eq. 3) and define the anomalous fields (primed variables) as the GHG (or SST) ensemble minus the NAT ensemble 200 hPa fields. To test whether the barotropic model responses are linear, we multiply the input forcings by \(10^{-6}\) (and then scale the output fields back up by \(10^6\)). Sensitivity experiments with and without the linearisation applied display no differences, and so the remainder of the barotropic experiments use the unscaled forcings. To first test that the barotropic model can produce the stationary wavelike response in the full GCMs, we force the barotropic model using the anomalous June RWS forcings from the GHG and SST ensembles, with the June NAT vorticity background state. The June forcing and background state are chosen as sensitivity tests using different background state months and anomalous forcing months (not shown) show this combination gives the largest amplitude and clearest Rossby wave response. The June background state has the strongest vorticity gradients which are necessary for the barotropic model to propagate a wave response across. The July, August and JJA vorticity gradients are weaker, which suggests why the barotropic model with the June background state reproduces the wave response best.
Barotropic model forcing and response. June Rossby wave source forcing from HadAM3P a GHG and b SST runs. The pink box demarcates the region used to force the barotropic model (\(0^\circ{-}15^\circ \hbox {N}\)). Barotropic model meridional wind response averaged from day 16–20 for c the GHG forcing and d the SST forcing. Both cases use the NAT ensemble mean June 200 hPa vorticity as the background state
Idealised barotropic model results. Weights from idealised patch experiments for NAT and NCEP2 backgrounds and HadAM3P Rossby wave source for a GHG ensemble response and b SST ensemble response. Rossby wave source is averaged over \(0^\circ {-}15^\circ \hbox {N}\) and then normalised so its maximum corresponds to the June weight maximum. The weights in the SST case have been multiplied by − 1. Idealised meridional wind responses are shown for c West Atlantic, d East Atlantic and e Indian Ocean forcing patches (location marked by pink cross). Combined response of Western and Eastern Atlantic and Indian Ocean forcings with f NAT background state and g NCEP2 background state
The results of forcing the barotropic model with the GHG and SST RWS are shown in Fig. 5. Anomalous forcing is only applied between \(0^\circ{-}15^\circ \hbox {N}\) (pink box in Fig. 5a, b). The decision to use forcing between \(0^\circ {-}15^\circ \hbox {N}\) in the barotropic model clearly has an impact on the wave response, and we restrict the forcing to equatorwards of \(15^\circ \hbox {N}\) to avoid over-constraining the model by imposing the wave response itself. Without conducting an in-depth sensitivity study to determine the best forcing latitudes (which is beyond the scope of this study), we feel our choice is valid given we can reproduce the wave 5 pattern. The forcings in the GHG and SST cases are opposite in several regions including the Western Atlantic, Eastern Atlantic and in the Indian Ocean, just off the east coast of Africa. Anomalous RWS forcings arise from changes in tropical convective heating (Sardeshmukh and Hoskins 1988), caused by the changes in precipitation in the tropics. The co-location of precipitation responses and anomalous RWS forcings suggest that the vertical motion associated with precipitation changes are responsible for the anomalous RWS forcings.
A comparison between the barotropic meridional wind responses (Fig. 5c, d) and the full model responses (Fig. 2c, d) reveals that the barotropic model can capture the main features of the full model. The wave pattern is clearly visible in both GHG and SST barotropic model experiments, with the same wavenumber as in the full model responses. Wave centres in the barotropic cases are shifted slightly eastward compared to the wave in the JJA mean in the Hadley experiments. However, the June mean wave centres in the Hadley experiments are also shifted by a similar amount eastward from the JJA mean (not shown), indicating that the shift between the wave in the barotropic model and the Hadley experiments could be due to the background winds differing between June and the JJA mean. Some wave centres are not as far poleward as in the full model response. This is evident in the jet exit regions, where climatological vorticity gradients are weak (e.g. over Northern Europe); there, a simple barotropic model will struggle to propagate the wave. Other reasons for the wave differences include the barotropic model not capturing important feedbacks that occur in the full model, such as zonal wind changes, eddy mean flow interactions, or potentially important non-linear orographic interactions (Ting 1994). Nevertheless, the fact that the barotropic model results bear strong similarity to the full model is remarkable given the model’s simplicity.
Figure 3c summarises the forcing used and the wave response in the barotropic model, taking the difference between GHG and SST RWS forcings and barotropic model meridional wind responses to highlight the areas of consistent change between the two ensemble responses. The strongest RWS signal is in the Indian Ocean; there is a dipole in the tropical Atlantic and various consistent regions across the Pacific too. The stationary wave responses in the barotropic model are very similar to the GCM responses (quantified in Table S1), suggesting the GCM responses are indeed forced from the tropics. Correlations are lower than between the full model responses, this is partly because, as mentioned before, the wave centres are shifted slightly eastward in the barotropic model, and also because the wave centres are slightly further equatorward in the barotropic model.
To test whether the observed wave is a new forced wave, or an excitation of a wave in the climatological background state, we perform the same experiments after removing wavenumbers 4–6 from the background state. The barotropic model responses in this case still display the same wave pattern with wavenumber five (not shown), implying that the wave is a new forced wave due to the anomalous RWS. We also test whether the change of the background state has a substantial impact on the summer stationary waves (cf. to the effect of the background state on winter stationary waves in Simpson et al. 2016) by using the barotropic model with the GHG ensemble background state and comparing it to results using the NAT ensemble background state. If the background state were to be having a substantial effect, one would expect the waves to differ between the two experiments noticeably, however we observe no large difference in the wave responses (not shown). These results suggest that the stationary wave arises from anomalous wave forcing, not from changes in the zonal winds.
4.2 Sensitivity tests
To determine the forcing locations responsible for producing the wave response in the barotropic model, we perform a set of sensitivity experiments using the barotropic model. Following Barsugli and Sardeshmukh (2002), we apply a series of 64 cosine-square patch forcings of the form:
on the rectangle \(\phi _0\pm \phi _w\), \(\lambda _i\pm \lambda _w\) (where \(\phi\) is the latitude and \(\lambda\) is the longitude), and zero elsewhere. The half-widths of the patches are fixed at two gridpoints in both the latitudinal and longitudinal directions, yielding \(\phi _w\approx 5.58^\circ\) and \(\lambda _w=5.625^\circ\). We apply the patch centres at a single fixed latitude \(\phi _0=7.0^\circ\), whilst increasing \(\lambda_i\) in \(5.625^\circ\) increments starting at \(0^\circ\), giving 64 patches in total. The amplitude of the patches, \(A=2.5\times 10^{-11}\hbox { s}^{-2}\), is chosen to be on the order of magnitude of, but slightly larger than, the forcing observed in the GHG forced ensemble so as to produce a strong signal in the barotropic model.
To assess the importance of a particular patch location in forcing the HadAM3P meridional wind response, we assign the following weight to each patch experiment response:
where \(v^{b}_{i}\) is the meridional wind response averaged between days 16–20 in the barotropic model for forcing \(F'_{i}\), and \(\bar{v}\) is the June ensemble mean meridional wind response from the HadAM3P model. The dot products are computed using cosine latitude weighting, and over the region \(30^\circ \hbox {N-}70^\circ \hbox {N}\) and all longitudes.
We perform two sets of sensitivity experiments, one using the HadAM3P NAT ensemble mean June background state, and the other using the NCEP Reanalysis 2 1979–2015 June mean background state (NCEP Reanalysis 2 data provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, from their website at http://www.esrl.noaa.gov/psd/). We then calculate a set of weights (comprising of 64 weights, one for each patch position) for each of the following four cases: the meridional wind responses of the barotropic model using the NAT ensemble mean background state projected onto the GHG ensemble mean meridional wind response, NAT background onto SST ensemble wind response, NCEP2 background onto GHG ensemble wind response and NCEP2 background onto SST ensemble wind response.
We calculate the weights for the sensitivity experiment responses with the full model GHG (Fig. 6a) and SST (Fig. 6b) responses in the 200 hPa meridional wind. Weights are shown for NAT background (blue). The RWS forcings from the full model (used to force the barotropic model in Fig. 5) averaged over \(0^\circ \hbox {-}15^\circ \hbox {N}\) are shown in red. Red lines are normalised so the maximum in each figure is the same as the respective blue line showing the NAT weights. Lines in Fig. 6b have been multiplied by − 1 to allow direct comparison with Fig. 6a. Regions where the amplitude of the full model forcing and weights agree and are large indicate regions where forcing is likely to be important in producing the full model wave responses. From the weights, we identify three key regions: the Western Atlantic, Eastern Atlantic and in the Indian Ocean, just off the east coast of Africa (marked by the crosses in Fig. 6c–e). For the SST case, there also seems to be a region of importance in the Pacific. Here we focus on the other three regions as they appear important in both GHG and SST cases. Fig. 6c–e show the wave responses for the HadAM3P background case at each of the identified forcing locations. The forcing in the Eastern Atlantic has a negative weight, and so we multiply the response of this patch experiment by − 1 to give the correct meridional wind response. When the three forcings are combined (Fig. 6f), they reproduce the wave response that the full model forcing produces in the barotropic model (compare to Fig. 5c). We combine the responses by summing them linearly to produce the response in Fig. 6f, but we verify that applying the three forcings in the same run produces the same wave response (not shown) indicating that the forcings combine linearly.
To test the robustness of the response to the identified forcing locations and jet conditions, we analyse the sensitivity results from the barotropic experiments run with the NCEP2 background state. The green lines in Fig. 6a, b show the weights when using the NCEP2 background state. The NCEP2 weights are broadly consistent with the NAT weights, albeit with a weaker sensitivity to the Indian Ocean region. When forced at the same three identified locations (marked by the crosses) the combined wave response is broadly the same as when using the NAT background state (Fig. 6g), with differences mainly arising over jet exit regions for the reasons previously discussed regarding weaker climatological vorticity gradients. From these sensitivity experiments we can conclude that there exist three important forcing locations to produce the full model wave response, and that the wave response also occurs on an observed background state (the NCEP2 case), which implies that the wave responses are not just possible in the three GCMs, but also in reality.
4.3 Discussion
Using the model RWS, it is only possible to replicate the wave 5 in the barotropic model when using the June RWS forcing and June background state from HadAM3P (in both the Hadley experiments and \(1.5^\circ \hbox {C}\) experiments). When using July, August or JJA forcing and their respective background states, a wave response is produced, but it does not closely resemble the wave 5 response. However, when the three idealized forcings from Fig. 6f are applied in July and August, the wave 5 response is recovered (not shown), albeit weaker than in the June case (as mentioned previously, this could be due to the weaker potential vorticity gradients in July and August). This suggests that the inability of the barotropic model to produce the wave 5 response when forced with the full model RWS forcing is due to the sensitivity of the response to details of the RWS.
When using the CAM4 and MIROC5 200 hPa vorticity fields as the background state, the correct wave 5 response cannot be replicated, even with the June RWS forcing and June background state. However, the idealized forcing on the June background states for both CAM4 and MIROC5 does produce a wave 5 pattern with many aspects similar to the full model responses (not shown). This suggests that the sensitivity of the response to the RWS forcing is still important, but that also the background states of the CAM4 and MIROC5 models are important. We investigate the three model background states and their biases to suggest possible reasons for not being able to reproduce the wave 5 pattern fully in CAM4 and MIROC5 even when using the idealized forcing.
Model zonal wind biases for June in a, b HadAM3P, c, d MIROC5 and e, f CAM4. Contours in a, c, e show the June 1979–2015 200 hPa zonal wind from the NCEP2 reanalysis (contours at \(5\hbox { ms}^{-1}\) intervals with the zero contour suppressed). Colours in a, c, e show the difference between the June 200 hPa zonal wind in the model (2006–2015) and the NCEP2 reanalysis (1979–2015). b, d, f show the zonal mean zonal winds and the bias, defined as the difference between the model and NCEP2 reanalysis means, shown in blue
Responses to GHG and SST forcing. \(\theta _e\) response for a HadAM3P GHG and b HadAM3P SST. See the “Appendix” for details of calculation
The first thing to note is that in MIROC5 and CAM4 the wave pattern in the ensemble mean is weaker, suggesting that the background states of these two models might be less conducive to propagating the wave response to forcing. Figure 7 shows the 200 hPa June ensemble mean zonal wind biases of the three models compared to the 1979–2015 200 hPa June mean zonal wind from the NCEP2 Reanalysis. The Pacific jet in both CAM4 and MIROC5 exhibits poleward biases, whilst in HadAM3P, the jet has a weak bias. All three model jets exhibit a poleward biased jet over land. Over the Atlantic, the biases in HadAM3P are again the smallest, with only a slightly weak biased jet compared to strong biased jets in the other two models. The HadAM3P jet is narrower in the zonal mean than the MIROC5 and CAM4 jets, and it has been suggested that this increases the ability of a jet to act as a waveguide (Manola et al. 2013). The biases in the zonal wind speeds could also be affecting the waveguiding properties of the jet due to the dependence of Rossby wave phase speed on jet speed (Ambrizzi et al. 1995). In the mean states, the HadAM3P jet exhibits a smaller poleward bias, meaning the waveguide is closer to the potential wave forcings in the tropics. In HadAM3P, the full model ensemble mean wave response is stronger than in CAM4 and MIROC5. This may be due to the narrow jet and weak jet bias, and suggests why the wave 5 pattern can be reproduced well when using the HadAM3P background state, even with the simple baroptropic model which has no structure in the vertical.
Differences in the three dimensional structure could also be important. We use the 200 hPa background vorticity state as this level has the largest anomalous tropical forcing and because the vorticity gradients, upon which the signal propagates out of the tropics, are stronger in the upper-troposphere. We find it necessary to have basic states with strong waveguides to achieve the response pattern. In reality, the equivalent barotropic level for external Rossby waves is lower in the troposphere (Held et al. 1985), and so lower model levels could be important in allowing the full model to produce the wave response.
With the large number of individual ensemble members, and the fact that the wave response is largest and biases smallest in HadAM3P, we have focused on analyzing the mean state forcing and background state, and just in the HadAM3P model. The logical next step to investigate and confirm the forcing mechanism from the tropics, and to reproduce the wave using the MIROC5 and CAM4 background states, is to perform experiments using a three-dimensional baroclinic model where we could cleanly test the tropical forcing hypothesis and the hypothesis that the changing background state is not important. However, we leave this more involved modelling approach for further work.
5 Forcing mechanisms
We identify two classes of mechanism which cause the changes in tropical precipitation in response to the \(\hbox {CO}_2\) and SST forcings. The first of these is due to thermodynamic changes. Increases in atmospheric \(\hbox {CO}_2\) concentration lead to an increase in the static stability of the atmosphere due to enhanced longwave absorption by the extra \(\hbox {CO}_2\), thus suppressing convection (Sugi and Yoshimura 2004; Andrews et al. 2009; Dong et al. 2009; Cao et al. 2012; Bony et al. 2013). On the other hand, an increase in SSTs results in increased atmospheric moisture, leading to an increase in precipitation across tropical wet regions (Held and Soden 2006; Seager et al. 2010). These thermodynamic effects are responsible for the model changes in precipitation over the tropical Western Atlantic. In the \(\hbox {CO}_2\) forcing cases, the suppressed convection leads to a decrease in precipitation in the tropical Western Atlantic (Figs. 1, 2a, c). In the SST forcing cases, the enhanced moisture leads to an increase in the precipitation in the tropical Western Atlantic (Fig. 2b, d).
The second mechanism arises from the land–sea \(\theta _e\) contrast. Increases in \(\hbox {CO}_2\) cause the land to warm in response to increased downwelling longwave radiation, enhancing the land–sea \(\theta _e\) contrast (Shaw and Voigt 2015) and leading to increases in precipitation over land (Chadwick et al. 2014; Richardson et al. 2016). However, when the SSTs are increased, the land–sea \(\theta _e\) contrast changes in the opposite direction (Shaw and Voigt 2015), causing an increase in the vertical velocity over the oceans (likely due to a reduction in static stability) thus enhancing convective precipitation over the oceans (Chadwick 2016). The changes in the land–sea \(\theta _e\) contrast in the GHG and SST responses are shown in Fig. 8. In the GHG case (Fig. 8a) on the east coast of Africa, there is a positive land–sea \(\theta _e\) gradient (along the blue arrow in Fig. 8a) and associated increase in precipitation over the same region in the \(\hbox {CO}_2\) forcing cases (Figs. 1, 2a, c). On the west coast Sahel region of Africa however, there is a negative land–sea \(\theta _e\) gradient (black arrow) which is associated with a decrease in precipitation. The changes in \(\theta _e\) correspond to the RWS forcing in the two regions: positive RWS for a positive land–sea \(\theta _e\) contrast and negative RWS for a negative contrast (see Fig. 5a). These regions of positive and negative RWS forcing are consistent with the Eastern Atlantic weight being opposite in sign to the Western Atlantic and Indian Ocean weights in Fig. 7a. In the SST case, the land–sea \(\theta _e\) gradient is negative on the east coast of Africa (along the blue arrow in Fig. 8b), and positive on the west coast Sahel region of Africa (black arrow). These \(\theta _e\) gradients again have corresponding changes in precipitation and RWS forcings: a decrease in precipitation (Fig. 2b, d) and negative RWS forcing on the east coast of Africa and an increase in precipitation and positive RWS forcing in the west coast Sahel region of Africa. Again, this is consistent with the opposite sign of the Eastern Atlantic weight in Fig. 7b. This forcing mechanism is the same mechanism responsible for summer stationary wave changes in response to direct radiative and SST forcings found by Shaw and Voigt (2015).
There is also a large change in RWS just off the west coast of South America (around \(90^\circ \hbox {W}\); Fig. 6a), which presumably arises due to the same mechanisms causing the other changes in RWS at land–sea interfaces. However, forcing the barotropic model here does not produce a response which projects onto the full model wave response. This may be due to the meridional distance of this RWS from large enough vorticity gradients needed to act as a waveguide.
The response of the land–sea \(\theta _e\) contrast on the west coast of Africa is tied to the precipitation response in the region, which arises due to a shift in the ITCZ (Fig. 2). The ITCZ shifts toward the anomalously warm hemisphere (e.g. Bischoff and Schneider 2014; Baker et al. 2018b): in the GHG case the ITCZ shifts northwards as the NH warms more due to having more land; in the SST case, the ITCZ shifts southwards as the Southern Hemisphere warms more due to having more ocean. Previous work has found the same sign ITCZ shifts in this region as this study finds: northwards due to greenhouse gas forcing and southwards due to global SST warming (e.g. Hoerling et al. 2006; Skinner et al. 2012). In the GHG case, on the west coast where the precipitation anomaly is negative, \(\theta _e\) decreases going from ocean to land, consistent with a decrease in convection. In the SST case, the precipitation anomaly is positive, with an increase in \(\theta _e\) from ocean to land, consistent with an increase in convection. The convection responses which arise from the ITCZ shift lead to the RWS responses over the Eastern Atlantic, which are opposite in sign compared to the Western Atlantic and Indian Ocean regions in both the GHG and SST responses.
We identify two key coastal regions just off the east coast of continents, the east coast of South America and just off the east coast of Africa (co-located with the western part of the Indian Ocean basin), and a further region just off the west coast of Africa. Positive RWS forcing in the east coast regions associated with decreased upper-level divergence, and negative RWS forcing in the west coast region associated with increased upper-level divergence, acts to force the NH stationary wave in summer.
The regions we identify for forcing this particular wave have been shown to be important in forcing extratropical Rossby waves in other studies. Changes in outgoing longwave radiation in observations in summer over the tropical Atlantic, coinciding with the regions where we see precipitation changes in this study, have been associated with summer circulation patterns over Europe (Cassou et al. 2005). The Summer East Atlantic pattern, as observed in reanalysis by Wulff et al. (2017) has an associated circumglobal wavenumber 5 wave, which is linked to an anomalous tropical precipitation pattern with similarities to the precipitation patterns we find in this study: drying in the Western Atlantic and wetting over the Sahel region in Africa, producing a similar convergent forcing as we find in this study. Yasui and Watanabe (2010) also find that precipitation changes over equatorial Africa are important in forcing the observed circumglobal teleconnection [CGT, see Ding and Wang (2005)] in boreal summer. The wave we observe is not an excitation of the CGT: the wave centres we observe do not coincide with the CGT, and as demonstrated in Sect. 4, the wave we force is not an excitation of a wave present in the background state. However, the fact that studies on the CGT find similar key forcing regions as this study suggests that these regions are important generally in forcing boreal summer Rossby waves. As well as equatorial Africa, the Indian summer monsoon region (which includes the area of ocean just off the east coast of Africa) has also been found important in forcing aspects of the CGT (Ding and Wang 2007), and other NH teleconnection patterns (Lin 2009).
6 Discussion
The opposing effects of radiative forcing versus sea surface warming have important implications on regional climates and extremes. Framed in terms of a global mean temperature target, the changes in regional climates and extremes depend significantly on the climate sensitivity (defined as the global mean temperature warming due to a doubling of atmospheric \(\hbox {CO}_2\) concentrations), which is subject to large uncertainties (IPCC 2014). If the Earth has a low climate sensitivity, the temperature target may be met, but with corresponding dangerous changes in certain regional extremes (Baker et al. 2018a), due to increases in tropical precipitation over land and the wavelike temperature increase pattern over the NH. For higher climate sensitivities, less \(\hbox {CO}_2\) would be emitted to reach the same temperature target, and so the opposing effect of the sea surface warming would balance out the direct \(\hbox {CO}_2\) effect to a greater extent. If the climate sensitivity is very high, the direct \(\hbox {CO}_2\) effect will be relatively unimportant compared to the sea surface warming effect, leading to drying over the land in the tropics, and different regions (those under the anticyclonic regions of the stationary wave pattern) experiencing increases in heat extremes. Geoengineering techniques aiming to tackle climate change impacts without removing \(\hbox {CO}_2\) would exacerbate the direct \(\hbox {CO}_2\) effect when stabilising at a temperature target as the techniques would reduce global mean temperature without removing \(\hbox {CO}_2\). Ultimately, the interplay of the two opposing effects will be dictated by the Earth’s climate sensitivity, and further work is need to quantify the exact magnitudes of the direct \(\hbox {CO}_2\) and sea surface warming effects on changes in precipitation and on the forced stationary wave.
On the question of the interaction between the direct \(\hbox {CO}_2\) effect and sea surface warming effect, Lambert et al. (2011) found no substantial nonlinearities in indices of atmospheric circulation when the doubling of \(\hbox {CO}_2\) and spatially uniform SST warming were added to an AGCM. Deser and Phillips (2009) also observe a high degree of linearity in the response to direct \(\hbox {CO}_2\) effects and sea surface warming in atmospheric circulation trends during 1950–2000 simulated in an AGCM. This suggests the opposing effects on circulation may combine linearly as in the barotropic modelling experiments in this study, although further work is needed to confirm this.
The SST forcing model results presented here rely on one global warming pattern change, and the direct \(\hbox {CO}_2\) runs all have the same fixed SST pattern. However, it has been suggested that the pattern of SST warming plays an important part in certain regional circulation responses (He and Soden 2015) and the tropical precipitation response to SST warming (Chadwick 2016). The robustness of the wave response in the AMIP4K response suggests that the wave is forced by changes in mean SST warming, but further work investigating the uncertainty arising from the SST pattern change is needed before quantitative predictions about the opposing effects of radiative forcing and sea surface warming can be made.
There are several other possible contributing factors to the direct \(\hbox {CO}_2\) effect, which require further study to quantify. Radiative changes in clouds have been linked to circulation changes (Voigt and Shaw 2015) and large scale cloud cover changes over the NH in summer are associated with the direct \(\hbox {CO}_2\) effect (Richardson et al. 2016), with a decrease in cloud cover over regions that see strong increases in temperature due to \(\hbox {CO}_2\). However, determining the causality between the cloud cover changes and the temperature changes is a complex issue. One possibility is that the anticyclonic regions of the forced stationary waves cause cloud to be less prevalent in these regions, adding to the increases in local temperature. Midlatitude stationary wave changes can also be affected by changes in the zonal mean westerlies in the sub-tropical upper troposphere (Simpson et al. 2016). We do not observe this effect in this study, and Grise and Polvani (2014) show that whilst there are differing effects on the zonal circulation under direct radiative forcing and sea surface warming, the effects are not opposite. However, with large variations among future predictions in zonal wind changes (Simpson et al. 2014), this effect could be important in dictating the characteristics of the forced stationary wave.
A modelling intercomparison project as part of the new CMIP6 ensemble, The Cloud Feedback Model Intercomparison Project Phase 3 (CFMIP3) (Webb et al. 2017), consists of AMIP style simulations designed to investigate effects on clouds and circulation of \(\hbox {CO}_2\) radiative effects, physiological effects, SST uniform warming and SST pattern effects. Chadwick et al. (2017) use several models from CFMIP3 to demonstrate in winter that the physiological effect and SST pattern change play important roles in the hydrological cycle and European circulation changes. The full CFMIP3 ensemble will enable more quantitative predictions and analysis surrounding the opposing effects of radiative forcing and sea surface warming in summer to be carried out.
7 Conclusions
Using results from three GCMs and CMIP5, we have shown here that there are opposing effects of direct \(\hbox {CO}_2\) forcing and sea surface warming on tropical precipitation and forced summer NH stationary waves. The direct effect of \(\hbox {CO}_2\) forcing leads to a drying over the land and wetting over the ocean in the tropics in boreal summer in key forcing locations. This forces a wavenumber 5 stationary wave pattern over the NH. We observe the opposite precipitation response due to sea surface warming, which forces the same wave over the NH but with opposite sign. The three key locations for forcing the summer wave are found to be the Western Atlantic, Eastern Atlantic and in the Indian Ocean off the east coast of Africa.
This study has important implications for changes in regional climates and extremes which depend heavily on the Earth’s climate sensitivity and land–sea temperature contrast response. The opposing effects of radiative forcing and sea surface warming and their relative importance at a specific global mean temperature are determined by how much \(\hbox {CO}_2\) is emitted to reach such a temperature. A low climate sensitivity means a greater contribution from the direct \(\hbox {CO}_2\) effect, i.e. enhanced precipitation and precipitation extremes (Baker et al. 2018a) over tropical land, and increases in heat extremes under the anticyclonic centres of the \(\hbox {CO}_2\) forced stationary wave. On the other hand, a high climate sensitivity means a greater contribution from the sea surface warming effect, i.e. reduced precipitation over tropical land, and increases in heat extremes shifted to the cyclonic centres of the \(\hbox {CO}_2\) forced stationary wave, which are anticyclonic for the sea surface warming forced wave. The future change in land–sea temperature contrast will also play an important role in determining the balance between the opposing effects. A larger land–sea temperature contrast response could lead to a larger forcing of the direct \(\hbox {CO}_2\) wave, compared to a smaller response. The relative magnitude of the combination of the opposing effects of direct radiative forcing and sea surface warming is still uncertain due to uncertainty in the Earth’s climate sensitivity and land–sea temperature contrast response (Byrne and O’Gorman 2013). This study points to the need to reduce the uncertainties in the climate sensitivity and land–sea contrast response to better constrain how regional precipitation and temperature patterns will change under global warming.
References
Alduchov OA, Eskridge RE (1996) Improved magnus form approximation of saturation vapor pressure. J Appl Meteorol 35(4):601–609. https://doi.org/10.1175/1520-0450(1996)035<0601:IMFAOS>2.0.CO;2
Allen M (1999) Do-it-yourself climate prediction. Nature 401(6754):642–642. https://doi.org/10.1038/44266
Ambaum MHP (2010) Thermal physics of the atmosphere. Wiley, New York. https://doi.org/10.1002/9780470710364
Ambrizzi T, Hoskins BJ, Hsu HH (1995) Rossby wave propagation and teleconnection patterns in the Austral winter. J Atmos Sci 52(21):3661–3672. https://doi.org/10.1175/1520-0469(1995)052%3c3661:RWPATP%3e2.0.CO;2
Andrews T, Forster PM, Gregory JM (2009) A surface energy perspective on climate change. J Clim 22(10):2557–2570. https://doi.org/10.1175/2008JCLI2759.1
Baker HS, Millar RJ, Karoly DJ, Beyerle U, Guillod BP, Mitchell D, Shiogama H, Sparrow S, Woollings T, Allen MR (2018a) Higher CO\(_2\) concentrations increase extreme event risk in a 1.5C world. Nat Clim Change 8(7):604–608. https://doi.org/10.1038/s41558-018-0190-1
Baker HS, Mbengue C, Woollings T (2018b) Seasonal sensitivity of the Hadley cell and cross-hemispheric responses to diabatic heating in an idealized GCM. Geophys Res Lett 45(5):2533–2541. https://doi.org/10.1002/2018GL077013
Barsugli JJ, Sardeshmukh PD (2002) Global atmospheric sensitivity to tropical SST anomalies throughout the Indo-Pacific basin. J Clim 15(23):3427–3442. https://doi.org/10.1175/1520-0442(2002)015<3427:GASTTS>2.0.CO;2
Bieli M, Pfahl S, Wernli H (2015) A Lagrangian investigation of hot and cold temperature extremes in Europe. Q J R Meteorol Soc 141(686):98–108. https://doi.org/10.1002/qj.2339
Bischoff T, Schneider T (2014) Energetic constraints on the position of the intertropical convergence zone. J Clim 13(27):4937–4951. https://doi.org/10.1175/JCLI-D-13-00650.1
Bolton D (1980) The computation of equivalent potential temperature. Mon Weather Rev 108(7):1046–1053. https://doi.org/10.1175/1520-0493(1980)108<1046:TCOEPT>2.0.CO;2
Bony S, Bellon G, Klocke D, Sherwood S, Fermepin S, Denvil S (2013) Robust direct effect of carbon dioxide on tropical circulation and regional precipitation. Nat Geosci 6(6):447–451. https://doi.org/10.1038/ngeo1799
Branstator G (2002) Circumglobal teleconnections, the jet stream waveguide, and the North Atlantic Oscillation. J Clim 15(14):1893–1910. https://doi.org/10.1175/1520-0442(2002)015<1893:CTTJSW>2.0.CO;2
Byrne MP, O’Gorman PA (2013) Link between land–ocean warming contrast and surface relative humidities in simulations with coupled climate models. Geophys Res Lett 40(19):5223–5227. https://doi.org/10.1002/grl.50971
Cao L, Bala G, Caldeira K (2012) Climate response to changes in atmospheric carbon dioxide and solar irradiance on the time scale of days to weeks. Environ Res Lett 7(3):034015. https://doi.org/10.1088/1748-9326/7/3/034015. http://stacks.iop.org/1748-9326/7/i=3/a=034015?key=crossref.b4a65cfba7f3fd7d4078736920eed250
Cassou C, Terray L, Phillips AS (2005) Tropical Atlantic influence on European heat waves. J Clim 18(15):2805–2811. https://doi.org/10.1175/JCLI3506.1
Chadwick R (2016) Which aspects of CO\(_2\) forcing and SST warming cause most uncertainty in projections of tropical rainfall change over land and ocean? J Clim 29(7):2493–2509. https://doi.org/10.1175/JCLI-D-15-0777.1
Chadwick R, Good P, Andrews T, Martin G (2014) Surface warming patterns drive tropical rainfall pattern responses to CO\(_2\) forcing on all timescales. Geophys Res Lett 41(2):610–615. https://doi.org/10.1002/2013GL058504
Chadwick R, Douville H, Skinner CB (2017) Timeslice experiments for understanding regional climate projections: applications to the tropical hydrological cycle and European winter circulation. Clim Dyn 49(9–10):3011–3029. https://doi.org/10.1007/s00382-016-3488-6
Compo GP, Sardeshmukh PD (2009) Oceanic influences on recent continental warming. Clim Dyn 32(2–3):333–342. https://doi.org/10.1007/s00382-008-0448-9
Deser C, Phillips AS (2009) Atmospheric circulation trends, 1950–2000: the relative roles of sea surface temperature forcing and direct atmospheric radiative forcing. J Clim 22(2):396–413. https://doi.org/10.1175/2008JCLI2453.1
Ding Q, Wang B (2005) Circumglobal teleconnection in the Northern Hemisphere summer. J Clim 18(17):3483–3505. https://doi.org/10.1175/JCLI3473.1
Ding Q, Wang B (2007) Intraseasonal teleconnection between the summer eurasian wave train and the Indian monsoon. J Clim 20(15):3751–3767. https://doi.org/10.1175/JCLI4221.1
Dong B, Sutton R (2015) Dominant role of greenhouse-gas forcing in the recovery of Sahel rainfall. Nat Clim Change 5(8):757–760. https://doi.org/10.1038/nclimate2664
Dong B, Gregory JM, Sutton RT (2009) Understanding land–sea warming contrast in response to increasing greenhouse gases. Part I: transient adjustment. J Clim 22(11):3079–3097. https://doi.org/10.1175/2009JCLI2652.1
Dong B, Sutton RT, Chen W, Liu X, Lu R, Sun Y (2016) Abrupt summer warming and changes in temperature extremes over Northeast Asia since the mid-1990s: drivers and physical processes. Adv Atmos Sci 33(9):1005–1023. https://doi.org/10.1007/s00376-016-5247-3
Donlon CJ, Martin M, Stark J, Roberts-Jones J, Fiedler E, Wimmer W (2012) The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens Environ 116:140–158. https://doi.org/10.1016/J.RSE.2010.017. https://www.sciencedirect.com/science/article/pii/S0034425711002197
Folland CK, Sexton DMH, Karoly DJ, Johnson CE, Rowell DP, Parker DE (1998) Influences of anthropogenic and oceanic forcing on recent climate change. Geophys Res Lett 25(3):353–356. https://doi.org/10.1029/97GL03701
Gent PR, Danabasoglu G, Donner LJ, Holland MM, Hunke EC, Jayne SR, Lawrence DM, Neale RB, Rasch PJ, Vertenstein M, Worley PH, Yang ZL, Zhang M (2011) The Community Climate System Model Version 4. J Clim 24(19):4973–4991. https://doi.org/10.1175/2011JCLI4083.1
Gordon C, Cooper C, Senior CA, Banks H, Gregory JM, Johns TC, Mitchell JFB, Wood RA (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16(2–3):147–168. https://doi.org/10.1007/s003820050010
Grise KM, Polvani LM (2014) The response of midlatitude jets to increased CO\(_2\): distinguishing the roles of sea surface temperature and direct radiative forcing. Geophys Res Lett 41(19):6863–6871. https://doi.org/10.1002/2014GL061638
Guillod BP, Jones RG, Bowery A, Haustein K, Massey NR, Mitchell DM, Otto FEL, Sparrow SN, Uhe P, Wallom DCH, Wilson S, Allen MR (2017) weather@home 2: validation of an improved global-regional climate modelling system. Geosci Model Dev 10(5):1849–1872. https://doi.org/10.5194/gmd-10-1849-2017. https://www.geosci-model-dev.net/10/1849/2017/
Haarsma RJ, Selten F (2012) Anthropogenic changes in the Walker circulation and their impact on the extra-tropical planetary wave structure in the Northern Hemisphere. Clim Dyn 39(7–8):1781–1799. https://doi.org/10.1007/s00382-012-1308-1
Haustein K, Otto FEL, Uhe P, Schaller N, Allen MR, Hermanson L, Christidis N, McLean P, Cullen H (2016) Real-time extreme weather event attribution with forecast seasonal SSTs. Environ Res Lett 11(6):064006. https://doi.org/10.1088/1748-9326/11/6/064006. http://stacks.iop.org/1748-9326/11/i=6/a=064006?key=crossref.3f0585e9af9b6a8e6e4ab5eaf240b920
He J, Soden BJ (2015) Anthropogenic weakening of the tropical circulation: the relative roles of direct CO\(_2\) forcing and sea surface temperature change. J Clim 28(22):8728–8742. https://doi.org/10.1175/JCLI-D-15-0205.1
Held IM, Soden BJ (2006) Robust responses of the hydrological cycle to global warming. J Clim 19(21):5686–5699. https://doi.org/10.1175/JCLI3990.1
Held IM, Panetta RL, Pierrehumbert RT (1985) Stationary external Rossby waves in vertical shear. J Atmos Sci 42(9):865–883. https://doi.org/10.1175/1520-0469(1985)042<0865:SERWIV>2.0.CO;2
Hoerling M, Hurrell J, Eischeid J, Phillips A (2006) Detection and Attribution of twentieth-century Northern and Southern African rainfall change. J Clim 19(16):3989–4008. https://doi.org/10.1175/JCLI3842.1
Hoskins BJ, Ambrizzi T (1993) Rossby wave propagation on a realistic longitudinally varying flow. J Atmos Sci 50(12):1661–1671. https://doi.org/10.1175/1520-0469(1993)050<1661:RWPOAR>2.0.CO;2
IPCC (2014) Climate change 2013: the physical science basis. Cambridge University Press, Cambridge. http://www.epa-pictaural.com/ctr/m/cc/transcript/stocker.pdf
Joseph PV, Srinivasan J (1999) Rossby waves in May and the Indian summer monsoon rainfall. Tellus A 51(5):854–864. https://doi.org/10.1034/j.1600-0870.1999.00021.x. http://tellusa.net/index.php/tellusa/article/view/14497
Joshi MM, Gregory JM, Webb MJ, Sexton DMH, Johns TC (2008) Mechanisms for the land/sea warming contrast exhibited by simulations of climate change. Clim Dyn 30(5):455–465. https://doi.org/10.1007/s00382-007-0306-1
Kamae Y, Shiogama H, Watanabe M, Kimoto M (2014a) Attributing the increase in Northern Hemisphere hot summers since the late 20th century. Geophys Res Lett 41(14):5192–5199. https://doi.org/10.1002/2014GL061062
Kamae Y, Watanabe M, Kimoto M, Shiogama H (2014b) Summertime land–sea thermal contrast and atmospheric circulation over East Asia in a warming climate—part II: importance of CO2-induced continental warming. Clim Dyn 43(9–10):2569–2583. https://doi.org/10.1007/s00382-014-2146-0
Krishnamurti TN, Stefanova L, Misra V (2013) Tropical meteorology: an introduction. Springer, Berlin
Lambert FH, Webb MJ, Joshi MM (2011) The relationship between land–ocean surface temperature contrast and radiative forcing. J Clim 24(13):3239–3256. https://doi.org/10.1175/2011JCLI3893.1
Lee MH, Lee S, Song HJ, Ho CH (2017) The recent increase in the occurrence of a boreal summer teleconnection and its relationship with temperature extremes. J Clim pp JCLI-D-16-0094.1. https://doi.org/10.1175/JCLI-D-16-0094.1
Lin H (2009) Global extratropical response to diabatic heating variability of the Asian summer monsoon. J Atmos Sci 66(9):2697–2713. https://doi.org/10.1175/2009JAS3008.1
Manola I, Selten F, de Vries H, Hazeleger W (2013) “Waveguidability” of idealized jets. J Geophys Res Atmos 118(18):10,432–10,440. https://doi.org/10.1002/jgrd.50758
Millar RJ, Fuglestvedt JS, Friedlingstein P, Rogelj J, Grubb MJ, Matthews HD, Skeie RB, Forster PM, Frame DJ, Allen MR (2017) Emission budgets and pathways consistent with limiting warming to 1.5C. Nat Geosci. https://doi.org/10.1038/ngeo3031
Mitchell JFB (1983) The seasonal response of a general circulation model to changes in CO\(_2\) and sea temperatures. Q J R Meteorol Soc 109(459):113–152. https://doi.org/10.1002/qj.49710945906
Mitchell D, AchutaRao K, Allen M, Bethke I, Forster P, Fuglestvedt J, Gillett N, Haustein K, Iverson T, Massey N, Schleussner CF, Scinocca J, Seland Ø, Shiogama H, Shuckburgh E, Sparrow S, Stone D, Wallom D, Wehner M, Zaaboul R (2017) Half a degree additional warming, projections, prognosis and impacts (HAPPI): background and experimental design. Geosci Model Dev Discuss 10(2):571–583. https://doi.org/10.5194/gmd-2016-203
O’Reilly CH, Woollings T, Zanna L, Weisheimer A (2018) The impact of tropical precipitation on summertime Euro-Atlantic circulation via a circumglobal wave-train. J Clim, pp JCLI-D-17-0451.1. https://doi.org/10.1175/JCLI-D-17-0451.1
Petoukhov V, Rahmstorf S, Petri S, Schellnhuber HJ (2013) Quasiresonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc Natl Acad Sci USA 110(14):5336–41. https://doi.org/10.1073/pnas.1222000110. http://www.ncbi.nlm.nih.gov/pubmed/23457264. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=PMC3619331
Pope VD, Gallani ML, Rowntree PR, Stratton RA (2000) The impact of new physical parametrizations in the Hadley Centre climate model: HadAM3. Clim Dyn 16(2–3):123–146. https://doi.org/10.1007/s003820050009
Richardson TB, Forster PM, Andrews T, Parker DJ (2016) Understanding the rapid precipitation response to CO\(_2\) and aerosol forcing on a regional scale. J Clim 29(2):583–594. https://doi.org/10.1175/JCLI-D-15-0174.1
Sardeshmukh PD, Hoskins BJ (1988) The generation of global rotational flow by steady idealized tropical divergence. J Atmos Sci 45(7):1228–1251. https://doi.org/10.1175/1520-0469(1988)045<1228:TGOGRF>2.0.CO;2
Schaller N, Kay AL, Lamb R, Massey NR, van Oldenborgh GJ, Otto FEL, Sparrow SN, Vautard R, Yiou P, Ashpole I, Bowery A, Crooks SM, Haustein K, Huntingford C, Ingram WJ, Jones RG, Legg T, Miller J, Skeggs J, Wallom D, Weisheimer A, Wilson S, Stott PA, Allen MR (2016) Human influence on climate in the 2014 southern England winter floods and their impacts. Nat Clim Change 6(6):627–634. https://doi.org/10.1038/nclimate2927. http://www.nature.com/articles/nclimate2927
Schubert S, Wang H, Suarez M (2011) Warm season subseasonal variability and climate extremes in the Northern Hemisphere: the role of stationary Rossby waves. J Clim 24(18):4773–4792. https://doi.org/10.1175/JCLI-D-10-05035.1
Screen JA, Simmonds I (2014) Amplified mid-latitude planetary waves favour particular regional weather extremes. Nat Clim Change 4(8):704–709. https://doi.org/10.1038/nclimate2271
Seager R, Naik N, Vecchi GA (2010) Thermodynamic and dynamic mechanisms for large-scale changes in the hydrological cycle in response to global warming. J Clim 23(17):4651–4668. https://doi.org/10.1175/2010JCLI3655.1
Seneviratne SI, Donat MG, Mueller B, Alexander LV (2014) No pause in the increase of hot temperature extremes. Nat Clim Change 4(3):161–163. https://doi.org/10.1038/nclimate2145
Sexton DMH, Grubb H, Shine KP, Folland CK (2003) Design and analysis of climate model experiments for the efficient estimation of anthropogenic signals. J Clim 16(9):1320–1336. https://doi.org/10.1175/1520-0442-16.9.1320
Shaw TA, Voigt A (2015) Tug of war on summertime circulation between radiative forcing and sea surface warming. Nat Geosci 8(7):560–566. https://doi.org/10.1038/ngeo2449
Simpson IR, Shaw TA, Seager R (2014) A diagnosis of the seasonally and longitudinally varying midlatitude circulation response to global warming. J Atmos Sci 71(7):2489–2515. https://doi.org/10.1175/JAS-D-13-0325.1
Simpson IR, Seager R, Ting M, Shaw TA (2016) Causes of change in Northern Hemisphere winter meridional winds and regional hydroclimate. Nat Clim Chang 6:65–70. https://doi.org/10.1175/1520-0469(1986)043<2944:LSOTSE>2.0.CO;2. http://www.nature.com/nclimate/journal/v6/n1/full/nclimate2783.html
Skinner CB, Ashfaq M, Diffenbaugh NS (2012) Influence of twenty-first-century atmospheric and sea surface temperature forcing on West African climate. J Clim 25(2):527–542. https://doi.org/10.1175/2011JCLI4183.1
Sugi M, Yoshimura J (2004) A mechanism of tropical precipitation change due to CO\(_2\) increase. J Clim 17(1):238–243. https://doi.org/10.1175/1520-0442(2004)017<0238:AMOTPC>2.0.CO;2
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Ting M (1994) Maintenance of Northern summer stationary waves in a GCM. J Atmos Sci 51(22):3286–3308. https://doi.org/10.1175/1520-0469(1994)051<3286:MONSSW>2.0.CO;2
Voigt A, Shaw TA (2015) Circulation response to warming shaped by radiative changes of clouds and water vapour. Nat Geosci 8(2):102–106. https://doi.org/10.1038/ngeo2345
Watanabe M, Suzuki T, O’ishi R, Komuro Y, Watanabe S, Emori S, Takemura T, Chikira M, Ogura T, Sekiguchi M, Takata K, Yamazaki D, Yokohata T, Nozawa T, Hasumi H, Tatebe H, Kimoto M (2010) Improved climate simulation by MIROC5: mean states, variability, and climate sensitivity. J Clim 23(23):6312–6335. https://doi.org/10.1175/2010JCLI3679.1
Webb MJ, Andrews T, Bodas-Salcedo A, Bony S, Bretherton CS, Chadwick R, Chepfer H, Douville H, Good P, Kay JE, Klein SA, Marchand R, Medeiros B, Siebesma AP, Skinner CB, Stevens B, Tselioudis G, Tsushima Y, Watanabe M (2017) The Cloud Feedback Model Intercomparison Project (CFMIP) contribution to CMIP6. Geosci Model Dev 10(1):359–384. https://doi.org/10.5194/gmd-10-359-2017
Wulff CO, Greatbatch RJ, Domeisen DI, Gollan G, Hansen F (2017) Tropical forcing of the Summer East Atlantic pattern. Geophys Res Lett. https://doi.org/10.1002/2017GL075493
Yasui S, Watanabe M (2010) Forcing processes of the summertime circumglobal teleconnection pattern in a dry AGCM. J Clim 23(8):2093–2114. https://doi.org/10.1175/2009JCLI3323.1
Acknowledgements
This work was supported by the Natural Environment Research Council (Grant NE/L002612/1 and NERC SummerTIME project, Grant NE/M005887/1). H. Shiogama was supported by the TOUGOU project of MEXT, Japan and by the Environment Research and Technology Development Fund (2-1702) of the Environmental Restoration and Conservation Agency, Japan. The authors thank Urs Beyerle for making the data from CAM4 available. This research used science gateway resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. We thank the two anonymous reviewers for their suggestions and comments which helped us to improve this manuscript. We would like to thank our colleagues at the Oxford eResearch Centre: A. Bowery, M. Rashid, P. Uhe and D. Wallom for their technical expertise. We would like to thank the Met Office Hadley Centre PRECIS team for their technical and scientific support for the development and application of weather@Home. Finally, we would like to thank all of the volunteers who have donated their computing time to climateprediction.net and weather@home.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendix: Equivalent potential temperature
Appendix: Equivalent potential temperature
To analyse differences in the response to SST versus \(\hbox {CO}_2\) forcing, we compute the equivalent potential temperature, \(\theta _e\), the temperature a parcel of air would reach if brought adiabatically to a standard reference pressure (taken to be 1000 hPa) and all the water vapour in the parcel were to condense, releasing its latent heat (Ambaum 2010). Following Bolton (1980), \(\theta _e\) can be calculated as follows:
\(\theta _L\) is the dry potential temperature (in Kelvin) at the lifted condensation level,
\(T_L\) is the approximate temperature (in Kelvin) at the lifted condensation level,
Here, T is the temperature (in Kelvin) of the air at pressure p (in hPa), \(p_0\) is a standard reference pressure (taken to be 1000 hPa) and \(\kappa _d=R_d/c_{pd}=0.2854\) is the ratio of the specific gas constant to the specific heat of dry air at constant pressure. e is the water vapour pressure in hPa, calculated from relative humidity by \(RH = \frac{e}{e_s}\times 100\%\), where the saturated water pressure \(e_s\left( T\right) = 6.1094\exp \left[ \frac{17.625(T-273.15)}{T-30.11}\right]\) (Alduchov and Eskridge 1996). \(r=0.622\frac{e}{p-e}\) is the mixing ratio of water vapour per mass (kg/kg). \(T_d\) is the dew point temperature which can be calculated from the relative humidity \(RH=e_s\left( T_d\right) /e_s\left( T\right)\) (Ambaum 2010).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Baker, H.S., Woollings, T., Mbengue, C. et al. Forced summer stationary waves: the opposing effects of direct radiative forcing and sea surface warming. Clim Dyn 53, 4291–4309 (2019). https://doi.org/10.1007/s00382-019-04786-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-019-04786-1