Abstract
The impact of an idealised scenario of future mass release of major ice sheets on the Atlantic ocean is studied. A freshwater forcing is applied to the ocean surface in a coupled climate model forced in accordance with a high-end future climate projection for mass loss from the Greenland and Antarctic ice-sheet, together with the RCP8.5 emission scenario. The added freshwater dilutes the entire ocean by increasing total volume, but changes in freshwater budget are non-linear in time, especially in the Atlantic Ocean. In the Atlantic the initial dilution mainly comes from Greenland freshwater, but the increase in mass is counteracted by the mass flux across the boundaries of the Atlantic, with the outflow into the Southern Ocean becoming larger than the inflow through Bering Strait. Associated with this mass divergence, salt is exported to the Southern Ocean by the barotropic flow. Further freshening is associated with more freshwater import by the Atlantic Meridional Overturning Circulation across the southern boundary of the Atlantic. Also, the subtropical gyre exports salt and imports freshwater across the Atlantic’s southern boundary, especially when freshwater from the Antarctic Ice Sheet arrives at the boundary of the basin. It appears that the response to Northern Hemisphere (NH) sources (the Greenland Ice Sheet) and Southern Hemisphere (SH) sources (the Antarctic Ice Sheet) are opposite. In the case of NH-only freshwater forcing, sea surface height (SSH) increases in the Arctic, causing a reduction of the SSH gradient over the Bering Strait, and hence the barotropic throughflow across the Arctic–Atlantic basin reduces. In case of SH-only freshwater forcing, SSH increases in the Pacific, enhancing the barotropic throughflow in the Arctic–Atlantic. When both NH and SH freshwater forcings are present, the response in the Atlantic is dominated by NH forcing. Changes in overturning transport to either NH or SH forcing counteract the response to changes in barotropic transport. These changes are not due to volume transport but mainly due to salinity changes, in particular across the southern boundary of the Atlantic. Only when both SH and NH freshwater forcing are present changes in barotropic transport and overturning transport reinforce each other: the barotropic transport more strongly reacts to NH forcing, while the overturning transport reacts more strongly to SH forcing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The climate warms due to anthropogenic emissions of greenhouse gasses and, as a consequence, the ice sheets on Greenland and Antarctica are expected to loose mass (e.g. Joughin and Alley 2011). Mass losses may increase further due to non-linear effects associated with ice sheet interactions with the atmosphere and ocean (see Hanna et al. (2013) for an overview). Upper limit estimates go as far as a 1 m global mean sea-level rise from Antarctica alone by 2100 and \(> 10\) m by 2500 (DeConto and Pollard 2016). The response to ice cap melting in the climate system is not well understood, since most climate models used for projections do not incorporate the complex interactions that lead to increased ice loss from the ice sheets. In principle, coupled climate models (CCMs) could simulate such mass loss by including ice sheet (see Vizcaino 2014) and iceberg modules that simulate calving and iceberg drift in response to changing atmospheric and ocean temperatures. The current generation of CCMs used in the CMIP5 ensemble, and likely used in the CMIP6 ensemble (Eyring et al. 2016), is not equipped with such modules and therefore cannot simulate the mass loss of ice sheets to the ocean interactively with the other components of the climate system.
An alternative to explicit modelling ice mass loss is to prescribe the freshwater release from the large ice sheets to the ocean by estimating the amount of mass loss under present and future conditions. Examples of such approaches are Bakker et al. (2016); Marsh et al. (2010); Swingedouw et al. (2012); Stammer (2008); Stammer et al. (2011); Weijer et al. (2012) where Greenland meltwater was applied to Greenland coastal grid cells of numerical ocean models. The latter three studies have the intensity of the forcing vary around the coast to reflect the non-uniform meltwater run-off. In Stammer (2008) mass loss from Antarctica was also included (with a similar approach in Stammer et al. 2011 using a coupled atmosphere-ocean model). Also, in each study the total amount of freshwater release was varied within a range of values to determine the sensitivity of the ocean circulation to a set of idealised forcing scenarios.
In this paper the effect of a more plausible freshwater release scenario to the ocean is assessed for the coming century using a coupled-climate model (Van den Berk and Drijfhout 2014). After the year 2100 the forcing reverses, which is clearly no longer realistic, but would reveal effects operating on multi-decadal or centennial timescales. Different from earlier studies is the use of a spatial pattern of freshwater release occurring for a large part outside the coastal area to reflect the meltwater deposition due to iceberg drift. This pattern has the effect that less meltwater is directly applied around the coasts of Greenland and Antarctica and more freshwater reaches the open ocean where deep water formation takes place in the coupled model, potentially affecting the global circulation. We vary the amount of freshwater release over time (with a seasonal cycle) in accordance with the RCP8.5 emission scenario (Riahi et al. 2011; Taylor et al. 2012). The increase is not uniform, with separate areas, such as the West Antarctic Ice Sheet and individual glaciers, having different projections. The mass loss from Antarctica is typically three to four times larger than the mass loss associated with Greenland, reaching more than \(1\hbox { Sv }(=10^{6} \hbox {m}^{3}\hbox { s}^{-1})\hbox { towards }2100\).
Earlier work that compared the effects of Greenland and Antarctic mass loss (e.g. Stouffer et al. (2007); Hu et al. (2013)) noted that the Southern Ocean winds induce a northward transport that transfers Antarctic meltwater northward and that the resultant sea-surface salinity and AMOC responses are different when the two freshwater sources are taken separately. In the model used here, the AMOC response is rather weak (Sterl et al. 2012), with low sensitivity to warming and freshening (Van den Berk and Drijfhout 2014). The salinity changes, on the other hand, can be very intricate and non-linear. Here, we will focus on the Atlantic and Arctic salinity budget and how barotropic and barotropic mass and freshwater/salt fluxes over the boundaries (i.e. Bering Strait and a zonal section near Cape Agulhas) are modified by the freshwater release. In particular, Coupled Climate Model (CCM) studies forced with realistic amounts of Greenland meltwater loss do not simulate a strong response of the AMOC (Swingedouw et al. 2012; Weijer et al. 2012; Van den Berk and Drijfhout 2014), and also the model used here features a rather weak response.
The aim of this paper is, therefore, to evaluate how the ocean, and in particular the distribution of salt, responds to a plausible high-end scenario of freshwater release against a background of global warming, and to which extent the response to Northern Hemisphere (NH; Greenland) and Southern Hemisphere (SH; Antarctica) mass sources reinforce or counteract each other. Also, it is investigated whether non-linear or non-reversible effects arise by simulating a century of decreasing CO\(_2\) concentrations and freshwater release (ramp-down) after a century of increase (ramp-up) following the RCP8.5 emission scenario. The ramp-up and ramp-down scenarios used are exactly symmetric about the year 2100.
The paper is structured as follows. Section 2 consists of an overview of the simulations done. In Sect. 3 the framework of the analysis is presented. In Sect. 4 the main results from the analysis are shown. A discussion and final conclusions are presented in Sect. 5.
2 Experiments
Figure 1 shows the forcing profiles used to prescribe atmospheric CO\(_2\) and freshwater forcing (from the continental ice sheets) to the ocean (or ‘hosing’). Till 2100 there is an increase in both forcings, followed by a symmetric decrease of the forcing, ending in 2195. These two phases are labelled ‘ramp-up’ and ‘ramp-down’ (see also Sgubin et al. 2014 for a similar experimental set-up). The atmospheric forcing follows the RCP8.5 scenario (Taylor et al. 2012) during the ramp-up, the freshwater forcing is as described in Van den Berk and Drijfhout (2014). The scenario follows a high-end mass-loss scenario from Greenland and Antarctica, but is less extreme than, e.g., DeConto and Pollard (2016).
Top: The two forcing profiles applied in our simulations. Top-left panel: atmospheric CO\(_2\) concentration. Top-right panel: cumulative global freshwater forcing (global: black, northern hemisphere: green, southern hemisphere: purple). Bottom-left: iceberg melt pattern (see Van den Berk and Drijfhout 2014 for technical details). Bottom-right: melt rates; the top-right panel shows the time-integrated curves of these
This forcing profile is idealised and the symmetry of the profile is clearly unrealistic. The motivation for using this symmetric forcing profile is to investigate possible non-linear effects, as the mechanisms responding to the linear increase in forcing, which operate on different timescales, will decouple after the reversal point in 2100 (see also Boucher et al. 2012). In particular, mechanisms that almost instantaneously follow the forcing will still behave symmetrically, while those which respond with a lag will deviate from the forcing trend. The simulations start in 2005 after a spin-up of 440 years with pre-industrial atmospheric forcing and historical forcing from 1850 to 2005 (see Sterl et al. (2012) for details). The simulations are continued until 2195.
Table 1 gives an overview of the simulations. We performed an ensemble of 4 control runs with only the atmospheric forcings changing according to the RCP8.5 scenario (ensemble C), and a similar-sized ensemble in which the freshwater forcing is applied to the run in C (ensemble H). Simulations N and S are single runs with a forcing like in the first run of H, but with the freshwater forcing only applied to either the Northern or Southern Hemisphere. All output variables are recorded as monthly mean output.
The experiments are performed with the CCM ‘EC-Earth’. EC-Earth consists of three components. The atmosphere and land surface are modelled with the Integrated Forecast System (IFS–cycle 31r1) which resolves 62 layers in the vertical and uses a triangular truncation at wavenumber 159 (ECMWF 2006) (effectively resolving \(\approx 130\) km). The ocean is modelled by the Nucleus for European Modelling of the Ocean (NEMO) developed by the NEMO European Consortium at a resolution of approximately 1\(^{\circ }\) in the horizontal (\(\approx 110\) km) and 42 levels in the vertical (Madec 2008). The effect of mesoscale eddies is parametrised with an eddy-induced advection term Gent and Mcwilliams (1990). Both the horizontal diffusivity and the eddy-induced advection term use a constant diffusivity parameter of \(10^3\)m s\(^{-2}\) NEMO is equipped with a free surface formulation for the ocean surface, implying that freshwater release adds volume to the ocean, instead of using a virtual salt flux. Ocean and atmosphere are synchronised along the interface every three model-hours by the OASIS3 coupler developed at the Centre Europe en de Recherche et Formation Avances et Calcul Scientifique (Valcke et al. 2004). The ocean model is coupled to a sea-ice model developed by the University of Louvain-la-Neuve (LIM2) (Fichefet T 1997; Bouillon et al. 2009). The general characteristics of EC-Earth simulations are described by Hazeleger et al. (2012); Sterl et al. (2012) shows more detail on the ocean aspects.
3 Methods
The total freshwater flux into the ocean surface (F) is \(F = -E + P + R + I + M\), with E evaporation, P precipitation, R runoff, I meltwater from sea-ice, and M the meltwater we apply as a forcing. For a global domain with only a free surface there must be changes in volume due to freshwater fluxes, but the salt content must remain conserved. The salt balance is expected to differ by latitude. Apart from the extra freshwater forcing applied in the model, the salinity is affected by ocean advection and changes in the other terms in F. A change in volume transport will change the advected amount of salt, as will a change in the local salinity. Below we derive some quantities that help differentiate between these components. EC-Earth’s ocean component, NEMO, uses a linear free surface formulation: a closure term related to changes in SSH is needed to close the salt budget. This term could be interpreted as a change in the salt content of the upper layer, and as such is an artifact of the lack of a true free surface of the model.Footnote 1 For a zonally bounded box B with surface a, depth H and sea surface height of \(\eta\), conservation of salt then leads to the balance (see also Treguier et al. 2012),
Here \(\zeta\) is the salt content, S the salinity, \(\rho _0\) the reference density of sea water in the model, V the meridional velocity, \(F_D\) salt diffusion, and \(\zeta _i\) salt forcing due to brine rejection. Because salt can only be transported across the north (n) and south (s) ocean sections these are explicitly present. The ocean component in our model formulates the (linear) free surface (Roullet and Madec 2000) and only involves advection and diffusion below \(z=0\),
The velocities \(V_s\) and \(V_n\) are the meridional velocities at the northern and southern boundaries of a box. The salt content is now split into the components, indicated by the given subscripts (\(\zeta _{0}\) for volume, \(\zeta _{\eta }\) for surface, \(\zeta _{n,s}\) for advection, \(\zeta _{D}\) for diffusion, and \(\zeta _{0}\) for brine rejection). Meltwater and other surface fluxes do not affect the total amount of salt in the ocean, but does add to its volume.
Salt advection through the basin is primarily a result of the overturning, gyres, and a net barotropic flow. We define three variables describing the changes in salt advection (see “Appendix” for details on notation used below). We start with advection by the overturning component, i.e. an analogue of \(M_{\text {ov}}\) (Rahmstorf 1996),
Here, \(\langle \rangle\) is a zonal averaging operator and is defined in the Appendix.
Similarly, Eq. 5 is associated with the azonal component of salt advection, i.e. advection by the gyre and an analogue of \(M_{\text {az}}\) (Rahmstorf 1996) of the salt content \(\zeta\);
and the remainder is advection by the net barotropic flow, resulting from Bering Strait transport and the integrated net freshwater forcing between Bering Strait and the relevant latitude (i.e the running integral of \(P+R-E\)),
Salt advection can change because the volume transport changes, or because the salinity changes. The salt advection anomaly into a box can be split into two quantities (where H for hosing series, C for control),
The operator \(\varDelta ^{S}\) retains the anomalous salinity, but uses the average of the volume transport, while \(\varDelta ^{V}\) averages the salinity profile while retaining the anomalous volume transport. These two operators indicate whether the change in salt advection is primarily due to salinity changes or volume changes.
For a single (zonal) section b the cumulative effects on salt, transported across a section b, have a similar expression to Eq. 7 as its time-integral,
Eq. 8 decomposes the changes in salt transport into a part that is driven by changes in salinity (keeping the volume transport constant) and into a part that is driven by changes in volume transport, keeping the salinity constant. Below, these two terms will be indicated as being the ‘salinity-driven’ and ‘volume-driven’ part of the salt transport anomaly, respectively. (All decompositions are calculated at the model gridpoint level).
4 The salt redistribution
We start our analysis by showing the global response in sea surface salinity to freshwater forcing from the large ice-sheets in four chunks of 45 years (see also e.g. Morrill et al. (2014); Otto-Bliesner and Brady (2010); Stouffer et al. (2007) for similar work in other models). As stated before, for a description of the mean ocean state in EC-Earth, see Sterl et al. (2012).
4.1 The spatial pattern of redistribution
In Fig. 2 the panels display ensemble-averaged differences between runs H and C (Table 1). Figure 2 shows that low salinity waters from the East and West Greenland Current pile up at the eastern boundary of the subtropical gyre. The distribution around the subpolar gyre (SPG) and the eastern boundary current of the subtropical gyre (STG), i.e. the Canary current, indicates that the redistribution is advective in nature. The low-salinity water partly follows the pathway of the boundary currents and mid-latitude jet, which divides the subpolar and subtropical gyres, and is partly affected by surface Ekman flow. The low salinity signature along the Canary current has been also observed in the hosing experiments of Swingedouw et al. (2012), which contains further details of how the salinity anomaly in the North Atlantic develops. Low salinity waters are also found around the coast of Antarctica. At the Antarctic Peninsula in particular there is a patch of low salinity waters which spreads further northward and eastward, and there is some indication of these waters being carried into the South Atlantic. A rapid adjustment takes place, as is evident from the congruence in the transport signals at both Bering Strait and the Agulhas section. This cannot be due to advection, but only through wave adjustment. This becomes especially visible after 2050. The conspicuous increase of sea surface salinity in the Arctic is not due to changes increases in sea-ice growth, but has an advective origin as will become apparent below.
Figure 3 shows the same for the depth-averaged salinity. By comparing the two figures it becomes clear that, while along the boundaries of the subpolar gyre the surface signal weakens in the last 45 years due to reducing freshwater input, the depth-averaged signal keeps increasing in the subpolar gyre region. During this period the time-integrated freshwater input still increases. Also, the signal is more mixed over the whole subpolar gyre. Apparently, during the last 45 years, more of the surface signal is vertically mixed or subducted reducing the net freshwater anomaly in the surface layers. Also, it becomes apparent that the northward spreading of the anomaly originating from Antarctica remains more confined to the surface layers and must be primarily transported by the Ekman flow.
4.2 The basin-wide Arctic–Atlantic salt export
The zonally-averaged salt anomaly in the Atlantic shows that after 50 years most of the freshening occurs primarily in the subtropical gyre (Fig. 4, between \(10^{\circ }N\) and \(45^{\circ }N\)). This implies that the subtropical gyre receives more freshwater from the north than it transports to the south, leading to convergence of freshwater. After about 100 years, the South Atlantic freshens as well, preceded by a mild salinification during the initial 50 years. Later, we will show that this freshening originates from the Antarctic. The subpolar gyre (between \(45^{\circ }N\) and \(65^{\circ }N\)) remains relatively unaffected until 2150 when considerable freshening starts, on par with subtropical gyre freshening.
A small part of the change in salinity (and salt content through changes in advection) is due to a response in evaporation and precipitation. After 50 years, a reduction in the precipitation north of the equator appears, with an excess in precipitation south of it (not shown). This pattern is indicative of a southward shift of the InterTropical Convergence Zone (ITCZ). A shifting ITCZ is a known effect for a warmer climate in which the AMOC slows down, reducing the relatively high NH surface temperatures compared to the SH (see e.g. Stouffer et al. (2006). The effects of the ITCZ shift, however, appear minimal compared to the freshwater forcing from the ice sheets and will not be discussed further (but see e.g. Zhang and Delworth (2005)). As a result, the basin-integrated effect of changes in EPRI are minor in the Arctic/Atlantic salinity budget (dotted line in Fig. 5). Remarkably, the Atlantic is not only diluted by the freshwater from the Greenland ice cap (Fig. 5), there is also a net salt export from the basin, which starts after five decades of forcing. As a result, the decrease in salinity is much stronger than dilution by the northern forcing would imply (left panel), even though part of the excess volume is transported out of the basin. There is no change in the salt transport across the Strait of Gibraltar (not shown). This leaves Bering Strait and the section at Cape Agulhas as the two locations where net salt exchange can adjust. The connection between Bering Strait and South Atlantic volume transport has been noted before by, e.g. Reason and Power (1994); De Boer and Nof (2004); Hu et al. (2008). These studies focus on the effects of closing Bering Strait on the overturning. Bering Strait is thought to have been closed during paleo-climatic times such as glacial periods (Hu et al. 2008). A closed Bering Strait leads to a more unstable overturning (Hu et al. 2012, 2015). The freshwater import via Bering Strait can be affected by Greenland meltwater, even reversing to an export (Hu et al. 2011). We, however, are interested in the connection during present and near-future times with Bering Strait in its current state. To this end we analyse the salt distribution in the transient response in greater detail (and with a more appropriate melt scenario) than has been done in the literature so far.
Left panel: the anomaly (\(H-C\)) of average salinity in the Arctic + Atlantic. More freshwater is taken in than is to be expected from the Greenland freshwater (dashed line), than can be explained from the increase in surface elevation (dash-dotted line), or the net freshwater anomaly into the ocean (dotted line). Right panel: the salt content in the basin. Ensemble averages are plotted in a darker hue. Individual anomalies are plotted to indicate the ensemble spread
Anomaly (\(H-C\)) of salt content in the Atlantic-Arctic basin by contribution. The components are the anomaly values of the terms in Eq. 3. In solid red \(\varDelta \left( \zeta _n + \zeta _s\right)\), the advected salt through the basin. In dash-dotted black \(\varDelta \zeta _0\), the salt in the fixed volume. In dashed green \(\varDelta \zeta _{\eta }\), the surface elevation accumulation term. The sea-ice contribution \(\varDelta \zeta _i\) in blue, and in grey the remainder (\(\approx \zeta _D\), diffusion, mixing and accumulated numerical errors). Ensemble averages are plotted in a darker hue
The inference from Fig. 5 that salt is exported from the Atlantic by advective processes is confirmed by decomposing the salt balance into its components as in Eq. 1. It is then found that salt loss is indeed due to anomalous salt advection (the green and black line \(\approx\) red) out of the basin (Fig. 6). Sea-ice and other coupled processes only affect the salt content in the basin very little. To determine which parts of the circulation are responsible for the salt loss we split the anomalous salt advection into components.
4.3 A decomposition of salt advection
Left panel: anomaly (\(H-C\)) of net advected salt into the Atlantic-Arctic basin decomposed into a barotropic (solid line), overturning (dashed line), and gyre (dash-dotted line) components. The grey line is their sum and equal to the total salt advection (red line in Fig. 6). Right panel: The three components in the left panel split into S (red) and V (blue) components. All lines are the ensemble averages of the runs. Note the difference in scale between the two panels
The anomalous salt advection can be split into three dynamic components, which reflect changes in salt transport by the overturning, gyre, and barotropic circulation, respectively (Eqs. 4, 5, 6). This decomposition is shown in the left panel of Fig. 7. The anomalous salt advection can also be split into components reflecting changes in either volume transport or salinity (Eq. 8). This is shown in the right panel of Fig. 7 for each of these three dynamic components.
The two baroclinic components (overturning and gyre) are responsible for 75% of the salt export at the end of the simulation, with the remaining 25% due to barotropic flow. Figure 7 shows that the overturning is associated with anomalous transport of salt out of the basin. The overturning component itself remains relatively unaffected during the ramp-up (blue dashed line, right panel). Thus, the AMOC response to hosing is relatively weak in this model; \(\mathcal {O}\)(1 Sv). This implies that the change in salt transport by the overturning is primarily due to changes in salinity (dashed red line, right panel). Because there is no overturning component in Bering Strait, the overturning at the Agulhas section either imports fresher water or exports saltier water. With a freshening of the surface due to the applied forcing, the expected response is a freshening of the inflow. Given the timing, this change must be associated with the arrival of freshwater, originating from the Antarctic Ice Sheet, at the southern boundary of the Atlantic.
It is only during the last half of the 22nd century that volume-driven changes affect the salt transport by the overturning. The overturning weakens and exports less salt from the Atlantic, counteracting the dilution of salt in the basin. It should be noted that this response, occurring after 2150, does not exclude changes in the volume transport (weakening) of the overturning, which occurs before 2150. It merely indicates that such changes have not yet reached the Agulhas section during the first century and a half. The gyre component in Fig. 7 is dominated by volume-driven changes. The gyre imports freshwater into the South Atlantic and the increase in import indicates a strengthening of the gyre at the Agulhas section, see Sect. 4.5 for details.
Top panel: Anomaly (\(H-C\)) of time-integrated mass transport into the Atlantic-Arctic basin. The solid line is the basin-integrated divergence (net transport through the basin), which is the difference between Bering Strait in the North (dashed line) and Cape Agulhas in the south (dash-dotted line). The EPRI contribution (dotted line) is negligible. The grey line is the Greenland freshwater forcing. Bottom panel: the ramp-down EPRI pattern plus forcing
The barotropic component also exports salt from the basin, both through a stronger volume transport and increased salt contrast between Bering Strait inflow and outflow across the Agulhas section (Fig. 7). Net volume transport changes across the basin in Fig. 8a result from a difference between changes in Bering Strait transport and transport across the section at Cape Agulhas. The mass loss due to divergence of the barotropic flow is at least an order of magnitude larger than changes in freshwater flux between ocean and atmosphere. The result is a steady export of water out of the basin due to an imbalance between the two barotropic transport terms. This transport divergence partly counteracts the volume increase due to adding freshwater from Greenland. The divergence in volume transport means that either the outflow across the Agulhas section increases, or it decreases less than the inflow through Bering Strait. The mass advection in Fig. 8a shows that the transport increases across both sections during the first 50 years, but decreases after that time. The bottom panel in Fig. 8 illustrates why the atmospheric response in EPRI is basin-integrated negligible over the Arctic/Atlantic basin. The anomalous EPRI field shows clearly the sign of a displaced ITCZ, with a southward shift occurring in the Atlantic. The net effect (i.e. net EPRI anomaly) integrated over the tropical belt, however, is small. This is consistent with the weak response of the AMOC.
The export of salt by the barotropic component especially increases during the ramp-up (solid black line in Fig. 7), and is steady during the ramp-down. We see that the initial salt export from the Atlantic by the barotropic flow is volume-driven and the effect of salinity changes only sets in during the ramp-down. In this phase (i.e. after 2100) the two effects largely cancel. It should be noted that the effect of volume-driven response in barotropic flow on the salinity budget is different than in Hu et al. (2011), where a reduction in Bering Strait throughflow was found to lead to an increase salinity. Here, changes in Bering Strait inflow and outflow across the Agulhas section are not in balance. The effect on salinity is not driven by the barotropic flow becoming stronger or weaker, but by the divergence between inflow and outflow, with the outflow being larger, hence export of volume and salt. This change in barotropic response is again associated with the arrival of freshwater from Antarctica at the southern boundary of the Atlantic.
The main drivers of the salt export from the Atlantic are thus a dilution due to water imported by the overturning across the Agulhas section because of the arrival of freshwater from the Antarctic, an increase in the volume-driven export by the South Atlantic gyre, and a divergent barotropic transport across the basin, which partly compensates the volume increase due to freshwater input. We conclude that the salt export from the Atlantic is a compound effect involving all three different circulation types.
4.4 Bering Strait changes
Results from previous sections and from existing literature (De Boer and Nof 2004; Hu et al. 2007, 2012; Weijer et al. 2001; Hu et al. 2015; Reason and Power 1994) indicate an important role for Bering Strait in the adjustment of the salt budget in the Atlantic in response to high latitude freshwater perturbations.
The flow through Bering Strait starts increasing salt and mass into the basin, while the flow across the Agulhas section decreases salt and mass even more, indicating that both barotropic flows increase. After 50 years the barotropic salt transport anomaly changes sign at each section, indicating the barotropic flow has become less than the control run C. However, at each moment in time the salt (and mass) transport are divergent, that is, mass and salt are exported from the basin. The mass export is a response to the volume added to the Atlantic by Greenland freshwater release. This added volume alters the sea surface height (SSH) difference between the Atlantic and Pacific.
The Pacific typically features higher sea level than the Atlantic, with the pressure drop across Bering Strait driving a northward flow through Bering Strait (Aagaard et al. 2006). The initial increase in barotropic flow through Bering Strait must be due to an increase in sea-level gradient, either by a Pacific-side increase, or an Arctic-side decrease. Initially, Greenland meltwater is carried southward via currents and wave adjustment, while Antarctic meltwater is carried northward into the Pacific along the eastern boundary, also likely dominated by wave adjustment processes via boundary and Kelvin waves. As a result, the Arctic does not gain volume, while SSH does increase in the Pacific (Fig. 9). After 40–50 years the SSH anomaly—coupled to a negative salinity anomaly—is carried by the North Atlantic Drift and Norwegian Current into the Arctic, reversing the anomalous SSH gradient across Bering Strait. This drives the sign reversal in salinity and mass transport anomaly through Bering Strait and across the Agulhas section seen in Fig. 8.
Though the large-scale changes in north-south SSH gradient are the driver of the Bering Strait throughflow flowing down the pressure gradient, within the Bering Strait the flow should largely obey geostrophy. Geostrophy is ensured by the warmer and lighter Pacific surface layer outcropping at the eastern side of Bering Strait, while the colder water in the Arctic is connected with the western boundary of the Arctic. As a result, the north-south gradient in SSH is transmitted to the east-west SSH gradient within Bering Strait. This effect is illustrated by Fig. 10, which shows the change in total transport versus geostrophic transport. The match is not completely perfect, as the flow is partly frictionally controlled, but the signals in both transports are still in qualitative agreement. Wind and density gradient contributions, shown as the Ekman transport anomaly and the baroclinic transport anomaly, are negligible.
4.5 The South Atlantic subtropical gyre response
The South Atlantic is separated from the Southern Ocean by a strong front associated with the Antarctic Circumpolar Current (ACC), known as the Subtropical Front (STF) (Peeters et al. 2004). At the STF, the Agulhas Return Current (ARC) encounters the ACC, with the winds exerting a strong influence on the position of the STF (Biastoch et al. 2009; de Boer et al. 2013; Durgadoo et al. 2013). Across the STF a large salinity and temperature gradient exists. In addition, the SH supergyre (the flow that connects the three wind-driven gyres in the SH in terms of barotropic volume transport) strengthens in the Indian and Atlantic sector in response to hosing. The strength of the SH supergyre and the position of the STF are strongly controlled by the wind; this response leads to the question whether the changes in transport can be attributed to changes in wind stress.
During the first 50 years, the gyre imports more salt into the South Atlantic due to a more saline inflow, partly counteracted by a spin-up of the South Atlantic subtropical gyre, which, as a whole, imports freshwater (Fig. 7). In those first 50 years the wind response shifts the STF to the south and enhances the SH supergyre. Thereafter, the barotropic streamfunction continues to show consistent anomalies that enhance the South Atlantic subtropical gyre (Fig. 11). The associated change in windstress does not only show an increase in winds, but also a noticeable southward shift of the westerlies. This is in contradiction with Menviel et al. (2010), who showed that an increase in SH sea ice shifts the wind northward. Here, the Antarctic ice sheet releases large amounts of freshwater. This not only increase sea-ice but also reduces buoyancy near the Antarctic continent due to large-scale freshening of surface waters, reducing, instead of increasing the meridional density gradient between pole and equator, and changing the density pattern. It is beyond the scope to explain the wind response to this type of surface forcing here, but the reversed change in equator-to-pole density gradient may partly explain the opposite shift in westerlies, as found in Menviel et al. (2010). As a result, Agulhas leakage does not decrease, but increases instead (Sijp and England 2008).
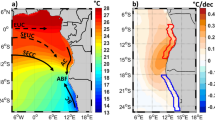
To quantify these effects, we relate the increased volume transport to the Sverdrup balance and gyre spin-up associated with buoyancy forcing. In this case the section is chosen at 35\(^\circ\)S, between 20\(^\circ\)E and 20\(^\circ\)W. We should stress that, because of the non-linearities associated with Agulhas leakage, we do not expect the South Atlantic gyre to be fully controlled by local windstress and buoyancy forcing, nor the strength of the Agulhas leakage feeding into this gyre (Beal et al. 2011).
Figure 12 clearly illustrates that buoyancy forcing plays no role, and that during the first 100 years the change in volume transport is adequately described by changes in Sverdrup transport associated with the wind response to increased meridional temperature gradients. After 100 years, however, the increase in volume transport becomes considerably larger than the change in Sverdrup transport, indicating that this change is associated with non-local effects further upstream (roughly at the same time the overturning starts to freshen the entire basin).
4.6 The different response to NH and SH sources
The results shown so far indicate a different role for both NH and SH freshwater sources on the Atlantic salt budget. The H set of simulations cannot distinguish between the impact of both sources of freshwater. To be able to do so, simulations with separate NH and SH freshwater forcing were conducted (N and S).
In Fig. 13 the barotropic transport anomalies are shown for NH forcing (\(N-C\)) and SH forcing (\(S-C\)) only. The barotropic component already shows the opposite effect of the forcing on salt import/export into/from the Atlantic and Arctic basins in the two experiments. With only Antarctic freshwater forcing, there is a steadily increasing salt import. With only Greenland freshwater forcing, there is a salt export from the Atlantic. In the NH forcing experiment, Greenland freshwater anomalies are advected with some time delay into the Arctic, similar to the full freshwater anomaly experiment. At the same time as in \(H-C\), the SSH gradient across Bering Strait starts to decrease and, as a result, the transport through Bering Strait, decreases as well. The throughflow across the Agulhas section follows this response. The reduced barotropic throughflow is associated with a diminished import of fresher water and also less export of saltier water. The reduced inflow, however, outweighs the reduced outflow in terms of salt and mass balance. Figure 13 clearly demonstrates this for the salt balance. The mass balance (not shown) displays the same behaviour.
This reduction in barotropic transport implies a positive feedback by Greenland meltwater on freshening the Atlantic and Arctic basins. Direct freshening occurs by adding freshwater to the ocean and this added volume reduces the inflow of mass and salt across Bering Strait. Although the barotropic flow across the Agulhas section also decreases, this decrease is smaller than the Bering Strait transport. As a result, salt transport divergence by the barotropic flow occurs in response to volume added from the Greenland Icesheet.
Note that even though the Pacific water entering through Bering Strait is fresher than the Arctic water, the positive feedback above relates to the mass advection through the Strait. In terms of salinity, a reduction in Bering Strait on its own is a negative feedback because less freshening through the strait takes place (Hu et al. 2011).
In the SH forcing experiment the opposite occurs. Added volume from Antarctica reaches the North Pacific with some time delay, enhancing the barotropic flow through Bering Strait. The effect on the salt balance is also the opposite of the one seen in the NH forcing experiment (Fig. 13). Flow through Bering Strait and across the Agulhas section both increase under SH forcing, but the increase across the Agulhas section is smaller than the increase of Bering Strait transport. As a result, the response of the barotropic flow is now a convergence of salt into the Arctic–Atlantic basin.
In the experiment H, with both NH and SH forcing, we saw a net freshening by the barotropic component. Ultimately, the effect of NH forcing outweighs the effect of SH forcing in terms of salt divergence in the Atlantic, even though the SH forcing in terms of added volume to the ocean is much stronger than the NH forcing (by roughly a factor four in our scenario). Also, we found that the NH forcing leads to a positive feedback on the freshwater budget, amplifying the freshening in the Arctic–Atlantic basin. In Fig. 14 the geostrophic transport is compared against the total transport for \(N-C\) and \(S-C\). For N there is even better agreement between geostrophic transport and the total transport than in H (forcing in both hemispheres), while in S the agreement is slightly less, even though wind and density gradients do not contribute significantly in each case. So, the Bering Strait response is driven by changes in sea surface height, which are attributed to wave adjustment to the freshwater release, although attribution in this case is difficult because of the large variability in sea surface height, making it difficult to identify the boundary/Kelvin waves included in the wave adjustment process.
Left panel: Salt increase in Atlantic–Arctic basin by barotropic flow advection for Northern Hemispheric melt (green) and southern Hemisphere melt (purple) scenarios. Right panel: anomaly \(N-C\) in green and \(S-C\) in purple of time-integrated barotropic salt advection component, split in northern (Bering Strait, darker hue) and southern (Agulhas section, lighter hue) boundary contributions
Counterparts of Fig. 10 for \(N-C\) (left) and \(S-C\) (right). The Bering geostrophic transport anomaly (solid line) is compared against the total transport anomaly (dashed line). The baroclinic contribution (dash-dotted line) and Ekman transport (dotted line) are negligible
5 Discussion and conclusion
Freshwater forcing, derived from a Greenland and Antarctic ice sheet melt scenario, was applied to the ocean in a coupled climate model, otherwise forced by an RCP8.5 scenario until 2100 (ramp-up) and a reversal in greenhouse gas concentrations and freshwater forcing after 2100 (ramp-down). It was found that the Atlantic exports both excess freshwater (volume anomalies) and salt during the latter half of the 21st and the 22nd century. The salinity decrease in the Atlantic and Arctic is more than would be expected from a mere dilution response from the freshwater forcing. In addition to the dilution, the salt transport across the Atlantic boundaries changes in such a way that additional freshening occurs.
In response to the freshwater forcing, the net volume transport across zonal sections at the latitude of Cape Agulhas and through Bering Strait develop almost similar anomalies. Initially transports increase, but after 50 years they start decreasing. At the same time a small residual imbalance between these two transports develops, becoming larger in time, with a larger outflow anomaly at the southern boundary than the inflow anomaly through Bering Strait. This net flow divergence in the Atlantic allows export of part of the excess volume of freshwater released from the Greenland Ice Sheet to the Southern Ocean across the Cape Agulhas section.
Splitting the salt advection into three dynamic components indicates not only a barotropic response, but also that the baroclinic gyre and overturning effects have a major share in the export of salt. During the first 50 years the salt export due to barotropic circulation changes is compensated by the South Atlantic subtropical gyre importing saltier waters (not shown). The positive salinity anomaly is subsurface and not visible in the sea surface salinity anomaly shown in Fig. 2. After 2070, when freshwater from the Antarctic Ice Sheet arrives at the eastern boundary of the South Atlantic, both gyre and overturning components freshen the basin. The baroclinic signal is almost solely determined by changes at the Agulhas section, while the barotropic signal is a residual between the inflow in the north and outflows in the south.
In Fig. 15 a summary of the long-term integrated effects of the hosing scenario are depicted. Larger arrows indicated a larger response, but they are not to scale. Black arrows indicate the mass transport, blue the volume-driven salt transport, and red the salinity-driven salt transport.
The freshwater from the Greenland and Antarctic ice sheets results in an adjustment of the Atlantic on longer timescales than studied here. The simulations show the beginning of this process and an equilibrium-response would take much longer time. Nevertheless, the experiments discussed here show a delicate interplay between the impact of Greenland meltwater and Antarctic meltwater release that can have opposing effects in the Atlantic. For instance, freshwater from Antarctica and freshwater from Greenland have opposite effects on the large-scale north-south density gradient, and this gradient is often used as a metric for the strength of the AMOC (Thorpe et al. 2001). Also, meltwater release from the Antarctic Ice Sheet might negatively impact Antarctic Bottom Water formation, and a reduced deep overturning cell might impede weakening of the AMOC through the bipolar seesaw effect (Green and Schmittner 2015; Seidov et al. 2001; Stocker and Johnsen 2003). The nature of the ramp-up/ramp-down experiment we have performed is by no means a realistic future scenario and was designed such that processes that take a long time to adjust become more apparent in the ocean response to freshwater forcing (e.g. the North Atlantic gyre responses). As a result, the integrated quantitative effects occurring in the model are far from a realistic future response to more realistic meltwater scenarios. Qualitatively, however, we have been able to demonstrate various–sometimes opposing–dynamic adjustments and feedbacks occurring in response to freshwater from both northern and southern sources.
After five decades the response at the Southern boundary changes sign. A slower, advective, oceanic response overtakes the effect of salinification by transporting Antarctic freshwater, associated with enhanced mass loss from the Antarctic Ice Sheet, to the South Atlantic and the whole Atlantic starts to freshen, even though the Agulhas leakage and the supergyre transport keep increasing. Also, the imbalance in barotropic transport affects the salinity budget in the Atlantic. Initially, Bering Strait transport increases less than the outflow across the Agulhas section from Africa to South America does. After 50 years, however, both start decreasing, with the response at Bering Strait being stronger than that of the Agulhas section. The initial increase appears due to SSH anomalies from added volume from Antarctica quickly arriving in the North Pacific, while similar anomalies resulting from added volume from Greenland initially travel southward. After 50 years, part of the volume excess originating from Greenland reaches the Arctic, being advected by the North Atlantic and Norwegian Current and spread further by the Beaufort Gyre.
While initially the SSH gradient over Bering Strait increases, after 50 years it starts to decrease. The integrated response to these barotropic changes is that the Atlantic freshens. It should be emphasized that this response cannot be explained by an increase or decrease in barotropic throughflow or Bering Strait inflow, since in such case the response in salinity would be opposite to the response in barotropic flow Hu et al. (2011). The salt export is due to the consistent divergence of barotropic flow, i.e. outflow across the Agulhas section increases more or decreases less than Bering Strait inflow.
Bering Strait can be important for the stability of the AMOC. After an AMOC collapse, recovery is more difficult with a closed Bering Strait (Hu et al. 2007, 2012). A closed Bering Strait traps low salinity anomalies in the Arctic, possibly destabilising the overturning, as shown in previous studies [e.g. Reason and Power (1994); De Boer and Nof (2004); Hu et al. (2015)]. In many coarse resolution models, Bering Strait is not well resolved, however. The model used here has one degree horizontal resolution, and Bering Strait features a realistic width and depth, allowing geostrophic processes to dominate over frictional processes. With a volume transport of \(\sim {1}\) Sv, the modelled Bering Strait throughflow is in agreement with observed values (Woodgate et al. 2006).
A main conclusion from this paper is that melting ice sheets do not merely dilute the ocean and increase sea-level. A much more complicated picture arises where both barotropic and baroclinic effects play a role. The salinity of the Atlantic depends not just on the dilution effects of Greenland meltwater, but also on the dynamic effects brought about by the Antarctic meltwater. The imbalance that develops between the mass flux anomaly at Bering Strait and at the zonal section at the latitude of Cape Agulhas eventually leads to additional freshening of the Atlantic (both through salinity and volume transport changes) beyond what would be expected from Greenland meltwater alone.
The freshwater releases from Greenland and from Antarctica have a distinctly different effect on the volume transports and salt balance of the Atlantic. In the case of SH meltwater forcing, the SSH gradient over Bering Strait increases, and subsequently the barotropic throughflow across the Arctic–Atlantic basin increases. Transport at the Agulhas section responds in a very similar way, but the increase is slightly less, leading to net convergence and salinification of the basin. With only NH meltwater forcing, the SSH gradient across Bering Strait decreases, with, again, transport across the Agulhas section following the decrease, but being slightly weaker. The result is a decrease and net divergence of the barotropic flow, leading to overall freshening of the basin.
Our study indicates that coupled ocean-atmosphere processes are of minor importance for the adjustment of the salt budget in the Atlantic in response to freshwater sources, while coupled processes are important in driving South Atlantic circulation changes. A resultant shift of the ITCZ is noted, but hardly affects the salt budget, when integrated over the whole Arctic/Atlantic basin, as areas of positive and negative EPRI response cancel out. Also, wind stress changes over the Southern Ocean affect the SH supergyre. Even though the model used is a state of the art coupled model for long climate integrations, there are limitations as well. Because the advection of the meltwater is likely affected by mesoscale eddies, both in the subpolar North Atlantic and by the Agulhas leakage bringing the meltwater from the Antarctic into the South Atlantic, the full effects of melting ice sheets on the Atlantic salt balance are difficult to quantify in our relatively coarse resolution model. The model uses the Gent-McWilliams parametrisation scheme, which is an idealisation (with a constant thickness diffusivity). The choice of eddy parametrisation can affect the results [e.g. Eden et al. (2009)]. We also do not know to what extent the melt scenario used here will be applicable to the real world. It is nonetheless clear that feedbacks in the Southern Ocean are of importance. The Southern Hemisphere forcing will eventually dominate the Northern Hemisphere forcing, because a larger volume of meltwater can be released from the Antarctic Ice Sheet compared to the Greenland Ice Sheet; the potential contribution from Antarctica to global sea level rise can be much larger than Greenland’s in a high-end scenario (DeConto and Pollard 2016; Katsman et al. 2011; Bars et al. 2017).
Notes
The surface elevation does not change the vertical metric (dz / dk–meaning the metric field is static and not dependent on the surface elevation as it should be for a real free surface formulation).
References
Aagaard K, Weingartner TJ, Danielson SL, Woodgate RA, Johnson GC, Whitledge TE (2006) Some controls on flow and salinity in Bering Strait. Geophys Res Lett. https://doi.org/10.1029/2006GL026612
Bakker P, Schmittner A, Lenaerts J, Abe-Ouchi A, Bi D, Broeke M, Chan WL, Hu A, Beadling R, Marsland S (2016) Fate of the Atlantic Meridional Overturning Circulation: strong decline under continued warming and Greenland melting. Geophys Res Lett 43(23):12–252
Bars DL, Drijfhout S, de Vries H (2017) A high-end sea level rise probabilistic projection including rapid Antarctic ice sheet mass loss. Environ Res Lett 12(4):044013
Beal LM, De Ruijter WP, Biastoch A, Zahn R (2011) On the role of the agulhas system in ocean circulation and climate. Nature 472(7344):429–436
Biastoch A, Böning CW, Schwarzkopf FU, Lutjeharms J (2009) Increase in agulhas leakage due to poleward shift of southern hemisphere westerlies. Nature 462(7272):495–498
de Boer AM, Graham RM, Thomas MD, Kohfeld KE (2013) The control of the southern hemisphere westerlies on the position of the subtropical front. J Geophys Res Oceans 118(10):5669–5675
Boucher O, Halloran PR, Burke EJ, Doutriaux-Boucher M, Jones CD, Lowe J, Ringer MA, Robertson E, Wu P (2012) Reversibility in an earth system model in response to CO\(_{2}\) concentration changes. Environ Res Lett 7(2):024013
Bouillon S, Maqueda MM, Legat V, Fichefet T (2009) An elastic-viscous-plastic sea ice model formulated on Arakawa b and c grid. Ocean Model 27:174–184. https://doi.org/10.1016/j.ocemod.2009.01.004
De Boer AM, Nof D (2004) The bering strait’s grip on the northern hemisphere climate. Deep Sea Res I Oceanogr Res Pap 51(10):1347–1366
DeConto RM, Pollard D (2016) Contribution of antarctica to past and future sea-level rise. Nature 531(7596):591–597
Durgadoo JV, Loveday BR, Reason CJ, Penven P, Biastoch A (2013) Agulhas leakage predominantly responds to the Southern Hemisphere westerlies. J Phys Oceanogr 43(10):2113–2131
ECMWF (2007) IFS documentation. http://www.ecmwf.int/research/ifsdocs/CY31R1/index.html. Accessed 2016
Eden C, Jochum M, Danabasoglu G (2009) Effects of diffferent closures for thickness diffusivity. Ocean Model 26(1–2):47–59
Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, Taylor KE (2016) Overview of the coupled model intercomparison project phase 6 (cmip6) experimental design and organization. Geosci Model Dev 9(5):1937–1958. https://doi.org/10.5194/gmd-9-1937-2016
Fichefet TMMM (1997) Sensitivity of a global sea ice model to the treatment of ice thermodynamics and dynamics. J Geophys Res 102(646):609–12. https://doi.org/10.1029/97JC00480
Gent PR, Mcwilliams JC (1990) Isopycnal mixing in ocean circulation models. J Phys Oceanogr 20(1):150–155
Green J, Schmittner A (2015) Climatic consequences of a Pine Island Glacier collapse. J Clim 28(23):9221–9234
Hanna E, Navarro FJ, Pattyn F, Domingues CM, Fettweis X, Ivins ER, Nicholls RJ, Ritz C, Smith B, Tulaczyk S et al (2013) Ice-sheet mass balance and climate change. Nature 498(7452):51–59
Hazeleger W, Wang X, Severijns C, Tefnescu S, Bintanja R, Sterl A, Wyser K, Semmler T, Yang S, Hurk B, Noije T, Linden E, Wiel K (2012) Ec-earth v2.2: description and validation of a new seamless earth system prediction model. Clim Dyn 39(11):2611–2629. https://doi.org/10.1007/s00382-011-1228-5
Hu A, Meehl GA, Han W (2007) Role of the bering strait in the thermohaline circulation and abrupt climate change. Geophys Res Lett. https://doi.org/10.1029/2006GL028906
Hu A, Otto-Bliesner BL, Meehl GA, Han W, Morrill C, Brady EC, Briegleb B (2008) Response of thermohaline circulation to freshwater forcing under present-day and LGM conditions. J Clim 21(10):2239–2258
Hu A, Meehl GA, Han W, Yin J (2011) Effect of the potential melting of the Greenland Ice Sheet on the Meridional Overturning Circulation and global climate in the future. Deep Sea Res II Top Stud Oceanogr 58(17–18):1914–1926
Hu A, Meehl GA, Han W, Timmermann A, Otto-Bliesner B, Liu Z, Washington WM, Large W, Abe-Ouchi A, Kimoto M (2012) Role of the bering strait on the hysteresis of the ocean conveyor belt circulation and glacial climate stability. Proc Natl Acad Sci 109(17):6417–6422
Hu A, Meehl GA, Han W, Yin J, Wu B, Kimoto M (2013) Influence of continental ice retreat on future global climate. J Clim 26(10):3087–3111. https://doi.org/10.1175/JCLI-D-12-00102.1
Hu A, Meehl GA, Han W, Otto-Bliestner B, Abe-Ouchi A, Rosenbloom N (2015) Effects of the bering strait closure on amoc and global climate under different background climates. Prog Oceanogr 132:174–196
Joughin I, Alley RB (2011) Stability of the West Antarctic ice sheet in a warming world. Nat Geosci 4(8):506–513
Katsman C, Sterl A, Beersma J, van den Brink H, Church J, Hazeleger W, Kopp R, Kroon D, Kwadijk J, Lammersen R, Lowe J, Oppenheimer M, Plag H, Ridley J, von Storch H, Vaughan D, Vellinga P, Vermeersen L, van de Wal R, Weisse R (2011) Exploring high-end scenarios for local sea level rise to develop flood protection strategies for a low-lying delta—the Netherlands as an example. Clim Change 109(3–4):617–645
Madec G (2008) NEMO ocean engine. Note du Pole de modelisation, vol 27. Institut Pierre-Simon Laplace (IPSL), Paris, pp 1288–1619
Marsh R, Desbruyères D, Bamber JL, de Cuevas BA, Coward AC, Aksenov Y (2010) Short-term impacts of enhanced Greenland freshwater fluxes in an eddy-permitting ocean model. Ocean Sci 6(3):749–760. https://doi.org/10.5194/os-6-749-2010
Menviel L, Timmermann A, Timm OE, Mouchet A (2010) Climate and biogeochemical response to a rapid melting of the west antarctic ice sheet during interglacials and implications for future climate. Paleoceanogr Paleoclimatol 25(4):PA4231
Morrill C, Ward EM, Wagner AJ, Otto-Bliesner BL, Rosenbloom N (2014) Large sensitivity to freshwater forcing location in 8.2 ka simulations. Paleoceanography 29(10):930–945
Otto-Bliesner BL, Brady EC (2010) The sensitivity of the climate response to the magnitude and location of freshwater forcing: last glacial maximum experiments. Quat Sci Rev 29(1):56–73
Peeters FJ, Acheson R, Brummer GJA, De Ruijter WP, Schneider RR, Ganssen GM, Ufkes E, Kroon D (2004) Vigorous exchange between the indian and atlantic oceans at the end of the past five glacial periods. Nature 430(7000):661–665
Rahmstorf S (1996) On the freshwater forcing and transport of the Atlantic thermohaline circulation. Clim Dyn 12(12):799–811
Reason C, Power S (1994) The influence of the bering strait on the circulation in a coarse resolution global ocean model. Clim Dyn 9(7):363–369
Riahi K, Rao S, Krey V, Cho C, Chirkov V, Fischer G, Kindermann G, Nakicenovic N, Rafaj P (2011) Rcp 8.5a scenario of comparatively high greenhouse gas emissions. Clim Change 109(1–2):33
Roullet G, Madec G (2000) Salt conservation, free surface, and varying levels: a new formulation for ocean general circulation models. J Geophys Res Oceans 105(C10):23927–23942. https://doi.org/10.1029/2000JC900089
Seidov D, Haupt BJ, Barron EJ, Maslin M (2001) Ocean bi-polar seesaw and climate: Southern versus northern meltwater impacts. In: Seidov D, Haupt BJ, Maslin M (eds) The ocean and rapid climate change: past, present, and future, Geophysical Monograph Series, vol 126. AGU, Washington, D. C., pp 147–167
Sgubin G, Swingedouw D, Drijfhout S, Hagemann S, Robertson E (2014) Multimodel analysis on the response of the AMOC under an increase of radiative forcing and its symmetrical reversal. Clim Dyn. https://doi.org/10.1007/s00382-014-2391-2
Sijp WP, England MH (2008) The effect of a northward shift in the southern hemisphere westerlies on the global ocean. Prog Oceanogr 79(1):1–19
Stammer D (2008) Response of the global ocean to Greenland and Antarctic ice melting. J Geophys Res Oceans. https://doi.org/10.1029/2006JC004079
Stammer D, Agarwal N, Herrmann P, Köhl A, Mechoso C (2011) Response of a coupled ocean-atmosphere model to Greenland ice melting. Surv Geophys 32(4–5):621
Sterl A, Bintanja R, Brodeau L, Gleeson E, Koenigk T, Schmith T, Semmler T, Severijns C, Wyser K, Yang S (2012) A look at the ocean in the ec-earth climate model. Clim Dyn 39(11):2631–2657
Stocker TF, Johnsen SJ (2003) A minimum thermodynamic model for the bipolar seesaw. Paleoceanography 18(4):1087
Stouffer RJ, Yin J, Gregory J, Dixon K, Spelman M, Hurlin W, Weaver A, Eby M, Flato G, Hasumi H (2006) Investigating the causes of the response of the thermohaline circulation to past and future climate changes. J Clim 19(8):1365–1387
Stouffer RJ, Seidov D, Haupt BJ (2007) Climate response to external sources of freshwater: North Atlantic versus the Southern Ocean. J Clim 20(3):436–448. https://doi.org/10.1175/JCLI4015.1
Swingedouw D, Rodehacke C, Behrens E, Menary M, Olsen MS, Gao Y, Mikolajewicz U, Mignot J, Biastoch A (2012) Decadal fingerprints of freshwater discharge around Greenland in a multi-model ensemble. Clim Dyn. https://doi.org/10.1007/s00382-012-1479-9
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Thorpe RB, Gregory JM, Johns TC, Wood RA, Mitchell JFB (2001) Mechanisms determining the Atlantic thermohaline circulation response to greenhouse gas forcing in a non-flux-adjusted coupled climate model. J Clim 14(14):3102–3116. https://doi.org/10.1175/1520-0442(2001)014%3c3102:MDTATC%3e2.0.CO;2
Treguier AM, Deshayes J, Lique C, Dussin R, Molines JM (2012) Eddy contributions to the meridional transport of salt in the North Atlantic. J Geophys Res Oceans 117(C5):18–26
Valcke S, Caubel A, Vogelsang R, Declat D (2004) OASIS 3 user’s guide. Technical Report TR/CMGC/04/68, CERFACS, Toulouse, France
Van den Berk J, Drijfhout S (2014) A realistic freshwater forcing protocol for ocean-coupled climate models. Ocean Model 81:36–48. https://doi.org/10.1016/j.ocemod.2014.07.003
Vizcaino M (2014) Ice sheets as interactive components of earth system models: progress and challenges. Wiley Interdiscip Rev Clim Change 5(4):557–568. https://doi.org/10.1002/wcc.285
Weijer W, De Ruijter WP, Dijkstra HA (2001) Stability of the atlantic overturning circulation: competition between bering strait freshwater flux and agulhas heat and salt sources. J Phys Oceanogr 31(8):2385–2402
Weijer W, Maltrud ME, Hecht MW, Dijkstra HA, Kliphuis MA (2012) Response of the Atlantic Ocean circulation to Greenland Ice Sheet melting in a strongly-eddying ocean model. Geophys Res Lett. https://doi.org/10.1029/2012GL051611
Woodgate RA, Aagaard K, Weingartner TJ (2006) Interannual changes in the Bering Strait fluxes of volume, heat and freshwater between 1991 and 2004. Geophys Res Lett. https://doi.org/10.1029/2006GL026931
Zhang R, Delworth TL (2005) Simulated tropical response to a substantial weakening of the Atlantic thermohaline circulation. J Clim 18(12):1853–1860
Acknowledgements
This work was funded by the European Commission’s 7th Framework Programme, under Grant Agreement number 282672, EMBRACE project. The authors thank Frank Selten for useful suggestions. The anonymous referees have contributed substantial improvements to the manuscript, for which the authors are also grateful.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 A Salt transport split
A zonal-depth variable (like on the zonal sections we consider in this paper) can be decomposed into a depth anomaly with respect to the zonal average and the remainder, \(V = \delta ^x V + \langle V \rangle _x\), where
Note that V and \(\delta ^x V\) are 2-dimensional, while \(\langle V \rangle _x\) only has the dimension of depth. We can split into these components,
but the cross terms integrate to zero, because (integrating over a section b)
We are then left with only two terms. We let
which is sensitive to azonal (not barotropic or overturning, but gyre related). The remaining term leaves
where we use \(\langle V \rangle\) for the barotropic (section-averaged) value of V. The two remaining terms are sensitive to the overturning and barotropic changes, respectively.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van den Berk, J., Drijfhout, S.S. & Hazeleger, W. Atlantic salinity budget in response to Northern and Southern Hemisphere ice sheet discharge. Clim Dyn 52, 5249–5267 (2019). https://doi.org/10.1007/s00382-018-4444-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4444-4