The interaction between the Western Indian Ocean and ENSO in CESM

Abstract

Several previous studies have suggested that a cool western Indian Ocean may induce convection over Indonesia, leading to surface convergence and easterlies over the western equatorial Pacific Ocean. These easterlies then increase the Pacific Warm Water Volume favouring El Niño in the next year. We investigate this mechanism of Indian-Pacific interaction using output from two simulations (at $0.1^\circ$ and $1^\circ$ ocean model resolution) with the Community Earth System Model (CESM). No conclusive evidence for the suggested interaction mechanism is found in CESM. Like many other coupled models, CESM has an overly strong sea surface temperature variability in the eastern Indian Ocean due to an exaggerated sensitivity of the sea surface temperature to thermocline variations. Due to this bias the effect of the western Indian Ocean signals on the Pacific, as found from observational analysis, is hidden. Our analysis shows that this bias can be traced to errors in the time-mean vertical temperature profile in the Indian Ocean. This bias needs to be reduced to allow a better investigation of the subtle interactions between the Indian and Pacific Oceans.

1 Introduction

Skilful predictions of El Niño-Southern oscillation (ENSO) events are still a challenge for the climate research community, especially at lead times longer than about 6 months (Barnston et al. 2012; L’Heureux et al. 2017). On the other hand, the basic processes in the equatorial Pacific are reasonably well understood (Zebiak and Cane 1987; Philander 1990; Neelin et al. 1998). Mean easterly winds along the equator cause a region of strong mean upwelling, shallow thermocline, and low Sea Surface Temperature (SST) in the eastern part of the basin (Dijkstra and Neelin 1995). The basic ENSO variability arises from an interplay of a positive ‘Bjerknes’ feedback and a delayed negative feedback due to ocean dynamics (Jin 1997a, b). Irregularities on the basic ENSO cycle, which limit prediction skill, arise through nonlinear resonance mechanisms (Tziperman et al. 1994; Jin et al. 1994) and atmospheric noise, the latter mainly in the form of westerly wind bursts (Lian et al. 2014). While the Indian Ocean was long thought to passively respond to ENSO (Latif and Barnett 1995), it was suggested by Luo et al. (2010) and Izumo et al. (2010) that Indian Ocean variability can add skill to ENSO predictions at up to two years lead time. Luo et al. (2010) explain this mainly by Indian Ocean variability in the year of El Niño onset, while Izumo et al. (2010) focus on Indian Ocean variability about 15 months before El Niño. Stimulated by this result, the degree to which the extratropical Pacific, the Atlantic Ocean, and the Indian Ocean affect ENSO is now an active field of research. In this study we will focus on the potential impact of the Indian Ocean on ENSO through atmospheric processes (the so-called ‘atmospheric bridge’).

The dominant Indian Ocean mode of SST variability is the Indian Ocean Basinwide (IOB) warming which is captured by the SST averaged over 40$^{\circ }$E–100$^{\circ }$E, 20$^{\circ }$S–20$^{\circ }$N (Saji et al. 2006). This is a spatially rather uniform warming (cooling) peaking a few months after El Niño (La Niña). The IOB tends to reduce the ENSO amplitude by facilitating the switch to the other ENSO phase (Kug et al. 2006), but due to its strong correlation to ENSO, it is of little use for ENSO predictions, as it does not add independent information [see e.g. Xie et al. (2009), Izumo et al. (2013), and Wieners et al. (2017)]. A second mode of Indian Ocean variability is the Indian Ocean Dipole (IOD). It becomes the dominant mode when removing the ENSO-related IOB signal in observations (Yamagata et al. 2003) or decoupling the tropical Pacific in a GCM (Behera et al. 2006). The IOD strength can be measured by the IOD index (Saji et al. 1999), which is computed as the average SST over 10$^{\circ }$N–10$^{\circ }$S, 50$^{\circ }$E–70$^{\circ }$E (the western pole of the IOD, IODwest) minus the average SST in 0$^{\circ }$N– 10$^{\circ }$S, 90$^{\circ }$E–110$^{\circ }$E (IODeast). A positive (negative) IOD is associated with cool (warm) SST anomalies off Sumatra and warm (cool) anomalies in the western Indian Ocean. The IOD is phase-locked to the Indian Ocean’s seasonal cycle. Westerlies prevail along the equator for most of the year, suppressing the Bjerknes feedback. However, in late boreal summer–autumn, southeasterly winds along the west coast of Sumatra cause coastal upwelling. In this season, the SST off Sumatra is sensitive to thermocline depth variability, and Bjerknes feedback can occur, allowing large SST anomalies which are often of opposite sign to the anomalies in the western Indian Ocean. It has been discussed (Schott et al. 2009, and references therein) whether the IOD is really an independent climate mode or an expression of ENSO. El Niño is associated with easterlies over the eastern Indian Ocean which can lead to upwelling anomalies and cooling there. Indeed, many positive (negative) IOD events co-occur with El Niño (La Niña), especially if the ENSO event develops early in the season, but strong IOD events have also been found in absence of an El Niño.

Fig. 1

Cartoon of the mechanisms to be investigated. a Gill response to western Indian Ocean (WIO) cooling. The low SST leads to cooling, subsidence and surface divergence of the air over the WIO, hence to the east of the WIO, westerly anomalies and upward motion prevail (grey arrows). The westerlies may cause a depletion of the western Pacific warm water volume. b If the upward motion induced by the Gill response (grey arrows) is amplified by convective heating over the warm and moist Maritime Continent, surface convergence is induced there (purple arrows). If this effect is strong enough, it might overcome the Gill-induced westerlies and lead to net easterly anomalies over the western Pacific, which in turn may build up the warm water volume. c If the SST anomaly is in the eastern Indian Ocean (EIO), i.e. if it is close to or even overlaps with the region with a warm and moist background state, Gill response (grey) and convection-induced upward motion (purple) co-act; hence a warm eastern Indian Ocean is also expected to yield easterlies over the western Pacific. Figure taken from Wieners et al. (2017), with permission of the AMS

Annamalai et al. (2005) and Santoso et al. (2012) suggested that the IOD has only an indirect impact on ENSO because the wind responses [‘Gill response’, see Gill (1980)] to its eastern and western poles cancel due to their close proximity. However, the results in Izumo et al. (2010) suggests that IOD events may affect ENSO development at 14 months lead time. Throughout this study we define year 0 as the year in which an IOD event occurs which possibly affects ENSO in the winter of year 1–2. One mechanism by which the IOD may impact ENSO is via a large-scale ‘atmospheric bridge’. Izumo et al. (2010) argue that a negative (positive) IOD in autumn of year 0 causes easterlies (westerlies) over the Pacific which lead to warm water accumulation (depletion) and thus favour the development of El Niño (La Niña) in the course of year 1. The suggested reason for this net wind response is that IODeast lies in the Indo-Pacific warm pool, i.e. a region with warm and moist air, so that local SST anomalies cause strong convection anomalies which re-enforce the Gill response. E.g. a warm IODeast causes enhanced convection, and thus a strong surface convergence and easterlies over the Pacific. IODwest lies in a region with a cooler, drier atmospheric background state and therefore its impact on the atmosphere should be smaller.

Wieners et al. (2016) found that IODeast in boreal summer-autumn of year 0 is not significantly correlated to ENSO indices like Nino3.4 in the winter of year 1–2, while the corresponding correlation for IODwest (autumn 0) and Nino 3.4 (winter 1–2) is significantly stronger than one would expect even when considering the influence of ENSO on the Indian Ocean. This seems to imply that it is IODwest, not IODeast, which contains information on ENSO. They also found by means of a composite analysis that a cool IODwest is accompanied by easterlies over the Pacific after filtering out the influence of simultaneous Nino3.4 anomalies, but the signal reaches only 80% confidence. However, the correlation between IODwest and the Pacific Warm Water Volume (WWV) a few months later is negative and significant at 95% confidence. The WWV is thought to increase following persistent easterlies. It may be that the low confidence for the correlation between IODwest and zonal wind is due to noise in the wind data, while the WWV provides a more steady, integrated measure. Wieners et al. (2016) hypothesised that the uplift which a cool IODwest causes above Indonesia as part of the Gill response (Fig. 1a) is re-enforced by convection there, such as to induce surface convergence over Indonesia (Fig. 1b). If this convection feedback is strong enough, then the easterly wind contribution induced by the convection above Indonesia might overcome the westerly contribution associated with the pure Gill response. In Wieners et al. (2017) this hypothesis was tested using an intermediate complexity model, namely an Indo-Pacific extension of the Zebiak-Cane model with a simple convective feedback above Indonesia and the eastern Indian Ocean. It was found, at least in principle, that a cool IODwest can cause easterlies over the Pacific, but it is unclear whether the strength of the convection feedback is large enough in reality. Also, within their model, a warm IODeast can cause much stronger easterlies (Fig. 1c) than a cool IODwest, and one would therefore expect that IODeast should have a larger impact on ENSO, which contradicts the observed correlations. This contradiction might arise because the model is idealised, but it might also be that the observational record is too short and/or too noisy.

The IOD-ENSO relationship has been studied in General Circulation Models (GCMs) before. Often this was done in partial decoupling experiments, for example by setting the SST in a certain area to climatological values, so as to suppress the impact of interannual variability in this regions on ENSO. Early studies like Yu et al. (2002) and Wu and Kirtman (2004) suggest that decoupling the Indian Ocean reduces the ENSO amplitude. However, these studies used relatively short simulations (about 50 years) from relatively coarse GCMs. More recent GCM studies including Terray et al. (2015) and Kajtar et al. (2017) find that removing Indian Ocean variability leads to larger amplitude of ENSO variability, which can be explained by the damping influence of the IOB. As mentioned, Santoso et al. (2012) suggest that the IOD can reduce the damping effect of the IOB. Dayan et al. (2015) forced an atmospheric GCM with climatological SSTs everywhere except certain regions, in which SST anomaly patterns such as the IOB were enforced and their impact on the zonal wind in the Western Pacific were assessed. Only the Indian Ocean was found to induce significant zonal wind anomalies in the western Pacific, the IOD being more important than the IOB.

A study that does not perform dedicated experiments but analyses the output of 23 CMIP5 models is Jourdain et al. (2016). That study focuses on the impact of the IOD on ENSO at about 15 months lead time suggested by Izumo et al. (2010). While in many CMIP5 models the correlation between IOD in autumn and ENSO 15 months later is stronger than expected based on the influence of ENSO on the IOD (which suggests a physical mechanism by which the IOD feeds back on ENSO), the authors cannot clearly confirm the mechanism suggested by Izumo et al. (2010) based on their multi-model study and advise a detailed analysis for the individual models.

In this study, we will investigate the Indo-Pacific interaction by analysing 100 years of output from two simulations of the Community Earth System Model (CESM), including one simulation at a very high horizontal resolution of 0.1$^{\circ }$ in the ocean and 0.5$^{\circ }$ in the atmosphere. In particular, we will investigate the influence of the IOD and its individual poles on convection above Indonesia and on the zonal wind over the western Pacific.

It should be kept in mind that GCMs may be biased. Cai and Cowan (2013) found that many CMIP3 and CMIP5 models have an overly strong IOD variability, which is mainly due to the exaggerated sensitivity of the SST to thermocline variations in the IODeast areas. Yao et al. (2016) confirmed their results for various CESM configurations at 1$^{\circ }$ and 2$^{\circ }$ resolution.

In Sect. 2 of the paper, a brief description of the model and the analysis tools are presented. In Sect. 3.1, it is checked whether the model is fit for purpose in representing both ENSO and IOD variability and a bias towards strong IODeast variability is found. In Sects. 3.2 and 3.3, evidence for and against an atmospheric bridge mechanism in CESM is presented, and in Sect. 4 possible causes for the IODeast bias are investigated. The paper ends with a summary and conclusions (Sect. 5).

2 Model, observational data, and techniques

The Community Earth System Model (CESM) contains model components for the oceans, sea ice, land surface, land ice, and the atmosphere (Hurrell et al. 2013). The ocean component is the Parallel Ocean Program (POP, version 2.1) model (Smith et al. 2010), while the atmosphere is modelled by the Community Atmosphere Model [CAM; Neale et al. (2012)]. In the simulations used in this study, the radiative forcing (solar, aerosol, and greenhouse gasses) is kept at observed year 2000 values.

Two control runs of CESM are used in this analysis. One of them, termed the Low Resolution (LR) simulation, is performed with CESM version 1.1.2 with CAM5 at a resolution of 1$^{\circ }$ for the atmosphere and a nominal resolution of 1$^{\circ }$ for the ocean and sea ice. The model uses a curvilinear, tripolar grid and the ocean has 60 non-equidistant depth levels. For the LR simulation, data from the model years 400–498 are used. The other simulation (indicated by High Resolution (HR)) is performed using CESM1.0.4 with CAM4 at a resolution of 0.5$^{\circ }$ for the atmosphere and 0.1$^{\circ }$ for the ocean, with 42 depth levels. Roughly 200 years are available for this simulation. The model is not perfectly equilibrated after this time, but spin-up related trends flatten out substantially after about 80 years (Supplementary material of Westen and Dijkstra 2017). It therefore seems justifiable to use detrended data from model years 93-192, especially since our analysis does not deal with deep sea processes. Although 100 years of data may not be sufficient to completely eliminate multidecadal variability (Wittenberg 2009; Deser et al. 2012), we found that at least for the LR simulation, for which several hundred years of data are available, the main results (in particular the correlations between the Indian Ocean and ENSO) do not depend much on which century of data is used. Data is available as monthly means, and is interpolated on a rectangular grid before use.

For comparison with observations (abbreviated as OBS), the following observational data sets were used. The SST fields over the years 1948-2016 are provided by the Hadley Centre (Rayner et al. 2003; Met Office Hadley Centre 2017). Surface wind, Outgoing Longwave Radiation (OLR, taken at the top of the atmosphere), and surface heat flux data for 1948-2016 were taken from the NCEP reanalysis (Kalnay et al. 1996; NOAA/OAR/ESRL PSD 2017), SODA data for 1948–2010 Carton and Giese (2008); SODA data (2017) was used for 3D ocean temperature and currents, as well as for the wind stress. Finally, the Warm Water Volume (WWV; the volume of water warmer than 20° between 5$^{\circ }$N–5$^{\circ }$S and 120°E–80°W) data set is available for 1980 onward and is provided by NOAA/PMEL Tropical Atmosphere Ocean Project (2014). Each of the model and observational time series used is detrended with a 23 years running mean. Anomalies are computed with respect to the seasonal cycle.

As mentioned in the introduction, year 0 is taken as the year in which an IOD event occurs. When defining criteria for, say, El Niño years, the following shorthand notation is used: $\hbox {Nino}3.4(ND(1)JF(2))>0.9$. This means that an El Niño is defined to occur in the winter of year 1–2 if the Nino3.4 index, averaged over November of year 1 to February of year 2, exceeds 0.9 times the standard deviation of this quantity. A definition in terms of standard deviations, rather than fixed temperature values, is preferable because the amplitude of ENSO variability differs considerably between the HR, LR and observations (OBS).

An important tool in this study is partial regression. If one regresses a time series y onto several time series $x_{k}$ ($k=1,2,\ldots$) which are mutually correlated, this affects the significance levels. As an extreme example, suppose $x_{1}=X+\epsilon z$ and $x_{2}=X-\epsilon z$ where $\hbox {std}(X)=\hbox {std}(z)=1$ and $\epsilon \ll 1$, and $y=Y+z$. Suppose also that X, Y,  and z are uncorrelated. Then $x_{1}$ and $x_{2}$ are strongly correlated, but while neither $x_{1}$ nor $x_{2}$ are strongly correlated to y, y is strongly correlated to $x_{1}-x_{2}$. Thus when linearly fitting $y=a_{1}x_{1}+a_{2}x_{2}+Res$, one might obtain relatively large coefficients $a_{1}$ and $a_{2}$ with $a_{1}\approx -a_{2}$.

This effect is taken into account in significance tests by letting the confidence limits depend on the correlations between the $x_{k}$. The actual regression coefficients are compared to results obtained from N randomly generated surrogate data sets $\{\tilde{x}_{k}\}$ where the correlations among the $\tilde{x}_{k}$ are the same as for the original $x_{k}$. A regression coefficient is considered significant at $s\%$ confidence (two-tailed) if its absolute value is larger than that of $s\%$ of the corresponding surrogate results. When using relatively moderate significance levels like $s=90$, $N=1000$ is a reasonable choice. When we are mainly interested in estimating the relative influence of the $x_{i}$ on y, rather than the amplitude of the time series, all time series are normalised by their standard deviation prior to performing the regression (this mainly applies to Sect. 3).

When wishing to check whether a correlation between two time series $z_{2}$ and $z_{3}$ can be explained by the fact that they are both also correlated to $z_{1}$, the ‘common cause test’ of Wieners et al. (2016) can be used. As argued in that study, $\text{ corr }(z_{2},z_{3})$ is significant against the ‘common cause’ $z_{1}$ if both $\text{ corr }(Z_{2},z_{3})$ and $\text{ corr }(z_{2},Z_{3})$ are significant, where $Z_{k}=z_{k}-a_{k1}z_{1}$ and the $a_{k1}$ are obtained from a linear fit of $z_{k}$ onto $z_{1}$.

3 Indo-Pacific interaction

Prior to investigating the Indo-Pacific connection in the Sects. 3.2 and 3.3, the CESM performance is evaluated in Sect. 3.1, in particular concerning basic properties of ENSO and the IOD and IOB.

3.1 Basic ENSO and Indian Ocean properties

Figure 2 shows normalised power spectra of several Indian and Pacific indices. Both HR and LR show a strong variability in the period band of 2–7 years, like the observations. However, LR has a much more regular spectrum with a single, relatively narrow peak at a period of about 4.3 years. All quantities in LR show this peak, suggesting that ENSO and the Indian Ocean are more strongly linked than in OBS. The HR spectra are less periodic and show two broader peaks, one at 5.7 and one at 3.6 years. The plot for OBS also has two peaks at similar periods, except for IOD which in OBS also has a strong bi-annual peak that lacks in HR and LR.

Fig. 2

Power spectra of various time series (after subtraction of the annual cycle) for OBS (a), HR (b), and LR (c). All curves were normalised by dividing by their peak value

Both HR and LR have ENSO and IOD variability with reasonable spatial patterns (Fig. 3). During the peak of ENSO (represented by composites of the SST anomaly in December, Fig. 3a–c), both the warm anomaly in the cold tongue and the surrounding cool anomaly, the ‘horse shoe pattern’, are well represented. For the positive IOD (represented by a composite in September in Fig. 3d–f), HR, LR and OBS all show a spatially extended warm anomaly in the western Indian Ocean and a more localised, strong cool anomaly off Sumatra. The figures show that El Niño tends to co-occur with a positive IOD and vice versa. In CESM, the IOD-related anomalies are stronger and the eastern one extends more to the west and to the north than in OBS, but little difference is noted between the two CESM versions, HR and LR. The IOB spatial pattern (Fig. 3g–i) is less well represented in CESM. In OBS, most parts of the Indian Ocean show a modest, but significant warm anomaly, whereas in CESM only the western Indian Ocean and the IODeast region are warm, whereas the northeast is cool. The dominance of IOD over IOB variability in CESM is confirmed by an EOF analysis of Indian Ocean SST (not shown): In OBS, the first EOF (explaining 40% of the variance) shows warming over most of the Indian Ocean, though it is weakest in the IODeast region, while only the second EOF (12%) represents IOD variability. In CESM, the IOD determines the first EOF with 34 and 47% of the variance for HR and LR, respectively, while the second mode does not resemble an IOB either.

Fig. 3

SST Composites of El Niño (top row; plots for December (1)), IOD [middle row; plots for September (1)] and IOB [bottom row; plots for March (2)] for OBS (left), HR (middle) and LR (right). The criteria for the composites are: Nino3.4(ND(1)JF(2))$>0.9\sigma$ for El Niño; IOD(ASON(1))$>0.9\sigma$ for IOD and IOB(FMAM(2))$>0.9\sigma$ for IOB. Black lines encircle areas where the anomaly is significant at 90% confidence

In order to investigate the strength and seasonality of the various modes of variability, the standard deviation of several indices for each calendar month is plotted in Fig. 4. Nino3.4 in CESM has its largest variability in boreal winter, as is the case for OBS. LR overestimates and HR underestimates the ENSO amplitude [e.g., std(Nino3.4) in December takes the values 1.66 K for LR, 0.83 K for HR and 1.11 K for OBS]. The variability in Nino1+2, relative to Nino3.4, is underestimated in CESM, especially in LR (i.e., LR El Niño has a comparatively weak signal at the Peruvian coast, while observed El Niños often start with coastal warming in boreal summer). As for OBS, std (IOD) in CESM peaks in autumn, but its peak values are much too high (for October, the values are 1.54 K for LR, 1.1 K for HR and 0.42 K for OBS, i.e. CESM overestimates std (IOD) by about a factor of three). This is mainly due to the very strong variability in the eastern pole of the IOD (IODeast) in CESM.

Fig. 4

Seasonal cycle of standard deviations of several indices for OBS (left), HR (middle), and LR (right)

While observed El Niños show a considerable diversity and can for example be grouped into central Pacific and eastern Pacific El Niños, or into eastward and westward propagating events (Wieners et al. 2016), no significantly distinct classes of ENSO events can be found in the CESM simulations. When attempting to sort the ENSO events by the criteria used in that study (with possible some shift in the exact threshold values), the groups are not significantly different at 90% confidence (not shown). We also tried to detect ENSO flavours by means of a Multichannel Singular spectrum Analysis (MSSA; a method to detect spatio-temporal oscillatory modes). The results are not shown here. HR has two ENSO modes with periods consistent with the spectra in Fig. 2b, but very similar spatial patterns. In LR, the second MSSA mode shows eastward propagation of SST anomalies, while the first does not. However, the first mode has almost 4 times as much variance as the second one, so apparently the second mode is of minor importance. Due to the lack of ENSO diversity in the model, the question whether Indian Ocean influence affects the ENSO flavour [as suggested in Wieners et al. (2016)] cannot be investigated using CESM.

In OBS, the IOD signal is seasonally strongly confined to boreal autumn (Fig. 5d). For example, the autocorrelation for the IOD index in September is above 0.3 only for lags of up to three months, indicating that IOD events start in boreal summer and end in early winter. For CESM, especially LR, this effect is weaker (Fig. 5e, f). In LR, autumn IOD is even positively correlated to next summer’s IOD, with a break in early spring. In other words, consecutive IOD events might occur. Often, the first event co-occurs with an ENSO event while the second does not. The first IOD event decays in boreal winter, as is the case for single events. However, in some years easterly winds arise in July and trigger a Kelvin wave leading to a second IOD event (not shown). These winds do not seem to be related to ENSO but may be linked to an SST anomaly around 15$^\circ$S, 100$^\circ$E.

Fig. 5

a–c Season-dependent lagged autocorrelations for Nino3.4 for OBS (left), HR (middle), and LR (right), d–f the same for the IOD index, g–i Season-dependent lagged correlation between IOD and Nino3.4. For plots g–i, the x-axis shows the month in which IOD is taken; the y-axis shows the lag in months (positive if Nino3.4 is taken at a later time than IOD). The data were detrended before correlating

Consecutive El Niño events also occur both in HR and LR, but not in OBS (not shown). Consecutive El Niño events are preceded by a higher Warm Water Volume than single El Niños. While single El Niños are typically accompanied by western Pacific cool anomalies and a positive IOD—which is possibly triggered by the cool western Pacific (Wang et al. 1999; Wallace et al. 1998; Wang et al. 2003) and might re-enforce the El Niño (Luo et al. 2010)—the first El Niños of a consecutive pair are not. In the single El Niño case, the westerly anomalies are stronger, possibly because of the stronger zonal SST gradients, and the Warm Water Volume anomaly becomes negative by December, while for consecutive El Niños this only happens in the following May. It is not clear whether the stronger westerlies in the single El Niño case lead to a faster depletion of the warm water, or whether the very high Warm Water Volume at the beginning of the consecutive El Niño case prevents western Pacific cooling and thus reduces the westerly anomalies. While in the single El Niño case an upwelling Kelvin wave ends the El Niño in the course of boreal spring, this does not happen in the consecutive El Niño case. Instead, vigorous westerly wind anomalies (possibly supported by the now-cooled western Pacific and a growing positive IOD) lead to a second El Niño which is stronger than the first one, but decays in the next spring. The El Niño events of 2014–2016 resemble the consecutive El Niño case of CESM to some extent, although the first El Niño (2014–2015) was very weak despite the high initial Warm Water Volume (Menkes et al. 2014). In particular, the atmospheric response to the eastern Pacific SST anomaly was very weak (Levine and McPhaden 2016), although this might be due to stochastic processes like easterly wind bursts (Levine and McPhaden 2016; Hu 2016), rather than (exclusively) to a weak zonal SST gradient. Note that oceanic processes such as warm subsurface anomalies (Zhang and Gao 2017), warm anomalies in the North Pacific (Alexander et al. 2010) and asymmetric wind stress w.r.t the equator (Abellán et al. 2018) may also have influenced the 2014–2016 El Niño event.

Both the consecutive IOD and consecutive El Niño events lead to unrealistically strong positive correlations between ENSO in winter and the IOD in the following autumn (see Fig. 5g–i), but this should have relatively little impact for the relationship between the IOD in autumn and ENSO about 15 months later, which is the main focus of this study.

3.2 Indo-Pacific correlations

In Fig. 5g–i, the correlations between IOD and Nino3.4 are plotted for OBS, HR and LR, respectively. OBS shows a strong seasonal dependence. At small lags, IOD peaking in autumn is positively correlated (about 0.65) to the ENSO event lasting from the previous summer to the next spring. For the IOD index in January-April, the correlation to Nino3.4 is close to zero. However, for CESM, this seasonal dependence is much weaker, correlations at relatively small lags are positive in all seasons, though weakest for the IOD index in spring. Especially in LR, IOD is also positively correlated to Nino3.4 at negative lags of about 10 months, i.e. a positive IOD is preceded by El Niño. This reflects the consecutive IOD and El Niño events mentioned in Sect. 3.1.

Fig. 6

Common cause test for Nino3.4 and IOD (a–c), IODwest (d–f), and IODeast (g–i) in OBS (left column), HR (middle), and LR (right). White dashed, orange dashed and white solid lines encircle values which are significant at 90$\%$, 95$\%$, and 99$\%$ confidence, respectively

More importantly, for OBS at lags beyond 1 year, we find a negative correlation at + 15 months lag (a negative IOD in summer-autumn is followed by El Niño 1.5 years later). No such strong correlation is found for negative lags longer than a year (IOD following ENSO). Thus at lags exceeding one year, the IOD predicts ENSO better than the other way round, suggesting a possible physical influence from the IOD on ENSO. Similar relations hold for HR. However, in LR we find strong negative correlations both for IOD leading ENSO by 15 months and for ENSO leading the IOD by about 25 months. This makes it doubtful whether the IOD is a useful ENSO predictor in LR—or vice versa.

In order to check whether the correlations at lags around 15 months are significant against the null hypothesis that they are a side effect of the stronger correlations at small negative lags and ENSO cyclicity, the common cause test described in Sect. 2 can be applied. The correlation of $z_{2}$ and $z_{3}$ is checked against the common influence of $z_{1}$, where $z_{2}$ is IOD or one of its poles, $z_{3}$ is Nino3.4 taken at lag $l_{23}$ later than $z_{2}$, and $z_{1}$ (the common cause) is Nino3.4 at lag $l_{12}$ later than $z_{2}$. Values $-14<l_{12}<6$ (measured in months) were used. The reason for including positive values is that IOD may be linked to a still growing El Niño peaking later than IOD itself. As one cannot tell a priori which value of $l_{12}$ is ‘correct’, corr ($z_2,z_3$) is only considered significant when passing the test for each individual value $l_{12}$.

In observations, IOD and IODwest in autumn are negatively correlated to Nino3.4 about 15 months later, and 99$\%$ confidence is reached for all both quantities (see Fig. 6a, d). The strongest correlations occur for IODwest. IODeast in autumn is weakly and non-significantly positively correlated to Nino3.4 1.5 years later (see Fig. 6g), suggesting that the western Indian Ocean has a stronger impact on ENSO than the eastern half. For HR, the correlations for IODwest and IOD are similar to those in OBS. As opposed to OBS, the positive correlation between IODeast and Nino3.4 is also significant. A greater influence of IODeast in CESM can possibly be explained by its very strong variability in CESM. A very warm IODeast can cause easterlies over the western Pacific, even if the atmospheric response is a pure Gill response. For LR, even though correlations are generally higher than for HR, the common cause test mostly gives negative results, suggesting that ENSO is so cyclic here that the Indian Ocean does not yield much independent information about ENSO. This does not mean that the Indian Ocean cannot physically influence ENSO. It just means that in LR, knowing the IOD does not help much in predicting ENSO, and the impact of the IOD cannot easily be disentangled from ENSO influence by linear statistical analysis.

3.3 Indo-Pacific atmospheric bridge

In this subsection, an attempt is made to verify that a negative (positive) IOD indeed leads to easterlies over the western Pacific, to assess the role of the two poles of the IOD and to investigate the role of convection.

First, the zonal wind in September is regressed onto the IOD in the same month. In order to filter out the effect of possible co-occurring ENSO events, partial regressions are used. For OBS, it suffices to regress onto IOD and Nino3.4 at zero lag. For CESM, the regression is carried out onto IOD and Nino3.4 at zero lag and Nino3.4 in the previous December (i.e. at $-9$ months lag), because Nino3.4 in December is significantly correlated to both IOD and the SST in an area around 5$^{\circ }$S, 200$^{\circ }$E (remnants of the ENSO-related SST anomaly; not shown) in the following September. This leads to spurious correlations between IOD and the southeastern Pacific SST and thus the south Pacific winds. Finally, in order to investigate the relative importance of both IOD poles, partial regressions are carried out onto Nino3.4, IODeast and IODwest (all at zero lag), and Nino3.4 in previous December (only for CESM). Prior to regressing, all time series and fields were normalised by their (local) standard deviation, so that the regression coefficients only contain information on the proportion of explained variance, and not on the standard deviation of the time series considered. Only the partial regressions onto Indian Ocean quantities are plotted.

Fig. 7

a, c, e Partial regression of zonal wind stress from OBS in Sept. onto the following indices at zero lag (regression to Nino3.4 not shown): a Nino3.4 and IOD; c, e Nino3.4, IODwest (c), and IODeast (e). All data (indices and local field time series) were normalised by their local standard deviation before regressing. Black lines encircle regions with 90% confidence (two-tailed). White lines are coastlines. b, d, f As a, c, e but for HR instead of OBS. In addition to the ENSO and Indian Ocean indices used for OBS, the influence of last winter’s ENSO (Nino3.4 in December 9 months earlier) is also regressed out

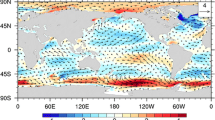
The IOD in OBS (Fig. 7a) for September has a significant positive regression with the zonal wind in a relatively narrow zone in the western Pacific. Significant correlations are also found between May and August (not shown). Though the regression coefficients are of the expected sign (negative IOD is associated with easterlies), they are not very strong. In order to see which IOD pole causes the wind anomalies, simultaneous regressions onto Nino3.4, IODwest, and IODeast were also performed (see Fig. 7c, e). For IODwest, a region of positive regression coefficients exists in the western Pacific, though they are hardly significant, but they are not negative; thus it might be that convection over the MC cancels the Gill response, but does not surpass it. However, in Wieners et al. (2016), the wind signal associated with a cool western Indian Ocean was found to be weak, whereas the correlation between western Indian SST in summer-autumn and Pacific Warm Water Volume (WWV) a few months later, was found to be significant in the common cause test. While wind data are often noisy, the WWV is expected to provide an integrated measure of the wind in the previous few months. IODeast in OBS is associated with negative regression coefficients in a zone in the western Pacific. Both poles thus may contribute to the IOD signal, but in general signals are weak and it is difficult to distinguish Indian Ocean-induced winds from winds that are caused by local Pacific SST gradients. Whether the data is too short and noisy or whether the impact of the IOD on the Pacific is just weak, is hard to tell.

In HR, the IOD shows positive regression coefficients in the west Pacific (Fig. 7b), and the signal is stronger than in OBS. In HR, IODeast seems to cause the winds, while IODwest yields no significant positive contribution at all in the western Pacific (Fig. 7d, f). This stronger impact of IODeast is in line with the positive results for IODeast in the common cause test (see Fig. 6h), and also with the results obtained with the model results in Wieners et al. (2017), which likewise supports the notion that IODeast has a stronger impact on ENSO than IODwest; but it disagrees to observations, which only show a weak, insignificant correlation between IODeast and ENSO at 15 months lag. In LR, winds associated with IOD and its poles are not significant over the Pacific (not shown). This may mean that the impact of the Indian Ocean is smaller than in HR (at least relative to the influence of ENSO, which has a high amplitude in LR, see Fig. 4), or that the strong correlation between ENSO and IOD makes it more difficult to distinguish their wind contributions by linear regression.

In order to gain insight into the possible impact of the Indian Ocean on convection, the above regression analysis for the IOD and its poles was repeated using Outgoing Longwave Radiation (OLR) instead of the zonal wind. OLR is a measure for convective activity, since vigorous convection leads to high cloud tops which have a low temperature and hence emit less radiation; low OLR thus corresponds to high convective activity. It should be noted that the “observed” OLR provided by NCEP for the pre-satellite era, i.e. before 1974, is based on reanalysis. As mentioned in Sect. 2, the OLR field was normalised by the local standard deviation at each point prior to regressing. Thus in an area with low (high) standard deviation, the same regression coefficient corresponds to a lower (larger) absolute value of the OLR signal. Therefore plots were added of the local standard deviations of the OLR field (Fig. 8a, b), which vary considerably in space. The highest standard deviations in September are found over the IODeast region, which has both a warm and moist climate and a reasonably strong variability in the temperatures of the underlying sea.

In OBS, the IOD is associated with a dipole pattern in OLR; its eastern pole extends over the Maritime Continent (see Fig. 8c). The positive OLR anomaly over the bay of Bengal is not related to a local SST anomaly (not shown) and might thus be induced non-locally. When regressing onto Nino3.4, IODwest and IODeast (Fig. 8e, g), one finds that IODwest seems to contribute also to the OLR anomaly over the IODeast region and vice versa. Both poles seem to contribute to the OLR anomalies over the Maritime Continent, though for IODwest the regression coefficients are significant only over a small area. As explained above, the same regression coefficient over the IODeast corresponds to a much larger OLR signal than over IODwest or the Maritime Continent.

For CESM (both HR and LR) one finds again for IOD a dipole pattern over the Indian Ocean (Fig. 8d; LR not shown). However, for CESM, the contribution from IODwest is smaller: in HR (Fig. 8f), there are some marginally significant regression coefficients in the south Maritime Continent (where IODeast does not have a significant contribution), while for LR no significant signal is present except over the IODwest region itself (not shown). Once again, the strong correlations between IOD (or its poles) and ENSO in LR make it harder to disentangle their impact on OLR by linear methods.

Fig. 8

a, b Standard deviation of the OLR in September, for OBS and HR, respectively. c–h Partial regressions as in Fig. 7a–f, but using OLR instead of zonal wind stress

To summarise, the CESM results do not support the hypothesis that IODwest causes easterlies over the western Pacific due to strong convection above the Maritime Continent. If an atmospheric bridge is present in CESM, it seems to be based on a Gill response to IODeast. On the one hand, this might mean that the results obtained by analysing observational data (in particular the common cause test for IODwest and IODeast) are easily misinterpreted, for example due to taking a too short, non-representative time series. On the other hand, it was shown in Sect. 3.1 that IOD variability is not reproduced entirely correctly in CESM; in particular, the variability in the IODeast region is far too strong. The artificially large SST variability in this region might lead to an overly large influence of the IODeast on western Pacific winds and thus ENSO.

4 IOD bias

In this section, the reasons for the overly large IODeast signal are investigated. Throughout the current section (Sect. 4), time series are not normalised by their standard deviations when applying linear regressions.

The IOD is linked to and probably partly forced by ENSO, but while in HR and LR the ENSO amplitude differs strongly, being too low in HR and too high in LR, both model versions have a similarly strong IOD variability. This suggests that the bias arises from processes within the Indian Ocean, rather than from external ENSO forcing.

Fig. 9

The climatological zonal wind stress in N/m$^{2}$ over the eastern Indian Ocean in September. Results are shown for OBS (left), HR (middle) and LR (right)

In boreal late summer to autumn, southeasterlies prevail along the west coast of Sumatra, allowing coastal upwelling and cooling. In addition, the zonal wind stress along the equator in the open ocean becomes less positive (i.e. less westerly) or even slightly negative (see Fig. 9). In CESM (both HR and LR), the wind stress along the equator is more negative than in OBS. These conditions resemble to some extent the cold tongue in the eastern Pacific and allow weak thermocline and upwelling feedbacks (involving the zonal wind, thermocline depth, upwelling, and SST), which may be a source of interannual variability in the IODeast area. Important factors in the strength of the thermocline feedback are the background upwelling at the lower boundary of the mixed layer and the effect of thermocline variations on the temperature just below the mixed layer, often indicated by $T_{sub}$. The upwelling feedback depends strongly on the mean difference between the SST and $T_{sub}$. Whether these feedbacks are able to cause SST anomalies also depends on the thermodynamic damping, i.e. the surface heat-flux response to SST anomalies.

Fig. 10

a–c The regression of the surface heat flux (in $W/m^{2}$, positive upward) in the eastern Indian Ocean onto IODeast. Results are shown for OBS (left), HR (middle) and LR (right) in October (a–c). White lines are coastlines. d–f Composites of the SST anomalies [K] in cool IODeast years (IODeast(ASON(0))$<-0.9$) in the eastern Indian Ocean. Results are shown for OBS (left), HR (middle) and LR (right), in October. The black line encircles areas where the results differ significantly from zero (90% confidence)

The surface heat flux Q is the sum of sensible and latent heat flux and long- and shortwave radiation flux. It is here defined as positive upwards, thus a positive value leads to ocean cooling. The dependence of the heat flux on SST is here represented by the regression of Q onto the index IODeast (Fig. 10a–c; for the spatial patterns of the SST during IODevents, compare the composites in Fig. 10d–f). This regression yields much larger values in CESM (both HR and LR) than in OBS, especially just south of the equator, away from the coast (the large values around 2°N–80°E in Fig. 10a is unrelated to local SST anomalies and does not contribute to the damping of the IODeast SST signal). The larger extent of IODeast-related heat flux anomalies in CESM is probably because the SST anomalies also extend further northwest in CESM. These findings imply that the thermodynamic damping is stronger for CESM than for OBS, so the high IODeast amplitude in CESM is not caused by lack of damping. When computing a correlation, rather than a regression, between the Q field and IODeast, CESM yields values well above 0.8 over large parts of the IODeast box west of Sumatra, while in OBS, only 0.6 is reached and only near the coast (not shown). Thus the damping depends less consistently on IODeast for OBS than for CESM, possibly because in CESM the local SST signal is so strong as to dominate over non-local forcing of the heat flux.

Fig. 11

The regression of the zonal wind stress (in 10⁻³ N/m²) in the eastern Indian Ocean onto IODeast (in K). Results are shown for OBS (left), HR (middle) and LR (right), in August (top row) and October (bottom row)

Fig. 12

The climatological temperature profile in $^{\circ }\text{C}$ along the equator in the eastern Indian Ocean in August. Results are shown for OBS (a), HR (b) and LR (c)

Fig. 13

Composites of the z20 anomalies [m] in cool IODeast years (IODeast(ASON(0))$<-0.9$) in the eastern Indian Ocean in October. Results are shown for OBS (a), HR (b) and LR (c). The black line encircles areas where the results differ significantly from zero (90% confidence)

The regression of the zonal wind stress onto IODeast (at zero lag) is given in Fig. 11. Until September, the regression shows somewhat higher values for CESM, especially LR, than for OBS. In October, OBS yields higher values. The maximum values in CESM (both HR and LR) are shifted northwards with respect to OBS, which is in line with the spatial patterns of the SST. Although it is plausible that a stronger wind stress response to IODeast SST anomalies early in the IOD season leads to stronger positive Bjerknes feedbacks, it is questionable whether this is the main driver for the difference between OBS and CESM, because the wind response between HR and LR also differs considerably, while their SST variability is similar, at least compared to OBS.

To assess the thermocline variability, composites over cool IODeast years (IODeast(ASON(0) < − 0.9)) of the 20 °C isotherm depth (z20) are made. Figure 12 shows that this isotherm indeed lies reasonably well within the thermocline, although at least for CESM, the vertical temperature gradient is strongest around the 23 °C isotherm. However, the results in the following do not depend on the exact choice of the thermocline proxy, and z20 was used to be consistent with Cai and Cowan (2013). The negative z20 anomalies in OBS (see Fig. 13) during cool IODeast years along the coast are somewhat weaker than those in LR, but similar to or slightly stronger than those in HR, though the area of shallow z20 extends somewhat further northwest in CESM than in OBS. Seeing that the thermocline variability differs most strongly between HR and LR, whereas the SST variability is much higher in both HR and LR than in OBS, the difference in thermocline variability seems not to be the main cause for the difference in SST variability.

Upwelling variability was likewise assessed by taking composites for cool IODeast years (IODeast(ASON(0) $< -0.9$)) of the vertical velocity, but the result is not signifiant at 90% confidence (not shown), although weak positive upwelling anomalies occur at around 50m depth in cool IODeast years. At 6°S, the upwelling anomalies are even much weaker than at the equator and spatially incoherent (not shown). The upwelling anomalies are of similar strength for LR and OBS, but weaker for HR. Therefore, the difference in upwelling anomalies cannot be the cause for the difference in SST anomalies. The fact that both upwelling and thermocline anomalies, which are related to wind stress anomalies, do not explain the strong difference in IODeast variability between CESM and OBS suggests that the difference in wind response discussed above is a consequence, rather than a cause, of the difference in SST variability.

Fig. 14

The climatological upwelling in 10⁻⁵ m/s over the eastern Indian Ocean. Results are shown for OBS (left), HR (middle) and LR (right), in August (top row) and October (bottom row)

Fig. 15

Composites of the temperature anomalies [K] in cool IODeast years (IODeast(ASON(0))$<-0.9$) along the equator. Results are shown for OBS (left), HR (middle) and LR (right), in June (top row), August (middle row) and October (bottom row). The black line encircles areas where the results differ significantly from zero (90% confidence)

Now, if the upwelling and thermocline variability is similar for OBS and CESM, the main difference between CESM and OBS must lie in the efficiency at which upwelling and thermocline anomalies influence the surface temperature. One way to achieve this is a strong background upwelling; another way, a strong impact of the thermocline on the subsurface temperature $T_{sub}$. Near the equator, where the differences between CESM and OBS SST are particularly large, the mean upwelling (see Fig. 14) at around 50m depth is positive in June-October for CESM (both HR and LR), and for July-September in OBS. Thus in CESM the IOD event can develop earlier in the season. However, in July-September, the values in OBS are, if anything, stronger than in CESM.

The cool IODeast composites of the temperature anomalies along the equator (see Fig. 15) show that at depth, the signal in OBS is not much weaker than in CESM; it just does not reach the surface well. The temperature minimum lies at greater depth in OBS (in August: around 70 m, rather than 40 m as in CESM), i.e. below the mixed layer, and also below the level where the background upwelling is strongest. The reason for the different depths of the temperature anomaly peaks is that in CESM, the strongest vertical mean temperature gradients are found at a smaller depths than in OBS (see Fig. 12). If one imagines thermocline depth anomalies to be associated with vertical shifts of the isotherms, then changes in the thermocline depth will cause large temperature changes where the mean vertical gradient is strong. In CESM, the vertical temperature gradient in the upper 70m is stronger than in OBS, especially in boreal summer. At 90°E, 0°N, the difference between the SST and the temperature at 70 m depth in June takes the values: 3.4 K (LR), 3.8 K (HR), and 1.3 K (OBS). In August, the temperature difference in OBS increases slightly to 2.1 K while HR and LR remain unchanged, and in October the values become 3.4 K (LR), 3.0 K (HR), and 1.9 K (OBS), i.e. the mean vertical temperature gradient in CESM remains stronger than in OBS throughout the IOD season, which allows upwelling anomalies to have a greater impact on the SST.

So the main driver for the bias in IODeast variability is traced to a bias in the temperature profile, leading to an exaggerated sensitivity of $T_{sub}$ to thermocline depth anomalies. Yao et al. (2016), who analysed various CESM runs at $2^{\circ }$ and $1^{\circ }$ resolution by performing regressions of time series obtained by spatially averaging the SST, zonal wind, $T_{sub}$, and the thermocline depths, likewise find that the largest discrepancy between the observed and model results lies in the sensitivity of $T_{sub}$, followed by the wind-SST-coupling, although they do not trace the sensitivity of $T_{sub}$ to the mean temperature profile.

5 Summary and conclusion

Simulations with the CESM were used to investigate the influence of the Indian Ocean on ENSO. In particular, we tested whether a cool western Indian Ocean can induce enhanced convection and surface convergence over Indonesia and easterlies over the western Pacific, which in turn lead to a strong western Pacific Warm pool acting as reservoir for next winter’s El Niño, as was suggested by Wieners et al. (2016) and Wieners et al. (2017). Using results from a GCM in addition to observations is particularly attractive because the observed easterly wind signal following a cool IODwest is rather weak in observations, possibly because of short and noisy data, so longer time series are desirable.

Two CESM simulations of about 100 years were used, one at $1^{\circ }$ resolution (low resolution / LR), and one at $0.1^{\circ }$ resolution for the ocean and $0.5^{\circ }$ for the atmosphere (high resolution/HR). Both capture the spatial pattern and interannual variability of ENSO reasonably well, although LR is too periodic. It might be interesting to investigate further why the ENSO variability is represented more realistically when increasing the resolution. On the one hand, more small-scale processes are included in HR, such as Tropical Instability Waves (TIW) (Graham 2014), which can act as noise and make ENSO more irregular. TIW tend to warm the cold tongue, especially during La Niña events, and have a damping effect, which might explain the lower ENSO amplitude in HR, compared to LR. Zhang (2014) find a cooling effects of TIW-induced wind stress, but it is an order of magnitude smaller than the warming by oceanic advection reported by Graham (2014). On the other hand, the smaller ENSO variability in HR might be caused by large-scale phenomena. In that case, the smaller amplitude might be the cause of the stronger irregularity in HR, because an oscillatory mode with stronger damping might be more susceptible to noise than a more self-sustained one. The modelled ENSO deviates from observations in the sense that CESM shows no distinct flavours of ENSO events. Therefore possible impacts of the Indian Ocean onto ENSO types (as suggested by Wieners et al., 2016) cannot be investigated using CESM.

The common cause test (see Sect. 3.2) suggests that in the HR simulation, Indian Ocean quantities may add skill to ENSO prediction. In the LR simulation, this does not hold, because ENSO is sufficiently regular that the Indian Ocean adds little linearly independent information. This does not mean that the Indian Ocean cannot influence ENSO, but other than linear methods would be needed to investigate this, for example dedicated decoupling experiments (Luo et al. 2010). In HR, not only the western pole of the Indian Ocean Dipole (IODwest), but also the eastern pole (IODeast) yields positive results in the common cause test, which disagrees with results from observations. No conclusive evidence is found in CESM that a cool western Indian Ocean induces easterlies over the western Pacific or strong convergence over the Maritime Continent. Such signals are weak even in observations, but more or less absent in CESM. However, in HR, a warm IODeast can lead to easterlies. In LR, due to the overly strong correlations between ENSO and Indian Ocean quantities, and the high regularity, it is very hard to disentangle the influence of ENSO and the Indian Ocean by linear techniques like regression. These findings may suggest that it is in fact the eastern Indian Ocean which dominates the influence on ENSO, as suggested by Izumo et al. (2010). This would be plausible in the sense that a warm IODeast needs no subtle convection effects to cause a wind reversal over Indonesia, but can cause easterlies over the western Pacific by a plain Gill response. The negative result of the common cause test for IODeast in observations might then be an artefact of inaccurate sampling and a relatively short record.

On the other hand, the CESM model clearly has some biases affecting the IO-ENSO interaction. For example, CESM (both HR and LR) exhibit consecutive IOD events and consecutive El Niño events which lead to unrealistic positive correlations between Nino3.4 in boreal winter and the IOD index in the following autumn. However, the effect on the correlations at 15 months lag - the main focus of this study - should be small. For the purpose of this study, the most important bias in CESM is that the amplitude of the IOD is too large. In particular, the standard deviation of the index IODeast in boreal autumn is too large by a factor of about 3 in both HR and LR, i.e. the higher resolution does not substantially reduce this bias. The slight difference in the IODeast variability between HR and LR may be due to the reduced ENSO forcing in HR.

The strong biases CESM exhibits in the Indian Ocean, particularly the exaggerated variability in IODeast, make it doubtful whether the model can realistically reproduce the subtle Indo-Pacific relationships. This bias is partly due to the fact that in CESM, the SST anomaly associated with IODeast variability extends further northwest into the open ocean, covering a greater area within the box over which IODeast is computed. It was found that the main cause for the strong IOD variability is the strong sensitivity of the subsurface temperature (i.e. the temperature of the water that can be upwelled into the mixed layer) to thermocline variations, especially in the equatorial region. This high sensitivity in turn may be due to differences in the mean temperature profile; in CESM, the vertical temperature gradients over the top 70m are considerably larger than in observations. Therefore a similar vertical displacement of isotherms may cause a stronger temperature anomaly. In addition, in observations, the temperature anomalies associated with a cool IODeast peak at greater depth (where the mean temperature gradients are stronger) than in CESM, which means that in observations, the temperature anomalies overlap less with the zone of strong climatological upwelling, so the temperature anomalies reach the surface less well.

Note that an overly large IOD variability is quite common in GCMs. Cai and Cowan (2013) find that in many CMIP3 and CMIP5 models, the SST is too sensitive to thermocline variability. However, in that study, it is suggested that unrealistically strong climatological easterlies and an unrealistically shallow eastern Indian thermocline are the cause. However, in our temperature profiles (Fig. 12), the 20 degrees isotherm [used as proxy for the thermocline by Cai and Cowan (2013)] in HR is actually deeper than in OBS. We propose that the whole temperature profile should be considered when investigating the reasons for the high IOD amplitude in GCMs.

It would be interesting to investigate in greater detail why the temperature profiles in CESM (and possibly other GCMs) differ from observations. One thing to check would be the parametrisation of vertical mixing, but other processes such as horizontal advection might play a role as well. Understanding the processes determining the temperature profile might help improving future model generations. However, for now we have to conclude that CESM has too strong biases to allow a detailed analysis of the subtle Indo-Pacific coupling. The mechanism suggested in Wieners et al. (2016, 2017) can neither be confirmed nor definitely falsified by analysing the CESM data.