Abstract
We assess the suitability of ECMWF Integrated Forecasting System (IFS) data for the global modeling of tropical cyclone (TC) storm surges. We extract meteorological forcing from the IFS at a 0.225° horizontal resolution for eight historical TCs and simulate the corresponding surges using the global tide and surge model. Maximum surge heights for Hurricanes Irma and Sandy are compared with tide gauge observations, with R2-values of 0.86 and 0.74 respectively. Maximum surge heights for the other TCs are in line with literature. Our case studies demonstrate that a horizontal resolution of 0.225° is sufficient for the large-scale modeling of TC surges. By upscaling the meteorological forcing to coarser resolutions as low as 1.0°, we assess the effects of horizontal resolution on the performance of surge modeling. We demonstrate that coarser resolutions result in lower-modeled surges for all case studies, with modeled surges up to 1 m lower for Irma and Nargis. The largest differences in surges between the different resolutions are found for the TCs with the highest surges. We discuss possible drivers of maximum surge heights (TC size, intensity, and coastal slope and complexity), and find that coastal complexity and slope play a more profound role than TC size and intensity alone. The highest surges are found in areas with complex coastlines (fractal dimension > 1.10) and, in general, shallow coastlines. Our findings show that using high-resolution meteorological forcing is particularly beneficial for areas prone to high TC surges, since these surges are reduced the most in coarse-resolution datasets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The strong winds and low pressures of tropical cyclones (TCs) often induce highly damaging storm surges, affecting people and economies over large coastal areas. In 2017, U.S. hurricane damage totals exceeded $265 billion, with Hurricanes Harvey, Irma, and Maria entering the top five of costliest hurricanes in recorded history (NOAA National Centers for Environmental Information 2018). Storm surges are influenced by TC intensity, size, and track and can be amplified by shallow coastal bathymetry or local geometry (Mori et al. 2014). Hence, even relatively weak TCs can induce high storm surges under certain conditions.
Hydrodynamic models are used to simulate storm surges, both for operational applications and risk assessments. These hydrodynamic models use wind speed and mean sea-level pressure (MSLP) as forcing, which is usually derived from general circulation models (GCMs). Until recently, these GCMs had horizontal resolutions of 0.45°–1.8° (ca. 50–200 km at the equator) (Saha et al. 2006; Yukimoto et al. 2006). Currently, all available climate reanalysis products have horizontal resolutions of up to 0.75°, including ERA-Interim (Dee et al. 2011) and NCEP/NCAR Reanalysis 1 (Kalnay et al. 1996). Such resolutions are insufficient to fully resolve TC intensity, size, and track (Murakami and Sugi 2010; Schenkel and Hart 2012; Walsh et al. 2007), and are especially problematic for weak TCs (Hodges et al. 2017; Murakami 2014). At the local scale, many studies have employed parametric models (Haigh et al. 2014; Harper and Holland 1999; Holland 1980; Lin and Chavas 2012; Lin et al. 2010) to obtain high-resolution wind and pressure fields. Such models fit MSLP and 10 m wind speeds (U10) to radial profiles with an exponential decay away from the eye. Limitations of such parametric models include the fact that they do not fully capture asymmetric cyclones (Harper and Holland 1999) and do not include dissipation effects over land (Jakobsen and Madsen 2004). Other studies have used high-resolution (down to 50 m) hindcasts to simulate TC characteristics and surge heights (Bunya et al. 2010; Dietrich et al. 2010). These hindcasts are based on regional downscaling and/or regional climate models, and consequently, hindcasts are not applicable in regions with sparse observational data (Nikulin et al. 2012).
A limited set of GCMs is run at horizontal resolutions of 10–30 km (0.09°–0.27°), a scale at which TCs can be resolved (Bacmeister et al. 2016; Mizuta et al. 2012). With the launch of ERA5 (0.25°) in 2017, reanalysis products are now also available at these horizontal resolutions. One high-resolution GCM is the European Centre for Medium-Range Weather Forecasting (ECMWF) Integrated Forecasting System (IFS). In addition to being an operational weather forecasting model, IFS has been used for producing reanalysis products such as ERA5 and ERA-Interim (Dee et al. 2011; ECMWF 2017c). In ERA-Interim, the average number of TCs per year is simulated well (Strachan et al. 2013), but modeled tracks differ from observed ones, and the intensity and size are underestimated (Murakami and Sugi 2010; Schenkel and Hart 2012). The underestimation of intensity is usually driven by resolution effects and poor physical schemes (Flato et al. 2013; Walsh et al. 2007). Previous updates in the ECMWF IFS tropical atmospheric conditions have improved tropospheric wind and convection compared to observations, (Fiorino 2008) and the model’s spatial resolution was increased from ± 0.225° at the equator in 2006 to its current resolution of ± 0.08° (ECMWF 2017a). These updates have significantly contributed to the improvement of the IFS TC track ensemble forecasts. A recent example of the improved performance is the IFS ensemble forecast for Hurricane Sandy’s track, which predicted Sandy’s landfall up to seven days in advance (Bassill 2014; Magnusson et al. 2014).
Apart from track ensemble forecasts, TC intensity forecasts have also improved in the latest model updates (ECMWF 2017a). Together with the emergence of global hydrodynamic models (Carrère and Lyard 2003; Jagers et al. 2014; Verlaan et al. 2015; Vitousek et al. 2017), it is possible to simulate TC surges at local to global scales using direct output from GCMs. These simulations are already carried out operationally, such as for the Atlantic Ocean using the NHC TC advisories, a parametric wind model and SLOSH model (Byrne et al. 2017; Jelesnianski et al. 1984). However, no research has been conducted on the use of ECMFS IFS meteorological forcing for high-resolution storm surge modeling. In addition, despite research focusing on methods to test the sensitivity of simulated storm surges to TC wind fields (Cardone and Cox 2009), few studies have analyzed the effects of the resolution of meteorological forcing on simulated storm surges. Wakelin and Proctor (2002) used three meteorological operational analysis datasets to analyze two storm surge events in the Adriatic Sea and concluded that their model works best using meteorological forcing with the highest spatial and temporal resolution. Recent research by Muis et al. (2016) has demonstrated the implications of using coarse-resolution meteorological forcing for global storm surge modeling. They generated time series of storm surges on a global scale using the six-hourly 0.75° ERA-Interim dataset (Dee et al. 2011; ECMWF 2016) and found that extreme sea levels induced by TCs are underestimated due to the coarse resolution of meteorological datasets. This raises the question: what resolution of meteorological forcing is needed to adequately simulate TC-induced storm surges?
In this paper, we test the suitability of ECMWF IFS as meteorological forcing for high-resolution global storm surge modeling. In addition, we analyze the effect of the horizontal resolution of meteorological forcing on maximum storm surge heights. We explore and discuss possible drivers of maximum surge heights.
2 Methodology
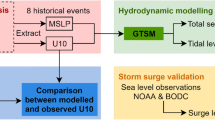
The overall methodology is illustrated in Fig. 1. The U10 and MSLP are derived from the ECMWF IFS and aggregated from their original resolution to T799 resolution (± 0.225° at the equator) and to various coarser resolutions between 0.25° and 1.0° (Sect. 2.1). Relevant meteorological parameters for the analysis (maximum U10, minimum MSLP, TC size) are derived by tracking each TC (Sect. 2.2). The U10 and MSLP fields are then used to model the associated surge heights using the Global Tide and Surge Model (GTSM) (Sect. 2.3). Storm surges modeled at T799-resolution forcing are compared with observations (Sect. 2.4). Lastly, the effects of different horizontal resolutions of meteorological forcing on maximum surge heights are explained through TC size and intensity, and coastline complexity and slope (Sect. 2.5).
Schematic overview of the approach followed in this study. Meteorological forcing is extracted from the ECMWF integrated forecasting system (IFS) at the native grid resolution (T799, ± 0.225°). Comparison to observations is performed for the 10 m wind speed (U10), mean sea-level pressure (MSLP) and maximum surge height (Hs). Land maps to derive coastal complexity are taken from the global administrative areas (GADM)
We focus on eight case studies of historical TCs (Fig. 2), one in each TC basin. We only consider landfalling TC events occurring after 5 June 2007 0 UTC, to allow for use of the new 4D-VAR data assimilation scheme, which considerably improved clouds and convection in IFS and thereby tropical troposphere forecasts (ECMWF 2017a). In the November 2007 update, lower tropospheric winds in the tropics are also improved.
2.1 ECMWF IFS forcing
For each case study, U10 and MSLP data are extracted from the ECMWF IFS (ECMWF 2017a). The ECMWF general circulation model is used for numerical weather predictions and consists of a dynamical, physical, and coupled ocean wave component (Persson and Grazzini 2005). The temporal resolution is 3 h. Because of continuous updates in IFS resolution (ECMWF 2017a), original model resolution varies between the different TCs. Therefore, we homogenize the horizontal resolution of all cases to T799 resolution. We use the 0 and 12 UTC runs and their + 3 h, + 6 h and + 9 h forecast runs. Upscaling is achieved by averaging over neighboring grid cells (first-order conservative remapping on all spatial variables in the dataset) (Jones 1999). This process is likely to produce lower differences in wind and pressure intensities between the different resolutions than re-running the global atmospheric model on a coarser resolution would, because small coherent features are typically poorly resolved in numerical models at coarser resolution, but they can still be included when upscaling from a high-resolution to a lower-resolution grid (Boer and Denis 1997).
2.2 TC tracking algorithm
To capture the TC characteristics at every time step and to enable comparison with the IBTrACS dataset (v03r10), we track the eight TCs and their characteristics throughout their lifetimes. We use IBTrACS because it is considered the most complete best-track dataset of global historical TC activity (Knapp et al. 2010). The cyclone’s position as given in IBTrACS is taken as the initial position of the eye in the tracking algorithm. The spatial resolution in IBTrACS is generally listed at 0.1°, whereas the spatial resolution in ECMWF IFS is approximately 0.225° at the equator. Because of this difference, we apply the tracking algorithm from Baatsen et al. (2015) to ensure we are looking at the ‘true’ position of the eye in ECMWF IFS. Following this tracking algorithm, we determine the location with the maximum relative vorticity (a measure of the rotation of the horizontal velocity field) is in a surrounding 5° × 5° box from the initial position of the eye. If this location corresponds to a lower MSLP than the initial position, the position of the eye is updated. We then set the location with the minimum MSLP in a surrounding 2.5° × 2.5° box as the final position of the eye. Using the tracking algorithm from Schenkel and Hart (2012), we extract the maximum U10 and minimum MSLP at every time step within a 7° radius of the final position of the eye. Using this 7° radius, we ensure that these two TC characteristics are captured inside the domain. Following Chavas et al. (2016), we determine TC size by using the radius of vanishing winds r0, defined as the average distance outside of the eye where U10 < 12 m/s.
2.3 Storm surge modeling
For each TC, storm surges are simulated by forcing GTSM with meteorological data (U10 and MSLP) from the ECMWF IFS. GTSM is a global hydrodynamic model implemented with unstructured grids, based on the Delft3D FM software developed by Deltares (Kernkamp et al. 2011). GTSM has a spherical grid with thinning at high latitudes, with cell size dependent on the bathymetry (also known as courant grid refinement) (Irazoqui Apecechea et al. 2017). Additional refinement is applied in areas with steep slopes, such as mid-oceanic ridges, to improve the representation of the internal tides. This allows for high computational efficiency with high resolution (lower than 7.5 km, and on average 5 km) near coasts and coarser resolutions (up to 50 km) in the deep ocean. The General Bathymetric Chart of Oceans (GEBCO) 2014 dataset (https://www.gebco.net/data_and_products/gridded_bathymetry_data/), defined in a 30″ grid, is used for bathymetry. The computational time step is 150 s.
GTSM and the output dataset GTSR (Muis et al. 2016) are used in many recent research, including Hiroaki et al. (2017), Irazoqui Apecechea et al. (2017), Muis et al. (2017), Vousdoukas et al. (2018) and Williams et al. (2018).
Muis et al. (2016) used 6-hourly ERA-Interim data (at 0.75°) as meteorological forcing in GTSM to obtain a global reanalysis of storm surges (1979–2014). They validate modeled sea levels against observed sea levels using a global set of 472 tide gauges stations from the University of Hawaii Sea Level Center (available at https://uhslc.soest.hawaii.edu/). A validation of the surge levels shows that 95% of all stations have a root–mean-square error (RMSE) lower than 0.2 m, with the average RMSE being 0.11 m (standard deviation 0.05 m). Extratropical storm surges are modeled relatively well, whereas TC storm surges are substantially underestimated. This is shown by the average correlation coefficient in tropical regions of 0.77 being significantly lower than the average correlation coefficient of 0.87 in extratropical regions. This underestimation is driven by the relatively coarse resolution of the meteorological forcing, which is unable to fully capture the strong wind and pressure gradients in the TCs in both space and time.
A storm surge is a rise of the sea level as a result of changes in atmospheric pressure and wind drag on the sea surface. The influence of atmospheric pressure is given by the inverse barometer effect (Ross 1854): every 1 hPa drop in atmospheric pressure is accompanied by a roughly 0.01 m increase in sea-level height. In addition, in shallow water there is an additional wind set up that can be approximated roughly as:
where g is the gravitational constant (m/s2), h the surface level above the reference height (m), x the horizontal distance (m), Cd the drag coefficient (−), U the average wind speed at 10 m perpendicular to the coast (m/s) and H the total water depth (m) (Weenink 1958). From this equation it follows that the largest surges occur in shallow water with a wide coastal shelf.
Hourly output data are extracted from the GTSM coastal grid points. For each TC, we consider an area of 15° × 15° around the landfall location and a time period of 3 days on either side of the moment of landfall. In this time period, we then select all coastal points in the T799-resolution forcing at which the maximum surge height is at least 50% of the overall maximum surge height, with a minimum height of 15 cm. This way, only coastal points with high storm surges are included in the statistical analysis. For the other resolutions, the same set of coastal grid points in GTSM is used, to ensure a direct comparison in storm surge heights at coarser resolutions.
2.4 Comparison of results
We compare the minimum MSLP and maximum U10 in the T799-resolution forcing against IBTrACS. The MSLP is given as an instantaneous value in both datasets. The U10 is given as a 7.5-min average in the T799-resolution forcing, and the observed U10 is the 10-min average wind speed in 3- or 6-hourly intervals. Since the conversion factor between these two averages is approximately 1 (Harper et al. 2008), we directly compare the two variables throughout this paper.
Before analyzing surge heights at coarser resolutions, we first need to demonstrate that our IFS-GTSM model setup is sufficient in simulating maximum surge heights. To do so, we analyze the performance of the model setup at the T799-resolution forcing by comparing the maximum surge heights modeled with the T799-resolution forcing to observed maximum heights. Because of the dense tide gauge network on the U.S. mainland, it is possible to compare modeled and observed storm surge heights for Irma and Sandy at multiple locations along the coastline. For this, we take tide gauge stations within 250 km of the TC track and subtract the daily maxima of tides from the daily maxima of the observed sea levels to calculate skew surge (NOAA 2017). Since these sea levels are referenced above the mean sea level, we correct for mean sea-level trends by removing the monthly mean sea level. We compare the tide gauge measurements to neighboring GTSM coastal grid points. For the other TCs, the observed maxima and any applied corrections are taken from the available literature.
2.5 Coastal slope and complexity
Apart from being driven by meteorological factors such as U10 and MSLP, storm surge heights can be further amplified when the surge is interacting with shallow coastal bathymetry and coastal complexity (Mori et al. 2014). For this reason, we will also look at coastal slope and coastal complexity as drivers for changes in storm surge heights between different resolutions.
The coastal slope is derived from GEBCO, and calculated as the average slope between the coastline and the bed level 100 km off the coast, perpendicular to the coastline.
Coastal complexity is assessed by calculating the fractal dimension D of the coastline around the landfall location (Mandelbrot 1967). A fractal dimension is the ratio of change between pattern details and measuring scales, calculated using different length scales to measure the length of the outline of an object, such as a coastline. The values of D lie between 1 and 2 for coastlines, where a high D implies a more complex coastline. To calculate D, we use high-resolution country maps (30 m) from the database of Global Administrative Areas (GADM 2017) and length scales between 1 and 100 km. The algorithm for calculating the coastline complexity is based on Hijmans (2016).
3 Results and discussion
3.1 IFS-GTSM model performance at T799-resolution forcing
3.1.1 Comparison of U10 and MSLP
The modeled and observed U10 and MSLP for all TCs are listed in Table 1. Spatial plots of U10 and MSLP at landfall can be found in Supplementary Material Figs. 1–4. We see that the modeled MSLP and U10 intensities are generally underestimated in the T799-resolution forcing as compared to the observed values. The modeled MSLP values are up to 60–70 hPa higher than the observed values (Hurricane Patricia and Typhoon Haiyan). Conversely, Cyclone Gonu has a lower modeled MSLP as opposed to the observed value (15 hPa). Although in most cases, the underestimation of U10 is between 10 and 30 m/s, Patricia’s U10 is underestimated by almost 50 m/s. These intensity underestimations for Patricia and Haiyan are likely related to the failure of the data resolution to fully capture their small eyes. The T799-resolution forcing is known to cause considerable intensity underestimations for relatively small TCs with a small eye (ECMWF 2017b), as was the case for Patricia and Haiyan, which had eyes of 13 and 15 km in diameter, respectively.
The R2-values show that there is good agreement between the observed and modeled values. However, the R2-values for Gonu are low compared to the other TCs. This discrepancy is likely due to the IFS update in November 2007, which significantly improved U10 values in the tropics (ECMWF 2017a).
3.1.2 Comparison of maximum surge heights
For Irma and Sandy, tide gauge records can be used to analyze the modeled maximum surge heights. The results are shown in Fig. 3. The R2-values are 0.86 for Irma and 0.74 for Sandy, demonstrating a good fit between the modeled and observed surge heights. These results show that GTSM is capable of capturing the spatial variability in surge heights in both cases, as is also shown in panels c and d of Fig. 3. However, when zooming in to the local level, we notice some deviations from observed values. Underestimations in modeled storm surges can be caused by various factors. One of these factors is that bays and estuaries are in general not captured by GTSM’s grid resolution (approximately 5 km near the coastline). In addition, uncertainties imposed by the meteorological forcing can also cause lower modeled storm surges. Overestimations in the modeled storm surges may be caused by differences in the locations of the coastal points and the tide gauges, such as a GTSM grid point at the coast versus a tide gauge located in a harbor or a semi-open inlet.
Upper panels show scatter plots of the modeled and observed maximum storm surge heights for Irma (a) and Sandy (b). Lower panels show the modeled and observed (dots) maximum storm surge heights for Irma (c) and Sandy (d). Observations are taken from NOAA tide gauge stations (14 stations for Irma, 22 stations for Sandy)
Because we compare the tide gauge locations to nearby GTSM coastal grid points, Irma’s maximum modeled surge height of 2.6 m near Everglades City (Table 1) is not included in the scatter plot (Fig. 3a). The nearest tide gauge station was located at Fort Myers, approximately 100 km north of Everglades City, so that a GTSM coastal point closer by was selected.
From Table 1, we see that Sandy’s modeled maximum U10 is more than 50% lower than observed. From the quadratic relation between wind and surge (Eq. 1), we would expect a 75% lower surge, but this is not seen in the simulations (Fig. 3). This is likely due to the fact that resolution effects of the climate model do not only lead to an underestimation of wind intensity and the pressure drop, but can also lead to an overestimation of the storm size (known as numerical diffusion). The relatively large wind field increases the storm surge, which compensates for the TC intensity underestimation.
For the other case studies, we refer to the maximum surge heights around the landfall location listed in the literature (see Table 1). The differences between the modeled and observed maximum surge heights are lower than 0.5 m for five TCs: Hurricanes Irma and Sandy and Cyclones Giovanna, Nargis, and Gonu. For Patricia, the modeled maximum surge height is approximately 0.2 m. However, there is no mention of a storm surge in the official tropical cyclone report (Kimberlian et al. 2016), from which we conclude that any possible storm surge would have been low. This conclusion is in line with our model results.
Larger differences between the modeled and observed maximum surge heights are seen for Haiyan and Yasi. In both cases, the maximum surge height was recorded in an inlet. Because of GTSM’s resolution of ~ 5 km near coastlines, these inlets are not (fully) captured by the model. For Haiyan, it is likely that the strong intensity underestimation adds to the underestimation of the storm surge.
Based on the performance, we conclude that the IFS-GTSM model setup at the T799-resolution framework is capable of capturing large-scale spatial patterns of maximum surge height sufficiently well for the analysis on the effect of using lower-resolution meteorological forcing.
3.2 Horizontal resolution effects
Our results confirm that storm surge simulations using coarse-resolution meteorological forcing generally result in lower storm surge heights (Wakelin and Proctor 2002). These reductions are shown in Fig. 4, where the gradual decrease in slope for the different scatter plots shows that the maximum surge heights at GTSM coastal points decrease with decreasing horizontal resolution. Scatterplots for the other TCs can be found in Supplementary Material Fig. 5.
The differences in surge heights are illustrated in Fig. 5, which displays surge heights during the storm’s lifetime for Irma, Giovanna, Yasi, and Nargis at T799 (left) and 1.0° (center) resolutions, and their difference (right). Differences in surge heights for the other TCs can be found in Supplementary Material Figs. 6, 7, 8, 9. We calculate the relative difference in maximum surge heights at all selected GTSM coastal points (black dots in Fig. 5) to illustrate the resolution effects for the different TCs (see also supplementary material, Table A.3). For both Giovanna and Irma, relative differences in the average maximum surge height between T799- and 1.0°-resolution forcing amount to 39%. Patricia, Sandy, Yasi, and Gonu each have relative differences smaller than 20%, and the largest relative difference is found for Nargis with 47%.
Maximum surge heights at T799- and 1.0°-resolution forcing and difference in maximum surge heights during the storm’s lifetime between T799- and 1.0°-resolution forcing for a–c Hurricane Irma (Florida), d–f Cyclone Giovanna (Madagascar), g–i Cyclone Yasi (Australia) and j, k Cyclone Nargis (Myanmar). Black dots represent GTSM coastal points used in the statistical analysis
For the remainder, we focus on the absolute differences in the average maximum surge heights. These absolute differences can directly affect inundation depths and flood risk estimates (De Moel et al. 2012). Comparing the average maximum surge heights for simulations using different resolutions, Table 2 shows that there are four TCs for which the absolute difference is approximately or less than 0.2 m for all resolutions: Patricia, Haiyan, Giovanna and Gonu. For Sandy and Yasi, the maximum differences are approximately 0.35 m. The largest differences are found for Irma and Nargis, with maximum surge heights around 1 m lower in the 1.0°-resolution forcing. These results show that six out of the eight TCs can still be modeled relatively well at low resolutions, with maximum storm surge underestimations lower than 0.5 m, whereas for Irma and Nargis, meteorological forcing resolutions lower than 0.75° result in storm surge underestimations of around 0.8 m. Underestimations of this magnitude have a considerable effect on impact calculations (De Moel et al. 2012).
From Table 2, it follows that the difference in simulated maximum surge heights between different model resolutions is larger for higher storm surges. The height of a storm surge is driven by a combination of factors, which can broadly be classified into TC characteristics and geographical characteristics. The TC characteristics include intensity (measured via maximum U10 and minimum MSLP) and TC size (Irish et al. 2008). In addition, storm surges can be amplified by certain geographical characteristics, most importantly coastal slope and coastal complexity (Mori et al. 2014). We represent coastal complexity here as a fractal dimension D, where higher values of D imply a more complex coastline. Table 3 shows the TC and geographical characteristics for our eight case studies at landfall. We see that intensity (U10 and MSLP) alone cannot explain the maximum storm surge heights. This insight corresponds with the results of Irish et al. (2008), who have shown that TC size also has a large effect on the storm surge (though we use the radius of vanishing winds (Chavas et al. 2016), where they use the radius to maximum winds as a proxy for TC size). In our cases, the effect of TC size is apparent with the storms Sandy and Yasi, which resulted in large storm surges, despite their relatively low maximum wind speed and high pressure. However, TC size alone is not enough to explain storm surge magnitudes, as some small storms (such as Nargis) still result in high storm surges.
Geographical characteristics also influence storm surges. Storms that make landfall on coasts with a low complexity and steep slopes generally result in low surges (e.g., Giovanna, Gonu, Patricia), while storms that make landfall on complex and shallow coastlines are associated with larger storm surges. Overall, both TC and geographical characteristics influence the size of the storm surge and, correspondingly, the underestimation that occurs when a coarse-resolution meteorological forcing is used.
4 Concluding remarks
In this paper, we have assessed the suitability of the ECMWF IFS as meteorological forcing for high-resolution storm surge modeling with GTSM. For this, we compared the modeled maximum surge heights of Hurricanes Irma (2017) and Sandy (2012) with observations from tide gauge stations. We found R2-values of 0.86 and 0.74 for Irma and Sandy, respectively, demonstrating that maximum surge heights and their spatial distributions are captured sufficiently well in our IFS-GTSM model setup to simulate historical TC storm surge events. For the other case studies, we compared the modeled maximum surge heights to observations and/or estimates from the literature. We found that modeled surge heights are generally lower than observed heights. For most case studies, the difference between the observed and modeled surge heights is less than 0.5 m, from which we conclude that the IFS-GTSM model setup at T799-resolution framework is capable of capturing the large-scale spatial patterns of the maximum surge heights sufficiently well.
In addition, we analyzed the effects of different horizontal resolutions of meteorological forcing data on the simulated maximum surge heights by upscaling the meteorological forcing of the eight selected TC case studies to various coarser resolutions between 0.25° to 1.0°. We found that simulated TC storm surges are lower using coarser resolution datasets, with differences between the highest-resolution and 1.0°-resolution forcing ranging between 0.01 m for Patricia and 1.02 m for Irma. Similar conclusions were reached by Appendini et al. (2013), who forced a wave model with three different atmospheric reanalyses datasets to model significant wave heights. Despite differences in the atmospheric models, they show that wave modeling is improved in finer spatial resolution datasets compared to coarser resolution forcings.
We also observed that the storms with the highest storm surges also generate the largest differences in storm surge heights between the different resolutions. Hence, TCs with high storm surges require high-resolution meteorological forcing for accurate storm surge and impact modeling. Apart from the atmospheric forcing, mesh resolution and bathymetry representation in the hydrodynamic model are also critical in storm surge modeling (Kerr et al. 2013), but the effects of these two elements were not explored here. Therefore, our results should be taken with some caution, as they only serve as a way of assessing the atmospheric resolution effects, rather than a way of validating the hydrodynamic model and providing accurate storm surge height estimates in a particular area.
Furthermore, we examined the relationship between storm surge heights and geographical characteristics known to influence them (Irish et al. 2008; Mori et al. 2014): intensity, TC size, coastal complexity, and coastal slope. It appears that storm surge height is a combination of all these factors. However, in the eight case studies examined in this study, it seems that the geographical characteristics have a larger effect than the TC characteristics: the highest storm surges are found in regions with high coastal complexity and, in general, a small slope. At a local scale, the orientation of the coastline can play a more dominant role in storm surge enhancements: this can be seen for small islands where on one side the surge is positive and negative on the other, both with the same complex coastline.
Despite the limited dataset, there are indications that coastal complexity is an important driver for maximum surge heights and, in turn, the decrease in maximum surge heights in coarser-resolution meteorological forcing datasets. To further test the relationship between coastal complexity and horizontal resolution effects, we propose the use of a hydrodynamic model in which coastal slope and complexity can be (independently) adjusted for the same TC case study. Since coastal topography (e.g., mountainous regions) can also affect wind fields (Raderschall et al. 2008), the coastal complexity should be adjusted simultaneously in the global atmospheric circulation model.
Our findings show that the use of high-resolution meteorological forcing is particularly beneficial for areas prone to high (several meters) TC storm surges, since these high storm surges are reduced most when using coarser-resolution datasets. For TC case studies with surges below 0.5 m, our results suggest that coarser-resolution datasets can be used with limited effects on maximum surge heights.
References
Appendini C, Torres-Freyermuth A, Oropeza F, Salles P, López J, Mendoza E (2013) Wave modeling performance in the Gulf of Mexico and Western Caribbean: wind reanalyses assessment. Appl Ocean Res. https://doi.org/10.1016/j.apor.2012.09.004
Baatsen M, Haarsma RJ, Van Delden AJ, de Vries H (2015) Severe Autumn storms in future Western Europe with a warmer Atlantic. Ocean Clim Dynam 45:949–964. https://doi.org/10.1007/s00382-014-2329-8
Bacmeister JT et al (2016) Projected changes in tropical cyclone activity under future warming scenarios using a high-resolution climate model. Clim Change. https://doi.org/10.1007/s10584-016-1750-x
Bassill NP (2014) Accuracy of early GFS and ECMWF Sandy (2012) track forecasts: Evidence for a dependence on cumulus parameterization. Geophys Res Lett 41:3274–3281 https://doi.org/10.1002/2014GL059839
Blake ES, Kimberlian TB, Cangialosi JP, Beven IIJL (2013) Tropical cyclone report: Hurricane Sandy. National Hurricane Centre, Miami
Boer GJ, Denis B (1997) Numerical convergence of the dynamics of a GCM. Clim Dyn 13:359–374. https://doi.org/10.1007/s003820050171
Bunya S et al (2010) A high-resolution coupled riverine flow, tide, wind, wind wave, and storm surge model for Southern Louisiana and Mississippi. Part I: Model development and validation. Mon Weather Rev 138:345–377. https://doi.org/10.1175/2009MWR2906.1
Bureau of Meteorology (2017) Severe Tropical Cyclone Yasi, 30 January–3 February 2011. Commonwealth of Australia. http://www.bom.gov.au/cyclone/history/yasi.shtml. Accessed 21 Jul 2017
Byrne D, Horsburgh K, Zachry B, Cipollini P (2017) Using remotely sensed data to modify wind forcing in operational storm surge forecasting. Nat Hazards 89:275–293. https://doi.org/10.1007/s11069-017-2964-6
Cangialosi JP, Latto AS, Berg R (2018) Tropical cyclone report: hurricane irma, 30 August–12 September 2017. National Hurricane Center, Miami
Cardone VJ, Cox AT (2009) Tropical cyclone wind field forcing for surge models: critical issues and sensitivities. Nat Hazards 51:29–47. https://doi.org/10.1007/s11069-009-9369-0
Carrère L, Lyard F (2003) Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing—comparisons with observations. Geophys Res Lett. https://doi.org/10.1029/2002GL016473
Chavas DR, Lin N, Dong W, Lin Y (2016) Observed tropical cyclone size. Revisit J Clim 29:2923–2939. https://doi.org/10.1175/jcli-d-15-0731.1
De Moel H, Asselman NEM, Aerts JCJH (2012) Uncertainty and sensitivity analysis of coastal flood damage estimates in the west of the Netherlands. Nat Hazards Earth Syst Sci 12:1045–1058. https://doi.org/10.5194/nhess-12-1045-2012
Dee DP et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597. https://doi.org/10.1002/qj.828
Dietrich JC et al (2010) A high-resolution coupled riverine flow, tide, wind, wind wave, and storm surge model for Southern Louisiana and Mississippi. Part II: Synoptic description and analysis of hurricanes Katrina and Rita. Mon Weather Rev 138:378–404
ECMWF (2016) ERA-Interim. European Centre for Medium-Range Weather Forecasts. http://www.ecmwf.int/en/research/climate-reanalysis/era-interim. Accessed 25 Oct 2016
ECMWF (2017a) Changes in ECMWF model: evolution of the IFS. http://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-model. Accessed 17 Mar 2017
ECMWF (2017b) Known IFS forecasting issues. European Centre for Medium-Range Weather Forecasts. https://software.ecmwf.int/wiki/display/FCST/Known+IFS+forecasting+issues. Accessed 22 Jun 2017
ECMWF (2017c) What is ERA5. https://software.ecmwf.int/wiki/display/CKB/What+is+ERA5. Accessed 20 Dec 2017
Fiorino M (2008) Record-setting performance of the ECMWF IFS in medium-range tropical cyclone track prediction. ECMWF Newsl 118(2008):20–27
Flato G et al (2013) Evaluation of Climate Models. In: Stocker TF et al (eds) Climate Change 2013: the physical science basis. Contribution of working group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, pp 741–866. https://doi.org/10.1017/CBO9781107415324.020
Fritz HM, Blount CD, Albusaidi FB, Al-Harthy AHM (2010) Cyclone Gonu storm surge in Oman. Estaur Coast Shelf Sci 86:102–106. https://doi.org/10.1016/j.ecss.2009.10.019
GADM (2017) GADM database of global administrative areas. http://www.gadm.org/. Accessed 17 Jul 2017
Haigh ID, MacPherson LR, Mason MS, Wijeratne EMS, Pattiaratchi CB, Crompton RP, George S (2014) Estimating present day extreme water level exceedance probabilities around the coastline of Australia: tropical cyclone-induced storm surges. Clim Dynam 42:139–157. https://doi.org/10.1007/s00382-012-1653-0
Harper B, Holland G (1999) An updated parametric model of the tropical cyclone. In: Proc. 23rd Conf. Hurricanes and Tropical Meteorology
Harper BA, Kepert JD, Ginger JD (2008) Guidelines for converting between various wind averaging periods in tropical cyclone conditions. World Meteorological Organization, Geneva
Hijmans R (2016) The length of a coastline. Feed the Future, The U.S. Government’s Global Hunger and Food Security Initiative. http://rspatial.org/cases/rst/2-coastline.html. Accessed 5 Jul 2017
Hiroaki I et al (2017) Compound simulation of fluvial floods and storm surges in a global coupled river-coast flood model: model development and its application to 2007 Cyclone Sidr in Bangladesh. J Adv Model Earth Syst 9:1847–1862. https://doi.org/10.1002/2017MS000943
Hodges K, Cobb A, Vidale PL (2017) How well are tropical cyclones represented in reanalysis datasets? J Clim 30:5243–5264. https://doi.org/10.1175/jcli-d-16-0557.1
Holland GJ (1980) An analytic model of the wind and pressure profiles in hurricanes Mon Weather Rev 108:1212–1218 https://doi.org/10.1175/1520-0493(1980)108%3C1212:aamotw%3E2.0.co;2
Irazoqui Apecechea M, Verlaan M, Zijl F, Le Coz C, Kernkamp H (2017) Effects of self-attraction and loading at a regional scale: a test case for the Northwest European. Shelf Ocean Dyn 67:729–749. https://doi.org/10.1007/s10236-017-1053-4
Irish JL, Resio DT, Ratcliff JJ (2008) The influence of storm size on hurricane surge. J Phys Oceanogr 38:2003–2013. https://doi.org/10.1175/2008jpo3727.1
Jagers B, Rego J, Verlaan M, Lalic A, Genseberger M, Friocourt Y, van der Pijl SA (2014) Global tide and storm surge model with a parallel unstructured-grid shallow water solver. In: AGU Fall Meeting Abstracts, p 05
Jakobsen F, Madsen H (2004) Comparison and further development of parametric tropical cyclone models for storm surge modelling. J Wind Eng Ind Aerod 92:375–391. https://doi.org/10.1016/j.jweia.2004.01.003
Jelesnianski C, Jye C, Shaffer W, Gilad A (1984) SLOSH—a hurricane storm surge forecast model. OCEANS 1984(1):314–317. https://doi.org/10.1109/OCEANS.1984.1152341
Jones PW (1999) First- and second-order conservative remapping schemes for grids in spherical coordinates Mon Weather Rev 127:2204–2210 https://doi.org/10.1175/1520-0493(1999)127%3C2204:fasocr%3E2.0.co;2
Kalnay E et al. (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77:437–471 https://doi.org/10.1175/1520-0477(1996)077%3C0437:tnyrp%3E2.0.co;2
Kernkamp HWJ, Van Dam A, Stelling GS, de Goede ED (2011) Efficient scheme for the shallow water equations on unstructured grids with application to the Continental. Shelf Ocean Dyn 61:1175–1188. https://doi.org/10.1007/s10236-011-0423-6
Kerr PC et al (2013) U.S. IOOS coastal and ocean modeling testbed: Evaluation of tide, wave, and hurricane surge response sensitivities to mesh resolution and friction in the Gulf of Mexico. J Geophys Res Oceans 118:4633–4661. https://doi.org/10.1002/jgrc.20305
Kimberlian TB, Blake ES, Cangialosi JP (2016) Tropical cyclone report: hurricane Patricia. National Hurricane Center, Miami
Knapp KR, Kruk MC, Levinson DH, Diamond HJ, Neumann CJ (2010) The international best track archive for climate stewardship (IBTrACS) unifying tropical cyclone data. Bull Am Meteorol Soc 91:363–376. https://doi.org/10.1175/2009BAMS2755.1
Lin N, Chavas D (2012) On hurricane parametric wind and applications in storm surge modeling. J Geophys Res Atmos. https://doi.org/10.1029/2011JD017126
Lin N, Emanuel KA, Smith JA, Vanmarcke E (2010) Risk assessment of hurricane storm surge for New York City J Geophys Res. https://doi.org/10.1029/2009JD013630
Magnusson L, Bidlot J-R, Lang STK, Thorpe A, Wedi N, Yamaguchi M (2014) Evaluation of medium-range forecasts for Hurricane Sandy. Mon Weather Rev 142:1962–1981. https://doi.org/10.1175/mwr-d-13-00228.1
Mandelbrot B (1967) How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 156:636–638. https://doi.org/10.1126/science.156.3775.636
Mizuta R et al (2012) Climate simulations using MRI-AGCM3.2 with 20-km Grid. J Meteorol Soc Jpn 90A:233–258. https://doi.org/10.2151/jmsj.2012-A12
Mori N et al (2014) Local amplification of storm surge by Super Typhoon Haiyan in Leyte Gulf. Geophys Res Lett 41:5106–5113. https://doi.org/10.1002/2014GL060689
Muis S, Verlaan M, Winsemius HC, Aerts JCJH, Ward PJ (2016) A global reanalysis of storm surges and extreme sea levels Nat Comm 7 https://doi.org/10.1038/ncomms11969
Muis S et al (2017) A comparison of two global datasets of extreme sea levels and resulting flood exposure. Earth’s Future. https://doi.org/10.1002/2016EF000430
Murakami H (2014) Tropical cyclones in reanalysis data sets. Geophys Res Lett 41:2133–2141. https://doi.org/10.1002/2014GL059519
Murakami H, Sugi M (2010) Effect of model resolution on tropical cyclone climate projections. SOLA 6:73–76. https://doi.org/10.2151/sola.2010-019
Nikulin G et al (2012) Precipitation climatology in an ensemble of CORDEX-Africa regional climate simulations. J Clim 25:6057–6078. https://doi.org/10.1175/jcli-d-11-00375.1
NOAA (2017) Tides and great lakes water levels. https://tidesandcurrents.noaa.gov/. Accessed 15 Oct 2017
NOAA National Centers for Environmental Information (2018) U.S. billion-dollar weather and climate disasters. https://www.ncdc.noaa.gov/billions/. Accessed 12 Jan 2018
Persson A, Grazzini F (2005) User guide to ECMWF forecast products, vol 4. ECMWF, Reading
Probst P, Franchelo G, Annunziato A, De Groeve T, Vernaccini L, Himer A, Andredakis I (2012) Tropical Cyclone GIOVANNA Madagascar, February 2012. Joint Res Centre Eur Comm. https://doi.org/10.2788/70858
Raderschall N, Lehning M, Schär C (2008) Fine-scale modeling of the boundary layer wind field over steep topography Water Resour Res. https://doi.org/10.1029/2007WR006544
Ross JC (1854) On the effect of the pressure of the atmosphere on the mean level of the ocean Phios. Tr R Soc 144:285–296
Saha S et al (2006) The NCEP climate forecast. Syst J Clim 19:3483–3517. https://doi.org/10.1175/jcli3812.1
Schenkel BA, Hart RE (2012) An examination of tropical cyclone position, intensity, and intensity life cycle within atmospheric reanalysis datasets. J Clim 25:3453–3475. https://doi.org/10.1175/2011JCLI4208.1
Strachan J, Vidale PL, Hodges K, Roberts M, Demory M-E (2013) Investigating global tropical cyclone activity with a hierarchy of AGCMs: the role of model. Resolut J Clim 26:133–152. https://doi.org/10.1175/JCLI-D-12-00012.1
Tasnim KM, Shibayama T, Esteban M, Takagi H, Ohira K, Nakamura R (2015) Field observation and numerical simulation of past and future storm surges in the Bay of Bengal: case study of cyclone. Nargis Nat Hazards 75:1619–1647
Verlaan M, De Kleermaeker S, Buckman L (2015) GLOSSIS: Global storm surge forecasting and information system. Paper presented at the Australasian Coasts & Ports Conference 2015: 22nd Australasian Coastal and Ocean Engineering Conference and the 15th Australasian Port and Harbour Conference, Auckland, New Zealand
Vitousek S, Barnard PL, Fletcher CH, Frazer N, Erikson L, Storlazzi CD (2017) Doubling of coastal flooding frequency within decades due to sea-level rise. Sci Rep 7:1399. https://doi.org/10.1038/s41598-017-01362-7
Vousdoukas MI, Mentaschi L, Voukouvalas E, Verlaan M, Jevrejeva S, Jackson LP, Feyen L (2018) Global probabilistic projections of extreme sea levels show intensification of coastal flood hazard. Nat Comm 9:2360. https://doi.org/10.1038/s41467-018-04692-w
Wakelin SL, Proctor R (2002) The impact of meteorology on modelling storm surges in the Adriatic Sea. Glob Planet Change 34:97–119. https://doi.org/10.1016/S0921-8181(02)00108-X
Walsh KJE, Fiorino M, Landsea C, McInnes KL (2007) Objectively determined resolution-dependent threshold criteria for the detection of tropical cyclones in climate models and reanalyses. J Clim 20:2307–2314. https://doi.org/10.1175/jcli4074.1
Weenink MPH (1958) A Theory and method of calculation of wind effects on sea levels in a partly-enclosed sea, with special application to the Southern coast of the North Sea. University of California, California
Williams J, Irazoqui Apecechea M, Saulter A, Horsburgh KJ (2018) Storm surge forecasting: quantifying errors arising from the double-counting of radiational tides. Ocean Sci Discuss 2018:1–21. https://doi.org/10.5194/os-2018-63
Yukimoto S et al (2006) Present-day climate and climate sensitivity in the meteorological research institute coupled GCM version 2.3 (MRI-CGCM2.3. J Meteorol Soc Jpn Ser II 84:333–363. https://doi.org/10.2151/jmsj.84.333
Acknowledgements
We would like to thank the reviewers for their thoughtful comments and efforts towards improving our manuscript. We thank ECMWF for the use of the ECMWF IFS dataset. Access to IFS data was granted by the national meteorological services of ECMWF Member and Co-operating States. All other users can gain access to ECMWF forecast product under various license agreement types, see https://www.ecmwf.int/en/forecasts/accessing-forecasts/order-historical-datasets. We thank Jan Barkmeijer for sharing his expertise on ECMWF IFS. We also thank the participants of the 6th International Summit on Hurricanes and Climate Change: from Hazard to Impact for the fruitful discussions on this topic. We thank SURFsara (http://www.surfsara.nl) for the support in using the Lisa Computer Cluster. NB, SM and JCJHA are funded by a VICI grant from the Netherlands Organisation for Scientific Research (NWO) (Grant Number 453-13-006). RJH is funded by the PRIMAVERA project in the European Commission’s Horizon 2020 research programme (Grant Number 641727). MV and MIA are funded by the European Union’s Horizon 2020 research and innovation programme (Grant Number 687323). PJW is funded by a VIDI grant from the Netherlands Organisation for Scientific Research (NWO) (Grant Number 016.161.324).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bloemendaal, N., Muis, S., Haarsma, R.J. et al. Global modeling of tropical cyclone storm surges using high-resolution forecasts. Clim Dyn 52, 5031–5044 (2019). https://doi.org/10.1007/s00382-018-4430-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4430-x