Assessment of aerosol–cloud–radiation correlations in satellite observations, climate models and reanalysis

Abstract

Representing large-scale co-variability between variables related to aerosols, clouds and radiation is one of many aspects of agreement with observations desirable for a climate model. In this study such relations are investigated in terms of temporal correlations on monthly mean scale, to identify points of agreement and disagreement with observations. Ten regions with different meteorological characteristics and aerosol signatures are studied and correlation matrices for the selected regions offer an overview of model ability to represent present day climate variability. Global climate models with different levels of detail and sophistication in their representation of aerosols and clouds are compared with satellite observations and reanalysis assimilating meteorological fields as well as aerosol optical depth from observations. One example of how the correlation comparison can guide model evaluation and development is the often studied relation between cloud droplet number and water content. Reanalysis, with no parameterized aerosol–cloud coupling, shows weaker correlations than observations, indicating that microphysical couplings between cloud droplet number and water content are not negligible for the co-variations emerging on larger scale. These observed correlations are, however, not in agreement with those expected from dominance of the underlying microphysical aerosol–cloud couplings. For instance, negative correlations in subtropical stratocumulus regions show that suppression of precipitation and subsequent increase in water content due to aerosol is not a dominating process on this scale. Only in one of the studied models are cloud dynamics able to overcome the parameterized dependence of rain formation on droplet number concentration, and negative correlations in the stratocumulus regions are reproduced.

1 Introduction

Systematic variations in aerosol amount and composition over time give rise to a forcing on the climate system, through aerosol interaction with clouds and with radiation. The estimate of aerosol forcing, from pre-industrial (PI) to present day (PD), is at present highly uncertain (Boucher et al. 2013) and to achieve the goal of constraining the estimate of aerosol forcing, including that from aerosol-interactions with clouds, a better understanding of the relations between aerosols, cloud microphysics and cloud macrophysics is necessary, although not sufficient.

In lack of long-term observations of variations in aerosol and cloud, it is customary to relate present-day, short-term relations between aerosol and cloud properties to those on the time scale of anthropogenic forcing. It has been shown, however, that present-day relations and their uncertainties may not be representative of those dominating the PI–PD changes, and the use of present-day variability to constrain PI–PD forcing has been questioned (Penner et al. 2011; Carlsaw et al. 2013; Ghan et al. 2016; Lee et al. 2016). Ghan et al. (2016) decompose the dependence of cloud radiative forcing on aerosol into individual sensitivity factors, and find from AeroCom (Aerosol Comparisons between Observations and Models) models that determining these relations from recent variability typically offers poor constraint on the anthropogenic forcing, and in some cases even results in sensitivities of opposite signs. Penner et al. (2011) suggest that satellite-derived sensitivity of cloud droplet number to aerosol optical depth strongly underestimates the actual change in cloud droplet number from PI to PD, while Gryspeerdt et al. (2017) demonstrate that by accounting for multiple predictors of cloud droplet number, the radiative forcing from aerosol–cloud interactions can be well constrained by PD relationships, provided that the anthropogenic aerosol component is known. Carlsaw et al. (2013) ascribe a large fraction of the uncertainty in anthropogenic aerosol forcing to uncertainty in the PI state, that may not necessarily be reduced by further constraint of PD conditions, and Lee et al. (2016) point at the fact that model uncertainty allows for multiple different models agreeing sufficiently well with PD aerosol observations, but still producing a large range of forcing estimates.

In this study, we do not attempt to constrain aerosol forcing, per se. Rather, we set out to test relations between various aerosol-, cloud-, and radiation-related variables on climatologically relevant scale, proposing a framework for evaluation, and thereby providing guidance to better model representation of these relations and continued model improvement. Even if agreement with PD observations is not sufficient for constraining model estimates of past or future forcing, a reasonable representation of the state, variability and co-variability of observable quantities is desired and required. It remains essential that global climate models (GCMs) used for process-studies as well as for future projections are able to realistically capture the relations between climatologically relevant aerosol and cloud properties, including those emerging from aerosol influence on cloud water content, which is central to aerosol–cloud interactions in warm clouds.

In terms of aerosol–cloud interactions, we focus on the effects of aerosols on cloud albedo (referred to as the Twomey effect, the cloud albedo effect, cloud brightening or the 1st indirect effect) and cloud amount (referred to as the Albrecht effect, the cloud lifetime effect, cloud thickening or the 2nd indirect effect). Although the classical nomenclature of aerosol indirect effects, as opposed to direct effects, has largely been abandoned (Boucher et al. 2013), it is instructive to separate the effects on cloud albedo and cloud amount.

Both the cloud brightening (1st indirect effect) and the cloud thickening (2nd indirect effect) act via the cloud droplet number concentration ($N_d$), the former instantaneously and the latter as a rapid adjustment. As the variability in $N_d$ has been found to be driven mainly by sulfate aerosol (Boucher and Lohmann 1995; McCoy et al. 2017), sulfate ($SO_4$) is the aerosol species we focus on.

Cloud brightening occurs when, all else equal, increased aerosol number yields more numerous and smaller cloud droplets (Twomey 1974, 1977). Cloud thickening in turn is an effect of the precipitation efficiency in such small-droplet clouds being reduced, leading to a build-up of condensate both in terms of prolonged cloud lifetime and larger fractional cloud cover, and in terms of cloud geometrical thickness (Albrecht 1989; Pincus and Baker 1994; Brenguier et al. 2000). Thereby a priori, the 1st indirect effect acting in isolation would lead to positive correlations between $N_d$ and cloud albedo ($\alpha _{cloud}$), and similarly the 2nd indirect effect acting in isolation would yield positive correlations between $N_d$ and cloud liquid water path (L) and/or cloud fraction ($f_c$).

However, neither of the two effects can be isolated from the other, nor from other processes. Just the fact that L-changes driven by the 2nd indirect effect will violate the conditions of the 1st indirect effect illustrates this difficulty, see e.g. McComiskey and Feingold (2012).

As discussed by Ackerman et al. (2004), Jiang and Feingold (2006), Stevens and Feingold (2009), Bretherton et al. (2007), Wood (2007), Small et al. (2009), Jiang et al. (2011), Rosenfeld et al. (2014) and Neubauer et al. (2017) among others, there are also other counteracting mechanisms related to aerosol and cloud dynamics, and these correlations do not necessarily protrude when all processes are allowed to act together, as must be expected to typically be the case in the real atmosphere. Therefore, a comparison of correlation strengths and directions can be of aid, indicating what matters and what does not, on a larger scale.

In a preceding attempt to compare observed and modelled relations between $N_d$ and L in particular, i.e. focusing on the 2nd indirect effect, Michibata et al. (2016) find that the cloud susceptibility to aerosol perturbation is region dependent, and also that the MIROC GCM overestimates the increase in L with increasing $N_d$ as compared to satellite observations. They ascribe the discrepancy to a too dominant role of microphysics in this model, not allowing for macrophysical feedbacks affecting the cloud water. It is noteworthy here, that the $N_d$ and L retrievals utilized by Michibata et al. (2016) may be biased in regions of broken cloud cover (Cho et al. 2015; Seethala and Hovath 2010). Prior to this, Quaas et al. (2009) used observed statistical relationships between aerosol optical depth ($\tau _a$) and various cloud parameters to estimate aerosol forcing, based on their finding that the same relationships in an ensemble of models are actually skilful in predicting simulated forcing. Quaas et al. (2009), similar to Michibata et al. (2016), draw the conclusion that the implementation of the 2nd indirect effect in models by delayed autoconversion from cloud droplet to drizzle at larger droplet number concentration, results in a too strong sensitivity of L to aerosol both in terms of $N_d$ and $\tau _a$. Neubauer et al. (2017) investigate in detail the influence of aerosol water uptake on the co-variability between aerosol and cloud water and find that dry aerosol better predicts the observed variability in L, and that water uptake, wet scavenging and cloud processing should all be minimized to isolate the susceptibility of cloud water to aerosol changes and compute aerosol forcing.

Several studies, e.g. Gassó (2008) and Toll et al. (2017) have made use of the natural experiment supplied by volcanic eruptions and their emissions of sulfate aerosol precursors, namely sulfur dioxide (SO$_2$), to study potential effects on cloud properties. McCoy and Hartmann (2015) specifically found that during the 2014–2015 eruption of Holohraun in Iceland, the cloud droplet size (represented by effective radius, $r_e$) significantly decreased in the area downwind of the volcano. Analysing the same volcanic eruption, Malavelle et al. (2017) indicate that $r_e$ is actually the only cloud-variable that responds to the increased $SO_2$ and $SO_4$. Malavelle et al. (2017) also suggest that the indifference of L to aerosol perturbation can be used to constrain models in a general sense; models with a significant 2nd indirect effect, i.e. in which L increases when aerosol and droplet number increases, should be considered less realistic. Toll et al. (2017) found that in volcano tracks, i.e. spatially limited, linear cloud modifications due to underlying volcanic emissions analogous to ship tracks, i.e. similar cloud features due to ship emissions, the L response to the aerosol perturbation varies and is on average close to zero, while the HadGEM model simulates a consistently positive response in L to aerosol.

To investigate the emerging relations between aerosol and cloud properties in an array of models and observations, we here look at several regions, in three main categories. Following recent literature (McCoy and Hartmann 2015; Mace and Abernathy 2016; Malavelle et al. 2017; McCoy et al. 2018) we include three regions of volcanic influence (Iceland, Vanuatu, Hawaii). While the Vanuatu and Hawaii regions have been assessed to be among the largest sources of volcanic SO$_2$ degassing in the past decade (Carn et al. 2017), the Iceland region is not degassing in the same way, but has experienced eruptive events during the time period studied (Grìmsvötn May 2011, Eyjafjallajökull March–June 2010, Holohraun Aug 2014–Feb 2015), as has Hawaii (Kilauea June–August 2008). In contrast to these natural sulfate-dominated regions we add two regions of strong anthropogenic influence (US, China). The Iceland region with its less remote location compared to the other two volcanic regions may also be expected to be anthropogenically influenced. Finally, we study five subtropical stratocumulus (Sc) regions (Californian, Peruvian, Namibian, Australian and Canarian, as defined by Klein and Hartmann (1993)), a category that serves as a reference, as aerosol–cloud–radiation relations in these regions have been studied rather extensively (Wood 2007; Bender et al. 2016; Frey et al. 2017, e.g.) and have been indicated as particularly susceptible to aerosol influence, at least in climate models (Kirkevåg et al. 2013; Carlsaw et al. 2013).

We add to the previous literature in several ways:

• Focus regions are selected based on aerosol signature as well as dynamical regime, motivated by the regional variability in aerosol–cloud relations discussed by e.g. Michibata et al. (2016), Zhang et al. (2016) and Neubauer et al. (2017).

• Compared to Quaas et al. (2009), Michibata et al. (2016) and Toll et al. (2017) we include additional years and sensors in the satellite data analysis, which provides an indication of retrieval biases and influence of temporal variability and sensitivity to time period.

• Monthly mean time scale is used, rather than daily (Quaas et al. 2009) or instantaneous (Neubauer et al. 2017). This is to emphasize not the process level, but the relations emerging at climatologically relevant time scales, which are not necessarily identical, cf. Bender et al. (2016), Konsta et al. (2016).

• We perform a multi-model comparison, rather than a single model evaluation or sensitivity experiments with one model as Neubauer et al. (2017), Michibata et al. (2016) or Toll et al. (2017), providing an evaluation of the subset of those models in the CMIP5 ensemble (see Section 2.3) that supply the necessary output variables. As pointed out in the model intercomparison made by Quaas et al. (2009), models evolve and therefore evaluations need to be continually updated.

• We include MERRA-2 (see Sect. 2.2), an independent set of reanalysis data that is useful because it includes dynamical and meteorological feedbacks but has no parameterized link between aerosol and cloud microphysics, and can therefore be used as a “no-indirect-effect” reference case.

• We focus not only on $N_d$–L relations (as Michibata et al. 2016; Malavelle et al. 2017; Neubauer et al. 2017) or on sensitivities to $\tau _a$ perturbations (as Quaas et al. (2009)) or on the specific relations behind the microphysical interactions assumed to drive the 1st and 2nd indirect effect (as Ghan et al. 2016), but give a broader picture of relations between macro- and microphysical cloud and aerosol properties, that can be used to test and evaluate models.

• Rather than “susceptibility” i.e. linear regression coefficients, we study correlations (with statistical significance estimates) and hereby avoid the problem of potentially assigning a large susceptibility to a relation between variables that are in fact not well correlated. We provide correlation matrices for individual regions that can readily be re-produced for the same or different regions, and used in the process of model development, tuning and evaluation.

2 Methods and data

We make use of three main data sources: satellite observations, nudged reanalysis and climate model output. With this data selection we illustrate the use of correlations between various micro- and macrophysical cloud and aerosol properties, as a way to evaluate models.

Correlation does not imply causation, and e.g. Engström and Ekman (2010) illustrate specifically how correlations between cloud and aerosol quantities can be strongly affected by other factors than microphysical relations. But conversely, if a specific microphysical coupling were strong enough to dominate on a climatologically relevant scale, it would give rise to a correlation. Thereby it follows that a lack of correlation indicates that no single microphysical coupling is dominating.

The study regions are defined in Table 1. All analysis is performed on monthly averaged data, corrected for a climatological seasonal cycle, i.e. values are given as anomalies relative to the regional mean climatology. Details on each of the data sources are provided in the following Sects. 2.1–2.3.

Table 1 Study regions, geographically specified and categorized based on aerosol signature or cloud regime

2.1 Satellite observations

Observed top-of-atmosphere shortwave (0.2–5 $\upmu \hbox {m}$) radiative fluxes from CERES [(Clouds and the Earth’s Radiant Energy System (Wielicki et al. 1996)] and cloud and aerosol properties from MODIS (MODerate resolution Imaging Spectroradiometer (Barnes et al. 1998) are taken from the CERES SSF (Single Scanner Footprint) Edition 4, level 3 product, available from the NASA Langley Research Center Atmospheric Science Data Center. Observed estimates of albedo ($\alpha$), clear-sky albedo ($\alpha _{clear}$), $f_c$, L, $r_e$ and $\tau _a$ averaged to 1$^{\circ }\times 1^{\circ }$ resolution on monthly mean time scale are analyzed.

In the SSF data set, clear-sky is determined by the CERES-MODIS cloud mask algorithm (Minnis et al. 2009) applied to the MODIS pixels within the CERES footprint. Each MODIS pixel (size at nadir ranging from 250 to 1000 m depending on wavelength) within the CERES footprint (20 km nominal resolution) is determined as either clear or cloudy and the cloud fraction is the ratio of cloudy pixels to the total number of pixels. MODIS cloud properties (collection 5) are derived from five channels in the visible and infrared (Minnis et al. 2009, 2011), and like the MODIS $\tau _a$ (Remer et al. 2005, 2008) are mapped to the lower CERES resolution.

CERES and MODIS are carried by the polar orbiting Aqua and Terra satellites, with local equator crossing times of 10.30 AM and 1.30 PM respectively. Observations from Aqua are used in the present study, following Malavelle et al. (2017). The gridded radiative fluxes are derived using angular distribution models as described by Loeb et al. (2005), and diurnally averaged assuming constant meteorology between the satellite overpasses, after which monthly means are created.

MODIS $N_d$ is calculated as a function of cloud optical thickness ($\tau _c$) and cloud top $r_e$ on daily mean scale at 1$^{\circ }\times$1$^{\circ }$ resolution, using level 2 MODIS swath data filtered to include only low, liquid clouds in cases where daily grid cloud fraction exceeds 80%, and to exclude pixels with solar zenith angle ($\theta$) greater than 65$^{\circ }$ and other problematic retrievals, as according to Grosvenor and Wood (2014). The daily data are then averaged to monthly means. See also McCoy et al. (2018) for a closer description and evaluation of the same $N_d$ data set.

In addition to MODIS L we make use of the Multisensor Advanced Climatology (MAC) L product (Elsaesser et al. 2016) that is based on the combination of data from SSM/I and SSMIS (Special Sensor Microwave Imager/Sounder), AMSR-E and AMSR-2 (Advanced Microwave Scanning Radiometers), TRMM (Tropical Rainfall Measuring Mission) and GPM (Global Precipitation Measurement) microwave imagers and WindSat satellite sensors. The compilation, inter-calibration and bias-correction of the data sets into a monthly gridded ($1^{\circ }\times 1^{\circ }$ resolution) global ocean L climatology is described by Elsaesser et al. (2017). An advantage of the MAC L is that it avoids the retrieval failures in regions of broken clouds, that may lead to sampling biases in the MODIS L (Seethala and Hovath 2010; Grosvenor and Wood 2014; Cho et al. 2015). The microwave measurements provide a grid-box average L, and to make this estimate consistent with that from MODIS, and more directly relatable to in-cloud $N_d$ estimates, MAC L is divided by the MODIS $f_c$, yielding an in-cloud L estimate. The two L estimates will be referred to as $L_{MODIS}$ and $L_{MAC}$ respectively, but we note that through the conversion to in-cloud L, the $L_{MAC}$ is not independent of MODIS.

All the observational data used span the time period January 2003 through December 2015, i.e. 13 years.

2.2 Reanalysis

MERRA-2 (Modern-Era Retrospective analysis for Research and Applications, version 2) is an atmospheric reanalysis dataset, based on the Goddard Earth Observing System Model, version 5 (GEOS-5) (Rienecker et al. 2011; Molod et al. 2015). In addition to assimilation of meteorological and cloud variables including rain-rate, water vapour path and wind speed, MERRA-2 also assimilates $\tau _a$ from satellite (AVHRR, MODIS, MISR) and surface based remote sensing (Aeronet), as described in Randles et al. (2016).

MERRA-2 also implements an on-line aerosol chemistry, radiation and transport model (Colarco et al. 2010). Hourly averages of the assimilated reanalysis product at $0.5^{\circ }\times$$0.625^{\circ }$ resolution are averaged to a monthly mean $1^{\circ }\times 1^{\circ }$ grid, in the case of all variables except the sulfate mass concentration for which monthly means are created from daily averages of the instantaneous 3-h reanalysis output. We note that the agreement with $\tau _a$ observations may vary during the analysis cycle, as a result of biases in model forecast compared to the assimilated MODIS observations, but the average product are in close agreement with the observed fields (Randles et al. 2016).

In MERRA-2, the aerosol module is coupled to the meteorology so that e.g. wet removal and humidification affect the aerosol distribution, but there is no parameterized microphysical link between aerosols and clouds, and MERRA-2 in our study therefore acts as a “no-indirect-effect” reference case. L is not directly assimilated in MERRA-2, and the only way for potential real-world aerosol effects to influence the reanalysis L would be via the assimilated water vapour path or rain rates, both weak links. MERRA-2 further has no $N_d$ estimate, but McCoy et al. (2017) have shown that SO$_4$ from MERRA-2 is a good predictor of observed $N_d$, and hence we use reanalysis SO$_4$ as a proxy for $N_d$, with global coverage. This metric will be referred to as $N_{dMERRA}$. MERRA-2 supplies a grid-box average L, that is divided by $f_c$ to yield an in-cloud estimate of L, consistent with MODIS observations.

2.3 Coupled climate models

We include seven models from the Coupled Model Intercomparison Project, phase 5 (CMIP5, (Taylor et al. 1996)) that provide the required output fields in their historical simulations, namely IPSL-CM5A-LR, IPSL-CM5A-MR, IPSL-CM5B-LR, MIROC5, MIROC-ESM, MRI-CGCM3 and MRI-ESM1. The two versions of IPSL-CM5A differ in resolution only, whereas the third model from the same institute, IPSL-CM5B-LR, has significantly different physics, including boundary layer, cloud and convection schemes (Dufresne et al. 2013; Hourdin et al. 2013), as further evaluated by Konsta et al. (2016). MIROC5 and MIROC-ESM both use the same aerosol scheme, but different cloud schemes; MIROC5 is based on Wilson and Ballard (1999) and MIROC-ESM is based on Treut and Li (1991). Further, MIROC-ESM in addition to the ocean, land surface and chemistry models includes atmospheric chemistry, ocean- and land ecosystem models with dynamic vegetation (Watanabe et al. 2010, 2011). Similarly, MRI-CGCM3 and MRI-ESM1 are based on the same atmosphere-ocean core component, but the ESM has a greater complexity including a sophisticated representation of the carbon cycle (Yukimoto et al. 2012). An error in the microphysics has been identified in the CMIP5-archived historical simulations of MRI, related to the prognostic equations for cloud droplet number concentration and yielding unrealistically large $N_d$ values (Kawai et al. 2017). As a reference we therefore also include analysis of an MRI-CGCM3 simulation in which this error has been rectified. This is an AMIP-type fixed-SST simulation with pre-industrial greenhouse gas forcing and year 2000 aerosol fields, and it will be referred to as MRI-fixed.

Whereas all the investigated models include a parameterization of the 1st indirect effect, they differ in their representation of $N_d$, and the 2nd indirect effect, as summarized in Table 2. MIROC5 and MIROC-ESM include parameterizations of the 1st and 2nd indirect effects, prognostic $N_d$ dependent on supersaturation as well as aerosol number and composition, and $r_e$ dependent on $N_d$ and cloud water mixing ratio (Watanabe et al. 2010, 2011; Takemura et al. 2005). MRI-CGCM3 and MRI-ESM1 similarly include the 1st and 2nd indirect effects, explicit treatment of aerosol activation into cloud droplets, and $r_e$ dependent on cloud droplet number density and cloud water (Yukimoto et al. 2012). IPSL-CM5A-LR, IPSL-CM5A-MR and IPSL-CM5B-LR include the 1st indirect effect but not the 2nd indirect effect, diagnose $N_d$ from total mass of water soluble aerosol, and $r_e$ from aerosol concentration (Dufresne et al. 2013; Hourdin et al. 2013).

Table 2 CMIP5 models used in the study, and their atmospheric resolutions and representation of $N_d$ and indirect effects

The CMIP time period analyzed differs from that of observations and reanalysis. With the exception of MIROC5 whose historical simulation reaches year 2012, the historical experiments in the models end in year 2005 and for consistency between models here we use a 10-year period 1996–2005, also avoiding large volcanic eruptions (like the Pinatubo eruption in 1992 that is parameterized in the MRI models). The Holohraun, Eyjafjallajökull and Vanuatu eruptions in the 2010’s are hence not included in the model simulations.

The grid-box average model L provided is divided by $f_c$, for consistency with in-cloud observations and estimates of $N_d$, cf. Jiang et al. (2012).

The model $N_d$ analyzed (cldncl) is the droplet number concentration at cloud top, considering liquid clouds only, and weighted by total liquid cloud fraction at each time step, before being averaged to a monthly mean. This is the droplet number measure that is available for the largest number of models, and is also most directly comparable to observations. A few models supply temporally evolving 3D-fields of $N_d$ (cdnc) and others provide only a vertically integrated droplet number concentration (cldnvi) that is inherently related to L, via cloud geometrical thickness.

2.4 Limitations to estimates of $\tau _a$, $N_d$ and L

As pointed out by e.g. Malavelle et al. (2017), MODIS $\tau _a$ is challenging as it is only retrieved under cloud-free conditions. This means that grid-box averaged $\tau _a$ values are calculated assuming that the cloud-free retrievals are representative for the entire grid box. This is standard procedure, (see e.g. Quaas et al. (2009), Bender et al. (2016)), but in cases of very large cloud cover, as frequently encountered over the mid-latitudes in winter, no $\tau _a$ retrievals can be made. MERRA-2 does not have this problem, but as MERRA-2 is nudged to satellite-observed $\tau _a$, corrected for swelling of aerosol near cloud, any residual MODIS $\tau _a$-issues may indirectly affect the MERRA-2 data.

On the other hand, we require a minimum cloud fraction of 80% for the $N_d$ retrievals to be considered valid (Bennartz et al. 2011). In addition, reliable $N_d$ retrievals cannot be made at high latitudes in winter months, because the low sun angle breaks the plane-parallel radiative transfer assumptions (Grosvenor and Wood 2014). The large $\theta$ afflicts also the MODIS L-retrievals, and for these reasons, the analyzed time series for the Iceland region exclude the monthly means for November through February for $\tau _a$ and $N_d$ as well as L.

2.5 Data aggregation issues

Aerosol influence on clouds span a range of spatiotemporal scales, and relations between relevant variables are scale-dependent (Bender et al. 2016; Konsta et al. 2016; Feingold et al. 2016).

Estimates of radiative forcing from aerosol–cloud interactions have also been found to vary depending on the spatial scale chosen in both models and observations, but in yet inconclusive ways (Grandey and Stier 2010; McComiskey and Feingold 2012; Possner et al. 2016).

In comparisons between models and observations, the differences in sampling and spatial and temporal resolution may introduce large biases, especially in attempts to evaluate models against point measurements. Such issues are discussed in detail by Schutgens et al. (2016).

The approach taken here is to aggregate data to a common spatial scale of regional averages, and a common temporal scale of monthly means. Spatio-temporal averaging reduces the influence of sampling errors (Schutgens et al. 2016), and allows for investigation of the ability of models to represent relations on observable and climatologically relevant scales.

3 Results

3.1 Regional characteristics

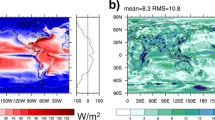
The focus regions listed in Table 1 are indicated in Fig. 1, also showing the 13-year average global distribution of $\tau _a$ from MODIS.

Fig. 1

Global ocean $\tau _a$ distribution, averaged from 2003 through 2015. Regions are (1) Iceland, (2) Vanuatu, (3) Hawaii, (4) US, (5) China, (6) Californian, (7) Peruvian, (8) Australian, (9) Namibian and (10), in all cases excluding land-covered grid points

Fig. 2

Observed monthly mean time series of albedo ($\alpha$), cloud fraction ($f_c$), aerosol optical depth ($\tau _a$), liquid water path (L), effective radius ($r_e$) and droplet number concentration ($N_d$) (corrected for climatological seasonal cycle) for three volcanic regions (Iceland, Vanuatu, Hawaii), two anthropogenically influenced regions (China, US) and five subtropical stratocumulus regions (Californian, Peruvian, Austalian Namibian, Canarian) as marked in Fig. 1. Total albedo (solid lines), clear-sky albedo (dashed lines) and cloud albedo (dotted lines) time series are shown separately, and L time series are shown for both MODIS (solid lines) and MAC (dashed lines). Eruptions of Kilauea (Hawaii) and Eyjafjallajökull and Holohraun (Iceland) are marked with grey in the left-most column. Corresponding time series for MERRA-2 (with SO$_4$ rather than $N_d$ and $r_e$) are shown in Supplementary Figure S2

Figure 2 shows regional mean time series of observed aerosol, cloud and radiation variables ($\alpha$, $\alpha _{cloud}$, $\alpha _{clear}$, $f_c$, $\tau _a$, L, $r_e$, $N_d$ ), over the same time period. There are several notable regional differences in absolute values and variability of both aerosol and cloud metrics.

3.1.1 Stratocumulus and anthropogenically influenced regions

The Sc regions are similar in dynamical cloud regime, and typically have high $f_c$ and low L, indicating thin clouds, which is also in agreement with the relatively low $\alpha _{cloud}$ in these regions. At the same time the regions differ in aerosol signature. The Canarian region, shows the greatest $\tau _a$ and $\tau _a$ variability, related to the dominance of desert dust and the $\tau _a$ is also high in the Namibian region, that has a comparatively strong signal of black carbon from biomass burning (cf. Frey et al. (2017)).

The anthropogenically influenced regions (US, China) have distinctively larger $N_d$ than the other regions. Their $r_e$ is also comparatively low, in particular in relation to the more remote volcanic regions. The $\tau _a$ is high, particularly for China. Both regions display decreasing trends in $\tau _a$ and $N_d$ during the given time period, consistent with emission reductions (Krotkov et al. 2016; Zhao et al. 2017; McCoy et al. 2018).

The MAC L estimates are typically higher than those from MODIS, which is likely in part related to MODIS retrieval biases in regions of broken clouds (Seethala and Hovath 2010; Cho et al. 2015).

3.1.2 Volcanic regions

For the Iceland region, $r_e$ drops at the time of the Holohraun eruption, as discussed in detail by McCoy and Hartmann (2015) and also confirmed by Malavelle et al. (2017). The MODIS and MAC L estimates agree well for this region, and neither of them indicate a peak at the time of the Holohraun eruption, in agreement with Malavelle et al. (2017). The spatial variability in L is large, however, and Malavelle et al. (2017) average over an area where positive anomalies in the south-west are balanced by negative anomalies in the north-east. Our Iceland domain is smaller, but still its average L does not show an increase during the months of September to October, when the volcanic emissions were at their peak (Schmidt et al. 2015). During the following winter months, most prominently December, see Figure S1, the MODIS data indicate an anomalously high L over the Iceland domain. This can not, however, be considered a reliable signal, due to the high $\theta$ biasing the few data points that are reported. The MAC-derived L, which is not afflicted with the same retrieval problems at high $\theta$ does not indicate a similar anomaly in L at the time of the eruption.

McCoy and Hartmann (2015) focus on the months of September–November, finding a negative $r_e$ anomaly that is more persistent in space and time. In that case the attribution to volcanic aerosol may rather be complicated by the fact that the flow pattern varies throughout the period, and is not consistently coincident with observed anomalies (see e.g. trajectory analysis in McCoy and Hartmann (2015)).

Despite the locally large L anomalies and the $r_e$ drop that appear during the time of the Holohraun eruption, no signal can be seen in $\alpha _{cloud}$ or $\alpha$, indicating that the actual radiative effect of the cloud property anomalies is weak. Corresponding drops in $r_e$ at the time of the eruptions of Eyjafjallajökull (Iceland March–June 2010) and Kilauea (Hawaii June–August 2008), the latter described by Yuan et al. (2012), Malavelle et al. (2017), are less marked and within the noise level of the monthly regional mean time series, and L peaks are not discernible at these points in time.

We note that Malavelle et al. (2017) convert the MODIS in-cloud L estimate to a grid-box average, which contributes to smaller L values than the in-cloud estimates shown here.

MERRA-2 explicitly includes eruptive volcanoes up until the end of 2010, but not later, and for degassing volcanoes, the pattern from year 2010 is repeated for the years following (Randles et al. 2016). Hence, in MERRA-2 data, a Holohraun effect is expected to be seen only as a response to assimilated $\tau _a$ observations, whereas Eyjafjallajökull and Kilauea aerosol emissions are explicitly included in the model. As in the observations, however, the effects are too localized in space and time to show in the monthly mean regional mean time series (Figure S2).

3.2 Correlations

We focus here on temporal correlations, i.e. the correlations between regional mean time series, corrected for a climatological seasonal variation. We emphasize again that correlation does not imply causation, and we also emphasize that correlations may be due to meteorological co-variation rather than driven by microphysics or cloud dynamics. The temporal correlation coefficients can indicate long-term co-variability as well as co-variations on shorter time scale that are frequent and uniform enough to create a signal in the monthly mean regional average, while lack of correlation can be indicative of a theoretical causal relation not being strong enough to protrude on the given scale. Spatial correlations, i.e. the correlations between temporally averaged latitude-by-longitude maps for each region may also be of interest, but more difficult to separate from meteorologically driven co-variability, in terms of persisting cloud regime differences within the regions chosen. For instance, spatial anti-correlations between aerosol and cloud properties in coastal regions may reflect near-land areas being more polluted (high $N_d$) and having thinner clouds (low L) because of local meteorology and transport respectively (Grosvenor et al. 2017).

Observations Figure 3 shows correlation matrices for observed monthly mean time series of $\alpha$, $\alpha _{clear}$, $\alpha _{cloud}$, $f_c$, $\tau _a$, L, $r_e$ and $N_d$ for each of the ten regions. As discussed in Sect. 2.4$\tau _a$, $N_d$ and L from MODIS are excluded for months November through February for the Iceland region.

Fig. 3

Observational correlation-matrices for albedo ($\alpha$), cloud fraction ($f_c$), aerosol optical depth ($\tau _a$), liquid water path (L), effective radius ($r_e$) and droplet number concentration ($N_d$). Temporal correlations of monthly mean, de-seasonalized time series for the period 2003–2015, with data from CERES, MODIS and MAC, respectively, are shown. Correlations significant at 95% confidence level (using a student t-test) are marked with an asterisk

Fig. 4

Reanalysis correlation-matrices for albedo ($\alpha$), cloud fraction ($f_c$), aerosol optical depth ($\tau _a$), liquid water path (L) and sulfate mass concentration (SO$_4$). Temporal correlations of monthly mean, de-seasonalized time series for the period 2003–2015, with data from MERRA-2 are shown. Correlations significant at 95% confidence level (using a student t-test) are marked with an asterisk

The observed correlations among macrophysical quantities are largely in agreement with expectations from previously established relations. The correlation between albedo and cloud fraction, $R(\alpha ,f_c)$, is strong and positive, confirming the first order dependence of albedo on cloud fraction (Cess 1976; Loeb et al. 2007; George and Wood 2010; Bender et al. 2011; Engström et al. 2015). $R(\alpha ,f_c)$ is stronger than $R(\alpha , \alpha _{cloud}$) or $R(\alpha ,\alpha _{clear})$ for instance, the former significantly positive for all regions, and the latter significant at the 95% level only in one region. $\alpha _{clear}$ has a significant positive correlation with $\tau _a$ in all regions except the Australian region.

The importance of L for $\alpha _{cloud}$ in Sc regions, discussed e.g. by Bender et al. (2016) and Frey et al. (2017), is confirmed by positive correlations $R(L, \alpha _{cloud})$ in all five Sc regions. $R(L,\alpha _{cloud})$ is further positive for all regions except with $L_{MAC}$ in the US region. $\alpha _{cloud}$ is here calculated based on the method derived in Bender et al. (2011) utilizing the near-linear dependence of $\alpha$ on $f_c$ on regional monthly mean scale.

The co-variation between satellite-retrieved $\tau _a$ and $f_c$ discussed in detail e.g. by Quaas et al. (2009), Gryspeerdt et al. (2016) and Christensen et al. (2017), but also Bender et al. (2016) and Neubauer et al. (2017), that is likely to be partly spurious, is manifest as positive $R(\tau _a,f_c)$ in all but one of the Sc and volcanic regions, but not in the anthropogenically influenced regions.

Fig. 5

Correlation L and $N_d$a in-cloud L and $N_d$from MODIS, b in-cloud L from MODIS and $N_d$ derived from MERRA-2 SO₄, c grid-average L from MAC and $N_d$ derived from MERRA-2 SO₄, d grid-average L from MERRA-2 and $N_d$ derived from MERRA-2 SO₄

Fig. 6

Spatial distribution of temporal correlation between L and $N_d$, for 8 CMIP5 models. De-seasonalized monthly means for 10 years are used for each model. As in Figs. 5c, d, L is here given as grid box average

Not unexpectedly, correlations involving microphysical parameters are more difficult to interpret. At constant L, $N_d$ can be expected to be closely negatively correlated with $r_e$. This is confirmed by temporal correlations between MODIS-derived $r_e$ and $N_d$, for all regions except China. On the other hand, $R(\alpha _{cloud},N_d)$, to which the 1st indirect effect is expected to contribute positively (more droplets leading to brighter clouds, given a constant L), is typically weak, significantly positive only in the Iceland, US and Peruvian regions. This is in agreement with the suggestion of a weak signal from the 1st indirect effect in satellite observations, made by Bender et al. (2016); there are simply too many other factors affecting cloud albedo for the influence of $N_d$ to come through on this scale. The link between $\tau _a$ and $N_d$ that is implicitly assumed by e.g. Bender et al. (2016) and found on global scale by Quaas et al. (2009), is also not conspicuous from the monthly and regional mean observational correlation matrix; $R(\tau _a,N_d)$ is positive for non-Sc regions, but not significant in Sc regions. This illustrates the influence of e.g. updrafts, cloud processes and humidity on $N_d$ and $\tau _a$ variation.

For a dominating 2nd indirect effect, considered in isolation, a positive correlation between $N_d$ and L is expected (more droplets leading to less rain and more L). However, none of the volcanic regions (Iceland, Vanuatu, Hawaii) show a significant correlation, which is consistent with the findings of Malavelle et al. (2017) that L is insensitive to $N_d$ variations in these regions. Correlations between L and $N_d$ are also mostly non-significant for the regions affected by anthropogenic aerosol (China, US); the US region displays a weakly positive $R(L,N_d)$ for $L_{MODIS}$, while China shows a weakly negative correlation with $L_{MAC}$. For L and $r_e$, correlations are also generally weak in these volcanic and anthropogenic aerosol regions, but Hawaii, China and US show positive correlations $R(L,r_e)$ for one of the L data sets.

Fig. 7

$R(L,N_d)$ for global observations, reanalysis and CMIP5 models as a function of vertical velocity. Solid black line relates MODIS L to MERRA-2 $N_d$, dashed lack line MAC L to MERRA-2 $N_d$ and dotted black line MERRA-2 L to MERRA-2 $N_d$, all binned by ERA $\omega _{500}$. Coloured lines relate model L to model $N_d$, binned by model $\omega _{500}$. Correlations have been averaged in bins of width 0.02 Pas$^{-1}$, and are displayed excluding bins containing less than 0.15% of the total number of cases

Fig. 8

Spatial distribution of temporal correlation between SO$_4$ and $N_d$, for 8 CMIP5 models. De-seasonalized monthly means for 10 years are used for each model

Fig. 9

Spatial distribution of temporal correlation between SO$_4$ and L, for 8 CMIP5 models. De-seasonalized monthly means for 10 years are used for each model

Turning to the Sc regions, Fig. 3 shows that $R(L,r_e)$ is consistently positive and $R(L,N_d)$ is negative, with the exception of the Australian region where $R(L,N_d)$ is not significant, and the Canarian region that shows a significant negative $R(L,N_d)$ only for $L_{MAC}$. The negative R(L, Nd) and positive $R(L,r_e)$ in these regions is contrary to the expectation from a dominating 2nd indirect effect. Wood (2007) has shown that the suppressed precipitation is in competition with enhanced entrainment in the Sc regions, and found that the sign of the L response to aerosol is dependent on environmental conditions including ambient humidity and stability as well as time scale. Other previous studies that have sought a causal explanation for a negative co-variation, such as that found here, have suggested competing effects of precipitation on cloud-top entrainment and sub-cloud mixing (Stevens and Feingold 2009), and increased cloud top cooling in optically thicker clouds leading to enhanced entrainment (Neubauer et al. 2017).

Replacing $L_{MODIS}$ with $L_{MAC}$ apparently changes the picture only slightly for the Sc regions, whereas the differences are somewhat more noticeable for the volcanic and anthropogenically influenced regions. Figure 3 also gives an indication of the general level of agreement between the two L data sets; $R(L_{MODIS},L_{MAC})$ is positive in all regions with values of 0.5 and above.

The emerging correlations are not primarily determined by the presence of volcanic aerosol during parts of the period studied. Exclusion of the months with volcanic eruptions, marked in the time series in Fig. 2, makes marginal difference to the correlation matrices; there are no changes of correlation signs in the affected regions, supplementary Figure S3), although, the positive correlation $R(a_{cloud},N_d)$ and $R(\tau _a,\alpha _{clear})$ in Iceland, is lost when volcano-years are excluded.

Reanalysis Correlation matrices based on MERRA-2 reanalysis are displayed in Fig. 4, and show some interesting differences from the observational correlations. Contrary to the satellite observations and the findings by Bender et al. (2016) and Frey et al. (2017), $R(L,\alpha _{cloud})$ is not significantly positive in any of the ten regions, but actually negative for Iceland, Vanuatu, China, Peruvian and Namibian. $R(L,f_c)$ is also in contrast with observations negative for all regions. This bias does not appear for MERRA-2 grid-box average L and hence these discrepancies involving L may be related to biases in the MERRA-2 $f_c$, used to calculated in-cloud L.

$R(\tau _a,f_c)$ is not pronounced here as in the satellite observations; the correlations are in some cases positive and in some cases negative, consistent with this correlation stemming from the near-cloud aerosol swelling, that biases observations but is corrected for when assimilated into the reanalysis (Randles et al. 2016; Chin et al. 2002).

$N_d$ is not available from MERRA-2, and as described in Sect. 2.2, we use MERRA-2 SO$_4$ as proxy for the droplet number concentration. $SO_4$ is positively correlated with $\tau _a$ for all regions, but $R(\alpha _{cloud},SO_4)$, to be compared with the observed $R(\alpha _{cloud},N_d)$, is generally weak. Correlations are significantly positive only in the Iceland region, while negative for Hawaii and China. Hence, as in the case of satellite observations, the correlations do not support a dominating 1st indirect effect on this temporal and spatial scale. With no parameterized coupling between aerosol and cloud microphysics in MERRA-2 this insensitivity to aerosol concentration is not unexpected.

Similarly, $R(L,SO_4)$ is generally weak. Significant negative correlations are seen in the Iceland and Australian regions, and positive correlations in the China and Vanuatu regions. Hence, taking SO$_4$ as a proxy for $N_d$, the observational negative correlations $R(L,N_d)$ in several of the Sc regions are not reproduced in the MERRA-2 data set. Again, lacking a parameterized aerosol–cloud coupling in MERRA-2, a weak correlation between aerosol ($SO_4$) and cloud (L) is not unexpected.

Excluding specific volcano-months (see markings in Fig. 2 time series) makes marginal difference with MERRA-2. Negative correlations between L and $\alpha$ and $\alpha _{cloud}$ respectively are lost when specific volcano-affected months are excluded (Figure S3).

Models We now compare the observational and reanalysis based correlation matrices with those from the CMIP5 models listed in Table 2. Correlation matrices for each of the models are found in Supplementary Figures S4–S11.

Differences from observations are particularly related to microphysical quantities, and specifically include the relations $R(N_d,r_e)$, $R(a_{cloud},N_d)$ and $R(L,N_d)$.

Contrary to observations, $R(N_d,r_e)$ is strongly positive for all regions in IPSL-CM5A-LR, IPSL-CM5A-MR and IPSL-CM5B-LR. For these models $r_e$ is a function of aerosol mass concentration (Hourdin et al. 2013). In the MRI models on the other hand, $R(N_d,r_e)$ is negative throughout when significant, and in the MIROC models slightly more variety is seen. These model families, as opposed to the IPSL models, parameterize $r_e$ as a function of droplet number concentration and liquid water content, which gives a more realistic $r_e$ estimate. The geographical distribution of $N_d$ is in general agreement among all the models, but the IPSL models are the only ones that display a global scale positive correlation $R(N_d,r_e)$ (not shown), rendering their $r_e$ estimates less trustworthy.

$R(\alpha _{cloud},N_d)$ is in many cases positive when significant, but there are several exceptions. MIROC5 shows negative $R(\alpha _{cloud},N_d)$ for the Vanuatu, Hawaii, Californian and Namibian regions, and IPSL-CM5B-LR for Iceland and Australian and IPSL-CM5A-MR for Californian, Australian and Iceland and IPSL-CM5A-LR for the Californian, Australian and Namibian regions. From the parameterized cloud albedo effect in the models, a positive correlation between $N_d$ and $\alpha _{cloud}$ is expected, as was also confirmed by Bender et al. (2016), but it is clear that this relation does not necessarily come through with the simple correlation approach taken, as many factors, not least L, influence the co-variation. Even for $R(\alpha _{cloud},\tau _a)$, that offers a more direct comparison with Bender et al. (2016), negative values are seen for the Namibian region in IPSL-CM5A-MR, for the US region in IPSL-CM5B-LR, the Namibian region in MIROC5, the Vanuatu region in MIROC-ESM and China and the Australian region in MRI-fixed.

The procedure in Bender et al. (2016), accounting for both seasonal and regional co-variability and investigating $\tau _a$-related albedo-variation at a given cloud fraction can better distil the actual aerosol-$\alpha _{cloud}$ coupling than mere correlations. Another caveat is that here we are using monthly mean data to calculate a monthly resolved cloud albedo, rather than producing an average value for a longer period, as originally done by Bender et al. (2011). Each regional mean cloud albedo value is hence based on albedo and cloud fraction observations in as many data points as there are grid boxes in the region, i.e. significantly fewer points than available for a temporal mean $\alpha _{cloud}$ calculation. Further, the condition of linearity between albedo and cloud fraction, and hence the cloud albedo estimate, is most reliable in the Sc regions, cf. Bender et al. (2011).

For consistency with MERRA-2 we also add in $SO_4$ in the model correlation matrices. We note that the sulfate mass measures are not the same in models and reanalysis; MERRA-2 $SO_4$ represents mass concentration ($\upmu \hbox {gm}^{-3}$) and CMIP5 $SO_4$ the integrated mass loading (kg m$^{-2}$), but surface and column sulfate can be expected to be tightly correlated. $R(SO_4,N_d)$ is typically positive, in models with diagnostic as well as prognostic $N_d$, and so is $R(\tau _a,SO_4)$.

The correlation $R(L,N_d)$ that in observations is found to be negative for Sc regions, and in other regions weaker and varying in sign, varies among models as well. For the IPSL models, which in contrast with the other studied models do not include the 2nd indirect effect, negative correlations appear in the Californian region (CM5A-LR, CM5A-MR), and positive correlations are seen for Hawaii and Peruvian (CM5A-LR, CM5A-MR, CM5B-LR), Iceland (CM5A-LR, CM5B-LR), China (CM5A-LR, CM5A-MR) and US, Namibian, Canarian regions (CM5B-LR).

MIROC5 produces negative $R(L,N_d)$ in the Californian, Australian and Canarian regions, and also for the Iceland, Vanuatu and Hawaii regions. MIROC-ESM on the contrary has weaker correlations, significantly positive only for the Vanuatu, Hawaii and Californian regions. MRI-CGCM shows significant negative correlations in the Vanuatu and US regions, and positive $R(L,N_d)$ in the Namibian and Canarian regions. This is similar to MRI-ESM1 which has negative $R(L,N_d)$ in Vanuatu and US, and positive $R(L,N_d)$ in the Peruvian, Namibian and Canarian regions. For MRI-fixed the picture is somewhat changed; correlations are negative for the Hawaii, US, Californian and Australian regions.

3.2.1 Global distribution of $R(L,N_d)$

The variation in $R(L,N_d)$ between the selected regions supports previous studies that have indicated that the susceptibility of cloud water to changes in aerosol, $dln(L)/dln(N_d)$, varies between geographical regions (Quaas et al. 2009) in response to variations in environmental regimes in terms of, for example, humidity, stability and the occurrence of precipitation (Michibata et al. 2016; Neubauer et al. 2017). We here look further at the $R(L,N_d)$ and its geographical distribution and relation to dynamical regime.

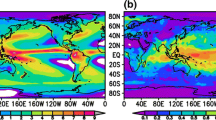
Figure 5a shows that with MODIS $N_d$ and L, $R(L,N_d)$ is positive in large areas, especially at mid-latitudes, while near-coast areas, particularly the subtropical Sc regions, display negative correlations, as also seen in the correlation matrices (Fig. 3). The MODIS $N_d$ has limited spatial coverage due to the restriction to $f_c>$80% and unreliable retrievals at high $\theta$ (see Sect. 2.1). Here we set a threshold value so that at least 70% of the points in the monthly mean time series at each grid point must be valid, for a correlation to be calculated. This can be compared with the correlation matrices (Sect. 3.2), where larger regional means are used, and correlations can be defined even in areas that are here screened out.

Following McCoy et al. (2017), we use MERRA-2 SO$_4$ to derive a global gridded $N_d$-approximation. The temporal correlation between this $N_d$-proxy ($N_{dMERRA}$) and L derived from MODIS is shown in Fig. 5b. The general pattern of negative correlations at low latitudes and positive correlations at high latitudes are in agreement with the results of Michibata et al. (2016) for both precipitating and non-precipitating clouds, with $N_d$ calculated from gridded MODIS $\tau$ and $r_e$. As in the case of L and $N_d$ both derived from MODIS (Fig. 5a) there is, however, indication that the Sc regions, display negative correlations.

In Fig. 5c, the correlation distribution is shown for N$_{dMERRA}$ and $L_{MAC}$, but the MAC L is in this case grid-averaged rather than in-cloud, i.e. L is not divided by $f_c$, which means it is sensitive to changes in cloud coverage as well as cloud thickness. As seen earlier, the conversion to in-cloud L gave rise to some biases in the comparison with observations. The $L_{MAC}$ estimate also includes broken or scattered clouds in which the MODIS cloud property retrieval is limited, but the picture for $R(L_{MAC},N_{dMODIS})$ is consistent with $R(L_{MODIS},N_{dMERRA})$ (Fig. 5b).

Figure 5d shows the correlation between MERRA-derived $N_d$ and MERRA grid-averaged L, and it is clear that compared to the observational and combined observation-reanalysis distributions of $R(L,N_d)$, the pure reanalysis correlations are weaker and show a much less pronounced pattern. As before, MERRA-2 can be seen as a “no-indirect-effect” reference, and hence this difference suggests that meteorological factors alone, without microphysical coupling between aerosols and clouds, are not sufficient for producing the observed relations between L and $N_d$.

The CMIP5 models display great variation in geographical distribution of $R(L,N_d)$, see Fig. 6. Several of the models show a region of strong positive correlations over the Southern Ocean, leading to a much more pronounced latitudinal gradient than in observations. In the IPSL models and MIROC-ESM strong positive correlations are also found over the tropics, in a way that is not supported by observations. With the exception of the two MIROC models, particularly MIROC5, the observational pattern of negative correlations over the subtropical stratocumulus regions is reversed, with pronounced positive correlations over these regions in the IPSL and MRI models. As stated previously, MRI ESM and MRI CGCM3 have a documented error in their $N_d$-parameterization, and for comparison we also show results for MRI-fixed. It is clear that this reduces the strong sensitivity of L to $N_d$ in the Sc regions, and in terms of magnitude of correlation coefficient, MRI-fixed shows the best general agreement with observations, whereas the other models typically overestimate the magnitudes (the colour scale is the same for Figs. 5 and 6.) IPSL-CM5A-LR and IPSL-CM5A-MR are as expected very similar, but IPSL-CM5B-LR shows a quite different pattern with positive correlations between L and $N_d$ nearly everywhere. Neither of the IPSL models include the 2nd indirect effect, and hence in these cases the correlation between $N_d$ and L is not driven by a lifetime effect, but is affected by the differences in physics that distinguish the IPSL-CM5A and IPSL-CM5B models (see Sect. 2.3). MIROC5 in contrast shows largely negative correlations, with exceptions of the high latitude oceans and regions of continental outflow, like China. Michibata et al. (2016) show that MIROC5 has a positive L to $N_d$ susceptibility more or less globally, but this result can only be reproduced if cloud-top $N_d$ is replaced with vertically integrated $N_d$ (see Sect. 1 for CMIP5 variable definitions), in which case variations in cloud-geometrical thickness result in a positive correlation between $N_d$ and L globally. MIROC5 here also shows some indication of local negative maxima coinciding with Sc regions, which is in line with the observational pattern. Although the two MIROC models share the same aerosol model, their separate cloud schemes give rise to pronounced differences in the relation between L and $N_d$.

To investigate a possible dependence of aerosol–cloud interaction on meteorological regime, adding to the findings of environmental regime dependence by Michibata et al. (2016), Zhang et al. (2016) and Neubauer et al. (2017), we investigate the dependence of $R(L,N_d)$ to vertical velocity in the upper troposphere.

Figure 7 shows the correlation $R(L,N_d)$ as a function of vertical velocity at 500 hPa, $\omega _{500}$. Relating MODIS and MAC L respectively to MERRA $N_d$, $R(L,N_d)$ is weakly positive at moderate ascent and subsidence. Stronger ascent around the Intertropical Convergence Zone (ITCZ) coincides with negative correlations, which may be an effect of efficient aerosol removal by precipitation. For these cases, however, McCoy et al. (2017), McCoy et al. (2018) do not offer a validation of the relation between SO$_4$ and $N_d$, and they are also less frequently occurring than the large areas of weak ascent and positive correlations over the Southern Ocean. Similarly, subsidence regions (including the Sc regions) partly coincide with negative correlations for both MODIS and MAC L. For most cases of stronger subsidence (corresponding to areas in the subtropics and mid-latitudes, of which the Sc regions are only a small part), correlations go to zero for MODIS but are positive for MAC L.

The $R(L,N_d)$ for MERRA-2 are overall small, suggesting that L-$N_d$ correlations arising from meteorology alone, with no indirect effects will introduce only small uncertainties in the correlations.

The CMIP5 models typically show stronger correlations, when binned in the same way by the model vertical velocity at 500 hPa. None of the models reproduce the weak correlations that observations and reanalysis indicate, and the patterns are also quite different from that seen in observations.

In agreement with Zhang et al. (2016) who studied L sensitivity to concentration of cloud condensation nuclei in a different set of GCMs, the model diversity is largest in regions of strong ascent (negative $\omega _{500}$), where correlations range from strongly positive (IPSL-CM5A) to strongly negative (MIROC5). Aerosol-cloud interaction in convection is not represented in the models, and to the extent $N_d$-L relations in these clouds are driven by such interactions a certain dis-agreement with observations is expected. As biases are both negative and positive it is not clear in which direction the lack of aerosol-aware convection affects the correlation.

It is interesting to note the close agreement between the two IPSL-CM5A models, that differ only in resolution, and their difference from the third IPSL model, that has different model physics, including convection representation. Noteworthy is also the agreement between the MRI models (MRI-CGCM3, MRI-ESM1 and MRI-fixed), where the correction of the $N_d$-related error appears to lead to somewhat weaker $R(L,N_d)$, especially in subsidence regions. The two MIROC models on the other hand have quite different behaviours. While MIROC-ESM largely shows positive correlations, MIROC5 almost exclusively shows negative correlations, although both MIROC models have cloud schemes including a dependence of autoconversion rate on the droplet spectrum. The IPSL models on the other hand do not have a parameterized dependence of rain rate on $N_d$ (2nd indirect effect), and the relatively strong correlations at all $\omega _{500}$-values in IPSL-CM5B-LR and at the limits of the displayed $\omega _{500}$ range for IPSL-CM5A cannot be ascribed to cloud lifetime effects.

3.2.2 Global distribution of $R(SO_4,N_d)$

McCoy et al. (2017) and McCoy et al. (2018) have demonstrated the usefulness of SO$_4$ as a predictor of $N_d$, in a range of regions, and on daily to decadal time scale. The correlation between SO$_4$ and $N_d$, combining satellite observations and MERRA-2 reanalysis is hence positive. Among the CMIP5 models we also find $R(SO_4,N_d)$ to be predominately positive in the ten focus regions. Figure 8 shows the global distribution of this correlation, indicating that positive correlations dominate globally for the MIROC and MRI models, the most striking exception being the negative correlations at $30^{\circ }\hbox {S}$ in MIROC5. There is a clear distinction between these model families, that have prognostic $N_d$, and the IPSL models with diagnostic $N_d$, where $R(SO_4,N_d)$ is weak and varying in sign. The corresponding linear regression coefficient of the relation $dlog(N_d)/dlog(SO_4)$, as quantified in McCoy et al. (2017), is shown in Figure S12.

In the MIROC and MRI models, $N_d$ further affects the autoconversion rate implying a link between SO$_4$ and L, and Fig. 9 displays the geographical distribution of $R(L,SO_4)$ that for these models can be compared to the observational $R(L,N_d)$ in Fig. 5. The agreement between models and observations is not particularly improved, although the elimination of $N_d$ dampens the spuriously strong L-sensitivity in the Sc regions in MRI-ESM1 and MRI-CGCM. For the IPSL models, where $N_d$ does not respond to SO$_4$ changes, and $R(L,SO_4)$ is weak.

4 Discussion

4.1 Model representation of $N_d$

$N_d$ is a central parameter in aerosol–cloud interactions, but in global models, its representation and relation to other variables is quite varying. Although $N_d$ is mostly positively correlated with SO$_4$ (supporting McCoy et al. (2017)) in the models where $N_d$ is a prognostic function of aerosol and supersaturation, this is not the case for models with diagnostic $N_d$. Further, the susceptibility $dlog(N_d)/dlog(SO_4)$ for column integral SO$_4$ varies largely between models and between regions, in contrast with what McCoy et al. (2017) showed for $N_d$ from satellite observations and surface level SO$_4$ mass concentration from reanalysis.

Technically, the model $N_d$ is also problematic to compare with observations. While a few models supply temporally evolving 3D-fields of $N_d$, others provide only a vertically integrated droplet number concentration. Here we utilize the droplet number concentration at cloud top, considering liquid clouds only, which is the measure that we consider most directly comparable to observations, and that is available for the largest number of models, which is, however, limited to seven. Given the importance of $N_d$, its representation in models as well as its requirement as an output field in model intercomparison projects should be considered more carefully.

$N_d$ has specific issues in the two MRI models MRI-CGCM3 and MRI-ESM1. In the AMIP simulation with corrected $N_d$-parameterization (MRI-fixed) the pattern of $R(L,N_d)$ is similar to that of the MRI-CGCM3 and MRI-ESM1 but with weaker positive correlations in the subtropics. By-passing the $N_d$-parameterization, i.e. analyzing $R(L,SO_4)$ instead of $R(L,N_d)$ has a similar effect in the MRI models. In general, however, discrepancies between models and observations in $R(L,N_d)$ cannot be solely attributed to mis-representation of the relation between SO$_4$ and $N_d$; replacing $R(L,N_d)$ with $R(L,SO_4)$ does not particularly improve the agreement with observations.

Models typically determine $r_e$ as a function of $N_d$ and L, see e.g. Peng and Lohmann (2003). This is the case for the MRI and MIROC models, but in the IPSL models $r_e$ is dependent on aerosol concentration, yielding positive correlations between $N_d$ and $r_e$, rather than the observationally supported negative correlations seen in MRI and largely in MIROC models.

Based on different observational estimates, Quaas et al. (2009) show positive coefficients between $N_d$ and $\tau _a$ on global scale, but we find that $\tau _a$ is not positively correlated with $N_d$ in all focus regions in MODIS observations. Significant positive correlations are seen for all the volcanic and anthropogenic regions except Vanuatu, but for the Sc regions, no correlations are significant. On the other hand, in MERRA-2, $\tau _a$ is consistently positively correlated with SO$_4$, which can arguably be used as an $N_d$ proxy. In the models, $R(\tau _a,SO_4)$ is typically positive whereas $R(\tau _a,N_d)$ varies more in sign in the different regions.

Ekman (2014) showed that models with an explicit parameterization of $N_d$, as a function of aerosol as well as supersaturation, better reproduce observed temperature trends, while the inclusion of aerosol effects on precipitation formation was a less useful determiner of model skill. We see that the MRI and MIROC models produce a more realistic SO$_4$-Nd relation, assuming that the positive correlation between $N_d$ and SO$_4$ described by McCoy et al. (2017) is realistic, but otherwise no clear distinction in model skill can be easily made based on the level of sophistication of aerosol–cloud interactions.

4.2 $R(L,N_d)$ as indicator of the 2nd indirect effect

A striking result is that in the Sc regions observed L is rather consistently negatively correlated with $N_d$ and positively with $r_e$, both spatially and temporally. This is contrary to what may be expected from a dominance of the 2nd indirect effect (Albrecht 1989) where more, smaller droplets would prevent rainfall and lead to greater L.

Wood (2007) points at the competition between effects on precipitation and entrainment of dry air from above in determining the L-response to aerosol changes in stratiform clouds. Stevens and Feingold (2009) have suggested that counteracting effects of enhanced cloud-top entrainment and reduced sub-cloud mixing in response to suppressed precipitation may lead to a net cloud thinning. Negative correlations in the given Sc regions may also be related to the fact that these clouds typically give rise to little precipitation, limiting the effects of precipitation suppression. Negative susceptibility of L to aerosol in non-raining regions has been suggested to be related to enhanced entrainment due to decreased droplet sedimentation when cloud droplets are smaller (Bretherton et al. 2007; Small et al. 2009; Chen et al. 2015; Neubauer et al. 2017). Neubauer et al. (2017) also suggest that improved representation of cloud-top entrainment could reduce the L-susceptibility in unstable and/or dry regions in models.

Compared to the observations, the models show more variability and more positive values for the correlation between L and $N_d$, particularly in the Sc regions. The model that best reproduces the observed negative correlations $R(L,N_d)$ in Sc regions is MIROC5. This model has the same parameterized dependence of autoconversion rate on droplet number concentrations as MIROC-ESM, based on Berry (1968), but unlike MIROC-ESM, MIROC5 still produces negative correlations in three Sc regions, and also in the three volcanic regions.

Quaas et al. (2009) previously questioned the implementation of the lifetime effect only through autoconversion, as did Michibata et al. (2016). Wang et al. (2012) rightly emphasize that many cloud dynamical feedbacks that are not included in climate models affect cloud fraction, water content, and lifetime. From our analysis, although the differences in sensitivity between models, observations and reanalysis suggest that models have too strong L–$N_d$ links for the specific studied regions, it is not clear that parameterized dependence of autoconversion on $N_d$ directly leads to exaggerated positive $R(L,N_d)$.

In MIROC5 and MIROC-ESM that share the same aerosol scheme and the same autoconversion scheme, quite different patterns of $R(L,N_d)$ appear. Hence other differences between their cloud schemes are more decisive in this relation than the autoconversion parameterization. Michibata and Takemura (2015) compare different autoconversion schemes, finding high L-sensitivity to the scheme used, but also pointing at other common factors, including too large dependence on autoconversion in diagnostic rain schemes, as causing biases. Neubauer et al. (2017) show, by comparing a prognostic and a diagnostic precipitation scheme, that overestimation of $N_d$-dependent autoconversion is not the primary reason for overestimated L-susceptibility in their model. Based on the argument that cloud top entrainment competes with suppressed precipitation (Wood 2007), MIROC5 seems to better capture this entrainment process than MIROC-ESM. Noting that MIROC5 uses fewer vertical levels than MIROC-ESM (see Table 2) this is not due to better vertical resolution.

Even models that do not parameterize the 2nd indirect effect by relating rain formation to droplet number concentration, in particular IPSL-CM5B, show positive correlations $R(LWP,N_d)$ in several areas. Hence positive correlations $R(L,N_d)$ may have other origins than increased cloud lifetime as prescribed by the 2nd indirect effect, related to meteorology or other aerosol–cloud interactions. For example, Wilcox (2010), Wilcox et al. (2016) propose dynamical pathways for increased L at higher loading of absorbing aerosol, through suppressed turbulence in the boundary-layer and reduced entrainment of dry air from above in response to the aerosol-induced changes in stability.

For MERRA-2 there is no parameterized aerosol–cloud interaction and no $N_d$ estimate. $R(L,SO_4)$ is used as a proxy for $R(L,N_d)$, resulting in correlations that are neither as negative as seen for observations in the Sc regions, or as positive as seen in many cases in the CMIP5 models. This indicates that in reality microphysical or small-scale dynamical couplings not included in the reanalysis play a role, but that in models these processes are not correctly represented.

Investigating the dependence of the 2nd indirect effect on ambient meteorological conditions, Neubauer et al. (2017) found that their model is less sensitive to environmental regimes than what is suggested by observations. Michibata et al. (2016) found that their model produced positive susceptibility of L to $N_d$ regardless of environmental regime, but this appears to be related to the dependence of both L and vertically integrated $N_d$ on cloud geometrical thickness, rather than a microphysical coupling between $N_d$ and L. We find that $R(L,N_d)$ varies with larger amplitude with varying upper tropospheric vertical velocity in models than in observations, but that reanalysis has yet weaker dependence on dynamical regime, again using SO$_4$ to approximate $N_d$ variations, and again indicating that the lack of aerosol–cloud coupling in the reanalysis can underestimate the observed correlations between L and $N_d$.

5 Concluding remarks

We study relations between several macro- and microphysical cloud and aerosol properties, in a range of regions with different characteristics in terms of meteorology and aerosol loading. An ensemble of coupled climate models is compared to satellite observations and reanalysis, where the latter assimilates aerosol optical depth as well as meteorological fields but does not parameterize a microphysical coupling between aerosols and clouds. Hence models can be evaluated against the observed state and a reference case with no prescribed aerosol–cloud interactions.

Some general differences between categories of regions can be seen; e.g. the US and China regions, representing dominance of anthropogenic aerosol, show decreasing trends in $\tau _a$ and $N_d$ over the period 2003–2015, and also larger $N_d$ and smaller $r_e$ than the Iceland, Vanuatu and Hawaii regions, representing influence from volcanic aerosols. The Iceland region is different from the two other volcanic regions as degassing does not provide a strong source of SO$_2$, and the region is not as remote, and hence more influenced by anthropogenic aerosol than Vanuatu and Hawaii.

Our observational data analysis confirms previous findings of decreases in $r_e$ in association with an eruptive volcanic event in Iceland (McCoy and Hartmann 2015; Malavelle et al. 2017). At the time of the Holohraun eruption in 2014–2015, satellite observations also indicate large local variations in L, but their spatial and temporal extents are not in agreement with the peak emission time and transport direction from the eruption, and neither MODIS nor MAC indicate a regional mean L-signal co-incident with the emission of volcanic aerosol. The $r_e$-anomalies too are spatially and temporally confined, and the cloud property changes do not result in discernible signals in $\alpha _{cloud}$ or $\alpha$. Temporal correlations in the volcanically influenced regions are found to be insensitive to the inclusion or exclusion of specific periods affected by volcanic eruptions.

In observations, several correlation combinations of macrophysical properties confirm expected relations among cloud, aerosol and radiation quantities, with which models can be compared. For instance, observations show that $f_c$ variability is closely related to variation in $\alpha$, and that L co-varies with $\alpha _{cloud}$. Models typically agree with observations in these cases, yielding positive $R(f_c,\alpha )$ and $R(L,\alpha _{cloud})$ with few exceptions.

Observational $f_c$ and in-cloud L are positively correlated in all regions, whereas the calculated in-cloud L in reanalysis and models is in several cases negatively correlated with $f_c$. Correlations are generally not sensitive to the choice of L (MAC or MODIS), particularly in the Sc regions where both can robustly perform retrievals, and the two L data sets are consistently positively correlated in all regions.

$R(\alpha _{cloud},N_d)$, which may be seen as an indicator for the 1st indirect effect, is weak in observations, indicating that droplet number is not the primary driver of the variation in cloud albedo. Given the numerous dynamical and meteorological processes acting simultaneously, the 1st indirect effect can hardly be expected to be seen as acting in isolation. In models, however, $R(\alpha _{cloud},N_d)$ is in many cases positive, consistent with the parameterization of the 1st indirect effect. Still, there are also cases of weak and negative correlations, even in the Sc regions where previous studies have found that the cloud brightening in models is strong (Bender et al. 2016), and we emphasize that the monthly resolved $\alpha _{cloud}$ estimate used in the present study must be interpreted with discretion.

$R(L,N_d)$ in observations is positive for large areas of the globe, but conspicuously negative for Sc regions, contrary to the expectation from the 2nd indirect effect, and this is not well captured by models. Counteracting effects of entrainment in response to aerosol variations may explain the negative correlations, and meteorologically driven co-variation between aerosol and cloud properties always remains a possible cause of the relations seen (see e.g. Toll et al. 2017), but still model-produced relations in many ways differ from those observed. The global geographical distribution of $R(L,N_d)$ is in poor agreement with observations for all models, and the variation in $R(L,N_d)$ with dynamical regime is much stronger in models than in observations and reanalysis. Hence we can make a more general comparison of sensitivity of cloud water to aerosol amount, in models, observations and reanalysis. Both geographical distribution of $R(L,N_d)$ and $R(L,N_d)$ as a function of vertical velocity give a picture of reanalysis (no parameterized aerosol–cloud interaction) showing weak correlations, models (parameterized aerosol–cloud interaction) strong correlations, and satellite observations somewhere in-between. In other words, it appears that microphysical aerosol–cloud interactions contribute to the relations seen on larger scale, but that in models these relations may be too dominant. We do not, however, find support for this being caused directly by a too strong link between L and $N_d$ through autoconversion, as suggested by e.g. Quaas et al. (2009) and Michibata et al. (2016). Models without autoconversion dependence on $N_d$ (three IPSL models) create positive correlations $R(L,N_d)$ and models with the same parameterization of that link (two MIROC models) create different patterns of $R(L,N_d)$. Along these lines, Michibata and Takemura (2015) also suggest that not only microphysics parameterizations need to be improved for models to better represent the relations between clouds, precipitation and radiation.

Our results with consistent non-zero correlations $R(L,N_d)$ for the Sc regions also challenge the view that L should not respond to aerosol at all (Malavelle et al. 2017). Co-variations are clearly region-dependent, and more work remains to be done to understand the counteracting processes on water content, and to what extent they dampen the microphysical response to aerosol, in different aerosol and meteorological regimes.

Although representation of large scale effects of aerosol–cloud interactions in agreement with observations is a necessary condition for a trustworthy model, it is not sufficient for constraining model estimates of aerosol forcing, not least due to the vast number of possible model configurations that can pass the test of agreeing sufficiently well with PD observations (Lee et al. 2016; Johnson et al. 2018). The presented correlation-based approach is a method for model evaluation and points out variations in performance among the tested models.

It is clear from our results, as well as from previous studies, that individual aerosol–cloud interaction pathways do not dominate the relations between variables across regional and temporal scales (Stevens and Feingold 2009; Rosenfeld et al. 2014; Bender et al. 2016). Our contribution here is an evaluation of emerging correlations, microphysics, macrophysics and meteorology taken together, in satellite observations, in reanalysis with no modelled aerosol–cloud interactions, and in global models, and thereby a way of testing models and pointing at ways of improving their performance.