1 Introduction

The Earth’s climate system and its components, including the atmosphere, oceans and sea ice, are a complex adaptive system that can exhibit multiple equilibria over a wide spectrum of characteristic spatial and temporal scales (Dijkstra 2013; Serreze and Barry 2014). Nonlinear geophysical fluid dynamics that govern the motion of climate system components can lead to the emergence of quasi-stationary flow regimes in the form of persistent or recurrent large-scale modes or patterns. Weather regimes are examples of such flow regimes that are manifested as particular atmospheric conditions on a regional scale with time scales roughly on the range of 10–100 days (Reinhold and Pierrehumbert 1982; Barnston and Livezey 1987; Vautard and Legras 1988; Ghil and Robertson 2002). The application of the concept of weather regimes in the analysis of mid- and high-latitude synoptic systems has provided us with a deeper understanding of intrinsic climate variability (Molteni et al. 1990; Michelangeli et al. 1995; Cassou et al. 2004; Guemas et al. 2009), with potential benefits to weather and climate prediction capability (Mo and Ghil 1988; Brankovic and Molteni 1997; Cassou 2008; Riddle et al. 2013) and possibly to long-term climate change (Corti et al. 1999).

A set of preferred circulation patterns is also identified in other atmospheric phenomena, such as the monsoon systems around the globe that can be represented through the prism of active and break phases (Jones and Carvalho 2002; Goswami 2005; Taraphdar et al. 2010; Cook et al. 2012; Meehl et al. 2012). Also, a spectrum of tropical and mid-latitude regimes of cloud variability has been determined by clustering methods (Jakob and Tselioudis 2003; Gordon et al. 2005; Cheruy and Aires 2009; Gordon and Norris 2010). The ocean circulation, with dominant wind-driven elements, also exhibits coherent flow regimes in dynamic regions such as the Antarctic circumpolar current and the Kuroshio extension (Hughes 2005; Qiu and Chen 2005).

Sea ice circulation, which is primarily driven by surface winds and upper-ocean currents (Lepparanta 2011), also has the potential to exhibit regime behavior. Sea ice thickness (SIT) is an integrating medium of the surface ocean and atmosphere conditions: it has the capability to contain climate information on time scales longer than seasonal (Blanchard-Wrigglesworth et al. 2011; Chevallier and Salas y Mélia 2012; Guemas et al. 2014b). Fučkar et al. (2016) extended the conceptual framework of recurrent large-scale modes to the sea ice system and identified modes of the northern hemisphere (NH) sea ice cover variability that persist from intraseasonal to interannual time scales. They applied the K-means clustering technique (Hastie et al. 2009; Wilks 2011) on SIT from a forced historical reconstruction of global sea ice cover (based on the approach in Guemas et al. 2014a) over the 1958–2013 period to determine three optimal modes or clusters of variability of the NH SIT, and the associated time series of cluster occurrences. Particularly the dynamics and distribution of multi-year ice strongly depend on surface wind patterns, which opens the possibility of imprinting of the high- and mid-latitude winter surface conditions onto the sea ice system.

In this study we examine the prediction skill of these three NH SIT modes in a state-of-the-art coupled climate forecast system. We aim to determine a hierarchy in quality of dynamical and statistical forecast systems for the NH SIT modes, representing predictable aspects of the Arctic sea ice system on monthly and longer time scales, based on a suite of prediction skill indices. The rest of the manuscript is structured in the following way. Section 2 briefly describes the historical reconstruction of sea ice cover (also used in the next section as one of the initialization datasets for dynamical prediction), the clustering methodology used to extract Arctic sea ice modes of variability and a selection of corresponding results. Section 3 describes the coupled dynamical forecast system used to produce climate predictions and two statistical reference forecast systems. Section 4 assesses the skill of the NH SIT cluster predictions with several widely-used forecast quality metrics for categorical (here cluster or mode) predictions. The final Sect. 5 includes conclusions, discussions and suggestions for future research.

2 Historical reconstruction, clustering methodology and mode decomposition

Making in situ or remote observations of SIT is a demanding task at any scale (e.g. Haas 2003; Kwok 2010). Hence the most practical option for obtaining spatially and temporarily complete SIT is a combination of general circulation models (GCMs) and available observations (which typically contain gaps) through various data assimilation or reconstruction techniques (e.g. Zhang and Rothrock 2003; Massonnet et al. 2013). We focus on the NH SIT obtained from the NEMO ocean-sea-ice GCM historical multi-member reconstructions of Guemas et al. (2014a). Specifically, we use 5 ensemble members that reconstruct the variability and change of the global sea ice field from 1958 to 2013 with the Louvain-la-Neuve sea ice model version 2 (LIM2) embedded into the version 3.2 of the Nucleus for European Modelling of the Ocean (NEMO) model using the standard tripolar ORCA1L42 grid (approximately 1° resolution with enhanced resolution in the tropics and two poles in the NH). To account for the oceanic sources of sea ice uncertainty, the ocean temperature and salinity in historical reconstructions are nudged (restored) towards their monthly values in the five-member ORAS4 ocean reanalysis (Mogensen et al. 2011; Balmaseda et al. 2012). Together with introduced surface wind perturbations to account for the atmospheric uncertainty, nudging each member of the sea ice reconstruction towards a different ORAS4 member allows us to sample sea ice uncertainty. Guemas et al. (2014a) shows that the reconstructed SIT field is in reasonable agreement with the available ICESat observations (Kwok and Cunningham 2008) and a reanalysis (Massonnet et al. 2013). We employ the ensemble mean of these 5 historical reconstructions as the best available estimate of complete SIT field in our modeling framework.

We build on the results of Fučkar et al. (2016) where the K-means clustering was used on the ensemble monthly mean SIT from the 1958–2013 reconstruction discussed above to determine K cluster centroids or modes (where the optimal number of cluster for the NH SIT is K = 3) and their time series of occurrences. The applied clustering methodology aims to minimize the Euclidean distance between the members of a given cluster and maximizing the distance between the centroids of the different clusters, so the time series of cluster occurrences reveals the unique centroid (mode) to which the system is the closest in a particular month (Wilks 2011). K-means clustering was chosen to reduce the data dimensionality in a simple manner (using Euclidian distance) that avoids the statistical constraints inherent in other unsupervised learning methods like principal component analysis (PCA), such as orthogonality and linearity. Prior to cluster analysis, the Arctic SIT was first coarse grained into 32 regions to make the method computationally efficient and because there are typically less than 15 effective degrees of freedom of the Arctic SIT fields in a GCM (Blanchard-Wrigglesworth and Bitz 2014). Also, to determine robust Arctic SIT variability clusters, a 2nd order polynomial approximation of the long-term change was removed prior to applying the K-means clustering. This step is necessary because, otherwise, the time series of NH SIT cluster occurrences in each month or season is overwhelmed by the strong long-term decline in the NH SIT field (Kwok and Rothrock 2009). The monthly SIT centroid or mode patterns are determined as the average of the anomalous NH SIT in each month belonging to each cluster or mode over the period of interest.

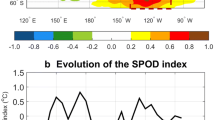
The three NH SIT modes that were identified over the 1958–2013 period are: the Central Arctic Thinning (CAT) mode (cluster 1), the Atlantic Pacific Dipole (APD) mode (cluster 2) and the Canadian Siberian Dipole (CSD) mode (cluster 3). Furthermore, Fučkar et al. 2016 shows that their anomalous patterns range from predominately negative (thinning) CAT mode to predominately positive (thickening) CSD mode. These three modes are consistent throughout the calendar year but with small seasonal cycle variations in their centroid patterns. For example, Fig. 1 shows the anomalous pattern of the CSD mode for different calendar months. The monthly time series of the NH SIT mode occurrences are combined into an occurrence matrix in Fig. 2 that markedly exhibits persistence on intraseasonal to interannual time scales of the CAT, APD and CSD modes in the historical reconstruction.

Fig. 1
figure 1

Monthly centroid patterns of the NH sea ice thickness (SIT) for the Canadian-Siberian dipole (CSD) mode or cluster 3—on average the thickest of three NH SIT modes—in a historical reconstruction of sea ice cover from 1958 to 2013. The occurrence rate of the CSD mode in the specific month, over the period of interest, is shown in the lower left corner of each panel

Full size image
Fig. 2
figure 2

Time-series map of occurrences of the ensemble-mean monthly NH SIT modes or clusters in a historical reconstruction of sea ice cover from 1958 to 2013

Full size image

3 Dynamical prediction system and two statistical reference methods

In this study we analyze five-member EC-Earth2.3 climate predictions in the standard configuration. EC-Earth2.3 is a state-of-the-art coupled Earth system model (http://www.ec-earth.org/) based on the operational seasonal forecast system of the European Centre for Medium-Range Weather Forecasts (ECMWF) (Hazeleger et al. 2010, 2012). The atmospheric component is the ECMWF’s Integrated Forecasting System (IFS) with the standard horizontal resolution T159 and 62 vertical layers up to 5 hPa. IFS also contains the land-surface H-TESSEL model (Balsamo et al. 2009). This EC-Earth version includes the NEMO2 ocean model (Madec 2008), embedding the LIM2 sea ice model (Fichefet and Morales Maqueda 1997; Bouillon et al. 2009), in the standard ORCA1L42 tripolar grid and 42 vertical layers. NEMO-LIM2 is coupled with IFS/H-TESSEL through OASIS3 every 3 h (Valcke 2013).

We performed 12-month ensemble climate predictions using a full-field initialization from the selected atmospheric and oceanic reanalyses and sea ice reconstruction on every 1 May and 1 November from 1979 to 2010. The atmospheric component is initialized from the ERA-interim reanalysis (Dee et al. 2011) with initial perturbations between the members computed using singular vectors (Du et al. 2012). The oceanic component of each climate prediction member is initialized from one of the five members of the ORAS4 ocean reanalysis (Balmaseda et al. 2012). The associated sea ice component of each climate prediction member is initialized using one of the five members from the global sea ice reconstruction of Guemas et al. (2014a).

This study addresses the question of how skillful the EC-Earth2.3 monthly predictions of Arctic SIT modes are out to a 12-month forecast horizon. However, in the rest of this section we first focus on two benchmark statistical forecasts: climatological probability forecast and a first-order Markov chain (Wilks 2011). A simple climatological forecast is based on recorded frequency of the three Arctic SIT modes, separately for each climatological month, in the historical reconstruction. We cross-validate all statistical forecasts by excluding the forecast year from the training data. For example, based on Fig. 2, the climatological probability forecast for May 1979 is 22/55, 15/55 and 18/55 for CAT, APD and CSD modes, respectively.

A more elaborate statistical method that can potentially account for the historical persistence of Arctic SIT modes is a three-state first-order Markov Chain (Wilks 2011). It has the Markovian property, i.e. the future state of the system depends only on the current state of the system and not on any previous state: Pr{Xt+1 | Xt, Xt−1, ..., X1} = Pr{Xt+1 | Xt}. Markov chain models of discrete states have been applied to determine the evolution of a number of weather and climate phenomena (e.g. Fraedrich and Klauss 1983; Ghil and Robertson 2002; Jones 2009). For continuous variables this process is referred to as a first-order autoregressive (AR1) model or red noise process. For the three Arctic SIT modes and their discrete occurrences, the Markovian property means that the probability of occurrence of a particular mode in month f + 1 depends only on which of three modes occurred in month f based on the matrix of transition probabilities. We estimate conditional transition probabilities pji (which indicate the probability of mode i in the current month transitioning to mode j in the next month) combined for all months from the reconstructed historical record of Arctic SIT mode occurrences shown in Fig. 2.

A K-state first-order Markov chain transition probabilities constitute a K x K transition matrix T, where K = 3 is for the Arctic SIT modes The diagonal elements of T (the probability of the Arctic SIT mode remaining in its current state) represent the persistence of the Arctic SIT mode, whereas the off-diagonal elements represent the transition to other modes. The initial state vector for this problem consists of a value of 1 for the initial monthly state of Arctic SIT mode and 0 for the two other modes. For example, if we are making a forecast for May through the following April, and if the Arctic mode in the preceding April is in CAT mode (or cluster 1), then the initial state vector is:

$${X^{\left( 0 \right)}}=\left[ {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}} \right].$$
(1)

For a first-order Markov chain forecast, the state vector indicating the probability of Arctic SIT mode occurrences at forecast month f months is given by

$${x^{(f)}}={{\mathbf{T}}^{f~}}{{\mathbf{x}}^{(0)}}.$$
(2)

For the present application, x(f) represents a probabilistic SIT mode forecast, where f varies from 1 to 12 months. For a very large forecast horizon f the first-order Markov chain forecast converges to the climatological forecast.

We now assess the quality of probabilistic forecasts of Arctic SIT modes generated by the three-state first-order Markov chain (2) with respect to a climatological frequency forecast. We generate 12-month forecasts for 1 May and 1 November start dates over the 1979–2010 period matching the period of available EC-Earth2.3 predictions. For each forecast, in our cross-validation approach, we estimate a new transition matrix T based on the transition frequencies for the whole historical reconstruction excluding the 12 target forecast months, as explained above. Hence, our estimate of the transition matrix T varies slightly for each of the 32 forecast years and both start dates in order to ensure that the training and forecast data remain independent, but T has no other dependence. The Arctic SIT modes tend to persist for multiple seasons, including through the changes between sea-ice growing and melting seasons (Fig. 2), hence we constructed T without seasonal dependence. Table 1 shows the mean T of CAT, APD and CSD modes for the 1958–2013 period constituted as the average of cross-validated transition matrices for forecast years from 1979 to 2010 (using both start dates).

Table 1 The first-order Markov chain transition matrix of conditional probabilities for the three NH SIT modes of clusters reconstructed over the 1958–2013 period
Full size table

We evaluate the skill of the first-order Markov chain forecasts with the ranked probability skill score (RPSS) based on the ranked probability score (RPS). RPS is the sum of squared differences between the cumulative forecast and reconstruction vectors that is defined for a single month as

$${\text{RPS}}=\mathop \sum \limits_{{i=1}}^{K} {\left( {\mathop \sum \limits_{{j=1}}^{i} {F_j} - \mathop \sum \limits_{{j=1}}^{i} {O_j}} \right)^2}~~~,$$
(3)

where Fj is forecast probability of occurrence of SIT cluster j and Oj is the reconstructed historical occurrence of Arctic SIT mode j (either 0 for non-occurrence or 1 for occurrence). RPS is an extension of the Brier Score for the assessment of probabilistic categorical forecast having more than two categories that also ranges from 0 for perfect skill to 1 for no skill (Wilks 2011). Through the incorporation of cumulative probabilities, this measure takes into account that the clusters are generally ordered from lowest to highest SIT anomalies. The RPSS for a single monthly forecast is computed as

$${\text{RPSS}}=1 - \frac{{{\text{RPS}}}}{{{\text{RP}}{{\text{S}}_{ref}}}},$$
(4)

where RPSref in this case stands for the RPS of climatological probability forecast RPSclim. RPSS values greater than zero indicate greater skill of the first-order Markov chain than a climatological forecast, while 1 indicates perfect skill, and values below 0 indicate lower skill than a climatological forecast.

Figure 3 shows the RPSS median, \(RPSS=1 - ~RPS/RP{S_{ref}}\), from start year 1979 to 2010 of the first-order Markov chain forecasts, with respect to the climatological forecast, as a function of forecast month for both start dates of EC-Earth2.3 seasonal predictions. For the first 5 forecast months the median RPSS of both 1 May and 1 November start dates indicate significantly positive skill. Afterwards the median RPSS of forecast initialized in autumn drops rapidly to the vicinity of zero. This rapid skill drop in Fig. 3 coincides with a switch from the boreal sea-ice growing season to melting season in April. This is compatible with findings of Holland et al. (2011) with the NCAR Community Climate System Model, version 3, where summer thermodynamic forcing reduces inherent predictability. Similarly, Day et al. (2014) shows that a melt season “predictability barrier” is a robust feature of five global climate models.

Fig. 3
figure 3

Ranked probability skill scores (RPSS) as a function of forecast month for three-state first-order Markov chain forecast of the NH SIT modes with respect to climatological forecast as the reference. Red and blue curves show the median of RPSS for 1 May and 1 November start dates, respectively, over the 1979–2010 period

Full size image

A skill index or single-number summary of forecast quality such as the RPSS provides valuable insight, but more comprehensive understanding of forecast performance requires analysis of the joint distribution of the forecasts and the historical reconstruction used for verification. The reliability diagram shows the historical event frequency versus the forecast probability divided into a number of bins (Wilks 2011; Jolliffe and Stephenson 2012). It examines how well forecast probabilities correspond to the actual event frequencies, or how well “calibrated” the forecast probabilities are. Figure 4 shows that first-order Markov chain forecasts of the CSD mode (bottom panels) are on average less reliable, i.e. the calibration function lies farther away from the perfect reliability diagonal, than the forecasts of the CAT and APD modes (top and middle panels). The observed relative frequency of the CSD mode tends to be higher than the forecast probability, which indicates a negative forecast bias in the Markov chain forecasts. Other than this bias, the Markov chain forecasts are relatively reliable for the other modes, with no clear tendency for overconfidence or underconfidence. The histograms of the forecast probabilities in the lower right corner of each plot are peaked near the climatological frequency of occurrence of each mode, which reflects the loss of sharpness (i.e., the range of probabilities) in the forecasts as the forecast horizons advance.

Fig. 4
figure 4

Reliability diagrams of the three-state first-order Markov chain forecasts of the NH sea ice thickness CAT, APD and CSD modes in the top, middle and bottom panels, respectively, encompassing all forecast months. The left (right) panels show forecasts with 1 May (1 November) start dates from 1979 to 2010. The grey consistency bars indicate 95% confidence interval (after 1000 bootstrap resamples). Each panel contains refinement histogram (number of events per bin) in the lower right corner

Full size image

In summary, the three-state first-order Markov chain model provides better skill and more insight into the predictability of the Arctic SIT modes than a simple climatology. Persistence could account for useful skill for about 5 months, and longer in the case of spring initialization. The skill of the Markov chain and climatological forecast will be used in the following section as benchmarks for the Arctic mode predictions with EC-Earth2.3.

4 Skill assessment of dynamical predictions of Arctic SIT modes

After introduction of two statistical models for reference forecasts we assess the performance of five-member 12-month-long EC-Earth2.3 coupled climate predictions of the Arctic SIT modes in capturing the reconstructed historical SIT mode variability over the 1979–2010 period. EC-Earth2.3 monthly predictions of mean SIT in the 32 selected regions in the NH defined in Fučkar et al. (2016) are trend bias corrected (Kharin et al. 2012; Fučkar et al. 2014) to minimize their root mean square error. We use various prediction skill measures, such as accuracy, RPSS, reliability diagram and relative operating characteristic (ROC: hit rate versus false alarm rate) diagram to examine dynamical forecast quality.

Accuracy simply tells us what fraction of the ensemble forecasts in a specific month predicts the correct Arctic SIT mode. Figure 5 shows matrices of accuracy of ensemble EC-Earth2.3 SIT mode forecasts as a function of the forecast month on the abscissa and the start year on the ordinate (along with the historical SIT mode in a month just before the start date). Specifically, if the majority of ensemble members make a wrong prediction (accuracy less than 0.6) in a forecast month, this month is shaded with grey color in Fig. 5, otherwise it is shaded with the designated primary color of the recorded historical SIT mode (from Fig. 2). For the first 6 forecast months, on average the accuracy of EC-Earth2.3 predictions is larger when initialized in fall than in spring. For the longer forecast horizons in Fig. 5, the opposite is indicated. This indicates that the switch from sea-ice melting season to growing season in the dynamical system typically leads to improvement of prediction skill, while often the opposite is the case for the switch from growing season to melting season. Also, every forecast month shaded with one of the primary colors in Fig. 5 has RPS values smaller than 0.2 (not shown).

Fig. 5
figure 5

Accuracy of EC-Earth2.3 12-month five-member ensemble predictions of the NH SIT modes for 1 May and 1 November start dates in the left and right panels, respectively, from 1979 to 2010. The color of a forecast month is saturated to the designated primary color of a historical reconstructed NH SIT mode if the majority of 5 EC-Earth2.3 ensemble members correctly predict this mode (accuracy of 0.6, 0.8 and 1.0), otherwise the forecast month is marked grey (accuracy of 0, 0.2 and 0.4). The additional first column in both panels—April(0) and October(0)—shows the historical NH SIT mode in the month just before the start date

Full size image

RPSS matrices of EC-Earth2.3 SIT mode forecasts as a function of the forecast month on the abscissa and the start year on the ordinate in Fig. 6 (using a three-state first-order Markov chain as the statistical reference forecast) roughly resemble the accuracy matrices shown in Fig. 5. Particularly after spring initialization for the forecast horizons longer than 5 months, when a majority of ensemble members correctly predict the historical mode, RPSS exhibits high skill (marked by darker shades of purple color), which demonstrates a significant added value of the dynamical forecast over the first-order Markov chain in growing season. Figure 7 compresses RPSS matrices by presenting the RPSS median in Fig. 6 along the start years 1979–2010 (i.e. along the ordinate) to show that the first-order Markov chain initialized on 1 May outperforms EC-Earth2.3 forecasts in the first month. This could be potentially attributed to initialization shock and missing or crudely represented physical processes in the sea ice model LIM2 such as melt ponds, wind redistribution of snow and simple solar penetration scheme. These processes are very important during the melting season, but much less so during the growing season (Notz 2012). The RPSS median of the dynamical forecasts initialized in spring (red curve in Fig. 7) show the emergence of positive skill with respect to the first-order Markov chain model after the first forecast month. Figure 7 shows a higher skill of the dynamical forecast initialized in autumn than in spring over the first 5 months, but on the longer forecast horizons this relationship reverses with the switch between melting and growing seasons. Such behavior is in accord with findings that SIT and sea ice volume have typically greater skill in winter than in any other season (Day et al. 2014; Guemas et al. 2014b). Overall, the RPSS medians in Fig. 7 corroborate the information in Figs. 5 and 6. Furthermore, the prevailing dominance of dynamical system over the Markov chain model emphasizes the importance of well-resolved physical processes for the skill of the forecast system.

Fig. 6
figure 6

RPSS of EC-Earth2.3 12-month five-member ensemble predictions of the NH SIT modes—with respect to three-state first-order Markov chain forecast as the reference—for 1 May and 1 November start dates in the left and right panels, respectively, from 1979 to 2010

Full size image
Fig. 7
figure 7

RPSS as a function of forecast month for EC-Earth five-member ensemble prediction of the NH SIT modes with respect to three-state first-order Markov chain forecast as the reference. Red and blue curves show the median of RPSS for 1 May and 1 November start dates, respectively, over the 1979–2010 period

Full size image

The RPSS matrices of EC-Earth2.3 mode forecasts with respect to climatological probability forecasts as the reference (Fig. S1) show a better match with the accuracy matrices in Fig. 5 than with the RPSS matrices in Fig. 6. This again indicates that the first-order Markov chain forecast is a more challenging statistical benchmark for the dynamical forecast system than the climatological forecast. Furthermore, the RPSS median (over the start years 1979–2010) of the dynamical forecasts with respect to the climatological reference in Fig. 8 confirms that the Markov chain model is better than climatological probabilities in capturing the persistence of Arctic SIT modes in the historical reconstruction. The RPSS medians in Fig. 8 show a monotonic decline of positive skill with forecast time in contrast to emergent RPSS median behavior with forecast time in Fig. 7 for 1 May initialization.

Fig. 8
figure 8

RPSS as a function of forecast month for EC-Earth five-member ensemble prediction of the NH SIT modes with respect to climatological forecast as the reference. Red and blue curves show the median of RPSS for 1 May and 1 November start dates, respectively, over the 1979–2010 period

Full size image

How reliable are dynamical forecasts of the three Arctic SIT modes in comparison with the three-state first-order Markov chain model? The left panels in Fig. 9 indicates that the EC-Earth2.3 probabilistic mode forecasts initialized on 1 May are more reliable than the corresponding Markov chain forecasts (the left panels in Fig. 6), i.e. they are on average closer to the diagonal of perfect reliability. There is only a slight tendency for overconfidence in the CAT mode forecasts (Fig. 9a), but overall the dynamical forecasts are well calibrated. The forecast probability histograms have greater spread than those of the Markov chain model, indicating the dynamical forecasts have greater sharpness, particularly at the longer forecast horizons. Overall, the left panels in Fig. 9 indicate that the five-member ensemble is sufficient for producing reliable probabilistic forecasts of SIT mode occurrences when the forecasts are initialized in spring.

Fig. 9
figure 9

Reliability diagrams of EC-Earth2.3 five-member ensemble predictions of the NH sea ice thickness CAT, APD and CSD modes in the top, middle and bottom panels, respectively, encompassing all forecast months. The left (right) panels show forecasts with 1 May (1 November) start dates from 1979 to 2010. The grey consistency bars indicate 95% confidence interval (after 1000 bootstrap resamples). Each panel contains refinement histogram (number of events per bin) in the lower left corner

Full size image

The EC-Earth2.3 probabilistic SIT mode forecasts initialized on 1 November, however, are not nearly as well calibrated (the right panels in Fig. 9). All of Arctic SIT mode forecasts are overconfident, especially those of the APD mode (Fig. 9e). These results suggest that the ensemble size of five members is insufficient for reliable probabilistic mode forecasts when EC-Earth2.3 is initialized in autumn: the model is underdispersive (i.e. ensemble spread is too small). A possible explanation is that the dynamic SIT modes are more sensitive to the large internal atmospheric variability in the winter months, hence more ensemble members of EC_Earth2.3 would probably better capture the wide range of possible realizations of internal variability of the Arctic sea ice system.

How good is the ability of the EC-Earth2.3 multi-member forecast system to discriminate between the correct and incorrect Arctic SIT mode predictions? Resolution is an attribute of forecast quality (Murphy 1993) that measures the success of a forecast system in distinguishing one type of event, i.e. one SIT mode from another. To gain insight into the resolution of probabilistic prediction skill, we combine hit rates and false alarm rates of the three Arctic SIT modes. The hit rate of a mode k tells us what fraction of mode k is correctly forecasted: it is equal to the number of correct mode k forecasts (hits) divided by the total number of mode k events (hits plus misses). The false alarm rate of a mode k tells us what fraction of forecasts produced mode k when mode k did not occur: it is equal to the number of false alarms of mode k divided by the total number of not-k mode events. The hit rate ignores false alarms, while false alarm rate ignores misses so they are commonly combined in a ROC diagram that shows hit rate against false alarm rate as the decision threshold varies (Wilks 2011; Jolliffe and Stephenson 2012). The decision threshold is the probability threshold that discriminates between one action (forecasting the occurrence of mode k) versus an alternative action (not forecasting mode k).

Figure 10 shows ROC diagrams for each Arctic SIT mode separately (in different rows of panels) and compares their potential skill in EC-Earth2.3 forecasts and two statistical forecasts for two selected start dates (in different columns of panels) combined over all 12 forecast months. The aim of a forecast system is to attain the perfect resolution that would correspond to a hit rate of 1 and false alarm rate of 0, i.e. the point in the upper left corner of a ROC diagram. The diagonal in the ROC diagram represents zero skill level (random forecast with equal probability of hit rate and false alarm rate). Figure 10 overall confirms a hierarchy in prediction skill of our three forecast systems: EC-Earth2.3 mode forecasts have better resolution than the first-order Markov chain forecasts (except for the CSD mode forecasts initialized on 1 November in Fig. 10f), while the Markov chain forecasts never have less resolution than the climatological probability forecasts. The area under the ROC curve (AROC) is a practical scalar measure of skill on the range from 0.5 for no skill (diagonal) to 1 for perfect forecast (ROC curve passing through the upper-left corner). AROC values in the lower right corner in panels of Fig. 10 show that for each Arctic SIT mode EC_Earth2.3 and Markov chain forecasts have slightly higher skill when initialized on 1 May than on 1 November over the 1979–2010 period. AROC values also indicate that the difference of resolution between EC-Earth2.3 and Markov chain forecasts, on average, is bigger after initialization on 1 November than on 1 May possibly to due better resolved key processes and higher predictability in winter than in summer.

Fig. 10
figure 10

Relative operating characteristic (ROC) diagrams of the various forecasts of the NH sea ice thickness CAT, APD and CSD modes in the top, middle and bottom panels, respectively, encompassing all forecast months. The solid, dashed and dotted curves show EC-Earth2.3, three-state first-order Markov chain and climatological forecast, respectively. The values in the right bottom corner of each panel show areas under ROC curves. The left (right) panels show forecasts with 1 May (1 November) start dates from 1979 to 2010

Full size image

How does the resolution of the EC-Earth2.3 and Markov chain forecast systems evolve with forecast time? Fig. 11 and the associated Table 2 compare their ROC curves and the areas under the ROC curves, respectively, in sequential steps of 3 forecast months. We see that the dynamical forecasts of each Arctic SIT mode typically have better resolution than the Markov chain forecasts, for both start dates, during each 3-month forecast range. This is furthermore evident when one compares the AROC values in (x.1) and (x.2) columns in the same row in Table 2. We can attest that dynamical forecasts have better resolution than the Marko Chain forecasts in all instances except one (4–6 forecasts months of CSD mode initialized in fall). Furthermore, it appears that the dynamical forecast resolution degrades with advancing forecast horizon at a faster rate after spring initialization than after fall initialization for CAT and APD modes while the opposite is the case for CSD mode. This indicates that on average the sea-ice growing season has potentially a higher predictability than melting season. The first-order Markov chain Arctic SIT mode forecasts initialized in autumn can reach skill even below the diagonal (i.e., the area under the ROC curve of less than 0.5) at longer forecast horizons, which represents the same level of resolution as they would if reflected with respect to the diagonal.

Fig. 11
figure 11

Relative operating characteristic (ROC) diagrams of the various forecasts of the NH sea ice thickness CAT, APD and CSD modes in the top, middle and bottom panels, respectively. The set of solid and dashed curves show EC-Earth2.3 forecasts in (x.1) columns and three-state first-order Markov chain (MC1) forecast in (x.2) columns, respectively, sequentially encompassing 3 forecast months at the time. The two left (right) panels show forecasts with 1 May (1 November) start dates from 1979 to 2010

Full size image
Table 2 The areas under ROC curves (AROC) in Fig. 11 for a sequence of forecasts advancing in time, combining three forecast months at the time (1–3, 4–6, 7–9 and 10–12), with 1 May and 1 November start dates over the 1979–2010 period
Full size table

5 Summary, conclusions and future directions

The concept of weather regimes offers a framework for the analysis of weather and climate variability through decomposition into dominant modes and their associated time series. Fučkar et al. (2016) has extended this concept of regime behavior to the NH SIT variability and determined three Arctic clusters or modes (CAT, APD and CSD) by applying the K-means cluster analysis on a historical reconstruction of SIT from 1958 to 2013 (Guemas et al. 2014a). The focus is on SIT because it has a capability to act as a buffer of climate signals on intraseasonal and longer time scales (e.g. Blanchard-Wrigglesworth et al. 2011; Guemas et al. 2014b). The K-means nonhierarchical clustering is a type of unsupervised statistical learning method complementary to the PCA, but not constrained by the orthogonality and linearity assumption inherent to the PCA (Hastie et al. 2009; Wilks 2011).

A state-of-the-art EC-Earth2.3 coupled forecast system (Hazeleger et al. 2010, 2012) is used to produce five-member 12-month climate predictions using full-field initialization on 1 May and 1 November every year from 1979 to 2010. Dynamically forecasted monthly SIT in the Arctic, after trend bias correction (e.g. Fučkar et al. 2014) is classified into three Arctic SIT modes from the historical reconstruction discussed above. We apply a three-state first-order Markov chain model and climatological probability forecasts of the Arctic SIT modes as statistical benchmarks for our EC-Earth2.3 mode predictions. The median RPSS of the Markov chain forecasts with respect to climatology forecasts shows prevailing positive skill over the first 5 forecast months after both fall and spring initialization.

The RPSS of the dynamical SIT mode forecasts with respect to the Markov chain forecasts shows negative skill for the first forecast month after initialization on 1 May, likely due to initialization shock and missing physical processes, but afterwards the RPSS is positive for both start dates. An interesting feature of RPSS is that the dynamical forecasts initialized in spring perform better than the dynamical forecasts initialized in fall from forecast month 6 onward. Such behavior indicates that the transition from the sea-ice melting season to growing season in EC-Earth2.3 typically leads to improvement of skill. This is also likely related to a higher inherent predictability of SIT in winter than in other seasons (Day et al. 2014; Guemas et al. 2014b). The reliability diagrams of EC-Earth2.3 forecasts show high reliability of all modes after initialization on 1 May, while after initialization on 1 November the dynamical system appears to be overconfident (possibly due to a small ensemble size). The ROC diagrams confirm the existence of this hierarchy in forecast quality of the forecast systems: EC-Earth2.3 Arctic SIT mode predictions have on average a higher skill than the first-order Markov chain predictions which are a notable improvement from the climatological probability forecasts. Further analysis of the ROC curves across different forecast horizons reveals that the dynamical CAT and APD mode forecasts initialized in fall lose resolution at a lower rate in forecast time than forecasts initialized in spring, In other words, the inferior performance of dynamical model during melting season may lead to higher SIT forecast errors, which would hint at the existence of “a summer predictability barrier”.

Possible future lines of investigation could include the application of the multivariate K-means clustering encompassing a set of polar climate variables using different types of observations, reanalyses and reconstructions. Also, such promising climate prediction skill of “coarse-grained” aspects of the Arctic system such as CAT, APD and CSD modes of SIT field will hopefully encourage exploration of their skill in other state-of-the-art coupled climate models. Our and many other coupled climate models still miss some of the critical physical processes with high impacts on sea ice cover in summer such as melt ponds, wind-driven snow dynamics, etc. Hence, a possibility of improved skill and utility of dynamical climate predictions during the boreal sea-ice melting season should also guide efforts to improve the physics of sea ice models and initialization methods of coupled forecast systems.