Abstract
Coordinated numerical ensemble experiments with six different state-of-the-art atmosphere models have been used in order to evaluate the respective impact of the observed Arctic sea ice and sea surface temperature (SST) variations on air temperature variations in mid and high latitude land areas. Two sets of experiments have been designed; in the first set (EXP1), observed daily sea ice concentration and SST variations are used as lower boundary forcing over 1982–2014 while in the second set (EXP2) the SST variations are replaced by the daily SST climatology. The observed winter 2 m air temperature (T2m) variations are relatively well reproduced in a number of mid and high latitude land areas in EXP1, with best agreement in southwestern North America and northern Europe. Sea ice variations are important for the interannual T2m variations in northern Europe but have limited impact on all other mid and high latitude land regions. In particular, sea ice variations do not contribute to the observed opposite variations in the Arctic and mid latitude in our model experiments. The spread across ensemble members is large and many ensemble members are required to reproduce the observed T2m variations over northern Europe in our models. The amplitude of T2m anomalies in the coldest observed winters over northern Europe is not reproduced by our multi-model ensemble means. However, the sea ice conditions in these respective winters and mainly the thermodynamic response to the ice anomalies lead to an enhanced likelihood for occurrence of colder than normal winters and extremely cold winters. Still, the main reason for the observed extreme cold winters is internal atmospheric dynamics. The coldest simulated northern European winters in EXP1 and EXP2 between 1982 and 2014 show the same large scale T2m and atmospheric circulation anomaly patterns as the observed coldest winters, indicating that the models are well able to reproduce the processes, which cause these cold anomalies. The results are robust across all six models used in this study.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Observations in the Arctic indicate a rapid change of climate in the last decades. The annual mean Arctic surface air temperature (SAT) increased by more than 2 °C since 1850, which is 2–3 times faster than the global mean warming (Stocker et al. 2013; Richter-Menge and Jeffries 2011). The ice-albedo feedback (Serreze et al. 2009; Screen and Simmonds 2010a, b), enhanced meridional energy transport in atmosphere (Graversen et al. 2008; Li et al. 2015; Park et al. 2015) and ocean (Spielhagen et al. 2011; Koenigk and Brodeau 2014; Zhang 2015; Yeager et al. 2015), changes in clouds and water vapour (Graversen and Wang 2009; Liu et al. 2008), the vertical mixing in Arctic winter inversion (Bintanja et al. 2011), the temperature feedback (Pithan and Mauritsen 2014) and the reduced air pollution in Europe (Navarro et al. 2016) have been discussed as potential contributors to this Arctic temperature amplification. Together with the warming, sea ice cover and volume have strongly decreased in the last decades (Comiso et al. 2008; Devasthale et al. 2013). The year 2016 showed record low ice extents in the Arctic during 7 months, and most of the year, the ice extent was more than two standard deviations below the average for 1981–2010. Also snow cover on the sub-Arctic continents is subject to extreme changes (Brown and Robinson 2011) and might affect local and large scale atmospheric conditions (Cohen and Entekhabi 1999; Gong et al. 2002; Cohen et al. 2012; Orsolini and Kvamstø 2009).
The world’s largest observed surface heat fluxes are found near the ice edge in the Barents Sea with up to 500W/m2 (Simonsen and Haugan 1996). Changes and variations in sea ice strongly affect amplitude and positon of these heat fluxes and play an important role for both local and remote climate (Årthun and Schrum 2010; Koenigk et al. 2009). A large number of recent studies investigated the link between ice variations and trends of autumn Arctic sea ice extent and winter mid-latitude conditions (e.g. Petoukhov and Semenov 2010; Francis et al. 2009; Yang and Christensen 2012; Overland and Wang 2010; Hopsch et al. 2013; Garcia-Serrano and; Frankignoul 2016; Nakamura et al. 2016). Although controversial, most of these studies indicated that reduced sea ice in late summer or autumn is linked to a negative phase of the North Atlantic Oscillation (NAO) in the following winter. Sea ice changes in the Barents Sea—Kara Sea area have been identified as particularly important for the impact on lower latitudes (Inoue et al. 2012; King et al. 2016; Garcia-Serrano et al. 2015; Koenigk et al. 2016; Yang et al. 2016). A sea ice reduction in the Barents Sea—Kara Sea also leads to snow cover changes over Siberia, through a larger moisture flux from the Arctic into central Eurasia, and snow and sea ice changes were suggested to act together to impact the atmosphere over the Northern Hemisphere (Wegmann et al. 2015; Gastineau et al. 2017).
In contrast to the recent Arctic warming, there is a cooling trend in winter SAT over large areas of the northern hemisphere continents during past decades, in particular since around 2000. Recent studies linked the negative ice trend to more frequent occurrence of extreme cold weather situations, particularly in Eurasia (Semenov and Latif 2015; Mori et al. 2014; Gao et al. 2015), but also in North America (Francis and Vavrus 2012; Liu et al. 2012). Therefore, a better understanding of the Arctic impacts on climate would be of great benefit to improve forecasts of cold weather situations in winter.
However, the observed time series are still short and it remains uncertain if the observed linkages between sea ice and atmospheric circulation are really robust or if they might be due to natural variations (Barnes 2013; Screen et al. 2014; Sun et al. 2016; Koenigk and Brodeau 2017; Ogawa et al. 2018). Screen et al. (2015) showed that increased greenhouse gas forcing will reduced the risk for cold days over North America. Furthermore, the climate system is complex and many variables have changed over the last years, which makes it uncertain if the sea ice really is the main driver for mid-latitude climate events (McCusker et al. 2016). It was also suggested that the cooling over the northern continents is linked to changes in the Atlantic (Peings and Magnusdottir 2014) and/ or the Pacific (Kosaka and Xie 2013). The problem is further complicated by the suggested non-linear large-scale atmosphere circulation response to the same sign boundary forcing anomalies (Petoukhov and Semenov 2010; Semenov and Latif 2015; Semenov 2016; Overland et al. 2016) that, in particular, makes model results sensitive to a correct simulation of the present climate state.
The aforementioned results are mainly based on observational based data sets or on single model ensemble experiments. As discussed above, the observational time series are still short, which makes it difficult to distinguish between variations and trends. Studies based on single models do not answer the question of the robustness across different models (Cohen et al. 2014). Comparison of results from early studies is also complicated by the generally differing boundary conditions. To overcome this problem, coordinated multi-model ensemble experiments have been performed in the GREENICE-project. So far only Screen et al. (2013) and Sun et al. (2016) used two different atmosphere model CAM for their sensitivty studies. This present study uses the by far largest number of models for coordinated sensitivity experiments. We use these large ensemble simulations to investigate the effect of sea ice variations on climate variations in mid and high latitude land areas. A recent study by Ogawa et al. (2018), which is based on the same model simulations, focused on the impact of ice and SST trends on atmospheric trends in mid and high northern latitudes.
After this introduction, we describe the model simulations and data in Sect. 2. In Sect. 3, we focus first on the linkage between temporal variations of temperature, sea ice and SST before investigating specific cold winter cases in more detail. In the final section, we summarize the results and conclude.
2 Model experiments and data
Six different global atmosphere models (AGCMs, Table 1) have been used to perform two sets of ensemble experiments.
In the first set of experiments (EXP1), the NOAA-OISST v2 (Reynolds et al. 2007; downloaded from http://www.ncdc.noaa.gov/sst/index.php) daily product of sea ice concentration (SIC) and SST from 1982 to 2014 is used to force five of our six AGCMs (CAM4. IFS, WACCM, LMDZOR, IAP4). External forcing follows the CMIP5 protocol. After 2005, external forcings following the RCP8.5 emission scenario are used. This forcing differs from the classical AMIP experiment as we use daily SST and sea ice, so that the sea ice edge and the gradient of air temperature above it are well specified as boundary condition, and not smoothed as when using monthly data. This might lead to a better simulation of ocean–atmosphere interaction in lower latitudes (Zhou et al. 2015). We performed 10–30 ensemble members with each of the models (Table 1).
The second set of experiments (EXP2) is identical to EXP1 but instead of using daily SST values, the daily climatological annual cycle of SST (averaged over 1982–2014) is used. Again, 10–30 ensemble members have been performed with each of the models. Following Screen et al. (2013), we further adjusted SST and sea ice concentration (SIC) to avoid large inconsistencies at the sea ice edge: North of 40°N, if the daily mean SIC deviates from daily climatology by > 10%, the grid box is set to the observed SIC and SST; otherwise and elsewhere the observed SIC and climatological SST are used.
EXP2 isolates the effect of the observed sea ice variations from 1982 to 2014. The difference between EXP1 and EXP2 highlights the role of SST forcing and the similarities highlight the role of the sea ice and the direct radiative impacts of external forcing.
The NOAA-OISSTv2 sea ice data showed an inconsistency at year 2005. From 2005 onwards, a number of coastal points, particularly in the Canadian Archipelago, show sea ice while they have been treated as land points (with an ice concentration of zero) before 2005. This leads to a positive offset of the Arctic sea ice extent after year 2005 in the original data. To avoid this offset, we corrected the data after 2005 in these coastal points. Two other data errors were corrected by linear interpolation of the daily anomalies [29 Nov 1987 to 18 Jan 1988 (SIC) and 27 Apr 2009 to 19 May 2009].
The sixth model, AFES4.1, follows the same experiment set up as the other five models but uses daily sea ice and SST forcing data from Hurrel et al. 2008. Since we did not find systematical deviations between the results from AFES4.1 and the other five models, we decided to include the AFES4.1-simulation in this study. All multi-model ensemble means include thus the AFES4.1-simulations as well.
We use ERA-interim reanalysis data (Dee et al. 2011) as reference data for most of our comparisons to the model experiments as it was shown to provide good performances over the Arctic (Jacobson et al. 2012; Lindsay et al. 2014). Note that ERA-interim data are not observations and might be uncertain as well. Particularly in the Arctic, where very few observations are available, data assimilation used in reanalysis obviously provides less value, although effects from more southerly locations with better observational coverage should have a positive impact. Nevertheless, large discrepancies are found in reanalysis in the Arctic (Lindsay et al. 2014).
In order to focus on the interannual variability, we perform most analyses after subtraction of a linear least squared trend from our model data.
3 Results
3.1 Impact of temporal sea ice variations on the temperature variability
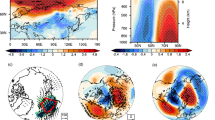
As discussed in the introduction, a number of studies have linked winter variations, trends and extremes in different northern hemisphere land regions to variations and trends in Arctic sea ice. Further, the so called “warm Arctic—cold continents (or cold mid-latitudes)” pattern have become a common expression (Overland et al. 2011). Figure 1 shows the zonal mean winter temperature (average over December, January, February; DJF) anomalies in ERA-interim data and the multi-model ensemble means (MMEM) of EXP1 and EXP2. The ERA-interim data show warm winters in the Arctic before 1985, followed by mainly cold winters between the end of the 1980s and 2000 and warm winters again after 2005. In mid-latitudes, this decadal scale variation is less pronounced but one might see a tendency towards the opposite signal in mid-latitudes compared to polar latitudes. Particularly after 2010, slightly colder than normal zonal means in mid-latitudes occur while the Arctic shows strong positive anomalies. This pattern agrees with the proposed warm Arctic—cold mid-latitudes pattern. The detrended data show generally very similar relations between warm (cold) Arctic and cold (warm) mid-latitudes and we find a significant correlation of − 0.48 between winter T2m, averaged over 70°N–90°N, and T2m, averaged over 30°N–50°N, in ERA-interim. However, if we look more in detail at individual winters, we find quite a number of exceptions, where this cold (warm) Arctic—warm (cold) mid-latitudes pattern is not pronounced or not at all existing (e.g., the winters 1987, 1988, 1991, 1994, 1996, 2000, 2001, 2006, 2007).
The experiments show that Arctic sea ice variations largely capture the observed decadal variations in winter Arctic temperature, but not those in mid-latitudes. In particular, we see that EXP1 simulates warm values in the 1980s, generally colder years in the 1990s, and then warmer winters again. However, single years can strongly deviate from the observed one. The correlation of zonal mean winter T2m in EXP1 and ERA interim reaches 0.6 to 0.7 north of 75°N but is low between 30°N and 60°N (not shown). EXP2 reproduces most of the Arctic T2m variations in EXP1 pretty well, indicating the strong coupling between the Arctic sea ice variations and local SAT. As for EXP1, the correlation of zonal mean T2m with ERA-interim reaches 0.6–0.7 for arctic latitudes. In mid-latitudes (30°N–60°N), EXP1 does not reproduce the observed zonal mean T2m anomalies well. Also, the warm (cold) Arctic—cold (warm) mid-latitude pattern is not well shown. Particularly, the warm Arctic temperature anomalies after 2005 extend into the mid-latitudes in EXP1. EXP2 shows generally small mid-latitude T2m anomalies, indicating little impact of the sea ice variations on zonally averaged mid-latitude temperature anomalies. The detrended zonal mean anomalies (Fig. 1b, d, f) show similar results: Observed decadal temperature variations are relatively well reproduced in the experiments in the Arctic but not in lower latitudes. The correlation of detrended winter T2m in 70°N–90°N and T2m in 30°N–50°N is − 0.2 in EXP1 and 0.02 in EXP2.
Winter cold extremes have often been reported in specific areas of mid-latitudes and might not occur as anomalies in the zonal mean. An example for this is the winter 2005/2006, which was the coldest winter between 1983 and 2009 in parts of Asia (Petoukhov and Semenov 2010) but does not appear as a cold winter in the zonal mean in ERA-interim. In the following, we thus concentrate on winter temperature variations in different land regions. We define ten different mid and high latitude regions (see Table 2) and average the T2m over each of the regions. We only took grid boxes into account where at least 50% of the box is land-covered. Figure 2 shows the time series of DJF T2m in the ten regions for ERA-interim and the MMEMs of EXP1 and EXP2. Interannual variations in ERA-interim are large, particularly in the northern land areas. The variations of the MMEMs of T2m in EXP1 and EXP2 are much smaller than in ERA-interim in all areas except for EXP1 in SE, SW and NW N America. This is expected from the ensemble averaging that greatly reduce the amount of internal atmospheric variability, while keeping the influence of boundary conditions onto the atmosphere. Over the three N America regions, the EXP1 MMEM reproduces well the observed interannual variations, while EXP2 MMEM does not reproduce the variability and amplitude in these three regions. Thus, here the SST-forcing seems to be the main driver of winter temperature variations, which is consistent with the dominant teleconnection from the tropical Pacific region. The El Niño Southern Oscillation is known to drive the Pacific North American Pattern in winter, which has a dominant impact on the winter climate over North America (Wallace and Gutzler 1981). Individual model ensemble members simulate a realistic amplitude of interannual winter variations but the spread among members is very large (Fig. 3); this is consistent with the large internal atmospheric variability over midlatitudes. The spread in EXP1 and EXP2 is of similar size, even in those regions where the SST is the main driver for interannual variation. Thus, using climatological SST boundary conditions is not reducing the internal variability in EXP2 as one might expect. The standard deviation of T2m across the model members in our experiments is also comparable to the standard deviation of T2m over time in the ERA-interim data in most of the regions (Fig. 3). Interestingly, we see for some of the regions, e.g. in NW Asia or for some time periods in N Europe, that the MMEM spreads in EXP1 and EXP2 show peaks in the same years, which might indicate that the specific sea ice conditions of these years play a role for the internal variability of temperature in these land regions. If we instead of calculating the standard deviation for each winter, calculate the standard deviation over time in EXP1 and EXP2, we get a small increase of the standard deviation. This increase is slightly larger in EXP1 than in EXP2 due to a stronger trend in the temperature. For most of the areas, the standard deviation, calculated over time, agrees slightly better with ERA-interim as the one across members for each winter.
The low MMEM amplitude of interannual winter variations in most regions indicates that the response of the atmosphere to sea ice and SST is rather weak. Still, T2m shows a significant correlation between the MMEM of EXP1 and ERA-interim in all regions except for NE and NW Asia (Table 2), and the correlation between T2m in EXP2 and ERA-interim is high in N Europe and NE N America. For N Europe, the correlation between EXP2 and ERA-interim reaches 0.68. This shows that it is possible to extract the rather small signal from the sea ice on the atmosphere in N Europe by using a large number of ensemble members. Sea ice might thus be an important predictor for T2m-variations in N Europe.
The correlations of the detrended time-series are for most regions slightly higher than for the raw data (Table 2, lower rows). This is especially the case for NW Asia, where the observed trend of T2m (− 0.38 K/decade) is opposite to the simulated one in EXP1 (0.45 K/decade, Table 3) and thus degrading the correlation. The trends in ERA-interim and the EXP1 MMEM agree relatively well for the European regions and are small in both observed and simulated western North American areas. NE N America shows a very high trend in ERA-interim, which is only partly reproduced by the models. The trends in EXP2 are much weaker than in EXP1, except for NE N America, indicating that the sea ice reduction is not the main driver for trends in most of the mid and high northern latitude regions. This result is rather robust across models.
All single model ensemble means of EXP2 are significantly correlated with ERA-interim for the N Europe and NE N America regions but almost none of the models show signifcant correlations for any of the other regions (except for AFES4.1 for NE Asia, with a correlation of 0.35 and WACCM for SW Asia with r = 0.38). The trends and the impact of sea ice reduction on trends in our model simulations are discussed in detail in an article, which has been submitted by Ogawa et al. (Geophysical Research Letters).
Figure 4 shows grid point correlations between the MMEMs of EXP1 and EXP2 and ERA-interim for SLP and T2m in winter. The SLP in EXP1 is significantly correlated with ERA-interim over the northeastern North Pacific and mid-latitude North America as well as over a region extending from western Europe into the North Atlantic. EXP2 shows only small areas with significant correlations, mainly over the Nordic Seas and North Atlantic Arctic sector. T2m in EXP1 is highly correlated with ERA-interim over all ocean regions. Correlations over land areas are significant over Europe with particularly high correlations over Northern Europe, and in a band across N America between 40°N and 50°N. T2m in EXP2 is only significantly correlated with T2m in ERA-interim over the Arctic, parts of the northern North Pacific, the northwestern North Atlantic and over Northern Europe. A comparison of the grid point correlations with the correlation of the regional averages (Table 2) shows substantially higher correlations for regional averages. The averaging leads to reduced noise and filters out the larger scale signal. This is a well known effect from climate predictions where the prediction skill increases with increasing spatial and temporal scales (Koenigk et al. 2012).
If we compare T2m variations in EXP1 to EXP2, we find significant correlations for a number of high and mid-latitude Eurasian regions (Table 4). Particularly, in the N Europe and NE Asia regions, the sea ice variations seem to be responsible for a large fraction of the temperature variability. In these two regions, the correlations between EXP1 and EXP2 remain almost unchanged when using detrended data. For the other Eurasian regions, correlations are reduced in the detrended data indicating that part of the correlation is due to common trends in EXP1 and EXP2.
3.2 Cold winters in Northern Europe
Section 3.1 showed that N Europe is the continental region with the largest impact (in the sense of highest correlation between MMEM with ERA-interim data) of Arctic ice variations on the T2m variability. Therefore, we focus in the following on this region.
Figure 5 shows the temporal variations of winter T2m in N Europe for all individual model ensemble means, the MMEM and the ERA-interim data. Note, that the ERA-interim data are divided by a factor of three for better visualization. The MMEM of EXP1 and EXP2 and all individual model ensemble means follow relatively well the T2m-evolution of ERA-interim from 1982 to 2014. T2m of all individual model ensemble means is significantly correlated with ERA-interim in both EXP1 and EXP2. The correlations vary between 0.45 (WACCM) and 0.66 (AFES4.1) for EXP1 and between 0.40 (CAM4) and 0.64 (IFS and LMDZOR) for EXP2. Thus, the MMEMs are in better agreement with ERA-interim than any single model ensemble mean.
Top left: Winter T2m anomalies in N Europe in ERA-interim, the multi-model ensemble mean in EXP1 and the individual model ensemble means. Note that ERA-interim T2m anomalies have been divided by 3 for better comparison. Top right: the same for ERA-interim and EXP2, Bottom left: standard deviations across all members of the multi-model ensemble and the individual model ensembles for EXP1. Bottom right: the same as bottom left but for EXP2
The amplitude of the anomalies of the MMEMs and also of the individual model ensemble means is much smaller than in ERA-interim. This is caused by a large spread among individual members. However, the standard deviations of the detrended winter temperatures over the entire 1982–2014 time period in the single model simulation agree relatively well with ERA-interim. In individual model simulation, the standard deviation varies between 1.2 and 2.3 K. This compares to a value of 2.0 K in ERA-interim. The standard deviation over time agrees with the variation across the ensemble members in EXP1 and EXP2 (Fig. 5 bottom). All individual models have a relatively similar spread among their ensemble members. There is no trend in the spread, and the variations over time are relatively small. We do not find any relation between the temperature spread across members (Fig. 5 bottom) and the temperature anomalies (Fig. 5 top). Also periods with high or low NAO are not reflected in the intra-model ensemble spread (not shown).
In the following, we focus on the coldest observed winters in N Europe; we selected those winters from the detrended ERA-interim data, which exceed an anomaly of − 1.5 standard deviations (which means T2m anomalies exceeding − 3 K). Based on this criterion, the four winters 1984/1985 (DJF 1985), 1986/1987 (DJF 1987), 2009/2010 (DJF 2010) and 2010/2011 (DJF 2011) are selected. These winters were also some of the coldest winters over Central and Eastern Europe and larger parts of Asia and have in common that anomalously easterly or northeasterly winds advect cold air to N Europe, as seen in the ERA-interim data (Figs. 6, 7). These winds are related to a pronounced NAO-like pattern with positive SLP anomalies over the Nordic Seas and the Arctic and negative SLP anomalies over the North Atlantic that are associated with anticyclonic anomalies from Scandinavia to the Ural Mountains, and low pressure anomalies south of it. DJF 1987 and DJF 2011 show at the same time a negative SLP-anomaly over the Aleutian Islands, while in DJF 1985 and DJF 2010, positive SLP anomalies occur in the North Pacific; these are consistent with ENSO teleconnection (Di Lorenzo et al. 2010), as weak to moderate El Niño conditions are observed in 1987 and 2010, and La Niña conditions in 1985 and 2011.
EXP1 reproduces the Pacific SLP anomalies very well in DJF 1985, DJF 1987 and DJF 2010 while there are some differences in DJF 2011 (Fig. 6). In DJF 2010, also the SLP anomalies in the North Atlantic, Arctic and Eurasian areas are relatively well reproduced but with reduced amplitude. The observed positive SLP-anomaly over the Arctic in DJF 1985, 1987 and 2011 are not well reproduced in EXP1. The observed SLP-anomalies in the North Pacific area are not well reproduced in EXP2. Thus, the agreement between EXP1 and ERA-interim in this area is caused by the SST-forcing and not due to sea ice variations. Over parts of the North Atlantic, Europe and along the Asian Arctic coast, the SLP-anomalies in EXP2 have some agreement with EXP1 and to an even smaller degree also with ERA-interim. However, the amplitude of the anomalies is small and only parts are significant at the 95% significance level. Still, this agreement, although mainly restricted to winds being either from land or ocean, might explain the fact that EXP2 reproduces the sign of the temperature anomalies over N Europe in the cold winters relatively well, except for DJF 1985 (Fig. 7).
In the ERA-interim data, the cold anomalies extend from N Europe across large parts of Asia almost until the Pacific Ocean. This is only partly reproduced in our experiments. All four observed cold winters show positive T2m anomalies in the Labrador Sea region, which extend into northern Canada. The southern boarder of this warm anomaly varies somewhat between winters. South of this warm area, we find again cold anomalies, which extend, to varying degree, into the North Atlantic. EXP1 reproduces a large part of the observed T2m anomalies over the Pacific, the North American and the North Atlantic areas. Over Eurasia and the Arctic, the agreement is worse. However, in all winters, cold anomalies occur over parts of Europe and Asia but with strongly reduced amplitude. EXP2 fails to reproduce most of the T2m anomalies in ERA-interim and EXP1, except for N Europe. This suggests again that sea ice variations are not the main driver for the winter cold extremes outside the Arctic and N Europe during the analyzed period.
3.2.1 Inter-model and intra-model spread
The inter-model spread in the cold winters is large. Figure 8 shows the ensemble mean anomalies of SLP in all the six individual models in the winter 2010. In this year, the MMEM of EXP1 is relatively well reproducing the observed large scale SLP-anomalies (compare Fig. 6g–i). All single EXP1-model ensemble means reproduce the large scale anomaly patterns over the North Pacific–North American region well. Also, the observed negative SLP-anomalies over the mid-latitude/sub-tropical North Atlantic and positive SLP anomalies over the Arctic regions are partly reproduced by most single models. However, larger differences occur over Eurasia and also on more regional scales. This strongly affects the temperature anomalies at regional scales (not shown). The EXP2-ensemble means of the individual models differ from each other, also over the North Pacific, and the ensemble mean anomalies are generally weaker than in EXP1.
Also in the other three cold North European winters, all EXP1-model ensemble means show a robust signal in the North Pacific–North American region. However, in the other regions, the spread among individual models is large (not shown). The agreement of the anomalies in the single model means with ERA-interim varies depending on the winter. We cannot identify any model that generally agrees best to ERA-interim. E.g., the EXP1-ensemble mean of CAM4 agrees best with ERA-interim in the winter 2010 but it agrees worst of all models in the winter 2011 (not shown). EXP2 is neither agreeing well with ERA-interim nor reproducing the EXP1 anomalies very well.
The spread among individual model ensemble members is extremely large. Figure 9 shows as an example the SLP-anomaly of the first ten ensemble members of the CAM4-model for DJF 2010. Although in this winter, the ensemble mean shows a pronounced negative NAO/AO state, some individual members show atmospheric circulation anomalies that do not resemble the NAO/AO—pattern at all. This highlights the importance of large ensembles in order to get robust responses to ice and SST variations. It also highlights the difficulty in attributing the circulation patterns to sea ice loss/SST changes from observations/reanalysis alone, as we only have one “realization” of the real world.
3.2.2 Probability distribution of N European winters in the models
In the following, we will investigate the spread and the probability for temperature anomalies in the cold observed winters in N Europe in more detail. We analyze here every individual member from all the models. Figure 10 shows the Probability Density Function (PDF) over all winter averaged T2m anomalies in N Europe. The ERA-interim data seem to show a slightly right-skewed distribution with highest probability for winters with slightly positive anomalies but with a longer tail for cold anomalies. Further, the distribution shows a secondary maximum of probability at T2m anomalies of − 3 °C, but this is probably due to the small number of winters in ERA-interim. The PDF of EXP1 and EXP2 are similar to ERA-interim but do not show the secondary maximum at − 3 °C. Both show a slightly right-skewed distribution that agrees well with the PDF of ERA-interim, with stronger cold extremes than warm extremes. About 48 and 47% of all winters show a negative temperature anomaly in EXP1 and EXP2, respectively (Table 5). The probability for the occurrence of very cold winters, with T2m anomalies below − 3°, is about 50% smaller in the model simulations compared to ERA-interim. However, the statistic for these extremes in ERA-interim is not very robust since the time-series is short with 32 winters.
In all four cold winters, the PDF shows a wide range of T2m anomalies in both EXP1 and EXP2 ensemble members (Fig. 11). The distribution is, however, moved towards colder temperatures compared to the PDF taking all winters into account (Fig. 10). In EXP1, the probability for a colder than normal winter is increased by 21% (DJF 1985) to 48% (DJF 2011) compared to the EXP1-distribution of T2m anomalies in all winters. In EXP2, the increase reaches between 21% in DJF 1985 and 43% in DJF 2011 (Table 5). In order to test if these increases could just be due to internal variability, we selected 200 sets of 120 randomly chosen winters (to mimic the number of ensemble members from each of the chosen extreme winters) from the total 3840 winters (32 winters, 120 ensemble members) and analyzed the distribution of the T2m anomalies over these 200 sets (Fig. 12). The maximum percentage of colder than normal winters does not exceed 57% and 55% in EXP1 and EXP2, respectively, in any of the sets of randomly chosen winters. In each of the cold winters, DJF 1985, DJF 1987, DJF 2010, DJF 2011, we found a higher probability for colder than normal winters than 57 and 55% in EXP1 and EXP2 (Table 5). This indicates clearly the significance of the shift towards colder winters in EXP1 and EXP2 in the four observed cold winters. However, only few members in EXP1 and EXP2 show anomalies exceeding the observed T2m anomalies in these winters (Table 6), although we note a slightly increased probability for occurrence of very cold winters as well. Also, the similarity in the probability distribution with skewness toward cold winters for both EXP1 and EXP2 is worth noting, implying the contribution of sea ice changes.
Our results indicate that the observed SST and sea ice conditions in these cold winters lead to enhanced probability for occurrence of both colder than normal winters and extremely cold winters. However, the main reason for the occurrence of the extremely cold winters in reality in these particular years is probably natural variability as the distribution of these years are not well separated from the climatological distribution. The structure of intra-seasonal, synoptic variability may also be affected by the recent climate changes. E.g., analysis of the observed Moscow daily T2m anomalies in winter indicates an increased probability of longer cold spells in the recent decade despite insignificant DJF mean changes (Shukurov and Semenov 2017, in print).
3.2.3 Cold N European winters in the models
Above, we show that the coldest observed N European winters are only partly reproduced in the models in these specific years. Now, we investigate if the coldest simulated winters in the models in the entire time period 1982–2014 agree with the large scale atmospheric and temperature anomaly patterns of the coldest observed winters. We build a composite over all individual model members, including all winters in N Europe with detrended temperature anomalies exceeding − 3 K. In total, we find 145 individual winters in EXP1 and 154 winters in EXP2, which show T2m anomalies of more than − 3 K in N Europe. The SLP and T2m anomalies, averaged over these winters are compared to the anomalies in the cold ERA-interim winters in Fig. 13 (the same 4 winters as used before; all with T2m cold anomalies exceeding − 3 K). The anomalies in EXP1 and EXP2 agree very well with ERA-interim. They show pronounced, positive AO- type SLP anomalies—that however somewhat differ from the canonical pattern. The maximum positive anomalies occur in the Barents Sea region with more than 8 hPa. The negative anomalies over the North Atlantic are more pronounced in ERA-interim but the extension of this negative anomaly into Europe and Asia agrees well between ERA-interim, EXP1 and EXP2. The T2m-anomalies are most pronounced over northeastern Europe (below − 5K) and extend across the entire of mid and high latitudes of Asia to the Pacific Ocean. Over the Canadian Arctic area, we see large positive anomalies. The cooling over the United States is more pronounced in ERA-interim compared to our experiments. This comparison clearly shows that the models are well able to reproduce the large scale patterns, which are connected to cold winters over N Europe.
Winter (DJF) SLP (top) and T2m (bottom) anomalies in cold Northern European winters in ERA-interim, EXP1 and EXP2. All winters, with N European anomalies colder than − 3 K (exceeding − 1.5 standard deviations) have been taken into account. For EXP1 and EXP2, all individual ensemble members have been analyzed. All data have been detrended
3.2.4 Relation between N European winter and preceding ice anomalies
Our results show a correlation of winter T2m in N Europe in both EXP1 and EXP2 with T2m in ERA-interim of around 0.75, indicating the importance of sea ice variations for winter T2m variations in this region. However, from the experiment setup, we only know that sea ice matters, but not in which specific regions and at which specific time periods it is particularly important for the winter T2m in N Europe. A more detailed analysis of this question will be subject to another study. However, here we provide some first results based on grid-point regressions and correlations between Arctic sea ice concentration and N European winter T2m (Fig. 14). Figure 14 a–c shows the linear regression coefficient between detrended DJF sea ice concentration and T2m in ERA-interim, EXP1 and EXP2 at lag 0. The regression patterns are similar in all three data sets with positive values from the Labrador Sea across the Canadian Archipelago to the Beaufort Sea and negative values with centre in the Barents Sea region. Although the signal is largest in Labrador Sea and Barents Sea, the highest correlations occur in the Beaufort Sea with up to 0.6 (not shown). The regresssion and correlation patterns seem to reflect mainly the sea ice response to the atmospheric circulation anomalies (NAO+ in warm North European winters and NAO− in cold winters). For single autumn months, we find the highest correlation between sea ice concentration and the following N Europe winter T2m in November (also higher than for the autumn average). If we regress November sea ice concentration with the next winter T2m, we find over the western Arctic part from Labrador Sea to Beaufort Sea positive coefficents, similar as for lag 0. In the Barents Sea region, values are in contrast to winter mostly positive. The correlations between autumn sea ice concentration and N European winter show the largest and significant correlations over parts of the Beaufort Sea but the variations of sea ice in the Beaufort Sea in November are rather small. Over the Barents Sea, correlations are small and only in ERA-interim partly significant.
a–c Linear regression coefficient between detrended winter (DJF) sea ice concentration and winter T2m in Northern Europe in ERA-interim (NOAA-OISST for sea ice) and the multi-model means of EXP1 and EXP2 for 1982–2014. Shown are ice concentration anomalies in % per standard deviation change of winter T2m. d–f The same as a–c but for November sea ice and the following winter T2m. The thin black lines indicate where the correlation is significant at the 95% level
The correlation between the entire autumn Arctic sea ice area and winter T2m in N Europe is small (0.18 and 0.08 for EXP1 and EXP2); the correlation between Barents/Kara Seas autumn ice area and T2m reaches 0.27 and 0.22 in EXP1 and EXP2, respectively. Correlations between sea ice concentration in single months and the following winter show the highest values between November ice in the Beaufort Sea (integrated over 70°N–82°N, 90°W–160°W) and DJF T2m in N Europe (0.38 and 0.46 in EXP1 and EXP2).
We further analyze the relation between both autumn ice in the Barents-Kara Seas and the Beaufort Sea and N Europe winter T2m. It turns out that the relationship between November Beaufort Sea ice and winter N Europe temperature is substantially larger compared to the linkage between Barents–Kara Seas ice and N Europe winter T2m. Figure 15 shows the regression coefficient between the November Beaufort Sea ice area and winter T2m and SLP. High ice in the Beaufort Sea is followed by postive T2m-anomalies over Barents Sea, which extend towards northern Europe. The signal is significant in both EXP1 and EXP2 but smaller than in ERA-interim data. Here, we find a much stronger regression with the winter SLP, with reduced SLP over the Arctic Ocean and Nordic Seas and increased SLP further to the south. This positive AO-like pattern leads to strong warming over most of Central, Eastern and Northern Europe and the Eurasian Arctic. The SLP regression pattern in EXP1 is partly reproducing the ERA-interim results (but with much smaller amplitude) while EXP2 shows only some similarities to the ERA-interim pattern over the northeastern North Atlantic–northern European area. Despite the large response in ERA-interim and the large number of simulations in EXP1 and EXP2, the SLP-signal is except for a few small patches not significant.
Linear regression coefficient between detrended November sea ice area in the Beaufort Sea (averaged over 70°N–82°N, 90°W–160°W) and winter SLP (a–c) and T2m (d–f) in Northern Europe in ERA-interim and the multi-model means of EXP1 and EXP2 for 1982–2014. Shown are winter T2m and SLP anomalies in K and hPa per standard deviation change of November ice area in the Beaufort Sea. The thin black lines indicate where the correlation is significant at the 95% level
The warm anomaly over the Barents Sea in winter, shown in Fig. 15, is linked to negative sea ice anomalies in the Barents Sea. Figure 16 reveals that reduced winter sea ice in the Barents Sea follows high autumn ice in the Beaufort Sea.
Linear regression coefficient between detrended November sea ice area in the Beaufort Sea (averaged over 70°N–82°N, 90°W–160°W) and sea ice concentration in the following winter (NOAA-OISST-data, 1982–2014). Shown are winter sea ice concentration anomalies in % per standard deviation change of November ice area in the Beaufort Sea. The thin black lines indicate where the correlation is significant at the 95% level
The weak circulation response in EXP1 and EXP2 (EXP1 and EXP2, Fig. 15d–f) indicates that the response is mainly of thermodynamic character and only to a smaller part of dynamic character. To further investigate the thermodynamical and dynamcial contributions to the T2m-anomalies in N Europe, we use a simple estimation: To estimate the dynamical contribution for the nth winter in each model, we project over a region including Northern Europe and its upstream regions (40°W–40°E, 20°N–80°N) the winter SLP anomalies onto SLP ensemble mean anomalies of the nth winter.
where X(e,t) designates the SLP anomalies for DJF of year t for ensemble e. XEM,n are the SLP anomalies of the ensemble mean of the nth winter. Angle brackets designate the area-weighted average. In(e,t) provides a SLP index measuring the intensity of the atmospheric circulation pattern simulated in the ensemble mean anomalies of the nth winter. The T2m-anomalies (noted T) are then regressed onto this SLP index, using the outputs of all members and winters:
we define the result from this regression as TDyn, the dynamical T2m contribution at the year tn. The difference of the ensemble mean T2m and the dynamical T2m provides an estimate TThermo, the thermodynamical contribution.
We repeat this procedure in each model separately, as the mean state and the signature of atmospheric variability is different in each model. This simple estimation is based on linear assumption, and a more advanced estimation of the dynamical and thermodynamical influence could be constructed using circulation analogs (Van der Dool et al. 2003, or more recently; Deser et al. 2016a, b).
The results (Figs. 17, 18) indicate that the dynamical contribution can be large in specific years in specific models, particularly in winters with large T2m-anomalies. We quantify the importance of the dynamical and thermodynamical contribution with the root mean squared anomalies and the correlation of each terms with the total T2m-anomalies, as given by the numbers in Figs. 17 and 18. In both EXP1 and EXP2, the thermodynamical contribution is dominant, as the T2m trend in N Europe is mostly governed by the thermodynamic part in both EXP1 and EXP2, due to the warming SST and reducing sea-ice extent. However the correlations of the dynamical components with the total T2M-anomalies are more important in EXP2, which demonstrate that our experiments simulate a dynamical response to the interannual sea-ice anomalies.
Time series of T2m anomalies, in K, for DJF averaged over Northern Europe (5E–40E, 50N–70N) for ensemble mean total T2m (black), dynamical T2m (green) and thermodynamical T2m parts (red). The upper six figures indicate the results for each model separately. Bottom panel shows the result of the multi model ensemble mean (MMM). The numbers given on top of each panel are the root mean squared anomalies of the dynamical (green) and the thermodynamical T2m (red), and the correlation of the dynamical (green) and thermodynamical T2m (red) with the total T2m anomalies
As Fig. 17 but for EXP2
Most recent studies (e.g. Inoue et al. 2012; Garcia-Serrano et al. 2016; King et al. 2016; Koenigk et al. 2016) suggested that autumn ice variations in the Barents and Kara Sea are important for winter temperature in lower latitudes. Our model results do not support a particularly strong role of autumn ice variations in this area for T2m in the N Europe region. However, the sea ice conditions in winter in the Barents Sea seems to be important for the T2m in N Europe. We find a negative correlation of around − 0.35 in with the winter T2m in N Europe in EXP1 and EXP2. This rather low correlation agrees well with the large spread among individual model members and explains why many ensemble members are needed to obtain a robust response.
3.3 Cold winters in Asia
Above, we showed that sea ice has an impact on winter T2m variability in N Europe but little effect in most of the other land regions. However, Asia is the region where winter trends are negative and a lot literature has focused on the impact of sea ice on Asian temperature trend. Thus, we will here shortly discuss the representation of cold winters in the Asian land regions in our models. As in Sect. 3.2.3, we investigate if the the large scale atmospheric and temperature anomaly patterns in the coldest simulated winters in the models agree with those of the coldest observed winters in 1982–2014.
Again, we use all winters exceeding a cold anomaly of more than − 1.5 standard deviations (based on the ERA-interim data) of the detrended time series. The large scale circulation and temperature fields connected to cold winters in the four Asian regions (see Table 1) agree, as for N Europe, very well in EXP1 and EXP2. Thus, we only compare EXP1 to ERA-interim in Fig. 19. The standard deviation of winter T2m in ERA-interim is slightly higher than in EXP1 in all four Asian regions and also the occurrence of very cold winters is slightly higher in ERA-interim compared to EXP1 and EXP2. While ERA-interim shows 2–5 winters, which exceed − 1.5 standard deviation in the period 1982–2014, EXP1 and EXP2 show between 150 and 200 cold winters (of 3840 individual winters) with anomalies below − 1.5 standard deviation of the ERA-interim values.
Cold winters in the two northern Asian regions are connected to a NAO-like pattern with the largest positive SLP anomaly over the Barents–Kara Seas in ERA-interim (Fig. 18 a, b). On the east side of this high pressure anomaly, anomalously cold air is transported from the Arctic to the south. Large parts of Eurasia show a strong, cold anomaly in both cases. Particularly during cold NE Asian winters, cold anomalies occur also over North America mainly due to positive SLP-anomalies over western North America/eastern North Pacific. The positive SLP anomaly with centre over the Barents–Kara Seas and the related cold anomalies over large parts of Eurasia are reproduced in EXP1 but the cold anomaly is somehwat more confined to the NE Asian region itself in cold winters in this region. The negative SLP anomalies over the North Atlantic are weaker and shifted further to the east. The postive SLP over western North America/Eastern North Pacific in cold NE Asian winters is not reproduced and thus the cooling over North America not either in our model simulations.
For the southern Central Asian regions, particularly SE Central Asia, differences between the large scale patterns of ERA-interim and models differ somewhat more, but in all cases, the main driver for the cold winters is an anticyclonic anomaly with centre over northeastern Europe. ERA-interim data show warm anomalies in the Barent Sea region, which is slightly less pronounced in EXP1 and EXP2. We see also slightly colder than normal temperatures over North America in ERA-interim, while the models show warm anomalies. This is in line with the weaker warm Arctic-cold continent pattern in the models compared to ERA-interim.
Note that the large scale circulation patterns can strongly deviate from year to year in ERA-interim (similar as in Fig. 6 for the cold winters in N Europe). Given the small number of cold cases, this might explain some of the differences between ERA-interim and the model simulations.
As for the N Europe area, we calculated the thermodynamic and dynamic contributions to the temperature anomalies in EXP1 and EXP2 (not shown). The dynamical contribution is dominating the Asian temperature anomalies in EXP2 while both dynamical and thermodynamical contributions are of similar size in EXP1. The area where dynamcial effects are largest in EXP2, is the region between 40°N–60°N, 80°E–13°E. This region is far away from the oceans and agrees well to the area that shows largest negative temperature trends in observations.
4 Conclusions
This study analyzed the impact of sea ice and SST on temperature variations in mid and high northern latitudes. We analyzed two sets of multi-model ensemble experiments performed in the GREENICE-project with six different global atmosphere models. The first experiment (EXP1) used observed varying SST and SIC data as lower boundary forcing while the second experiment (EXP2) used varying SIC but climatological SST as lower boundary forcing.
The models used in this study have been widely used in many scientific investigations; still shortcomings in the models and the experiment set-up might affect the results. The usage of AGCMs, which do not allow for coupled ocean–atmosphere feedback processes, might lead to an underestimation of the magnitude of the response to sea ice loss (Deser etal. 2016). The description of sea ice in the AGCMs is simplified and most AGCMs use a constant sea ice thickness and a climatological cycle of sea ice albedo. Since ice thickness and ice albedo (Koenigk et al. 2014) have been reduced in the last decades, this might lead to an underestimated response to ice reduction and variability. Further, the usage of climatological SSTs in EXP2 leads to a smoothing of SST-gradients and might affect the response in the EXP2-experiments.
Despite these potential short-comings, our model experiments reveal robust results across our six atmosphere models.
The correlation between winter T2m variations in EXP1 and ERA-interim data is high for all ocean areas but lower over land. However, the T2m average over most of ten different mid and high latitude continental sub domains is significantly correlated with the ERA-interim data. In contrast, T2m in EXP2 is only significantly correlated with ERA-interim over the Arctic Ocean, in northern Europe and northeastern North America. This indicates that sea ice variations have only a limited impact on T2m variations in most mid and high northern latitude regions. Further, the suggested warm Arctic—cold continent pattern (Overland et al. 2011) is only partly reproduced in EXP1 and not reproduced in EXP2 as a response to lower boundary and radiative forcing. Thus, according to our experiments this pattern is unlikely to be due to sea ice variations in reality and might represent internal atmospheric circulation variability.
The ice variations are important for the interannual variations of winter T2m in N Europe although the amplitude of the anomalies in the multi-model ensemble mean is about three times smaller than in ERA-interim. This is mainly due to a large spread of simulated T2m-anomalies across the individual ensemble members and shows that many ensemble members are needed to simulate the observed T2m variations over N Europe. November sea ice anomalies in the Beaufort Sea seems to play an important role for the T2m in N Europe in the following winter. They are highly negatively correlated with winter sea ice in the Barents Sea. Those in turn contribute thermodynamically to T2m anomalies in N Europe.
Our results revealed a robust response of the ice impact on N Europe T2m across the individual model ensemble means. The T2m in N Europe of each single model ensemble mean is significantly correlated with ERA-interim. However, as for the multi-model ensemble mean, the amplitude of the single model ensemble mean T2m responses are about three times weaker than the observed anomalies (Fig. 2). Such characteristics of the ensemble response may be related to the forced one-way interaction in our AGCM simulations, when the simulated ensemble mean response represents a feedback from the SST and sea ice anomalies originally caused by internal atmosphere variability (Bretherton and Battisti 2000). However, it could also suggest a too weak atmospheric response to surface forcing (Eade et al. 2014).
The sea ice conditions in the four coldest observed winters (exceeding cold anomalies of 1.5 standard deviations) in ERA-interim in N Europe since 1982, increase the probability for cold winters in N Europe in the models. However, only few ensemble members simulate T2m anomalies that are as large as the observed ones in these winters. Further, we found that T2m and SLP amplitudes and patterns in the coldest simulated winters in N Europe (which can differ from the observed winters) in the models since 1982 agree well with the coldest winters in ERA-interim. This shows that the models are able to realistically reproduce large-scale circulation and T2m anomaly patterns during extremely cold winters in N Europe. Thus, the fact that the models do not fully reproduce the observed cold winters in these specific winters is not caused by a general failure of the models to reproduce large scale conditions and processes that cause cold winters in N Europe. Therefore, we conclude, that the occurrence of the observed extremely cold winters in these specific years is mainly due to natural variations of the atmospheric circulation and only to a smaller part caused by the underlying sea ice and SST conditions.
The results from our study, in contrast to those studies, which suggested a clear link between sea ice and mid latitude cold winters, do not reveal a robust sea ice impact. Our results suggest instead the major role of internal variability for the recent climate anomalies in lower latitudes.
References
Årthun M, Schrum C (2010) Ocean surface heat flux variability in the Barents Sea. J Mar Syst 83:88–98
Barnes EA (2013) Revisiting the evidence linking Arctic amplification to extreme weather in midlatitudes. Geophys Res Lett 40:4734–4739. https://doi.org/10.1002/grl.50880
Bintanja R, Graversen RG, Hazeleger W (2011) Arctic winter warming amplified by the thermal inversion and consequent low infrared cooling to space. Nat Geosci Lett https://doi.org/10.1038/NGEO1285
Bretherton CS, Battisti DS (2000) An interpretation of the results from atmospheric general circulation models forced by the time history of the observed sea surface temperature distribution. Geophys Res Lett 27:767–770
Brown RD, Robinson DA (2011) Northern Hemisphere spring snow cover variability and change over 1922–2010 including an assessment of uncertainty. Cryosphere 5:219–229. https://doi.org/10.5194/tc-5-219-2011
Cohen J, Entekhabi D (1999) Eurasian snow cover variability and Northern Hemisphere climate predictability. GRL 26(3):345–348
Cohen JL, Furtado JC, Barlow MA, Alexeev VA, Cherry JE (2012) Arctic warming, increasing snow cover and widespread boreal winter cooling. Environ Res Lett. https://doi.org/10.1088/1748-9326/7/1/014007
Cohen J, Screen JA, Furtado JC, Barlow M, Whittleston D, Coumou D, Francis J, Dethloff K, Entekhabi D, Overland J, Jones J (2014) Recent Arctic amplification and extreme mid-latitude weather. Nat Geosci 7:627–637. https://doi.org/10.1038/ngeo2234
Comiso JC, Parkinson C, Gersten R, Stock L (2008) Accelerated decline in the Arctic sea ice cover. Geophys Res Lett 35 (L01703), https://doi.org/10.1029/2007GL031972
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Holm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thepaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597. https://doi.org/10.1002/qj.828
Deser C, Sun L, Tomas RA, Screen J (2016a) Does ocean coupling matter for the northern extratropical response to projected Arctic sea ice loss? Geophys Res Lett 43:2149–2157. https://doi.org/10.1002/2016GL067792
Deser C, Terray L, Phillips AS (2016b) Forced and internal components of winter air temperature trends over North America during the past 50 years: mechanisms and implications. J Clim 29(6):2237–2258. https://doi.org/10.1175/JCLI-D-15-0304.1
Devasthale A, Sedlar J, Koenigk T, Fetzer EJ (2013) The thermodynamic state of the Arctic atmosphere observed by AIRS: comparisons during the record minimum sea ice extents of 2007 and 2012. Atmos Chem Pys 13:7441–7450. https://doi.org/10.5194/acp-13-7441-2013
Di Lorenzo E, Cobb KM, Furtado JC, Schneider N, Anderson BT, Bracco A, Alexander MA, Vimont DJ (2010) Central Pacific El Nino and decadal climate change in the North Pacific Ocean. Nat Geosci 3(11):762–765. https://doi.org/10.1038/ngeo984
Eade R, Smith D, Scaife A, Wallace E, Dunstone N, Hermanson L, Robinson N (2014) Do seasonal-to-decadal climate predictions under-estimate the predictability of the real world? Geophys Res Lett 41:5620–5628. https://doi.org/10.1002/2014GL061146
Francis JA, Vavrus SJ (2012) Evidence linking Arctic amplification to extreme weather in mid-latitudes. Geophys Res Lett 39 (L06801), https://doi.org/10.1029/2012GL051000
Francis JA, Chan W, Leathers DJ, Miller JR, Veron DE (2009) Winter Northern Hemisphere weather patterns remember summer Arctic sea-ice extent. Geophys Res Lett 36 (L07503), https://doi.org/10.1029/2009GL037274
Gao Y, Sun J, Li F, He S, Sandven S, Yan Q, Zhang Z, Lohmann K, Keenlyside N, Furevik T, Suo L (2015) Arctic sea ice and Eurasian climate: a review. Adv Atmos Sci 32:92–114. https://doi.org/10.1007/s00376-014-0009-6
García-Serrano J, Frankignoul C (2016) On the feedback of the winter NAO-driven sea ice anomalies. Clim Dyn 47(5–6):1601–1612
García-Serrano J, Frankignoul C, Gastineau G, De La Càmara A (2015) On the predictability of the winter Euro-Atlantic climate: lagged influence of autumn Arctic sea ice. J Clim 28(13):5195–5216
Gastineau G, García-Serrano J, Frankignoul C (2017) The influence of autumnal eurasian snow cover on climate and its link with Arctic sea ice cover. J Clim. https://doi.org/10.1175/JCLI-D-16-0623.1
Gong G, Entekhabi D, Cohen J (2002) A large-ensemble model study of the wintertime AO–NAO and the role of interannual snow perturbations. J Clim 15(23):3488–3499
Graversen RG, Wang M (2009) Polar amplification in a coupled climate model with locked albedo. Clim Dyn 33:629–643. https://doi.org/10.1007/s00382-009-0535-6
Graversen RG, Mauritsen T, Tjernström T, Källén E, Svensson G (2008) Vertical structure of recent Arctic warming. Nature 541. https://doi.org/10.1038/nature06502
Hazeleger W, Severijns C, Semmler T, Stefanescu S, Yang S, Wang X, Wyser K, Baldasano JM, Bintanja R, Bougeault P, Caballero R, Dutra E, Ekman AML, Christensen JH, van den Hurk B, Jimenez P, Jones C, Kållberg P, Koenigk T, MacGrath R, Miranda P, van Noije T, Schmith T, Selten F, Storelvmo T, Sterl A, Tapamo H, Vancoppenolle M, Viterbo P, Willén U (2010) EC-Earth: a seamless earth system prediction approach in action. Bull Am Meteorol Soc 91:1357–1363. https://doi.org/10.1175/2010BAMS2877.1
Hopsch S, Cohen J, Dethloff K (2012) Analysis of a link between fall Arctic sea ice concentration and atmospheric patterns in the following winter. Tellus A 64 (18624), https://doi.org/10.3402/tellusa.v64i0.18264
Hourdin F, Foujols MA, Codron F, Guemas V, Dufresne JL, Bony S, Braconnot P (2013) Impact of the LMDZ atmospheric grid configuration on the climate and sensitivity of the IPSL-CM5A coupled model. Clim Dyn 40(9–10):2167–2192
Hurrell JW, Hack JJ, Shea D, Caron JM, Rosinski J (2008) A new sea surface temperature and sea ice boundary dataset for the community atmosphere model. J Clim 21:5145–5253. https://doi.org/10.1175/2008JCLI2292.1
Inoue J, Masatake HE, Koutarou T (2012) The role of Barents sea ice in the wintertime cyclone track and emergence of a warm-Arctic cold-Siberian anomaly. J Clim 25(7):2561–2568
Jakobson E, Vihma T, Palo T, Jakobson L, Keernik H, Jaagus J (2012) Validation of atmospheric reanalyses over the central Arctic Ocean. GRL. https://doi.org/10.1029/2012GL051591
King MP, Hell M, Keenlyside N (2016) Investigation of the atmospheric mechanisms related to the autumn sea ice and winter circulation link in the Northern Hemisphere. Clim Dyn 46:1185–1195
Koenigk T, Brodeau L (2014) Ocean heat transport into the Arctic in the twentieth and twenty-first century in EC-Earth. Clim Dyn 42:3101–3120. https://doi.org/10.1007/s00382-013-1821-x
Koenigk T, Brodeau L (2017) Arctic climate and its interaction with lower latitudes under different levels of anthropogenic warming in a global coupled climate model. Clim Dyn 49:471–492. https://doi.org/10.1007/s00382-016-3354-6
Koenigk T, Mikolajewicz U, Jungclaus J, Kroll A (2009) Sea ice in the Barents Sea: seasonal to interannual variability and climate feedbacks in a global coupled model. Clim Dyn 32:1119–1138. https://doi.org/10.1007/s00382-008-0450-2
Koenigk T, König Beatty C, Caian M, Döscher R, Wyser K (2012) Potential decadal predictability and its sensitivity to sea ice albedo parameterization in a global coupled model. Clim Dyn 38(11–12):2389–2408. https://doi.org/10.1007/s00382-011-1132-z
Koenigk T, Devasthale A, Karlsson K-G (2014) Summer sea ice Albedo in the Arctic in CMIP5 models. Atmos Chem Phys 14: 1987–1998. http://www.atmos-chem-phys.net/14/1987/2014/. https://doi.org/10.5194/acp-14-1987-2014
Koenigk T, Caian M, Nikulin G, Schimanke S (2016) Regional Arctic sea ice variations as predictor for winter climate conditions. Clim Dyn 46:317–337. https://doi.org/10.1007/s00382-015-2586-1
Kosaka Y, Xie (2013) Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 501:403–407. https://doi.org/10.1038/nature12534
Li F, Wang HJ, Gao YQ (2015) Extratropcial ocean warming and winter Arctic sea ice cover since the 1990s. J Clim 28:5510–5522. https://doi.org/10.1175/JCLI-D-14-00629.1
Lindsay R, Wensnahan M, Schweiger A, Zhang J (2014) Evaluation of seven different atmospheric reanalysis products in the Arctic. J Clim 27(7):2588–2606
Liu Y, Key JR, Wang X (2008) The influence of changes in cloud cover on recent surface temperature trends in the Arctic. J Clim 21:705–715
Liu J, Curry JA, Wang H, Song M, Horton RM (2012) Impact of declining Arctic sea ice on winter snowfall. Proc Natl Acad Sci 109(11):4074–4079. https://doi.org/10.1073/pnas.1114910109
McCusker KE, Fyfe KC, Sigmond M (2016) Twenty-five winters of unexpected Eurasian cooling unlikely due to Arctic sea-ice loss. Nat Geosci 9:838–842. https://doi.org/10.1038/NGEO2820
Mori M, Watanabe M, Shiogama H, Inoue J, Kimoto M (2014) Robust Arctic sea-ice influence on the frequent Eurasian cold winters in past decades. Nat Geosci 7:869–873. https://doi.org/10.1038/NGEO2277 (published online)
Nakamura T, Yamazaki K, Iwamoto K, Honda M, Miyoshi Y, Ogawa Y, Ukita J (2015) A negative pahse shift of the winter AO/NAO due to the recent Arctric sea-ice reduction in late autumn. JGR 120:3209–3227
Nakamura T, Yamazaki K, Iwamoto K, Honda M, Miyoshi Y, Ogawa Y, Tomikawa Y, Ukita J (2016) The stratospheric pathway for Arctic impacts on midlatitude climate. GRL 43(7):3494–3501
Navarro JCA, Varma V, Riipinen I, Seland Ö, Kirkevåg A, Struthers H, Iversen T, Hansson HC, Ekman AML (2016) Amplification of Arctic warming by past air pollution reductions in Europe. Nat Geosci 9:277–281. https://doi.org/10.1038/ngeo2673
Neale RB, Richter J, Park S, Lauritzen PH, Vavrus SJ, Rasch PJ et al (2013) The mean climate of the community atmosphere model (CAM4) in forced SST and fully coupled experiments. J Clim 26:5150–5168
Ogawa F, Keenlyside N, Gao Y, Koenigk T, Yang S, Suo L et al. (2018) Evaluating impacts of recent Arctic sea ice loss on the northern hemisphere winter climate change. Geophys Res Lett 45, https://doi.org/10.1002/2017GL076502
Orsolini YI, Kvamstø NG (2009) Role of Eurasian snow cover in wintertime circulation: decadal simulations forced with satellite observations. J Geophys Res Atmos 114 (D19), https://doi.org/10.1029/2009JD012253
Overland JE, Wang M (2010) Large-scale atmospheric circulation changes are associated with the recent loss of Arctic sea ice. Tellus. https://doi.org/10.1111/j.1600-0870.2009.00421.x
Overland JE, Wood KR, Wang M (2011) Warm Arctic—cold continents: climate impacts of the newly open Arctic Sea. Polar Res. https://doi.org/10.3402/polar.v30i0.15787
Overland J, Dethloff K, Francis J, Hall R, Hanna E, Kim SJ, Screen J, Shepherd TG, Vihma T (2016) Nonlinear response of mid-latitude weather to the changing Arctic. Nature CC 6:992–999. https://doi.org/10.1038/NCLIMATE3121
Park HS, Lee S, Son SW, Feldstein SB, Kosaka Y (2015) The impact of poleward moisture and sensible heat flux on Arctic winter sea ice variability. J Clim 28(13):5030–5040
Peings Y, Magnusdottir G (2014) Forcing of the wintertime atmospheric circulation by the multidecadal fluctuations of the North Atlantic ocean. Environ Res Lett. http://iopscience.iop.org/1748-9326/9/3/034018)
Petoukhov V, Semenov VA (2010) A link between reduced Barents–Kara sea ice and cold winter extremes over northern continents. J Geophys Res. https://doi.org/10.1029/2009JD013568
Pithan F, Mauritsen T (2014) Arctic amplification dominated by temperature feedbacks in contemporary climate models. Nat Geosci. https://doi.org/10.1038/NGEO2071
Reynolds RW et al (2007) Daily high-resolution-blended analyses for sea surface temperature. J Clim 20:5473–5496
Richter-Menge J, Jeffries M (2011) The Arctic, in “state of the climate in 2010”. Bull Am Meteorol Soc 92(6):S143–S160
Screen JA (2014) Arctic amplification decreases temperature variance in northern mid- to high-latitudes. Nat Clim Change 4:577–582. https://doi.org/10.1038/NCLIMATE2268
Screen JA, Simmonds I (2010a) Increasing fall-winter energy loss from the Arctic Ocean and its role in Arctic temperature amplification. Geophys Res Lett. https://doi.org/10.1029/2010GL044136
Screen JA, Simmonds I (2010b) The central role of diminishing sea ice in recent Arctic temperature amplification. Nature. https://doi.org/10.1038/nature09051
Screen JA, Deser C, Simmonds I, Tomas R (2013) The atmospheric response to three decades of observed Arctic sea ice loss. J Clim 26:1230–1248. https://doi.org/10.1175/JCLI-D-12-00063.1
Screen JA, Deser C, Simmonds I, Tomas R (2014) Atmospheric impacts of Arctic sea-ice loss, 1979–2009: separating forced change from atmospheric internal variability. Clim Dyn 43(1–2):333–344
Screen JA, Deser C, Sun L (2015) Reduced risk of North American cold extremes due to continued Arctic Sea ice loss. Bull Am Meteorol Soc. https://doi.org/10.1175/BAMS-D-14-00185.1
Semenov VA (2016) Link between anomalously cold winters in Russia and sea-ice decline in the Barents Sea. Izv Atmos Ocean Phys 52:225–233. https://doi.org/10.1134/S0001433816030105
Semenov VA, Latif M (2015) Nonlinear winter atmospheric circulation response to Arctic sea ice concentration anomalies. Environ Res Lett. https://doi.org/10.1088/1748-9326/10/5/054020
Serreze MC, Barrett AP, Stroeve JC, Kindig DN, Holland MM (2009) The emergence of surface-based Arctic amplification. Cryosphere 3:11–19
Shukurov KA, Semenov VA (2017) Changes of the characteristics of Moscow winter surface air temperature anomalies in Moscow in 1970–2016 in a contexst of winter the Barents Sea ice reduction. Izv Atm Ocean Phys (in print)
Simonsen K, Haugan PM (1996) Heat budgets of the Arctic Mediterranean and sea surface heat flux parameterization for the Nordic Seas. J Geophys Res 101:6553–6576
Smith KL, Neely RR, Marsh DR, Polvani L (2014) The specified chemistry whole atmosphere community climate model (SC-WACCM). J Adv Model Earth Syst 6(3):883–901 (ISSN 1942-2466)
Spielhagen RF, Werner K, Aagaard Sörensen S, Zamelczyk K, Kandiano E, Budeus G, Husum K, Marchitto TM, Hald M (2011) Enhanced modern heat transfer to the Arctic by warm Atlantic water. Science 331(6016):450–453. https://doi.org/10.1126/science.1197397
Stocker T et al (2013) Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Sun HC, Zhou GQ, Zeng QC (2012) Assessments of the climate system model (CAS-ESM-C) using IAP AGCM4 as its atmopsheric component. Chin J Atmos Sci 36:215–233
Sun L, Perlwitz J, Hoerling M (2016) What caused the recent “warm Arctic, cold continents” trend pattern in winter temperatures? Geophys Res Lett 43:5345–5352. https://doi.org/10.1002/2016GL069024
Van den Dool HM, Huang J, Fan Y (2003) Performance and analysis of the constructed analogue method applied to U.S. soil moisture over 1981–2001. J Geophys Res. https://doi.org/10.1029/2002JD003114
Wallace JM, Gutzler DS (1981) Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon Weather Rev 109(4):784–812
Wegmann M, Orsolini Y, Vázquez M, Gimeno L, Nieto R, Bulygina O, Sterin A (2015) Arctic moisture source for Eurasian snow cover variations in autumn. Env Res Lett 10(5):054015
Yang S, Christensen JH (2012) Arctic sea ice reduction and European cold winters in CMIP5 climate change experiments. Geophys Res Lett. https://doi.org/10.1029/2012GL053333
Yang XY, Yuan X, Ting M (2016) Dynamical link between the Barents–Kara Sea ice and the Arctic oscillation. J Clim 29(14):5103–5122
Yeager SG, Karspeck AR, Danabasoglu G (2015) Predicted slowdown in the rate of Atlantic sea ice loss. GRL. https://doi.org/10.1002/2015GL065364
Zhang R (2015) Mechanisms for low-frequency variability of summer Arctic sea ice extent. Proc Natl Acad Sci 112(15):4570–4575
Zhou G, Latif M, Greatbatch RJ, Park W (2015) Atmospheric response to the North Pacific enabled by daily sea surface temperature variability. GRL 42(18):7732–7739
Acknowledgements
This study has been made possible by support of the Rossby Centre at the Swedish Meteorological and Hydrological Institute (SMHI) together with the NORDFORSK Top Level Research Initiative, Project no. 61841—GREENICE and the JPI-Climate—Belmont Forum project 407, InterDec. T. Nakamura was also supported by the Japanese Arctic Challenge for Sustainability (ArCS) project. Y. Orsolini was also supported by the Norwegian Research Council (Project #244166 SNOWGLACE). Simulations with IFS were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the National Supercomputer Centre at Linköping University (NSC). LMDZOR simulations were performed using HPC resources from GENCI TGCC (Grant 2016-017403).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Koenigk, T., Gao, Y., Gastineau, G. et al. Impact of Arctic sea ice variations on winter temperature anomalies in northern hemispheric land areas. Clim Dyn 52, 3111–3137 (2019). https://doi.org/10.1007/s00382-018-4305-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4305-1