Abstract
The enhancement of warming rates with elevation, so-called elevation-dependent warming (EDW), is one of the regional, still not completely understood, expressions of global warming. Sentinels of climate and environmental changes, mountains have experienced more rapid and intense warming trends in the recent decades, leading to serious impacts on mountain ecosystems and downstream. In this paper we use a state-of-the-art Global Climate Model (EC-Earth) to investigate the impact of model spatial resolution on the representation of this phenomenon and to highlight possible differences in EDW and its causes in different mountain regions of the Northern Hemisphere. To this end we use EC-Earth climate simulations at five different spatial resolutions, from \(\sim\) 125 to \(\sim\) 16 km, to explore the existence and the driving mechanisms of EDW in the Colorado Rocky Mountains, the Greater Alpine Region and the Tibetan Plateau–Himalayas. Our results show that the more frequent EDW drivers in all regions and seasons are the changes in albedo and in downward thermal radiation and this is reflected in both daytime and nighttime warming. In the Tibetan Plateau-Himalayas and in the Greater Alpine Region, an additional driver is the change in specific humidity. We also find that, while generally the model shows no clear resolution dependence in its ability to simulate the existence of EDW in the different regions, specific EDW characteristics such as its intensity and the relative role of different driving mechanisms may be different in simulations performed at different spatial resolutions. Moreover, we find that the role of internal climate variability can be significant in modulating the EDW signal, as suggested by the spread found in the multi-member ensemble of the EC-Earth experiments which we use.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The enhancement of warming rates with elevation, a phenomenon which is referred to as elevation-dependent warming (EDW, e.g. MRI 2015), is one of the regional manifestations of global warming. Impacts of EDW include changes in the high-altitude cryosphere system and mountain ecosystems, in future water availability and distribution, with possible consequences on populations depending on these resources.
Monitoring the dependence of warming rates on elevation is complicated by different factors. First of all, the complexity and heterogeneity inherent in mountain environments and in mountain climate would require a dense and homogeneous network of ground stations up to the highest altitudes, which are generally not available for most mountain areas. The picture provided by all observation-based datasets is thus biased towards lower elevations. In addition, long-term time series are required to assess the dependence on elevation of temperature trends and to filter out any inter-decadal variability from the detected trends. Unfortunately, meteorological stations with at least 30 years of records (the classical length of time to calculate climatic normals as defined by the World Meteorological Organization; Bye et al. 2011) are very few at high elevations (MRI 2015). EDW is a complex process also because it occurs in response to many different mechanisms that have feedbacks at different scales (Rangwala and Miller 2012). It is, therefore, difficult to disentangle the causal correlations among the relevant variables and to distinguish what are the main drivers of EDW.
A great number of studies on EDW has been performed in the recent decades. Most of them are based on the analysis of surface station observations, in spite of the limitations outlined above, and a few of them are based on estimates of land surface temperatures from satellite observations (e.g., Qin et al. 2009). A summary of individual studies on EDW is provided in MRI (2015) and its supplementary information. Most studies based on observations indicate that warming rates are amplified with elevation, depending on the season, the region of study and the analysed variable (usually either the minimum or maximum daily temperature), but there are also studies showing no clear correlation between temperature trends and surface elevation. Mixed results on EDW can be highly dependent on the limitations of the current networks of in situ stations, on the presence of possible non-climatic artifacts associated with changes in measurement practices, on the different methods adopted to homogenize time series and on procedures used to interpolate in situ station data to derive gridded products. All these aspects are sources of uncertainty that are exacerbated by the relative scarcity of observations in high mountains (e.g., You et al. 2010; Oyler et al. 2015).
The use of climate models, both global and regional, to study EDW allows to overcome some of the inadequacies inherent in all observing systems when trying to identify the main mechanisms at work. In fact, the output of numerical models includes all the variables (and their dynamical relations) needed to build a picture of the mechanisms driving EDW, at a given spatial and temporal resolution, and long simulations can be run both to reproduce the past and to study future projections.
There are some examples of studies on EDW using regional climate models (RCMs), whose fine scales should allow to capture the effects of the complex mountain topography on climate variability and processes better than coarser resolution global climate models (GCMs). Giorgi et al. (1997), for example, analyzed both a present-day and a doubled CO\(_2\) concentration experiment over the Alpine region with the RegCM regional climate model (Giorgi et al. 1993), run at 50 km resolution. They showed enhanced warming rates in response to a doubling of CO\(_2\) concentrations, with more pronounced changes at higher elevations in winter and spring, mostly associated with a decrease in snowpack. Another study by Rangwala et al. (2012) analyzed future projections in the minimum and maximum daily temperatures by mid-twenty-first century using four RCMs at 50 km, run over specific mountain ranges of the southwestern US Rocky Mountains. They found large increases in the maximum temperature at higher elevations in summer associated with drying conditions. Another regional climate model at 20 km resolution was used to investigate the elevational dependency of the temperature changes over Korea (Im and Ahn 2011) showing that enhanced warming occurs for minimum temperature at higher elevations, especially during winter, mostly because of the snow-albedo feedback. Still another study used the PRECIS (Providing REgional Climates for Impacts Studies) RCM at \(\sim\) 25 km resolution (Jones et al. 2004) nested into the Hadley Centre’s global atmospheric model HadAM3P to study climate change in Central America and Mexico (Karmalkar et al. 2011), highlighting the expected amplification of future warming with elevation in the lower troposphere and its significant implications for mountainous regions (e.g., Bradley et al. 2006). The paper by Minder et al. (2018) explored the characteristics and causes of EDW in the Rocky Mountains using very high resolution simulations (\(\le\) 12 km) with the Weather Research and Forecasting Model (WRF) and found very complex patterns of warming with elevation, including cases of warming nearly independent of height. They found that warming is maximum in regions of maximum snow loss and albedo reduction, identifying the snow-albedo feedback as the primary cause of EDW. Their simulations showed that EDW depends strongly on the adopted RCM configuration including the dependence not only on the spatial resolution but also on the land surface model used in the RCM.
A majority of model studies on EDW is based on global climate models, in spite of their coarse horizontal resolutions (on average coarser than 120 km; Taylor et al. 2012). Some studies used simulations from a single GCM (e.g., Fyfe and Flato 1999; Liu et al. 2009; Rangwala et al. 2010; Yan et al. 2016), while others analysed the output of several models with different characteristics, such as the latest Climate Model Intercomparison Project (CMIP5) GCM ensemble (e.g., Rangwala et al. 2013, 2016; Palazzi et al. 2017). In a recent study, Yan et al. (2016) performed specific experiments to test the sensitivity of the CCSM3 GCM to changes in CO\(_2\) concentrations and found that the changes in snow depth and cloud cover in and around the Tibetan Plateau in response to CO\(_2\) quadruplication would lead to EDW. Rangwala et al. (2013) analysed the CMIP5 GCMs up to 2100 and found that warming rates are projected to be amplified at higher altitudes with respect to the adjacent areas in the Tibetan Plateau and in the Rocky Mountains in North America, especially in the cold season. They found enhanced increases in the minimum temperature in the Tibetan Plateau related to increases in the downward longwave radiation and in the maximum temperature in the Rocky Mountains associated with snow reduction and snow-albedo feedbacks. In a previous study (Palazzi et al. 2017) we investigated elevation-dependent warming in the Tibetan Plateau–Himalayas using a subset of the CMIP5 ensemble and we found, on average, enhanced warming rates at higher elevations in both historical simulations and in future projections. In that work we used a set of physical criteria and correlations of possible variables driving EDW both with elevation and with changes in temperature to disentangle their role, and we used a multiple regression model to assess their relative importance. We found that the most important driving variable for the models in the Tibetan Plateau–Himalayas is the change (i.e., decrease) in albedo with elevation, followed by changes in atmospheric humidity and downward longwave radiation. That study, while analysing a rather large ensemble of CMIP5 models, used the multi-model mean of all GCMs to draw conclusions on EDW.
Over the recent decades, global climate models have considerably increased the number of components incorporated within them and the degree of detail in the description of the key climate processes (IPCC 2013). At the same time, global models have been tested at increasing horizontal resolutions, reaching even grid scales that are typically achieved by numerical weather prediction models (e.g., Demory et al. 2014; Davini et al. 2017).
In this paper we exploit an ensemble of climate simulations performed with the EC-Earth GCM (Hazeleger et al. 2010, 2012), run at five atmospheric horizontal resolutions from about 125 km down to about 16 km, which were produced in the framework of the PRACE project “Climate SPHINX” (Stochastic Physics HIgh resolutioN eXperiments, Davini et al. 2017; Watson et al. 2017). This represents a quite comprehensive and unprecedented set of simulations performed with a global model, able to span a large range of spatial resolutions up to those generally not achieved with GCMs for long climate simulations, and thus giving us the opportunity to test the sensitivity of specific processes or climate mechanisms to the spatial resolution which is employed. The aim of this study is to assess if and to what extent the representation of EDW (and of its driving processes) is dependent on the model resolution, as it might be expected for processes that largely depend on the orography. To our knowledge, there are only few studies that have to some extent explored the impact of the model resolution on the simulation of EDW. One is the work by Rangwala et al. (2016), in which the authors analysed various CMIP5 GCMs with spatial resolution varying between 1\(^\circ\) and 3\(^\circ\) longitude–latitude and studied EDW focusing on the Rocky Mountains and the Tibetan Plateau/Himalayas. They did not find any significant indication on the role of the spatial resolution on the simulation of EDW. Another study by Yan et al. (2016) used the data from the 1990 control and 4 \(\times\) CO\(_2\) runs by the CCSM3 GCM with horizontal resolutions of T85 (1.4\(^\circ\) lon–lat) and T31 (3.75\(^\circ\) lon–lat) and found that the increase in net radiation at the surface (influenced by the effects of decreases in total cloud and snow at ground) resulted in EDW on the Tibetan Plateau and its surroundings but that this effect was evident only at the finest model resolution (1.4\(^\circ\)). In our study we explore significantly higher resolutions, comparable to those usually achieved only by RCMs. We consider EC-Earth GCM simulations run at five horizontal resolutions from T159 (\(\sim\) 125 km) to T1297 (\(\sim\) 16 km), the coarsest of which being finer than the finest considered in the two studies mentioned above. We focus our analysis on three mountain ranges of the northern hemisphere—the Tibetan Plateau–Himalayas (already dealt with in our previous study, Palazzi et al. 2017), the Greater Alpine Region in Europe, and the Colorado Rocky mountains—in order to highlight possible regional differences in EDW. It is worth noticing that in the three regions which we consider, all located in mid-latitudes, EDW is not influenced by another important mechanism active in tropical areas, that is latent heat release in response to enhanced diabatic heating of the upper troposphere (e.g., Bradley et al. 2009).
The paper is organized as follows: Sect. 2 presents the three mountain regions considered in this study and provides a short summary on the observed EDW in each of them based on the literature. The EC-Earth model data and the methods employed for their analysis are also presented in Sect. 2. In Sect. 3 we describe the results of our analysis in terms of presence and characteristics of EDW in the three regions and in the different seasons and we discuss the differences in the model representation of the phenomenon as a function of the model resolution. The driving EDW mechanisms are described in Sect. 4, while Sect. 5 summarizes and discusses the main results and concludes the paper.
2 Study areas, data and methods
2.1 Study areas
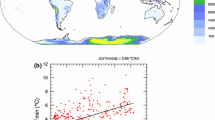
We consider three mountainous regions shown in Fig. 1: part of the Rocky Mountains in United States (Rockies, − 125\(^\circ\)E to − 95\(^\circ\)E longitude, 34\(^\circ\)N–49\(^\circ\)N latitude), the Greater Alpine Region (GAR, 4\(^\circ\)E–19\(^\circ\)E longitude, 43\(^\circ\)N–49\(^\circ\)N latitude) and the Hindu Kush–Karakoram–Himalaya–Tibetan Plateau (HKKH-TP, 70\(^\circ\)E–105\(^\circ\)E longitude and 25\(^\circ\)N–40\(^\circ\)N latitude). Please note that the green areas in Fig. 1 indicate the regions lying below 500 m a.s.l.; these areas have been filtered out in our analysis of EDW, as explained in Sect. 2.3. Besides the literature review reported in Sect. 1, here we provide a brief overview and characterization of observed EDW in the three regions, as from previous studies based on measurements:
-
In the Colorado Rocky mountains, EDW and its possible impacts on snowpack characteristics and timing of seasonal melting, forests and vegetation have been documented in past studies (e.g., Diaz and Eischeid 2007; Clow 2010; Pederson et al. 2011; Stewart et al. 2005). One of them (Diaz and Eischeid 2007), for example, documented enhanced warming rates in the period 1987–2006 with respect to the early twentieth century above about 2000 m a.s.l. with trends exceeding by about 1\(^\circ\)C the average temperature increase in the Western United States. This and other studies (e.g., Daly et al. 2008; Williams et al. 2010; Clow 2010; Pederson et al. 2011, 2013) assessed EDW in this region using measurements from the high-elevation Snowpack Telemetry (SNOTEL) network and related gridded climate products, without evaluating these data for possible inhomogeneities, an issue which was subsequently dealt with by Oyler et al. (2015).
-
In the Alpine region from the late ninteenth century until the end of the twentieth century temperatures have risen at a rate about twice as large as the northern-hemispheric average (mean temperature increase of about 2 \(^\circ\)C, Auer et al. 2007). Warming occurred with a rate of 0.5 \(^\circ\)C/decade from 1980 onwards (EEA 2009) and Philipona (2013) suggested mainly water vapor-enhanced greenhouse warming as a cause. Previous studies also suggested that larger increases in average surface air temperature at higher elevations in the Alps occurred in winter and spring compared to other seasons, particularly in the Swiss Alps (Beniston et al. 1997), mainly associated with a strong snow-albedo feedback. Another study focusing on the southern part of the Eastern Alps (the Trentino region), however, found significant negative elevation-dependent warming in the period 1975–2010, consistent for mean, maximum and minimum air temperature, attributed to solar brightening and increased radiative forcing at lower elevations (Tudoroiu et al. 2016);
-
In the Tibetan Plateau the existence of EDW was first demonstrated by Liu and Chen (2000), showing that temperature variations during the last 100 years in this high-mountain region have a larger magnitude of change and appear at an earlier time compared to the whole Northern Hemisphere, particularly in the cold season. This led to the development of many other studies focused on EDW in this area. Liu et al. (2009), for example, analysed the elevation dependency in monthly mean of daily minimum temperature finding more prominent warming at higher than lower elevations during winter and spring most likely caused by a combination of cloud-radiation and snow-albedo feedbacks. Yan and Liu (2014) also showed a dependence of warming on elevation over the last 50 years, particularly amplified in most recent decades. Increasing warming rates with elevation between 3000 m and 5000 m have also been detected from satellite in this region, through the analysis of land surface temperature data (e.g., MODIS observations, Qin et al. 2009). Another study (You et al. 2010) used homogenized surface stations at elevations higher than 2000 m a.s.l. and two reanalysis products to investigate EDW in the Tibetan Plateau and found a lack of any linear relationship between temperature trends and elevation in the surface data and an inconsistent picture in the two reanalyses. Their results, while highlighting the complexity of the phenomenon, also suggest that different datasets can provide different pictures and that caution should be taken when using reanalysis products to identify climatic trends in this topographically complex region.
Topographic maps of the three study areas (left: Rocky Mountains; middle: Greater Alpine Region; right: Hindu Kush–Karakoram–Himalaya–Tibetan Plateau) from a high-resolution Digital Elevation Model at \(\sim\) 0.0167 ° resolution (ETOPO1 Global Relief Model from the NOAA’s National Geophysical Data Center). Green areas lie below 500 m a.s.l. See text for details
2.2 Model data
We analyze the output of historical and future simulations of the state-of-the-art Earth System Model EC-Earth, version 3.1 (Hazeleger et al. 2010, 2012; http://www.ec-earth.com) performed in the framework of the PRACE project Climate SPHINX (Stochastic Physics HIgh resolutioN eXperiments). All technical aspects and the scientific setup of the Climate SPHINX experiments are described in Davini et al. (2017) and on the main project web pages http://www.to.isac.cnr.it/sphinx/. The simulations performed with the EC-Earth GCM in SPHINX are atmosphere-only experiments extending for 30 years in the past (from 1979 to 2008) and 30 years in the future (from 2039 to 2068) using forcing conditions from the Representative Concentration Pathway emission scenario RCP 8.5 (Riahi et al. 2011). EC-Earth was run exploring five different horizontal resolutions, labelled as low (spectral resolution T159, corresponding to \(\sim\) 125 km in the meridional direction), moderate (T255, \(\sim\) 80 km), intermediate (T511, \(\sim\) 40 km), high (T799, \(\sim\) 25 km), and very high (T1279, \(\sim\) 16 km). The vertical resolution is kept constant across all of the simulations and accounts for 91 levels up to 0.01 hPa. The coarsest resolution, T159, is the one typically used in state-of-the-art global climate model simulations (e.g. in the latest CMIP5 intercomparison project), while the finest, T1279, is a resolution typically used for numerical weather prediction. Due to computational costs, a different number of EC-Earth members is available for each resolution: twenty members were run at T159 and at T255, twelve at T511, six at T799 and two at T1279. A peculiarity of the SPHINX experiment is that half of the members at each resolution was run including base physics while the other half using stochastic parameterizations (Davini et al. 2017). Introducing randomness into parameterizations represents a way to include small-scale processes in coarse resolution models with the advantage of being less computationally-demanding than increasing the spatial resolution of numerical models (Palmer 2012). These ensembles give us the opportunity to gauge, at the same time, the internal variability of the EC-Earth model (thus, also, climate variability in EDW) through the spread of the multi-member ensemble as well as the uncertainty associated with the specific model chosen, i.e., a model implementing either base physics or stochastic parameterizations. In our EDW analysis we do not find any significant difference between simulations with and without stochastic physics (discussed in Sect. 3 and shown in the Supplementary Information), and thus we consider all individual members, irrespective of whether stochastic physics is implemented or not, as part of a single ensemble. In addition, our results are mostly based on the analysis of the multi-member ensemble mean as a representative measure of the whole ensemble.
We analyze the following set of model variables which are relevant for the study of EDW, as also done in previous studies (e.g. Palazzi et al. 2017): surface altitude and monthly averages of daily minimum and maximum near surface air temperature (tasmin and tasmax, respectively, using standard CMIP5 nomenclature), surface downwelling longwave and shortwave radiation (rlds and rsds, respectively), surface upwelling shortwave radiation (rsus), near surface specific humidity (huss). The surface albedo is calculated as the ratio between the upward (i.e., reflected) and downward (i.e., incoming) shortwave radiation at the surface. The height of the mean orography (elevation) used by the model is available for each simulation resolution. For the observed elevation data shown in Fig. 1, we use the ETOPO1 Global Relief Model from the NOAA’s National Geophysical Data Center (NGDC) available at http://www.ngdc.noaa.gov/mgg/global/global.html, a digital elevation model (DEM) available for the whole globe with a grid spacing of 1 arc-minute (approximately 0.0167°).
2.3 Methods
The first step to assess elevation-dependent warming is to quantify a warming signal. In this study, this is evaluated as the difference, or change, between the 2039–2068 climatology and the 1979–2008 climatology of the minimum and of the maximum daily temperature (\(\Delta tasmin\), \(\Delta tasmax\)). For each of the three regions, the temperature change between the future and past climatology is evaluated on a seasonal basis using the standard definition of the seasons for the Northern Hemisphere mid-latitudes: winter (December–February, DJF), spring (March– May, MAM), summer (June–August, JJA), and autumn (September–November, SON). It is generally recommended to analyze minimum and maximum temperatures separately because different mechanisms driving EDW can be at play during nighttime and daytime.
The second step is to assess whether a warming signal in minimum and maximum temperatures exhibits a dependence on elevation. As commonly done in the literature (e.g. Liu and Chen 2000; Vuille et al. 2003; Pepin and Lundquist 2008; Liu et al. 2009; Qin et al. 2009; Rangwala et al. 2010, 2012; Palazzi et al. 2017), we calculate the slope obtained by linear regression of timeseries of daily minimum or maximum temperature against the model elevation and we assess its statistical significance. The regression is performed both at each grid point and using data averaged into elevational bands. The statistical significance of the linear slopes is assessed using a Student's t test, which tests against the null hypothesis that the coefficient of the regression is zero (no slope). We also explore a new methodology based on grouping the temperature change data into elevation bins and then fitting the Probability Density Function (PDF) of the temperature changes evaluated for each bin with a LOcal regrESSion (LOESS) method. In fact, the uneven distribution of points at different elevations may have an impact on the slope evaluation and the dependence of the temperature changes with elevation may not be linear. Using the PDF solves the first issue while the LOESS regression would highlight possible departures from linearity.
Only grid cells with elevation above 500 m a.s.l. are considered in the analysis, to reduce some of the influence of the coastal areas or of other areas generating potential interference, such as the Po Valley in the Greater Alpine Region. Another geographical filter is applied in the analysis of the HKKH-TP region to exclude the area of the Taklamakan desert, a region bounded by the Kunlun Mountains to the south, the Pamir Mountains and Tian Shan to the west and north, and the Gobi Desert to the east. This is done in order to avoid the excessive contribution to warming of this desert area, similar to the approach applied in Giorgi et al. (2014) who filtered out desert areas with extreme large (small) values of the indices that the authors used to assess hydro-climatic extremes.
Using a similar methodological approach as in Palazzi et al. (2017), we proceed with the identification of the variables that may potentially contribute to EDW. These include all factors whose changes may alter the surface energy balance and cause temperature variations, and thus include albedo, surface downwelling longwave (thermal) and shortwave radiation, and near-surface specific humidity, as already suggested by previous studies (e.g. Rangwala and Miller 2012; Palazzi et al. 2017). As done for the minimum and the maximum temperature, we calculate the change between the average in the period 2039–2068 and the average in the period 1979–2008 of the possible EDW drivers and, in particular, the absolute change for albedo (\(\Delta albedo\)) and the fractional (or normalized) change for rlds, rsds, and huss (\(\Delta rlds/rlds_{0}\), \(\Delta rsds/rsds_{0}\), \(\Delta huss/huss_{0}\)). Fractional changes are calculated relative to the averaged climatology between the mean in the years 1979–2008 and the mean in the years 2039–2068. Previous studies showed that temperature changes may be more sensitive to the fractional changes of those variables rather than to their absolute changes (e.g. Rangwala et al. 2013, 2016).
In order for the four variables listed above—\(\Delta albedo\), \(\Delta rlds/rlds_{0}\), \(\Delta rsds/rsds_{0}\), \(\Delta huss/huss_{0}\) – to be actual EDW drivers, the following conditions have to be satisfied: (1) they have to exhibit a dependence on the elevation and the sign of that dependence has to be physically consistent with enhanced warming with elevation, and (2) they have to spatially correlate with temperature variations even if the dependence on elevation is removed. Condition (1) implies that the changes in radiations (rsds, rlds) and in huss have to exhibit the same elevational dependence as the temperature change does: if these variables increase (decrease) also the temperature change increases (decreases). On the contrary, changes in albedo have to exhibit an elevational gradient of opposite sign, since an increase in albedo leads to a reduction of absorbed radiation at the surface and, therefore, to a decrease in surface warming. Basically, condition (1) ensures that the variation with altitude of a given variable and the altitudinal dependence of temperature changes are related with each other by some known physical mechanisms. Condition (2) is essential to identify those variables which still (spatially) correlate with temperature changes independently of elevation.
Finally, to disentangle the relative importance of the identified EDW drivers in each season and region, we set up a multiple linear regression model (see Eq. 1) in which the change in daily minimum or maximum temperature is the predictand and the possible drivers are the predictors (as in Palazzi et al. 2017). Predictors and the predictand are altitude-detrended, by removing the linear fit on elevation, and standardized, by dividing each change by its standard deviation over the whole spatial domain.
In Eq. 1 the drivers correspond to the variables that, among \(\Delta albedo\), \(\Delta rlds/rlds_{0}\), \(\Delta rsds/rsds_{0}\), and \(\Delta huss/huss_{0}\), fulfill the conditions (1) and (2) described above. This approach allows to test all the possible combinations of the n predictors that lead to a different regression model. Overall, the possible regression models are (2\(^n -\) 1) and their ability in predicting the temperature change is quantified by the coefficient of determination R\(^2\) that measures the proportion of the variance of the predictand that they can explain: the closer R\(^2\) is to 1, the better the prediction is. At the same time, the value of R\(^2\) allows to quantify how much of the EDW response in the model is not explained by the drivers (predictors) considered. By construction, the regression models including a larger number of predictors are associated with higher values of R\(^2\). Therefore, to measure the relative quality of the regression models and avoid a ranking biased by the number of predictors, we use the Akaike information criterion corrected for finite sample sizes (AICc, Burnham and Anderson 2003), which favors the models with less predictors and penalizes those with more (the lower the AICc, the better the model).
3 The simulated elevational dependence of surface warming
We analyse EDW by exploring the dependence of the minimum and maximum temperature changes on elevation for the three areas and for each season, and at each model resolution. One example is shown in Fig. 2, where EDW is analysed for the minimum temperature in autumn (SON) in the Rockies, GAR, and HKKH-TP. All other cases are displayed in Figs. S1–S6 of the Supplementary Information (SI). Figure 2 shows in black the regression line evaluated using all data, in green the regression line evaluated fitting the average of the data (green dots) in each 100 m-thick elevational bin, and in blue the LOESS fitting curve. Purple shading indicates the probability density of a given minimum temperature change in each elevation bin (see also Sect. 2.3). Figures 3, 4, and 5 show, for each model resolution (displayed along the x-axis) and season (each column plot), the value of the slope describing the linear relationship between either the minimum or maximum temperature changes and the elevation (corresponding to the slope of the green line in Fig. 2 and in Figs. S1–S6 of the SI). Each grey circle indicates the output of one individual model member at each resolution, while the black circle denotes the multi-member mean. Empty symbols indicate elevational gradients of surface warming that are not statistically significant. Positive slopes in Figs. 3, 4 and 5 indicate EDW, while negative slopes highlight the situations in which there is still warming but it is larger at lower elevations (assuming a linear relationship) and we do not focus on this kind of occurrences. Finally, Table 1 summarizes the information provided in Figs. 3, 4 and 5 with regard to the multi-member mean, highlighting with a “Y” entry EDW cases and with a “N” the cases with no EDW. ‘Y” or “N” entries in parentheses denote the cases in which the slope of the elevational gradient of warming rate is not statistically significant against the hypothesis of no slope.
Dependence of minimum daily temperature (tasmin) on elevation in SON for the Rocky Mountains (left panels), the GAR (middle panels) and the HKKH–TP (right panels) at the different EC-Earth model resolutions. The black line is the regression line evaluated using all data while the green line that evaluated fitting the average of the data (green dots) into each elevational bin. Superimposed is the PDFs of the temperature change calculated for each bin (shading), as explained in Sect. 2.3. The LOESS curved fitting line is also shown in blue. See also Figs. S1–S6 of the SI to look at all remaining cases
Elevational gradients of the seasonal temperature change in the Rocky Mountains, for each ensemble member at different model resolutions. The minimum and maximum temperature changes are shown in the top and bottom panels, respectively, while different seasons are organized in the different columns. Each gray circle is the output of one individual model ensemble member at each resolution, while the black circle denotes the multi-member mean (corresponding to the slope of the green line in Fig. 2 and in Figs. S1–S6 of the SI). The open symbols represent statistically non-significant elevational gradients of warming rates
The same as Fig. 3, for the GAR
The same as Fig. 3, for the HKKH-TP
We use the information extracted from Figs. 2-5, S1–S6 of the SI and from Table 1 to analyse in detail how the EC-Earth model represents seasonal EDW in the three areas:
-
Rockies (Figs. S1 and S2, left column plots of Fig. 2 and Fig. 3): The model simulates EDW in both the minimum temperature and the maximum temperature in autumn at all model resolutions, with more intense EDW as the resolution becomes coarser (more evident for tasmax). As suggested in Figs. 2 and S1–S2, autumn is also the season in which the relationship between changes in tasmin or tasmax and the elevation is rather well described by a linear model. In the other seasons the EDW signal is either absent or less evident throughout all resolutions. In winter EDW is not detected, and larger temperature increases are expected at lower than higher elevations. This signal is robust across all model resolutions and almost all model members at each resolution. More precisely, Figs. S1 and S2 of the SI show a more complex pattern of temperature changes with elevation in winter (left column plots): in fact, there is an elevational range, between about 1000 and 2000 m a.s.l., where EDW in both tasmin and tasmax is found, while the negative elevational gradients of warming found at lower and higher elevations dominate the overall trend, indicating no EDW. Rangwala et al. (2012), using mid-twenty-first century projections of four regional climate models with a spatial resolution of about 50 km, found similar results showing a more amplified response in the minimum temperature (relative to the maximum temperature) in lower-elevation regions of the Colorado Rocky Mountains during winter months. In spring EDW is significantly simulated only at the two coarsest resolutions, while in summer EDW is only detected at some resolutions with no particular pattern. Further, in spring the LOESS fit suggests the existence of different warming regimes with height: the temperature change increases with elevation up to about 1500–2000 m and then it either decreases or remains almost constant (see Figs. S1 and S2 of the SI). This may explain the non significance of the EDW slope at the highest resolutions.
-
GAR (Figs. S3 and S4, middle column plots of Fig. 2 and Fig. 4): EDW is detected in summer and autumn at the three finest resolutions, while in winter and spring it is detected only at the coarsest resolutions (T255 and T159 in winter, T159 in spring). The relationship between warming rates and elevation is well represented by a linear model. Further, for this region, the PDF of the temperature change in each bin is well peaked around its mean value, which allows to have an unambiguous estimate of the warming expected at each elevation.
-
HKKH–TP (Figs. S5 and S6, right column plots of Fig. 2 and Fig. 5): This area shows the most robust and the clearest EDW. Here, the elevational gradients of warming rates, for both the maximum and the minimum temperature, are always positive and statistically significant with only four exceptions all occurring at the coarsest resolution (T159). For both tasmin and tasmax the largest EDW occurs in autumn at almost all model resolutions. Further, in autumn the elevational gradient of warming rates is characterized by a clear twofold behaviour (green dots and LOESS curved fitting), with the temperature change increasing with elevation up to about 4000-4500 m (EDW) and then decreasing at higher elevations. This behaviour is coherent throughout all model resolutions except the coarsest, corroborating previous modelling (e.g., Palazzi et al. 2017) and satellite-based (e.g., Qin et al. 2009) studies.
To summarize, the season showing the most striking evidence of EDW in both tasmin and tasmax in all regions is autumn. In fact, the elevational gradients of warming rates in SON exhibit always a positive and statistically significant slope (except in two cases found in the GAR) and the spread among the individual model realizations at each resolution is overall smaller than in the other seasons. The region that is expected to be more prone to EDW in all seasons is the HKKH–TP. As shown in Table 1, these findings are quite robust across all model resolutions. EC-Earth does not simulate EDW in DJF in the Rockies for both tasmin and tasmax at any resolutions (Fig. 3), and this signal is coherent across all model members (except a few ones at the two coarsest resolutions). Also, EDW is not simulated for tasmin in DJF and in MAM in the GAR (Fig. 4) where, in fact, the statistically significant slopes which we found are all negative. In some cases, we find considerable variability of the response among the ensemble members at a given resolution, particularly in the Rockies (Fig. 3) and in the GAR (Fig. 4) and, in a few cases, some members present both positive and negative slopes. As already mentioned in Sect. 2.2, we do not find any clear signal in the response of the different members to be directly ascribable to the two possible models used in SPHINX (i.e., the use of either base physics or stochastic parameterizations). This is visible in Figs. 3, 4 and 5 looking at the highest resolution (T1279) results, as the two members available at this resolution, run either with or without stochastic parameterizations, do not provide significantly different EDW response. Also, the results obtained by averaging only the members implementing the base physics did not differ significantly from those shown in Figs. 3, 4 and 5 which refer to the average of all members at each resolution (see Figs. S7–S9 of the SI). The relationship between warming rates and elevation is not necessarily linear, as we find in the HKKH-TP region and in the Rockies. This corroborates previous studies showing that enhanced warming can occur at intermediate elevations in the vicinity of the 0 \(^\circ\)C isotherm (e.g., Pepin and Lundquist 2008; Ceppi et al. 2012; Palazzi et al. 2017) where positive feedbacks from ice and snow at the surface may play a crucial role. Our results do not suggest any clear or universal relationship between the EDW representation and the model resolution, at least using this model. A previous study by Rangwala et al. (2016), using an ensemble of CMIP5 GCMs with spatial resolutions from 1\(^\circ\) to 3\(^\circ\) and thus coarser than the EC-Earth simulations analysed in our paper, did not find any difference as well in the EDW simulated by GCMs having different spatial resolutions.
4 Drivers of elevation-dependent warming
Next we analyse the role of the four variables possible drivers of EDW (\(\Delta albedo\), \(\Delta rlds/rlds_{0}\), \(\Delta rsds/rsds_{0}\), \(\Delta huss/huss_{0}\)) in the different seasons, highlighting regional differences and assessing whether model simulations performed at different spatial resolutions present different behaviours. From a practical point of view we proceed with the calculation of the three linear Pearson correlation coefficients described below, useful to check if the conditions (1) and (2) discussed in Sect. 2.3 are fulfilled:
-
R1, between either \(\Delta tasmin\) or \(\Delta tasmax\) and elevation, and its statistical significance, to highlight the cases with or without EDW.
-
R2, between each of the four possible EDW drivers and elevation, and its statistical significance;
-
R3, between the (minimum, maximum) temperature change and each of the four possible EDW drivers, and its statistical significance. R3 is calculated after having removed the dependence on elevation of each variable, which is obtained by considering the residuals compared to a linear fit respect to elevation.
From the considerations reported in Sect. 2.3, a positive sign of R2 for \(\Delta rlds/rlds_{0}\), \(\Delta rsds/rsds_{0}\), \(\Delta huss/huss_{0}\) and − \(\Delta albedo\) is physically consistent with EDW (i.e., with the condition R1 > 0). Therefore, having R2 greater than zero and statistically significant is one necessary condition for those variables to be actually drivers of EDW. For the variables that fulfill this condition we compute the correlation coefficient R3, measuring their spatial correlation with the temperature change, after having first detrended all variables for elevation. We recall that, in this case, we do not explore the results individually for each ensemble member but the calculation of the correlation coefficients was performed on the average of all members available at each model resolution. The R3 values are shown in Figs. 6 and 7 for tasmin and for tasmax, respectively. Grey boxes indicate the cases in which there is no EDW or it is not statistically significant, based on the values of R1 and in agreement with the analysis presented in Sect. 3, while white boxes identify the situations in which:
-
for a given variable, R2 is negative or not statistically-significant, which indicates that the variable certainly cannot be a driver of EDW. We recall that the condition R2 < 0 applies also to the change in albedo since we use \(-\,\Delta albedo\) in the calculations,
-
the spatial correlation between a possible driver of EDW and the temperature change is negative.
Figures 6 and 7 thus indicate what are the possible drivers of EDW and how much they correlate (value of R3) with the change in the minimum (Fig. 6) and maximum (Fig. 7) temperature. The relative contribution to EDW of the different drivers can be assessed using the multiple linear regression model described by Eq. 1. Since we noticed that the season showing evidence of EDW in all three regions is SON, for simplicity in the following we will discuss in detail the results of application of the multiple linear regression model for SON only, while qualitatively discussing the EDW drivers in all cases.
Correlation coefficient (called R3 in Sect. 4) between each of the seven possible EDW drivers and the minimum temperature change, in the three regions (columns) and four seasons (rows). The drivers are displayed along the x-axis. Grey boxes indicate the cases in which there is no EDW or it is not statistically significant. White boxes identify the cases in which R2 is negative or not statistically-significant and the spatial correlation between a possible driver of EDW and the temperature change is negative. See also the text for details
The same as Fig. 6, for maximum temperature
-
Rockies: The most robust signal emerging from our analysis is found in SON, where the EC-Earth GCM identifies in \(\Delta albedo\) and \(\Delta rlds/rlds_{0}\) the two main EDW drivers for both \(\Delta tasmin\) and \(\Delta tasmax\) and across all model resolutions except the coarsest. In the other seasons either no EDW is found (as in DJF) or none of the variables turned out to be one contributing significantly to EDW according to conditions (2) and (3) outlined in Sect. 2.3, or \(\Delta albedo\) and \(\Delta rlds/rlds_{0}\) emerge as important but the signal is not robust at the different resolutions. Using the multiple linear regression equation (Eq. 1) with \(\Delta albedo\) and \(\Delta rlds/rlds_{0}\) as drivers, we can quantify the explained variance (R\(^2\)) and the AICc values associated with the two regression models having a single predictor (either \(\Delta albedo\) or \(\Delta rlds/rlds_{0}\)) and with the regression model accounting for the combination of the two predictors, as summarized in Table 2. The single-predictor model with \(\Delta rlds/rlds_{0}\) has higher R\(^2\) than the single-predictor model with \(\Delta albedo\). While, as expected, the two-predictors model has the highest R\(^2\) for all EC-Earth resolutions which we considered, we also observe that the coarser the resolution the higher the R\(^2\). This is an indication that at high resolution additional small-scale processes, not included in simulations at lower resolutions and not related to the simple predictors considered here, are at work. We also note that \(\Delta albedo\) contributes in a non-negligible way to the explained variance only at T255, while at the other EC-Earth resolutions the value of R\(^2\) associated with the two-predictors model is similar to the value of R\(^2\) associated with the model with \(\Delta rlds/rlds_{0}\) as single predictor.
Overall, the same considerations apply to the prediction of \(\Delta tasmax\) (see Table 2, right columns). The low R\(^2\) value shown by the regression model at T1279, in particular, indicates that the two predictors, \(\Delta albedo\) and \(\Delta rlds/rlds_{0}\), are not able to explain a large proportion of the variance of \(\Delta tasmax\) in SON, and that some other relevant drivers which we are neglecting may contribute to EDW.
-
GAR: The three drivers of the changes in tasmin in JJA and SON (in DJF and MAM EC-Earth did not show EDW) are \(\Delta albedo\), \(\Delta rlds/rlds_{0}\), and \(\Delta huss/huss_{0}\) (see Fig. 6). The only EC-Earth resolutions able to identify the simultaneous contribution of all three drivers are T1279 and T799 and we apply the multiple linear regression model only for these two resolutions and in SON (we recall that three predictors give rise to seven regression models). The results are summarized in Table 3, left columns. At T1279, the four models including \(\Delta rlds/rlds_{0}\) as a predictor show the highest values of explained variance (R\(^2\)) among the seven regression models. At T799 the first three models and the fifth in the rank include \(\Delta rlds/rlds_{0}\), the model combining \(\Delta albedo\) and \(\Delta huss/huss_{0}\) ranking fourth. At both resolutions, among the three single-predictor models, the one with \(\Delta rlds/rlds_{0}\) shows the highest R\(^2\). The three multi-predictor models including \(\Delta rlds/rlds_{0}\) in conjunction with any other driver are capable of accounting for more than half the variance of the predictand at T799 (more than 20\(\%\) at T1279). Therefore, \(\Delta rlds/rlds_{0}\) is found, among the drivers which we considered, essential to drive the changes in tasmin in SON.
As for the changes in tasmax (see Fig. 7), we identify as drivers in DJF \(\Delta albedo\), \(\Delta rlds/rlds_{0}\), and \(\Delta huss/huss_{0}\) at T255 and \(\Delta albedo\) and \(\Delta huss/huss_{0}\) at T159. In JJA, the drivers are \(\Delta albedo\) and \(\Delta rlds/rlds_{0}\) and the signal is robust across all EC-Earth resolutions (T1279, T799, T511) at which EDW is found. In SON, the drivers are \(\Delta albedo\) and \(\Delta rlds/rlds_{0}\) at T511 and \(\Delta albedo\), \(\Delta rlds/rlds_{0}\) and \(\Delta huss/huss_{0}\) at T1279 and T799. For the latter two resolutions we discuss the results of application of the multiple linear regression model to study the relative contribution of the three identified drivers (see the right columns in Table 3). \(\Delta huss/huss_{0}\) emerges as the most important driver at T1279, while \(\Delta albedo\) is the most important driver at T799. In both cases the proportion of the maximum variance explained by the best-performing regression model is quite low (44\(\%\) at T1279 and 41\(\%\) at T799).
-
HKKH–TP: \(\Delta albedo\), \(\Delta rlds/rlds_{0}\) and \(\Delta huss/huss_{0}\) are identified as EDW drivers at almost all model resolutions in SON for both \(\Delta tasmin\) and \(\Delta tasmax\). As shown in Figs. 6 and 7 (right column plots), the R3 coefficient associated with \(\Delta rlds/rlds_{0}\) and that associated with \(\Delta huss/huss_{0}\) vary in the same way with the model resolution, though having a different intensity for the two drivers. This is not surprising since these variables are related to each other, in that increases in downward longwave radiation occur in conjunction with globally increasing specific humidity. This is a non-linear relationship, however, with the sensitivity of a change in rlds being higher for lower initial water vapor concentration, a situation typically found at high elevations during the cold season (e.g., Rangwala and Miller 2012). Table 4 shows the results of the application of the multiple linear regression model for the prediction of \(\Delta tasmin\) and \(\Delta tasmax\) in SON. We have applied the regression model only to the EC-Earth resolutions able to identify all three variables mentioned above (\(\Delta albedo\), \(\Delta rlds/rlds_{0}\) and \(\Delta huss/huss_{0}\)) as drivers, that is T1279, T511 and T255 for tasmin and T511 and T255 for tasmax. Overall, \(\Delta albedo\) emerges as the most important driver of both tasmin and tasmax changes. For the prediction of \(\Delta tasmin\) (left columns of Table 4), the four models including \(\Delta albedo\) as a predictor show the highest values of explained variance at T1279 and T255, and the same is true at T511 except for the model where \(\Delta albedo\) is the only predictor. The maximum variance explained by the model combining all three predictors is about 70\(\%\). These results corroborate a previous study focused on assessment of EDW characteristics and drivers in the Tibetan Plateau-Himalayas using the CMIP5 model ensemble (Palazzi et al. 2017). Similarly for \(\Delta tasmax\), \(\Delta albedo\) emerges as the most important driver. It appears in the first three regression models and in the fifth model at T511 and in the first four regression models at T255; the model having \(\Delta albedo\) as single predictor has an R\(^2\) larger than that of the other single-predictor regression models.
In general, our analysis shows that the more frequent EDW drivers in all regions and seasons are the changes in albedo and in downward thermal radiation and this is reflected in both daytime and nighttime warming. In HKKH–TP, and to a lesser extent in the GAR, an additional EDW driver is the change in specific humidity. In autumn, the change in albedo is found to be the most important driver of EDW in the HKKH–TP, while in the Rockies and in the GAR, EDW appears to be mainly driven by changes in downward thermal radiation. Still, it is also clear that our picture omits other factors which may contribute to EDW in the different regions.
5 Discussion and conclusions
There is growing evidence that mountain areas are responding faster and more intensely, in comparison to the global mean and other regions, to climate change (MRI 2015). Among other indicators, elevation-dependent warming is an expression of this enhanced sensitivity. EDW occurs when a statistically significant dependence of the temperature trends on surface elevation exists. As shown by the available observations, this dependence can be either positive or negative and it can be linear or characterized by a more complex pattern of altitudinal variability. There is not a unique and well-defined way to describe the relationship between warming rates and elevation which applies for all mountain regions of the world. However, there is increasing evidence that amplification of warming with elevation is the situation most often encountered in high-elevation areas. As yet, also model studies have indicated that the enhancement of warming rates with elevation is expected to continue and in some cases to be significantly amplified in the future (e.g., Rangwala et al. 2013, 2016; Palazzi et al. 2017).
Our analysis has focused on elevation-dependent warming in an ensemble of model simulations performed with one state-of-the-art GCM, the EC-Earth Earth System Model, run at five different horizontal resolutions, from 125 to 16 km, over three different mountain areas of the northern hemisphere mid-latitudes, the Colorado Rocky Mountains, the Greater Alpine Region and the Himalayas-Tibetan Plateau. Our aims were to understand whether the representation of EDW and of its driving mechanisms is dependent on the model spatial resolution and to highlight possible differences among the different geographical areas which we analysed.
There is a lack of consistency in the methods used so far to quantify EDW (e.g., MRI 2015; Liu et al. 2009). When dealing with model data, the various methods include correlating warming rates with elevation, either considering the data at each individual grid point or grouping them into elevation bands, or comparing high elevation averages with adjacent lowland (or global) averages. In this study we assessed the dependence of the temperature changes on elevation using the first two approaches and quantified the EDW intensity by calculating the slope of the linear regression between warming rates and elevation, which is the accepted method used by the scientific community. In most of the cases the linear model turned out to fairly reproduce the actual pattern of temperature changes with height. It is otherwise clear that when the data distribution shows different slopes at different height ranges, a non-linear approach would be desirable. Here we assessed deviations from linearity using a further regression approach based on a LOESS fitting.
The existence of various mechanisms, possible drivers of EDW, makes the picture even more complex and may in part explain why describing the dependence of warming rates on elevation through a linear relationship is not really possible and simplifies the reality. For example, the relationship between specific humidity and downward longwave radiation is nonlinear and the percentage increase in downward longwave radiation following an increase in atmospheric water vapour amount is particularly large in dry regions, when the initial humidity is low, as found at high elevations during the cold season. The solar dimming effect of aerosol particles is most pronounced at low elevations and reduced in high elevation zones. Also, through deposition on snow surfaces, aerosol can reduce their albedo and enhance warming rates. On the other hand, aerosol is among the forcing factors not usually accounted for in model evaluations of EDW, thus representing one of the missing components when quantifying the role of the different drivers.
We found that if the EC-Earth GCM simulates EDW (i.e., positive elevational gradients of warming) in one season and region, in most of the cases the signal is coherent throughout all model resolutions, though the simulated EDW intensity may be different and the response of the individual model realisations at each resolution exhibits some spread. The ensemble spread shown in Figs. 3, 4 and 5 just measures the climate variability associated with the EDW representation in the EC-Earth model simulations which we analysed. The region which is found to be more prone to EDW is the HKKH-TP, while the season showing the most striking evidence of EDW in both tasmin and tasmax in all regions is autumn. In mountain regions autumn is generally the “transition season” between snow-free and snow-covered surface. Climate warming is delaying the onset of snow cover at low and mid altitudes (Terzago et al. 2014, 2017) and this trend is expected to continue and intensify in the future, involving higher elevations. Therefore, larger snow free areas are expected in autumn, as many areas that used to be snow covered in the past might not be anymore in the future in this season. The decrease in snow cover lowers the surface albedo, resulting in increased absorption of solar radiation and enhanced warming. Our study identifies albedo changes as a driver of EDW in SON, even though other variables and mechanisms are also at play. Also the spring transition between snow-covered and snow-free areas is expected to happen earlier in the future, with a corresponding decrease in the surface albedo and enhanced warming, but we rarely found EDW significantly correlated with changes in albedo in MAM in our analysis, except in the HKKH-TP and to a lesser extent in the Rockies. It is interesting to observe that in the Alps, and at the coarsest horizontal resolutions only, a significant EDW signal related to albedo changes is observed in the DJF season. At the coarsest resolutions, the orography is smooth, and the highest elevations are not realistically represented in the climate model. This result seems to suggest that the “model’s highest elevations” might undergo an earlier (winter) transition from being snow covered to being snow free in the future in winter months. Of course this signal is an artifact typical of the coarsest resolutions and disappears at finer resolutions when the orography is represented with more accuracy. On the contrary, the finest resolutions are the only ones able to catch the change in albedo as an EDW driver in SON in the GAR. This result would suggest an added value of the finest resolution simulations in the Alpine area.
In general, each study area considered in our paper shows a different dependence of the EDW intensity on the resolution. In the Rockies EDW is generally more intense at lower than at higher resolutions. The only season with a significant EDW at most resolutions in both tasmin and tasmax is SON, with no clear dependence on resolution. In the GAR, it is evident that the lower resolutions suffer from an underrepresentation of the highest altitudes, leading to a difficult estimate and comparison of EDW. This is particularly evident for summer and autumn where a strong warming dependence on altitude can be found at the highest resolutions (starting from 40 km) but not in coarse scale simulations. In the HKKH-TP, EDW intensity increases with the model resolution up to the intermediate resolution T511 (in almost all cases) but then it decreases as the resolution increases. Whether this behaviour is related to a different representation of the snow cover extent (snow cover is not among the output variables of the EC-Earth simulations which we considered) at the different model resolutions or to the way other surface processes are simulated still remains to be understood and will be subject of further investigations.
Overall these results seem to indicate that model resolution plays a crucial role only in small areas such as the Alps, where a too coarse resolution would lead to an underrepresentation of the highest altitudes. In fact, elevational dependency of warming, as well as of other mechanisms or variables, could not be easily identified if the range of altitudes is too limited. There are two reasons why model resolution may play a role for EDW, in particular for the modelling setup used to produce the EC-Earth simulations employed in this study. On one hand model parameterizations, such as convective and microphysical schemes controlling clouds and the representation of surface processes, were developed for a specific resolution and most of them are not resolution aware, so that the same parameterization is used at all scales. As a consequence it is not entirely surprising that a complex phenomenon such as EDW which depends strongly on these processes, does not show great sensitivity to the resolution. On the other hand, as discussed in Davini et al. (2017), it has to be considered that when the model is pushed to the highest resolutions, it is very far from the resolution at which it was tuned (80 km, in the case of the EC-Earth model for the SPHINX experiment), with a possible impact on large scale-features of the model such as circulation patterns and climatology. This in turn may explain why the highest resolutions seem often to behave differently in terms of EDW compared to other resolutions. It has also to be remembered that a larger uncertainty is associated with the highest resolution results, since they are based on a smaller number of ensemble members in the model simulations which we used. Finally, in our opinion it is important to stress that enhancing the spatial resolution in climate models may be crucial especially in complex topography, but also improvements in model parameterizations, particularly those involving surface processes in high-mountain areas, the snow-albedo and cloud-radiation feedbacks, may allow for a better simulation of EDW in the models. Considering the importance that mountains have as early warning indicators of the consequences of global warming, EDW is a phenomenon that calls for further research and efforts, both in terms of observations and of model simulations.
References
Auer I, Böhm R, Jurkovic A, Lipa W, Orlik A, Potzmann R, Schöner W, Ungersböck M, Matulla C, Briffa K, Jones P, Efthymiadis D, Brunetti M, Nanni T, Maugeri M, Mercalli L, Mestre O, Moisselin J-M, Begert M, Müller-Westermeier G, Kveton V, Bochnicek O, Stastny P, Lapin M, Szalai S, Szentimrey T, Cegnar T, Dolinar M, Gajic-Capka M, Zaninovic K, Majstorovic Z, Nieplova E (2007) HISTALP-historical instrumental climatological surface time series of the Greater Alpine Region. Int J Climatol 27:17–46. https://doi.org/10.1002/joc.1377
Beniston M, Diaz H, Bradley R (1997) Climatic change at high elevation sites: an overview. Clim Chang 36:233–251. https://doi.org/10.1023/A:1005380714349
Bye J, Fraedrich K, Kirk E, Schubert S, Zhu X (2011) Random walk lengths of about 30 years in global climate. Geophys Res Lett 38:L05806. https://doi.org/10.1029/2010GL046333
Bradley RS, Vuille M, Diaz HF, Vergara W (2006) Threats to water supplies in the tropical Andes. Science 312(5781):1755–1756
Bradley RS, Keimig FT, Diaz HF, Hardy DR (2009) Recent changes in freezing level heights in the Tropics with implications for the deglacierization of high mountain regions. Geophys Res Lett 36:L17701. https://doi.org/10.1029/2009GL037712
Burnham KP, Anderson DR (2003) Model selection and multimodel inference: a practical information-theoretic approach. Springer Science & Business Media, New York
Ceppi P, Scherrer S, Fischer A, Appenzeller C (2012) Revisiting Swiss temperature trends 1959–2008. Int J Climatol 32:203–213. https://doi.org/10.1002/joc.2260
Clow DW (2010) Changes in the timing of snowmelt and streamflow in Colorado: a response to recent warming. J Clim 23:2293–2306. https://doi.org/10.1175/2009JCLI2951.1
Daly C, Halbleib M, Smith JI, Gibson WP, Doggett MK, Taylor GH, Curtis J, Pasteris PP (2008) Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int J Climatol 28:2031–2064. https://doi.org/10.1002/joc.1688
Davini P, von Hardenberg J, Corti S, Christensen HM, Juricke S, Subramanian A, Watson PAG, Weisheimer A, Palmer TN (2017) Climate SPHINX: evaluating the impact of resolution and stochastic physics parameterisations in the EC-Earth global climate model. Geosci Model Dev 10:1383–1402. https://doi.org/10.5194/gmd-10-1383-2017
Demory M-E, Vidale PL, Roberts MJ, Berrisford P, Strachan J, Schiemann R, Mizielinski MS (2014) The role of horizontal resolution in simulating drivers of the global hydrological cycle. Clim Dyn 42:2201–2225
Diaz HF, Eischeid JK (2007) Disappearing ’alpine tundra’, Köppen climatic type in the western United States. Geophys Res Lett 34:L18707. https://doi.org/10.1029/2007GL031253
EEA (2009) Regional climate change and adaptation: the Alps facing Query ID="Q3" Text="Author: Kindly upadte Ref EEA (2009) With publisher name and location." --> the challenge of changing water resources, vol 8
Fyfe JC, Flato JM (1999) Enhanced climate change and its detection over the Rocky Mountains. J Clim 12:230–243. https://doi.org/10.1175/1520-0442-12.1.230
Giorgi F, Marinucci MR, Bates GT (1993) Development of a second-generation regional climate model (RegCM2). Part I: Boundary-layer and radiative transfer processes. Mon Weather Rev 121:2794–2813. https://doi.org/10.1175/1520-0493(1993)121%3cC2794:DOASGR%3e2.0.CO;2
Giorgi F, Hurrell JW, Marinucci MR, Beniston M (1997) Elevation dependency of the surface climate change signal: a model study. J Clim 10:288–296. https://doi.org/10.1175/1520-0442(1997)010%3c0288:EDOTSC%3e2.0.CO;2
Giorgi F, Coppola E, Raffaele F (2014) A consistent picture of the hydroclimatic response to global warming from multiple indices: Models and observations. J Geophys Res Atmos 119:11695–11708. https://doi.org/10.1002/2014JD022238
Hazeleger W, Severijns C, Semmler T, Ştefănescu S, Yang S, Wang X, Wyser K, Dutra E, Baldasano JM, Bintanja R, Bougeault P, Caballero R, Ekman AML, Christensen JH, van den Hurk B, Jimenez P, Jones C, Kȧllberg P, Koenigk T, McGrath R, Miranda P, Van Noije T, Palmer T, Parodi JA, Schmith T, Selten F, Storelvmo T, Sterl A, Tapamo H, Vancoppenolle M, Viterbo P, Willén U (2010) EC-Earth: a seamless earth-system prediction approach in action. Bull Am Meteorol Soc 91:1357–1363. https://doi.org/10.1175/2010BAMS2877.1
Hazeleger W, Wang X, Severijns C, Ştefănescu S, Bintanja R, Sterl A, Wyser K, Semmler T, Yang S, van den Hurk B, van Noije T, van der Linden E, van der Wiel K (2010) EC-Earth V2.2: description and validation of a new seamless earth system prediction model. Clim Dyn 39:2611–2629. https://doi.org/10.1007/s00382-011-1228-5
Im E-S, Ahn J-B (2011) On the elevation dependency of present-day climate and future change over Korea from a high resolution regional climate simulation. J Meterol Soc Japan 89:89–100. https://doi.org/10.2151/jmsj.2011-106
IPCC (2013) Climate Change 2013: The Physical Science Basis. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, and Midgley PM (eds.) Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Jones RG, Noguer M, Hassel DC, Hudson D, Wilson SS, Jenkins GJ, Mitchell JFB (2004) Generating high resolution climate change scenarios using PRECIS. Met Office, Hadley Center, Exeter, p 40
Karmalkar AV, Bradley RS, Diaz HF (2011) Climate change in Central America and Mexico: regional climate model validation and climate change projections. Clim Dyn 37:605. https://doi.org/10.1007/s00382-011-1099-9
Liu X, Chen B (2000) Climatic warming in the Tibetan Plateau during recent decades. Int J Climatol 20:1729–1742. https://doi.org/10.1002/1097-0088(20001130)20:14%3c1729::AID-JOC556%3e3.0.CO;2-Y
Liu X, Cheng Z, Yan L, Yin Z-Y (2009) Elevation dependency of recent and future minimum surface air temperature trends in the Tibetan Plateau and its surroundings. Global Planet Chang 68:164–174. https://doi.org/10.1016/j.gloplacha.2009.03.017
Minder JR, Letcher TW, Liu C (2018) The character and causes of elevation-dependent warming in high-resolution simulations of Rocky Mountain climate change. J Clim 31:2093–2113. https://doi.org/10.1175/JCLI-D-17-0321.1
MRI EDW Working Group (Pepin N, Bradley R S, Diaz HF, Baraer M, Caceres EB, Forsythe N, Fowler H, Greenwood G, Hashmi MZ, Liu XD, Miller JR, Ning L, Ohmura A, Palazzi E, Rangwala I, Schöner W, Severskiy I, Shahgedanova M, Wang MB, Williamson SN, Yang DQ) (2015) Elevation-dependent warming in mountain regions of the world. Nat Clim Chang 5:424–430. https://doi.org/10.1038/nclimate2563
Oyler JW, Dobrowski SZ, Ballantyne AP, Klene AE, Running SW (2015) Artificial amplification of warmingtrends across the mountains of the western United States. Geophys Res Lett 42:153–161. https://doi.org/10.1002/2014GL062803
Palazzi E, Filippi L, von Hardenberg J (2017) Insights into elevation-dependent warming in the Tibetan Plateau–Himalayas from CMIP5 model simulations. Clim Dyn 48(11–12):3991–4008. https://doi.org/10.1007/s00382-016-3316-z
Palmer TN (2012) Towards the probabilistic Earth-system simulator: a vision for the future of climate and weather prediction. Q J R Meteorol Soc 138:841–861. https://doi.org/10.1002/qj.1923
Pederson GT, Gray ST, Ault T, Marsh W, Fagre DB, Bunn AG, Woodhouse CA, Graumlich LJ (2011) Climatic controls on the snowmelt hydrology of the northern Rocky Mountains. J Clim 24:1666–1687. https://doi.org/10.1175/2010JCLI3729.1
Pederson GT, Betancourt JL, McCabe GJ (2013) Regional patterns and proximal causes of the recent snowpack decline in the Rocky Mountains, US. Geophys Res Lett 40:1811–1816. https://doi.org/10.1002/grl.50424
Pepin NC, Lundquist JD (2008) Temperature trends at high elevations: patterns across the globe. Geophys Res Lett 35:L14701. https://doi.org/10.1029/2008GL034026
Philipona R (2013) Greenhouse warming and solar brightening in and around the Alps. Int J Climatol 33:1530–1537
Qin J, Yang K, Liang S, Guo X (2009) The altitudinal dependence of recent rapid warming over the Tibetan Plateau. Clim Chang 97:321–327. https://doi.org/10.1007/s10584-009-9733-9
Rangwala I, Miller JR, Russell GL, Xu M (2010) Using a global climate model to evaluate the influences of water vapor, snow cover and atmospheric aerosol on warming in the Tibetan Plateau during the twenty-first century. Clim Dyn 34:859–872. https://doi.org/10.1007/s00382-009-0564-1
Rangwala I, Miller JR (2012) Climate change in mountains: a review of elevation-dependent warming and its possible causes. Clim Chang 114:527–547. https://doi.org/10.1007/s10584-012-0419-3
Rangwala I, Barsugli J, Cozzetto K, Neff J, Prairie J (2012) Mid-21st century projections in temperature extremes in the southern Colorado Rocky Mountains from regional climate models. Clim Dyn 39:1823–1840. https://doi.org/10.1007/s00382-011-1282-z
Rangwala I, Sinsky E, Miller RJ (2013) Amplified warming projections for high altitude regions of the Northern hemisphere mid-latitudes from CMIP5 models. Environ Res Lett 8:024040. https://doi.org/10.1088/1748-9326/8/2/024040
Rangwala I, Sinsky E, Miller RJ (2016) Variability in projected elevation dependent warming in boreal midlatitude winter in CMIP5 climate models and its potential drivers. Clim Dyn 46(7):2115–2122. https://doi.org/10.1007/s00382-015-2692-0
Riahi K, Rao S, Krey V, Cho C, Chirkov V, Fischer G, Kindermann G, Nakicenovic N, Rafaj P (2011) RCP 8.5–a scenario of comparatively high greenhouse gas emissions. Clim Chang 109:33–57. https://doi.org/10.1007/s10584-011-0149-y
Stewart IT, Cayan DR, Dettinger MD (2005) Changes toward earlier streamflow timing across western North America. J Clim 18:1136–1155. https://doi.org/10.1175/JCLI3321.1
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498. https://doi.org/10.1175/BAMS-D-11-00094.1
Terzago S, von Hardenberg J, Palazzi E, Provenzale A (2014) Snowpack Changes in the Hindu KushKarakoramHimalaya from CMIP5 Global Climate Models. J Hydrometeorol 15:2293–2313. https://doi.org/10.1175/JHM-D-13-0196.1
Terzago S, von Hardenberg J, Palazzi E, Provenzale A (2017) Snow water equivalent in the Alps as seen by gridded data sets, CMIP5 and CORDEX climate models. Cryosphere 11:1625–1645. https://doi.org/10.5194/tc-11-1625-2017
Tudoroiu M, Eccel E, Gioli B, Gianelle D, Schume H, Genesio L, Miglietta F (2016) Negative elevation-dependent warming trend in the Eastern Alps. Environ Res Lett 11:044021. https://doi.org/10.1088/1748-9326/11/4/044021
Vuille M, Bradley RS, Werner M, Keimig F (2003) 20th Century climate change in the tropical Andes: observations and model results. Clim Chang 59:75. https://doi.org/10.1023/A:1024406427519
Watson PAG, Berner J, Corti S, Davini P, von Hardenberg J, Sanchez C, Weisheimer A, Palmer TN (2017) The impact of stochastic physics on tropical rainfall variability in global climate models on daily to weekly time scales. J Geophys Res Atmos 122:5738–5762. https://doi.org/10.1002/2016JD026386
Williams AP, Allen CD, Millar CI, Swetnam TW, Michaelsen J, Still CJ, Leavitt SW (2017) Forest responses to increasing aridity and warmth in the southwestern United States. Proc Natl Acad Sci 107:21289–21294. https://doi.org/10.1073/pnas.0914211107
Yan L, Liu X (2014) Has climatic warming over the Tibetan Plateau paused or continued in recent years? J Earth Ocean Atmos Sci 1:13–28
Yan L, Liu Z, Chen G, Kutzbach JE, Liu X (2016) Mechanisms of elevation-dependent warming over the Tibetan plateau in quadrupled CO\(_2\) experiments. Clim Chang 135:509–519. https://doi.org/10.1007/s10584-016-1599-z
You Q, Kang S, Pepin N, Flgel W-A, Yan Y, Behrawan H, Huang J (2010) Relationship between temperature trend magnitude, elevation and mean temperature in the Tibetan Plateau from homogenized surface stations and reanalysis data. Global Planet Chang 71:124–133. https://doi.org/10.1016/j.gloplacha.2010.01.020
Acknowledgements
This work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 641762 (ECOPOTENTIAL) and under grant agreement 641816 (CRESCENDO). This work was also supported by the Italian project of Interest NextData of the Italian Ministry for Education, University and Research.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Palazzi, E., Mortarini, L., Terzago, S. et al. Elevation-dependent warming in global climate model simulations at high spatial resolution. Clim Dyn 52, 2685–2702 (2019). https://doi.org/10.1007/s00382-018-4287-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4287-z