1 Introduction

The South Asian high (SAH) is a planetary-scale anticyclonic circulation in the upper troposphere, with its main body zonally elongated over the Iranian Plateau (IP)–Tibetan Plateau (TP) and the surrounding areas during summer (Mason and Anderson 1963; Tao and Zhu 1964; Krishnamurti 1973). As a member of the Asian summer monsoon system, the SAH’s spatiotemporal variability and impacts on the weather and climate over Asia and beyond have been investigated (Zhang et al. 2002, 2005, 2016; Liu et al. 2004, 2007, 2013; Duan and Wu 2005; Randel and Park 2006; Zarrin et al. 2010; Huang et al. 2011; Jiang et al. 2011; Qu and Huang 2012; Wei et al. 2014; Yang et al. 2014; Ren et al. 2015; Wu et al. 2015; Chen and Zhai 2016; Shi and Qian 2016; Yang and Li 2016). Especially, variations of the SAH on subseasonal time scale have attracted more attention in recent years. Because some high-impact events (e.g. persistent heavy rainfall or long-lived heat wave) are often induced by anomalies in atmospheric circulation and water vapor transport accompanied by the SAH’s subseasonal variations (Ren et al. 2015; Yang et al. 2017; Chen and Zhai 2016; Ge et al. 2017).

Previous studies (Tao and Zhu 1964; Zhang et al. 2002; Jia and Yang 2013; Ren et al. 2015; Yang and Li 2016) have identified two dominant modes of the SAH’s variations on subseasonal time scale. One mode demonstrates zonal movement of the SAH’s main body (denoted as “zonal oscillation”). Another one depicts the intensity variation of the SAH’s main body (hereafter “intensity variation”). The SAH’s zonal oscillation around its climatology position for periods of weeks were firstly revealed by Mason and Anderson (1963), and Tao and Zhu (1964). Zhang et al. (2002) suggested the bimodality of the SAH at 100 hPa and identified them as the Iranian pattern and the Tibetan pattern, respectively. Further investigations have studied the features of subseasonal zonal shift of the SAH and its connection with precipitation and diabatic heating over eastern Asia (Ren et al. 2015; Shi and Qian 2016; Yang and Li 2016). Other literature mentioned about the SAH’s subseasonal intensity variation. For example, Jia and Yang (2013) demonstrated that the northwestward propagation of the quasi-biweekly oscillation over the western North Pacific is accompanied by the strengthening of SAH, which contributes to the upper level divergence pattern over the subtropical east Asian region. Yang et al. (2017) suggested that the SAH is enhanced with eastward and westward extensions when the quasi-biweekly oscillation in the eastern TP summer precipitation transits from its dry to wet phase. Compared to the studies about the SAH’s zonal oscillation, our understanding of characteristics and mechanisms for SAH’s intensity variation on subseasonal time scale is incomplete. This makes up the core subject of the present study.

The SAH is considered as a thermal-driven circulation (Jin and Hoskins 1995; Liu et al. 2004; Lin 2009). Diabatic heating induced by precipitation is an important dynamical factor responsible for the SAH’s variations (Liu et al. 2004, 2007, 2013; Ren et al. 2015; Chen and Zhai 2016; Wang and Ge 2016; Ge et al. 2017). Ren et al. (2015) suggested that a north–south dipolar structure of the condensation heating/rainfall over eastern Asia performed a positive feedback in the SAH’s subseasonal zonal oscillation. Similar relationship between condensation heating over eastern Asia and the zonal oscillation of the SAH were also advocated by Yang and Li (2016), Chen and Zhai (2016) and Wang and Ge (2016). The strengthening/weakening of SAH is also accompanied by precipitation anomalies over monsoon region (Jia and Yang 2013; Yang et al. 2017). The corresponding change in diabatic heating should be a no-negligible factor responsible for the SAH’s subseasonal intensity variation. The present study focuses on this factor. We intend to reveal the role of precipitation induced diabatic heating on the SAH’s intensity variation through performing a diagnosis on relative vorticity.

Besides, we also evaluate the model performances in reproducing the features of the SAH’s subseasonal intensity variation and the corresponding dynamical mechanisms. The World Climate Research Programme (WCRP) Working Group on Coupled Modelling (WGCM) has employed the phase 5 of Coupled Model Intercomparison Project (CMIP5) since September 2008 (Taylor et al. 2012). Evaluating the ability of the CMIP5 models in simulating the Asian summer monsoon has been carried out (Duan et al. 2013; Huang et al. 2013; Cherchi et al. 2014; Lee and Wang 2014; Freychet et al. 2015; Gao et al. 2015; Sooraj et al. 2016; Li et al. 2017). Some studies have assessed the capacity of climate models in simulating the SAH’s climatology and its variations. Xue et al. (2017) studied the climatology and interannual variations of the SAH in 38 CMIP5 models. They pointed out that two-thirds of these models can simulate the observed relationship between the El Niño–Southern Oscillation (ENSO) and the SAH. Qu and Huang (2015) evaluated the performance of CMIP5 models in reproducing the decadal relationship between the SAH and sea surface temperature in the tropical Indian Ocean. The above investigations assessed the SAH’s interannual to decadal variations simulated by the CMIP5 models. The present evaluation focuses on the subseasonal intensity variation of the SAH.

The paper is organized as follows. Section 2 introduces the datasets, CMIP5 models and analysis methods. Section3 presents the features of climatology and the subseasonal intensity variation of the SAH, and investigates the relationship between precipitation and the SAH in the observation and CMIP5 models. Section 4 reveals the corresponding dynamical mechanism. A summary and discussion is shown in Sect. 5.

2 Datasets and methods

2.1 Datasets

The datasets used include (1) daily reanalysis data on a 1° × 1° horizontal resolution in 1979–2005 derived from the European Center for Medium-Range Weather Forecasts (ECMWF) (ERA-Interim, Dee et al. 2011), (2) daily mean outgoing longwave radiation (OLR) data on a 2.5° × 2.5° grid from the National Oceanic and Atmospheric Administration (NOAA) (Liebmann and Smith 1996) for 1979–2005, and (3) gauge-based analysis of global daily precipitation data from NOAA Climate Prediction Center (CPC) for the period 1979–2005 on 0.5° × 0.5° horizontal resolution. Further details for the precipitation dataset can be found in Xie et al. (2007) and Chen et al. (2008). The observational and reanalysis datasets are called “observation” in the present study.

The historical experiments for daily mean fields of 18 CMIP5 models from 1979 to 2005 are used in this study (Taylor et al. 2012). Table 1 shows the detail information, including the institutes, horizontal resolutions of these models. Given the large volume of data, only one run from each model and experiment was used in this study. The model outputs are interpolated onto 1° × 1° resolution to match the ERA-Interim reanalysis data. More information about the 18 CMIP5 models can be referred to http://cmip-pcmdi.llnl.gov/cmip5/.

Table 1 Information of CMIP5 climate models
Full size table

2.2 Extracting subseasonal daily anomalies and the SAH’s subsesonal intensity variation

We use the method adopted by Krishnamurthy and Shukla (2000) and Ren et al. (2015) to extract the subseasonal daily anomalies both for observation and for model data for all the variables. The process is as follows. First, a 5-day running mean is preformed to remove the high-frequency fluctuations in the daily data, and then remove the daily climatology to get daily anomalies, finally, remove the interannual signal by subtracting seasonal anomaly.

The amplitudes of 100 hPa geopotential height (Z100) anomalies are increased rapidly from the tropical to extratropical latitudes. To avoid the variance of the EOF being dominated by the signals in the middle latitudes, the EOF analysis is performed on standardized subseasonal anomalies of Z100 over the SAH’s main body region during summer (June, July and August) of 1979–2005 (27 × 92 = 2484 days in total). We also perform the latitudinal weight before EOF analysis and the EOF results are similar. The main body region (20°–40°N, 35°–110°E) covers the climatological 16,750 gpm contour line of the SAH at 100 hPa (Fig. 1a). A power spectrum analysis (Gilman et al. 1963) is used to identify the dominant periodicity on the principal components of EOF.

Fig. 1
figure 1

Climatological summer (June, July and August) fields of Z100 (contour and shaded with interval of 50 gpm) during 1979–2005 for a ERA-Interim and b–s results of the 18 CMIP5 models. The spatial correlation coefficients between the ERA-interim and individual CMIP5 models over the region of 15°–45°N,10°–140°E are shown at each of the top-right corners. The red box in a denotes the region for EOF analysis in Fig. 2. The grey line in each is the outline of the Tibetan Plateau

Full size image
Fig. 2
figure 2

Spatial pattern of the first EOF mode of normalized subseasonal anomalies of Z100 over the region of 20°–40°N, 35°–110°E. a ERA-Interim and b–s the results of the 18 CMIP5 models. The spatial correlation coefficients between the first EOF of the ERA-Interim and those of the CMIP5 models (rEOF) are displayed at each of the top-right corners. The purple contour in a is the climatological 16,750 gpm contour line of the SAH at 100 hPa

Full size image

The observed first EOF mode (EOF1) demonstrates a monopole pattern centered over the IP–western TP. This mode indicates the SAH’s intensity variation on subseasonal time scale. The observed second EOF mode displays a positive center of anomalous Z100 over East Asia and a negative one over the IP. It represents the subseasonal zonal oscillation of the SAH, which has been intensively studied (Zhang et al. 2002; Ren et al. 2015; Shi and Qian 2016; Yang and Li 2016; Chen and Zhai 2016). We focus on the EOF1 in this study. Time-lagged regressions of the observed subseasonal variables on the normalized first principal components of EOF (observed normalized PC1) are calculated. The same process is then done on each of the 18 models’ simulation. The time-lagged regression is used. Day 0 is simultaneous in regression. The simultaneously regression fields can show the anomalous pattern when the SAH gets it strongest stage (the positive peak of normalized PC1). The lead-lag regression can demonstrate the evolution pattern of anomalies accompanied by the evolution of the SAH. A negative lag day (a positive lag day) is obtained by shifting backward (forward) the number of the leading (lag) days.

2.3 Diagnosis on relative vorticity equation

Following the Ertel potential vorticity equation (Ertel 1942; Hoskins et al. 1985), the relatively vorticity equation is expressed as (Wu and Liu 1998; Wu et al. 1999; Liu et al. 2001, 2004, 2013).

$$\frac{{\partial \zeta }}{{\partial t}}= - {{\text{V}}_h} \cdot {\nabla _h}\zeta - \beta v - (f+\zeta ){\nabla _h} \cdot {{\text{V}}_h}+\frac{{f+\zeta }}{{{\theta _z}}}\frac{{\partial {Q_1}}}{{\partial z}}+S,$$
(1)
$$S= - \frac{1}{{{\theta _z}}}\frac{{\partial v}}{{\partial z}}\frac{{\partial {Q_1}}}{{\partial x}}+\frac{1}{{{\theta _z}}}\frac{{\partial u}}{{\partial z}}\frac{{\partial {Q_1}}}{{\partial y}},$$
(2)

where \(\zeta\) is relative vorticity, \({V_h}=(u,v)\) the horizontal wind, \({V_h}\) the horizontal gradient operator, f the planetary vorticity, and \({\theta _z}\) and \({Q_1}\) are the static stability and diabatic heating, respectively. According to Eq. (1), the changes of \(\zeta\) are contributed by the following processes: the horizontal advection of relative vorticity, \(\beta ~\) effect, divergence of atmospheric circulation, and vorticity sources induced by vertical and horizontal gradients of \({Q_1}\).

Diabatic heating \({Q_1}\) (also known as apparent heating source) and apparent moisture sink \({Q_2}\) and their vertically integrated values \(\left\langle {Q_1} \right\rangle\) and \(\left\langle {Q_2} \right\rangle\) are calculated based on the following formulas (Yanai et al. 1973; Luo and Yanai 1984)

$$Q_1=\frac{{\partial T}}{{\partial t}}+{{\text{V}}_h} \cdot {\nabla _h}T+\omega \left( {\frac{{\partial T}}{{\partial p}} - \frac{{RT}}{{{c_p}P}}} \right),$$
(3)
$$~Q_2= - L\left[ {\frac{{\partial q}}{{\partial t}}+{{\text{V}}_h} \cdot {\nabla _h}q+{{\left( {\frac{P}{{P_0}}} \right)}^k}\omega \frac{{\partial q}}{{\partial t}}} \right],$$
(4)
$$\left\langle {Q_1} \right\rangle =\frac{1}{g}\mathop \int \limits_{{{p_t}}}^{{{p_s}}} Q_1dp,$$
(5)
$$\left\langle {Q_2} \right\rangle =\frac{1}{g}\mathop \int \limits_{{{P_t}}}^{{Ps}} Q_2dp,$$
(6)

where \(T\) is the air temperature; \(q\) is the water vapor, \(\omega\) is the vertical velocity in pressure (\(P\)) coordinates; \(k=\frac{R}{{{c_p}}},\)\(R~\) and \({c_p}\) are the gas constant and specific heat at constant pressure of dry air, respectively; \(L~\) is the latent heat of condensation; P0 = 1000 hPa. g is the gravitational acceleration; \({P_t}\) and \({P_s}\) are tropopause pressure and surface pressure, respectively. The components of diabatic heating \({Q_1}\) include: radiative heating, turbulent sensible heating at the earth surface, and condensation latent heating induced by precipitation. The apparent moisture sink \({Q_2}\) is mainly related to the condensation latent heating. A similar pattern of \(\left\langle {{Q_1}} \right\rangle\) and \(\left\langle {{Q_2}} \right\rangle\) over summer monsoon region indicates that condensational heating induced by precipitation is the major component of diabatic heating (Yanai and Tomita 1998; Jin et al. 2013).

A variable is decomposed into its time mean (denoted with an overbar) and subseasonal (denoted with a prime), and non-subseasonal components (Zhang and Ling 2012; Ren et al. 2015). The horizontal advection of relative vorticity and the two vorticity generation terms in Eq. (1) which contribute to the subseasonal anomaly of local vorticity change \(\left( {\tfrac{{\partial \zeta ^{\prime}}}{{\partial t}}} \right),\) can be expressed as follows:

$$\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv~= - \left( {\bar {u}\frac{{\partial {\zeta ^\prime }}}{{\partial x}}+\bar {v}\frac{{\partial {\zeta ^\prime }}}{{\partial y}}} \right) - \left( {{u^\prime }\frac{{\partial \bar {\zeta }}}{{\partial x}}+{v^\prime }\frac{{\partial \bar {\zeta }}}{{\partial y}}} \right)+residue,$$
(7)
$$\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z~=\frac{1}{{{{\bar {\theta }}_z}}}\left( {f+\bar {\zeta }} \right)\frac{{\partial Q_{1}^{\prime }}}{{\partial z}}+\frac{1}{{{{\bar {\theta }}_z}}}{\zeta ^\prime } \frac{{\partial \overline {{Q_1}} }}{{\partial z}}+residue,$$
(8)
$$\begin{aligned}\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S~&=\frac{1}{{{{\bar {\theta }}_z}}}\left( {\frac{{\partial \bar {u}}}{{\partial z}}\frac{{\partial Q{_1^\prime }}}{{\partial y}} - \frac{{\partial \bar {v}}}{{\partial z}}\frac{{\partial Q{_1^\prime }}}{{\partial x}}} \right)\\ &\quad +\frac{1}{{{{\bar {\theta }}_z}}}\left( {\frac{{\partial {u^\prime }}}{{\partial z}}\frac{{\partial \overline {{Q_1}} }}{{\partial y}} - \frac{{\partial {v^\prime }}}{{\partial z}}\frac{{\partial \overline {{Q_1}} }}{{\partial x}}} \right)+residue \end{aligned},$$
(9)

Where residue terms represent the contributions from nonlinear interaction between subseasonal and non-subseasonal components. The residue terms in (7)–(9), \(\beta ~\) effect, and divergence term in (1) are much smaller than the others and thus ignored hereinafter.

3 Characteristics of subseasonal intensity variation of SAH

3.1 Subseasonal intensity variation of the SAH

Before showing the EOF results, we depict the observed and simulated climatological summer mean fields of Z100 for 1979–2005. The observed SAH is located over the IP–TP and its surrounding areas, with its center value slightly higher than 16,800 gpm (Fig. 1a). The simulations by 18 CMIP5 models reproduce the zonally elongated structure of the SAH in general (Fig. 1b–s). Among the 18 models, CanESM2 slightly overestimates the intensity of the SAH with the center higher than 16,850 gpm, while the SAH’s centers of FGOALS-g2, GFDL-ESM2G, IPSL-CM5A-LR, MRI-CGCM3 are less than 16,700 gpm. Based on the pattern correlation between the observation and the 18 models, MPI-ESM-LR, BNU-ESM, CanESM2, MPI-ESM-MR and NorESM1-M show better skills on simulation of the climatological SAH. Their pattern correlation coefficients are above 0.95. HadGEM2-CC and HadGEM2-ES produce a slightly northward center of SAH compared to the observation. Their pattern correlations are around 0.6.

The spatial pattern of the observed EOF1 is plotted in Fig. 2a. It demonstrates a monopole pattern with a center over the IP–western TP region. As mentioned earlier, this pattern exhibits the spatial structure of subseasonal intensity variation of SAH. The variance of the observed EOF1 is 43%. Figure 2b–s depict the EOF1 patterns of each CMIP5 models. The 18 models simulate the monopole pattern to a certain extent with variances ranging from 33 to 44%. We calculate the subseasonal pattern correlation coefficients (rEOF) between the observed EOF1 and each model’s. ACCESS1-0, ACCESS1-3, BNU-ESM, HadGEM2-CC, HadGEM2-ES, MIROC-ESM-CHEM, MRI-CGCM3, and NorESM1-M reasonably reproduce a similar EOF1 pattern to the observation’s with rEOF ≥ 0.8. Some other models show differences in the location of the monopole center, compared to the observation. For example, the anomalous centers simulated by CanESM2, GFDL-CM3, IPSL-CM5A-LR and IPSL-CM5A-MR are located slightly poleward. Their subseasonal pattern correlation coefficients rEOF are under 0.5.

We divide the 18 models into three groups, according to the value of rEOF. (1) Better-simulated group (BG) with rEOF ≥ 0.8, includes ACCESS1-3 (0.98), HadGEM2-CC (0.96), ACCESS1-0 (0.93), HadGEM2-ES (0.93), MIROC-ESM-CHEM (0.90), BNU-ESM (0.89), MRI-CGCM3 (0.84), NorESM1-M (0.8). (2) General-simulated group (GG) with rEOF between 0.8 and 0.5, includes MRI-ESM1 (0.72), MIROC5 (0.68), MPI-ESM-MR (0.68), MPI-ESM-LR (0.67), GFDL-ESM2G (0.67), FGOALS-g2 (0.58). (3) The rest of the models with rEOF less than 0.5 are lower-simulated group (LG), which includes GFDL-CM3 (0.46), CanESM2 (0.44), IPSL-CM5A-LR (0.43) and IPSL-CM5A-MR (0.41). We select one model from each group as their individual representatives. They are ACCESS1-3 from the BG, MRI-ESM1 from the GG, and IPSL-CM5A-MRall the three models from the LG.

Figure 3 displays the power spectrum of PC1 for the observation and 18 models. A 10-36-day periodicity is seen in the observation (Fig. 3a) with the peak around 27-day. Figure 3b to s are sorted according to rEOF from the greatest to least. Most of the BG models and GG models (Fig. 3b-o) simulate the peaks within 15-30-day, while the GG models show slightly lower variance. The four LG models, CanESM2, GFDL-CM3, IPSL-CM5A-LR and IPSL-CM5A-MR, all simulate no significant peak period.

Fig. 3
figure 3

The 27-year averaged mean power spectra (blue solid line) of the principal component of the first EOF (PC1) for a ERA-Interim and b–s results of the 18 CMIP5 models. The pink dashed line is the red noise spectrum and red dashed line is the spectrum of 95% confidence level. The values at each of the top-right corners is each models’ rEOF. b–s are sorted according to rEOF from the greatest to least

Full size image

Figure 4a–e plot the regression of subseasonal Z100 and 100 hPa wind field anomalies on the normalized PC1 for the observation, from days − 9 to + 3 with interval of 3 days. In the observation, it is seen that an anomalous high is in control of the SAH area at 100 hPa centered over the IP–western TP and East Asia at day 0. Meanwhile, a cyclonic one exists over the Barents Sea and Novaya Zemlya poleward of the anomalous high. Such anomalous pattern is seen on day − 9 with a weak amplitude. From days − 6 to − 3, the anomalous high and low centers become more significant with intensified amplitudes. The above pattern matures on day 0 and fades away locally after day 0.

Fig. 4
figure 4

Regression fields of subseasonal Z100 anomalies (contour with interval of 4 gpm) and 100 hPa wind field anomalies (vector; m s− 1, only values above the 95% confidence level are shown) on PC1, from day − 9 to day + 3 with interval of 3 days, for a–e ERA-Interim, f–j ACCESS1-3, k–o MRI-ESM1, and p–t IPSL-CM5A-MR. The dashed lines denote negative values. The negative (positive) lag days mean Z100 and wind fields anomalies leading (lagging) PC1. Shaded areas denote regions of statistically significant at 95% confidence level

Full size image

The regression of subseasonal anomalies in Z100 and 100 hPa wind field for the three selected models, ACCESS1-3 (BG), MRI-ESM1 (GG) and IPSL-CM5A-MR (LG) on each model’s normalized PC1, are shown in Fig. 4f–t. In general, all the three models can simulate the anomalous anticyclonic band over the SAH’s main body region. However, the simulation results show differences in the intensity of the anomalous anticyclone and its center location. ACCESS1-3 (BG, Fig. 4f–j) simulates most of the observed features of the Z100 anomalous circulation, especially the anomalous anticyclonic center anchored over the IP–western TP region with an amplitude close to the observation. The evolution process simulated by ACCESS1-3 from days − 9 to + 3 also bears resemblance with that in the observation. MRI-ESM1 (GG, Fig. 4k–o) reproduces the anomalous anticyclonic band over the SAH’s main body region with slightly weaker amplitude and with the center shifting to the western part of TP compared to ACCESS1-3 and the observation. IPSL-CM5A-MR (LG, Fig. 4p–t) simulates a much weaker anomalous anticyclone over the IP–TP region from days − 9 to + 3, compared to the observation, ACCESS1-3 (BG) and MRI-ESM1 (GG).

3.2 The precipitation anomaly associated with SAH

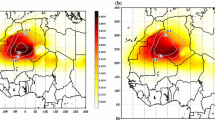
Figure 5a–d plot the time-lagged regression of precipitation and OLR anomalies on PC1 for the observation. The northward propagation of the anomalous rainfall belt is seen in the observation. During the early stage of the SAH’s strengthening (prior to day − 6), positive precipitation anomalies are located between the equator and 20°N, consistent with the local negative OLR anomalies. Increased precipitation also scatters over the regions to the east of TP, southern Korea and southern Japan. During days − 6 to − 4, the area with increased rainfall expands northward to almost all over the Indian subcontinent, Indo-China Peninsula and subtropical east Asian region. When the SAH’s intensity reaches its peak stage (day 0), the positive rainfall belt propagates northward furthermore covering almost the whole of south Asian and east Asian summer monsoon regions between 20° and 40°N. After day 0, the above increased precipitation region becomes shrink, especially over the area to the east of TP.

Fig. 5
figure 5

Regression fields of subseasonal precipitation anomalies (shaded; mm d− 1) on PC1, averaged between days − 9 and − 7, − 6 and − 4, − 3 and 0, + 1 and + 3, for a–d the observation (CPC), e–h ACCESS1-3, i–l MRI-ESM1, and m–p IPSL-CM5A-MR. The regressed OLR anomalies are plotted by contours in a–d (with interval of 1 W m− 2), with the dashed contours being negative. Shaded areas denote regions of statistically significant at 90% confidence level

Full size image

The simulated time-lagged regression of precipitation anomalies on PC1 for the three models are shown in Fig. 5e to p. ACCESS1-3 reproduces the northward propagation of the precipitation anomalies with the strengthening of the SAH, though with a slightly stronger amplitude and weaker signals over the Indian subcontinent compared to the observation (Fig. 5e–h). MRI-ESM1 simulates the northward propagation of the precipitation anomalies in general (Fig. 5i–l). However, its zonal rainfall belt is not well organized. The simulated precipitation anomaly over the eastern Asian continent is too weak. IPSL-CM5A-MR’s simulations of rainfall belt and its northward propagation are much weaker, compared to the observation and the other two models’ (Fig. 5m to p).

We plot latitude–time section of the precipitation anomalies for the observation (Fig. 6a) and 18 models (Fig. 6b–s), averaged over 70°–120°E, to further demonstrate the simulated northward propagating feature of precipitation anomaly. Figure 6b–s are sorted according to rEOF from the greatest to least. The BG models (Fig. 6b to i) can overall simulate well the northward propagation of the precipitation anomalies from tropical areas to subtropical Asia. The GG models (Fig. 6j–o) also can display the northward propagation of precipitation anomalies to a certain extent. However, the propagation patterns are slightly different with that of the observation. The propagation signals in the LG models (Fig. 6p–s) are rather weak, compared to the BG and GG models. Meanwhile, the propagation signals in the LG models are not alike those in the observation.

Fig. 6
figure 6

Lag-regression of subseasonal precipitation anomalies (shaded; mm d− 1) on PC1 averaged over 70°–120°E, for a the observation (CPC) and b–s the 18 CMIP5 models. The values at each of the top-right corners are the same as those in Fig. 3. The regressed observation OLR anomaly is plotted in a (contour; with dashed contour being negative and interval of 1 W m− 2)

Full size image

To show the relationship between intensity anomaly of the SAH and precipitation anomaly over the south and east Asian monsoon regions, we average the simultaneous regression of subseasonal Z100 anomalies on the normalized PC1 over the region of (20°–40°N, 35°–110°E) (denoted as Z100’SAH). The same process is done for precipitation anomalies over the region of (20°–40°N, 70°–120°E) (denoted as R’ASIA). Figure 7 displays the scatter diagrams between Z100’SAH and R’ASIA for the observation and 18 models. It is seen that an enhanced SAH is always accompanied by an above-normal precipitation over south and east Asian regions. Furthermore, a quasi-linear relationship is shown between Z100’SAH and R’ASIA. The correlation coefficient between Z100’SAH and R’ASIA in BG, GG, and LG group are 0.69, 0.61 and 0.62, respectively. This result means the stronger (weaker) precipitation is accompanied by the enhanced (damped) SAH. For example, the BG (models showing in Fig. 7 as ‘*’) overall reproduces reasonably the enhanced SAH and accompanied positive precipitation anomaly. The GG (showing as ‘O’) simulate smaller values of positive Z100′ and positive R’ASIA compared to the observation and the BG models. For the LG (showing as ‘+’), their positive values of Z100’SAH and R’ASIA are both the smallest.

Fig. 7
figure 7

Scatter diagrams showing the relationship between subseasonal Z100 anomalies (gpm; x-axis) averaged over 20°–40°N, 35°–110°E and precipitation anomalies (mm d− 1; y-axis) averaged over 20°–40°N, 70°–120°E both at day 0, for the ERA-Interim and 18 CMIP5 models

Full size image

4 Mechanism for the subseasonal intensity variation of SAH

In this section, we diagnose the three dynamical processes contributing to the subseasonal relatively vorticity anomaly at 100 hPa over the SAH’s region: horizontal advection of relativity vorticity \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv,\) vorticity sources induced by vertical gradients \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z~\) and by horizontal gradients \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) of diabatic heating, respectively.

4.1 The dynamic processes in observation

Figure 8a, b show the latitude-time sections of regressed anomalies in \(\left\langle {{Q_1}} \right\rangle ,\)\(\left\langle {{Q_2}} \right\rangle ,\)\(~\left( {\frac{{\partial \zeta '}}{{\partial t}}} \right){Q_1}\_z~\) at 100 hPa and precipitation against PC1 averaged over 70°–120°E for the observation. As mentioned before, a northward propagation of the positive rainfall band can be seen with the strengthening of the SAH. The positive diabatic heating as well as positive moisture sink also propagate from the tropical to the south and east Asian regions. The similar northward propagation of \(\left\langle {{Q_1}} \right\rangle\) and \(\left\langle {{Q_2}} \right\rangle\) anomalies indicates that the anomalous condensational heating induced by the rainfall anomalies dominates the anomalous diabatic heating (Yanai and Tomita 1998; Jin et al. 2013). Thus a northward propagation of negative \(~\left( {\frac{{\partial \zeta '}}{{\partial t}}} \right){Q_1}\_z\) band is produced in Fig. 8b due to the increased vertical gradient of \({Q_1}'\) in the upper level. When the negative \(~\left( {\frac{{\partial \zeta '}}{{\partial t}}} \right){Q_1}\_z\) band reaches the SAH’s main body region, it contributes directly to the strengthening of the SAH. We also used a Linear Baroclinic Model (LBM) experiment to examine the locally responses of circulation to the condensation heating. The results (figure omitted) verify again the effect of condensation heating to the SAH, which is similar to the results showing in Zhang et al. (2016).

Fig. 8
figure 8

latitude-time section (averaged over 70°–120°E) of regressed subseasonal anomalies on PC1 for ERA-Interim in a vertically integrated apparent heating source \(\left\langle {{Q_1}} \right\rangle\) (shaded; W m− 2) and vertically integrated apparent mositure sink \(\left\langle {{Q_2}} \right\rangle\) (purple contour with interval of 2 W m− 2); b\(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) (shaded; 10− 11 s− 2) and precipitation (purple contour with interval of 0.2 mm d− 1); c\(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) (shaded; 10− 11 s− 2) and \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) (contour with interval of 2 × 10− 11 s− 2); d longitude-time section (averaged over 20°–35°N) of regressed subseasonal anomalies on PC1 of vorticity advection (\(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\)) (shaded; 10− 11 s− 2)

Full size image

The contour in Fig. 8c plots observed regression of \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\). Within the heating region the vertical heating gradient dominates the forcing, whereas at the border of the diabatic heating the horizontal heating gradient plays a more important role (Wu and Liu 1998; Liu et al. 2001). In Fig. 8c, on the north flank of the heating, a negative vorticity source which is induced by the horizontal gradient of diabatic heating is generated and propagates northward as well. When the positive rainfall belt propagates northward and reaches around 15°N (about day − 9), the generated weak negative tendency of vorticity anomalies begins to favor the enhancement of the southern part of SAH. The observed regression of \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv,\) is plotted in Fig. 8d. During the summertime, the climatological easterly flow is located over the southern part of the SAH. It can be seen that the negative vorticity anomalies with the climatological easterly flow together induce a westward advection of the negative vorticity, which is conducive to the westward expansion of the SAH.

To demonstrate further the evolutions of above dynamical processes, the three dynamic processes are averaged over the SAH’s main body region and plotted in Fig. 9. In the observation, the northward propagating of rainfall band during days − 9 to − 6 is on the south flank of SAH. Thus, the process of \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) plays a negative vorticity source in favor of enhancement of the SAH’s southern part. The process of \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) acts to contribute to the enhancement of SAH after day − 6. It has the most significant role in the strengthening of SAH around day 0, when the anomalous rainfall band occupies the south and east Asian regions. The horizontal advection process of \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\) is also favorable to the SAH’s enhancement, especially during days − 6 to days 0.

Fig. 9
figure 9

Regression of observed subseasonal anomalies in \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) (green line; 10− 11 s− 2), \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\) (purple line; 10− 11 s− 2), \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z~\) (blue line; 10− 11 s− 2) and \({\zeta ^\prime }\) (red line; 10− 6 s− 1) on PC1 averaged over 20°–40°N, 40°–120°E

Full size image

4.2 The models performances

We next evaluate the selected three models’ performances of above dynamical processes. Figure 10 displays the latitude-time sections of regression of simulated subseasonal anomalies of \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z,\)\(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) and \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\) onto each models’ normalized PC1. ACCESS1-3 simulates the northward propagation of negative vorticity tendency generated by \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) and \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) (Fig. 10a, b). The simulated westward advection of negative vorticity anomalies is mainly located between 90°and 120°E (Fig. 10c). MRI-ESM1 reproduces the northward propagation of \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) and \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) in general (Fig. 10d, e). However, the signal is weaker than the observation and ACCESS1-3, due to the weaker simulation of the rainfall band shown in Fig. 6j. The three dynamical processes simulated by IPSL-CM5A-MR are rather weak (Fig. 10g–i).

Fig. 10
figure 10

Upper panels: latitude-time section of regressed subseasonal anomalies in \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) (10− 11 s− 2) on PC1 averaged over 70°–120°E for a ACCESS1-3, d MRI-ESM1 and g IPSL-CM5A-MR. Middle panels: the same as upper panels, but for \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S.\) Bottom: the same as upper panels, but for longitude-time section (averaged over 20°–35°N) of regressed subseasonal anomalies in \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\)

Full size image

Figure 11 shows the three dynamic processes of the three models averaged over the SAH’s main body region. The evolutions and amplitudes of the three area-averaged dynamic processes simulated by ACCESS1-3 resemble those of the observation (Fig. 9). The amplitudes simulated by MRI-ESM1 are weaker compared to the observation and ACCESS1-3, though the evolutions are similar to the observation. The evolutions of the three dynamic processes simulated by IPSL-CM5A-MR are too weak. Meanwhile, the amplitudes are underestimated dramatically.

Fig. 11
figure 11

Regression of subseasonal anomalies in \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) (green line; 10− 11 s− 2), \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\) (purple line; 10− 11 s− 2), \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z~\)(blue line; 10− 11 s− 2) and \({\zeta ^\prime }\) (red line; 10− 6 s− 1) on PC1 averaged over 20°–40°N, 40°–120°E for a ACCESS1-3, b MRI-ESM1 and c IPSL-CM5A-MR, respectively

Full size image

5 Summary and discussion

The present study investigates the features and dynamical mechanism of the subseasonal intensity variation of SAH at 100 hPa based on the observational data and 18 CMIP5 models during 1979–2005. In the observation, the SAH at 100 hPa is located over the IP–TP and its surrounding areas, with its center value slightly higher than 16,800 gpm. An EOF analysis is carried out on the standardized subseasonal Z100 anomalies over the region of (20°–40°N, 35°–110°E). The observed EOF1 pattern demonstrates the strengthening/weakening of the SAH’s main body with its center over the IP–western TP region. The intensity variation of SAH displays a periodicity of 10–36-day with the peak around 27-day.

The regressions of the observed anomalies in Z100, 100 hPa wind fields, and precipitation onto the observed normalized PC1 reveal the following features: The SAH’s strengthening begins with a weak anomalous high centered over the IP–western TP, and a low poleward of the high located over the Barents Sea and Novaya Zemlya. Above pattern is invigorated gradually and matures on day 0. Before day − 6, an enhanced rainfall belt migrates northward conspicuously from the equatorial Indian Ocean, the Bay of Bengal, the South China Sea and the Western North Pacific and finally occupies almost the whole Indian subcontinent, Indochina Peninsula and subtropical East Asian regions between 20°–40°N on day 0.

Three dynamical processes responsible for the subseasonal intensity variation of SAH are investigated, respectively: vertical gradient of diabatic heating \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)Q{}_{1}\_z~,\) horizontal gradient of diabatic heating \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S,\) and horizontal advection of relative vorticity \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv.\) The dynamical process of \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)S\) plays a role in the enhancement of the southern part of SAH around days − 9 to -6 due to the horizontal gradient of diabatic heating. The process of \(~\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right){Q_1}\_z\) contributes most significantly to the enhancement of SAH during days − 3 to + 3 when the anomalous rainfall band occupies 20°–40°N of the south and east Asian monsoon regions. The horizontal advection process of \(\left( {\frac{{\partial {\zeta ^\prime }}}{{\partial t}}} \right)adv\) induces a westward transportation of the negative vorticity, being favorable to the westward expansion of SAH.

The 18 CMIP5 models capture the zonally elongated structure of the climatological SAH in general. All the 18 CMIP5 models simulate the SAH’s monopole pattern of EOF1 to a certain extent. The models are divided into three groups according to the subseasonal pattern correlation coefficient (rEOF) between the observed EOF1 and the models’. One model is selected from each group as their individual representatives: ACCESS1-3 from the BG with rEOF above 0.8, MRI-ESM1 from the GG with rEOF between 0.8 and 0.5, and IPSL-CM5A-MR from the LG with rEOF less than 0.5. ACCESS1-3 (BG) simulates a realistic subseasonal intensity anomaly of SAH. MRI-ESM1 (GG) reproduces a slightly weaker one with the center of anticyclonic anomaly shifting to the western part of TP. IPSL-CM5A-MR (LG) simulates a much weaker one compared to the observation, ACCESS1-3 and MRI-ESM1.

Our results indicate that, the capacity of the 18 models to simulate the SAH’s intensity variation has a close conjunction with simulations of the strength as well as the northward propagating features of anomalous rainfall band over the south and east Asian monsoon regions. The realistic simulation of precipitation anomalies in BG models befits reproduction of the dynamical processes related to diabatic heating. When the simulated subseasonal precipitation anomalies (for example, LG models) are too weak and show deficiency in propagating features, the simulated SAH’s subseasonal intensity anomalies are dramatically weakened.

The present study shows that the strength and northward propagation of precipitation from the tropics is important for the reproduction of the subseasonal variation of the SAH. Why some of the models cannot reproduce this northward propagation of precipitation anomalies? Comparison of Figs. 1 and 2, it seems that the model’s ability to reproduce subseasonal intensity variation of the SAH has no robust connection with its capacity in simulating the SAH climatology. One of the possible reasons may result from the horizontal resolution of models. In CMIP5, the simulation of precipitation has been further improved to a certain extent compared to the CMIP3. However, the bias of the precipitation simulation is still seen in current general couple models (Chen and Frauenfeld 2014; Yao et al. 2017; Fang et al. 2017). In this paper, it can be found that the top four models in BG models have the same horizontal resolution (192 × 144), which could be a suitable horizontal resolution for the precipitation simulation related to the SAH subseasonal variation. The lower or higher horizontal resolution can both influence the models performance, which may due to the convective parameterization scheme or microphysis scheme (Giorgi and Marinucci 1996; Chan et al. 2013; Huang et al. 2013; Kan et al. 2015; Yang et al. 2015).

Moreover, the boreal summer intraseasonal oscillation (BSISO) is a dominant signal over the tropical and Asian monsoon region (Yasunari 1979; Krishnamurti and Subramanian 1982; Lau and Chan 1986; Jiang et al. 2004; Annamalai and Sperber 2005; Wang et al. 2005; Lee et al. 2013; Demott et al. 2013). The simulation of large-scale circulation such as mean wind, moisture fields, or western North Pacific subtropical high (WNPSH), and the ocean boundary conditions such as sea surface temperature (SST) could also lead to the bias of models reproduction of northward propagation BSISO signal (Fu and Wang 2004; Park et al. 2009; Levine and Turner 2012; Demott et al. 2013, 2014; Fang et al. 2017), and thus may influence the ability of model to the simulation of SAH variation. The relationship between the subseasonal variations of SAH and the BSISO is not analyzed thoroughly in this study and need a further investigation both in observation and models. More exploration about the above issues should be taken into account in future studies.