Abstract
The Caribbean low-level jet (CLLJ) is an important component of the atmospheric circulation over the Intra-Americas Sea (IAS) which impacts the weather and climate both locally and remotely. It influences the rainfall variability in the Caribbean, Central America, northern South America, the tropical Pacific and the continental Unites States through the transport of moisture. We make use of high-resolution coupled and uncoupled models from the Geophysical Fluid Dynamics Laboratory (GFDL) to investigate the simulation of the CLLJ and its teleconnections and further compare with low-resolution models. The high-resolution coupled model FLOR shows improvements in the simulation of the CLLJ and its teleconnections with rainfall and SST over the IAS compared to the low-resolution coupled model CM2.1. The CLLJ is better represented in uncoupled models (AM2.1 and AM2.5) forced with observed sea-surface temperatures (SSTs), emphasizing the role of SSTs in the simulation of the CLLJ. Further, we determine the forecast skill for observed rainfall using both high- and low-resolution predictions of rainfall and SSTs for the July–August–September season. We determine the role of statistical correction of model biases, coupling and horizontal resolution on the forecast skill. Statistical correction dramatically improves area-averaged forecast skill. But the analysis of spatial distribution in skill indicates that the improvement in skill after statistical correction is region dependent. Forecast skill is sensitive to coupling in parts of the Caribbean, Central and northern South America, and it is mostly insensitive over North America. Comparison of forecast skill between high and low-resolution coupled models does not show any dramatic difference. However, uncoupled models show improvement in the area-averaged skill in the high-resolution atmospheric model compared to lower resolution model. Understanding and improving the forecast skill over the IAS has important implications for highly vulnerable nations in the region.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Intra-Americas region, also known as the Intra-Americas Sea (IAS), is defined as a broad area including the Gulf of Mexico, southern United States, Mexico, the Caribbean Sea with its islands, northern South America, Central America and the ocean off the west coast of Central America and Colombia (IASCLIP 2005). The most important physical mechanisms controlling the rainfall in the region are associated with the semi-annual strengthening and westward excursion of the North Atlantic Subtropical High (NASH; Wang 2007a), and its relationship with the variability of the Atlantic side of the Western Hemisphere Warm Pool (WHWP; Wang and Enfield 2001, 2003), cold surges emanating from the North America (Schultz et al. 1997, 1998), annual migration of the ITCZ (Hastenrath 2002; Higgins and Shi 2001; Hu and Feng 2002; Nogues-Paegle and Mo 2002) and the Caribbean Low Level Jet (CLLJ; Amador 1998, 2008; Amador and Magana 1999; Mo et al. 2005; Wang 2007a).
NASH’s zonal migrations in summer and winter modify both the surface-level pressure (SLP), winds and thus sea-surface temperature (SST) gradients (via wind-evaporation-SST feedback) in the Caribbean, being associated with well defined bands of strong easterly winds and SST gradients, which are maximum in the July–September (JAS) season (Wang 2007a). These further induce the horizontal SLP gradients that force the low-level atmospheric winds and produce the CLLJ, which is one of causes for the CLLJ formation. Furthermore, an important positive atmosphere–ocean feedback mechanism has been suggested that helps self-sustain the CLLJ: the easterly winds induce positive and negative wind stress curls to the north and the south of the jet, respectively, that further increase the SST gradient through oceanic Ekman dynamics warming the WHWP via downwelling, and cooling the southern part of the Caribbean via upwelling (Inoue et al. 2002; Wang 2007a). Thus, the CLLJ can be considered a central climate driver for the Intra-Americas, sensitive to the variability of NASH, WHWP and to SST patterns in both the Pacific and the Atlantic (Amador 2008; Krishnamurthy et al. 2015). In consequence, we pay special attention to the CLLJ in this work.
The seasonal evolution of rainfall in the Intra-Americas region varies based on the geographical location. For example, in the Central America, there is a pronounced difference in the seasonality of rainfall between the Pacific and the Caribbean coasts, mainly attributed to the interaction of the dominant easterly winds with the local topography (Taylor and Alfaro 2005; Maldonado et al. 2016a; Magaña et al. 1999). In addition, several regions in the Intra-Americas, such as southern Mexico, Central America and Caribbean exhibit a bimodal distribution of rainfall that correlates well with the semi-annual variability of the CLLJ (Magaña et al. 1999; Amador 2008). The precipitation peaks before and after the Mid-Summer Drought (MSD) in July, when the easterly winds are at their maximum intensity on the Pacific slope of Central America (Magaña et al. 1999). In addition to contribution of the Choco jet from the Pacific side (Poveda and Mesa 2000, Durán-Quesada et al. 2010), rainfall is seasonally modulated by the Caribbean low-level jet from the Caribbean side via its control of moisture advection, vertical wind shear and easterly waves (Amador 1998, 2008; Amador and Magana 1999; Wang 2007a; Durán-Quesada et al. 2010; Maldonado et al. 2016a). Further, the region of intense precipitation maxima near Costa Rica and Nicaragua in the southwestern Caribbean region during July and the low-level convergence–divergence patterns are suggested to be strongly associated with large-scale CLLJ dynamics (Amador 2008). It is expected that models that have a fair representation of the CLLJ characteristics also have a better representation of the rainfall characteristics for most of the Intra-Americas.
As mentioned before, atmosphere–ocean feedback is an important driver of the CLLJ, and hence it is important for climate models to have accurate representation of the feedback mechanisms between the atmosphere and ocean. The state-of-the-art coupled global models have been shown to have important biases leading to misrepresentation of the rainfall variability in the region (Ryu and Hayhoe 2014), while global atmospheric models forced with observed SSTs have a better representation of the CLLJ characteristics and associated rainfall (Martin and Schumacher 2011; Diro et al. 2012) although these studies suggest a slight underestimation of magnitude of the CLLJ. However, it is logical to think that coupled models will have an accurate representation of the involved key physical processes related to air-sea feedback than uncoupled models. This contradiction between the perceived notion about coupled models and previous studies which indicate that the uncoupled models are better, motivates us to have a comparative study for the region between the coupled and uncoupled models.
Studies based on Coupled Model Intercomparison Project Phase 3 (CMIP3; Martin and Schumacher 2011) models reveal that most of the state-of-the-art coarse resolution coupled models fail to capture the correct magnitude of the CLLJ, its semiannual cycle and associated rainfall. Their CMIP3 study suggests the need for high-resolution models to precisely simulate the mean state and variability of the CLLJ, and to further capture the local small-scale relationships between the jet in the IAS and the surrounding regions. Muñoz et al. (2008) suggest that the surface temperature and orographic effects also contribute to the strength of the CLLJ, in agreement with Wang (2007a). However, Maldonado et al. 2016a suggests that topography may not have influence on the simulation of the CLLJ. They note that this result needs to be treated with caution due to instability issues. Further model sensitive studies and those with higher resolution (higher than 80 km as used in Maldonado et al. 2016a) may be needed to support above hypothesis. The low-level jet, while transporting moisture to the surrounding inhabited continents, encounters orographic influences on its path such as Greater Antilles and mountains of the northern South America which confines the jet structure and the mountain range of the Central America on the western side of the Caribbean. Thus, high-resolution coupled models with accurate representation of orography may be required for a precise simulation of the structure and strength of CLLJ.
The highest atmospheric resolution used so far to study the CLLJ is 1.125° (Martin and Schumacher 2011), although other studies have used higher resolution to understand different aspects of IAS such as representation of SSTs, ocean currents and heat flux with changing bathymetry (Misra et al. 2016). In this study, we use the Geophysical Fluid Dynamics Laboratory (GFDL) Forecast-oriented Low Ocean Resolution (FLOR) model which has a high-resolution atmospheric component at approximately 50 km (0.5° × 0.5°), and the low-resolution GFDL Coupled Model version 2.1 (CM2.1) at approximately 111 km (1° × 1°) to understand the climatological structure and seasonal cycle of the CLLJ, as well as its variability and associated teleconnections. We also compare with uncoupled simulations of FLOR and CM2.1, referred to as AM2.5 and AM2.1, respectively. Further, we also assess the skill of these coupled and uncoupled models in predicting rainfall over the Intra-Americas Seas.
Most common seasonal prediction schemes used in Central America, northern South America and the Caribbean employ statistical models based on empirical relationships between predictors like observed sea-surface temperature (SST) and rainfall. For example, the Central American Climate Outlook Forum (CACOF) uses this approach to provide accumulated rainfall forecasts for the May–June–July (MJJ), August–September–October (ASO) and December–January–February–March (DJFM) seasons (García-Solera and Ramírez 2012; Alfaro et al. 2017).
A number of studies (Alfaro 2007; Fallas-López and Alfaro 2012a, b; Maldonado et al. 2013, 2016a, b) has analyzed the predictability of rainfall at seasonal timescale using cross-validated statistical forecasts based on the observed tropical Atlantic and Pacific SST anomalies with a lead time ranging from a month to a season. Using several kind of metrics, these studies show that the predictive skill is high enough as to be of potential use for the development of climate services (Vaughan and Dessai 2014) over a large portion of Central America.
On the other hand, since 2008, the Latin American Observatory for Climate Events (http://ole2.org; Muñoz et al. 2010, 2012) has been issuing high-resolution regional-scale seasonal forecasts for different variables relevant to climate services. Although originally their approach used a multi-physics dynamical downscaling with a combination of regional climate models (Muñoz et al. 2010), the Observatory has more recently migrated to predictions of “seasonal scenarios” computed using the same kind of SST-based statistical models mentioned above, and Model Output Statistics (MOS) applied on the Climate Forecast System version 2 (CFSv2) ensemble-mean rainfall predictions. The skill assessment for both types of seasonal scenarios, using a variety of metrics, is publicly available on the Observatory’s Datoteca (Chourio 2016; see also details in http://datoteca.ole2.org/maproom/Sala_de_Validacion/index.html.es). In terms of accumulated rainfall predictive skill, the Observatory reports values of the spatially averaged Kendall’s tau correlation coefficient that range from 0.040 (March–May, or MAM) to 0.180 (OND).Footnote 1 Thus, so far, either statistical models, regional models and/or coupled dynamical model with resolution up to 1° x 1° have been used for seasonal prediction of rainfall over the IAS. To the best of the author’s knowledge, this is the first study for this region that assesses the rainfall predictive skill using high-resolution global coupled models with a statistical correction to account for biases in the model variables in the context of seasonal prediction. Alfaro et al. (2017) have applied similar statistical correction over Central America.
The rest of the paper is organized as follows. Section 2 presents observational datasets, models and model data, as well as the methods of analysis used in this research. The main results are discussed in Sect. 3 and the concluding remarks are stated in Sect. 4.
2 Observational data, model and method of analysis
2.1 Observational data
The high-resolution reanalysis data on 0.5° × 0.5° in longitude by latitude for sea-level pressure, and for zonal and meridional winds are obtained from NASA’s (National Aeronautics and Space Administration) Modern-Era Retrospective Analysis for Research and Applications (MERRA), for the period 1979–2012 (Rienecker et al. 2011). The MERRA was generated using the Goddard Earth Observing System version 5.0 and its data assimilation system. The zonal and meridional winds are available at 42 vertical levels from 1000 to 0.1 hPa. The monthly SST data is derived from HadISST1.1 version from the Hadley Centre for Climate Prediction and Research. It spans for the period 1870–2012 on 1° × 1° grid (Rayner et al. 2003).
Two independent rainfall datasets are used in this study. One is the Climate Prediction Center (CPC) Merged Precipitation analysis (CMAP) provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, available at their web site (http://www.esrl.noaa.gov/psd/). This is a merged precipitation dataset derived from the combination of gauge measurements, satellite observations and National Center for Ensemble Prediction (NCEP)—National Center for Atmospheric Research (NCAR) reanalysis (Xie and Arkin 1997). It is known to have better quality than the individual estimates. The data is available on 2.5° × 2.5° grid, and for the period 1979–2013. The second dataset is the East Anglia University’s Climate Research Unit product known as CRUTS3.23 (Harris and Jones 2015), that uses surface rainfall gauges and state-of-the-art-interpolation methods to build a gridded precipitation dataset at a horizontal resolution of 0.5° × 0.5° and for the period 1979–2012.
2.2 Model data
As indicated in the Introduction, the models used in this study are CM2.1 and FLOR, a modified version of Climate Model version 2.5 (CM2.5). The CM2.1, CM2.5 and FLOR models are described in detail in Delworth et al. (2006), Delworth et al. (2012) and Vecchi et al. (2014), respectively. The physics is similar in both the atmospheric component of the models, the main difference being associated with the horizontal resolution. CM2.1 comprises of Atmospheric Model version 2 (AM2) which has a resolution of approximately 200 km, and has 24 vertical levels. The oceanic component is the Ocean Model version 3.1 (OM3.1), with 1° × 1° horizontal resolution and 50 vertical levels. FLOR includes the same atmospheric component as CM2.5, but the oceanic component is from CM2.1. The atmospheric component of FLOR is on a 0.5° × 0.5° longitude by latitude grid, with 32 levels in vertical. The mean state and variability of the upper surface variables (such as rainfall, SST, SLP and the upper and lower-level zonal and meridional winds) in FLOR is very similar to that of CM2.5 (Jia et al. 2015). Thus, we focus on FLOR for the rest of this analysis. FLOR is shown to have better climate simulation than CM2.1 which further leads to improved simulation of teleconnections and predictions (Vecchi et al. 2014; Jia et al. 2015; Yang et al. 2015; Krishnamurthy et al. 2015, 2016, 2018; Zhang and Delworth 2015).
All the results presented in Sect. 3.1, have been verified with the CM2.5 simulation and they yield similar results, suggesting that the increased ocean resolution plays a secondary role. The 1990 control simulations of CM2.1 and FLOR are used in this study, where the greenhouse gases, aerosols and solar forcing are prescribed at 1990 levels. The CM2.1 and FLOR simulations span from year 101–300 and year 601–1200, respectively, to avoid spin-up issues. We analyze these runs to investigate the ability of the models to simulate CLLJ, its impacts and relationship to large-scale SST forcing. Further, we use forecast runs from CM2.1 and FLOR model to asses the forecast skill of the models in predicting rainfall patterns during July-August-September (JAS) that may be driven by CLLJ. We analyze the forecast runs starting from 1981 to 2013, with initial conditions starting from June 1st.
2.3 Model output statistics
Due to uncertainties associated with boundary and initial conditions, inadequate representation of physical processes and the chaotic nature of the climate system, models always exhibit errors. Part of these errors, the systematic ones, can be corrected via a statistical approach generally known as Model Output Statistics (MOS; Glahn and Lowry 1972; Wilks 2006). In this work, Canonical Correlation Analysis (Barnston and Ropelewski 1992; Wilks 2006), or CCA, is used as MOS to correct the biases in the model output. In brief, CCA identifies modes of variability by maximizing the correlation between linear combinations of predictor and predictand empirical orthogonal functions (EOFs).
CCA is a common statistical method frequently used to forecast rainfall using a purely empirical approach (Mason and Baddour 2008; Barnston et al. 2012), especially in developing countries and in particular in the Intra-Americas nations. For example, considering 30 years of data,Footnote 2 if the predictor field is observed SST of the previous month to be forecast (e.g., June), and the predictand is the observed rainfall for the season to be forecast (e.g., July–September), CCA can be used to build a statistical model to predict the behavior of certain linear combinations of the observed rainfall EOFs in terms of linear combinations of the June sea-surface temperature EOFs. In a MOS approach, the predictand, or variable to be forecast, is still the observed rainfall for the season of interest, and the predictor is the raw model output rainfall for the same season. CCA in this case corrects both biases in the magnitude and in the spatial location of the modeled precipitation patterns. In this work, CCA is applied to both model rainfall (over the domain 4°S–33°N, 120°W–50°W) and SST fields, and for the JAS season. MOS correction is applied for every grid point.
This work uses a 5-year-out cross-validation window, meaning that when “training” the CCA model, five continuous years are purposely left out of the record. Further, the regression coefficients are computed with the remaining time series, and the resulting model is validated by comparing the prediction’s the third year (the middle year in the 5-year out window) against observations. The 5-year-long window is redefined a year at a time, thus moving from the beginning of the record to its end. The mean value of the validation metric computed for each iteration is reported as the cross-validated goodness-of-fit index.
The Kendall’s tau rank correlation coefficient is used in this work as an overall metric for assessing rainfall skill (the goodness index). A negative Kendall’s tau means that the forecast is worse than using climatology, while a value of one corresponds to a perfect set of forecasts. The values are computed for each gridbox and then spatially averaged in order to have an overall assessment of skill. The Generalized Relative Operating Characteristics (GROC), also called 2AFC score (2AFC = (tau + 1)/2; Mason and Weigel 2009), is used to evaluate precipitation skill at a local scale, i.e., via spatial maps. A value of 50% corresponds to climatological values, and thus regions with a 2AFC lower than 50% are worse than the climatology. A value of 100% indicates perfect discrimination. This score is similar to Kendall’s tau, and measures the “proportion of all available pairs of observations of differing category whose probability forecasts are discriminated in the correct direction” (Mason and Weigel 2009). It has an intuitive interpretation, as an indication of how often the forecasts are correct.
3 Results
3.1 Simulation of CLLJ, its impacts and relation to large-scale SST forcing
-
(a)
Climatological structure and seasonality of the CLLJ
The CLLJ is considered to be predominantly zonal and is known to have maximum wind speeds in the Caribbean region defined by the domain 70°W–80°W and 12°N–16°N (Muñoz et al. 2008; Wang 2007a; Whyte et al. 2008). The vertical profile of the CLLJ is defined in terms of area-averaged climatological zonal winds for the Caribbean region, to examine its structure and seasonality (Fig. 1). The observed vertical structure in Fig. 1a indicates peak values of zonal wind at 925 hPa during winter and summer, with the wind speeds being strongest in July. In addition to the strengthening of winds in July, the jet structure also deepens vertically. The minimum in the low-level jet occurs in May and October. The CM2.1 model shows the summer peak in June and weakens much earlier compared to observations, failing to capture the July peak and the minimum in May (Fig. 1b). Figure 1f shows that the high-resolution model FLOR successfully captures the summer peak in July and vertical deepening of the jet (only with a difference of slight deepening beyond 650 hPa, compared to observations). This is an important improvement in the representation of CLLJ peak in summer over CM2.1. The representation of CLLJ is better in AM2.1 and AM2.5 compared to their coupled counterparts. This highlights the role of SSTs on the adequate simulation of the CLLJ. AMIP runs have SSTs close to observations, and hence may lead to improved simulation of the CLLJ.
Pressure–time section of climatological zonal wind area-averaged in the domain 80°W–70°W, 12°N–16°N for (a) Observations (c) AM2.1, (d) AM2.5 (e) CM2.1 (f) FLOR. Units of zonal wind are in m/s. The wind speeds greater than 9 m/s are shaded in blue and contour interval is 1 m/s. (b) Timeseries of climatological zonal wind speed at 925 hPa area-averaged in the domain 80°W–70°W, 12°N–16°N. The units of zonal wind speed are in m/s for observations (black), CM2.1 (red), FLOR (green), AM2.1 (dark blue) and AM2.5 (light blue)
The vertical structure of zonal wind in the Caribbean region suggests a peak at 925 hPa level in the observations that is successfully simulated by both CM2.1 and FLOR. Thus, in the following, we focus on that level and define the time series of climatological CLLJ at 925 hPa for both observations and models (Fig. 1b). The observed time series shows a semiannual cycle with peaks in January and July, and minimum in May and October (Fig. 1b). Similar to the vertical profile, the time series also shows that the FLOR model captures the summer peak accurately in July (though it overestimates its magnitude), in contrast to CM2.1 which exhibits its summer peak in June, as mentioned before. However, both models indicate that the peak persists from winter to summer, which is in contrast to observations. The slight underestimation of the CLLJ in AM2.1 during summer and fall is consistent with Martin and Schumacher (2011) and Diro et al. (2012) suggesting an underestimation in uncoupled models during these seasons. However, this general bias in uncoupled models is absent in AM2.5 with accurate simulation of magnitude of the CLLJ during summer and fall. The lack of vertical deepening in AM2.1 and CM2.1 is similar to the issue in the atmospheric model used in Amador (2008). The issue with lack of minimum in May in coupled and uncoupled models leading to lack of semiannual cycle, as noted by Martin and Schumacher (2011), is yet to be resolved in GFDL models. Further, both versions of the coupled and uncoupled models fail to simulate the minimum in May and hence the CLLJ in these GFDL models is characterized by an absence of semiannual cycle. This seems to be a persistent problem with most of AR4 models also (Martin and Schumacher 2011; Ryu and Hayhoe 2014). We explored the possible causes for deficiency of the GFDL model in simulating the spring minimum. The lack of minimum of the low-level jet during spring may be attributed to the northeastward excursion of NASH. The FLOR model has southwestward extension of NASH compared to observations in May as evident in the climatological SLP (figure not shown). This may lead to stronger SLP gradients in the Caribbean in FLOR and hence the stronger CLLJ and the lack of minimum in May. FLOR-FA, which is a flux-adjusted version of FLOR with SSTs close to observational estimates, also shows similar behavior (figure not shown), even though the model has better simulation of SSTs, which points again towards possible deficiency in the atmospheric model. FLOR AGCM forced with observed SSTs also hints towards a similar hypothesis, where correcting SSTs seems to not necessarily improve the simulation of CLLJ during May (figure not shown). It also suggests stronger SLP gradients during May along with stronger CLLJ. However, correcting SSTs does improve the simulation of magnitude of the CLLJ during summer and fall. Other coupled model [for e.g., National Center for Atmospheric Research (NCAR) Community Climate System Model Version 4 (CCSM4)] studies also showed similar results (Grodsky et al. 2012) and their AGCM runs with prescribed SSTs from observations did not correct the bias in SLP. However, improvements in the convection scheme in their atmospheric model reduced the biases to a certain extent.
This lack of simulation of mean state during spring may have implications for teleconnections associated with the CLLJ. For example, the variations in the CLLJ have been connected to the variability of tornado activity in the southern US during spring. This may also have implications for bimodal distribution of rainfall over the Caribbean region which has peak rainfall during May. Stronger than observed CLLJ may lead to reduced rainfall during this month and may have adverse implications for forecasting rainfall during spring over the Caribbean.
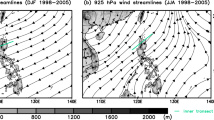
Hereafter, we analyze the simulation of the CLLJ and its teleconnection for JAS season as the models successfully simulate the CLLJ during this season; this is attributed to a fair representation of the meridional SST gradient and the involved mechanisms as described in the Introduction. These months are also of interest due to the effect of the CLLJ on the US rainfall over the central and southeastern regions (Weaver et al. 2009) and on the tropical storms and Atlantic hurricanes (Wang and Lee 2007b). We analyzed the spatial structure of the CLLJ in the longitude-latitude domain in JAS. Both the coupled and uncoupled versions 2.1 and 2.5 models show realistic simulation of the climatological structure of the CLLJ (Fig. 2), although FLOR shows slightly higher magnitude.
-
(b)
Interannual variability of CLLJ and its teleconnections
Figure 3 shows that AM2.1, AM2.5, CM2.1 and FLOR models have realistic simulation of the JAS variability of CLLJ in the Caribbean region, with AM2.5 and FLOR showing a slight improvement in the longitudinal extent and strength of the jet. In addition to the improvements locally, FLOR also shows improvement in the simulation of the easterlies extending into the eastern Pacific. This improvement may be related to better simulation of SLP gradients (figure not shown) and SST gradients in FLOR (Fig. 4e). Both, the coupled and uncoupled models have realistic representation of CLLJ-related SST teleconnection patterns (Fig. 4). CLLJ-related SSTs shows westward extension of SST in CM2.1 in the western tropical Pacific and the magnitude of SSTs are slightly higher in the tropical Atlantic. However, these biases are improved in FLOR, which has better representation of CLLJ-related SSTs in the tropical Pacific and Atlantic Oceans compared to observations. Thus, the FLOR model has improved simulation of the observed relationship of the CLLJ with the tropical Pacific and Atlantic SSTs (Fig. 4e) which might translate into better SST gradients between the tropical Pacific and tropical Atlantic. The SST gradients further influence the CLLJ (Amador 2008; Krishnamurthy et al. 2015). The strength of regression coefficients is slightly higher in coupled models. This may be attributed to increased strength of amplitude of ENSO in CM2.1 and FLOR (Fig. 5). Weaker amplitude of the CLLJ may also be the contributing factor in FLOR in addition to stronger ENSO (Fig. 6e). We also notice slightly higher regression values in AMIP runs, which may be related to slightly weaker amplitude of the CLLJ (Fig. 6b, c). Above results are based on the comparison with MERRA, uncertainties in the reanalysis product will affect our conclusions.
Regression of JAS seasonal anomalies of U925 on the JAS seasonal CLLJ for a observations, b AM2.1, c AM2.5, d CM2.1 and e FLOR. CLLJ is area-averaged U925 over the domain 80°W–70°W; 12°N–16°N. Units are in m/s per standard deviation of corresponding time series. Dotted regions indicate values significant at 5% level. Significant values are shown for every 4th grid point in a, 2nd grid point in b, 10th grid point in c, 2nd grid point in d and 8th grid point in e
Regression of JAS seasonal anomalies of SST on the JAS seasonal CLLJ for a observations, b AM2.1, c AM2.5, d CM2.1 and e FLOR. CLLJ is area-averaged U925 over the domain 80°W–70°W; 12°N–16°N. Units are in °C per standard deviation of corresponding time series. Dotted regions indicate values significant at 5% level. Significant values are shown for every 8th grid point in a, 3rd grid point in b, 12th grid point in c–e. We have plotted negative of regression values to depict the El Niño phase associated with easterlies (the case of a stronger CLLJ)
The CLLJ affects rainfall in the Caribbean region and beyond, over the United States and the tropical Pacific Ocean. The regression of rainfall over CLLJ is shown in Fig. 7 to examine the model’s ability to capture such teleconnections. The observed relation suggests reduced rainfall associated with a stronger CLLJ in the Caribbean region, Central America and northern South America, while enhanced rainfall over the southeastern US and the tropical Pacific (Fig. 7a). The reduced rainfall is related to lack of moisture in the jet entrance region and large-scale dynamics of the jet in the Caribbean and Central America, while enhanced rainfall in the jet exit region in the tropical Pacific due to moisture transported by the CLLJ. AM2.1 and CM2.1 fairly capture the observed relation but the magnitude of rainfall anomalies are lower in the Caribbean and Central America (Fig. 7b, d). FLOR and AM2.5 also have a realistic simulation of the observed relation, with improvements in teleconnections over the Caribbean and oceanic regions (Fig. 7c, e).
Regression of JAS seasonal anomalies of precipitation on the JAS seasonal CLLJ for a observations, b AM2.1, c AM2.5, d CM2.1 and e FLOR. Red color shading corresponds to wet and blue to dry. Units are in mm/day per standard deviation of corresponding time series. Dotted regions indicate values significant at 5% level. Significant values are shown for every 20th grid point in a, 3rd grid point in b, 10th grid point in c, 3rd grid point in d and 10th grid point in e
3.2 Forecast skill for the JAS season
From Sect. 3.1, we notice that the CLLJ has significant impact on the rainfall over the IAS. Both the coupled and uncoupled versions of 2.1 and 2.5 have realistic simulation of CLLJ and its teleconnections with SST and rainfall with FLOR showing slight improvements than its counterparts. Thus, we make use of hindcasts from coupled and uncoupled versions of 2.1 and 2.5 to explore the forecast skill of rainfall over the IAS during JAS, with hindcasts initialized in June. We also highlight the role of coupling and resolution in predicting the rainfall over the IAS.
First, we show timeseries of the CLLJ in CM2.1 and FLOR forecasts and compare with observations. As seen in Fig. 8, both CM2.1 and FLOR forecasts capture the time variations of the CLLJ with correlation of 0.84 for each model with observations. The coupled model forecasts tend to capture the peak CLLJ events especially when accompanied with ENSO events; for example, a weaker CLLJ event during 1982, 1987, 1997 and 2009 is accompanied by an El Niño event and a La Niña accompanies a stronger CLLJ event during 2010. We also compare the rainfall indices from CM2.1 and FLOR forecasts over North America, Central America, Caribbean and South America to observations (the domain over which area-averaged rainfall is calculated is shown in Fig. 9). Both the models tend to forecast rainfall better over Central America, Caribbean and northern South America than over North America (Fig. 10).
Map showing the indices used in Fig. 10. Red box corresponds to the domain over North America (120°W–80°W; 18°N–32°N), green box over Central America (92°W–78°W; 7°N–18°N), blue box over Caribbean (85°W–60°W; 12°N–25°N) and yellow box over northern South America (78°W–50°W; 5°N–13°N)
Further, we apply MOS to forecasts to correct for systematic errors and compare with raw forecasts to investigate its effect in improving the forecast skill. In this analysis, the predictand is always observed rainfall. In addition to coupled models, we have computed the forecast skill in two perfect-prognosis experiments, AM2.1 and AM2.5, as it helps us to estimate the upper limit of predictability. These simulations are called “perfect prognosis”, because the atmospheric model is forced with observed SST as in a typical AMIP experiment (Gates et al. 1999). These are frequently considered in the literature to provide a measure of the upper limit of predictability (see Barnston and Ropelewski 1992; Wilks 2006; Barnston et al. 2012; Muñoz et al. 2016 and references therein). As indicated in the methodology, we selected the Kendall’s tau correlation coefficient as an overall measure of model performance, using a 5-years-out cross-validated window (Table 1). Initially, we analyze the model output without any kind of statistical correction in uncoupled and coupled versions of 2.1 and 2.5 to understand the effect of biases on the model performance. The forecast skill calculated based on raw data with rainfall as predictor suggests that AM2.1 has considerably higher skill than AM2.5. However, there is no dramatic difference between the hindcasts produced by CM2.1 and FLOR (Table 1). This result is consistent with Fig. 5e, f in Jia et al. (2015) for the JAS season, although for a global domain.
Further we apply statistical correction using Canonical Correlation Analysis on the raw model output, and then calculate the forecast skill using both modeled rainfall and SST as predictors. We computed the cross-validated skill using the model’s precipitation (PRCP) and SST as independent predictors. Overall, the forecast skill is notably enhanced in all models when raw model output is corrected based on MOS approach (Table 1). AMIP models, AM2.1 and AM2.5, show higher skill with model rainfall as predictor based on MOS-corrected data compared to raw rainfall data as predictor. Coupled models also show a dramatic improvement with respect to the raw model output, but there is no outstanding difference in rainfall skill when comparing the results between the two MOS-corrected experiments.
We also examined the spatial distribution in skill (Fig. 11). Spatial correlation skill with rainfall as predictor appears to be better in AM2.1 compared to AM2.5 in most of the Intra-Americas region, and is comparable between CM2.1 and FLOR, consistent with Table 1. In general, the skill is improved only over South America in CM2.1 and FLOR, and over both South and North America in AM2.5. Nonetheless, AM2.1 exhibits lower skill over parts of Honduras and Nicaragua, northern Colombia and western Venezuela after MOS has been applied. Hence, forecasts with rainfall as predictor show overall better skill in the entire domain after MOS correction is applied compared to the raw model output, but certain regions experience a decrease in skill (Fig. 11). With SST as predictor, improvements in skill is mostly over northern South America in AM2.5 and FLOR, and over both North and South American countries in the domain of study for CM2.1.
Further, we investigate the role of coupling (Fig. 12) and horizontal resolution (Fig. 13) in the improvement of skill over IAS before and after MOS correction. Coupled models tend to show improvement in skill over South America after MOS correction relative to uncoupled models with both rainfall and SST as predictor (Fig. 12b, c, e, f). However, neither rainfall or SST as predictor shows any considerable enhancement in skill between coupled and uncoupled models over North America, except moderate improvement in CM2.1 compared to AM2.1 with SST as predictor.
As in Fig. 12, but for the difference between high and low resolution model output
Figure 13 highlights the role of resolution on forecast skill. High-resolution raw predictions for rainfall tend to show improved skill compared to low-resolution models over Mexico, Northern Venezuela and Western Cuba with rainfall as predictor (Fig. 13). However, experiments with higher horizontal resolution tend to provide lower skill in the uncorrected hindcasts, especially in Colombia and Venezuela (Fig. 13a, d). After MOS correction has been applied to the dynamically forecast rainfall, the role of resolution is less clear and it depends on the location of interest (Fig. 13b, e). Although uncoupled models show improvement in skill over Northern Mexico, Guatemala and Florida, resolution is of little or no relevance for the MOS experiments based on dynamically forecast SST fields, especially when considering FLOR and CM2.1 (Fig. 13c, f). This may be related to having the same ocean resolution in both CM2.1 and FLOR. Thus, improving the atmospheric resolution in coupled models with same lower resolution ocean models does not improve skill in SST-corrected MOS experiments. Further research is needed in order to explore this issue.
4 Conclusions and discussion
The IAS encompasses the Caribbean Sea and its island nations, the Gulf of Mexico in addition to surrounding land regions, such as southern United States, Mexico, Central America, and northern South America. The CLLJ is considered an integral part of IAS climate system, due its large influence on weather and climate in the region by acting as an important moisture corridor to the surrounding oceanic and continental regions. IPCC AR4 multimodel studies suggest that the state-of-the-art coarse resolution coupled models fail to simulate the magnitude of the CLLJ and its teleconnections, which warrant high-resolution coupled models. In this study we used high-resolution coupled and uncoupled models to analyze the simulation of the CLLJ and its teleconnections and further compare them with low-resolution coupled and uncoupled models. Considering that the CLLJ has pronounced impact on the rainfall variability over the IAS, we also analyzed the forecast skill of rainfall over this region in both coupled and uncoupled models with high and low-resolution.
Observed CLLJ shows two peaks in summer and winter, with maximum wind speed in July and associated vertical deepening. CM2.1 erroneously peaks in June; however, FLOR successfully captures the summer peak with vertical deepening of the jet. The jet is better represented in uncoupled simulations forced with observed SSTs (AM2.1 and AM2.5) compared to their coupled counterparts, emphasizing the role of SSTs and their gradients in the simulation of the CLLJ. We focus on the JAS season to explore the simulation of jet and the associated teleconnections in addition to the forecast skill of rainfall, as the CLLJ contributes to the variability of rainfall over US and to the tropical storms and hurricanes during JAS.
The high and low-resolution versions of coupled and uncoupled models have realistic simulation of the variability of the CLLJ for the JAS season. FLOR and AM2.5 show slightly improved simulation compared to their low-resolution counterparts; this is attributed to better simulation of SST and SLP gradients which influence the variability of the CLLJ. A stronger CLLJ leads to reduced rainfall in the jet entrance region over the Caribbean region, Central and northern South America, due to lack of moisture and enhanced rainfall over the southeastern US and the tropical Pacific due to abundance of moisture transported by the CLLJ in the jet exit region. FLOR and AM2.5 show slightly improved simulation of CLLJ-related rainfall compared to CM2.1 and AM2.1 especially over the Caribbean and ocean regions.
Further, we analyzed the forecast skill of rainfall in the IAS during JAS using hindcasts initialized in June. The forecast skill in the model is measured in terms of Kendall’s tau correlation coefficient. In this study, we highlighted the role of applying statistical correction to account for model biases, coupling and resolution in predicting the rainfall over the IAS. The raw model forecasts without any statistical correction suggests that there is no dramatic difference in skill between the CM2.1 and FLOR. But uncoupled models indicate considerable difference in skill, with AM2.1 showing higher skill than AM2.5. After applying MOS to correct for model biases, we determined the forecast skill in predicting rainfall using both rainfall and SST as predictors. After MOS correction, we notice a dramatic improvement in forecast skill in all models, AM2.1, AM2.5, CM2.1 and FLOR. There is no striking difference in forecast skill with rainfall as predictor versus SST as predictor.
However, the spatial distribution in skill suggests that the improvement in skill from raw forecasts to bias-corrected forecasts is region dependent. For example, with rainfall as predictor, AM2.5, CM2.1 and FLOR show better skill over North and South America after MOS correction, but AM2.1 has lower skill over parts of Honduras and Nicaragua, northern Colombia and western Venezuela. Improvements in forecast skill is also dependent on certain regions with SST as predictor with higher skill mostly over northern South America in AM2.5 and FLOR, and over both North and South American countries in the domain of study for CM2.1. Other studies have also shown useful skill in North American rainfall during JASO season (Misra and Li 2014; Misra et al. 2014; Misra and Chan 2009).
In addition to analyzing the sensitivity of forecast skill to bias correction, we also determine the effect of coupling and horizontal resolution in predicting the rainfall over the IAS. Forecast skill is sensitive to coupling only over South America in bias corrected forecasts with both rainfall and SST predictors. We do not see any improvements in skill over North America between uncoupled and coupled models except with moderate improvement in CM2.1 compared to AM2.1, when using forecast SST as predictor. Forecast skill is not sensitive to resolution, especially in the coupled models, CM2.1 and FLOR, using SST as predictor. This may be attributed to the same ocean resolution in both models, thus suggesting that coupled models with improved atmospheric resolution but with the same lower resolution in ocean may not contribute to better forecasts. However, uncoupled models do show higher skill with high-resolution atmosphere compared to those with low-resolution atmosphere.
The IAS region is heavily populated with high vulnerability to changes in rainfall variability (IASCLIP 2005). In most of Central America, the Caribbean and northwestern South America, JAS is a transition season between the two rainfall peaks. Having predictability for this season is key because soil moisture content and state of vegetation tend to enhance or decrease the intensity of impacts associated with droughts or floods during the second rainfall peak. This also has important repercussions for food security, water management, disaster planning and even epidemic preparedness in those highly vulnerable nations. Thus, it is important to improve our ability to predict rainfall over the region. In this study, we performed a comprehensive analysis of forecast skill with and without bias correction. We also compared the skill among coupled and uncoupled models, and sensitivity to improvements in atmospheric resolution. In present times, where most of the resources are invested in coupled models and improving resolution, this study provides insights on sensitivity of forecast skill to coupling and resolution, which may help plan future efforts in model development.
Notes
This spatial average is calculated using the Observatory’s seasonal forecast system, that involves the entire Latin America and the Caribbean. Hence, it is not directly comparable with the values corresponding to only the Intra-Americas region. Nonetheless, the range provided offers an idea of typical forecast skill for rainfall.
References
Alfaro E (2007) Uso del análisis de correlación canónica para la predicción de la precipitación pluvial en Centroamérica. Ing Compet 9:33–48
Alfaro EJ, Chourio X, Muñoz AG, Mason SJ (2017) Improved seasonal prediction skill of rainfall for the Primera season in Central America. Int J Climatol. https://doi.org/10.1002/JOC.5366
Amador JA (1998) A climatic feature of the tropical Americas: the trade wind easterly jet. Top Meteor Oceanogr 5(2):1–13
Amador J (2008) The Intra-Americas sea low level jet: overview and future research. Ann N Y Acad Sci 1146:153–188
Amador JA, Magana V (1999) Dynamics of the low level jet over the Caribbean Sea. In: Preprints, the 23rd conference on hurricanes and tropical meteorology, American Meteorological Society, Dallas, pp 868–869
Barnston AG, Ropelewski CF (1992) Prediction of ENSO episodes using canonical correlation analysis. J Clim 11:1316–1345
Barnston AG, Tippett MK, L’Heureux ML, Li S, DeWitt DG (2012) Skill of real-time seasonal ENSO model predictions during 2002–11: is our capability increasing? Bull Am Meteorol Soc 93(5):631–651
Chourio X (2016) The Latin American Observatory’s Datoteca. Climate Service Partnership Newsletter April: 6. p 6. http://www.climate-services.org/wp-content/uploads/2015/05/CSP-newsletter-April-2016-2.pdf. Accessed 2017
Delworth TL, Broccoli AJ, Rosati A, Stouffer RJ, Balaji V, Beesley JA, Cooke WF, Dixon KW, Dunne J, Dunne KA, Durachta JW (2006) GFDL’s CM2 global coupled climate models. Part I: formulation and simulation characteristics. J Clim 19(5):643–674
Delworth TL, Rosati A, Anderson W, Adcroft AJ, Balaji V, Benson R, Dixon K, Griffies SM, Lee HC, Pacanowski RC, Vecchi GA (2012) Simulated climate and climate change in the GFDL CM2. 5 high-resolution coupled climate model. J Clim 25(8):2755–2781
Diro GT, Rauscher SA, Giorgi F, Tompkins AM (2012) Sensitivity of seasonal climate and diurnal precipitation over Central America to land and sea surface schemes in RegCM4. Clim Res 52:31–48
Durán-Quesada AM, Gimeno L, Amador JA, Nieto R (2010) Moisture sources for Central America: identification of moisture sources using a Lagrangian analysis technique. J Geophys Res 115:D05103. https://doi.org/10.1029/2009JD012455
Fallas-López B, Alfaro E (2012a) Uso de herramientas estadísticas para la predicción estacional del campo de precipitación en América Central como apoyo a los Foros Climáticos Regionales. 1: Análisis de tablas de contingencia. Rev Climatol 12:61–79
Fallas-López B, Alfaro EJ (2012b) Uso de herramientas estadísticas para la predicción estacional del campo de precipitación en América Central como apoyo a los Foros Climáticos Regionales. 2: análisis de Correlación Canónica. Rev Climatol 12:93–105
García-Solera I, Ramírez P (2012) Central America’s Seasonal Climate Outlook Forum. The climate services partnership. http://www.climate-services.org/sites/default/les/CRRH_Case_Study.pdf. Accessed 2017
Gates WL, Boyle J, Covey C, Dease C, Doutriaux C, Drach R, Fiorino M, Gleckler P, Hnilo J, Marlais S, Phillips T, Potter G, Santer BD, Sperber KR, Taylor K, Williams D (1999) An overview of the results of the Atmospheric Model Intercom-parison Project (AMIP I). Bull Am Meteorol Soc 80:29–55
Glahn H, Lowry D (1972) The use of model output statistics (MOS) in objective weather forecasting. J Appl Meteorol 11:1203–1211
Grodsky SA, Carton JA, Nigam S, Okumura YM (2012) Tropical Atlantic biases in CCSM4. J Clim 25:3684–3701
Harris I, Jones PD (2015) CRU TS3.23: Climatic Research Unit (CRU) Time-Series (TS) Version 3.23 of High Resolution Gridded Data of Month-by-month Variation in Climate (Jan. 1901–Dec. 2014). Centre for Environmental Data Analysis. https://doi.org/10.5285/4c7fdfa6-f176-4c58-acee-683d5e9d2ed5
Hastenrath S (2002) The intertropical convergence zone of the eastern Pacific revisited. Int J Clim 22:347–356
Higgins RW, Shi W (2001) Intercomparison of the principal modes of interannual and intraseasonal variability of the North American monsoon system. J Clim 14:403–417
Hu Q, Feng S (2002) Interannual rainfall variations in the North American summer monsoon region: 1900–98. J Clim 15:1189–1202
IASCLIP (2005) A prospectus for an Intra-Americas Study of Climate Processes (IASCLIP). Report prepared by the VAMOS panel. http://www.clivar.org/sites/default/files/documents/vamos/IASCLIP.pdf. Accessed 2017
Inoue M, Handoh IC, Bigg GR (2002) Bimodal distribution of tropical cyclogenesis in the Caribbean: characteristics and environmental factors. J Clim 15:2897–2905
Jia L, Yang X, Vecchi GA, Gudgel RG, Delworth TL, Rosati A, Stern WF, Wittenberg AT, Krishnamurthy L, Zhang S, Msadek R, Kapnick S, Underwood S, Zeng F, Anderson WG, Balaji V, Dixon K (2015) Improved seasonal prediction of temperature and precipitation over land in a high-resolution GFDL climate model. J Clim 28:2044–2062
Krishnamurthy L, Vecchi G, Msadek R, Wittenberg A, Delworth T, Zeng F (2015) The seasonality of the great plains low-level jet and ENSO relationship. J Clim 28:4525–4544
Krishnamurthy L, Vecchi GA, Msadek R, Murakami H, Wittenberg A, Zeng F (2016) Impact of strong ENSO on regional tropical cyclone activity in a high-resolution climate model in the North Pacific and North Atlantic Oceans. J Clim 29(7):2375–2394
Krishnamurthy L, Vecchi GA, Yang X, Van der wiel K, Balaji V, Kapnick S, Jia L, Zeng F, Paffendorf K, Underwood S (2018) Causes and probability of occurrence of extreme precipitation events like Chennai 2015. J Clim 31:3831–3848
Magaña V, Amador JA, Medina S (1999) The midsummer drought over Mexico and Central America. J Clim 12:1577–1588
Maldonado T, Alfaro E, Fallas-López B, Alvarado L (2013) Seasonal prediction of extreme precipitation events and frequency of rainy days over Costa Rica, Central America, using canonical correlation analysis. Adv Geosci 33:41–52. https://doi.org/10.5194/adgeo-33-41-2013
Maldonado T, Rutgersson A, Alfaro E, Amador J, Claremar B (2016a) Interannual variability of the midsummer drought in Central America and the connection with sea surface temperatures. Adv Geosci 42:35–50. https://doi.org/10.5194/adgeo-42-35-2016
Maldonado T, Alfaro E, Rutgersson A, Amador JA (2016b) The early rainy season in Central America: the role of the tropical North Atlantic SSTs. Int J Climatol. https://doi.org/10.1002/joc.4958
Martin ER, Schumacher C (2011) The Caribbean low-level jet and its relationship with precipitation in IPCC AR4 models. J Clim 24:5935–5950
Mason SJ, Baddour O (2008) Statistical modelling. In: Troccoli A, Harrison M, Anderson DLT, Mason SJ (eds). Seasonal climate: forecasting and managing risk. Nato Science Series. IV: earth and environmental sciences, vol 82. Springer, Dordrecht
Mason SJ, Weigel AP (2009) A generic forecast verification framework for administrative purposes. Mon Weather Rev 137:331–349
Misra V, Chan S (2009) Seasonal predictability of the Atlantic Warm Pool in the NCEP CFS. Geophys Res Lett 36:L16708
Misra V, Li H (2014) The seasonal climate predictability of the Atlantic Warm Pool and its teleconnections. Geophys Res Lett 41(2):661–666
Misra V, Wang C, Lee SK, Enfield D, Douglas A (2014) IASCLiP implementation strategy. https://www.eol.ucar.edu/projects/iasclip/documentation/IASCLIP-CLIVAR2014-live.pdf. Accessed 2017
Misra V, Mishra A, Li H (2016) The sensitivity of the regional coupled ocean atmosphere simulations over the Intra-Americas Seas to the prescribed bathymetry. Dyn Atmos Ocean. https://doi.org/10.1016/j.dynatmoce.2016.08.007
Mo K, Chelliah M, Carrera M, Higgins R, Ebisuzaki W (2005) Atmospheric moisture transport over the United States and Mexico as evaluated in the NCEP regional reanalysis. J Hydrometeorol 6:710–728
Muñoz E, Busalacchi A, Nigam S, Ruiz-Barradas A (2008) Winter and summer structure of the Caribbean low-level jet. J Clim 21:1260–1276
Muñoz AG, López MP, Velásquez R, Monterrey L, León G, Ruiz F, Recalde C, Cadena J, Mejía R, Paredes M, Bazo J (2010) An environmental watch system for the Andean countries: El Observatorio Andino. Bull Am Meteorol Soc 91:1645–1652. https://doi.org/10.1175/2010BAMS2958.1
Muñoz AG, Ruiz D, Ramírez P, León G, Quintana J, Bonilla A, Torres W, Pastén M, Sánchez O (2012) Risk Management at the Latin American Observatory. In: Banaitiene N (ed) Risk management—current issues and challenges, InTech, pp 532–556
Muñoz ÁG, Goddard L, Mason SJ, Robertson AW (2016) Cross–time scale interactions and rainfall extreme events in southeastern South America for the austral summer. Part II: predictive skill. J Clim 29:5915–5934
Nogués-Paegle J, Mo K (2002) Linkages between Summer Rainfall Variability over South America and Sea Surface Temperature Anomalies. J Clim 15:1389–1407
Poveda G, Mesa OJ (2000) On the existence of Lloró (the rainiest locality on Earth): enhanced ocean-atmosphere-land interaction by a low-level jet”. Geophys Res Lett 27(11):1675–1678
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atm 108(D14):4407
Rienecker MM, Suarez MJ, Gelaro R, Todling R, Bacmeister J, Liu E, Bosilovich MG, Schubert SD, Takacs L, Kim GK, Bloom S, Chen J, Collins D, Conaty A, da Silva A (2011) MERRA: NASA’s modern-Era retrospective analysis for research and applications. J Clim 24:3624–3648. https://doi.org/10.1175/JCLI-D-11-00015.1
Ryu JH, Hayhoe K (2014) Understanding the sources of Caribbean precipitation biases in CMIP3 and CMIP5 simulations. Clim Dyn 42(11–12):3233–3252
Schultz DM, Bracken WE, Bosart LF et al (1997) The 1993 Superstorm cold surge. Frontal structure, gap flow, and tropical impact. Mon Weather Rev 125:5–39
Schultz DM, Bracken WE, Bosart LF (1998) Planetary- and synoptic-scale signatures associated with central american cold surges. Mon Weather Rev 126:5–27. https://doi.org/10.1175/1520-0493(1998)126<0005:PASSSA>2.0.CO;2
Taylor MA, Alfaro E (2005) Climate of Central America and the Caribbean. In: Oliver J (ed) The encyclopedia of world climatology. Springer, New York, pp 183–189. https://doi.org/10.1007/1-4020-3266-8
Vannitsem S, Nicolis C (2008) Dynamical properties of model output statistics forecasts. Mon Wea Rev 136:405–419. https://doi.org/10.1175/2007MWR2104.1
Vaughan C, Dessai S (2014) Climate services for society: origins, institutional arrangements, and design elements for an evaluation framework. Wiley Interdiscip Rev Clim Chang 5:587–603
Vecchi GA, Delworth T, Gudgel R, Kapnick S, Rosati A, Wittenberg AT, Zeng F, Anderson W, Balaji V, Dixon K, Jia L, Kim HS, Krishnamurthy L, Msadek R, Stern WF, Underwood SD, Villarini G, Yang X, Zhang S (2014) On the seasonal forecasting of regional tropical cyclone activity. J Clim 27:7994–8016
Wang C (2007a) Variability of the Caribbean low-level jet and its relations to climate. Clim Dyn 29:411–422
Wang C, Enfield DB (2001) The tropical Western Hemisphere warm pool. Geophys Res Lett 28:1635–1638
Wang C, Enfield DB (2003) A further study of the tropical Western Hemisphere warm pool. J Clim 16:1476–1493
Wang C, Lee SK (2007b) Atlantic warm pool, Caribbean low-level jet, and their potential impact on Atlantic hurricanes. Geophys Res Lett 34:L02703. https://doi.org/10.1029/2006GL028579
Weaver SJ, Schubert S, Wang H (2009) Warm season variations in the low-level circulation and precipitation over the central United States in observations, AMIP simulations, and idealized SST experiments. J Clim 22(5401):5420
Whyte F, Taylor M, Stephenson T, Campbell J (2008) Features of the Caribbean low level jet. Int J Climatol 28:119–128
Wilks DS (2006) Statistical methods in the atmospheric sciences. 2nd edn. Academic Press, London
Xie P, Arkin PA (1997) Global precipitation: a 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull Am Meteorol Soc 78:2539–2558
Yang X, Vecchi GA, Gudgel RG, Delworth TL, Zhang S, Rosati A, Jia L, Stern WF, Wittenberg AT, Kapnick S, Msadek R, Underwood SD, Zeng F, Anderson W, Balaji V (2015) Seasonal predictability of extratropical storm tracks in GFDL’s high-resolution climate prediction model. J Clim 28:3592–3611
Zhang L, Delworth TL (2015) Analysis of the characteristics and mechanisms of the Pacific Decadal Oscillation in a suite of coupled models from the Geophysical Fluid Dynamics Laboratory. J Clim 28:7678–7701
Acknowledgements
We would like to thank Xiaosong Yang and Liping Zhang for helpful comments on the manuscript. We also thank three anonymous reviewers for their valuable input. This work is supported by MAPP Intra Americas Seas proposal funded by NOAA Climate Program Office and National Science Foundation (award number 1262099).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Krishnamurthy, L., Muñoz, Á.G., Vecchi, G.A. et al. Assessment of summer rainfall forecast skill in the Intra-Americas in GFDL high and low-resolution models. Clim Dyn 52, 1965–1982 (2019). https://doi.org/10.1007/s00382-018-4234-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-018-4234-z