1 Introduction

Atmospheric climate model biases have been shown to be sensitive to large-scale sea surface temperature (SST) biases, for example in the North Atlantic–European region (e.g., Keeley et al. 2012; Scaife et al. 2011). The more recent generations of models have reduced many of these large-scale SST biases, for example in this same mid-North Atlantic region in the Met Office Global Coupled 2 model (Williams et al. 2015). However despite improvements on the large-scale, smaller regions of SST biases remain and when they are located in regions of deep atmosphere–ocean interactions, there is potential for a propagation of biases.

In general, the local response mechanism to dissipate anomalous diabatic heating in the mid-latitudes, for example from an SST anomaly or bias, may be via any of the following mechanisms: (1) meridional heat advection by a mean wind anomaly; (2) meridional heat advection by the transient eddies; and/or (3) ascent and the associated adiabatic cooling if over the western boundary currents (WBC) and their extensions. Mechanisms 1 and 2 are considered to act mostly in the horizontal plane, whereas 3 is in the vertical. The response mechanisms have been studied within the context of the WBCs, their extensions, and storm track regions.

A local meridional mean wind response in the extratropics is the response suggested by large-scale steady linear dynamics, from theoretical and simple modeling studies (Hoskins and Karoly 1981; Hendon and Hartmann 1982; Hall et al. 2001). There would be a surface cyclonic anomaly slightly downstream of the low-level diabatic heating, acting to balance the SST-induced warming with cold air advection. Aloft there would be subsidence and column shrinking (to conserve vorticity and balance the equatorward flow), yielding a baroclinic structure with a downstream upper-level anticyclonic anomaly. Sato et al. (2014) hypothesised, using a reanalysis dataset, that warm southerly advection is induced from warm Gulf Stream SST anomaly conditions (via a poleward shift of the SST front) and noted that a meridionally-propagating planetary wave response is triggered.

In the second option it is the eddies which remove the anomalous heat. Hoskins and Valdes (1990) showed that mean diabatic heating in the storm track regions favors maintenance of co-located large mean baroclinicity. Ocean-to-atmosphere heat and moisture fluxes in the WBC regions anchor the latitude of the storm tracks and therefore influence the mean state of the atmospheric circulation (Kwon et al. 2010). Ambaum and Novak (2014) constructed a nonlinear oscillator model to show that these regions oscillate between periods of intense storm track activity, during which baroclinicity decreases, and longer periods of lower activity, during which the baroclinicity increases. Numerical simulations have been used to explore the role of midlatitude SST gradients, and find that these can influence storm track activity (e.g., Brayshaw et al. 2008; Hand et al. 2014). Simulations have also been used to investigate the sensitivity to SST front gradient strengths, suggesting that a sharper front acts to generate stronger meridional eddy heat flux (and associated storm track activity) and shift the eddy-driven jet polewards (e.g., Nakamura et al. 2008; Sampe et al. 2010; Small et al. 2014; Piazza et al. 2016; O’Reilly et al. 2016).

The third response mechanism to dissipate anomalous diabatic heating is enhanced deep ascent/moist convection to convect the heat throughout the depth of the troposphere and potentially give an adiabatic cooling. Surface heat fluxes damp the low-frequency SST anomalies over the WBC regions and therefore anomalous heat fluxes, originating from the ocean, have the potential to drive the overlying atmospheric circulation (Kwon et al. 2010). In the annual mean, Minobe et al. (2008) show that the atmospheric response to the presence of the Gulf Stream SST front can extend through the depth of the troposphere. This is through the process of convergence in the atmospheric boundary layer, upward motion, cloud formation, and precipitation along the Gulf Stream. Czaja and Blunt (2011) estimate that conditions for this moist convection throughout the troposphere occur for up to 50% of the time in winter over the WBC regions and their extensions. In winter, the heating redistribution over the Gulf Stream has been shown to be primarily through sensible heating and confined to the lower troposphere (Minobe et al. 2010).

Parfitt and Czaja (2016), and later O’Neill et al. (2017) demonstrate from reanalysis and satellite observations, respectively, that the time mean upward motion over the Gulf Stream reflects the cumulative effect of synoptic systems, rather than the response of slower forms of motion to diabatic heating (e.g., the Hoskins and Karoly 1981 mechanism). This suggests that co-location of mean vertical motion and diabatic heating in the Gulf Stream region found by Minobe et al. (2008) arises as a residual of synoptic systems. Vannière et al. (2017) have proposed a ‘cold path’ mechanism by which the Gulf Stream front anchors atmospheric mean state features through cold-sector air–sea interactions. This mechanism potentially explains the limited vertical (lower tropospheric) response of vertical wind to the SST gradient, consistent with the strongly stratified midtroposphere and subsidence of the cold sector.

Parfitt and Czaja (2016) suggest that the majority of this synoptic vertical motion is due to the diabatic contribution that takes place near the atmospheric front within the synoptic systems. They also suggest that the key ocean-storm track physical process may be the interaction of atmospheric fronts within the synoptic systems, with the underlying SST distribution. Therefore it is important to address whether this interaction leads to strengthening or a weakening of upward motion within these fronts (Parfitt and Czaja 2016).

Downstream, the Gulf Stream extension region is also suggested to be capable of perturbing the free-tropospheric circulation via vertical motion anomalies as analysed from the SST variability on subseasonal timescales (Wills et al. 2016). Hoskins and Karoly (1981) used a baroclinic model to study the steady, linear response to thermal forcing, and found that when the vertical distribution of the source was sufficient, equivalent Rossby wavetrains are generated and propagate along the jets—similar to barotropic ray paths or waveguides (e.g., Hoskins and Ambrizzi 1993; Branstator 2002; Manola et al. 2013). Branstator and Teng (2017) showed how the upper tropospheric jets in the winter season can act as waveguides circumglobally. Since the large heat and moisture fluxes can enhance latent heating associated with cyclones, this acts to organise bands of precipitation over the Gulf Stream, and as a heat source forcing for atmospheric planetary waves, number 5 and 6 (Minobe et al. 2008).

Using numerical simulations of the extended winter atmospheric response to midlatitude SST anomalies, Smirnov et al. (2015) suggest that response mechanisms may vary depending on the spatial resolution of the atmospheric model. The steady linear dynamical response prevails in lower resolution climate simulations, and the deep ascent in the high resolution configuration of the model. Given the potential for forcing planetary waves, this separation by resolution has the potential to alter the planetary-scale circulation. Parfitt et al. (2016) also highlight the importance of ocean resolution in ocean–atmospheric front interactions, finding significant changes in the frequency of the fronts, particularly cold fronts. The authors argue that the role and influence of the Gulf Stream on the tropospheric time-mean state may become more important and accurate as the ocean resolution increases, particularly around \(\frac{1}{4}^{\circ }\).

The aim of this paper is to investigate the impact of a spatially small region of Gulf Stream SST biases from a high resolution fully coupled global climate model on the global circulation in the atmospheric model component in the context of large-scale biases. The model used is the HadGEM3-GC2 version of the UK Met Office Unified Model™ (UM). The \(\frac{1}{4}^{\circ }\) coupled ocean used in this model does not have large mid-Atlantic biases seen in previous generations of the UM climate models (Keeley et al. 2012; Scaife et al. 2011), however there is a spatially small, but large in magnitude bias where the Gulf Stream separates from the US eastern sea board at Cape Hatteras in the winter season. Masato et al. (2016) hypothesised that this bias might lead to eddy heat flux and consequent jet biases in the atmosphere of the model.

Since the \(\frac{1}{12}^{\circ }\) configuration of the ocean model does not have large Gulf Stream region SST biases (Hewitt et al. 2016), this suggests that this bias originates in the ocean component at the lower resolution. SSTs and surface winds are positively correlated in frontal regions with high mesoscale activity, such as those associated with WBCs, implying that the ocean is driving the atmosphere in the WBC region (Bryan et al. 2010). These considerations justify the approach taken here of imposing parts of the coupled model SST bias in atmosphere-only experiments.

Three sensitivity experiments are performed to impose the coupled model SST bias, differing by domain size to cover a small and medium section of the Gulf Stream, and, for context, the wider North Atlantic. Imposing this warm SST bias onto the fixed SST field in the atmosphere-only model over the Gulf Stream acts to shift and change the strength of the SST gradients in the Gulf Stream, and the strength of these gradients has been shown to be important to ocean-atmosphere interactions, as discussed above (e.g. Parfitt et al. 2016). The experimental results are compared with atmosphere-only and coupled configurations to investigate the degree to which the coupled model mean bias state is reproduced. The coupled and atmosphere-only configurations of the model are also compared with the ERA-Interim reanalysis where relevant. As well as the impacts and atmospheric response to the SST bias, the mechanisms introduced above will also be examined in the sensitivity experiments and model configurations.

A further description of the model, reanalysis, and statistical methods used are given in the next section, followed by an overview of the experiments performed in Sect. 3. Section 4 highlights the main results from the sensitivity experiments and concluding remarks are presented in Sect. 5.

2 Model, reanalysis, and statistics

The ECMWF Interim reanalysis (ERA-Interim; Dee et al. 2011) is used along with Global Coupled model version 2.0 (GC2; Williams et al. 2015) of the UK Met Office Unified Model (MetUM; Cullen 1993). GC2 is used for the seasonal forecast system (GloSea5), decadal prediction system (DePreSys3), and climate projection system (HadGEM3). GC2 comprises the following components: Global Atmosphere version 6.0 (GA6; Walters et al. 2017), Global Land version 6.0 (GL6; Walters et al. 2017), Global Ocean version 5.0 (GO5; Megann et al. 2014), and Global Sea Ice version 6.0 (GSI6; Rae et al. 2015). GA6 features a semi-implicit semi-Lagrangian dynamical core, and all results presented here use an N216 horizontal resolution (\(\sim 60\,\hbox {km}\) in the mid-latitudes) with 85 vertical levels (with a top at \(85\,\hbox {km}\)). GL6 has four soil levels, GSI6 has five sea-ice thickness categories, and GO5 has 75 levels (with a \(1\,\hbox {m}\) top level) and here uses a resolution of \(\frac{1}{4}^{\circ }\) on a tri-polar grid.

ERA-Interim has a horizontal resolution of T255 (approximately \(79\,\hbox {km}\)), and 60 vertical levels. Within the period used here, the sea-surface temperature (SST) field used in the ERA-Interim dataset is prescribed from the following datasets (exact dates are detailed in Dee et al. 2011): NCEP 2D-Var, NCEP OISSTv2, and NCEP RTG. While ERA-Interim is used here as an observational comparison, this of course has its own biases. For example, it is known that the reanalysis used lower resolution SST data prior to 2002, with impacts on ocean-atmosphere interactions (Masunaga et al. 2015; Parfitt et al. 2017). In contrast, the comparisons between the coupled and atmosphere-only configurations examine the impact of the coupled model SST bias within the same model, with a constant SST resolution throughout.

The fields have been interpolated to the resolution of the ERA-Interim grid before further analysis. The period used is the December-January-February (DJF) winter season from 1981 to 2008 for ERA-Interim and GA6. 27 years of the GC2 simulation are also used, however they do not correspond to particular years in the real world as the simulation uses perpetual present-day forcing. Where daily data are used, these are taken as daily means.

The significance of differences has been assessed by using a Monte-Carlo method to obtain the distributions. Half of the days in the combined time-series from both datasets were randomly selected to difference against the other half. This process was calculated for 10 000 trials and the difference between the two datasets compared against this distribution. Two tailed significance levels are displayed at \(95 \%\) (black stippling), and \(99 \%\) (white stippling).

3 Experimental design

Figure 1a shows the time mean SSTs in the North Atlantic in ERA-Interim; of note is the tight SST gradient as the Gulf Stream separates from the US eastern seaboard at Cape Hatteras, with its extension reaching the mid North Atlantic, beyond Grand Banks. The region of largest SST gradient is also the region of largest variability (Fig. 1a). The GC2-Coupled (here named GC2-C) configuration has a winter warm SST bias in the time mean (Fig. 1b). This bias is located northeast of Cape Hatteras and is up to \(6.75\,\hbox {K}\) warmer relative to ERA-Interim, and \(6\,\hbox {K}\) relative to OISSTv2 (not shown; Banzon et al. 2014). The warm bias is centered along the tight SST gradient as the Gulf Stream separates from North America.

Fig. 1
figure 1

Time mean sea surface temperatures (shading, units: K) in a ERA-Interim, b GC2-C minus ERA-Interim, c GC2-C minus GC2-A, and sensitivity experiments d GC2-S minus GC2-A from the small red box region, e GC2-M minus GC2-A from the medium orange box region, and f GC2-L minus GC2-A from the large purple box region. Monthly frequency standard deviation of ERA-Interim is shown in a (white line contours, units: K). Zero differences in d–f are shown in white

Full size image

The warm bias is seen in the \(\frac{1}{4}^{\circ }\) ocean model but not in the higher resolution \(\frac{1}{12}^{\circ }\) configuration (Hewitt et al. 2016). The \(\frac{1}{4}^{\circ }\) ocean model has a reduced returning cold water current, the Northern Recirculation Gyre, by the northeastern US seaboard, coming from the Labrador Sea in the real world. Met Office experiments reducing the ocean bathymetry resolution, comparing a \(\frac{1}{12}^{\circ }\) ocean model with \(\frac{1}{4}^{\circ }\) bathymetry and a \(\frac{1}{12}^{\circ }\) ocean model also reproduce a similar SST difference as the GC2-C bias (Pierre Mathiot, personal communication).

The warm bias extends to \(43^{\circ }\hbox {W}\), with a cool bias beyond (further east). Most of the subtropical North Atlantic has a smaller negative bias of around \(-1\,\hbox {K}\) to \(-2\,\hbox {K}\), while there is a small positive bias (\(<1\,\hbox {K}\)) in the Sargasso Sea (south of the strong warm Gulf Stream bias and east of the Carolinas). There is also a small positive SST bias in the Labrador Sea, with biases over \(3\,\hbox {K}\) towards the southwest coast of Greenland.

Time mean winter SST GC2-C biases in other WBCs are much smaller relative to the Gulf Stream bias (not shown). In the Kuroshio in the North Pacific, biases are generally around \(-1\,\hbox {K}\) to \(-1.5\,\hbox {K}\). Just northeast of the separation from the Kuroshio western boundary at the Boso Peninsula in the Oyashio sector, however, there are biases of up to \(-5\,\hbox {K}\) over a very small area covering around \(100\,\hbox {km}^2\) to \(200\,\hbox {km}^2\).

The time mean difference in Gulf Stream SSTs between GC2-C and GC2 atmosphere-only (GA6) configuration (here named GC2-A; Fig. 1c) are similar to the biases relative to ERA-Interim since the GA6 SSTs are also derived from observation-based analyses.

To create the new SST fields for the sensitivity experiments, the GC2-C SST bias (as a monthly mean difference) is imposed on the GC2-A daily SST boundary condition field for three different sized boxes to examine the atmospheric response in the GC2-A model. This aims to test the importance of the Gulf Stream biases relative to the larger scale biases. The horizontal spatial boundaries of the boxes are linearly tapered by two gridpoints (\(1^{\circ }\) in latitude; \(1\frac{2}{3}^{\circ }\) in longitude) each side. The boundaries of the three boxes (displayed over the time mean differences in Fig. 1d–f) are as follows:

  • \(50^{\circ }\hbox {N}\), \(60^{\circ }\hbox {W}\), \(35^{\circ }\hbox {N}\), \(75.5^{\circ }\hbox {W}\)—a ‘small’ box to capture the main region of the largest positive Gulf Stream SST bias (Fig. 1d; box in red). The GC2-A run which includes this box is here named GC2-S.

  • \(50^{\circ }\hbox {N}\), \(43^{\circ }\hbox {W}\), \(35^{\circ }\hbox {N}\), \(75.5^{\circ }\hbox {W}\)—a ‘medium’ box expanding GC2-S to include the eastward extension of the smaller positive SST Gulf Stream bias (Fig. 1e; box in orange). The GC2-A run which includes this box is here named GC2-M.

  • \(70^{\circ }\hbox {N}\), \(4^{\circ }\hbox {E}\), \(10^{\circ }\hbox {N}\), \(84^{\circ }\hbox {W}\)—a ‘large’ box to give a context to the Gulf Stream SST bias experiments. This box was intended to capture most of the North Atlantic SST biases including the large region of \(-1\,\hbox {K}\) to \(-\,2\,\hbox {K}\) in the subtropical North Atlantic and the region of larger SST biases around southern Greenland and Iceland (Fig. 1f; box in purple). The GC2-A run which includes this box is here named GC2-L.

Each experiment consists of one ensemble member for the 1981–2008 period. The SST biases from GC2-C are imposed continuously, throughout all months in the timeseries, however again only the DJF winter season is considered here for analysis, throughout.

4 Results

4.1 Flux response

To examine the surface response to the replaced SSTs, Fig. 2 examines the combined surface upward sensible and latent heat flux. GC2-C biases (Fig. 2b) correspond with the SST biases, being positive (up to \(+\,240\,\hbox {W}\,\hbox {m}^{-2}\), \(200\%\) of ERA-Interim climatology) over the warm Gulf Stream SSTs and negative to the east (downstream) and immediately to the west (upstream). Both the Sargasso Sea and Labrador Sea regions also have corresponding positive flux biases (up to \(+\,80\,\hbox {W}\,\hbox {m}^{-2}\), \(140\%\) of ERA-Interim climatology) associated with the weakly positive SST biases. Flux differences between GC2-C and GC2-A (Fig. 2c) are similar to the GC2-C biases over the Gulf Stream region.

Fig. 2
figure 2

Time mean surface upward sensible and latent heat flux (shading, units: \(\hbox {W}\,\hbox {m}^{-2}\)) in a ERA-Interim, b GC2-C minus ERA-Interim, c GC2-C minus GC2-A, and sensitivity experiments d GC2-S minus GC2-A, e GC2-M minus GC2-A, and f GC2-L minus GC2-A. Values between \(\pm \,40\,\hbox {W}\,\hbox {m}^{-2}\) in b–f are masked in white

Full size image

The GC2-S flux response differences (Fig. 2d) are similar to the GC2-C minus GC2-A. The GC2-M flux response differences (Fig. 2e) are also similar to the GC2-C minus GC2-A, except in the downward flux region on the southern side of the box, where the fluxes are slightly larger, while the GC2-L flux responses (Fig. 2f) have some small differences south of Bermuda and Iceland.

4.2 Global impacts

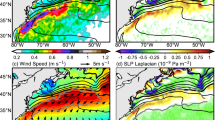
The mid-tropospheric response is now examined with the geopotential height field at \(500\,\hbox {hPa}\) (Fig. 3). GC2-C biases (Fig. 3b) show lower heights throughout the mid-latitudes, in particular a deeper and eastward-extended Pacific trough, while in the northern North Atlantic the trough-ridge climatology is weaker, indicating that the tilt in the Atlantic storm track is too weak. GC2-C has some similar differences compared with GC2-A (Fig. 3c), in particular in the Pacific bias and the reduced Scandinavian ridge. The three sensitivity experiments (Fig. 3d–f) all show increased heights over the North Pole and significant anomalies of both signs around the mid-latitudes. Particularly over the pole, the North Pacific and Scandinavia the responses can potentially explain some of the coupled model bias shown in Fig. 3b. In these regions, for example, GC2-S explained up to \(77\%\), \(19\%\) and \(25\%\), respectively, of the GC2-C differences relative to GC2-A. GC2-M differences (Fig. 3e) also show increased heights over the region of imposed warmer SSTs.

Fig. 3
figure 3

Time mean geopotential height at \(500\,\hbox {hPa}\) (shading, units: m) in a ERA-Interim, b GC2-C minus ERA-Interim, c GC2-C minus GC2-A, and sensitivity experiments d GC2-S minus GC2-A, e GC2-M minus GC2-A, and f GC2-L minus GC2-A. Monte-Carlo resampling is used to calculate significance at \(95\%\) (black stippling), and \(99\%\) (white stippling) levels

Full size image

The upper-tropospheric response is examined next. The mean meridional wind field at \(250\,\hbox {hPa}\) has biases in GC2-C (Fig. 4b), generally reproducing the planetary wave-trains seen in ERA-Interim (Fig. 4a), but with some shifts in their phase. The largest differences are mostly located nearer to the zero points in the original fields, which may imply a difference or shift in wavelength—we shall return to this later. Comparing GC2-C with GC2-A (Fig. 4c), some of the differences are located in approximately the same locations (e.g., around the Pacific rim) whereas in other regions this is not the case (e.g., over northeast: North America, Europe, and Asia).

All three sensitivity experiments (Fig. 4d–f) indicate a significant circumglobal planetary Rossby wave response to the imposed SST forcing, however magnitudes are smaller than the GC2-C minus GC2-A differences. Several of the main centres of action are broadly similar between the three experiments, though there are some differences. The GC2-S response (Fig. 4d) appears to have its centres of action most similar to the GC2-C minus GC2-A differences including the arc around the Pacific, while GC2-M has the most zonally oriented and straightest response. It is important to remember that this is the response in the time mean, and so the composite may be formed of many individual arcing waves rather than waves that span the whole globe. Many of these responses are not inconsistent with the often circumglobal waveguides of Hoskins and Ambrizzi (1993), Branstator (2002) and Branstator and Teng (2017). Differences between the three experiments are also significant across their centers of action (not shown).

The vertical profiles of meridional wind in the mid-latitudes indicate an equivalent barotropic response in all experiments (zonal-height profiles not shown, however Fig. S1 shows the meridional wind at \(850\,\hbox {hPa}\) for comparison with Fig. 4 at \(250\,\hbox {hPa}\)), with the exception of GC2-L over the region of forcing where the response has a westward tilt with height of \(\frac{1}{4}\) of a wavelength immediately downstream of the forcing. A key conclusion from these analyses is that the model is not responding with the linear mean circulation response to balance the heating. In some forced experiments in the literature, the response to forcing projects onto leading empirical orthogonal functions (EOFs) of internal (or ‘natural’) variability (the indirect response; Deser et al. 2004). In the present study this was tested by computing EOFs of meridional winds. The wave patterns are found to be quite distinct from the dominant patterns of internal variability and the wavenumbers differ (not shown). The global response in these simulations does not, therefore, arise from a projection of the forcing onto a preferred mode of the model’s internal variability.

To analyze the zonal wave biases in the meridional wind field at \(250\,\hbox {hPa}\) (Fig. 4), zonal wavenumber power spectra have been computed for each dataset using daily (Fig. 5a) and climatological time mean (1981–2008) frequency fields (Fig. 5b). The power spectra are computed for each latitude between \(20^{\circ }\hbox {N}\) and \(60^{\circ }\hbox {N}\) using the one-dimensional discrete Fourier transform, squared. The mean of these power spectra from each latitude is then obtained for each zonal wavenumber. On daily timescales ERA-Interim has larger power than the GC2 models, implying that the models are biased towards lower variance. The largest daily power differences between GC2-C and GC2-A are similar at all wavelengths except zonal wavenumber 1. On climatological timescales GC2-C is biased towards low power in zonal wavenumbers 2 and 3, and towards high power in zonal wavenumbers 4 and 5. In the three sensitivity experiments, it is only at wavenumbers 2 and 5 where differences between GC2-C and GC2-A are significant. At wavenumber 5, GC2-M has similar power to GC2-C, thereby being significantly different from GC2-A and giving rise to the large differences seen in Fig. 4e. While GC2-S and GC2-L also have wavenumber 5 differences, they are not statistically different from any other experiment or configuration, and the wavetrains are less zonal (Fig. 4d, f) so some of this power difference is not seen at any individual latitude band. There is also a difference in wavenumber 3 in GC2-L, with the power spectrum becoming even less similar to GC2-C, but not statistically significant. Together, the regional SST experiments reproduce in the range of 45 to \(95\%\) of the wavenumber 5 climatological difference between GC2-C and GC2-A.

Fig. 4
figure 4

Time mean meridional wind at \(250\,\hbox {hPa}\) (shading, units: \(\hbox {m}\,{\hbox {s}}^{-1}\)) in a ERA-Interim, b GC2-C minus ERA-Interim, c GC2-C minus GC2-A, and sensitivity experiments d GC2-S minus GC2-A, e GC2-M minus GC2-A, and f GC2-L minus GC2-A. Monte-Carlo resampling is used to calculate significance at \(95\%\) (black stippling), and \(99\%\) (white stippling) levels

Full size image

Motivated by the equivalent barotropic hemispheric response in the meridional wind, the wavetrain response has been tested in a barotropic wave model (see Supplement for method). The barotropic model was initialised on the GC2-A background state at 300–\(400\,\hbox {hPa}\), with a forcing imposed at some locations over the imposed Gulf Stream bias region. The barotropic wave model results do not replicate the responses of the sensitivity experiments further downstream over eastern Asia and the Pacific (not shown), with the wavetrain being less zonal, and favouring zonal wavenumbers 3 and 4, over zonal wavenumber 5. This suggests that the wave response may not be well represented by the steady response to a constant imposed forcing.

The mean zonal wind field at \(250\,\hbox {hPa}\) in GC2-C has a zonal and equatorward bias relative to ERA-Interim (Fig. 6b) and to GC2-A (Fig. 6c). This bias is particularly strong over the central and eastern North Pacific, incorrectly representing the southwest-northeast tilt of the jet. This has a consequence downstream over eastern North America and the start of the North Atlantic jet. The GC2-S and GC2-L experiments (Fig. 6d, f) partially but significantly recreate these biases over the central Pacific, and the eastern USA region where the jet is slightly southward shifted. This response over the Pacific is part of the hemispheric wave pattern. It explains only about \(15\%\) of the zonal wind bias over the Pacific, but it is a fairly robust signal across the three experiments. Masato et al. (2016) showed when the Pacific jet is shifted north in GC2-C (i.e. when it exhibits a reduced equatorward bias), the Atlantic eddy-driven jet distribution is weighted south, with an increased occurrence of the south regime and reduced occurrences at higher latitudes. GC2-L also has a southward shifted jet over the southeastern US, with significantly positive values over the Gulf of Mexico bias, partially reproducing the bias of GC2-C. The GC2-M differences (Fig. 6e) show fewer similarities to any other comparisons, likely associated with the more zonal Rossby wave path discussed with Fig. 4.

Fig. 5
figure 5

Power spectrum of \(250\,\hbox {hPa}\) meridional winds, \(20^{\circ }\hbox {N}\)–\(60^{\circ }\hbox {N}\), computed on a daily, and b climatological (time mean). The two-sigma (\(\sim \,95\%\)) envelope from 1000 bootstraps of the seasons (shading) is shown for ERA-Interim, GC2-C and GC2-A only

Full size image
Fig. 6
figure 6

Time mean zonal wind at 250 hPa (shading, units: \(\hbox {m}\,{\hbox {s}}^{-1}\)) in a ERA-Interim, b GC2-C minus ERA-Interim, c GC2-C minus GC2-A, and sensitivity experiments d GC2-S minus GC2-A, e GC2-M minus GC2-A, and f GC2-L minus GC2-A. Monte-Carlo resampling is used to calculate significance at \(95\%\) (black stippling), and \(99\%\) (white stippling) levels

Full size image

4.3 Meridional heat advection

To examine the local response mechanism to dissipate anomalous diabatic heating from the Gulf Stream SST bias, first the meridional heat advection by a mean wind anomaly was investigated by looking at the mean meridional wind field at \(850\,\hbox {hPa}\). No large response was detected in this field (Fig. S1), suggesting the linear response of Hoskins and Karoly (1981) is not dominant.

To examine the storm track activity, the meridional eddy heat flux at \(850\,\hbox {hPa}\) (\(\overline{\text {v}'\text {T}'}\); Fig. 7) has been derived from high-pass time-filtered eddies (with a period shorter than 10 days) using the Lanczos method (Duchon 1979). There is too little storm track activity in the model simulations relative to ERA-Interim in the Pacific and upstream Atlantic storm tracks, which is in agreement with the lower power in synoptic wavelengths at high-frequency timescales (Fig. 5a). Over the North Atlantic ocean the storm track has a slight poleward bias. The bias is up to \(30\%\) less storm track activity in the region of the Gulf Stream SST biases in the GC2-C simulation (Fig. 7b). GC2-C has larger negative biases than GC2-A in the central and east North Pacific, whereas the Atlantic storm track has higher eddy heat flux towards the poleward/northern flank. The GC2-S and GC2-L experiments (Fig. 7d, f) show no clear differences from GC2-A, while GC2-M (Fig. 7e) shows a small, significant, and localised storm track response of around \(+\,15\%\) over the region of SST heating. Intercomparisons between the three experiments (Fig. S2d–f) also show GC2-S and GC2-L as significantly different from GC2-M.

Fig. 7
figure 7

Time mean high-pass Lanczos filtered meridional heat flux (\(\overline{\text {v}'\text {T}'}\)) at \(850\,\hbox {hPa}\) (shading, units: \(\hbox {K}\,\hbox {m}\,\hbox {s}^{-1}\)) in a ERA-Interim, b GC2-C minus ERA-Interim, c GC2-C minus GC2-A, and sensitivity experiments d GC2-S minus GC2-A, e GC2-M minus GC2-A, and f GC2-L minus GC2-A. Monte-Carlo resampling is used to calculate significance at \(95\%\) (black stippling), and \(99\%\) (white stippling) levels. Values between \(\pm 1\,\hbox {K}\,\hbox {m}\,\hbox {s}^{-1}\) in b–f are masked in white

Full size image

The low-pass meridional heat flux (not shown) exhibits a positive mean bias in GC2-C over Eastern Canada, north of the warm SST bias. This bias is also in GC2-A, despite no SST bias being present. A large GC2-C-ERA-Interim positive bias in the Bering Sea region may partly compensate the negative transient heat flux bias (Fig. 7b), which is shifted further north in GC2-C compared with GC2-A. Low-pass differences are also generally small in the three sensitivity experiments. Hence, the additional heating in the perturbation experiments is not balanced by either high- or low-pass eddy meridional heat fluxes.

4.4 Vertical motion

The analysis above has shown that the heating perturbations are not fully balanced in the horizontal by either the linear response or by the meridional eddy heat transports. In this section we study the changes in vertical motion over the Gulf Stream, which act as another mechanism to dissipate the anomalous heating and additionally trigger the hemispheric wave train. This mechanism is particularly important to consider once the resolution is sufficient to be able to resolve the atmospheric and oceanic fronts and their interactions (e.g. Smirnov et al. 2015; Parfitt et al. 2016).

Figure 8 is a narrow zonal mean height cross section of vertical ascent and zonal wind across the Gulf Stream from \(69.75^{\circ }\hbox {W}\) to \(68.25^{\circ }\hbox {W}\) and from \(25^{\circ }\hbox {N}\) to \(45^{\circ }\hbox {N}\). The main region of mean ascent over the Gulf Stream is shown from around \(35^{\circ }\hbox {N}\) to \(37^{\circ }\hbox {N}\) in ERA-Interim (Fig. 8a), bounded by regions of descent to the north and south. This ascent over the Gulf Stream is directly below the core of the upper level jet (line contours) at around 200 hPa in the time-mean (Fig. 8a). GC2-C (Fig. 8b) has a stronger and wider region of ascent throughout the troposphere in this region with the differences clearly significant (Fig. 8d). GC2-A (Fig. 8c) has deep ascent similar to that of ERA-Interim, with almost no regions of both large and significant differences (Fig. 8e), and similar jet profiles. Given this similarity, the GC2-C comparison with GC2-A is similar to that with ERA-Interim, highlighting the significantly stronger and wider region of deep ascent (Fig. 8f). The region of positive mean ascent also has a positive meridional wind difference in GC2-C relative to GC2-A (e.g. meridional winds at \(850\,\hbox {hPa}\) are shown in Fig. S1), consistent with slantwise ascent. To test this, the angle of the climatological isentropic slopes, as computed from \(\arctan (^{\frac{d\theta }{dp}}/_{\frac{d\theta }{dy}})\), is compared with the angle of anomalous climatological ascent in GC2-C relative to GC2-A, as computed from \(\arctan (^{-\omega }/_v)\). The mean anomalous slantwise ascent in GC2-C is up to \(20^{\circ }\) steeper than the climatological GC2-A dry isentropes in the lower troposphere over the SST bias (showing the ascent is likely between the local moist and dry rate), with the potential for increased latent heat release. This reduces to zero by the mid troposphere (\(\sim 500\,\hbox {hPa}\)), indicating along-isentropic flow. Over the southern region (\(30^{\circ }\hbox {N}\)–\(35^{\circ }\hbox {N}\)) of mean ascent, the anomalous mean slantwise ascent is around \(1^{\circ }\)–\(2^{\circ }\) steeper in GC2-C in the lower troposphere, potentially indicating increased moist convective ascent over this SST bias in the time mean.

Fig. 8
figure 8

Time mean omega (\(\bar{\omega }\), shading, units: \(\hbox {Pa}\,\hbox {s}^{-1}\)) and zonal wind (contours, units: \(\hbox {m}\,\hbox {s}^{-1}\)) averaged from \(69.75^{\circ }\hbox {W}\) to \(68.25^{\circ }\hbox {W}\). Shading in panels d-i are differences in omega, as labelled. Monte-Carlo resampling is used to calculate significance at \(95\%\) (black stippling), and \(99\%\) (white stippling) levels. Zonal wind contours in black correspond to the data labelled in black, and contours in grey correspond to the data labelled in grey

Full size image

Over the Gulf Stream SST anomaly, all three sensitivity experiments (Fig. 8g–i) recreate the northern extension of the region of deep ascent throughout most of the troposphere, despite the lack of any clear southward tropospheric zonal jet shift (c.f. Fig. 8f). Statistical significance of this feature is confined to the lower half of the troposphere in GC2-S, while in GC2-M and GC2-L the significant increases extend throughout the depth of the troposphere. The responses appear consistent between the three different experiments, however an intercomparison suggests that each experiment has a slightly stronger response with increasing anomalous SST box size, such that the difference between GC2-S and GC2-L is significant (Fig. S3). The differential mean slantwise ascent is between \(4^{\circ }\) and \(10^{\circ }\) steeper in the lower- to mid-troposphere in the three sensitivity experiments (Fig. S3g–i) over the imposed SST bias, again indicating the potential for increased latent heat release.

This response of enhanced deep ascent over the region of SST bias is similar to the ‘high’ atmospheric resolution (\(\frac{1}{4}^{\circ }\)) response seen in the CAM model to SST front shifts from ocean variability by Smirnov et al. (2015), something not seen in their ‘low’ atmospheric resolution (\(1^{\circ }\)) configuration, which saw a linear dynamical response, despite using the same parameterization schemes. This difference is likely associated with the less well resolved fronts in the low resolution configuration, which are highly important for setting the time-mean state as discussed in the introduction. This may suggest that such close coupling of ocean–atmosphere biases (in both location and intensity) found here may be more prevalent in higher resolution coupled global climate models, given that fronts are better resolved. Willison et al. (2013) also find differences between a high and low resolution model comparison, with an enhanced positive feedback between cyclone intensification and latent heat release seen at their higher resolution configuration.

Neither GC2-S nor GC2-M recreate the GC2-C enhanced convection south of the Gulf Stream over the Sargasso Sea (since this is south of the region of the imposed SST biases in these two experiments), however GC2-L does also reproduce the southern regions of enhanced convection seen in GC2-C, with significance. The Sargasso Sea region of enhanced anomalous ascent has a similar slope to the climatological isentropes (Fig. S3i), a bias which is also extending upstream to the entire Gulf of Mexico in GC2-C (not shown). This may link with the partially reproduced southward shift in the upper jet over the southeastern US/Gulf of Mexico region in GC2-L (and GC2-C; Fig. 6b, c, f). The profile of this jet shift at the \(69.75^{\circ }\hbox {W}\)–\(68.25^{\circ }\hbox {W}\) section in the GC2-L experiment is around \(1^{\circ }\) south, not as far south as the GC2-C bias. GC2-M has its jet shifted north by around \(1^{\circ }\), while there is no change in the GC2-S jet here.

Daily frequency distributions of omega ascent at \(850\,\hbox {hPa}\) are shown in Fig. 9 for ERA-Interim and all model configurations/experiments along the longitude section in Fig. 8, from \(69.75^{\circ }\hbox {W}\) to \(68.25^{\circ }\hbox {W}\), at three different latitudes: \(32.25^{\circ }\hbox {N}\) to \(33^{\circ }\hbox {N}\) to cover the Sargasso Sea bias (Fig. 9a); \(36^{\circ }\hbox {N}\) over the region of maximum mean omega in ERA-Interim (Fig. 9b); and \(38.25^{\circ }\hbox {N}\) to \(39^{\circ }\hbox {N}\) over the region of largest Gulf Stream SST bias in GC2-C (Fig. 9c).

Figure 9a shows ERA-Interim with an \(850\,\hbox {hPa}\) omega distribution very similar to GC2-A over the Sargasso Sea. GC2-C has a distribution shifted with more values of stronger ascent than GC2-A from around 0.05 to 0.4 (\(\times -1\)) \(\hbox {Pa}\,\hbox {s}^{-1}\) (and with a mean positive value: vertical line), corresponding with the differences seen in the height profile over the \(33^{\circ }\hbox {N}\) region (Fig. 8f). The GC2-S and GC2-M distributions are similar to GC2-A, which is to be expected since the region of SST imposed from GC2-C did not cover this region. GC2-L has an omega distribution similar to GC2-C and significantly different from GC2-A, demonstrating the ability of even a small SST bias to enhance transient ascent in this region along the isentropes. There is little difference between any of the model versions during the periods of descent.

Fig. 9
figure 9

Omega at \(850\,\hbox {hPa}\) frequency distributions (note the field has been multiplied by \(-1\) so that positive values represent ascent; units: \(\hbox {Pa}\,\hbox {s}^{-1}\)) over \(1.5^{\circ }\) box-means along the longitude section in Fig. 8, from \(69.75^{\circ }\hbox {W}\) to \(68.25^{\circ }\hbox {W}\), at three different latitudes: a \(32.25^{\circ }\hbox {N}\) to \(33^{\circ }\hbox {N}\), b \(36^{\circ }\hbox {N}\), and c \(38.25^{\circ }\hbox {N}\) to \(39^{\circ }\hbox {N}\). Distribution mean (thick solid lines), the two-sigma (\(\sim \,95\%\)) envelope from 1000 bootstraps of the seasons (shading), and mean omega amplitude (thin vertical lines) are shown for ERA-Interim (black), GC2-C (blue), GC2-A (green), and sensitivity experiments: GC2-S (red), GC2-M (orange), and GC2-L (purple)

Full size image
Fig. 10
figure 10

Jet latitude distributions over \(60^{\circ }\hbox {W}\)–\(0^{\circ }\hbox {E}\), \(20^{\circ }\hbox {N}\)–\(70.5^{\circ }\hbox {N}\) (thick lines). Distribution mean (thick solid lines), the two-sigma (\(\sim \,95\%\)) envelope from 1000 bootstraps of the seasons (shading), and mean latitudinal position (thin vertical lines) are shown for ERA-Interim (black), GC2-C (blue), GC2-A (green), and sensitivity experiments: a GC2-S (red), b GC2-M (orange), and c GC2-L (purple)

Full size image

Over the region of maximum mean omega in ERA-Interim at \(36^{\circ }\hbox {N}\), all \(850\,\hbox {hPa}\) omega distributions are similar to each other except GC2-C and GC2-L, being statistically different from ERA-Interim during medium intensity ascent, from around 0.1 to 0.2 (\(\times -1\)) \(\hbox {Pa}\,\hbox {s}^{-1}\) (Fig. 9b). This agrees with the time mean omega profile differences at \(36^{\circ }\hbox {N}\) (Fig. 8).

There are clear changes in the \(850\,\hbox {hPa}\) omega distribution for GC2-C and the three sensitivity experiments, relative to GC2-A and ERA-Interim, over the region of SST bias (in the case of GC2-C) and imposed SST heating bias (in the sensitivity experiments) (Fig. 9c). From around \(-0.2\) to 0 (\(\times -1\)) \(\hbox {Pa}\,\hbox {s}^{-1}\) GC2-C and the sensitivity experiments have fewer occurrences of weak descent relative to GC2-A, and more occurrences of strong ascent from around 0.1 to 0.5 (\(\times -1\)) \(\hbox {Pa}\,\hbox {s}^{-1}\). The mean in the distributions (thin vertical lines) further emphasises this difference, agreeing with Fig. 8 around \(39^{\circ }\hbox {N}\). The mean change in omega over the imposed SSTs is achieved via more frequent occurrence of strong ascent, while the statistics of strong descent do not change. Hence the distribution of omega is broadened, rather than shifted, over the positive SST bias and imposed bias. Analysis of high-pass filtered omega-prime-squared (\(\overline{\omega ^{\prime 2}}\)) fields (Fig. S4), as meridional profiles along the section used in Fig. 8, also supports large increases in ascent in the transient eddies over the SST bias and imposed bias.

The vertical eddy moisture and vertical eddy heat fluxes at 850 hPa (\(\overline{\omega '\text {q}'}\): Fig. S5b; \(\overline{\omega '\text {T}'}\): not shown) are negatively biased in GC2-C relative to ERA-Interim in parts of both storm tracks, particularly the North Pacific. The vertical eddy moisture flux GC2-C differences from GC2-A (Fig. S5c) in the Pacific are similar to those of the meridional eddy heat flux (Fig. 7c), while in the North Atlantic storm track the differences are confined to a southward shift towards the Gulf of Mexico from the southeastern US. All three sensitivity experiments and GC2-C minus GC2-A (Fig. S5d–f) show a very localized northward shift over the region of large SST bias in both vertical eddy moisture and vertical eddy heat fluxes, likely associated with the shift and change in maximum SST gradient.

While the meridional-height section at \(69.75^{\circ }\hbox {W}\)–\(68.25^{\circ }\hbox {W}\) in Figs. 8 and 9 reveals the impact of vertical motion over the region of greatest SST biases, further analysis (not shown) reveals this continues further downstream over this bias (e.g. at \(61^{\circ }\hbox {W}\)) in the three sensitivity experiments. Further downstream, analysis of ascent (not shown) indicates similar processes are occurring. This is both within the region including the positive bias of the Gulf Stream extension (within the GC2-M box), and the cold bias in the mid North Atlantic. Wills et al. (2016) found that anomalous heating of the lower troposphere in regions to the northeast of the Gulf Stream extension extends to the upper-tropospheric circulation in analysis of ERA-Interim data. Therefore, in the GC2-M and GC2-L experiments, the warm Gulf Stream extension SST bias (in both experiments) and the cold bias to the northeast (in GC2-L) may both also have impacts up to the upper troposphere.

4.5 North Atlantic eddy-driven jet

The heat and moisture fluxes from the WBCs into the atmosphere anchor the latitude of the storm tracks to the WBCs (Kwon et al. 2010). The position and strength of the Gulf Stream SST gradient are important to accurately capture the eddy-driven jet latitude over the North Atlantic, with a realistic gradient resulting in more frequent occurrences of the northern jet location relative to a smoothed SST gradient via eddy heat flux differences (e.g., O’Reilly et al. 2016). Figure 10 investigates the jet response to the sensitivity experiments and the downstream dynamical impact of the imposed Gulf Stream SST bias. Jet latitude distributions are derived following the methodology of Woollings et al. (2010), using the \(850\,\hbox {hPa}\) zonal wind field which is zonally averaged over the North Atlantic region (\(60^{\circ }\hbox {W}\)–\(0^{\circ }\hbox {E}\), \(20^{\circ }\hbox {N}\)–\(70.5^{\circ }\hbox {N}\)), 10-day low-pass Lanczos filtered with a window of 61 days and subtracting the smoothed seasonal cycle (Duchon 1979), and then smoothed with a Gaussian kernel density estimation. The spread on the jet latitude distributions show the two-sigma (\(\sim \,95\%\)) envelope of 1000 bootstrap realisations, randomly selecting whole seasons from the 27 years with replacement.

Figure 10 shows the trimodal distribution of preferred jet-stream locations, often called ‘regimes’, in ERA-Interim (black) and the GC2 models, with the time-mean jet position shown by the thin vertical lines. It highlights the bias towards the high-latitude regime in GC2-C (blue) when compared with GC2-A (green), as found by Masato et al. (2016), and agrees with the storm track analysis above (Fig. 7c, in the northern N. Atlantic). The GC2-S (red; Fig. 10a) experiment reproduces the high-latitude regime GC2-C bias, while GC2-M (orange; Fig. 10b) and, in particular, GC2-L (purple; Fig. 10c) both appear to have only small shifts north from GC2-A. Differences between the sensitivity experiments may arise from an impact of the larger scale SST gradients, however note that the internal variability is large as is shown by the spread in Fig. 10, thus the differences cannot be considered significant.

5 Conclusions

In this study the tropospheric response to Gulf Stream biases have been investigated during the winter season. The state-of-the-art Met Office HadGEM3-GC2 coupled model configuration (GC2-C) at N216 atmospheric resolution (\(\sim \,60\,\hbox {km}\) in the mid-latitudes), \(\frac{1}{4}^{\circ }\) ocean resolution has a winter warm bias of up to \(6.75\,\hbox {K}\) in a small region where the Gulf Stream separates from North America, which is associated with surface heat flux biases and linked to eddy-driven jet biases in the North Atlantic. The three sensitivity experiments analysed were created by imposing the warm SST bias from GC2-C onto the atmosphere-only configuration (GC2-A). Imposing this warm SST bias here acts to shift and change the strength of the SST gradients in the Gulf Stream which have been shown to be important to ocean–atmosphere interactions (e.g. Parfitt et al. 2016). The three experiments differ by imposing increasingly larger areas of SST bias from the Gulf Stream and North Atlantic. The ‘small’ box (GC2-S) covers the Gulf Stream separation region east of Cape Hatteras including biases of up to between \(+\,6\) and \(+\,6.75\,\hbox {K}\), and the ‘medium’ box (GC2-M) extends this area eastward towards the mid Atlantic, where this warm bias ends. In order to give a context to this Gulf Stream bias in amongst other SST biases in the North Atlantic, the ‘large’ box (GC2-L) covers most of the North Atlantic, including a warm bias of \(+\,1\,\hbox {K}\) in the Sargasso Sea and a large region of around \(-\,1\,\hbox {K}\) cool bias in the subtropical North Atlantic.

The anomalous heating imposed over the Gulf Stream appears to be dominated by enhanced ascent, in comparison to meridional heat transport, either mean or eddy. GC2-M is the one exception where there is also a significant eddy heat flux response in addition to the enhanced ascent. The increased ascent is not a constant perturbation, but rather occurs during periods of transient ascent. Hence the distribution of vertical velocity is broadened rather than shifted. This deep ascent is twice as strong in GC2-C relative to ERA-Interim reanalysis, and is mostly made up of ascent which is over the fronts as seen in the transient field, steeper than the isentropes in the lower troposphere, and slantwise ascent along the isentropes in the upper troposphere. This is associated with another much weaker Sargasso Sea region of warm SST bias (adding a small absolute SST increase in GC2-L) and enhanced vertical motion in the transients below the southward shifted jet in GC2-C.

A resolution comparison climate modeling experiment using variability forced SSTs by Smirnov et al. (2015) found a similar enhanced deep ascent response only in the high resolution configuration. Atmospheric and oceanic fronts and their interactions are the key process which must be sufficiently resolved to improve their impact on the time-mean state (Parfitt and Czaja 2016; Parfitt et al. 2016; O’Neill et al. 2017; Smirnov et al. 2015). Together, this may suggest that such close coupling of biases found here may be more prevalent in higher resolution coupled global climate models (such as this N216 atmosphere, \(\frac{1}{4}^{\circ }\) ocean configuration), given their increased sensitivity to errors in location and intensity.

Over the Gulf Stream extension and further northeast there are further impacts on the vertical ascent, agreeing with the findings of Wills et al. (2016). Together this implies that a similar transfer of biases throughout the troposphere is also possible.

Together with the imposed Gulf Stream heating bias, the response affects the troposphere not only locally but also in remote regions of the Northern Hemisphere via a quasi-zonal planetary barotropic Rossby wave response, at wavenumber 5. The circumglobal nature of this wave response is found in nature and models during the winter season due to the jet configuration acting as a waveguide (Branstator and Teng 2017). The Rossby wave response appears to be triggered by the increased ascent over the Gulf Stream. The wavenumber 5 response seen in the sensitivity experiments could not be reproduced in an idealised barotropic vorticity equation model, possibly because the forcing is not constant, but rather modulated by the transient regions of ascent. The baroclinic nature of the response immediately downstream of the heating may be important, and the response might be highly sensitive to the position of the jet, atmospheric and oceanic fronts, convection and latent heat release. The wavenumber 5 response also does not emerge as a leading pattern of internal variability in GC2.

The Rossby wave response is consistent with other studies investigating enhanced deep ascent over the Gulf Stream (e.g., Minobe et al. 2008), and a wave response has been seen in a study investigating the linear dynamical response although their path is arcing rather than zonal (Sato et al. 2014). This planetary response appears to be consistent with the partial reproduction of the south-shifted bias from GC2-C in the Pacific upper tropospheric jet as well as over the southeastern US in some of the experiments. Other coupled model biases are also partially reproduced including the extended trough over the Pacific (up to \(19\%\) reproduction in GC2-S) and the reduced ridge over Scandinavia (up to \(25\%\) reproduction in GC2-S).

A full reproduction of the GC2-C biases should not be expected since there are multiple other sources of bias in addition to the small Gulf Stream region, the focus of this paper. Such other sources of bias and/or systematic errors include a cool SST bias in the central North Pacific, a warm SST bias over the Southern Ocean (related to atmospheric heat flux biases), and low levels of rainfall over India and West Africa during the summer monsoons (partly related to a southward displaced Intertropical Convergence Zone, ITCZ). A full model evaluation, including these biases, is presented by Williams et al. (2015).

Some of the differences between the three experiments may be accounted for by differing internal variability since the runs are only 27 years in length to match the GC2-A standard period. However, even when the response to the forcing is small, it is nevertheless consistent between the three perturbed experiments, which adds confidence to the results.

The transient ascent, and wave response pathways may have implications for the ability of the model to respond correctly to variability or changes in the Gulf Stream. While the higher wavenumber stationary waves, such as wavenumber 5, represent a small fraction of the stationary eddy variance, they have been shown to respond sensitively to changes in radiative forcing (Simpson et al. 2016), with important implications for regional climate. Better global prediction requires particular attention be paid to reducing western boundary current SST biases in such highly coupled and sensitive regions, such as the Gulf Stream, where they occur. Through the mechanisms shown in this paper, a focus on reducing ocean and SST biases in these regions of high ocean–atmosphere interaction may also reduce some of the global atmospheric biases in coupled global climate models.