Abstract
Interannual rainfall variability in China affects agriculture, infrastructure and water resource management. To improve its understanding and prediction, many studies have associated precipitation variability with particular causes for specific seasons and regions. Here, a consistent and objective method, Empirical Orthogonal Teleconnection (EOT) analysis, is applied to 1951–2007 high-resolution precipitation observations over China in all seasons. Instead of maximizing the explained space–time variance, the method identifies regions in China that best explain the temporal variability in domain-averaged rainfall. The EOT method is validated by the reproduction of known relationships to the El Niño Southern Oscillation (ENSO): high positive correlations with ENSO are found in eastern China in winter, along the Yangtze River in summer, and in southeast China during spring. New findings include that wintertime rainfall variability along the southeast coast is associated with anomalous convection over the tropical eastern Atlantic and communicated to China through a zonal wavenumber-three Rossby wave. Furthermore, spring rainfall variability in the Yangtze valley is related to upper-tropospheric midlatitude perturbations that are part of a Rossby wave pattern with its origin in the North Atlantic. A circumglobal wave pattern in the northern hemisphere is also associated with autumn precipitation variability in eastern areas. The analysis is objective, comprehensive, and produces timeseries that are tied to specific locations in China. This facilitates the interpretation of associated dynamical processes, is useful for understanding the regional hydrological cycle, and allows the results to serve as a benchmark for assessing general circulation models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Seasonal precipitation variability over China is mainly influenced by the East Asian Monsoon (EAM) system, characterized by strong southwesterly winds in summer (the East Asian Summer Monsoon, EASM), and strong northeasterly winds in winter (the East Asian Winter Monsoon, EAWM). Figure 1 shows that there is a strong seasonal cycle in precipitation, with 51% of China-wide annual precipitation falling during summer (JJA), 23% during spring (MAM), 19% during autumn (SON) and 7% during winter (DJF), based on 1952–2007 data (Sect. 2.1). The EASM circulation transports large amounts of moisture into East Asia, whereas dry and cold air enters China during winter. The EAM system exhibits substantial intraseasonal, interannual and decadal variability, which affects the risk of disastrous regional extremes such as droughts, floods and cold surges (Huang et al. 1998, 2012b; Huang and Zhou 2002; Gu et al. 2008). Individual extreme events can cause economic losses of the order of billions of US dollars by damaging industrial and agricultural production; such events affect the lives of millions of people through impacts on water resource management, infrastructure and the ecological environment (Huang et al. 1998, 1999, 2012b; Huang and Zhou 2002; Barriopedro et al. 2012).
The EAM is a highly complex system influenced by various atmosphere–ocean–land coupled mechanisms on daily-to-decadal scales. The El Niño Southern Oscillation (ENSO) has an important influence on East Asian climate (e.g. Fu and Teng 1988; Huang and Wu 1989; Zhang et al. 1996, 2014; Zhang and Huang 1998; Wang et al. 2000; Wu and Hu 2003; Lau and Nath 2006; Wu et al. 2009). Summer flooding in the Yangtze River valley can occur during the decaying stage of El Niño, while the developing stage of El Niño favors droughts in northern China (Huang and Zhou 2002). The ENSO SST anomalies over the eastern tropical Pacific are communicated to precipitation anomalies over East Asia through low-level circulation anomalies over the western North Pacific. After El Niño an anticyclonic circulation anomaly usually starts to appear during autumn and winter and can persist into the following summer (e.g., Harrison and Larkin 1996; Wang and Zhang 2002). A variety of dynamical mechanisms have been proposed to address the origin and persistence of this anticyclonic circulation. Zhang et al. (1996) suggested it is induced by suppressed convection over the western equatorial Pacific due to a weakened Walker circulation during El Niño. Wang et al. (2000) argued instead that its development is a response to Rossby waves triggered by SST anomalies over the western tropical Pacific (Matsuno 1966; Gill 1980), and that its long persistence could be attributed to a local wind-evaporation-SST feedback. Other studies found the delayed Indian Ocean warming after the El Niño to be important for the development and maintenance of the anomalous anticyclone over the western North Pacific (e.g., Yang et al. 2007; Xie et al. 2009). The delayed Indian Ocean warming can give rise to equatorial surface easterly wind anomalies and suppressed convection in the western North Pacific region through a baroclinic atmospheric Kelvin wave response. Another recent theory involves the combination mode (C-mode), resulting from the nonlinear atmospheric interaction between the annual cycle and ENSO variability (Stuecker et al. 2013, 2015); the antisymmetric circulation response during the El Niño peak phase and the following spring is associated with the seasonal warm pool migration to the southern hemisphere. Xie and Zhou (2017) argued that the C-mode is important for establishing the anticyclone but that the Indian Ocean capacitor effect is what causes it to persist (Yang et al. 2007; Xie et al. 2009). These circulation anomalies in the western North Pacific do not only have an effect on summer precipitation, but also on spring rainfall in southern China (Zhang et al. 2016). In winter, a weaker EAWM has been associated with the mature phase of El Niño, and a stronger EAWM with La Niña (Zhang et al. 1996; Tomita and Yasunari 1996; Ji et al. 1997; Wang et al. 2000; Hamada et al. 2002; Chan and Li 2004). However, the impact of ENSO on the EAM is modulated by the Pacific Decadal Oscillation during summer, winter and spring (Zhang et al. 1997; Wang et al. 2008; Yang and Zhu 2008; Wu and Mao 2016).
Extratropical teleconnection patterns also play an important role in affecting interannual rainfall variability over East Asia. Chen and Huang (2014) found two teleconnection patterns that modulate July precipitation in northwest China. One is the Silk Road pattern, which starts from the Mediterranean and Caspian Seas and propagates zonally along the Asian jet stream. The Silk Road pattern has previously been identified by Lu et al. (2002). Enomoto et al. (2003) found that it is instrumental in the formation of the barotropic ridge near Japan during August, also known as the Bonin high. The second pattern identified by Chen and Huang (2014), the Europe–China pattern, consists of positive anomalous centers over western Europe and northwestern China and negative anomalous centers over eastern Europe and southeastern China. Other northern-hemisphere teleconnection patterns that are not zonally aligned but have arc-like shapes include the East Atlantic, East Atlantic/Western Russia, Polar/Eurasia, and Scandinavian patterns. Their influence on the atmospheric circulation over Eurasia and the Pacific was examined by Tao et al. (2016). A wave train resembling the Scandinavian pattern was also identified by Wang and Feng (2011) who found that winter precipitation in south China is associated with a barotropic wave train originating over the Atlantic.
Important connections between regional precipitation variability and large-scale drivers have been found for specific locations and seasons, with a primary focus on winter and summer, but no studies have examined the causes of variability across China in all seasons and across timescales using a consistent method.
This study aims to objectively identify regions in China that show strong coherent interannual variability in seasonal precipitation, and to understand the associated local and large-scale atmospheric and coupled air–sea processes that drive it. A complementary study (part II of this work) conducts a similar analysis for intraseasonal precipitation (Stephan et al. 2017). In both studies, we analyze gridded precipitation observations and determine spatial patterns of rainfall variability objectively, instead of relying on predefined regions or standard correlation analysis. We analyze all seasons to compile a comprehensive catalog of the drivers of rainfall variability in China, which can serve as a basis for model assessments. Our analysis technique, Empirical Orthogonal Teleconnection (EOT) analysis, does not maximize the percentage of explained space–time variance, unlike other algorithms that seek eigenvectors. Instead, it emphasizes regions of strong coherent variability. Benefits of our analysis technique include that the EOT timeseries and spatial patterns have undeniable physical meaning, as they can be connected directly to particular regions of coherent variability. They can be useful in predicting precipitation variability over larger regions by creating forecasts for only a few selected points in space. Even in cases where no associated large-scale dynamical pattern can be identified for an EOT, an empirical prediction of regional precipitation variability may be possible by taking advantage of the orthogonality to other EOT timeseries.
Section 2 describes the data sets and analysis methods. Results from the EOT analysis are shown in Sect. 3. Section 4 is a discussion; Sect. 5 summarizes the main results.
2 Data and methods
2.1 Seasonal precipitation over China
Daily precipitation over China is obtained from the Asian Precipitation-Highly-Resolved Observational Data Integration Towards Evaluation (APHRODITE) data set, which is a long-term (1951–2007) continental-scale product, produced mainly from daily rain-gauge data (Yatagai et al. 2012). The resolution is 0.5\(^{\circ }\times 0.5^{\circ }\). Before the data are gridded, 14 objective quality control steps are applied to the rain-gauge data as detailed in Hamada et al. (2011). The high quality of the data has been confirmed in previous studies (Rajeevan and Bhate 2009; Krishnamurti et al. 2009; Wu and Gao 2013).
We use the seasonal-total precipitation for winter (DJF), spring (MAM), summer (JJA) and autumn (SON). Throughout China the spatial coverage of rain gauges is consistently high except in northwest China and the Tibetan Plateau, which are climatologically dry regions (see Yatagai et al. 2012, for a map of rain-gauge locations). All patterns of rainfall variability that are identified in this study are located in areas of high-density observations. Figure 1 shows the average seasonal total precipitation and its interannual standard deviation for each season. During all seasons the magnitude of rainfall variability closely follows the contours of seasonal total precipitation, and total precipitation and its variability are largest in southeast China.
2.2 Empirical orthogonal teleconnections
EOT analysis was introduced by Van den Dool et al. (2000). Unlike Empirical Orthogonal Functions (EOFs), which are orthogonal in space and time, EOTs are orthogonal either in space or time. We choose orthogonality in time to investigate temporal rainfall variability. The Van den Dool et al. (2000) method defines the first EOT as the timeseries at the point within a two-dimensional spatial domain that best explains the variance at all points combined including the base point itself. The associated spatial pattern is a map of correlation coefficients at each point with this so-called base point. To compute the second EOT timeseries, the first EOT timeseries is removed from all points in the domain by linear regression, and the above steps are repeated. This algorithm can be repeated as many times as there are gridpoints in a domain, although the lowest order patterns often explain vanishingly small amounts of variance.
For continents or countries with multiple climate zones, like Australia and China, often a large fraction of total rainfall variance is concentrated in relatively small areas. This is also evident from Fig. 1. Smith (2004) showed that under these circumstances it can be beneficial to modify the Van den Dool et al. (2000) technique: instead of searching for the point that best explains the variance at all other points combined, we compute the domain area-averaged timeseries of rainfall anomalies and search for the point that best explains the variance of this single timeseries. The EOT method allows us to identify independent regional patterns of coherent rainfall variability, which can then be connected to regional and large-scale atmospheric and coupled atmosphere–ocean patterns, as has been demonstrated successfully for other regions (Smith 2004; Rotstayn et al. 2010; Klingaman et al. 2013; King et al. 2014). Unlike other methods that seek eigenvectors, EOT analysis does not maximize the percentage of explained space–time variance. Instead, the timeseries are connected to specific points and most of the explained variance is derived from nearby positively correlated points. Therefore, EOT spatial patterns are dominated by monopoles, rather than dipolar or tripolar patterns. The EOT method has several benefits: the timeseries and spatial patterns have undeniable physical meaning, as they can be connected directly to particular regions of coherent variability. They can be useful in predicting precipitation variability over larger regions by creating forecasts for only a few selected points in space. Even in cases where no associated large-scale dynamical pattern can be identified for an EOT, an empirical prediction of regional precipitation variability may be possible by taking advantage of the orthogonality to other EOT timeseries.
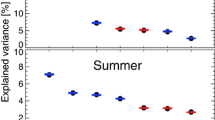
Van den Dool et al. (2000) argued that a ’rule of thumb’ derived for testing degeneracy in EOF analysis by North et al. (1982) should also apply to EOTs: modes are considered degenerate if, for a given mode, the uncertainty in an eigenvalue is of the same order of magnitude as the difference between neighbouring eigenvalues. As a measure of uncertainty due to a limited sample size in time, we compute the percentage of total explained space–time variance for each EOT, leaving out 1 year at a time. The error is considered to be the difference between the greatest and smallest percentages. We discard an EOT as degenerate when its error is greater than half the difference between its total explained variance (using the full EOT timeseries) and that of either of its neighbours. Results for all seasons are shown in Fig. 2. In DJF, for example, EOTs 1 and 2 are distinct from the other EOTs, but EOTs 3 and 4 are degenerate. EOTs 5 and higher explain only small fractions of the total space–time variance and cannot be distinguished from one another. Therefore, we analyze only EOTs 1 and 2 for DJF precipitation. The number of EOTs analyzed differs from season to season because some EOTs are degenerate; we show only EOTs that explain at least 5% of the total space–time variance.
Fraction of total space–time variance explained by the 11 leading EOTs for DJF, JJA, MAM and SON precipitation. Error bars are computed by omitting 1 year at a time and are shown as horizontal bars. Red bars denote EOTs that are ‘degenerate’ (i.e., that are not distinctly different from all other EOTs) following the procedure outlined in Sect. 2.2. We only analyze EOTs that are shown in blue and that explain at least 5% of the total space–time variance (marked by dashed lines)
Connections between rainfall patterns and drivers are established by linearly regressing atmospheric and oceanic data sets onto timeseries corresponding to each EOT pattern. All computations involving multiple data sets are performed for the respective common record periods. Regressions show the change associated with a one standard deviation increase in the EOT timeseries, but all discussions hold for negative anomalies in the EOT timeseries, with patterns in the opposite phase of variability. We use Spearman’s rank correlations because the rainfall data are not normally distributed. Nevertheless, tests showed high agreement between Pearson’s and Spearman’s rank correlation coefficients. ’Significant’ always refers to the 95% confidence level.
2.3 Atmospheric and oceanic data
The following fields from the European Centre for Medium-Range Weather Forecasting Interim global reanalysis (ERA-Interim), available at \(0.7^{\circ }\times 0.7^{\circ }\) resolution from 1979–2007 (Dee et al. 2011) are regressed against the EOT timeseries: horizontal wind at 200 and 850 hPa, streamfunction and divergence of horizontal wind at 200 hPa, geopotential at 500 and 200 hPa, surface pressure, and vertically integrated moisture flux.
Monthly-mean 1870–2010 SSTs are obtained from the 1\(^{\circ }\times 1^{\circ }\) Hadley Centre sea Ice and SST data set (HadISST; Rayner et al. 2003). We employ monthly means of 2.5\(^{\circ }\times 2.5^{\circ }\) interpolated satellite-retrieved outgoing longwave radiation data (OLR; Liebmann and Smith 1996) for 1974–2013, as a proxy for convective activity.
We also perform lead–lag correlations of EOT timeseries with the Niño3.4 index, defined as the average SST anomaly in 5\(^{\circ }\)S–5\(^{\circ }\)N and 170\(^{\circ }\)W–120\(^{\circ }\)W. The index is available from the National Center for Environmental Prediction’s Climate Prediction Center at http://www.cpc.ncep.noaa.gov.
2.4 Rossby wave diagnostics
Many patterns of coherent precipitation variability in China are associated with extratropical waves. To understand their propagation and origins, we compute the Rossby wave source (RWS) function and diagnose the direction of wave energy propagation, as given by the wave activity flux vector W.
For the RWS function we use the definition given by Sardeshmukh and Hoskins (1988) in their Eq. (3), which combines the absolute vorticity \(\eta\), horizontal wind divergence D, and the divergent horizontal wind vector \({v}_{\chi }\) to
Hence, the RWS is defined as the rate of change of vorticity due to vortex stretching (first term) and vorticity advection by the divergent part of the wind (second term). The first term is related to divergence and convergence above ascending or descending air, respectively, which drives the upper atmospheric rotational wind field. The second term implies that RWS can be generated non-locally (i.e. far away from anomalous heating), when divergent wind encounters sharp horizontal vorticity gradients (such gradients would exist, for example, approaching a jet stream). We choose the 200 hPa level for calculating the RWS, as this is where its vertical profile peaks (Scaife et al. 2016). Convective outflow and hence divergent horizontal winds are strong at 200 hPa. In addition vorticity gradients associated with a vertical peak in the jet stream are maximum.
To compute the wave activity flux vector W, we first regress the perturbation stream function \(\psi\) onto an EOT timeseries, then compute W from \(\psi\) and the climatological mean flow \(\bar{U}=(\bar{u}(x,y),\bar{v}(x,y))\). Takaya and Nakamura (2001) derived the horizontal components for stationary Rossby waves in a zonally varying basic flow:
where subscripts denote partial derivatives.
To investigate wave propagation, we perform Rossby wave ray tracing. The dispersion relation of a barotropic Rossby wave in a slowly varying zonal flow with velocity U is given by
where \(\omega\) is the frequency, \(K=\sqrt{(k^2+l^2)}\) is the total wavenumber, and k and l are the zonal and meridional wavenumbers, respectively; and \(\beta ^*=\beta -U_{yy}\) is the meridional gradient of the absolute vorticity of the mean flow, which combines the gradient in planetary vorticity \(\beta\) and the curvature of the flow \(U_{yy}\) (Hoskins and Karoly 1981). For a stationary wave, \(\omega =0\), and (3) gives
The zonal and meridional group velocities of a stationary wave are given by
and
respectively. For a wave with zonal wave number k, points where \(K^2=k^2\) correspond to \(l=0\) and constitute a reflecting surface where the wave reverses its meridional propagation direction. Points where l and therefore K approach infinity form critical lines where \(U=0\) and the propagation of Rossby waves is not supported. We trace Rossby waves of a given zonal wavenumber k by computing l from (3), then using (5) and (6) to find the location of the wave front, in steps of 2 h, taking into account the spherical geometry of the globe. We continue to trace the wave until it terminates at a critical line.
To illustrate the waveguides that are associated with the positive phase of a particular EOT, we show maps of the stationary Rossby wavenumber K. The background wind is computed using the seasonal mean 200 hPa zonal wind averaged over the five most positive years of the EOT timeseries. We further use a 60\(^{\circ }\) zonal average for the background wind field U, and a full 360\(^{\circ }\) zonal average for the curvature term \(U_{yy}\). Our choices of pressure level, timestep, and smoothing of the background wind field follow the recommendations of Scaife et al. (2016).
3 Results
We proceed with each season in turn, discussing first winter and summer, followed by spring and autumn. We only analyze EOTs that are not degenerate (blue in Fig. 2) and that explain at least 5% of the total space–time variance.
3.1 Winter
3.1.1 DJF EOT 1
DJF EOT 1 describes rainfall variability in large areas of eastern China and explains 34% of the total space–time variance (Fig. 3a). The associated timeseries (black and red lines in Fig. 3a) exhibits a strong 2–3 years variability as well as a multidecadal modulation with mostly negative anomalies between the late 1950s and mid-1980s and mostly positive ones since then, but with a tendency towards another negative phase after 2000.
Left correlations of DJF rainfall anomaly timeseries at each point with the EOT base point. The base point is marked by the black inverted triangle. Magenta lines identify regions where correlations are significant at the 5% level. Right the corresponding EOT timeseries (black) with their 11-year running averages (red)
DJF EOT 1 is significantly correlated with Niño3.4 during the previous spring, summer and autumn, the concurrent winter and following spring (correlation coefficients of \(\rho =0.29, 0.47, 0.48, 0.47, 0.40\), respectively). Figure 4a confirms a positive relationship between ENSO SSTs and DJF EOT 1. The surface pressure pattern is characteristic of a weakened Walker circulation, with negative anomalies in the eastern tropical Pacific and a broad area of positive anomalies in the western tropical Pacific and eastern Indian Ocean (Fig. 4b). A regression of 850 hPa winds (Fig. 4b) confirms a weakened EAWM with anomalous southerly flow over China. The anomalous southwesterlies along the coast of southeast China are consistent with moisture transport from the Bay of Bengal and the South China Sea, where SSTs are anomalously warm.
Regression maps of DJF sea surface temperatures (a), and surface pressure and 850 hPa horizontal wind (b) onto the normalized DJF EOT 1. Colours show the regression slopes and stippling indicates correlations that are significant at the 10% level. Wind vectors in b are drawn when at least one component of the horizontal wind vector is significant at the 10% level
Using DJF precipitation over China, Wang and Feng (2011) also found that the EOF 1 pattern was centered over eastern China south of the Yangtze river. They also reported a 2–4 year period with similar multidecadal variability, and associated their EOF 1 with ENSO-driven changes in the strength of the East Asian winter monsoon. Their principal component timeseries showed correlations of 0.2–0.5 with the Niño3 index from the preceding June to the following May. This agreement demonstrates that EOT and EOF analysis are capable of identifying robust patterns of coherent variability with similar associated timeseries and thus further supports our choice of method.
3.1.2 DJF EOT 2
DJF EOT 2 explains 12% of the total space-time variance with a peak along the southeast coast and another small area of coherent variability in north China (Fig. 3b). Low 200 hPa geopotential is seen over China, with a positive 200 hPa geopotential anomaly over and to the east of Japan (Fig. 5b). Statistically significant positive geopotential anomalies in this area are not only present at 200 hPa, but also at 500 hPa, and positive surface pressure anomalies are also statistically significant (not shown). They force anomalous westward onshore flow, visible in 850 hPa wind (Fig. 5a). Precipitation increases where the topography rises steeply from sea level, which is the case for both the southern and northern regions of DJF EOT 2. The signature of orography is also seen in a small region of variability of opposite phase in southeast China, the Shaoyang basin. Negative OLR anomalies are present over the western equatorial Indian Ocean and positive OLR anomalies over the eastern equatorial Atlantic Ocean (Fig. 5a). Divergence of wave activity flux indicates that a Rossby wave source region is located over Africa (blue star in Fig. 5b). This Rossby wave source is due to anomalous vertical motion, creating significant divergent or convergent winds, respectively, at 200 hPa (not shown). Through the terms in Eq. (1) these upper level divergent winds can create anomalous vorticity, either locally through vortex stretching, or by advecting vorticity in interacting with the subtropical westerly jet. The blue points show the path of a zonal wavenumber-three Rossby wave originating from this location, with one point every 2 h. The ray passes through a significant positive 200 hPa geopotential anomaly over the Arabian Sea and India (Fig. 5b), before crossing the above-mentioned negative and positive pressure anomalies over China and Japan. The wave propagation continues across the Pacific, intersecting another significant 200 hPa geopotential anomaly before diverting southward. We conclude that wintertime rainfall variability along the southeast coast of China is associated with anomalous convection over the tropical eastern Atlantic and is mediated through a Rossby wave with zonal wavenumber three.
Regression maps of DJF outgoing longwave radiation (OLR) and 850 hPa wind (a), and 200 hPa eddy geopotential (GP) and 200 hPa wave activity flux (b) onto the normalized DJF EOT 2. Colours show the regression slopes and stippling indicates correlations that are significant at the 10% level. Wind vectors in a are drawn when at least one component of the horizontal wind vector is significant at the 10% level. Wave activity flux vectors in b are omitted for magnitudes less than 0.3 m\(^2\)s\(^{-2}\). Blue points show the propagation of a zonal wavenumber-three Rossby wave from the location marked with a star for 5 days at intervals of 2 h
3.2 Summer
3.2.1 JJA EOT 1
JJA EOT 1 describes a pattern of coherent precipitation variability along the southern reaches of the Yangtze River (Fig. 6a). JJA EOT 1 was mostly negative from the late 1950s to the early 1980s and transitioned to a positive phase afterward, with a tendency towards another negative phase after 2000, similar to DJF EOT 1. A lead-lag correlation reveals that JJA EOT 1 lags ENSO. Significant positive correlations with Niño3.4 exist during the preceding 5 seasons with a maximum correlation of \(\rho =0.42\) for the preceding DJF. A connection between the decaying state of El Niño and flooding in the Yangtze region was previously found by Huang and Zhou (2002), who performed a composite analysis of summer monsoon rainfall anomalies for different stages of ENSO.
Left correlations of JJA rainfall anomaly timeseries at each point with the EOT base point. The base point is marked by the black inverted triangle. Magenta lines identify regions where correlations are significant at the 5% level. Right the corresponding EOT timeseries (black) with their 11-year running averages (red)
The temporal evolution of SSTs and wind in Fig. 7 is consistent with the schematics shown in Fig. 12 of Stuecker et al. (2015) and Fig. 9 of Xie and Zhou (2017). Stuecker et al. (2013, 2015) showed that the atmospheric response over the equatorial Indian and Pacific Oceans to ENSO consists of two dominant modes: a meridionally quasi-symmetric direct response to ENSO and an antisymmetric response, which arises from the nonlinear atmospheric interaction between ENSO variability and the seasonal cycle of SST and circulation and is referred to as the combination mode (C-mode). During SON and DJF, there is a quasi-symmetric response with anticyclonic off-equatorial circulations in the Indian Ocean and cyclonic circulations in the western Pacific. During the following spring the antisymmetric circulation response develops, featuring an anticyclonic circulation in the western North Pacific. Stuecker et al. (2015) explain that this is associated with the migration of the seasonal warm pool to the southern hemisphere, which is also visible as stippling in the MAM SST regression (Fig. 7). Finally, the anticyclone strengthens during JJA. This amplification and persistence into summer is linked to the Indo-western Pacific Ocean Capacitor effect (Xie and Zhou 2017). Delayed warming of the Indian Ocean can induce equatorial surface easterlies and suppressed convection in the western North Pacific through a baroclinic atmospheric Kelvin wave response (e.g., Yang et al. 2007; Xie et al. 2009), thereby reinforcing the western North Pacific anticyclone.
Regression maps of previous SON, DJF, MAM and simultaneous JJA sea surface temperatures and 850 hPa wind onto the normalized JJA EOT 1. Stippling indicates correlations that are significant at the 10% level. Green wind vectors indicate that at least one component of the horizontal wind vector is significant at the 10% level. Vectors are omitted for magnitudes <0.1 ms\(^{-1}\)
3.2.2 JJA EOT 2
JJA EOT 2 peaks along the northern reaches of the Yangtze valley (Fig. 6b). The timeseries has a pronounced periodicity with a peak at about 2 years. Precipitation variability in this region could not be associated with any large-scale circulation pattern. Instead, the JJA EOT 2 timeseries is significantly correlated with increased pressure over a small area of south China. This creates a regional lower tropospheric circulation anomaly with increased westerlies along the Yangtze River (not shown).
Our JJA EOT 1 and JJA EOT 2 patterns compare well with EOF 1 and EOF 2 identified by Zhou and Yu (2005) (their Fig. 2). Their EOF patterns also peak in the southern and northern reaches of the Yangtze River valley, respectively. They associated EOF 1 with atmospheric circulation changes that included a southwestward extension of the subtropical high. While they did not make any connections with SSTs, their circulation changes (their Fig. 4) are consistent with Fig. 7. Based on circulation changes associated with both EOFs, Zhou and Yu (2005) hypothesized that they may be associated with the Pacific-Japan/East-Asia-Pacific (PJ) teleconnection pattern, but did not test this hypothesis. The PJ teleconnection results from Rossby wave dispersion due to anomalous heating around the Philippines (Nitta 1987; Huang and Sun 1992). We searched for evidence for the PJ teleconnection in JJA EOT 2 by regressing OLR, atmospheric vorticity and wave activity flux fields as in Kosaka and Nakamura (2006). However, those regressions did not support the PJ pattern, which suggests that the EOF patterns in Zhou and Yu (2005) may have a different physical origin as well.
3.3 Spring
3.3.1 MAM EOT 1
MAM EOT 1 explains 20% of the total space-time variance with a peak in southeast China (Fig. 8a). During the positive phase, northeastward flow along the western side of an anomalous anticyclonic circulation in the tropical western Pacific transports additional moisture into south China (Fig. 9d). Furthermore, there are cold SST anomalies in the western tropical Pacific and warm SST anomalies in the central Pacific south of the equator. These areas also correspond to anomalously enhanced and suppressed convection, respectively (not shown).
Left correlations of MAM rainfall anomaly timeseries at each point with the EOT base point. The base point is marked by the black inverted triangle. Magenta lines identify regions where correlations are significant at the 5% level. Right the corresponding EOT timeseries (black) with their 11-year running averages (red)
The circulation in Fig. 9 strongly resembles the antisymmetric C-mode response to ENSO (Sect. 3.2.1; compare to Fig. 1b of Zhang et al. 2016). In addition, the area of significantly correlated coherent precipitation in Fig. 8a agrees very well with the area that experiences increased spring precipitation related to the C-mode (compare Fig. 5 in Zhang et al. 2016). To further support this hypothesis, we use the second principal component of surface wind over the tropical Pacific as an index for the C-mode (EOF analysis based on 1979–2016 data in 10\(^{\circ }\)S–10\(^{\circ }\)N, 100\(^{\circ }\)E–80\(^{\circ }\)W after applying a 6–120 days bandpass filter, data obtained from Zhang et al. 2016). The correlation coefficient of MAM EOT 1 with this index averaged over MAM is 0.56 with a confidence >99%. The evolution of SSTs, however, is different from Stuecker et al. (2015). Instead of a mature El Niño state in DJF, Fig. 9 shows warm SST anomalies in the eastern Pacific mostly south of the equator, and the MAM EOT 1 timeseries is not significantly correlated with Niño3.4 during any season. This suggests that the MAM precipitation variability does not project as strongly onto ENSO SST anomalies as it does on the ENSO-associated circulation. This is consistent with Zhang et al. (2016), who showed that there is little connection between DJF ENSO SSTs and spring precipitation over southeastern China, but that the impact of ENSO on precipitation over southeastern China is conveyed via the C-mode.
Regression maps of previous JJA, SON, DJF and simultaneous MAM sea surface temperatures and 850 hPa wind onto the normalized MAM EOT 1. Stippling indicates correlations that are significant at the 10% level. Green wind vectors indicate that at least one component of the horizontal wind vector is significant at the 10% level. Vectors are omitted for magnitudes <0.1 ms\(^{-1}\)
It must be noted that Stuecker et al. (2015) and Zhang et al. (2016) analyzed a period when the PDO was is a mostly positive phase. Wu and Mao (2016) showed that the PDO modulates the relationship between ENSO and MAM rainfall in south China. When ENSO and PDO are in phase rainfall anomalies in south China are strongly correlated with ENSO. In contrast, when ENSO and PDO are out of phase, the relationship between ENSO and precipitation over China weakens or becomes insignificant. We quantified the influence of the PDO on MAM EOT 1 by computing the average phase (in units of standard deviations) of the EOT timeseries for the four combinations of PDO and ENSO phases, based on the years listed in Table 1 of Wu and Mao (2016). We find values of 0.45 for El Niño-PDO+ (9 years), –0.43 for El Niño-PDO− (10 years), 0.00 for La Niña-PDO+ (8 years) and –0.38 for La Niña-PDO− (7 years). This is consistent with the findings in Wu and Mao (2016); it could explain why the relationship between the Niño3.4 index and MAM EOT 1 differs from Stuecker et al. (2015) and Xie and Zhou (2017).
3.3.2 MAM EOT 2
MAM EOT 2 peaks in the Yangtze valley region with variability of opposite phase in parts of northwest China and south China (Fig. 8b). It explains 8% of the total space–time variance and is associated with upper-tropospheric geopotential perturbations in the high and midlatitudes (Fig. 10a). The upper-level trough extending from Kazakhstan to north China, combined with a band of increased pressure extending from south China into the North Pacific, creates significant upper-level divergence over the Yangtze River, and convergence over the coastline of south China (Fig. 10b). Vectors of vertically integrated moisture flux indicate moisture convergence in the Yangtze valley. The direction of this flow is consistent with the upper-tropospheric dynamics. The upper-level geopotential anomalies over China are part of a Rossby wave pattern of Atlantic origin, as can be seen from the zonal wavenumber-one Rossby wave ray (Fig. 10a). In the Atlantic significant warm SST anomalies are collocated with positive geopotential anomalies; cold SST anomalies are collocated with negative geopotential anomalies (not shown). The SST anomalies appear in the preceding autumn, but since the SST and geopotential anomalies are of the same sign we may suspect that the SST anomalies arise in response to the atmospheric motion and associated cloud cover, rather than forcing them. Nevertheless, the wavenumber-one Rossby wave ray in Fig. 10a originates in one of the hotspots of Rossby wave generation, as can be seen from the climatologically high variability of the RWS function off the east coast of the US (Fig. 10c). Therefore, the western North Atlantic is the most likely origin of the wave pattern associated with MAM EOT 2.
Regression maps of MAM 200 hPa eddy geopotential (GP) and 200 hPa wind (a), and 200 hPa divergence and vertically integrated moisture flux (b) onto the normalized MAM EOT 2. Colours show the regression slopes and stippling indicates correlations that are significant at the 10% level. Vectors are drawn when at least one component of the horizontal vector is significant at the 10% level. The rays of a zonal wavenumber-one Rossby wave from the location marked with a star are shown at 2-h intervals. The interannual standard deviation of the Rossby wave source function (RWS) is shown in c
3.3.3 MAM EOT 3
The spatial pattern of MAM EOT 3 includes large areas in eastern China except for the very south (Fig. 8c). It explains 7% of the total space–time variance and variability occurs mainly at periods of about 3 years. MAM EOT 3 is positively correlated with Niño3.4 in the previous autumn and winter (\(\rho\) = 0.32). Low OLR in the eastern tropical Pacific and significantly increased OLR over the Maritime Continent (Fig. 11a) indicate a decaying El Niño state. In the zonal band of 20\(^{\circ }\)–30\(^{\circ }\)N, increased 200 hPa geopotential occurs at the same longitudes as enhanced equatorial convection (low OLR), and reduced 200 hPa geopotential at the same longitudes as suppressed equatorial convection (high OLR) (Fig. 11b). Over the western Pacific and northwestern Africa at 20\(^{\circ }\)–40\(^{\circ }\)N there are significant positive and negative geopotential anomalies, which are indicative of anomalous descent and ascent of air, respectively, and hence anomalous upper-tropospheric convergence and divergence. Upper-tropospheric divergence or convergence can generate Rossby waves through the first term in Eq. (1). There are indeed statistically significant Rossby wave sources over the western Pacific and northwestern Africa at 20\(^{\circ }\)–40\(^{\circ }\)N (Fig. 11d), and we conclude that these are the source regions for the wave train that propagates at low latitudes along the subtropical westerly jet stream stretching from northwestern Africa into the North Pacific (Fig. 11d). At longitudes 0\(^{\circ }\)–100\(^{\circ }\)E wave flux remains confined southwards of 30\(^{\circ }\)N, consistent with the location of the wave guide (Fig. 11c). As can be seen in Fig 11b, both southeastward propagating waves from high latitudes and northeastward propagating waves from south China terminate over Korea and Japan in a region of high pressure, indicating blocking conditions. In addition, a center of low pressure is found over south China as part of this circumglobal geopotential pattern. The waves terminate in this region because the zonal group velocity is reduced near the jet exit as a consequence of the reduced zonal wind speed (Eq. 5). This process has been referred to as Rossby-wave blocking by Nakamura (1994) and as accumulation by Swanson (2000) and Enomoto et al. (2003). The resulting pressure distribution over East Asia creates a broad band of northward moisture flux into the region where EOT 3 peaks.
Regression maps of MAM, a outgoing longwave radiation (OLR) and vertically integrated moisture flux and b 200 hPa eddy geopotential (GP) and 200 hPa wave activity flux onto the normalized MAM EOT 3, c a map of the stationary Rossby wave number K computed as described in Sect. 2.4 and d regression of the 200 hPa Rossby wave source (RWS) function onto the normalized MAM EOT 3, showing only values that are significant at the 10% level. Colours in a, b show the regression slopes and stippling indicates correlations that are significant at the 10% level. Vectors in a are drawn when at least one component of the horizontal vector is significant at the 10% level. Wave activity flux vectors in b are omitted for magnitudes less than 0.3 m\(^2\)s\(^{-2}\). Contours in d show the 200 hPa zonal wind speed at intervals of 8 ms\(^{-1}\) averaged over the five most positive years of MAM EOT 3
3.4 Autumn
3.4.1 SON EOT 1
SON EOT 1 describes large areas in southeast China and explains 13% of the total space–time variance (Fig. 12a). Figure 13b shows that precipitation anomalies are associated with a circumglobal wave pattern in the northern hemisphere. Vectors of wave activity flux indicate eastward propagation following the wave guide in Fig. 13c. Areas of wave flux divergence can be found in many locations along the wave train, suggesting that there exist multiple source regions for the wave pattern associated with SON EOT 1. In fact, areas of divergent wave flux agree well with the climatological key source regions of Rossby waves (Fig. 13d). Locally, a high-pressure anomaly is visible both in Fig. 13b and in the lower tropospheric circulation southeast of China, Fig. 13a. This anomaly is associated with southerly flow into the areas of southeast China that experience increased rainfall.
Left correlations of SON rainfall anomaly timeseries at each point with the EOT base point. The base point is marked by the black inverted triangle. Magenta lines identify regions where correlations are significant at the 5% level. Right the corresponding EOT timeseries (black) with their 11-year running averages (red)
Regression maps of a 850 hPa wind >0.2 ms\(^{-1}\), and b SON 200 hPa eddy geopotential (GP) and 200 hPa wave activity flux onto the normalized SON EOT 1. c A map of the stationary Rossby wave number K computed as described in Sect. 2.4, and d the interannual standard deviation of the Rossby wave source function (RWS); colours in a, b show the regression slopes and stippling indicates correlations that are significant at the 10% level. Wave activity flux vectors in b are omitted for magnitudes less than 0.3 m\(^2\)s\(^{-2}\). Wind vectors in violet colour indicate that at least one component of the horizontal vector is significant at the 10% level
3.4.2 SON EOT 2
The base point of SON EOT 2 is located near the coast of southern China. It explains 9% of the total rainfall variability, with decreasing correlations away from the coast. Figure 14a shows anomalously high OLR in the western tropical Pacific, indicating suppressed convection. A high-pressure anomaly exists east of the Philippines (not shown), associated with an anticyclonic circulation and southerly onshore winds into the region described by SON EOT 2 (Fig. 14a). Furthermore, the region of coherent rainfall is located below the right-hand entrance region of a 200 hPa jet stream anomaly, creating upper-level divergence over the northern portion of the peak region of SON EOT 2 (Fig. 14b). This may support increased vertical motion and further increase the northward lower-tropospheric winds.
Regression maps of a SON outgoing longwave radiation and 850 hPa wind and b 200 hPa divergence and wind onto the normalized SON EOT 2. Colours show the regression slopes and stippling indicates correlations that are significant at the 10% level. Wind vectors are drawn when at least one component of the horizontal vector is significant at the 10% level
4 Discussion
The EOT analysis method used in this study identifies the spatial point that best explains the temporal variability in area-averaged precipitation (or in area-averaged residual precipitation for higher orders) over China. This has several implications. First, all identified patterns peak in the eastern part of the country because these areas have the greatest precipitation and hence dominate the area-averaged rainfall and its variability, as can also be seen from Fig. 1. The fact that there is little covariability with the western part of China implies that precipitation in the west responds to different processes to precipitation in the east. Secondly, all results are domain-dependent because adding or removing regions with large precipitation variability would change the domain-averaged rainfall anomaly timeseries; different patterns could have been found had we chosen a broader East Asian domain or restricted the domain to include only a fraction of China. Thirdly, EOT spatial patterns are dominated by positive correlations due to the high covariance between the base point and points in the surrounding region.
It is instructive to compare EOT to EOF analysis, as the latter is a frequently used method for diagnosing causes of precipitation variability. The first two points above apply to EOF analysis as well, but EOT and EOF analysis differ with respect to the third. EOF analysis seeks to maximize the explained space-time variance. This is partly achieved by maximizing the area of coherent variability, which often results in spatial dipole- or tripole patterns (e.g., as in Zhao and Fu 2006; Wang and Feng 2011; Huang et al. 2011b, 2012). EOTs, on the other hand, are constrained to be orthogonal only in time, and by choosing this technique we searched for the regions in China that best explain the temporal variability in the domain-averaged rainfall. As expected from mathematical arguments, there is good agreement between the methods when the EOF spatial patterns are monopoles, i.e. when the variability is of the same sign everywhere. This can be seen by comparing our leading DJF EOT to the leading DJF EOF in Wang and Feng (2011), as well as by comparing our two leading JJA EOTs to the corresponding EOFs of Zhou and Yu (2005).
Previous studies have classified the spatial distribution of JJA rainfall anomalies over eastern China into three patterns, as was first proposed by Liao et al. (1981). The three patterns are characterized by (I) positive rainfall anomalies north of the Yellow River, (II) between the Yangtze Basin and the Yellow River, and (III) in and south of the Yangtze Basin, respectively (e.g., Fig. 1 in Shi et al. 2009). An increased occurrence of Pattern III and decreased occurrences of Patterns I and II in recent decades have created a ’South Flood and North Drought’ pattern (Shi et al. 2009; Zhao and Feng 2014). Our EOT 1 and EOT 2 correspond well to Patterns III and II, respectively, but we do not expect our EOT method to identify Pattern I for two reasons. First, as was shown by Zhou and Yu (2005) in their EOF analysis, Pattern I only explains 6.7% of the space-time variance, compared to 16.3 and 12.4% for the leading two modes; it is not well separated from other EOFs according to North’s rule of thumb (North et al. 1982). Since the EOT method does not seek to maximize the explained space-time variance, it is unlikely that Pattern I would show up as one of the leading EOTs. Secondly, the EOT method can identify several patterns inside a region of high variance, since the EOT patterns are not orthogonal in space. Because JJA precipitation variability is large in southeast China (Fig. 1c), most EOTs are located there and not in the Yellow River.
We chose EOT analysis over other methods for two reasons. First, it is mathematically less constrained, which facilitates the interpretation of the EOT timeseries and patterns; in studying the first-order impacts of dynamical mechanisms on precipitation variability, we can focus on specific locations, i.e. the EOT base points. Using our analysis of observations as a benchmark to assess general circulation models will benefit from this simplification. Secondly, from an operational predictional point, it appears plausible that information about regions with high and coherent variability could be more useful than knowledge about patterns that maximize variance in space and time. For example, a confident prediction of flooding in the Yangtze valley and surrounding areas could be more useful than predicting simultaneous wet conditions in the Yangtze valley and dry conditions somewhere else. Focusing on coherent regional patterns is also helpful for investigating the causes of fluctuations and trends in the regional hydrological cycle.
With regard to connecting precipitation variability to large-scale circulation patterns, we can conclude that EOT and EOF analysis are equally successful. For the above-mentioned patterns in DJF and JJA where a direct comparison to EOF analysis was possible, we were able to support previously reported links and contribute additional information.
To investigate the potential for predicting precipitation variability based on rainfall in previous seasons or years, we computed lead-lag correlations between all EOTs. Only three lead-lag correlations and three autocorrelations, with correlation coefficients between −0.29 and −0.36, exist amongst all EOT timeseries. This lack of useful relationships between EOT timeseries highlights the importance of understanding what causes precipitation variability from a physical perspective, as there is no potential to predict precipitation variability in China based on observed precipitation in previous seasons or years. The origin of this problem is that neither the large-scale drivers of precipitation variability, i.e. modes of climate variability, nor regional atmospheric or coupled atmosphere–ocean processes, exhibit a single, consistent period. In addition, even in cases where an EOT pattern could be connected with a particular local or large-scale feature, there are additional processes that can interfere to influence the precipitation response. And lastly, unlike modes of large-scale variability, rainfall is inherently a local phenomenon.
5 Summary
Using Empirical Orthogonal Teleconnection analysis, we identified the dominant regions of coherent interannual variability in seasonal precipitation in China, and linked that variability to large-scale and regional mechanisms. Table 1 lists the geographic regions, percentages of total explained space–time variance, magnitudes of variability, and key features for each EOT. A summary of the main results follows.
Our analysis technique successfully reproduced robust known relationships to the El Niño Southern Oscillation, which include that winter precipitation variability in large parts of eastern China is mainly driven by ENSO, with increased precipitation during El Niño and reduced precipitation during La Niña (Figs. 3a, 4). Furthermore, we discovered that winter rainfall variability along the southeast coast of China is associated with anomalous convection over the tropical eastern Atlantic and communicated to China through a zonal wavenumber-three Rossby wave (Figs. 3b, 5). During the wet phase, a positive pressure anomaly over Japan forces anomalous westward onshore flow.
Key regions for summer precipitation variability are found along the Yangtze River (Fig. 6). Rainfall variability in the southern reaches of the Yangtze River lags ENSO (Fig 7), and the associated circulation appears to be closely connected with the feedback loops shown in Fig. 12 of Stuecker et al. (2015) and Fig. 9 of Xie and Zhou (2017), and involve the C-mode response to ENSO (Stuecker et al. 2013, 2015). Wet summer conditions in the northern areas of the Yangtze region are associated with a local pressure anomaly over south China with increased lower-tropospheric westerlies along the Yangtze River.
Precipitation variability in southeast China during spring is highly correlated with the C-mode (Figs. 8a, 9), as had previously been reported by Zhang et al. (2016). Our results for the other key regions of coherent spring rainfall variability are new: a lagged relationship with ENSO SSTs is found for the northern parts of eastern China: rainfall is enhanced when a dipole of high pressure over the Korean peninsula and low pressure over southern China channels moisture northwestwards (Figs. 8c, 11). Spring rainfall variability in the Yangtze region is related to upper-tropospheric midlatitude perturbations with associated upper-level divergence over the Yangtze River. These anomalies over China are part of a Rossby wave pattern with its origin in the North Atlantic (Figs. 8b, 10).
Our results for autumn are new as well: a circumglobal wave pattern in the northern hemisphere is associated with precipitation variability in large areas of eastern China centred around the Yangtze–Huaihe River basin during autumn (Figs. 12a, 13). Locally, increased southerly flow into southeast China occurs during phases of increased precipitation. The coastal area of southern China is affected by the circulation response to anomalous convection in the tropical western Pacific. Enhanced onshore flow is key for increased precipitation during autumn (Figs. 12b, 14).
In Sect. 4 we argued that a direct comparison to previous studies that used EOF analysis is possible when EOF spatial patterns are dominated by variability of the same sign. Our EOT regions and their associated local and large-scale circulation patterns in DJF and JJA are consistent with studies by Wang and Feng (2011) and Zhou and Yu (2005), for which such a comparison was possible. This shows that the EOT method is a robust analysis technique. Unlike previous studies, which mainly focused on DJF and JJA, we report results for all seasons, and patterns of regional rainfall variability that are tied to specific locations in China. This simplification is useful for understanding the drivers of interannual variability in the regional hydrological cycle, and allows our analysis of observations to serve as a benchmark for assessing general circulation models.
References
Barriopedro D, Gouveia CM, Trigo RM, Wang L (2012) The 2009/10 drought in China: possible causes and impacts on vegetation. J Hydrometeorol 13:1251–1267. doi:10.1175/JHM-D-11-074.1
Chan JCL, Li C (2004) The East Asia winter monsoon. World Sci Ser Meteorol East Asia 2:54–106
Chen G, Huang R (2014) Excitation mechanisms of the teleconnection patterns affecting the July precipitation in northwest China. J Clim 25:7834–7851. doi:10.1175/JCLI-D-11-00684.1
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137:553–597
Enomoto T, Hoskins BJ, Matsuda Y (2003) The formation mechanism of the Bonin high in August. Q J R Meteorol Soc 129:157–178
Fu CB, Teng XL (1988) Relationship between summer climate in China and El N ino/Southern Oscillation phenomenon. Chin J Atmos Sci 12:133–141 (in Chinese)
Gill AE (1980) Some simple solutions for heat-induced tropical circulation. Q J R Meteorol Soc 106:447–462. doi:10.1002/qj.49710644905
Gu L, Wei K, Huang RH (2008) Severe disaster of blizzard, freezing rain and low temperature in January 2008 in China and its association with the anomalies of East Asian monsoon system. Clim Environ Res 13:405–418 (in Chinese)
Hamada A, Arakawa O, Yatagai A (2011) An automated quality control method for daily rain-gauge data. Glob Environ Res 15:183–192
Hamada JI, Yamanaka M, Matsumoto J, Fukao S, Winarso P, Sribimawati T (2002) Spatial and temporal variations of the rainy season over Indonesia and their link to ENSO. J Meteorol Soc Jpn 80:285–310
Harrison DE, Larkin NK (1996) The COADS sea level pressure signal: a near-global El Nino composite and time series view, 1946–1993. J Clim 9:3025–3055. doi:10.1175/1520-0442(1996)009,3025:TCSLPS.2.0.CO;2
Hoskins BJ, Karoly DJ (1981) The steady linear response of a spherical atmosphere to thermal and orographic forcing. J Atmos Sci 38:1179–1196. doi:10.1175/1520-0469(1981)038,1179:TSLROA.2.0.CO;2
Huang RH, Chen JL, Liu Y (2011b) Interdecadal variation of the leading modes of summertime precipitation anomalies over Eastern China and its association with water vapor transport over East Asia. Chin J Atmos Sci 35:589–606. doi:10.1029/2009JD011733
Huang RH, Chen JL, Wang L, Lin ZD (2012) Characteristics, processes, and causes of the spatio-temporal variabilities of the East Asian monsoon system. Adv Atmos Sci 29:910–942. doi:10.1007/s00376-012-2015-x
Huang RH, Liu Y, Wang L, Wang L (2012b) Analyses of the causes of severe drought occurred in Southwest China from the fall of 2009 to the spring to 2010. Chin J Atmos Sci 36:443–457 (in Chinese)
Huang RH, Sun FY (1992) Impacts of the tropical western Pacific on the East Asian summer monsoon. J Meteorol Soc Jpn 70:243–256. doi:10.1029/2009JD011733
Huang RH, Wu YF (1989) The influence of ENSO on the summer climate change in China and its mechanism. Adv Atmos Sci 6:21–32
Huang RH, Xu YH, Wang PF, Zhou LT (1998) The features of the catastrophic flood over the Changjiang river basin during the summer of 1998 and cause exploration. Clim Environ Res 3:300–313 (in Chinese)
Huang RH, Xu YH, Zhou LT (1999) The interdecadal variation of summer precipitations in China and the drought trend in North China. Plateau Meteorol 18:465–476 (in Chinese)
Huang RH, Zhou LT (2002) Research on the characteristics, formation mechanism and prediction of severe climatic disasters in China. J Nat Disasters 1:910–942 (in Chinese)
Ji LR, Shuqing S, Arpe K, Bengtsson L (1997) Model study on the interannual variability of Asian winter monsoon. Adv Atmos Sci 14:1–22
King AD, Klingaman NP, Alexander LV, Donat MG, Jourdain NC, Maher P (2014) Extreme rainfall variability in Australia: patterns, drivers, and predictability. J Clim 27:6035–6050. doi:10.1175/JCLI-D-13-00715.1
Klingaman NP, Woolnough SJ, Syktus J (2013) On the drivers of inter-annual and decadal rainfall variability in Queensland. Aust Int J Clim 33:2413–2430. doi:10.1002/joc.3593
Kosaka Y, Nakamura H (2006) Structure and dynamics of the summertime Pacific-Japan teleconnection pattern. Q J R Meteorol Soc 132:2009–2030. doi:10.1256/qj.05.204
Krishnamurti TN, Mishra AK, Simon A, Yatagai A (2009) Use of a dense rain-gauge network over India for improving blended TRMM products and downscaled weather models. J Meteorol Soc Jpn 87A:393–412. doi:10.2151/jmsj.87A.393
Lau N-C, Nath MJ (2006) ENSO modulation of the interannual and intraseasonal variability of the East Asian monsoon-A model study. J Clim 19:4508–4530. doi:10.1175/JCLI3878.1
Liao QS, Chen GY, Chen GZ (1981) Collection of long time weather forecast. Meteorological Press, Beijing, pp 103–114 (in Chinese)
Liebmann B, Smith CA (1996) Description of a complete (interpolated) outgoing longwave radiation dataset. Bull Am Meteorol Soc 77:1275–1277
Lu R-Y, Oh J-H, Kim B-J (2002) A teleconnection pattern in upper-level meridional wind over the North African and Eurasian continent in summer. Tellus 54A:44–55
Matsuno T (1966) Quasi-geostrophic motion in the equatorial area. J Meteorol Soc Jpn 44:25–43
Nakamura H (1994) Rotational evolution of potential vorticity associated with a strong blocking configuration over Europe. Geophys Res Lett 21:2003–2006
Nitta T (1987) Convective activities in the tropical western Pacific and their impact on the Northern Hemisphere summer circulation. J Meteorol Soc Jpn 65:373–390
North GR, Bell TL, Cahalan RF, Moeng FJ (1982) Sampling errors in the estimation of empirical orthogonal functions. Mon Weather Rev 110:699–706
Rajeevan M, Bhate J (2009) A high resolution daily gridded rainfall dataset (1971–2005) for mesoscale meteorological studies. Curr Sci 96:558–562. doi:10.1175/JHM-D-11-074.1
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophy Res 108(4407):37. doi:10.1029/2002JD002670
Rotstayn LD, Collier MA, Dix MR, Feng Y, Gordon HB, O’Farrell SP, Smith IN, Syktus J (2010) Improved simulation of Australian climate and ENSO-related rainfall variability in a global climate model with an interactive aerosol treatment. Int J Climatol 30:1067–1088
Sardeshmukh PD, Hoskins BJ (1988) The generation of global rotational flow by steady idealized tropical divergence. J Atmos Sci 45:1228–1251. doi:10.1175/1520-0469(1988)045<1228:TGOGRF>2.0.CO;2
Scaife AA, Comer RE, Dunstone NJ, Knight JR, Smith DM, MacLachlan C (2016) Tropical rainfall Rossby waves and regional winter climate predictions. Q J R Meteorol Soc. doi:10.1002/qj.2910
Shi Y, Wang Y-G, Giorgi F (2009) Simulation and projection of monsoon rainfall and rain patterns over eastern China under global warming by RegCM3. Atmos Ocean Sci Lett 2:308–313. doi:10.1080/16742834.2009.11446816
Smith I (2004) An assessment of recent trends in Australian rainfall. Aust Meteorol Mag 53:163–73
Stephan CC, NP Klingaman, PL Vidale, AG Turner, M-E Demory, L Guo (2017) A comprehensive analysis of coherent rainfall patterns in China and potential drivers. Part II: Intraseasonal variability. Climate Dyn (under review)
Stuecker MF, Jin F-F, Timmermann A, McGregor S (2015) Combination mode dynamics of the anomalous northwest Pacific anticyclone. J Clim 28:1093–1111. doi:10.1175/JCLI-D-14-00225.1
Stuecker MF, Timmermann A, Jin F-F, McGregor S, Ren H-L (2013) A combination mode of the annual cycle and the El Nino/Southern Oscillation. Nat Geosci 6:540–544. doi:10.1038/ngeo1826
Swanson KL (2000) Stationary wave accumulation and the generation of low frequency variability on zonally varying flows. J Atmos Sci 57:2262–2280
Takaya K, Nakamura H (2001) A formulation of phase-independent wave-activity flux for stationary and migratory quasigeostrophic eddies on a zonally varying basic flow. J Atmos Sci 57:608–627
Tao G, Yu J-Y, Paek H (2016) Impacts of four northern-hemisphere teleconnection patterns on atmospheric circulations over Eurasia and the Pacific. Theor Appl Climatol. doi:10.1007/s00704-016-1801-2
Tomita T, Yasunari T (1996) Role of the northeast winter monsoon on the biennial oscillation of the ENSO/monsoon system. J Meteorol Soc Jpn 74:399–413
Van den Dool HM, Saha S, Johansson A (2000) Empirical orthogonal teleconnections. J Clim 13:1421–1435. doi:10.1175/1520-0442(2000)013<1421:EOT>2.0.CO;2
Wang B, Wu R, Fu X (2000) Pacific-East Asian teleconnection: how does ENSO affect East Asian climate? J Clim 13:1517–1536. doi:10.1175/1520-0442(2000)013,1517:PEATHD.2.0.CO;2
Wang B, Zhang Q (2002) Pacific-East Asian teleconnection. Part II: How the Philippine Sea anomalous anticyclone is established during El Nino development. J Clim 15:3252–3265. doi:10.1175/1520-0442(2002)015,3252:PEATPI.2.0.CO;2
Wang L, Feng J (2011) Two major modes of wintertime precipitation over China. Chin J Atmos Sci 35:1105–1116. doi:10.1175/JCLI-D-15-0105.1 (in Chinese)
Wang LW, Chen W, Huang RH (2008) Interdecadal modulation of PDO on the impact of ENSO on the east Asian winter monsoon. Geophys Res Lett. doi:10.1029/2008GL035287
Wu J, Gao XJ (2013) A gridded daily observation dataset over China region and comparison with the other datasets. Chin J Geophys 56:1102–1111. doi:10.6038/cig20130406
Wu R, Hu ZZ (2003) Evolution of ENSO-related rainfall anomalies in East Asia. J Clim 16:3742–3758. doi:10.1175/1520-0442(2003)016,3742:EOERAI.2.0.CO;2
Wu X, Mao J (2016) Interdecadal modulation of ENSO-related spring rainfall over South China by the Pacific Decadal Oscillation. Clim Dyn 47:3203–3220. doi:10.1007/s00382-016-3021-y
Wu Z, Wang B, Li J, Jin F-F (2009) An empirical seasonal prediction model of the East Asian summer monsoon using ENSO and NAO. J Geophys Res. doi:10.1029/2009JD011733
Xie SP, Hu K, Hafner J, Tokinaga H, Du Y, Huang G, Sampe T (2009) Indian Ocean capacitor effect on Indowestern Pacific climate during the summer following El Nino. J Clim 22:730–747. doi:10.1175/2008JCLI2544.1
Xie S-P, Zhou Z-Q (2017) Seasonal modulations of El Nino-related atmospheric variability: Indo-western Pacific ocean feedback. J Clim 30:3461–3774. doi:10.1175/JCLI-D-16-0713.1
Yang J, Liu Q, Xie SP, Liu Z, Wu L (2007) Impact of the Indian Ocean SST basin mode on the Asian summer monsoon. Geophys Res Lett. doi:10.1029/2006GL028571
Yang XQ, Zhu YM (2008) Interdecadal climate variability in China associated with the Pacific Decadal Oscillation, vol 15. Springer, Berlin, pp 97–118
Yatagai A, Kamiguchi K, Arakawa O, Hamada A, Yasutomi N, Kitoh A (2012) APHRODITE: Constructing a long-term daily gridded precipitation dataset for Asia based on a dense network of rain gauges. Bull Am Meteorol Soc 93:1401–1415. doi:10.1175/BAMS-D-11-00122.1
Zhang RH, Huang RH (1998) Dynamical roles of zonal wind stresses over the tropical Pacific on the occurring and vanishing of El Nino. Part I: Diagnostic and theoretical analyses. Chin J Atmos Sci 22:587–599 (in Chinese)
Zhang RH, Sumi A, Kimoto M (1996) Impact of El Nino on the East Asian monsoon: a diagnostic study of the 86/87 and 91/92 events. J Meteorol Soc Jpn 74:49–62
Zhang W, Jin F-F, Turner A (2014) Increasing autumn drought over southern China associated with ENSO regime shift. Geophys Res Lett 41:4020–4026. doi:10.1002/2014GL060130
Zhang W, Li H, Stuecker MF, Jin F-F, Turner AG (2016) A new understanding of El Nino’s impact over East Asia: dominance of the ENSO Combination Mode. J Clim 29:4347–4359. doi:10.1175/JCLI-D-15-0104.1
Zhang Y, Wallace JM, Battisti DS (1997) ENSO-like interdecadal variability: 1900–93. J Clim 10:1004–1020. doi:10.1175/1520-0442(1997)010<1004:ELIV>2.0.CO;2
Zhao J, Feng G (2014) Reconstruction of conceptual prediction model for the Three Rainfall Patterns in the summer of eastern China under global warming. Sci China Earth Sci 57:3027–3061. doi:10.1007/s11430-014-4930-4
Zhao T, Fu C (2006) Comparison of products from ERA-40, NCEP-2, and CRU with station data for summer precipitation over China. Adv Atmos Sci 23:593–694. doi:10.1007/s00376-006-0593-1
Zhou T-J, Yu R-C (2005) Atmospheric water vapor transport associated with typical anomalous summer rainfall patterns in China. J Geophys Res. doi:10.1029/2004JD005413
Acknowledgements
The authors thank the two anonymous reviewers for their constructive comments to improve the manuscript. This work and its contributors (Claudia Christine Stephan, Pier Luigi Vidale, Andrew Turner, Marie-Estelle Demory and Liang Guo) were supported by the UK-China Research and Innovation Partnership Fund through the Met Office Climate Science for Service Partnership (CSSP) China as part of the Newton Fund. Nicholas Klingaman was supported by an Independent Research Fellowship from the Natural Environment Research Council (NE/L010976/1). APHRODITE data are available from http://www.chikyu.ac.jp/precip/. OLR data are provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, at http://www.esrl.noaa.gov/psd/. The Rossby wave source function was computed using code from the python package windspharm v1.5.0 available at http://ajdawson.github.io/windspharm. We thank Dr. Wenjun Zhang for providing us with the results of EOF analysis on equatorial surface winds. We are also grateful to Prof. Adam Scaife, Dr. Edwin Gerber, Prof. Oliver Bühler and Dr. Nick Dunstone for helpful discussions regarding Rossby wave ray tracing.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Stephan, C.C., Klingaman, N.P., Vidale, P.L. et al. A comprehensive analysis of coherent rainfall patterns in China and potential drivers. Part I: Interannual variability. Clim Dyn 50, 4405–4424 (2018). https://doi.org/10.1007/s00382-017-3882-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3882-8