Abstract
The Madden-Julian Oscillation (MJO) simulation diagnostics developed by MJO Working Group and the process-oriented MJO simulation diagnostics developed by MJO Task Force are applied to 37 Coupled Model Intercomparison Project phase 5 (CMIP5) models in order to assess model skill in representing amplitude, period, and coherent eastward propagation of the MJO, and to establish a link between MJO simulation skill and parameterized physical processes. Process-oriented diagnostics include the Relative Humidity Composite based on Precipitation (RHCP), Normalized Gross Moist Stability (NGMS), and the Greenhouse Enhancement Factor (GEF). Numerous scalar metrics are developed to quantify the results. Most CMIP5 models underestimate MJO amplitude, especially when outgoing longwave radiation (OLR) is used in the evaluation, and exhibit too fast phase speed while lacking coherence between eastward propagation of precipitation/convection and the wind field. The RHCP-metric, indicative of the sensitivity of simulated convection to low-level environmental moisture, and the NGMS-metric, indicative of the efficiency of a convective atmosphere for exporting moist static energy out of the column, show robust correlations with a large number of MJO skill metrics. The GEF-metric, indicative of the strength of the column-integrated longwave radiative heating due to cloud-radiation interaction, is also correlated with the MJO skill metrics, but shows relatively lower correlations compared to the RHCP- and NGMS-metrics. Our results suggest that modifications to processes associated with moisture-convection coupling and the gross moist stability might be the most fruitful for improving simulations of the MJO. Though the GEF-metric exhibits lower correlations with the MJO skill metrics, the longwave radiation feedback is highly relevant for simulating the weak precipitation anomaly regime that may be important for the establishment of shallow convection and the transition to deep convection.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Madden-Julian oscillation (MJO) is the dominant mode of tropical intraseasonal variability, and is characterized by eastward-propagating, planetary-scale envelops of convective cloud clusters that are tightly coupled with the large-scale wind field. It is distinguished from other convectively coupled equatorial disturbances by its large spatial extent and low frequency (zonal wavenumbers 1–3 and 30–90 days period). The MJO interacts with a wide range of tropical weather and climate phenomena that include the onset and break of monsoons (Yasunari 1979, 1980; Lau and Chan 1986; Hendon and Liebmann 1990; Sperber et al. 2000; Sultan et al. 2003; Annamalai and Sperber 2005; Wheeler and McBride 2005; Lorenz and Hartmann 2006; Wheeler et al. 2009), tropical cyclone activity (Nakazawa 1988; Liebmann et al. 1994; Maloney and Hartmann 2000; Bessafi and Wheeler 2006; Klotzbach 2010; Jiang et al. 2012), and the El Niño Southern Oscillation (Kessler et al. 1995; McPhaden 1999; Takayabu et al. 1999; Kessler and Kleeman 2000; Bergman et al. 2001; Kessler 2001; Zhang and Gottschalck 2002; Hendon et al. 2007). The MJO also influences mid- and high-latitudes through atmospheric teleconnections (Weickmann et al. 1985; Ferranti et al. 1990; Berbery and Nogués-Paegle 1993; Higgins and Mo 1997; Matthews et al. 2004; Vecchi and Bond 2004; Cassou 2008; L’Heureux and Higgins 2008; Lin et al. 2009; Johnson and Feldstein 2010; Seo and Son 2011; Garfinkel et al. 2012; Guan et al. 2012; Yoo et al. 2012; Henderson et al. 2016; Mundhenk et al. 2016).
Despite the important role of the MJO in the weather-climate system, our understanding of the fundamental mechanism of the MJO is incomplete (e.g., Zhang 2005; Wang 2005; Maloney and Zhang 2016). The lack of understanding of MJO dynamics suggests that the community has been unable to guide modelers to improve the MJO simulation by highlighting key processes responsible for good MJO simulations. Without the critical processes being identified, simulation of a realistic MJO has remained a challenging task for most general circulation models (GCMs) (Slingo et al. 1996; Waliser et al. 2003; Sperber et al. 2005; Lin et al. 2006; Kim et al. 2009; Hung et al. 2013; Jiang et al. 2015). For example, Hung et al. (2013) compared 20 CMIP5 models with 14 CMIP3 models’ results evaluated by Lin et al. (2006) and showed that the CMIP5 models exhibit an overall modest improvement over the CMIP3 models in the simulation of the MJO and several convectively coupled equatorial waves (CCEWs). However, many GCMs exhibit shortcomings in representing the realistic MJO variance and eastward propagation. Jiang et al. (2015) showed that only about one-fourth of the 27 GCM simulations participating in the Working Group on Numerical Experimentation MJO Task Force (MJOTF)/GEWEX Atmospheric System Study (GASS) MJO global model comparison project were able to simulate eastward propagation and the associated tilted vertical structure of the MJO. Thus, the majority of GCMs continue to exhibit shortcomings in representing a realistic MJO. However, the cause of these shortcomings is still elusive. To this end, various MJO skill metrics and process-oriented MJO diagnostics are applied to evaluate the 37 CMIP5 models in order to assess and highlight model processes that help distinguish the quality of MJO simulations.
To facilitate evaluation of model performance and tracking of model improvement, the CLIVAR MJO Working Group (MJOWG) developed a diagnostics package (MJOWG 2009) that can be used to evaluate GCMs’ MJO representation in a standardized way. When applied to GCM simulations, the diagnostic package enables modelers to objectively gauge their models’ strengths and weaknesses in representing the MJO. The diagnostics package has been widely used by the climate modeling community (Kim et al. 2009; Liu et al. 2009; other references).
The first objective of the current study is to assess the performance of the GCMs that participated in the CMIP5 through use of the MJO simulation diagnostics package. The focus of the evaluation is on the fundamental features of the simulated MJO—amplitude, period, and coherent eastward propagation. More than one diagnostic is used for a particular attribute (e.g., amplitude of the MJO) to test the consistency among different diagnostics that aim to characterize a model’s fidelity at capturing the same feature of the MJO. Scalar metrics are derived from select diagnostics for a quantitative comparison between models and observations.
While GCM simulations of the MJO have largely remained at an unsatisfactory level in multi-model intercomparison studies, it has been continuously demonstrated that MJO simulation can be improved by making appropriate changes to parameterizations, especially that of cumulus convection (Tokioka et al. 1988; Wang and Schlesinger 1999; Maloney and Hartmann 2001; Lin et al. 2008; Zhang and Song 2009; Hannah and Maloney 2011; Kim and Kang 2012; Kim et al. 2012), as summarized in Kim and Maloney (2017). However, the knowledge and experience from these studies have not been fully utilized in operational versions of climate and NWP models, possibly because the methods that improve the MJO often degrade other aspects of model simulation, such as the mean state (e.g., Kim et al. 2011). These deficiencies reflect continued shortcomings in our parameterizations relevant to MJO simulation.
This gap between parameterization development and improving model performance motivated the recent development of the ‘process-oriented’ MJO simulation diagnostics by the MJOTF and others (Maloney 2009; Kiranmayi and Maloney 2011; Andersen and Kuang 2012; Kim et al. 2014, 2015; Benedict et al. 2014; Chikira 2014; Hannah and Maloney 2014; Arnold and Randall 2015; Klingaman et al. 2015a, b; Xavier et al. 2015; Wolding and Maloney 2015; Wolding et al. 2016). These process-oriented diagnostics are designed to characterize resolved-scale processes that are strongly affected by certain aspects of parameterization schemes, and that are relevant to MJO dynamics. The tight connection to parameterizations distinguishes the process-oriented diagnostics from ‘conventional’ diagnostics, such as simple characterization of the mean state. By applying these process-oriented diagnostics, modelers can obtain guidance into where further parameterization development is necessary.
Thus, the second objective of the current study is to apply process-oriented MJO simulation diagnostics to the CMIP5 models. After deriving scalar metrics from the process-oriented diagnostics, we examine relationships between models’ MJO simulation skill and their representation of particular processes that are strongly affected by parameterized physics. Kim et al. (2014) presented the RHCP (Relative Humidity Composite based on Precipitation) diagnostic that indicates the sensitivity of simulated convection to low-level environmental moisture. They showed that the amount of 700–850 hPa RH increase required for a transition from weak to strong rain regimes had a robust statistical relationship with the East/West power ratio of equatorial precipitation (correlation coefficient is about 0.72 when 28 models are used). Benedict et al. (2014) presented the NGMS (Normalized Gross Moist Stability) diagnostic that indicates the efficiency of vertical advection in a convecting atmosphere to export Moist Static Energy (MSE) out of the column. In 6 GCM simulations that consist of 3-pairs of GCMs, each with a good and poor MJO, they found a tight relationship between the time-mean vertical component of the NGMS over the Indo-Pacific warm pool region and the East/West power ratio of equatorial precipitation (correlation coefficient is about −0.89). In addition, Jiang et al. (2015) also examined the relation between the time-mean vertical component of the GMS over the warm pool area and the East/West power ratio of equatorial precipitation using a different model dataset, and showed a weaker, but statistically significant relationship (correlation coefficient is about −0.36). Note that Benedict et al. (2014) and Jiang et al. (2015) used slightly different domains for their GMS calculations. Most recently, Kim et al. (2015) presented the GEF (Greenhouse Enhancement Factor) diagnostic that indicates the strength of anomalous column-integrated longwave radiative heating due to cloud-radiation interaction. The GEF in the weak precipitation anomaly regime (<5 mm day−1) showed a statistical relationship with the East/West power ratio of equatorial precipitation with a correlation coefficient of 0.58 (0.67) when 29 models (without one outlier model) are used.
This paper is organized as follows. The participating models and validation data are described in Sect. 2. The MJO simulation diagnostics and formulation of the MJO skill metrics are described in Sect. 3. Three process-oriented diagnostics are investigated and related to the MJO skill metrics in Sect. 4. A summary and discussion are presented in Sect. 5.
2 Participating models and validation datasets
The MJO is analyzed using 20 years (1985–2004) of daily mean data from the historical runs obtained from the CMIP5 data portal (http://pcmdi9.llnl.gov). The MJO simulation diagnostics are applied to 37 models, while the process-oriented diagnostics are applied to a subset of these models because of limited data availability. The model designation, host institution, convection scheme, and stratiform cloud scheme are given in Table 1. The reader is referred to Taylor et al. (2012) for a more detailed description of the CMIP5 models.
The CMIP5 models are validated against daily rainfall analyses from the Global Precipitation Climatology Project (GPCP; Huffman et al. 2001) for 1997–2010 and the Tropical Rainfall Measuring Mission (TRMM 3B42 version 6; Huffman et al. 2007) for 1998–2010, outgoing longwave radiation (OLR) from the Advanced Very High Resolution Radiometer (AVHRR; Liebmann and Smith 1996) for 1985–2004 and the Clouds and the Earth’s Radiant Energy System (CERES; Loeb et al. 2009) for 2001–2010, specific humidity, air temperature, geopotential height, pressure velocity from the ECMWF Reanalysis (ERA-interim; Dee et al. 2011) for 1985–2004, upper (250 hPa) and lower (850 hPa) tropospheric zonal winds (U250 and U850 hereafter) from the ECMWF Reanalysis and the NCEP–NCAR reanalysis (Kalnay et al. 1996) for 1985–2004. All participating models and validation datasets are interpolated onto 2.5° × 2.5° horizontal resolution and analyzed for the boreal winter (November–April).
3 MJO simulation diagnostics and MJO skill metrics
In this section, the MJO simulation diagnostics developed by MJOWG are applied to 37 CMIP5 models and MJO skill metrics are formulated to capture a model’s ability to simulate prominent features of the MJO, and report this ability in the form of a scalar. Statistical methods that have been employed to diagnose the realism of spatial and temporal scales and propagation characteristics of the MJO include (1) wavenumber-frequency power spectra (Hayashi 1982; Salby and Hendon 1994; Wheeler and Kiladis 1999), and (2) combined EOF (CEOF) analysis (Wheeler and Hendon 2004). These methods are components of the CLIVAR MJO simulation diagnostics (CLIVAR MJOWG 2009).
-
a.
Wavenumber-frequency power spectrum analysis
The wavenumber-frequency power spectrum analysis assesses the distribution of variance (i.e. power) in the wavenumber-frequency domain and provides a convenient diagnostic of planetary-scale structure and behavior of the MJO. Figure 1 shows the wavenumber-frequency power spectra and the “MJO band” (eastward propagating, periods of 30–60 days, and wavenumbers 1–3) averaged coherence-squared (coh2) of 10°S–10°N averaged precipitation (shaded) and U850 (contoured) obtained from observations and 37 CMIP5 models. The power spectra and coh2 were calculated for each year and then averaged over all years. The observed spectral power of precipitation and the U850 are concentrated at the MJO band, whereas most CMIP5 models show a diverse range of spectral power over a broader range of periods and wavenumbers. In observations, the consistency between the space–time characteristics of precipitation and U850 is clear (coh2 of observation is about 0.71), whereas most CMIP5 models show a lack of correspondence (the average coh2 across models is about 0.6).
November–April wavenumber-frequency power spectra of 10°S–10°N averaged precipitation (shaded) and 850 hPa zonal wind (contoured with 0.015 interval) and coh2 (texted on the upper right of each plot) averaged over MJO band (period 30–60 days and wavenumber 1–3). Power spectra and coh2 were calculated for each year and then averaged over all years of data. Units of power spectra for the precipitation and 850 hPa zonal wind are \(mm^{2} ~day^{{ - 2}}\) and \(m^{2} ~s^{{ - 2}}\) per frequency interval per wavenumber interval, respectively
For a quantitative evaluation of model simulations, four MJO simulation skill metrics are formulated from the wavenumber-frequency power spectra and the coh2. The first skill metric is obtained by dividing the sum of spectral power over the MJO band by that of its westward propagating counterpart. This metric, which is often called as the Eastward/Westward power ratio (E/W ratio hereafter), indicates the robustness of eastward propagating feature of the MJO (Zhang and Hendon 1997) and has been frequently used in observational (e.g., Zhang and Hendon 1997; Hendon et al. 1999) and modeling studies (e.g., Lin et al. 2006; Kim et al. 2009).
The observed E/W ratio is about 2.3, 4.0, 4.2, and 2.8 for precipitation, OLR, U850, and U250, respectively (Fig. 2a). This suggests that the observed MJO’s eastward propagation is more robust in OLR and U850 than that in precipitation and U250. Most CMIP5 models underestimate the E/W ratio of all variables, especially that of OLR. As an exception, CNRM-CM5 shows outstandingly strong E/W ratios compared to other models, with that of U850 (11.1) out of range in the figure. A majority of the models exhibit E/W ratios of U850 that are greater than that of other variables, consistent with the finding of Zhang et al. (2006). IPSL-CM5A-LR and IPSL-CM5B-LR are developed from same modeling center, but they exhibit substantially different E/W ratios, particularly in the wind fields (difference between two models is about 3.2 and all CMIP5 inter-model spread is about 2 for the U850 E/W ratio). The change in MJO performance across models from the same center could be related to impacts from changing parameterization schemes among model versions. IPSL-CM5A-LR and IPSL-CM5B-LR use different convection and stratiform cloud schemes (Table 1). Kim et al. (2015) attributed the stronger MJO in IPSL-CM5B-LR to the stronger cloud-longwave radiation feedback in that model, likely due to the difference in parameterization schemes.
a East/West power ratio (E/W ratio), b Normalized East power by observation (E/O ratio), c coh2 of precipitation with precipitable water and U850, and d dominant eastward period from the wavenumber-frequency power spectra (PWFPS). Closed squares, closed triangles, closed circles, and open circles indicate observations [GPCP (1997–2010), AVHRR (1985–2004), ERA-int (1985–2004)], additional observations [TRMM (1998–2010), CERES (2001–2010), NCEP1 (1984–2010)], multi-model means, and CMIP5 models, respectively. Vertical lines indicate inter-model spreads. Different color indicates each variable. The observed East powers for normalization of models are 0.02 \(mm^{2} ~day^{{ - 2}},\) 1.20 \(W^{2} ~m^{{ - 4}}\), 0.026 \(m^{2} ~s^{{ - 2}}\), and 0.10 \(m^{2} s^{{-2}}\) for the PRCP (GPCP), OLR (AVHRR), U850 and U250 (ERA-int), respectively. The value of CNRM-CM5’s E/W ratio of U850 (11.1) and E/O ratio of U850 (3.44) and U250 (2.33) are out of range in the figure
The second skill metric from the wavenumber-frequency power spectrum, which we refer to as the E/O ratio, is formulated by normalizing the sum of spectral power within the MJO band by the observed value. The observed values are 0.02 \(mm^{2} ~day^{{ - 2}}\), 1.20 \(W^{2} ~m^{{ - 4}}\), 0.026 \(m^{2} ~s^{{ - 2}}\), and 0.10 \(m^{2} ~s^{{ - 2}}\) for precipitation, OLR, U850, and U250, respectively. The use of the second metric is complementary to the E/W ratio and it is motivated by the possibility that a model with large E/W ratio could still exhibit unrealistically small eastward propagating power. Figure 2b shows that most CMIP5 models underestimate the E/O ratios, especially for variables that are more directly related to convection (precipitation and OLR). As for the E/W ratio, CNRM-CM5 shows an excessively strong E/O ratio compared to other models, with its E/O ratio of U850 (3.44) and U250 (2.33) off scale in the figure. Models that show superior skill in the E/O ratio also perform better in the E/W ratio. Table 2 shows the correlation coefficient between the E/W ratios and the E/O ratios among the models. The correlation coefficient is especially high for U850 (0.93) and U250 (0.96). The high correlation between the E/W ratio and E/O ratio suggests that the E/W ratio is well correlated with eastward propagation within MJO band. Thus, the E/W power ratio that has been used in many studies is a reasonable choice to assess how well a model captures the robust eastward propagation of the MJO.
The third skill metric is obtained by the MJO band averaged coh2 of precipitation with U850 and precipitable water. The observed values of the coh2 of precipitation with U850 and precipitable water are about 0.7 and 0.75, respectively. It indicates the strong coupling of precipitation with U850 and precipitable water. These results are consistent with those of Yasunaga and Mapes (2012) who also showed the coh2 of precipitation with precipitable water in observations. Most CMIP5 models underestimate the coh2 of precipitation with U850 and precipitable water. The CNRM-CM5, which simulated excessively strong E/W ratio and E/O ratio, shows larger coh2 than other models and even observations. Table 2 shows the correlation between coh2 and other MJO skill metrics. The coh2 between precipitation and U850 is well correlated with the E/W ratio and the E/O ratio of all variables, especially the E/O ratio of precipitation and U850 that have a correlation greater than 0.8.
For the fourth skill metric we estimate the MJO periodicity (PWFPS, Fig. 2d) by dividing the sum of power-weighted period (i.e. 1/frequency) by the sum of power over the period of 20–100 days and for each of these sums, considering only wavenumbers 1–3. In observations, the PWFPS obtained from the four variables used in this study ranges from 38 days (U250) to 42 days (U850). Some models (BCC-CSM1-1, BCC-CSM1-1-m, MIROC-ESM, MIROC-ESM-CHEM, and MIROC4h) exhibit shorter-than-observed periodicity across all four variables. These models also tend to show the E/W ratio and the E/O ratio that are smaller than that of other models. The CMCC model group (CMCC-CESM, CMCC-CM, CMCC-CMS) exhibits relatively large spread (~10 days) in PWFPS estimated from different variables, with longer and shorter periodicity in OLR and U250, respectively. Overall, PWFPS from U250 is shorter than those from other variables.
-
b.
CEOF analysis
In the CEOF analysis (Wheeler and Hendon 2004), a standard EOF analysis is performed using three variables—OLR, U850, and U200. Each variable is meridionally averaged and normalized individually before being merged. The use of the combined field is motivated by the observation that the large-scale convective and circulation anomalies are tightly coupled. In observations, the leading pair of CEOFs of intraseasonal (20–100-day bandpass filtered) anomalies explains more than 40% of total intraseasonal variability and represents an eastward propagation with periodicity of about 40 days.
We calculate the CEOFs using 15°S–15°N averaged 20–100-day band-pass filtered variables, following the protocol of the MJOWG (2009). This is slightly different from the original method used by Wheeler and Hendon (2004), who used unfiltered fields, since they were developing an approach useful for real-time monitoring and prediction. OLR, U850, and U250 (instead of U200) are used in the CEOF analysis because of limited data availability of the CMIP5 models. Nine models are excluded from the CEOF analysis because at least one of the three variables required was unavailable.
Figure 3 shows the first two CEOFs from the observations and models, noting that the sign and order of the model Eigen modes are adjusted to best match observations. In observations, the first (second) CEOF mode captures a convective signal (negative OLR) centered at about 90°E (130°E) with associated low-level convergence and upper-level divergence. Most CMIP5 models simulate reasonably well the first two CEOF patterns, especially the circulation anomalies (mean values of spatial correlation coefficients along longitude between observations and each model are about 0.67, 0.79 and 0.73 for the OLR, U850 and U250, respectively). The magnitude of the peak convective signal over the warm pool tends to be weaker in the models compared to observations (Fig. 3a, d). Figure 3g also shows the lead-lag correlation of first two CEOF principal component time series (PCs) formulated by projecting the unfiltered anomaly data onto the CEOF’s eigenvector. Because we use unfiltered anomalies to calculate PCs, it is not guaranteed that the PCs have intraseasonal time scales. If a model has variability of a shorter-than-intraseasonal time scale whose spatial patterns of OLR, U850, and U200 resemble that of the MJO, PCs and lag-correlation between them would show this shorter time scale. Thus, using unfiltered anomalies in the calculation of the PCs is a stricter test for GCMs than using filtered anomalies. In observations, the first CEOF mode (convection center over the Indian Ocean) leads the second CEOF mode (convection center over the west Pacific) by about 10 days, indicating the eastward propagation of MJO from Indian Ocean to Western Pacific. The models are in general able to capture the lead-lag relationship between the two leading modes, while they show large spread in values of maximum correlation, and the lag day at which the correlation maximizes. Most models simulate lower correlations between the leading PCs than observed.
First two Combined EOF’s of 15°S–15°N averaged 20–100-day OLR, U850, and U250. a–c are first mode, and d–f are second mode. Sign and order of each Eigen mode are adjusted to be similar to observation. The values on the upper right of each plot indicate the mean of correlation coefficients between observation and each model. g Lead-lag correlation of first two PC time series formulated by projecting the unfiltered anomaly data onto the Combined EOF’s eigenvector. The thick black curves and thin grey curves indicate observations and the CMIP5 simulations, respectively
In order to visualize the propagation of the MJO represented in each model, Fig. 4 shows the hovmӧller diagrams of MJO-phase composited 20–100-day precipitation averaged between 10°S–10°N. The MJO phase composites are based on the phase-space plots of the PC time series formulated by projecting the 20–100-day filtered anomaly data onto the CEOF’s eigenvector, as described in MJOWG (2009). In observations, the MJO rainfall signal propagates from Indian Ocean to Western Pacific, whereas many CMIP5 models fail to produce coherent eastward propagation of MJO rainfall signal compared to observations. Some models struggle to propagate the signal into the Western Pacific (BCC-CSM1-1-m, BNU-ESM, FGOALS-s2, NorESM1-M, HadGEM2-CC, MIROC4h), some models have standing oscillation over Maritime Continent (GFDL-ESM2G, GFDL-ESM2M, IPSL-CM5A-LR, IPSL-CM5A-MR, MIROC-ESM, MIROC-ESM-CHEM, INMCM4), and some models show a very weak signal over all longitudes (CanESM2, FGOALS-2g). For example, when considering the 150°E as a critical region, only about 6–8 out of 28 CMIP5 models propagate MJO rainfall east of 150°E reasonable well (BCC-CSM1-1, CMCC-CM, CMCC-CMS, CNRM-CM5, IPSL-CM5B-LR, MRI-CGCM3). Hung et al. (2013) and Jiang et al. (2015) showed similar results using lead-lag correlation diagram of MJO time-scale filtered precipitation.
Hovmӧller diagrams of MJO phase composited 20–100-day precipitation averaged between 10°S and 10°N. The MJO phase composites are based on the PC time series formulated by projecting the 20–100-day filtered anomaly data onto the CEOF’s eigenvector shown in Fig. 3. The vertical dotted lines in each plot indicate the 150°E longitude
Four skill metrics are derived from the CEOF analysis. The first metric is the percentage variance explained by the two leading modes. In observations, the leading two CEOFs explain about 41% of the total variance (Fig. 5a). These two modes also explain 59, 39, and 31% of the variance of U850, U250, and OLR respectively. The sequence of variance explained by each variable of the CEOF is well simulated in CMIP5 models, but most CMIP5 models underestimate the magnitude of the variance explained by each variable, especially for OLR.
a Percentage variance (pct) obtained from sum of first two combined EOF modes, b spatial correlation between observations and models for the MJO phase hovmӧller diagram averaged between 10°S–10°N and first two combined EOF’s, c maximum correlation (CMAX) between first two combined EOF PC time series, and d dominant eastward period from the first two combined EOF modes (PCEOF). Closed squares, closed circles, and open circles indicate observations, multi-model means, and CMIP5 models, respectively. Vertical lines indicate inter-model spreads. Different color indicates each variable. The percentages of variance for individual variables in a are obtained using the variance of each variable explained by the first and second CEOFs and the total variance of the variable
The second skill metric is obtained from the spatial correlation coefficients between observations and models for the hovmӧller diagrams of MJO phase composited precipitation in Fig. 4 and for the first two CEOFs in Fig. 3. For the skill metric of the first two CEOFs, the spatial correlation coefficients of mode-1 and mode-2 are averaged to produce a single scalar metric. In the models, the lowest spatial correlation coefficient of the CEOFs appeared in the OLR among three variables. The FGOALS-g2 model showed an especially large difference of correlation between OLR and the wind variables. The FGOALS-g2 model also showed weak coupling of precipitation with the wind field and moisture (Figs. 2c, 7a). The multi-model mean of the spatial correlation coefficients for the hovmӧller diagrams of MJO phase composited precipitation is about 0.48.
The third and fourth skill metrics are derived from the lead-lag correlation between PCs of the two leading modes (Fig. 3g). The third metric, a measure of the coherency in the MJO propagation, is formulated by averaging the absolute values of maximum and minimum lead-lag correlation coefficients (c.f. Sperber and Kim 2012). The third metric will be referred to Cmax. The observed Cmax is about 0.47, whereas the value of CMIP5 multi-model mean is about 0.36 indicating that most CMIP5 models’ MJO propagation is not as coherent as observed. The fourth metric, an estimate of MJO periodicity from the CEOF analysis (PCEOF), is formulated by twice the time interval between maximum lag-correlation and minimum lag-correlation. The observed PCEOF is about 36 days, whereas the value of CMIP5 multi-model mean is about 34 days, which is similar to PWFPS (Fig. 2d). The correlation coefficients between the modeled values for PCEOF and PWFPS are 0.58, 0.69, 0.63, and 0.58 for precipitation, OLR, U850, and U250, respectively (Table 3).
4 Process-oriented diagnosis
In this section, we examine whether good and poor MJO models are characterized by a different representation of processes that are hypothesized to be important for simulation of a realistic MJO. These process-oriented diagnostics aim to provide insights into how parameterizations of physical processes in GCMs can be modified to improve the MJO simulation. Here we study three process-oriented diagnostics (RHCP-, NGMS-, and GEF-diagnostics; see Sect. 1). Scalar metrics are derived from each process-oriented diagnostic to investigate their relationship with the MJO skill metrics developed in Sect. 3.
To formulate the RHCP-diagnostic presented by Kim et al. (2014), the low-level (850–700 hPa) RH composite based on precipitation percentile is performed over the Indo-Pacific warm pool (60°E–180°E, 15°S–15°N) with land masked out (Fig. 6). In observations, the low-level RH increases as the precipitation percentile increases, indicating coupling between convection and low-level moisture. Most CMIP5 models exhibit a low-level RH increase as the precipitation percentile increases, but the RH for a given precipitation percentile can vary substantially compared to the observations. To objectively evaluate the relationship between convection and low-level moisture, the RHCP-metric is formulated as the low-level RH difference between upper 10% precipitation percentile and lower 20% precipitation percentile (Kim et al. 2014):
Relative Humidity Composite based on PRCP percentile (RHCP) averaged between 850 hPa and 700 hPa. The Indian Ocean area (60°E–180°E, 15°S–15°N) is used and land area is excluded from thecalculation. Thick black solid, long-dash, short-dash curves indicate GPCP (1997–2010), TRMM (1998–2010), ERA-int (1985–2004) precipitation respectively combined with ERA-interim RH, and thin grey curves indicate the CMIP5 simulations
The observed RHCP-metric ranges from 28.8 to 42.5, depending on the precipitation dataset used in the analysis (Fig. 7a). The large uncertainty of the observed RHCP-metric is caused by the uncertainty of the magnitude of weak precipitation (less than about the 45 percentile). Most CMIP5 models show RHCP-metric values that are within the uncertainty range of observed values (Fig. 7a).
a RHCP-metric for observations and the CMIP5 simulations. Closed square, X mark, closed triangle, closed circle, and open circles indicate GPCP (1997–2010), TRMM (1998–2010), ERA-int (1985–2004), multi-model mean, and CMIP5 models, respectively. Vertical lines indicate the inter-model spread. b Correlation coefficient between RHCP-metric and MJO skill metrics. The dotted line indicates 5% significance level when 27 models are used
The correlation between the simulated RHCP-metric and various MJO skill metrics is assessed in Fig. 7b. The RHCP-metric is significantly correlated with most MJO skill metrics, including the E/W ratio and E/O ratio of precipitation, coh2 of precipitation with precipitable water and U850, CEOF percentage variance of OLR, the spatial correlation between observations and models for the MJO phase hovmӧller diagram, and for the CEOF eigenvector of OLR for which R ~ 0.6. This indicates that models with stronger (weaker) coupling strength between low-tropospheric moisture and convection have a better (poorer) MJO. For models with too weak a coupling strength, improvement in this quantity would lead to a better MJO. Even considering the highest correlation score between this diagnostic and MJO skill, this only leads to an explained variance of about 35–40%, and thus additional parameterized quantities have to be investigated to more fully improve MJO fidelity.
In many previous studies, the gross moist stability (GMS) is presented to examine the relationship between convection and large-scale circulation. For example, Benedict et al. (2014) showed that the E/W ratio of precipitation is more related to the vertical component of normalized GMS (NGMS) than the horizontal component of NGMS. The relationship between vertical component of NGMS obtained from the mean state and various MJO skill metrics are examined in this study. The NGMS-metric is formulated using the time-mean vertical profiles of omega, moist static energy (MSE), and dry static energy (DSE) over the Indo-Pacific warm pool area (60°E–180°E, 15°S–15°N) with land masked out:
where the over-bar indicates the time mean, angle bracket indicates the column vertical integration from 1000 to 100 hPa, \(MSE = CpT + gz + Lq\) is the moist static energy, and \(DSE = CpT + gz\) is the dry static energy. The magnitude and shape of the mean vertical profile of omega is diverse across the CMIP5 models, and the MSE of all levels is underestimated in most CMIP5 models (Fig. 8). The NGMS-metric is mainly influenced by the combination of mean vertical profiles of omega and MSE.
The NGMS-metric is about 0.25 for the observations and about 0.33 for the multi-model mean, with many CMIP5 models overestimating the NGMS-metric (Fig. 9a). This indicates that most CMIP5 models more efficiently discharge MSE from the column through vertical convective motions compared to the observations. The simulated NGMS-metric has a significant negative correlation with half of the MJO skill metrics, including the E/W ratio and E/O ratio of most variables, PWFPS of most variables, and PCEOF (Fig. 9b). This indicates that a smaller NGMS, which means a less efficient discharge of MSE from the column through vertical convective motions, should result in a stronger MJO amplitude, and a slower and more realistic MJO propagation speed.
a The Normalized Gross Moist Stability (NGMS) metric for the observations and the CMIP5 simulations. Closed square, closed circle, and open circles indicate observations, the multi-model mean, and the CMIP5 models, respectively. Vertical lines indicate the inter-model spread. b Correlation coefficient between the NGMS-metric and the MJO skill metrics. The dotted line indicates the 5% significance level when 23 models are used
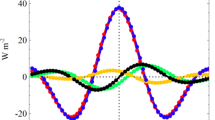
For the third process-oriented diagnostic we use the GEF-diagnostic presented by Kim et al. (2015). It is calculated over the Indo-Pacific warm pool area (60°E–180°E, 15°S–15°N) with land masked out, as the ratio of column-integrated longwave radiative heating to column-integrated latent heating and is calculated for precipitation anomaly bins (Fig. 10):
The Greenhouse Enhancement Factor (GEF) diagnostics for the observations (AVHRR and GPCP (1997–2010): thick black curve, AVHRR and TRMM (1998–2010): long-dashed curve) and the CMIP5 simulations (thin grey curves). The Indo-Pacific warm pool area (60°E–180°E, 15°S–15°N) is used and land gridpoints have been excluded from the calculation. Note that precipitation anomaly is plotted on a log-scale. The inset plot is expanded plot with different range of x and y axis
where the \(GEF = \frac{{ - OLR~anomaly~}}{{L \times PRCP~anomaly~}}\) is the latent heat of condensation. Note that the precipitation anomaly bins are defined in log-scale following Kim et al. (2015). The surface longwave anomaly is assumed to be small; hence the OLR anomaly is used as a measure of the column-integrated longwave radiative heating anomaly. In observations and in models, the maximum GEF tends to appear in relatively weak precipitation anomaly regimes, and the GEF decreases as the precipitation anomaly increases. This indicates that the cloud-longwave radiation feedback is larger in the weak precipitation anomaly regime than in the strong precipitation anomaly regime. All CMIP5 models underestimate the GEF in the weak precipitation anomaly, but the GEF in the strong precipitation anomaly is relatively well simulated.
Kim et al. (2015) found that the maximum correlation between the E/W ratio of precipitation and the GEF appeared when the latter was quantified using only the weak precipitation anomaly regime. Accordingly, they formulated the GEF-metric as the weighted average of GEF over 1-5mm/day precipitation anomaly regime. The GEF-metric is about 0.31 for the observations and about 0.25 for the multi-model mean, with most CMIP5 models underestimating the GEF-metric (Fig. 11a). The correlation between the simulated GEF-metric and various MJO skill metrics is presented in Fig. 11b. Compared to the RHCP- and NGMS-metric, the GEF-metric does not show as robust a relationship with the MJO skill metrics. The GEF-metric is most correlated with the E/W ratio of precipitation and the E/O ratio of precipitation and OLR. This suggests that the MJO in the CMIP5 models has the possibility to improve with an increase of longwave radiative heating in the weak precipitation anomaly regime. To increase the longwave radiative heating in the weak precipitation anomaly regime, the parameterizations of cloud properties and cloud-radiation interaction need to be modified. Kim et al. (2015) showed that the model with strong longwave radiative heating in the weak precipitation anomaly has a larger cloud fraction, larger cloud ice water content, lower cloud liquid water content, and larger precipitable water.
a The GEF-metric for the observations and the CMIP5 simulations. Closed square, closed triangle, closed circle, and open circles indicate observations [AVHRR and GPCP (1997–2010)], additional observations [AVHRR and TRMM (1998–2010)], the multi-model mean, and the CMIP5 models, respectively. Vertical lines indicate the inter-model spread. b Correlation coefficient between GEF-metric and MJO skill metrics. The dotted line indicates the 5% significance level when 28 models are used
5 Summary and discussion
This study applies the MJO diagnostics developed by the MJOWG to 37 CMIP5 models, and formulates numerous MJO skill metrics that are used to assess the model performance in simulating the prominent features of the MJO. The common problems found in this study are that most models underestimate MJO amplitude, especially in OLR, and struggle to generate coherent eastward propagation. Additionally, most models simulate an MJO that propagates too fast compared to observations, similar to previous model studies of the MJO (e.g., Kim et al. 2009). On the other hand, Hung et al. (2013) and Jiang et al. (2015) showed that the MJO propagation speed of some CMIP5 models in the Indian Ocean tends to be slower than observed, but they indicated that this is due to too strong a persistence of precipitation. When considering the zonal extent of the propagating signal in convection, most models did not propagate the MJO rainfall signal from Indian Ocean to Pacific region, as observed.
Additionally, the MJO skill metrics formulated in this study are compared statistically with MJO process-oriented diagnostics to ascertain which aspects of physical process parameterizations should be improved in GCMs to result in better MJO simulations. We find that (1) the RHCP-metric is positively correlated with nearly all of the MJO metrics, (2) the NGMS-metric is negatively correlated with the E/W power ratio of precipitation and OLR, the E/O ratio of OLR, and PWFPS of all variables, and (3) the GEF-metric is correlated with the E/W ratio of precipitation and the E/O ratio of precipitation and OLR. Thus, the simulation of the MJO is influenced by many processes suggesting a variety of approaches for improving MJO simulation.
Jiang et al. (2015) also examined the relationship between the MJO skill metric and MJO process-oriented metrics using 27 GCM simulations participating in the MJOTF/GASS MJO global model comparison project. They showed that the low-level RH difference between high- and low-rain events (consistent with RHCP-metric in this study) and the seasonal mean gross moist stability (consistent with NGMS-metric in this study) are significantly correlated with the E/W power ratio of precipitation, which is consistent with results of this study. They also showed that the cloud-radiative feedback is negatively but insignificantly correlated with the E/W power ratio of precipitation, which is an inconsistent result with this study that uses the GEF-metric. This inconsistency might be caused by the difference in the cloud-radiative feedback metrics used. Jiang et al. (2015) formulated their cloud-radiative feedback metric based on regressed radiative heating and latent heating against 20–100-day precipitation for all data, while the GEF-metric used in the present study is based on the radiative heating and latent heating on each precipitation anomaly bin, and only weak precipitation bins are used to construct the GEF-metric. Kim et al. (2015) showed that GEF-metrics from mid- and strong- precipitation bins are insignificantly correlated with the E/W power ratio of precipitation.
The process-oriented diagnostics used in this study have a more direct link to parameterization schemes than the conventional performance-oriented diagnostics. The moisture-convection coupling measured by the RHCP-metric has been shown to be affected by parameters in the convection scheme such as the fractional entrainment rate and the efficiency of convective rain re-evaporation (e.g., Kim et al. 2012). The models that exhibit lower-than-observed values of the RHCP-metric would benefit by increasing the values of these parameters in the convection scheme. The NGMS-metric is sensitive to the vertical distribution of the vertical motion in a convecting column, with a more top- (bottom-) heavy profile making the NGMS-metric higher (lower). The vertical profile of vertical motion is affected by the cumulus massflux, whose vertical profile is determined by the fractional entrainment and detrainment rates. This suggests that improving the fractional entrainment and detrainment rates would improve the NGMS-metric of a model. The GEF-metric could potentially be affected by the parameterizations of convection, clouds, and radiation. This is because the calculation of the longwave radiative flux is affected by (1) how much of the water vapor and cloud condensates are transported upward in convective towers to form large-scale clouds (convection scheme), (2) how large-scale clouds are distributed in the grid cell and how long the clouds persist in association with the anomalous precipitation (large-scale cloud scheme), and (3) the optical properties of the cloud condensates (radiation scheme). Modelers should focus on parameters that affect these features to improve the GEF-metric.
Our insight into the processes relevant to the MJO has improved over the last 20 years, and importantly the advent of standardized experimentation (e.g., AMIP and CMIP) and more extensive high frequency model output have contributed to our improved insights. Despite the comparative paucity of data in the AMIP1 era simulations, it is possible to address the question of whether models have improved in the intervening 20 years. Pioneering MJO model studies, such as Slingo et al. (1996), recognized the utility of evaluating the space–time structure of the MJO using wavenumber-frequency analysis, an essential technique utilized herein. Though not a primary field analyzed today due to the more comprehensive model output presently available, the upper-tropospheric velocity potential, used in Slingo et al. (1996) for AMIP1 fields, clearly captures the eastward propagation of the MJO. As such, Fig. 12 shows the percentage of simulated 250 hPa velocity potential (VP250) spectral power relative to observations within periods of 30–70 days for wavenumber 1 using 10°N–10°S averaged data. The upper panel is for the CMIP5 models and lower panel is for the AMIP1 models, estimated from Fig. 8 of Slingo et al. (1996). When considering a 50% threshold, the results indicate that the CMIP5 models are better than the AMIP1 models, with only 4 out of 15 AMIP1 models but 13 out of 32 CMIP5 models exceeding this threshold (AMIP1 vs CMIP5 is 27 vs. 40%). Recently, Hung et al. (2013) compared the CMIP5 and CMIP3 models using the same diagnostics as Lin et al. (2006). When considering the 50% threshold of observed MJO variance over the Indo-Pacific warm pool (60°E–180°E, 15°S–15°N), only 4 out of 20 CMIP5 models (20%) and 2 out of 14 CMIP3 models (14%) exceeded this threshold, as estimated from Fig. 7a of Hung et al. (2013) and Fig. 9a of Lin et al. (2006).
The percentage of simulated 250 hPa velocity potential (VP250) spectral power relative to the observations within 30–70 day period and wavenumber 1 component based on the wavenumber-frequency power spectra of 10°N–10°S averaged VP250 (Jun–May) for a CMIP5 and b AMIP1 estimated from the Fig. 8 of Slingo et al. (1996). The 50% lines are indicated by dashed line
Though progress is evident, MJO simulation in GCMs remains a challenging problem. Intraseasonal precipitation variability is a poorly simulated quantity among CMIP5 models (Fig. 13). Little mean precipitation spread exists among individual models over the Indo-Pacific warm pool area, especially in the Western Pacific with most models within about 20% of the multi-model average (Fig. 13d-f). On the contrary, the intraseasonal and total variability of precipitation, measured by standard deviation of intraseasonal filtered and raw precipitation anomalies, exhibits substantial spread that is about three times larger than that of mean precipitation in the Western Pacific. The large spread in intraseasonal precipitation variability would at least partly be associated with that of the MJO, the dominant mode of tropical intraseasonal variability. This suggests that we need to better constrain the MJO to reduce the spread in intraseasonal variability among models.
Scatter plots of the difference (%) from the multi-model mean for the a, d mean state and total standard deviation, b, e mean state and 20–100-day filtered standard deviation, c, f mean state and MJO (30–60 days, 1–3 wavenumber) filtered standard deviation of precipitation over the a–c Indian Ocean (60°E–120°E, 15°S–15°N) and d–f Western Pacific (120°E–180°E, 15°S–15°N). The difference % is calculated by “(model-mmm)*100/mmm”, the “mmm” is multi-model mean
Our results suggest that modifications to processes associated with the relative humidity and convective coupling, and the gross moist stability might be the most fruitful, as these have significant correlations with the largest number of MJO skill metrics. The Greenhouse enhancement factor exhibits fewer significant correlations with the MJO skill metrics, and correlates best with the E/W ratio of precipitation and the E/O ratio of precipitation and OLR. In this case, the longwave radiation feedback for the weak precipitation anomaly regime requires the most attention.
References
Andersen JA, Kuang Z (2012) Moist static energy budget of MJO-like disturbances in the atmosphere of a zonally symmetric aquaplanet. J Climate 25:2782–2804
Annamalai H, Sperber KR (2005) Regional heat sources and the active and break phases of boreal summer intraseasonal (30–50 day) variability*. J Atmos Sci 62:2726–2748
Arnold NP, Randall DA (2015) Global-scale convective aggregation: Implications for the Madden-Julian Oscillation. J Adv Model Earth Syst 7:1499–1518
Benedict JJ, Maloney ED, Sobel AH, Frierson DMW (2014) Gross moist stability and MJO simulation skill in three full-physics GCMs. J Atmos Sci 71:3327–3349
Berbery EH, Nogués-Paegle J (1993) Intraseasonal interactions between the tropics and extratropics in the Southern hemisphere. J Atmos Sci 50:1950–1965
Bergman JW, Hendon HH, Weickmann KM (2001) Intraseasonal air–sea interactions at the onset of El Niño. J Climate 14:1702–1719
Bessafi M, Wheeler MC (2006) Modulation of South Indian Ocean tropical cyclones by the Madden–Julian oscillation and convectively coupled equatorial waves. Mon Weather Rev 134:638–656
Cassou C (2008) Intraseasonal interaction between the Madden-Julian Oscillation and the North Atlantic Oscillation. Nature 455:523–527
Chikira M (2014) Eastward-propagating intraseasonal oscillation represented by Chikira–Sugiyama cumulus parameterization. Part II: understanding moisture variation under weak temperature gradient balance. J Atmos Sci 71:615–639
Dee DP, Coauthors (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Quart J Roy Meteor Soc 137:553–597
Ferranti L, Palmer TN, Molteni F, Klinker E (1990) Tropical-extratropical interaction associated with the 30–60 day oscillation and its impact on medium and extended range prediction. J Atmos Sci 47:2177–2199
Garfinkel CI, Feldstein SB, Waugh DW, Yoo C, Lee S (2012) Observed connection between stratospheric sudden warmings and the Madden-Julian Oscillation. Geophys Res Lett 39. doi:10.1029/2012GL053144
Guan B, Waliser DE, Molotch NP, Fetzer EJ, Neiman PJ (2012) Does the Madden–Julian oscillation influence wintertime atmospheric rivers and snowpack in the Sierra Nevada? Mon Weather Rev 140:325–342
Hannah WM, Maloney ED (2011) The role of moisture-convection feedbacks in simulating the Madden–Julian oscillation. J Climate 24:2754–2770
Hannah WM, Maloney ED (2014) The moist static energy budget in NCAR CAM5 hindcasts during DYNAMO. J Adv Modeling Earth Sys 6. doi:10.1002/2013MS000272.
Hayashi Y (1982) Space-time spectral analysis and its applications to atmospheric waves. J Meteor Soc Japan 60:156–171
Henderson SA, Maloney ED, Barnes EA (2016) The influence of the Madden-Julian oscillation on Northern Hemisphere winter blocking. J Climate 29:4597–4616. doi:10.1175/JCLI-D-15-0502.1
Hendon HH, Liebmann B (1990) A composite study of onset of the Australian summer monsoon. J Atmos Sci 47:2227–2240
Hendon HH, Zhang C, Glick JD (1999) Interannual variation of the Madden–Julian oscillation during austral summer. J Climate 12:2538–2550
Hendon HH, Wheeler MC, Zhang C (2007) Seasonal dependence of the MJO–ENSO relationship. J Climate 20:531–543
Higgins RW, Mo KC (1997) Persistent North Pacific circulation anomalies and the tropical intraseasonal oscillation. J Climate 10:223–244
Huffman GJ et al (2001) Global precipitation at onedegree daily resolution from multisatellite observations. J Hydrometeor 2:36–50
Huffman GJ et al (2007) The TRMMMultisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J Hydrometeor 8:38–55
Hung M-P, Lin J-L, Wang W, Kim D, Shinoda T, Weaver SJ (2013) MJO and convectively coupled equatorial waves simulated by CMIP5 climate models. J Climate 26:6185–6214
Jiang X, Zhao M, Waliser DE (2012) Modulation of tropical cyclones over the Eastern Pacific by the intraseasonal variability simulated in an AGCM. J Climate 25:6524–6538
Jiang X et al (2015) Vertical structure and physical processes of the Madden-Julian oscillation: exploring key model physics in climate simulations. J Geophys Res Atmos 120:4718–4748
Johnson NC, Feldstein SB (2010) The continuum of North Pacific Sea Level pressure patterns: intraseasonal, interannual, and interdecadal variability. J Climate 23:851–867
Kalnay E, Coauthors (1996) The NCEP/NCAR 40-year reanalysis project. Bull Amer Meteor Soc 77:437–471
Kessler WS (2001) EOF representations of the Madden–Julian oscillation and Its connection with ENSO*. J Climate 14:3055–3061
Kessler WS, Kleeman R (2000) Rectification of the Madden–Julian oscillation into the ENSO cycle. J Climate 13:3560–3575
Kessler WS, McPhaden MJ, Weickmann KM (1995) Forcing of intraseasonal Kelvin waves in the equatorial Pacific. J Geophys Res Oceans 100:10613–10631
Kim D, Kang I-S (2012) A bulk mass flux convection scheme for climate model—description and moisture sensitivity. Clim Dyn 38:411–429
Kim D et al (2009) Application of MJO simulation diagnostics to climate models. J Climate 22:6413–6436. doi:10.1175/2009JCLI3063.1
Kim D, Sobel AH, D. M. W. Frierson, Maloney ED, Kang I-S (2011a) A systematic relationship between intraseasonal variability and mean state bias in AGCM simulations. J Climate 24:5506–5520
Kim D, Sobel AH, Del Genio AD, Chen Y, Camargo SJ, Yao M-S, Kelley M, Nazarenko L (2012) Tropical intraseasonal variability simulated in the NASA GISS general circulation model. J Climate 25:4641–4659
Kim D et al (2014) Process-oriented MJO simulation diagnostic: moisture sensitivity of simulated convection. J Climate 27:5379–5395
Kim D, Ahn M-S, Kang I-S, Del Genio AD (2015) Role of longwave cloud–radiation feedback in the simulation of the Madden–Julian oscillation. J Climate 28:6979–6994
Kim D, Maloney ED (2017) Review: Simulation of the Madden-Julian oscillation using general circulation models. In: Chang C-P et al (eds) The Global Monsoon System, 3rd edn, p 119–130. doi:10.1142/9789813200913_0009
Kiranmayi L, Maloney ED (2011) Intraseasonal moist static energy budget in reanalysis data. J Geophys Res 116:D21117
Klingaman NP, Woolnough SJ, Jiang X, Waliser D, Xavier PK, Petch J, Caian M, Hannay C, Kim D, Ma H-Y, Merryfield WJ, Miyakawa T, Pritchard M, Ridout JA, Roehrig R, Shindo E, Vitart F, Wang H, Cavanaugh NR, Mapes BE, Shelly A, Zhang G (2015a) Vertical structure and physical processes of the Madden–Julian Oscillation: linking hindcast fidelity to simulated diabatic heating and moistening. J Geophys Res doi:10.1002/2014JD022374
Klingaman NP, Jiang X, Xavier PK, Petch J, Waliser D, Woolnough SJ (2015b) Vertical structure and physical processes of the Madden–Julian oscillation: synthesis and summary, J Geophys Res doi:10.1002/2015JD023196
Klotzbach PJ (2010) On the Madden–Julian Oscillation–Atlantic hurricane relationship. J Climate 23:282–293
L’Heureux ML, Higgins RW (2008) Boreal winter links between the Madden–Julian Oscillation and the Arctic Oscillation. J Climate 21:3040–3050
Lau K-M, Chan PH (1986) Aspects of the 40–50 day oscillation during the northern summer as inferred from outgoing longwave radiation. Mon Weather Rev 114:1354–1367
Liebmann B, Smith CA (1996) Description of a complete (interpolated) outgoing longwave radiation dataset. Bull Amer Meteor Soc 77:1275–1277
Liebmann B, Hendon HH, Glick JD (1994) The relationship between tropical cyclones of the western pacific and Indian Oceans and the Madden-Julian oscillation. J Meteorol Soc Jpn Ser II 72:401–412
Lin JL et al (2006) Tropical intraseasonal variability in 14 IPCC AR4 climate models. Part I: convective signals. J Climate 19:2665–2690. doi:10.1175/JCLI3735.1
Lin JL, Lee M-I, Kim D, Kang I-S, Frierson DMW (2008) The impacts of convective parameterization and moisture triggering on AGCM-simulated convectively coupled equatorial waves. J Climate 21:883–909
Lin H, Brunet G, Derome J (2009) An observed connection between the North Atlantic Oscillation and the Madden–Julian oscillation. J Climate 22:364–380
Liu P et al (2009) Tropical intraseasonal variability in the MRI-20km60L AGCM. J Climate 22:2006–2022
Loeb NG, Wielicki BA, Doelling DR, Smith GL, Keyes DF, Kato S, Manalo-Smith N, Wong T (2009) Toward optimal closure of the Earth’s top-of-atmosphere radiation budget. J Climate 22:748–766
Lorenz DJ, Hartmann DL (2006) The effect of the MJO on the North American monsoon*. J Climate 19:333–343
Madden RA, Julian PR (1971) Detection of a 40–50 day oscillation in the zonal wind in the tropical pacific. J Atmos Sci 28:702–708
Madden RA, Julian PR (1972) Description of global-scale circulation cells in the tropics with a 40–50 day period. J Atmos Sci 29:1109–1123
Maloney ED (2009) The moist static energy budget of a composite tropical intraseasonal oscillation in a climate model. J Climate 22:711–729
Maloney ED, Hartmann DL (2000) Modulation of Eastern North Pacific hurricanes by the Madden–Julian oscillation. J Climate 13:1451–1460
Maloney ED, Hartmann DL (2001) The sensitivity of intraseasonal variability in the NCAR CCM3 to changes in convective parameterization. J Climate 14:2015–2034
Maloney ED, Zhang C (2016) Dr. Yanai’s contribution to the discovery and science of the MJO. Meteor Monographs 56. doi:10.1175/AMSMONOGRAPHS-D-15-0003.1
Matthews AJ, Hoskins BJ, Masutani M (2004) The global response to tropical heating in the Madden–Julian oscillation during the northern winter. Q J R Meteorolog Soc 130:1991–2011
McPhaden MJ (1999) Genesis and evolution of the 1997–98 El Niño. Science 283:950–954
MJOWG, 2009: MJO simulation diagnostics. J Climate 22:3006–3030
Mundhenk BD, Barnes EA, Maloney ED (2016) All-season climatology and variability of atmospheric river frequencies over the North Pacific. J Climate. doi:10.1175/JCLI-D-15-0655.1
Nakazawa T (1988) Tropical super clusters within intraseasonal variations over the Western Pacific. J Meteorol Soc Jpn Ser II 66:823–839
Salby ML, Hendon HH (1994) Intraseasonal behavior of clouds, temperature, and motion in the Tropics. J Atmos Sci 51:2207–2224
Seo K-H, Son S-W (2011) The global atmospheric circulation response to tropical diabatic heating associated with the Madden–Julian oscillation during Northern Winter. J Atmos Sci 69:79–96
Slingo JM, Coauthors (1996) Intraseasonal oscillations in 15 atmospheric general circulation models: results from an AMIP diagnostic subproject. Climate Dyn 12:325–357
Sperber KR, Kim D (2012) Simplified metrics for the identification of the Madden–Julian oscillation in models. Atmos Sci Lett 13:187–193
Sperber KR, Slingo JM, Annamalai H (2000) Predictability and the relationship between subseasonal and interannual variability during the Asian summer monsoon. Q J R Meteorol Soc 126:2545–2574
Sperber KR, Gualdi S, Legutke S, Gayler V (2005) The Madden–Julian oscillation in ECHAM4coupled and uncoupled general circulation models. Climate Dyn 25:117–140. doi:10.1007/s00382-005-0026-3
Sultan B, Janicot S, Diedhiou A (2003) The West African monsoon dynamics. Part I: documentation of intraseasonal variability. J Climate 16:3389–3406
Takayabu YN, Iguchi T, Kachi M, Shibata A, Kanzawa H (1999) Abrupt termination of the 1997-98 El Nino in response to a Madden–Julian oscillation. Nature 402:279–282
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93:485–498
Tokioka T, Yamazaki K, Kitoh A, Ose T (1988) The equatorial 30–60-day oscillation and the Arakawa–Schubert penetrative cumulus parameterization. J Meteor Soc Japan 66:883–901
Vecchi GA, Bond NA (2004) The Madden–Julian Oscillation (MJO) and northern high latitude wintertime surface air temperatures. Geophys Res Lett 31. doi:10.1029/2003GL018645
Waliser DE, Schubert S, Kumar A, Weickmann K, Dole R (2003) Proceedings from a workshop on ‘‘modeling, simulation and forecasting of subseasonal variability.’’ NASA/TM 2003-104606 25:67
Wang (2005) Theory. Intraseasonal Variability in the Atmosphere-Ocean Climate System. In: Lau WK-M, Waliser DE (eds). Praxis, pp 307–360
Wang WQ, Schlesinger ME (1999) The dependence on convection parameterization of the tropical intraseasonal oscillation simulated by the UIUC 11-layer atmospheric GCM. J Climate 12(5):1423–1457
Weickmann KM, Lussky GR, Kutzbach JE (1985) Intraseasonal (30–60 day) fluctuations of outgoing longwave radiation and 250 mb streamfunction during Northern Winter. Mon Weather Rev 113:941–961
Wheeler MC, Hendon HH (2004) An all-season real-time multivariate MJO index: development of an index for monitoring and prediction. Mon Weather Rev 132:1917–1932
Wheeler M, Kiladis GN (1999) Convectively coupled equatorial waves: analysis of clouds and temperature in the wavenumber–frequency domain. J Atmos Sci 56:374–399
Wheeler MC, McBride JL (2005) Australian–Indonesian monsoon. Lau WKM, Waliser DE (eds) Intraseasonal variability in the atmosphere-ocean climate system. Springer, Berlin, pp 125–174
Wheeler MC, Hendon HH, Cleland S, Meinke H, Donald A (2009) Impacts of the Madden–Julian oscillation on australian rainfall and circulation. J Climate 22:1482–1498
Wolding BO, Maloney ED (2015) Objective diagnostics and the Madden–Julian oscillation. Part II: application to moist static energy and moisture budgets. J Climate 28:7786–7808
Wolding BO, Maloney ED, Branson M (2016) Vertically resolved weak temperature gradient analysis of the Madden–Julian oscillation in SP-CESM. J Adv Model Earth Syst 8:1586–1619. doi:10.1002/2016MS000724
Xavier PK, Petch JC, Klingaman NP, Woolnough SJ, Jiang X, Waliser DE, Caian M, Hagos SM, Hannay C, Kim D, Cole J, Miyakawa T, Pritchard M, Roehrig R, Shindo E, Vitart F, Wang H (2015) Vertical structure and physical processes of the Madden-Julian Oscillation: biases and uncertainties at short range. J Geophys Res doi:10.1002/2014JD022718
Yasunaga K, Mapes B (2012) Differences between more divergent and more rotational types of convectively coupled equatorial waves. Part I: space–time spectral analyses. J Atmos Sci 69:3–16
Yasunari T (1979) Cloudiness fluctuations associated with the northern hemisphere summer monsoon. J Meteorol Soc Jpn Ser II 57:227–242
Yasunari T (1980) A Quasi-stationary appearance of 30 to 40 day period in the cloudiness fluctuations during the summer monsoon over India. J Meteorol Soc Jpn Ser II 58:225–229
Yoo C, Lee S, Feldstein SB (2012) Mechanisms of Arctic surface air temperature change in response to the Madden–Julian oscillation. J Climate 25:5777–5790
Zhang C (2005) Madden–Julian oscillation. Rev Geophys 43:RG2003. doi:10.1029/2004RG000158
Zhang C, Gottschalck J (2002) SST anomalies of ENSO and the Madden–Julian oscillation in the equatorial Pacific*. J Climate 15:2429–2445
Zhang C, Hendon HH (1997) Propagating and standing components of the intraseasonal oscillation in tropical convection. J Atmos Sci 54:741–752
Zhang GJ, Song XL (2009) Interaction of deep and shallow convection is key to Madden-Julian Oscillation simulation. Geophys Res Lett 36. doi:10.1029/2009GL037340
Zhang C, Dong M, Gualdi S, Hendon HH, Maloney ED, Marshall A, Sperber KR, Wang WQ (2006) Simulations of the Madden-Julian oscillation in four pairs of coupled and uncoupled global models. Clim Dyn 27:573–592
Acknowledgements
The authors wish to acknowledge the U.S. CLIVAR MJO Task Force members for their insightful comments and suggestions. M.-S. Ahn and I.-S. Kang were supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MEST) (NRF-2009-C1AAA001-0093065) and by the Brain Korea 21 Plus. D. Kim was supported by National Aeronautics and Space Administration Grant NNX13AM18G and by the Korea Meteorological Administration Research and Development Program under Grant KMIPA 2016–6010. K. Sperber was supported by the Regional and Global Climate Modeling Program, Office of Science (BER), U.S. Department of Energy through Lawrence Livermore National Laboratory contract DE-AC52-07NA27344. E. Maloney acknowledges support by the NOAA MAPP program under awards NA15OAR4310099 and NA15OAR4310098, and by National Science Foundation (NSF) Climate and Large-Scale Dynamics Program under award AGS-1441916. D. Waliser’s contribution was carried out on behalf of the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA.
Author information
Authors and Affiliations
Consortia
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ahn, MS., Kim, D., Sperber, K.R. et al. MJO simulation in CMIP5 climate models: MJO skill metrics and process-oriented diagnosis. Clim Dyn 49, 4023–4045 (2017). https://doi.org/10.1007/s00382-017-3558-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3558-4