Abstract
The present study is an effort to deepen the understanding of Indian summer monsoon rainfall (ISMR) on decadal to multi-decadal timescales. We use ensemble simulations for the period AD 1600–2000 carried out by the coupled Atmosphere-Ocean-Chemistry-Climate Model (AOCCM) SOCOL-MPIOM. Firstly, the SOCOL-MPIOM is evaluated using observational and reanalyses datasets. The model is able to realistically simulate the ISMR as well as relevant patterns of sea surface temperature and atmospheric circulation. Further, the influence of Atlantic Multi-decadal Oscillation (AMO), Pacific Decadal Oscillation (PDO), and El Niño Southern Oscillation (ENSO) variability on ISMR is realistically simulated. Secondly, we investigate the impact of internal climate variability and external climate forcings on ISMR on decadal to multi-decadal timescales over the past 400 years. The results show that AMO, PDO, and Total Solar Irradiance (TSI) play a considerable role in controlling the wet and dry decades of ISMR. Resembling observational findings most of the dry decades of ISMR occur during a negative phase of AMO and a simultaneous positive phase of PDO. The observational and simulated datasets reveal that on decadal to multi-decadal timescales the ISMR has consistent negative correlation with PDO whereas its correlation with AMO and TSI is not stationary over time.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Indian summer monsoon rainfall (ISMR) has a vital impact on the agrarian economy of this region. Understanding the variability of the ISMR on decadal to multi-decadal timescales is essential for adequate planning of farming and relevant infrastructure development, and for adapting to the consequences of future climate change (Krishnamurthy et al. 2014; Joshi and Rai 2015). Other than on inter-annual timescales the ISMR varies on decadal to multi-decadal timescales as various studies identified the presence of a ~60-year cycle in it (see, Mooley and Parthasarathy 1984; Verma et al. 1985; Kripalani et al. 1997; Krishnamurthy and Goswami 2000; Goswami 2006a; Zhou et al. 2009a). The potential factors which cause the decadal to multi-decadal scale variability of the ISMR are Pacific decadal oscillation (PDO), Atlantic multi-decadal oscillation (AMO), and external climate forcings i.e. greenhouse gases (GHGs), volcanic eruptions, and Total Solar Irradiance (TSI). Understanding the interaction of these modes and forcings with ISMR can help us to better predict the ISMR on decadal to multi-decadal timescales.
Several studies show the individual influence of the AMO and the PDO on ISMR. The AMO is a pattern of Sea Surface Temperatures (SSTs) in the North Atlantic with a period of ~55–80 years (e.g., Knight et al. 2006; Wei and Lohmann 2012) and an amplitude of 0.4 °C (e.g., Wang et al. 2009). Whether the AMO is caused by internal processes or related to external forcings is currently under discussion (see, Otterå et al. 2010; Booth et al. 2012; Zhang et al. 2013). The observational, paleoclimate, and simulated datasets show increased (decreased) ISMR during positive (negative) phase of the AMO (see, Gupta et al. 2003; Zhang and Delworth 2006; Goswami et al. 2006b; Lu et al. 2006; Feng and Hu 2008; Li et al. 2008; Wang et al. 2009; Msadek and Frankignoul 2009; Joshi and Pandey 2011; Joshi and Rai 2015; Luo et al. 2011; Krishnamurthy and Krishnamurthy 2014, 2015). In contrast to the AMO, the PDO, the leading mode of SSTs in the North Pacific Ocean with periodicities of 15–25 years and 50–70 years (e.g., Mantua and Hare 2002), is suggested having an opposite effect on ISMR (see, Krishnan et al. 2003; Roy et al. 2003; Krishnamurthy and Krishnamurthy 2013). Further, these studies found that dry (wet) events are more likely over India when the positive (negative) phase of El Niño Southern Oscillation (ENSO) coincides with the positive (negative) phase of PDO. Although the above-mentioned studies indicate the influence of decadal to multi-decadal scale ocean modes on ISMR they do not show the stability of their relationship (sign of correlation and magnitude) with the ISMR.
Only little effort has been made to explore the combined influence of AMO and PDO on ISMR. Recently, Joshi and Rai 2015 using the gridded Indian Meteorological Department (IMD) dataset over the period AD 1901–2004 found that the impact of AMO and Inter-decadal Pacific oscillation (IPO) over India is not homogeneous and their simultaneous opposite phases can cause wet and dry periods depending upon the sign of phase. The combined influence of these ocean modes on ISMR was studied only over the twentieth century and requires further investigation using long-term datasets. Thereby, long-term climate model simulations can help us to further understand the combined influence of AMO and PDO on ISMR and to know if this combined influence did exist in the past.
Other than internal climate variability (e.g., AMO and PDO), the external forcings also play a role in modulating the decadal to multi-decadal variability of ISMR. Bhattacharyya et al. (2005, 2007) employed the homogeneous ISMR data (AD 1871–1990) for studying the connection between solar activity and ISMR on multi-decadal time scale. They found that ISMR is above-normal (below-normal) during decades of above-normal (below-normal) solar activity. Mehta and Lau (1997) hypothesized that multi-decadal positive anomalies in TSI may shift the ISMR towards its positive phase for 20–30 years. Agnihotri et al. (2002) observed a periodicity of 60 ± 10 years in both ISMR and solar activity. Further research is required to assess whether solar activity contributes in controlling the dry events over the Indian monsoon region. There is evidence of the influence of volcanic eruptions on ISMR. Employing the superposed epoch analysis, Anchukaitis et al. (2010) in Monsoon Asia Drought Atlas (MADA) and Man et al. (2014) in coupled ocean–atmosphere climate model simulations found dry conditions after volcanic eruptions over most parts of the Indian region. In atmosphere-only climate model simulations Wegmann et al. (2014) also found dry conditions over most parts of the Indian region after strong tropical volcanic eruptions. Liu et al. (2009) found multi-decadal to longer time scale periodicities after volcanic eruptions in coupled ocean atmosphere climate model simulations. They further suggested that this low frequency component of the volcanic response is positively correlated with the global monsoon (correlation coefficient: 0.37). The influence of external forcings on ISMR is presently being debated and requires further investigation to better understand the variability of ISMR on decadal to multi-decadal timescales.
In order to reasonably simulate the effect of solar activity on ISMR it is important to use a model capable of reproducing the stratospheric influence on the troposphere and ocean. Various studies have indicated the importance of top-down and bottom-up mechanisms for studying the influence of the sun on monsoons as well as on the ocean. Meehl et al. (2009) and Kodera (2004) observed indirect dynamical response of solar forcing on air circulation through stratospheric heating at solar maximum periods. Meehl et al. (2009) simulated the stratospheric response to Ultraviolet (UV) solar forcing (top-down mechanism) and coupled ocean–atmosphere surface response (bottom-up mechanism) and found a cold event like La Niña in the eastern Pacific Ocean with negative temperature anomalies larger than −0.60 °C which is close to the observed value of −0.80 °C. From the study of Meehl it can be hypothesized that strong solar activity can strengthen the La Niña events and hence the Indian monsoon which is known to be negatively correlated with eastern Pacific SST anomalies. The AOCCM-SOCOL-MPIOM has the advantage of simulating both the top-down stratospheric ozone mechanism and bottom-up coupled air-sea mechanism, which is important for studying the solar influence on climate system, as described by Meehl et al. (2009) who showed enhanced vertical ascent (descent) over 10°–20°N (5°N) for the month of June when both mechanisms are simulated together.
Kodera (2004) found that more monsoon precipitation occurs over India during solar maximum periods due to the stratospheric variations by solar forcing. He proposed that the solar influence on monsoon is not due to direct heating of the troposphere through radiative changes; instead it comes through the stratosphere by modulation of the upwelling in the equatorial troposphere. He found a very little correlation of solar radio flux at 10.7 cm (F10.7 index) and JA (July–August) northward near-surface (10 m) wind velocity with Indian Ocean SSTs which indicates that most of the variations in near-surface winds originate from atmospheric variations Kodera (2004). Furthermore, he studied the spatial structure of JA zonal means of zonal wind (U), temperature (T), and vertical velocity (ω) by correlating them with near-surface winds and F10.7 index from the surface up to 10 hPa. He found strong positive correlations of near-surface winds and F10.7 index with T in the equatorial region and northern hemisphere sub-tropics from the upper troposphere to the stratosphere. He observed that near-surface winds and F10.7 index have significant positive correlations with U in stratospheric subtropics. The spatial relationship of ω with near-surface winds and F10.7 index showed a strong downwelling at the equator and upwelling above the Indian region. Kodera also found that the Brewer Dobson circulation (BDC) is weak (strong) during high (low) solar activity. From a previous study of Hood and Soukharev (2003) he concluded that weak BDC increases the temperature of the tropopause region, consequently reducing the convective activity in the equatorial troposphere. It is evident from the above-mentioned studies that solar forcing indirectly causes precipitation anomalies in the Indian and Pacific Ocean. Hence, coupled ocean-atmospheric effects as well as stratospheric dynamics should be considered for studying the influence of the sun on Indian monsoon which can be done by using a coupled atmosphere-ocean-chemistry climate model.
The stratosphere can induce multi-decadal variability in the ocean circulation through the polar vortex, for instance the Atlantic Meridional Overturning Circulation (AMOC) is modulated by stratospheric dynamics (see, Reichler et al. 2012). Reichler et al. (2012) suggested that models capable of coupling stratosphere, troposphere, and ocean can help better predict decadal climate variability. Kodera (2005) also suggested the solar modulation of ENSO through the stratosphere. Keeping in view the dynamical effects of the stratosphere we employ the AOCCM SOCOL-MPIOM for studying the link between ocean modes of variability and ISMR on decadal to multi-decadal timescale.
The key objectives of the present research are to (1) evaluate the AOCCM SOCOL-MPIOM for the Indian monsoon region, (2) evaluate the model skill in simulating ocean modes of variability (e.g., ENSO, AMO, and PDO), (3) study the individual influence of AMO, PDO, and external climate forcings on ISMR, and (4) study the combined influence of AMO and PDO on ISMR. Further, we investigate if the climate model is capable of simulating the combined influence and if this combined influence did exist in the past. Finally, we investigate the stability of relationship of AMO, PDO, and TSI with ISMR.
Section 2 provides an introduction to the climate model, datasets, and methods employed. The climate model evaluation is presented in Sect. 3. Section 3 also presents the statistical analysis for studying the influence of internal climate variability and external climate forcings. Section 4 presents the summary and conclusion.
2 Data and methods
2.1 Model description
In this study we have used the atmosphere-ocean-chemistry-climate model (AOCCM) SOCOL-MPIOM simulations for the period AD 1600–2000. The model has 39 sigma pressure levels (L39) from the surface up to 0.01 hPa (≈80 km). As the model does not simulate the QBO, it was nudged to a QBO reconstruction (Brönnimann et al. 2007). The model has a horizontal resolution of T31 (approximately 3.75° × 3.75°). The horizontal resolution of the ocean component (MPIOM) is nominal 3°, but varies between 22 km (Greenland) and 350 km (Tropical Pacific). The model calculation time step for dynamical processes is 15 min and 144 min for the ocean component. The coupling of the atmosphere and ocean takes place every 24 h (Anet et al. 2013a, b; Muthers et al. 2014).
Four different sets of transient simulations for the period AD 1600–2000 including all major forcings (solar, volcanic, GHGs, and aerosol) have been studied (L1, L2, M1 and M2 simulations of Muthers et al. 2014). The simulations differ by the solar forcing and ocean initial conditions. In all model simulations, solar spectral irradiance reconstructions by Shapiro et al. (2011) have been used, with a strong amplitude (6 W/m2) in the L1 and L2 simulations, and weaker amplitude (3 W/m2) in the M1 and M2 simulations. The amplitude refers to the TSI differences between the Maunder Minimum and present day. Simulations with indices 1 and 2 have different initial ocean conditions. For more details of the model and simulations the reader is referred to Muthers et al. (2014).
The simulations were carried out under the framework of the SNSF (Swiss National Science Foundation) project FUPSOL I (Future and Past Solar Influence on Terrestrial Climate I). In the project we started with a model consisting of only the components for atmosphere and the atmospheric chemistry. Then the ocean model was coupled and to that time, when simulations were started, it was only feasible to simulate a certain number of model years. As the model needs to be run into an equilibrium state (as the initial conditions, except the external forcing, are unknown) and such a simulation is normally several hundreds of years long, it was only possible to simulate the last 400 years. Still the selected period contains the Maunder and the Dalton Minimum, as well as several major volcanic eruptions so that external forcing impacts can be assessed. Due to the high computational demand the model was not applied with higher spatial resolution for any special time slices.
The AOCCM SOCOL-MPIOM is based on the middle atmosphere model MA-ECHAM5 which uses a mass-flux convection scheme based on Tiedtke (1989) with a modification by Nordeng (1994). The applied convection scheme has been checked in previous studies (e.g., Tost et al. 2006; Kucharski et al. 2009; Zhou et al. 2009b). Zhou et al. (2009b) evaluated the performance of various climate models including SOCOL (with mass-flux convection scheme) for Asian-Australian monsoon circulation indices and found that the Webster-Yang-Index, Indian Monsoon Index, Western North Pacific monsoon index, Australian monsoon index, and East Asian monsoon meridional wind index for ensemble mean of 9 SOCOL realizations are significantly positively correlated with observations (CC: ~0.58, ~0.36, 0.37, 0.32, and 0.60 respectively, see, Fig. 3 in Zhou et al. 2009b). Kucharski et al. (2009) used the SOCOL model (with mass-flux convection scheme) for simulating the Indian summer monsoon variability on inter-annual to decadal timescale under the CLIVAR C20C project. They found that the multi-model ensemble can simulate decadal variability of Indian monsoon reasonably well whereas the skill on inter-annual timescale is modest. Annamalai et al. (2007) evaluated 18 global climate models and found that only 6 (including ECHAM5) were capable of realistically reproducing the Asian summer monsoon. They found that all these 6 models have problem in simulating the high rainfall over the west coast of India however relative to observations the ECHAM5 shows a pattern correlation of 0.6 over the Indian monsoon region (7°–30°N, 65°–95°E). These studies indicate that SOCOL which is based on ECHAM5 is well capable of reproducing the monsoon phenomenon.
2.2 Datasets
2.2.1 Global Precipitation Climatology Centre (GPCC)
GPCC Full v7 (Schneider et al. 2015) monthly-totals precipitation data are used over the period AD 1901–2000 for evaluation of the model precipitation for land areas. The GPCC has a horizontal resolution of 0.5° × 0.5°. GPCC precipitation data is provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA (http://www.esrl.noaa.gov/psd/).
2.2.2 Longest instrumental rainfall series of the Indian region (AD 1813–2006)
Sontakke et al. (2008) reconstructed highly quality-controlled area averaged monthly rainfall time series using 316 rain gauges spread across the Indian region. The dataset is available for the period AD 1813–2006 from the website of Indian Institute of Tropical Meteorology (IITM; http://www.tropmet.res.in, hereafter IITM-Precip). This dataset is used for evaluating the model and for further statistical analysis.
2.2.3 Reanalyses datasets
Three reanalyses datasets, the Twentieth Century Reanalysis (20CR; AD 1854–2000) version 2c (v2c) (Compo et al. 2011), ERA-20C (AD 1901–2000; Poli et al. 2015, 2016), and ERA-Interim (AD 1979–2000; Dee et al. 2011) are used. The 20CR v2c (ERA-20C) have a horizontal resolution of 2° × 2° (≈1.25° × 1.25°). The 20CR v2c and ERA-20C monthly mean values of 2-m surface air temperature (SAT), precipitation, 300-hPa geopotential heights (GPH), 500-hPa vertical velocity (omega), and zonal (u) and meridional (v) winds at 850 hPa are used for the evaluation of the model over the period AD 1901–2000. The 20CR v2c precipitation data over the period AD 1854–1999 (hereafter 20CR-Precip) are used to assess the relationship of ISMR with AMO and PDO indices. The ERA-Interim monthly mean precipitation data is also used in the present research. The ERA-Interim dataset has a horizontal resolution of approximately 79 km (T255). The 20CR dataset was provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA (http://www.esrl.noaa.gov/psd/). The ERA-20C and ERA-Interim datasets were downloaded from European Centre for Medium Range Weather Forecasting (ECMWF) web site (http://www.ecmwf.int/).
2.2.4 NOAA Extended Reconstructed Sea Surface Temperature (ERSST)
The ERSST v3b (ERSSTv3b) (Xue et al. 2003; Smith et al. 2007) and ERSST v4 (ERSSTv4) (Huang et al. 2015, 2016; Liu et al. 2014) are used in this study. The v3b and v4 has a global grid with a horizontal resolution of 2° × 2°. The v4 is the latest improved version and is used to evaluate the simulated Niño3, AMO, and PDO indices over the period AD 1901–2000. The NOAA ERSST v3b and v4 data are provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA (http://www.esrl.noaa.gov/psd/).
The PDO and AMO indices based on both v3b and v4 are used to study their relationship with ISMR over the period AD 1854–1999. The PDO index based on v3b and v4 is downloaded from the web site of NOAA National Centers for Environmental Information (NCEI) (http://www.ncdc.noaa.gov/teleconnections/pdo/) whereas for model evaluation it is calculated over the period 1901–2000 using the method of Mantua et al. (1997) (see, Sect. 3.2.3). The two versions of ERSST are used because they produce different results for the relationship of AMO with ISMR and both versions give different PDO indices. Note that the v3b and v4 indicate that PDO prior to 1930 is not well defined and both versions show larger differences especially before 1900 (see Fig. S1).
2.2.5 External climate forcing dataset
All external forcing datasets, i.e., CO2 (Ramaswamy et al. 2001), Tropospheric Aerosol Optical Depth (TropAOD) based on CAM3.5 simulations with a bulk aerosol model driven by fixed SSTs and AD 1850–2000 CMIP5 emissions (S. Bauer, personal communication, 2011), Stratospheric Aerosol Optical Depth (StratAOD) in the visible band as proxy for the volcanic activity (Arfeuille et al. 2014), and TSI (Shapiro et al. 2011) are obtained from the input of the AOCCM SOCOL-MPIOM. All these external forcing variables are used for temporal and spatial correlation analysis.
2.3 Methods
The AOCCM SOCOL-MPIOM is evaluated for ISMR (JJAS), atmospheric circulation, and ocean indices using observational, reanalyses, and reconstructed datasets. For comparison purposes the model dataset is re-gridded to GPCC/20CR/ERA-20C/ERA-Interim/ERSST datasets using bilinear interpolation. The geographic domain selected for evaluation purposes covers an area between 6°N–40°N and 56°E–100°E as shown in Fig. 1. For comparing the similarity between the model output and observational datasets, the root mean squared (rms) error, bias (model minus observations), and pattern correlation are used. To check the periodicities of ocean indices (Niño3, AMO, and PDO) the power spectrum is calculated using the Fast Fourier Transform as in the built-in MATLAB function (fft). The significance is tested using the power spectrum of a red noise process as null hypothesis. For calculating the temporal correlation coefficients, ISMR is averaged over 5.56°N–35.25°N and 67.5°E–97.5°E (land and ocean) for the model simulation, over 8.25°N–34.75°N and 68.25°E–96.75°E (land only) for GPCC, and over 6.66°N–35.24°N and 67.5°E–97.5°E (land and ocean) for 20CR-Precip.
Mean precipitation climatology in mm/day (AD 1951–2000 from a–d and AD 1979–2000 in e; shaded) for a L1, b ERA-20C, c 20CR and d GPCC. Contours (interval 4 mm/day) in b-e show difference of precipitation of L1 with ERA-20C, 20CR, GPCC, and ERA-Interim respectively. Topographical differences (in meters) between f model and 20CR
The ensemble of four 400-year (AD 1600–1999) climate model simulations is the basis to study the temporal and spatial correlations of de-trended and low-pass filtered (11-year running mean) monsoon precipitation with de-trended and low-pass filtered internal climate variability and external climate forcings. The low pass filter removes the first and the last 5 years. The effective number of degrees of freedom (EDF) for the low-pass filtered datasets is calculated by dividing the total number of observations with the window size of the moving average filter. We also calculated the EDF using the autoregressive approach of Quenouille (1952) and Chen (1982) which in most cases generated larger EDF than our method. Therefore, the statistical significance is tested using two-tailed Student t-test at the EDF calculated by our method.
The statistically significant decadal to multi-decadal timescales anomalies of ISMR are identified using Cramer’s t-test statistic as described by Kripalani et al. (2003). We compare these statistically significant wet and dry decades of ISMR with phases (positive or negative) of AMO, PDO, and TSI. To study the joint influence of AMO and PDO, composites are estimated according to Joshi and Rai (2015). The statistical significance of composite anomalies is tested using the Wilcoxon rank sum test. Finally, the stationarity of relationship of AMO, PDO and TSI with ISMR is investigated using running correlation with a 51-yr running window. The significance of the running correlations is tested by using Monte Carlo simulation. For the original time series we generate 5000 surrogate samples using Corrected Amplitude Adjusted Fourier Transform (CAAFT) algorithm which is a conservative approach for significance testing (Kugiumtzis 2002). Unless otherwise stated all temporal and spatial correlations shown are Spearman’s rank correlation coefficients.
3 Results
3.1 Climatology of Indian Summer Monsoon (ISM)
3.1.1 Precipitation
We compared the 100-year (AD 1901–2000) and 50-year (AD 1951–2000) mean climatology of ISMR for the AOCCM SOCOL-MPIOM, ERA-20C, 20CR, and GPCC but found no considerable differences over these two time periods (not shown). Therefore, here we will show the model evaluation with ERA-20C, 20CR, and GPCC for the period AD 1951–2000, whereas with ERA-Interim over the period AD 1979–2000. The four ensemble members (L1, L2, M1, and M2) of the model do not differ from each other in their 50-year mean climatology (not shown); thus for model evaluation we will mostly show results for the L1 simulation. The spatial pattern of ISMR in L1 (shading; Fig. 1a) resembles with that of ERA-20C (shading; Fig. 1b), 20CR (shading; Fig. 1c), GPCC (shading; Fig. 1d), and ERA-Interim (shading; Fig. 1e) over most parts of the Indian monsoon region except over the Western Ghats where the model fails to capture the spatial pattern of relatively higher rainfall. The difference of the L1 mean precipitation with ERA-20C (contours; Fig. 1b), 20CR (contours; Fig. 1c), GPCC (contours; Fig. 1d), and ERA-Interim (contours; Fig. 1e) shows that the model underestimates the precipitation over Hilly regions, the Western Ghats, the Himalayan Region, Northeast India, and over the west coast of Myanmar, which may be due to the lower spatial resolution and topographical differences of the model (Fig. 1f). As compared to GPCC for most parts of the Indian region the precipitation differences are within ±4 mm/day. Thus, except the Western Ghats we can be relatively more confident about subsequent results for most parts of India, Afghanistan, Pakistan, the Tibetan Plateau, and the Arabian Sea where model reasonably captures the spatial pattern and also the precipitation differences are comparatively lower, or approximately zero over some regions.
Although the ERA-20C and 20CR mean summer precipitation climatology show a spatial pattern similar to that of GPCC, both reanalyses also underestimate precipitation over the Western Ghats, Himalaya, Northeast India, and the west coast of Myanmar. The model’s topography over most parts of the Tibetan Plateau, central parts of India, and the Western Ghats is lower than in 20CR whereas it is higher over the foothills of Himalayas, and western part of the Tibetan Plateau (Fig. 1f). The model ensemble mean shows a bias (rms error) of −0.93 (2.48) mm/day, −1.61 (3.97) mm/day, −1.18 (3.88) mm/day, −5.82(8.59) mm/day with ERA-20C, 20CR, GPCC, and ERA-Interim respectively. In general, the model simulates the ISMR reasonably well as evident from the pattern correlation of four ensemble members with ERA-20C (L1: 0.82, L2: 0.82, M1: 0.82, M2: 0.82), 20CR (L1: 0.76, L2: 0.76, M1: 0.77, M2: 0.77), ERA-Interim (L1: 0.82, L2: 0.82, M1: 0.81, M2: 0.82), and GPCC (L1: 0.67, L2: 0.67, M1: 0.67, M1: 0.67), thus the model can be used for studying the ISMR.
The comparison of the model mean annual cycle of precipitation, averaged over the period AD 1951–2000, with GPCC, ERA-20C, 20CR, and the instrumental dataset (IITM-Precip) for the selected geographic domain is presented for land (Fig. 2a), land and ocean (Fig. 2b), and within the political boundary of India (Fig. 2c). Although the model’s monthly mean summer (JJAS) precipitation is higher compared to other seasons it underestimates summer rainfall compared to GPCC, ERA-20C, 20CR, and IITM-Precip. It appears that the model is better in simulating the precipitation for seasons other than for summer. This could be due to the low resolution and the convection scheme of the model. Tost et al. (2006) employed several convection schemes, including the mass-flux convection scheme, on atmospheric chemistry general circulation model ECHAM5/MESSy. They found that these convection schemes are capable of reproducing the observed rainfall patterns, however except the convection parametrisation of the ECMWF; these schemes have significant problems over the Himalaya/Tibet region owing to the complex topography of this region. Despite all the problems our model simulates the annual cycle of precipitation reasonably well.
The ensemble mean annual cycle of the model shows an rms error of 0.69 (0.68/1.06) mm/day with GPCC (ERA-20C/20CR) over the geographic domain shown in Fig. 1d (Fig. 1b, c), whereas, within the political boundary of India, the ensemble mean annual cycle of model shows an rms error of 1.47 (1.08/1.42) mm/day with GPCC (ERA-20C/20CR) and 1.44 mm/day with IITM-Precip. The model ensemble mean for JJAS within the political boundary of India has a deficit of 55, 24, 21, and 15% with ERE-Interim, GPCC, 20CR, and ERA-20C respectively. The large deficit of the model with ERA-Interim is due to the reason that relative to GPCC ERA-Interim overestimates the monsoon precipitation by 40%.
3.1.2 Vertical velocity
To evaluate the model skill for simulating the ascending and descending air during JJAS, we have compared the 500-hPa vertical velocity of the model (shading; Fig. 3a) with ERA-20C (shading; Fig. 3b) and 20CR (shading; Fig. 3c) for the time period AD 1951–2000 over the selected geographic domain. The spatial pattern of 500-hPa vertical velocity is mostly consistent with ERA-20C with only differences in the magnitude. The strong ascending motions can be seen over the Western Ghats, Himalayas, and parts of Northeast India and Myanmar whereas descending vertical velocities are evident over the Rajasthan region, Pakistan, and Afghanistan. The model underestimates the vertical velocity over Western Ghats, the Himalayan region, Northeast India, west coast of Myanmar, and the Bay of Bengal (positive contours; Fig. 3b, c) which can be one of the reasons that model underestimates precipitation over these regions. The overestimation of vertical velocity can be seen over the Tibetan Plateau and northern part of Pakistan (negative contours; Fig. 3b, c). The difference of vertical velocity is approximately zero over Rajasthan, central parts of India, and Arabian Sea. The ensemble member L1 shows a bias (rms error) of 0.01 (0.03) Pa/s, and 0.02 (0.08) Pa/s with ERA-20C and 20CR, respectively. The model simulates the vertical velocity reasonably well as evident from the pattern correlation of L1 with ERA-20C (0.73). The model has lower pattern correlation with 20CR (0.35) which may be due to the reason that in contrast to ERA-20C, 20CR does not reasonably simulate vertical velocities over the Hilly regions, parts of Central-Northeast and Northeast India, and parts of Myanmar and the Tibetan Plateau.
JJAS mean climatology (AD 1951–2000) of ISM: vertical velocity (Pa/s; shaded) for a L1, b ERA-20C, and 20CR (c), contours (interval 0.04 Pa/s) in b–c show difference of vertical velocity of L1 with ERA-20C, and 20CR respectively; SAT (°C; shaded) and geopotential height at 300 hPa (gpm; contours) for d L1, e ERA-20C and f 20CR; LLJ at 850 hPa with direction (arrows) and magnitude (m/s; shaded) for g L1, h ERA-20C and i 20CR. The zonal and meridional components of 850 hPa wind are used to calculate the magnitude and direction of LLJ using Fathom toolbox provided by David L Jones (http://www.marine.usf.edu/user/djones/)
3.1.3 Surface air temperature
The comparison of the 50-yr (AD 1951–2000) mean climatology of JJAS SAT is presented for L1 simulation (shading; Fig. 3d), ERA-20C (shading; Fig. 3e), and 20CR (shading; Fig. 3f). There is a good coherence of the SAT pattern between the L1 simulation and ERA-20C/20CR. The highest temperatures can be seen over Northwest India whereas a temperature gradient between the warm plains of India and the cold mountains of the Tibetan Plateau is also represented. The model has a bias (rms error) of 3.45 (4.92) °C with ERA-20C, and 1.53 (3.01) °C with 20CR, respectively. The pattern correlation between the L1 simulation and ERA20-C (20CR) is 0.92 (0.94) for SAT. The model has good skill for SAT and can be used for further analysis of ISMR.
3.1.4 Geopotential height
We compare the GPHs of the L1 simulation (contours; Fig. 3d) with ERA-20C (contours; Fig. 3e), and 20CR (contours; Fig. 3f) at 300 hPa over the selected geographic domain for the period AD 1951–2000. The 300-hPa GPHs are higher over Northwest India and Northeast India compared to the Indian Peninsula, West-Central India, and most parts of the Tibetan Plateau in L1 simulation which shows the presence of a trough over Northwest India and a ridge over the Tibetan Plateau. Resembling the reanalyses datasets, the model simulates the presence of a trough over India and an anticyclone over the Tibetan Plateau (Fig. 3d). However, the model overestimates 300-hPa GPHs in comparison to ERA-20C and 20CR. The model has a bias (rms error) of 130.6 (133.1) gpm with ERA-20C, and 71.2 (78.1) gpm with 20CR, respectively. The pattern correlation between the L1 simulation and ERA20-C (20CR) is 0.81 (0.70) for 300 hPa GPH. Thus, the simulated GPHs can be used for further analysis of the ISMR.
3.1.5 Low Level Jet (LLJ)
To evaluate the model skill for simulating the LLJ during JJAS, we have compared the 850 hPa wind of the model (Fig. 3g) with ERA-20C (Fig. 3h) and 20CR (Fig. 3i) for the time period AD 1951–2000 over the selected geographic domain. There is a good coherence between the L1 simulation and ERA-20C/20CR for spatial pattern of LLJ. The rms error is 2.02 (2.26) m/s for u850 between the model and ERA-20C (20CR). The rms error is 1.67 (1.79) m/s for v850 between the model and ERA-20C (20CR). The pattern correlation between L1 simulation and ERA-20C (20CR) is 0.92 (0.90) for u850 and 0.81 (0.84) for v850. The model has good skill for simulating the zonal and meridional winds over the Indian monsoon region and can be used for studying the ISMR.
3.2 Ocean variability modes
3.2.1 El Niño Southern Oscillation (ENSO)
We compare the JJAS mean spatial pattern (AD 1901–2000) between the simulated SSTs and ERSSTv4 over the Niño3 region (5°N–5°S, 150°W–90°W) (Fig. 4a, b). To cover the area between 5°N–5°S and 150°W–90°W the SSTs both for model and ERSSTv4 are re-gridded to 1° × 1° using bilinear interpolation. The mean climatology of Niño3 for all ensemble members (L1, L2, M1, and M2) is very similar, therefore we show spatial pattern only for L1.The bias (rms) of four simulations (L1, L2, M1, & M2) with ERSSTv4 is −0.45, −0.50, −0.47, −0.43 °C (1.12, 1.17, 1.14, 1.13 °C) and the pattern correlations are 0.61, 0.67, 0.64, and 0.63, respectively, over the Niño3 region. The spectral analyses of Niño3 index based on model simulations and ERSSTv4 shows statistically significant ENSO periodicities between 2- and 7-year (Fig. S2a–e).
We conclude that the model can reasonably simulate SSTs over the Niño3 region; however, the cold bias relative to observations is visible.
3.2.2 Atlantic Multi-decadal Oscillation (AMO)
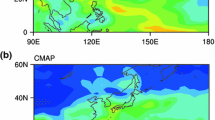
The model-skill for simulating the AMO spatial pattern (Fig. 5a, b, and S3) is evaluated using ERSSTv4 over the period AD 1901–2000 (the filtering of data from AD 1901–2000 reduces it to AD 1906–1995). The AMO index is calculated by using the method of Enfield et al. (2001). First, the global (60°N–60°S) SST anomalies (relative to 1951–1980) are calculated and then SST anomalies are averaged, de-trended, and low pass filtered (11-year running mean) over the north Atlantic region (0°N–60°N, 0°W–80°W). The spatial pattern is calculated by correlating the AMO index with de-trended and low pass filtered (11-year running mean) global SST anomalies (60°N–60°S). The AMO calculated using ERSST hereafter is referred to as AMO-ERSST.
The warming present over the North Atlantic both in the simulated (Fig. 5a and S3a-c) and observed (Fig. 5b) spatial pattern is a characteristic feature of the AMO. The model seems to capture the AMO spatial pattern reasonably well. The simulated spatial pattern of AMO shows statistically significant positive correlations over the Indian Ocean and equatorial Pacific which is not evident in the observed pattern. Luo et al. (2011) used the Bergen Climate Model Version 2.0 to study the influence of the AMO on Indian summer monsoon and found that the simulated spatial pattern of the AMO over the South Atlantic and Indian Ocean is warmer compared to the observed spatial pattern. They attributed this warming to the limitation in the observational data owing to dearth of long instrumental records. Other climate models also show a similar kind of warming over the Indian Ocean (see, Lu et al. 2006; Msadek et al. 2011).
The spectral analyses of the AMO index performed for the four model simulations and the observational datasets show statistically significant multi-decadal periodicity of ~50-year (Fig. S4a-e). The model has reasonable skill in simulating the AMO and hence can be used to study the influence of AMO on ISMR.
3.2.3 Pacific Decadal Oscillation (PDO)
The model is evaluated with respect to the PDO over the period AD 1901–2000 (the filtering of data from AD 1901–2000 reduces it to AD 1906–1995). The PDO index has been calculated as described by Lapp et al. (2012) who followed the method of Mantua et al. (1997). The 1st Principal Component (PC) from the Empirical Orthogonal Function (EOF) analysis of monthly residuals over the north Pacific is used as PDO index. The residuals are obtained by subtracting global (60°N–60°S) monthly SST anomalies (relative to 1961–1990) from monthly SST anomalies (relative to 1961–1990) over the PDO region (20°N–60°N, 120°E–90°W). The simulated PDO spatial pattern is evaluated using ERSSTv4. The PDO calculated using ERSST hereafter is referred to as PDO-ERSST.
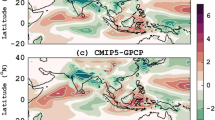
The model simulates the PDO spatial pattern reasonably well for all four simulations (Fig. 6a and S5a–c) compared to the observed PDO spatial pattern (Fig. 6b). Cold anomalies extend from the central to the western Pacific and warm anomalies are centred over the eastern Pacific. The simulated warm anomalies (Fig. 6a and S5a–c) in the eastern Pacific resemble the observed anomalies (Fig. 6b) whereas the simulated cold anomalies are more centred over the western Pacific. The variances explained by the modelled EOFs (L1: 18.1%, L2: 19.8%, M1: 20.8%, M2: 20.2%) are also comparable to that of the observed EOF (20.7%).
Observed and simulated PDO spatial patterns from 1901 to 2000 a L1, b ERSSTv4. The numbers in the braces show the variance explained by each EOF over the north Pacific region. The spatial correlations of PDO Index with de-trended low pass filtered global SST anomalies for c L1, and d ERSSTv4. Stippling indicates correlations significant at 90%. The EDF are 9 for L1 and ERSSTv4. The EOF is calculated by using PCAtool provided by Guillaume Maze (http://www.mathworks.com/matlabcentral/fileexchange/17915-pcatool)
The PDO index is correlated with de-trended and low pass filtered (11-year running mean) global (60°N–60°S) SST anomalies for observed and simulated datasets (Fig. 6c, d, and S5d–f). Global spatial patterns for L2 and M2 simulations show low SSTs over some parts of the equatorial Pacific region compared to the observed pattern. The global spatial pattern for the M1 simulation is almost similar to the observed one. The spectral analyses of PDO index performed for four model simulations shows statistically significant decadal to multi-decadal scale periodicities (~10 to 50 year), which are reasonably comparable with observed periodicities (Fig. S6a–e). The model has reasonable skill in simulating the PDO and hence can be used to study the influence of PDO on ISMR.
3.3 Relation of ISMR with internal climate variability and external climate forcings
3.3.1 ENSO and its effect on ISMR
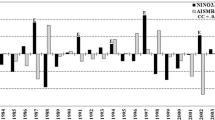
The ISMR is found to be negatively correlated with Niño3 index which is well simulated by the model (Fig. 7). The mean climatological relationship between standardized anomalies of Niño3 index (averaged over 5°N–5°S and 150°W–90°W) and ISMR over the period AD 1901–2000 for model simulations (Fig. 7a–d), 20CR-Precip (Fig. 7e), GPCC (Fig. 7f), and IITM-Precip (Fig. 7g) is presented in Fig. 7. The observed Niño3 standardized anomalies are calculated using ERSSTv4 and then correlated with 20CR-Precip, GPCC, and IITM-Precip. Ample rainfall occurs over the Indian region during the years when Niño3 anomalies are <−1 and ISMR anomalies are >+1, whereas dry events occur when Niño3 anomalies are >1 and ISMR anomalies are <−1 (red dots in Fig. 7a–g) (Kumar et al. 2006). The simulated correlation coefficients (L1:−0.49; L2: −0.26; M1: −0.43; M2: −0.49) reasonably coincide with the observed relationship (20CR-Precip: −0.28, GPCC: −0.60, IITM-Precip: −0.59) between Niño3 and ISMR. All these correlation coefficients are significant at 95% using two-sided Student t-test, and bootstrap method. Thus, the model is suitable for studying the relationship of ISMR with ENSO.
Correlation between standardized anomalies of ISMR and Niño3 over the time period AD 1901–2000 for a L1, b L2, c M1, d M2, e 20CR, f GPCC and g IITM-Precip. Red dots indicate the drought events and green line is a linear fit between ISMR and Niño3 anomalies. Correlation coefficients are shown above each figure with significance at 95% (Student t-test and bootstrap method)
3.3.2 Spatial and temporal correlations of ISMR with AMO and PDO
The negative temporal correlation of ISMR with PDO is successfully simulated by the model (except for M2) and is comparable with the observational dataset (Table 1; Fig. 8). In general, PDO is negatively correlated with the Indian monsoon as can be seen in L1, L2, and M1 simulations (Fig. 8 upper horizontal panel). Statistically significant (at 90% confidence level) negative spatial correlations are observed over parts of India, Pakistan, the Tibetan Plateau, Arabian Sea, and Bay of Bengal. The precipitation spatial pattern of PDO in M2 simulation is considerably different than the other three simulations (L1, L2, and M1). As noticed in Sect. 3.2.3 that the global spatial pattern of PDO shows reduced SSTs over parts of equatorial Pacific which could be a reason that M2 does not show negative spatial correlations over most parts of India. Our findings are consistent with Krishnamurthy and Krishnamurthy (2013) who in climate model (CCSM4) simulations for the period AD 1850–2005 found negative correlations over most parts of India except over Northeast India. Contrary to the findings of Krishnamurthy and Krishnamurthy (2013), in general all ensemble members show negative correlations over Northeast India. This inconsistency may be due to the reason that model largely underestimates precipitation and 500 hPa vertical velocities over the Northeast India.
The model successfully simulates the positive correlation of ISMR with AMO only in L1 and is comparable with observational findings (Table 1; Fig. 8). The spatial correlations between AMO and ISMR are not consistent among the four ensemble members (Fig. 8 lower horizontal panel) and compared to that of PDO are less homogeneous. The L1 simulation compared to other simulations shows stronger positive spatial correlations between AMO and precipitation. The negative spatial correlations between AMO and ISMR are also evident over various parts. Statistically significant (at 90% confidence level) positive influence of AMO is observed over the foothills of the Himalayas, over parts of West-Central India, Central-Northeast India, Myanmar, the Arabian Sea, and the Bay of Bengal. Three model simulations (L1, L2, and M1) indicate positive correlations over the southern part of Northeast India, parts of Central-Northeast India, Nepal, Bhutan, and Myanmar region.
By using climate model simulations (CCSM4 model simulations for the period AD 1850–2005) and an observational dataset (IMD gridded data for the period AD 1901–2004) Krishnamurthy and Krishnamurthy (2015) found positive rainfall anomalies over central and northern part of India, whereas negative rainfall anomalies over the Indian Peninsula (consistent with L2, M1 and M2 simulations) were found during the positive phase of AMO. In climate model simulations for the twentieth century (Zhang and Delworth 2006) also found a strengthening of rainfall over West-Central India (consistent with L1 and M2). However, Zhang and Delworth (2006) and Wang et al. (2009) found decreased rainfall in the north during the positive phase of AMO, which is not consistent with the findings of Krishnamurthy and Krishnamurthy (2015). Wang et al. (2009) also found increased rainfall over central and southern India in climate model simulations. Using Bergen Climate Model (BCM) Luo et al. (2011) found enhanced rainfall over central India and Indian Peninsula; however, they identified an opposite pattern over north India for JJA over the time period 1850–1999. Some other studies based on climate models by Sutton and Hodson (2007), Knight et al. (2006), and Lu et al. (2006) showed increased rainfall over north India but reduced rainfall over central India during positive phase of AMO. All these studies indicate inconsistent results over Indian region. Lu et al. (2006) found enhancement of precipitation over the Southeast Asia (Myanmar) in Hadley Centre Coupled Model version 3 (HadCM3) which is consistent with the four model simulations of this study for southern part of Myanmar. They found that the warm phase of AMO causes positive SST anomalies over the eastern Indian Ocean and Maritime continent. Based on the current and aforementioned climate model studies we conclude that the influence of AMO on ISMR is not conspicuous and homogeneous over the Indian monsoon region.
3.3.3 Spatial and temporal correlations of ISMR with external climate forcings
In order to see the influence of external forcings on ISMR we spatially and temporally correlate the ISMR with external forcings (Fig. S7). Only the L1 and M2 simulations show statistically significant positive temporal correlations between ISMR and TSI. The observational data (IITM-Precip; AD 1854–1999) also shows a statistically non-significant weak positive correlation between ISMR and TSI (Table 1). We do not see statistically significant (at 90% confidence level) positive/negative spatial correlations between TSI and ISMR over the Indian region except over the southern part of West-Central India in M2. We conclude that there is no conspicuous linear correlation of TSI with precipitation over the Indian region.
CO2 shows statistically significant positive temporal correlation with ISMR only in L1 which could be due to stronger influence of CO2 on precipitation over the Arabian Sea. The observed precipitation (IITM-Precip, AD 1854–1999) shows a statistically non-significant negative temporal correlation with CO2 (Table 1). Statistically significant (at 90% confidence level) positive spatial correlations between ISMR and CO2 are observed over parts of Central-Northeast India, Myanmar, and Arabian Sea.
The temporal and spatial correlations between ISMR and TropAOD are very similar to that of ISMR with CO2. The observed precipitation (IITM-Precip, AD 1859–1994) has statistically non-significant negative correlation (Table 1) with TropAOD.
The spatial correlations of StratAOD with ISMR are mostly statistically non-significant positive in L2, M1, and M2, and statistically non-significant negative in L1 over the Indian region. The observed and simulated temporal correlations are also not statistically significant (Table 1).
In general, we do not see statistically significant strong spatial correlations between ISMR and external climate forcings.
3.3.4 Combined influence of AMO, PDO, and TSI on ISMR
We explore the combined relationship of AMO, PDO, and TSI with ISMR using instrumental (IITM-Precip: AD 1854–1999), and climate model simulated (AD 1600–1999) datasets. We identify statistically significant wet and dry decades of ISMR in model simulations and instrumental dataset by using Cramer’s test statistics with 11-yr running window and compare the mean of each 11-yr running window with the overall mean of the data (AD 1600–1999 for model and AD 1854–1999 for IITM-Precip) (Fig. 9).
Decadal to multi-decadal scale anomalies of ISMR along co-variability with TSI, PDO and AMO for a L1, b L2, c M1, d M2 and e IITM-Precip with PDO and AMO indices based on ERSSTv3b f IITM-Precip with PDO and AMO indices based on ERSSTv4. Brown bars indicate dry events for simultaneous PDO+ and AMO− phases. Green bars indicate dry events for simultaneous TSI−, PDO+, and AMO- phases. The numeric values above each figure towards left in braces indicate the correlation coefficients of ISMR with TSI, PDO, and AMO. The numeric values above each figure towards right show the total number of dry events, dry events during PDO+ and AMO−, and dry events during TSI−, PDO+ and AMO− respectively. For model anomalies have been calculated over land and ocean (5.56°N–35.25°N, 67.5°E to 97.5°E)
The wet (blue curves) and dry (red curves) decades in four model simulations and instrumental data along with co-variability of AMO (magenta line), PDO (cyan line), and TSI (black line) with 11-year running Cramer’s t-value are presented in Fig. 9. As expected, the wet and dry decades of ISMR in the individual model simulations do not coincide with each other as the effects of external forcings are smaller than that of internal variability. It is worth noting that out of 24 statistically significant dry events (decades) in four model simulations (1600 years of model simulations), 22 occur during negative phase of AMO and a simultaneous positive phase of PDO, 18 dry periods occur during simultaneous negative phase of TSI, positive phase of PDO, and negative phase of AMO, 23 (23) dry periods occur during negative (positive) phase of AMO (PDO), and 20 dry periods occur during negative phase of TSI (Table 2). In model simulations and observations several other statistically non-significant dry events also occur during simultaneous positive phase of PDO and negative phase of AMO (Fig. 9, brown bars).
Regarding the influence of TSI on ISMR, our findings are consistent with those of Agnihotri, et al. (2011) who, exploited instrumental (AD 1871–2004) and a paleoclimate (AD 1700–2004) dataset, found that most of the dry periods (droughts) of ISMR coincide with decades of low solar activity, whereas the wet periods are likely to occur during decades of high solar activity. Out of twelve decades of low TSI seven occurred in parallel with severe dry periods.
Our findings are also consistent with Joshi and Rai (2015) who, using the IMD gridded dataset, found that the simultaneous opposite phases of AMO and IPO can cause wet and dry periods depending upon the sign of the phase. Thus, our climate model based study confirms the previous observational findings of Joshi and Rai (2015) and provides additional evidence of the combined effect of AMO and PDO on ISMR.
Further, it is interesting to note that the intense and prolonged dry period around AD 1900 in the observational dataset (Fig. 9e) occurred when both TSI and AMO were negative and PDO was positive. However, it could be an artifact of the ERSST data because PDO is not well defined prior to AD 1930. The climate model simulations (except for M1) also show a dry period around AD 1900 with simultaneous positive phase of PDO and negative phases of AMO and TSI. Other than this particular dry epoch (around AD 1900), several intense and prolonged dry periods in model simulations tend to occur when PDO is positive and AMO and TSI are simultaneously negative. We postulate that the dry period around AD 1900 is due to statistically significant stronger positive anomalies of PDO and negative anomalies of AMO and TSI.
3.3.5 Composites of ISMR during different phases of AMO and PDO
To further verify the combined influence of AMO and PDO on ISMR in the long-term climate model simulations we compute composites of ISMR under various regimes of AMO and PDO as defined by Joshi and Rai (2015) i.e. Regime1 (positive AMO and positive PDO), Regime2 (positive AMO and negative PDO), Regime3 (negative AMO and negative PDO), and Regime4 (negative AMO and positive PDO). The statistical significance is tested at 80% confidence level as done by Joshi and Rai (2015).
It is observed that during Regime2 (Regime4) the rainfall increases (decreases) over most parts of India in all model simulations except in M2 (Fig. 10e–h, m–p) consistent with observational findings of Joshi and Rai (2015). The Regime1 (Fig. 10a–d) shows an overall reduced precipitation whereas Regime3 (Fig. 10i–l) indicates enhanced precipitation. It appears that the positive (negative) phase of PDO in Regime1 (Regime3) dominates over the positive (negative) phase of AMO in Regime1 (Regime3). In general, PDO seems to have a dominant effect on ISMR as compared to that of AMO. Further, we compare these four regimes by the individual composites corresponding to the phase of AMO and PDO alone in that regime (Joshi and Rai 2015). It seems that, in general, Regime1 (+ AMO, +PDO) produces less rainfall (in L1, L2 and M1; Fig. S8a-d) compared to positive phase of AMO-alone and more rainfall compared to positive phase of PDO-alone (in L1, M1, M2; Fig. S8e-h), Regime2 (+ AMO, -PDO) produces more rainfall compared to positive phase of AMO-alone (in L1, L2, and M1; Fig. S9a–d) and the negative phase of PDO-alone (in L1, L2, and M1; Fig. S9e–h), Regime3 (-AMO, -PDO) produces more rainfall than the negative phase of AMO-alone (L1, L2, M1; Fig. S8i-l) and less rainfall than the negative phase of PDO-alone (L1, L2, M1; Fig. S8m-p), and Regime4 (-AMO, +PDO) produces less rainfall compared to the negative phase of AMO (L1, L2, M1, M2; Fig. S9i-l) and positive phase of PDO (in L1, M1, M2; Fig. S9m-p). Again the results for M2 are not consistent with other three ensemble members (L1, L2, and M1) that may be due to lower SSTs over parts of equatorial Pacific as evident in global spatial pattern of PDO (Fig. S5f).
Composites of standardized anomalies of ISMR for four model simulations for Regime1 (a–d), Regime2 (e–h), Regime3 (i–l) and Regime4 (m–p). Black stippling indicates significance at 80% using Wilcoxon rank sum test. Significance of anomalies for regimes is tested relative to the whole period AD 1600–1999
When AMO and PDO are out of phase their positive/negative influence on ISMR is reinforced depending upon the phase whereas when both are in phase PDO seems to play a dominating role and suppresses the influence of AMO. From all the above analyses we conclude that the joint effect of AMO and PDO on ISMR is not restricted to the twentieth century (as found by Joshi and Rai 2015) and can be seen in long-term model simulations.
3.3.6 Stationarity of relationship of ISMR with AMO, PDO, and TSI
By employing the model simulated (AD 1600–1999) and observational (IITM-Precip and ERSSTv4; AD 1854–1999) datasets, running correlations of ISMR with AMO, PDO, and TSI are calculated using a 51-yr running window (Fig. 11). The purpose is to analyse if the precipitation maintains the stationarity in sign and magnitude of its overall temporal correlations (as shown in Table 1) with TSI, PDO, and AMO. The examination of the running correlations indicates that the overall temporal positive correlations of ISMR with AMO and TSI are non-stationary over time, and fluctuate between positive and negative values, whereas there is consistent and stable negative correlation (statistically significant over most of the time windows) between ISMR and PDO with variations in its magnitude.
51-yr running correlations between ISMR and a AMO, b PDO, c TSI in model simulations and observational (IITM-Precip and ocean indices calculated from ERSSTv4) datasets. The dashed lines indicate the correlation coefficient critical values for corresponding running correlations to be significant at 90%
Wu and Hu (2015), using reconstructed and long-term model simulated (CCSM4) datasets, found a non-stationary relationship between AMO and ISMR. The non-stationary relationship between AMO and ISMR may be due to more dominating influence of PDO than that of AMO on ISMR as noticed in Sect. 3.3.5. In a monsoon reconstruction over the period AD 600–1550, Berkelhammer et al. (2010) found that on multi-decadal timescales the sun-monsoon relation is non-stationary and exists only for the period AD 950–1300. They posited that multi-decadal variability of North Atlantic SSTs is the main driver of multi-decadal variability of ISMR and solar activity plays a nominal role. However, here we do not find any evidence of a consistent positive relationship of AMO with ISMR. Berkelhammer et al. (2010) hypothesized that variations in the ocean atmosphere system (e.g., ENSO) may disrupt or strengthen the relationship between ISMR and TSI and cause a non-stationary relationship between them. We propose that the Pacific Ocean atmosphere system may also disturb the relationship between AMO and ISMR which requires further investigation.
Various studies have shown that ocean modes of variability (e.g., AMO, PDO, and ENSO) are tele-connected and influence the variability of each other (e.g., Schneider and Cornuelle 2005; Newman 2007; Zhang et al. 2007; Wu et al. 2011; Frauen and Dommenget 2012; Kang et al. 2014; Kayano and Capistrano 2014). These ocean modes of variability, especially AMO and ENSO, are also found to be influenced by external forcings (e.g., Meehl et al. 2009; Narashima and Bhattacharyya 2010; Otterå et al. 2010; Zanchettin et al. 2012; Knudsen et al. 2014; Pausata et al. 2015). This presents a convoluted picture of the dynamics of the ISMR with ocean modes of variability and external forcings. Thus, stationarity of the relationship of the ISMR with ocean modes of variability not just depends on internal variability of ISMR but also on the complex interaction among the ocean modes and their link to external forcings. The modulation of the ocean modes by any means may change the nature as well as stationarity of their relationship with ISMR.
The AOCCM SOCOL-MPIOM reasonably simulated the spatial and temporal patterns of ocean modes of variability as well as the climatological patterns of the Indian summer monsoon. Further, the model has the necessary components (e.g., ocean, atmosphere, and chemistry) to simulate the dynamical effects of external forcings on atmosphere and ocean which can help understand the lack of stationarity of relationship between ISMR and ocean modes. The non-stationarity of the relationship of the AMO and TSI with ISMR may pose further challenges to reliably predict the ISMR. Though more coupled climate model studies are needed, from present investigation the PDO turns out to be a relatively more reliable factor for prediction of ISMR on decadal to multi-decadal timescales.
4 Summary and conclusions
We evaluate the AOCCM SOCOL-MPIOM for the Indian monsoon and assess the influence of internal and external climate forcings on temporal and spatial variability of ISMR. Additionally, the combined influence of AMO and PDO on ISMR is investigated on decadal to multi-decadal time scales over the period AD 1600–1999.
The model simulates the spatial pattern of ISMR reasonably well with major differences of precipitation over the Western Ghats, the Himalayan region, and western coast of Myanmar. The ERA-20C/20CR data also underestimate ISMR over these elevated areas. The observed relationship of ISMR with various ocean indices (Niño3, AMO, and PDO) holds within the model, however the relationship of ISMR with PDO does not exist in 20CR-Precip. We conclude that our model has reasonable capability to simulate the ocean indices and their relation with ISMR, atmospheric circulation over the Indian monsoon region, and the combined influence of AMO and PDO on ISMR.
The climate model simulations with AOCCM SOCOL-MPIOM show a weakening of ISMR during positive phase of the PDO; however, the linear relationship of ISMR with AMO is not conspicuous. The decadal to multi-decadal timescales anomalies of ISMR in climate model simulations indicate the individual as well as combined effect of AMO, PDO, and TSI on dry/wet periods over Indian region. The AMO, PDO, and TSI seem to play a significant role in controlling the dry periods over the Indian region. The combined effect of AMO and PDO seems stronger than that of AMO, PDO, and TSI as more dry periods (22 compared to 18) occur when simultaneously AMO is in negative phase and PDO is in positive phase. Despite the fact that dry decades of monsoon tend to occur during the simultaneous negative phase of AMO and positive phase of PDO, and during negative phases of TSI, we conclude that the sign of correlation of ISMR with AMO and TSI is not stationary over time.
In general, we do not see statistically significant strong spatial correlations between ISMR and external climate forcings. The temporal correlation between TSI and ISMR is positive both in observational (statistically not significant) and climate model simulations (statistically significant in L1 and M2). The observed precipitation shows statistically significant negative temporal correlations with CO2 and StratAOD.
Despite the low spatial resolution of the model, it reasonably simulates the spatial and temporal patterns of ocean modes of variability. Although the model largely underestimates the ISMR, it realistically reproduces the spatial patterns of its climatology and can further help in understanding the physical processes that govern the decadal to multi-decadal scale variability of the ISMR. Further, in future the model can be used for understanding the influence of solar activity and volcanic eruptions on ocean modes owing to its ability to simulate them and to couple the dynamical effects of the stratosphere with ocean and the troposphere.
References
Agnihotri R, Dutta K, Bhusan R, Somayajulu BLK (2002) Evidence for solar forcing on the Indian monsoon during the last millennium. Earth Planet Sc Lett 198:521–527. doi:10.1016/S0012-821X(02)00530-7
Agnihotri R, Dutta K, Soon W (2011) Temporal derivative of Total Solar Irradiance and anomalous Indian summer monsoon: an empirical evidence for a Sun-climate connection. J Atmos Sol-Terr Phy 73(13):1980–1987. doi:10.1016/j.jastp.2011.06.006
Anchukaitis KJ, Buckley BM, Cook ER (2010) Influence of volcanic eruptions on the climate of the Asian monsoon region. Geophys Res Lett 37(22). doi:10.1029/2010GL044843
Anet JG, Muthers S, Rozanov EV, Raible CC, Peter T, Stenke A, Shapiro AI, Beer J, Steinhilber F, Brönnimann S, Arfeuille FX, Brugnara Y, Schmutz W (2013a) Forcing of stratospheric chemistry and dynamics during the Dalton Minimum. Atmos Chem Phys 13:10951–10967. doi:10.5194/acp-13-10951-2013
Anet JG, Rozanov EV, Muthers S, Peter T, Brönnimann Stefan, Arfeuille FX, Beer J, Shapiro AI, Raible CC, Steinhilber F, Schmutz WK (2013b) Impact of a potential 21st century “grand solar minimum” on surface temperatures and stratospheric ozone. Geophys Res Lett 40(16). doi:10.1002/grl.50806
Annamalai H, Hamilton K, Sperber KR (2007) The South Asian summer monsoon and its relationship with ENSO in the IPCC AR4 simulations. J Clim 20:1071–1092. doi:10.1175/JCLI4035.1
Arfeuille F, Weisenstein D, Mack H, Rozanov E, Peter T, Brönnimann S (2014) Volcanic forcing for climate modeling: a new microphysics-based data set covering years 1600-present. Clim Past 10:359–375. doi:10.5194/cp-10-359-2014
Berkelhammer M, Sinha A, Mudelsee M, Chang H, Edwards RL, Cannariato K (2010) Persistent multidecadal power of the Indian summer monsoon. Earth Planet Sc Lett 290:166–172. doi:10.1016/j.epsl.2009.12.017
Bhattacharyya S, Narasimha R (2005) Possible association between Indian monsoon rainfall and solar activity. Geophys Res Lett 32(L05813). doi:10.1029/2004GL021044
Bhattacharyya S, Narasimha R (2007) Regional differentiation in multidecadal connections between Indian monsoon rainfall and solar activity. J Geophys Res 112(D24103). doi:10.1029/2006JD008353
Booth BBB, Dunstone NJ, Halloran PR, Andrews T, Bellouin N (2012) Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 484(7393):228–232. doi:10.1038/nature10946
Brönnimann S, Annis JL, Vogler C, Jones PD (2007) Reconstructing the quasi-biennial oscillation back to the early 1900s. Geophys Res Lett 34(L22805). doi:10.1029/2007GL031354
Chen WY (1982) Fluctuations in northern hemisphere 700mb height field associated with the Southern Oscillation. Mon Weather Rev 110:808–823. doi:10.1175/1520-0493(1982)110<0808:FINHMH>2.0.CO;2
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ, Yin X, Gleason BE, Vose RS, Rutledge G, Bessemoulin P, Brönnimann, S, Brunet M, Crouthamel RI, Grant AN, Groisman PY, Jones PD, Kruk M, Kruger AC, Marshall GJ, Maugeri M, Mok HY, Nordli Ø, Ross TF, Trigo RM, Wang XL, Woodruff SD, Worley SJ (2011) The Twentieth Century Reanalysis Project. Quarterly J Roy Meteorol Soc 137:1–28. doi:10.1002/qj.776
Dee DP, Uppalaa SM, Simmonsa AJ, Berrisforda P, Polia P, Kobayashib S, Andraec U, Balmasedaa MA, Balsamoa G, Bauera P, Bechtolda P, Beljaarsa ACM, van de Bergd L, Bidlota J, Bormanna N, Delsola C, Dragania R, Fuentesa M, Geera AJ, Haimbergere L, Healya SB, Hersbacha H, Hólma EV, Isaksena L, Kallbergc P, Köhlera M, Matricardia M, McNallya AP, Monge-Sanzf BM, Morcrettea JJ, Parkg BK, Peubeya C, de Rosnaya P, Tavolatoe C, Thèpauta JN, Vitarta F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J Roy Meteor Soc 137:553–597. doi:10.1002/qj.828
Enfield DB, Mestas-Nunez AM, Trimble PJ (2001) The Atlantic Multidecadal Oscillation and its relationship to rainfall and river flows in the continental U.S. Geophys Res Lett 28:2077–2080. doi:10.1029/2000GL012745
Feng S, Hu Q (2008) How the North Atlantic Multidecadal Oscillation may have influenced the Indian summer monsoon during the past two millennia. Geophys Res Lett 35(L01707). doi:10.1029/2007GL032484
Frauen C, Dommenget D (2012) Influences of the tropical Indian and Atlantic Oceans on the predictability of ENSO. Geophys Res Lett 39(L02706). doi:10.1029/2011GL050520
Goswami BN (2006a) The Asian monsoon: Interdecadal variability. In: Wang B (ed) The Asian monsoon. Springer, Berlin Heidelberg, pp 295–328
Goswami BN, Madhusoodanan MS, Neema CP, Sengupta D, (2006b) A physical mechanism for North Atlantic SST influence on the Indian summer monsoon. Geophys Res Lett 33(2). doi:10.1029/2005GL024803
Gupta AK, Anderson DM, Overpeck JT (2003) Abrupt changes in the Asian southwest monsoon during the Holocene and their links to the North Atlantic Ocean. Nature 421:354–357. doi:10.1038/nature01340
Hood LL, Soukharev BE (2003) Quasi-decadal variability of the tropical lower stratosphere: the role of extratropical wave forcing. J Atmos Sci 60:2389–2403. doi:10.1175/1520-0469(2003)060<2389:QVOTTL>2.0.CO;2
Huang B, Banzon VF, Freeman E, Lawrimore J, Liu W, Peterson TC, Smith TM, Thorne PW, Woodruff SD, Zhang HM (2015) Extended Reconstructed Sea Surface Temperature version 4 (ERSST.v4): part I. upgrades and intercomparisons. J Clim 28:911–930. doi:10.1175/JCLI-D-14-00006.1
Huang B, Thorne P, Smith T, Liu W, Lawrimore J, Banzon V, Zhang H, Peterson T, Menne M (2016) Further exploring and quantifying uncertainties for Extended Reconstructed Sea Surface Temperature (ERSST) Version 4 (v4). J Clim 29:3119–3142. doi:10.1175/JCLI-D-15-0430.1
Joshi MK, Pandey AC (2011) Trend and spectral analysis of rainfall over India during 1901–2000. J Geophys Res 116(D06104). doi:10.1029/2010JD014966
Joshi MK, Rai A (2015) Combined interplay of Atlantic multidecadal oscillation and the interdecadal Pacific oscillation on rainfall and its extremes over Indian subcontinent. Clim Dynam 44:3339–3359. doi:10.1007/s00382-014-2333-z
Kang IS, No HH, Kucharski F (2014) ENSO amplitude modulation associated with the mean SST changes in the tropical Central Pacific induced by Atlantic Multidecadal Oscillation. J Clim 27:7911–7920. doi:10.1175/JCLI-D-14-00018.1
Kayano MT, Capistrano VB (2014) How the Atlantic multidecadal oscillation (AMO) modifies the ENSO influence on the South American rainfall. Int J Climatol 34(1):162–178. doi:10.1002/joc.3674
Knight JR, Folland CK, Scaife AA (2006) Climate impacts of the Atlantic Multidecadal Oscillation. Geophys Res Lett 33(L17706). doi:10.1029/2006GL0262
Knudsen MF, Jacobsen BH, Seidenkrantz MS, Olsen J (2014) Evidence for external forcing of the Atlantic Multidecadal Oscillation since termination of the Little Ice Age. Nat Commun 5(3323). doi:10.1038/ncomms4323
Kodera K (2004) Solar influence on the Indian Ocean monsoon through dynamical processes. Geophys Res Lett 31(L24209). doi:10.1029/2004GL020928
Kodera K (2005) Possible solar modulation of the ENSO cycle. Pap Meteorol Geophys 55(1/2):21–32. doi:10.2467/mripapers.55.21
Kripalani RH, Kulkarni A, Singh SV (1997) Association of the Indian summer monsoon with the northern hemisphere mid-latitude circulation. Int J Climatol 17:1055–1067. doi:10.1002/(SICI)1097-0088(199708)17:10<1055::AID-JOC180>3.0.CO;2-3
Kripalani RH, Kulkarni A, Sabade SS, Khandekar ML (2003) Indian monsoon variability in a global warming scenario. Nat Hazards 29(2):189–206. doi:10.1023/A:1023695326825
Krishnamurthy V, Goswami BN (2000) Indian monsoon-ENSO relationship on interdecadal time scales. J Clim 13:579–595. doi:10.1175/1520-0442(2000)013<0579:IMEROI>2.0.CO;2
Krishnamurthy L, Krishnamurthy V (2013) Influence of PDO on South Asian summer monsoon-ENSO relation. Clim Dynam 42(9–10):2397–2410. doi:10.1007/s00382-013-1856-z
Krishnamurthy L, Krishnamurthy V (2014) Decadal scale oscillations and trend in the Indian monsoon rainfall. Clim Dynam 43:319–331. doi:10.1007/s00382-013-1870-1
Krishnamurthy L, Krishnamurthy V (2015) Teleconnection of Indian monsoon rainfall with AMO and Atlantic Tripole. Clim Dynam 46(7): 2269–2285. doi:10.1007/s00382-015-2701-3
Krishnan R, Sugi M (2003) Pacific decadal oscillation and variability of the Indian summer monsoon rainfall. Clim Dynam 21:233–242. doi:10.1007/s00382-003-0330-8
Kucharski F, Scaife AA, Yoo JH, Folland CK, Kinter J, Knight J, Fereday D, Fischer AM, Jin EK, Kröger J, Lau NC, Nakaegawa T, Nath MJ, Pegion P, Rozanov E, Schubert S, Sporyshev PV, Syktus J, Voldoire A, Yoon JH, Zeng N, Zhou T (2009) The CLIVAR C20C project: skill of simulating Indian monsoon rainfall on interannual to decadal timescales. Does GHG forcing play a role? Clim Dynam 33(5):615–627. doi:10.1007/s00382-008-0462-y
Kugiumtzis D (2002) Surrogate data test on time series. In: Soofi AS, Cao L (ed) Modelling and forecasting financial data: techniques of nonlinear dynamics, Springer, US, pp 267–282
Kumar KK, Rajagopalan B, Hoerling M, Bates G, Cane M (2006) Unraveling the mystery of Indian monsoon failure during El Niño. Science 314:115–119. doi:10.1126/science.1131152
Lapp SL, Jacques SJM, Elaine BM, David SJ (2012) GCM projections for the Pacific Decadal Oscillation under greenhouse forcing for the early 21st century. Int J Climatol 32(9):1423–1442. doi:10.1002/joc.2364
Li S, Perlwitz J, Quan X, Hoerling MP (2008) Modelling the influence of North Atlantic Multidecadal warmth on the Indian summer rainfall. Geophys Res Lett 35(L05804). doi:10.1029/2007GL032901
Liu J, Wang B, Ding Q, Kuang X, Soon W, Zorita E (2009) Centennial variations of the global monsoon precipitation in the last millennium: results from ECHO-G model. J Climate 22:2356–2371. doi:10.1175/2008JCLI2353.1
Liu W, Huang B, Thorne PW, Banzon VF, Zhang HM, Freeman E, Lawrimore J, Peterson TC, Smith TM, Woodruff SD (2014) Extended reconstructed sea surface temperature Version 4 (ERSST.v4): part II. parametric and structural uncertainty estimations. J Clim 28:931–951. doi:10.1175/JCLI-D-14-00007.1
Lu R, Dong B, Ding H (2006) Impact of the Atlantic Multidecadal Oscillation on the Asian summer monsoon. Geophys Res Lett 33(L24701). doi:10.1029/2006GL027655
Luo F, Li S, Furevik T (2011) The connection between the Atlantic Multidecadal Oscillation and the Indian summer monsoon in Bergen Climate Model Version 2.0. J Geophys Res 116(D19117). doi:10.1029/2011JD015848
Man W, Zhou T, Jungclaus JH (2014) Effects of large volcanic eruptions on global summer climate and East Asian monsoon changes during the last millennium: analysis of MPI-ESM simulations. J Clim 27:7394–7409. doi:10.1175/JCLI-D-13-007
Mantua NJ, Hare ST (2002) The Pacific Decadal Oscillation. J Ocenogr 58(1):35–44. doi:10.1023/A:1015820616384
Mantua NJ, Hare SR, Zhang Y, Wallace JM, Francis RC (1997) A Pacific interdecadal climate oscillation with impacts on salmon production. Bull Amer Meteor Soc 78:1069–1079. doi:10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2
Meehl GA, Arblaster JM, Matthes K, Sassi F, Loon HV (2009) Amplifying the Pacific climate system response to a small 11-year solar cycle forcing. Science 325(5944). doi:10.1126/science.1172872
Mehta VM, Lau WKM (1997) Influence of solar irradiance on the Indian monsoon-ENSO relationship at decadal-multidecadal time scales. Geophys Res Lett 24(2):159–162. doi:10.1029/96GL03778
Mooley DA, Parthasarathy B (1984) Fluctuations in all India summer monsoon rainfall during 1871–1978. Clim Change 6:287–301. doi:10.1007/BF00142477
Msadek R, Frankignoul C (2009) Atlantic multidecadal oceanic variability and its influence on the atmosphere in a climate model. Clim Dynam 33:45–62. doi:10.1007/s00382-008-0452-0
Msadek R, Frankignoul C, Li LZX (2011) Mechanism of the atmospheric response to North Atlantic multidecadal variability: a model study. Clim Dynam 36:1255–1276. doi:10.1007/s00382-010-0958-0
Muthers S, Anet JG, Stenke A, Raible C, Rozanov E, Brönnimann S, Peter T, Arfeuille FX, Shapiro AI, Beer J, Steinhilber F, Brugnara Yuri, Schmutz W (2014) The coupled atmosphere-chemistry-ocean model SOCOL-MPIOM. Geoscientific Model Dev 7(5):2157–2179. doi:10.5194/gmd-7-2157-2014
Narashima R, Bhattacharyya S (2010) A wavelet cross-spectral analysis of solar-ENSO rainfall connections in the Indian monsoons. Appl Computational Harmonic Anal 28:285–295. doi:10.1016/j.acha.2010.02.005
Newman M (2007) Interannual to decadal predictability of tropical and North Pacific sea surface temperatures. J Clim 20:2333–2356. doi:10.1175/JCLI4165.1
Nordeng TE (1994) Extended versions of the convective parameterization scheme at ECMWF and their impact on the mean and transient activity of the model in the tropics. Technical Memorandum 206, ECMWF, Reading, UK
Otterå OH, Bentsen M, Drange H, Suo L (2010) External forcing as a metronome for Atlantic multidecadal variability. Nat Geosci 3(10):688–694
Pausata FS, Chafik L, Caballero R, Battisti DS (2015) Impacts of high-latitude volcanic eruptions on ENSO and AMOC. Proc Natl Acad Sci USA 112(45):13784–13788. doi:10.1073/pnas.1509153112
Poli P, Hersbach H, Berrisford P, Dee DP, Simmons A, Laloyaux P (2015) ERA-20C Deterministic. ERA Report Series 20
Poli P, Hersbach H, Dee DP, Berrisford P, Simmons AJ, Vitart F, Laloyaux P, Tan DGH, Peubey C, Thépaut J-N, Trémolet Y, Hólm EV, Bonavita M, Isaksen L, Fisher M (2016) ERA-20C: an atmospheric reanalysis of the twentieth century. J Clim 29:4083–4097. doi:10.1175/JCLI-D-15-0556.1
Quenouille MH (1952) Associated measurements. Academic, New York
Ramaswamy V, Boucher O, Haigh J, Hauglustaine D, Haywood J, Myhre G, Nakajima T, Shi GY, Solomon S (2001) Radiative forcing of climate change. In: Houghton J, Ding Y, Griggs D et al (eds) IPCC Third Assessment Report: Climate Change 2001. Cambridge University Press, Cambridge, pp 350–416
Reichler T, Kim J, Manzini E, Kröger J (2012) A stratospheric connection to Atlantic climate variability. Nat Geosci 5:783787. doi:10.1038/ngeo1586
Roy SS, Goodrich GB, Jr RCB (2003) Influence of El Nino/Southern oscillation, Pacific Decadal Oscillation, and local sea-surface temperature anomalies on peak season monsoon precipitation in India. Clim Res 25:171–178. doi:10.1002/joc.2065
Schneider N, Cornuelle BD (2005) The forcing of the Pacific Decadal Oscillation. J Clim 18:4355–4373. doi:10.1175/JCLI3527.1
Schneider U, Becker A, Finger P, Meyer-Christoffer A, Rudolf B, Ziese Ma (2015) GPCC Full Data Reanalysis Version 7.0 at 0.5°: monthly land-surface precipitation from rain-gauges built on GTS-based and historic data. doi:10.5676/DWD_GPCC/FD_M_V7_050
Shapiro AI, Schmutz W, Rozanov E, Schoell M, Haberreiter M, Shapiro AV, Nyeki S (2011) A new approach to the long-term reconstruction of the solar irradiance leads to large historical solar forcing. Astron Astrophys 529(A67). doi:10.1051/0004-6361/201016173
Smith TM, Reynolds RW, Peterson TC, Lawrimore J (2007) Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J Clim 21:2283–2296. doi:10.1175/2007JCLI2100.1
Sontakke NA, Singh N, Singh HN (2008) Instrumental period rainfall series of the Indian region (1813–2005): revised reconstruction, update and analysis. The Holocene 18(7):1055–1066. doi:10.1177/0959683608095576
Sutton R, Hodson DLR (2007) Climate response to basin-scale warming and cooling of the North Atlantic Ocean. J Clim 20:891–907. doi:10.1175/JCLI4038
Tiedtke M (1989) A comprehensive mass flux scheme for cumulus parameterization in largescale models. Mon Weather Rev 117:1779–1800. doi:10.1175/1520-0493(1989)117<1779:ACMFSF>2.0.CO;2
Tost H, Jöckel P, Lelieveld J (2006) Influence of different convection parameterisations in a GCM. Atmos Chem Phys 6:5475–5493. doi:10.5194/acp-6-5475-2006
Verma RK, Subramaniam K, Dugam SS (1985) Interannual and long-term variability of the summer monsoon and its possible link with northern hemispheric surface air temperature. Proc Indian acad Sci (Earth Planet Sci) 94(3):187–198. doi:10.1007/BF02839197
Wang Y, Li S, Luo D (2009) Seasonal response of Asian monsoonal climate to the Atlantic Multidecadal Oscillation. J Geophys Res 114(D02112). doi:10.1029/2008JD010929
Wegmann M, Brönnimann S, Bhend J, Franke J, Folini D, Wild M, Luterbacher J (2014) Volcanic influence on European summer precipitation through monsoons: possible cause for “Years without Summer”. J Clim 3683–3691. doi:10.1175/JCLI-D-13-00524.1
Wei W, Lohmann G (2012) Simulated Atlantic Multidecadal oscillation during the. Holocene J Climate 25(20):6989–7002. doi:10.1175/JCLI-D-11-00667.1
Wu Q, Hu Q (2015) Atmospheric circulation processes contributing to a multidecadal variation in reconstructed and modeled Indian monsoon precipitation. J Geophys Res-Atmos 120(2):532–551. doi:10.1002/2014JD022499
Wu S, Liu Z, Zhang R (2011) On the observed relationship between the Pcific Decadal Ocillation and the Atlantic Multi-decadal Oscillation. J Oceanogr 67:27–35. doi:10.1007/s10872-011-0003-x
Xue Y, Smith TM, Reynolds RW (2003) Interdecadal changes of 30-year SST normals during 1871–2000. J Clim 16:1601–1612
Zanchettin D, Timmreck C, Graf HF, Rubino A, Lorenz S, Lohmann K, Krüger K, Jungclaus JH (2012) Bi-decadal variability excited in the coupled ocean-atmo-sphere system by strong tropical volcanic eruptions. Clim Dynam 39(1–2): 419–444. doi:10.1007/s00382-011-1167-1
Zhang R, Delworth TL (2006) Impact of Atlantic Multidecadal Oscillations on India/Sahel rainfall and Atlantic hurricanes. Geophys Res Lett 33(L17712). doi:10.1029/2006GL026267
Zhang R, Delworth TL (2007) Impact of Atlantic multidecadal oscillation on north Pacific climate variability. Geophys Res Lett 34(L23708): doi:10.1029/2007GL031601
Zhang R, Delworth TL, Sutton R, Hodson DLR, Dixon KW, Held IM, Kushnir Y, Marshall J, Ming Y, Msadek R, Robson J, Rosati AJ, Ting MF, Vecchi GA (2013) Have aerosols caused the observed Atlantic multidecadal variability? J Atmos Sci 70(4):1135–1144. doi:10.1175/JAS-D-12-0331.1
Zhou T, Brönnimann S, Griesser T, Fischer AM, Zou L (2009a) A reconstructed dynamic Indian monsoon index extended back to 1880. Clim Dynam 34:573–585. doi:10.1007/s00382-009-0552-5
Zhou T, Wu B, Scaife AA, Brönnimann S, Cherchi A, Fereday D, Fischer AM, Folland CK, Jin KE, Kinter J, Knight JR, Kucharski F, Kusunoki S, Lau LC, Li L, Nath MJ, Nakaegawa T, Navarra A, Pegion P, Rozanov E, Schubert S, Sporyshev P, Voldoire A, Wen X, Yoon JH, Zeng N (2009b) The CLIVAR C20C project: which components of the Asian-Australian monsoon circulation variations are forced and reproducible? Clim Dynam 33:1051–1068. doi:10.1007/s00382-008-0501-8
Acknowledgements
We acknowledge support from the Federal Commission for Scholarships for Foreign Students for the Swiss Government Excellence Scholarship (ESKAS No. 2013.0516) for the academic year(s) 2013-16/17, SNF project FUPSOL2 (CRSII2-147659), and the EC FP7 project ERA-CLIM2: 607029. We are grateful to NOAA/OAR/ESRL PSD, Boulder, Colorado, USA (http://www.esrl.noaa.gov/psd/) for providing GPCC, 20CR, and ERSST datasets. We are also thankful to the Indian Institute of Tropical Meteorology for providing the homogeneous Indian monsoon rainfall dataset, and the anonymous reviewers for improving the manuscript through their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Malik, A., Brönnimann, S., Stickler, A. et al. Decadal to multi-decadal scale variability of Indian summer monsoon rainfall in the coupled ocean-atmosphere-chemistry climate model SOCOL-MPIOM. Clim Dyn 49, 3551–3572 (2017). https://doi.org/10.1007/s00382-017-3529-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-017-3529-9