Abstract
The statistical characteristics of the atmospheric internal variability (hereafter internal atmospheric noise) for surface pressure (PS) in twentieth century simulations of a coupled general circulation model are documented. The atmospheric noise is determined from daily post-industrial (1871–1998) Community Climate System Model 3 simulations by removing the SST and externally forced responses from the total fields. The forced responses are found from atmosphere-only simulations forced by the SST and external forcing of the coupled runs. However, we do not address the influence of the SST variability on the synoptic scale high frequency weather noise.The spatial patterns of the main seasonal modes of atmospheric noise variability are found for boreal winter and summer from empirical orthogonal function analyses performed globally and for various regions, including the North Atlantic, the North Pacific, and the equatorial Pacific. The temporal characteristics of the modes are illustrated by power spectra and probability density functions (PDF) of the principal components (PC). Our findings show that, for two different realizations of noise, the variability is dominated by large scale spatial structures of the atmospheric noise that resemble observed patterns, and that their relative amplitudes in the CGCM and AGCM simulations are very similar. The regional expression of the dominant global mode, a seasonally dependent AO-like or AAO-like pattern is also found in the regional analyses, with similar time dependence. The PCs in the CGCM and the corresponding SST forced AGCM simulations are uncorrelated, but the spectra and PDFs of the CGCM and AGCM PCs are similar.The temporal structures of the noise PCs are white at timescales larger than few months, so that these modes can be thought of as stochastic forcings (in time) for the climate system. The PDFs of the noise PCs are not statistically distinguishable from Gaussian distributions with the same standard deviation. The PDFs do not change substantially between the first and second half of the twentieth century.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
An important role for intrinsic atmospheric noise (equivalently “noise” or “atmospheric noise” in the following) in forcing climate variability, and in particular, SST variability, was proposed by Hasselmann (1976). Hasselmann’s single-point model represented forcing of SST by atmospheric noise as a specified white noise heat flux. The model solutions demonstrate that the large heat capacity of the ocean filters out the high frequencies, leading to a red noise SST response for intermediate frequencies and a white noise response for low frequencies that resembles the spectrum of observed SST variability.
Figure 1 illustrates Hasselmann’s mechanism through the solution to
where T represents the temperature of a slab mixed layer ocean of depth H, density \(\rho\), and heat capacity c. The atmosphere is represented by the forcing N, and linear damping of T with coefficient \(\lambda\). The forcing N is taken to be white in frequency \(\omega\), with dependence on \(\omega\) given by \(N\left( \omega \right) = Re\left( {N_{\omega } e^{i\omega t} } \right)\) and \(\left| {N_{\omega } } \right| = N_{0}\), where N 0 is constant. Taking \(T\left( \omega \right) = Re\left( {T_{\omega } e^{i\omega t} } \right)\), the solution to (1) is then \(T_{\omega } = \frac{{N_{\omega } }}{\lambda + i\omega \rho cH}\), and the power spectrum of the solution for T is
Power spectrum of response of \({\mathbf{T}}_{{\varvec{\upomega}}}\) to white noise forcing, for an H = 50 m slab mixed layer ocean with damping \({\varvec{\uplambda}}\) = 15 W m−2 K, \({\mathbf{N}}_{0} = 1\) W m−2 Hz−1, from Eq. (2)
The power spectrum (2) is red (\(\propto \omega^{ - 2} )\) for high frequencies, \(\omega \gg \lambda /\left( {\rho cH} \right)\), and white (\(\propto \omega^{0} )\) for low frequencies, \(\omega \ll \lambda /\left( {\rho cH} \right)\). In the red regime, the balance is between heat storage and the noise forcing, so that T and N are in quadrature, while in the white regime (energy balance regime) the balance is between forcing and damping, and T and N are in phase. The values used for the results presented in Fig. 1 are \(\lambda =\) 15 W m−2 K−1, H = 50 m, \(\rho\) = 103 kg m−3, and c = 4.18 \(\times\) 103 J kg−1 deg−1. For these parameters, the power spectrum is red for periods P ≪ 3 year and white for P ≫ 3 year. The power at the 10 year period is about 93% of the power at infinite period, so that the reddening of the spectrum is noticeable even at decadal periods, as is evident in Fig. 1. Viewed in a log–log plot, the turnover from red to white noise is more abrupt and appears to be at a period of about 6 years. As H increases, the turnover moves to longer periods, but the power level in the energy balance regime is not affected, while the red part of the spectrum flattens. This simple example demonstrates that it is plausible that the Hasselmann mechanism can produce reddening of the SST variability out to decadal time scales, even in regions with modest mixed layer depths. However, the simple model is not sufficient to show that this mechanism can explain the observed spectrum, as the choice of parameters H and \(\lambda\) and the amplitude/frequency structure of the atmospheric noise forcing are crucial.
Barsugli and Battisti (1998) developed a stochastically forced single column linear coupled atmosphere–ocean model, where the internal atmospheric noise is represented by a specified stochastic forcing of the atmosphere to simulate the SST response to atmospheric internal variability. That paper demonstrated that if the SST anomalies are forced by the atmospheric noise, the noise and the SST anomalies are linearly simultaneously correlated, and it is therefore not appropriate to use the assumption of no simultaneous correlation of the noise with SST anomalies to infer the atmospheric noise, as has been done by some investigators.
Atmospheric internal noise is also a strong candidate to explain ENSO irregularity and phase locking (Neelin et al. 1998; Kleeman 2008). The stochastic modeling approach has been extended to include the use of linear stochastically forced models for prediction of ENSO SST patterns, with Gaussian white noise forcing representing neglected process including atmospheric noise (Penland and Magorian 1993).
In atmospheric simulations forced by climatological SST and constant external forcing, that is, when there is are no SST anomalies, all of the simulated atmospheric variability can be thought of as intrinsic noise. In this case, a single long simulation can be used to infer the properties of the noise. Schneider and Kinter (1994) examined properties of the noise in this way in multi-century simulations with a low resolution AGCM. They found polar-trapped zonally symmetric modes as the leading EOFs of the global surface pressure, similar to what are now known as the Arctic Oscillation (AO) and the Antarctic Oscillation (AAO). Deser (2012) made a 10,000 year run of the CAM3 AGCM with current day external forcing and climatological SST and chose a measure of atmospheric noise to be 56-year trends in variables such as sea level pressure in this run. This noise measure was used as a null hypothesis for the detection of externally forced climate change in externally forced CGCM simulations.
The noise evolution is not predictable, however, the noise that has occurred in a model simulation or observations can be diagnosed after the fact. A method consistent with the conceptual model of Barsugli and Battisti (1998) is used here to extract the space and time varying noise from a coupled climate model generated data set. In order to isolate the noise in this situation, the SST and externally forced signals need to be determined and removed. In the following discussion, both analyses of the observed climate system and CGCM simulated fields are referred to as “observations” or “observed”. In this approach, the SST forced signal is taken to be the ensemble mean of an ensemble of atmospheric model simulations forced by the observed SST (“AMIP ensemble”; Gates et al. 1999). The noise in the AMIP ensemble members is uncorrelated with the SST, since the SST is specified and is not affected by the surfaces fluxes from the atmosphere. However, the noise in the observations is expected to be correlated with the observed SST. The noise in an AMIP ensemble member is also uncorrelated with the noise in the other ensemble members. The ensemble averaging reduces the noise in the AMIP ensemble mean compared to the individual ensemble members, but preserves the SST and externally forced signal. The observed noise is then found by removing the time-dependent SST forced signal (the AMIP ensemble mean) from the observational time series. Hurrell et al. (2009) used the above decomposition to evaluate the forced and free (called noise here) precipitation variances in AGCM ensembles from several models forced by observed SST. Results from applying the AMIP ensemble method to determination of the intrinsic atmospheric noise in various fields and some of their gross properties have been reported by Schneider and Fan (2007), where the observations were generated by a long coupled model simulation with constant external forcing using the COLA CGCM; by Fan and Schneider (2012), where the observations were from the 1950–2000 NCEP reanalysis and the forced signal was found from AMIP simulations using the COLA AGCM; by Chen et al. (2013) and Chen and Schneider (2014), where it was shown that noise variance in a long control simulation of the CCSM3 CGCM was indistinguishable from that in the associated AMIP ensemble members, but that only the atmospheric noise evolution in the CGCM was consistent with noise forcing of the SST; and by Colfescu et al. (2013), where the method was extended to evaluating the noise in CCSM3 simulations with estimated twentieth century external forcing.
However, the studies described above did not examine the spatial or temporal properties of the noise in much detail. Here, having gained some confidence that the methodology produces consistent and meaningful results, we examine the statistical properties of the intrinsic atmospheric noise of surface pressure (PS) in twentieth century Community Climate System Model 3 (CCSM3) CGCM simulations more closely.
In particular, the analysis is directed towards comparing the inferred properties of the presumably somewhat realistic CGCM noise to the noise properties assumed in simplest stochastically forced models. The paper seeks to address the following questions: Are the spatial and temporal patterns for the coupled and SST forced simulations similar and how can they be characterized statistically (e.g. as white)?; Are the local noise patterns linked to global noise variability?; Are the noise characteristics for two different noise realizations similar?; Is the noise probability density function Gaussian? Is the noise influenced by the changing external forcing?.
The method can be applied to the analysis of the noise in any prognostic or diagnostic field. In this first study of the more detailed properties of the noise, we have chosen to concentrate on the properties of the noise in the PS field for the boreal winter December–January–February (DJF) and summer June–July–August (JJA) seasons, as the variability and predictability of this field is of general interest to the weather and climate community. In addition, since it is a prerequisite for the validity of the method that the noise statistics in the coupled and uncoupled simulations should be indistinguishable, a more detailed comparison between coupled and uncoupled model results is made than in previous work.
2 Methodology
The experimental design is the same as the one used in Colfescu et al. (2013). The models are the coupled model, the Community Climate System Model (CCSM3) (Collins et al. 2006) and its atmospheric component, the Community Atmosphere Model (CAM3) (Collins 2006b). As in Colfescu et al. (2013) CGCM simulations and AGCM simulations forced with the SST from the CGCM simulations are performed in order to calculate the atmospheric noise.
Two CGCM simulations with differing initial state are analyzed, called Cont1 and Cont2 in the following, covering the 1871–1998 period and forced by the same prescribed twentieth century historical forcing. The purpose of this comparison is to study the stability of the noise statistics when the internally generated SST evolves differently. For each CGCM simulation, an ensemble of six twentieth century externally forced AGCM simulations with SST forcing prescribed from its respective coupled run is performed. The SST and externally forced response (equivalently “forced response”) for each CGCM simulation is defined as the ensemble mean of the AGCM ensemble with same SST. The atmospheric noise in the coupled simulation is obtained by removing its forced response. Therefore, two noise data sets, one for each of the CGCM simulations, are calculated and analyzed. The noise is also evaluated for each AGCM ensemble member using the forced response from the appropriate ensemble mean, leaving out the member for which the noise is being calculated.
December–January–February (DJF) and June–July–August (JJA) seasonal noise is found for the surface pressure (PS) of the CGCM and the AGCM ensemble members. The monthly means are calculated based on daily noise estimates. In order to examine the regional differences in noise patterns, four regions are used as described by Table 1: global domain (GL), Equatorial Pacific (EP), North Pacific (NP) and North Atlantic Ocean (NA).
Although we are performing a comparison of local and global noise patterns, this analysis is a description of the properties of the noise but a mechanistic understanding of the causes (i.e. teleconnections, local mechanisms etc.) found is beyond the scope of the paper.
First, the spatial and temporal structures of the main modes of variability of the noise are studied by calculating the Empirical Orthogonal Functions (EOF), the spatial patterns (normalized) and the corresponding Principal Components (PC), the time series corresponding to the EOFs, of the area-weighted noise fields for each coupled run and their corresponding AGCM members. The first three EOFs and their associated PCs are described here. For the global as well as for the regional EOFs, the total variance explained by these three is about 70%, and the third EOF explains only about 5% of the total variance.
The first part of the analysis examines the spatial properties of the noise EOFs. Also, global regressions of the noise fields (without area weighting) onto the standardized regional noise PCs are performed In order to address the question of local noise linkage with global large scale variability modes.
A spectral analysis of the PCs is performed in order to study the temporal noise behavior. The significance of whether the noise spectra differ from red noise is evaluated in each case using a Markov “red noise” confidence spectrum with upper and lower confidence curves of 5 and 95% respectively.
Probability density functions of the standardized noise PCs are calculated for the whole time period and for the first and last 30 year periods of study to examine the temporal structure of the noise modes and whether their temporal behavior (e.g. extremes) are sensitive to the externally forced climate change. A Monte-Carlo approach is developed and applied to quantify whether the noise PDFs differ from Gaussian structure or from each other.
3 Results
3.1 Noise spatial characteristics: global surface pressure EOF analysis
An EOF analysis of PS is carried out for each of the regions defined in Table 1. The analysis is performed seasonally for DJF/winter and JJA/summer for the two noise realizations found for the coupled runs Cont1 and Cont2 and each of their associated SST forced AGCM ensemble members. The AGCM EOF patterns shown are the averages of the six individual EOF patterns for the associated AGCM ensemble members, which are in fact almost identical in both structure and explained variance.
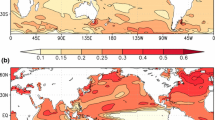
The first, second, and third EOFs for DJF and JJA, for the global domain (GL) and each CGCM simulation (Figs. 2, 3) show similar percentages of explained variance for the AGCM and CGCM (Table 2). Only the explained variances for the Cont1 and its corresponding AGCM ensemble are given in Table 2, since the results for Cont2 are very similar.
Same as in Fig. 2 but for Cont2 and its respective AGCM ensemble mean
In DJF, the dominant modes of variability for Cont1, Fig. 2a–f, show similar patterns for the CGCM and AGCM in the northern Hemisphere and tropical band between 25°S and 25°N. The structure seen in EOF1 can be associated with the Arctic Oscillation, with negative PS anomalies in the Arctic, and opposite sign anomalies with the center of maxima over the Icelandic and Aleutian lows. EOF2 (Fig. 2c, d) is dominated by Antarctic Oscillation patterns in the Southern Hemisphere. The third DJF EOFs, Fig. 3e, f, also show a strong resemblance between the AGCM and CGCM and explain about six percent of the total variance (Table 2). A zonal wavenumber three pattern with maximum amplitude in the region of the Aleutian low and a suggestion of meridional propagation can be seen in EOF3 for both the AGCM and CGCM. The AGCM and CGCM EOFs have a dominant hemisphere in which the pattern is much stronger than the other hemisphere, NH for EOF1 and EOF3, and SH for EOF2. The AGCM and CGCM patterns are very similar in the dominant hemisphere, with weaker agreement in the other hemisphere.
For JJA, Fig. 2g–l, the dominant hemisphere is switched, SH for EOF1 and EOF3 and NH for EOF2. EOF1 has an Antarctic Oscillation-like pattern, EOF2 and Arctic Oscillation, while EOF 3 has a zonal wavenumber 1–2 wavelike structure.
Figure 3 for the noise in Cont2 and its associated AGCM ensemble, shows very similar dominant hemisphere structures to those found for Cont1. This demonstrates that the noise structures and other statistics are not sensitive to the initial conditions, and consequently not sensitive to the different evolutions of the noise and the SST anomalies. Also, in both different CGCM realizations of internal atmospheric noise, the variability is dominated by large scale spatial structures that resemble observed patterns with their relative strengths in the CGCM and associated AGCM simulations being very similar.
We have compared the tropical structures of the CGCM and AGCM EOFs (not shown). High similarity between the two noise realizations is found in this region for the CGCM and AGCM in both noise realizations and both seasons. Moreover, for DJF both the coupled model and AGCM ensemble mean EOF1 show an east–west dipole pattern for the equatorial suggestive of the Southern Oscillation. A similar structure but zonally shifted, can be seen for the second EOF of Cont2 for DJF.
3.2 Noise spatial characteristics: linkage of regional and global noise patterns
Regressions of the PS noise anomalies onto the standardized PS noise PCs for each region were carried out in order examine the spatial structures of the noise and how the noise in the various regions is linked. The patterns found globally as well as for the regional ones for the CGCM and AGCM correspond very well; therefore, only the ones for the CGCM will be shown (Fig. 4). The structures in the global case (not shown) are very similar to the ones of the global EOFs (Fig. 2, the regressions and EOFs would be identical if the regressions were carried out against the area weighted noise).
In both summer and winter, the patterns of the regressions against both the NA and NP PCs are confined to the extratropical Northern Hemisphere. This contrasts with the regressions against the EP PCs, which have substantial amplitude either in both hemispheres (e.g. EP PC1 DJF) or are confined more to the local winter hemisphere (e.g. EP PC2 DJF, PC2 JJA). The regressions against the GL PCs show strong amplitudes in both hemispheres in each season (although not for each regression). Some of the patterns from regressions on PCs from different regions are quite similar. Considering DFJ first, the regressions against NA PC1, NP PC1, and the negative of EP PC2 all have very similar structures, with strong positive centers in the midlatitude North Atlantic and North Pacific, and a zonally uniform negative polar region. There is, however, no analog to this pattern in the DJF GL structures in Fig. 2. The NP PC1 regression Pacific center is stronger and the Atlantic center is weaker than the NA PC1 regression, as might be expected. The EP PC2 regression structure resembles more the NA PC1 regression.
The regression against NP PC2 appears to resemble the one against NP PC1, but in fact is spatially orthogonal by construction, a characteristic mainly related to the southward displacement of the centers of action over the extra topical North Pacific in NP PC2. In fact, the regression against NP PC2 corresponds well in the Northern Hemisphere with that against EP PC1, as well as GL PC1. The regressions against NA PC2 and PC3 are localized in the North Atlantic, while that against NP PC3 is localized in the North Pacific, although there these structures also show evidence of zonal propagation to the other hemisphere. EP PC3 has large amplitude in the Northern Hemisphere extratropics, but no analog (in this limited set of patterns) to NA or NP patterns. We conclude that several of these DJF noise patterns show strong evidence of regional interconnections, since they are found from analyses of noise data in unconnected regions.
For JJA regressions, NA PC1 and NP PC1, and GL PC1 are related, in this case in both hemispheres, but with a Southern Hemisphere emphasis for GL PC1 and stronger amplitude in the Northern Hemisphere for the NA and NP patterns. Also, The EP PC1 and GL PC1 patterns resemble each other in the Southern Hemisphere.
3.3 Noise temporal characteristics: PS noise power spectrum analysis
Power spectra of the PCs are examined to determine if the noise patterns had temporal behavior consistent with white noise, as is commonly assumed in idealized stochastic models. Another aim is to examine whether the CGCM and AGCM spectra are distinguishable from each other, and if so, in what ways.
As noted above, the spatial structures of the first three global or regional spatial patterns/EOFs correspond well between pairs of AGCM ensemble members and between an AGCM member and the associated CGCM. This provides justification that direct comparison between the temporal structures of the associated PCs is meaningful. The ensemble means of the six individual spectra of the PCs for each AGCM ensemble, the envelopes of the individual AGCM spectra and the power spectra for their associated CGCM runs are shown for DJF and JJA in Fig. 5 for Cont1 and Fig. 6 for Cont2. The results are shown for the various regions defined in Table 1 and for the first three modes. The statistical test that the ensemble mean AGCM spectra (dark blue curve in Figs. 5, 6) are different from red noise is uses a Markov red noise spectrum with upper and lower confidence limits of 5 and 95% respectively. Two tests of similarity of the CGCM and the AGCM ensemble mean spectra are first, if the CGCM spectrum is inside the 5 and 95% confidence limits for the AGCM ensemble spectrum, and second, whether the CGCM spectrum is inside of the cloud of spectra of the individual AGCM runs.
Each panel shows power spectrum of Cont1 (red line), average spectra of the six AGCM simulations corresponding to Cont1 (dark blue line) envelope of AGCM ensemble members’ spectra (blue shading) 5 and 95% confidence intervals for the AGCM ensemble mean spectrum (light blue lines) as fitted by an AR1 model (black line). The rows are for the different regions: GL (top), NA (second), North Pacific (third) and Equatorial Pacific (bottom). Columns show PC1 DJF/JJA (columns 1/2); PC2 DJF/JJA (columns ¾); PC3 DJF/JJA (columns 5 and 6). Period is cycles per year
Same as in Fig. 5 but for Cont2 and AGCM2
For both sets of noise realizations none of the PCs shows significant peaks for the ensemble mean of the AGCM spectra. The ensemble mean AGCM spectrum becomes flat, suggesting white noise, for period longer than about 2 years for all regions. The envelope of the spectra of the individual AGCM simulations does exceed the confidence limits, but these peaks and valleys are not consistent, as is evident from the ensemble mean of the spectra. Thus the peaks in the individual AGCM spectra can be interpreted as due to random noise, as expected to occur with 5% probability.
The Cont1 spectra (Fig. 5) and Cont2 spectra (Fig. 6) also have peaks exceeding the confidence limits, but the Cont1 and Cont2s spectra are also generally consistent with the clouds of associated AGCM spectra. Additionally, the significant peaks in Cont1 and Cont2 spectra do not agree. We conclude that there is no compelling evidence that the CGCM or AGCM noise spectra are different from white noise at time scales longer than about two years, and that the CGCM and associated AGCM spectra are indistinguishable. The analysis should be repeated with much larger ensembles of CGCM simulations and much larger ensembles of AGCM simulations to clarify this result.
3.4 Noise temporal characteristics: noise probability density functions
The final issue we address is whether the noise characteristics change as the climate changes. In order to do this PDFs (Probability Density Function) of the noise PCs are constructed for the periods 1871–1901 and 1951–1998, as well as for the total period 1871–1998. A Monte Carlo approach is used to test whether the PDFs are Gaussian and whether their properties differ. The PDFs of the PCs, with 128 moments of time for each, are generated using 23 bins spanning from −4 to +4 standard deviations.
For each of the two periods, the centered, standardized PDFs (i.e. PDfs with the x-axis measured in standard deviations and mean removed from the data) were calculated.
As an example, Figs. 7 and 8 show the PDFs for the global PCs of Cont1 the mean of the PDFs of the associated AGCM ensemble members, and the approximate Gaussian distribution generated from the average of the PDFs of 1000 realizations of standardized random data with the same number of points in each realization as the number of data points in the PCs. The spread of 7 arbitrarily selected PDFs out of the 1000 random noise realizations is shown in yellow and the shaded dark orange color represents the cloud of the 6 AGCM PDFs. The selection of 7 out of the 1000 approximate Gaussians is meant to represent a rough statistical test for the similarity of the PDFs from the noise data to the PDF generated from the same amount of data taken from a Gaussian distribution.
Each panel shows a PDF of standardized data for global domain PCs of Cont1 (red line), mean of PDFs from AGCM PCs (blue line), cloud of AGCM PDFs (orange shading), and cloud of PDFs for random data (yellow). Also shown is the Gaussian distribution generated by averaging the PDFs from 100 realizations of random data. Shown are results for PC1 (left column), PC2 (middle column), PC3 (right column), 1871–1901 DJF (top row), JJA (second row), and 1951–1998 DJF (third row), JJA (bottom row)
Same as in Fig. 7 but for the entire period, 1871–1998
To test if the coupled or SST forced model PDF characteristics are different from those of a Gaussian distribution, the Cont1/Cont2 PDFs and associated AGCM ensemble of PDFs should fall inside the cloud of the Gaussian spread. To test if the CGCM is not different from the AGCMs, the CGCM PDF should fall inside the AGCM PDF cloud.
Figure 7 shows the DJF and JJA PDFs of the PCs found over the global domain for the 1871–1901 and 1951–1998 periods, while Fig. 8 shows the PDFs of the global domain PCs for the whole 1871–1998 period. Both tests produce negative results—the PDFs of the standardized model noise modes are consistent with those generated from random data (temporally white noise). Therefore, differences between the distributions can be detected by applying standard statistical tests evaluating differences between the means and standard deviations.
4 Conclusions
The paper addressed three main questions about the internal atmospheric noise occurring in twentieth century CGCM simulations: (1) What are the spatial characteristics of the noise; (2) What are its temporal characteristics, and in particular can it be represented by a stochastic process; (3) How do the noise characteristics change as climate changes. We chose to analyze the noise in the surface pressure in this initial study, and we compared the noise in the CGCM simulations with that found in AGCM simulations forced by the CGCM SST.
The spatial characteristics of the noise in two twentieth century CGCM simulations and their corresponding AGCM simulations were investigated through EOF analyses. The spatial patterns from the CGCM and corresponding AGCM simulations correspond closely to each other. This result was independent the domain that the EOFs were calculated over, which included global, North Atlantic, North Pacific and the Equatorial Pacific. Several of the patterns found by regression against the PCs of the noise modes show similarity to well known modes of variability such as the NAO, AO, or AAO. Some of the patterns found using the regional PCs corresponded to global patterns, indicating that the dominant regional patterns could be viewed as part of a larger scale coherent phenomenon.
The time variability of the noise was characterized by examining the power spectra of the PCs. These spectra were not distinguishable from white noise at timescales longer than a couple of years. The CGCM spectra were not distinguishable from those of the corresponding AGCM simulations. The probability density functions of the DJF and JJA noise were constructed. We found that their structures were not distinguishable from Gaussian distributions.
The connection between externally forced climate change and changes in the noise was examined by comparing PDFs from the late nineteenth/early twentieth century periods of the simulations with those from the latter half of the twentieth century. The structures of the PDFs could not be distinguished between the two periods. Perhaps changes in the noise PDFs could be detected if the external forcing change was strong enough (e.g. as large as the annual cycle change between DJF and JJA), or if the simulations were long enough (e.g. 1000 year time slice simulations with early vs. late twentieth century external forcing).
We have presented a pilot study of how atmospheric noise might be quantitatively defined and analyzed. This was carried in conjunction with the evaluation of the climate “signal” as determined from AMIP-type AGCM simulations. Our results support that viewing the atmospheric noise as a stochastic additive process is reasonable for the current climate and for the relatively weak changes in external forcing that occurred over the last century.
As this is a first attempt at this type of analysis, we would be happy if our results stimulated further investigations. For example, although in out analysis the SST forced SLP patterns are removed by the analysis, the synoptic scale variability, e.g. the position of the storm tracks, is definitely expected to be influenced by the state of large scale modes. It would be interesting to investigate this issue, which is beyond the scope of this paper. Also, a deeper understanding the dependence of the noise on SST is needed and constitutes an interesting future direction of study as we didn’t directly address it in our analysis.
References
Barsugli JJ, Battisti DS (1998) The basic effects of atmosphere—ocean thermal coupling on midlatitude variability. J Atmos Sci 55:477–493. doi:10.1175/1520-0469(1998)055
Chen H, Schneider EK (2014) Comparison of the SST forced responses between coupled and uncoupled climate simulations. J Clim 27:740–756. doi:10.1175/jcli-d-13-00092.1
Chen H, Schneider EK, Kirtman BP, Colfescu I (2013) Evaluation of weather noise and its role in climate model simulations. J Clim 26:3766–3784. doi:10.1175/JCLI-D-12-00292.1
Colfescu I, Schneider EK, Chen H (2013) Consistency of 20th century sea level pressure trends as simulated by a coupled and uncoupled GCM. Geophys Res Lett 40:3276–3280. doi:10.1002/grl.50545
Collins WD, Rasch PJ, Boville BA, Hack JJ, McCaa JR, Williamson DL, Williamson BPDL, Briegleb BP (2006a) The formulation and atmospheric simulation of the Community Atmosphere Model version 3 (CAM3). J Clim 19:2144–2161
Collins WD et al (2006b) The Community Climate System Model version 3 (CCSM3). J Clim 19:2122–2143. doi:10.1175/JCLI3760.1
Deser C, Phillips A, Bourdette V, Teng H (2012) Uncertainty in climate change projections: the role of internal variability. Clim Dyn 38:527–546. doi:10.1007/s00382-010-0977-x
Fan M, Schneider EK (2012) Observed Decadal North Atlantic Tripole SST Variability. Part I: weather Noise Forcing and Coupled Response. J Atmos Sci 69:35–50. doi:10.1175/JAS-D-11-018.1
Gates W, Boyle J, Covey C, Doutriaux C, Drach R, Fiorino M, Gleckler P, Hnilo J, Marlais S, Phillips T, Potter G, Santer B, Sperber K, Taylor K, Williams D (1999) An overview of the results of the Atmospheric Model Intercomparison Project (AMIP). Bull Amer Meteor Soc 80:29–55
Hasselmann K (1976) Stochastic climate models.Part I:theory. Tellus 28:473–485
Hurrell J, Meehl GA, Bader D, Delworth TL, Kirtman B, Wielicki B (2009) A unified modeling approach to climate system prediction. Bull Am Meteorol Soc 90:1819–1832
Kleeman R (2008) Stochastic theories for the irregularity of ENSO. Philos Trans R Soc A 366:2509–2524
Neelin JD, Battisti DS, Hirst AC, Jin F-F, Wakata Y, Yamagata T, Zebiak SE (1998) ENSO theory. J Geophys Res Oceans 103:14261–14290
Penland C, Magorian T (1993) Prediction of Niño 3 Sea Surface Temperatures Using Linear Inverse Modeling. J Clim 6:1067–1076
Schneider EK, Fan M (2007) Weather noise forcing of surface climate variability. J Atmos Sci 64:3265–3280
Schneider EK, Kinter JL III (1994) An examination of internally generated variability in long climate simulations. Clim Dyn 10:181–204
Acknowledgements
We thank the anonymous reviewers for their constructive and insightful comments on this work. The contributions of Colfescu were supported by the National Center for Atmospheric Science (NCAS). The contributions of Colfescu and Schneider were supported by NSF Grants ATM-0653123. Schneider was also supported by NSF Grant AGS 1338427, NOAA Grant MAPP NA14OAR4310160, and NASA Grant NNX14AM19G. The NCAR CISL and NASA Advanced Super Computer Division provided computer resources for the simulations. Data analyses and plotting were done using NCL and GrADS.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Colfescu, I., Schneider, E.K. Internal atmospheric noise characteristics in twentieth century coupled atmosphere–ocean model simulations. Clim Dyn 49, 2205–2217 (2017). https://doi.org/10.1007/s00382-016-3440-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3440-9