Advertisement

Climate Dynamics

, Volume 48, Issue 9–10, pp 3115–3138 | Cite as

An empirical model for probabilistic decadal prediction: global attribution and regional hindcasts

  • Emma B. Suckling
  • Geert Jan van Oldenborgh
  • Jonathan M. Eden
  • Ed Hawkins
Open Access
Article
First Online:

Abstract

Empirical models, designed to predict surface variables over seasons to decades ahead, provide useful benchmarks for comparison against the performance of dynamical forecast systems; they may also be employable as predictive tools for use by climate services in their own right. A new global empirical decadal prediction system is presented, based on a multiple linear regression approach designed to produce probabilistic output for comparison against dynamical models. A global attribution is performed initially to identify the important forcing and predictor components of the model . Ensemble hindcasts of surface air temperature anomaly fields are then generated, based on the forcings and predictors identified as important, under a series of different prediction ‘modes’ and their performance is evaluated. The modes include a real-time setting, a scenario in which future volcanic forcings are prescribed during the hindcasts, and an approach which exploits knowledge of the forced trend. A two-tier prediction system, which uses knowledge of future sea surface temperatures in the Pacific and Atlantic Oceans, is also tested, but within a perfect knowledge framework. Each mode is designed to identify sources of predictability and uncertainty, as well as investigate different approaches to the design of decadal prediction systems for operational use. It is found that the empirical model shows skill above that of persistence hindcasts for annual means at lead times of up to 10 years ahead in all of the prediction modes investigated. It is suggested that hindcasts which exploit full knowledge of the forced trend due to increasing greenhouse gases throughout the hindcast period can provide more robust estimates of model bias for the calibration of the empirical model in an operational setting. The two-tier system shows potential for improved real-time prediction, given the assumption that skilful predictions of large-scale modes of variability are available. The empirical model framework has been designed with enough flexibility to facilitate further developments, including the prediction of other surface variables and the ability to incorporate additional predictors within the model that are shown to contribute significantly to variability at the local scale. It is also semi-operational in the sense that forecasts have been produced for the coming decade and can be updated when additional data becomes available.

Keywords

Empirical modelling Decadal prediction Hindcast skill 

1 Introduction

Near-term climate prediction, on seasonal to multi-decadal timescales, has been widely recognised as an important field in recent years (Smith et al. 2012; Kirtman et al. 2013; Doblas-Reyes et al. 2013a; Meehl et al. 2014; Kirtman et al. 2014). In theory, good quality near-term regional scale forecasts, with reliable uncertainty estimates, have the potential to inform decisions and activities across sectors that are susceptible to, and influenced by, climate variability and change. This in turn could benefit business, society and the environment (Soares and Dessai 2014). In recent years much progress has been made in the development of seasonal-to-decadal prediction systems based on both dynamical and statistical models (Smith et al. 2007; Weisheimer et al. 2009; Meehl et al. 2010, 2014; van Oldenborgh et al. 2012; Smith et al. 2012, 2013; Doblas-Reyes et al. 2013a, b; Ho et al. 2013b; Eden et al. 2015). Operational forecasting on seasonal timescales is now a regular activity across many forecast centres (Arribas et al. 2011; Stockdale et al. 2011; Saha et al. 2013). Challenges remain for decadal prediction, however, in terms of understanding sources and limits of predictability as well as quantifying forecast uncertainties (Meehl et al. 2009; Doblas-Reyes et al. 2013a; Weisheimer and Palmer 2014).

Seasonal-to-decadal prediction occupies an intermediate ground between weather forecasting and climate projection. It may be characterised as the combination of both an initial condition problem, in which uncertainties arise due to estimating the initial state of the atmosphere, ocean, cryosphere and land surface, and a boundary condition problem, which suffers from uncertainties in the forcings and feedback processes that play a central role in constraining climate projections (Meehl et al. 2009). Figure 1 illustrates this for surface air temperature forecasts at De Bilt, the Netherlands (52°N, 5°E) in terms of the correlation coefficient between forecasts and observations at different time scales: averaged over the first N days, weeks, months and years of the forecasts, from 1-day weather forecasts to 10-year decadal forecasts. For comparison, the skill of a simple persistence forecast is also shown. Weather forecasts, which depend wholly on the initial state, far outperform persistence forecasts. At the other side of the spectrum, 10-year forecasts again show good skill in this measure due to the forced trend. Seasonal-to-decadal forecasts currently have much lower skill and often do not clearly outperform persistence. Delivering reliable predictions on these timescales is particularly challenging on regional scales because internal variability can be large relative to the effects of the initial conditions and signals of change (Hawkins and Sutton 2009).
Fig. 1

Correlation of model forecasts and persistence with observations across time scales for temperatures at De Bilt, the Netherlands (52°N, 5°E). The temperature of the first N days, weeks, months and years, averaged from the analysis time to the indicated time on the x-axis, is verified against the observed temperature. The forecasts used are: 1–10 days: ensemble mean of the ECMWF ensemble prediction system (Palmer et al. 1997) over 2010–2013, 1–3 weeks: KNMI monthly forecasts based on damped persistence from the ECMWF EPS for the first week over 2006–2013, 1–6 months: multi-model mean of the Demeter (Palmer et al. 2004) ECMWF, Met Office and Météo France seasonal hindcasts over 1959–2001, 1–9 years: multi-model mean of the ENSEMBLES (van Oldenborgh et al. 2012) ECMWF, UKMO, Météo France and MPI-MET decadal hindcasts over 1960–2013. Observations are from the KNMI database

Predictability on seasonal-to-decadal timescales is influenced by components of the climate system that evolve at a slower rate than the atmosphere, such as in the ocean and land-surface, as well as by the interactions between them (Palmer and Hagedorn 2006; Boer 2011; Meehl et al. 2009). The coupled ocean-atmosphere El-Niño Southern Oscillation (ENSO) phenomenon is a source of predictability on seasonal timescales (Trenberth et al. 2000; Alexander et al. 2002; van Oldenborgh et al. 2005a; Balmaseda et al. 2009; Weisheimer et al. 2009; Wu et al. 2009), and has been a large factor in the success of seasonal forecasting using both dynamical and statistical models (van Oldenborgh et al. 2005b; Coelho et al. 2006; Weisheimer et al. 2009; Wu et al. 2009). Multidecadal variations of sea surface temperatures (SSTs) in the North Atlantic, often referred to as the Atlantic Multidecadal Oscillation (AMO), as well as the interdecadal Pacific oscillation (IPO) (Power et al. 1999), are sources of potential skill for prediction on decadal timescales (Meehl et al. 2014).

In addition to variations of large-scale dynamical processes such as ENSO and the AMO, evolution of the climate system on seasonal-to-decadal timescales can be considered as externally forced low frequency variability due to natural and anthropogenic forcing superimposed on the natural variability of the system (Smith et al. 2012; Meehl et al. 2014). As such, the development of dynamical seasonal-to-decadal prediction systems has focused not only on simulating responses to external forcing factors, but also on initialisation of model simulations using observations. Initialised prediction has been relatively successful for seasonal forecasting, however the advantages are less clear at longer lead times. As such decadal prediction using initialised GCMs remains an experimental exercise, rather than an operational activity.

Model intercomparison projects such as ENSEMBLES (van der Linden and Mitchell 2009) and CMIP5 (Taylor et al. 2012) have advanced the science base for decadal prediction using dynamical models by defining frameworks within which the skill and viability of different modelling, initialisation and calibration techniques could be assessed in a consistent way over a historical hindcast period. Projects such as the Decadal Forecast Exchange (Smith et al. 2013) have enabled these decadal prediction frameworks to be further developed and tested in real-time. Challenges still remain, however, in terms of achieving consensus on the approach to decadal forecast calibration and evaluation given the relatively sparse and non-independent nature of the forecast-observation archive (Goddard et al. 2013). Furthermore, decadal prediction systems based on dynamical models currently suffer from relatively large errors in their representation of the mean climate and variability, even when their simulations are shown to capture long-term forced trends consistent with observations. The mechanisms underlying the decadal vacillations in the dynamical models also vary wildly from model to model (Branstator et al. 2012; Hazeleger et al. 2013; Sutton et al. 2015).

An alternative to complex and computationally demanding dynamical forecast models are empirical forecast approaches. Empirical models, which exploit known statistical relationships to represent physical mechanisms between the atmosphere and oceans, serve not only as useful benchmarks for comparison against dynamical forecast systems, but also offer potential as informative tools in their own right. Empirical methods have been successfully employed for forecasting on seasonal timescales (van den Dool 2007) and include simple approaches, such as persistence, as well as more sophisticated models that can be used for real-time prediction (Penland and Matrosova 1998; van Oldenborgh et al. 2005b; Coelho et al. 2006; Eden et al. 2015). Similar approaches have been applied for decadal prediction, including simple analogue methods such as dynamic climatology (Suckling and Smith 2013), statistical methods aimed at estimating trends and variability due to different components of the climate system (Lean and Rind 2008, 2009; Folland et al. 2013; Newman 2013), and methods for the prediction of SST patterns (Hawkins et al. 2011; Ho et al. 2013b).

Here, a new empirical model for predicting surface air temperatures over the globe is developed and evaluated in terms of its hindcast skill. The model, based on a multiple linear regression approach similar to Lean and Rind (2008) and Eden et al. (2015), uses observed and projected global forcings based on well-understood physical relationships, as well as large-scale predictors that have been shown to represent aspects of local scale variability, for example ENSO. This approach is used to produce probabilistic hindcasts and predictions on time scales of 1 year to a decade ahead. Hindcasts covering the period 1960–2014 are generated in four different prediction ‘modes’ and are evaluated in terms of both their deterministic and probabilistic skill. The definition of different prediction modes is designed to allow investigation of sources of potential skill and predictability within the model and offer the opportunity to test different approaches for the design of decadal prediction systems that would be too computationally expensive to do with dynamical models. The hindcast data and forecasts produced from the model are publicly available at: http://dx.doi.org/10.17864/1947.39.

This paper is structured as follows: Sect. 2 describes the empirical model set up, the data used and sources of predictability, while Sect. 3 outlines each of the prediction modes used and the approach for generating hindcasts. Section 4 is dedicated to a discussion of deterministic and probabilistic skill of the model in each of the prediction modes for global mean and regional surface air temperature. Section 5 highlights some of the choices made when designing the prediction system for semi-operational use and presents forecasts of surface air temperature for the period 2016–2025. Section 6 summarises the key findings and discusses directions for future efforts.

2 Empirical model design

The empirical model is based on a multiple linear regression approach that uses global forcings and large-scale sea surface temperature (SST) patterns as predictors for local (grid scale) annual mean surface air temperatures over the whole globe. The system has been designed with the flexibility to facilitate future development, for the prediction of any number of variables, or the ability to incorporate additional components, such as regionally-varying forcings and variable-, season- and region-specific predictors. In practice, empirical methods are dependent on the quality and quantity of the input data (historical observations and future forcing scenarios), so the present study is focused on prediction of surface air temperature using global mean radiative forcings since there is a relative abundance of data with which to build and evaluate the system. Future work will focus on prediction of temperature and precipitation at the regional scale in locations where long observational records exist and where strong teleconnections are shown to play a role in local scale variability. The prediction system incorporates uncertainty information through the generation of ensembles (the methods for which are discussed in Sect. 3.5), which are output in a similar format to those of dynamical models in order to aid comparisons. The selection of forcings and predictors is based on physical principles and well-understood observed relationships to the fullest extent, yet is as simple as possible, using as few predictors as necessary to minimise the risk of overfitting.

2.1 Data

For the purposes of model development and evaluation the target variable (predictand) that we focus on here is surface air temperature anomalies. The Cowtan and Way interpolated observational dataset (Cowtan and Way 2014) is chosen as it provides monthly mean coverage over the whole globe. This data is based on the HadCRUT4 ensemble (Morice et al. 2012), which uses air temperatures over land and sea ice and sea surface temperatures over the open ocean. In the present study annual mean (January-December) temperature anomalies, covering the period 1900–2014 (with anomalies relative to a 1961–1990 baseline), are used within the model. Data prior to 1900 (from 1850) is available, however the uncertainties are larger, especially in the Southern hemisphere, so this data is only considered later to test the sensitivity of the model. The Cowtan and Way dataset includes an ensemble of observed historical values that represent uncertainties due to data coverage and due to the bias correction procedure (Cowtan and Way 2014), allowing investigation of these sources of uncertainty within the empirical model. The majority of results discussed here are, however, based on fitting the empirical model to the ensemble median of the dataset. The robustness of the model skill to other observational datasets has also been explored and shows broad consistency across locations of the globe that have ample station data coverage.

The empirical model uses several globally observed forcings and predictors, which are fitted on a gridpoint by gridpoint basis over the historical training period. In all forecasts predictive information is exploited from the externally forced variability associated with natural and anthropogenic activity. This includes greenhouse gas (GHG) forcing, solar irradiance, volcanic aerosols and ‘other’ anthropogenic radiative forcings (OA). These forcings are prescribed in the model as global averages according to the CMIP5 historical scenario (up to 2005) and Representative Concentration Pathway (RCP) 4.5 (Meinshausen et al. 2011; Thomson et al. 2011) for future projections (beyond 2005), which are all given in units of W/m2 relative to a 1750 baseline. The OA forcing component includes factors such as aerosols, ozone and land use changes and is simply the total radiative forcing prescribed by CMIP5 after removing the greenhouse gas, solar and volcanic forcing components. In Sect. 3 onwards the GHG and OA components are combined to define a total anthropogenic forcing (AF) component. The sensitivity of the model skill and predictions is also examined using other RCP scenarios (see Sects. 4, 5).

An additional predictor included in the model is the large-scale ENSO mode of variability, which is prescribed according to the observed Niño3.4 index from the HadISST dataset (anomalies relative to a 1961–1990 baseline) (Rayner et al. 2003). The AMO and IPO modes of variability are also investigated as a potential source of model skill. In the present study all forcings are applied equally across the globe (i.e. as globally averaged forcing values, rather than spatially varying ones) and the ENSO, AMO and IPO predictors are also included across the whole globe, regardless of whether they are shown to provide a significant influence in a particular region. It may be the case that alternative or additional predictors provide better descriptors for climates in specific regional locations, and their inclusion may lead to increased forecast skill in these regions. However, such possibilities are left for future investigation.

2.2 Identifying important predictors

Having identified a set of potential forcings and predictors to be included in the model based on physical principles (as described in Sect. 2.1), we consider the importance of the individual contributions to the simulated surface air temperature over the historical period 1900–2014. To justify the inclusion of each of the forcings and predictors for a given predictand a multivariate analysis is performed in order to understand the relative influence of each component. For a predictor to be included in the model it must satisfy the following criteria: (1) Demonstrate a significant correlation with the predictand, (2) Increase the total fraction of the variance explained by the model and (3). Its inclusion leads to minimal increases in the uncertainties of the individual parameters of the model. The approach adopted here assumes that each climate variable (the predictand) responds linearly, with some lag, to the various influences, which are analysed in terms of their individual contributions using a multiple linear regression analysis, which has the form:
$$T(t)=C+\sum _{i=1}^{N}(\alpha _i F_i(t-\ell _i)) + \varepsilon _i,$$
(1)
where N is the number of predictors to be included in the model, \(\alpha _i\) are the regression coefficients that transform the predictors, \(F_i\) into their respective contributions to the modelled predictand, C is the constant term in the multiple linear regression that relates predictors relative to some baseline period to the baseline period of the predictand and \(\varepsilon\) is the set of residuals of the fit. The lag \(\ell _i\) between each predictor and the predictand is a free parameter within the model and is selected based on maximising the total fraction of the variance explained by the model, while minimising any increase in model parameter uncertainty. Isolating and quantifying the changes arising from individual components forms the basis for understanding the physical factors that have governed past variability and change and provide a first step towards determining the predictive potential of such an empirical approach, assuming the availability of plausible future scenarios for each of the significant influences.

Figure 2 shows an analysis of the relative contributions of each of the forcings and predictors used to construct the model for annual global mean surface air temperature anomalies over the period 1900–2014. The temperature anomalies are constructed from global annual mean GHG forcing, solar irradiance, volcanic aerosol, plus other anthropogenic forcings, as well as ENSO (via the Niño3.4 index). The GHG forcing is included with a 10 years lag as it was shown in Lean and Rind (2008) that most of the delay from emissions to temperature was due to ocean uptake. In this study a 10 years lag is also found to maximise the variance of the surface air temperature anomaly explained by the model, athough differences are small across the range of lags explored. The ENSO component is also included with a four month lag (i.e. a September-August mean). The fitted model coefficients convert the individual components from their native units (W/m2 for the forcings and K for ENSO) to equivalent global annual mean surface air temperature anomalies relative to the baseline 1750 (once the constant term in the linear regression is removed from the model and the observed global surface temperature). Sections 2.2.1 and 2.2.2 explore the contributions of these components to global and regional surface air temperatures in more detail. Section 3 uses the approach described above to generate decadal hindcasts.

2.2.1 Factors influencing global mean temperature

The model shown in Fig. 2 has a correlation of r = 0.95 with the observed temperature timeseries. The combination of component influences accounts for 90 % of the variance in the dataset over the period 1900–2014. The lag one autocorrelation of the model residuals is 0.57. These results are broadly consistent with Lean and Rind (2008), although small discrepancies occur due to a difference in the particular target and predictor datasets used for construction of the model, as well as the period over which the model is analysed. The GHG and other anthropogenic forcing (OA) components show correlations of \(r_{GHG}=0.91\) and \(r_{OA}=-0.82\) with the temperature anomalies respectively, although it is noted that there is a large colinearity (0.93) between the components, which leads to large uncertainties on the parameter values. Combining these components into a single anthropogenic forcing (AF) leads to a small increase in the total fraction of the variance explained by the model (91 %), as well as a small decrease (∼5–10 %) in the uncertainty on all model parameters. For the purposes of analysing hindcast skill and generating forecasts these two components will therefore be combined in Sect. 3 and thereafter. It is nevertheless still interesting to consider their individual contributions to surface air temperature variability. The solar, volcanic and ENSO components are also shown to be significant sources of variance in the historical temperature record, so are also included in the ‘standard’ version model for the analysis of hindcast skill in Sect. 4. The addition of AMO and IPO indices as predictors are found to have a minimal impact on the fraction of the variance of global mean temperature explained by the model, and generally increase the uncertainties on all the model parameters so are therefore excluded here. Their influence is however important for regional scale prediction (see Sect. 4).

The model in Fig. 2 clearly follows the observed pattern of variability better over the latter half of the twentieth century than over the first half. While the uncertainty range on the observations is generally larger in the earlier part of the period, the model still falls outside this uncertainty range on several occasions. The fitted model parameters have also been used to generate a backwards projection of global mean surface temperature over the period 1850–1900 to test the capability of the model to reproduce past observed temperatures given the known historical forcings (not shown). In this case the model was found to have a correlation with global mean surface air temperature of r = 0.67 over the period 1855–1900 (1855 coincides with the start date of the available observed Niño3.4 index), reflecting the larger uncertainties on the estimate of the global mean temperature and of the model fit before 1900.
Fig. 2

Top panel Annual mean (January–December) global surface air temperature anomaly reconstructed from the empirical model, compared against global mean Cowtan and Way interpolated HadCRUT4 observations (Cowtan and Way 2014). Bottom panels Each of the components contributing to temperature variability are shown in units of temperature change [K] determined from the multiple linear regression analysis. The model has a correlation of r = 0.95 with the observed temperature timeseries and the combination of component influences accounts for 90 % of the variance. Forward projections of each contribution to surface air temperature anomalies are shown in grey, using the RCP4.5 scenario for the period 2005–2025

Each of the forcing components in the model is prescribed according to the CMIP5 historical observations relative to a 1750 pre-industrial baseline. The constant term in the multiple linear regression approach, found to be C = −0.47 ± 0.23 K, therefore provides an estimate of the total temperature change from the baseline period of the observations to the pre-industrial baseline. When subtracted from the observations and model time series (as shown in the top panel of Fig. 2), the resulting temperature anomaly provides an estimate of the observed warming from the pre-industrial baseline in 1750, something which is not possible to derive from direct observations.

Similarly, the temperature change attributed to each of the individual influences can be estimated using a linear trend analysis. Figure 3 shows a quantification of these influences using an approach consistent with the IPCC AR5 [see figure TS.10 in Stocker et al. (2013)], based on a trend analysis over the period 1951–2010. The empirical model warms 0.78 ± 0.22 K from 1951 to 2010 (or 0.77 ± 0.13 K if a combined AF component is used), which is larger than the observed warming from Cowtan and Way (2014) of 0.68 ± 0.02 K, but within the uncertainty range of observed warming quoted by the IPCC of around 0.65 ± 0.15 K. Uncertainty on the observed trend in Fig. 3 is derived from the one-sigma uncertainty from the 100-member observational ensemble (Cowtan and Way 2014). The GHG component contributes to a warming of 0.89 ± 0.11 K, while the OA forcings contribute to a global cooling of −0.14 ± 0.10 K. Thus, the total anthropogenic forcing contributes to an overall warming of 0.75 ± 0.11 K (or 0.74 ± 0.03 K for the model using the combined AF forcing). Natural forcings contribute a small global warming component of 0.01 ±< 0.01 K, while internal variability, defined as the difference in 60 years trends between observations and the model excluding the ENSO component, is found to be −0.08 ± 0.02 K. A similar analysis of internal variability trends over all possible 60 years periods within the historical record shows a range between −0.28 K and 0.26 K. The small cooling contribution from internal variability over the period 1951–2010 is therefore a temporary effect in this empirical model and implies that it may contribute a positive (warming) effect to global temperature trends in future decades. These results are broadly consistent with the attributed global warming components quoted by Lean and Rind (2008), Stocker et al. (2013) and Johansson et al. (2015). The uncertainty ranges on the model components shown in Fig. 3 are derived from the one-sigma uncertainties on individual model parameters from the multiple linear regression and are the square root of the summed variance of the uncertainties in the case of combined forcing trends, having taken into account the covariance between the GHG and OA parameters. Currently, uncertainties on the forcings are not considered, however, sensitivity to the natural forcing component has been tested using radiative forcing data from Schmidt et al. (2014), which includes adjustments to volcanic aerosols and solar irradiance, as well as to GHGs over the period 1985–2004 and includes updated observations from 2005–2013. In general the model results are robust to these small adjustments in forcing, showing similar correlations and warming trends.

It is also possible to estimate the global climate system’s temperature response to external radiative forcing in terms of the transient climate response (TCR) metric. To a first approximation TCR can be estimated from the GHG regression coefficient (\(\alpha _{GHG}=0.49\,\pm 0.06\,{\hbox {K}}/\hbox {Wm}^{-2}\)) and the forced response to a doubling of \({\hbox {CO}}_2\,(3.7\,{\hbox {W}}/\hbox {m}^{2}\)) (Boucher et al. 2001), which leads to a TCR range of 1.55 K to 2.07 K. Such a range is consistent with the IPCC quoted 5–95 % TCR range of 1.5 K to 2.8 K and consistent with several studies based on estimates of TCR using the recent observational period, which suggest that TCR may fall at the lower end of the IPCC quoted range (Otto et al. 2013; Shindell 2014). However, unlike Shindell (2014), we find the aerosol (OA) component to have a lower efficacy (defined as the ratio of the climate sensitivity parameter for a given forcing agent to the climate sensitivity for \({\mathrm{CO}}_2\) changes (Joshi et al. 2003; Hansen et al. 2005)) than that of \({\mathrm{CO}}_2\) (or more precisely GHG in this case) over the recent period, which has a regression coefficient of \(\alpha _{OA}=0.30\,\pm 0.21\,{\hbox {K}}/{\hbox {Wm}}^{-2}\). However, the large uncertainty associated with the OA component suggests that it is not possible to make robust statements about OA (and consequently GHG) in isolation.
Fig. 3

Modelled warming trends contributing to annual mean global surface air temperature anomalies over the period 1951–2010 due to individual influences and forcings. The uncertainty ranges on each model component are derived from the one-sigma uncertainties on the individual model parameters from the multiple linear regression. The uncertainty on warming trends from combined components is the square root of the sum of the individual variances from the one-sigma parameter uncertainties, having taken into accound any co-linearity between the model components. The observed annual mean global warming trend from the Cowtan and Way interpolated HadCRUT4 dataset over the same period is shown as the left-hand bar for comparison, including an uncertainty estimate using the full ensemble. The global warming trend from the empirical model is consistent with the observed trend, and the modelled contributions from individual components are consistent with figure TS.10 in the IPCC AR5 (Stocker et al. 2013)

2.2.2 Regional patterns of temperature change

Figure 4 shows regional patterns for the observed and modelled trends (top panels) over the period 1951–2010, as well as contributions to the modelled trend from different forcing components of the model (middle panels). Estimates of the contribution to the modelled trend from ENSO (bottom left panel) and other internal variability (bottom right panel) are also shown. The model, which is fitted independently at each grid point, shows similar patterns of warming to that of the observations, with the largest warming between 1951–2010 having occurred in the high latitudes, over Asia and parts of Africa. The magnitude of the warming trends are shown to be slightly lower in the model over the Asia region than in the observations, but slightly larger over the Pacific and Atlantic Oceans. Stippling in the figures indicates regions where the uncertainties on the trend (calculated from combining the one-sigma uncertainties from individual model parameters) is as large, or larger, in magnitude than the trend itself. The largest uncertainties are found in the high latitudes, typically in regions where the observed warming trends are already large. The second row in Fig. 4 shows temperature trends from the anthropogenic (left) and natural (right) forcings respectively, and suggest that while anthropogenic forcings have had a warming effect over most of the globe, natural (combined solar and volcanic) forcings have contributed to a small cooling effect over many land regions (with the exception of Europe). The third row in Fig. 4 shows a further decomposition of the anthropogenic component into GHG (left) and OA (right) forcing and they suggest while GHGs have contributed to a warming in the Northern hemisphere, OA has contributed to a cooling. The model indicates a cooling effect from GHGs in the Southern Ocean, which is consistent with recent evidence of a cooling effect of the meltwater from the land ice (Bintanja et al. 2013). The model also suggests a warming effect from OA in the Southern Ocean, however observational data for this region over the early twentieth century is generally sparse and so comparisons should be treated with some caution. The bottom panels in Fig. 4 (note the different scale necessary to show these small contributions) illustrate the contribution to the surface air temperature trend from the ENSO component (left) and from an estimate of the internal variability of the model (right). The internal variability trend is calculated as the difference between the observed timeseries and a model which has had the ENSO component removed. Defining internal variability in this way means that model deficiency is also included in this component. The estimated internal variability of the system is largest over the same regions exhibiting the largest overall trends, which may have implications for detecting significant signals of climate change from the noise. This model, however, considers the cooling in the North Atlantic to be a decadal fluctuation of the AMO.
Fig. 4

Modelled (top left) and observed (top right) warming trends in surface air temperature anomalies [K] over the period 1951–2010. Second row shows contributions to the modelled warming trend from anthropogenic (left) and natural (right) components, while the third row shows the GHG (left) and OA (right) components of the anthropogenic warming trend. The bottom panels (note the different scale) show the warming trend contribution from ENSO (left) and an estimate of the internal variability, defined here as the difference between the observed annual mean observed temperature anomalies and the modelled temperature anomalies without the ENSO component (right). Regions of stippling indicate locations where the one-sigma uncertainties in the trend due to model parameter uncertainty is as large, or larger than the magnitude of the trend. The modelled trends are similar to the observed patterns of warming, with the largest contribution coming from the anthropogenic forcing component

Figure 5 shows the total fraction of the variance of the observed surface air temperature anomaly explained by individual model components, as well as by the combined components of the model (top left). The combination of components in the model explain at least 40 % of the observed temperature variance over a large fraction of the planet, and up to 90 % of the variance in the Indian Ocean region. The inclusion of each component in turn is shown to increase the overall correlation of the model with the observed surface air temperature anomalies, as well as increase the total variance explained by the model. Only global mean forcings are currently employed in the model, however, so further increases to the correlation of the model in some locations may arise from the inclusion of regionally-varying forcings. Furthermore, a version of the model was also generated that does not include the ENSO component (i.e. a model that includes only the external forcing components—not shown). Such a model could be considered as equivalent to a historical projection and similar to the uninitialised simulations that are often performed alongside initialised simulations in decadal prediction experiments. In this case the correlation of the uninitialised model with global mean surface air temperature anomalies is reduced to r = 0.93 (and 85 % of total variance is explained by the model). In general the patterns of temperature trends and variance explained from individual components are robust to different observed surface air temperature datasets (not shown), particularly in regions where observations are ample.
Fig. 5

Fraction of the variance of observed annual mean surface air temperature anomaly explained by the model by each component. The fraction of the total variance explained by the model (top left) and the ENSO component (top right) are shown, along with individual contributions from greenhouse gas forcings (GHG, middle left), other anthropogenic forcing (OA, middle right), solar irradiance (bottom left) and volcanic aerosol (bottom right). The combination of model components explain at least 40 % of the variance over much of the globe, with up to 90 % of the variance explained by the model in regions such as the Indian Ocean

It is clearly shown that each of the components used to construct the empirical model have had at least some influence on the trend and variability of surface air temperatures both globally and regionally over the twentieth century. A common criticism of empirical systems, however, concerns their applicability in a future, perturbed, climate. Climate system nonlinearities have the potential to undermine predictions from empirical models if, for example, the relationships underpinning the statistical model do not remain stationary under climate change. This is a concern for long timescale prediction, but is less so over timescales of a decade or two. It has also previously been found that, within statistical uncertainties, no detectable changes have been seen in ENSO teleconnections over the last half of the century (Sterl et al. 2007), and similar results are expected in other teleconnection modes.

3 Decadal hindcasts

Having explored the contributions of individual forcings and large-scale predictors to global and regional temperature variability, the question arises about how this knowledge can be applied to the problem of prediction. The forcings described in Sect. 2, along with an estimate of ENSO variability, are shown to explain a substantial fraction of the variance of global mean temperature, and are investigated in terms of decadal prediction skill in Sect. 4.1. This ‘standard’ version of the empirical model uses a single anthropogenic forcing (AF) component, which combines the GHG and OA forcing contributions, as well as solar irradiance and volcanic aerosol forcing, and also the ENSO predictor. For regional prediction, however, additional modes are important and some of them, in particular AMO and IPO, are explored further in Sect. 4.2. The predictive capabilities of the empirical model for forecast lead times of 1–10 years is investigated in Sect. 4 within a hindcast framework similar to those carried out by the dynamical modelling centres participating in the ENSEMBLES and CMIP5 decadal prediction experiments (van der Linden and Mitchell 2009; Taylor et al. 2012).

The empirical model is calibrated and evaluated based on a set of decadal hindcasts, starting each year, covering the period 1960–2014. The model coefficients are established over a historical training period for each hindcast start date using the forcing components, with lags, outlined in Sect. 2, in which the combined AF component has a 10 years lag. The regression coefficients for the ENSO component (as well as the AMO and IPO components explored in Sect. 4.2) are then estimated for lags of 1–10 years, corresponding to each annual lead time of the decadal prediction system. The training period for the model and the prescription of ‘future’ forcings and predictors in each hindcast are defined according to a series of different prediction ‘modes’. The investigation of skill under each of these prediction modes allows comparison between different experimental designs chosen for various decadal prediction experiments using dynamical models. It also allows an exploration of the sources of potential predictability and uncertainty, which in turn may aid future development, and in particular the experimental design, of operational decadal prediction systems.

A set of hindcasts with prediction lead times of 1–10 years is generated, both for global mean surface air temperature anomalies, as well as for spatial maps over the full global domain. The hindcasts are launched every year over the hindcast period and each contain 51 ensemble members (generated as described in Sect. 3.5). The skill of these hindcasts has been investigated in four different prediction ‘modes’, as described below.

3.1 ‘Real-time’ mode

Hindcasts are generated using a causal approach in which the model parameters are estimated over a historical training period from 1900 up to the hindcast start date. All radiative forcings are prescribed over the training period with a lag corresponding those described in Sect. 2, and ENSO is prescribed according to their observed value with a lag corresponding to the hindcast lead time. The volcanic aerosol component is then set to zero at the hindcast start date (i.e. no future information about volcanic aerosol forcing is assumed to be known), reflecting the set of observational data that would have been available for each hindcast were it produced in real-time. The 11-year solar cycle is also repeated from the previous cycle for the coming decade at each hindcast launch. The ENSO component is set to the observed Niño3.4 index value in the year before the hindcast start date and uses the regression coefficient corresponding to a lead-lag relationship that reflects the lead time of the hindcast. The anthropogenic forcing during each hindcast is prescribed according to the CMIP5 historical values or the RCP4.5 scenario. This approach is similar to the decadal prediction studies of Smith et al. (2007) using the DePreSys system based on the UK Met Office HadCM3 dynamical model. In their approach volcanic aerosols were prescribed at each hindcast start date and contain an exponentially decaying component with a lifetime of 1 year. A damped volcanic forcing component was also tested in this study but was found to have little impact on the overall skill of the model.

Since this approach uses only information that would be available in an operational setting, the evaluation of these hindcasts provides an estimate of out-of-sample skill of the model.

3.2 ‘Prescribed natural forcing’ mode

Volcanic aerosols are known to have an important impact on the climate system, particularly a few months after a large volcanic eruption in the tropics. Although volcanic eruptions cannot be predicted in advance it is still interesting to consider the impact of known future volcanic aerosol forcings on the models ability to capture the observed variability of the system.

Hindcasts are generated using the causal approach as above. All other forcings and predictors are also prescribed in the same manner, but volcanic aerosols and the solar cycle are prescribed for each hindcast according to their historically observed values. This approach is often used by the dynamical modelling centres in decadal prediction experiments such as ENSEMBLES and CMIP5 (van der Linden and Mitchell 2009; Taylor et al. 2012). Although such an approach uses information about the future that would not have been available in real time, it provides a useful estimate of the potential skill of the model, or more precisely an insight into the predictability of the response to volcanic forcing and other known important drivers of climate variability. It also allows investigation into the impact of initialisation through comparisons with free-running dynamical models that also include this information.

Even in this case, which only uses data prior to the start date of each hindcast to determine the model parameters, there is the potential to underestimate the level of skill that an operational forecast system may have, since the hindcasts generated in a causal manner do not fully exploit predictability due to the forced trend in AF over the full period of the hindcast set.

3.3 ‘Exploiting the trend’ mode

In this prediction mode, the hindcasts are generated using model parameters that are determined over the full range of the historical data archive (1900–2014). That is, the training period for each hindcast is identical across all start dates, so that the model uses predictand and predictor information which occurs after the start of the hindcast itself. This approach is designed to exploit maximum knowledge about each of the model components by using data from the future to compensate for the limited amount of data available to train the model during the earlier hindcasts. Approaches such as ‘Optimal Climate Normals’ (Huang et al. 1996) also attempt to exploit knowledge about forced trends by taking reference periods of the recent past, however for the model presented here the relatively short training period for the earlier hindcasts, combined with a change in trend between global AF forcing during the first and second halves of the twentieth century result in a difficulty in producing reliable estimates of the forced trend using only data prior to the hindcast start date. As a result, hindcasts are found to warm too quickly during these periods (not shown), leading to large forecast errors. While the ‘exploiting the trend’ approach to hindcast generation will undoubtedly produce overestimates of overall skill of the model hindcasts, it is useful in terms of gauging more robust estimates of model bias for the purposes of calibrating a forecast system which is to be used for operational decadal predictions.

Figure 6 shows a subset of the hindcasts (every fifth start date) produced in the ‘exploiting the trend’ mode for the global mean surface air temperature anomaly over the period 1960–2014. The observations are shown in black and the ensemble mean from every fifth hindcast start date is shown in blue. The 51 ensemble members are generated as described in Sect. 3.5. In general the observed temperature anomalies are captured well by the ensemble members and fall within the 5–95 % confidence intervals of the hindcast probabilities around 90 % of the time (as expected). The hindcasts themselves are bias corrected according to a lead-time dependent estimate of the mean forecast error over the full set of hindcasts using a leave-one-out cross-validation methodology similar to that described in Suckling and Smith (2013) and Goddard et al. (2013). Similar sets of hindcasts are generated and calibrated in each of the prediction modes discussed and their skill contrasted according to a variety of performance measures in Sect. 4.
Fig. 6

Hindcasts of global (land and ocean) annual mean surface air temperature anomalies (relative to 1961–1990) covering the period 1960–2014. Every fifth start date is shown for hindcasts generated in the ‘exploiting the trend’ prediction mode. Each hindcast contains 51 ensemble members, generated from the residuals of the model fit over the training period and are bias corrected using a leave-one-out (i.e. leaving out one ten year period) cross-validation procedure. The 5–95 % confidence intervals, shown as thin black lines, are calculated from the one-sigma uncertainties of individual model parameters. Observations are shown in black for comparison and the ensemble mean is shown in blue

3.4 ‘Two-tier system’

Dynamical models are often shown to perform better at capturing the features of large-scale low frequency phenomena in the oceans than local-scale variability of the coupled system (Smith et al. 2012; Meehl et al. 2014). The empirical model outlined in this paper is designed to exploit the observed statistical relationships between large-scale drivers of variability and local patterns in surface variables, so if a dynamical model were capable of reliably estimating future large-scale ocean patterns, such as ENSO or the AMO for example, then this knowledge could be incorporated into the empirical model with the aim of improving the skill of the prediction system. Such two-tier approaches have been employed within dynamical models in the past by using predicted SST as boundary conditions in atmospheric models (Deser and Phillips 2009; Hoerling et al. 2011). An empirical two-tier approach is developed here and its potential skill investigated within a ‘perfect knowledge’ framework (i.e. without the need for assessing the skill of any particular dynamical model) using future information about the ENSO, AMO and IPO predictors to generate the hindcast set.

Hindcasts are generated in a similar manner to the ‘exploiting the trend’ approach, however future information about the large-scale predictors, corresponding to the state of Pacific and Atlantic Ocean SSTs at each hindcast lead time, is included as a component of the model. In the perfect knowledge framework future knowledge about these components is taken from the historically observed values of the Niño3.4, AMO and IPO indices. If such an approach showed the potential to improve the skill of the empirical model then further investigation would be necessary to evaluate the skill of any dynamical (or statistical) prediction system used, as well as the sensitivity of hindcast skill of the two-tier system to the inclusion of different predictions of these large-scale modes of variability.

In an operational setting, future information about the predictors would have to be included from dynamical (or statistical) model predictions. The two-tier approach could further be extended to incorporate predictions of other large-scale mechanisms and drivers of local-scale variability in regions where strong teleconnections (and skillful model predictions of the mechanisms themselves) have been demonstrated. Future development of such an approach will focus on the ability of such large-scale predictors to enhance the skill of the empirical model in specific regions using predictions from dynamical models.

3.5 Generating ensembles

A key component of the empirical prediction system is the provision of probabilistic output. Each of the hindcast experiments described above produces ensemble output containing 51 members. The ensemble size is comparable to that used by dynamical forecast centres who produce operational seasonal predictions (Molteni et al. 2011). It is, however, much larger than any of the current decadal prediction experiments based on dynamical models, since they are computationally expensive to run.

There are several approaches to generating ensemble members from the multiple linear regression model, which is designed to find the single best combination of model components with some estimate of uncertainty on the fit. Each approach samples uncertainty in a different way, and allows uncertainty from different sources within the system to be explored.

The simplest approach, and the method used for the reporting of probabilistic skill throughout this paper, is to sample randomly from the residuals of the regression fit over the training period without replacement (allowing exploration of a wide variety of possible futures without replicating ensemble members). When considering spatial predictions, the residuals are sampled so that the ensemble members are spatially coherent, i.e. each ensemble member is generated by selecting a spatial map from the residuals, rather than independently selecting a residual at each location over the globe.

An alternative approach to ensemble generation would involve sampling from the individual components of the model parameter uncertainties, taking into account the covariance between each of the parameters. Such an approach has not been adopted here since it is less straightforward to sample uncertainties in a spatially coherent way. Further developments in terms of ensemble generation in the model could also be developed to account for serial correlation in the predictand and component timeseries. Such an approach may be important if considering the temporal dependence of individual model trajectories, however, may not be important in terms of statistical analyses based on the ensemble mean or probabilistic distributions that assume individual ensemble members are exchangeable and temporally independent. Generating temporally coherent ensembles would also benefit from a larger historical data archive than the present study considers.

In addition, the Cowtan and Way interpolated surface air temperature observations (Cowtan and Way 2014) used here as the target predictand are available as a 100-member ensemble of historical trajectories. Each trajectory samples uncertainty in a way that is consistent with the available station data and bias correction procedure. The hindcast evaluation presented is based on fitting the empirical model to the ensemble median of this dataset. However, a further estimate of uncertainty has been calculated by fitting a model to each member of the full 100-member ensemble, and using the resulting ensemble of hindcasts to estimate model skill (see Sect. 4.1).

Finally, a further source of uncertainty regarding future predictions involves a lack of knowledge about the externally forced component of the climate system. Future forcings are treated using RCP4.5 projections for anthropogenic forcings and solar radiation, but other scenarios could also be sampled (also see Sects. 4, 5 in the context of hindcast skill and forecast spread). However, over the timescale of a decade, uncertainties due to the magnitude of internal variability are likely to be larger than uncertainties in external forcing (Hawkins and Sutton 2009).

In principle, other more advanced methods may be available for exploring and combining uncertainties from different sources within the prediction model. The approach of selecting residuals has the advantage of being simple while at the same time accounting for many of the uncertainties discussed in an implicit way. Analysis of the ensemble characteristics suggest that such an approach does not lead to any significant systematic over- or under-confidence within the hindcasts, particularly after any mean bias in the model is removed.

3.6 Bias correction

Dynamical models typically suffer from biases in their representation of mean climate due to misrepresentations of the physical processes within the climate system and the nonlinear feedbacks between them. Such model biases are usually removed once raw ensembles of simulations are transformed into probabilistic forecast products. Several approaches exist to account for biases due to model error with the simplest approach [and the suggested approach in, for example Goddard et al. (2013)] being to apply a lead-time dependent correction to the forecast variable, estimated from the average error of the ensemble mean over a hindcast set under cross-validation. A similar approach is also adopted here to account for biases in the empirical model. More sophisticated methods for bias correction of initialised hindcasts include time-dependent methods (Kharin et al. 2012; Fuc̆kar et al. 2014) and approaches that account for the rate of sampling of the internal variability (Hawkins et al. 2013) are not explored in the present study.

Biases in the empirical model arise due to a change in the quality and quantity of information available to train the model (which by definition is fit so that the mean residual, or bias, over the training period is zero) compared to generating the hindcasts. Biases also arise due to uncertainties in determining model parameters using linear constraints based on relatively few data points. As expected, biases are larger in the hindcasts generated from the real-time and prescribed natural forcings prediction modes (approximately 0.1–0.2 K for global mean temperature) than for hindcasts which exploit full knowledge of the AF trend and use perfect knowledge about future SSTs in the two-tier approach (approximately −0.01–0.04 K for the global mean). In general the biases grow as the lead time of the forecast increases. Once these mean biases are removed from each of the hindcasts, based on estimating the bias under cross-validation, their skill is assessed according to both deterministic and probabilistic measures.

4 Hindcast skill

Hindcast skill is evaluated as a function of lead time, both as annual means (Fig. 7) and as the more commonly quoted time aggregates, 2–5 and 6–9 years (Fig. 8) for the standard version of the model (Sect. 4.1) and a version containing additional AMO and IPO predictors (Sect. 4.2). Skill is assessed according to both deterministic and probabilistic scores.

4.1 The standard model

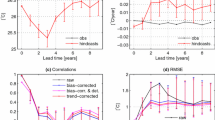
Figure 7 shows skill of the hindcasts for global mean surface air temperature anomalies in each of the four prediction modes, which use the AF, solar irradiation and volcanic aerosol forcings, as well as the ENSO predictor within the model. The top panels show the correlation and root mean squared error (RMSE) of the ensemble mean for each set of hindcasts, as well as the skill of persistence hindcasts for comparison. All hindcasts from the empirical model are shown to perform better than persistence at all lead times and generally the skill of the model increases as extra information is added beyond what would have been known in real-time. Prescribing volcanic aerosol forcings is shown to have a small impact on the overall level of skill in the model at all lead times. However, its impact on skill will be much larger in the years following any large eruption. The correlation and RMSE of the single best model and of the ensemble mean for each prediction mode are almost identical in this case (not shown), which is a reflection on the manner in which ensembles members are generated and the fact that there are enough of them to converge on a robust estimate of skill.

The bottom two panels in Fig. 7 show the probabilistic, proper skill scores Ignorance and the continuous ranked probability skill score (CRPSS). In this case the hindcast ensemble members are transformed into probabilistic distributions through kernel dressing (Bröcker and Smith 2008) and the skill scores are assessed relative to reference hindcasts of persistence. In the case of Ignorance, scores below zero indicate that the empirical model on average outperforms persistence (by the empirical model systematically placing more probability density on the outcome than persistence does). Scores above zero for CRPSS indicate the degree to which the empirical model shows improvement over persistence, with scores of 1.0 indicating the empirical model to be a perfect forecast system. It is clearly shown that the empirical model is more skillful than persistence in all prediction modes. The vertical bars in the bottom panels of Fig. 7 show a 10–90 % bootstrap resampling range from the set of hindcast scores for each lead time with replacement. In all cases the bootstrap bars indicate that the skill relative to persistence is statistically significant at the 10 % level (i.e. the scores do not cross zero).

For Ignorance (bottom left panel of Fig. 7), scores of ∼0.6 indicate that hindcasts in the real-time and prescribed natural forcings mode typically place around 0.6 bits, or 20.6 (that is around 50 %) more probability density on the observed outcome than the persistence hindcasts. The hindcasts that exploit the trend place on average twice as much probability on the observed outcome than persistence. For CRPSS (bottom right panel of Fig. 7) the general conclusions are the same, with the empirical model demonstrating a 20–60 % improvement over persistence, depending on the hindcast lead time and prediction mode.

In Fig. 7, a lead time of zero indicates hindcasts based on training the model using all forcing and predictor information available at the time of the hindcast launch (i.e volcanic aerosol data is included and all predictor information on the hindcast start date is also included). Lead time one corresponds to a forecast at 1 year ahead, in which the ENSO predictor (and AMO, IPO predictors in Sect. 4.2) takes the observed value at lead time zero with a regression parameter that corresponds to a lead-lag relationship with surface air temperature of 1 year, and so on. The fact that skill does not appear to diminish as lead time increases indicates that much of the skill in decadal predictions of global mean temperature comes from the forced trend component associated with AFs [see, for example van Oldenborgh et al. (2012)]. The proportion of skill that comes from the large-scale modes of variability within the model has been tested by comparing the skill of the model in each prediction mode to an equivalent version of the model that does not contain any ENSO component (i.e. an uninitialised model). In most cases a small but significant improvement (∼15–20 %) in skill is found by including the ENSO component for lead time zero (not shown), but any increase in skill is negligible after 1 year, reflecting the rapidly decreasing forecast skill of Pacific SSTs at increasing timescales. However, it is found that having perfect knowledge of Pacific SSTs during each hindcast increases the skill of the model significantly at all lead time (up to a 30 %, or ∼0.5 bit improvement) over an empirical model that includes no SST information, suggesting that any future information about the temperatures in the Pacific Ocean (or other large-scale patterns) could greatly improve the skill of a decadal prediction system based on a two-tier model described in Sect. 3.4.
Fig. 7

Hindcast skill of the empirical model for annual (January–December) global (land and ocean) mean surface air temperature in each of the four prediction modes as a function of lead time (in years). The top panels show the correlation (left) and RMSE (right) of the ensemble mean, while the bottom two panels show Ignorance (left) and CRPSS (right) of the ensemble relative to hindcasts of persistence. Hindcasts generated in all prediction modes show significant skill above that of persistence and generally as information is added to the model (beyond what would have been known in real time) the skill of the model increases according to all skill measures

A further test of probabilistic skill based directly on the raw ensemble can be examined through the dispersion characteristics of the hindcast ensemble members for each of the approaches discussed in Sect. 3.5. The ensemble dispersion (Ho et al. 2013a) is defined as:
$$d=\sqrt{\left( \frac{n+1}{n} \right) \frac{\sigma ^2}{R^2}},$$
(2)
where n is the number of ensemble members in each hindcast, \(\sigma ^2\) is the mean variance across the ensemble over the full hindcast set and \(R^2\) is the mean squared error of the ensemble mean. Dispersion values with \(d<1\) indicate that the ensembles are systematically over-confident (or under-dispersed) in their predictions, whereas \(d>1\) suggest that the prediction ensembles are systematically under-confident (or over-dispersed). It is found that selecting from the residuals of the model fit over the training period typically leads to hindcast ensembles for global mean temperature that are slightly over-confident in the real-time hindcast mode (\(d\approx 0.85-0.95\)) and slightly under-confident when using exploiting the trend mode (\(d\approx 1.1-1.3\)). Similar results are obtained if ensemble members are sampled directly from the combined uncertainties of the individual model parameters. However if an ensemble of models is generated using the uncertainty on the observations alone (i.e. using the ensemble of observations from the Cowtan and Way interpolated HadCRUT4 dataset) then the hindcasts are shown to be over-confident in all hindcast modes (\(d\approx 0.6\), not shown).

Figure 8 shows maps of hindcast skill for surface air temperature from the standard model at lead times of 1, 2–5 and 6–9 years in the exploiting the trend mode. The top panels in Fig. 8 show the correlation of the model with observed surface air temperature anomalies for each lead time. Strong correlations are shown over land in many regions, particularly over parts of Asia and Africa, with correlations increasing to over 0.8 in many regions at lead times of 6–9 years, due to the forced trend component and the longer time averaging relative to the short decorrelation times. Stippling in the top panels indicates regions that are not statistically significant at the 10 % level. The second row in Fig. 8 shows the RMSE of the ensemble mean and indicates that model errors are largest at high latitudes and in the tropical Pacific at lead time one, although this error is removed once longer time averages are considered. In general the correlations and RMSEs are of a similar order of magnitude to those of recent decadal hindcasts from dynamical models and show similar spatial patterns of skill (van Oldenborgh et al. 2012; Shaffrey et al. 2016). More comprehensive comparisons between the empirical model and dynamical systems (or against benchmarks other than persistence) are beyond the scope of the current study.

The third row in Fig. 8 shows the dispersion characteristics of the ensemble, as defined in Eq. 2. In general as lead time increases the ensemble becomes more under-dispersive (over-confident), although at lead time 6–9 years there are still some regions which show the ensemble to be under-confident, particularly over the East Asia and North America regions. Finally, the bottom panels in Fig. 8 show the probabilistic Ignorance skill score for hindcasts from the empirical model relative to persistence. In almost all locations over the globe the empirical model is shown to be significantly more skillful than persistence At lead time one the empirical model consistently places ∼50 % (or ∼0.6 bits) more probability density on the observed outcome than persistence forecasts do, while at longer lead times (and larger time aggregates) this grows up to 3 times more probability density in some locations, likely due to the forced trend component in the empirical model compared to persistence.

The levels of skill found in the empirical model are similar whether computing the global mean surface air temperature from individual model temperatures across the globe, or whether fitting the model to global mean temperature directly (as expected under the application of a linear model), and the general conclusions are robust to alternative observational datasets and adjustments to the model training periods (not shown). The patterns of skill found in Fig. 8 are similar across all of the prediction modes investigated, but generally skill decreases as information is removed from the model, with hindcasts made in the real-time mode still demonstrating significant skill compared to persistence (by up around 0.2 to 0.6 bits of additional information depending on the region). A small, but statistically significant (up to 5 %) decrease in skill is found at all lead times and in most locations if the ENSO component is removed from the model (i.e. equivalent to generating uninitialised historical projections).
Fig. 8

Various measures of hindcast skill of the empirical model for annual mean surface air temperature anomalies for lead time 1 year (left panels), 2–5 years (middle panels) and 6–9 years (right panels). Hindcasts are generated annually over the period 1960–2014, containing 51 ensemble members and are shown for the ‘exploiting the trend’ prediction mode. The correlation (top row) and RMSE (second row) of the ensemble mean are shown, along with the ensemble dispersion characteristics (third row) and Ignorance relative to persistence (bottom row). The stippling indicates locations that do not exhibit statistically significant skill at the 10 % level. Almost all locations over the globe are shown to outperform persistence (bottom panels) at all lead times, while strong correlations (top panels) with the observed temperatures are shown, particularly over land at all lead times, mainly due to the forced trend

4.2 Additional predictors

The skill of a set of hindcasts that also includes the AMO predictor (as well as hindcasts that include AMO and IPO predictors) is generated using exploiting the trend mode. The skill of the hindcasts which include AMO is also shown in Fig. 7 (light blue lines). The inclusion of the AMO predictor, or the IPO predictor, does not lead to any significant improvement in skill over the standard model (dark blue lines), which is perhaps not surprising for prediction of global mean temperature. However these components are expected to have larger impacts on regional scale prediction. The two-tier system (purple lines in Fig. 7), which includes perfect knowledge of SSTs in the ENSO region, as well as from AMO, shows improvement over all other modes and demonstrates a small improvement over a two-tier approach which only includes ENSO (not shown). This suggests there may be potential to increase the skill of an operational prediction system by incorporating predictions of large-scale ocean patterns and their relationship to local-scale variability within the model. However, the perfect knowledge framework used here assumes perfect predictability of the state of the Pacific and Atlantic Oceans several years in advance and in reality the skill of any such system will depend also on the quality of these predicted large-scale patterns. The addition of the IPO component in the two-tier model, however, shows no significant improvement over a model which includes the ENSO and AMO components (not shown).
Fig. 9

Improvements in skill (in terms of Ignorance) relative to the standard version of the empirical model as additional predictors are included within the model for hindcasts of annual mean surface air temperature anomalies for lead times of 1 year (top panels), 2–5 years (middle panels) and 6–9 years (bottom panels). The left-hand panels show the standard version of the empirical model plus the inclusion of the AMO predictor, the middle column shows the two-tier model which uses observed values of the ENSO predictor thrughought the hindcasts, and the right-hand panels show the two-tier model with the additional AMO predictor. Stippling indicates locations that do not exhibit statistically significant skill relative to the standard version of the model at the 10 % level. The inclusion of the AMO component leads to significant increases in skill in the North Atlantic region at 1 year ahead (with hindcasts placing around 10 % more probability on the observed temperatures in this region than the standard model). This improvement diminishes at longer lead times, however. Significant improvements in skill are shown in many locations at all lead times for the two-tier models

Figure 9 shows the hindcast skill (in terms of Ignorance) for different versions of the model relative to the standard version of the model in which hindcasts are generated in the exploiting the trend prediction mode. At lead times of 1 year (top panels) there is clearly a benefit of including the AMO predictor for skill in the North Atlantic and Greenland region (left panels), which show improvements over the standard version of up to 0.2 bits (or an increase of around 15 % probability density being placed on the outcome compared to the standard model). Including the AMO predictor also leads to small but statistically significant improvements over some areas of the globe, particularly in the Pacific Ocean and over parts of Europe. At longer lead times (bottom panels) much of the improvement has diminished and there are even a few locations (parts of South America and Africa in the tropics for example, and also in the Southern Ocean) that show a degradation of skill compared to the standard version of the model. The two-tier approach, which includes either an ENSO component only (middle panels) or SST information from both the Pacific and Atlantic regions (i.e. includes ENSO and AMO—right panels), also clearly demonstrates the potential for significant improvements in model skill, particularly over North America and southern Africa. The level of improvement that could be gained is clearly contingent on the predictability of SSTs at these timescales and the skill of any prediction system used within such a two-tier approach. The potential improvements in skill over the standard model approach diminish as lead time increases, showing no improvement, or even a degradation of skill in much of the Southern hemisphere at lead times beyond 1 year (middle and bottom panels).

At lead time 6–9 (bottom panels), the diminished skill compared to lead time 2–5 in the standard + AMO case (left panel) is due to the decreasing skill of the relationship between the ENSO and AMO predictors with observed surface air temperatures at longer lead-lag times (since the model in the exploiting the trend prediction mode is generated from a single set of regression parameters across all hindcasts). In the two-tier approach (middle and right panels) the differences in skill between lead times 2–5 and 6–9 are simply an effect of the differing start and end points of the verification period between the two lead times (since in this case the ENSO and AMO predictors are set to their observed values throughout the hindcasts). These differences in skill between the two lead times highlight that there are sensitivities to particular verification events over the hindcast period and illustrate the importance of considering consistent verification periods when making like-for-like skill comparisons between models (Hawkins et al. 2013).

The IPO predictor also shows very small improvements in skill compared to a model that includes ENSO and AMO at lead times of 1 year (not shown), however, any improvement in skill is small relative to the extra uncertainty introduced on the individual model parameters. Furthermore, at longer lead times the inclusion of the IPO index within the model leads to a significant degradation of skill over much of the Southern hemisphere (by up to 0.25 bits in some locations) relative to the standard version of the model. These results suggest that large-scale predictors such as AMO and IPO should only be included within the model where they are shown to significantly improve skill for the specific variable, region and timescale of interest, as was done in Eden et al. (2015). For the purpose of prediction the standard version of the model is therefore employed in Sect. 5. A more comprehensive analysis of the benefits of including additional predictors within the empirical model for regional prediction is left for future work.

5 Forecast for 2016–2025

The analysis of hindcast skill in the empirical model has identified sources of predictability from different components, as well as provided useful insight into which approaches to experimental design might be most appropriate for real-time prediction. These approaches have been applied to produce forward forecasts of surface air temperature anomalies (relative to 1961–1990) over the globe for the period 2016–2025. Figures 10 and 11 show these forecasts for a lead time of 1 year, i.e. 2016 (Fig. 10) and for time aggregated lead times of up to 10 years (Fig. 11). The forecast is generated in a similar manner as described in Sect. 3.1 using the standard version of the model, with projected AF forcings prescribed according to RCP4.5, volcanic aerosol set to zero at the forecast launch and ENSO taking the observed Niño3.4 value in 2015 (with a four month lag), using regression parameters that correspond to the lead-time of the forecast (i.e. using the relevant lead-lag relationships). The empirical model is trained over the period 1900–2014 and ensembles are generated from the residuals of the model fit, with a lead-time dependent bias correction applied based on an estimate of the mean forecast error over the hindcast period in the exploiting the trend prediction mode.

Figure 10 shows the ensemble mean prediction (top left), the standard deviation across the 51-member ensemble (top right) and a subset of ensemble members (chosen to reflect the range of spatial patterns predicted by the model—middle and bottom panels) for 2016. Temperature anomalies are generally predicted to be warmer than the 1961–1990 baseline period over much of the globe, particularly in Northern latitudes and over the African and Asian continents, with anomalies above 1.6 K in some regions. Despite the ensemble mean showing a warming over much of the Northern hemisphere, there is diversity across the ensemble members in terms of their predicted spatial patterns. The standard deviation across the ensemble members ranges from 0.1 K up to 0.5 K in some regions. A small number of ensemble members even predict cooler temperature anomalies relative to the 1961–1990 baseline in some regions (e.g. a cooling of ∼1.4 K over Eastern Europe, Asia, or in the Southern and Pacific Oceans, as shown in the middle panels of Fig. 10). However the majority of ensemble members show a warming over much of the globe for 2016.

Globally, temperature anomalies are predicted to be 0.71 ± 0.12 K (\(1\sigma\) ‘likely’ range) above the 1961–1990 baseline in 2016 (observed anomaly ranges across a variety of datasets for 2014 and 2015 are 0.57–0.62 and 0.74–0.77 K respectively), rising to 0.88 ± 0.13 K in 2025 (not shown). Similar results are obtained based on fitting the empirical model to a variety of different global mean surface temperature datasets, including HadCRUT4 (Morice et al. 2012), the Berkeley Earth Surface Temperature dataset, BEST, (Rohde et al. 2013), the GISS Surface Temperature Analysis, GISTEMP (Hansen et al. 2010) and NOAA/NCDC (Smith et al. 2008), which are all found to have similar correlation and RMSE scores across their hindcast sets. Ensemble mean predictions based on each of these observational time series range from 0.62 K to 0.72 K above a 1961–1990 baseline for 2016 and 0.83 K to 0.89 K for 2025. The predicted temperature trend over the 10 years period 2016–2025 is 0.17 ± 0.11 K. Furthermore, hindcasts and forecasts have also been examined using other forcing scenarios, specifically RCP2.6 and RCP8.5 (Meinshausen et al. 2011). Once again the hindcasts show similar levels of skill across the different scenarios. Over the coming decade predictions based on the RCP2.6 scenario predict the largest warming by 2025, with a global mean temperature anomaly of 0.90 ± 0.13 K relative to 1961–1900, compared to 0.89 ± 0.13 K for RCP8.5. These results are consistent with predictions from dynamical models, which suggest that the larger warming in RCP2.6 compared to RCP8.5 is due to the effects of less negative aerosol forcing adding to the global temperature response over the near-term (Chalmers et al. 2012).
Fig. 10

Predictions of surface air temperature anomalies (relative to 1960–1990) for the year 2016 (January–December mean) from the empirical model. The top left panel shows the ensemble mean of the 51-member ensemble and the top right panel shows the standard deviation across the ensemble members. The bottom four panels show a subset of the individual ensemble members, selected randomly. The full ensemble is generated by sampling from residuals of the empirical model fit over the period 1900–2014 without replacement. Each ensemble member is bias corrected using an estimate of the mean forecast error from the set of hindcasts produced using the ‘exploiting the trend’ approach

Figure 11 shows the ensemble mean (left panels) and standard deviation (right panels) of the predicted regional patterns for the empirical model at lead times of 2–5 years (i.e. 2017–2020—top panels), 6–9 years (i.e 2021–2024—middle panels) and 1–10 years (i.e. 2016–2025—bottom panels) ahead. The ensemble variance is naturally suppressed as longer time aggregates are taken, while the ensemble mean patterns are similar across all time scales, predicting a warming above the 1961–1990 baseline period of over 1.6 K over land across most of the Northern hemisphere by the end of 2025. Only a few small regions, including in the North Atlantic, over South America and in the Southern Ocean show a predicted relative cooling in the ensemble mean over the coming decade, which is consistent with similar forecasts based on dynamical models (Hermanson et al. 2014). In the Southern Ocean region, however, where the predicted cooling is largest, the data available to train the model contains larger uncertainties due to a relative lack of observations.

Such predictions of surface temperature warming over the next decade have important implications for adaptation planning and risk management decisions in the near term. However, the quantitative output from any single model should be taken with caution. While operational decadal forecasting is still in its infancy, the ability to compare predictions from a variety of empirical and dynamical models in real time is potentially beneficial, not only in terms of understanding the range of predicted climates over the coming years, but also in terms of analysing methodologies and approaches to real-time prediction. As such, a similar set of empirical forecasts to those presented here for surface air temperature anomalies, over the period 2015–2024, have contributed to the Decadal Forecast Exchange project (Smith et al. 2013), alongside those from dynamical modelling centres across the world. Further developments to the empirical forecast system will aim at expanding that range of variables that are predicted and by the model, thus allowing further comparisons against predictions from dynamical models, as well as additional contributions to decadal prediction projects, such as the Decadal Forecast Exchange.
Fig. 11

Empirical predictions of annual mean surface air temperature anomalies (relative to 1961–1990) for the period 2016–2025. The left-hand panels show the ensemble mean from 51 ensemble members and the right-hand panels show the standard deviation across the ensemble. Prediction lead times of 2–5 years (top panels), 6–9 years (middle panels) and 1–10 years (bottom panels) are shown. The largest warming is predicted to be over land, particularly in teh Northern Hemisphere, although these regions are also associated with the largest ensemble spread. Only a few regions, such as in the North Atlantic and in the Southern Ocean are predicted to cool compared to the 1961–1990 baseline

6 Conclusions

A new global empirical decadal prediction system for surface air temperature has been presented, based on a multiple linear regression approach using observed and projected global forcings, as well as ENSO and other large-scale modes of variability as predictors. Ensembles of hindcasts covering the period 1960–2014 were generated under a series of different prediction modes and predictability and skill of the model were evaluated according to both deterministic and probabilistic metrics. The model was shown to be significantly more skillful than persistence at all lead times, up to 10 years ahead, for all prediction modes. Small improvements in skill are found at all lead times once future volcanic forcings are prescribed in the hindcasts and it is suggested that hindcasts which exploit knowledge of the forced trend throughout the hindcast period can provide more robust estimates of model bias for the calibration of the empirical model in an operational setting. Although there is some sensitivity to the datasets, training period and future scenarios employed, it is possible to draw robust conclusions about the skill within the empirical prediction system. A two-tier system shows potential for improved real-time prediction, given the assumption that skillful forecasts of the large-scale modes of local-scale variability, such as ENSO and AMO, are available. However, the two-tier model investigated here only considers Pacific and Atlantic Ocean SSTs as important predictors and does so under the assumption of perfect knowledge about the future, so additional work is needed to investigate the viability of such an approach to decadal prediction given a more realistic analysis of predictability and forecast skill of the mechanisms themselves.

The empirical model has been designed with the flexibility to facilitate further developments, including the prediction of other surface variables, improved ensemble generation methodologies and the ability to incorporate additional predictors within the model. It is also semi-operational in the sense that forecasts have been produced for the coming decade and have contributed to the Decadal Forecast Exchange project. The hindcast data and forecasts produced from the model are also publicly available at: http://dx.doi.org/10.17864/1947.39. However, at present only globally averaged annual mean forcings are included within the model in all locations over the globe. The inclusion of regionally-varying forcings may lead to improvements in skill. Furthermore, the inclusion of additional predictors that describe decadal-scale variability, and that are specific to the predictand variable, region and season of interest, may improve such an operational empirical system beyond the present study. Such developments will be explored in future.

Notes

Acknowledgments

The research leading to these results has received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under SPECS project (Grant Agreement No. 308378). ES was supported by the UK-China Research and Innovation Partnership Fund through the Met Office Climate Science for Service Partnership (CSSP) China as part of the Newton Fund. EH received funding from NERC (Grant NE/I020792/1) and the National Centre for Atmospheric Science.

References

  1. Alexander MA et al (2002) The atmospheric bridge: the influence of ENSO teleconnections on air–sea interactions over the global oceans. J Clim 15(16):2205–2231. doi: 10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2 CrossRefGoogle Scholar
  2. Arribas A et al (2011) The GloSea4 ensemble prediction system for seasonal forecasting. Mon Weather Rev 139(6):1891–1910. doi:  10.1175/2010MWR3615.1 CrossRefGoogle Scholar
  3. Balmaseda M et al (2009) Impact of initialization strategies and observations on seasonal forecast skill. Geophys Res Lett 36(1):L01701. doi: 10.1029/2008GL035561 CrossRefGoogle Scholar
  4. Bintanja R et al (2013) Important role for ocean warming and increased ice-shelf melt in Antarctic sea-ice expansion. Nat Geosci 6:376–379. doi: 10.1038/NGEO1767 CrossRefGoogle Scholar
  5. Boer GJ (2011) Decadal potential predictability of twenty-first century climate. Clim Dyn 36(5):1119–1133. doi: 10.1007/s00382-010-0747-9 CrossRefGoogle Scholar
  6. Boucher O et al (2001) 6.3.1 Carbon dioxide. In: Houghton JT et al (eds) Chapter 6: radiative forcing of climate change. Climate change 2001: the scientific basis. Contribution of working group I to the third assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp 351–416Google Scholar
  7. Branstator G, Kimoto M, Knight JR, Latif M, Rosati A (2012) Systematic estimates of initial value decadal predictability for six AOGCMs. J Clim 25:1827–1846. doi: 10.1175/JCLI-D-11-00227.1 CrossRefGoogle Scholar
  8. Bröcker J, Smith LA (2008) From ensemble forecasts to predictive distribution functions. Tellus A 60(4):663–678. doi: 10.1111/j.1600-0870.2008.00333.x CrossRefGoogle Scholar
  9. Chalmers N et al (2012) Aerosol contribution to the rapid warming of near-term climate under RCP 2.6. Geophys Res Lett 39:L18709. doi: 10.1029/2012GL052848 CrossRefGoogle Scholar
  10. Coelho CAS et al (2006) Towards an integrated seasonal forecasting system for South America. J Clim 19(15):3704–3721. doi: 10.1175/JCLI3801.1 CrossRefGoogle Scholar
  11. Cowtan K, Way RG (2014) Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q J R Meteorol Soc 140(683):1935–1944. doi: 10.1002/qj.2297 CrossRefGoogle Scholar
  12. Deser C, Phillips AS (2009) Atmospheric circulation trends, 1950–2000: the relative roles of sea surface temperature forcing and direct atmospheric radiative forcing. J Clim 22(2):396–413. doi: 10.1175/2008JCLI2453.1 CrossRefGoogle Scholar
  13. Doblas-Reyes FJ et al (2013a) Seasonal climate predictability and forecasting: status and prospects. WIREs Clim Change 4(4):245–268. doi: 10.1002/wcc.217 CrossRefGoogle Scholar
  14. Doblas-Reyes FJ et al (2013b) Initialized near-term regional climate change prediction. Nat Commun 4:1715. doi: 10.1038/ncomms2704 CrossRefGoogle Scholar
  15. Eden JM et al (2015) A global empirical system for probabilistic seasonal climate prediction. Geosci Model Dev Discuss 8:3941–3970. doi: 10.5194/gmdd-8-3941-2015 CrossRefGoogle Scholar
  16. Folland CK et al (2013) High predictive skill of global surface temperature a year ahead. Geophys Res Lett 40(4):761–767. doi: 10.1002/grl.50169 CrossRefGoogle Scholar
  17. Fuc̆kar NS, Volpi D, Guemas V, Doblas-Reyes FJ (2014) A posteriori adjustment of near-term climate predictions: accounting for the drift dependence on the initial conditions. Geophys Res Lett 41(14):5200–5207. doi: 10.1002/2014GL060815 CrossRefGoogle Scholar
  18. Goddard L et al (2013) A verification framework for interannual-to-decadal prediction experiments. Clim Dyn 40(1):245–272. doi: 10.1007/s00382-012-1481-2 CrossRefGoogle Scholar
  19. Hansen J et al (2005) Efficacy of climate forcings. J Geophys Res 110:D18104. doi: 10.1029/2005JD005776 CrossRefGoogle Scholar
  20. Hansen J et al (2010) Global surface temperature change. Rev Geophys 48:RG4004. doi: 10.1029/2010RG000345 CrossRefGoogle Scholar
  21. Hawkins E et al (2011) Evaluating the potential for statistical decadal predictions of sea surface temperatures with a perfect model approach. Clim Dyn 37(11):2495–2509. doi: 10.1007/s00382-011-1023-3 CrossRefGoogle Scholar
  22. Hawkins E et al (2013) The interpretation and use of biases in decadal climate prediction. J Clim 27(8):2931–2947. doi: 10.1175/JCLI-D-13-00473.1 CrossRefGoogle Scholar
  23. Hawkins E, Sutton R (2009) The potential to narrow uncertainty in regional climate predictions. Bull Am Meteorol Soc 90(8):1095–1107. doi: 10.1175/2009BAMS2607.1 CrossRefGoogle Scholar
  24. Hazeleger W et al (2013) Predicting multiyear North Atlantic Ocean variability. J Geophys Res 118(3):1087–1098. doi: 10.1002/jgrc.20117 CrossRefGoogle Scholar
  25. Hermanson L et al (2014) Forecast cooling of the Atlantic subpolar gyre and associated impacts. Geophys Res Lett 41(14):5167–5174. doi: 10.1002/2014GL060420 CrossRefGoogle Scholar
  26. Ho CK et al (2013a) Examining reliability of seasonal to decadal sea surface temperature forecasts: the role of ensemble dispersion. Geophys Res Lett 40(21):5770–5775. doi: 10.1002/2013GL057630 CrossRefGoogle Scholar
  27. Ho CK et al (2013b) Statistical decadal predictions for sea surface temperatures: a benchmark for dynamical GCM predictions. Clim Dyn 41(3):917–935. doi: 10.1007/s00382-012-1531-9 CrossRefGoogle Scholar
  28. Hoerling M et al (2011) On North American decadal climate for 2011–2020. J Clim 24(16):4519–4528. doi: 10.1175/2011JCLI4137.1 CrossRefGoogle Scholar
  29. Huang J, van den Dool HM, Barnston AG (1996) Long-lead seasonal temperature prediction using optimal climate normals. J Clim 9(4):809–817. doi: 10.1175/1520-0442(1996)009<0809:LLSTPU>2.0.CO;2 CrossRefGoogle Scholar
  30. Johansson DJA et al (2015) Equilibrium climate sensitivity in light of observations over the hiatus warming. Nat Clim Change 5:449–453. doi: 10.1038/nclimate2573 CrossRefGoogle Scholar
  31. Joshi M et al (2003) A comparison of climate response to different radiative forcings in three general circulation models: towards an improved metric of climate change. Clim Dyn 20(7):843–854. doi: 10.1007/s00382-003-0305-9 Google Scholar
  32. Kharin VV et al (2012) Statistical adjustment of decadal predictions in a changing climate. Geophys Res Lett 39:19. doi: 10.1029/2012GL052647 CrossRefGoogle Scholar
  33. Kirtman B et al (2013) Near-term climate change: projections and Predictability. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, pp 953–1028. doi: 10.1017/CB09781107415324.023
  34. Kirtman B et al (2014) The North American multimodel ensemble: phase-1 seasonal-to-interannual prediction; phase-2 towards developing intraseasonal prediction. Bull Am Meteorol Soc 95:585–601. doi: 10.1175/BAMS-D-12-00050.1 CrossRefGoogle Scholar
  35. Lean JL, Rind DH (2008) How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys Res Lett 35:L18701. doi: 10.1029/2008GL034864 CrossRefGoogle Scholar
  36. Lean JL, Rind DH (2009) How will Earth’s surface temperature change in future decades? Geophys Res Lett 36:L15708. doi: 10.1029/2009GL038932 CrossRefGoogle Scholar
  37. Meehl GA et al (2009) Decadal prediction: can it be skillful? Bull Am Meteorol Soc 90(10):1467–1485. doi: 10.1175/2009BAMS2778.1 CrossRefGoogle Scholar
  38. Meehl GA, Hu A, Tebaldi C (2010) Decadal prediction in the Pacific region. J Clim 23(11):2959–2973. doi: 10.1175/2010JCLI3296.1 CrossRefGoogle Scholar
  39. Meehl GA et al (2014) Decadal climate prediction: an update from the trenches. Bull Am Meteorol Soc 95:2. doi: 10.1175/BAMS-D-12-00241.1 CrossRefGoogle Scholar
  40. Meinshausen M et al (2011) The RCP greenhouse gas concentrations and their extension from 1765 to 2300. Clim Change 109(1):213–241. doi: 10.1007/s10584-011-0156-z CrossRefGoogle Scholar
  41. Molteni F et al (2011) The new ECMWF seasonal forecast system (System 4), ECMWF Tech. Memo., 656, 49pp., ECMWF, Reading, UKGoogle Scholar
  42. Morice CP et al (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 dataset. J Geophys Res 117:D08101. doi: 10.1029/2011JD017187 CrossRefGoogle Scholar
  43. Newman M (2013) An empirical benchmark for decadal forecasts of global surface temperature anomalies. J Clim 26(14):5260–5269. doi: 10.1175/JCLI-D-12-00590.1 CrossRefGoogle Scholar
  44. Otto A et al (2013) Energy budget constraints on climate response. Nat Geosci 6:415–416. doi: 10.1038/ngeo1836 CrossRefGoogle Scholar
  45. Palmer TN, Barkmeijer J, Buizza R, Petroliagis T (1997) The ECMWF ensemble prediction system. Meteorol Appl 4(4):301–304. doi: 10.1017/S1350482797000649 CrossRefGoogle Scholar
  46. Palmer TN et al (2004) Development of a European multimodel ensemble system for seasonal-to-interannual prediction (DEMETER). Bull Am Meteorol Soc 85(6):853–872. doi: 10.1175/BAMS-85-6-853 CrossRefGoogle Scholar
  47. Palmer T, Hagedorn R (eds) (2006) Predictability of weather and climate. Cambridge University Press, Cambridge. ISBN 9780511225017Google Scholar
  48. Penland C, Matrosova L (1998) Prediction of tropical Atlantic sea surface temperatures using linear inverse modelling. J Clim 11(3):483–496. doi: 10.1175/1520-0442(1998) 011<0483:POTASS>2.0.CO;2 CrossRefGoogle Scholar
  49. Power S et al (1999) Interdecadal modulation of the impact of ENSO on Australia. Clim Dyn 15(5):319–324. doi: 10.1007/s003820050284 CrossRefGoogle Scholar
  50. Rayner NA et al (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407. doi: 10.1029/2002JD002670 CrossRefGoogle Scholar
  51. Rohde R et al (2013) A new estimate of the average Earth surface land temperature spanning 1753 to 2011. Geoinform. Geostat. 1:1. doi: 10.4172/gigs.1000101 Google Scholar
  52. Saha S et al (2013) The NCEP climate forecast system version 2. J Clim 27(6):2185–2208. doi: 10.1175/JCLI-D-12-00823.1 CrossRefGoogle Scholar
  53. Schmidt GA, Shindell DT, Tsigaridis K (2014) Reconciling warming trends. Nat Geosci 7:158–160. doi: 10.1038/ngeo2105 CrossRefGoogle Scholar
  54. Shaffrey LC, Hodson D, Robson J, Stevens DP, Hawkins E, Polo I, Stevens I, Sutton RT, Lister G, Iwi A, Smith D, Stephens A (2016) Decadal predictions with the HiGEM high resolution global coupled climate model: description and basic evaluation. Clim Dyn. doi: 10.1007/s00382-016-3075-x Google Scholar
  55. Shindell DT (2014) Inhomogeneous forcing and transient climate sensitivity. Nat Clim Change 4:274–277. doi: 10.1038/nclimate2136 CrossRefGoogle Scholar
  56. Smith DM et al (2007) Improved surface temperature prediction for the coming decade from a global climate model. Science 317(5839):796–799. doi: 10.1126/science.1139540 CrossRefGoogle Scholar
  57. Smith TM et al (2008) Improvements to NOAA’s historical merged land-ocean surface temperature analysis. J Clim 21(10):2283–2296. doi: 10.1175/2007JCLI2100.1 CrossRefGoogle Scholar
  58. Smith DM, Scaife AA, Kirtman BP (2012) What is the current state of scientific knowledge with regard to seasonal and decadal forecasting? Environ Res Lett 7(1):015602. doi: 10.1088/1748-9326/7/1/015602 CrossRefGoogle Scholar
  59. Smith DM et al (2013) Real-time multi-model decadal climate prediction. Clim Dyn 41(11):2875–2888. doi: 10.1007/s00382-012-1600-0 CrossRefGoogle Scholar
  60. Soares MB, Dessai S (2014) On the use of seasonal to decadal climate prediction for decision-making in Europe. SRI Papers, 62, Sustainability Research Institute, University of Leeds, ISSN:1753-1330Google Scholar
  61. Sterl A et al (2007) On the robustness of ENSO teleconnections. Clim Dyn 29:469–485. doi: 10.1007/s00382-007-0251-z CrossRefGoogle Scholar
  62. Stockdale TN et al (2011) ECMWF seasonal forecast system 3 and its prediction of sea surface temperature. Clim Dyn 37(3):455–471. doi: 10.1007/s00382-010-0947-3 CrossRefGoogle Scholar
  63. Stocker TF et al (2013) Technical Summary. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USAGoogle Scholar
  64. Suckling EB, Smith LA (2013) An evaluation of decadal probability forecasts from state-of-the-art climate models. J Clim 26(23):9334–9347. doi: 10.1175/JCLI-D-12-00485.1 CrossRefGoogle Scholar
  65. Sutton R, Suckling E, Hawkins E (2015) What does global mean temperature tell us about local climate? Philos Trans A 373:2054. doi: 10.1098/rsta.2014.0426 CrossRefGoogle Scholar
  66. Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498. doi: 10.1175/BAMS-D-11-00094.1 CrossRefGoogle Scholar
  67. Thomson AM et al (2011) RCP4.5: a pathway for stabilization of radiative forcing by 2100. Clim Change 109(1):77–94. doi: 10.1007/s10584-011-0151-4 CrossRefGoogle Scholar
  68. Trenberth KE et al (2000) The Southern Oscillation revisited: Sea level pressures, surface temperatures and precipitation. J Clim 13(24):4358–4365. doi: 10.1175/1520-0442(2000) 013<4358:TSORSL>2.0CO;2 CrossRefGoogle Scholar
  69. van den Dool HM (2007) Empirical methods in short-term climate prediction. Oxford University Press, OxfordGoogle Scholar
  70. van der Linden P, Mitchell JFB (eds) (2009) ENSEMBLES: climate change and its impacts: summary of research and results from the ENSEMBLES project, Met Office Hadley Centre, FitzRoy Road, Exeter EX1 3PB, UK, 160ppGoogle Scholar
  71. van Oldenborgh G-J et al (2005a) Evaluation of atmospheric fields from the ECMWF seasonal forecasts over a 15-year period. J Clim 18(16):3250–3269. doi: 10.1175/JCLI3421.1 CrossRefGoogle Scholar
  72. van Oldenborgh G-J et al (2005b) Did the ECMWF seasonal forecast model outperform statistical ENSO forecast models over the last 15 years? J Clim 18(16):3240–3249. doi: 10.1175/JCLI3420.1 CrossRefGoogle Scholar
  73. van Oldenborgh G-J et al (2012) Decadal prediction skill in a multi-model ensemble. Clim Dyn 38(7):1263–1280. doi: 10.1007/s00382-012-1313-4 CrossRefGoogle Scholar
  74. Weisheimer A et al (2009) ENSEMBLES—a new multi-model ensemble for seasonal-to-annual predictions: skill and progress beyond DEMETER in forecasting tropical Pacific SSTs. Geophys Res Lett 36(21):L21711. doi: 10.1029/2008GL040896 CrossRefGoogle Scholar
  75. Weisheimer A, Palmer T (2014) On the reliability of seasonal climate forecasts. J R Soc Interface 11(96):20131162. doi: 10.1098/rsif.2013.1162 CrossRefGoogle Scholar
  76. Wu R, Kirtman BP, van den Dool H (2009) An analysis of ENSO prediction skill in the CFS retrospective forecasts. J Clim 22(7):1801–1818. doi: 10.1175/2008JCLI2565.1 CrossRefGoogle Scholar

Copyright information

© The Author(s) 2016

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Emma B. Suckling
    • 1
  • Geert Jan van Oldenborgh
    • 2
  • Jonathan M. Eden
    • 2
  • Ed Hawkins
    • 1
  1. 1.NCAS-Climate, Department of MeteorologyUniversity of ReadingReadingUK
  2. 2.Royal Netherlands Meteorological Institute (KNMI)De BiltNetherlands

Personalised recommendations