Non-stationary analysis of the frequency and intensity of heavy precipitation over Canada and their relations to large-scale climate patterns

Abstract

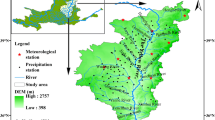
In recent years, because the frequency and severity of floods have increased across Canada, it is important to understand the characteristics of Canadian heavy precipitation. Long-term precipitation data of 463 gauging stations of Canada were analyzed using non-stationary generalized extreme value distribution (GEV), Poisson distribution and generalized Pareto (GP) distribution. Time-varying covariates that represent large-scale climate patterns such as El Niño Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), Pacific decadal oscillation (PDO) and North Pacific Oscillation (NP) were incorporated to parameters of GEV, Poisson and GP distributions. Results show that GEV distributions tend to under-estimate annual maximum daily precipitation (AMP) of western and eastern coastal regions of Canada, compared to GP distributions. Poisson regressions show that temporal clusters of heavy precipitation events in Canada are related to large-scale climate patterns. By modeling AMP time series with non-stationary GEV and heavy precipitation with non-stationary GP distributions, it is evident that AMP and heavy precipitation of Canada show strong non-stationarities (abrupt and slowly varying changes) likely because of the influence of large-scale climate patterns. AMP in southwestern coastal regions, southern Canadian Prairies and the Great Lakes tend to be higher in El Niño than in La Niña years, while AMP of other regions of Canada tends to be lower in El Niño than in La Niña years. The influence of ENSO on heavy precipitation was spatially consistent but stronger than on AMP. The effect of PDO, NAO and NP on extreme precipitation is also statistically significant at some stations across Canada.

Appendices

Appendix 1: GEV distribution

Let M = max {Z ₁,…, Z _n } for large n, where Z ₁, Z ₂,… is a sequence of independent (or weakly dependent) identically distributed observations. In this study, Z _t represents daily observed precipitation recorded at a particular station on day t, and M is the AMP. Asymptotic results state that under some regularity conditions, normalizing sequences{a _n } and {b _n  > 0} can be found such that (Coles 2001):

$$\Pr \left( {\frac{{M - a_{n} }}{{b_{n} }} \le y} \right) \to {\text{GEV}}\left( y \right)$$

(1)

as n → ∞, for a non-degenerate distribution function, which is the GEV distribution with the cumulative distribution function:

$${\text{GEV}}\left( {y;\mu ,\sigma ,\xi } \right) = \left\{ {\begin{array}{*{20}l} {\exp \left\{ { - \left[ {1 + \xi \frac{y - \mu }{\sigma }} \right]^{{ - {1 \mathord{\left/ {\vphantom {1 \xi }} \right. \kern-0pt} \xi }}} } \right\}} \hfill & {\xi \ne 0} \hfill \\ {\exp \left[ { - \exp \left( {\frac{(y - \mu )}{\sigma }} \right)} \right]} \hfill & {\xi = 0} \hfill \\ \end{array} } \right.$$

(2)

where 1 + ξ(y − μ)/σ > 0, μ, σ and ξ are the location, scale, and shape parameters, respectively. The shape parameter ξ determines the type of tail behavior. ξ < 0, ξ = 0 and ξ > 0 correspond to the Weibull (Type III), Gumbel (Type I) and Fréchet (Type II) distributions, respectively.

For a non-stationary process, the time-varying GEV parameters can be estimated by time-varying covariates. For instance, the GEV location parameter is defined through a linear function of covariates:

$$\mu = \beta X = \beta_{0} + \beta_{1} x_{1} + \cdots + \beta_{m} x_{m}$$

(3)

where X = (1, x ₁,…, x _m ) is a matrix of the time-varying covariate vectors x ₁,…, x _m , β = (β ₀, β ₁, …β _m ) is the parameter vector to be estimated, in which β ₀ is the intercept and β ₁,…β _m are the regression coefficients for the corresponding covariates; m is the number of covariates considered. The scale and shape parameters of the GEV distribution can be similarly expressed as Eq. (3).

Appendix 2: Poisson regression

The numbers of days (counts) of extreme values exceeding a threshold over a specified time interval (a year in this study) can be modeled by a Poisson distribution with an equal-dispersion (the mean equals the variance). However, the variance of observed data tends to be larger than the mean, known as over-dispersion, which can partly be attributed to the effect of temporal clustering (Mallakpour and Villarini 2015; Pinto et al. 2013; Villarini et al. 2011, 2013). The statistical significance of dispersion coefficients different from unity at 5 % significance level can be tested using the regression-based tests (Cameron and Trivedi 1990) for testing over-dispersion in a Poisson model.

A Poisson regression models discrete data, in which the predict and follows a Poisson distribution. The counts in year i as N _i have a conditional Poisson distribution with the rate of occurrence parameter λ _i , given that:

$$P\left( {N_{i} = k\left| {\lambda_{i} } \right.} \right) = \frac{{e^{{ - \lambda_{i} }} \lambda_{i}^{k} }}{k!} \, \quad \left( {k = 0,1,2, \ldots } \right)$$

(4)

where λ _i is a non-negative random variable. In a Poisson regression model, λ _i can be modeled as a function of predictors x _1i , x _2i ,…, x _mi in a manner similar to parameters of a non-stationary GEV (see Eq. 3):

$$\lambda_{i} = \exp \left( {\beta_{0} + \beta_{1} x_{1i} + \beta_{2} x_{2i} + \cdots + \beta_{m} x_{mi} } \right)$$

(5)

where β _j is the coefficient for the j-th predictor (x _ji ) estimated by the maximum likelihood method. If β _j estimated is non-zero at a 5 % significance level, then there is a statistically significant relationship between the occurrence of extreme events and the predictor x _j . By relating λ _i to the time using an exponential function λ _i  = exp (β ₀ + β ₁ i), changes in the mean number of occurrences of heavy precipitation with time can be examined. If β ₁ is non-zero at the 5 % significance level, temporal changes in the mean number of extreme events are statistically significant (Villarini et al. 2011, 2012, 2013). The abrupt change points of the occurrences of extreme events can be further identified by a segmented regression in which the relation between the predictand and the predictor is piecewise linear. We used the function segmented in the R package ‘segmented’ (Muggeo 2003) to detect change points and to estimate β ₀ and β ₁ for the Poisson regression model.

Appendix 3: GP distribution

The exceedance, Q = Z – u (where Z is the observed precipitation and u the threshold) can be modeled as a GP distribution (Coles 2001):

$$\Pr \left( {Q \le q\left| {Z > u} \right.} \right) = GP_{\sigma ,\xi } \left( q \right) = \left\{ {\begin{array}{*{20}l} {1 - \exp \left[ {{{ - q} \mathord{\left/ {\vphantom {{ - q} \sigma }} \right. \kern-0pt} \sigma }} \right]} \hfill & {\xi = 0} \hfill \\ {1 - \left[ {1 + {{\xi q} \mathord{\left/ {\vphantom {{\xi q} \sigma }} \right. \kern-0pt} \sigma }} \right]^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} \xi }} \right. \kern-0pt} \xi }}} } \hfill & {\xi \ne 0} \hfill \\ \end{array} } \right.$$

(6)

For q ≥ 0 and 1 + ξq/σ > 0, where σ and ξ are the scale and shape parameters of a GP distribution. For ξ = 0, GP reduces to an exponential distribution. The GP distribution can be set up to model non-stationary processes, usually by making the scale parameter σ depend on particular covariate(s) (Coles 2001; Khaliq et al. 2006). The log of σ is regressed against covariates X, log (σ) = βX, as shown in Eqs. 3 and 5.

The return level y _l is exceeded on average l times over a fixed period. Since there are on average λ peaks in the whole time series, the probability that an arbitrary peak exceeds y _l equals l/λ. Thus, y _l is obtained by adding the threshold to the (1 − l/λ) quantile of the excess distribution (Coles 2001):

$$y_{l} = u + GP_{\sigma ,\xi }^{ - 1} \left( {{{1 - l} \mathord{\left/ {\vphantom {{1 - l} \lambda }} \right. \kern-0pt} \lambda }} \right) = \left\{ \begin{aligned} u + \sigma \ln \left( {{l \mathord{\left/ {\vphantom {l \lambda }} \right. \kern-0pt} \lambda }} \right) \quad \xi = 0 { } \hfill \\ u + \frac{\sigma }{\xi }\left[ {1 - \left( {\frac{l}{\lambda }} \right)^{ - \xi } } \right] \quad \xi \ne 0 \hfill \\ \end{aligned} \right.$$

(7)

For presentation, it is often more convenient to give return levels on an annual scale, so that the N-year return level is the level expected to be exceeded once every N years.

Appendix 4: The likelihood-ratio test

The likelihood-ratio test can compare results obtained from GEV and GP distributions of parameters expressed with covariates of various complexities, such that the base covariate (e.g., M ₀) is a subset of a more complex covariate (e.g., M ₁). The likelihood-ratio test can determine which sets of model parameters will lead to the overall best model performance for GEV and GP. Suppose a base model M ₀ is nested within a model M ₁, and L ₀ (L ₁) is the negative log-likelihood value for M ₀ (M ₁), then a deviance statistics is given by (Coles 2001):

$$D = - 2\left( {L_{1} - L_{0} } \right)$$

(8)

Large values of D indicate that M ₁ is more adequate for representing the data than its base counterpart M ₀. The D statistic follows a Chi square distribution with degree of freedom, ν (difference between the number of parameters of the models M ₀ and M ₁). D _α is the (1 − α) quantile of the Chi square distribution at the α significant level. The null hypothesis D = 0 is rejected if D > D _α . We used functions in the R package ‘extRemes’ (Gilleland and Katz 2011) for inferring the parameters of GEV and GP distributions and testing the significance of the relations between parameters and covariates.