Roles of convective heating and boundary-layer moisture asymmetry in slowing down the convectively coupled Kelvin waves

Abstract

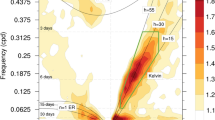
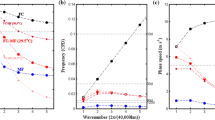
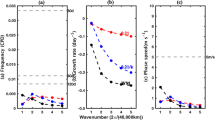
Mechanisms for an in-phase relationship between convection and low-level zonal wind and the slow propagation of the convectively coupled Kelvin wave (CCKW) are investigated by analyzing satellite-based brightness temperature and reanalysis data and by constructing a simple theoretical model. Observational data analysis reveals an eastward shift of the low-level convergence and moisture relative to the CCKW convective center. The composite vertical structures show that the low-level convergence lies in the planetary boundary layer (PBL) (below 800 hPa), and is induced by the pressure trough above the top of PBL through an Ekman-pumping process. A traditional view of a slower eastward propagation speed compared to the dry Kelvin waves is attributed to the reduction of atmospheric static stability in mid-troposphere due to the convective heating effect. The authors’ quantitative assessment of the heating effect shows that this effect alone cannot explain the observed CCKW phase speed. We hypothesize that additional slowing process arises from the effect of zonally asymmetric PBL moisture. A simple theoretical model is constructed to understand the relative role of the heating induced effective static stability effect and the PBL moisture effect. The result demonstrates the important role of the both effects. Thus, PBL-free atmosphere interaction is important in explaining the observed structure and propagation of CCKW.

Appendix: Derivation of the 2.5-layer model for CCKW

Consider a simple atmospheric model that consists of two-level atmosphere and a well-mixed planetary boundary layer (PBL) (see Fig. 11), where p _s, p _e and p ₀ stand for pressures at the surface, the top of PBL and the top of free atmosphere, respectively. The free atmosphere is divided by two equal pressure levels with $p_{2} = (p_{0} + p_{e} )/2$. Neglecting the meridional wind component, the horizontal momentum and continuity equations are written at levels p ₁ ($p_{1} = (p_{2} + p_{0} )/2$) and p ₃ ($p_{3} = (p_{2} + p_{e} )/2$) and thermodynamic equation at p ₂.

$$\frac{{\partial u_{1} }}{\partial t} = - \frac{{\partial \phi_{1} }}{\partial x},$$

(12)

$$\frac{{\partial u_{3} }}{\partial t} = - \frac{{\partial \phi_{3} }}{\partial x},$$

(13)

$$\frac{{\partial u_{1} }}{\partial x} + \frac{{\omega_{2} - \omega_{0} }}{\Delta p} = 0,$$

(14)

$$\frac{{\partial u_{3} }}{\partial x} + \frac{{\omega_{e} - \omega_{2} }}{\Delta p} = 0,$$

(15)

$$\frac{\partial }{\partial t}\left( {\frac{{\phi_{3} - \phi_{1} }}{\Delta p}} \right) + \sigma_{2} \omega_{2} = - \frac{{R\dot{Q}}}{{p_{2} C_{p} }},$$

(16)

where C _p is specific heat at constant pressure; $u$, $\phi$ and $\omega$ denote the zonal wind, geopotential and vertical pressure velocity respectively; $\sigma_{2}$ and $\dot{Q}$ are the static stability parameter and the diabatic heating rate at p ₂ respectively; $\Delta p$ is the half-depth of the free atmosphere ($\Delta p = (p_{e} - p_{0} )/2$).

Fig. 11

Schematic vertical structure of the 2.5-layer model

Introducing barotropic and baroclinic components of zonal winds and geopotentials defined by

$$u_{ + } = \left( {u_{3} + u_{1} } \right)/2,\;\phi_{ + } = \left( {\phi_{3} + \phi_{1} } \right)/2,$$

(17)

$$u_{ - } = \left( {u_{3} - u_{1} } \right)/2,\;\phi_{ - } = \left( {\phi_{3} - \phi_{1} } \right)/2,$$

(18)

The sums and differences of corresponding momentum and continuity equations at levels p ₁ and p ₃ then yield

$$\frac{{\partial u_{ + } }}{\partial t} = - \frac{{\partial \phi_{ + } }}{\partial x},$$

(19)

$$\frac{{\partial u_{ + } }}{\partial x} + \frac{{\omega_{e} - \omega_{0} }}{2\Delta p} = 0,$$

(20)

$$\frac{{\partial u_{ - } }}{\partial t} = - \frac{{\partial \phi_{ - } }}{\partial x},$$

(21)

$$\frac{{\partial u_{ - } }}{\partial x} + \frac{{\omega_{e} + \omega_{0} - 2\omega_{2} }}{2\Delta p} = 0,$$

(22)

$$\frac{{\partial \phi_{ - } }}{\partial t} + \frac{{\sigma_{2} \Delta p}}{2}\omega_{2} = - \frac{{\Delta pR\dot{Q}}}{{2p_{2} C_{p} }},$$

(23)

By assuming $\omega_{e} = \omega_{0}$, the barotropic and baroclinic modes are decoupled; this assumption was shown to be quite useful to simplify tropical atmospheric motion (Wang and Li 1993). As a result, one only needs to consider the linear governing Eqs. (21–23), with $u_{ - }$ and $\phi_{ - }$ representing lower tropospheric zonal wind and geopotential anomaly fields, respectively. The mid-tropospheric vertical motion is determined by the vertical motion at the top of PBL and the low-level convergence as

$$\omega_{2} = \omega_{e} + \Delta p\frac{{\partial u_{ - } }}{\partial x},$$

(24)

Following Wang and Li (1993), PBL momentum and continuity equations may be written as

$$Eu_{B} - \beta^{*} yv_{B} = - \frac{{\partial \phi_{e} }}{\partial x},$$

(25)

$$Ev_{B} + \beta^{*} yu_{B} = - \frac{{\partial \phi_{e} }}{\partial y},$$

(26)

$$\frac{{\partial u_{B} }}{\partial x} + \frac{{\partial v_{B} }}{\partial y} - \frac{{\omega_{e} }}{{p_{s} - p_{e} }} = 0,$$

(27)

where $u_{B}$ and $v_{B}$ are vertically averaged horizontal winds in the boundary layer; $\phi_{e}$ denotes the geopotential at the top of PBL; E is the friction coefficient; $\beta^{*}$ is the planetary vorticity gradient. Here we have assumed the vertical motion is zero at $p_{s}$. As a result, $\omega_{e}$ could be explicitly solved as a function of $\phi_{e}$ (i.e., $\omega_{e} = \left( {p_{s} - p_{e} } \right)\left( {\frac{{\partial u_{B} }}{\partial x} + \frac{{\partial v_{B} }}{\partial y}} \right) = f(\phi_{e} )$). For simplicity, one may directly link $\omega_{e}$ to $\phi_{e}$ as

$$\omega_{e} = \beta_{0} \phi_{e} ,$$

(28)

where $\beta_{0}$ is a scale parameter which could be estimated based on reanalysis data, and $\phi_{e}$ may be approximately represented by $\phi_{ - } .$

Consider that atmospheric diabatic heating consists of two parts: a simultaneous heating process (denoted by $\dot{Q}_{s}$) associated with the deep convection of CCKW and a delayed heating process (denoted by $\dot{Q}_{d}$) related to PBL moistening ahead of the convection (i.e., $\dot{Q} = \dot{Q}_{s} + \dot{Q}_{d}$), where $\dot{Q}_{s}$ is induced by the mid-level upward motion associated with the deep convection and could be parameterized as $\dot{Q}_{s} = - I\sigma_{2} C_{p} p_{2} \omega_{2} /R,$ where I represents the ratio of the simultaneous heating against the adiabatic cooling; the $\dot{Q}_{d}$ is associated with the pre-moistening of PBL. The effect of the PBL moistening at the east side of pre-existing CCKW convection is to destabilize the atmosphere through increased convective instability and induce the onset of shallow cumulus and congestus. The delayed heating process may be parameterized by the pre-moistening of PBL as

$$ {\dot{Q}_{d} = \beta_{1} q_{B}}_{ \left( {t - \tau_{1} } \right),} $$

(29)

where β ₁ is a scale parameter and τ ₁ represents the time-lag between the PBL moisture ($q_{B}$) and the subsequent convective heating. Therefore, free-atmospheric governing equations may be written as

$$\frac{{\partial u_{ - } }}{\partial t} = - \frac{{\partial \phi_{ - } }}{\partial x},$$

(30)

$$\frac{{\partial \phi_{ - } }}{\partial t} + C_{0}^{2} (1 - I)\frac{{\partial u_{ - } }}{\partial x} = - \frac{{\Delta pR\dot{Q}_{d} }}{{2p_{2} C_{p} }} - (1 - I)\frac{{C_{0}^{2} }}{\Delta p}\omega_{e} ,$$

(31)

where $C_{0} = \sqrt {{{\sigma_{2} \Delta p^{2} } \mathord{\left/ {\vphantom {{\sigma_{2} \Delta p^{2} } 2}} \right. \kern-0pt} 2}}$ denotes the dry Kelvin wave speed.

To reveal the cause of the pre-moistening in PBL, a vertically (1000–800 hPa) integrated moisture budget analysis was performed over the PBL moistening region (5°S–5°N, 100°–120°E). Applying a CCKW-filtering operator (denoted by a prime) to the total moisture tendency equation, one may derive the CCKW moisture budget equation as the following:

$$\frac{{\partial q^{\prime}_{B} }}{\partial t} = - \left( {u_{B} \frac{{\partial q_{B} }}{\partial x}} \right)^{\prime } - \left( {v_{B} \frac{{\partial q_{B} }}{\partial y}} \right)^{\prime } - \left( {\omega \frac{\partial q}{\partial p}} \right)^{\prime } - \left( {\frac{{Q_{2} }}{{L_{v} }}} \right)^{\prime } ,$$

(32)

where $Q_{2}$ is the atmospheric apparent moisture sink (Yanai et al. 1973) and L _v is the latent heat of condensation. Figure 12 shows the contribution from each of the PBL moisture budget terms. The largest positive contribution is the vertical moisture advection term. The cause of the positive vertical advection is primarily due to the advection of the mean moisture (which has a maximum at the surface and decays with height) by anomalous ascending motion, in a way similar to the MJO moistening process (Hsu and Li 2012). For simplicity, a PBL moisture tendency equation may be written as $\frac{{\partial q_{B} }}{\partial t} = - \omega_{B} \frac{{\partial \bar{q}}}{\partial p} = - \frac{{\omega_{e} }}{2}\frac{{\partial \bar{q}}}{\partial p} = \lambda \omega_{e}$ where $\lambda = \frac{{\partial \bar{q}}}{2\partial p}$. As $\omega_{e}$ is associated with the PBL convergence, which is mainly induced by the low pressure at the top of PBL through Ekman pumping effect (as demonstrated in Fig. 5), an alternative way is to directly link $q_{B}$ to $\omega_{e}$ or $\phi_{e}$ with a time lag, based on reanalysis data analysis. Thus, the PBL moisture equation could be simplified as a linear diagnostic equation:

$${ q_{B} = - \beta_{2} \phi_{e}}_ {(t - \tau_{2} ),} $$

(33)

where β ₂ is a scale parameter and $\tau_{2}$ represents the time-lag between $- \phi_{e}$ and $q_{B}$.

Fig. 12

PBL averaged CCKW moisture budget terms over the max PBL moistening tendency region (5°S–5°N, 100°–120°E). From left to right, observed specific humidity tendency, zonal moisture advection, meridional moisture advection, vertical moisture advection, latent heating and sum of these budget terms. Unit is 10⁻⁵ g kg⁻¹ s⁻¹

Equations (28)–(31) and (33) formulate a simple analytical model for CCKW, with the parameters β ₀, β ₁, β ₂, $\tau_{1}$ and $\tau_{2}$ estimated by using the reanalysis data (discussed in Sect. 5.1).