Abstract
This study forms part II of two papers describing ECHAM6-FESOM, a newly established global climate model with a unique multi-resolution sea ice-ocean component. While part I deals with the model description and the mean climate state, here we examine the internal climate variability of the model under constant present-day (1990) conditions. We (1) assess the internal variations in the model in terms of objective variability performance indices, (2) analyze variations in global mean surface temperature and put them in context to variations in the observed record, with particular emphasis on the recent warming slowdown, (3) analyze and validate the most common atmospheric and oceanic variability patterns, (4) diagnose the potential predictability of various climate indices, and (5) put the multi-resolution approach to the test by comparing two setups that differ only in oceanic resolution in the equatorial belt, where one ocean mesh keeps the coarse ~1° resolution applied in the adjacent open-ocean regions and the other mesh is gradually refined to ~0.25°. Objective variability performance indices show that, in the considered setups, ECHAM6-FESOM performs overall favourably compared to five well-established climate models. Internal variations of the global mean surface temperature in the model are consistent with observed fluctuations and suggest that the recent warming slowdown can be explained as a once-in-one-hundred-years event caused by internal climate variability; periods of strong cooling in the model (‘hiatus’ analogs) are mainly associated with ENSO-related variability and to a lesser degree also to PDO shifts, with the AMO playing a minor role. Common atmospheric and oceanic variability patterns are simulated largely consistent with their real counterparts. Typical deficits also found in other models at similar resolutions remain, in particular too weak non-seasonal variability of SSTs over large parts of the ocean and episodic periods of almost absent deep-water formation in the Labrador Sea, resulting in overestimated North Atlantic SST variability. Concerning the influence of locally (isotropically) increased resolution, the ENSO pattern and index statistics improve significantly with higher resolution around the equator, illustrating the potential of the novel unstructured-mesh method for global climate modeling.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Understanding the internal variability of the climate system is essential in order to assess the significance of observed climate changes, including the global surface warming over the last decades and the apparent warming slowdown (‘hiatus’) during the period 1998–2012. There is substantial evidence that, in contrast to the long-term warming, the hiatus can be attributed to internal variability of the climate system that masked the externally forced long-term warming (Stocker et al. 2013; Hawkins et al. 2014; Chen and Tung 2014; Huber and Knutti 2014; Watanabe et al. 2014). Given that the temporal span of the observational record is too short to address multidecadal variability reliably, this evidence is primarily based on numerical models of the climate system. These models are also the main tools to project the future evolution of the climate system, where internal variations again play a key role. The internal variability is thus one of the most crucial aspects of any climate model and needs to be carefully explored and documented.
In most current climate models, including those contributing to the most recent phase of the Coupled Model Intercomparison Project (CMIP5; Taylor et al. 2012), the governing equations are discretized in space based on quasi-regular grids or truncated expansions in spherical harmonics. These regular-mesh models are rather similar with respect to their numerical core; this may contribute to the effective number of global climate models being a factor 3 smaller than the total number of models (Pennell and Reichler 2011).
To increase resolution locally in regular-mesh ocean models one can apply ’geometrical tricks’ such as the telescoping of ocean grid boxes in the tropics (e.g. Delworth et al. 2006) and the strategic placement of the mesh poles to exploit the convergence of meridians (e.g. Marsland et al. 2003). Another approach is 2-way nesting, where coarse and high resolution regular-mesh models are running in parallel such that the fine-resolution model is embedded into a coarser one. However, apart from high technical demands of this approach, inconsistencies along the boundaries pose considerable numerical problems (Harris and Durran 2010). In general, the flexibility to distribute the computational nodes in regular-mesh models is strongly limited: to increase the horizontal resolution in arbitrary regions of the ocean can only be achieved by increasing resolution globally, which poses strong constraints in terms of computational costs.
Recently, a suite of multi-resolution (i.e. irregular- or unstructured-mesh) ocean models has emerged (e.g. Chen et al. 2003; Danilov et al. 2004; Ringler et al. 2013; Wang et al. 2014), adding to the diversity in the current zoo of ocean models. These models employ numerical cores that are different, in essence, to today’s CMIP-type models and allow for locally increased resolution in arbitrarily chosen regions of the global ocean with smooth transitions. Currently, the Finite Element Sea ice–Ocean Model (FESOM) is the only multi-resolution ocean model which is available in a coupled configuration with a state-of-the-art atmospheric general circulation model (ECHAM6-FESOM; Sidorenko et al. 2015). Sidorenko et al. (2015) showed that the realism of the mean climate simulated by ECHAM6-FESOM (run with 1990 aerosol and greenhouse gas concentrations) is comparable to that of standard CMIP5 models. In Sidorenko et al. (2015), the potential of the multi-resolution approach has been demonstrated in the equatorial Pacific, where an increased resolution from 1° to 0.25° in the equatorial belt results in an improved simulation of the narrow equatorial current system and a reduced cold sea surface temperature (SST) bias.
In this study, ECHAM6-FESOM is validated regarding the simulated internal climate variability, using the same model and experimental setup (apart from longer integration) as in Sidorenko et al. (2015). Instead of detailing selected modes of variability and their mechanisms, a broad spectrum of important modes is analyzed to document and assess the overall performance of this new climate model. The potential of the multi-resolution approach is demonstrated further by inspection of the resolution dependence of the variability in the equatorial Pacific associated in particular with the El Niño–Southern Oscillation (ENSO). Apart from this aspect, the multi-resolution approach is not exploited in this study.
The aim of this study is threefold:
-
1.
To validate the internal climate variability of a long (1500-year) present-day control run with ECHAM6-FESOM on different time scales, compare to observations and to other models where appropriate;
-
2.
To assess whether the observed hiatus in global mean surface temperature rise could have been caused by internal variability alone, and to diagnose the potential predictability of various climate variables;
-
3.
To put the multi-resolution approach to the test in the tropical Pacific by studying the influence of mesh refinement in the tropical ocean on ENSO.
The paper is organized as follows. Section 2 describes the model setup and two different grid configurations. Section 3 describes the data sets which are used and discusses utilized detrending methods. The climate variability is analyzed in Sect. 4 and comprises 5 steps where we (a) analyze the global mean surface temperature characteristics; (b) discuss hiatus-analog events in global mean surface temperature and statistics of various climate indices during these events; (c) examine in more detail the climate indices discussed in part b) regarding their spatio-temporal patterns compared to observations and other models; (d) investigate the influence of the tropical mesh resolution on the modeled ENSO pattern and variability; (e) conclude with an analysis of the potential predictability of all climate indices considered in this study. The paper closes with a summary and conclusion in Sect. 5.
2 Model setup
The global multi-resolution model ECHAM6-FESOM (E6-F) is applied in two configurations differing only in the tropical horizontal resolution in the ocean. The atmosphere component ECHAM6 (Stevens et al. 2013) is employed at T63L47 resolution (approx. 1.875° horizontal resolution with 47 vertical levels and a 10 min time step). The ocean component FESOM is a multi-resolution sea ice-ocean model (Danilov et al. 2004; Wang et al. 2008, 2014) that has been developed at the Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research (AWI). FESOM discretizes the model domain with triangular surface grids. In the current setup, FESOM operates on 46 unevenly spaced z-levels in the vertical, with a spacing of 10 m in the upper 100 m and increasing steps below. The time step is 30 min. FESOM and ECHAM6 are coupled every 6 h via the OASIS3-MCT coupler (Valcke et al. 2013). For more details see Sidorenko et al. (2015).
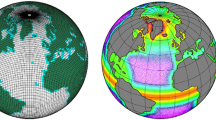
As in Sidorenko et al. (2015), FESOM is employed here in two configurations (Fig. 1) regarding the horizontal mesh: (1) The reference mesh (REF) has a nominal resolution of 150 km in the open ocean. The mesh is gradually refined towards the equator down to ~25 km. Refinement is also applied in the northern part of the North Atlantic as well as near coastlines. Note that the triangular surface grid refinement is always isotropic, i.e. equally in meridional and zonal direction, in contrast to the ’telescoping’ of grid boxes at the equator applied in some regular-mesh models (e.g. Delworth et al. (2006)). The triangular surface mesh contains approximately 87,000 surface nodes, resulting in a total of about 2,900,000 nodes in all dimensions. (2) The low resolution mesh (LOW) is identical to REF except for the refinement in the equatorial belt. In LOW the surface mesh contains ~44,000 nodes, resulting in ~1,300,000 nodes in all dimensions.
Arctic and Pacific sectors of the ocean meshes used in this study. The REF simulation is based on a mesh with resolution up to 0.25° in the tropics. A depiction of the Atlantic sector of this mesh can be found in Sidorenko et al. (2015). The LOW simulation is based on a mesh identical to the REF mesh except for missing local refinement in the tropics
The computational requirement is proportional to the total number of nodes, which is about half in LOW compared to REF. Taking the unchanged computational demand of the atmospheric model into account, REF is more expensive by a factor 1.5 compared to LOW in the coupled model.
Two E6-F simulations with the REF and LOW configurations have been conducted with present-day greenhouse gas and aerosol concentrations from the year 1990. Compared to part I of this study (Sidorenko et al. 2015), the REF simulation has been extended to 1500 years and the LOW simulation has been extended to 520 years to allow for a robust assessment of the long-term climate variability.
Given the extension of the simulations, it is appropriate to give an update on the performance of E6-F REF and E6-F LOW in simulating the mean climate state by means of objective performance indices (PI, Table 1; see Appendix 1 for their computation). Note that, in contrast to the PI reported in Sidorenko et al. (2015), these PI include an assessment of the simulated sea ice concentrations in addition to the atmospheric variables used in Sidorenko et al. (2015). According to the PI, E6-F REF performs very similar to E6-F LOW across the considered large-scale regions. The PI for E6-F REF slightly worsen with advancing simulation length because of a slow transient warming of the deep ocean. It is not clear to what extent this is a model bias or a realistic commitment warming due to the constant present-day forcing. Despite the slow warming all PI remain below 1 (except for Antarctica, see discussion in Sect. 4.5), indicating an above-average performance compared to the considered set of CMIP5 models (Sidorenko et al. 2015). Thus, the main findings from Sidorenko et al. (2015) still apply to the extended simulations examined here.
3 Validation data and detrending methods
Several observational data sets are used in this study for the validation of the model results. Near-surface temperatures over land and ocean are taken from the UK Met Office Hadley Centre’s HadCRUT4 data set (Morice et al. 2012) for the period 1850–2012. Due to spatio-temporally varying data coverage, this data set includes gaps. In addition, the HadISST data for sea surface temperature anomalies between 1870 and 2012 with global coverage is used where data gaps have been filled by an optimal interpolation procedure (HadISST; Rayner et al. 2003). More data are taken from the atmospheric ERA-Interim reanalysis provided by ECMWF (Dee et al. 2011). Finally, objective performance indices for the variability of E6-F are also compared to the PI for one of the MPI-ESM-LR (Giorgetta et al. 2013) CMIP5 historical runs spanning the period 1950–2005.
These data have been detrended linearly at every grid point in order to remove externally forced trends, and also the mean annual cycle has been subtracted. This way only the non-seasonal internal climate variability is retained. Note that, since the externally forced warming trend is unlikely to be linear, a residual signal may remain.
Due to the experimental setup that resembles a dynamical system converging asymptotically towards a quasi-equilibrium state under constant forcing, the E6-F data are treated differently. An exponential 3-parameter fit of the form
to the last 1000 years of the 3D integrated potential ocean temperature results in high-quality residuals (Fig. 2), with \(\tau \approx 813\) years being the deep-ocean equilibration time scale. Exponential fits to sufficiently long subintervals of the time series show only a weak dependence on the exact period used for estimating the parameters a, b and \(\tau\) (not shown), indicating the robustness and physical plausibility of the method.
Time series of annual global volume-averaged ocean potential temperature for E6-F REF (grey), years 1–1500. An exponential function \(a*\exp (-y/\tau )+b\) has been fitted to the last 1000 years (blue) of the integration and the best fit corresponds to the time scale \(\tau \approx 813\) years. The discrepancy left of the vertical line (where the fitted curve is extrapolated) illustrates the contamination from transient effects on time scales shorter than \(\tau\). In the analysis below we mostly use only years 501–1500
Unless otherwise specified, an exponential detrending of the form of Eq. (1) with \(\tau \approx 813\) years is applied at each grid point to the last 1000 years of the E6-F REF simulation. Because of possibly varying trends in different seasons, the detrending is performed separately for each month, which entails the removal of the seasonal cycle, leaving again only the non-seasonal part of the variability. Note that the time scale \(\tau\) of the deep ocean adjustment is used to remove the model drift from all E6-F data because the generally lower drift to noise ratio, e.g. for the temperature at a single surface grid point, allows no meaningful estimation of individual time scales. Moreover, it stands to reason that the longest-time scale equilibration associated with the deep ocean imprints on any other climate variables, which is confirmed by high-quality residuals obtained for virtually all examined quantities (not shown).
In the first ~500 years of the simulations, shorter time scale adjustments take place that interfere with the long-term equilibration. Therefore, where the first ~500 years are used to compare the REF and LOW simulations, the data are detrended linearly. Otherwise, the exponentially detrended last 1000 years of the E6-F REF simulation are used, neglecting the previous 500 years.
Note that, even with the careful detrending applied to the simulation data, the drift of the background climate state (~0.4 K global-mean surface warming over the last 1000 years) may imprint on the modes of variability. To supplement the below analyses we have therefore investigated whether the results depend systematically on simulation time, with the general outcome that no significant dependence can be detected (not shown).
4 Simulated climate variability
4.1 Performance indices (PI)
We start the discussion of the simulated internal climate variability using objective variability performance indices (Table 2) which, analogously to the PI for the mean state, integrate over large spatial areas and a number of important quantities (see Appendix 1) based on standard deviations. The PI are normalized such that an index larger (smaller) than 1 implies that the model performs worse (better) than the average over the selected set of CMIP5 models in comparison to observational data.
According to the PI (Table 2) E6-F REF and LOW perform similarly well in terms of large-scale non-seasonal variability in the polar regions and in the Northern and Southern mid-latitudes, irrespective of the time period considered. If any, there is a tendency towards improved non-seasonal variability in the tropics and especially in the inner tropics due to increased resolution in REF (also compared to MPI-ESM-LR), but the error bars for REF and LOW overlap. Because, according to the PI, E6-F REF and LOW perform similarly in the extratropics, the analysis of possible improvements due to increased tropical resolution is limited to the tropical regions only (Sect. 4.6).
4.2 Global surface temperature
4.2.1 Spatial distribution of surface temperature variability
Following the methodology in Collins et al. (2001), the E6-F results are compared to the HadCRUT4 dataset which is provided on a \(5\,^\circ \times 5\,^\circ\) regular grid with variable data coverage in space and time. We interpolated the model data onto the coarser HadCRUT4 grid prior to the analysis. The model data are then split into six non-overlapping chunks of the same length as the HadCRUT4 data set (163 years). Afterwards, the data in every chunk is masked to match the missing values in HadCRUT4 in both space and time. As a result, an ensemble of six model realizations that mimic the HadCRUT4 dataset in terms of spatio-temporal coverage is obtained. Based on these data we compute a pattern of standard deviations for the monthly surface temperature for every grid box (Fig. 3).
(Top) Standard deviation of non-seasonal monthly near-surface temperature anomalies from HADCRUT4 (1850 to 2012) based on its 1961–1990 climatology. Only grid boxes with at least 10 years of data are considered. White boxes represent data gaps. (Bottom) Average non-seasonal monthly surface temperature standard deviation in the last 1000 years of the E6-F REF simulation, derived from the six non-overlapping 163-year chunks as the square root of the ensemble-mean variance. The model data have been interpolated to the HADCRUT4 grid (\(5\,^\circ \times 5\,^\circ\)) prior to the analysis
E6-F simulates an average non-seasonal monthly surface temperature variability that is in broad agreement with observations from HadCRUT4 (Fig. 3). Naturally, the variability is most pronounced over land and is largest over the northern continents. Overall, the agreement between model and data over land is rather accurate with ratios of modeled to observed variability between 0.75 and 1.25 (not shown). In some tropical regions the simulated variability is higher by 25–50 %, namely in northern Australia, South America, India, and Central Africa.
Over the ocean, both E6-F and HadCRUT4 show increased variability over the Gulf stream extension and the Kuroshio region. The increased variability in the equatorial Pacific west of the Peruvian coast, associated with the El Niño–Southern Oscillation (see Sect. 4.6), is well reproduced. Overall, the model however tends to have too weak variability over the ocean, in particular over wide areas of the Southern Ocean, probably related to unresolved eddy activity. An exception occurs in the North Atlantic near the Labrador and Barents Seas where the simulated variability is by a factor two larger compared to observations. This agrees with the findings in Sidorenko et al. (2015) where the authors show that E6-F has indeed deficiencies in simulating those areas: sporadically occurring decadal-scale ‘cold events’ with increased sea-ice coverage in later winter in the Labrador and Barents Seas are associated with strongly augmented SST variability (see Sect. 4.5).
4.2.2 Global mean surface temperature
We now analyze internal variations of the global mean surface temperature (GMST)—the probably most discussed integrated quantity of the climate system. The GMST (Fig. 4, top) is computed as the average of the northern hemisphere (NH; Fig. 4, middle) and southern hemisphere (SH) values (Fig. 4, bottom) to ensure equal weighting of the hemispheres despite the variable data coverage (Morice et al. 2012). The standard deviation of the modeled annual-mean GMST is 0.13 K while it is 0.16 K for HadCRUT4 after a linear detrending. As pointed out by Collins et al. (2001), the standard deviation analysis is complicated by the fact that after a simple linear detrending a residual signal of the externally forced warming trend (resulting in overestimated internal variability) may remain. A polynomial detrending of order two results in a reduced estimate for the internal variability of 0.12 K, suggesting that the annual-mean GMST variability in E6-F is consistent with observations.
(Top) Blue line: Exponentially detrended anomaly of global mean surface temperature from the E6-F REF control run (1500 years). Black line: Linearly detrended time series of observed global mean nearsurface temperature anomaly from the HadCRUT 4 dataset (163 years). Grey lines depict the original time series, with anomalies relative to the climatology of the last 300 years for E6-F and relative to 1961–1990 for HadCRUT4. (Middle and bottom) Same as top panel, but for the Northern and Southern Hemispheres
The annual-mean NH-mean surface temperature anomaly (Fig. 4, middle) exhibits slightly higher than observed variability (standard deviation 0.20 K compared to 0.19 K (0.16 K) after linear (quadratic) detrending of the observed values). As already mentioned, the model overestimates surface temperature variability in the Labrador and Barents Seas (Fig. 3), possibly resulting in an overall overestimation of NH variability. The abrupt GMST increase around the model year 1200 by approximately 0.4 °C, for example, can be attributed to a strong warming in the Labrador Sea by 3–5 °C, accompanied by a smaller but pan-Arctic warming of more than 1 °C. Many climate indices in E6-F show connections to the variability in the Labrador Sea, which is discussed in Sect. 4.5 in more detail. The modeled annual-mean SH-mean surface temperature anomaly (Fig. 4, bottom), on the other hand, exhibits variability that is consistent with observations: The corresponding standard deviation is 0.11 K in E6-F while it is 0.14 K (0.11 K) in HadCRUT4 after linear (quadratic) detrending.
We next examine variance spectra of the global, NH, and SH time series of monthly mean surface temperature anomalies for the model and for the HadCRUT4 data (Fig. 5). The one-sided power spectral densities (PSD) are computed using Welch’s method (Welch 1967) with a relative chunk length of 1/4 (i.e. 40.75 years) and a Blackman window. The six model PSDs (each based on a 163 years interval) provide a possible range of PSDs that mirrors the sampling uncertainty associated with the single realization of HadCRUT4. Red spectra for fitted AR(1) processes (von Storch and Zwiers 1999, p. 204–205) and their confidence bands, estimated with a Monte-Carlo approach, are shown for comparison.
(Top) Black line: Power spectral density (PSD) of the linearly detrended HadCRUT4 non-seasonal GMST anomaly (163 years) with respect to the 1961–1990 climatology. Cyan lines: PSDs for six 163 years intervals of E6-F REF. The grey area depicts the 5–95 % confidence interval of an AR(1)-process fitted to the HadCRUT4 data, based on 10,000 random realizations. (Middle and bottom) Same as top panel, but for the Northern and Southern Hemispheres
Overall, the GMST PSDs for E6-F are in remarkable quantitative agreement with the observed GMST PSD from HadCRUT4 over the entire frequency range (Fig. 5). Compared to the AR(1) spectra, both HadCRUT4 and the model exhibit less power on time scales between 1 and 2 years and more power on time scales of 20 years and longer. As pointed out by Collins et al. (2001), a possible residual (low-frequency) warming signal after the linear detrending may bias the lowest frequency of the HadCRUT4 spectrum. As a result, the increased variance on the longest time scale can not be reliably attributed to multi-decadal variability, though slow processes like the Atlantic Multidecadal Oscillation (AMO) can actually generate increased power at these time scales (see Sect. 4.4). In the Southern Hemisphere the model does not show increased multi-decadal variability, which stands in contrast to the HadCRUT4 data (Fig. 5, bottom). Again, however, the increased variance in the observations on the longest time scale might be unreliable.
4.2.3 Modeled versus observed internal GMST trends
Having shown that E6-F reproduces GMST variability of reasonable amplitude over a wide range of frequencies, the 1000-year present-day control simulation (REF) is now used to study internally generated trends in GMST and to put observed trends into perspective. Following Stouffer et al. (1994) and Collins et al. (2001), we calculate successively longer GMST trends for HadCRUT4, all ending in either 1998 or 2012, and compare these to all model trends of equal length. The motivation to compute not only most recent trends but also trends ending in 1998 is to enable direct comparison to Collins et al. (2001). Since there was an extreme El Niño event in 1997/1998, short GMST trends ending in 1998 are exceptionally large. Regarding the model data, for each trend length we determine the maximum number of non-overlapping segments in the 1000-year simulation with trends greater or equal to the observed trend. By this means we prohibit possible clustered trends from being counted multiple times as might be the case for the overlapping segments in Collins et al. (2001).
Under the assumption that E6-F features realistic GMST variability, short term trends over 20 years or less in the observational record—even the large trend of \(0.72\,^\circ \hbox {C}\) per decade between 1994 and 1998—can be easily explained by internal variability (Table 3). Recent observed trends over longer periods, however, become less likely with increasing period length: Regardless of the ending year (1998 or 2012), recent observed trends over more than 25 years occur at most once in the 1000-year simulation. These results support the prevailing conclusion (e.g. Stouffer et al. 1994; Collins et al. 2001) that the observed global warming over the last decades can not be ascribed to internal climate variability alone.
4.2.4 Hiatus analogs
The 15-year period 1998–2012 exhibits a decreased global warming trend (\(0.04\,^\circ \hbox {C}\) per decade) compared to the 60-year reference period 1953–2012 (\(0.11\,^\circ \hbox {C}\) per decade). The period 1998–2012 is defined by the IPCC as the ’hiatus’ or slowdown in GMST rise (AR5WG1; Stocker et al. 2013, boxTS.3). The reference and hiatus periods are labeled accordingly in Table 3. Internal variability of the climate system can either weaken or strengthen the externally forced warming on decadal time scales, a prominent example being the augmented GMST rise associated with the Pacific climate shift in 1976/77 (Trenberth and Hurrell 1994; Miller et al. 1994).
Following a similar approach as in the previous section, we use the 1000-year present-day control simulation (REF) to assess how (un)usual the observed warming slowdown is. As the period 1998–2012 includes both externally forced and internally generated trend components, we investigate negative GMST trends that are large enough to counteract an overlaid externally forced warming trend. As an estimate of the externally forced trend in 1998–2012, we use the CMIP5 historical ensemble-mean trend of \(0.21\,^\circ \hbox {C}\) per decade (AR5WG1; Stocker et al. 2013, boxTS.3). Thus, we consider 15-year periods with a GMST cooling trend of 0.04 - 0.21 = −0.17 °C per decade (or less) as hiatus analogs.
Twelve hiatus analogs occur in the 1000-year E6-F simulation (Table 3), meaning that a hiatus analog is roughly a once-in-one-hundred-years event. The associated median trend pattern of surface temperature (Fig. 6, top) shows a significant cooling in the Arctic and in the tropical equatorial Pacific. At the same time the sea level pressure in the tropical equatorial Pacific increases (Fig. 6, middle). The southern part of the tropical Atlantic, the Indian Ocean, and adjacent land areas also depict a negative temperature trend. This is also reflected in the trend pattern of the 500 hPa geopotential height (Z500; Fig. 6, bottom), depicting a general decrease in the tropics between \(30\,^\circ\)N and \(30\,^\circ\)S. The Pacific surface temperature trend pattern strongly resembles the Pacific Decadal Oscillation (PDO) pattern (see Sect. 4.4) and suggests a shift of E6-F to a more negative PDO phase during hiatus analogs (see also, e.g., Trenberth and Fasullo 2013; Meehl et al. 2011). However, while not all (9 out of 12) hiatus analogs coincide with a decreasing PDO index (Fig. 7), all realizations exhibit a trend to more La Niña-like conditions (decreasing Niño 3.4 index over 15 years), suggesting a more robust link of hiatus analogs to ENSO-related variability than to PDO shifts.
Median trend patterns associated with the twelve hiatus analogs in the 1000-year E6-F REF simulation: (top) surface temperature trends [K/decade], (middle) sea level pressure trends [hPa/decade] with vector trends of the 10 m wind [ms\(^{-1}\)/decade] overlaid, and (bottom) 500 hPa geopotential height (Z500) trends [m/decade]. Stippling indicates that at least 11 out of the 12 hiatus analogs agree on the trend sign, corresponding to a significance level of ~99.4 %. Vector trends of the 10 m wind are shown where at least one direction shows a significant trend according to the same criterion
Trends of various climate indices during the twelve model hiatus analogs, being represented in each case by a distinct colored marker. The mean trend is shown by horizontal black lines where significantly different from zero at the 95 % significance level according to a two-sided one-sample Gauß test, with horizontal grey lines denoting the 95 % significance threshold. Vertical grey bars span the 5–95 % quantiles of all 15-year trends within the 1000-year simulation. GMST: Global mean surface temperature; AMO: Atlantic Multi-decadal Oscillation; PDO: Pacific Decadal Oscillation; N34: Niño 3.4 index; Ind1 & Ind2: Basin-wide & zonal dipole mode of SST variability in the Indian Ocean; Atl1 & Atl2: Atlantic Niño & meridional dipole mode of SST variability in the tropical Atlantic; NAO: North Atlantic Oscillation; PNA: Pacific North American pattern; AO: Arctic Oscillation; AAO: Antarctic Oscillation; OHC_a700 (OHC_b700): Global ocean heat content for the ocean column above (below) ~700 m; AMOC: Atlantic meridional overturning circulation transport; Ice M./S. NH/SH: March/September sea ice cover in the northern/southern hemispheres (annual values). Monthly values are used for all other indices. All time series are normalized by their standard deviation prior to the computation of trends, resulting in unitless time series. Trends are thus given in units of [decade\(^{-1}\)]
Tropical regions are known to influence the climate of the extratropics through atmospheric teleconnections, in particular through the atmospheric bridge (Alexander et al. 2002). Indeed, the simulated Niño 3.4 index correlates in phase with global surface temperatures at high latitudes in both hemispheres, such as the Bering Strait and Ross Sea regions (not shown). Consequently, those regions also show significant negative 15-year GMST trends during hiatus analogs. At the same time, the winds associated with the North and South Pacific subtropical highs, in particular the southeasterly trade winds, as well as the Southern Hemisphere westerlies around the Antarctic continent intensify. An intensification of the Pacific trades has also been identified to be associated with the recent observed hiatus in GMST warming, but the involved processes and causal relations remain unclear (England et al. 2014). In the following we analyze the hiatus analogs further by investigating the evolution of other important climate indices during the 15-year hiatus analogs in E6-F.
The basin-wide SST mode in the Indian Ocean (Ind1, Sect. 4.4) is closely connected to ENSO (e.g. Deser et al. 2010) and shows significant basin-wide cooling over the 15-year long hiatus analogs, consistent with the trend to more La Niña-like conditions. A similar trend is observed for the Atlantic Niño mode (Atl1, Sect. 4.4), connected with cooling of the equatorial Atlantic’s cold tongue. Of the dipole modes in the Atlantic (Atl2) and the Indian Ocean (Ind2) (Sect. 4.4), only the latter shows a marginally significant trend towards warmer (colder) SSTs in the western (eastern) Indian Ocean. In contrast to the PDO, the AMO shows no significant trend towards one side during the hiatus analogs: Trends of both signs are possible in the model, suggesting a minor link between AMO phase changes and the appearance of hiatus analogs.
Regarding atmospheric teleconnection patterns (Sect. 4.3), the Antarctic Oscillation (AAO) index significantly increases and the Pacific-North American (PNA) index significantly decreases during hiatus periods, whereas the Arctic Oscillation (AO) and the North Atlantic Oscillation (NAO) show no significant trends. The AAO trend is consistent with the intensified westerly winds around Antarctica (Fig. 6). Despite the significant trend in the AAO index, the integrated Antarctic sea ice area for March and September do not show significant trends, suggesting that other components unrelated to the hiatus analogs play a larger role for the Antarctic sea ice cover.
The negative PNA trend can be explained by its strong link with ENSO and the negative Niño 3.4 trend. A negative PNA index tends to be associated with positive (negative) surface temperature anomalies in the eastern (western) United States, explaining the surface temperature trends in those regions (Fig. 6).
It has been argued that there is a redistribution of heat in the ocean during warming slowdowns (Meehl et al. 2011; Trenberth and Fasullo 2013), with more heat being stored in the deep ocean and less in the upper layers. Indeed, the global depth-averaged ocean heat content for the ocean column above about 700 m (OHC_a700m) decreases during all twelve hiatus analogs in E6-F. At the same time, the heat content below about 700 m (OHC_b700m) increases in most realizations, suggesting that a redistribution of heat from the upper to the deeper ocean often plays a role. During three hiatus analogs, however, the ocean heat content below 700 m decreases along with the ocean heat content in the upper ocean, accompanied by an exceptionally high net radiative heat loss at the top of the atmosphere (TOA). This suggests the existence of distinct flavors of hiatus analogs: They all share the predominance of La Niña-like conditions, but they differ in the relative importance of a vertical redistribution of heat between the upper and the deep ocean and radiative heat loss at the TOA.
In summary, consistent with earlier studies (Meehl et al. 2011; Meehl and Teng 2014) we conclude from the E6-F simulation that a slowdown in GMST warming such as the recently observed one can be caused by internal climate variations that mask the externally forced global warming. Sufficiently strong internal cooling periods are roughly once-in-one-hundred-years events in E6-F. These hiatus analogs are mainly associated with (1) a decreasing PDO index along with an increasing (decreasing) frequency of La Niña (El Niño) events, and (2) a vertical redistribution of heat from the upper to the deeper ocean and/or a net radiative imbalance at the TOA. In contrast, our results suggest a minor role of the AMO in the appearance of hiatus analogs.
4.3 Atmospheric teleconnection patterns
Because a large part of the low-frequency atmospheric variability is represented by atmospheric teleconnection patterns, we now evaluate the spatial structure of the most important teleconnections, namely, the Arctic Oscillation (AO), the Antarctic Oscillation (AAO), the North-Atlantic Oscillation (NAO), and the Pacific-North-American Pattern (PNA).
The AO and AAO, also termed Northern and Southern Annular Mode (NAM and SAM), describe north-south shifts in atmospheric mass between the polar regions and the mid-latitudes, caused by interactions between baroclinic transients and/or planetary waves and the zonal mean flow (e.g. Feldstein and Lee 1996). The two most important NH winter teleconnection patterns on a regional scale are the NAO over the North Atlantic and Eurasia, and the PNA over the North Pacific and North America. While the positive phase of the NAO is related to strengthened westerlies over the North Atlantic due to a shift of the North-Atlantic jet, the positive phase of the PNA is associated with a strengthening of the North-Pacific jet.
The simulated AO, AAO, NAO, and PNA patterns are very similar to their counterparts from the reanalysis data (Fig. 8); all corresponding pattern correlations are larger than 0.9. There are slight differences with regard to the strength and position of the centers of action: For the simulated AO, the Pacific center of action is stronger and the Atlantic center of action is shifted to the east. The simulated AAO is more zonally symmetric than its counterpart from ERA-Interim.
Spatial patterns (from left to right) of the Arctic Oscillation (AO), the Antarctic Oscillation (AAO), the North Atlantic Oscillation (NAO), and the Pacific North American pattern (PNA). Upper row: Patterns from ERA-Interim reanalysis data for 1979–2011. Lower row: Patterns from years 501–1500 of the E6-F REF simulation. The AO pattern corresponds to the leading empirical orthogonal function (EOF) of the year-round monthly-mean anomalies of the geopotential height field at 1000 hPa north of \(20\,^\circ\)N; the AAO pattern corresponds to the leading EOF of the year-round monthly-mean anomalies of the geopotential height field at 700 hPa south of \(20\,^\circ\)S; the PNA and NAO patterns correspond to the first and second rotated EOFs of the 500 hPa geopotential height (Z500) anomaly fields for winter (DJF). The explained variances are given in the upper right corner. All simulated fields have been detrended with the exponential method described in Sect. 3 prior to the EOF analyses. Units are geopotential meters (gpm)
Also in terms of pattern correlation, root-mean-square difference, and standard deviation, E6-F is able to reproduce the most important atmospheric teleconnections very well (Fig. 9). When compared to the range of CMIP3 models analysed in Handorf and Dethloff (2012, compare their Figures 2 and 4), E6-F performs favorably with regard to the NAO and PNA patterns.
4.4 Oceanic variability patterns
Compared to atmospheric teleconnection patterns, oceanic variability patterns are associated with longer time scales, from monthly to multi-decadal, potentially even up to multi-centennial (e.g. Martin et al. 2014). In this section we analyze some of the most prominent modes of SST variability, namely the extratropical Atlantic Multi-decadal Oscillation (AMO) and Pacific Decadal Oscillation (PDO), and more briefly the faster tropical modes of SST variability in the Atlantic (Atl1, Atl2) and Indian Ocean (Ind1, Ind2) occurring on monthly to interannual time scales. ENSO is discussed separately in Sect. 4.6.
The AMO is considered to be an intrinsic oceanic mode (Deser et al. 2010) associated with fluctuations in North Atlantic SSTs and in the strength of the North Atlantic thermohaline circulation (Delworth and Mann 2000). While the AMO has originally been described as a mode with a distinct periodicity of 65–70 years (Schlesinger and Ramankutty 1994), now the AMO is sometimes also called the Atlantic Multi-decadal Variability (AMV) pattern to stress the potential absence of real periodicity (Park and Latif 2010). The AMO is usually diagnosed as a simple SST index of area-averaged anomalies in the North Atlantic region between \(0^\circ\)–\(70^\circ\) N (Deser et al. 2010). We basically use this definition to compute the AMO index for the last 1000 years of the E6-F REF simulation, but to achieve comparability with the observed AMO, where a largely forced global signal needs to be removed, we subtract the global-mean SST anomalies as suggested by Trenberth and Shea (2006).
Surface temperature anomalies associated with a positive AMO index are positive in the whole North Atlantic region in E6-F. They differ considerably in amplitude from the corresponding HadISST anomalies for the period 1870–2012 (Fig. 10, top left), especially in the Labrador Sea where the model features AMO-associated SST anomalies increased by a factor of 4 compared to HadISST. The decadal-scale variations of deep-water formation intensity and late-winter sea ice coverage in this region (Sect. 4.5) appear to be directly linked to the AMO in E6-F. The surface temperature anomalies in the Pacific associated with a positive AMO index differ in sign between the model and the (shorter) HadISST data, with the pattern of the anomalies resembling the PDO (see below). Ruiz-Barradas et al. (2013) analyzed historical simulations from CMIP3 and CMIP5 and found a similar discrepancy compared to HadISST, which they refer to as the ’fictitious tropical Pacific signature of the AMO’. However, repeating our model data analysis for chunks of the same length as the HadISST data reveals considerable spread of the AMO-associated regression pattern, including neutral values in the Pacific (not shown), and suggests that the discrepancy is not statistically robust. Therefore, future research should focus not only on the still challenging representation of the AMO in models (Ruiz-Barradas et al. 2013) but also on the observed AMO signature and its apparent uncertainty.
Linear regression patterns (K per standard deviation) corresponding to the (top left) AMO index and the (bottom left) PDO index for the 1000-year E6-F REF simulation and for the observations from HadISST (1870–2012). The explained variance for the PDO is given in the top right corner. Spectra are computed for the (top right) AMO index and the (bottom right) PDO index based on the full 1000 years of E6-F data (blue), seven 143-year sub-intervals of the E6-F data (cyan), and based on one 143-year observation from HadISST (black). Grey shading depicts the red spectrum for an AR(1) process fitted to the model data, with 5–95 % confidence interval based on 10,000 random realizations
A spectral decomposition of the AMO index reveals highest power at a period of about 100 years (Fig. 10, top right). However, the simulation is not long enough to infer whether this can be attributed to quasi-periodicity or to long-time scale AR(1)-type components that are not captured by the background AR(1) spectrum shown in Fig. 10 (top right).
The PDO, sometimes also called the Pacific Decadal Variability (PDV) pattern (Park and Latif 2010), is a pan-Pacific mode of SST variability (Mantua et al. 1997; Deser et al. 2010). Its pattern and index time series are usually diagnosed from monthly SST anomaly data as the first EOF and corresponding principal components in the North Pacific between \(20^\circ\)–\(70^\circ\) N, again with the global-mean SST removed prior to the EOF analysis (Deser et al. 2010). Computed accordingly, the simulated PDO pattern resembles the observed pattern from HadISST (Fig. 10, bottom left). Generally, the PDO regression pattern looks similar to the ENSO regression pattern (see Sect. 4.6) but shows differences in relative weighting between the tropical and North Pacific (Deser et al. 2010). The observational record is too short to determine a reliable spectral peak of the PDO index. In the model, the PDO spectrum is largely consistent with an AR(1)-process (Fig. 10, bottom right). This has also been suggested by Pierce (2001) and Newman et al. (2003), the latter of which interpret the PDO as a slow AR(1)-process that is driven by quasi random forcing by ENSO.
The dominant modes of SST variability in the tropical Atlantic and Indian Oceans are commonly diagnosed as the two leading EOFs of monthly SST anomalies between \(20\,^\circ\)N and \(20\,^\circ\)S. These are (1) the Atlantic Niño mode (Atl1), (2) a meridional dipole mode in the Atlantic (Atl2), (3) a basin-wide mode in the Indian Ocean (Ind1), and (4) a zonal dipole mode in the Indian Ocean (Ind2) (Deser et al. 2010). We compute these modes accordingly for E6-F and HadISST (Fig. 11). The pattern of the Atlantic Niño mode Atl1 is well represented in the model. The second EOF Atl2 features a meridional dipole similar to the observations, but includes an additional tongue of warm anomalies along the coast of Angola and along the equator (which appears in the third EOF of HadISST, not shown). The first and second modes in the Indian Ocean (Ind1 and Ind2; explained variance of 22.4 and 15.5 %) are not as clearly separated in E6-F when compared to HadISST (38.8 and 11.6 %), but still represent a near basin-wide mode and a zonal dipole mode. All in all, the modes of SST variability in the tropical Atlantic and Indian Ocean are reasonably well represented in E6-F when compared to corresponding patterns from HadISST. The corresponding index time series are included in the hiatus analog and potential predictability analyses in Sects. 4.2.4 and 4.7. For mechanisms behind these modes we refer to Deser et al. (2010).
Surface temperatures regressed onto (top row) the Atl1 index, (second row) the Atl2 index, (third row) the Ind1 index, and (bottom row) the Ind2 index in (left column) the 1000-year E6-F REF simulation and for (right column) the observations from HadISST (1900–2008). The indices are based on the first and second principal components of EOF analyses of SSTs in the corresponding basins between \(20\,^\circ\)N and \(20\,^\circ\)S. The explained variances are given in brackets
4.5 Sea ice variability
The mean Arctic sea ice extent over the last 1000 years of the E6-F simulation amounts to 13.61 \(\times\)10\(^6\) km\(^2\) in March and 5.74 \(\times\)10\(^6\) km\(^2\) in September. These values are lower than those reported in Sidorenko et al. (2015) for the first 350 years of the simulation, which the authors already showed to be lower than observational estimates of 15.7 \(\times\)10\(^6\) km\(^2\) in March and 7.0 \(\times\)10\(^6\) km\(^2\) in September for the period 1979–2000 (Fetterer et al. 2002, made available online from the NASA Earth Observatory website). As mentioned in Sidorenko et al. (2015), the underestimation of Arctic sea ice in the present model setup is partly an artifact of inaccurate Arctic coastlines in the Canadian Arctic Archipelago (CAA) and at the Siberian coast, resulting in a 10 % smaller area of the Arctic ocean in the model compared to reality. The slight decline of Arctic sea ice from the values reported in Sidorenko et al. (2015) is due to the slow warming associated with the equilibration of the deep ocean.
Compared to the Arctic, the Antarctic sea ice is much more affected by the slow deep-ocean warming (Fig. 12; note that the figure shows sea ice area, not extent). Averaged over the 1000-year period, the Antarctic sea ice extent in E6-F REF amounts to 0.42 \(\times\)10\(^6\) km\(^2\) in March and 13.61 \(\times\)10\(^6\) km\(^2\) in September, which is well below observational estimates of 2.9 \(\times\)10\(^6\) km\(^2\) in March and 18.7 \(\times\)10\(^6\) km\(^2\) in September for the period 1979–2000 (Fetterer et al. 2002). In the Antarctic summer the ice nearly vanishes in some years. The stronger long-time scale adjustment to greenhouse gas forcing in the Southern Ocean compared to the Arctic Ocean has been found in earlier modeling studies (Goosse and Renssen 2001; Marshall et al. 2013). The latter argue that the delayed Antarctic warming is related to the fact that the Southern Ocean forms part of the upwelling branch of the Meridional Overturning Circulation (Marshall and Speer 2012) and is thus stronger influenced by the slowly responding deep ocean (see also Marshall et al. 2014). Note that the simulated Antarctic sea ice cover depicts almost no trend when constant pre-industrial CO\(_2\) concentrations are applied, as verified by sensitivity experiments branching off from the E6-F REF control run (not shown).
(top) Integrated sea ice area in March and September for the northern hemisphere (blue) and the southern hemisphere (green). Values for the maximum (minimum) month are shown in strong (light) colors. (middle) Maximum AMOC transport at \(45\,^\circ\)N in Sv (\(10^6\,\) m3s-1 ). (bottom) Maximum Labrador mixed layer depth (MLD) in JFM (blue) as well as its 30-year running mean (black). Episodes with a shallow mixed layer (defined as episodes where the 30-year running mean mixed layer depth is smaller than 500 m, grey shading) alternate with episodes with a deep mixed layer. No detrending has been performed for these quantities
The Arctic sea-ice area displays pronounced multidecadal to centennial variability (Fig. 12). This variability is linked to persistent episodes of either weak or strong convection in the Labrador Sea, as already discussed in Sidorenko et al. (2015). During the episodes with a shallow mixed layer, the Labrador Sea features decreased surface temperatures and salinities and an extensive sea-ice cover in March (not shown) that is clearly visible in the pan-Arctic sea-ice area (see grey shaded boxes in Fig. 12). The reduced or nearly blocked deep water production in the Labrador Sea during these episodes is accompanied by a weakened Atlantic meridional overturning circulation (AMOC), which drops below 12 Sv at 45 \(^\circ\)N compared to 15 to 18 Sv during episodes with strong deep convection (Fig. 12, middle).
The AMOC slightly drifts towards higher transports during the 1500-year simulation, possibly because of an increased wind stress around Antarctica due to the decreasing sea ice cover, which would then reinforce the upwelling branch of the AMOC. At the same time, the episodes of shallow mixed layer in the Labrador Sea apparently become less frequent at the end of the simulation. This fits the discussion by Sidorenko et al. (2015) that a relatively weak AMOC transport (and corresponding northward heat transport) in E6-F might be responsible to some extent for the episodic extensive sea ice coverage in the Labrador Sea.
It shall be mentioned that sporadically collapsing convection in the Labrador Sea is a feature shared by other climate models and might be a manifestation of an important mechanism related to abrupt climate shifts that needs to be understood (Drijfhout et al. 2013) rather than removed through model tuning.
4.6 ENSO and the effects of increased tropical resolution
The El Niño–Southern Oscillation (ENSO) is a coupled mode of the ocean-atmosphere system in the tropical Pacific and arguably the most important mode of climate variability on monthly to interannual time scales. Warm El Niño and cold La Niña events grow and decay according to two main feedback mechanisms: the positive Bjerknes feedback (Bjerknes 1966) and a negative dynamic oceanic feedback involving the re-adjustment of the thermocline (e.g. Deser et al. 2010). The state of ENSO, i.e. warm/cold or neutral conditions, has far-reaching consequences around the world, e.g. due to shifting precipitation patterns.
In part I of this work (Sidorenko et al. 2015) it has been shown that the increased tropical resolution in REF compared to LOW results in an improved simulation of the narrow equatorial current systems, including a more vigorous Equatorial Undercurrent and a reduction of the “cold tongue” SST bias in the western Pacific warm pool region by up to 1 K. Potentially associated benefits for the representation of ENSO variability are analyzed in this section. We start with a discussion of the global ENSO signature, followed by a more detailed analysis of SST variability in the tropical Pacific and its change with locally increased ocean resolution in REF compared to LOW.
The global ENSO signature is here defined as surface temperature regressed onto the area-averaged SST anomalies in the Niño 3.4 region (\(170\,^\circ\)W–\(120\,^\circ\)W, \(5\,^\circ\)N–\(5\,^\circ\)S). In HadISST, this results in a broad pattern of positive SST anomalies associated with a positive Niño 3.4 index in the eastern tropical Pacific, enclosed by a horseshoe-like pattern of negative SST anomalies. Teleconnections of smaller amplitude to the Indian and (tropical) Atlantic Oceans are present (Fig. 13, top). This general pattern is similarly well reproduced by the REF and LOW configurations (Fig. 13, middle and bottom), but with subtle differences. While REF and LOW both show narrower patterns of positive SST anomalies compared to HadISST, reaching too far to the west into the area of observed negative SST anomalies, the REF pattern extends less to the west and is slightly broader than the LOW pattern. The patterns outside the tropical Pacific are virtually the same for REF and LOW.
In HadISST, the interannual SST standard deviation in the tropical Pacific has two distinct maxima near the Peruvian coast (0.8–0.85 K) and east of \(120\,^\circ\)W (0.75–0.8 K) (Fig. 14, top). Increased SST variability reaches as far west as the dateline, again enclosed in a horseshoe-like pattern of low amplitude. In comparison, high SST variability in E6-F extends farther to the west (Fig. 14, middle and bottom), especially in the LOW simulation which has a pronounced spurious third maximum in SST variability in the western Pacific warm pool region. Generally, the simulated SST variability pattern in the coarse setup depicts too strong variability and is meridionally too broad. In REF the variability pattern is more confined to the equator and shows reduced variability in the Niño 3 region (\(150\,^\circ\)W–\(90\,^\circ\)W, \(5\,^\circ\)S–\(5\,^\circ\)N), in closer agreement to HadISST. SST variability in the Niño 1+2 (0–\(10\,^\circ\)S, \(90\,^\circ\)W–\(80\,^\circ\)W) region near the Peruvian coast is similarly well represented in both simulations, probably related to the fact that the oceanic resolution in the proximity of coasts is relatively high already in LOW. The improved ENSO pattern in REF is connected to its reduced cold SST bias in the tropical Pacific compared to LOW. While in the latter simulation, there is a pronounced cold mean SST bias of -2 K along the equator in the central Pacific, this bias in the mean state is significantly reduced with higher resolution in REF (blue contour lines in Fig. 14). The improvement in REF might be related to resolved Tropical Ocean Instability Waves (TIWs) at 0.25° resolution and the associated meridional heating along the equator (Graham 2014), while these waves are not resolved in LOW (not shown).
Interannual SST standard deviation for (top) HadISST (1870–2012), (middle) the first 520 years of REF and (bottom) the same years of LOW. Solid (dashed) contour lines show the positive (negative) mean SST bias with respect to HadISST; contours for the \(+2\) K (\(-2\) K) SST biases are colored red (blue)
Higher statistical moments of SSTs in the commonly considered El Niño regions (Fig. 15) reveal that ENSO-related variations become more realistic in terms of amplitude and asymmetry with higher resolution. While the decrease of standard deviations from east to west is well captured in both E6-F simulations, the absolute values of the standard deviations are consistent with observations only in REF; in LOW the amplitude of ENSO-related variability is too high (Fig. 15, top, consistent with Fig. 14).
Statistics for different Niño indices from HadISST (black dashed lines, 143 years), and for 4 (slightly overlapping) 143-year chunks from the E6-F REF (red dots) and LOW (blue dots) simulations. N12, N3, N34, and N4 denote the area-averaged SST anomalies in the Niño 1+2 (0–\(10\,^\circ\)S, \(90\,^\circ\)W–\(80\,^\circ\)W), Niño 3 (\(150\,^\circ\)W–\(90\,^\circ\)W, \(5\,^\circ\)S–\(5\,^\circ\)N), Niño 3.4 (\(170\,^\circ\)W–\(120\,^\circ\)W, \(5\,^\circ\)N–\(5\,^\circ\)S), and Niño 4 (\(160\,^\circ\)E–\(150\,^\circ\)W, \(5\,^\circ\)S–\(5\,^\circ\)N) regions. SST anomalies for REF and LOW (years 1–520) are with respect to the last common 100 years. (Top) Standard deviation and (bottom) skewness of the Niño indices. Note that the subsampling of the model results serves to estimate the uncertainty associated with the single observational values
Except for the Niño 4 region, in the observations the warm El Niño events are typically stronger than the cold La Niña events, reflected in positive skewness of the Niño indices (Fig. 15, bottom, dashed lines). The observed decrease of skewness from east to west may be explained as follows. First, high positive skewness values in the Eastern Pacific upwelling regions are connected to the already shallow thermocline so that warm anomalies are easier to develop than (even) colder anomalies (Burgers and Stephenson 1999). Also, another potential mechanism leading to ENSO asymmetry in the Eastern Pacific is related to TIWs, which generally damp the ENSO amplitude but are more active during La Niña events than during El Niño events (An 2008). Second, negative skewness values in the western Pacific warm pool region are connected to the fact that SSTs tend to saturate at about \(30\,^\circ \hbox {C}\) (Marshall and Plumb 2007, p. 231f) due to the nonlinear dependence of convection and outgoing longwave radiation on SSTs (Burgers and Stephenson 1999). This prohibits strong warm SST anomalies from developing and results on the whole in a negative skewness.
In the Eastern Pacific Niño 1+2, Niño 3, and Niño 3.4 regions, the E6-F simulation with increased tropical ocean resolution (REF) captures the observed positive skewness of SST anomalies (Fig. 15, bottom), though the skewness is too weak in the Niño 1+2 region. In contrast, the LOW simulation depicts generally too low, mostly negative, skewness in the Eastern Pacific Niño regions. This difference between REF and LOW might again be related to the resolved TIW activity in REF compared to LOW. However, because the east-west gradient of skewness is opposed to the observed gradient in both model simulations, the skewness is more realistic in LOW for the westernmost Niño 4 region where negative skewness in the observations stands against a strongly positive skewness in REF. An explanation could be that SST saturation has not yet happened anywhere in the Niño 4 region due to the persistent cold bias, so that a stronger positive skewness due to increased resolution is erroneously sustained. This suggests that a more realistic simulation of the SST asymmetry in the Niño 4 region demands an even further reduction of the cold bias in this area.
To investigate ENSO-related variability in E6-F in more detail, we now analyze the spectral composition of the SST fluctuations. The Niño 3.4 index shows a broad spectral peak between about 4 and 7 years both in HadISST and in the E6-F REF simulation when compared to the red-noise spectrum of a fitted AR(1) process (Fig. 16, middle). Not only the frequency range of the peak is well reproduced but also the absolute value of the variance in this range. The LOW simulation tends to have a broader than observed spectral peak: the overestimated total variance in LOW for the Niño 3.4 region is due to the overestimated variability associated with the flanks of the spectral peak.
Power spectral densities (PSDs) for different Niño boxes from HadISST (black, 143 years) and for 4 (slightly overlapping) 143-year chunks from the REF (red) and LOW (blue) simulations. The grey area depicts the 5–95 % confidence interval of an AR(1)-process fitted to the HadISST data, based on 10,000 random realizations. Model SST anomalies for REF and LOW (years 1–520) are with respect to the last common 100 years. (Top) Niño 1+2, (middle) Niño 3.4 and (bottom) Niño 4. Note that the subsampling of the model data allows to estimate the uncertainty associated with the single observational spectra. The total (integrated) variances \([\text {K}^2]\) for HadISST are 0.81 (Niño 1+2), 0.58 (Niño 3.4), and 0.31 (Niño 4), which is in the range of the total variances in REF (0.64–0.82; 0.36–0.63; 0.27–0.46) while the total variances are systematically overestimated in LOW (0.92–0.98; 0.69–0.82; 0.49–0.63)
The behavior is qualitatively similar in the Niño 4 region, where the improvement in REF compared to LOW concerning the frequency range between about 2 and 10 years is even more obvious (Fig. 16, bottom). As for the statistical moments, the variability in the Niño 1+2 region is similarly well represented in both simulations regarding spectral characteristics (Fig. 16, top).
To summarize, the higher tropical ocean resolution in REF has clearly beneficial effects on the representation of ENSO-related variability. This conclusion is supported not only by spatial improvements, which are especially strong in the western Pacific warm pool (identified by a reduced westward extension of the ENSO signature and strongly decreased interannual SST standard deviation in this region), but also by more realistic temporal characteristics (statistical moments and spectral composition of the SST fluctuations in the different Niño regions). Furthermore, lower performance indices for the variability in REF compared to LOW in the whole tropics (Table 2) confirm the beneficial effect of the higher tropical ocean resolution. Due to strong known teleconnections between ENSO and the extratropics, this should also translate into improvements regarding the mean state and certain aspects of variability in the extratropics, i.e. in the regions where the ocean resolution is not refined compared to LOW. The extratropical response to the improved spatial and temporal ENSO characteristics in REF is apparently weak or too localized to show up as a decrease of performance indices that evaluate just the amplitude of variability, averaged over large-scale regions (Table 2). More detailed analyses would be required to quantify the potential benefits for the extratropics, but this is beyond the scope of the current paper.
4.7 Diagnostic potential predictability
An essential question linked to the internal modes of climate variability is to what extent these fluctuations can be predicted. We end our analysis of the internal climate variability in E6-F with an assessment of the potential predictability of the most important modes of variability considered above. We confine this part of the analysis again to the long E6-F REF integration.
The most comprehensive way to determine the inherent limits of predictability is to run large ensembles of simulations that are completely identical except for slight random perturbations of the initial state, and to analyze how the individual simulations diverge from each other due to the chaotic nature of the climate system (the so-called perfect-model approach, giving estimates of the prognostic potential predictability (PPP); e.g. Boer 2000). This is obviously beyond the scope of the current paper, but it has been shown that one can approximate the PPP remarkably well with the diagnostic potential predictability (DPP) which requires a single long quasi-equilibrium climate model integration (Pohlmann et al. 2004). The DPP of a quantity characterized by a time series with a constant time step \({\varDelta }t\) is defined here as follows:
where \(\sigma ^2\) is the total variance and \(\sigma _m^2\) is the variance of the running mean over m time steps (implying that \(\sigma ^2 = \sigma _1^2\)). This definition is slightly different from the ones used in Boer (2000) and Pohlmann et al. (2004) in the way the noise contribution to the variance fraction \(\sigma _m^2 / \sigma ^2\) is corrected for; in our case the DPP is normalized such that it can take the whole range of values between 0 and 1 for any \(m > 1\), with 0 implying pure random noise and 1 implying that all variance is retained in the running means, corresponding to perfect predictability at the time scale \(m \cdot {\varDelta }t\).
Not surprisingly the atmospheric modes of variability are least predictable, with the AAO being more predictable than the AO, NAO, and PNA (Fig. 17). The dependence of DPP on time scale corresponds approximately to AR(1) processes with time scales between 1.5 (NAO, PNA) and 2.5 (AAO) months, with the AO falling inbetween. The PNA however deviates from AR(1)-type behavior in the sense that the DPP decreases more slowly with time scale, indicating that slower processes imprint on the PNA; the link between ENSO and the PNA is an obvious candidate.
Diagnostic potential predictability (DPP; Eq. (2)) for various climate (variability) indices as a function of time scale \(m \cdot {\varDelta }t\), where \({\varDelta }t = 1\,\text {month}\), based on years 501–1501 of E6-F REF with exponential detrending. Dashed black lines and grey bands depict the DPP of AR(1)-processes with the indicated time scales \(\tau\) (decorrelation time in von Storch and Zwiers 1999, p. 371ff.) along with their 5–95 % confidence bands based on 10,000 random realizations. Note that the confidence bands are indicative of the uncertainty associated with the DPP estimates for the climate indices. The long names of the considered climate indices are given in the caption to Fig. 7
The more predictable tropical modes of SST variability (Niño 3.4, Ind1, Ind2, Atl1, Atl2) tend to deviate from AR(1)-type behavior in the opposite way (Fig. 17): the variance fraction retained in running means (i.e. the DPP) decreases faster with time scale than typical of an AR(1) process. This is indicative of quasi-periodic behavior and is most prominent for the Niño 3.4 index, with a DPP that corresponds to an AR(1) process with \(\tau \approx 2\) years at the monthly time scale, dropping to \(\tau \approx 6\) months at the decadal time scale.
The largely extratropical modes of SST variability feature the highest predictability (Fig. 17). While the predictability of the PDO corresponds to an AR(1) process with \(\tau \approx\) 2–2.5 years at all time scales, the DPP associated with the AMO decreases much slower than AR(1)-like, indicating that the AMO index encapsulates processes with different time scales, the slowest of which appears to have a time scale of ~32 years.
For the DPP of the global mean surface temperature (GMST), the influence from multiple processes and associated time scales is even more obvious (Fig. 17). A relatively large variance fraction (~20 %) is already lost when averages are taken over two months. This is partly due to the inclusion of land temperatures that are much less persistent than SSTs. At the same time, substantial predictability remains even at multi-decadal time scales, highlighting the influence of slow processes like the AMO on the GMST. At intermediate time scales one can even discern the influence of ENSO: the DPP associated with the GMST drops relatively fast where also the predictability of ENSO ceases.
5 Summary and conclusions
The current CMIP5 generation of global climate models is based exclusively on the long-established approach of structured-mesh discretization. These models share typical biases that are partly attributed to a lack of resolution in key regions. New dynamical cores utilizing unstructured meshes are thus a promising way to overcome some of the typical model biases. In part I of this study, Sidorenko et al. (2015) describe the mean climate state of the newly developed climate model ECHAM6-FESOM (E6-F) with a sea ice-ocean component based on unstructured meshes. Sidorenko et al. (2015) conclude that, in its present configuration with only relatively moderate mesh-stretching factors, E6-F performs slightly better than the average of five well-established CMIP5 models according to objective performance indices. In the present follow-up study, the internal variability of E6-F is analyzed. The main findings can be summarized as follows:
-
1.
The internal climate variability in E6-F is largely consistent with observations of the real climate system: Measured by objective variability performance indices, the model performs overall favorably compared to five well-established CMIP5 models with regard to its internal variability. In particular, oceanic and atmospheric variability patterns are realistically simulated.
-
2.
The model generates unforced 15-year periods of strong cooling in GMST that are strong enough to explain the observed warming slowdown (hiatus) observed from 1998–2012. Sufficiently strong cooling periods – hiatus analogs – in E6-F are roughly once-in-one-hundred-years events and are mainly associated with (1) a trend to more La Niña-like conditions and (2) a vertical redistribution of heat from the upper layers to deeper layers of the ocean. In some realizations, however, the latter mechanism does not occur; instead, a net radiative heat loss at the TOA takes place, suggesting the existence of different flavors of hiatus analogs. The ’hiatus analog’ method could easily be extended to the long pre-industrial control integrations from the CMIP5 archive to assess the robustness of our results.
-
3.
The simulated pattern of ENSO-related interannual SST variability and the index statistics in the different Niño regions clearly improve with a locally increased resolution of ~0.25° around the equator compared to a simulation where the ~1° resolution of the adjacent open-ocean regions is retained at the equator. Specifically, this results in a reduced westward extension of the ENSO signature and strongly decreased interannual SST standard deviation in the western Pacific warm pool, but also in improved temporal characteristics of the SST fluctuations in the different Niño regions. Performance indices that evaluate the large-scale extratropical mean state and variability do however not decrease, suggesting a weak or only localized extratropical response to the improved ENSO characteristics in the current model configuration. In this paper the potential of the multi-resolution approach is demonstrated only in the equatorial belt; the impact of increased resolution in other key regions, e.g. the western boundaries and overflow regions, needs to be addressed in future studies.
The investigated setup of E6-F shares some typical deficits with regular-mesh models using a similar average resolution. These biases are in particular (1) too weak non-seasonal variability of SSTs over large parts of the ocean, (2) episodic periods of almost absent deep-water formation in the Labrador Sea, resulting in overestimated North Atlantic SST variability, and (3) slow deep-ocean warming and salinization of the Atlantic (see Sidorenko et al. 2015). There is evidence that the latter two of these typical biases can be strongly reduced by better resolving key regions of the North Atlantic, for which the multi-resolution approach is ideally suited. Future meshes, such as those to be utilized in AWI’s planned CMIP6 activities (where the synonym AWI Climate Model (AWI-CM) will be used), will further exploit the multi-resolution approach to reduce long-standing model biases.
Despite remaining deficits, we conclude that E6-F can be considered a “state-of-the-art” global coupled climate model that can be used as a tool to investigate the functioning of the climate system and to examine past and future climate changes. With its unique dynamical core, E6-F increases the diversity in the current zoo of climate models. Further it appears likely that the benefits from increased resolution in key regions will outweigh the disadvantage unstructured-mesh models have in terms of computational costs per grid point, though this remains to be demonstrated more systematically (e.g. in the comprehensive multi-model framework of CMIP6). The significant improvement of ENSO-related variability through locally (isotropically) increased resolution around the equator reported here already hints at the high potential of the multi-resolution approach in global climate modeling.
References
Adler RF, Huffman GJ, Chang A, Ferraro R, Xie P-P, Janowiak J, Rudolf B, Schneider U, Curtis S, Bolvin D, Gruber A, Susskind J, Arkin P, Nelkin E (2003) The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J Hydrometeorol 4(6):1147–1167
Alexander MA, Blad I, Newman M, Lanzante JR, Lau N-C, Scott JD (2002) The atmospheric bridge: the influence of ENSO teleconnections on air–sea interaction over the global oceans. J Clim 15(16):2205–2231. doi:10.1175/1520-0442(2002)015<2205:TABTIO>2.0.CO;2
An S-I (2008) Interannual variations of the tropical ocean instability wave and ENSO. J Clim 21(15):3680–3686. doi:10.1175/2008JCLI1701.1
Bjerknes J (1966) A possible response of the atmospheric Hadley circulation to equatorial anomalies of ocean temperature. Tellus 18(4):820–829. doi:10.1111/j.2153-3490.1966.tb00303.x
Boer GJ (2000) A study of atmosphere-ocean predictability on long time scales. Clim Dyn 16(6):469–477. doi:10.1007/s003820050340
Burgers G, Stephenson DB (1999) The “normality” of El Niño. Geophys Res Lett 26(8):1027–1030. doi:10.1029/1999GL900161
Chen C, Liu H, Beardsley RC (2003) An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries. J Atmos Ocean Technol 20(1):159–186. doi:10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2
Chen X, Tung K-K (2014) Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345(6199):897–903
Collins M, Tett SFB, Cooper C (2001) The internal climate variability of HadCM3, a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 17(1):61–81. doi:10.1007/s003820000094
Collins WJ, Bellouin N, Doutriaux-Boucher M, Gedney N, Halloran P, Hinton T, Hughes J, Jones CD, Joshi M, Liddicoat S, Martin G, O’Connor F, Rae J, Senior C, Sitch S, Totterdell I, Wiltshire A, Woodward S (2011) Development and evaluation of an Earth-system model - HadGEM2. Geosci Model Dev Discuss 4(2):997–1062
Danilov S, Kivman G, Schröter J (2004) A finite-element ocean model: principles and evaluation. Ocean Model 6(2):125–150
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot L, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Holm EV, Isaksen L, Kallberg P, Koehler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thepaut JN, Vitart F (2011) The ERA-interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137(656, Part a):553–597
Delworth TL, Mann ME (2000) Observed and simulated multidecadal variability in the Northern Hemisphere. Clim Dyn 16(9):661–676. doi:10.1007/s003820000075
Delworth TL et al (2006) GFDL’s CM2 global coupled climate models. Part I: formulation and simulation characteristics. J Clim 19:643–674
Deser C, Alexander MA, Xie S-P, Phillips AS (2010) Sea surface temperature variability: patterns and mechanisms. Annu Rev Mar Sci 2(1):115–143
Drijfhout S, Gleeson E, Dijkstra HA, Livina V (2013) Spontaneous abrupt climate change due to an atmospheric blocking-sea-ice-ocean feedback in an unforced climate model simulation. Proc Nat Acad Sci 110(49):19713–19718
England MH, McGregor S, Spence P, Meehl GA, Timmermann A, Cai W, Gupta AS, McPhaden MJ, Purich A, Santoso A (2014) Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat Clim Change 4:222–227
Feldstein S, Lee S (1996) Mechanisms of zonal index variability in an aquaplanet GCM. J Atmos Sci 53(23):3541–3555
Fetterer F, Knowles K, Meier W, Savoie M (2002) Updated 2009. Sea ice index, digital media. National Snow and Ice Data Center, Boulder
Gent PR, Danabasoglu G, Donner LJ, Holland MM, Hunke EC, Jayne SR, Lawrence DM, Neale RB, Rasch PJ, Vertenstein M, Worley PH, Yang Z-L, Zhang M (2011) The community climate system model version 4. J Clim 24(19):4973–4991
Giorgetta MA, Jungclaus JH et al (2013) Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the coupled model intercomparison project phase 5. J.Adv Model Earth Syst 5(3):572–597
Gleckler PJ, Taylor KE, Doutriaux C (2008) Performance metrics for climate models. J Geophys Res Atmos. doi:10.1029/2007JD008972
Goosse H, Renssen H (2001) A two-phase response of the southern ocean to an increase in greenhouse gas concentrations. Geophys Res Lett 28(18):3469–3472. doi:10.1029/2001GL013525
Graham T (2014) The importance of eddy permitting model resolution for simulation of the heat budget of tropical instability waves. Ocean Model 79:21–32
Griffies SM, Winton M, Donner LJ, Horowitz LW, Downes SM, Farneti R, Gnanadesikan A, Hurlin WJ, Lee H-C, Liang Z, Palter JB, Samuels BL, Wittenberg AT, Wyman BL, Yin J, Zadeh N (2011) The GFDL CM3 coupled climate model: characteristics of the ocean and sea ice simulations. J Clim 24(13):3520–3544
Handorf D, Dethloff K (2012) How well do state-of-the-art atmosphere-ocean general circulation models reproduce atmospheric teleconnection patterns? Tellus 64:19777
Harris LM, Durran DR (2010) An idealized comparison of one-way and two-way grid nesting. Mon Weather Rev 138(6):2174–2187. doi:10.1175/2010MWR3080.1
Hawkins E, Edwards T, McNeall D (2014) Pause for thought. Nat Clim Change 4(3):154–156. doi:10.1038/nclimate2150
Huber M, Knutti R (2014) Natural variability, radiative forcing and climate response in the recent hiatus reconciled. Nat Geosci 7(9):651–656
King MD, Menzel WP, Kaufman YJ, Tanre D, Gao B-C, Platnick S, Ackerman SA, Remer LA, Pincus R, Hubanks PA (2003) Cloud and aerosol properties, precipitable water, and profiles of temperature and water vapor from MODIS. IEEE Trans Geosci Remote Sens 41(2):442–458
Loeb NG, Kato S, Su W, Wong T, Rose FG, Doelling DR, Norris JN, Huang X (2012) Advances in understanding top-of-atmosphere radiation variability from satellite observations. Surv Geophys 33:359–385
Mantua NJ, Hare SR, Zhang Y, Wallace JM, Francis RC (1997) A Pacific interdecadal climate oscillation with impacts on salmon production. Bull Am Meteorl Soc 78(6):1069–1079. doi:10.1175/1520-0477(1997)078<1069:APICOW>2.0.CO;2
Marshall J, Plumb R (2007) Atmosphere, ocean and climate dynamics: an introductory text, 93rd edn., International geophysics series, Elsevier, Amsterdam
Marshall J, Speer K (2012) Closure of the meridional overturning circulation through Southern Ocean upwelling. Nat Geosci 5(3):171–180. doi:10.1038/ngeo1391
Marshall J, Scott J, Armour K, Campin J-M, Kelley M, Romanou A (2013) The ocean’s role in the transient response of climate to abrupt greenhouse gas forcing. Clim Dyn 44(7):2287–2299
Marshall J, Armour KC, Scott JR, Kostov Y, Hausmann U, Ferreira D, Shepherd TG, Bitz CM (2014) The ocean’s role in polar climate change: asymmetric Arctic and Antarctic responses to greenhouse gas and ozone forcing. Philos Trans R Soc Lond A Math Phys Eng Sci 372(2019):20130040 doi:10.1098/rsta.2013.0040
Marsland S, Haak H, Jungclaus J, Latif M, Röske F (2003) The Max-Planck-Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Model 5(2):91–127
Martin T, Park W, Latif M (2014) Southern Ocean forcing of the North Atlantic at multi-centennial time scales in the Kiel Climate Model. Deep Sea Res Part II Top Stud Oceanogr. http://www.sciencedirect.com/science/article/pii/S0967064514000320
Meehl GA, Arblaster JM, Fasullo JT, Hu A, Trenberth KE (2011) Model-based evidence of deep-ocean heat uptake during surface-temperature hiatus periods. Nat Clim Change 1:360–364
Meehl GA, Teng H (2014) CMIP5 multi-model hindcasts for the mid-1970s shift and early 2000s hiatus and predictions for 2016–2035. Geophys Res Lett 41(5):1711–1716
Miller A, Cayan D, Barnett T, Graham N, Oberhuber J (1994) The 1976–77 climate shift of the Pacific Ocean. Oceanography 7(1):21–26
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 dataset. J Geophys Res 117:D08101. doi:10.1029/2011JD017187
Newman M, Compo GP, Alexander MA (2003) ENSO-forced variability of the Pacific decadal oscillation. J Clim 16(23):3853–3857. doi:10.1175/1520-0442(2003)016<3853:EVOTPD>2.0.CO;2
Park W, Latif M (2010) Pacific and Atlantic multidecadal variability in the Kiel Climate Model. Geophys Res Lett. doi:10.1029/2010GL045560
Pennell C, Reichler T (2011) On the effective number of climate models. J Clim 24(9):2358–2367
Pierce DW (2001) Distinguishing coupled ocean-atmosphere interactions from background noise in the North Pacific. Prog Oceanogr 49(1–4) 331 – 352. http://www.sciencedirect.com/science/article/pii/S0079661101000295
Platnick S, King MD, Ackerman SA, Menzel WP, Baum BA, Riedi JC, Frey RA (2003) The MODIS cloud products: algorithms and examples from Terra. IEEE Trans Geosci Remote Sens 41(2):459–473
Pohlmann H, Botzet M, Latif M, Roesch A, Wild M, Tschuck P (2004) Estimating the decadal predictability of a coupled AOGCM. J Clim 17(22):4463–4472. doi:10.1175/3209.1
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108(D14):4407
Reichler T, Kim J (2008) How well do coupled models simulate today’s climate? Bull Am Meteorol Soc 89(3):303–311
Ringler T, Petersen M, Higdon RL, Jacobsen D, Jones PW, Maltrud M (2013) A multi-resolution approach to global ocean modeling. Ocean Model 69:211–232
Ruiz-Barradas A, Nigam S, Kavvada A (2013) The Atlantic Multidecadal Oscillation in twentieth century climate simulations: uneven progress from CMIP3 to CMIP5. Clim Dyn 41(11):3301–3315
Schlesinger ME, Ramankutty N (1994) An oscillation in the global climate system of period 65–70 years. Nature 367(6465):723–726. doi:10.1038/367723a0
Sidorenko D, Rackow T, Jung T, Semmler T, Barbi D, Danilov S, Dethloff K, Dorn W, Fieg K, Goessling HF, Handorf D, Harig S, Hiller W, Juricke S, Losch M, Schröter J, Sein D, Wang Q (2014) Towards multi-resolution global climate modeling with ECHAM6-FESOM. Part I: model formulation and mean climate. Clim Dyn 1–24. doi:10.1007/s00382-014-2290-6
Stevens B, Giorgetta M, Esch M, Mauritsen T, Crueger T, Rast S, Salzmann M, Schmidt H, Bader J, Block K et al (2013) The atmospheric component of the MPI-M earth system model: ECHAM6. J Adv Model Earth Syst 5(2):146–172
Stocker T, Qin D, Plattner G-K, Alexander L, Allen S, Bindoff N, Bron F-M, Church J, Cubasch U, Emori S, Forster P, Friedlingstein P, Gillett N, Gregory J, Hartmann D, Jansen E, Kirtman B, Knutti R, Kumar KK, Lemke P, Marotzke J, Masson-Delmotte V, Meehl G, Mokhov I, Piao S, Ramaswamy V, Randall D, Rhein M, Rojas M, Sabine C, Shindell D, Talley L, Vaughan D, Xie S-P (2013) Technical Summary. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Climate Change 2013: The physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Stouffer RJ, Manabe S, Vinnikov KY (1994) Model assessment of the role of natural variability in recent global warming. Nature 367(6464):634–636
Sumata H, Lavergne T, Girard-Ardhuin F, Kimura N, Tschudi MA, Kauker F, Karcher M, Gerdes R (2014) An intercomparison of Arctic ice drift products to deduce uncertainty estimates. J Geophys Res Oceans. doi:10.1002/2013JC009724
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Meteorol Soc 93(4):485–498
Trenberth KE, Fasullo JT (2013) An apparent hiatus in global warming? Earth’s Future 1(1):19–32
Trenberth KE, Hurrell JW (1994) Decadal atmosphere-ocean variations in the Pacific. Clim Dyn 9(6):303–319. doi:10.1007/BF00204745
Trenberth KE, Shea DJ (2006) Atlantic hurricanes and natural variability in 2005. Geophys Res Lett. doi:10.1029/2006GL026894
Uppala SM, Kallberg PW, Simmons AJ, Andrae U, Bechtold VD, Fiorino M, Gibson JK, Haseler J, Hernandez A, Kelly GA, Li X, Onogi K, Saarinen S, Sokka N, Allan RP, Andersson E, Arpe K, Balmaseda MA, Beljaars ACM, Van De Berg L, Bidlot J, Bormann N, Caires S, Chevallier F, Dethof A, Dragosavac M, Fisher M, Fuentes M, Hagemann S, Holm E, Hoskins BJ, Isaksen L, Janssen PAEM, Jenne R, McNally AP, Mahfouf JF, Morcrette JJ, Rayner NA, Saunders RW, Simon P, Sterl A, Trenberth KE, Untch A, Vasiljevic D, Viterbo P, Woollen J (2005) The ERA-40 re-analysis. Q J R Meteorol Soc 131:2961–3012
Valcke S, Craig T, Coquart L (2013) OASIS3-MCT user guide, OASIS3-MCT 2.0. Technical report, TR/CMGC/13/17, CERFACS/CNRS SUC URA No 1875, Toulouse, France
von Storch H, Zwiers FW (1999) Statistical analysis in climate research. University Press, Cambridge
Wang Q, Danilov S, Schröter J (2008) Finite element ocean circulation model based on triangular prismatic elements, with application in studying the effect of topography representation. J Geophys Res 113(C5):C05015 doi:10.1029/2007JC004482
Wang Q, Danilov S, Sidorenko D, Timmermann R, Wekerle C, Wang X, Jung T, Schröter J (2014) The finite element sea ice-ocean model (fesom) v.1.4: formulation of an ocean general circulation model. Geosci Model Dev 7(2) 663–693. http://www.geosci-model-dev.net/7/663/2014/
Watanabe S, Hajima T, Sudo K, Nagashima T, Takemura T, Okajima H, Nozawa T, Kawase H, Abe M, Yokohata T, Ise T, Sato H, Kato E, Takata K, Emori S, Kawamiya M (2011) MIROC-ESM 2010: model description and basic results of CMIP5-20c3m experiments. Geosci Model Dev 4(4):845–872
Watanabe M, Shiogama H, Tatebe H, Hayashi M, Ishii M, Kimoto M (2014) Contribution of natural decadal variability to global warming acceleration and hiatus. Nat Clim Change 4(10):893–897
Welch PD (1967) The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. Audio Electroacoust IEEE Trans 15(2):70–73
Acknowledgments
Computational resources were made available by the German Climate Computing Center (DKRZ) through support from the German Federal Ministry of Education and Research (BMBF), and by the North-German Supercomputing Alliance (HLRN). We also thank Axel Timmermann, Sergey Danilov, and Stephan Juricke for helpful discussions and Patrick Scholz for providing a mesh-visualization script.
Author information
Authors and Affiliations
Corresponding author
Appendix 1: Computation of performance indices
Appendix 1: Computation of performance indices
To obtain an objective view of the skill of a model to simulate basic quantities compared to observations, performance indices (PI) have been developed (e.g. Reichler and Kim 2008; Gleckler et al. 2008). Sidorenko et al. (2015) have adapted and extended the PI defined by Reichler and Kim (2008) to include seasonal variations of the variables and to stratify the PI in latitudinal belts such as 60–\(90\,^\circ\)S (Antarctica), 30–\(60\,^\circ\)S (southern mid-latitudes), \(30\,^\circ\)N–\(30\,^\circ\)S (tropics), 30–\(60\,^\circ\)N (northern mid-latitudes) and 60–\(90\,^\circ\)N (Arctic). As reference data sets 2-m temperature, 10-m wind speed, 500-hPa geopotential height, and 300-hPa u-component from the 40-year ECMWF reanalysis (ERA-40; Uppala et al. 2005), precipitation from the Global Precipitation Climatology Project (GPCP; Adler et al. 2003), total cloud cover from the Moderate Resolution Imaging Spectroradiomenter (MODIS; Platnick et al. 2003; King et al. 2003), and top-of-the-atmosphere outgoing longwave radiation data from the Clouds and the Earth’s Radiant Energy System (CERES; Loeb et al. 2012) have been chosen. In the present study we include sea ice concentration for the Arctic and Antarctic, the reference data set being the sea ice concentration data set from the Ocean and Sea Ice Satellite Application Facility (OSISAF; Sumata et al. 2014).
1.1 Appendix 2: PI for mean climate state
For each grid cell n of a common \(2\,^\circ \times 2\,^\circ\) degree grid to which all data have been interpolated, each season s, and each variable v the absolute errors of the climatological seasonal means of a model m to the observation data have been calculated. Afterwards for each season and each variable global averages and averages over the latitudinal belts have been computed—in the present study in addition for the inner tropics (\(15\,^\circ\)N–\(15\,^\circ\)S):
with e being the mean absolute error, w the weighting factor for the area of a grid cell, s the simulated value, and o the observed value. The overbars represent climatological means.
These mean absolute errors have been calculated for our ECHAM6-FESOM (E6-F) model as well as for 56-year long historical simulations from 1950 to 2005 of five state-of-the-art CMIP5 models: MPI-ESM-LR (Giorgetta et al. 2013; Stevens et al. 2013), HadGEM2 (Collins et al. 2011), CCSM4 (Gent et al. 2011), GFDL-CM3 (Griffies et al. 2011), and MIROC-ESM (Watanabe et al. 2011). The first ensemble member of each of these simulations has been chosen, respectively. Finally, the mean absolute errors of E6-F have been normalized by the mean absolute errors averaged over the five CMIP5 models:
where PI represents the normalized performance index and \(\overline{~\cdot ~}^{~\tiny {\text {CMIP5}}}\) the average over the five CMIP5 models.
For comparison, the PI of the MPI-ESM-LR which shares the atmospheric component with E6-F have been calculated. In this case MPI-ESM-LR mean absolute errors have been normalized with the ones of the five CMIP5 models. In Table 1 we present averages of these performance indices over the four seasons and the nine variables in the Arctic and Antarctic and eight variables in the remaining areas.
The inclusion of sea ice concentration explains the slight changes in the performance indices in our Table 1 for the Arctic and Antarctic in E6-F REF (51–350) and MPI-ESM-LR (56 years) compared to Sidorenko et al. (2015). For E6-F REF (501–1500), E6-F REF (1–500) and LOW (1–500) we calculate the PI for all consecutive 50-year chunks in the given time period and present means and standard deviations over all chunks as error estimates.
1.2 Appendix 3: PI for interannual climate variability
The focus of the present paper is on the variability. Therefore we extend our PI to include the representation of interannual variability of seasonal means. We use the same observation data sets as for the mean values. Like for the climatological mean values in Sidorenko et al. (2015), for each grid point, each season, and each variable we calculate the absolute errors of the interannual standard deviation of seasonal means to the observation data and average these globally and over the latitudinal belts. Therefore, in Eq. (3) the overbars are replaced by interannual standard deviation of seasonal means. It should be noted that for the calculation of the interannual standard deviation a detrending is necessary to avoid that a long term trend contributes to the interannual variability. Therefore we applied the exponential detrending of Sect. 3 to the E6-F data. Furthermore, we did not only apply a linear detrending to the observation data used as a reference and the CMIP5 model data but also to the 50-year chunks of the exponentially detrended E6-F data. We did this to filter out the variability on long time scales which is also filtered out by the linear detrending from the observation data and the 56-year historical simulation chunks from the CMIP5 model data. We calculate the mean absolute errors of interannual standard deviations for our E6-F model as well as for the five selected CMIP5 models. Finally, we normalize the mean absolute errors of E6-F or MPI-ESM-LR by the mean absolute error averaged over the five CMIP5 models according to Eq. (4).
In Table 2 we present averages of these performance indices over the four seasons and the nine variables in the Arctic and Antarctic and eight variables in the remaining areas. Like for the PI of the climatological seasonal means, for E6-F REF (501–1500), E6-F REF (1–500) and E6-F LOW (1–500) we calculate the PI for all consecutive 50-year chunks in the given time period and present means and standard deviations over all chunks as error estimates.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rackow, T., Goessling, H.F., Jung, T. et al. Towards multi-resolution global climate modeling with ECHAM6-FESOM. Part II: climate variability. Clim Dyn 50, 2369–2394 (2018). https://doi.org/10.1007/s00382-016-3192-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3192-6