1 Introduction

The Indian Ocean dipole (IOD) is an important ocean–atmosphere coupled phenomenon in the tropical Indian Ocean, which produces an anomalous zonal sea surface temperature (SST) gradient along the equator (Saji et al. 1999; Webster et al. 1999; Murtugudde et al. 2000). The anomalous zonal SST gradient is strongly coupled with anomalous equatorial winds (Saji et al. 1999; Webster et al. 1999). Specifically, positive phase of IOD events are characterized by anomalous SST warming in the western Indian Ocean and cooling in the eastern Indian Ocean, accompanied by easterly winds at the equator (Saji et al. 1999; Webster et al. 1999; Murtugudde et al. 2000; Li et al. 2002, 2003; Saji and Yamagata 2003a); negative phase of IOD events are characterized by opposite SST and wind anomaly patterns. In addition to this, the subsurface sea temperature anomalies present an east–west dipole pattern (Rao et al. 2002; Feng and Meyers 2003). In association with the anomalous sea temperatures and winds, positive IOD events often cause severe flooding in eastern Africa and serious droughts in Indonesia and Australia; negative IOD events have the opposite effects on the climate (Ansell et al. 2000; Black et al. 2003; Zubair et al. 2003; Behera et al. 2005). Not only do IOD events affect rim regions (Birkett et al. 1999; Ansell et al. 2000; Black et al. 2003), they also modulate the climate in remote areas by planetary atmospheric waves (Saji and Yamagata 2003b).

Phase-locking is an important characteristic of IOD events, whereby the occurrence, peak, and decay of IOD events are phase-locked to the seasonal cycle (Saji et al. 1999; Webster et al. 1999; Li et al. 2002, 2003; Krishnamurthy and Kirtman 2003; Lau and Nath 2004; Cai et al. 2005; Zhong et al. 2005; Behera et al. 2006). Wajsowicz (2004) showed that IOD events often reverse their sign in winter, peak in autumn, and reverse their sign again in the following winter; this is observed both in reanalysis and model results. The results indicate that winter is important as IOD variability often emerges or decays during this period.

Due to the large influence of IOD events on the climate in near and far regions, there is great interest in studying the predictability of the events. Previous studies have shown that the lead time for skillful IOD prediction is about 1–2 seasons (Wajsowicz 2004, 2005; Luo et al. 2005, 2007; Zhao and Hendon 2009; Shi et al. 2012). On one hand, the poor skill may be due to imperfect numerical models unable to simulate the basic characteristics of IOD events (Gualdi et al. 2003; Wajsowicz 2004; Yamagata et al. 2004; Cai et al. 2005). Alternatively, errors in the initial fields due to the sparse availability of observation data may also be a major limitation to improved skills. It has been observed that whatever the start month the predictive skills for the IOD region decrease rapidly during winter, and this is called the winter predictability barrier (WPB) phenomenon (Luo et al. 2007). By calculating the anomaly correlation coefficients of the IOD indices between the ideal observation (i.e., the “true state” of the positive IOD events in the model) and the model predictions (i.e., the predicted positive IOD events, with initial errors superimposed) in the Geophysical Fluid Dynamics Laboratory Climate Model version 2p1 (GFDL CM2p1), Feng et al. (2014a) demonstrated the existence of the WPB in both the growing and decaying phases of the positive IOD events, as a result of initial errors. Feng and Duan (2014) further reported that the dominant pattern of initial sea temperature errors, which are most likely to cause the occurrence of a significant WPB, shows an east–west dipole in both the surface and subsurface components. Therefore initial sea temperature errors with an east–west dipole pattern probably cause the occurrence of the WPB and, in turn, result in the failure of predicting the occurrence and decay of IOD events, which usually happen in winter (Wajsowicz 2004). This emphasizes the importance of initial field accuracy in skillfully predicting IOD events.

To improve the initial field accuracy, the Indian Ocean Observing System (IndOOS; http://www.incois.gov.in/Incois/iogoos/home_indoos.jsp) has been developed, which is a long-term observational network, based on multiple platforms. Despite this, the low resolution of the current observations in the tropical Indian Ocean is still a limitation to improved forecasts. Therefore, there is an urgent need for more observations. However, collecting observational data over the vast Indian Ocean is costly and not easy to implement. A strategy called targeted observations may reduce prediction errors to a greater degree than the same number of non-targeted observations; that is to say, a small number of targeted observations will reduce the prediction errors as much as a large number of non-targeted observations (Morss et al. 2001; Kim et al. 2004). This strategy where observations are collected in specific regions that are sensitive to IOD events to reduce the prediction uncertainties may be an effective solution to reduce the WPB in IOD prediction. The key question from this is: how do we find the observing locations (i.e., the sensitive areas) for advancing beyond the WPB of IOD predictions?

Different methods were applied to explore the sensitive areas of the El Niño Southern Oscillation (ENSO) and tropical cyclones for targeted observations; these methods can generally be divided into two categories. One category consists of the adjoint-based methods, in which the adjoints of the forward tangent propagator of the models were calculated (Kim et al. 2004), such as singular vectors (SVs; Palmer et al. 1998) and conditional nonlinear optimal perturbation (CNOP; Mu and Duan 2003). The second category was ensemble-based methods, such as the ensemble Kalman filter (Hamill and Snyder 2002), the ensemble transform technique (Bishop and Toth 1999) and the ensemble transform Kalman filter (Bishop et al. 2001). Some results of these studies have already been implemented in field experiments, showing the efficiency of these proposed methods (Bergot 1999; Szunyogh et al. 2000).

To the authors’ knowledge, there were no adaptive observational studies targeting IOD events. In this study, we will conduct perfect model predictability experiments to explore the observing locations (i.e., the sensitive areas) for advancing beyond the WPB of IOD predictions with an ensemble approach. As positive IOD events have larger effects on the climate and more frequently occur under current climate change conditions, compared with negative ones (Ashok et al. 2001, 2003; Vinayachandran et al. 2002; Abram et al. 2003; Black et al. 2003; Annamalai and Murtugudde 2004; Yamagata et al. 2004; Behera et al. 2005; Hong et al. 2008; Cai et al. 2009; Weller and Cai 2013), only positive IOD events are considered.

The remainder of the paper is organized as follows. The model and experimental strategy are described in Sect. 2. The effects of initial error patterns on prediction uncertainties in the model are described in Sect. 3. The sensitive areas to enable advancement beyond the WPB in predicting positive IOD events are explored in Sect. 4. And finally, a summary and discussion are presented in Sect. 5.

2 Model and experimental strategy

The model used in this study is the GFDL CM2p1, an ocean–atmosphere–land–ice coupled model. The oceanic component of the coupled model is the Modular Ocean Model version 4 (MOM4p1), released in December 2009, which is a numerical representation of the ocean’s hydrostatic primitive equations (Griffies 2009). The horizontal resolution is 1 × 1 in most regions, with the meridional resolution reducing to 1/3 at the equator. In total, there are 50 unevenly spaced vertical levels, with a 10 m resolution in the upper 225 m of ocean. The atmospheric component of the GFDL CM2p1 is the GFDL atmosphere model, AM2p12b (GFDL Global Atmospheric Model Development Team 2004). Its horizontal resolution is 2.5 × 2, and there are 24 vertical levels in total. The different components are coupled with each other through the Flexible Modeling System and exchange fluxes every two hours. The GFDL CM2p1 has been used to study the predictability of IOD events in previous research (Feng et al. 2014a, b; Feng and Duan 2014; Song et al. 2008) and was found to simulate the climatoloty and interannual variability of the Indian Ocean well.

In the present study, the GFDL CM2p1 is run for 150 years, including the forcing of aerosols, land cover, tracer gases and insolation in 1990; the last 100 years are analyzed after a 50 year spin-up, to reduce the effects of initial adjustments. Ten positive IOD events are randomly chosen as the “true states” (i.e., reference states) to be predicted (Fig. 1), from all of those in which the IOD index exceeds 0.5 standard deviations for at least 3 consecutive months (Song et al. 2007). The IOD indices of these positive IOD events usually reverse their signs from negative to positive in winter, peak in autumn and reverse the signs again in the following winter (Feng et al. 2014a), which is consistent with the observational results (Wajsowicz 2004). The winter season here refers to the time period from January to March. In perfect model predictability experiments, the model is assumed to be perfect and so any prediction errors are caused by initial errors. The detailed experimental strategy is stated below.

Fig. 1
figure 1

IOD indexes of 10 reference state IOD events used in this study. R1–R10 denote the IOD events with the model year 1, 3, 11, 20, 59, 81, 88, 90, 92, 95, respectively. The stars signify the start months July(−1), October(−1), and January(0) (“−1” indicates the year preceding the IOD year; “0” indicates the IOD year), and the integrations starting from these start months bestride the winter in the growing phase of positive IOD events; the triangles signify the start months April(0), July(0), and October(0), and the predictions from these start months bestride the winter in the decaying phase

Full size image

As the ocean actively forces the atmosphere in the tropical Indian Ocean, we only perturbed the sea temperature and analyzed the effect of initial sea temperature errors on the prediction uncertainties of IOD events in this study. Considering the mean thermocline depth is about 110–130 m in the tropical Indian Ocean (Song et al. 2007), the sea temperature anomalies at 95-m depth can reflect the variation of the thermocline depth to some extent, which is closely related to the evolution of IOD events (Rao et al. 2002; Vinayachandran et al. 2002). Besides, the SST anomalies are also closely linked with the evolution of IOD events. Therefore, initial errors are only superimposed on sea temperatures at the sea surface and at 95-m depth in the reference state IOD events, which could probably reflect the effects of sea temperature perturbations on the prediction uncertainties of positive IOD events.

Recent researches have shown that initial errors causing significant prediction errors for coupled ocean–atmospheric modes (e.g., El Niño-Southern Oscillation (ENSO), Kuroshio Large Meander (KLM), Atlantic and Pacific blockings, etc.) may have dynamical growth behavior similar to the events themselves (Yu et al. 2009; Jiang and Wang 2010; Duan et al. 2013; Wang et al. 2012). Furthermore, Duan et al. (2009) demonstrated that such kinds of initial errors for El Niño would be most likely to cause a significant “spring predictability barrier”. These results encourage us to investigate the sensitive initial errors related to the WPB of IOD events with an ensemble approach by superimposing initial errors derived from IOD-related sea temperature anomalies. Moreover, due to a 4-year dominant period of IOD events in the GFDL CM2p1 model (Feng and Duan 2014), there is usually a positive IOD event and a negative IOD event within 4 years; therefore, the patterns of sea temperature anomalies within 4 years are plentiful. So we sample the temperature anomalies at the sea surface and at 95-m depth in the tropical Indian Ocean every other month from the 4 years preceding each reference state IOD event to make initial errors as plentiful as possible; that is, there are 24 pairs of initial errors altogether for each positive IOD event.

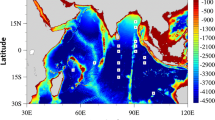
Based on the above discussions, for each positive IOD event, 24 pairs of initial errors are superimposed on the initial sea temperature fields at both the sea surface and 95 m depth, in the tropical Indian Ocean (45°E–115°E, 10°S–10°N) (Fig. 2). Then the model is integrated for 12 months from six different start months: July, October in the year preceding the IOD year, and January, April, July and October in the IOD year (Fig. 1). For simplicity, the six start months are respectively labeled as July(−1), October(−1), January(0), April(0), July(0), and October(0) in the following discussions (where “−1” indicates the year preceding the IOD year and “0” indicates the IOD year). The integrations starting from July(−1), October(−1), and January(0) bestride the winter in the growing phase of the positive IOD events, and from April(0), July(0), and October(0) bestride the winter in the decaying phase. The prediction errors are then obtained, which are the absolute values of the difference in the IOD index between the predicted positive IOD events and the “true state” of the positive IOD events.

Fig. 2
figure 2

Schematic diagram of the experimental design. The black bold line R indicates the IOD index of a reference state IOD event. The 24 colored lines indicate the predictions with 24 different initial errors superimposed on the initial fields of the reference state IOD event. These predictions are integrated for 12 months from the same start month. The prediction errors are the absolute values of the difference in the IOD index between the predicted positive IOD events and the reference state IOD event

Full size image

To impartially compare the relative impact of different initial errors on the predictability of positive IOD events, the initial errors are constrained by T ′1  = T 1/δ 1 and T ′2  = T 2/δ 2, where T 1 and T 2 represent the surface and subsurface components of the original initial errors, T ′1 and T ′2 represent the surface and subsurface components of the final initial errors, superimposed on the “true state” of positive IOD events, and δ 1 and δ 2 represent positive numbers which are chosen to ensure the same magnitude between T ′1 and T ′2 . The norms \(\left\| {T^{\prime}_{1} } \right\| = \sqrt {\sum\nolimits_{i,j} {(T^{\prime}_{1ij} )^{2} } }\) and \(\left\| {T^{\prime}_{2} } \right\| = \sqrt {\sum\nolimits_{i,j} {(T^{\prime}_{2ij} )^{2} } }\) are set as 2.4°, where the grid point (i, j) ranges over 45°E–115°E, 10°S–10°N. In this case, the initial error at any gridpoint (i, j) in the tropical Indian Ocean is smaller than the standard deviation of analysis errors of sea surface temperature along the equator (i.e., 0.2 °C; Kaplan et al. 1998), indicating that the initial errors analyzed in this study may exist in the analysis errors and that the magnitude of our initial errors is reasonable set. As only two levels of sea temperatures are perturbed in the tropical Indian Ocean and the perturbations on the sea temperatures are small, no significant initial shock exists during the integrations even though regid boundaries are used in this study (not shown).

3 Effect of initial error patterns on the prediction uncertainties

Based on the same experimental strategy, Feng and Duan (2014) chose initial errors that cause the fastest error growth in winter and analyzed their dominant pattern using Combined Empirical Orthogonal Function (CEOF) analysis. They demonstrated that the dominant pattern of those initial errors that are most likely to cause a significant WPB presents a large-scale east–west dipole, in both the surface and subsurface (i.e., 95 m depth) components (hereafter referred to as the dipole pattern).

In this paper, by comparing the relative effects of the dipole pattern initial errors and spatially correlated noise on prediction uncertainties, we verify the effect of initial error patterns on the prediction uncertainties of positive IOD events. Specifically, we superimpose spatially correlated noises on the initial fields of the positive IOD events and integrate them for 12 months from the start months July(−1) and July(0). The integrations starting from these 2 months are used to illustrate predictions spanning winter, in the growing phase and the decaying phase, respectively, of the positive IOD events. Then the prediction errors in winter caused by spatially correlated noises are compared with those caused by dipole pattern initial errors, to verify the effect of initial error patterns on IOD predictions.

For each start month, we choose ten pairs of initial errors that are most likely to cause a significant WPB from the 240 pairs of initial errors mentioned in Sect. 2 and ensure that the absolute values of the pattern correlation coefficients between those initial errors and the corresponding leading mode of the aforementioned CEOF analysis are largest (Fig. 3a–d, also see Feng and Duan 2014). These initial errors therefore represent the initial errors of the dipole pattern and are hereafter called the dipole pattern initial errors. The corresponding prediction errors for these initial errors are analyzed.

Fig. 3
figure 3

The surface component (a) and subsurface component (b) for the leading mode of the Combined Empirical Orthogonal Function analysis of initial errors that are most likely to cause a significant WPB for start month July(−1); c and d are as above, but for the start month July(0); A, B, C, and D in the black boxes represent the areas where the large values of the dominant pattern are located. e, g, and i are the surface components of three pairs of fields with spatially correlated noise in the tropical Indian Ocean; and f, h, and j are the subsurface components (units:  °C)

Full size image

In consideration that analysis fields are based on both first guess (FG) fields and observations, and errors in analysis fields are likely correlated both horizontally and vertically due to the use of FG fields that have strongly correlated errors, we generated three pairs of fields with spatially correlated noise to contrast with the dipole pattern initial errors. They possess the surface and subsurface components and have the same magnitude as the dipole pattern initial errors. For simplicity, the surface and subsurface components of the spatially correlated noise fields are the same; and they are generated to follow a multivariable normal distribution X~\(N_{p} ({\mathbf{0}},\sum )\) with mean (0, …, 0) p and covariance matrix ∑. The subscript p denotes the total number of the grid points in the tropical Indian Ocean (45°E–115°E, 10°S–10°N). Each value in ∑ describes the correlation coefficient between the grid point x and y and is defined as \(\langle s(x)s(y) \rangle = e^{{ - \frac{{\left| {x - y} \right|}}{\xi }}}\), where |x − y| denotes the distance between the grid point x and y, and the correlation length ξ is defined as 220 km. As ∑ is not a diagonal matrix, these noise fields are spatially correlated.

To ensure that the magnitude of spatially correlated noises is the same as that of the dipole pattern initial errors, the spatially correlated noises are constrained by T ′ = T/δ, where T represents the surface and subsurface components of the original spatially correlated noises, T ′represents the surface and subsurface components of the final spatially correlated noises, superimposed on the “true state” of positive IOD events, and δ represents a positive number. The norm \(\left\| {T^{\prime}_{{}} } \right\| = \sqrt {\sum\nolimits_{i,j} {(T^{\prime}_{ij} )^{2} } }\) is set as 2.4°, where the grid point (i, j) ranges over 45°E–115°E, 10°S–10°N. Three pairs of spatially correlated noises are generated in total and their spatial patterns are shown in Fig. 3e–j, which are in striking contrast to the dipole pattern initial errors. These three pairs of spatially correlated noises are respectively superimposed on the initial fields of each “true state” positive IOD event. After 12 months of integration, 30 predictions are obtained for each start month.

The prediction errors in winter that are caused by the spatially correlated noises are then compared with those caused by the dipole pattern initial errors (Fig. 4). In most cases, the prediction errors in winter caused by the dipole pattern initial errors are larger than those caused by the three pairs of spatially correlated noises; this is particularly apparent in their composite and is true for both of the start months July(−1) and July(0). These results indicate that the dipole pattern initial errors have a larger effect on the prediction uncertainties of positive IOD events in winter, compared with the spatially correlated noises. Therefore, they probably result in a failure of the predictions for the occurrence and decay of positive IOD events.

Fig. 4
figure 4

The prediction errors in winter for each individual case superimposed with the dipole pattern initial errors and three pairs of fields with spatially correlated noise for (a) start month July(−1), and (b) start month July(0) (color plots). The bars represent the average mean of each kind of initial errors

Full size image

To further evaluate the effects of initial errors with different spatial patterns on the prediction uncertainties of positive IOD events, the seasonal growth rate of prediction errors is calculated. The error growth rate (κ) in a season is defined as κ = (γ n+1 − γ n-1)/2, where γ n-1 is the prediction error in the first month of the season and γ n+1 is the prediction error in the last month. A positive κ signifies an increase of the prediction error for a given season, and a negative κ signifies a decrease; the larger the positive value of κ, the faster the prediction error grows in that season. For the dipole pattern initial errors, κ is positive and largest in winter, indicating that the prediction errors grow fastest in winter and show a strong seasonally dependent evolution; therefore, the dipole pattern initial errors favor the occurrence of a significant WPB. By contrast, for almost all of the spatially correlated noises, the seasonal growth rates of prediction errors are small or even negative in winter, indicating that no WPB occurs. This contrast is also reflected in their composite (Table 1). Based on these results, it is considered that the dipole pattern initial errors cause larger prediction errors, and are more favorable for the fastest error growth in winter, compared with the spatially correlated noises; therefore, the dipole pattern initial errors are more likely to lead to the occurrence of a significant WPB.

Table 1 The composite error growth rates during each of the four seasons for IOD events superimposed with dipole pattern initial errors and three pairs of fields with spatially correlated noise for start months July(−1) and July(0)
Full size table

These results emphasize the close relationship between the spatial patterns of initial errors and the occurrence of a significant WPB. If we can filter out the initial errors of dipole structure by carrying out intensive observations over the tropical Indian Ocean, we could probably decrease the prediction errors in winter and, in turn, greatly improve the forecast skills for the occurrence and decay of positive IOD events. However, carrying out intensive observations over the vast tropical Indian Ocean is costly and not easy to implement; therefore, targeted observations may be an effective solution to this issue, as discussed in the introduction. Feng and Duan (2014) showed that the large values of the dipole pattern initial errors are localized within a few areas. This indicates that the initial errors in these regions may make a large contribution to the prediction uncertainties and provide information regarding the sensitive areas for advancing beyond the WPB of IOD predictions, which is further explored in the following section.

4 Identification of sensitive areas to advance beyond the WPB

For start month July(−1), the large values of the dipole pattern initial errors are mainly located at 10°S–Equator, 90°E–110°E (A of Fig. 3a) in the surface component and 5°S–5°N, 85°E–105°E (B of Fig. 3b) in the subsurface component. For start month July(0), the large values are mainly located at 10°S–Equator, 70°E–90°E (C of Fig. 3c) in the surface component and at 5°S–5°N, 85°E–105°E (D of Fig. 3d) in the subsurface component. The four areas A, B, C, and D have the same size. Two experiments are conducted on each pair of initial errors, which are most likely to cause a significant WPB. 26 pairs of initial errors for start month July(−1) and 24 pairs for start month July(0), which show the fastest growth in winter and are most likely to cause a significant WPB, are respectively chosen to participate in these experiments.

Firstly, for each pair of initial errors (hereafter referred to as “the whole initial errors”), the errors at A and C from the surface component and at B and D from the subsurface component are eliminated (for start months July(−1) and July(0), respectively), and the remaining errors in the tropical Indian Ocean (45°E–115°E, 10°S–10°N), are superimposed on the same initial fields as the whole initial errors. After 12 months of integration, the prediction errors are obtained. This type of experiments is called Exp-S, in which errors over small areas are eliminated from the whole initial errors. Secondly, and in contrast, for each pair of initial errors, only the errors at A and C in the surface component, and at B and D in the subsurface component (for start months July(−1) and July(0), respectively), are superimposed on the same initial fields as the whole initial errors, and the rest of the initial errors in the tropical Indian Ocean (45°E–115°E, 10°S–10°N) are eliminated. Then they are integrated for 12 months and the prediction errors are obtained. This type of experiments is referred to as Exp-L, in which errors over large areas are eliminated from the whole initial errors. In addition, the predictions with the whole initial errors superimposed are called Exp-all. The only difference among these three types of experiments is in the different initial errors.

The prediction errors in different experiments are compared in Fig. 5. The points beneath the diagonal line indicate that the prediction errors in winter in Exp-all are larger than those in Exp-S (Figs. 5a, c) and Exp-L (Figs. 5b, d). For most cases, the prediction errors in Exp-all are larger than 1; however, by partially eliminating the initial errors (i.e., the Exp-S or the Exp-L), the prediction errors decrease rapidly, which is highlighted by the concentration of the points in the bottom right part of Fig. 5. These results indicate that partially eliminating the initial errors in the tropical Indian Ocean can reduce the prediction errors in winter and improve the forecast skills of IOD events spanning winters. This conclusion is true for both of the start months, July(−1) and July(0). We further take a case as an example to examine the SST component of prediction error fields in winter in different experiments (Fig. 6). Apparently, the errors in Exp-all are large in both the western pole (50°E–70°E, 10°S–10°N) and the eastern pole (90°E–110°E, 10°S–0°) of IOD events, resulting in large prediction uncertainties in winter. However, the temperature errors decrease in both Exp-S and Exp-L, especially in Exp-S. These results again demonstrate that the prediction errors decrease largely when partially eliminating initial errors in the tropical Indian Ocean.

Fig. 5
figure 5

The prediction errors in winter for each individual case; the y-axis represents the prediction errors in Exp-S (a and c), and in Exp-L (b and d); the x-axis represents those in Exp-all. Graphs a and b show those for start month July(−1), and c and d are for start month July(0)

Full size image
Fig. 6
figure 6

SST component of prediction error fields in winter for a case in Exp-all (a), Exp-S (b), and Exp-L(c) (units:  °C)

Full size image

It is worth noting that, the total area from which the initial errors in Exp-S are eliminated, is only one-sixth of that in Exp-L; therefore, to impartially compare the impacts of eliminating initial errors, per unit area, on the prediction uncertainties of positive IOD events in different experiments, the cost effectiveness, CE, is defined as CE = I/N = ((P 1 − P 0)/P 0)/N, where I is the impact of partially eliminating initial errors on the prediction uncertainties in winter in the different experiments, P 1 is the prediction errors in Exp-S or Exp-L, P 0 is the prediction errors in Exp-all, and N is the size of the areas from which the initial errors are eliminated. For convenience, N is set as 1 in Exp-S and 6 in Exp-L. The negative or positive CE indicates an improvement or decline, respectively, of the forecast skills of IOD events spanning winter, by eliminating the initial errors per unit area; the larger the absolute value of the negative CE, the greater the improvement of the forecast skills.

It is apparent that the CE is negative for most cases in Exp-S and Exp-L (Fig. 7); this indicates an improvement of the forecast skills of IOD events spanning winter, by eliminating the initial errors, per unit area in these experiments. In addition, the absolute values of the negative CE in Exp-S are significantly larger than those in Exp-L, suggesting a greater improvement of the forecast skills by Exp-S. This is also reflected in their average values: the average cost effectiveness is −50.94 and −40.92 % in Exp-S, and −6.34 and −8.01 % in Exp-L, for start months July(−1) and July(0), respectively. That is to say, by solely eliminating the initial errors in one-seventh of the tropical Indian Ocean (45°E–115°E, 10°S–10°N) in Exp-S, the prediction errors in winter could largely be reduced by more than 40 %. Physically, the large values of the dipole pattern initial errors in Exp-L develop rapidly under the Bjerknes feedback and cause large prediction errors. By contrast, the errors in Exp-S do not show a large development and cause small prediction errors (not shown). Therefore, the improvement of the forecast skills is greater by Exp-S than Exp-L, and the prediction uncertainties of positive IOD events in winter are more sensitive to the initial errors at A and B for start month July(−1), and C and D for start month July(0).

Fig. 7
figure 7

The cost effectiveness of each individual case in Exp-S and Exp-L for a start month July(−1); and b start month July(0); the numbers above each graph are the average mean of the cost effectiveness in Exp-S and Exp-L

Full size image

By eliminating the initial errors over areas A and B, the prediction errors in the winter of the growing phase will probably decrease rapidly, and the forecast skills for the occurrence of positive IOD events will be largely improved. Corresponding to this, by eliminating the initial errors over areas C and D, the prediction errors in the winter of the decaying phase will probably decrease rapidly, and the forecast skills for the decay of positive IOD events will be largely improved. These sensitivity experiments, showed that, these areas [i.e., A and B for start month July(−1), C and D for start month July(0)] have great effects on the IOD predictions spanning winter for most cases.

The analysis in this study demonstrates that the prediction uncertainties of positive IOD events in winter are sensitive to the initial errors in the areas where the large values of the dipole pattern initial errors are located. Feng and Duan (2014) showed that the errors in the subsurface component of the dipole pattern initial errors are larger than those in the surface component. The question then arises, as to whether the prediction uncertainties of positive IOD events in winter are more sensitive to the initial errors in the subsurface large value areas (i.e., B and D) than those in the surface large value areas (i.e., A and C).

For each pair of initial errors that are most likely to cause a significant WPB (i.e., the whole initial errors), by eliminating the initial errors in the surface and subsurface large value areas respectively, their impacts on the prediction uncertainties of positive IOD events can be compared. Specifically, for start months July(−1) and July(0), respectively, the initial errors at A and C are eliminated from the surface component of the whole initial errors, and the remaining initial errors are superimposed on the original initial fields. After 12 months of integration, the prediction errors are obtained. These experiments are called Exp-surf, in which the initial errors in the surface large value areas are eliminated. Similarly, the initial errors at B and D (respectively, for each start month) are eliminated from the subsurface component, and the remaining initial errors are superimposed on the original initial fields. These experiments are referred to as Exp-sub, in which the initial errors in the subsurface large value areas are eliminated.

The points beneath the diagonal line within Fig. 8 indicate that the prediction errors in winter in Exp-all are larger than those in Exp-surf or Exp-sub. The solid lines in red and green represent the linear best fit for the points in Exp-surf and Exp-sub, respectively; the slopes of these lines indicate the ratio of the prediction errors in winter in Exp-surf and Exp-sub, respectively, to those in Exp-all. If the slope is smaller than that of the diagonal line, by eliminating the initial errors in the surface or subsurface large value areas, the prediction errors in winter for most cases decrease and, on average, they improve the forecast skills; the smaller the slope, the greater the improvement. It is apparent that most red and green points concentrate in the bottom right part of the figures, indicating that the prediction errors in winter largely decrease with the elimination of the initial errors from the surface or subsurface large value areas; therefore, the forecast skills of the IOD events spanning winter greatly improve. This is in accordance with the results showing that the slopes of the red and green lines are smaller than that of the diagonal line. The conclusions are true for both of the start months July(−1) and July(0). Furthermore, the slope of the green line is smaller than that of the red line for both of the start months July(−1) and July(0), indicating that, in general, the improvement of the forecast skills of the IOD events spanning winter in Exp-sub is greater than that in Exp-surf. That is to say, the prediction uncertainties in winter are generally more sensitive to the initial errors in the subsurface large value areas than to those in the surface large value areas.

Fig. 8
figure 8

The prediction errors in winter for each individual case; the y-axis represents the prediction errors in Exp-surf and Exp-sub; the x-axis represents those in Exp-all; the solid lines in red and green represent the linear best fit for the points in Exp-surf and Exp-sub, respectively. Graphs a and b show those for start month July(−1) and July(0), respectively

Full size image

Furthermore, the impacts of partially eliminating initial errors on the prediction uncertainties of the IOD events in winter (i.e., I) in both Exp-surf and Exp-sub are shown in Fig. 9. As the areas A and B, as well as C and D, have the same size, the impact I could impartially compare the effects of eliminating initial errors on the prediction uncertainties of positive IOD events in different experiments. Negative and positive impacts indicate a decrease or increase, respectively, of the prediction errors in winter. It is apparent that, for most cases, the impacts are negative in Exp-surf and Exp-sub, indicating a decrease of the prediction errors and an improvement of the forecast skills for the IOD events spanning winter. Moreover, the average extent of improvement by eliminating the initial errors in the subsurface large value areas is greater than that by eliminating the initial errors in the surface large value areas, with an average impact of −50.14 and −59.96 % in Exp-sub, and −36.52 and −45.77 %, in Exp-surf, for start months July(−1) and July(0), respectively, indicating that the prediction uncertainties in winter are more sensitive to the initial errors in the subsurface large value areas.

Fig. 9
figure 9

The impacts of each individual case on the prediction uncertainties in winter in Exp-surf and Exp-sub (a) at start month July(−1); and (b) at start month July(0); the numbers above each graph are the average impacts in Exp-surf and Exp-sub

Full size image

It should be noted, that the average impact on the prediction uncertainties of IOD events in Exp-sub is approximately equal to, and even greater than, that in Exp-S, for start months July(−1) and July(0), respectively, but the size of the areas where initial errors are eliminated in Exp-sub is only half of that in Exp-S. Therefore, in consideration of the CE, eliminating the initial errors in just the subsurface large value areas could effectively decrease the prediction errors in winter and largely improve the forecast skills of IOD events; that is, the prediction uncertainties of IOD events are exquisitely sensitive to initial errors over the subsurface large value areas. These results suggest that the subsurface large value areas are the sensitive areas for advancing beyond the WPB of IOD predictions. As the subsurface large value areas (i.e., B and D) for start months July(−1) and July(0) are in the same general area, if initial errors are reduced by carrying out intensive observations at 95 m depth in the eastern tropical Indian ocean (5°S–5°N, 85°E–105°E), the forecast skills for the occurrence and decay of positive IOD events will probably be largely improved.

5 Summary and conclusions

The Indian Ocean dipole (IOD), which is an important ocean–atmosphere coupled phenomenon at the inter-annual timescale in the tropical Indian Ocean, has strong effects on the climate in rim regions and areas further afield. In this study, using the GFDL CM2p1 model, the observing locations (i.e., the sensitive areas) are explored, to advance beyond the winter predictability barrier (WPB) of predicting positive IOD events; this is done using perfect model predictability experiments, in which the model is assumed to be perfect and any prediction errors are only caused by initial errors.

Firstly, the effects of initial error patterns on the prediction uncertainties of positive IOD events are explored. By superimposing dipole pattern initial errors and spatially correlated noises on the initial fields of the true state IOD events, in turn, we found that the prediction errors in winter caused by dipole pattern initial errors are larger than those caused by the spatially correlated noises. Further, the prediction errors caused by dipole pattern initial errors show a significant seasonally dependent evolution, with the fastest growth in winter, indicating the occurrence of the WPB. By contrast, the seasonal growth rates of the prediction errors caused by spatially correlated noises are small or negative in winter, indicating that no WPB occurs. Feng et al. (2014b) pointed out that the climatology in winter (i.e., the weakest coupling) may favor the rapid variation of perturbations in winter closely related to IOD events. Under such climatology, the dipole pattern initial errors are more likely to cause the fastest error growth in winter, and in turn a significant WPB.

Secondly, we further identified the areas that have large effects on the prediction uncertainties of positive IOD events in winter. Two experiments were conducted (i.e., Exp-S and Exp-L) on each pair of initial errors that were most likely to cause a significant WPB. In Exp-S, the initial errors in the areas where the large values of the dipole pattern initial errors are located, were eliminated. In Exp-L, only the initial errors in these areas were retained, and the rest of the initial errors were eliminated. We found that partially eliminating initial errors in the tropical Indian Ocean can reduce the prediction errors in winter and improve the forecast skills of IOD events spanning winter. The absolute values of the cost effectiveness in Exp-S are significantly larger than those in Exp-L; that is, the improvement in Exp-S is significantly greater than that in Exp-L, per unit area. These conclusions are true for both of the start months, July(−1) and July(0). These sensitivity experiments showed that, by eliminating the initial errors over the areas, where the large values of the dipole pattern initial errors are located, the prediction errors in winter will largely decrease and the forecast skills for the occurrence and decay of positive IOD events will be greatly improved. Therefore, the prediction uncertainties of IOD events in winter are sensitive to the initial errors over these areas. If initial errors are reduced by carrying out intensive observations in these areas, the prediction errors in winter will probably be reduced, and in turn improve the forecast skill, which provides information regarding the sensitive areas of the positive IOD events for advancing beyond the WPB.

Of further interest, we investigated the relative effects of the initial errors in the surface and subsurface large value areas on the prediction uncertainties of IOD events. We demonstrated that the average extent of improvement on the forecast skills spanning winter by eliminating the initial errors in the subsurface large value areas is greater than that by eliminating the initial errors in the surface large value areas, for both of the start months July(−1) and July(0); that is to say, the prediction errors in winter are more sensitive to the initial errors in the subsurface large value areas than those in the surface large value areas. Based on this, in consideration that the absolute values of the cost effectiveness in Exp-sub are larger than those in Exp-S, eliminating the initial errors at only 95 m depth in the eastern tropical Indian Ocean (5°S–5°N, 85°E–105°E) (i.e., the subsurface large value areas) could effectively decrease the prediction errors of the growing and decaying phases of IOD events in winter and largely improve the forecast skills for the occurrence and decay of IOD events. Therefore, the prediction uncertainties of IOD events are exquisitely sensitive to initial errors over these areas and these areas probably are the observing locations (i.e., the sensitive areas) for advancing beyond the WPB of IOD predictions. Intensive observations should be carried out in the eastern tropical Indian Ocean (5°S–5°N, 85°E–105°E) at 95 m depth, which would probably largely reduce the prediction errors in winter and greatly improve the forecast skills for the occurrence and decay of positive IOD events.

We should realize the limitation of the results presented in this article. Actually, limited to the experimental strategy used in the present study, we could not reveal the optimal observing locations that have the most potential for advancing beyond the WPB. That is to say, in addition to the observing locations identified in the present study, there may exist other observing locations for advancing beyond the WPB. Considering that the sensitivity experiments have verified the validity of the observing locations identified here in advancing beyond the WPB of IOD predictions, we argue that these observing locations are valid and acceptable, although they may not be the optimal ones. These results are preliminary and only qualitatively indicative; however, they encourage us to further explore the optimal observing locations for IOD predictions by using advanced mathematical methods such as the CNOP (Mu and Duan 2003), which is a fully nonlinear method and has been adopted in tropical cyclones for targeted observations (Qin and Mu 2011). In addition, in the present study we only explored the effects of sea temperatures in the tropical Indian Ocean on IOD predictions and identified the sensitive areas for advancing beyond the WPB. In fact, one should further investigate how the Pacific Ocean or other oceans affect IOD predictions and explore the associated sensitive areas. And the validity of the sensitive areas in improving IOD forecast skill should also be tested by OSSEs and OSEs (observing system experiments) with a data assimilation method. In any case, for targeted observations associated with IOD predictions, substantial work remain to be done. It is expected that the IOD forecast skill can be greatly improved based on comprehensive studies.