Abstract
The Nordic Seas and the Barents Sea is the Atlantic Ocean’s gateway to the Arctic Ocean, and the Gulf Stream’s northern extension brings large amounts of heat into this region and modulates climate in northwestern Europe. We have investigated the predictive skill of initialized hindcast simulations performed with three state-of-the-art climate prediction models within the CMIP5-framework, focusing on sea surface temperature (SST) in the Nordic Seas and Barents Sea, but also on sea ice extent, and the subpolar North Atlantic upstream. The hindcasts are compared with observation-based SST for the period 1961–2010. All models have significant predictive skill in specific regions at certain lead times. However, among the three models there is little consistency concerning which regions that display predictive skill and at what lead times. For instance, in the eastern Nordic Seas, only one model has significant skill in predicting observed SST variability at longer lead times (7–10 years). This region is of particular promise in terms of predictability, as observed thermohaline anomalies progress from the subpolar North Atlantic to the Fram Strait within the time frame of a couple of years. In the same model, predictive skill appears to move northward along a similar route as forecast time progresses. We attribute this to the northward advection of SST anomalies, contributing to skill at longer lead times in the eastern Nordic Seas. The skill at these lead times in particular beats that of persistence forecast, again indicating the potential role of ocean circulation as a source for skill. Furthermore, we discuss possible explanations for the difference in skill among models, such as different model resolutions, initialization techniques, and model climatologies and variance.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Climate predictions with an interannual-to-decadal forecast horizon merge the gap between seasonal forecasts and future climate projections. In other words, it is both an initial value problem and a boundary condition problem. For this reason, decadal predictions require unique information combining both the present state of climate and external forcing, such as changes in greenhouse gases, anthropogenic and volcanic aerosols. Although global climate is expected to warm over the present century in response to increasing levels of greenhouse gases, regional climate (e.g., in the Nordic Seas) on timescales of years to decades are likely to be dominated by internal climate variability. Much of the internal climate variability is thought to be related to the slow variations in the ocean, which provides memory to the climate system.
The North Atlantic Current extends into the Nordic Seas (Fig. 1), carrying warm and saline water masses of subtropical origin northward. The Nordic Seas comprises the Greenland Sea, Iceland Sea, and the Norwegian Sea, and is constrained by the Greenland-Scotland Ridge in the south, Norway in the east, the Fram Strait in the north, and Greenland in the west. The amount of heat carried by the North Atlantic Current and its related heat loss influences the atmospheric circulation (e.g., Overland et al. 2008), the extent of the sea ice (Årthun et al. 2012; Sandø et al. 2014), marine ecosystems (Loeng and Drinkwater 2007; Drinkwater et al. 2014), and the dense Nordic Seas overflows across the Greenland-Scotland Ridge (Mauritzen 1996; Eldevik et al. 2009), contributing to the lower limb of the Atlantic Meridional Overturning Circulation (AMOC). The capacity to predict changes in the state of the ocean years in advance would therefore be of great potential impact.
Sea surface temperature in winter (Jan–Apr) from the HadISST data, averaged over the period 1961–2010. The black box embraces the eastern Nordic Seas (66–79°N and 0–18°E), and the dashed black line indicates the Greenland-Scotland Ridge. The extension of the North Atlantic Current, carrying warm and saline Atlantic Water into the Nordic Seas and the Barents Sea, is illustrated by magenta arrows
Sea surface temperature (SST) anomalies occurring along the pathway of the North Atlantic Current are brought northwards and eventually into the Nordic Seas (Sutton and Allen 1997; Chepurin and Carton 2012). Several observation-based studies have shown that SST anomalies propagate from the northeast North Atlantic, via the Nordic Seas, and towards the Barents Sea and the Arctic Ocean (e.g., Polyakov et al. 2005; Holliday et al. 2008; Eldevik et al. 2009). If this occurs recurrently, the temperature in the Nordic Seas would be predictable some years ahead. Based on retrospective predictions (“hindcasts”) with three coupled climate models, we herein take a first step and investigate the multiyear predictive skill of SST in the Nordic Seas and Barents Sea for the 50-year long time period 1961–2010.
In the present study we focus on the eastern Nordic Seas (as defined in Fig. 1). This is a climatically complicated and economically important region with the northernmost surface signature of Atlantic Water; subsequently it either extends east into Barents Sea, or enters the Fram Strait as a sub-surface water mass to recirculate south or to progress into the Arctic Ocean. The eastern Nordic Seas remain ice-free during winter as the Atlantic layer of relatively warm and saline water extends to the surface (Swift 1986). A thin mixed layer is overlaying the Atlantic Water in summer (Nilsen and Falck 2006). Herein we focus on the months January to April, when SST is representative of the Atlantic layer in general. These months are also the coldest in the eastern Nordic Seas and when the Nordic Seas in general exhibit the largest sea ice extent (Fig. 2).
Based on both observational and model studies, the northward propagation of SST anomalies in the subpolar region have been attributed to changes in purely advective signals from the subtropics, changes in local atmosphere–ocean interaction, or a combination of these two processes (Sutton and Allen 1997; Hátún et al. 2005; Sarafanov et al. 2008; Häkkinen et al. 2011). Accordingly, ocean circulation is an important factor when it comes to predicting SST anomalies in the subpolar North Atlantic. For example, Matei et al. (2012) explain predictive skill for SST on longer lead times in the subpolar North Atlantic with the northward advection of subtropical water by the Atlantic Meridional Overturning Circulation. Similarly, a suite of models (e.g., Robson et al. 2012; Yeager et al. 2012; Msadek et al. 2014) show that retrospective predictions are able to reproduce the subpolar warming in the 1990s due to increased northward advection of warm water. On the other hand, the Nordic Seas and the Barents Sea have been poorly investigated with respect to ocean predictability on interannual-to-decadal time scales. One recent “perfect model” twin-experiment shows encouraging results with predictive skill in heat content in the eastern and northernmost Nordic Seas up to a decade (Counillon et al. 2014). In this perfect model study the synthetic data used for initialisation and verification is taken from a free-running simulation with the same climate model.
The manuscript is organized as follows. The CMIP5 simulations, initialization data sets, and the observational based data, as well as the methods used in our study, are presented in Sect. 2. In Sect. 3, the retrospective predictability of SST in the Nordic and Barents Seas is assessed and inter-compared among the three models. In Sect. 4, we discuss why there is different skill among the models and which factors can limit SST predictability in our focus region. Finally, the conclusions are given in Sect. 5.
2 Data and methods
In the following, the simulations and observation-based data are introduced, including a description of the model resolutions and initialization process used for the hindcast experiments. Finally, we describe how the predictive skill is calculated.
2.1 CMIP5 simulations (decadal hindcasts and historical runs)
In this study we use a suit of initialized hindcast simulations (or retrospective predictions) performed within the framework of the fifth phase of the Coupled Model Intercomparison Project (CMIP5; Taylor et al. 2012). CMIP5 includes simulations that have been assessed in the Intergovernmental Panel on Climate Change Fifth Assessment Report (IPCC 2013). Each model provides several ensemble members, which have been initialized every fifth year between 1960 and 2010 (end of 1960, end of 1965…end of 2005). Here, we are using observations over the period 1961–2010. That means that we are investigating only the hindcasts started between 1960 and 2005 (the 2006 decadal hindcast simulates the 2006–2015 period that is outside our observational data set). All hindcasts have a time length of 10 years. Some of the CMIP5 models provide hindcasts initialized every year, but initialization every fifth year was a minimum requirement for CMIP5 decadal experiments. For consistency, we use the hindcasts initialized every fifth year from all models. Additionally we also check the predictive skill robustness in the hindcasts initialized every year from MPI-ESM-LR system, the model showing the most promising results (as shown later).
There are 16 different models that contribute with decadal hindcast experiments to the CMIP5 data archive (Meehl et al. 2014). Herein we are focusing on three of these models: MPI-ESM-LR (Giorgetta et al. 2013; Jungclaus et al. 2013), CNRM-CM5 (Voldoire et al. 2013), and IPSL-CM5 (Dufresne et al. 2013). The first two models have a reasonable seasonal cycle of ice area export in the Fram Strait (Langehaug et al. 2013). A realistic ice export is one of the important factors for correctly simulating the Arctic Ocean sea ice (Smedsrud et al. 2011). We also include IPSL-CM5 in the present study, which has been widely used in previous climate studies (e.g., also including previous versions of the model, Mignot et al. 2011; Langehaug et al. 2012; Mignot et al. 2013). In Langehaug et al. (2012), both IPSL-CM and MPI-ESM were included, and the study demonstrated large model differences in the properties of the North Atlantic Current in the subpolar region. Another recent study (Deshayes et al. 2014) combines all three models herein, and shows that the models have clear differences in the extent of Atlantic Water in the subpolar region: MPI-ESM-LR is the warmest model of the three models studied herein with respect to Atlantic Water, whereas IPSL-CM5 is the coldest, and CNRM-CM5 is intermediate compared to the two other. This is also expressed in the seasonal cycle of the sea ice area in the Nordic Seas (Fig. 2, lower panel): underestimated sea ice in MPI-ESM-LR, overestimated in CNRM-CM5, and largely overestimated in IPSL-CM5.
It is in a modelling and dynamical aspect of interest to analyse models that differ, thus representing a range of different model climates. This is particularly relevant for Sect. 4, discussing why different predictability is found in different models. The present study is accordingly not only an assessment of predictability in the three hindcast experiments, but also an evaluation of how model-dependent mechanisms affect actual predictive skill. An appreciation of why these models show different predictability in the Nordic Seas and the Barents Sea will help to pinpoint the mechanisms carrying predictability in this region.
The model resolution of the oceanic component in the three models is given in Table 1, and a visualization of the horizontal resolution can be obtained from the spatial Figures, e.g., Fig. 12. MPI-ESM-LR has a bipolar grid with 1.5° resolution, but the northern pole is located over Greenland, and hence, close to Greenland the resolution can be as high as 12 km. IPSL-CM5 has a tripolar grid with 2° resolution, and is the model with the lowest resolution of the three models in the North Atlantic/Nordic Seas. CNRM-CM5 also has a tripolar grid, but with an intermediate resolution (1°) compared to the two other models, and the resolution is similar to that of the observation-based data set (see Sect. 2.3 for further description of this data set).
In order to assess the impact of the initialization of the hindcasts, we compare the predictive skill of the hindcasts against the benchmark skill of the non-initialized historical simulations. The historical simulations cover the period 1850–2005, and the RCP4.5 scenario simulations are used to extend the historical simulations up to 2010. The combined historical and RCP4.5 runs are in the following called historical+ runs. Even if the number of ensemble members in the historical simulations for a particular model might be higher, the number of historical+ runs at hand is limited by the number of available RCP4.5 simulations. This numbers is for the three models as follows: three members for MPI-ESM-LR, four members for IPSL-CM5, whereas the historical+ run for CNRM-CM5 consist only of one member (as given in Table 1). The ensemble mean is used for MPI-ESM-LR and IPSL-CM5.
2.2 Initialisation data sets and techniques
The three models in this study use different techniques and different data sets in the initialization process for their decadal hindcast experiments (Meehl et al. 2014).
The initial state in the hindcasts from MPI-ESM-LR is extracted from a nudged simulation using the coupled MPI-ESM-LR. In this so-called assimilation experiment, the 3D temperature and salinity fields of the second historical ensemble member of MPI-ESM-LR are relaxed towards the temperature and salinity anomalies of a simulation with the MPI ocean model forced with NCEP-NCAR daily atmospheric reanalysis (Matei et al. 2012; Müller et al. 2012). The relaxation time scale is 10 days. In the regions covered by sea-ice an additional relaxation proportional with the ice-free fraction is applied in the upper 12 levels of the ocean model. This anomaly initialisation scheme aims at reducing model drift toward its own imperfect climatology. An ensemble simulation of ten members for the hindcasts initialized every fifth year (and three members for yearly initialized hindcasts) is subsequently made.
The initial state in the hindcasts from CNRM-CM5 is extracted from a nudged simulation using the coupled CNRM-CM5 (Germe et al. 2014). In this simulation the 3D temperature and salinity are nudged towards the full fields from the ECMWF ocean reanalysis NEMOVAR–COMBINE (Balmaseda and Mogensen 2010). The nudging is 3D Newtonian damping with a vertical dependence of the relaxing time-scale ranging from 10 days below the mixed layer to 360 days at the bottom of the ocean. No nudging is applied within the mixed layer (Germe et al. 2014). An ensemble simulation of ten members for the hindcasts initialized every fifth year is subsequently made.
The initial state in the hindcasts from IPSL-CM5 is extracted from a nudged simulation using the coupled IPSL-CM5 (Swingedouw et al. 2013). This nudged simulation is based on the first historical ensemble member of IPSL-CM5, where SST anomalies are nudged towards observed SST anomalies (ERSST data, Reynolds et al. 2007). That means that no initialization is included below the ocean surface in IPSL-CM5-LR. Additionally, there is no initialization where the sea ice concentration is higher than 50 % (Swingedouw et al. 2013). A relaxing timescale of around 60 days is used in the nudged simulation (for a mixed layer of 50 m depth), and hence, the nudging is weaker in IPSL-CM5 than in MPI-ESM-LR and CNRM-CM5. An ensemble simulation of six members for the hindcasts initialized every fifth year is subsequently made.
Another main difference among the models is whether anomaly or full field initialization has been applied. MPI-ESM-LR and IPSL-CM5 use anomaly initialization, whereas CNRM-CM5 uses a full field initialization (Meehl et al. 2014). An expected hindcast evolution for the full field initialization approach is a drift toward the model climatology. The model state in CNRM-CM5 is colder than the observed state, and hence, sea ice area in the Nordic Seas increases and SST in the eastern Nordic Seas decreases in each hindcast (not shown).
2.3 HadISST sea surface temperature and sea ice data
Observation-based SST and sea ice concentration is obtained from the Hadley Centre Sea Ice and SST data set, version 1.1 (HadISST). This data set from the Met Office Hadley Centre is a combination of monthly global SST and sea ice concentration on a 1-degree latitude-longitude grid from 1870 to present. A detailed description of the dataset and its production process is given in Rayner et al. (2003).
The HadISST sea ice data are in reasonable agreement with data from National Snow Ice Data Center (NSIDC, lower panel in Fig. 3). The monthly sea ice concentration from the NSIDC for the period 1979–2010 is estimated from passive microwave satellite data on a 25 km × 25 km grid (Cavalieri et al. 1996). Due to the short time period of this data set, we are using the HadISST sea ice data to assess the realism of the CMIP5 models. The accuracy of the data before 1979 is lower compared to the period after 1979, due to the higher resolution and more homogenous data in the modern satellite period (from 1979 and onwards). However, note that we here only use the mean and the standard deviation of the sea ice concentration over the period 1961–2010 and the mean seasonal cycle over the same period. We do not compare the year-to-year variability from HadISST and the CMIP5 models.
For the spatial distribution of predictive skill (i.e., skill is calculated grid point wise), the HadISST data are interpolated to each of the three ocean model grids using bilinear interpolation. The HadISST SST data is set to “missing” for grid boxes with 100 % sea ice concentration, and hence, fully sea ice covered regions will appear as regions with no data in the spatial maps showing predictive skill of SST. The sea ice concentration in the models is also indicated in the relevant figures (Figs. 8, 9, 10). Furthermore, when calculating average SST in the eastern Nordic Seas for the models we exclude regions with 100 % sea ice concentration (as is the case for HadISST).
2.4 Assessment of decadal hindcasts
In interannual-to-decadal predictability studies it is common to use one independent observation-based data set (e.g., HadISST) to compare with the hindcast experiments (e.g., Smith et al. 2007; Kim et al. 2012; Hazeleger et al. 2013; Robson et al. 2013; Caron et al. 2014), although the hindcasts are initialized with a different data set. If there are large differences between the independent observation-based data set and the data sets used for initialisation (which is possible in our region of interest), the assessment of predictive skill can be expected to underestimate the actual predictability for a given model. In this study, we have therefore tested the predictive skill for each model against the data set that has been used for initialisation, in addition to an independent observation-based data set. This provides a more robust evaluation of the predictive skill, which can be divided in two parts: (1) how skilful are predictions compared to the data actually used for initialization, and (2) how skilful are predictions compared to a reference climate as it evolved (in our case chosen to be HadISST).
Regarding the data used for initialization, it is important to note that we here consider these data sets before their eventual modification in the specific assimilation procedure of the models. Hence, the hindcasts and the initialization data sets may differ at the starting point of each hindcast (as is shown later). However, the initialization data sets are generically more consistent with the respective hindcasts than the HadISST data, and therefore, higher predictive skill is expected when evaluating against the initialization data sets. More details on the initialization data sets are given in Table 1, and Fig. 3 (upper panel) shows how they differ. The initialization data sets for MPI-ESM-LR (NCEP forced ocean hindcast) and CNRM-CM5 (NEMOVAR-COMBINE; Balmaseda and Mogensen 2010) are most similar to the HadISST data, whereas the initialization data set for IPSL-CM5 (ERSST; Reynolds et al. 2007) has a temporal variability that is rather different from the others.
2.5 Calculation of predictive skill
We are calculating predictive skill according to lead time (e.g., Matei et al. 2012) to investigate how many years in advance SST in the Nordic Seas and Barents Sea is skilfully predictable. The two main measures for predictive skill are the anomaly correlation coefficient (or correlation skill) and the Root Mean Square Error (RMSE) skill. Herein we will focus on the former, since we are interested in whether or not the models are able to predict the observed SST anomalies.
To calculate the anomaly correlation coefficient, we construct a time series from the hindcasts for each lead time and correlate it with the corresponding observation-based time series. Since we are interested in the year-to-year variability and not the long-term trend, a linear trend is removed from the constructed time series at each lead time, prior to the calculation of the correlation. The anomaly correlation coefficient is calculated both for the ensemble mean and for the different ensemble members. Regarding the latter, a random ensemble member is chosen for each hindcast at each lead time. This process is repeated 100 times at each lead time to get a picture of the spread in correlation for the ensemble members. Correlation close to 1 indicates good predictive skill, while low correlation indicates poor skill. The statistical significance level at 90 % is achieved by the standard two-sided Student’s t test (e.g., O’Mahony 1986). With 9 data points available at each lead time, a significant correlation must be higher than 0.58. We believe that the two-sided t test is the more relevant in our case. If we use a one-sided t test we disregard the possibility of a relationship in the other direction (i.e., negative correlations), which does not represent predictive skill, but it is possible. In the presence of strong negative correlation it is normal to check if such a value can be obtained by chance or if it is a real issue (e.g., initialization shock, unrealistic model behaviour/variability), and then one needs to use a two-sided t test (e.g., Matei et al. 2012). The two-sided t test gives a higher statistical threshold compared to a one-sided t test.
The anomaly time series are smoothed to increase the signal-to-noise ratio (e.g., Kim et al. 2012; Matei et al. 2012). More specifically, a 3-year moving average has been applied to the hindcasts, and hence, we are considering lead times 1–3, 2–4, 3–5…and 8–10 years. The HadSST data and the historical+ runs have also been smoothed the same way.
As mentioned, CNRM-CM5 shows a clear drift in the initialized hindcasts. A drift correction is therefore done at each lead time by subtracting the mean difference between the hindcast and the observation-based data from each hindcast (Fig. 4). By doing this, the drift is removed, but variability is maintained in the hindcasts. There are other ways of doing the drift correction, but the one used herein is reasonable when having a small number of hindcasts (initialized only every fifth year between 1960 and 2010; Gangstø et al. 2013).
Hindcast winter SST in the eastern Nordic Seas for three CMIP5 models (coloured curves). The black curves show the data sets used to initialise the three models. Grey shading represents the range of one standard deviation of the spread in the ensemble members at each time step. The starting time of each hindcast is indicated by a magenta circle
We compare the hindcast correlation skill not only against the benchmark skill of the non-initialized historical simulations, but also against the skill of the persistence forecast. More specifically, at lead time 1–3 years (i.e., 1961–1963, 1966–1968…), the persistence forecast is constructed from the observation-based data by using the last year before the first forecasting year (i.e., 1960, 1965…).
3 Results
Predictive skill for the average SST in the eastern Nordic Seas is presented for each model in this section, comparing the skill of initialized hindcasts, non-initialized historical runs, and the persistence forecast. To achieve a better understanding of the skill, we also present spatial maps showing the anomaly correlation coefficient grid point by grid point. Assessing maps for each lead time give the possibility to detect regions where ocean advection appears to be important for the skill.
3.1 Predictive skill in the eastern Nordic Seas differs among the climate models
Eastern Nordic Seas SST displays a positive trend in all initialization data sets (Fig. 4, black curves). With respect to the initialized hindcasts (Fig. 4, coloured curves), a positive trend is most clearly seen in CNRM-CM5. In IPSL-CM5 there is a drift in some of the individual hindcasts (e.g., 1981–1990). Since a drift with the same sign is not present in all hindcasts, i.e., the model is not drifting back to its mean state (as CNRM-CM5), drift correction is not applied for this model. Note that we show the time series for the ensemble mean hindcast for each model (Fig. 4), which has a smaller variance than each individual ensemble member. From Fig. 4, it is difficult to deduce how well the models predict SST in the eastern Nordic Seas. Hence, we turn to the anomaly correlation coefficient that is calculated for each lead time. In order to assess the practical robustness of correlations, hindcasts are compared both with the respective initialization data set and the observational-based reference (HadISST). Note that NEMOVAR-COMBINE only provides data up to 2008, and therefore the predictive skill for CNRM-CM5 can only be calculated for lead times up to 6–8 years.
The number of data points at each lead time is too low to estimate robustly any lagged auto-correlation, and hence the effective degrees of freedom. However, the indicated significance level (0.58; Fig. 5, and cf. Sect. 2.5) should be representative as a bootstrap-like procedure resulted in practically the same significance level. In this procedure the time series of SST in the eastern Nordic Seas based on initialization data were correlated with 9 randomly chosen numbers from the first historical ensemble member for the period 1961–2010 (i.e., from a 50-datapoint time series). This procedure was repeated 5000 times for each lead time. This resulted in a distribution of all correlations with the 5 and 95 % percentile almost matching the significance level based on the two-sided t test (mean for all lead times is 0.6, except the 95 % percentile for CNRM which is 0.64). Using the concatenated first three historical+ runs (i.e., 150 data points) from MPI-ESM-LR and IPSL-CM5 gives the same result (0.6).
Left panel Anomaly correlation coefficient of winter SST in the eastern Nordic Seas for three CMIP5 models: the solid coloured lines show the correlation between the ensemble mean of the hindcasts and the data used to initialise the hindcasts. The grey curves show the spread in the ensemble members. For comparison, also the ensemble mean of the non-initialised runs (historical+ runs) and the persistence forecast are shown. At each lead time, the time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation. Note that NEMOVAR-COMBINE only provides data up to 2008, and therefore the predictive skill for CNRM-CM5 can only be calculated for lead-times up to 6–8 years. Right panel Same as left panel, but HadISST data is used instead of the initialisation data
Both MPI-ESM-LR and IPSL-CM5 display increased correlation skill with increasing lead times (Fig. 5, left panel). The peak correlation is reached at a different lead time for IPSL-CM5 (4–6 years) and MPI-ESM-LR (8–10 years). MPI-ESM-LR also shows significant correlation at shorter (1–3 years) lead time. CNRM-CM5 has the highest correlation at the shortest lead time (1–3 years), although not significant; contrary to the two other models, there is no increase of skill towards long lead times.
Comparing predictive skill using the initialization data and HadISST data (right panel, respectively) we find that the overall results agree (Fig. 5). However, there are some differences that are worth mentioning; the correlation at short lead time for MPI-ESM-LR is not significant and the lead time for the peak correlation is shifted from 8–10 to 7–9 years when considering HadISST. On the other hand, IPSL-CM5 shows higher correlations when using HadISST data instead of initialization data, e.g., the peak correlation at lead time 4–6 years is now significant. This is somewhat surprising, as one would maybe expect the highest predictive skill from consistency, i.e., from evaluating against the data also used for initialization. However, it could also reflect the fact that we only have nine data points to be correlated at each lead time. Furthermore, all three models show most negative correlations when using HadISST instead of initialisation data sets. These negative correlations appear to arise from sampling issues, as the negative correlations are greatly reduced when considering hindcasts initialized every year for MPI-ESM-LR (this will be shown later at the end of the current subsection). A thorough investigation of the reason for the drop in the correlation is beyond the scope of this study. In the remainder of this subsection, the results are valid for evaluations both with respect to initialization data sets and HadISST data.
The non-initialized (historical+) runs are included here as a reference forecast and a direct comparison for the eventual benefit of initialization. At each lead time, the same years are taken from the non-initialized runs as from the hindcasts. A linear trend is also removed at each lead time from the historical+ time series prior to the calculation of the correlation skill. The historical+ run from MPI-ESM-LR has no significant skill (Fig. 5). This shows that SST in the eastern Nordic Seas in MPI-ESM-LR benefit from the initialization (which also holds for the hindcasts initialized every year, as shown below). However, the benefit for SST in the eastern Nordic Seas in IPSL-CM5 is not clear, as neither the initialized hindcasts nor the historical+ runs display any general significant skill (Fig. 5). Regarding CNRM-CM5, the situation is different; the historical+ run is significantly correlated with the initialization data at nearly all lead times, and for some lead times when evaluated against HadISST data (Fig. 5).
To further corroborate the covariance of the historical+ runs and the HadISST data, we correlate the continuous time series from the historical+ runs with HadISST over the full study period (1961–2010; Fig. 6). This means that 50 data points from each data set is correlated, as opposed to the nine data points that have been correlated for each lead time in Fig. 5. Effective degrees of freedom were estimated according to the decorrelation time scale (following Pyper and Peterman 1998). As Fig. 5 suggests, the historical+ run from CNRM-CM5 is significantly in phase with HadISST (0.48, Fig. 6). This analysis shows that the single non-initialized historical simulation from CNRM-CM5 has higher skill than the initialized hindcasts (both for individual members and ensemble mean). Hence, for SST in the eastern Nordic Seas, CNRM-CM5 hindcasts do not benefit from the initialization. The other two models have no significant correlation between historical+ and HadISST at zero time lag (Fig. 6), consistent with Fig. 5.
Cross-correlation of time series of SST in the eastern Nordic Seas for the period 1961–2010; ensemble mean of the non-initialised runs (historical+ runs) from the CMIP5 models have been correlated with HadISST data. The auto-correlation of HadISST data is shown by the black dashed curve. The time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation
There is little persistence of HadISST in the eastern Nordic Seas at short lead time, i.e., at lead time 1–3 years the correlation is slightly above 0.2 (Fig. 5, right panel); the auto-correlation of HadISST is negligible at lag year three (Fig. 6). At the subsequent lead times, the persistence forecast shows negative correlations, and particularly high negative correlations at lead time 5–7 years. On the other hand, considering the initialization data sets (Fig. 5, left panels), persistence is ranging from essentially zero (for IPSL-CM5) to nearly 0.6 (for MPI-ESM-LR) at short lead time. At increasing lead times, correlations are negative (at least for MPI-ESM-LR and CNRM-CM5), similar to the persistence forecast based on HadISST data, but the values do not exceed the significance level.
The positive peak correlations at longer lead time for the MPI-ESM-LR hindcasts are higher than those for the persistence forecast. This underlines the potential role of ocean dynamics in bringing predictability to the Nordic Seas and Barents Sea, and similar result for the North Atlantic has been stressed using a different version of the MPI-ESM (Matei et al. 2012) as well as other models (Robson et al. 2012; Yeager et al. 2012; Msadek et al. 2014).
The significant negative correlation for the persistence forecast using HadISST data at lead times 4–6 and 5–7 years (Fig. 5) is consistent with the auto-correlation for HadISST data (Fig. 6), where a significant negative correlation is found at a time lag of ±6 years. This suggests a characteristic time scale of variance for SST in the eastern Nordic Seas of about 12 years, in line with the recent findings of Årthun and Eldevik (2016) combining both HadISST and a multi-century model control simulation. Accordingly, a warm anomaly in the eastern Nordic Seas should be followed by a cold anomaly about 6 years later, and a warm anomaly about 12 years thereafter.
As MPI-ESM-LR is showing the most skilful results in terms of SST anomalies in the eastern Nordic Seas, we have further assessed this model with respect to the impact of sampling size on the robustness of predictive skill also considering the available extended suite of hindcasts initialized every year (Fig. 7). The SST anomalies in eastern Nordic Seas are assessed both against HadISST data and the initialisation data set (Fig. 7). We see that negative correlations are greatly reduced compared to what is shown in Fig. 5. Hence, the negative correlations in Fig. 5 appear to be a result of sampling issues (at least for MPI-ESM-LR), as also suggested above. Another difference between Fig. 5 and Fig. 7 is the reduced positive correlation at short lead time when evaluating against HadISST data. Otherwise the shape of the curves is similar to what we got for the hindcasts initialised every fifth year, with increasing skill for increasing lead time and significant correlations at lead times 7–10 years (for evaluation against both data sets). Regarding the non-initialized historical experiments we see that the shape of the non-initialized historical experiments skill is now more similar to that of the initialized hindcasts, however, at lower non-significant levels. The similarity of the curves could suggest that the radiative forcing also contributes to the predictive skill.
Left panel Anomaly correlation coefficient of winter SST in the eastern Nordic Seas for MPI-ESM-LR with yearly initialization: the solid coloured lines show the correlation between the ensemble mean of the hindcasts and the data used to initialise the hindcasts. The grey lines show the spread in the ensemble members. For comparison, also the ensemble mean of the non-initialised runs (historical+ runs) and the persistence forecast are shown. At each lead time, the time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation. Right panel Same as left panel, but HadISST data is used instead of the initialisation data
3.2 Differences in predictive skill north and south of the Greenland-Scotland Ridge
We here describe the predictive skill of SST in three regions: the subpolar North Atlantic, the Nordic Seas, and the Barents Sea (see Fig. 1 for the location of the different regions). These results give a better understanding of the predictive skill of the average SST in the eastern Nordic Seas (Fig. 5). The following results are based on assessment of the initialized hindcasts only against HadISST data. Note that also the extent of the sea ice cover for each of the models is shown in Figs. 8, 9 and 10. MPI-ESM-LR has the smallest extent of sea ice of the three models, IPSL-CM5 the largest extent, and CNRM-CM5 is somewhere between the two other models. The sea ice extent is more closely discussed in the following section.
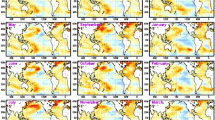
Anomaly correlation coefficient, point-by-point, of winter SST for MPI-ESM-LR between HadISST data and the ensemble mean of the hindcasts at different lead times. Significant correlations at the 90 % level are embraced by the black solid (dashed) curves for positive (negative) correlations. At each lead time, the time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation. The magenta curve shows the position where the sea ice concentration is 50 %
Anomaly correlation coefficient, point-by-point, of winter SST for CNRM-CM5 between HadISST data and the ensemble mean of the hindcasts at different lead times. Significant correlations at the 90 % level are embraced by the black solid (dashed) curves for positive (negative) correlations. At each lead time, the time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation. The magenta (grey) curve shows the position where the sea ice concentration is 50 (95) %
Anomaly correlation coefficient, point-by-point, of winter SST for IPSL-CM5 between HadISST data and the ensemble mean of the hindcasts at different lead times. Significant correlations at the 90 % level are embraced by the black solid (dashed) curves for positive (negative) correlations. At each lead time, the time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation. The magenta (grey) curve shows the position where the sea ice concentration is 50 (95) %
In general, high predictive skill is found in the subpolar North Atlantic in MPI-ESM-LR (red colours are dominating south of the Greeland-Scotland Ridge, Fig. 8), consistent with previous studies (e.g., Matei et al. 2012; Hazeleger et al. 2013; Bellucci et al. 2015). In contrast, the predictive skill in the Nordic Seas and Barents Sea is poorer than in the subpolar North Atlantic (blue colours are dominating in the north, Fig. 8). However, at short time after initialization (1–3 years), MPI-ESM-LR has significant predictive skill in parts of the Nordic Seas and the Barents Sea. Thereafter, the skill becomes overall poorer as we move away from the initialization time. In the subpolar North Atlantic the skill becomes higher again at longer lead times (4–6 years). Interestingly, in the following lead times, domains of high skill are propagating from the subpolar North Atlantic and into the eastern Nordic Seas, and finally the Barents Sea (6–8 years). The increase of skill at longer lead times is consistent with the skill for the averaged SST in the eastern Nordic Seas (Fig. 5).
Similar to MPI-ESM-LR, CNRM-CM5 shows overall high predictive skill in the subpolar North Atlantic and poor skill in the Nordic Seas and the Barents Seas (Fig. 9). However, at short time after initialization (1–3 years), CNRM-CM5 has significant predictive skill in parts of the Nordic Seas and the Barents Sea. Thereafter, the skill becomes overall poorer as we move away from the initialization time. In the subpolar North Atlantic the skill becomes higher again at longer lead times (6–8 years). But, in contrast to MPI-ESM-LR, the domains of high skill are only reaching as far north as the southernmost part of the Nordic Seas. This is consistent with the no skill we find for the averaged SST in the eastern Nordic Seas (Fig. 5).
In IPSL-CM5, the subpolar North Atlantic has poor predictive skill at nearly all lead times, in contrast to the other two models (Fig. 10). The southern part of the Nordic Seas has high skill at short lead times. Similarly to what was found in MPI-ESM-LR, this region of high skill appears to spread further northward and into the Barents Sea (at lead times 4–6 and 5–7 years). Again, these findings are consistent with the skill for the averaged SST in the eastern Nordic Seas (Fig. 5). The Barents Sea at short lead times has poor skill in contrast to other two models. Possible reasons for the differences in skill among models are discussed in the following section.
3.3 Relationship between SST in the eastern Nordic Seas and AMOC
Matei et al. (2012) has investigated the relation between SST in the subpolar North Atlantic and AMOC (at 26.5°N), and find significant correlations between the two at time lags from 4 to 10 years. Matei et al. (2012) therefore suggested that in their decadal prediction system, the SST skill in the subpolar region at longer lead times is a consequence of initialization AMOC variability, while the SST skill at shorter lead times can be attributed to persistence. These findings supports that skill at long lead time is a delayed response to ocean circulation (advective time lag). In the present study, we also find a significant correlation between the AMOC (at 48°N) and SST in the eastern Nordic Seas for MPI-ESM-LR and IPSL-CM5, where AMOC is leading with 5 and 1–2 years (Fig. 11), respectively. The time lag between the two appears to be related to the timing of predictive skill in the southeastern Nordic Seas for MPI-ESM-LR (Fig. 8, lead time 4–6 years) and IPSL-CM5 (Fig. 10, lead time 2–4 years). Regarding CNRM-CM5, there is no significant correlations between AMOC and SST in the eastern Nordic Seas (Fig. 11), consistent with no SST skill in the eastern Nordic Seas (Fig. 5). The AMOC-SST relationships (Fig. 11) come from the non-initialized historical experiments that are the basis for the hindcast experiments for MPI-ESM-LR and IPSL-CM5 (as described in Sect. 2.2). Examining the cross-correlation with other ensemble members from the historical experiment shows that the AMOC-SST relationship is different from one ensemble member to another.
Cross-correlation between AMOC at 48°N and SST in the eastern Nordic Seas for the period 1961–2010 based on ensemble members from the historical+ runs from the CMIP5 models. The legend denotes which model and ensemble member (given in the parentheses). The time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation. The significance level is shown by the dashed lines
4 Discussion
We have investigated predictive skill of SST in the Nordic Seas and Barents Sea, with a particular focus on the eastern Nordic Seas, based on initialized hindcasts with three coupled climate models. The previous section showed that the predictive skill differs among the three models. In this section we are firstly discussing possible reasons for why the predictive skill differ, and then secondly we discuss more closely the characteristics of the model (MPI-ESM-LR) that showed the most promising results in the previous section.
4.1 Potential sources (causes) for the spread in predictive skill among models
A robust prediction would ideally require that the predictive skill in the eastern Nordic Seas is high and similar across different models. However, this is not the case in the present study. There are several reasons that could lead to these differences, such as the different horizontal resolution of the models. There appears to be a link between the resolution and the SST skill of the three models. MPI-ESM-LR is the model with the highest resolution of the three models, and is also the one showing the most promising results (Figs. 5, 8). IPSL-CM5, on the other hand, has the lowest resolution among the three, a poor skill in the subpolar region, no robust skill for the averaged SST in the eastern Nordic Seas, and a largely overestimated sea ice cover in comparison to the two other models (Figs. 5, 10). CNRM-CM5 has an intermediate resolution compared to the other two models. Also this model has no robust skill for averaged SST, but it has skill in the subpolar region (Figs. 5, 9).
Another source for the differences among the models that could limit the SST skill is the initialization process. The three models in this study use different initialization techniques for their decadal hindcast experiments. Initialization is one of the important challenges to the decadal climate prediction (Meehl et al. 2014). The predictive skill in IPSL-CM5 is fairly different than in the other two models. This model uses initialization of SST only. This could imply that an initialization not taking into account subsurface variability and salinity is not enough to get ocean dynamics correct. In addition, IPSL-CM5 has no initialization of SST where the sea ice concentration is higher than 50 % (Swingedouw et al. 2013), e.g., the Barents Sea in wintertime, which could also contribute to the poor skill.
Systematic model errors are a major challenge in climate predictions. We here assess two important aspects of the climate at northern high latitudes in the models, which might influence the skill of SST in the Nordic Seas and the Barents Sea: the sea ice cover and the pathway of Atlantic Water. In the following we discuss the mean and variance of the sea ice concentration and SST in the three models based on the historical+ runs (Figs. 12, 13, respectively). For the SST discussion, we also compare the results with the hindcast experiments, as SST is the key variable in this study. We note that skill is not only related to how accurate the simulated mean state is. The variability and realism of various processes and mechanisms are also important for models’ predictive capacity.
Winter sea ice concentration (SIC) from HadISST data and three CMIP5 models for the period 1961–2010. The colour shows standard deviation (std), whereas the single black curve shows where the SIC is equal to 10 %. The models are represented by one ensemble member from the historical+ runs to exemplify the typical variance in the runs
Winter SST from HadISST data and three CMIP5 models for the period 1961–2010. The colour shows standard deviation (std), whereas the two black curves are isolines for 2 and 6 °C. The models are represented by one ensemble member from the historical+ runs (left) and hindcasts (right) to exemplify the typical variance in the runs. Only one hindcast period is chosen here (time length of 10 years)
The sea ice cover in IPSL-CM5 is expanding too far south during wintertime compared to observed sea ice, and high variance in the sea ice is therefore found in the central and eastern part of the Nordic Seas where the sea ice edge is located (Fig. 12). In the Barents Sea, IPSL-CM5 clearly differs from the two other models, since the region is almost completely sea ice covered in wintertime, and therefore only allows for very small changes in SST (Fig. 13). The large sea ice cover in this model is consistent with the Atlantic Meridional Overturning Circulation being weaker than the observation-based estimate and also compared to other CMIP5 models (Escudier et al. 2013; Zhang and Wang 2013). Furthermore, with an earlier version of IPSL-CM, it has been shown that the North Atlantic Current subducts in the subpolar North Atlantic due to an overly fresh surface layer in the North Atlantic region (Mignot and Frankignoul 2010; Langehaug et al. 2012). After travelling at subsurface, Atlantic Water emerges in the Nordic Seas. This subduction could be one suggestion for why we find poor skill in the subpolar North Atlantic in IPSL-CM5. However, unrealistic location of the convection in the subpolar region (Langehaug et al. 2012), limited initialization and low resolution, as mentioned above, or too weak nudging (Sect. 2.2) could also be possible reasons for the poor skill in the subpolar region. On the other hand, a recent study using the IPSL-CM5 hindcasts do find potential predictability of AMOC (Swingedouw et al. 2013), which might explain some of the skill that we find in Nordic Seas.
CNRM-CM5 is more similar to the observed sea ice and SST than IPSL-CM5 (Figs. 12, 13). However, the extent in CNRM-CM5 advances too far eastward in the southern part of Nordic Seas compared to observations; the isoline for 10 % sea ice concentration is located east of Iceland in the model, whereas it is located west of Iceland in HadISST data (Fig. 12, left panels). This overestimation of sea ice could obscure the SST signals coming from the south. In addition, the oceanic heat transport from the Nordic Seas and into the Barents Sea is weak in this model in comparison with observed values (Sandø et al. 2014).
Furthermore, CNRM-CM5 has the largest difference of the three models regarding SST variance in the Nordic Seas between the historical+ run and initialized hindcast experiment (Fig. 13, compare left and right panel for CNRM-CM5), where SST variance is greatly enhanced northeast of Iceland in the hindcast experiment. Note that Fig. 13 (right panel) only shows the SST variance for the last hindcast, i.e., the hindcast starting in 2001. Interestingly, this region also coincides with the most skilful region in the Nordic Seas at lead time 1–3 years (Fig. 9), and one could speculate whether the SST skill is enhanced by the change in the SST variance due to the initialization of the model. However, Germe at el. (2014) describe differences between the historical and hindcast experiments for CNRM-CM5. They find that the historical experiment has less sea ice northeast of Iceland in the period after 1987 compared to period prior to 1987, which is consistent with the observational record. On the other hand, a similar reduction in the sea ice extent northeast of Iceland was not seen in the hindcast experiment (Germe et al. 2014). The enhanced SST variance northeast of Iceland in the hindcast experiment could therefore simply be due to co-location of the sea ice edge northeast of Iceland, and not due to the initialization of temperature and salinity.
MPI-ESM-LR compares similarly to observed sea ice and SST as CNRM-CM5, although these two models also have differences between them with MPI-ESM-LR being generally warmer than CNRM-CM5 (Figs. 12, 13). However, MPI-ESM-LR is the one out of the three models showing the highest predictive capacity of SST for a broader region (subpolar region, Nordic Seas, and Barents Sea) for the period 1961–2010 (Figs. 5, 8). In particular, on longer lead times, only MPI-ESM-LR shows SST skill along the pathway of the Atlantic Water all the way from the subpolar North Atlantic to the Barents Sea. In the following, the discussion is therefore concentrated on MPI-ESM-LR.
4.2 Predictive capacity of MPI-ESM-LR
Previous studies find predictive skill for SST in the subpolar region at lead times up to a decade with MPI hindcasts experiment, but the persistence forecast beats the hindcasts at short lead time (Matei et al. 2012). Likewise, multi-model ensembles show predictive skill for the ocean surface in the North Atlantic up to a decade (Hazeleger et al. 2013; Bellucci et al. 2015). Consistently, MPI-ESM-LR used herein also shows predictive skill in large parts of the northeast subpolar region up to lead times of 6–8 years (Fig. 8). Furthermore, another study using sea surface salinity from MPI-ESM-LR with yearly initialization also shows predictive skill up to decade in the subpolar region (Lohmann et al., in preparation).
Moving further north, to the Nordic Seas, MPI-ESM-LR shows skill in predicting both sea surface temperature (Fig. 8) and salinity (Lohmann et al., in preparation) along the pathway of Atlantic Water at longer lead times. Since skill is found both for sea surface temperature and salinity, it indicates that the skill is caused by ocean advection. The northward spread of skilful regions is consistent with what is known from observational studies; ocean surface temperature and salinity anomalies progress northward as they are carried by the mean flow from the subpolar North Atlantic and towards the Arctic Ocean (e.g., Holliday et al. 2008; Eldevik et al. 2009; Årthun and Eldevik 2016). Based on both observations and a tracer simulation, Gao et al. (2005) demonstrated that the transit time is about 5 years during the 1970s for a passive tracer originating from the Irish Sea (eastern North Atlantic) to reach the Barents Sea. Starting from the entrance of the Nordic Seas and considering thermohaline properties, the travel time reduces to 1–3 years (Eldevik et al. 2009). Similarly, Årthun and Eldevik (2016) finds a travel time of about 3 years for SST anomalies propagating the same distance. The travel time through the eastern Nordic Seas in MPI-ESM-LR can be estimated from the spatial maps of predictive skill to about 2 years (Fig. 7; lead time 3–5 and 5–7 years), which is comparable to observations.
As MPI-ESM-LR appears to be the more adequate model to predicting SST in the Nordic and Barents Seas, we also show predictive skill for the Barents Sea ice cover (assessed against HadISST; Fig. 14). Similar to the anomaly correlation coefficient for the averaged SST in the eastern Nordic Seas, the correlation for the sea ice in the Barents Sea is highest at short lead time and then increases at longer lead times, with peak correlation at 6–8 years lead time. Although none of the correlations are significant, the result point in the same direction as recent studies. These studies highlight the potential of predicting the sea ice in the Barents Sea a couple of year ahead using heat transports through the Barents Sea Opening as a predictor (Schlichtholz 2011; Årthun et al. 2012; Smedsrud et al. 2013; Onarheim et al. 2015).
Anomaly correlation coefficient of winter sea ice area in the Barents Sea for MPI-ESM-LR: the solid blue line show the correlation between the ensemble mean of the hindcasts and HadISST data. For comparison, also the ensemble mean of the non-initialised runs (historical+ runs) and the persistence forecast are shown. At each lead time, the time series are smoothed by a 3 year-moving average and the linear trend is subtracted prior to correlation
5 Conclusions
This study is based on initialized hindcasts for the period 1961–2010 with three coupled climate models. The maybe most promising results are related to one model, MPI-ESM-LR, which shows aspects of SST predictability in the eastern Nordic Seas on longer lead times, i.e., 7–10 years after the initialization. The skill at these lead times beats the skill of a persistence forecast, underlining the potential role of ocean circulation in bringing predictability to the Nordic Seas and the Barents Sea. Regions of high skill propagate from the subpolar North Atlantic towards the Barents Sea as forecast time progresses, similar to observed ocean temperature anomalies. This appears to be a source for skill on interannual time scale in this region.
In the other two models, the northward propagation of skilful regions as forecast time progresses is found to a varying and lesser degree. In IPSL-CM, the subpolar North Atlantic shows no skill, but skilful regions is found between the entrance to the Nordic Seas and the entrance to the Barents Sea (where the model sea ice edge is located). In CNRM-CM5, there is northward propagation of skill from the subpolar North Atlantic, similar to MPI-ESM-LR, but the skill does not extend beyond the southern part of the Nordic Seas. The reason for model differences such as these, and how they translate into skill or lack thereof, needs to be better understood to improve future decadal predictions.
For all models, skilful regions are found in parts of the Nordic and Barents Seas 1–3 years after the initialization (regions are model dependent). However, for longer lead times we generally find that the predictive skill of SST in the Nordic Seas and Barents Sea is more limited than the relatively high skill that appears relatively robust for the subpolar North Atlantic (e.g., Matei et al. 2012; Hazeleger et al. 2013; the IPSL-CM5 is neither associated with skill in the subpolar North Atlantic). Large areas even display significant negative correlations with observations, particularly in the Nordic Seas. This underlines the need for a better understanding of the mechanisms and processes giving rise to skill in the Nordic Seas and the Barents Sea. As an example, a recent study argues that realistic eddy fluxes and volume of Atlantic Water in the Lofoten Basin are needed in climate models in order to better represent the transport of Atlantic Water into the Arctic (Chafik et al. 2015).
There are several factors that can limit predictive skill of SST in the Nordic Seas and the Barents Sea: insufficient horizontal resolution, an imperfect initialization technique, and model biases, such as an unrealistic sea ice cover. For instance, an overestimation of sea ice in the Barents Sea would mute SST variance, and hence, predictions would not be useful for that region. In order to improve the predictive skill of climate models it is essential to reduce model biases and improve the representation of mechanisms and processes relevant for predictability. Regarding SST in the Nordic Seas and the Barents Sea, it appears essential to simulate a realistic poleward propagation of SST anomalies. More specifically, this means a continuous propagation of anomalies from the subpolar North Atlantic to the Fram Strait along a realistic pathway and with a realistic time scale of propagation.
References
Årthun M, Eldevik T (2016) On anomalous ocean heat transport toward the Arctic and associated climate predictability. J Clim. doi:10.1175/JCLI-D-15-0448.1
Årthun M, Eldevik T, Smedsrud LH, Skagseth Ø, Ingvaldsen RB (2012) Quantifying the influence of Atlantic heat on Barents Sea ice variability and retreat. J Clim 25:4736–4743. doi:10.1175/JCLI-D-11-00466.1
Balmaseda MA, Mogensen K (2010) Evaluation of ERA-Interim forcing fluxes from an ocean perspective. ERA Report Series No. 6. ECMWF: Reading, UK
Bellucci A, Haarsma R, Gualdi S, Athanasiadis PJ, Caian M, Cassou C, Fernandez E, Germe A, Jungclaus J, Kröger J, Matei D, Müller W, Pohlmann H, y Mélia DS, Sanchez E, Smith D, Terray L, Wyser K, Yang S (2015) An assessment of a multi-model ensemble of decadal climate predictions. Clim Dyn 44:2787–2806. doi:10.1007/s00382-014-2164-y
Caron L, Jones C, Doblas-Reyes F (2014) Multi-year prediction skill of Atlantic hurricane activity in CMIP5 decadal hindcasts. Clim Dyn 42:2675–2690. doi:10.1007/s00382-013-1773-1
Cavalieri DJ, Parkinson CL, Gloersen P, Zwally HJ (1996) updated yearly. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data. Boulder, Colorado USA: National Snow and Ice Data Center. Digital media
Chafik L, Nilsson J, Skagseth Ø, Lundberg P (2015) On the flow of Atlantic water and temperature anomalies in the Nordic Seas towards the Arctic Ocean. J Geophys Res Oceans. doi:10.1002/2015JC011012
Chepurin GA, Carton JA (2012) Subarctic and Arctic sea surface temperature and its relation to ocean heat content 1982-2010. J Geophys Res Oceans. doi:10.1029/2011JC007770
Counillon F, Bethke I, Keenlyside N, Bentsen M, Bertino L, Zheng F (2014) Seasonal-to-decadal predictions with the ensemble Kalman filter and the Norwegian Earth System Model: a twin experiment. Tellus A 66:21074. doi:10.3402/tellusa.v66.21074
Deshayes J, Curry R, Msadek R (2014) CMIP5 model intercomparison of freshwater budget and circulation in the North Atlantic. J Clim 27:3298–3317. doi:10.1175/JCLI-D-12-00700.1
Drinkwater KF, Miles M, Medhaug I, Otterå OH, Kristiansen T, Sundby S, Gao Y (2014) The Atlantic Multidecadal Oscillation: its manifestations and impacts with special emphasis on the Atlantic region north of 60 N. J Mar Syst 133:117–130. doi:10.1016/j.jmarsys.2013.11.001
Dufresne J, Foujols M, Denvil S et al (2013) Climate change projections using the IPSL-CM5 Earth System Model: from CMIP3 to CMIP5. Clim Dyn 40:2123–2165. doi:10.1007/s00382-012-1636-1
Eldevik T, Nilsen JEO, Iovino D, Anders Olsson K, Sando AB, Drange H (2009) Observed sources and variability of Nordic seas overflow. Nat Geosci 2:406–410
Escudier R, Mignot J, Swingedouw D (2013) A 20-year coupled ocean-sea ice-atmosphere variability mode in the North Atlantic in an AOGCM. Clim Dyn 40:619–636. doi:10.1007/s00382-012-1402-4
Gangstø R, Weigel A, Liniger M, Appenzeller C (2013) Methodological aspects of the validation of decadal predictions. Clim Res 55:181–200
Gao Y, Drange H, Bentsen M, Johannessen OM (2005) Tracer-derived transit time of the waters in the eastern Nordic Seas. Tellus B 57:332–340. doi:10.1111/j.1600-0889.2005.00153.x
Germe A, Chevallier M, y Mélia DS, Sanchez-Gomez E, Cassou C (2014) Interannual predictability of Arctic sea ice in a global climate model: regional contrasts and temporal evolution. Clim Dyn 43:2519–2538. doi:10.1007/s00382-014-2071-2
Giorgetta MA, Jungclaus J, Reick CH et al (2013) Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J Adv Model Earth Syst 5:572–597. doi:10.1002/jame.20038
Häkkinen S, Rhines PB, Worthen DL (2011) Warm and saline events embedded in the meridional circulation of the northern North Atlantic. J Geophys Res Oceans. doi:10.1029/2010JC006275
Hátún H, Sandø AB, Drange H, Hansen B, Valdimarsson H (2005) Influence of the Atlantic subpolar gyre on the thermohaline circulation. Science 309:1841–1844
Hazeleger W, Wouters B, van Oldenborgh GJ, Corti S, Palmer T, Smith D, Dunstone N, Kröger J, Pohlmann H, von Storch J (2013) Predicting multiyear North Atlantic Ocean variability. J Geophys Res Oceans 118:1087–1098. doi:10.1002/jgrc.20117
Holliday NP, Hughes SL, Bacon S, Beszczynska-Möller A, Hansen B, Lavín A, Loeng H, Mork KA, Østerhus S, Sherwin T, Walczowski W (2008) Reversal of the 1960s to 1990s freshening trend in the northeast North Atlantic and Nordic Seas. Geophys Res Lett. doi:10.1029/2007GL032675
IPCC (2013) Climate change 2013: the physical science basis. In: Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds). Contribution of Working Group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, p 1535. doi:10.1017/CBO9781107415324
Jungclaus JH, Fischer N, Haak H, Lohmann K, Marotzke J, Matei D, Mikolajewicz U, Notz D, von Storch JS (2013) Characteristics of the ocean simulations in MPIOM, the ocean component of the MPI-Earth system model. J Adv Model Earth Syst 5:422–446. doi:10.1002/jame.20023
Kim H, Webster PJ, Curry JA (2012) Evaluation of short-term climate change prediction in multi-model CMIP5 decadal hindcasts. Geophys Res Lett. doi:10.1029/2012GL051644
Langehaug HR, Rhines PB, Eldevik T, Mignot J, Lohmann K (2012) Water mass transformation and the North Atlantic Current in three multicentury climate model simulations. J Geophys Res Oceans. doi:10.1029/2012JC008021
Langehaug HR, Geyer F, Smedsrud LH, Gao Y (2013) Arctic sea ice decline and ice export in the CMIP5 historical simulations. Ocean Model 71:114–126. doi:10.1016/j.ocemod.2012.12.006
Loeng H, Drinkwater K (2007) An overview of the ecosystems of the Barents and Norwegian Seas and their response to climate variability. Deep Sea Res Part II 54:2478–2500. doi:10.1016/j.dsr2.2007.08.013
Lohmann K, Matei D, Bersch M, Jungclaus JH. Predictability of upper-ocean salt content in the subpolar North Atlantic and Nordic Seas—a multi-model study. In preparation for Climate Dynamics
Matei D, Pohlmann H, Jungclaus J, Müller W, Haak H, Marotzke J (2012) Two tales of initializing decadal climate prediction experiments with the ECHAM5/MPI-OM Model. J Clim 25:8502–8523. doi:10.1175/JCLI-D-11-00633.1
Mauritzen C (1996) Production of dense overflow waters feeding the North Atlantic across the Greenland–Scotland Ridge. Part 1: evidence for a revised circulation scheme. Deep Sea Res Part I 43:769–806. doi:10.1016/0967-0637(96)00037-4
Meehl GA, Goddard L, Boer G et al (2014) Decadal climate prediction: an update from the trenches. Bull Am Meteorol Soc 95:243–267. doi:10.1175/BAMS-D-12-00241.1
Mignot J, Frankignoul C (2010) Local and remote impacts of a tropical Atlantic salinity anomaly. Clim Dyn 35:1133–1147. doi:10.1007/s00382-009-0621-9
Mignot J, Khodri M, Frankignoul C, Servonnat J (2011) Volcanic impact on the Atlantic Ocean over the last millennium. Clim Past 7:1439–1455. doi:10.5194/cp-7-1439-2011
Mignot J, Swingedouw D, Deshayes J, Marti O, Talandier C, Séférian R, Lengaigne M, Madec G (2013) On the evolution of the oceanic component of the IPSL climate models from CMIP3 to CMIP5: A mean state comparison. Ocean Model 72:167–184. doi:10.1016/j.ocemod.2013.09.001
Msadek R, Delworth TL, Rosati A, Anderson W, Vecchi G, Chang Y, Dixon K, Gudgel RG, Stern W, Wittenberg A, Yang X, Zeng F, Zhang R, Zhang S (2014) Predicting a decadal shift in North Atlantic climate variability using the GFDL forecast system. J Clim 27:6472–6496. doi:10.1175/JCLI-D-13-00476.1
Müller WA, Baehr J, Haak H, Jungclaus JH, Kröger J, Matei D, Notz D, Pohlmann H, von Storch JS, Marotzke J (2012) Forecast skill of multi-year seasonal means in the decadal prediction system of the Max Planck Institute for Meteorology. Geophys Res Lett. doi:10.1029/2012GL053326
Nilsen JEØ, Falck E (2006) Variations of mixed layer properties in the Norwegian Sea for the period 1948–1999. Prog Oceanogr 70:58–90. doi:10.1016/j.pocean.2006.03.014
O’Mahony M (1986) Sensory evaluation of food: statistical methods and procedures. Dekker, New York
Onarheim IH, Eldevik T, Årthun M, Ingvaldsen RB, Smedsrud LH (2015) Skillful prediction of Barents Sea ice cover. Geophys Res Lett. doi:10.1002/2015GL064359
Overland JE, Wang M, Salo S (2008) The recent Arctic warm period. Tellus A 60:589–597. doi:10.1111/j.1600-0870.2008.00327.x
Polyakov IV, Beszczynska A, Carmack EC et al (2005) One more step toward a warmer Arctic. Geophys Res Lett. doi:10.1029/2005GL023740
Pyper BJ, Peterman RM (1998) Comparison of methods to account for autocorrelation in correlation analyses of fish data. Can J Fish Aquat Sci 55:2127–2140. doi:10.1139/f98-104
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atmos. doi:10.1029/2002JD002670
Reynolds RW, Smith TM, Liu C, Chelton DB, Casey KS, Schlax MG (2007) Daily high-resolution-blended analyses for sea surface temperature. J Clim 20:5473–5496. doi:10.1175/2007JCLI1824.1
Robson JI, Sutton RT, Smith DM (2012) Initialized decadal predictions of the rapid warming of the North Atlantic Ocean in the mid 1990s. Geophys Res Lett. doi:10.1029/2012GL053370
Robson J, Sutton R, Smith D (2013) Predictable climate impacts of the decadal changes in the ocean in the 1990s. J Clim 26:6329–6339. doi:10.1175/JCLI-D-12-00827.1
Sandø AB, Gao Y, Langehaug HR (2014) Poleward ocean heat transports, sea ice processes, and Arctic sea ice variability in NorESM1-M simulations. J Geophys Res Oceans 119:2095–2108. doi:10.1002/2013JC009435
Sarafanov A, Falina A, Sokov A, Demidov A (2008) Intense warming and salinification of intermediate waters of southern origin in the eastern subpolar North Atlantic in the 1990s to mid-2000s. J Geophys Res Oceans. doi:10.1029/2008JC004975
Schlichtholz P (2011) Influence of oceanic heat variability on sea ice anomalies in the Nordic Seas. Geophys Res Lett 38(5):L05705. doi:10.1029/2010GL045894
Smedsrud LH, Sirevaag A, Kloster K, Sorteberg A, Sandven S (2011) Recent wind driven high sea ice area export in the Fram Strait contributes to Arctic sea ice decline. Cryosphere 5:821–829
Smedsrud LH, Esau I, Ingvaldsen RB, Eldevik T, Haugan PM, Li C, Lien VS, Olsen A, Omar AM, Otterå OH, Risebrobakken B, Sandø AB, Semenov VA, Sorokina SA (2013) The role of the Barents Sea in the Arctic Climate System. Rev Geophys 51:415–449. doi:10.1002/rog.20017
Smith DM, Cusack S, Colman AW, Folland CK, Harris GR, Murphy JM (2007) Improved surface temperature prediction for the coming decade from a global climate model. Science 317:796–799. doi:10.1126/science.1139540
Sutton RT, Allen MR (1997) Decadal predictability of North Atlantic sea surface temperature and climate. Nature 388:563–567
Swift JH (1986) The Arctic waters. In: Hurdle BG (ed) The Nordic Seas. Springer, New York, pp 129–154. doi:10.1007/978-1-4615-8035-5_5
Swingedouw D, Mignot J, Labetoulle S, Guilyardi E, Madec G (2013) Initialisation and predictability of the AMOC over the last 50 years in a climate model. Clim Dyn 40:2381–2399. doi:10.1007/s00382-012-1516-8
Taylor KE, Stouffer RJ, Meehl GA (2012) An Overview of CMIP5 and the Experiment Design. Bull Am Meteorol Soc 93:485–498. doi:10.1175/BAMS-D-11-00094.1
Voldoire A, Sanchez-Gomez E, y Mélia DS et al (2013) The CNRM-CM5.1 global climate model: description and basic evaluation. Clim Dyn 40:2091–2121. doi:10.1007/s00382-011-1259-y
Yeager S, Karspeck A, Danabasoglu G, Tribbia J, Teng H (2012) A decadal prediction case study: late twentieth-century North Atlantic Ocean heat content. J Clim 25:5173–5189. doi:10.1175/JCLI-D-11-00595.1
Zhang L, Wang C (2013) Multidecadal North Atlantic sea surface temperature and Atlantic meridional overturning circulation variability in CMIP5 historical simulations. J Geophys Res Oceans. doi:10.1002/jgrc.20390
Acknowledgments
The research leading to these results have received funding from the European Union 7th Framework Programme (FP7 2007–2013) under Grant agreement n.308299 (HRL, DM, KL, YG). HRL and TE acknowledge support from the NFR EPOCASA project (Grant 229774) and also the NFR NORTH project (Grant 229763). In addition, this study was also funded by the German BMBF RACE project (DM). We thank the two reviewers for constructive comments, and also Francois Counillon and Laurent Bertino for useful discussions. Thanks also to Didier Swingedouw for providing IPSL-CM5 initialization data and model data. We acknowledge the NSIDC for providing satellite data of sea ice concentration and the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP. We also thank the climate modeling groups (listed in Table 1 of this paper) for producing and making available their model output. For CMIP the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organisations for Earth System Science Portals.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Langehaug, H.R., Matei, D., Eldevik, T. et al. On model differences and skill in predicting sea surface temperature in the Nordic and Barents Seas. Clim Dyn 48, 913–933 (2017). https://doi.org/10.1007/s00382-016-3118-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3118-3