Abstract
A warming hiatus is a period of relatively little change in global mean surface air temperatures (SAT). Many studies have attributed the current warming hiatus to internal climate variability (ICV). But there is less work on discussion of the dynamics about how these ICV modes influence cooling over land in the Northern Hemisphere (NH). Here we demonstrate the warming hiatus was more significant over the continental NH. We explored the dynamics of the warming hiatus from a global perspective and investigated the mechanisms of the reversing from accelerated warming to hiatus, and how ICV modes influence SAT change throughout the NH land. It was found that these ICV modes and Arctic amplification can excite a decadal modulated oscillation (DMO), which enhances or suppresses the long-term trend on decadal to multi-decadal timescales. When the DMO is in an upward (warming) phase, it contributes to an accelerated warming trend, as in last 20 years of twentieth-century. It appears that there is a downward swing in the DMO occurring at present, which has balanced or reduced the radiative forced warming and resulted in the recent global warming hiatus. The DMO modulates the SAT, in particular, the SAT of boreal cold months, through changes in the asymmetric meridional and zonal thermal forcing (MTF and ZTF). The MTF represents the meridional temperature gradients between the mid- and high-latitudes, and the ZTF represents the asymmetry in temperatures between the extratropical large-scale warm and cold zones in the zonal direction. Via the different performance of combined MTF and ZTF, we found that the DMO’s modulation effect on SAT was strongest when both weaker (stronger) MTF and stronger (weaker) ZTF occurred simultaneously. And the current hiatus is a result of a downward DMO combined with a weaker MTF and stronger ZTF, which stimulate both a weaker polar vortex and westerly winds, along with the amplified planetary waves, thereby facilitating southward invasion of cold Arctic-air and promoting the blocking formation. The results conclude that the DMO can not only be used to interpret the current warming hiatus, it also suggests that global warming will accelerate again when it swings upward.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
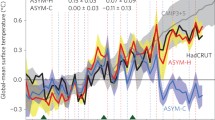
The carbon dioxide in the Earth’s atmosphere has increased monotonically over the past 100 years (IPCC 2013) and is considered the main cause of global warming for that period. Although this increase in atmospheric carbon dioxide has been associated with increasing temperatures, the global mean surface air temperature (SAT) has leveled off since 1998, a phenomenon known as a warming hiatus (IPCC 2013; Kosaka and Xie 2013; England et al. 2014; Meehl et al. 2014; Trenberth et al. 2014; Dai et al. 2015; Steinman et al. 2015; Guan et al. 2015) (Fig. 1a). Furthermore, there was another significant warming hiatus during the period of 1940–1975 (Fig. 1a; Beamish et al. 1998; Klyashtorin 1998; Klyashtorin and Lyubushin 2007; Van Loon et al. 2007; Wyatt and Curry 2014), which was a longer hiatus period than the recent warming hiatus. The warming hiatus has attracted great attention worldwide because it appears to contradict the theory of human-induced global warming (IPCC 2013). As the previous projection by the scientific community, the global warming will go on in the first two decades of twenty-first century (IPCC 2007). However, the unexpected warming hiatus declared a failure of the projection and a doubt to the credibility of climate science. Hitherto, many explanations on the warming hiatus have been presented by the scientific community, which increased the knowledge of hiatus process.
a The SAT anomaly time series relative to the 1961–1990 global annual mean for land and ocean (black), land (red), ocean (blue), and SST (green). The marks at the line indicate the recent warming hiatus period. b Same as a but for the NH cold season; only the SAT anomalies over land (red) and ocean (blue) are shown, and the black dashed lines are the linear trend for 2001–2013. Note that the boreal warm season runs from May to September, while the cold season runs from November to the following March
Previous studies have suggested that the warming hiatus was mainly induced by internal climate variability (ICV), especially the oceanic ICV. Steinman et al. (2015) concluded that the hiatus has been induced primarily by a strong negative-trend in Pacific multidecadal variability, with only a small contribution from Atlantic variability. However, the Pacific multidecadal variability defined by Steinman et al. (2015) did not follow the classic ICV modes that are generally used to represent the Pacific variability (Kravtsov et al. 2015). The suggested classic Pacific variability related with the recent warming hiatus mainly were the La-Niña-like cooling induced by accelerated trade winds (Kosaka and Xie 2013; England et al. 2014), and a negative phase of the Pacific Decadal Oscillation (PDO), or (more generally) the Interdecadal Pacific Oscillation (IPO) (Dai et al. 2015; Meehl et al. 2014; Trenberth et al. 2014). The Atlantic variability represented by the Atlantic Multidecadal Oscillation (AMO) plays a significant role in the variability of the Northern Hemisphere (NH) or global mean temperature (Kravtsov and Spannagle 2008; Wyatt et al. 2012; Tung and Zhou 2013; Wyatt and Curry 2014). As suggested by Wyatt et al. (2012) and Wyatt and Curry (2014), the AMO signal culminates in an opposite signal in the NH temperature about 30 years later via a sequence of atmospheric and lagged oceanic teleconnections. These studies indicate that the previous warming hiatus (about 1940–1975) was significantly related with the AMO signal. The atmospheric ICV over the Atlantic is generally represented by the North Atlantic Oscillation (NAO) (Huang et al. 1998; Higuchi et al. 1999; Wyatt et al. 2012), which is suggested to have contributed to the recent warming hiatus (Guan et al. 2015). In addition, from an energy balance perspective, the hiatus may have been caused by heat transported to deeper layers of the Atlantic and Southern oceans (Chen and Tung 2014).
Exactly, most of these studies have mainly focused on individual oceanic ICV modes and their influence on global cooling and do not fully describe how these ICV modes have influenced SAT over NH land. The recent cooling over NH land (Cohen et al. 2012) was reversed from the previous enhanced warming, which was probably related to the circulation change over extratropical NH (Huang et al. 2012; Wallace et al. 2012; He et al. 2014; Huang et al. 2016a; Guan et al. 2015; Huang et al. 2016b). As suggested by Wallace et al. (1995) and He et al. (2014), the land-sea thermal contrast can excite feedbacks related with circulation and induces the transition between the pattern of “cold ocean and warm land” (COWL) and “warm ocean and cold land” (WOCL). In addition, some studies suggest the recent cold winters in Eurasian and North America were influenced by the accelerated Arctic warming and sea ice decline (Frolov et al. 2009; Outten and Esau 2012; Zakharov 2013; Cohen et al. 2014; Mori et al. 2014; Screen and Simmonds 2014; Xie et al. 2015). Response to these thermal forcing variation, the circulation over extratropical NH represented by the atmospheric pressure field has also changed, which was suggested to contribute much to the previous enhanced wintertime warming and recent warming hiatus (Wallace et al. 2012; Guan et al. 2015).
This body of literature greatly promoted the understanding of ocean’s effect on the process of hiatus, but the hiatus is also a significant phenomenon over land, especially in mid-to high-latitude of North Hemisphere. So how the cooling over continental NH developed is a key question to understand the recent warming hiatus. In this study, we explore the dynamics of the warming hiatus from a hemispheric perspective and examine the combined effects of ICV modes and Arctic climate on SAT over NH land. The recorded sea surface temperatures (SST) suggest a bias toward colder temperatures in recent decades, and which has induced the corresponding SAT over the oceans to also become colder (Karl et al. 2015). However, the bias in SAT over land was small, especially when averaged over a large scale (Karl et al. 2015; Jones 2016). Our results show that approximately one-half of the recent hiatus in global mean SAT was accounted by cooling over land. We attempt to address how the ICV modes and Arctic amplification induced the hiatus and examine how the IPO or the PDO, the AMO, and other decadal ICV modes influence the hiatus, especially the cooling over the continental NH.
The paper is arranged as follows. The details of the datasets and the methodology used are given in Sect. 2. In Sect. 3, a theoretical model used in this study is introduced. The global pattern of the warming hiatus and the relative contribution to hiatus are presented in Sect. 4. Section 5 discussed the decadal modulated oscillation. Section 6 examined the circulation change responding to thermal forcing during the warming hiatus. Section 7 presents circulation abrupt shift under thermal forcing change. Discussion and conclusion are presented in Sect. 8.
2 Data and methods
2.1 Temperature
The GISTEMP dataset from the National Aeronautics and Space Administration Goddard Institute for Space Studies (GISS) has a resolution of 2° × 2° and covers the period from 1880 to the present day (Hansen et al. 2010). The Extended Reconstructed Sea Surface Temperature (ERSST) dataset is provided by National Oceanic and Atmospheric Administration (NOAA)/OAR/ESRL PSD, from their Web site at http://www.esrl.noaa.gov/psd/data/gridded/data.noaa.ersst.html. These data are version 4, and begins in January 1854 continuing to the present (Huang et al. 2015). The Nino3.4, PDO, and AMO indexes were calculated using the ERSST data. Furthermore, the Merged Land–Ocean Surface Temperature Analysis (MLOST) (Smith et al. 2008) and HadCRUT4 (Morice et al. 2012) datasets were compared with GISTEMP dataset to assess the uncertainty of SAT data (Fig. S1). The SAT time series for low- and mid- latitudes were very consistent among the three datasets, especially for the period from about 1960 onward (Fig. S1 a, b). The discrepancies among the three datasets were larger for high-latitudes, because the MLOST and HadCRUT4 datasets have more missing data over high-latitudes than GISTEMP (Fig. S1c). Therefore, only the results of the GISTEMP dataset were presented in the paper. The SST data from ERSST v3b (Smith et al. 2008) and COBE (Ishii et al. 2005) datasets were compared with ERSST v4 datasets, and showed a colder bias for both the ERSST v3b and COBE datasets during the recent warming hiatus (Fig. S2). The ERSST v4 datasets have been recently corrected and updated (Karl et al. 2015), so only the results from the ERSST v4 dataset were presented in the paper. For more details about these SAT and SST datasets, see the Supplementary Material.
2.2 Oscillation indexes
The Nino3.4 index was the SST averaged over [5°S–5°N, 170°W–120°W] as defined by Trenberth (1997). The PDO index was first empirical orthogonal function (EOF) pattern and associated time series of monthly SST over field [20°N–70°N, 110°E–100°W] with subtracted global mean SST series (Mantua et al. 1997). The AMO index was SST anomalies averaged over field [0°–70°N, 0°–80°W] with the global mean SST was removed (Trenberth and Shea 2006). Furthermore, the oscillation indexes calculated from other SST datasets and definitions were compared with ours to access the uncertainty of the indexes (Fig. S3). The Nino 3.4 indexes calculated from both the HadISST (Rayner et al. 2003) and COBE datasets were very consistent with the results from the ERSST v4 dataset (Fig. S3a). Two methods—removing the global-warming fingerprint represented by the global mean SST or the linear trends series—used in calculations of PDO and AMO indexes were compared (Fig. S3 b, c). The PDO indexes calculated by both methods from the ERSST v4, HadISST combined with OISST (Reynolds et al. 2007), and COBE datasets were also very consistent (Fig. S3b). The AMO indexes calculated by both methods from the ERSST v4, Kaplan SST (Kaplan et al. 1998), and COBE datasets had some differences at the interannual time scale (Fig. S3c). However, they were very consistent at decadal and multi-decadal time scales (Fig. S3c), and therefore had little influence on our results. In addition, the AMO index calculated by a method that removed the spatio-temporal signal of the global-warming fingerprint was also similar when calculated by the method that removed the linear trend series (Kravtsov and Spannagle 2008). Therefore, we only presented the results from the ERSST v4 dataset and used the global mean SST removal method to calculate the PDO and AMO indexes. More details about these oscillation indexes and SST datasets are provided in the Supplementary Material.
2.3 Reanalysis products
The wind speed, geopotential height data were from NCEP/NCAR Reanalysis I (Kalnay et al. 1996), NCEP-DOE Reanalysis II (Kanamitsu et al. 2002), and ERA-interim (Dee et al. 2011) reanalysis product sets. All these reanalysis products have a resolution of 2.5° × 2.5°. But the ERA-interim has many different resolution choices. The NCEP/NCAR Reanalysis I was from 1948 to present, and the other two products were from 1979 to present. Because the reanalysis products are model-based, the modelled outputs may differ from real observations, especially on decadal-plus time scales (Wyatt and Peters 2012; Kravtsov et al. 2014). To access some of the uncertainties in the results based on these reanalysis products, all the results associated with these three products were presented by the ensemble mean of them. Furthermore, the wind speed and geopotential height data from the NOAA–CIRES Twentieth Century Reanalysis V2c (Compo et al. 2011) and the ERA-20C (Hersbach et al. 2015) reanalysis product sets were used to examine the atmospheric dynamics during the previous warming hiatus. The NOAA–CIRES Twentieth Century Reanalysis V2c products have a resolution of 2° × 2°, and are available from 1851 to 2012 (Compo et al. 2011). The ERA-20C products has a resolution of 2° × 2°, but has many different resolution choices, and is available for the period 1900–2010 (Hersbach et al. 2015). All the results associated with these two reanalysis products were also presented by the ensemble mean of them.
2.4 EEMD decomposition
The ensemble empirical mode decomposition (EEMD) method was used in our study. EEMD is an adaptive one-dimensional data analysis method; it is temporally local and therefore can reflect the nonlinear and nonstationary nature of climate data. Climate variability can be split into different oscillatory components with intrinsic timescales, including interannual, decadal and multidecadal extents. The steps followed in the EEMD method are taken from Ji et al. (2014) and are as follows:
-
(1)
Add a white noise series with an amplitude 0.2 times that of the standard deviation of the raw data to the raw data series x(t);
-
(2.1)
Set \(x_{1} (t) = x(t)\) and find the maxima and minima of x1(t), and obtain the upper envelope e u (t) and lower envelope e l (t) using cubic splines to connect the maxima and minima, respectively;
-
(2.2)
Find the local mean \(m(t) = [e_{u} (t) + e_{l} (t)]/2\), and then determine whether m(t) is close to zero (equivalent to the symmetric of the upper and lower envelopes with respect to the zero line) at any location based on the given criterion;
-
(2.3)
If yes, stop the sifting process; otherwise, set \(x_{1} (t) = x(t) - m(t)\) and repeat steps 2.1 to 2.2;
-
(2.4)
In this manner, we obtain the first intrinsic mode function (IMF), and by subtracting it from x(t), we obtain a remainder. If the remainder still contains oscillatory components, we again repeat steps 2.1 to 2.2 but with the new x1(t) as the remainder.
So, each time series is decomposed into different IMFs, which can be expressed as:
where c j (t) represents the jth IMF, which is an amplitude-frequency-modulated oscillatory component, and R n (t) is the residual of data x(t), which is either monotonic or contains only one extreme.
-
(3)
Repeat steps 1 and 2 again and again but with different white noise series added each time and obtain the (ensemble) means for corresponding IMFs of the decompositions as the final result.
In the EEMD calculation as outlined in Ji et al. (2014), the noise added to data has an amplitude that is 0.2 times the standard deviation of the raw data, and the ensemble number is 400. The number of IMFs is 6. A MATLAB EMD/EEMD package with the above stoppage criteria and end treatment is available for download at http://rcada.ncu.edu.tw/research1.htm (Wang et al. 2014).
3 Theoretical model
The model used in this study is governed by the nondimensional quasi-geostrophic barotropic vorticity equation for a sphere (Källén 1981; Charney and DeVore 1979):
where \(\psi\) is the nondimensional streamfunction, \(\psi^{*}\) is the nondimensional streamfunction forcing, t is nondimensional time, \(\nabla^{2}\) is the nondimensional horizontal Laplacian operator, J is the nondimensional Jacobian operator, \(\lambda\) is the longitude, \(\mu\) is the sine of the latitude \((\mu = \sin (\varphi ))\), h is the nondimensional topographic height parameter and k is the nondimensional dissipation rate.
A purely zonal component and two wave components are taken into account in the low-order model for simplicity; thus, we select three spherical harmonics
and truncate the expansions for \(\psi\), \(\psi^{*}\) and \(h\) as follows:
The standardized associated Legendre function is defined as
so that
The flow of the atmosphere is confined in the Northern Hemisphere in the model (i.e., \(\lambda \in [0,2\pi ], \, \mu \in [ 0 , 1 ]\)). Inserting the expansions (2)–(5) into Eq. (1), we can obtain
where
Solving for the equilibrium solution of the system given by Eq. (8), we obtained the following equation using \(\psi_{\text{A}}\)
and
The cubic Eq. (9) shows that we can, at most, have three equilibria for certain values of the forcing parameters. The stability of an equilibrium solution is determined by the characteristic values of the three-order coefficient matrix of the linear perturbation equations resulting from (8), i.e., from
4 Global distribution of the SAT trend and its relative contribution
As shown in Fig. 1, the temperature changes have varied depending on the season, land/sea, and the hemisphere (Wu et al. 2011; Huang et al. 2012; Ji et al. 2014). The change of mean SAT over land is much faster than the ocean, especially in the previous decades before the recent warming hiatus. Although both the land and ocean show the hiatus during recent decades, it shows that the land SAT have been to a higher level after the enhanced warming during 80–90s in last century. Compared with land, the SAT and SST of ocean maintain a relatively moderate warming rate before the recent hiatus period (Fig. 1a). The SAT over NH exhibits the largest warming trend before the recent hiatus, and it also exhibits the most obvious hiatus in recent decades (Fig. 1b). The SAT of land over NH takes an obvious cooling trend in the boreal cold season during recent decades, accompanied by a weak increase of mean SAT of ocean (Fig. 1b).
The linear trends of SAT in the boreal warm and cold season for 2001–2013 are presented in Fig. 2. The apparent differences in the spatial patterns of SAT changes between the warm and cold seasons during the recent hiatus are shown in Fig. 2. There are more cooling regions and larger cooling trends in the boreal cold season than in the warm season during the recent hiatus. The cooling centers in warm season are mainly located in small regions over Eurasia continents and some regions over Pacific (Fig. 2a). Most regions of NH land still show the warming trend in warm season. However, large parts of NH land exhibit the obvious cooling trend in cold season (Fig. 2b). Besides, the cooling over the equatorial central and eastern Pacific (ECEP) (Kosaka and Xie 2013; Dai et al. 2015) is also more significant in cold season (Fig. 2b). Therefore, we confine our analysis to SAT changes in the NH during the boreal cold season.
To quantify the spatial features of the recent hiatus, we calculated the areal weighted relative contribution of the SAT for each grid cell to the global mean cooling or warming trend during the boreal cold season (Fig. 3). The relative contribution identified in Fig. 3 was calculated using Eq. (13). The global mean cooling SAT trend was calculated as \(\sum\nolimits_{i}^{N} {K_{i} \omega_{i} }\), and N is the number of the whole grids whose SAT trends were negative. The same procedure is used to calculate the global mean warming trend. For Table 1, the relative contribution of the regional mean cooling trend to global mean cooling is the sum of the relative contribution of all the grids in a region (Fig. 3). The relative contributions of the regional mean cooling trends to NH, land or ocean were the ratio of the regional mean relative contributions to the average relative contributions over NH, land, and ocean, respectively.
where K i is the SAT trend of grid i, \(\omega_{i} = \cos (\theta_{i} \cdot \pi /180.0)\), θ i is the latitude of the grid, and N is the number of grids whose SAT trend is negative (cooling) or positive (warming), e.g., N is the number of the whole grids whose SAT trend is negative when the SAT trend of the grid i is negative.
Areal weighted relative contribution of the SAT trend in each grid cell to the global mean warming/cooling trend during the boreal cold season for 2001–2013. The relative contribution was calculated using Eq. (13). The blue (red) number in left (right) corner is the global mean cooling (warming) trend in °C per 13 years. The black squares represent the North American (NA), the Eurasian continents (EUA), and the Equatorial Central and Eastern Pacific region (ECEP), respectively
Figure 3 shows that the cooling centers of the recent warming hiatus are mainly located above the Eurasian (EUA) and North American (NA) continents as well as in the ECEP regions. Meanwhile, continued warming centers have been identified over the Arctic, in some regions around the Mediterranean, and over the North Pacific Ocean. The areal weighted global mean warming trend was 0.47 °C per 13 years, which is slightly lower than the global cooling trend of −0.50 °C per 13 years. The EUA and NA continents contributed 18 % (60 %) and 43 % (25 %) to NH (terrestrial) mean cooling, respectively (Table 1). Although the oceanic ICV played a major role in explaining the hiatus (Steinman et al. 2015), the local cooling contribution by the ocean was only 52 % (Table 1), which indicates that 48 % is explained by terrestrial cooling, a figure that should not be ignored.
5 Decadal modulated oscillation
We refer to the ICV modulated components of SAT variation on the decadal to multi-decadal scale as the decadal modulated oscillation (DMO). To examine the DMO components of SAT, we used the EEMD method, which can split the evolution of SAT into long-term trends and oscillation components (Wu et al. 2011; Ji et al. 2014). The long-term warming trend is related primarily to radiative forcing (Wu et al. 2011; Guan et al. 2015), and the oscillation component is thought to be induced mainly by ICV (Wu et al. 2011; Wallace et al. 2012; Guan et al. 2015). The DMO components of the global annual mean SAT and NH cold season mean SAT are presented in Fig. 4a, b respectively. The DMO component is the sum of IMF 3, 4, 5 from the EEMD, and the long-term trend is the IMF 6. The DMO enhances or suppresses the long-term trend on decadal to multi-decadal timescale. The DMO’s magnitude is comparable to that of the long-term trend at the decadal scale (Fig. 4). When the DMO is in an upward (warming) phase, it contributes to an accelerated warming trend, as in 1985–1998. It appears that there is a downward swing in the DMO occurring since about 2000, which has balanced or reduced the radiative forced warming and resulted in the recent global warming hiatus. During the boreal cold season, the DMO’s cooling trend is greater than the long-term warming trend, which is shown as obvious cooling in the mean SAT over the NH (Fig. 4b).
To examine the modulated effect of the oceanic ICV modes on the NH SAT during the cold season, the multiple linear regression (MLR) and EEMD methods were used to create the DMO index. First, the EEMD method was applied to the indices of three classic oceanic modes: the PDO, Nino3.4, AMO, and Arctic Oscillation (AO), respectively. Then, the DMO component of the NH SAT during the cold season (Fig. 4b) was regressed with standardized IMF 3, 4, 5, for each index using a stepwise MLR. The regressed DMO component in Fig. 5 is expressed in Eq. (14). The regression-based approximation of DMO component for NH SAT using PDO, Nino3.4, AMO, and Arctic Oscillation (AO) indexes can explain 88 % of its variance during the boreal cold season (Fig. 5). The three classic oceanic ICV modes—PDO, Nino3.4 and AMO—contributed 22, 18 and 56 %, respectively.
a The DMO component of the NH SAT anomalies during the cold season (black line) and its regression using the decadal variability of the PDO, Nino3.4, AMO, and AO indices (bar). b The contribution of PDO (blue), Nino3.4 (grey), and AMO (red) to the regressed DMO component in a. Note that the regression in a explained 88 % of the variance in corresponding SAT anomalies, and the PDO, Nino3.4, AMO, and AO contributed 22, 18, 56, and 4 %, respectively. As the contribution of AO was little, the line that represents AO’s contribution was not shown in b
Moreover, a similar method was applied to the temporal coefficients in the first three empirical orthogonal function (EOF) modes of the de-trended global SST (Fig. 7) and the AO index. The results are shown in Fig. 6 and expressed in Eqs. (15, 16). To obtain the results shown in Fig. 6a, the EOF analysis was first applied to the linear de-trended global SST for the boreal cold season (Fig. 7). Then, methods similar to those used to derive Fig. 5 were applied to the temporal coefficients of the first three EOF modes and the AO index. The results in Fig. 6c were derived by employing similar methods but replaced the EEMD method with the 11-year running mean method, which is expressed using Eq. (16). The first EOF mode of the de-trended global SST closely correlates with the PDO and Nino3.4 indices, with correlation coefficients of 0.69 and 0.93, respectively (Table 2). The second and third SST’s EOF modes closely correlate with the AMO and present the correlation coefficients of 0.61 and 0.64, respectively (Table 2). The relative contribution of each classic oceanic ICV mode or SST’s EOF mode and AO to the regressed DMO component was calculated following the method described by Huang and Yi (1991).
a The DMO component for the NH cold season mean SAT anomalies (black line), and its regression using decadal variability of EOF modes for global SST, and AO indexes (bar). b The contribution of first (blue), second (orange), and third (red) EOF modes to the regressed DMO component in a. c, d The same as a, b but using the 11-year running mean instead of the EEMD method. Note that the regression in a, c explained 93 and 95 % of the variance in corresponding SAT anomalies, respectively. The EOF1, EOF2, EOF3, and AO contributed 33, 45, 15, and 7 % in b, and contributed 11, 42, 43, and 4 % in d, respectively. The lines that represent AO’s contributions were not shown in b, d
a, b The spatial pattern and temporal coefficient of the first EOF mode for the linear de-trended global SST anomaly over the 1900–2013 period with respect to the 1961–1990 reference period for the boreal cold season, respectively. c–f The same as a, b but for the second and third EOF modes, respectively. Note that the three black rectangles in a indicate the ocean regions where the PDO, AMO and Nino3.4 indices are defined
Figures 5 and 6 suggest that the Atlantic Ocean’s decadal variability makes the largest contribution to the DMO, whereas the North Pacific and tropical Pacific’s decadal variability have the relative weaker effect. However, the sum of North Pacific and tropical Pacific’s contribution is comparable with Atlantic’s contribution. The North Pacific’s contribution to SAT variability of NH is larger than tropical Pacific for decadal timescale. Nevertheless, the recent warming hiatus was mainly the contribution of decadal variability in the Pacific Ocean (Kosaka and Xie 2013; England et al. 2014; Meehl et al. 2014; Trenberth et al. 2014; Dai et al. 2015). It seems that the AO make little contribution to the DMO for the decadal scale as suggested by the results, which showed the relative contributions of AO were 4, 7, and 4 % in Figs. 5, 6b, d, respectively. However, there are many studies indicated that the Arctic sea ice and enhanced Arctic warming influenced the SAT variability over mid-latitude NH continents significantly in last decades (Outten and Esau 2012; Cohen et al. 2014; Mori et al. 2014; Screen and Simmonds 2014). So the Arctic’s influence on recent warming hiatus will be examined further in next section. As most parts of NH are land, how the suggested oceanic modulation influence the SAT variability of NH land will be examined in next section as well.
6 Thermal forced atmospheric circulation change
Atmospheric circulation change is the dominant factor affecting the decadal variability of terrestrial SAT over the NH during the boreal cold season (Van Loon et al. 2007; Wallace et al. 2012; Guan et al. 2015), and oceanic ICV influences that atmospheric circulation via oceanic thermal forcing (Latif and Barnett 1994; Rodwell et al. 1999). To study the thermally forced atmospheric circulation change, the surface thermal forcing fields were examined firstly. Figure 8 shows the regional mean SAT time series with 11-year running mean over different latitudinal zones (Fig. 8a), and two warming and two cooling centers in the mid-latitude (Fig. 8b), respectively. Although warming over the mid- to high NH latitudes has paused over the past decades for boreal cold season, Arctic warming accelerated during the same period (Fig. 8a, b), which is consistent with Cohen et al. (2014) and Wyatt and Curry (2014). The obvious enhanced Arctic warming during the period of warming hiatus was also suggested by the Fig. 9a, which shows the zonal mean SAT time series of NH. The zonal mean SAT over Arctic regions shows the persistent increasing trends, but the mid-latitude regions have no significant trend during recent hiatus (Fig. 9a). Despite the obvious differences in varied latitudinal zones, the SAT change also shows a difference over varied longitudinal zones (Fig. 8b). As shown in Fig. 8b, the SAT over NA and EUA show significant decreasing trends, but the western EUA (regions around the Mediterranean) and Pacific regions still show the warming trend. The meridional mean SAT time series shown in Fig. 9b also confirm these results. The specific locations of these four regions are presented in Fig. 9c. The red and orange filled regions are two warming centers during the warming hiatus, and the green and blue filled regions are two cooling centers (Fig. 9c). The regional mean SAT in Fig. 8b was calculated over the color filled regions in Fig. 9c. The meridional mean SAT in Fig. 9b also was calculated over the color filled regions, but the skyblue filled regions of NA were not used in the calculation of the meridional mean.
a The 11-year running mean SAT time series for the boreal cold season averaged across 10°–30°N (green), 30°–50°N (blue), 50°–70°N (black), and 70°–90°N (red) latitudinal zones. b The 11-year running mean SAT time series for the boreal cold season averaged over North America (NA, black), Eurasia (EUA, blue), Western EUA (green), and the Pacific (red)
a The 11-year running zonal mean SAT time series for the boreal cold season. b The 11-year running meridional mean SAT time series for the boreal cold season. The dashed lines indicate the edges of the NA and EUA continents, and the western EUA regions. c The distribution of the regions. The colored zones represent the regions in a, b. Note that both the sky blue and blue regions represent NA in Fig. 8b, but only blue regions are used to calculate the meridional mean in b
Figure 10 shows the meridional thermal forcing (MTF) and zonal thermal forcing (ZTF) evolution over NH for boreal cold season, and the corresponding atmospheric circulation response. The MTF represents the meridional temperature gradients between the mid- and high-latitudes. The ZTF represents the asymmetry in temperatures between the extratropical large-scale warm and cold zones in the zonal direction, especially the land-sea thermal contrast. As shown in Fig. 10a, the different SAT changes over the mid-latitudes and the Arctic induced a rapidly weakened meridional temperature gradient over the NH extratropics, which induced an accelerated weakening of the extratropical MTF during the recent warming hiatus. However, the asymmetric ZTF, which is related to the land-sea thermal contrast, has heightened during the hiatus, shifting from a decreasing trend to a significant increasing trend (Fig. 10b). This enhanced extratropical ZTF was induced by the rapidly increasing discrepancy between the two cooling centers over the EUA and NA continents and the two warming centers over the western EUA and the North Pacific (also see Figs. 3, 8, 9).
a The meridional temperature gradient represented by the difference between the regional mean SAT over the 30°–50°N and 70°–90°N latitudinal zones. b Zonal asymmetry thermal forcing represented by the SAT difference between North America (NA), eastern Eurasia (EUA) and Pacific, western EUA. The solid line with arrows in a, b is the linear trend for 2001–2013. The difference in the time series is the anomaly relative to the 1981–2010 reference period. c The difference in the mean geopotential height (GPH) over the 500-hPa layer for 2002–2013 and 1990–2001. The vector indicates the corresponding wind field difference. d The difference in the mean meridional wind speeds over the 500-hPa level for 2002–2013 and 1990–2001. Note that the minimum latitude of c, d is 20°N, and the dashed circle lines are 30°N and 60°N. Only the wind vectors over the regions in which the meridional and zonal wind speed change that calculated from three reanalysis products (ERA-interim, NCEP I and NCEP II) had the same sign are presented in c. The black dots in d indicate the regions in which the signs for the results from the three reanalysis products did not agree
The weaker MTF followed a pattern of “warm Arctic and cold land” (WACL) (Overland et al. 2011; Mori et al. 2014) (see Fig. 3), which corresponded to an obvious positive anomaly at 500-hPa geopotential height (GPH) over the Arctic (Fig. 10c). As shown in Fig. 11a, c, e, the positive GPH anomalies were also shown in other three height levels, the 200- and 850-hPa GPH, and sea level pressure (SLP) fields, which indicate the low pressure system over Arctic–referred as polar vortex in upper troposphere was quite weak in the recent warming hiatus. In addition, the mid-latitudes over the eastern EUA, NA, the Atlantic, and the Mediterranean all exhibited a negative 500-hPa GPH anomaly (Fig. 10c). Similar situations occurred above other three height levels (Fig. 11a, c, e). As shown in Figs. 10c and 11a, c, e, the changes in the GPH or SLP fields over the Arctic and the mid-latitudes are asymmetric. These asymmetries induced the weaker polar vortex and slower westerly winds over the high-latitudes as shown in the wind fields (Figs. 10c, 11a, c, e). Besides, the weakened meridional GPH gradient and slower westerly winds will induce a slower speeds and a larger amplitude in planetary waves (Screen and Simmonds 2014), which will facilitate the invasion of extremely cold air at the mid-latitudes, leading to cooling over the EUA and NA during the recent hiatus. Furthermore, during the previous warming hiatus period (1940–1975), the Arctic experienced cooling trends, and the corresponding polar vortex was strengthened (Fig. S4). Therefore, the Eurasian extratropical regions (poleward of 45°N) showed warming trends because of the stronger MTF in high-latitudes (Fig. S4). However, the Eurasian mid- and low-latitudes (southward of 45°N) experienced cooling trends, because of the weaker MTF over these regions (Fig. S4, Table 3). The North America high-latitudes showed significant cooling trends during the previous warming hiatus period, because the stronger polar vortex expanded to high-latitudes over North America (Fig. S4b).
a, b Same as Fig. 10c, d but for the 200-hPa level. c–f Represent 850-hPa and sea level, respectively. Note that the wind speed in e, f was measured at 10 m height above the surface
The enhanced ZTF generally followed a “warm ocean and cold land” (WOCL) pattern (Wallace et al. 1995; He et al. 2014), but one warm center was over the western EUA regions rather than over the Atlantic Ocean (see Fig. 3). The North Pacific had one of the most obvious warming centers (see Fig. 3), which corresponded to a negative PDO phase and a positive 500-hPa GPH anomaly (Fig. 10c). As shown in Fig. 11a, c, e, the positive anomalies over North Pacific are also shown in other heights. As the Aleutian Low is defined in SLP fields, it indicates a quite weaker Aleutian Low in recent warming hiatus (Fig. 11e). The positive GPH or SLP anomalies over the North Pacific enhanced the southward flow of air over NA (Figs. 10d, 11b, d, f), which caused the cooling across NA (Fig. 3). Furthermore, the positive GPH anomalies over the North Pacific were also presented during the previous warming hiatus period, which also contributed to the NA’s cooling during that period (Fig. S4, Fig. S6 a, c, e). Previous studies (e.g. Beamish et al. 1998; Klyashtorin 1998; Klyashtorin and Lyubushin 2007; Van Loon et al. 2007; Wyatt and Curry 2014) also suggested the evident positive GPH anomalies and the weaker Aleutian Low over the North Pacific during the previous warming hiatus period. In addition, these studies examined the atmospheric circulation changes throughout a period (about 1915–1975) that contains the entire evolutions form the accelerated warming (about 1915–1940) to the warming hiatus (1940–1975). By examine the Pacific Circulation Index and Atmospheric Circulation Index that represent the large-scale winds and atmospheric-mass-transfer, and the Aleutian Low Pressure Index, they suggested the GPH and Aleutian Low over the North Pacific changed significantly during both the accelerated warming (about 1915–1940) and the previous warming hiatus period (Vangenheim 1940; Girs 1971a, b; Beamish et al. 1998; Klyashtorin 1998; Klyashtorin and Lyubushin 2007; Van Loon et al. 2007; Wyatt and Curry 2014). The cyclone-like negative 500-hPa GPH anomaly over the eastern EUA also enhanced the flow of air southward over EUA, and cold Arctic air was carried by the southward airflow and the cyclone anomaly to large parts of the eastern EUA (Fig. 10c, d), which induced obvious cooling in that areas (Fig. 3). Furthermore, the similar cyclone anomaly also occurred during the previous warming hiatus period, but its location was over the Eurasian mid- and low-latitudes (Fig. S4). In addition, the opposite SLP or GPH anomaly at 850-hPa between Greenland and the mid-latitude Atlantic indicated a negative phase NAO-like pattern (Fig. 11d, f), which also contributed to the recent warming hiatus (Guan et al. 2015). However, there was a positive NAO-like pattern during the previous warming hiatus period, which probably contributed to the warming trends in extratropical regions over the Eurasian continent during that period (Fig. S4).
7 Abrupt shift in thermally forced atmospheric circulation
A theoretical dynamic model (Källén 1981; Charney and DeVore 1979) was used to confirm the responses of circulation patterns to the MTF and ZTF changes over the extratropical Northern Hemisphere suggested above. Charney and DeVore (1979) found multiple equilibrium states for a given topographic and thermal forcing using this model. Among the multiple equilibrium states, two stable equilibrium states vary distinctly: one state is a low-index flow with a strong wave component and a weaker zonal component (Fig. 12e), whereas the other is a high-index flow with a weaker wave component and a stronger zonal component (Fig. 12c). The low-index equilibrium is a colder state with more blocking events over extratropical NH, but the high-index equilibrium is a warmer state with less blocking (Charney and DeVore 1979). In addition, there is an abrupt shift between the low-index and high-index equilibrium with the change of MTF and ZTF over the extratropical NH (Charney and DeVore 1979) (see Fig. 12a).
a The equilibrium bifurcation associated with the change both in the parameter of MTF (\(\psi_{A}^{*}\)) and the parameter of ZTF (\(\psi_{K}^{*}\)). Note that \(\psi_{A}^{*}\) is the opposite of MTF, and \(\psi_{K}^{*}\) is same-phase with ZTF. All points in the orange and skyblue surface indicate high-index and low-index equilibrium states, respectively. All the points with unstable equilibria are not shown. The black line is a possible track of equilibrium states that correspond to the change of both \(\psi_{A}^{*}\) and \(\psi_{K}^{*}\). The thin black lines over the skyblue and orange surfaces in a represent the streamfunction field corresponding to the two black points. b, c The heating field and streamfunction field corresponding to the black point on the orange surface, respectively. d, e The same as b, c but for the black point on the skyblue surface. The colored background shows the topography distribution in the model, and the warm tone indicates the “land”; the cool tone indicates the “ocean”. “C” and “W” in b, d represent cold and warm, respectively. “H” and “L” in c, e represent high and low pressure, respectively. The contour intervals are all 0.1 units. Parameter values are: k = 0.05, \(h_{0} = - 0.15\), \(\psi_{A}^{*} = - 0.42\), \(\psi_{K}^{*} = 0.2\) in b and \(\psi_{A}^{*} = - 0.32\), \(\psi_{K}^{*} = 0.3\) in d
To evaluate the thermally forced atmospheric circulation changes that occur with the simultaneous changes of both MTF and ZTF over the extratropical NH, we first separately examine MTF and ZTF to assess each pattern’s individual impact profile. The equilibrium bifurcation associated with the changes to the parameter of MTF (\(\psi_{A}^{*}\); \(\psi_{A}^{*}\) is opposite to MTF) is shown in Fig. 13. \(\psi_{A}^{*} < 0\) indicates that thermal forcing decreases from low to high latitudes. \(\psi_{A} < 0\) indicates that the large-scale flow is a westerly wind, whereas \(\psi_{A} > 0\) indicates that the large-scale flow is an easterly wind. When the absolute value of \(\psi_{A}\) is greater than the absolute value of \(\psi_{K}\) and \(\psi_{L}\), the zonal component is stronger than the wave component. We can see that when the MTF is large (\(\psi_{A}^{*} < - 0.42\)), the large-scale flow has only one possible equilibrium state, which has a large zonal component (Fig. 13a) and small wave components (Fig. 13b, c) and is a high-index flow. When the MTF is small (\(- 0.3 < \psi_{A}^{*} < 0\)), the large-scale flow has only one possible equilibrium state, which has a small zonal component (Fig. 13a) and large wave components (Fig. 13b, c) and is a low-index flow. When the MTF falls between the two cases outlined above (\(- 0.42 < \psi_{A}^{*} < - 0.3\)), there are two stable equilibrium solutions; one is a high-index flow, and the other is a low-index flow. Which stable flow regime the atmosphere is attracted to depend on the initial state of the flow and the way in which the MTF changes over time (Shabbar et al. 2001).
The equilibrium bifurcation associated with the changes in the parameter of MTF (\(\psi_{A}^{*}\)). The ordinate gives the equilibrium values \(\psi_{A}\) in a, \(\psi_{K}\) in b and \(\psi_{L}\) in c, respectively. A numerical evaluation of the eigenvalues shows stability properties as indicated by the black (stable) and red dashed (unstable) lines. Parameter values are: k = 0.05, \(h_{0} = - 0.15\), and \(\psi_{K}^{*} = 0.2\)
The equilibrium bifurcation associated with the changes to the parameter of ZTF (\(\psi_{K}^{*}\)) is shown in Fig. 14. \(\psi_{K}^{*} > 0\) indicates that the ocean’s warming is stronger than the land’s, whereas \(\psi_{K}^{*} < 0\) means that the ocean’s cooling is stronger than the land’s. When the ZTF with a “warm ocean and cold land” pattern (WOCL, Fig. 12d) is large (\(\psi_{K}^{*} > 0.8\)), the large-scale flow has only one possible equilibrium state, which has a small zonal component (Fig. 14a) and large wave components (Fig. 14b, c) and is a low-index flow. When the ZTF is small (\(\psi_{K}^{*} < 0.2\)), or if the ZTF exhibits a “cold ocean and warm land” pattern (COWL, \(\psi_{K}^{*} < 0\)), the large-scale flow has only one possible stable equilibrium state, which has a large zonal component (Fig. 14a) and small wave components (Fig. 14b, c) and is a high-index flow. When the ZTF falls between the two cases outlined above (\(0.2 < \psi_{K}^{*} < 0.8\)), there are also two stable equilibrium solutions.
Same as Fig. 13, except that the abscissa all give the parameter of ZTF (\(\psi_{K}^{*}\)) and have a parameter value \(\psi_{A}^{*} = - 0.42\)
Figures 13 and 14 suggest that both a decrease in MTF and an increase in ZTF favored the occurrence of a low-index flow. The equilibrium bifurcation associated with the simultaneous change in the parameters of MTF (\(\psi_{A}^{*}\)) and ZTF (\(\psi_{K}^{*}\)) is shown in Fig. 12a.
In addition, blocking corresponding to the low-index flow occurred more frequently over the EUA and NA during the recent hiatus (Fig. 15). Figure 15a shows the decadal variability of sector blocking frequency over EUA (50°E–140°E) and NA (170°E–80°W) regions. Figure 15b compares the 5-year mean difference of local blocking frequency between the beginning of hiatus (1999–2003) and present (2009–2013). The sector and local blocking was calculated following the procedure outlined in D’Andrea et al. (1998). As shown in Fig. 15a, the blocking frequency over EUA increased by 8 % in boreal cold season since 2001, which is nearly one-third of its climatology, which is about 27 %. Such a severe increase of the blocking events will definitely induce the EUA’s cooling during recent hiatus. The blocking frequency over NA also increased by 6 %, which led the NA’s cooling too (Fig. 15a). Besides, the blocking frequency over EUA and NA decreased significantly during the enhance warming period (Huang et al. 2012, He et al. 2014) before the recent warming hiatus. The frequency of blocking events also contributed to the enhanced warming. The increase frequency of the local blocking over the longitude zones of EUA and NA also indicated the more frequent blocking events during the recent hiatus (Fig. 15b). Over all, the Arctic amplification (Cohen et al. 2014; Mori et al. 2014), land-sea thermal contrast (Wallace et al. 1995; He et al. 2014), the negative phase of PDO (England et al. 2014; Dai et al. 2015), and negative phase of NAO (Luo 2005; Luo et al. 2010; Guan et al. 2015) jointly induced the weaker MTF and stronger ZTF, and then made the frequent blocking events in recent warming hiatus (Table 3).
a The 11-year running mean sector blocking frequency for the boreal cold season over EUA (blue line) and NA (red line). The shading represents the one standard deviation range of results from the ERA-interim, NCEP I and II reanalysis products. b The local blocking frequency for the boreal cold season average from 1999 to 2003 (black line) and from 2009 to 2013 (red line). The pink and grey shading represent the one standard deviation range of results from the ERA-interim, NCEP I and II reanalysis products. The blue area represents the positive difference between the average of the results for 2009–2013 and 1999–2003 over the EUA and NA regions. Note that the sector and local blocking was calculated following the procedure outlined in D’Andrea et al. (1998)
8 Discussion and conclusion
The recent warming hiatus was identified several years ago (Easterling and Wehner 2009), however, it attracted worldwide attention since the famous scientific community-Intergovernmental Panel on Climate Change (IPCC) highlighted it in recently IPCC report (IPCC 2013). Although the IPCC has discussed some possible causes for the hiatus, they were not enough to win the confidence of people to the fact of global warming and climate science. Many papers about the hiatus have been published since then. The hiatus has stirred debate within the community of climate science, on topics such as the influence of internal climate variability on global temperature change (Kravtsov et al. 2014; Meehl et al. 2014; Dai et al. 2015; Steinman et al. 2015; Guan et al. 2015), and projection of climate in interdecadal time scale (Meehl and Teng 2014; England et al. 2015; Roberts et al. 2015). However, some important aspects of the hiatus, such as the global dynamical figure of it, are still unclear.
Although cooling over land contributed 48 % to the global warming hiatus, the manner in which ICV modes influenced this cooling remains unclear. Our research concludes that these oceanic ICV modes and Arctic influenced the terrestrial SAT by eliciting both weaker MTF and stronger ZTF, which then induced a weaker polar vortex and westerly winds, slower but amplified planetary waves, and specific variations in meridional wind speeds. Thus, extremely cold air was able to invade the mid-latitude regions easily. In addition, there will be more frequent blocking events under the weaker MTF and stronger ZTF situation. We use the term DMO to denote the modulation effect of these oceanic ICV modes and Arctic on the SAT change at decadal to multidecadal timescales. When the DMO trended upward, the warming was accelerated by an associated stronger asymmetric MTF and weaker ZTF, and vice versa. In addition, the asymmetrical thermal forcing and terrestrial SAT change may elicit positive feedbacks, which may further induce amplified regional cooling or warming (Wallace et al. 1995; He et al. 2014). The enhanced warming in the Arctic (Cohen et al. 2014; Mori et al. 2014; Wyatt and Curry 2014) and the downtrend PDO (England et al. 2014; Meehl et al. 2014; Trenberth et al. 2014; Dai et al. 2015) and NAO (Guan et al. 2015) were the main classic ICV modes responsible for the current warming hiatus.
The robust twenty-first century warming projection presented when considered only the ensemble members from the Coupled Model Intercomparison Project Phase 5, which captured the recent hiatus (England et al. 2015). Regardless of the model’s projections, our study also suggests that warming will accelerate again when the DMO enters its upward phase. However, when this change is likely to occur, and how much time we have left to prepare for the accelerated warming expected in the near future are questions that remain unanswered. Furthermore, although the contributions of the temperature change in the warm seasons contributed little to the recent warming hiatus, the warm seasons made a large contribution during the pervious warming hiatus (Fig. S7). Compared with the recent warming hiatus, the spatial patterns of the pervious warming hiatus and its atmospheric dynamics also showed some differences in the cold season (Fig. S4, S6 a, c, e; Table 3). Therefore, more studies about the previous warming hiatus should be undertaken in the future.
References
Beamish RJ, McFarlane GA, Noakes D, King JR, Sweeting R (1998) Evidence of a new regime starting in 1996 and the relation to Pacific salmon catches (NPAFC Doc 321). Department of Fisheries and Oceans, Sciences Branch-Pacific Region, Pacific Biological Station, Nanaimo
Charney JG, DeVore JG (1979) Multiple flow equilibria in the atmosphere and blocking. J Atmos Sci 36(7):1205–1216
Chen X, Tung K-K (2014) Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345(6199):897–903
Cohen JL, Furtado JC, Barlow M, Alexeev VA, Cherry JE (2012) Asymmetric seasonal temperature trends. Geophys Res Lett. doi:10.1029/2011gl050582
Cohen J, Screen JA, Furtado JC, Barlow M, Whittleston D, Coumou D, Francis J, Dethloff K, Entekhabi D, Overland J, Jones J (2014) Recent Arctic amplification and extreme mid-latitude weather. Nat Geosci 7(9):627–637. doi:10.1038/ngeo2234
Compo GP, Whitaker JS, Sardeshmukh PD, Matsui N, Allan RJ, Yin X, Gleason BE, Vose RS, Rutledge G, Bessemoulin P (2011) The twentieth century reanalysis project. Q J R Meteor Soc 137(654):1–28
Dai A, Fyfe JC, Xie S-P, Dai X (2015) Decadal modulation of global surface temperature by internal climate variability. Nat Clim Change 5(6):555–559. doi:10.1038/nclimate2605
D’Andrea F, Tibaldi S, Blackburn M, Boer G, Déqué M, Dix M, Dugas B, Ferranti L, Iwasaki T, Kitoh A (1998) Northern Hemisphere atmospheric blocking as simulated by 15 atmospheric general circulation models in the period 1979–1988. Clim Dyn 14(6):385–407
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteor Soc 137(656):553–597. doi:10.1002/qj.828
Easterling DR, Wehner MF (2009) Is the climate warming or cooling? Geophys Res Lett. doi:10.1029/2009GL037810
England MH, McGregor S, Spence P, Meehl GA, Timmermann A, Cai W, Gupta AS, McPhaden MJ, Purich A, Santoso A (2014) Recent intensification of wind-driven circulation in the Pacific and the ongoing warming hiatus. Nat Clim Change 4(3):222–227
England MH, Kajtar JB, Maher N (2015) Robust warming projections despite the recent hiatus. Nat Clim Change 5(5):394–396. doi:10.1038/nclimate2575
Frolov IE, Gudkovich AM, Karklin BP, Kvalev EG, Smolyanitsky VM (2009) Climate change in Eurasian arctic shelf seas. Springer-Praxis Books. ISBN 978-3-540-85874-4
Girs AA (1971a) Multiyear oscillations of atmospheric circulation and long-term meteorological forecasts. Gidrometeroizdat, Moskva, Russia, p 480 (in Russian)
Girs AA (1971b) Long-term fluctuations of the atmospheric circulation and hydrometeorological forecasts. Gidrometeroizdat, St. Petersburg, Russia, p 280 (in Russian)
Guan X, Huang J, Guo R, Pu L (2015) The role of dynamically induced variability in the recent warming trend slowdown over the Northern Hemisphere. Sci Rep 5:12669. doi:10.1038/srep12669
Hansen J, Ruedy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophys 48:29. doi:10.1029/2010rg000345
He Y, Huang J, Ji M (2014) Impact of land–sea thermal contrast on interdecadal variation in circulation and blocking. Clim Dyn 43(12):3267–3279. doi:10.1007/s00382-014-2103-y
Hersbach H, Peubey C, Simmons A, Berrisford P, Poli P, Dee D (2015) ERA-20CM: a twentieth-century atmospheric model ensemble. Q J R Meteor Soc 141:2350–2375. doi:10.1002/qj.2528
Higuchi K, Huang J, Shabbar A (1999) A wavelet characterization of the North Atlantic oscillation variation and its relationship to the North Atlantic sea surface temperature. Int J Climatol 19:1119–1129
Huang J, Yi Y (1991) Inversion of a nonlinear dynamic-model from the observation. Sci China Ser B Chem Life Sci Earth Sci 34(10):1246–1251
Huang J, Higuchi K, Shabbar A (1998) The relationship between the North Atlantic Oscillation and El Niño–Southern Oscillation. Geophys Res Lett 25(14):2707–2710
Huang J, Guan X, Ji F (2012) Enhanced cold-season warming in semi-arid regions. Atmos Chem Phys 12(12):5391–5398. doi:10.5194/acp-12-5391-2012
Huang B, Banzon VF, Freeman E, Lawrimore J, Liu W, Peterson TC, Smith TM, Thorne PW, Woodruff SD, Zhang H-M (2015) Extended reconstructed sea surface temperature version 4 (ERSST.v4). Part I: upgrades and intercomparisons. J Clim 28(3):911–930. doi:10.1175/JCLI-D-14-00006.1
Huang J, Ji M, Xie Y, Wang S, He Y, Ran J (2016a) Global semi-arid climate change over last 60 years. Clim Dyn 46:1131–1150. doi:10.1007/s00382-015-2636-8
Huang J, Yu H, Guan X, Wang G, Guo R (2016b) Accelerated dryland expansion under climate change. Nat Clim Change 6(2):166–171. doi:10.1038/nclimate2837
IPCC (2007) In: Solomon S et al (eds) Summary for policymakers in climate change 2007: the physical science basis. 12–12
IPCC (2013) In: Stocker TF et al (eds) Summary for policymakers in climate change 2013: the physical science basis. 3–29
Ishii M, Shouji A, Sugimoto S, Matsumoto T (2005) Objective analyses of sea-surface temperature and marine meteorological variables for the 20th century using ICOADS and the Kobe collection. Int J Climatol 25:865–879
Ji F, Wu Z, Huang J, Chassignet EP (2014) Evolution of land surface air temperature trend. Nat Clim Change 4(6):462–466. doi:10.1038/nclimate2223
Jones P (2016) The reliability of global and hemispheric surface temperature records. Adv Atmos Sci 33(3):269–282. doi:10.1007/s00376-015-5194-4
Källén E (1981) The nonlinear effects of orographic and momentum forcing in a low-order, barotropic model. J Atmos Sci 38(10):2150–2163
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J (1996) The NCEP/NCAR 40-year reanalysis project. Bull Am Meteorol Soc 77(3):437–471
Kanamitsu M, Ebisuzaki W, Woollen J, Yang S-K, Hnilo J, Fiorino M, Potter G (2002) NCEP-DOE AMIP-II reanalysis (r-2). Bull Am Meteorol Soc 83(11):1631–1643
Kaplan A, Cane MA, Kushnir Y, Clement AC, Blumenthal MB, Rajagopalan B (1998) Analyses of global sea surface temperature 1856–1991. J Geophys Res 103(C9):18567–18589
Karl TR, Arguez A, Huang B, Lawrimore JH, McMahon JR, Menne MJ, Peterson TC, Vose RS, Zhang H-M (2015) Possible artifacts of data biases in the recent global surface warming hiatus. Science 348(6242):1469–1472. doi:10.1126/science.aaa5632
Klyashtorin LB (1998) Long-term climate change and main commercial fish production in the Atlantic and Pacific. Fish Res 37:115–125
Klyashtorin LB, Lyubushin AA (2007) Cyclic climate changes and fish productivity. VNIRO Publishing, Moscow (Editor for English version: Dr. Gary D. Sharp, Center for Climate/Ocean Resources Study, Salinas)
Kosaka Y, Xie S-P (2013) Recent global-warming hiatus tied to equatorial Pacific surface cooling. Nature 501(7467):403–407
Kravtsov S, Spannagle C (2008) Multidecadal climate variability in observed and modeled surface temperatures. J Clim 21(5):1104–1121
Kravtsov S, Wyatt MG, Curry JA, Tsonis AA (2014) Two contrasting views of multidecadal climate variability in the twentieth century. Geophys Res Lett 41(19):6881–6888. doi:10.1002/2014GL061416
Kravtsov S, Wyatt MG, Curry JA, Tsonis AA (2015) Comment on “Atlantic and Pacific multidecadal oscillations and Northern Hemisphere temperatures”. Science 350(6266):1326. doi:10.1126/science.aab3570
Latif M, Barnett TP (1994) Causes of decadal climate variability over the North Pacific and North-America. Science 266(5185):634–637. doi:10.1126/science.266.5185.634
Luo D (2005) Why is the North Atlantic block more frequent and long-lived during the negative NAO phase? Geophys Res Lett. doi:10.1029/2005GL022927
Luo D, Zhou W, Wei K (2010) Dynamics of eddy-driven North Atlantic Oscillations in a localized shifting jet: zonal structure and downstream blocking. Clim Dyn 34(1):73–100
Mantua NJ, Hare SR, Zhang Y, Wallace JM, Francis RC (1997) A Pacific interdecadal climate oscillation with impacts on salmon production. Bull Am Meteorol Soc 78(6):1069–1079
Meehl GA, Teng H (2014) CMIP5 multi-model hindcasts for the mid-1970s shift and early 2000s hiatus and predictions for 2016–2035. Geophys Res Lett 41(5):1711–1716
Meehl GA, Teng H, Arblaster JM (2014) Climate model simulations of the observed early-2000s hiatus of global warming. Nat Clim Change 4(10):898–902. doi:10.1038/nclimate2357
Mori M, Watanabe M, Shiogama H, Inoue J, Kimoto M (2014) Robust Arctic sea-ice influence on the frequent Eurasian cold winters in past decades. Nat Geosci 7(12):869–873. doi:10.1038/ngeo2277
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J Geophys Res Atmos (1984–2012) 117(D8):D08101. doi:10.1029/2011JD017187
Outten SD, Esau I (2012) A link between Arctic sea ice and recent cooling trends over Eurasia. Clim Change 110(3–4):1069–1075
Overland JE, Wood KR, Wang M (2011) Warm Arctic-cold continents: climate impacts of the newly open Arctic Sea. Polar Res. doi:10.3402/polar.v30i0.15787
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atmos (1984–2012) 108(D14):4407. doi:10.1029/2002JD002670
Reynolds RW, Smith TM, Liu C, Chelton DB, Casey KS, Schlax MG (2007) Daily high-resolution-blended analyses for sea surface temperature. J Clim 20(22):5473–5496
Roberts C, Palmer M, McNeall D, Collins M (2015) Quantifying the likelihood of a continued hiatus in global warming. Nat Clim Change 5:337–342. doi:10.1038/NCLIMATE2531
Rodwell MJ, Rowell DP, Folland CK (1999) Oceanic forcing of the wintertime North Atlantic Oscillation and European climate. Nature 398(6725):320–323. doi:10.1038/18648
Screen JA, Simmonds I (2014) Amplified mid-latitude planetary waves favour particular regional weather extremes. Nat Clim Change 4(8):704–709. doi:10.1038/nclimate2271
Shabbar A, Huang J, Higuchi K (2001) The relationship between the wintertime North Atlantic Oscillation and blocking episodes in the North Atlantic. Int J Climatol 21(3):355–369
Smith TM, Reynolds RW, Peterson TC, Lawrimore J (2008) Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J Clim 21(10):2283–2296
Steinman BA, Mann ME, Miller SK (2015) Atlantic and Pacific multidecadal oscillations and Northern Hemisphere temperatures. Science 347(6225):988–991. doi:10.1126/science.1257856
Trenberth KE (1997) The definition of El Nino. Bull Am Meteorol Soc 78(12):2771–2777
Trenberth KE, Shea DJ (2006) Atlantic hurricanes and natural variability in 2005. Geophys Res Lett. doi:10.1029/2006GL026894
Trenberth KE, Fasullo JT, Branstator G, Phillips AS (2014) Seasonal aspects of the recent pause in surface warming. Nat Clim Change 4(10):911–916. doi:10.1038/nclimate2341
Tung KK, Zhou JS (2013) Using data to attribute episodes of warming and cooling in instrumental records. Proc Natl Acad Sci 110(6):2058–2063. doi:10.1073/pnas.1212471110
Van Loon H, Founda D, Psiloglou BE (2007) Circulation changes on the Northern Hemisphere in winter associated with trends in the surface air temperature. Acad Athens Res Centre Atmos Phys Climatol Publ 17:1–29
Vangenheim GY (1940) The long-term temperature and ice break-up forecasting. Proc State Hydrol Inst 10:207–236 (in Russian)
Wallace JM, Zhang Y, Renwick JA (1995) Dynamic contribution to hemispheric mean temperature trends. Science 270(5237):780–783. doi:10.1126/science.270.5237.780
Wallace JM, Fu Q, Smoliak BV, Lin P, Johanson CM (2012) Simulated versus observed patterns of warming over the extratropical Northern Hemisphere continents during the cold season. Proc Natl Acad Sci 109(36):14337–14342. doi:10.1073/pnas.1204875109
Wang YH, Yeh CH, Young HWV, Hu K, Lo MT (2014) On the computational complexity of the empirical mode decomposition algorithm. Phys A Stat Mech Appl 400:159–167. doi:10.1016/j.physa.2014.01.020
Wu Z, Huang NE, Wallace JM, Smoliak BV, Chen X (2011) On the time-varying trend in global-mean surface temperature. Clim Dyn 37(3–4):759–773
Wyatt MG, Curry JA (2014) Role for Eurasian Arctic shelf sea ice in a secularly varying hemispheric climate signal during the 20th century. Clim Dyn 42(9–10):2763–2782
Wyatt MG, Peters J (2012) A secularly varying hemispheric climate-signal propagation previously detected in instrumental and proxy data not detected in CMIP3 data base. SpringerPlus 1(1):1–25. doi:10.1186/2193-1801-1-68
Wyatt MG, Kravtsov S, Tsonis AA (2012) Atlantic multidecadal oscillation and Northern Hemisphere’s climate variability. Clim Dyn 38(5–6):929–949
Xie Y, Liu Y, Huang J (2015) Overestimated Arctic warming and underestimated Eurasia mid-latitude warming in CMIP5 simulations. Int J Climatol. doi:10.1002/joc.4644
Zakharov VF (2013) Sea ice in the climate system. A Russian view. National Snow and Ice Data Center, Boulder, CO. Special report #16 (same as 1997 version, with updates). https://nsidc.org/pubs/special/16/NSIDC-special-report-16.pdf
Acknowledgments
We thank anonymous reviewers for comments on the earlier versions of the manuscript, which helped improve the paper. This work was supported by the National Science Foundation of China (41521004, and 41575006), the National Basic Research Program of China (2012CB955301), the Fundamental Research Funds for the Central Universities (lzujbky-2015-ct03) and the China 111 Project (No. B 13045).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, J., Xie, Y., Guan, X. et al. The dynamics of the warming hiatus over the Northern Hemisphere. Clim Dyn 48, 429–446 (2017). https://doi.org/10.1007/s00382-016-3085-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3085-8