Abstract
The global mean 1900–2015 warming simulated by 42 Coupled Models Inter-comparison Project, phase 5 (CMIP5) climate models varies between 0.58 and 1.70 °C. The observed warming according to the NASA GISS temperature analysis is 0.95 °C with a 1200 km smoothing radius, or 0.86 °C with a 250 km smoothing radius. The projection of the future 2015–2100 global warming under a moderate increase of anthropogenic radiative forcing (RCP4.5 scenario) by individual models is between 0.7 and 2.3 °C. The CMIP5 climate models agree that the future climate will be warmer; however, there is little consensus as to how large the warming will be (reflected by an uncertainty of over a factor of three). A parsimonious statistical regression model with just three explanatory variables [anthropogenic radiative forcing due to greenhouse gases and aerosols (GHGA), solar variability, and the Atlantic Multi-decadal Oscillation (AMO) index] accounts for over 95 % of the observed 1900–2015 temperature variance. This statistical regression model reproduces very accurately the past warming (0.96 °C compared to the observed 0.95 °C) and projects the future 2015–2100 warming to be around 0.95 °C (with the IPCC 2013 suggested RCP4.5 radiative forcing and an assumed cyclic AMO behavior). The AMO contribution to the 1970–2005 warming was between 0.13 and 0.20 °C (depending on which AMO index is used) compared to the GHGA contribution of 0.49–0.58 °C. During the twenty-first century AMO cycle the AMO contribution is projected to remain the same (0.13–0.20 °C), while the GHGA contribution is expected to decrease to 0.21–0.25 °C due to the levelling off of the GHGA radiative forcing that is assumed according to the RCP4.5 scenario. Thus the anthropogenic contribution and natural variability are expected to contribute about equally to the anticipated global warming during the second half of the twenty-first century for the RCP4.5 trajectory.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the past century the Earth has experienced a considerable warming. Although most of the warming has been attributed to the burning of fossil fuels, the division between natural and anthropogenic components remains uncertain. Most climate research has been centered on the use of AOGCMs (atmosphere–ocean general circulation models) to simulate the climate system using fundamental physical, chemical and biological processes. At the same time semi-empirical statistical models (Otterman et al. 2002; Lean and Rind 2008; Humlum et al. 2011; Scafetta 2012; Mascioli et al. 2012; Zhou and Tung 2013; Canty et al. 2013; Chylek et al. 2014a, b) have been developed to provide additional insight into the anthropogenic and natural components of climate variability, and to point out components of the climate system that are not yet properly captured by the AOGCMs.
Multiple linear regression analysis (e.g. Wilks 2006) has been used recently (Lean and Rind 2008; Foster and Rahmstorf 2011; Zhou and Tung 2013; Canty et al. 2013; Chylek et al. 2014a, b; Miksovsky et al. 2015) to estimate the relative importance of the natural and anthropogenic components of the past warming. The method assumes a linear relation between the observed temperature and a set of selected physically plausible explanatory variables or predictors. A typical set of explanatory variables contains the known radiative forcing and an additional factors characterizing the oceanic influence on climate (Compo and Sardeshmukh 2009; Zhou and Tung 2013; Canty et al. 2013; Chylek et al. 2014a, b; Miksovsky et al. 2015).
The natural radiative forcing includes the top of the atmosphere solar variability (SOL) and volcanic aerosols (VOLC) (Douglass and Clader 2002; Haigh 2003; Scafetta and West 2006; Camp and Tung 2007; Lean and Rind 2008). The anthropogenic component includes anthropogenic well mixed greenhouse gases (GHG) and anthropogenic aerosols (AER). The oceanic influences are usually characterized by the El Nino Southern Oscillation (ENSO) index (Lean and Rind 2008; Foster and Rahmstorf 2011). However, the Atlantic Multi-decadal oscillation (AMO) (Schlesinger and Ramankutty 1994; Delworth and Mann 2000; Gray et al. 2004; Canty et al. 2013) and the Pacific Decadal Oscillations (PDO) have also exerted a considerable influence on the past century global and regional climate (Polyakov and Johnson 2000; Zhang et al. 2007; Mahajan et al. 2011; Frankcombe and Dijkstra 2011; Zhou and Tung 2013; Canty et al. 2013; Muller et al. 2013; Chylek et al. 2014a, b; Li et al. 2014).
In this note we compare simulations of the past and projections of the future mean global warming by 42 CMIP5 climate models and the statistical regression model. The projections are all based on the assumption of a future moderate increase in anthropogenic greenhouse gas radiative forcing such that it will plateau before 2100 with a magnitude of 4.5 W/m2 above its pre-industrial value. This plausible future trajectory of radiative forcing is described by the IPCC as a Representative Concentration Pathway RCP4.5. We also show that the relative contribution of the natural climate variability (characterized by the AMO) to the anticipated global warming will likely increase during the second half of the current century due to the expected levelling off of the anthropogenic forcing under the RCP4.5 scenario.
2 Data
In our analysis we use the global mean annual temperatures as compiled by the NASA GISS (Goddard Institute for Space Studies) available at http://data.giss.nasa.gov/gistemp/. The NASA GISS procedure includes filling the regions without observations and smoothing the data using correlations with stations up to 1200 km radius (Hansen and Lebedeff 1987; Hansen et al. 2010). This may prevent an underestimation of temperature variability from unobserved parts of the globe—especially the Arctic—which might have occurred in other temperature data sets. However, since the highest rate of anthropogenic warming is not necessarily limited to the Arctic (Lean and Rind 2008) the procedure may also overestimate the warming. To demonstrate the range of uncertainty we consider also the NASA GISS temperature data set constructed with a smaller (250 km) smoothing radius.
The historic radiative forcing used in our analysis is shown in Fig. 1. The forcing by anthropogenic greenhouse gases (GHG) and aerosols (AER), SOL, and VOLC are from IPCC (2013). The annual ENSO index is obtained by averaging monthly data from the NOAA website http://www.esrl.noaa.gov/psd/data/correlation/censo.long.data, and the PDO is from the website http://jisao.washington.edu/pdo/PDO.latest. Since we are interested in decadal scale variability we use an annually averaged ENSO index, rather than the monthly data used in earlier studies (e.g. Lean and Rind 2008; Foster and Rahmstorf 2011; Canty et al. 2013).
a Radiative forcing due to carbon dioxide (CO2), all well mixed greenhouse gases (GHG), anthropogenic aerosols (AER), combined CO2, GHG, and aerosols (CO2GHGAER), and volcanic aerosol (VOLC) after IPCC (2013). b Solar radiative forcing after IPCC (2013). c Three of the considered versions of the AMO indices after NOAA (AMO_K), van Oldenborgh (AMO_O), and Trenberth and Shea (AMO_TS). d The ENSO and PDO indices from sources described in the text
There are several different AMO indices (Fig. 1 ) resulting from different de-trending of the North Atlantic temperature data (Kaplan et al. 1998; Trenberth and Shea 2006; van Oldenbogrh et al. 2009), or from the principal component analysis (Parker et al. 2007). Without trying to resolve the differences of opinions and argue for one specific index, we use either the average of these most often used AMO indices, or all of them separately (when we need to show the dependence of the climate variable of interest on the selected form of the AMO index).
As previously stated, for future climate change projections up to the year 2100 we use the total radiative forcing (CO2, CH4, O3, N2O, halocarbons, and anthropogenic aerosols) prescribed by the IPCC (2013) for the RCP4.5 scenario. This number represents an approximate increase of 4.5 W/m2 between the year 2100 and its pre-industrial value.
3 Aerosol and GHG radiative forcing
Multiple regression analysis can lead to results with a larger uncertainty of regression coefficients when explanatory variables are significantly correlated (e.g. Wilks 2006). Since the degree of association between the GHGs and anthropogenic aerosol (AER) forcing is generally high, some of the previous regression analyses (e.g. Lean and Rind 2008; Chylek et al. 2014a) combined the GHGs and aerosol forcing into one effective forcing (GHGA), represented by the sum of the GHGs and aerosol radiative forcing. We follow the same procedure. We use the notation GHGA for the combined effect of GHG and tropospheric aerosols.
The large temporal and spatial variability of atmospheric aerosols makes global measurements of the aerosol optical depth and composition difficult. Although the direct aerosol effect (aerosol interaction with solar and terrestrial radiation) is reasonably well understood, the aerosol indirect effect (e.g. Chylek et al. 2006) (interaction affecting the cloud micro-structure, cloud albedo and cloud life cycle) remains a major source of uncertainty. The aerosol treatment in climate models varies, with some of the Coupled Models Inter-comparison Project phase 5 (CMIP5) models restricting their treatment to a direct aerosol effect; others attempt to include indirect effects as well (e.g. Wilcox et al. 2013; Flato et al. 2013), while some models do not consider an aerosol effect at all. In the following regression analysis we consider aerosol radiative forcing including an indirect effect as prescribed by the IPCC (2013), and we classify the CMIP5 models according to their aerosol treatment following the description in Table 9.1 of Flato et al. (2013).
In addition to the GHG and AER there are pairs of other potential explanatory variables (Table 1) that are also significantly correlated (e.g. GHGA and SOL). Whenever any of these pairs appears among the set of explanatory variables, their regression coefficients carry a considerable uncertainty. Although the collinearity affects the interpretability of the regression model, it does not affect its predictability.
4 Regression analysis of the 1900–2015 annual mean global temperature
Using the set of conventional explanatory variables (e.g. Lean and Rind 2008) GHGA, SOL, VOLC, and ENSO, we expand the annual mean global temperature as
where GHGA(t), SOL(t), VOLC(t) are respectively the prescribed 1900–2015 annual radiative forcing due to anthropogenic GHG and aerosols, the variability of solar radiation at the top of the atmosphere, and volcanic aerosols. The ENSO(t) is a time series of the annual ENSO index. The regression coefficients Ao to A4 are determined by a least squares fit. When only some of the explanatory variables are considered for a particular regression model, the coefficients of those variables not considered are set to zero. Additional terms are added when the AMO and PDO are considered as potential predictors. The fraction of the dependent variable variance accounted for by regression is given by R2, the square of the multiple regression coefficient.
The regression models using the usual explanatory variables (GHGA, SOL, VOLC, and ENSO) account for 93.68 % of the observed 1900–2015 temperature variance (Table 2). The residual (difference between the observed and modeled temperature) of this model (model #1 in Table 2) was found to be correlated with the AMO (Chylek et al. 2014a), suggesting the AMO as an additional potential explanatory variable, in agreement with previously reported results (e.g. Canty et al. 2013; Zhou and Tung 2013). The use of the PDO as a potential explanatory variables has also been explored. When both the AMO and PDO are added to the set of explanatory variables, the fraction of accounted for temperature variance increases to 95.68 %. However, the VOLC, ENSO and PDO are found not to be statistically significant predictors (model #2 in Table 2). In order to eliminate non-essential predictors we use a backward selection algorithm with the p value as a selection parameter; a statistically not significant predictor with the highest p value is thereby eliminated. Although the PDO may affect the AMO behavior (Guan and Nigam 2009; Chylek et al. 2014a), the PDO itself (p = value 0.72) is not a significant predictor in the context of our set of explanatory variables, as found earlier also by Canty et al. (2013). A compromise between complexity and accuracy leads to a parsimonious model with just three statistically significant explanatory variables, namely GHGA, SOL, and AMO, which still accounts for 95.51 % of the observed (1900–2015) temperature variance (Table 2). We shall use this three predictor regression model (GHGA, SOL and AMO) below to estimate future warming and to compare the regression model’s predicted future warming with the warming projected by the CMIP5 models.
5 The AMO as an explanatory variable
The origin of the Atlantic Multi-decadal Oscillation is not yet fully understood (Dima and Lohmann 2007). Some studies (e.g. Mahajan et al. 2011; Delworth and Zeng 2012; Zhang et al. 2013) suggest a connection to the Atlantic Meridional Overturning Circulation (AMOC), while others point to the upwelling of warm water along the Antarctic Circumpolar Current (Toggweiler and Russell 2008). Cycles of about 20 and 60–70 years have been identified in tree rings and ice cores records (Delworth and Mann 2000; Gray et al. 2004, Frankcombe and Dijkstra 2010; Chylek et al. 2011).
Since the AMO index is derived from the North Atlantic sea surface temperature, it represents not only the basic multi-decadal variability connected possibly to the AMOC, but also the imprints of other processes affecting the North Atlantic temperature (e.g. solar variability, volcanic aerosol, cloudiness). The direct warming effect due to increasing atmospheric concentration of greenhouse gases is assumed to be removed from the AMO index by different de-trending methods leading to slightly different AMO indices (Kaplan et al. 1998; Trenberth and Shea 2006; van Oldenborgh et al. 2009).
Although the twentieth century AMO-like cycle has been mimicked by an aerosol effect in some of the CMIP5 models (Booth et al. 2012; Wilcox et al. 2013; Zhang et al. 2013; Chylek et al. 2014b), analysis of the central England temperature (Tung and Zhou 2013), tree rings (Delworth and Mann 2000; Gray et al. 2004) and ice core data (Chylek et al. 2011) suggest that the AMO cyclic behavior existed for hundreds and possibly thousands of years before the beginning of anthropogenic influences. Thus the addition of the AMO to a set of predictors seems to be a justifiable choice (Mascioli et al. 2012; Zhou and Tung 2013; Canty et al. 2013; Kavvada et al. 2013; Muller et al. 2013; Miksovsky et al. 2015).
6 CMIP5 models simulations of the past (1900–2015) global warming
The global mean temperature as simulated by 42 individual CMIP5 models varies between 12 and 15 °C in 1860, and increases under the RCP4.5 forcing to 14–18 °C in 2100. The ensemble mean of the CMIP5 simulations increases by 2.6 °C, from 13.6 to 16.2 °C (Fig. 2).
Simulation of the global mean temperature (1860–2100) by 42 CMIP5 models with the prescribed historic and RCP4.5 radiative forcing. The thick black line (CMIP5_Ave) is a simulation by ensemble mean of all CMIP5 RCP4.5 simulations. The red thick line (T1200) is the observed global mean temperature variability after NASA GISS with 1200 km smoothing normalized to the CMIP5 mean in the year 1900
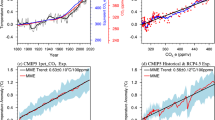
The temperature increase between the years 1900 (average of 1900–1910) and 2015 (average of 2005–2015) by individual models (Fig. 3a) under the RCP4.5 scenario varies between 0.58 and 1.70 °C with the CMIP5 models mean increase of 1.05 °C. The observed global warming (1900–2015) is 0.95 °C with the GISS smoothing radius of 1200 km, or 0.86 °C with the 250 km smoothing radius (red columns in Fig. 3a). Of the 42 CMIP5 models, 28 models simulate the 1900–2015 temperature increase within ±0.25 °C of the observed range, while 13 models show the warming higher (and one model lower) than that. This represents a partial success of the first principle physics based CMIP5 climate models in reproducing the observed past (1900–2015) warming. The three predictor (GHGA, SOL, and AMO) regression model (blue column in Fig. 3a) reproduces the observed NASA GISS T1200 mean global temperature increase quite accurately (0.96 °C compared to the observed value of 0.95 °C). The reproduction of the past is of course no guarantee of reliable future projections.
a The 1900–2015 warming (defined as a difference between the decadal means of 1900–1910 and 2005–2015) simulated by individual CMIP5 models and their average (red column CMIP5_Ave), together with the observed temperature increase (black columns for T1200 and T250), and the warming reproduced by the regression model of the T1200 (blue column Reg1200). b The projected 2015–2100 warming (defined as the difference between decadal averages of 2090–2100 and 2005–2015) by individual CMIP5 models; the CMIP5 models’ mean (red column CMIP5_Ave); and the warming predicted by the regression model (blue column Reg1200) of the T1200 temperature
7 CMIP5 models projections of the future 2015–2100 mean global warming under the RCP4.5 scenario
As noted in the Introduction, the IPCC (2013) prescribes several pathways (Representative Concentration Pathways—RCP) to the year 2100 specified by an assumed increase of anthropogenic radiative forcing between the year 2100 and its pre-industrial value. The RCP4.5, RCP6.0 and RCP8.5 pathways describe respectively radiative forcing increases of about 4.5, 6.0, and 8.5 W/m2. Most simulations done by the CMIP5 models assume RCP4.5 radiative forcing, which we consider in the following analysis. The radiative forcing equivalent to the doubling of CO2 (about 3.7 W/m2) is reached within the decade of the 2060s under RCP4.5.
The correlation coefficient for the period 2015–2100 between the radiative forcing and the CMIP5 ensemble mean projected warming is extremely high: 0.99 for the case of the RCP4.5 scenario. Thus the ensemble mean of all CMIP5 temperature simulations is a simple linear transformation of applied forcing. The response of individual models, however, varies depending on the parameterization of the model’s physical processes. For the RCP4.5 scenario the individual models’ projected 2015–2100 warming varies between 0.71 and 2.22 °C (Fig. 3b), with a mean of all CMIP5 RCP4.5 simulations of 1.47 °C.
To project the future temperature using the regression model we need, in addition to the RCP prescribed radiative forcing, an estimate of the future natural variability represented by the AMO and solar variability (SOL). For the AMO we assume a cyclic behavior that repeats the twentieth century AMO cycle. Similarly the solar variability is assumed to repeat its past behavior.
Comparing the CMIP5 climate models and the statistical regression model (Fig. 3), we have nine CMIP5 models that simulate both the historic global mean temperature increase (1900–2015) and the models’ projected 2015–2100 warming within ±0.25 °C of that obtained by a regression model (also within ±0.25 °C of the observed 1900–2015 warming). Thus we consider these CMIP5 models and the three predictor statistical regression model to be in a broad agreement. On the other hand there are seven CMIP5 models that project the future 2015–2100 warming to be at least 1.0 °C higher than that suggested by the regression model and more than 0.5 °C over the mean of all the CMIP5 models (Fig. 3b). We note further that all seven of these CMIP5 models with the highest projected future warming have a fully interactive aerosol-cloud interaction (an indirect aerosol effect) incorporated. As has been pointed out earlier in the case of Arctic warming (Chylek et al. 2016), the CMIP5 models classified as having fully interactive aerosols (Flato et al. 2013, their Table 9.1) project generally a higher warming than the rest of the models.
Concerning the total 1900–2100 warming, we have eight CMIP5 models and the regression model that project the total 1900–2100 warming (Fig. 4) to stay below 2 °C under the RCP4.5 scenario. The mean warming (2.8 °C) of models with fully interactive aerosols is statistically significantly different (p = 0.001 for the Welch two sample t test) from the mean (2.3 °C) of models without it. Thus the aerosol indirect effect, as it is presently represented in climate models, leads to higher models’ projected global warming than models without an indirect effect. In this regard it should be recalled that the aerosol indirect effect is regarded presently as a relatively poorly understood and simulated phenomenon.
The mean global warming between 1900 and 2100 as projected by 42 CMIP5 models and the regression model under the RCP4.5 scenario. Black columns designate models with a fully interactive aerosol (Flato et al. 2013; Table 9.1) and gray columns designate models without it. The red column is the mean warming of the CMIP5 models and the blue column is the global warming according to the regression model. Eight CMIP5 models and the regression model project the total 1900–2100 warming to stay below 2 °C under the RCP4.5 scenario. The mean warming of models with a fully interactive aerosol effect (2.8 °C) is statistically significantly different (p = 0.001 for the Welch two sample t test) from the mean (2.3 °C) of models without it
The choice of different forms of the AMO index in the regression model has little effect on the regression model total temperature (Fig. 5). However, the fraction of the AMO contribution (Table 3) to global warming increases significantly (by about a factor of two) in the second half of the twenty-first century (Fig. 5) due to the levelling off of the anthropogenic radiative forcing according to the RCP4.5 scenario (IPCC 2013).
a Assumed form of a cyclic AMO extended to 2100. b Simulated past and projected future temperatures by regression models with different AMO indices [after NOAA-Kaplan (T_K), van Oldenborgh (T_O), Trenberth and Shea (T_TS), and Parker (AMO_P)] are close to each other. The temperature projected by an ensemble mean of all CMIP5 RCP4.5 simulations (CMIP5-black dashed line) and the temperature variability projected by the CMIP5 model with the highest (GFDL-CM3-blue dash line) and the lowest (GFDL-ESM2G-orange dash line) projected warming. The observed NASA GISS temperature (T1200) is shown in red color. All temperature anomalies are 5 year moving averages normalized to zero within 1900–1910 mean. c Individual contributions of the anthropogenic greenhouse gases and aerosols (GHGA), solar variability (SOL), and the average AMO index towards the 1900–2015 warming and d towards 2015–2100 warming under the RCP4.5 scenario. Due to the levelling off of the GHGA radiative forcing during the second half of the twenty-first century, the relative contribution of the AMO (representing natural climate variability) to the GHGA in the twenty-first century is more than double what it was during the twentieth century (see also Table 3). The AMO in c, d stands for an average for the four considered AMO indices
8 Discussion and summary
In addition to the usual explanatory variables of the regression model (anthropogenic greenhouse gases and aerosols, solar variability, volcanic aerosols, and ENSO) we have included the AMO and the PDO as potential proxies for additional unforced natural climate variability. In agreement with earlier studies we confirm that the AMO is an effective explanatory variable (predictor) for the 1900–2015 global mean temperature while the PDO is not (Table 2). The parsimonious regression model (i.e., the version providing a balance of simplicity and accuracy) that accounts for 95.5 % of the global mean temperature variance (1900–2015) contains only three explanatory variables: radiative forcing due to anthropogenic greenhouse gases and aerosol (GHGA), the AMO index, and the solar variability (SOL). The regression model reproduces accurately the 1900–2015 warming (0.96 °C modeled compared to the observed 0.95 °C), and projects another 0.95 °C warming before the end of the twenty-first century under radiative forcing specified by the RCP4.5 pathway (IPCC 2013). There is a broad agreement between the projection of the future warming by the CMIP5 climate models and the regression model.
However, seven the CMIP5 models (GFDL-CM3, MIROC-ESM, MIROC-ESM-CHEM, HadGEM2-ES, HadGEM2-CC, CESM1-CAM5, and CSIRO-Mk3-6-0) project the future (2015–2100) global warming to be by a more than 1 °C higher that the regression model projection (Fig. 3b). All these models projecting the highest warming include a fully interactive aerosol effect (Flato et al. 2013). At the other end there are five CMIP5 models (Fig. 3b) that project a future global warming that is below that of the regression model.
Eight of the CMIP5 models (GFDL-ESM2G, GFDL-ESM2M, GISS-E2-R-p2, GISS-E2-R-CC, GISS-E2-R-p1, FIO-ESM, inmcm4, and FGOALS_g2) and the regression model project the total 1900–2100 global warming to stay below 2 °C, as long as anthropogenic radiative forcing does not exceed that specified by the RCP4.5 (IPCC 2013). We note that none of these models has a fully interactive aerosol as defined by (Flato et al. 2013, their Table 9.1).
The relative influence of the AMO (natural variability) is expected to increase during the second half of the twenty-first century, when the GHGA forcing, under the RCP4.5 scenario, will level off (Fig. 5). Our analysis shows that the anthropogenic warming will be of the same magnitude as natural variability during the second half of the twenty-first century if we limit GHG emissions to keep radiative forcing within the RCP4.5 scenario.
References
Booth B, Dunstone N, Halloran P, Andrews T, Bellouin N et al (2012) Aerosols implicated as a prime driver of twentieth-century North Atlantic climate variability. Nature 484:228–232
Camp C, Tung KK (2007) Surface warming by the solar cycle as revealed by the composite mean difference projection. Geophys Res Lett 34:L14703. doi:10.1029/2007GL030207
Canty T, Mascioli N, Smarte M, Salawitch R (2013) An empirical model of global climate—part 1: a critical evaluation of volcanic cooling, Atmos. Chem Phys 13:3997–4031. doi:10.5194/acp-13-3997
Chylek P, Dubey MK, Lohmann U, Ramanathan V, Kaufman YJ, Lesins G, Hudson J, Altman G, Olsen S (2006) Aerosol indirect effect over Indian Ocean. Geophys Res Lett 33:L06806. doi:10.1029/2005GL025397
Chylek P, Folland CK, Dijkstra H, Lesins G, Dubey MK (2011) Ice-core data evidence for a prominent near 20 year time-scale of the Atlantic Multidecadal Oscillation. Geophys Res Lett 38:L13704. doi:10.1029/2011GL047501
Chylek P, Hengartner N, Lesins G, Klett JD, Humlum O, Wyatt M, Dubey MK (2014a) Isolating the anthropogenic component of arctic warming. Geophys Res Lett 41:L14801. doi:10.1002/2014GL060184
Chylek P, Klett JD, Lesins G, Dubey MK, Hengartner N (2014b) The Atlantic Multi-decadal Oscillation as a dominant factor of oceanic influence on climate. Geophys Res Lett. doi:10.1002/2014GL059274
Chylek P, Vogelsang TJ, Klett JD, Hengartner N, Higdon D, Lesins G, Dubey MK (2016) Indirect aerosol effect increases CMIP5 models’ projected arctic warming. J Clim 29:1417–1428. doi:10.1175/JCLI-D-15-0362.1
Compo G, Sardeshmukh P (2009) Oceanic influences on recent continental warming. Clim Dyn 32:333–342
Delworth TL, Mann ME (2000) Observed and simulated multidecadal variability in the Northern Hemisphere. Clim Dyn 16:661–676. doi:10.1007/s003820000075
Delworth T, Zeng F (2012) Multicentennial variability of the Atlantic meridional overturning circulation and its climatic influence in a 4000 year simulation of the GFDL CM2.1 climate model. Geophys Res Lett 39:L13702. doi:10.1029/2012GL052107
Dima M, Lohmann G (2007) A hemispherical mechanism for the Atlantic Multidecadal Oscillation. J Clim 20:2706–2719
Douglass D, Clader B (2002) Climate sensitivity of the earth to solar irradiance. Geophys Res Lett. doi:10.1029/2002GL015345
Flato G et al (2013) Evaluation of climate models. In: Stocker T et al (eds) Climate change 2013: the physical science basis. Contribution of working group I to the 5th AR of the IPCC. Cambridge University Press, Cambridge
Foster G, Rahmstorf S (2011) Global temperature evolution 1979–2010. Environ Res Lett 6:044022. doi:10.1088/1748-9326/6/4/044022
Frankcombe L, Dijkstra H (2010) North Atlantic Multidecadal climate variability: an investigation of dominant time scales and processes. J Clim 23:3626–3638. doi:10.1175/2010JCLI3471.1
Frankcombe L, Dijkstra H (2011) The role of Atlantic-Arctic exchange in North Atlantic multidecadal climate variability. Geophys Res Lett. doi:10.1029/2011GL048158
Gray S, Graumlich L, Betancourt J, Pederson G (2004) A tree-ring based reconstruction of the Atlantic Multidecadal Oscillation since 1567 AD. Geophys Res Lett 31:L12205. doi:10.1029/2004GL019932
Haigh J (2003) The effect of solar variability bon the earth’s climate. Philos Trans R Soc Lond Ser A 361:95–111
Hansen J, Lebedeff S (1987) Global trends of measured surface air temperature. J Geophys Res 92:13345–13372
Hansen J, Ruedy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophysics 48:1–29
Humlum O, Solheim JE, Stordahl K (2011) Identifying natural contributions to late Holocene climate change. Glob Planet Change 79:145–156
IPCC (2013) Annex II: Climate System Scenario Tables [Prather M, Flato G, Friedlingstein P, Jones C, Lamarque J-F, Liao H, Rasch P (eds)]. In: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds)]. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA
Kaplan A, Cane M, Kushnir Y, Clement A, Blumenthal M, Rajagopalan B (1998) Analyses of global sea surface temperature 1856–1991. J Geophys Res 103:18567–18589
Kavvada A, Ruiz-Barradas A, Nigam S (2013) AMO’s structure and climate footprint in observations and IPCC AR5 climate simulations. Clim Dyn 41:1345–1364. doi:10.1007/s00382-013-1712-1
Lean JL, Rind DH (2008) How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys Res Lett 35:L18701. doi:10.1029/2008GL034864
Li X, Holland D, Gerber E, Yoo C (2014) Impacts of the north and tropical Atlantic Ocean on the Antarctic Peninsula and sea ice. Nature. doi:10.1038/nature12945
Mahajan S, Zhang R, Delworth T (2011) Impact of the Atlantic meridional overturning circulation (AMOC) on arctic surface air temperature and sea ice variability. J Clim 24:6573–6581
Mascioli N, Canty T, Salawitch R (2012) An empirical model of global climate—part 2: implications for future temperature. Atmos Chem Phys Discuss 12:23913–23974. doi:10.5194/acpd-12-23913-2012
Miksovsky J, Holtanova E, Pisoft P (2015) Imprints of climate forcings in global gridded temperature data. Earth Syst Dyn Discuss 6:2339–2381. doi:10.5194/esdd-6-2339-2015
Muller RA et al (2013) Decadal variations in the global atmospheric land temperatures. J Geophys Res 118:5280–5286. doi:10.1002/jgrd.50458
Otterman J et al (2002) Are stronger North-Atlantic southwesterlies the forcing to the late-winter warming in Europe? Int J Climatol 22:743–750. doi:10.1002/joc.681
Parker D, Folland C, Scaife A, Knight J, Colman A, Baines P, Dong B (2007) Decadal to multidecadal variability and the climate change background. J Geophys Res 112:D18115. doi:10.1029/2007JD008411
Polyakov I, Johnson M (2000) Arctic decadal and interdecadal variability. Geophys Res Lett 27:4097–4100
Scafetta N (2012) Multi-scale harmonic model for solar and climate cyclical variation throughout Holocene based on Jupiter-Saturn tidal frequencies plus the 11-year solar dynamo cycle. J Atmos Solar Terrestr Phys 80:296–311. doi:10.1016/j.jastp.2012.02.016
Scafetta N, West B (2006) Phenomenological solar contribution to the 1900–2000 global surface warming. Geophys Res Lett 33:L05708. doi:10.1029/2005GL025539
Schlesinger ME, Ramankutty N (1994) An oscillation in the global climate system of period 65–70 years. Nature 367:723–726. doi:10.1038/367723a0
Toggweiler JR, Russell J (2008) Ocean circulation in a warming climate. Nature 451:286–288. doi:10.1038/nature06590
Trenberth K, Shea D (2006) Atlantic hurricanes and natural variability in 2005. Geophys Res Lett 33:L12704. doi:10.1029/2006GL026894
Tung K, Zhou J (2013) Using data to attribute episodes of warming and cooling in instrumental records. PNAS 110:2058–2063. doi:10.1073/pnas.1212471110
van Oldenborgh G, te Raa L, Dijkstra H, Philip S (2009) Frequency- or amplitude-dependent effects of the Atlantic meridional overturning on the tropical Pacific Ocean. Ocean Sci 5:293–301. doi:10.5194/os-5-293-2009
Wilcox L, Highwood E, Dunstone N (2013) The influence of anthropogenic aerosol on multi-decadal variations of historical global climate. Env Res Lett. doi:10.1088/1748-9326/8/2/024033
Wilks DS (2006) Statistical methods in the atmospheric sciences. Academic Press, Cambridge
Zhang R, Delworth TL, Held IM (2007) Can the Atlantic Ocean drive the observed multidecadal variability in Northern Hemisphere mean temperature? Geophys Res Lett 34:L02709. doi:10.1029/2006GL028683
Zhang R, Delworth TL, Sutton R et al (2013) Have aerosol caused the observed Atlantic Multidecadal variability? J Atmos Sci 70:1135–1144. doi:10.1175/JAS-D-12-0331.1
Zhou J, Tung KK (2013) Deducing multidecadal anthropogenic warming trend using multiple regression analysis. J Atmos Sci 70:3–8. doi:10.1175/JAS-D-12-0208.1
Acknowledgments
Reported research (LA-UR-14-27366) was supported in part by the Los Alamos National Laboratory Center for Space and Earth Sciences. The authors thank to Chris Folland for providing an updated AMO_P index.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chylek, P., Klett, J.D., Dubey, M.K. et al. The role of Atlantic Multi-decadal Oscillation in the global mean temperature variability. Clim Dyn 47, 3271–3279 (2016). https://doi.org/10.1007/s00382-016-3025-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3025-7