Abstract
Sea-level variability in the Mediterranean Sea was investigated by means of in-situ (tide-gauge) and satellite altimetry data over a period spanning two decades (from 1993 to 2012). The paper details the sea-level variations during this time period retrieved from the two data sets. Mean sea-level (MSL) estimates obtained from tide-gauge data showed root mean square differences (RMSDs) in the order of 40–50 % of the variance of the MSL signal estimated from satellite altimetry data, with a dependency on the number and quality of the in-situ data considered. Considering the individual time-series, the results showed that coastal tide-gauge and satellite sea-level signals are comparable, with RMSDs that range between 2.5 and 5 cm and correlation coefficients up to the order of 0.8. A coherence analysis and power spectra comparison showed that two signals have a very similar energetic content at semi-annual temporal scales and below, while a phase drift was observed at higher frequencies. Positive sea-level linear trends for the analysis period were estimated for both the mean sea-level and the coastal stations. From 1993 to 2012, the mean sea-level trend (\(2.44\pm 0.5\) mm year\(^{-1}\)) was found to be affected by the positive anomalies of 2010 and 2011, which were observed in all the cases analysed and were mainly distributed in the eastern part of the basin. Ensemble empirical mode decomposition showed that these events were related to the processes that have dominant periodicities of \(\sim\)10 years, and positive residual sea-level trend were generally observed in both data-sets. In terms of mean sea-level trends, a significant positive sea-level trend (\(>\)95 %) in the Mediterranean Sea was found on the basis of at least 15 years of data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The sea level is a key indicator of climate change. Estimating sea-level rise is one of the most important scientific issues, with a large societal benefit and impact. In the Fifth Assessment Report (AR5) of the Intergovernmental Panel on Climate Change (IPCC), Church et al. (2013) underline the importance of instrumental records to analyze the past sea-level changes. The focus of the present study is the sea-level variability retrieved from observational datasets.
The difficulties in estimating reliable sea-level changes are due mainly to the sampling shortcomings of the two observational datasets: tide gauges provide measurements of the sea-level relative to the solid Earth, with a coarse spatial resolution, while the altimeter measures the range between the satellite and the sea surface (Cazenave and Nerem 2004) covering approximately only two decades.
Despite the sparse sampling, tide gauges have been fundamental in highlighting the trend in the rise in sea levels in the last century (Douglas 1991, 1997). Tide-gauge records have also always been used to calibrate altimeter sea level measurements, in order to obtain a highly accurate mean sea level (Mitchum 2000, 1998, 1994; Leuliette et al. 2004). The combination of the two data-sets has been used in previous works for several purposes. Fenoglio-Marc (2004) and García et al. (2012) combined satellite altimetry and tide gauge data in the Mediterranean Sea to estimate vertical motions of the Earth’s crust. Using a generalized least squares method, Mangiarotti (2007) performed a joint analysis of TOPEX/Poseidon satellite altimetry and tide gauge data to estimate sea level trends along the Mediterranean Sea coasts.
Global and regional sea-level reconstructions (Church and White 2011; Church et al. 2010; Calafat and Gomis 2009) aim to reproduce the multi-decadal sea-level variability over a continuous spatial domain, combining the spatial and the temporal information from the two data-sets.
The two data-sets are generally combined in order to fill the space and time gaps, however in order to do this we first needed to examine the consistency of the two data-sets at the regional scale. A key issue is to assess the reliability of the mean sea-level (MSL) estimate obtained from tide-gauge stations and to compare it with the estimate derived from satellite altimetry in the Mediterranean basin.
The Mediterranean Sea is a particularly interesting area for investigating mean sea-level variability and trends. As explained in Pinardi et al. (2014), when considering a limited area of the world ocean, the mean sea-level tendency is also dominated by lateral mass transport fluxes, which makes the regional mean sea-level very different from the global level (Church et al. 2013). In the Mediterranean Sea, Gibraltar mass transport almost balances the surface water flux, thus changing the nature of the mean sea-level trend.
In the literature, the works that focus on sea-level variability and trends in the Mediterranean Sea by comparing tide-gauge and satellite altimetry data, usually consider a limited number of tide-gauge stations in sub-regional basins, using along-track satellite altimetry data (Vignudelli et al. 2005; Pascual et al. 2007; Fenoglio-Marc et al. 2012; Birol and Delebecque 2014). In addition multi-mission gridded satellite altimetry data are used (Fenoglio-Marc 2002; Cazenave et al. 2002; Pascual et al. 2009), which in the version for the global ocean are not suitable for resolving the sea-level variability due to the meso-scale dynamics in the Mediterranean Sea (Robinson and Golnaraghi 1994; Robinson et al. 2001; Pinardi et al. 2015).
In this work we investigated how satellite altimetry data resolve the sea-level near the coasts. We used a regional multi-mission satellite altimetry gridded data-set and all the tide-gauge records available in the Mediterranean Sea over a 20-year period (1993 to 2012). The aim was to understand whether the offshore sea-level altimetry signals were representative of the local sea-level recorded by tide gauges along the basin coasts, in terms of temporal variability and linear trends, focusing on the significance of the linear trend estimates.
Recent works have investigated non-linear sea-level variability and long-term residual trends (Spada et al. 2014; Galassi and Spada 2015) on the basis of tide-gauge time series and performing Empirical Mode Decompositions (EMDs) (Huang et al. 1998; Wu and Huang 2009; Torres et al. 2011).
We also set out to identify the temporal scales of the processes that characterize the sea-level variations in the Mediterranean basin. We used EMD methods to compare sea-level signals from coastal tide-gauge records, distributed almost over the entire Mediterranean basin, together with time-series retrieved from satellite altimetry data, which to the best of our knowledge have never been analysed in the study area using this method. The expected result was to identify the leading modes of oscillation of the sea level in the Mediterranean Sea and to obtain the long-term residual trend, from both data-sets.
The paper is organized as follows. Section 2 describes the data used in the sea-level signal analysis. An analysis of sea-level components retrieved by each observational instrument is provided in Sect. 3. The MSL estimates in the Mediterranean Sea retrieved from both data-sets are compared in Sect. 4. The coastal sea level from tide gauges and the open-ocean sea level from altimetry are compared in terms of temporal variability and trends in Sect. 5. Section 6 focuses on the non-linear sea-level variations. The sea-level trend significance is discussed in Sect. 7. All the results are summarized in Sect. 8 and some conclusions are drawn.
2 Data sets
2.1 Tide gauge data
The Permanent Service for Mean Sea Level (PSMSL) records for the Mediterranean Sea are available from around 1900, however these records suffer from a discontinuous spatial distribution and a significant gap in the southern part of the basin (North Africa). In-situ sea-level data are provided by the PSMSL (Holgate et al. 2013; PSMSL 2015) as monthly means. Our focus is on the Revised Local Reference (RLR) dataset (Woodworth and Player 2003), which is recommended for scientific purposes. The RLR data-set reduces all the records collected to a common datum for the analysis of time series. In order to avoid negative numbers in the resulting RLR monthly and annual mean values, this reduction is performed using the tide gauge datum history and a common reference level of approximately 7000 mm below the average sea-level (Klein and Lichter 2009).
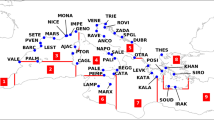
In the Mediterranean basin there are 100 tide gauge stations of the RLR dataset covering the period from 1993 to 2012 (satellite time window). Less than half of these show a complete time series. We selected 23 stations that have at least 85 % of the complete time series during the analysis period. Figure 1, top panel, shows the spatial distribution of tide gauge stations over the basin: black points represent the positions of the stations selected. The bottom panel in Fig. 1 shows the number of tide-gauge stations available during our analysis period.
Note that during the last few years (e.g. 2012) the total number of stations available in the Mediterranean basin has been very close to the number of stations selected. Table 1 shows the metadata of these stations and the completeness of their time-series expressed as a percentage (Columns from 1 to 4).
Vertical land motion (VLM) can affect sea-level measurements over different temporal scales with different processes. Local sea-level measurements are influenced by VLM due to Glacial Isostatic Adjustment (GIA), tectonics, subsidence, sedimentation and self-attraction and loading (SAL; Tamisiea et al. 2010) which can contaminate the trends (Calafat and Gomis 2009) and affect the estimate of reliable sea-level rates purely associated with the ocean dynamics.
Permanent GPS stations co-located at tide-gauge stations (GPS@TG; Santamaría-Gómez et al. 2012) accurately estimate the long-term VLM and correct tide-gauge records (Wöppelmann et al. 2007, 2009; Wöppelmann and Marcos 2012). Although much has been done to combine the information from tide-gauge and GPS measurements (Santamaría-Gómez et al. 2012; http://www.sonel.org/), however GPS@TG still do not cover all tide-gauge sites, either at a global or regional scale (e.g. the Mediterranean Sea). On the other hand, land motions related to GIA can be simulated in global geodynamic models (Peltier 2001, 2004b). Aware of VLM processes that are not taken into account using a GIA model, in this work we follow the approach typically used in the literature (e.g., Church and White 2011) and consider the GIA as the only VLM correction to be applied to both observational data-sets. The GIA computations (Table 1, Column 11) were performed with the aid of an improved version of SELEN (Spada and Stocchi 2007; Spada et al. 2012) which solves the sea-level equation assuming a spherically symmetric, and rotating Earth model. The sea-level equation is solved at a harmonic degree \(\ell _{max}=128\) on a quasi–regular icosahedral grid with a spacing of \(\sim 40\) km, adopting the ICE-5G(VM2) deglaciation chronology of Peltier (2004a). Mantle incompressibility is assumed, and the formulation by Milne and Mitrovica (1998) was used to describe the rotational feedback on sea-level changes.
2.2 Satellite data
The specific satellite Sea Level Anomaly (SLA) fields used in this study are described by Pujol and Larnicol (2005) and Landerer and Volkov (2013). Along track sea-level data are corrected for long wavelength errors (Traon et al. 1998; Le Traon et al. 2003) and an estimate of the inverse barometer (IB) effect is subtracted as well as wind and tidal effects in addition to other atmospheric corrections (taken together these are called dynamic atmospheric corrections; Carrère and Lyard 2003). The dynamic atmospheric correction (DAC) combines the high frequency sea-level variability (time scales less than 20 days) of the MOG2D-G model with the low frequency signals (greater than 20 days) of the IB correction (Carrère and Lyard 2003; Landerer and Volkov 2013).
The data set used in this analysis is based on six satellites: TOPEX/Poseidon (September 1992 to October 2005), Jason-1 (August 2002 onwards), Jason-2 (January 2009 onwards), ERS-1 (October 1992 to May 1995), ERS-2 (May 1995 to June 2003), Envisat (June 2003 onwards). Starting with different satellite along-track data, the different SLA signals are interpolated with objective analyses (Ducet et al. 2000), thereby producing a field on a regular grid with a horizontal resolution of \(1/8^{\circ }\) (\(\sim\) 13 km), every seven days. Gridded fields were collected from the merged regional products for the Mediterranean Sea, distributed by Archiving, Validation, and Interpretation of Satellite Oceanographic data (AVISO), which are freely available at http://www.aviso.altimetry.fr. Data were averaged monthly in order to use the same temporal resolution as the in-situ data.
3 Analysis of sea-level components
The formalism for the description of the sea-level signal components in the in-situ and satellite sea-level measurements is given in Appendix 1.
In order to compare satellite SLA and tide gauge sea-level data, we start by defining the SLA signal from the satellite. The SLA is given by the difference between the sea-level and its mean, calculated over a reference period from 1993 to 1999 (Pujol and Larnicol 2005). We assume that this mean value contains an approximation of the height of the geoid above the reference ellipsoid (Cazenave et al. 1998, 2002) and the mean dynamic topography. The resulting component, shown in Eq. (1), is corrected for tides and the inverse barometer effect, as well as wind effects, as explained in Sect. 2.2.
Following the literature (Cazenave et al. 2003; Cazenave and Llovel 2010) we define the MSL as the average area of the previous component (Eq. 2).
As described in Pinardi et al. (2014) the MSL in the Mediterranean Sea is composed of two parts: an incompressible or mass component due to the balance between the net volume transport at the Gibraltar Strait (normalized by the Mediterranean basin area) and the net surface water flux, and a steric component due to the buoyancy fluxes that account for the thermosteric and halosteric components (Eq. 3).
Subtracting our estimate of MSL from the SLA signal from the satellite, we obtain the space and time dependent sea-level component from the satellite, which is then compared with in-situ data (Eq. 4).
Next we consider the in-situ sea-level measured by tide gauges. Tide-gauge records provide a sea-level signal without any corrections applied. We can assume that the in-situ measured sea-level contains the MSL, geoid, the low frequency response of the sea surface to the atmospheric pressure, the high frequency response to the atmospheric pressure and wind (both accounted for by the DAC in the satellite data), the local datum correction and a time- and space-dependent local sea-level component (Eq. 5). The local datum correction is computed by removing the temporal mean from each tide gauge station time series. The effect of the high frequency response to the atmospheric pressure and wind is minimized in our analysis, considering monthly averaged data. The low frequency response to the atmospheric pressure (inverse barometer effect) can be considered as in Dorandeu and Traon (1999), as shown in Eq. (6). In order to account for this component, we used the Mean Sea Level Pressure (MSLP) of the European Centre for Medium-Range Weather Forecasts (ECMWF) Re-analysis dataset (ERA-Interim; Dee et al. 2011).
The effects of the atmospheric forcings on the free surface also affect the sea-level trends (Tsimplis et al. 2005; Marcos and Tsimplis 2007; Gomis et al. 2008). Considering DAC, Pascual et al. (2008) observed a sea-level trend, over the period 1993–2001, due to the effect of the atmospheric forcings, of the order of \(\sim\)0.6 mm year\(^{-1}\). On the other hand, the same authors observed minimum values in the Western Mediterranean basin and maximum values in the Levantine basin, up to 2 mm year\(^{-1}\).
In order to compare analogous signals in tide gauges and satellite altimetry products, in our approach we only need to use the space- and time- dependent components described above (\(\eta _{ins}^{var}\) and \(\eta _{sat}^{var}\) in Eqs. 4, 5 respectively).
4 Mean sea-level estimates
In this section we compare the possible MSL estimates considering satellite altimetry and tide-gauge data in the Mediterranean Sea.
In order to examine the reliability of the MSL estimate obtained from tide-gauge stations and to compare it with the estimate derived from satellite altimetry, which provides a much better spatial coverage, a bootstrap analysis (Efron and Tibshirani 1997) was carried out, considering an increasing number of randomly distributed tide-gauge stations in the computation of the MSL estimate.
Figure 2, top panel, shows the MSL estimates obtained from satellite altimetry (solid red line) and tide-gauge data, considering both all the stations available during the analysis period (dashed blue line) and only the stations selected for our analysis (solid black line). The bottom panel in Fig. 2 shows the results of the bootstrap analysis in terms of the correlation coefficient (black lines) and Root Mean Square Difference (RMSD), normalized by the standard deviation of the satellite altimetry data (red lines; hereafter RMSD* in the text), both considering the total number of tide-gauge stations available (dashed lines) and only the stations selected for this work (solid lines). The results show that MSL estimates from tide gauges are clearly dependent on the number of stations considered and on the quality of the data considered, given the completeness of the tide-gauge time-series. In general considering a larger number of stations, the correlation coefficient tended to increase, while the RMSD* tended to decrease, up to 0.87 and 0.53, respectively, considering the total number of tide-gauges available. When only the 23 tide-gauge stations selected for our analysis were taken into account, the MSL estimates from tide gauges were slightly more reliable than the estimate using all stations of a lower quality, with correlation coefficients up to the order of 0.9 (0.4 of RMSD*). Despite the high correlation, due to the seasonal signal contained in the MSL estimates, the RMSD* of the MSL estimates obtained from the tide-gauges were in the order of 40–50 % of the variance of the MSL signal obtained considering satellite altimetry data. Thus we conclude that tide-gauge stations do not give a good enough estimate of MSL in the Mediterranean Sea, and that satellite MSL estimates should be used to correct tide-gauge sea levels for these effects.
5 Comparison of in-situ and satellite altimetry data
A comparison of satellite and tide-gauge signals (\(\eta _{ins}^{var}\) and \(\eta _{sat}^{var}\) in Appendix 1) at tide-gauge stations is shown in Table 1 using the nearest satellite altimeter grid point.
In general satellite altimetry and tide-gauge signals were comparable in most of the cases considered, with RMSDs that ranged between 2.5 and 5 cm against a trough–to–peak amplitude of the in-situ sea-level signal that ranged between 20 and 30 cm. The two data-sets also were significantly correlated up to 0.8.
In the western part of the basin, moving from Gibraltar up to the Gulf of Lion, the two sea-level signals were positively correlated with a lower correlation coefficient (0.5) in the Alboran Sea, which reached higher values (\(\sim\)0.6 and 0.7) along the Catalan and the southern French coasts respectively. Figure 3 shows Malaga, L’Estartit (top panels) and Marseilles (central left panel).
Higher correlations were found in the northern Adriatic (Fig. 3), where the Trieste station (central right panel) showed a very high correlation (0.87) among altimetry and tide gauges. Similar correlations patterns were observed in Dubrovnik and Split (bottom left panel).
In the central part of the basin, the Valletta station (Fig. 3 bottom left panel), showed a high correlation between the two signals (0.78), which mean that the sea-level signal captured by the tide gauge station in Malta is an open-ocean signal.
In the Ionian Sea the coastal sea-level signals were well correlated between tide gauge and satellite altimetry (0.55–0.75), with RMSDs that ranged between 3 and 5.5 cm, i.e. Levkas, Preveza, Katakalon and Kalamai Fig. 4, top right panel), located along the Greek coasts as far as the Peloponnesus peninsula.
In the Aegean Sea, altimetry and tide gauges were comparable in terms of correlation coefficients which ranged between 0.6 to the order of 0.8. Figure 4 shows the cases of: Thessaloniki and Alexandroupolis (top left panel) in the northern part of the sub-basin; Khios (central right panel) in the Sporades archipelago; Leros and Siros (central left panel) in the Cyclades archipelago; and Soudhas (bottom right panel) in Crete.
In the Levantine basin, we only analyzed one tide gauge station (the only one available). Figure 4 shows the Hadera station (bottom left panel), where satellite data are representative of the decadal variability in the sea-level signal captured by the tide gauge measurements, resulting in a correlation coefficient of the order of \({\sim}0.65\) and RMSD of 5 cm.
Note that in all stations analysed, there were large positive sea-level anomalies in 2010 and 2011. This is in agreement with findings by Landerer and Volkov (2013) during the same period in the Mediterranean Sea.
Landerer and Volkov (2013) also found the highest correlation patterns between wind stress in the Gibraltar Strait and the sea-level signal in Mediterranean Sea, the Northern Adriatic, the Central Mediterranean and in the Levantine basin.
Considering satellite altimetry data in the years 2010–2011, Fig. 5 shows the difference between the sea-level anomaly field and climatology computed without considering 2010 and 2011.
Most of the large positive differences (\(>\)5 cm) occur in the Adriatic, along the Tunisian shelf and in the Levantine basin. Large positive anomalies are also evident in front of the Gulf of Sirte and in the Aegean Sea.
In order to compare the \(\eta _{ins}^{var}\) and \(\eta _{sat}^{var}\) in detail, Fig. 6 shows the average of all the tide-gauge stations with the average satellite altimetry at the same stations.
Figure 6 (top panel) shows that the signals are highly correlated (0.9) and that the RMSD is low (1.3 cm), which corresponds to 40 % of the variance in the tide-gauge signal.
The tide gauge-satellite altimetry sea-level comparison was also evaluated by a power spectra comparison and coherency analysis. For the coherency analysis, smoothing was performed over eight adjacent frequencies. A frequency window between 60 and 2 months was selected in order to clearly represent the power spectra, given the relevant temporal scales of sea-level variability and the amount of data available.
It is clear that the tide-gauge and satellite sea-level signals reach a similar energy content in the spectral window between 60 and 6 months.
Considering higher frequency processes, differences can be noted in the energy content and a phase drift between the two signals (Fig. 6, bottom left panel). In the window between 5 and 3 months, satellite data have a higher energy content than the tide-gauge signal. The opposite is observed considering the window between 3 and 2 months (Fig. 6, bottom right panel).
6 Non-linear sea-level variations
In this section we investigate the non-linear sea-level variations and trends in the Mediterranean Sea, during our analysis period, using EMD methods (Huang et al. 1998). EMD is particularly suitable for analyzing non-linear and non- stationary time series (Barnhart 2011). Ezer and Corlett (2012) applied this method to monthly sea-level in-situ data, as we did in this work, explaining that each oscillatory mode (Intrinsic Mode Function, IMF) represents different oceanic processes from the highest frequency to the lowest frequency oscillating mode. The remaining non-oscillating mode is the residual, or the trend in the case of sea level. Spada et al. (2014) used an improved version of the EMD method, the Complete Ensemble EMD (CEEMD; Torres et al. 2011) to study the long term sea-level variations in Greenland using the longest tide-gauge time-series. In this study, we used CEEMD to compare sea-level signals from our observational data sets. Considering 20 years of monthly data, CEMMD gives 7 IMFs in both data-sets considered. Significant correlations were found for all the modes (0.8–0.9), which increase up to 0.97 considering the residual trend (mode 7). The almost identical EMD trends in both data-sets showed a non-linear trend with an increased slope in recent years. Figure 7 shows the combination of IMFs that explain the high-frequency (top panel) and the low-frequency (central panel) modes of oscillation, and the residual trend (bottom panel). Note that modes 5 (3.5 years) and 6 (7 years) show the maxima in 2010. The combination of these two IMFs (Fig. 7 central panel) shows a positive peak of 4 cm, which once added to the other modes of variability, explains the large anomalies observed during 2010 (Fig. 6). According to this analysis, the sea-level anomalies observed during 2010 and 2011 are associated with the result of signals with dominating periodicities of \(\sim\)10 years. On the other hand, the positive peaks observed during 1996 and 1997 and 2000 and 2001, as well as the negative anomalies in 2001 and 2006, are associated with processes that act over shorter temporal scales, in particular with modes 1 to 4 that explain from the intra-annual (\(<\)1 years) up to the \(\sim\) 2 year periodicity of sea-level variability (Fig. 7 top panel).
7 Significance of the linear sea-level trend
In this section we compare the tide-gauge and altimetry in terms of sea-level linear trends. A trend analysis was performed using the least squares method, as described in Spada and Galassi (2012). The formalism for the trend analysis is given in Appendix 2.
Figure 8 shows the marked spatial variability of the sea-level \(\eta _{sat}^{var}\) trend, as well as for \(\eta _{ins}^{var}\) in a representative number of tide gauge locations (seventeen out of twenty-three stations analysed). Interestingly the Adriatic and Aegean Seas have high positive trends, up to 3 mm year\(^{-1}\). There are also positive values in most of the Eastern basin, especially where recurrent gyres and eddies in the circulation are found. Maximum positive values, with more than 6 mm year\(^{-1}\), have been found in the Levantine basin, west of Crete (Pelops gyre) (Pinardi et al. 2006). Similar peaks have been shown at the location of the Mersa-Matruh gyre. On the other hand, a negative trend (<−4 mm year−1) has been observed in the Ionian Sea as a consequence of an important change in the circulation observed in this basin since the beginning of the 1990s. (Demirov and Pinardi 2002; Pinardi et al. 2015). We found a maximum negative trend in the Levantine basin, south-east of Crete associated with the Ierapetra gyre.
The trend for \(\eta _{MSL}\), shows a rise of \(2.44\pm 0.5\) mm year\(^{-1}\) from 1993 to 2012, after first removing the seasonally repeating cycle and considering the contribution of GIA as a mean value (Peltier 2004b, 2009; Stocchi and Spada 2009; Meyssignac et al. 2011). The observed positive sea-level trend is in agreement with the resuts of Haddad et al. (2013) obtained by performing a singular spectrum analysis (SSA) with satellite altimetry data to estimate the seasonal cycle and trend, in almost the same analysis period.
The significance of linear trends can be analysed by the method described in Liebmann et al. (2010) to estimate the global surface temperature trends. Considering the MSL signal obtained from satellite altimetry data, Fig. 9 (top left panel) shows every possible trend (mm year\(^{-1}\)) computed as a function of the length of the period considered (2-year changes discarded). Each point in the diagram indicates a sea-level trend up to a specific year (x-axis) obtained by considering the number of years expressed on the y-axis. The results are multiplied by the number of years considered to emphasize the differences.
One of the most interesting results of this analysis is that there is no clear trend between 1998 and 2009, as confirmed by the trend significance analysis (bottom left panel) performed by bootstrapping the results. This analysis underlines the fact that to find a significant positive trend in the Mediterranean basin, it is necessary to consider at least 15 years of data, from 1993 to 2007. A period of 17 years gives a trend significance level of 99.9 %. If we calculate the trend between 1993 and 2009, only a value of \(2 \pm 0.6\) mm year\(^{-1}\) is found. This evidence also suggests that the sea-level trend from 1993 to 2012 is associated with 2010–2011 events, as previously discussed.
8 Summary and conclusions
The sea-level dynamics of the Mediterranean Sea were evaluated in terms of variability and trends using tide-gauge and satellite altimetry data over two decades (from 1993 to 2012). An initial result of this work regards the reliability of the MSL estimates that can be retrieved from sparse in-situ data in the Mediterranean Sea, compared to those obtained from satellite altimetry data. Bootstrap analysis showed a dependency on the number of stations considered (spatial dependency due to sampling error) and on the quality of the data considered. Considering the total number of tide-gauge stations showing the most complete time-series (\(>\)85 %), the two MSL estimates showed the highest level of reliability, with a correlation coefficient up to the order of 0.9. Despite the high correlation patterns observed, due to the seasonal signal contained in the MSL estimates, the RMSDs* of the MSL estimates obtained from tide-gauge signals were in the order of 40–50 % of the variance of the MSL signals obtained considering satellite altimetry data.
When in-situ and satellite altimetry data were processed in order to select similar geo-physical signals (Sect. 3), the sea-level variability between the two data sets was comparable in terms of amplitude and temporal evolution. In general we found RMSDs between the in-situ and satellite sea-level that ranged between 3–5 cm against a through-to-peak amplitude of the in-situ sea-level signal that ranged between 20 and 30 cm. In all the cases, the two data sets were significantly correlated up to 0.5–0.8.
In all the stations analysed there were large positive sea-level anomalies in 2010 and 2011, with a spatial pattern mainly distributed in the eastern part of the basin (Fig. 5). These positive anomalies were also observed by averaging the individual time-series. Averaging tide-gauge and satellite data in the tide-gauge positions, the correlation between the two data-sets increased to 0.9 and a small RMSD value (1.3 cm) was observed, compared to those found by analysing each location individually (Table 1). Evaluating the resulting time-series by power spectra comparison and coherence analysis, the results showed that between the inter-annual (5 years) and semi-annual (6 months) time scales, the two signals had a similar energy content and were highly coherent, while differences in the energy content and a phase drift were observed considering higher frequency processes (\(<\)6 months). CEEMD analysis, performed to investigate the non-linear sea-level variability, produced 7 IMFs in both data-sets considered. All the IMFs identified, which account for different temporal scales of variability, were very significantly correlated, up to the order of 0.9. The residual trends were almost identical in the two data-sets and showed a non-linear trend with an increased slope in recent years. The large anomalies observed in 2010 were related to the result of signals with dominating periodicities of \(\sim\)10 years, described by IMFs 5 and 6. On the other hand, the maxima observed in 1996–1997 and the negative anomalies in 2001 and 2006, were related to higher frequency variability.
Turning now to the local sea-level trends, almost in all the cases analysed positive rates were observed. A good agreement between the rates estimated from tide gauge data and satellite data was found only in the cases where the most complete time series were available, and where the two signals had a similar standard deviation (Columns 7 and 8 in Table 1), with a few exceptions.
In all the cases analysed, sea-level signals were characterized by large positive anomalies in 2010 and 2011, which were mainly due to large positive differences (with respect to climatology) observed in the eastern part of the basin (Fig. 5). This in agreement with Oddo et al. (2014) who, looking at the sensitivity of the Mediterranean sea level to atmospheric pressure, observed a large scale zonal gradient, which produces higher sea-level values and a larger variance in the sea-level signal in the Levantine basin. These events have already been observed at the basin scale (Calafat et al. 2010, 2012; Tsimplis et al. 2013) and defined as non-steric fluctuations due to mass transport through the Strait of Gibraltar driven by wind, occurring during a strong negative phase of the North Atlantic Oscillation (Landerer and Volkov 2013).
Considering the longest tide-gauge time-series in the Adriatic Sea, Galassi and Spada (2015) associated these anomalies with the periodic occurrence of opposite phases of the NAO and Atlantic Multidecadal Oscillation (AMO) indices, which show a similar periodicity (\(\sim\)20 years) with one of the most energetic modes of variability in the sub-basin.
With regard to the mean sea-level trend, a positive trend of \(2.44\pm 0.5\) mm year\(^{-1}\) was estimated during the period from 1993 to 2012. However local sea-level changes were large and very different: the highest values were found in the central Mediterranean Sea, in the Adriatic, and along the Tunisian coasts. Different sea-level positive rates were observed by averaging tide-gauge and satellite altimetry data in the tide-gauge positions, which were higher considering in-situ data (\(3.5\pm 0.7\) mm year\(^{-1}\)) compared to altimetry data (\(2.64\pm 0.6\) mm year\(^{-1}\)). These results were confirmed by applying a least squares method to the residual signals given by EMD, which obtain more accurate sea-level trend estimates.
The trend sensitivity study of the time series length shows that in order to obtain a significant and stable positive trend between 1993 and 2012, more than 15 years of data should be considered, and a 17 year period obtains a trend significance level of 99.9 %. Computing the mean sea-level trend between 1993 and 2009, only a value of \(2.06\pm 0.67\) mm year\(^{-1}\) was found. This evidence also suggests that the sea-level trend from 1993 to 2012 is associated with events from 2010 to 2011.
References
Barnhart BL (2011) The Hilbert-Huang transform: theory, applications, development. Ph.D. thesis, University of Iowa
Birol F, Delebecque C (2014) Using high sampling rate (10/20 Hz) altimeter data for the observation of coastal surface currents: a case study over the northwestern Mediterranean Sea. J Mar Syst 129:318–333
Calafat F, Chambers D, Tsimplis M (2012) Mechanisms of decadal sea level variability in the eastern North Atlantic and the Mediterranean Sea. J Geophys Res Oceans 117(C9):1978–2012
Calafat FM, Gomis D (2009) Reconstruction of Mediterranean sea level fields for the period 1945–2000. Glob Planet Change 66(3–4):225. doi:10.1016/j.gloplacha.2008.12.015
Calafat FM, Marcos M, Gomis D (2010) Mass contribution to Mediterranean Sea level variability for the period 1948–2000. Glob Planet Change 73(3):193–201
Carrère L, Lyard F (2003) Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing - comparisons with observations. Geophys Res Lett 30(6):1275. doi:10.1029/2002GL016473
Cazenave A, Llovel W (2010) Contemporary sea level rise. Annu Rev Mar Sci 2:145–173. doi:10.1146/annurev-marine-120308-081105
Cazenave A, Nerem RS (2004) Present-day sea level change: observations and causes. Rev Geophys 42:RG3001. doi:10.1029/2003RG000139
Cazenave A, Dominh K, Gennero M, Ferret B (1998) Global mean sea level changes observed by Topex-Poseidon and ERS-1. Phys Chem Earth 23(9–10):1069–1075. doi:10.1016/S0079-1946(98)00146-3, http://www.sciencedirect.com/science/article/pii/S0079194698001463
Cazenave A, Bonnefond P, Mercier F, Dominh K, Toumazou V (2002) Sea level variations in the Mediterranean Sea and Black Sea from satellite altimetry and tide gauges. Glob planet change 34(1–2):59–86
Cazenave A, Cabanes C, Dominh K, Gennero MC, Le Provost C (2003) Present-day sea level change: observations and causes. Space Sci Rev 108(1):131–144. http://www.springerlink.com/content/l5uh627038364344/
Church JA, White NJ (2011) Sea-level rise from the late 19th to the early 21st century. Surv Geophys 32:585–602
Church J, Woodworth P, Aarup T, Wilson S (2010) Understanding sea-level rise and variability. Wiley-Blackwell, Hoboken
Church J, Clark P, Cazenave A, Gregory J, Jevrejeva S, Levermann A, Merrifield M, Milne G, Nerem R, Nunn P, Payne A, Pfeffer W, Stammer D, Unnikrishnan A (2013) Sea level change. In: Stocker T, Qin D, Plattner G, Tignor M, Allen Allen S, Boschung J, Nauels A, Xia Y, Bex V, Midgley P (eds) Climate change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, Cambridge, United Kingdom and New York
Dee D, Uppala S, Simmons A, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda M, Balsamo G, Bauer P et al (2011) The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q J R Meteorol Soc 137(656):553–597
Demirov E, Pinardi N (2002) Simulation of the Mediterranean Sea circulation from 1979 to 1993: part I. The interannual variability. J Marine Syst 33:23–50
Dorandeu J, Le Traon PY (1999) Effects of global mean atmospheric pressure variations on mean sea level changes from TOPEX/Poseidon. J Atmos Ocean Technol 16(9):1279–1283
Douglas BC (1991) Global sea level rise. J Geophys Res Oceans 96: doi:10.1029/91jc00064, http://gen.lib.rus.ec/scimag/index.php?s=10.1029/91jc00064
Douglas BC (1997) Global sea rise: a redetermination. Surv Geophys 18: doi:10.1023/a:1006544227856, http://gen.lib.rus.ec/scimag/index.php?s=10.1023/a:1006544227856
Ducet N, Le Traon PY, Reverdin G (2000) Global high-resolution mapping of ocean circulation from TOPEX/Poseidon and ERS-1 and -2. J Geophys Res 105(C8):19477–19498. doi:10.1029/2000JC900063
Efron B, Tibshirani RJ (1997) An introduction to the bootstrap. Chapman & Hall, London
Ezer T, Corlett WB (2012) Is sea level rise accelerating in the Chesapeake Bay? A demonstration of a novel new approach for analyzing sea level data. Geophys Res Lett 39:L19605. doi:10.1029/2012GL053435
Fenoglio-Marc L, Dietz C (2004) Vertical land motion in the mediterranean sea from altimetry and tide gauge stations. Marine Geodesy 27: doi:10.1080/01490410490883441, http://gen.lib.rus.ec/scimag/index.php?s=10.1080/01490410490883441
Fenoglio-Marc L (2002) Long-term sea level change in the Mediterranean Sea from multi-satellite altimetry and tide gauges. Phys Chem Earth Parts A/B/C 27(32—-34):1419–1431. doi:10.1016/S1474-7065(02)00084-0
Fenoglio-Marc L, Braitenberg C, Tunini L (2012) Sea level variability and trends in the adriatic sea in 19932008 from tide gauges and satellite altimetry. Phys Chem Earth Parts A/B/C 40–41(0):47–58, doi:10.1016/j.pce.2011.05.014, http://www.sciencedirect.com/science/article/pii/S1474706511001008, the Climate of Venetia and Northern Adriatic
Galassi G, Spada G (2015) Linear and non-linear sea-level variations in the Adriatic Sea from tide gauge records (1872–2012). Ann Geophys 57(6). doi:10.4401/ag-6536
García F, Vigo M, García-García D, Sánchez-Reales J (2012) Combination of multisatellite altimetry and tide gauge data for determining vertical crustal movements along northern mediterranean coast. Pure Appl Geophys 169(8):1411–1423
Gomis D, Ruiz S, Sotillo M, AlvarezFanjul E, Terradas J (2008) Low frequency Mediterranean sea level variability: the contribution of atmospheric pressure and wind. Glob Planet Change 63(2–3):215. doi:10.1016/j.gloplacha.2008.06.005
Greatbatch RJ (1994) A note on the representation of steric sea level in models that conserve volume rather than mass. J Geophys Res 99(C6):12767–12771
Griffies SM, Greatbatch RJ (2012) Physical processes that impact the evolution of global mean sea level in ocean climate models. Ocean Model 51:37–72. doi:10.1016/j.ocemod.2012.04.003, http://www.sciencedirect.com/science/article/pii/S1463500312000637
Haddad M, Hassani H, Taibi H (2013) Sea level in the Mediterranean Sea: seasonal adjustment and trend extraction within the framework of SSA. Earth Sci Inf 6(2):99–111
Holgate SJ, Matthews A, Woodworth PL, Rickards LJ, Tamisiea ME, Bradshaw E, Foden PR, Gordon KM, Jevrejeva S, Pugh J (2013) New data systems and products at the permanent service for mean sea level. J Coastal Res 29(3):493–504
Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, Yen NC, Tung CC, Liu HH (1998) The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond A Math Phys Eng Sci R Soc 454:903–995
Klein M, Lichter M (2009) Statistical analysis of recent Mediterranean Sea-level data. Geomorphology 107(1–2):3–9. doi:10.1016/j.geomorph.2007.06.024
Landerer FW, Volkov DL (2013) The anatomy of recent large sea level fluctuations in the Mediterranean Sea. Geophys Res Lett 40(3):553–557
Le Traon PY, Nadal F, Ducet N (1998) An improved mapping method of multisatellite altimeter data. J Atmos Ocean Technol 15(2):522–534
Le Traon PY, Faugère Y, Hernandez F, Dorandeu J, Mertz F, Ablain M (2003) Can we merge GEOSAT follow-on with TOPEX/Poseidon and ERS-2 for an improved description of the ocean circulation? J Atmos Ocean Technol 20:889–895. doi:10.1175/1520-0426(2003)020<0889:CWMGFW>2.0.CO;2
Leuliette EW, Nerem RS, Mitchum GT (2004) Calibration of TOPEX/Poseidon and Jason Altimeter Data to Construct a Continuous Record of Mean Sea Level Change. Marine Geodesy 27(1):79–94. doi:10.1029/2001JC000964
Liebmann B, Dole RM, Jones C, Bladé I, Allured D (2010) Influence of choice of time period on global surface temperature trend estimates. Bull Am Meteorol Soc. doi:10.1175/2010BAMS3030.1
Mangiarotti S (2007) Coastal sea level trends from TOPEX-Poseidon satellite altimetry and tide gauge data in the Mediterranean Sea during the 1990s. Geophys J Int 170: doi:10.1111/j.1365-246x.2007.03424.x, http://gen.lib.rus.ec/scimag/index.php?s=10.1111/j.1365-246x.2007.03424.x
Marcos M, Tsimplis MN (2007) Variations of the seasonal sea level cycle in southern Europe. J Geophys Res Oceans 112(C12):c12011. doi:10.1029/2006JC004049
Mellor GL, Ezer T (1995) Sea level variations induced by heating and cooling: an evaluation of the Boussinesq approximation in ocean models. J Geophys Res Oceans 100(C10):20565–20577. doi:10.1029/95JC02442
Meyssignac B, Calafat FM, Somot S, Rupolo V, Stocchi P, Llovel W, Cazenave A (2011) Two-dimensional reconstruction of the Mediterranean sea level over 1970–2006 from tide gauge data and regional ocean circulation model outputs. Glob Planet Change 77(1–2):49–61. doi:10.1016/j.gloplacha.2011.03.002 (ISSN 0921-8181)
Milne G, Mitrovica J (1998) Postglacial sea-level change on a rotating Earth. Geophys J Int 133(1):1–19. doi:10.1046/j.1365-246X.1998.1331455.x
Mitchum GT (1994) Comparison of TOPEX sea surface heights and tide gauge sea levels. J Geophys Res Oceans 99: doi:10.1029/94jc01640, http://gen.lib.rus.ec/scimag/index.php?s=10.1029/94jc01640
Mitchum GT (1998) Monitoring the stability of satellite altimeters with tide gauges. J Atmos Oceanic Technol 15(3):721–730
Mitchum GT (2000) An improved calibration of satellite altimetric heights using tide gauge sea levels with adjustment for land motion. Marine Geodesy 23: doi:10.1080/01490410050128591, http://gen.lib.rus.ec/scimag/index.php?s=10.1080/01490410050128591
Oddo P, Bonaduce A, Pinardi N, Guarnieri A (2014) Sensitivity of the Mediterranean sea level to atmospheric pressure and free surface elevation numerical formulation in NEMO. Geosci Model Dev 7:3001–3015. doi:10.5194/gmd-7-3001-2014
Pascual A, Pujol MI, Larnicol G, Traon PYL, Rio MH (2007) Mesoscale mapping capabilities of multisatellite altimeter missions: first results with real data in the mediterranean sea. J Marine Syst 65(1–4):190–211, doi:10.1016/j.jmarsys.2004.12.004, http://www.sciencedirect.com/science/article/pii/S0924796306002922, marine Environmental Monitoring and Prediction Selected papers from the 36th International Lige Colloquium on Ocean Dynamics 36th International Lige Colloquium on Ocean Dynamics
Pascual A, Marcos M, Gomis D (2008) Comparing the sea level response to pressure and wind forcing of two barotropic models: validation with tide gauge and altimetry data. J Geophys Res Oceans 113(C7):c07011. doi:10.1029/2007JC004459
Pascual A, Boone C, Larnicol G, Le Traon PY (2009) On the quality of real-time altimeter gridded fields: comparison with in situ data. J Atmos Oceanic Technol 26(3):556–569
Peltier W (2001) Global glacial isostatic adjustment and modern instrumental records of relative sea level history. Int Geophys 75:65–95
Peltier W (2004a) Global glacial isostasy and the surface of the ice-age Earth: the ICE-5G (VM2) Model and GRACE. Annu Rev Earth Planet Sci 32:111–149. doi:10.1146/annurev.earth.32.082503.144359
Peltier W (2004b) Global glacial isostasy and the surface of the ice-age Earth: the ICE-5G (VM2) model and GRACE. Annu Rev Earth Planet Sci 32(111):149
Peltier W (2009) Closure of the budget of global sea level rise over the GRACE era: the importance and magnitudes of the required corrections for global glacial isostatic adjustment. Quaternary Sci Rev 28(17):1658–1674
Pinardi N, Arneri E, Crise A, Ravaioli M, Zavatarelli M (2006) The physical, sedimentary and ecological structure and variability of shelf areas in the Mediterranean sea. Sea 14:1243–1330
Pinardi N, Bonaduce A, Navarra A, Dobricic S, Oddo P (2014) The mean sea level equation and its application to the mediterranean sea. J Climate. doi:10.1175/JCLI-D-13-00139.1
Pinardi N, Zavatarelli M, Adani M, Coppini G, Fratianni C, Oddo P, Simoncelli S, Tonani M, Lyubartsev V, Dobricic S, Bonaduce A (2015) Mediterranean Sea large-scale low-frequency ocean variability and water mass formation rates from 1987 to 2007: a retrospective analysis. Progress Oceanogr 132(0):318–332, doi:10.1016/j.pocean.2013.11.003, http://www.sciencedirect.com/science/article/pii/S007966111300222X, oceanography of the Arctic and North Atlantic Basins
PSMSL (2015) Tide Gauge Data, Retrieved 26 Jan 2015 from http://www.psmsl.org/data/obtaining/. Tech. rep., Permanent Service for Mean Sea Level (PSMSL)
Pujol MI, Larnicol G (2005) Mediterranean sea eddy kinetic energy variability from 11 ys of altimetric data. J Marine Syst 58(3–4):121–142. doi:10.1016/j.jmarsys.2005.07.005
Robinson AR, Golnaraghi M (1994) The Physical and Dynamical Oceanography of the Mediterranean Sea. doi:10.1007/978-94-011-0870-6_12, http://gen.lib.rus.ec/scimag/index.php?s=10.1007/978-94-011-0870-6_12
Robinson AR, Leslie WG, Theocharis A, Lascaratos A (2001) Mediterranean sea circulation. A Derivative of the Encyclopedia of Ocean Sciences, Ocean Currents, pp 1689–1705
Santamaría-Gómez A, Gravelle M, Collilieux X, Guichard M, Míguez BM, Tiphaneau P, Wöppelmann G (2012) Mitigating the effects of vertical land motion in tide gauge records using a state-of-the-art GPS velocity field. Glob Planet Change 98:6–17
Spada G, Galassi G (2012) New estimates of secular sea level rise from tide gauge data and GIA modelling. Geophys J Int 191(3):1067–1094. doi:10.1111/j.1365-246X.2012.05663.x
Spada G, Stocchi P (2007) SELEN: A Fortran 90 program for solving the “Sea-Level Equation”. Comput Geosci 33(4):538–562. doi:10.1016/j.cageo.2006.08.006
Spada G, Melini D, Galassi G, Colleoni F (2012) Modeling sea level changes and geodetic variations by glacial isostasy: the improved SELEN code. arXiv:12125061
Spada G, Galassi G, Olivieri M (2014) A study of the longest tide gauge sea-level record in Greenland (Nuuk/Godthab, 1958–2002). Glob Planet Change 118:42–51
Stocchi P, Spada G (2009) Influence of glacial isostatic adjustment upon current sea level variations in the Mediterranean. Tectonophysics 474(1–2):56–68
Tamisiea M, Hill E, Ponte R, Davis J, Velicogna I, Vinogradova N (2010) Impact of self-attraction and loading on the annual cycle in sea level. J Geophys Res 115(07):004. doi:10.1029/2009JC005687, http://adsabs.harvard.edu/abs/2010JGRC..11507004T
Torres ME, Colominas MA, Schlotthauer G, Flandrin P (2011) A complete ensemble empirical mode decomposition with adaptive noise. In: Acoustics, Speech and Signal Processing (ICASSP), 2011 IEEE International Conference on, IEEE, pp 4144–4147
Tsimplis M, Calafat FM, Marcos M, Jordá G, Gomis D, Fenoglio-Marc L, Struglia M, Josey SA, Chambers D (2013) The effect of the NAO on sea level and on mass changes in the Mediterranean Sea. J Geophys Res Oceans 118(2):944–952
Tsimplis MN, Álvarez-Fanjul E, Gomis D, Fenoglio-Marc L, Pérez B (2005) Mediterranean sea level trends: atmospheric pressure and wind contribution. Geophys Res Lett 32(20):-20,602. doi:10.129/2005GL023867
Vignudelli S, Cipollini P, Roblou L, Lyard F, Gasparini GP, Manzella G, Astraldi M (2005) Improved satellite altimetry in coastal systems: case study of the Corsica channel (Mediterranean Sea). Geophys Res Lett 32:L07608. doi:10.1029/2005GL022602
Woodworth PL, Player R (2003) The permanent service for mean sea level: an update to the 21st century. J Coast Res 19(2):287–295, http://www.jstor.org/pss/4299170
Wöppelmann G, Marcos M (2012) Coastal sea level rise in southern Europe and the nonclimate contribution of vertical land motion. J Geophys Res Oceans 117(C1):1978–2012
Wöppelmann G, Miguez BM, Bouin MN, Altamimi Z (2007) Geocentric sea-level trend estimates from GPS analyses at relevant tide gauges world-wide. Glob Planet Change 57(3):396–406
Wöppelmann G, Letetrel C, Santamaria A, Bouin M-N, Collilieux X, Altamimi Z, Williams SDP, Martin Miguez B (2009) Rates of sea-level change over the past century in a geocentric reference frame. Geophys Res Lett 36:L12607. doi:10.1029/2009GL038720
Wu Z, Huang NE (2009) Ensemble empirical mode decomposition: a noise-assisted data analysis method. Adv Adapt Data Anal 1(01):1–41
Acknowledgments
This work was supported by the University of Bologna, Ph.D. program in Environmental Science and CMCC-TESSA project (PON-01 02823). N. Pinardi was supported by the contract TESSA given to the University of Bologna and by the European Commission MyOcean 2 Project (FP7-SPACE-2011-1-Prototype Operational Continuity for the GMES Ocean Monitoring and Forecasting Service, GA 283367). INGV activities were supported by the MyOcean 2 FP7 Project and by the Italian Project RITMARE, la RIcerca iTaliana per il MARE (MIUR-Progetto Bandiera 2012-2016). G. Spada was partially funded by a DiSBeF research grant. The DUACS system that generates the AVISO data used in this study is a joint CLS/CNES system maintained and operated with support from the SALP project from CNES. It benefits from co-funding from the MyOcean 2 FP7 Project. All the data used in this work are freely available through the PSMSL and AVISO web portals.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
The satellite altimetry SLA signal is obtained by the difference between the sea-level (\(\eta _{sat}\)) and its mean (\(\eta _{sat}^{mean}\)), calculated over a reference period from 1993 to 1999 (Pujol and Larnicol 2005). We assume that \(\eta _{sat}^{mean}\) contains an approximation of the height of the geoid above the reference ellipsoid (Cazenave et al. 1998, 2002) and the mean dynamic topography, hence:
where \(\eta _{sat}(x,y,t)\) is corrected for effects caused by tides, inverse barometer and wind. Following the literature (Cazenave et al. 2003; Cazenave and Llovel 2010) we define the mean sea-level, \(\eta _{MSL}(t)\), as:
where the double square brackets indicate a normalized area average, defined as \(\frac{1}{\Omega } \int \int _\Omega d\Omega\), where \(\Omega\) is the sea surface area.
As described in Pinardi et al. (2014) the mean sea-level in the Mediterranean Sea is composed of two parts:
where \(\eta _{I}(t)\) is the incompressible or mass component and \(\eta _{S}(t)\) is the steric contribution (Mellor and Ezer 1995; Greatbatch 1994; Griffies and Greatbatch 2012). While \(\eta _{I}(t)\) is due to the balance between net volume transport at the Gibraltar Strait (normalized by the Mediterranean basin area) and the net surface water flux, \(\eta _{S}(t)\) is due to the buoyancy fluxes that account for the thermosteric and halosteric components.
The space and time dependent sea-level component from the satellite, which will be then compared with in-situ data, is thus:
We next consider the in-situ sea-level \(\eta _{ins}\) measured by tide gauges:
where \(x_{i},y_{i}\) are the station coordinates, \(\eta _{MSL}(t)\) and \(\eta _{sat}^{mean}(x_{i},y_{i})\) are the same as in (1) and (3) but interpolated at the station locations by considering four grid points around the tide gauge position, and assigning weights to each one according to their distance from the station position. \(\eta ^{IB}(x_{i},y_{i},t)\) is the inverse barometer effect due to the low frequency response of the sea-surface to the atmospheric pressure, and \(\eta _{HF}(x_{i},y_{i},t)\) is the high frequency response to the atmospheric pressure and wind (both accounted for by the DAC in the satellite data). \(\eta _{ins}^{var}(x,y,t)\) is the time- and space-dependent local sea-level component and \(C_{ins}(x_{i},y_{i})\) the local datum correction. The local datum correction is computed by removing the temporal mean from each tide gauge station time series.
The effect of \(\eta _{HF}(x_{i},y_{i},t)\) is minimized in our analysis since monthly averaged data were considered. The inverse barometer effect considered here is the same as Dorandeu and Traon (1999):
where \(\rho\) is the sea water density, P the Mean Sea Level Pressure (MSLP) from the European Centre for Medium-Range Weather Forecasts (ECMWF) Re-analysis dataset (ERA-Interim; Dee et al. 2011) and \(P_{ref}\) is the MSLP spatial mean over the global ocean computed from 1993 to 2012.
Appendix 2
The sea-level linear trend is defined using basics statistics by Spada and Galassi (2012) as the regression coefficient estimated using the least squares method. In the case of a linear fit applied to a sea-level time-series, the regression coefficient r, considered as the best estimate of the sea-level rate, is given by the equation:
with \(i=1,\ldots ,n\), where n is the number of sea-level records considered, \(y_{i}\) is a sea-level measure at the time \(x_{i}\). The standard error of the regression coefficient is a measure of the uncertainty of the obtained estimate. Spada and Galassi (2012) describe the formal uncertainty on the estimated sea-level rate defining a 95 percent confidence interval (\(\mu\)) for the slope, given by:
where \(\overline{x}\) is the average of the \(x_{i}\)’s and \(t_{0.975}\) is the 0.975-th quartile of Students t-distribution with \(k = n - 2\) degrees of freedom. In Eq. (1 8) \(\sigma\) is defined by:
where \(y_{i}\) is the actual sea-level value and \(\hat{y}_{i}\) the estimated value.
Thus to account for uncertainties on the rate r, the sea-level trend is given by:
where r and \(\mu\) are given in Eqs. (7) and (8), respectively.
Tide-gauge station distribution in the Mediterranean between 1993 and 2012. In the top panel black points represent the tide gauge stations with the most complete time series (at least 85 %) between 1993 and 2012. The bottom panel shows the number of tide-gauge stations available during the analysis period
Reliability of Mediterranean Sea MSL estimates. Top panel MSL estimates as obtained from satellite altimetry (solid red line), all available tide-gauge data (dashed blue line) and selected tide-gauge data (solid black line). Bottom panel correlation coefficient (black lines) and RMSD* (red lines) between satellite altimetry, all available tide-gauge data (dashed lines) and selected tide-gauge data (solid lines)
\(\eta ^{var}(t)\) from tide gauge (solid black line) and satellite altimetry (solid red line) comparison. From the western part of the basin to the Adriatic Sea, the following cases are shown: Malaga (a), Marseille (b), L’Estartit (c), Trieste (d), Split (e) and Valletta (f); y-axis values expressed as [cm]
Spatial pattern of sea-level positive anomalies during the years 2010–2011 [cm]. The map shows the difference between the satellite altimetry, averaged over the period 2010–2011, compared to climatology computed from 1993 and 2012 and removing the years 2010 and 2011; differences below 5 cm are not shown
Satellite altimetry and tide-gauge time-series and coherency. Top panel \(\eta _{ins}^{var}\) (black line) and \(\eta _{sat}^{var}\) (red line) time-series averaged over the tide gauge positions shown in Fig.1 (black dots) [cm]. Left middle panel \(\eta _{ins}^{var}\) and \(\eta _{sat}^{var}\) power spectra [cm\(^{2}\)]. Right middle, left bottom and right bottom panels coherence, phase (degrees) and gain computed between \(\eta _{ins}^{var}\) and \(\eta _{sat}^{var}\), respectively. X-axis is expressed as periods in months
Ensemble Empirical Model Decomposition Analysis (EEMD) performed using satellite altimetry (red lines) and tide-gauge data (black lines). The sea-level signals are decomposed into 7 Intrinsic Modes Functions (IMFs), shown are the combined high-frequency modes 1–4 (top panel) and the low-frequency modes 5–6 (central panel). Bottom panel shows the EEMD residual signal. Y-axis expressed as [cm]
Satellite altimetry trend [mm year\(^{-1}\)] spatial variability in the Mediterranean Sea (1993–2012). Seasonal signal removed, glacial-isostatic adjustment (GIA) applied. Boxes show a representative number of locations (17 out of 24 stations analyzed) where the sea-level trend was estimated both from tide gauge data (values on the left side in the brackets) and altimetry (values on the right side in the brackets) [mm year\(^{-1}\)]
Satellite Trend as a function of the length of the period considered. The left panel shows all the possible trends ending at the year indicated in the x-axis, obtained considering the number of years shown over the y-axis. Thus, the points x = 2000 and y = 10, express the sea-level trend value up to the year 2000, obtained considering 10 years of data. The right panel shows the trend significance obtained performing a bootstrap analysis; values below 90 % are not shown
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bonaduce, A., Pinardi, N., Oddo, P. et al. Sea-level variability in the Mediterranean Sea from altimetry and tide gauges. Clim Dyn 47, 2851–2866 (2016). https://doi.org/10.1007/s00382-016-3001-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-016-3001-2