AMOC sensitivity to surface buoyancy fluxes: Stronger ocean meridional heat transport with a weaker volume transport?

Abstract

Oceanic northward heat transport is commonly assumed to be positively correlated with the Atlantic meridional overturning circulation (AMOC). For example, in numerical “water-hosing” experiments, imposing anomalous freshwater fluxes in the northern Atlantic leads to a slow-down of the AMOC and the corresponding reduction of oceanic northward heat transport. Here, we study the sensitivity of the ocean heat and volume transports to surface heat and freshwater fluxes using a generalized stability analysis. For the sensitivity to surface freshwater fluxes, we find that, while the direct relationship between the AMOC volume and heat transports holds on shorter time scales, it can reverse on timescales longer than 500 years or so. That is, depending on the model surface boundary conditions, reduction in the AMOC volume transport can potentially lead to a stronger heat transport on long timescales, resulting from the gradual increase in ocean thermal stratification. We discuss the implications of these results for the problem of steady state (statistical equilibrium) in ocean and climate GCM as well as paleoclimate problems including millennial climate variability.

1 Introduction

The Atlantic meridional overturning circulation (AMOC) is a basin-scale baroclinic ocean circulation with a northward flow of warm water and cold return flow at depth (e.g. Wunsch 2002; Gagosian 2003; Sévellec and Fedorov 2011; Srokosz et al. 2012). During its northward travel, the surface water exchanges heat with the atmosphere, modifying the climate of the Northern Atlantic region and contributing to the relative mild climate in Europe. This overturning circulation is a meridional plane portrait of a much more complex three-dimensional circulation in the Atlantic, which can be conditionally split into wind-driven and thermohaline circulations (e.g. Fedorov et al. 2007; Barreiro et al. 2008). This latter circulation depends in part on oceanic density gradients and hence on temperature and salinity gradients controlled by warming/cooling and evaporation/precipitation at the surface of the ocean.

Recent studies also emphasize the important role of the Southern Ocean wind stress for the AMOC dynamics (Toggweiler and Samuels 1998; Gnanadesikan 1999; Vallis 2000; Sévellec and Fedorov 2011; Wolfe and Cessi 2010, 2011; Haertel and Fedorov 2012; Nikurashin and Vallis 2012). Indeed, competing effects of eddy fluxes and wind stress in the Antarctic Circumpolar Current region are critical in setting the depth of the thermocline, and hence the intensity of the AMOC. Still, the ocean mean density field, which is affected by surface buoyancy fluxes particularly in the northern Atlantic and around Antarctica, is equally important. Our analysis will focus on the role of these buoyancy fluxes.

The goal of this study is to explore the impacts that anomalies in the surface fluxes of freshwater and heat can have on the AMOC, as measured by meridional volume and heat transports in the North Atlantic, and to determine the upper bound of these impacts on timescales ranging from decadal to multi-millennial. As we will demonstrate, the character of the impacts can change dramatically on these longer, millennial timescales.

The sensitivity of ocean circulation to changes in oceanic surface fluxes is relevant to a number of problems ranging from global warming to abrupt climate changes of the past. In the context of anthropogenic global warming, it is being debated whether changes in surface conditions over the ocean are already affecting the thermohaline circulation (IPCC 2007, 2013). For example, Hansen et al. (1999), Mann et al. (1999) and subsequent studies discuss the increase of surface air temperatures over the Northern hemisphere and its impacts. Wang et al. (2010) argue that the long-term trends are such that the upper ocean subpolar North Atlantic is becoming cooler and fresher, whereas the subtropical North Atlantic becomes warmer and saltier, although decadal variability may differ from the long-term trends (Wang et al. 2010; Hátún et al. 2005; Thierry et al. 2008).

A number of authors have argued that surface waters in the northern Atlantic are already freshening at a relatively rapid pace (Dickson et al. 2002; Curry et al. 2003; Curry and Mauritzen 2005), possibly as a consequence of increase in precipitation in the subpolar gyre region (Josey and Marsh 2005). More recently, Durack and Wijffels (2010) have demonstrated that the spatial structure of salinity changes in the Atlantic over the last 50 years agrees well with the expected changes in the hydrological cycle over the same time interval. Although it is not fully clear whether these salinity changes represent decadal fluctuations or a gradual trend, the freshening of high-latitude oceans can intensify in the future, should global warming enhance high-latitude precipitation or accelerate freshwater loss from continental ice sheets (Ekstrom et al. 2006).

Such changes in oceanic freshwater and heat fluxes modify surface density gradients and influence the AMOC. This is of a major concern as it is believed that freshwater discharges played an important role in past climate changes (e.g. Broecker et al. 1990; Rahmstorf 2002; Clarke et al. 2003; Alley et al. 2003) by affecting deep-water formation and meridional overturning in the Atlantic. Evidence from geological records (Broecker 1991, 2003; McManus et al. 2004; Lynch-Stieglitz et al. 2007) suggests that reorganizations of the AMOC can lead to temperature changes of several Kelvins or more in a few decades.

Many modeling studies considered the consequences of such a freshening for the climate of the North Atlantic (e.g. Rahmstorf 1995; Manabe and Stouffer 1995, 1999; Rind et al. 2001; Stouffer et al. 2006; Fedorov et al. 2007; Barreiro et al. 2008 and references therein). This includes studies with coupled ocean-atmosphere climate models used for making projections for future global warming (e.g. Vellinga and Wood 2002; Zhang and Delworth 2005; Stouffer et al. 2006; Barreiro et al. 2008). Typically, applying a freshwater flux equivalent of 1 Sv over the northern Atlantic causes a shutdown of the AMOC. The ensuing large drop in sea surface temperatures in the northern Atlantic is accompanied by a substantial cooling of Northern Europe. In contrast, the equatorial and southern Atlantic become warmer, leading to a global displacement of rainfall patterns in low latitudes, including the southward shift of the ITCZ (also see Vellinga and Wood 2002; Zhang and Delworth 2005), and deepening the tropical thermocline (e.g. Fedorov et al. 2007; Barreiro et al. 2008). In general, the system’s response to freshwater forcing depends on the stability of the AMOC (i.e. whether it is mono- or bi-stable, following Stommel 1961), as discussed by Sévellec and Fedorov (2011), Liu and Liu (2013) or Liu et al. (2013) amongst others. For example, many climate models are arguably in the monostable regime due to surface temperature biases (Liu et al. 2014), so that a short freshwater pulse does not result in a lasting AMOC collapse. Overall, “water-hosing” experiments have become a useful tool to study the sensitivity of ocean circulation to surface perturbations.

Another approach to assess the ocean circulation sensitivity involves adjoint methods (e.g. Marotzke et al. 1999; Czeschel et al. 2010). Using such an approach, Bugnion et al. (2006a) and Bugnion et al. (2006b) studied the sensitivity of ocean circulation to surface forcing and identified critical sensitivity patterns in surface heat and freshwater fluxes and wind stress. In these studies, the AMOC intensity is sensitive to surface flux anomalies over the northern regions of the North Atlantic, especially along its western boundary. These authors assumed that the ocean reaches its steady state after 400 years of time integration. Whereas this timescale is plausible for advective adjustment, it is too short for diffusive adjustment for which the characteristic timescale $h^2/k_d \simeq 7000\hbox{ years}$, where $k_d=10^{-5}\hbox { m}^2\hbox { s}^{-1}$ is a typical diapycnal diffusivity for the ocean interior and $h=1500\hbox { m}$ is a typical pycnocline depth. This suggests that to assess ocean sensitivity to surface fluxes one should consider longer timescales as well.

Here, to study the sensitivity of the AMOC to surface perturbations, we will follow the methodology developed by Sévellec et al. (2007) and recently used in different contexts by Sévellec and Fedorov (2010), Sévellec and Fedorov (2013b), and Sévellec and Fedorov (2015). This methodology will be used to compute optimal surface fluxes of heat and freshwater (or salt) for the AMOC. Here, the optimal fluxes are defined as the most efficient steady fluxes that would perturb the AMOC the most, as measured by its meridional volume and heat transports, after a time delay. We will conduct a set of 16 experiments varying from one experiment to the next (1) the measure of the AMOC used, (2) the type of surface perturbation (salt or heat), (3) the type of surface boundary conditions (mixed or flux), and imposing or not (4) the freshwater and heat conservation constraints (i.e. in some experiments we set the net area integral of surface perturbations to zero thus conserving net mass and heat in the system).

Our analysis shows that the sensitivity of the AMOC to the imposed surface fluxes still exists after several millennia. Furthermore, it also shows that whereas the positive correlation between the meridional volume and heat transports persists on centennial timescales, this correlation can become negative on longer timescales. This change in the correlation sign is linked to the gradual adjustment of the ocean thermocline. Consequently, on sufficiently long timescales the AMOC weakening could potentially lead to an increase in poleward heat transport by the ocean and a warming of the northern Atlantic.

The structure of this paper is as follows: in Sect. 2 we will describe the ocean model and its seasonal cycle. The results of the AMOC sensitivity study to ocean surface heat and freshwater fluxes, as relevant to meridional volume and heat transports, will be presented in Sect. 3. In Sect. 4, we will discuss the results and possible directions for future work.

2 The ocean model, configuration and seasonal cycle

2.1 The model configuration

In this study we use the ocean General Circulation Model (GCM) OPA 8.2 (Océan PArallélisé, Madec et al. 1998) in its 2° global configuration (ORCA2, Madec and Imbard 1996). There are 31 levels in the vertical—with the layer thickness varying from 10 m at the surface to 500 m at depth. The model is integrated using an Arakawa C-grid and z-coordinates, with a rigid-lid approximation.

Although a number of climate models included in the last IPCC report (2013) have a 0.25° resolution in the ocean, here we use an ocean model with a lower resolution of 2° (note that the IPSL climate model, with OPA as the oceanic component, has the same 2° resolution; see Marti et al. 2010). The main reason for applying a relative coarse ocean model is to avoid small-scale baroclinic instability existing in eddy-permitting models. Within the linear framework of this study such instability would not saturate, contaminating the solutions of our experiments.

The present model configuration uses the following parameterizations: convection is parameterized by an increase in vertical diffusion when vertical stratification becomes unstable; double diffusion is taken into account by using different terms for temperature and salinity mixing; eddy-induced velocities are described by the Gent and McWilliams (1990) parameterization; viscosity coefficients follow the turbulent closure scheme of Blanke and Delecluse (1993) and are functions of longitude, latitude and depth; and diffusion coefficients for temperature and salinity vary in longitude and latitude (Redi 1982).

The linear and adjoint models are provided by the OPATAM code (OPA Tangent Adjoint Model, Weaver et al. 2003). The tangent linear model is a linearization of the OPA’s primitive equations of motion with respect to the ocean seasonally varying basic state.

In the present study, we use either flux boundary conditions (with surface heat and freshwater fluxes specified) or mixed boundary conditions [(with a sea surface temperature (SST)—restoring term used in addition to specified freshwater fluxes]. The restoring coefficient for SST is set to $40\hbox { W m}^{-2}\hbox { K}^{-1}$. The time-mean ocean fluxes were computed by running the full nonlinear model forced with a combination of prescribed climatological fluxes and restoring terms (restoring to the climatological seasonal cycle). This approach produces a realistic seasonal cycle for both linear and adjoint models, while reducing the damping and allowing SST anomalies to develop more easily (Huck and Vallis 2001; Arzel et al. 2006; Sévellec et al. 2009).

Several additional approximations have been introduced for the tangent-linear and adjoint models: viscosity coefficients in the momentum equations, tracer diffusivities, and eddy-induced advection are calculated only for the basic ocean state—further variations in those coefficients are neglected.

The same ocean model, and its tangent linear and adjoint versions, has been used in different contexts in several studies by the authors (Sévellec and Fedorov 2010, 2013a, b, 2015). In particular, these authors have estimated the upper bound on the ocean sensitivity to initial perturbations in surface temperature and salinity for various ocean metrics.

2.2 The model basic state

The seasonally-varying basic state of the ocean, also referred to as the annual model “trajectory”, is obtained by the direct integration of the OPA model subject to the climatological surface boundary forcing (varying with the annual cycle). In particular, we used the ECMWF heat fluxes averaged in the interval from 1979 to 1993, the ERS wind stress blended with the TAO data between 1993 and 1996, and an estimate of the climatological river runoff. In addition, we applied a surface temperature restoring to the Reynolds climatological values averaged from 1982 to 1989, together with a surface salinity restoring to the Levitus (1989) climatology (we emphasize that the restoring term can be switched off in the experiments with the linear and adjoint models). A mass restoring term to the Levitus climatological values of temperature and salinity was applied in the Red and Mediterranean Seas. Starting with the Levitus climatology as the initial conditions, the model produces a quasi-stationary annual cycle of the ocean basic state after 200 years of integration.

The Atlantic meridional overturning circulation in the full ocean GCM (Fig. 1) is characterized by a northward mass transport above the thermocline, a southward return flow below 1000-1500 m and extending about 3000 m, and a recirculation cell below 3000 m associated with the Antarctic Bottom Water. The maximum volume transport of the AMOC is around 14 Sv, which is slightly below but still within the errorbars of the observations (e.g. 18 ± 5 Sv, Talley et al. 2003). The AMOC poleward heat transport reaches 0.8 PW at 25°N, whereas estimates from inverse calculations and hydrographic sections give 1.3 PW at 24°N (Ganachaud and Wunsch 2000).

As expected, the SST field develops a strong meridional gradient in the northern Atlantic, especially across the North Atlantic Current (NAC); it also develops a salinity maximum at about 20°N (Fig. 1). The plot of barotropic streamfunction shows an intense subtropical gyre and a weaker subpolar gyre centered at about 60°N. The two gyres are separated by the Gulfstream and the NAC.

Fig. 1

The climatological basic state of the ocean in the Atlantic as reproduced by the full ocean GCM. (Top left) Sea surface temperature; contour intervals (CI) are 2 °C, the heavy line corresponds to 20 °C. (Top right) Sea surface salinity; CI are 0.2 psu, the heavy line corresponds to 35 psu. (Middle left) Barotropic streamfunction; CI are 3 Sv. (Middle right) Ocean meridional heat transport as a function of latitude. (Bottom) Zonally-averaged streamfunction of the Atlantic meridional overturning circulation; CI are 1 Sv. In the two plots of the streamfunction, solid, dashed and dotted lines indicate positive, negative and zero values. In the bottom and middle-right panel, thick dashed lines indicate the latitudes and depth at which AMVT and AMHT are evaluated. These two variables are used as AMOC measures in the optimization problem

In this study we use a climatological mean seasonal forcing to study the AMOC long-term asymptotic behavior. The chosen asymptotic approach precludes us from using a realistic observed forcing that would include a full variety of timescales, from diurnal to decadal. In principle, using climatological forcing can weaken mean ocean circulation and oceanic variability (e.g. Frankignoul and Hasselmann 1977) by restricting extremes important for winter deep water formation. For example, this might explain why the mean AMOC strength in the model is 14 Sv, which is arguably a bit too weak.

Overall, the full nonlinear model produces a realistic (seasonally-varying) basic state of the ocean. Next, we will conduct a sensitivity analysis of the model, focusing on the ocean response to constant in time anomalies in freshwater and heat fluxes.

3 Asymptotic sensitivity of the AMOC

To evaluate the sensitivity of the AMOC to surface heat and freshwater fluxes, we have conducted a set of 16 experiments. Each experiment corresponds to a different combination of four major controlling factors for the problem, including

• 1. the type of surface perturbation forcing (surface heat flux or freshwater flux—SHF or SFF, respectively),

• 2. the AMOC measure used in the maximization problem (Atlantic meridional volume transport or Atlantic meridional heat transport—AMVT or AMHT, respectively),

• 3. the type of boundary conditions used in the linear model (flux boundary conditions or mixed boundary conditions—FBC or MBC, respectively), and

• 4. whether a zero-mean constraint on flux perturbations is imposed or not (ensuring freshwater and heat conservation).

A full mathematical description of the calculations is given in the “Appendix” and the main results are summarized in Table 1. Throughout the paper we will focus on the results obtain under FBC without the zero-mean constraint (this was the initial set of experiments we performed) and then describe differences with other calculations, if any. Also note that, within our linear approach, solutions for an arbitrary SST restoring coefficient can be found using a linear combination of MBC and FBC.

Table 1 The magnitude of the impact of optimal surface heat and freshwater flux perturbations on the AMOC volume and heat transports for all 16 experiments

The first result of our analysis is the long timescales needed to reach a steady state (statistical equilibrium) after a surface heat or freshwater flux perturbation has been imposed. Evaluating expression (12) in the “Appendix” numerically, we estimate that ocean dynamics need several thousands of years to equilibrate (Fig. 2). Especially in the case of AMHT experiments, ocean and its heat transport are still not fully equilibrated even after 3000 years (Fig. 2c, d). This result has significant implications for climate modeling studies. Since meridional heat transport (more than volume transport) is directly related to temperature imbalances, it suggests that climate models should be time-integrated for 3000 years or even longer to be considered in a steady state. With shorter time-integration the models still remain in a transient state. This timescale is consistent with the scaling analysis for both horizontal and vertical diffusion of heat and salt in our model: $L^2/k_h \simeq h^2/k_v \simeq 5000\,{\hbox{years}}$, where $k_h=2\times 10^3\hbox { m}^2\hbox { s}^{-1}$ and $k_v=1.2\times 10^{-5}\hbox { m}^2\hbox { s}^{-1}$ are the horizontal and vertical diffusivities in the ocean interior, and $L=1.8\times 10^7\hbox { m}$ and $h=1500\,{\hbox{m}}$ are the basin length scale and pycnocline depth.

Fig. 2

The magnitude of impacts of surface a, b heat and c, d freshwater fluxes that modify meridional a, c heat and b, d volume transports in the North Atlantic (AMHT and AMVT, respectively) most efficiently, as a function of integration timescale (i.e. corresponding to the duration of the imposed fluxes, $\tau$). These results are obtained from expressions (11) and (12) of the “Appendix” with normalized surface fluxes such that $\sqrt{{\langle {{{\varvec{f}}}|{{\mathbf {\mathsf{{S}}}}}|{{\varvec{f}}}}\rangle }}=1\hbox { W m}^{-2}$ or $1\,{\hbox{cm year}}^{-1}$. Computations were conducted for the flux boundary conditions without the freshwater and heat conservation constraints

The second result, generally consistent with previous studies, is that AMVT is primarily sensitive to surface heat and freshwater flux perturbations in the northern Atlantic and the Arctic regions (Fig. 3b, d). The location of the highest sensitivity coincides with the region of deep mixed layer depth, which has been shown to provide an efficient way for stimulating AMVT changes on decadal timescales in the exact same model (Sévellec and Fedorov 2015). Accordingly, a persistent surface warming or freshening of these regions reduces the AMVT. This sensitivity has already been established in previous studies and is at the root of “water-hosing” experiments with comprehensive climate GCMs (e.g. Rahmstorf 1995; Manabe and Stouffer 1995, 1999; Vellinga and Wood 2002; Stouffer et al. 2006; Barreiro et al. 2008), and zonally-average ocean models (Marotzke et al. 1988; Wright and Stocker 1991; Sévellec and Fedorov 2011), all going back to the pioneering work of Stommel (1961). Such sensitivity has also been demonstrated through adjoint analyses in other ocean GCM using similar or more idealized configurations (e.g. Bugnion and Hill 2006; Bugnion et al. 2006a, b).

In some contrast to these adjoint-sensitivity analyses and typical “water-hosing” experiments that impose uniform fluxes over the high-latitude North Atlantic, we find a clear east-west gradient in the optimal surface heat and freshwater fluxes. This result is consistent with Hirschi and Marotzke (2007) decomposition of the AMVT (used operationally by RAPID-MOCHA monitoring system, see McCarthy et al. 2012). This east-west gradient corresponds to surface warming or freshening along the ocean western boundary, required to reduce AMVT. Thus, the ocean sensitivity to both freshwater and heat fluxes is linked to buoyancy fluxes characterized by a large-scale zonal gradient that tends to modify the North Atlantic Current and hence reduce AMVT.

Fig. 3

The spatial structure of optimal perturbations in a, b heat and c, d freshwater fluxes that modify meridional a, c heat and b, d volume transports in the North Atlantic most efficiently on asymptotic timescales ($\tau >3000\,{\hbox{years}}$, see Fig. 2). Surface fluxes are normalized so that $\sqrt{{\langle {{{\varvec{f}}}|{{\mathbf {\mathsf{{S}}}}}|{{\varvec{f}}}}\rangle }}=1\hbox { W m}^{-2}$ or $1\,{\hbox{cm year}}^{-1}$; the magnitude of the impacts of these surface perturbations are specified in the respective titles. Thick black lines indicate zero values. Computations were conducted for the flux boundary conditions without the freshwater and heat conservation constraints

This sensitivity to surface fluxes in the North Atlantic is paralleled by the system’s sensitivity to fluxes along the coast of Antarctica (Fig. 3b, d). The latter is related to the fact that AMVT is partially controlled by the competition between the North Atlantic Deep Water (NADW) and AntArctic Bottom Water (AABW) cells. A weaker NADW formation or a stronger AABW formation would act to fill the North Atlantic with waters originating in the Southern Ocean and reduce AMVT, which is typical for the AMOC off-state for example (e.g. Sévellec and Fedorov 2011).

Quantitatively this can be understood from a broadly used ad hoc relation between the meridional gradient of baroclinic pressure ($\partial _yP_b$, where $P_b$ is the baroclinic pressure) and meridional stream function ($\psi$): $\partial _yP_b \propto \psi$. For further discussion on this realtionship we refer the reader to Sévellec and Huck (2015), and references therein. Integrating this relationship meridionally yields that the mean value of stream function is proportional to the north-south difference in baroclinic pressure. A zero mean stream function would imply that along the meridional plane there is exactly as much water moving clockwise as counterclockwise, whilst positive or negative values of the mean stream function indicate the dominance of the clockwise or counterclockwise cell, respectively. Thus, the norths-south pressure difference controls the relative dominance of the NADW cell over the AABW cell and hence the AMVT intensity. Consequently, making NADW more buoyant and/or AABW denser contributes to the overall weakening of the NADW cell relative to the AABW cell, leading to a decrease in AMVT (Fig. 3a, b). Specifically, anomalous salt fluxes along the Antarctic coast weaken AMVT (Fig. 3c)—a finding consistent with Shin et al. (2002), Liu et al. (2005) and Ferrari et al. (2014).

The third and perhaps most surprising result is different asymptotic sensitivities of the Atlantic volume and heat transports (i.e. on long timescales). On the one hand, both measures of ocean dynamics show a high sensitivity to heat fluxes perturbations in the high-latitude North Atlantic and the Arctic ocean (Fig. 3a, b)—surface warming in these regions would lead to the weakening of the AMVT and AMHT. However, the asymptotic sensitivity of these two measures to freshwater fluxes differ radically—surface freshening is required to weaken the AMVT (analogously to the heat flux case, Fig. 3d), whereas making surface waters more saline is necessary to weaken the AMHT (Fig. 3c). In other words, within our computations ocean meridional volume and heat transports have opposite asymptotic sensitivities to surface freshwater fluxes!

To verify this last result we have conducted a series of calculations testing non-asymptotic effects of the optimal freshwater flux on the AMHT (see the “Appendix” for the details on the methodology). These results indicate that, when the duration of the imposed surface perturbation is sufficiently short, a freshening of high latitudes reduces both AMVT and AMHT (Fig. 4). That is, on shorter timescales the AMVT and AMHT behave similarly (i.e. they are positively correlated, as typically assumed). However, if the imposed surface flux persists for longer than $500\,{\hbox{years}}$, making surface waters less saline (and hence reducing AMVT) is needed to increase AMHT, which implies a negative correlation between the ocean meridional volume and heat transports as discussed above (Fig. 4).

Fig. 4

The spatial structure of optimal perturbations in freshwater flux, influencing AMHT most efficiently, for different lengths $\tau$ of time integration (i.e. different durations of the imposed fluxes), see expression (12) of the “Appendix”. a–f correspond to $\tau$ = 50, 100, 200, 500, 1000, 2600 (${\simeq} \infty$) years. The surface flux has been normalized so that $\sqrt{{\langle {{{\varvec{f}}}|{{\mathbf {\mathsf{{S}}}}}|{{\varvec{f}}}}\rangle }}=1\,{\hbox{cm year}}^{-1}$. Thick black lines indicate zero values. Note that panel f is similar to c in Fig. 3. Computations were conducted for the flux boundary conditions without the freshwater conservation constraint

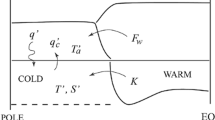
To explain this finding, we can use a simple zonally-averaged treatment of ocean dynamics in the Atlantic, considering only baroclinic component of the ocean heat transport (Fig. 5); a further discussion of the barotropic (horizontal) contribution will be given in Sect. 4. Within a linear framework, a baroclinic heat transport anomaly can be split into two terms:

$$\begin{aligned} \mathrm {AMHT}'\simeq W\int _{-H}^0dz\, \left( v'\overline{T}+\overline{v}T'\right) , \end{aligned}$$

(1)

where z is the vertical coordinate, T—zonal-averaged temperature, v—zonally-averaged meridional velocity, H—the total ocean depth, and W—the zonal basin extent. The bars and primes indicate mean values and perturbations, respectively. Note that the schematic approach described in (1) and Fig. 5 is diagnostic—its role is to show how the poleward heat transport in the North Atlantic is affected by the two different terms in the heat equation—one related to changes in ocean stratification ($T'$) and the other to meridional overturning circulation ($v'$). However, in general, $T'$ and $v'$ are dynamically connected (e.g. Gnanadesikan 1999).

Fig. 5

A schematic of the thermocline shoaling in response to the strengthening of the ocean meridional overturning. Here, y and z are the latitudinal and vertical coordinates, respectively; v and w are the meridional and vertical velocities; l is the latitudinal extent of the thermocline and h is its depth. T is temperature. Bars and primes indicate mean and perturbation values, respectively. The solid and dashed lines represent the mean and the perturbed thermoclines. Similarly, the weakening of the AMOC would lead to the deepening of the thermocline

From this expression one can see that the strengthening of ocean heat transport (positive AMHT anomalies) can result from the strengthening of the meridional flow ($v'$) or from heat redistribution in the water column ($T'$). The former mechanism is directly linked to AMVT change and implies a positive correlation between heat and volume transports (since the vertical temperature gradient is positive). However, the latter mechanism suggests that the vertical displacement of the thermocline can also modify the meridional heat transport. Since the mean meridional overturning circulation ($\overline{v}$) is comprised of a northward flow in the upper ocean compensated by a southward flow at depth, the shoaling of the thermocline should lead to a decrease in the heat transport (Fig. 5). Because ocean flow is non-divergent in the interior, the strengthening of the AMOC should result in the thermocline shoaling, while the AMOC weakening should result in the deepening of the thermocline. Thus, such heat redistribution in the water column by itself would make AMHT and AMVT negatively correlated.

Note that typically in the ocean there exists positive correlations between temperature and salinity gradients (warm waters are often saline and cold waters are relatively fresh), hence we expect that increase/decrease in heat content can coincide with increase/decrease in salt content, respectively. Therefore, because the two gradients have opposite effects on density, the shoaling of the thermocline can be partially compensated by the halocline shoaling, in terms of impacts on density.

In summary, there operates two competing processes or feedbacks that affect ocean meridional heat transport. The first one is directly related to change in oceanic volume transport, acting almost immediately after the surface forcing was imposed. The second one, acting on longer timescales, is related to thermocline adjustment, which is only indirectly linked to the volume transport. In fact, our experiments suggest that the adjustment of the thermocline can potentially become more important on timescales longer than ~$500\,{\hbox{years}}$. On such timescales anomalies in heat transport, as in our FBC experiments, are primarily controlled by the mean advection of anomalous temperature (and changes in AMHT and AMVT become negatively correlated).

The competition between these two processes is rooted in the conservation of heat. Since there is no heat loss or gain in our experiments that test the system’s sensitivity to surface freshwater fluxes (under FBC), on long timescales, when an equilibrium state is reached, all terms need to be compensated in a time-average sense. This implies that the integral of positive heat advection by anomalous flow has to be compensated by a negative heat transport. This is achieved by heat redistribution through the water column, equivalent to thermocline adjustment. In other words, the two terms on the right-hand-side of (1) can be considered as two feedbacks affecting ocean heat content on different timescales, but compensating one another at the equilibrium state.

To further confirm our results, we compute the response of AMVT and AMHT to the optimal surface freshwater fluxes for volume transport as a function of time (Fig. 6). These computations take advantage of the stationarity of the asymptotic optimal surface fluxes and adjoint outputs and, within a linear framework, yield results equivalent to running a forward model (previously it has been demonstrated that the tangent linear model we use produces identical results for forward and backward trajectories, e.g. Sévellec et al. 2008). The mathematical treatment of this method is explained in the “Appendix”. For comparison, we use optimal surface freshwater fluxes obtained with and without freshwater conservation (i.e. with and without the zero-mean constraint imposed on freshwater flux anomalies).

Our computations indicate a reduction in volume transport of 0.6–0.7 Sv together with an increase of heat transport on the order of $0.1\times 10^{-2}\,{\hbox{PW}}$ on a millennial timescale (Fig. 6). Further, our estimates suggest a deficit in water subduction on the order of 50 Pt (${\equiv} 10^{18}\hbox { kg}$) and excessive heat accumulation of several GJ (${\equiv} 10^{9}\,{\hbox{J}}$) after 2500 years. The experiment with the freshwater conservation constraint imposed is especially instructive. As suggested by the previous analysis (Fig. 4), the negative correlation between AMVT and AMHT develops after ${\sim} 500\,{\hbox{years}}$, but on shorter timescales changes in the two metrics are positively correlated (Fig. 6).

Fig. 6

Response of a AMVT and b AMHT to the asymptotic optimal surface freshwater fluxes for volume transport as a function of time. The computations are based on expression (13) of the “Appendix” with FBC. Red dashed and black solid lines correspond to the optimal surface freshwater fluxes with and without the freshwater conservation constraint, respectively. Mass deficit (in $\hbox {Pt }\equiv 10^{18}\hbox { kg}$) and heat excess (in $\hbox {GJ }\equiv 10^9\,\hbox {J}$) are computed as time integrals of AMVT and AMHT over 2500 years of simulation. Note that initially, on centennial timescales, the weakening of the AMOC is accompanied by a reduction in poleward volume transport (negative anomalies in AMVT and AMHT). However eventually, over several thousand years, the system will transport more heat despite the weaker AMOC. This result is especially striking for the computations with the freshwater conservation constraint

4 Discussion and conclusion

The AMOC carries roughly 1.3 PW of heat northward in the North Atlantic (Ganachaud and Wunsch 2000; Lumpkin and Speer 2007). Conceptually, this baroclinic circulation can be described as a northward surface flow of relatively warm water with a cold southward equatorward return flow at depth (e.g. Srokosz et al. 2012; Sévellec and Fedorov 2011), even though three-dimensional details of the flow and its adjustment are rather complicated (e.g. Lozier 2012; Johnson and Marshall 2002; Thomas et al. 2012). The warm surface branch exchanges heat with the atmosphere, warming northern high latitudes (Gagosian 2003). This process strongly affects air temperatures over the ocean and contributes to the relative mild European climate. It has been argued, based on GCM experiments, that a shutdown of the AMOC could cool down Europe by 1-3 K on multi-decadal to centennial timescales (e.g. Vellinga and Wood 2002; Zhang and Delworth 2005; Stouffer et al. 2006; Barreiro et al. 2008).

Likewise, changes in northward oceanic heat transport in the North Atlantic are often considered to be positively correlated with changes in the AMOC intensity (i.e. stronger/weaker overturning circulation leads to a stronger/weaker northward transport of heat by the ocean). Whereas this result clearly holds for relatively short, transient timescales of decades to centuries (e.g. Sévellec et al. 2008; Sévellec and Fedorov 2015), we have demonstrated that it becomes less straightforward when dealing with very long, asymptotic timescales required for reaching a new equilibrium ocean state. We have shown that under right circumstances (no perturbations in surface heat flux are allowed), on millennial timescales the ocean northward heat transport can potentially decrease after a persistent, long-lasting increase in the AMOC intensity.

To demonstrate this result, we have computed optimal perturbations of surface heat and freshwater fluxes in a realistic ocean GCM (OPA 8.2 in its 2° configuration Madec et al. 1998) within a linear framework. The optimality was defined in terms of oceanic meridional volume and heat transports in the North Atlantic (AMVT and AMHT, respectively). The role of oceanic surface boundary conditions (mixed versus flux) and the freshwater and heat conservation for the optimal perturbations were also tested, leading to a set of 16 experiments.

For all these experiments the convergence to asymptotic values takes several thousands of years. In fact, both the AMHT and AMVT exhibit sensitivity to the imposed surface heat and freshwater fluxes even after several thousands of years. This suggests that the full oceanic adjustment requires many millennia to reach full equilibrium (in agreement with the conclusions of Wunsch and Heimbach 2008; Siberlin and Wunsch 2011). This result is significantly different from that of Bugnion and Hill (2006), who suggested an equilibration timescale of some 400 years (despite their multi-millennial diffusive timescale). On such centennial timescales pycnocline adjustment is not completed, implying that Bugnion and Hill (2006) and Bugnion et al. (2006b) could have overestimated the sensitivity of the AMOC.

Unlike meridional volume transport, which is only sensitive to large-scale perturbations on these timescales, heat transport is also sensitive to more intricate smaller-scale structures. Specifically, both optimal heat and freshwater flux perturbations for the AMHT show a signature in the middle of the North Atlantic (around 25°N). This is related to local stimulation of heat transport by horizontal barotropic circulation via the strengthening of the ocean subtropical gyre.

In the set of 16 experiments we have also tested the addition of the conservation constraint (which removes the mean freshwater or heat flux from the perturbations and allows maintaining exact mass or heat conservation in the system under flux boundary conditions). This constraint has only a minor impact on the spatial structure of the optimal perturbations (Table 1), since it does not affect the gradients of surface fluxes. This constraint can however reduce the sensitivities—in particular it reduces by a factor of 2 the impact of surface heat fluxes on AMHT by preventing the net warming of the ocean.

Unlike the conservation constraint, the use of MBC versus FBC significantly modifies the sensitivity of the relevant ocean dynamics (Table 1). Under MBC, there is a restoring term, which dampens SST variations. This effect causes a strong reduction of the sensitivity to surface heat fluxes of both AMVT and AMHT. In contrast, the sensitivity to freshwater fluxes is increased (also for both AMVT and AMHT). Moreover, restoring SST under MBC, thus maintaining ocean thermal stratification more or less unchanged, reestablishes the positive correlation between the AMVT and AMHT (responding to freshwater flux perturbations) at all timescales. That is, when ocean thermal stratification is maintained by the surface restoring term, the negative feedback due to thermocline adjustment is not sufficiently strong to overcome the positive advective feedback.

To further test the role of these two feedbacks affecting poleward heat transport in (1), we have generated a 40-members ensemble set of experiments in a coupled climate model. The model is IPSL-CM5 (Marti et al. 2010) and the ensemble is a larger set of experiments similar to the ensemble of Persechino et al. (2013), see Germe et al. (2015) for further details. Ensemble members are generated by choosing slightly different initial conditions. Short (20-year) simulations are conducted just to test the schematic proposed in Fig. 5. In these particular runs, the AMOC intensity of the ensemble mean increases on a decadal timescale (Fig. 7a). As expected from our analysis, we are able to detect indications of the second proposed feedback: upper-ocean heat content increases when the AMOC strengthens (correlation of +0.82, Fig. 7b), whereas at intermediate depths ocean heat content decreases (correlation of $-0.91$, Fig. 7c). Upper-ocean and intermediate depths correspond to 200–300 and 1200–2000 m, respectively, whereas the area of integration goes from the equator to 60°N in the Atlantic. These results suggest that variations in the depth of the thermocline are negatively correlated with variations in meridional volume transport. In other words, the strengthening of the AMOC entails a shoaling of the thermocline, consistent with this second feedback. This ocean thermal stratification adjustment during AMOC change is also consistent with the coupled climate modeling and observational studies of Marcott et al. (2011). However, on short timescales this second feedback is too weak to affect the direct relationship between oceanic volume and heat transports. It is thus unclear whether this negative feedback will ultimately be able to reverse the direct relationship or just partially compensate for the positive feedback in the coupled system. To further validate our idea in the coupled context one would need to use much longer simulations with slower AMOC changes.

Fig. 7

Ensemble mean (solid line) and spread (dashed lines indicating the mean plus/minus one standard deviation) for a the AMOC intensity, b Ocean Heat Content (OHC) anomaly between 200 and 300 m, and c OHC anomaly between 1200 and 2000 m obtained in coupled climate simulations using the IPSL-CM5 model. The area of integration for OHC is from the equator to 60°N in the Atlantic. The two correlation coefficients shown are between the AMOC variations and the respective OHC anomaly. As expected from our analysis in Fig. 5, the upper-ocean heat content is strongly and positively correlated with the AMOC changes, whereas at intermediate depths this correlation becomes negative. This plot illustrates the second (negative) feedback for decadal timescales. Similar results are found on much longer timescales (see Fig. 2e of Liu et al. 2009 for example)

In summary, our analysis of the sensitivity of the AMOC volume and heat transports suggests that a persistent slow-down of the overturning circulation could lead to a cooling of the North Atlantic ocean over decadal to centennial timescales; however, over millennial timescales this cooling will decrease and could potentially give way to surface warming. This latter effect is related to the thermocline adjustment that can compensate the initial reduction of oceanic heat transport. In our study the strength of this effect depends on the type of the model’s surface boundary conditions and thus on atmospheric processes that maintain the ocean thermal structure.

Indirect evidence for this behavior may come from data for the transition between the Last Glacial Maximum and Heinrich event 1 (H1). From $-18$ to $-15\hbox {kyr}$ before present, AMVT proxies exhibit a negative trend whereas proxies for the North Atlantic SST exhibit a warming trend (McManus et al. 2004). This interval between the Last Glacial and the Holocene is a period of net surface freshwater transport to the ocean due to the melting of continental ice sheets. However, since during this period SSTs were also affected by increasing greenhouse gas forcing (e.g. Clark et al. 2012), applying our results directly to this transition would be too speculative at this point. Nevertheless, this transition provides a hypothetical example of how the traditional thinking (that the slowdown of the AMOC due to surface freshwater fluxes necessarily leads to a colder North Atlantic) might fail on millennial timescales.

These results stress the importance of long time integration of climate GCMs, several thousand years long, in order to achieve a fully equilibrated climate state—shorter integrations may contain transient features vanishing in longer runs. These findings, consistent with those of Wunsch and Heimbach (2008) and Siberlin and Wunsch (2011) who looked at the tracer propagation timescales, has important implication for the interpretation of paleoclimate proxy data, as relevant to both cold and warm climate states. For example, a persistently weaker AMOC does not necessarily imply a cold North Atlantic climate at equilibrium or vice versa.

On shorter, centennial timescales our study is useful to estimate the upper bound on the impacts of surface heat and freshwater fluxes on oceanic volume and heat transports as relevant to contemporary global warming. To this end, for each individual experiment we selected the most efficient cases with a 100 years delay (Table 2) and scaled them with the magnitude of expected changes in surface fluxes.

• Assuming a change in surface heat fluxes of $4\hbox { W m}^{-2}$ over the ocean (IPCC 2007, 2013), we estimate a reduction of AMVT by 6.9 Sv and AMHT by 0.2 PW.

• Global warming is expected to increase the hydrological cycle by 4 % (Held and Soden 2006) within the next century, corresponding to an anomalous freshwater flux of about $3\hbox { cm year}^{-1}$. We estimate that such a forcing can lead to a reduction of AMVT by 3.8 Sv and AMHT by 0.1 PW.

Acting together, these changes would imply the upper bounds on the weakening of the AMVT and AMHT of nearly 80 and 40 %, respectively, after 100 years, but the actual impacts will be probably weaker.

Table 2 As in Table 1 but for a flux’s duration of $\tau =100\,{\hbox{years}}$ (transient experiments)

Finally, we should emphasize that, despite testing different surface boundary conditions (i.e. FBC and MBC experiments) and having some confirmation for the proposed mechanisms in a coupled system (Fig. 7), our study has been conducted in a forced oceanic paradigm. Thus, one natural extension is to take into account the role of ocean-atmospheric interactions. We expect that in the coupled ocean-atmosphere system the results will fall between the results of our two sets of experiments (those using FBC wherein atmospheric feedbacks are neglected and those using MBC wherein atmospheric heat capacity is infinite). However, at this point we cannot say whether in the fully coupled ocean-atmosphere system the proposed negative feedback will necessarily overwhelm the positive feedback or only partially compensate for it. Some available long coupled simulations with a nearly complete shut-down of the AMOC (Liu et al. 2009) show persistent cooling in the North Atlantic, but such results go beyond the applicability of our study dealing with small perturbations around the equilibrium. Thus, the coupled problem needs to be addressed in future work.

Appendix: Computing optimal surface flux perturbations

Notations of the linear framework. Firstly, we introduce key notations used in this study. The prognostic equations of the ocean GCM can be written as a general non-autonomous dynamical system:

$$\begin{aligned} d_t{|{{{\varvec{U}}}}\rangle }=\mathcal {N}\left( {|{{{\varvec{U}}}}\rangle },t\right) , \end{aligned}$$

(2)

where t is time, $\mathcal {N}$ is a time-dependent nonlinear operator and ${|{{{\varvec{U}}}}\rangle }$—the state vector consisting of all prognostic variables. We also defined ${\langle {{{\varvec{U}}}}|}$ through the Euclidean scalar product ${\langle {{{\varvec{U}}}|{{\varvec{U}}}}\rangle }$ and decompose the state vector as ${|{{{\varvec{U}}}}\rangle }={|{{\bar{{\varvec{U}}}}}\rangle }+{|{{{\varvec{u}}}}\rangle }$, where ${|{\bar{{{\varvec{U}}}}}\rangle }$ is the model’s non-linear trajectory (i.e. the seasonally varying basic state) and ${|{{{\varvec{u}}}}\rangle }$ is a perturbation (hereafter called ocean state anomaly). The time evolution of the anomaly reads as:

$$\begin{aligned} d_t{|{{{\varvec{u}}}}\rangle }={{\mathbf {\mathsf{{A}}}}}(t){|{{{\varvec{u}}}}\rangle }+{{\mathbf {\mathsf{{B}}}}}{|{{{\varvec{f}}}}\rangle },\; {{\mathbf {\mathsf{{A}}}}}(t)=\left. \frac{\partial \mathcal {N}}{\partial {|{{{\varvec{U}}}}\rangle }}\right| _{{|{{\bar{{\varvec{U}}}}}\rangle }},\; {{\mathbf {\mathsf{{B}}}}}=\frac{\partial \mathcal {N}}{\partial {|{{\varvec{\mathcal {F}}}}\rangle }}, \end{aligned}$$

(3)

where ${{\mathbf {\mathsf{{A}}}}}(t)$ is a Jacobian matrix, which is a function of the trajectory ${|{{\bar{{\varvec{U}}}}}\rangle }$, ${|{{{\varvec{f}}}}\rangle }$ is a surface flux anomaly, ${|{{\varvec{\mathcal {F}}}}\rangle }$—the total surface flux, and ${{\mathbf {\mathsf{{B}}}}}$—the linearized flux operator. Further, we introduce the propagator operator of the linearized dynamics to obtain the temporal evolution of ocean state anomalies as:

$$\begin{aligned} {|{{{\varvec{u}}}(t_2)}\rangle }=\int _{t_1}^{t_2}ds\,\left[ {{\mathbf {\mathsf{{A}}}}}(s){|{{{\varvec{u}}}(s)}\rangle }+{{\mathbf {\mathsf{{B}}}}}{|{{{\varvec{f}}}}\rangle }\right] ={{\mathbf {\mathsf{{M}}}}}(t_1,t_2){|{{{\varvec{u}}}(t_1)}\rangle }+\int _{t_1}^{t_2}ds\,{{\mathbf {\mathsf{{M}}}}}(t_1,s){{\mathbf {\mathsf{{B}}}}}{|{{{\varvec{f}}}}\rangle }, \end{aligned}$$

(4)

where ${{\mathbf {\mathsf{{M}}}}}(t_1,t_2)$ is the propagator of the linearized dynamics from the time $t_1$ to the time $t_2$, and s is a time variable. Without loss of generality, we can use the time delay $\tau =t_2 - t_1$ as our main variable ($\tau$ will give the length of the time integration). We also set ${|{{{\varvec{u}}}(0)}\rangle }=0$, since the impact of optimal initial perturbations in surface temperatute and salinity on the AMOC has been extensively studied in Sévellec et al. (2008) and Sévellec and Fedorov (2015) for the same model configuration. Thus, we obtain a simple result for the ocean state anomaly as a function of the steady surface flux perturbation and the time delay (also see Sévellec et al. 2007):

$$\begin{aligned} {|{{{\varvec{u}}}(\tau )}\rangle }=\int _{0}^\tau ds\,{{\mathbf {\mathsf{{M}}}}}(s){{\mathbf {\mathsf{{B}}}}}{|{{{\varvec{f}}}}\rangle }, \end{aligned}$$

(5)

Defining the optimality for the problem. To obtain optimal surface flux perturbations, we also need to define a measure of optimality, which is often referred to as the cost function. For the Atlantic Meridional Volume Transport (AMVT) we define the cost function as:

$$\begin{aligned} {\langle {{{\varvec{F}}}|{{\varvec{u}}}}\rangle }= & {} \left. \mathrm {AMVT}'\right| _{\left\{ \phi =\phi _{\max },z=z_{\max }\right\} },\nonumber \left\{ \exists \left\{ \phi _{\max },z_{\max }\right\} \in \left\{ \Phi ,Z\right\} :\left. \overline{\mathrm {AMVT}}\right| _{\left\{ \phi =\phi _{\max },z=z_{\max }\right\} }=\max \left( \overline{\mathrm {AMVT}}\right) \right\} , \end{aligned}$$

(6)

where ${|{{{\varvec{F}}}}\rangle }$ is a vector defining the cost function, $\max$ stand for the maximum, $\phi$ is latitude, $\phi _{\max }$—the latitude of the maximum of AMVT, $\Phi$—the ensemble of all possible latitudes $\phi$, $z_{\max }$—the depth of the maximum of AMVT, Z—the ensemble of all possible depths z. This particular choice of latitude and depth ($\phi =\phi _{\max }$ and $z=z_{\max }$, respectively) allows an exact definition of the maximum since

$$\begin{aligned} {\langle {{{\varvec{F}}}|{{\varvec{U}}}}\rangle } &= {} {\langle {{{\varvec{F}}}|{\bar{{\varvec{U}}}}}\rangle }+{\langle {{{\varvec{F}}}|{{\varvec{u}}}}\rangle }, & \max \left( \mathrm {AMVT}\right) = {} \max \left( \overline{\mathrm {AMVT}}\right) +\left. \mathrm {AMVT}'\right| _{\left\{ \phi =\phi _{\max },z=z_{\max }\right\} }. \end{aligned}$$

The same approach could be applied to the other measure used in the study: the Atlantic Meridional Heat Transport (which depends only on latitude). In our experiments, the location of the maximum of AMVT or AMHT are $\phi _{\max }=50^\circ \hbox {N}$ and $z_{\max }=-1000\hbox { m}$ or $\phi _{\max }=25^\circ \hbox {N}$. At these latitudes for our model configuration, the eddy-induced velocities are weak, so that the Eulerian volume and heat transports are nearly equivalent to the Lagrangian transports. On the other hand, we acknowledge that eddy-resolving models could in future show other sensitivities, but exploring these issues goes beyond our current numerical capabilities.

In summary, we intend to find surface fluxes that would lead to the maximum change of the AMVT or AMHT. Thus, we need to solve a maximization problem.

Defining of a norm constraining the optimal flux perturbations. To avoid degeneracy of the maximization problem in a linear framework, we introduce a norm for the fluxes. One simple example of such a norm is a spatial average of the square of surface fluxes, such as:

$$\begin{aligned} {\langle {{{\varvec{f}}}|{{\mathbf {\mathsf{{S}}}}}|{{\varvec{f}}}}\rangle }=\frac{\iint d\sigma \,\left[ f\left( x,y\right) \right] ^2}{\iint d\sigma }, \end{aligned}$$

(7)

where ${{\mathbf {\mathsf{{S}}}}}$ is the operator defining the norm, f—surface fluxes, $d\sigma$—a unit surface, x—the zonal coordinate, and y—the meridional coordinate.

Heat and freshwater conservation constraints. One of the control parameters in our experiments is the conservation constraint that controls the conservation of heat or salt in the ocean. This conservation is achieved by introducing an explicit constraint setting the average of surface heat or freshwater fluxes to zero:

$$\begin{aligned} {\langle {{{\varvec{C}}}|{{\varvec{f}}}}\rangle }=\iint d\sigma \,f\left( x,y\right) =0, \end{aligned}$$

(8)

where ${|{{{\varvec{C}}}}\rangle }$ is a vector yielding the heat or freshwater flux spatial average. We refer to these constraints as the zero-mean constraints on the fluxes or heat and freshwater conservation constraints.

Finding the optimal flux perturbations. Now we can define a Lagrangian function maximizing the cost function asymptotically ($\tau \rightarrow \infty$) under the constraint that surface flux perturbations are normalized (${\langle {{{\varvec{f}}}|{{\mathbf {\mathsf{{S}}}}}|{{\varvec{f}}}}\rangle }=1$, a necessary condition for maximization in a linear framework):

$$\begin{aligned} \mathcal {L}=\lim _{\tau \rightarrow \infty }\left[ {\langle {{{\varvec{F}}}|{{\varvec{u}}}(\tau )}\rangle }\right] -\gamma _1\left[ {\langle {{{\varvec{f}}}|{{\mathbf {\mathsf{{S}}}}}|{{\varvec{f}}}}\rangle }-1\right] -\gamma _2{\langle {{{\varvec{C}}}|{{\varvec{f}}}}\rangle }, \end{aligned}$$

where $\gamma _1$ and $\gamma _2$ are Lagrange multipliers associated with the two constraints. The maximization procedure corresponds to solving the equation:

$$\begin{aligned} d\mathcal {L}=0. \end{aligned}$$

We now obtain an explicit solution of the flux perturbation maximizing ${\langle {{{\varvec{F}}}|{{\varvec{u}}}(\infty )}\rangle }$:

$$\begin{aligned} {|{{{\varvec{f}}}}\rangle }=\lim _{\tau \rightarrow \infty }\left\{ \pm \frac{1}{\gamma _1}\int _0^\tau ds\,{{\mathbf {\mathsf{{S}}}}}^{-1}\left[ {{\mathbf {\mathsf{{B}}}}}^\dagger {{\mathbf {\mathsf{{M}}}}}^\dagger (s){|{{{\varvec{F}}}}\rangle }-\gamma _2{|{{{\varvec{C}}}}\rangle }\right] \right\} , \end{aligned}$$

(9)

where ${{\mathbf {\mathsf{{M}}}}}^\dagger(\tau)$ is an adjoint of the propagator (the one defined through the Euclidean scalar product) over the duration $\tau$,

$$\begin{aligned} \gamma _1^2= & {} \lim _{\tau \rightarrow \infty }\iint _0^\tau ds ds'\, {\langle {{{\varvec{F}}}|{{\mathbf {\mathsf{{M}}}}}(s){{\mathbf {\mathsf{{B}}}}}{{\mathbf {\mathsf{{S}}}}}^{-1}{{\mathbf {\mathsf{{B}}}}}^\dagger {{\mathbf {\mathsf{{M}}}}}^\dagger (s')|{{\varvec{F}}}}\rangle }-\gamma _2{\langle {{{\varvec{F}}}|{{\mathbf {\mathsf{{M}}}}}(s){{\mathbf {\mathsf{{B}}}}}{{\mathbf {\mathsf{{S}}}}}^{-1}|{{\varvec{C}}}}\rangle }\nonumber \\&-\gamma _2{\langle {{{\varvec{C}}}|{{\mathbf {\mathsf{{S}}}}}^{-1}{{\mathbf {\mathsf{{B}}}}}^\dagger {{\mathbf {\mathsf{{M}}}}}^\dagger (s')|{{\varvec{F}}}}\rangle }+\gamma _2^2{\langle {{{\varvec{C}}}|{{\mathbf {\mathsf{{S}}}}}^{-1}|{{\varvec{C}}}}\rangle }, \end{aligned}$$

(10a)

$$\begin{aligned} \gamma _2= & {} \lim _{\tau \rightarrow \infty }\int _0^\tau ds\,\frac{{\langle {{{\varvec{C}}}|{{\mathbf {\mathsf{{S}}}}}^{-1}{{\mathbf {\mathsf{{B}}}}}^\dagger {{\mathbf {\mathsf{{M}}}}}^\dagger (s)|{{\varvec{F}}}}\rangle }}{{\langle {{{\varvec{C}}}|{{\mathbf {\mathsf{{S}}}}}^{-1}|{{\varvec{C}}}}\rangle }}. \end{aligned}$$

(10b)

The impact of this perturbation on the circulation is then:

$$\begin{aligned} \mathrm {AMVT}'=\lim _{\tau \rightarrow \infty }\left[ \pm \frac{1}{\gamma _1}\iint _0^\tau dsds'\,{\langle {{{\varvec{F}}}|{{\mathbf {\mathsf{{M}}}}}(s){{\mathbf {\mathsf{{B}}}}}{{\mathbf {\mathsf{{S}}}}}^{-1}{{\mathbf {\mathsf{{B}}}}}^\dagger {{\mathbf {\mathsf{{M}}}}}^\dagger (s')|{{\varvec{F}}}}\rangle }-\gamma _2{\langle {{{\varvec{F}}}|{{\mathbf {\mathsf{{M}}}}}(s){{\mathbf {\mathsf{{B}}}}}{{\mathbf {\mathsf{{S}}}}}^{-1}|{{\varvec{C}}}}\rangle }\right] , \end{aligned}$$

(11)

or similar for $\hbox {AMHT}'$ depending on the cost function defined in (6). Results based on numerical evalution of (9) and (11) are given in Sect. 3.

To measure the convergence of the solution, we also define a transient (non-asymptotic) impact of the flux perturbation on the circulation as

$$\begin{aligned} \int _0^{\tau _\infty } ds\,{{\mathbf {\mathsf{{M}}}}}^\dagger (s){|{{{\varvec{F}}}}\rangle }\simeq \lim _{\tau \rightarrow \infty }\int _0^\tau ds\,{{\mathbf {\mathsf{{M}}}}}^\dagger (s){|{{{\varvec{F}}}}\rangle }, \end{aligned}$$

(12)

where $\tau _\infty$ represents the convergence timescale of the adjoint model. After this time $\tau _\infty$, the difference with the asymptotic limit can be considered sufficiently small to be neglected in (12). Thus, we will be able to use (9) to compute ${|{{{\varvec{f}}}}\rangle }$ and the sensitivity to the forcing of the measure, ${|{{{\varvec{F}}}}\rangle }$. Transient solutions (as in Figs. 2, 4) can be obtained by using intermediate values of the time delay (such that $0< \tau < \tau _\infty$).

Finally, to diagnose the impact of the asymptotic optimal surface fluxes on volume and heat transports at an arbitrary time after the fluxes were imposed, we can start from (5) and (6), take advantage of the steadiness of the asymptotic optimal surface fluxes ($d_t{|{{{\varvec{f}}}}\rangle }=0$) as shown in (9), and obtain:

$$\begin{aligned} {\langle {{{\varvec{F}}}|{{\varvec{u}}}(t)}\rangle }={\langle {{{\varvec{F}}}}|}\left[ \int _{0}^t ds\,{{\mathbf {\mathsf{{M}}}}}(s){{\mathbf {\mathsf{{B}}}}}{|{{{\varvec{f}}}}\rangle }\right] ={\langle {{{\varvec{f}}}}|}\left[ \int _{0}^t ds\,{{\mathbf {\mathsf{{B}}}}}^\dagger {{\mathbf {\mathsf{{M}}}}}^\dagger (s){|{{{\varvec{F}}}}\rangle }\right] , \end{aligned}$$

(13)

Previously it has been demonstrated that the tangent linear model we use produces identical results for “forward” and “backward” trajectories (e.g. Sévellec et al. 2008). Therefore, this diagnostic, based on adjoint outputs (Fig. 6), is actually equivalent to forward simulation within a linear framework where the asymptotic optimal surface fluxes were imposed from time $t = 0$.