1 Introduction

The increase in the atmospheric water vapor content with global warming is expected to change the hydrological cycle (e.g. Turner and Annamalai 2012; IPCC 2013). Increases in frequency and intensity of extreme rainfall events are thought to be one of the major consequences of changes in the hydrological cycle, and this yields a larger risk for severe flood events. To assess the climate change impact on the precipitation extremes is a difficult task, as the extremes are not well represented in global climate models. However, several studies suggest that the heaviest precipitation events should increase at a higher rate than the mean precipitation (e.g. Pall et al. 2007; O’Gorman and Schneider 2009), and also that the extreme precipitation on sub-daily time scale is expected to increase significantly (Westra et al. 2014).

The Indian subcontinent is particularly vulnerable to extreme rainfall events, since a large part of the population is poor, the infrastructure and crop yield is easily destructed by heavy precipitation events and early warning systems are not always reaching out to the people that are being affected, thus the people are not being notified or evacuated when these events arise (World bank 2013). Many of the extreme rainfall events in India occur during the Southwest monsoon, which is the rainy season starting in the beginning of June until the end of September. During these 4 months the west coast of India (along the Gaths Mountains), the north-northeast (along the Himalayan rim) and some areas over central India are most exposed to extreme rainfall events (Pattanaik and Rajeevan 2010). The west coast of India and the north-northeast are both regions that are characterized by steep orography, thus the extreme rainfall that occurs in these regions are often a result of forced ascent over the mountains. The extreme rainfall events over central India are a result of the synoptic scale monsoon low-pressure systems (LPS), which occur frequently during the monsoon season (Goswami et al. 2006; Sikka 2006; Pattanaik and Rajeevan 2010). The monsoon LPS have been investigated extensively in several studies (e.g. Sikka 2006; Ajayamohan et al. 2010; Krishnamurthy and Ajayamohan 2010). The reason for this interest is due to the fact that they are very rain bearing, where as much as 50 % of the precipitation during the monsoon season comes from these systems (Yoon and Chen 2005).

Throughout the South Asian monsoon severe flood hazards occurs almost every year (Mirza 2011). The Pakistan flooding during the 2010 monsoon season and the North-India flooding in 2013 both affected several hundred thousand of people, caused thousands of fatalities and led to large economic losses (Houze et al. 2011; Webster et al. 2011; Joseph et al. 2014; Dube et al. 2014). Different weather conditions was leading to these two extreme rainfall incidents, however, monsoon LPS were present in the atmospheric circulation for both events. For the Pakistan flood a depression from the Bay of Bengal was bringing air with high moisture content to arid regions of Pakistan, and when this moist air met southeasterly flow due to a high pressure over Tibetan Plateau, intense convective towers with very heavy precipitation rates, was generated over Pakistan (Houze et al. 2011). The flooding in North-India was associated with a weaker monsoon LPS, that moved northwestward from the Bay of Bengal with air containing large amount of moisture. Strong low-level convergences were generated leading to deep convective towers over the state Uttarakhand in India, when the moist air from Bay of Bengal met a western disturbance that moved eastward (Joseph et al. 2014; Dube et al. 2014). These two flood incidents were both a result of a very anomalous weather condition. An abnormal propagation of the depression was seen for the Pakistan flooding, and for the northern Indian flooding the propagation of the monsoon was 1 month earlier than expected. To what extent these weather conditions are results of climate change or natural variability are not known. To investigate if the atmospheric condition in the future is more favorable to develop LPS with such abnormal behavior, it is necessary to use climate models where the atmospheric dynamics of the monsoon circulation and the embedded disturbances are well represented.

The Fifth Assessment report (AR5) from the Intergovernmental Panel on Climate Change (IPCC) purposes that there will be enhanced summer monsoon precipitation over India, and there will be increased rainfall extremes from cyclones that makes landfall on the coast of Bay of Bengal and the Arabian Sea (IPCC 2013). Stowasser et al. (2009) investigated the frequency and intensity of monsoon depressions by downscaling a climate scenario of a four times CO2—concentration, and hypothesized that the warmer climate is favorable to develop more frequently and intense depressions. Downscaling climate models with regional models is an important method when it comes to perform climate impact studies, and is invaluable for the end used (Maraun et al. 2010). However, several studies argue that since the climate models cannot reproduce the current climate accurately, the climate scenario projections are not reliable (e.g. Sabeerali et al. 2015; Sooraj et al. 2014), thus the downscaled projections will be influenced by the bias in the climate models. The Coupled Model Inter-comparison Project 5 (CMIP5) models underestimate the precipitation of the current climate in the central Indian region, and this can be linked to a poor representation of the monsoon LPS in the climate models (e.g. see Figure 3 in Sooraj et al. 2014).

Precipitation extremes should be studied with respect to their dynamical and thermo-dynamical forcing. The dynamical forcing is associated with the large-scale atmospheric circulation, whereas the thermo-dynamical forcing is connected with the moisture content of the atmosphere. To study how sensitive the dynamical forcing is to a changing climate, it is necessary that all the components of the large-scale monsoon circulation are represented in the climate model. As discussed above, this is still a challenging task, since the current climate models have difficulties in simulating the present climate (Turner and Annamalai 2012; Sabeerali et al. 2015; Sooraj et al. 2014). However, there are methods to keep the large-scale flow “unchanged”, and thus only change the thermodynamic properties. This surrogate climate change method is good for sensitivity studies, and separates the effect of the change in the atmospheric moisture and temperature from changes in the large-scale atmospheric circulation (Schär et al. 1996). We here perform sensitivity experiment on 10 different monsoon LPS that developed during 1979–2010, originally detected by a tracking algorithm in the ERA-Interim reanalysis (Sørland and Sorteberg 2015; from hereafter SS2015a). The ten LPS cases are connected to an observed extreme rainfall event over India. Each LPS case is first simulated with unperturbed lateral and boundary conditions (LBC), called the control runs. Then two sets of perturbed runs are performed on each LPS case, where the temperature is increased, and since the relative humidity (RH) is kept constant, the moisture increases as the Clausius–Clapeyron (CC) relation (i.e. ~6.5 %/K).

In this study we are focusing on the short duration extreme precipitation that is released over the central India region. Even though these systems have the largest precipitation rate over the ocean, it is important to understand how the precipitation might change where people are living. The LPS are in several studies connected to extreme rainfall events in the central India region (e.g. Goswami et al. 2006; Sikka 2006; Pattanaik and Rajeevan 2010; Ajayamohan et al. 2010), we therefore want to examine how sensitive the LPS generated extreme rainfalls are, to a warmer and more humid environment. A separate study, which investigates the intensity and mean precipitation following the low-pressure systems, will be presented in a manuscript in the near future.

The paper is divided as follows: in Sect. 2 the design of the sensitivity experiments is described and the model evaluation is given in Sect. 3. Section 4 covers the area of study and the results are presented in Sect. 5 and we end with a summary of the main findings in Sect. 6.

2 Selection of the LPS cases and the design of the sensitivity simulations

2.1 LPS cases

The ten cases are chosen from the 39 LPS identified in SS2015a. In all cases both the ERA-Interim (Dee et al. 2011), which we use as boundary conditions, and the observations, taken from the Indian Meteorological Department (IMD) rainfall (Rajeevan et al. 2006), indicate occurrence of extreme precipitation in the vicinity of the LPS propagation path. All the LPS simulated develop over the BoB and propagate towards the central Indian continent. Table 1 lists the selected LPS with their respective lifetime.

Table 1 The lifetime of the ten different LPS simulated in this study
Full size table

2.2 Model configurations

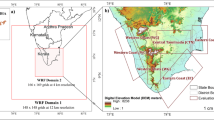
Version 3.4.1 of the regional Weather Research and Forecasting (WRF) model (Skamarock et al. 2008) is used to perform the simulations. WRF is a fully compressible and non-hydrostatic model, which makes it suitable for very high-resolution simulations. The Advanced Research WRF dynamical core is used. The domain contains 694 × 694 grid points with a 4 km horizontal resolution and 50 vertical (eta) model levels, covering India and parts of BoB, Himalaya and Arabian Sea (Fig. 1). The domain size is a compromise between two competing factors. The domain must be small enough to be constrained by the large-scale boundary conditions, but be large enough so that the model can develop its own LPS dynamics.

Fig. 1
figure 1

The WRF domain used for the simulations (the whole figure), and the central India box used in this study (black box). The track density of the LPS in the CTR (left), 2 K (middle) and 4 K (right) runs are also shown

Full size image

The simulations start 24 h before the initiation of the LPS, and continue throughout the LPS lifetime. The first 24-h are to allow for the model spin-up of precipitation. Using 12 h is enough for spinning up precipitation, but since we are comparing the model precipitation with the IMD rainfall, the latter being given as 24-h accumulated precipitation, we added 12 h to the spin up time. We found no major differences between a 12 and 24-h initialization before the LPS.

The 6-h ERA-Interim reanalysis data (Dee et al. 2011), interpolated to ~0.5°, provide initial and lateral boundary conditions, for both the control and perturbed runs. The generation of perturbed initial and boundary conditions is described in Sect. 2.3. The transition from the coarse ERA-Interim data to the high resolution WRF is thought to be too large. Therefore we tested the use of two nested domains, where the outer domain was spectrally nudged towards the reanalysis. The results with the nudging did not differ much from the current set-up we are using, with one domain and no nudging. An outer domain with no nudging would give large deviations in the large-scale flow of the climate simulation, and undermine the whole idea of the pseudo climate setup. The advantage of using only one high-resolution domain without coarser resolution outer domain is that we do not use any cumulus parameterization scheme.

The runs were performed with the Thompson microphysical scheme (Thompson et al. 2008), Yonsei University Planetary Boundary layer scheme (YSU) (Hong et al. 2006), Community Atmosphere Model’s (CAM) longwave and shortwave radiation scheme (Collins et al. 2006), and the Noah Land Surface Model scheme (Niu et al. 2011). No convection parameterization scheme was enabled for these 4 km-horizontal resolution simulations. The model was run with SST update every 6 h, and we also included an alternative initialization of the lake water temperatures. This method uses the diurnal average temperature taken from the area close to the lake, instead of the SST from the closest ocean.

2.3 Boundary conditions

The control run uses the unperturbed ERA-Interim boundary conditions. The perturbed runs are generated using the method of surrogate climate change scenarios described in Schär et al. (1996), and involves changing all the temperature fields in the boundary conditions uniformly. Hence we add a change in the temperature, ΔT, to the temperature fields on all pressure levels in the atmosphere, the SST, the skin-temperature and all the soil temperature fields in the ERA-Interim data, while keeping the relative humidity constant, and adjust the specific humidify according to the CC-relation. In generating initial and lateral boundary conditions the surface pressure is adjusted to keep pressure gradients unchanged. Thus for each LPS case, the three simulations are conducted with three different boundary conditions, consisting of one unperturbed control run (CTR), and two perturbed runs, which respectively corresponds to: 2 K perturbations where ΔT = +2 K and Δq ≈ +13 %, and 4 K perturbations where ΔT = +4 K and Δq ≈ +26 %.

3 Model evaluation

3.1 The Central India mean precipitation

CTR runs are evaluated against the IMD rainfall data (Rajeevan et al. 2006), which provide 24-h accumulated rainfall on a 1° × 1° grid. We make a spatial average comparison of the precipitation over an area covering central India bounded by the latitudes 19–27°N and longitudes 74–85°E. The evaluation of the WRF control simulations is performed by comparing the central India mean total accumulated precipitation against the IMD rainfall (Fig. 2). Table 1 lists the mean percentage error (MPE) of total accumulated precipitation, whereas the MPE is defined as:

$$ MPE = 100\,\% \cdot \frac{{P_{WRF} - P_{IMD} }}{{P_{IMD} }} $$
(1)

where PIMD (PWRF) is the total accumulated precipitation from the IMD dataset (WRF) at the end of the simulations. In general, the CTR runs capture the observational evolution of the precipitation in most cases (see Fig. 2). On average, the accumulated precipitation during the LPS lifetime is underestimated by 4.9 %. However, there is a great variation in the model performance for different LPS cases. Thus there is no systematic error in the WRF precipitation as compared to the IMD precipitation. The mean absolute percentage error (MAPE), which is similar to MPE except that the absolute value of the error is considered instead, is 17.5 % for the total accumulated precipitation. The MAPE of the daily accumulated precipitation is 54.8 %. To summarize, WRF reasonably reproduces the accumulated precipitation over the central India during the LPS lifetime, but the timing of the precipitation is not always correct.

Fig. 2
figure 2

The first and third column shows the central India mean 24 h accumulated precipitation during the simulation of each LPS case. The second and forth column shows the trajectories for the different LPS cases. For the accumulated precipitation (trajectories) the green line is the IMD precipitation (the trajectory from the ERA-Interim), the blue line is from the CTR simulations

Full size image

In this study we have not investigated the sensitivity of the modeled precipitation to the choice of parameterization. Rajeevan et al. (2010) investigated the sensitivity to different microphysical schemes in simulating a thunderstorm over Southeast India. They found that the WRF simulations were closest to the observations when the Thompson scheme was used. Even though 4 km is too coarse to adequately resolve small-scale convection, the results from Rajeevan et al. (2010) strengthened our confidence in the model configuration used herein. Moreover, the IMD rainfall dataset with 1° × 1° horizontal resolution is rather coarse, and the number of stations in each grid box and interpolation method both affect the data quality. Thus the gridded dataset should not be seen as the truth, but an approximation to the truth.

3.2 Comparing the simulated synoptic conditions

The LPS trajectories in the WRF simulations (CTR, 2 and 4 K runs) are determined by visual inspection of the 850 hPa geopotential height field every 6 h. All simulations have a well-defined low-pressure system. However, the lifetime and the position of the lows differ slightly between the CTR run and the two perturbed runs of each LPS case (Fig. 1). At 4 km horizontal resolution the model geopotential height is noisy, therefore a subjective assessment of the position of the low is made by identifying the lowest (deepest) local minimum in the vicinity of the low-pressure center detected in the previous time step. We include an additional constraint that the low had to contain at least two or more closed contours (where the contour interval is 5 m), otherwise, the low-pressure system was assumed to have dissipated.

We compare the LPS trajectories in control simulations with those in the ERA-Interim reanalysis. The LPS detection follows a tracking algorithm, described in SS2015a. The trajectories from the reanalysis and the control simulation are reasonably well co-located in most of the LPS cases (Fig. 2). The start-position is not exactly the same since we start the integration 24-h before the identification of the LPS in the ERA-Interim. In some cases the trajectory slightly diverges as the integration progresses. Given the relatively large domain size, the model results are not always well constrained by the LBC.

The trajectories from the three sets of simulations (CTR, 2 and 4 K) are compared in Fig. 1. There is a small change in the path of the lows from the CTR-simulations to the two perturbed runs. The large-scale flow from the ERA-Interim reanalysis, which is imposed as the LBC, is kept unchanged in the surrogate climate change method. However, the large domain size enables the development of different LPS dynamics in the three simulations. As shown in Fig. 1, a great similarity of the trajectories is present among the three sets of simulations, suggestive of a dynamical consistency between the control run and perturbed runs. However, in a couple cases the trajectories of the 4 K run differs considerably from the control run. The large domain allows the LPS dynamics to be influenced by feedbacks associated with the temperature warming.

4 Study area and analysis method

India is a country with a complex orography that is resulting in large heterogeneity in the precipitation characteristics. The Indian subcontinent is also consisting of a large network of river systems. The rivers downstream from the Himalayas are the largest ones, and these rivers (Indus, Ganges and Brahmaputra) drain large parts of the north-northeast of India. The central India region is also subject to several river networks, but in contrary to the rivers downstream from the mountainous Himalaya that are dependent on snow and ice melt as well as precipitation, the basins in the central India region are mainly rain fed (Singh et al. 2008).

The model domain used to perform the sensitivity experiments is mainly covering the Indian subcontinent, where parts of the adjoining oceans (Arabian Sea and Bay of Bengal) are included. In this study we pick out data in a box bounded by the longitude and latitude 74–88°E, 17–26.8°N, covering the central India region. Figure 1 shows the WRF model domain, together with the central India box, and compares the trajectories from the three sets of simulations. A small change in the path of the lows from the CTR-simulations to the two perturbed runs is seen in Fig. 1, however, in general the trajectories are well located inside the box.

The central India box includes several river basins, as parts of Ganges, Narmada, Godavari, Mahanadi, Brahmani, Subarnarekha and a few other smaller basins on the east coast of India. Precipitation analysis and the influence on runoff are best performed on catchment scale. However, we are looking at the whole central India box, instead of dividing into the different catchment. The main reason for this is that the lows do not have identical propagation path across the central India region, as seen in Fig. 1. Thus if we look at differences on the catchment scale, we could not know whether the differences were a result of the change in the thermodynamic properties, or due to slightly different paths of the lows. By averaging over a larger region, we hope to reduce this uncertainty.

The model results are analyzed with focus on understanding how sensitive the precipitation and runoff is to an increase in the temperature and the corresponding change in the atmospheric moisture content. Thus we look for differences between the control (CTR) and the perturbed runs (2 and 4 K). Statistical significance tests are performed to check whether the difference between the control and perturbed runs are statistical significant. We use the bootstrap method to find the 5 % confidence levels of the ten LPS cases for each set of simulation, and when the confidence levels do not overlap, the field is different at 95 % significance. The runoff is the sum of the surface runoff and deep soil drainage from the Noah Land Surface Model scheme (Niu et al. 2011) used in the WRF simulations. We pick out the land data within the central India box (i.e. removing grid points that are ocean in the box). First we investigate the mean changes in the precipitation and the runoff, followed by analysis of the extreme events.

5 Results

5.1 Sensitivity of areal mean precipitation and runoff to increased temperature

Before examining the changes in the extremes, we show the mean relative changes between the control and perturbed runs of the precipitation and runoff. Table 2 lists the central India mean precipitation and runoff (including dry and wet points) from the control run, and the fractional change from the control runs to the 2 and 4 K runs, scaled with the temperature perturbation. The change is largest from the control to the 4 K runs, where the precipitation (runoff) is increasing with 19.9 %/K (28.5 %/K). We use the relative change from each LPS case, from the control to the two perturbed runs, and combine the two scenarios, so that both the runoff and precipitation gets a sample of 20 simulations. Linear regression analyses of the area mean runoff response to changes in area mean precipitation shows a runoff response of 17.5 % per 10 % change in the precipitation (Fig. 3). A correlation of 0.84 between the variation in the changes of the precipitation and runoff is found, indicating that there is a strong relationship between the precipitation and runoff changes. When we perform the regression analysis for the 2 and 4 K separately, the correlation between the variation in the changes of the precipitation and runoff is 0.87 (2 K) and 0.81 (4 K). The same analysis was done where the change in the runoff was regressed on the precipitation minus the surface moisture flux, but it did not change the correlation between the precipitation and runoff.

Table 2 The central India mean precipitation, runoff and runoff coefficient calculated for the CTR simulations, including all points (wet and dry) (first row)
Full size table
Fig. 3
figure 3

Scatterplots with the one-to-one line of the fractional change in the precipitation (x axis) from the 2 and 4 K runs, and the fractional change in runoff (y axis). The fractional change is given as %/K. The correlation coefficient is given at the top of the figure. The blue (black) dots are from the 2 K (4 K) runs

Full size image

A dimensionless coefficient that is used as a measure of the ratio between the amounts of precipitation received and the runoff generated, is the runoff coefficient (Rc). During an extreme precipitation event the coefficient can be used as an indicator of the possibility of flooding, and is defined as:

$$ R_{c} = \frac{{Runoff \left[ {\text{mm}} \right]}}{{Precipitation \left[ {\text{mm}} \right]}} $$
(2)

The closer the runoff coefficient is to unity, the more of the precipitation is converted to runoff, and the closer the coefficient is to zero, the more of the precipitation is used to moisturize the ground or evapotranspiration. The runoff coefficient is dependent on the surface characteristics, where urban areas with asphaltic or concrete have a high runoff coefficient, and more rural or agriculture unsaturated areas have a lower runoff coefficient. In a climate perspective, the runoff coefficient may change, because the land-use is being altered. In India the population is expected to grow, thus the urbanization is most likely going to increase (World Bank 2013). In this study we are not including changes in the land-use. However, by calculating the runoff coefficient we can evaluate how sensitive the runoff is to a change in the precipitation. If the soil ground is close to saturation, and there is an increase in the precipitation, the relative response in the runoff can be much larger that the relative change in the precipitation, since most of the precipitation is directly converted to runoff. The central India mean runoff coefficient in the control runs is 0.46, indicating that on average 54 % of the precipitation goes to moisturize the ground, being evaporated or to plant transpiration. From the control to the 2 K (4 K) runs the runoff coefficient increases with 5.3 (4.6) %/K (Table 2). During strong precipitation events the evaporation is close to potential evapotranspiration and the soil is saturated. The increase in the precipitation in the perturbed runs is stronger than the increase in the potential evapotranspiration, and this is directly translated into increased runoff as the soil is saturated. Thus more of the precipitation in the perturbed runs is converted to runoff, which explains why the relative response in runoff is larger than the change in the precipitation, as found by the linear estimate.

As the LPS are moving in the east–west direction as seen in Fig. 1, an east–west cross-section of the central India box gives a good description of the storm as it moves inland. A cross section with the mean over the latitudes 17–26.8°N, shown for the longitudes 74–88°E is therefore constructed. Figure 4 show the mean vertical cross section of the cloud hydrometeors cloud water, rainwater and snow from the control runs. The cloud water has its maximum mass around 875–600 hPa, except in the eastern part where there is cloud water almost down to the surface. There is maximum cloud water at 80–82°E, and then the cloud water is decreasing towards the west. Most of the rainwater is situated between 950 and 550 hPa, with a peak around 900–750 hPa at 80–84°E. The snow is mostly above 550 hPa, and there is a snow maximum around 78–84°E. These east–west cross sections compare well with the active period composite shown in Rajeevan et al. (2013), where the longitude-height variation of the cloud and ice liquid water content is investigated. During the active period, which is when most of the LPS develop, there are positive anomalies of convective plumes across the central Indian continent.

Fig. 4
figure 4

The vertical distribution of the central India east (right) west (left) mean of the cloud water (a), rain-water (b) and snow (c) from the control runs. The cloud hydrometeors are averaged over the latitudes 17–26.8°N, shown for the longitudes 74–88°E. The cloud water is given in gram per volume [g/m3]. The black shading indicates the mean of the east–west orography in the central India region

Full size image

Figure 5a–c shows the east–west distribution of the 1 h-accumulated precipitation, runoff and runoff coefficient from the control runs. The east–west initial upper level soil moisture is shown in Fig. 5d. A peak in the precipitation and runoff is seen at the center of the box, corresponding to the region where the maximum rainwater, seen in Fig. 4b, is located. The runoff coefficient is largest in the eastern part and to the center of the box, where from the center and towards the western edge the runoff coefficient decreases. This can be due to several reasons: For instance, the western region is drier than the eastern part, shown in Fig. 5d, which means that a larger fraction of the precipitation is going to moisturize the ground. Another reason can be due to the less cloudy conditions in the western part, as seen in Fig. 4, where the sun is able to heat up the ground and lead to larger evapotranspiration.

Fig. 5
figure 5

The mean 1 h accumulated precipitation (a), runoff (b) and runoff coefficient (c) from the control runs, and the initial upper level soil moisture (d), averaged over the latitudes 17–26.8°N, shown for the longitudes 74–88°E. The units are mm/h for the precipitation and runoff, and m3/m3 for the soil moisture, whereas the runoff coefficient is dimension less

Full size image

The path of the lows is slightly different between the three sets of runs, seen in Fig. 1, and from a first guess it can be thought that the storms are moving further inland in the warmer runs. Figure 6 shows the difference between the 4 K and CTR runs of the mean cloud water, rainwater and snow. The results are similar for the difference between the 2 K and CTR runs, but the signals are stronger for the temperature scaled 4 K-CTR difference. Areas that are statistical different at 5 % confidence level are marked with black dots. It is clearly seen that there has been an increase in the cloud water from 76 to 83°E, where the increase is statistical significant over small areas mainly around 78–80°E. There is a decrease in the cloud water in the eastern part, except for a minor increase where the orography starts to rise. A small decrease in the cloud water is also seen in the western part of central India. There is a statistical significant increase in the cloud water above 550 hPa over the whole east west cross section, which can be due to a consistent increase in the height of the cloud due to warmer atmosphere column.

Fig. 6
figure 6

Same as Fig. 4, except for the difference between the 4 K and control runs. The black dots are where the results are statistical different at a 5 % confidence level

Full size image

The rainwater has mainly increased in the western part of the central India cross section, where it is statistical significant at all heights from 74 to 80°E. The reason for this large increase in the rainwater in the western part may be a result of cloud droplets being able to grow big enough to become rain droplets, which is a consistent result throughout the different LPS cases. A small increase at the point where the orography is becoming higher in the eastern part is seen, and a minor decrease in the rainwater is found slightly to the east of the center in the box.

As the altitude of production of snow has increased from the CTR to 4 K, there is a decrease in the snow around 550 hPa and an increase aloft. This corresponds to a leveling of the zero isotherm as the atmospheric column is warming. The increase (decrease) in the snow production is statistical significant in the western part (almost over the whole east–west cross section).

The east–west relative difference in the precipitation, runoff and the runoff coefficient is shown in Fig. 7. The east–west distribution of the temperature scale relative change [%/K] for the 2 and 4 K runs are similar for the precipitation and runoff, except in the western part of the box where the 4 K runs have a larger fractional difference in the runoff than the 2 K runs. The east–west distribution for the runoff coefficient is also similar for the 2 and 4 K runs, but here the 2 K runs have a higher relative change in some regions. It is clearly seen that the relative change in the precipitation, runoff and runoff coefficient is mainly to the west in the central India box. The relative change in the precipitation is up to 90 %/K in the western part, but from the center of the box and eastward the change is mainly around 10 %/K, with a small peak in the eastern region. The same feature is seen for the runoff but with a higher relative change in the western part, which is in the range of 180–220 %/K. This large change in the runoff in the western part corresponds to an increase in the runoff coefficient. In the western part the runoff coefficient is increasing up to 35 %/K. Thus the LPS in a warmer and more humid environment are bringing more cloud hydrometeors further inland, where the cloud droplets are able to grow big enough to become rain droplets, resulting in more precipitation being released in western part of central India. This large increase in the precipitation has a huge impact on the runoff, where the ground is saturated, or reduced evaporation due to more cloudy conditions, and therefore most of the precipitation is directly converted to runoff. The increase in the precipitation, runoff and runoff coefficient from the control to the 4 K runs is mainly statistical significant from 74 to 80°E for the precipitation and runoff, while only statistical significant over some areas from 76 to 78°E for the runoff coefficient.

Fig. 7
figure 7

Same as Fig. 5, except for the relative difference between the 4 K and control runs. The fractional change is scaled with the temperature perturbation, given as %/K. The black (gray) dots below each figure is where the results are statistical different at 5 % confidence level for the 2 K (4 K) runs

Full size image

5.2 Changes in the intensity, frequency and contribution of extreme events

The intensity, frequency and contribution of different precipitation and runoff categories are analyzed. We pick out all the grid points within the central India box, for all the time steps, for each simulation. A set of different percentiles (Table 3) based on the control simulations are calculated to investigate if the results are consistent throughout different time resolutions, where we use the 1, 6 and 24 h accumulated precipitation (accP) and runoff (accR). When we compare the percentiles intensities between the control and perturbed runs, we calculate the percentiles separately for the CTR, 2 and 4 K. Only wet events are considered when calculating the percentiles, and a wet event is defined as where the precipitation or runoff is >0.02 mm/h, 0.13 mm/6 h and 0.50 mm/24 h for the 1, 6 and 24 h accumulated precipitation and runoff. The temperature scaled relative differences between the control runs and the 2 and 4 K runs are very similar, in the following we therefore focus on the results from the 4 K and control differences.

Table 3 The definition of the different categories, where P and R is the precipitation or the runoff
Full size table

The precipitation frequency (fraction of wet events) is mainly connected with the moisture convergence generated by the synoptic scale circulation. However, within the central India box there can be changes in the frequency of the wet and dry grid points that can be explained by either a change in the horizontal extent of the system or that the system is precipitating more or less. Figure 8 shows the occurrence of wet events for the precipitation and runoff, and compares the control and perturbed runs for the three different time resolutions. In the control runs the LPS mean frequency of the wet events for the 1, 6 and 24 h accP (accR) is around 20 % (40 %), 35 % (45 %) and 55 % (50 %), respectively. There is an increase (decrease) in the occurrence of wet (dry) events for all the time resolutions, seen for both the precipitation and the runoff from the control runs to the perturbed runs, where the increase is larger for precipitation than the runoff. Thus the systems in a warmer and more humid environment are either precipitating over a larger area or precipitating more frequent, and this is contributing to an increase in the runoff.

Fig. 8
figure 8

The LPS mean frequency of the wet events from the three set of simulations (CTR dark gray; 2 K medium gray; 4 K white), for the 1, 6 and 24 h accP (accR) in the left (right) figure. The error bar is the 25th and 75th percentile of the ten simulations. The definition of a wet event is when the grid point precipitation (runoff) exceeds 0.02 mm/h, 0.13 mm/6 h and 0.50 mm/24 h, respectively

Full size image

The actual values for the different precipitation and runoff percentile intensities for the control runs are seen in Fig. 9. The intensity for the 24 h-accumulated precipitation is 1.9, 20 and 138 mm/24 h for the 25th, 75th and 99th percentile, which is in the same range as the values used to classify rainfall events in Pattanaik and Rajeevan (2010). All the percentile intensities have increased from the control to the perturbed runs for both the precipitation and runoff, and Fig. 9g–i show the scaled relative change from the CTR to the 4 K runs, and Table 3 lists the different scaled relative changes. For each time resolution, the precipitation intensity increases in the same range for the three percentiles: 6.2–9.9 %/K, 9–11.8 %/K and 13.5–15.1 %/K for the 1, 6 and 24 h accP, respectively. However, for the runoff the relative change is much larger for the 99th percentile intensity than the 25th and 75th percentile, consistent for the three time resolutions. Whereas the relative change for the lower runoff percentile intensities is in the same range as for the precipitation, the 99th percentile change is up to 23.8 %/K. Thus it is evident that the impact from the increase in the precipitation is largest on the most extreme runoff. One possibility for the larger response in extreme runoff rates may be that during the most extreme precipitation events the ground is already close to saturation and most of the precipitation is converted to runoff. To summarize the warming yields larger precipitation rate, that leads to an increase in runoff rates, and the impact is largest for the category with very heavy intensities.

Fig. 9
figure 9

The control run precipitation (a–c) and runoff (d–f) intensities [mm] of the 25th, 75th and 99th percentile for the 1, 6 and 24 h time resolutions. g–h shows the mean fractional change [%/K] from the control to the 4 K runs for the precipitation (dark gray) and runoff (light gray) for the three time resolutions and percentiles

Full size image

Categories of different precipitation and runoff intensities is found by calculating the percentiles given in Table 2 from the control runs, which is then used to category an event into low, moderate, heavy and very heavy intensity. Figure 10 show the precipitation and runoff frequency distributions for the different categories from the control runs. Low events have the highest frequency, and the frequency is decreasing towards the moderate, heavy and very heavy events, and this is consistent for the three time resolutions. The fractional change scaled with the temperature perturbation in the frequencies from the control to the 2 and 4 K runs is almost equal, we therefore only show the fractional change from the control to the 4 K runs, seen in Fig. 10c–d, and listed in Table 4. The fractional change is largest in the category with very heavy intensity, where the 1, 6 and 24 h accP (accR) shows an increase of 35 %/K (43.3 %/K), 48 %/K (67.6 %/K) and 85.9 %/K (97.8 %/K). There is a small increase for categories with the moderate and heavy intensity. This increase in the moderate, heavy and very heavy events is being compensated by a decrease in the low precipitation and runoff events. The increase in the heavy and very heavy events is statistical significant at a 5 % confidence level for all the three time resolutions for accP. For accR the increase is statistical significant for all time resolutions for very heavy events, and only for the 24 h accR for the heavy events. The large relative change in the extremes can be understood by considering a simplified example where the relative change in intensity is the same for the whole distribution. In such a case if the tail of the distribution is fat, this will lead to largest relative changes in the frequency of events for the most extreme events. This corresponds to the changes we see in the frequency distribution from the control to the 4 K simulations.

Fig. 10
figure 10

The mean frequency for the 1 h (black) 6 h (gray) and 24 h (white) accumulated precipitation (a) and runoff (b) within the different categories. The relative change in the frequency of the different precipitation (c) and runoff (d) events between the control and 4 K runs. The error bar is the 25th and 75th percentile of the ten LPS of the ten simulations. The black dots in c and d is where the results are statistical different at 5 % significance level

Full size image
Table 4 The relative change from the control to the 4 K simulations of the frequency, contribution and intensity, for the 1, 6 and 24 h time resolutions and the four different categories for the precipitation and runoff
Full size table

As seen in Fig. 10, most of the precipitation and runoff event are from the low-intensity category. However, the contribution from a given event is dependent on both the frequency and the intensity. Thus we are calculating the precipitation (runoff) contribution from the different categories by multiplying the frequency within each category with the actual intensity, and then dividing on the total precipitation (runoff) during each simulation. Figure 11 shows the contribution of the different events to the total precipitation (runoff) during the control simulations. 60–70 % (50–60 %) of the precipitation (runoff) comes form the category with heavy intensities, consistent for the 1, 6 and 24 h time resolution. Less than 5 % of the precipitation and runoff comes from low events, whereas 10–25 % (10–30 %) comes from moderate (very heavy) events. The relative change scaled with the temperature perturbation from the control runs to the 4 K runs is shown in Fig. 11c–d, and listed in Table 4. It is evident that with the warming there is a shift in which category that contributes the most to the total precipitation and runoff. More of the precipitation and runoff is coming from very heavy events (12–47.2 %/K), whereas there is a decrease in the contribution from the low and moderate event (5.8–13.4 %). Only a small decrease is seen for the heavy events (<5 %). All the precipitation changes from the control to the 4 K simulations are statistical significant at a 5 % confidence level, except for the small decrease seen for the contribution from heavy event for the 24 h accP. For the runoff the decrease in the contribution from the low events and the increase in the contribution from the very heavy events are statistical significant together with the 24 h accR (moderate) and 1 h accR (heavy). These results are consistent with our previous results, since there is an increase in the frequency of the very heavy events together with an increase in the intensities of the precipitation and runoff. Thus when we consider the total precipitation and runoff during the passage of a low-pressure, in the warmer runs more of the precipitation and runoff is coming from the category very heavy events, and this is occurring on the expenses of the low and moderate events. The increase in the atmospheric moisture is changing the character of the precipitation and the runoff. In the warmer simulations the most rainy events have experience a positive change in intensity. As a result of this thermodynamic effect, there is a shift in the whole distribution of rainfall toward larger values, which lead to a higher contribution to the total precipitation and runoff from the extreme events and less from the low and moderate events. The changing character of the precipitation affects the runoff in the way that more intense rainfall over a shorter time frame contributes to more extreme runoff events while the longer periods of no or weak rainfall rates gives a dryer ground (Trenberth et al. 2003). These shifts in rainfall and runoff characteristics may have a large impact on water resources in the future, with potentially negative impacts on the Indian society.

Fig. 11
figure 11

The mean 1 h (black), 6 h (gray) and 24 h (white) accumulated precipitation (a) and runoff (b) contribution from the different categories. The relative change in the contribution from the different precipitation (c) and runoff (d) categories between the control and 4 K runs. The error bar is the 25th and 75th percentile of the ten LPS of the ten simulations. The black dots in c and d is where the results are statistical different at 5 % significance level

Full size image

6 Summary

This study examines the sensitivity of precipitation and runoff changes in the central Indian region to an increase in the atmospheric temperature and moisture. We have used the surrogate climate change method by Schär et al. (1996) on ten different monsoon LPS cases that is connected to an observed extreme rainfall event. Three sets of simulations are performed, one control run and two perturbed runs. In the perturbed runs all the temperature (atmospheric specific moisture) fields have been increased by +2 K (13 %) and +4 K (26 %). We have analyzed the differences between the control runs to the perturbed runs, with focus on the changes in the central Indian region.

The mean central India precipitation change between the control and perturbed simulations is up to 19.9 %/K when the response is scaled with the initial temperature perturbation. This large response in the precipitation within the central India area can be explained by the fact that there are regions, which have not been subject to precipitation in the control runs, but in the perturbed runs there have been precipitation, probably due to an increased horizontal extent of the system and a slightly different propagation path. By performing linear regression of the mean central India precipitation and runoff, we find the runoff to respond by a 17.5 %/K change for a 10 % increase in the precipitation. The larger relative response in the runoff can be explained by an increase in the runoff coefficient, which indicates that the soil is being saturated and/or less evapotranspiration, thus more of the precipitation can be directly converted to runoff. By making an east–west cross section over central India, we see that the largest change in the precipitation, runoff and runoff coefficient are in the western region of central India. East–west cross section of the cloud water, rainwater and snow also show that there is an increase in the cloud hydrometeors further inland. Thus, in the warmer and more humid environment the LPS are able to bring more moisture across the central Indian continent, where the cloud droplets are able to grow big enough to become rain droplets, giving more precipitation further inland. This increase in the precipitation gives a larger fractional increase in the runoff.

There is an increase in the wet points from the control runs to the perturbed runs, shown in Fig. 7, suggesting the LPS to have increased the horizontal area where precipitation is being released. However, not only are the lows precipitating over a larger region, but the precipitation intensity is also increasing. This is seen for all the percentiles. The intensity in the runoff is also increasing for all percentiles. In the perturbed runs, an increase in the precipitation and runoff in the category moderate, heavy and very heavy events is also found, which is being compensated by a decrease in the frequencies within the category of low intensity. The increase in the frequency of the heavy and very heavy events together with the increase in the intensities, give a shift in which category most of the precipitation and runoff is coming from. More of the precipitation and runoff is coming from the category with very heavy intensities, while there is a decrease in the contribution from the other categories.

We have shown that the storms in the warmer climate are producing more precipitation further inland, and therefore the precipitation change is largest in the western region of the central India domain. Our results also indicate that the intensity of the precipitation associated with the LPS is increasing. Trenberth et al. (2003) argued that by increasing the moisture content of the atmosphere, the storms will become more vigorous with a larger precipitation rate. Several studies have reported on increased precipitation extremes with an increase in the temperature, seen by using both observations (e.g. Sen Roy and Balling, 2004; Rajeevan et al. 2008; Pattanaik and Rajeevan 2010; Westra et al. 2014) and model studies (e.g. Frei et al. 1998; Muller et al. 2011; Singh and O’Gorman 2014). Our results clearly show a shift in the precipitation categories, with more extreme precipitation in the perturbed runs. Figure 11, which shows the contribution from the different events, reveals this shift clearly: more of the precipitation is coming from very heavy events, whereas there is a reduction in the contribution from the other categories.

Our results demonstrate that there is a strong relationship between the precipitation and runoff, but there is not a one-to-one change in the two parameters. Figure 9 effectively shows this: the relative change in the 99th percentile intensity for the runoff is twice the relative change in the precipitation intensity, but for the lower percentiles the relative change is similar for the precipitation and runoff. From these results it may be suggested that LPS which develop in a warmer and moistener atmosphere, is more likely to induce heavy precipitation event that can lead to severe flooding events. It can also be speculated that there can be severe flooding in regions that has been less prone to flooding before, due to the further inland propagation of the storms. These statistical analysis have been performed on three different time resolutions, the 1, 6 and 24 h accumulated precipitation and runoff, and they all show the same clear signal, that there is an increase in the frequencies and contribution from the very heavy events, and a decrease in the low and moderate events. However, it should be stressed that this is only a sensitivity study, where the large-scale monsoon flow is kept unchanged. We cannot expect the lows to behave in the same manner in a warmer climate, since the large-scale dynamic will influence the propagation and frequency of the LPS. Factors as changes in land-use, increased aerosol content in the atmosphere and changes in the SST gradients in the Indian and Western pacific Oceans are also thought to have an impact on the changes in the extreme rainfall events in the central India region (e.g. Pattanaik and Rajeevan 2010). These are not included in this experiment. Nevertheless, this study highlights that once they are formed, the LPS are sensitive to an increase in the temperature and moisture, and that the consequence might be more energetic LPS, which are able to bring high moisture air to new regions, as seen in the Pakistan flooding for instance.