1 Introduction

The abrupt onset is one of the salient features of the Asian monsoon system (Yeh et al. 1959), which first occurs very explosively in the southern part of Bay of Bengal (BoB) (Lau and Yang 1997; Wu and Zhang 1998; Wang and LinHo 2002). During the monsoon transition, the development of an onset vortex (OV) is often observed in the lower troposphere (Krishnamurti et al. 1981; Rao and Sivakumar 1999). It is found recently that some OVs could evolve into tropical cyclones (TCs) and eventually lead to the monsoon onset by their northward movement (Wu et al. 2011, 2012). Moreover, some OVs even got quickly intensified into super cyclones along with the monsoon onset and hence loaded severe destruction to the local inhabitants. Two recent examples in 1991 and 2008 are widely known to cause more than 100,000 deaths in Bangladesh and Myanmar respectively (Webster 2008). Therefore, documenting and understanding of the OV development is of vital importance for the Southern Asia and beyond.

Recently there is much concern on the BoB OV genesis particularly due to its potential role in triggering the summer monsoon. Wu et al. (2011, 2012) emphasized the importance of strong surface sensible heating by the high sea surface temperature (SST) in the eastern BoB. Liu et al. (2013) argued that the cyclonic vorticity induced by the unstable development of the South Asian High also favors the OV genesis. These findings are generally consistent with the traditional understanding on how large scale environmental processes modulate the cyclone genesis (Gray 1968, 1979).

It is worth noting that BoB cyclones have two dominant time scales, i.e., seasonal and intra-seasonal ones. At seasonal scale, BoB TC activity exhibits a notable bimodal character with peaks in pre- and post-monsoon seasons, in contrast to the single peak distribution in the Pacific and Atlantic basins. This peculiar feature is attributed to the strong modulation by seasonal monsoon circulation (Gray 1968; Yanase et al. 2012; Li et al. 2013b). It is also identified that BoB TCs are strongly influenced by the intra-seasonal oscillation (ISO) (Camargo et al. 2009; Kikuchi and Wang 2010; Yanase et al. 2012; Krishnamohan et al. 2012). Monsoon onset represents the critical time when the seasonal transition is realized by the intrusion of the first northward-propagating intra-seasonal oscillations (FNISOs) into the central BoB (Li et al. 2013a). The FNISO is largely viewed as a critical event from the ISO winter mode to the summer mode and bears some peculiar features. Hence OVs are modulated by the slowly marching seasonal cycle (Wu et al. 2011, 2012; Li et al. 2013b) and as well by unique FNISOs. This interesting “ISO–TC–onset connection” was discussed in Li et al. (2013b) and Fosu and Wang (2014).

Though the modulation of OVs by the seasonal cycle is deeply documented, the modulation process by FNISO is still open, particularly considering the FNISO’s different 3-D structure with that of boreal summer monsoon ISO (Li et al. 2013a). The present study attempts to resolve the above issue. The rest of the paper is organized as following. The data and method are described in Sect. 2. In Sect. 3, we analyze the role of intra-seasonal modulations and clarify the dominant physical processes concerning to the OV genesis. Discussion is given in Sect. 4 and conclusion is provided in the last section.

2 Data and method

2.1 Data

Three daily gridded data sets are used here, including the satellite observed outgoing longwave radiation (OLR) (Liebmann and Smith 1996) as the proxy for convection from National Ocean and Atmosphere Administration (NOAA), atmospheric fields (horizontal winds, relative humidity, temperature, vertical velocity and sea level pressure) from European Center for Medium-Range Weather Forecast (ECMWF)-Interim reanalysis (Dee et al. 2011), and sea surface temperature (SST) from NOAA Optimum Interpolation SST (OISST) (Reynolds et al. 2007). All data sets above are spatially interpolated to 0.5° × 0.5° resolution and the temporal interval is spanning from 1991 to 2010.

The best-track TC data is from the Joint Typhoon Warning Center (JTWC). The genesis date of OV is defined as JTWC firstly reported date and the genesis location is represented by the mean position at the genesis date. OVs are defined from the JTWC TC archive based on the principle that if and only if the TC occurs before the BoB monsoon onset and its life cycle spans the onset date (Wu et al. 2012). Saffir–Simpson hurricane wind scale (Table 1) is adopted as a classification standard in reference to the maximum sustained wind of OVs.

Table 1 Saffir–Simpson hurricane wind scale
Full size table

To identify the modulation of environmental fields on the tropical cyclogenesis, running mean is applied to the above OLR, ERA circulation and SST data sets. Specifically, all the parameters are dealt with a 19-point smoothing in the horizontal direction and a 15-day running mean in the time domain. The filtering results are not significantly sensitive to the different choices of the spatial (from 17 to 21 points) and temporal (from 15 to 21 days) scales. Hereinafter, these spatially and temporally filtered data sets are referred to as the environmental fields, in which the TC-scale signals are filtered out.

2.2 Method

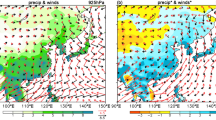
The composite analysis is adopted here for its mathematical simplicity but physical relevance to the governing process. To understand the common atmospheric circulation features corresponding to OVs genesis, the composite map of atmospheric 850 hPa wind and convection (represented by OLR) with reference to the 11 identified OVs (Table 2) are produced as Fig. 1, which clearly reflects the modulation effect from the seasonal transition. One striking feature is the occurrence of the northward propagating convection system that hosts the OVs. Its temporal evolution resembles the FNISO identified by Li et al. (2013a). Further composite is done to reveal the intra-seasonal modulation on OV activity. The ISO life cycle is divided into eight phases, as shown in Fig. 2a. Phases 1 and 8 correspond to the peak convection-suppressed period, while phases 4 and 5 correspond to the peak convection-enhanced interval. The composite based on 11 FNISO events (during which the 11 OVs were generated) is carried out according to the 8 phases (Fig. 2c). It is clearly seen that the 11 OVs occurs in the convection-enhanced phases 4 and 5, which provides the clue that OVs are modulated by FNISO. This phase-based composite avoids the complexity of the different length of the FNISO life cycles in days. Another environmental genesis potential index (GPI) composite based on the 11 OVs are also carried out in order to double check the cause-effect relation. It is confirmed (figure not shown) that the environmental GPI leads OV genesis by 3 days, pointing to the direction that the large-scale environment process, i.e. FNISO, modulates OV.

Table 2 Genesis date, location and maximum intensity (Saffir–Simpson scale) of BoB OVs
Full size table
Fig. 1
figure 1

Composite time–latitude diagram of OLR (shaded, W/m2, values lower than 230 are plotted) and 850 hPa wind (vector, m/s) along 80°–100°E relative to the genesis dates of BoB OVs. The blue and red pentacles indicate the genesis and peak latitudes of OVs respectively

Full size image
Fig. 2
figure 2

a Definition of eight ISO phases based on 15–90 day band-passed OLR anomalies in BoB (80°–100°E, 0°–15°N), one example in 2009. b Climatologically daily GPI (red solid), \(\overline{GPI}\)(blue dash) and monthly TC number (bar) in BoB during 1991–2010. c Composite GPI (red solid) and \(\overline{GPI}\) (blue dash) in terms of defined ISO phases, as well as the OVs clusters (bars) with their corresponding grades following Saffir–Simpson Scale. d Composite \(GPI^{{\prime }}\)(red solid) and the right-hand terms (bars) in Eq. (2) as a function of ISO phases. The blue solid indicates the sum of R1, R2, R3, and R4. The number of days for composite in each phase is given above the horizontal axis in c

Full size image

To explore key factors in modulating tropical cyclogenesis, the widely used empirical GPI (Emanuel and Nolan 2004) is adopted here:

$$GPI = \underbrace {{\left| {10^{5} \eta } \right|^{3/2} }}_{X1}\underbrace {{\left( {1 + 0.1V_{shear} } \right)^{ - 2} }}_{X2}\underbrace {{\left( {{H \mathord{\left/ {\vphantom {H {50}}} \right. \kern-0pt} {50}}} \right)^{3} }}_{X3}\underbrace {{\left( {{{PI} \mathord{\left/ {\vphantom {{PI} {70}}} \right. \kern-0pt} {70}}} \right)^{3} }}_{X4}$$
(1)

where \(\eta\) is the absolute vorticity at 850 hPa, \(V_{shear}\) is the magnitude of the vertical wind shear between 850 and 200 hPa, \(H\) is the relative humidity at 600 hPa, and \(PI\) is the potential intensity, which gives an upper limit on TC intensity (Bister and Emanuel 2002).

The climatological daily GPI based on the environmental fields is shown to correspond well with the observed cyclogenesis in BoB (Fig. 2b), which guarantees the fidelity of using GPI in studying the environmental modulation on BoB OVs.

We further proceed to assess the individual contributions from the four right-hand factors in Eq. (1) to the GPI intra-seasonal variations reflected in Fig. 2c. For clarification purpose, any environmental field \(X\) in Eq. (1) can be decomposed into an intra-seasonal anomaly (\(X^{\prime}\); periods of 15–90 days) and a low-frequency background state (\(\bar{X}\); periods longer than 90 days), i.e., \(X = \bar{X} + X^{\prime}\). The background component of GPI (\(\overline{GPI}\)) could be expressed as: \(\overline{GPI} = \overline{X1} *\overline{X2} *\overline{X3} *\overline{X4}\). Accordingly, the intra-seasonal component of GPI (\(GPI^{\prime}\)) could be expressed as the sum of four individual intra-seasonal factors, with the aid of the total differential formula, i.e.,

$$\begin{aligned} GPI^{{\prime }} \text{ } & = GPI - \overline{GPI} \\ & = \underbrace {{\overline{X2} *\overline{X3} *\overline{X4} *X1^{{\prime }} }}_{R1} + \underbrace {{\overline{X1} *\overline{X3} *\overline{X4} *X2^{{\prime }} }}_{R2} + \underbrace {{\overline{X1} *\overline{X2} *\overline{X4} *X3^{{\prime }} }}_{R3} + \underbrace {{\overline{X1} *\overline{X2} *\overline{X3} *X4^{{\prime }} }}_{R4} \\ \end{aligned}$$
(2)

The close resemblance of the red and blue lines in Fig. 2d indicates the validity of such linear decomposition given by Eq. (2). In fact, this diagnosis method is widely used and one recent successful application can be found in Li et al. (2013b), where BoB cyclone modulation by seasonal monsoon circulation is discussed. Hereafter, the four right-hand-side terms (R1, R2, R3 and R4) are named as vorticity term, vertical wind shear term, mid-level humidity term and PI term, respectively.

3 Results

3.1 Dominant process associated FNISO to modulate the OV genesis

According to the OV definition as well as the onset date of BoB monsoon in Wu et al. (2012), 11 OVs are identified from JTWC archive during 1991–2010 (Table 2), which means OV is a frequent phenomenon during the onset of BoB monsoon. Generally, the average genesis date for BoB OVs is 2nd May, with the earliest one in 2009 and the latest one in 2010. Among the 11 OVs, 5 developed into super cyclones with the maximum intensity exceeding category 4 (Saffir–Simpson scale), including the worldwide notorious cases in 1991 and 2008. Geographically they cluster in southeastern BoB, i.e., (3°N–13°N, 86°E–96°E). All these 11 OVs are found to occur in the FNISO convection-enhanced phases (Fig. 2c).

The strong modulation of OV activities by the mean monsoonal cycle is clearly seen in Fig. 1. This is consistent with the findings in Li et al. (2013b) that the first peak of BoB cyclones occurs in the pre-monsoon period. Our present emphasis is paid on the co-occurrence of the OV genesis and the FNISO, which is the most striking feature in Fig. 1. It is understood that the FNISO plays the critical role in triggering the southwest monsoon over the BoB and has unique structure different from boreal winter Madden–Julian Oscillation (MJO) and boreal summer intra-seasonal oscillation (BSISO) (Li et al. 2013a). Even though there are some previous studies on the ISO’s modulation on the BoB cyclones (Camargo et al. 2009; Kikuchi and Wang 2010; Yanase et al. 2012; Krishnamohan et al. 2012), there still lacks of the dedicated study about how the unique FNISO modulates OV, which is the present focus.

The significant FNISO modulation on OV genesis is clearly shown in Fig. 2c. The OVs are seen to cluster in the convection-enhanced 4th and 5th phases of the FNISO, when the environmental GPI (red solid line) peaks. Since the mean GPI value (blue dashed line in Fig. 2c) is not phase-sensitive and almost constant (around 0.7), the environmental GPI peak is attributed to the intra-seasonal component (\(GPI^{{\prime }}\)) with its maximum value at 0.6 in the 4th phase, which is further shown in Fig. 2d. It is therefore noted that the environmental GPI remarkably increases nearly 70 % in FNISO’s convection-enhanced 4th and 5th phases compared with its seasonal mean value, suggesting the critical role of FNISO in modulating the OV genesis.

Further in-depth diagnosis is carried out with the aid of Eq. (2) to explore the individual contribution from different environmental factors to the intra-seasonal \(GPI^{{\prime }}\). The decomposed individual contributions from the four right-hand terms of Eq. (2) are given in Fig. 2d, where the vorticity, vertical wind shear, and mid-level humidity are three leading terms in defining the intra-seasonal \(GPI^{{\prime }}\). The vorticity and mid-level humidity terms are shown to vary nearly in phase with the cyclogenesis, while the vertical wind shear and PI terms slightly lead, which is similar with Yanase et al. (2012).

Special attention is turned to the 4th phase, when a large cluster of OVs occur associated with the peak \(GPI^{{\prime }}\) value. Diagnosis shows the positive \(GPI^{{\prime }}\) comes respectively from the vertical wind shear term (with contribution of 0.21), mid-level humidity term (with contribution of 0.19), vorticity term (with contribution of 0.13) and PI term (with contribution of 0.01). Keeping in mind that ISO perturbations, such as the low- and high-level circulations, the mid-troposphere humidity and the SST, usually have regular spatial distributions (Zhang 2005), we further look at the corresponding spatial distribution of the key parameters (Fig. 3), trying to understand the way that they contribute. In the 4th phase, FNISO convection centers at southern BoB around 80°–95°E and 0°–10°N, and the associated convective heating induces a strong low-level cyclonic circulation (Fig. 3a). At the sea surface, positive (negative) SST anomaly appears northward (southward) of the convection (Fig. 3b). While at 600 hPa level, positive humidity anomaly is slightly northeast leading the convective center, which induces the northeastward movement of the convection center (Fig. 3a). In this phase, OVs naturally favor generate over the southeastern BoB in relation with the high total GPI (purple contours in Fig. 3c–f), which is contributed by the combined effect of four individual terms. Corresponding to the cyclonic disturbance at 850 hPa, the vorticity term (R1) exhibits a positive anomaly in southern BoB and its high value center well hosts the OVs’ genesis locations (Fig. 3c). The similar favorable pattern is also shown in Fig. 3e, where the high value center of mid-level humidity term (R3) is co-located with the OVs’ genesis locations. However, the high value centers of vertical wind shear term (R2) and PI term (R4) are found to be shifted northeastward and northward respectively from the OVs’ genesis locations (Fig. 3d, f). The spatial configuration of the R1–R4 distribution and the OVs’ genesis locations leads to the inference that the vorticity term (R1) and mid-level humidity term (R3) are likely more dominant than the other two terms (R2 and R4) to modulate the OVs genesis, which will be corroborated by further analysis below.

Fig. 3
figure 3

a, b Intra-seasonal anomalies of atmospheric and oceanic variables and c, d, e, f four \(GPI^{{\prime }}\) budget terms (shaded) in the 4th phase. The black dashed contours in each panel represent OLR anomaly (W/m2). In a, the vectors are intra-seasonal wind anomaly (red, m/s) and mean state component (cyan, m/s) at 850 hPa. In b, the shaded is RH anomaly (%) at 600 hPa, and purple contours are SST anomaly (°C). In c–f, purple contours are the total GPI and pentacles are the OVs genesis locations. The ISO movement is illustrated by the blue line connecting the convection centers of the 4th to 6th phases in a

Full size image

In contrast to the 3rd phase when none OV forms, most OVs occur in the 4th phase due to the \(GPI^{{\prime }}\) increase. We calculate the \(GPI^{{\prime }}\) tendency from the 3rd to 4th phase and decompose it into individual contributions from the 4 right-hand terms of Eq. (2), similarly with the aid of the total differential formula. The quantitative assessment (Table 3) reveals the overwhelming contribution comes from the mid-level humidity term (percentage contribution value 102 %), followed the vorticity term (percentage contribution value 22 %). Not very surprisingly, the vertical wind shear term and PI term have negative contribution. This calculation well supports the above inference from Fig. 3. It is now clear that the significant mid-level humidity anomaly induced by the FNISO is the dominant process to modulate the OV genesis, favoring its clustering in the convection-enhanced phase.

Table 3 GPI increase (∆GPI)from the 3rd to 4th phase and the corresponding individual contribution (value and percentage) from four environmental factors
Full size table

3.2 Moisture budget analysis

Considering the critical role of FNISO-induced mid-level moisture anomaly in the OV genesis, it is worth further clarifying the key physical processes accounting for the significant moisture increase from the 3rd to 4th phase. The perturbation moisture budget diagnosis is conducted over the southern BoB region (80°E–100°E, 0°–15°N) following Yanai et al. (1973),

$$\frac{{\partial q^{{\prime }} }}{\partial t} = - ({\mathbf{V}} \cdot \nabla q)^{{\prime }} - \left( {w \cdot \frac{\partial q}{\partial p}} \right)^{{\prime }} - {{(Q_{2} } \mathord{\left/ {\vphantom {{(Q_{2} } L}} \right. \kern-0pt} L})^{{\prime }}$$
(3)

where \(q\) is specific humidity, \({\mathbf{V}}\) is the horizontal velocity, \(w\) is the p-vertical velocity, \(L\) is latent heat constant, and \(Q_{2}\) represents the latent heating due to condensation or evaporation processes and subgrid-scale moisture flux convergences. In above equation, \(- {\mathbf{V}} \cdot \nabla q\) denotes horizontal moisture advection, \(- w \cdot \frac{\partial q}{\partial p}\) indicates vertical moisture advection, and \(- {{Q_{2} } \mathord{\left/ {\vphantom {{Q_{2} } L}} \right. \kern-0pt} L}\) represents the moisture source or sink. The prime at each term denotes the perturbation at the intra-seasonal timescale of 15–90 days. Again, each environmental field (\(X\)) in the Eq. (3) can be decomposed into a mean state component (\(\bar{X}\); periods longer than 90 days) and an intra-seasonal perturbation component (\(X^{\prime}\); periods of 15–90 days). Then Eq. (3) can be converted to the below form:

$$\frac{{\partial q^{{\prime }} }}{\partial t} = - {\mathbf{V}}^{{\prime }} \cdot \nabla q^{{\prime }} - {\mathbf{V}}^{{\prime }} \cdot \nabla \bar{q} - {\bar{\mathbf{V}}} \cdot \nabla q^{{\prime }} - w^{{\prime }} \cdot \frac{{\partial q^{{\prime }} }}{\partial p} - w^{{\prime }} \cdot \frac{{\partial \bar{q}}}{\partial p} - \bar{w} \cdot \frac{{\partial q^{{\prime }} }}{\partial p} - {{Q_{2}^{{\prime }} } \mathord{\left/ {\vphantom {{Q_{2}^{{\prime }} } L}} \right. \kern-0pt} L}$$
(4)

The moisture budget based on Eq. (4) is shown in Fig. 4. It is clear that the moisture accumulation is mainly contributed by vertical advection term, offset a large portion by the moisture sink term. More exactly, the anomalous vertical advection is mainly resulted by the perturbed vertical motion in the presence of mean vertical moisture gradient, i.e., \(- w^{{\prime }} \cdot \frac{{\partial \bar{q}}}{\partial p}\). The underlying physical process of the above term could be easily caught. In typical troposphere, \(\frac{{\partial \bar{q}}}{\partial p}\) has a positive value since mean moisture decreases in altitude while the barometric pressure drops. Meanwhile, a mid-troposphere anomalous ascending flow (\(w^{{\prime }}\) < 0) is induced by the surface convergence in the FNISO convective region. As a result, a positive moisture tendency is contributed at 600 hPa by the combined effect of the above two factors. Compared with the remarkable vertical moisture advection term, the horizontal moisture advection term (blue bars) is generally negligible despite a positive contribution, and the moisture sink term (purple bar) completely exhibits a significant negative contribution. Thus in physics, it is the moist air brought by the FNISO ascending flow from the low-level atmosphere that ultimately favors the OV genesis at intra-seasonal timescale.

Fig. 4
figure 4

The perturbed moisture budget diagnosis at 600 hPa in BoB (80°–100°E, 0°–15°N) accounting for the moisture increase from the 3rd to 4th phase. The black, blue, red and purple indicate respectively the tendency, the horizontal advection, the vertical advection and source/sink terms in Eq. (4)

Full size image

4 Discussion

Monsoon onset represents the sudden transition from dry season to wet season, which usually exhibits as an explosive convection event. This process often includes the tropical cyclone known as OV and is tied with one intra-seasonal oscillation known as FNISO (Wu et al. 2012; Li et al. 2013a).

Unlike northward propagating BSISO, FNISO bears some peculiar features in mechanisms and structures. It is understood that BSISO propagates northward during boreal summer monsoon due to the mean flow modulation (Jiang et al. 2004). FNISO occurs during the monsoon transition period, when the boreal summer monsoon mean flow is still not established yet. Its northward propagation is governed by the meridional asymmetry of background convective instability in conjunction with its north–south asymmetrical structure of the humidity perturbation (Li et al. 2013a). FNISO has no obvious north–south asymmetry in vorticity and low-level convergence fields as in BSISO.

Diagnosis in Sect. 3 clearly indicated that OVs are strongly modulated by FNISOs. The 20-year mean date of OV formation is May 2nd. This preferred date is consistent with the southwest monsoon onset time over BoB (Wang and LinHo 2002; Yu et al. 2012). The composite based on OV genesis also indicates that the environmental deep convection development leads 3 days. The preferred locations of historical OVs, as shown in Fig. 3e, are constrained by FNISO. Thus it is argued that OVs are modulated by FNISO when it triggers southwest monsoon over BoB.

However, OVs could be only identified in about half years between 1991 and 2010. It is then natural to examine the GPI difference between 11 OV-years and 9 no OV-years (Fig. 5). Not surprisingly, a significant positive GPI anomaly is observed in the favorite region of OV genesis around 85°–100°E and 0°–10°N. This GPI difference is largely due to the intra-seasonal component (\(GPI^{{\prime }}\), Fig. 5b) compared with the low-frequency component (\(\overline{GPI}\), Fig. 5a). The further decomposition of \(GPI^{{\prime }}\) indicates the vorticity term (Fig. 5c), vertical wind shear term (Fig. 5d) and mid-level humidity term (Fig. 5e) are comparable dominant in both values and spatial patterns, except for an evidently minor contribution from the PI term (Fig. 5f). Indeed, a further in-depth study is needed to reveal the underlying physical processes responsible for the year-to-year OVs variations.

Fig. 5
figure 5

Differences of a, b \(\overline{GPI}\), \(GPI^{{\prime }}\) and c, d, e, f four \(GPI^{{\prime }}\) budget terms between OV-years and no OV-years in the FNISO convection-enhanced phases (4th and 5th). The genesis locations of 11 OVs are plotted on each panel

Full size image

5 Conclusion

BoB TCs are active in pre-monsoon (April–May) and their majority (11 out of 16 TCs during 1991–2010) are generated in the monsoon onset phase helping trigger the summer monsoon (Wu et al. 2012). The OVs are obviously and strongly modulated by the FNISOs (Figs. 1, 2), whose underlying processes are not clear yet. With the aid of GPI, a quantitative assessment method is developed and applied to reveal the individual contributions from four important environmental factors to the favorable condition of the OV genesis at intra-seasonal timescale.

It is found that all OVs form in the convection-enhanced phases of the FNISO, and a majority (eight out of eleven OVs) occur in the 4th phase in accordance with the peak GPI anomaly. The above significant GPI anomaly (more than 70 % increase relative to its mean value) is attributed to the comparable contributions from the vorticity term, vertical wind shear term, mid-level humidity term, while PI term is negligible. Further examination on their spatial patterns and OV genesis locations, as well as the diagnosis of GPI increase from the 3rd to 4th phase identifies the overwhelming role of the mid-level humidity term.

The moisture budget analysis is further performed to explore the underlying physical processes responsible for the significant mid-troposphere humidity increase associated with the FNISO. It is found that the mid-level moisture accumulation is mainly due to the vertical advection as a result of the FNISO ascending flow interacted with the mean vertical moisture gradient.