Download PDF

Climate Dynamics

, Volume 46, Issue 11–12, pp 3807–3819 | Cite as

Irreducible uncertainty in near-term climate projections

  • Ed Hawkins
  • Robin S. Smith
  • Jonathan M. Gregory
  • David A. Stainforth
Open Access
Article
First Online:
Received:
Accepted:

Abstract

Model simulations of the next few decades are widely used in assessments of climate change impacts and as guidance for adaptation. Their non-linear nature reveals a level of irreducible uncertainty which it is important to understand and quantify, especially for projections of near-term regional climate. Here we use large idealised initial condition ensembles of the FAMOUS global climate model with a 1 %/year compound increase in \(\hbox {CO}_2\) levels to quantify the range of future temperatures in model-based projections. These simulations explore the role of both atmospheric and oceanic initial conditions and are the largest such ensembles to date. Short-term simulated trends in global temperature are diverse, and cooling periods are more likely to be followed by larger warming rates. The spatial pattern of near-term temperature change varies considerably, but the proportion of the surface showing a warming is more consistent. In addition, ensemble spread in inter-annual temperature declines as the climate warms, especially in the North Atlantic. Over Europe, atmospheric initial condition uncertainty can, for certain ocean initial conditions, lead to 20 year trends in winter and summer in which every location can exhibit either strong cooling or rapid warming. However, the details of the distribution are highly sensitive to the ocean initial condition chosen and particularly the state of the Atlantic meridional overturning circulation. On longer timescales, the warming signal becomes more clear and consistent amongst different initial condition ensembles. An ensemble using a range of different oceanic initial conditions produces a larger spread in temperature trends than ensembles using a single ocean initial condition for all lead times. This highlights the potential benefits from initialising climate predictions from ocean states informed by observations. These results suggest that climate projections need to be performed with many more ensemble members than at present, using a range of ocean initial conditions, if the uncertainty in near-term regional climate is to be adequately quantified.

Keywords

Ensembles Projections Initial conditions Uncertainty 
Download fulltext PDF

1 Introduction

Predictions of regional climatic changes during the next few decades are sought by decision makers. The use of climate models to guide scientific research on such predictions requires an acceptance that their non-linear nature generates irreducible uncertainty. To understand a model’s behaviour in response to rising greenhouse gas concentrations, therefore requires a probabilistic quantification of outcomes.

On regional spatial scales it has been argued that internal climate variability and model uncertainty dominate scenario uncertainty for near term temperatures (Hawkins and Sutton 2009). A key question is determining the size of the internal variability when compared to other sources of uncertainty and the magnitude of the expected change from causes other than internal climate fluctuations.

This question has previously been addressed by considering large ensembles of climate projections with a single climate model and a single future emissions trajectory (Selten et al. 2004; Sterl et al. 2008; Deser et al. 2012a, b; Kay et al. 2015). In these ensembles, multiple projections are simulated from a single ocean initial condition with many different atmospheric states to examine the magnitude of uncertainty associated with the non-linear nature of the atmosphere. It has also been suggested that some of the apparent model diversity may simply be due to internal variability (Deser et al. 2014).
Fig. 1

Inter-annual variability (standard deviation, in K) of near-surface temperature in ERA-40 (linearly detrended, left) and the FAMOUS control simulation (right)

Fig. 2

Distributions of transient climate response (TCR), defined as the average global temperature at years 61–80 minus the mean global temperature in the pre-industrial control simulation, for the four ensembles

Fig. 3

Warming for a doubling of \(\hbox {CO}_2\) concentration shown as a function of the starting \(\hbox {CO}_2\) value for each ensemble member (colours) and ensemble mean (black). The black bar shows the 25–75 and 5–95 % ranges for the standard measure of TCR. It is seen that warming apparently increases in all ensembles

In Deser et al. (2012b), each simulation warms by over 2 K in the first 50 years in the global average. However, the uncertainty in near-term regional climate trends can be substantial when compared to the size of the signal of change. For example, with 40 simulations it was possible to simulate both a 3 K warming and even a small cooling for winter (DJF) in Seattle, USA over the next 50 years, with the difference solely due to changes in the atmospheric initial conditions (Deser et al. 2012b). For winter precipitation, the ensemble ranged from a –25 to +25 % change over 50 years. The conclusion was that this uncertainty is essentially irreducible. This is an extreme example, and the caveat to this conclusion is that the simulated variability and the sensitivity of the response to initial conditions, may not be similar to the real world. However, there is a diverse range of simulated variability amongst climate models (Hawkins and Sutton 2012; Knutson et al. 2013), and given the relatively short observational record and complications in separating the internal variability from a forced trend, it is difficult to obtain a reliable estimate of climate variability from existing observations, especially on decadal timescales. In addition, different GCMs have varying predictability characteristics, particularly the timescales of memory (Collins et al. 2006; Branstator et al. 2012).

The large initial condition ensemble approach is in sharp contrast to the more usual climate projections which often use a single simulation (and at most ten ensemble members) for each climate model for multiple emission scenarios (Stocker et al. 2013). Computational resources and model complexity have restricted assessment of the implications of ensemble size in global climate models but analysis of a low-dimensional non-linear model suggests that ensembles of significantly more than 100 members are required to make confident statements at the 5 or 95 % level (Daron and Stainforth 2013). Although the number of ensemble members required will depend on the signal-to-noise characteristics of the variable considered, the quantities considered by Daron and Stainforth (2013) had relatively long timescales and are broadly representative of large scale ocean variables.

Several open questions remain which have particular relevance to the design of future ensembles of climate projections. Are these findings of significant irreducible uncertainty replicated in other climate models? Does uncertainty in oceanic initial conditions produce similar magnitudes and characteristics of response uncertainty? What is the shape of the irreducible uncertainty (i.e. are the distributions non-Gaussian)? And is this dependent on oceanic initial conditions? How large an ensemble is required to quantify these types of uncertainty?

In this study we utilise a fast atmosphere-ocean coupled general circulation model (AOGCM) to perform larger ensembles than have previously been possible, although at a lower resolution and complexity. Section 2 describes the FAMOUS AOGCM and the ensemble design. The relative role of atmospheric and oceanic initial conditions in producing uncertainty is explored and illustrated in Sect. 3. We summarise in Sect. 4.
Fig. 4

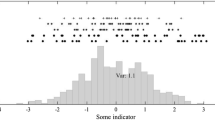
(Top row) Histograms of 10, 15 and 20-year global temperature trends in all the ensembles combined. The black lines represent the normalised distribution from the control simulation with its mean shifted to match the mean trend of the transient ensembles. The percentages indicate the fraction of cooling periods for the ensembles and (in brackets) inferred from the control simulation. Note that the first 20 years of each member is not included to remove any biasing effects of initialisation. The bottom row shows similar histograms, but only selecting trends for periods following cooling episodes of the same length. The black lines are repeated from the top row with the normalisation changed to match the number of trends available. The shift in the mean of the histograms is indicated as a percentage

Fig. 5

The fraction of simulations that show a cooling trend in the first N years of the four ensembles, for \(N = 20, 30\) and 50. The average fraction of the planet’s surface area which exhibits a cooling trend is also given

Fig. 6

a, b Ensemble spreads (1 standard deviation) of global and European annual temperatures as a function of time (thin lines), smoothed with an 11-year running mean (thick lines). c Map of the trends in MACRO ensemble spread over the first 90 years of the simulations. The grey box denotes the Europe region used

2 Large initial condition ensembles with FAMOUS

To examine the role of internal variability in near-term climate projections we analyse a 1200-year pre-industrial control simulation and four large ensembles with the FAMOUS AOGCM.

2.1 The FAMOUS AOGCM

FAMOUS is a lower resolution and retuned version of the third Met Office Hadley Centre AOGCM (HadCM3; Gordon et al. (2000)), and has an atmospheric component with a horizontal resolution of \(5^{\circ } \times 7.5^{\circ }\), with 11 vertical levels. The ocean component has a horizontal resolution of \(2.5^{\circ } \times 3.75^{\circ }\), with 20 vertical levels. No flux adjustments are used. The coarse resolution and fast computational speed of FAMOUS allows simulations to be performed at over 100 model years per wall-clock day, making it ideal for lengthy simulations and large ensembles. The version of FAMOUS used is xfxwb, described in Smith et al. (2008) and updated in Smith (2012).

In the control simulation, the standard deviation of global annual mean surface air temperature is 0.18K (with a range of 0.14–0.21 K for different 164 year segments), which is larger than all of the state-of-the-art CMIP5 models (range 0.06–0.15 K). A crude estimate from observations is \(0.12\,\hbox {K}\), obtained by removing a 4th order polynomial fit to the HadCRUT4 global temperature dataset (Morice et al. 2012) for 1850–2013. However, the pattern and autocorrelation characteristics of the variability are also important for assessing the realism of the simulations. For example, the CMIP5 GCMs show a diversity in the simulated patterns and amplitude of variability on regional scales (Hawkins and Sutton 2012; Knutson et al. 2013).
Fig. 7

Timeseries of Europe DJF temperatures in the various ensembles. The ensemble mean is shown in black. The equivalent figure for JJA is in the Supplementary Information

Fig. 8

Ensemble mean winter (DJF) trends over the first 20 years (top row) for the MICRO (left) and MACRO (right) ensembles, along with the maximum and minimum trend at any particular grid-point across the MICRO ensemble (second row). The distribution of trends for the domain average are shown in the bottom two rows for all four ensembles. The mean and standard deviation of the domain average for each ensemble is also given. The equivalent figure for JJA is in the Supplementary Information

Fig. 9

As Fig. 8 but for trends over the first 50 years. Note change of y-axis scales for the histograms. The equivalent figure for JJA is in the Supplementary Information

Interannual temperature variability in the FAMOUS control simulation shows a similar geographical pattern to, but with a much larger amplitude than, an observational estimate from ERA-40 (Fig. 1, for 1958–2001 after linear detrending) (Uppala et al. 2005). Although this has large implications for any comparison of these simulations with the real world, and is a caveat on the results, the speed of FAMOUS makes it a good test-bed to explore the role of variability and how to design ensembles to sample initial condition uncertainty.
Fig. 10

The annual maximum Atlantic meridional overturning circulation (AMOC) strength for the FAMOUS control simulation. The filled circles represent the initial conditions for MICRO (green), MINI MICRO 1 (orange), MINI MICRO 2 (grey) and MACRO (blue & all colours). The MACRO dates were chosen simply from the availability of initial condition data files

Fig. 11

The annual maximum Atlantic meridional overturning circulation strength for the control simulation (black) and the first 30 years of each ensemble (colours, panels as labelled)

Fig. 12

Regression between the AMOC and annual mean surface air temperature in the FAMOUS control simulation

Fig. 13

Signal-to-noise in future trends. Comparing the mean trend (grey) with the ensemble spread in the trend (black) for the MACRO (solid) and MICRO (dashed) ensembles for different seasons, regions and climate variable as labelled

2.2 Ensemble design

All the simulations assume an idealised 1 %/year compound increase in \(\hbox {CO}_2\) from pre-industrial levels until year 140, when a quadrupling of \(\hbox {CO}_2\) is reached.

Using terminology first suggested by Stainforth et al. (2007a), two separate ensembles were initially produced:
  1. 1.

    MACRO—30 different coupled initial conditions are chosen from well separated start dates in the long control run

     
  2. 2.

    MICRO—a single coupled initial condition from MACRO is chosen, and 100 ensemble members are produced, each with a \({\mathcal {O}}(10^{-3})\hbox {K}\) perturbation to sea surface temperature (SST) in a single, randomly chosen ocean grid point

     

The chosen start dates are indicated later in Fig. 10. The MICRO ensemble therefore samples the uncertainty in future model climate only due to the non-linear nature of its climate system (i.e. the irreducible uncertainty), whereas the MACRO ensemble samples the uncertainty due to both its non-linear nature and initial condition differences in large scale aspects of the atmosphere and ocean. A component of this uncertainty may be reducible due to the memory in the initial conditions (Griffies and Bryan 1997; Smith et al. 2007). MACRO is therefore designed to better sample the uncertainty in an uninitialised framework, and MICRO samples the uncertainty contingent on the particular initial conditions chosen.

After preliminary analysis, two further ensembles were produced:
  1. 3.

    and 4. MINI MICRO 1 and 2—each of these ensembles has 50 members and, like MICRO, are run from different coupled initial conditions, chosen from MACRO

     

The two initial conditions for MINI MICRO, which are only 20 years apart in the control run (see Fig. 10 later), were chosen because the corresponding MACRO members produced very different outcomes for the subsequent 30 years for European climate. These additional ensembles enable the sensitivity to the particular ocean initial condition to be assessed in terms of the irreducible response uncertainty resulting from uncertainty at the smallest scales.

In total, 33,400 simulated years have been analysed. The key issue that will be addressed with these ensembles is determining the size of the irreducible uncertainty in near-term climate projections. Other questions will be considered, such as: (1) what is the range of possible temperature trends? (2) how important is the oceanic initial state in near-term climate projections? (3) how long before the signal of climate change emerges from the internal variability? (4) how should future ensembles of near-term projections be designed?

3 The role of the initial conditions

We explore the variability within the transient ensembles using surface temperatures globally, and then illustrate the magnitude of the irreducible uncertainty and consequences for regional near-term temperatures and precipitation with a case study over Europe.

3.1 Transient climate reponse

It has recently been suggested (Liang et al. 2013) that the initial conditions may be a significant source of uncertainty in estimating the global temperature change at the time of \(\hbox {CO}_2\) doubling, or transient climate response (TCR). The primary reason for the uncertainty identified by Liang et al. (2013) was that the spin-up or drift in the GCM considered would produce different estimates of TCR for well-spaced initial conditions. However, it is also possible that the TCR could vary depending on the initial condition in a well spun-up GCM, such as FAMOUS.

We estimate TCR in each FAMOUS simulation using the global mean surface temperature in years 61–80, minus the mean of the entire pre-industrial control simulation. The four FAMOUS ensembles show that the spread (which we take to be one standard deviation throughout) in estimates of TCR is between 0.06 and 0.08 K, with a minimum to maximum range of 2.25–2.64 K (Fig. 2). The standard deviation of 20-year means in global temperature in the FAMOUS control simulation is also 0.08 K, suggesting that the ensembles are effectively sampling the same internal variability but around the point of \(\hbox {CO}_2\) doubling and that the transient response itself does not add additional uncertainty.

In the CMIP5 ensemble, the estimated TCR ranges from 1.1 to 2.5 K (Forster et al. 2013). FAMOUS is clearly a high sensitivity GCM, but the relatively small initial condition uncertainty suggests that the spread in CMIP5 GCM estimates is dominated by model diversity. In addition, these results suggest that uncertainty in TCR estimates using control simulation variability may provide a good first estimate if only small ensembles are available. Such an approach would, however, substantially reduce the likelihood of identifying non-linear, model-dependent feedbacks which could affect the TCR in different models. Ensemble sizes should in any case be sufficiently large to make a good estimate of the mean.

In all four FAMOUS ensembles, the warming is greater for later initial states, which are characterised by their starting \(\hbox {CO}_2\) concentration in Fig. 3. This effect is commonly observed in CMIP3 and CMIP5 AOGCMs (Gregory and Forster 2008; Gregory et al. in press). The main reason is likely to be the decrease in efficiency of heat loss from the upper ocean to deeper layers as the latter become warmer, and is related to the cold-start effect (e.g. Keen and Murphy 1997) and the long-term commitment to surface warming after forcing is stabilised (as discussed by Gregory et al. in press). It does not imply a dependence of ocean heat uptake processes on the state of the climate. However, non-linear behaviours may also enhance the warming under successive doublings, for instance due to decrease in the global climate feedback parameter (Gregory et al. in press) and various regional phenomena (Good et al. 2015). Because the warming per unit increase in \(\hbox {CO}_2\) in forcing tends to increase, its value inferred from historical observations might underestimate the future response (Gregory and Forster 2008).

3.2 Global temperature trends

When considering shorter timescales, there is considerable variability in global mean temperatures. Figure 4 (top row) shows distributions of all possible overlapping trends for 10, 15 and 20 year periods in all the ensembles combined, with decadal trends ranging from –0.5 to over +1 K/decade. For example, ~8 % of decades show a cooling trend and ~1 % of 15-year trends show a cooling, even though the climate is warming in the long-term. However, the regional patterns and causes of each cooling period can be very different (Sutton et al. 2015). The longest period with a global cooling trend is 24 years in FAMOUS. All trends are calculated using standard linear regression against time.

The variability in these short-term trends inferred from the long control simulation (solid black curves) matches that of the large transient ensembles fairly well, indicating that lengthy control simulations are of considerable value in determining the range of possible future climate changes in this model (also see Deser et al. 2014). However, the magnitude of the variability decreases slightly over time in the transient simulations (see Sect. 3.4) suggesting there is a limit to the assumption of stationary variance.

Interestingly, it is also possible to consider what happens after a cooling period. The bottom row of Fig. 4 shows the distributions of global mean temperature trends immediately following periods of the same length that had a cooling trend. The mean of these distributions are shifted towards more positive values by between 15 and 25 %, indicating that cooling periods are more likely to be followed by higher rates of warming (or ‘surges’), with relevance to the recent observed slowdown in global temperatures. In addition, this shift is not simply due to the removal of the cooling periods from the distributions, except for 10-year trends where about half of the shift in the mean is due to this effect.

3.3 Local temperature trends

We next consider local temperature trends in the initial decades of the experiments, as an idealised analogue of the coming decades. Figure 5 illustrates the fraction of simulations which exhibit a cooling trend at each grid point over the first N years, for different values of N. In the MACRO case, one third or more of the simulations show a cooling trend over the first 20 years in many regions, especially in the extra-tropics. In the MICRO case, the fraction of simulations is increased over the North Atlantic, Europe and some of the Southern Ocean and north western Pacific. For longer trend lengths, the fractions of simulations exhibiting a cooling trend decreases and the two ensembles converge, although even over 30 years substantial areas still have significant fractions which show cooling.

The two MINI MICRO ensembles demonstrate that the probability of a cooling trend in any specific region is highly dependent on the particular ocean initial condition chosen. All three MICRO ensembles exhibit areas where more than 50 % of the simulations have a cooling trend over the first 20, and sometimes 30, years but the spatial patterns of ensemble behaviour are strikingly different. By 50 years in, the long term trend is positive almost everywhere and the few regions where a few simulations are negative are similar across the ensembles (also see Branstator and Teng 2010).

These differences between ensemble types highlight how a single ocean initial condition (as in each MICRO case) is not effectively sampling the uncertainty in future trends. For example, over Europe there is a high chance of a cooling trend in MICRO and MINI MICRO 2 due to a decline in the Atlantic Ocean heat transport (see Sect. 3.6), but in MINI MICRO 1, there is a near zero chance. Thus a single MICRO ensemble is not representative of the full uncertainty in the absence of knowledge of the initial ocean conditions. On the other hand it is representative of the irreducible uncertainty conditioned on a particular set of ocean/atmosphere initial conditions, in this model. This regional case study is explored further in Sect. 3.5 where we also highlight that the different MICRO ensembles have different predictability properties.

However, the ensembles are more consistent in the fraction of the globe which exhibits a cooling. Looking across all the simulations, a median of \(21\,\%\) (with a 5–95 % range of 12–43 %) of the globe shows a cooling over the first 20 years, and \(10\,\%\) (with a 5–95 % range of 4–19 %) over the first 30 years. No simulation exhibits a warming everywhere. But, the simulations differ in where the warming and cooling regions are. This type of quantification may be of use to help communicate the odds of ‘unexpected’ trends.

3.4 Ensemble spread and variability

We next consider how the ensemble spread changes over time, and the implications for predictability characteristics in the future.

The ensemble spread of the MICRO ensemble is initially smaller than the MACRO case, as expected, but they converge after a few years for global temperatures, and after around 20 years for European average temperatures (Fig. 6a, b) (also see Sect. 3.6 later).

There is therefore a potential initial reduction in ensemble spread and increase in predictive skill of the future within the model through conditioning on a particular initial ocean state. Whether some of this potential can be realised for real world predictions depends on the quality of the simulated climate and is an area of active ongoing research (Smith et al. 2007; Meehl et al. 2014).

Interestingly, the MINI MICRO 1 ensemble produces a very different growth of spread than MICRO and MINI MICRO 2 for Europe, even though they are all only sampling the irreducible initial condition uncertainty. These differences highlight possible state dependence of regional predictability - predictability from certain states may be greater than from others (Griffies and Bryan 1997). Both MINI MICRO ensembles are similar to MICRO for the global average (not shown).

In addition, the ensemble spread decreases as the climate warms, at least for the first 100 years. For the global mean, this reduction is around \(10\,\%\), and for Europe it is around \(20\,\%\), although there is significant variability in both the annual and the running mean of the spread. It is also seen that there is a flattening in the ensemble spread after around 100 years. This change in ensemble spread suggests a corresponding decrease in the magnitude of simulated interannual variability [also see Stouffer and Wetherald (2007) and Holmes et al. (2015)].

The ensemble spread decline is particularly evident in the North Atlantic, Nordic Seas and Scandinavia (Fig. 6c), suggesting that it is due to the sea-ice edge retreating in a warmer climate (also see Screen 2014). This would also explain why the reduction in ensemble spread does not continue indefinitely as the sea-ice retreats further into the Arctic.

3.5 Regional trends: a European case study

We now examine possible future temperature trends over Europe in these ensembles. The timeseries of winter (DJF) temperatures are shown in Fig. 7 for the four ensembles. Note that MACRO undergoes a rather smooth warming in the ensemble mean, but the different MICRO ensembles show consistent deviations from a smooth trend in the first couple of decades. The equivalent temperatures for JJA are shown in Fig. S1.

We also consider examples of 20 and 50 year projections of winter (DJF) in Figs. 8 and 9. The equivalent figures for summer (JJA) are shown in Figs. S2 and S3. Other seasons, regions and trend lengths can be viewed at an interactive website,1 which includes results for both surface air temperature and precipitation.

The mean spatial trend for the MICRO and MACRO ensembles differ substantially when considering 20 year trends (Fig. 8). The MACRO ensemble shows a warming trend over the whole region. However, in the MICRO ensemble, there is a general cooling over Europe and much of the North Atlantic as a consequence of the particular ocean initial condition chosen. When considering each grid point independently there is the possibility of a trend smaller than –0.8 to larger than +0.8 K per decade for most land areas.

The histograms of trends for the European average temperature illustrate that the MACRO ensemble has a significantly wider spread than MICRO (at 99 % confidence using an f-test), and a mean which is positive, whereas the MICRO ensemble tends to produce a cooling, as seen in the maps.

However, the MINI MICRO ensembles clearly highlight how ocean initial conditions affect the subsequent distribution. Remarkably, the MINI MICRO 1 ensemble warms far more on average, and has no members which show a cooling. It also exhibits a distribution which hardly overlaps with the other MICRO ensembles.

When considering 50 year trends (Fig. 9), the differences between the ensembles have reduced, and all show a warming on average, and in all ensemble members (except one) for the European mean. However, considering grid points independently, it is still possible to have a cooling over Central and Eastern Europe. Again, the MACRO ensemble has a larger spread than the MICRO ensembles. The results for summer (JJA) give similar conclusions (Figs. S2, S3), but the variability is smaller, resulting in narrower distributions.

3.6 Regional trends: the role of the ocean state

The temperature timeseries for Europe in DJF (Fig. 7) show some interesting features. The particular ocean state chosen as the initial condition in each ensemble is clearly changing the distribution of the subsequent projections.

An important consequence of the initial ocean state, in this GCM, is the subsequent development of the Atlantic meridional overturning circulation (AMOC). Figure 10 shows the annual mean maximum of the AMOC streamfunction for the long FAMOUS control simulation. The filled circles represent the initial conditions used—green for the MICRO ensemble, orange and grey for MINI MICRO 1 and 2 respectively, and blue for the other MACRO states. We note again that a single realisation from each of the MICRO ensembles is also included in MACRO.

At first glance, there is nothing unusual about the chosen MICRO initial condition as the AMOC is relatively neutral. However, Fig. 11 shows that the vast majority of ensemble members follow a similar subsequent trajectory with an increase for a few years, followed by a rapid decline. There is a clear potentially predictable signal in the AMOC and the time structure matches the behaviour of temperatures over Europe.

Figure 12 shows the regression pattern between the AMOC and surface temperatures in the control simulation, highlighting the potential impact of the ocean on European temperatures in FAMOUS. In the control simulation, European temperatures change by around 0.17 K/Sv in response to the AMOC (also see Smith and Gregory 2009). This is in qualitative agreement with the variations seen in MICRO.

Figure 11 also shows the AMOC evolution for each MACRO state, reset to start from the same nominal year. Here the spread in projections is far wider initially, highlighting that a range of ocean states has been chosen. The ensemble spread of the MICRO experiments saturate to a similar level to MACRO after around 20–30 years (not shown), slightly longer than previous studies (Collins et al. 2006; Msadek et al. 2010).

The MINI MICRO 1 ensemble members undergo a rapid warming initially over Europe, consistent with the low state of the AMOC in the initial condition although the AMOC control timeseries does not reflect this (Figs. 10 and 11). It is not clear why MINI MICRO 1 has a high ensemble spread over Europe in the first few years (Fig. 6). In MINI MICRO 2, a similar situation to MICRO is seen, with an initial warming and subsequent cooling, also consistent with the AMOC initial state and evolution (Fig. 11).

The different behaviour of the ensembles over Europe are clearly related to the particular ocean initial condition in a complex fashion, highlighting the need to sample a wide range of ocean states to ensure a representative future ensemble.

3.7 Signal-to-noise in future trends

The issues of signal-to-noise in future temperature trends in this ensemble are summarised in Fig. 13. The mean signal (solid) and ensemble spread (dashed) are compared for two seasons (DJF & JJA) and two spatial averages (global & Europe).

The signal of the trend is larger than the ensemble spread for 20 year trends in global average temperature (top row)—i.e. where the dashed and solid lines cross, termed ‘emergence’. For Europe (middle row), this signal emergence time is later, at around 20–35 year trend length depending on the ensemble.

The ensemble spread declines as the period lengthens and the MACRO ensemble (blue) shows larger spreads than the MICRO ensemble (green) for all trend lengths in both seasons and both spatial averages. But, for trend lengths larger than around 40 years the differences are negligible. For shorter trends, the ocean initial conditions play a key role in determining the spread in future trends.

For precipitation, Fig. 13 (bottom row) demonstrates that the emergence times are generally later, except for DJF in MICRO, which is at a similar time to temperature. For European JJA rainfall, the signal remains smaller than the variability, even when considering trends of 90 years length.

Interestingly, the spreads in MICRO and MACRO do not completely converge, even for multi-decadal trend lengths, especially in DJF European temperature and precipitation. This suggests some memory of the initial conditions for an extended period.

4 Summary and discussion

We have performed four large initial condition ensembles of climate change simulations with the FAMOUS AOGCM to examine issues of state-dependent predictability in the context of irreducible uncertainty. Our main findings are:
  1. 1.

    The presence of initial condition uncertainty and non-linearity produces significant irreducible uncertainty in future regional climate changes. For trends of 20 years, the climate change signal rarely emerges from the noise of internal variability in FAMOUS. Uncertainty in future trends of temperature and precipitation reduce for longer trends as the initial condition uncertainty saturates.

     
  2. 2.

    An ensemble of different ocean states produces a wider spread in regional climate changes for a few decades, when compared with ensembles of different atmospheric states only.

     
  3. 3.

    Variability in the control simulation in this model is representative of the spread of possible trends for the near-term. However, large ensembles are required to estimate the expected changes over time.

     
  4. 4.

    There is an initial ocean state dependence of near-term climate trends. In FAMOUS, the initial state of the AMOC has a clear impact on subsequent temperature distributions over Europe.

     
  5. 5.

    Surface temperature ensemble spread decreases in a warmer climate, especially in the northern extra-tropics, suggesting a decline in the amplitude of internal variability in future.

     
  6. 6.

    Cooling periods in global mean surface temperature tend to be followed by more rapid warming periods in FAMOUS, suggesting that the recent slowdown may be followed by a warming ‘surge’.

     
  7. 7.

    The warming for a further doubling of \(\hbox {CO}_2\) concentration increases as time passes under the 1 %/year \(\hbox {CO}_2\) scenario in FAMOUS.

     

We stress again that the variability in FAMOUS appears larger than in the real world (Fig. 1), and so the precise numerical values for ensemble spreads and signal-to-noise cannot be directly related to reality. However, we consider the model to be qualitatively reliable to examine the effects of different types of initial condition perturbation. The results provide additional evidence that large ensembles of simulations with complex climate models are required to sample plausible near-term climate, and should be considered more widely (Kay et al. 2015). In addition, the average of a large ensemble provides a more robust estimate of mean projected changes than a small ensemble or single member. Such large ensemble studies have implications for the various types of ensembles produced to inform about future climate, and raise challenging questions regarding how such ensembles should be designed and interpreted.

Ensembles which explore a range of different macro initial conditions, addressed in this work through different ocean states, are essential to get an idea of the consequences of initial condition uncertainty and the range of plausible future behaviour within a model under changing forcing conditions. However, it is difficult to see how a completely representative sample of ocean states (or macro initial conditions more generally) could be generated. For example, selecting different AMOC states is important for Europe, but not elsewhere. In addition, different modes of variability may interact, increasing the dimensonality of producing initial conditions. In practical terms, a large set of transient simulations started in the nineteenth century would produce a range of outcomes which samples from the full distribution, but the resulting ensemble statistics cannot necessarily be interpreted as true probabilities. Such ensembles are likely to provide a lower bound [or ‘non-discountable envelope’, Stainforth et al. (2007b)] of responses within a given model.

This is in contrast to the irreducible uncertainty associated with initial condition uncertainty at the smallest scales, in this case tiny changes to SST at a single grid point. Here an ensemble can be interpreted as providing future probability distributions conditioned on the model structure and the ‘large scale’ initial conditions, allowing for some small uncertainty in the finest details. This situation is more like the experimental initialised decadal forecasts which are now being produced Smith et al. (2013). In addition, the original Deser et al. (2012b) large ensemble was a micro ensemble, with each member starting from an identical ocean state in the year 2005 to analyse near-term projections. According to our experiments with the FAMOUS AOGCM, this approach would underestimate the spread in future projections.

To more fully understand the behaviour of the model requires a ‘micro’ ensemble for each ocean state explored so that differences in the distributions can be quantified. For example, the three MICRO distributions in Fig. 8 are obviously different, but to better examine how they are different requires larger initial condition ensembles than are presented here. The ‘gold standard’ to understand the physical behaviour of a model would therefore be large micro initial condition ensembles for a range of different macro initial condition variations.

The results presented also highlight the potential benefit to near-term climate forecasts from appropriately constraining the macro ocean initial conditions with observations. Furthermore, if the evolution of the AMOC is predictable then some of the resulting regional temperature variability over Europe may also be predictable.

Footnotes

  1. 1.

Notes

Acknowledgments

We thank Erich Fischer, Rowan Sutton and Peter Good for helpful discussions, and two anonymous reviewers for their constructive comments which helped improve the paper. EH was funded by a NERC Advanced Fellowship. EH, RS and JG all received support from NCAS-Climate. DAS acknowledges the support of the LSE’s Grantham Research Institute on Climate Change and the Environment and the Centre for Climate Change Economics and Policy funded by the Economic and Social Research Council and Munich Re.

Supplementary material

382_2015_2806_MOESM1_ESM.pdf (155 kb)
Supplementary material 1 (pdf 154 KB)

References

  1. Branstator G, Teng H (2010) Two limits of initial-value decadal predictability in a CGCM. J Clim 23:62926311. doi:10.1175/2010JCLI3678.1 CrossRefGoogle Scholar
  2. Branstator G, Teng H, Meehl GA, Kimoto M, Knight JR, Latif M, Rosati A (2012) Systematic estimates of initial-value decadal predictability for six AOGCMs. J Clim 25:18271846. doi:10.1175/JCLI-D-11-00227.1 CrossRefGoogle Scholar
  3. Collins M, Botzet M, Carril AF, Drange H, Jouzeau A, Latif M, Masina S, Otteraa OH, Pohlmann H, Sorteberg A, Sutton R, Terray L (2006) Interannual to decadal climate predictability in the North Atlantic: a multimodel-ensemble study. J Clim 19:1195–1202. doi:10.1175/JCLI3654.1 CrossRefGoogle Scholar
  4. Daron JD, Stainforth DA (2013) On predicting climate under climate change. Environ Res Lett 8(034):021Google Scholar
  5. Deser C, Phillips AS, Bourdette V, Teng H (2012a) Uncertainty in climate change projections: the role of internal variability. Clim Dyn 38:527–546. doi:10.1007/s00382-010-0977-x CrossRefGoogle Scholar
  6. Deser C, Knutti R, Solomon S, Phillips AS (2012b) Communication of the role of natural variability in future north american climate. Nat Clim Change 2:775–779. doi:10.1038/nclimate1562 CrossRefGoogle Scholar
  7. Deser C, Phillips AS, Alexander MA, Smoliak BV (2014) Projecting North American climate over the next 50 years: uncertainty due to internal variability. J Clim 27:2271–2296. doi:10.1175/JCLI-D-13-00451.1 CrossRefGoogle Scholar
  8. Forster PM, Andrews T, Good P, Gregory JM, Jackson LS, Zelinka M (2013) Evaluating adjusted forcing and model spread for historical and future scenarios in the cmip5 generation of climate models. J Geophys Res Atmos 118:1139–1150. doi:10.1002/jgrd.50174 CrossRefGoogle Scholar
  9. Good P, Lowe JA, Andrews T, Wiltshire A, Chadwick R, Ridley JK, Menary MB, Bouttes N, Bouttes N, Dufresne JL, Gregory JM, Schaller N, Shiogama H (2015) Nonlinear regional warming with increasing CO2 concentrations. Nat Clim Change 5:138–142. doi:10.1038/nclimate2498 CrossRefGoogle Scholar
  10. Gordon C, Cooper C, Senior CA, Banks H, Gregory JM, Johns TC, Mitchell JFB, Wood RA (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16:147–168CrossRefGoogle Scholar
  11. Gregory JM, Forster PM (2008) Transient climate response estimated from radiative forcing and observed temperature change. J Geophys Res Atmos 113(D23):105. doi:10.1029/2008JD010405 CrossRefGoogle Scholar
  12. Gregory JM, Andrews T, Good P (in press) The inconstancy of the transient climate response parameter under increasing \(\text{ CO }_{2}\). Philos Trans R Soc LondGoogle Scholar
  13. Griffies SM, Bryan K (1997) A predictability study of simulated North Atlantic multidecadal variability. Clim Dyn 13:459–487CrossRefGoogle Scholar
  14. Hawkins E, Sutton R (2009) The potential to narrow uncertainty in regional climate predictions. Bull Am Met Soc 90:1095–1107. doi:10.1175/2009BAMS2607.1 CrossRefGoogle Scholar
  15. Hawkins E, Sutton R (2012) Time of emergence of climate signals. Geophys Res Lett 39(L01):702. doi:10.1029/2011GL050087 Google Scholar
  16. Holmes C, Woollings T, Hawkins E, de Vries H (2015) Robust future changes in temperature variability under greenhouse gas forcing and the relationship with thermal advection. J Clim (in press). doi:10.1175/JCLI-D-14-00735.1
  17. Kay J, Deser C, Phillips A et al (2015) The CESM large ensemble project. BAMS (in press). doi:10.1175/BAMS-D-13-00255.1
  18. Keen AB, Murphy JM (1997) Influence of natural variability and the cold start problem on the simulated transient response to increasing \(\text{ CO }_{2}\). Clim Dyn 13:847–864CrossRefGoogle Scholar
  19. Knutson TR, Zeng F, Wittenberg AT (2013) Multimodel assessment of regional surface temperature trends: CMIP3 and CMIP5 twentieth-century simulations. J Clim 26:8709–8743. doi:10.1175/JCLI-D-12-00567.1 CrossRefGoogle Scholar
  20. Liang MC, Lin LC, Tung KK, Yung YL, Sun S (2013) Transient climate response in coupled atmospheric-ocean general circulation models. J Atmos Sci 70:1291–1296. doi:10.1175/JAS-D-12-0338.1 CrossRefGoogle Scholar
  21. Meehl GA, Goddard L, Boer G, Burgman R et al (2014) Decadal climate prediction: An update from the trenches. BAMS 95:243. doi:10.1175/BAMS-D-12-00241.1 CrossRefGoogle Scholar
  22. Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 data set. J Geophy Res Atmos 117(D08):101. doi:10.1029/2011JD017187 Google Scholar
  23. Msadek R, Dixon KW, Delworth TL, Hurlin W (2010) Assessing the predictability of the Atlantic meridional overturning circulation and associated fingerprints. Geophys Res Lett 37(L19):608. doi:10.1029/2010GL044517 Google Scholar
  24. Screen JA (2014) Arctic amplification decreases temperature variance in northern mid- to high-latitudes. Nat Clim Change 4:577–582. doi:10.1038/nclimate2268 CrossRefGoogle Scholar
  25. Selten F, Branstator G, Dijkstra H, Kliphuis M (2004) Tropical origins for recent and future northern hemisphere climate change. Geophys Res Lett 31(L21):205. doi:10.1029/2004GL020739 Google Scholar
  26. Smith DM, Cusack S, Colman AW, Folland CK, Harris GR, Murphy JM (2007) Improved surface temperature prediction for the coming decade from a global climate model. Science 317:796–799. doi:10.1126/science.1139540 CrossRefGoogle Scholar
  27. Smith DM, Scaife AA, Boer GJ, Caian M, Doblas-Reyes FJ, Guemas V, Hawkins E, Hazeleger W, Hermanson L, Ho CK, Ishii M, Kharin V, Kimoto M, Kirtman B, Lean J, Matei D, Merryfield WJ, Muller WA, Pohlmann H, Rosati A, Wouters B, Wyser K (2013) Real-time multi-model decadal climate predictions. Clim Dyn 41:2875. doi:10.1007/s00382-012-1600-0 CrossRefGoogle Scholar
  28. Smith RS (2012) The famous climate model (versions xfxwb and xfhcc): description update to version xdbua. Geosci Model Dev 5:269–276. doi:10.5194/gmd-5-269-2012 CrossRefGoogle Scholar
  29. Smith RS, Gregory JM (2009) A study of the sensitivity of ocean overturning circulation and climate to freshwater input in different regions of the North Atlantic. Geophys Res Lett 36(L15):701. doi:10.1029/2009GL038607 Google Scholar
  30. Smith RS, Gregory JM, Osprey A (2008) A description of the FAMOUS (version XDBUA) climate model and control run. Geosci Model Dev 1(1):53–68CrossRefGoogle Scholar
  31. Stainforth DA, Allen MR, Tredger ER, Smith LA (2007) Confidence, uncertainty and decision-support relevance in climate predictions. Philos Trans A 365:2145–2161. doi:10.1098/rsta.2007.2074 CrossRefGoogle Scholar
  32. Stainforth DA, Downing TE, Washington R, Lopez A, New M (2007) Issues in the interpretation of climate model ensembles to inform decisions. Philos Trans A 365:2163–2177. doi:10.1098/rsta.2007.2073 CrossRefGoogle Scholar
  33. Sterl A, Severijns C, Dijkstra H, Hazeleger W, Jan van Oldenborgh G, van den Broeke M, Burgers G, van den Hurk B, Jan van Leeuwen P, van Velthoven P (2008) When can we expect extremely high surface temperatures? Geophys Res Lett 35(L14):703. doi:10.1029/2008GL034071 Google Scholar
  34. Stocker TF, Qin D, Plattner GK, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (2013) IPCC, 2013: summary for policymakers. In: Climate change 2013: the physical science basis. Contribution of working group I to the fifth assessment report of the intergovernmental panel on climate change. Cambridge University Press, CambridgeGoogle Scholar
  35. Stouffer RJ, Wetherald RT (2007) Changes of variability in response to increasing greenhouse gases. part 1: temperature. J Clim 20:5455–5467. doi:10.1175/2007JCLI1384.1 CrossRefGoogle Scholar
  36. Sutton R, Suckling E, Hawkins E (2015) What does global temperature tell us about local climate? Philos Trans A (in press)Google Scholar
  37. Uppala SM, Kallberg PW, Simmons AJ, Andrae U, Bechtold VDC, Fiorino M, Gibson JK, Haseler J, Hernandez A, Kelly GA, Li X, Onogi K, Saarinen S, Sokka N, Allan RP, Andersson E, Arpe K, Balmaseda MA, Beljaars ACM, Berg LVD, Bidlot J, Bormann N, Caires S, Chevallier F, Dethof A, Dragosavac M, Fisher M, Fuentes M, Hagemann S, Holm E, Hoskins BJ, Isaksen L, Janssen PAEM, Jenne R, Mcnally AP, Mahfouf JF, Morcrette JJ, Rayner NA, Saunders RW, Simon P, Sterl A, Trenberth KE, Untch A, Vasiljevic D, Viterbo P, Woollen J (2005) The ERA-40 re-analysis. QJRMS 131:2961–3012. doi:10.1256/qj.04.176 CrossRefGoogle Scholar

Copyright information

© The Author(s) 2015

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  1. 1.NCAS-Climate, Department of MeteorologyUniversity of ReadingReadingUK
  2. 2.Met Office Hadley CentreExeterUK
  3. 3.Grantham Institute, London School of EconomicsLondonUK
  4. 4.Department of PhysicsUniversity of WarwickCoventryUK
  5. 5.Environmental Change Institute, University of OxfordOxfordUK

Personalised recommendations