Variability of West African monsoon patterns generated by a WRF multi-physics ensemble

Abstract

The credibility of regional climate simulations over West Africa stands and falls with the ability to reproduce the West African monsoon (WAM) whose precipitation plays a pivotal role for people’s livelihood. In this study, we simulate the WAM for the wet year 1999 with a 27-member multi-physics ensemble of the Weather Research and Forecasting (WRF) model. We investigate the inter-member differences in a process-based manner in order to extract generalizable information on the behavior of the tested cumulus (CU), microphysics (MP), and planetary boundary layer (PBL) schemes. Precipitation, temperature and atmospheric dynamics are analyzed in comparison to the Tropical Rainfall Measuring Mission (TRMM) rainfall estimates, the Global Precipitation Climatology Centre (GPCC) gridded gauge-analysis, the Global Historical Climatology Network (GHCN) gridded temperature product and the forcing data (ERA-Interim) to explore interdependencies of processes leading to a certain WAM regime. We find that MP and PBL schemes contribute most to the ensemble spread (147 mm month⁻¹) for monsoon precipitation over the study region. Furthermore, PBL schemes have a strong influence on the movement of the WAM rainband because of their impact on the cloud fraction, that ranges from 8 to 20 % at 600 hPa during August. More low- and mid-level clouds result in less incoming radiation and a weaker monsoon. Ultimately, we identify the differing intensities of the moist Hadley-type meridional circulation that connects the monsoon winds to the Tropical Easterly Jet as the main source for inter-member differences. The ensemble spread of Sahel precipitation and associated dynamics for August 1999 is comparable to the observed inter-annual spread (1979–2010) between dry and wet years, emphasizing the strong potential impact of regional processes and the need for a careful selection of model parameterizations.

Introduction

The West African monsoon (WAM) is the most prominent feature of the West African climate. It accounts for the majority of the annual precipitation and is therefore of paramount importance for the West African population that primarily relies on agriculture. The WAM is forced by differential heating of the ocean and the land surface which causes a seasonal change of the large-scale wind systems during the boreal summer and results in the migration of the inter-tropical convergence zone (ITCZ) over the West African continent. Relatively cool moist air from the Gulf of Guinea is advected onto the hot dry continent, where the resulting rainband travels from the Guinea Coast to the Sahel and back again, following the movement of the ITCZ. The WAM is generally characterized by a strong intra-annual as well as inter-annual variability especially in the Sahel region (Barbe 2002; Lebel and Ali 2009), driven by a complex and not yet fully understood interplay of several dynamical features and multi-scale factors influencing the WAM intensity and continental coverage (e.g. Sultan and Janicot 2003; Grist and Nicholson 2001; Nicholson and Webster 2008).

For a better understanding of the related processes, regional climate models (RCM) are useful tools in this data sparse region. Nikulin et al. (2012) confirm that RCMs can considerably enhance the representation of precipitation in comparison to their coarser forcing dataset (ERA-Interim) over West Africa. Recent studies demonstrate the ability of state-of-the-art RCMs to represent the WAM (Paeth et al. 2011; Druyan et al. 2010; Sylla et al. 2013; Nikulin et al. 2012). Sylla et al. (2013) conclude that RCMs are suitable for the investigation of the dynamical features and their relation to precipitation patterns, despite some uncertainties related to the generation of convective systems, surface temperatures and differing model sensitivities to the dynamical elements of the WAM. All studies emphasize the progress in recent years in improving the WAM representation, but identify large uncertainties related to model physics. They also point out that a multi-model ensemble approach can help to reduce uncertainties in the simulation of WAM characteristics and variability. Research initiatives like the Coordinated Regional Downscaling Experiment (CORDEX, Giorgi et al. 2009) Africa aim at satisfying the demand for standardized RCM simulations over the West African region with diverse models, which facilitates a joint analysis. However, ensemble means do not always outperform individual models, and computational or temporal constraints often render ensemble approaches unfeasible. An alternative solution therefore is to optimize a given atmospheric model for a particular application.

For this, we use the Weather Research and Forecasting (WRF, Skamarock et al. 2008) model, which is a widely used community model, applicable for numerical weather prediction and regional climate modeling. It incorporates a vast number of physical parameterizations that make it highly adaptable but challenging to set up at the same time. Physical parameterizations are subroutines used to describe physical processes on scales too small or too complex to be represented physically in the model. These parameterizations are usually a key source of model uncertainty. The performance of any physics scheme depends amongst others on the dominant atmospheric processes in the region of interest, the model resolution and the suitability of the parameterization for the particular problem. It is well-known that the results of the model can change considerably with the choice of the model physics. The WRF model therefore incorporates many “different atmospheric models”, which is why a large number of WRF sensitivity studies for many regions of the world can be found in the literature.

So far, only a small number of studies utilize WRF for the West African region. These studies demonstrate the skill of the WRF model and its predecessor, the Mesoscale Meteorology model 5 (MM5, Grell et al. 1994) in representing specific features of the West African climate (Vizy and Cook 2002; Bliefernicht et al. 2013; Hagos and Cook 2007; Sijikumar et al. 2006), for RCM-based climate projections (Jung and Kunstmann 2007; Vigaud et al. 2011), for the investigation of tropical storms triggered over the region (Vizy and Cook 2009; Druyan et al. 2009; Chiao and Jenkins 2010) and for evaporation tagging (Knoche and Kunstmann 2013). These studies either simply mention which model configurations were employed, or include a pragmatic testing of model physics to minimize the bias against observations. However, they rarely discuss uncertainties introduced by their choice of parameterizations. Flaounas et al. (2011a) conducted a first comprehensive study of the sensitivity of WRF for three cumulus and two planetary boundary layer parameterizations during the WAM 2006. They investigate the behavior of the tested schemes by analyzing their capability in representing surface variables and some dynamical monsoon features but they find no consistently best-performing configuration. Noble et al. (2014) compared African Easterly Wave occurrences of 64 WRF configurations with those of two reanalysis datasets and radiosonde observations for 12-days time slices over 10 years. They give valuable insights into the development of these atmospheric disturbances and reveal deficiencies of the model in reproducing them.

However, these two sensitivity studies conclude on very different suggestions for a “best” configuration, which nicely illustrates that any kind of evaluation is subjective, depends on the variables of interest, the focus region and the verification methods. Fersch and Kunstmann (2013) evaluated a large set of different WRF configurations including parameterizations, changing driving data and nudging techniques for four climatological regions of the world, including a domain encompassing West Africa. They concluded that the positive skill of a particular model configuration is often limited to the specific case-study, and that new model applications always require a thorough performance testing. The choice of a feasible configuration is furthermore highly dependent on the chosen (imperfect) reference datasets, which Sylla et al. (2013) identified as a key factor preventing an unambiguous model evaluation.

The goal of this study therefore is to use the advantages of an ensemble approach to generalize the process-based impact of individual parameterization schemes in order to complement existing studies. We use the WRF model in an RCM set-up to investigate the ability of a WRF multi-physics ensemble to represent certain WAM features. All members share the same boundary forcing from reanalysis data. The uncertainties in the representation of a single rainy season introduced by the different parameterizations, are used to explore interdependencies of processes leading to a certain WAM regime. Precipitation is especially sensitive to the model configuration, since it is the result of a complex interplay of parameterizations and therefore combines the uncertainties of the various physics schemes in the ensemble. Thus, we concentrate on the qualitative impact on precipitation and associated monsoon dynamics.

The ensemble members represent all possible combinations of three schemes per parameterization of cumulus convection (CU), microphysical cloud processes (MP) and planetary boundary layer mixing (PBL), totaling in 27 different CU_MP_PBL combinations. These parameterizations modulate the atmospheric moisture distribution and thus can be used to indirectly assess the impact of different regional moisture circulations on the WAM dynamics, while the large-scale forcing at the domain boundaries remains the same for all simulations. Analyzing all possible combinations of parameterizations rather than taking an iterative approach allows us to identify the impact of each scheme, since it reveals robust tendencies for changing parameterization partners. This study therefore gives insights into the sensitivity of the WAM system to local processes, as represented by the model physics schemes. It can further help to trace back bad model behavior to a certain process, and suggest which parameterization scheme to change in order to improve the WAM representation in the WRF model.

Section 2 describes the experimental model set-up and the observational datasets used for model comparison. In Sect. 3, we analyze the model precipitation and uncertainties introduced by the different parameterizations. Section 4 presents the variability of WAM dynamics as represented in the WRF ensemble. Section 5 is devoted to a discussion of our results followed by summary and conclusions in Sect. 6.

Experimental set-up and reference datasets

Model configuration

The simulations in this study are conducted with the WRF/Advanced Research WRF model, version 3.5.1. For our approach, the selected physics schemes should (1) directly be linked to moisture transport and moisture redistribution in the atmosphere, and (2) differ in complexity or methodology to represent a particular process.

The investigated CU, MP and PBL schemes (see Table 1) include the effects of latent heat release through deep and shallow convection, microphysical cloud and precipitation processes, and vertical turbulent mixing due to eddy transports, respectively. The PBL scheme is determining the flux profiles of temperature and moisture within the whole atmospheric column, hence generating tendencies that serve as input for the CU and MP scheme at every model time step. The CU scheme is responsible for releasing instabilities in the atmospheric sounding, preventing the MP scheme from generating potentially unrealistic grid-scale convection. As a side-effect of the redistribution of temperature and moisture towards a stable profile, the CU scheme produces convective precipitation. In a last step, the MP scheme removes excess atmospheric moisture in case the air is still saturated, which we will refer to as non-convective precipitation.

Table 1 Cumulus, microphysics and planetary boundary layer schemes used for the ensemble members

For the CU, MP, and PBL groups, we combine parameterization schemes that follow different approaches to represent the same physical effects. The CU group includes a mass-flux type cloud model (KF), a sounding-adjustment type model (BMJ) and a mass-flux type model based on a stochastic approach, providing an ensemble mean (GF). For the KF scheme, the alternative trigger function (option 2) based on moisture advection was used instead of the default option because of reduced precipitation overestimations in preceding experiments.

The MP schemes used here differ in their classification of hydro-meteors. The WSM3 differentiates between three classes: cloud water/ice, rain/snow and vapor, depending on the temperatures being above or below freezing. LIN and TH take into account all six classes of hydro-meteors: cloud water, cloud ice, rain, snow, vapor and graupel. The more sophisticated TH scheme additionally predicts number concentrations for rain and ice species.

The PBL schemes can be divided into 1.5th order closure schemes based on prognostic turbulent kinetic energy (MYJ), and schemes which treat the turbulent mixing by a first order closure (YSU, ACM2). While the MYJ only considers local mixing into vertically adjacent grid cells, the YSU and ACM2 schemes consider non-local mixing through large convective eddies. In YSU, this is expressed by adding a counter-gradient term to non-local gradients of heat and momentum. ACM2 changes smoothly from local eddy diffusion in stable environments to combined local (downward fluxes) and non-local (upward fluxes) transport for heat, momentum and moisture components in unstable conditions. Further details about these schemes can be found in the literature listed in Table 1. All possible combinations of the schemes are included in the multi-physics ensemble, resulting in a total of twenty-seven members. Analyses of the ensemble or sub-ensembles always refer to the mean value.

Non-variable parameterizations that are shared by all simulations include the short-wave radiation scheme by Dudhia (1989), the Rapid Radiative Transfer Model (RRTM) long-wave radiation scheme (Mlawer et al. 1997), and the Noah land surface model (Chen and Dudhia 2001) with the 21-category MODIS land-use data.

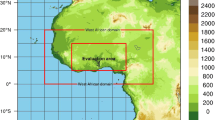
The model domain as shown in Fig. 1 encompasses the entire WAM system and its important features. If not specified otherwise, analyses are carried out for the study region depicted by the black box and for the three sub-regions with the sea masked out. To avoid problems with the so-called gray zone for convection (~3–20 km, Molinari and Dudek 1991), we operate the model at a medium horizontal resolution of 24 km, with 36 vertical levels and a model top of 50 hPa. The 6-hourly boundary conditions are provided by ERA-Interim reanalysis data (Dee et al. 2011) at a horizontal resolution of 0.75°. The sea surface temperature (SST) is given by the NCDC AVHRR_OI at 0.25° (NCDC 2007) at daily temporal resolution and is linearly interpolated to six hourly intervals. The integration time step is 120 s with adaptive time stepping enabled, and model results are stored every 3 h.

Fig. 1

WRF model domain and elevation (m) at 24 km horizontal resolution. The study region (10°W–10°E, 4°N–18°N) is depicted by the black box. Sub-regions indicate the humid Guinea Coast (4°N–8°N), the Sudano-Sahel (8°N–14°N) and the semi-arid Sahel (14°N–18°N)

For all simulations, the green vegetation fraction and albedo are taken from the monthly climatology. Lake temperatures are adjusted to correspond to the daily mean skin temperature of the surrounding area, rather than being interpolated from SSTs.

Simulation period

The rainy season of the wet year 1999 is simulated from March to September, including 1 month of spin-up time. This time span covers the two monsoonal phases as described by Thorncroft et al. (2011): the coastal phase from April to June (AMJ), and the continental phase from July to September (JAS). We choose a wet year to investigate the ensemble spread under a boundary forcing that favors moist conditions to ensure that the monsoon regime simulated by the RCM is not constrained by low incoming moisture fluxes and remote effects that dictate a weak WAM.

The year 1999 is characterized by an extraordinarily wide monsoon rainband with an extended zone of maximum precipitation (Fig. 2 a). At the same time, an above-average northward transition of the monsoon rainband leads to very wet conditions in the Sahel and the Guinea Coast, as can be seen from Fig. 2b. The year is among the three wettest years in the reference period since 1979 (Fig. 2c), for which the ERA-I dataset is available.

Fig. 2

a JAS 1999 average precipitation (mm day⁻¹) for TRMM (left) and GPCC (right); b Annual cycle of 1999 monthly average precipitation for TRMM and GPCC. In addition, the GPCC climatological mean (GPCC CLIM) for 1979–2010 is given. c Annual precipitation amounts for the study region with respect to the climatological mean for 1979–2010 from GPCC

Datasets

Model simulations are compared to satellite and observational data in order to evaluate the skills and physical plausibilities of the different model configurations. For precipitation, the NASA Tropical Rainfall Measuring Mission (TRMM) 0.25° resolution 3B42V7 (3-hourly, daily) and 3B43V7 (monthly) rainfall estimates (Huffman et al. 1995, 1997) and the Global Precipitation Climatology Centre (GPCC) 0.5° gridded gauge-analysis (Schneider et al. 2011) are used. The two datasets clearly show the wet regime at the Guinea Coast and over the Sahel with respect to the climatological mean from 1979–2010 (Fig. 2a, b).

Surface temperatures are compared to the Global Historical Climatology Network (GHCN) 5° monthly gridded temperature product Version 3 (Lawrimore et al. 2011). To address the question to which degree the regional model modifies the large-scale patterns, the ERA-Interim forcing data is taken as reference for the atmospheric dynamics and surface fluxes.

Precipitation

Seasonality of precipitation

WRF captures the seasonal cycle, as can be seen from the Hovmöller diagrams (Fig. 3) for the WRF ensemble mean (ENS) in comparison to TRMM. For both, the area of maximum precipitation from April to June is situated at the coast at about 5°N.

Fig. 3

Time-latitude Hovmöller diagrams of 1999 daily precipitation for TRMM (top), ERA-I (middle) and the WRF ensemble mean (ENS, bottom)

According to Hagos and Cook (2007), the Saharan Heat Low (SHL) reaches its maximum by the end of June when it is positioned around 20°N, and when the Atlantic cold tongue in the Gulf of Guinea is established which induces a pressure gradient strong enough to trigger the “monsoon jump”. This term refers to the sudden relocation of the precipitation maximum from the coast to approximately 10°N and represents the monsoon onset in the Sahel. We define the date of the monsoon jump as the first occurrence of two consecutive days with rainfall amounts within the 0.9 percentile for the period May–July between 9 and 11°N. For TRMM, the monsoon jump takes place on 1st of July, as can be seen in Fig. 3 from the extension and subsequent relocation of the precipitation maximum from the coast to ~12°N. ENS is also capturing the monsoon jump, although 3 days earlier. Most ensemble members are able to capture the monsoon jump close to the observed date with a mean absolute deviation of 4.3 days and a maximum shift of 16–20 days for three of the members.

Intense precipitation events are better represented in ENS than in ERA-I, because of the higher horizontal resolution of WRF. The rainband is slightly shifted to the south over the whole rainy season in comparison to TRMM, but less than for ERA-I. The shift is especially pronounced in August, when the monsoonal rainfall is at its peak and TRMM shows precipitation throughout the whole month in the northern Sahel between 16–20°N, while ERA-I and ENS are not able to capture all of these events. This also applies to all individual ensemble members. The retreat of the rainband to the Guinea Coast sets in by mid-August for TRMM and ERA-I. This movement is delayed in ENS, which results in a too dry coast in the late summer. On the other hand, the observed dry period at the coast during August, i.e., before the retreat of the rainbelt, is not very well represented in ENS, since for some members the rainband remains too far south for the whole period. All ensemble members show a seasonal relocation of the rainband, but strongly differ in the extent, intensity and width, which will be discussed in the following sections.

Spatial distribution of precipitation

In order to reveal the differences in precipitation with respect to certain physics influences, Fig. 4c shows the bias against the ensemble mean of the spatial average of JAS precipitation for each of the nine parameterization groups (following the approach of Pohl et al. 2011, Fig. 15), where one particular scheme is fixed for each group. For example, the KF ensemble consists of the average of the nine simulations that utilize the KF cumulus scheme, and so forth.

Fig. 4

JAS 1999 average precipitation a for TRMM, ERA-I, the ensemble mean (ENS), b the bias of ERA-I and ENS against TRMM and c the bias against ENS of each of the nine parameterization groups. Each group consists of nine members using the respective scheme

The rainband of ENS shown in Fig. 4a is mostly too narrow with excessive precipitation in its core zone and in Central Africa in comparison to TRMM. A persistent dry bias in the eastern part of the Gulf of Guinea is introduced, which stretches into the continent (Fig. 4b). It is most likely caused by too low SSTs in this area in the NCDC dataset. Further simulations using prescribed SSTs from ERA-I show a reduction of this dry bias in accordance with higher SSTs in that region (not shown).

The intensities of the rainbands in Fig. 4c cover the entire range from dry conditions (ACM2, WSM3) to wet conditions (TH, KF). None of the groups is able to capture the exceptional northward extension of the rainband in 1999, especially visible over Mali, which leads to a dry bias in the northern Sahel. Since this dry bias is also found for ERA-I, one might assume that the bias of the WRF simulations is caused by the bias of the driving data. However, in ERA-I the reason for the dry bias is a shift of the relatively broad rainband to the south, while in WRF it is the small North–South extent of the rainband. For GF and MYJ, the rainband is especially narrow with a daily precipitation of only 1–2 mm at the coast. ACM2 and WSM3 show very low precipitation intensities and induce an overall dry bias. BMJ shows closest rainfall amounts to TRMM, outperforming ENS with more precipitation at the coast and less overprediction in the Sudano-Sahel.

Parameterization influences on rainband intensity and position

In the following, we analyze the contribution of the three parameterization groups (CU, MP, PBL) to the above-mentioned differences in spatial rainfall distribution. Figure 5 shows boxplots of the parameterization groups, compared to the ensemble mean for the whole rainy season. The spread of the boxes indicates the tendency of a scheme towards a dry or a wet regime. Small boxes imply that the scheme is the dominating factor, since the resulting regime is hardly changed by different configuration partners. We differentiate between (1) the Guinea Coast, where peak precipitation occurs during the continental phase before monsoon onset, (2) the Sudano-Sahel, where the center of the rainbelt and thus the precipitation maximum are found after monsoon onset is found, and (3) the Sahel, where precipitation depends on the northernmost extent of the rainband (Fig. 1). With respect to the blue line that indicates the TRMM mean, ENS underestimates precipitation both, at the Guinea Coast and in the Sahel. However, except for the dry parameterization groups WSM3 and ACM2, we find an overestimation in the Sudano-Sahel. The largest bias reaches from −3.5 to 1.7 mm day⁻¹ at the Guinea Coast, −2.1 to 3.2 mm day⁻¹ in the Sudano-Sahel, and −1.4 to 0.5 mm day⁻¹ in the Sahel, indicated by the whisker difference of ENS to TRMM.

Fig. 5

Boxplots of the bias in average precipitation from April–September 1999 with respect to the ensemble mean in the Sahel (top), the Soudano-Sahel (middle) and at the Guinea Coast (bottom). The parameterization groups are defined as in Fig. 4. The boxes indicate the interquartile range and the whiskers stretch to minimum and maximum values of each group. Blue lines depict the TRMM average precipitation

The MP schemes show the same overall tendencies for the three regions, with a clear order (TH being the wettest and WSM3 being the driest). The mean precipitation difference between WSM3 and TH is 1.5 mm day⁻¹ at the Guinea Coast, 2.4 mm day⁻¹ in the Sudano-Sahel and 0.7 mm day⁻¹ in the Sahel. Thus, the average intra-ensemble spread induced by the MP schemes is close to the magnitude of the bias to TRMM, which underlines the considerable impact of the MP schemes.

Looking at the PBL schemes, the picture is more diverse for the different regions: While MYJ is dry at the Guinea Coast and wet in the Sahel, ACM2 behaves the opposite way. This indicates a shift of the monsoon rainband, dependent on the choice of the PBL scheme. YSU shows an almost as strong northward shift as MYJ, but with much wetter conditions at the Guinea Coast due to a generally wider rainband as can be seen from Fig. 4. In terms of northward shift of the monsoon rainband, the order of the PBL schemes is ACM2 < YSU < MYJ. The interquartile ranges of the ACM2 and MYJ parameterization groups do not intersect for any of the three regions, which underlines the opposing impact they have on the position of the rainband. However, the strongest northward shift does not necessarily coincide with largest precipitation amounts: YSU instead of MYJ shows largest values in the Sudano-Sahel, where the core of the rainband is situated.

The CU schemes show the largest interquartile-spreads and on average only weak dry/wet tendencies with respect to ENS. They also show the smallest mean difference in precipitation of only 0.6 mm day⁻¹ at the Guinea Coast, 0.9 mm day⁻¹ in the Sudano-Sahel and 0.4 mm day⁻¹ in the Sahel. This suggests an inferior role for the generation of precipitation in the model. However, this depends on the region: In the Sahel, KF (GF) shows a neutral (restrictive) behavior, but a restrictive (neutral) behavior at the Guinea Coast. BMJ dampens the effect of other schemes in both regions, indicated by the consistently smaller inter-quartile spread.

Convective and non-convective precipitation

The ability of an atmospheric model to simulate convective processes is crucial and at the same time a limiting factor for the quality of model precipitation in the tropics and sub-tropics. In the WRF model, precipitation from unresolved deep convection is generated by the CU scheme, while the MP scheme produces grid-scale precipitation in case the air is still super-saturated after the instabilities are released. Thus, the convective fraction of the model is artificial and related to the model resolution. Nevertheless, the partitioning into convective and non-convective precipitation helps to identify the impact of either scheme on the representation of convection.

The amount of non-convective precipitation follows the same order we found earlier for the MP schemes (WSM3 < LIN < TH), with a total spread of 93 mm month⁻¹ exceeding the spread of convective precipitation (68 mm month⁻¹). There is no clear correlation between the CU schemes and the amount of convective precipitation. Model configurations with KF or BMJ generate convective precipitation from 40 mm month⁻¹ to 110 mm month⁻¹, depending on the choice of MP and PBL scheme, while GF generates less convective precipitation and never exceeds 80 mm month⁻¹. In particular, the ACM2 scheme leads to small amounts of convective precipitation for all CU schemes and results in a very dry regime. The impact of a particular CU scheme depends on the chosen PBL scheme and vice versa. For example, for the MYJ PBL scheme, maximum convective precipitation is achieved in combination with KF, while for the YSU and ACM2 PBL schemes, BMJ produces almost consistently the largest amounts of convective precipitation. The mean convective fraction over the whole domain of the individual ensemble members varies between 24 and 63 %, with consistently lower values for ACM2 configurations and higher values for BMJ and YSU configurations.

Figure 6b illustrates more clearly the sensitivity of precipitation amounts with respect to each parameterization type. Each box consists of the nine precipitation spreads between ensemble members for which only the indicated parameterization type is rotated. For example, one of the nine spreads for CU is computed between (KF_LIN_YSU, GF_LIN_YSU, BMJ_LIN_YSU), another between (KF_TH_MYJ, GF_TH_MYJ, BMJ_TH_MYJ) and so forth. For non-convective precipitation, CU and PBL schemes show an average spread of about 20 mm month⁻¹ compared to ~60 mm month⁻¹ for MP, which indicates only minor influence. The average spread in convective precipitation is larger for configurations that differ in their PBL scheme than for those that differ in their CU scheme. However, the large inter-quartile spread of both illustrates their non-linear interplay for the production of convective rainfall. Here, the MP scheme is of minor importance. The sensitivity of total precipitation amounts to the MP and PBL choice is almost equal with average spreads of 67 ± 13 mm month⁻¹ and 62 ± 11 mm month⁻¹, respectively. The importance of the CU schemes is reduced and highly variable with a spread of 31 ± 21 mm month⁻¹.

Fig. 6

a Scatterplot of non-convective precipitation over convective precipitation for JAS 1999 over the whole study region for all ensemble members. b Boxplots of spreads (max–min) of each parameterization type for total precipitation (left), convective precipitation (middle) and non-convective precipitation (right). Each box consists of the nine spreads derived from the three members that differ in one parameterization scheme only (see text). ENS indicates the total ensemble spread for the respective precipitation fraction (mm month⁻¹)

However, their impact becomes stronger on finer temporal scales: KF and GF have difficulties to reproduce the amplitude of the diurnal cycle (Fig. 7a), which results in a large overestimation of precipitation in the morning hours. BMJ produces the convective peak about 3 h too early, but is close to the amplitude of TRMM, especially in combination with the YSU PBL scheme. However, the phase of the diurnal cycle is somewhat better captured by GF and KF with the convective peak at 18 h for most configurations (Fig. 7b). Nikulin et al. (2012) report a shift of the phase of the diurnal cycle for almost all models in an ensemble of CORDEX-Africa regional climate simulations that includes the WRF model. They relate this deficiency to the formulation of the cumulus parameterizations. In accordance to our findings, their WRF-KF configuration captures the phase of the diurnal cycle reasonably well, but with a stronger amplitude. Figure 7b confirms that differences in phase and amplitude mainly arise from the convective precipitation fraction (CU scheme). Non-convective precipitation amounts mostly show a uniform phase and the amplitude is closely related to the respective CU scheme activity. BMJ is almost inactive during night hours, as was also found by Pohl et al. (2014), leading to an underestimation of precipitation compared to TRMM. According to Marsham et al. (2013) and further experiments that we conducted at convection-allowing scales (12–4 km, not shown), the explicit treatment of convection greatly improves the representation of the diurnal cycle and removes the phase shift.

Fig. 7

Average diurnal cycle of JAS precipitation over the whole study region for CU and PBL parameterization groups and for TRMM (left) for total precipitation and (right) for convective and non-convective precipitation. Parameterization groups comprise of configurations that differ in the MP scheme but use the same CU and PBL scheme

Parameterization influences on large-scale dynamics

The WAM precipitation is strongly tied to the characteristics of several dynamical ingredients (see Nicholson 2013 for a comprehensive summary). The differences between the parameterization groups in rainfall raise the question whether these can be related to changes in the dynamics and whether these changes correspond to mechanisms known to cause inter-annual monsoon variability.

Figure 8 shows a cross section of the zonal wind for August 1999 for ERA-I, ENS and the parameterization groups. All groups show the major components of the West African monsoon such as the mid-tropospheric African Easterly Jet (AEJ, ~600 hPa), the high-level Tropical Easterly Jet (TEJ, ~200 hPa) and the near-surface south-westerly monsoon winds, but with clear differences in velocity and position. The degree to which WRF alters these features in comparison to ERA-I illustrates how regional processes can affect large-scale features. In this section, we concentrate on August only, since it contributes most to the inter-annual variability in precipitation (Dennett et al. 1985) and marks the maximum of the northward movement of the monsoon rainband over the continent.

Fig. 8

August 1999 cross section of zonal wind for ERA-I, the WRF ensemble mean (ENS) and the parameterization groups

The south-westerly monsoon wind

WRF captures the unusually thick monsoon layer that reaches up to over 750 hPa, but generally over-predicts the westerly winds with up to 6–8 m s⁻¹, compared to 3 m s⁻¹ for ERA-I. The overestimation in WRF is due to a deeper SHL by approximately 2 hPa, connected to higher near-surface temperatures north of 15°N (Fig. 9a, b) and a resulting stronger land-sea surface pressure gradient. In Fig. 10, we compare the monsoon wind velocity of the 27 ensemble members as a function of sea-level pressure (SLP) difference between the sea and two different regions on the continent. We find no correlation between the monsoon wind velocities and the land-sea SLP difference for the region north of 15°N where the SHL is positioned and where little to no rainfall occurs (Fig. 10a), but a clear correlation for the the moist region south of 15°N (Fig. 10b), r² = 0.63, p ≤ 0.01). This denotes that moist processes are causing the intra-ensemble spread in monsoon wind strength.

Fig. 9

a August 1999 average near-surface temperature and superimposed mean sea level pressure (hPa) for GHCN, ERA-I, the WRF ensemble mean (ENS), b the temperature bias of ERA-I and ENS against GHCN and c temperature gradients (ΔT) over the continent for GHCN, ERA-I, ENS and the parameterization groups. All data is interpolated on the ERA-I grid with ΔT computed over ~150 km (three ERA-I grid cells)

Fig. 10

Scatterplots of August 1999 average monsoon wind velocity at 850 hPa (positive meridional wind) versus a the mean sea level pressure difference (ΔSLP) between the sea (Atlantic cold tongue: 10°W–10°E; 5°S–0°N) and the region of the SHL (10°W–10°E, 15°N–25°N), b the ΔSLP between the sea and the region of continental monsoon rainfall (10°W–10°E; 4°N–15°N), c the maximum wind velocities at 250 hPa between 4 and 15°N representing the TEJ, d the same as c, but for each parameterization group with error bars indicating the standard deviation, e the latitudinal position of the AEJ for all ensemble members and ERA-I, f the same as e, but for each parameterization group with error bars indicating the standard deviation. The latitudinal position of the AEJ is defined as the first occurrence of the zonal wind velocity surpassing 10 m s⁻¹ between 650 and 550 hPa

The tropical easterly jet

Configurations with stronger monsoon winds tend to have a stronger core of the TEJ. For ERA-I, the maximum winds in the core exceed 20 m s⁻¹ at 200 hPa. The ensemble spread ranges from 20 m s⁻¹ for configurations using ACM2 to extensive cores with maximum winds exceeding 24 m s⁻¹ for MYJ (Fig. 8). While not yet fully understood, the intensity and inter-annual variability of the TEJ is usually related to non-local phenomena: the strength of the Indian summer monsoon (Flaounas et al. 2011b), the El Niño/Southern Oscillation (Chen and van Loon 1987), the intensity of the extratropical Southern Hemisphere westerlies (Dezfuli and Nicholson 2013), and latitudinal temperature gradients (Nicholson 2008). The impact of the TEJ on the WAM is mainly thought to be a causal one. The existence of the TEJ is linked to the Asian monsoon outflow and enhances the meridional Hadley-type overturning between sea and land by upper-level divergence over the West African continent. This divergence promotes vertical uplift and rainfall. Figure 10c illustrates that the strength of the westerly monsoon winds and the velocity of the TEJ are indeed correlated with r² = 0.72 (p ≤ 0.01). Since non-local effects are prescribed by ERA-I at the domain boundary, this suggests that the intensity of the TEJ can also be modified by local processes. These processes change the monsoon flow and thus the moisture supply that feeds the TEJ via latent heating, which, in turn, can further intensify the monsoon winds. Figure 10d summarizes the information by parameterization group. It demonstrates that the different schemes can be classified according to the strength of the TEJ (weaker < stronger):

$$\begin{gathered} {\text{BMJ }} < {\text{ KF }} < {\text{ GF}} \hfill \\ {\text{WSM3 }} < {\text{ LIN }} < {\text{ TH}} \hfill \\ {\text{ACM}}2 \, < {\text{ YSU }} < {\text{ MYJ}} \hfill \\ \end{gathered}$$

Schemes like TH (WSM3) that favor (dampen) deep vertical motion and trigger rapid (slow) precipitation are reinforcing (weakening) the TEJ because of efficient (inefficient) moisture transport and recycling. The vertical velocities in Fig. 11 correspond well to this ranking. Vertical motion between the axes of the TEJ and AEJ (contours) connects the upper troposphere with the lower troposphere and completes the meridional circulation which promotes rainfall. Consequently, the above ranking is in good agreement with the classification of a scheme as dry or wet (cf. Figure 4). These correlations denote the strength of the moist meridional overturning as the main factor for the variability of the ensemble members in monsoon strength, and explain the governing role of the resulting SLP south of 15°N (Fig. 10b). This is consistent with the findings of Sultan and Janicot (2003), who suggest an increased importance of the Hadley-type meridional circulation and deep convection for the prevailing atmospheric circulation as soon as the monsoon is established.

Fig. 11

August 1999 cross section of vertical wind for ERA-I, the WRF ensemble mean (ENS) and the parameterization groups. Contours indicate u-wind (m s⁻¹) and depict the position of the AEJ and TEJ

The African easterly jet

The mid-level AEJ is located at about 600 hPa for ERA-I and for the WRF simulations (Fig. 8). GF, KF and ACM2 are not able to capture the core wind speed, which exceeds 12 m s⁻¹. This jet develops to adjust for thermal wind balance and as such moves with the position of the maximum surface temperature gradient between the monsoon rainband and the periphery of the SHL. This gradient is caused by the different thermal properties of moist/vegetated and desert land surface (Cook 1999). According to Nicholson (2009), the position of the AEJ is typically far to the south (north) for dry (wet) years when the monsoon is weak (strong). The dry and wet ensemble members of the WRF ensemble follow the same pattern: There is a significant correlation (r² = 0.82, p ≤ 0.01) between the maximum strength of the monsoon winds and the position of the AEJ in Fig. 10e.

The classification by scheme in Fig. 10f reveals the same order as for the velocity of the TEJ. Schemes which favor extreme southward or northward displacements of the AEJ tend to dictate the strength of the monsoon flow, independent of the configuration partners, as indicated by the standard deviation of their respective parameterization group. Moderate schemes show a larger standard deviation and can be pushed to either side.

The impact of a parameterization scheme on the position of the AEJ comes from the displacement of the temperature gradient maximum, which is modified by the strength of the moisture advection from the ocean. The AEJ positions shown in Fig. 9c (depicted as points) correspond well to the regions of maximum temperature gradients for the member groups and ENS. The temperature gradient maximum seems to be shifted northward for ERA-I and is not in agreement with the AEJ position, which corresponds better to GHCN. In accordance to the dry bias in the Sahel (cf. Fig. 4), WRF generally exhibits a southward shift of the maximum temperature gradient compared to GHCN. Furthermore, parameterizations that show a weaker monsoon flow (ACM2, WSM3, BMJ) tend to have larger temperature gradients further to the South and correspondingly show the AEJ and the monsoon rainband further to the South, too. This is especially pronounced for the PBL group with clearly shifted temperature gradient maxima in accordance to their monsoon regime. Our findings are in agreement with Cornforth et al. (2009), who found that moist processes contribute to the meridional extent and intensity of the temperature gradient. We conclude that the position of the AEJ is a result of the northernmost extent of the rainband as described by Cook (1999), who attributes the maintenance of the jet to the negative meridional soil moisture gradient and the associated hydrodynamical response of the atmosphere. In her GCM experiments, the development of the AEJ was suppressed when a uniform soil moisture, corresponding to savanna conditions, was prescribed over the whole continent.

The AEJ plays a crucial role for the rainfall production by triggering atmospheric disturbances at its southern and northern border, so-called African Easterly Waves (AEWs). Especially along their southern track around 10°N, AEWs interact with convective processes and are amplified by them (Berry and Thorncroft 2012). At the same time they foster convective initiation and are thus strongly associated with the formation and the life cycle of mesoscale convective systems (MCS) (Fink and Reiner 2003; Sultan and Janicot 2000). Current theory relates the formation of such atmospheric disturbances in the vicinity of the AEJ to a barotropic-baroclinic energy conversion process (Cornforth et al. 2009, Hagos and Cook 2007). Therefore, wet years usually show a weaker AEJ, since more precipitation is related to a stronger wave activity, while dry years usually show a stronger AEJ (Grist and Nicholson 2001). Our WRF ensemble members do not display such a relationship between the strength of the AEJ (cf. Fig. 8) and the AEW activity, represented by the 3–5 days bandpass filtered variance of the meridional wind vector in Fig. 12. For example, LIN and KF show comparable wave activity, but KF has a weaker jet. This suggests that other factors that were found to maintain the AEJ might influence the modeled AEJ such as the surface temperature gradient in the vicinity of the jet and the (parameterized) atmospheric turbulence transporting the gradient into the atmosphere (e.g. Cook 1999). However, there is a correlation (r² = 0.69, p ≤ 0.01, not shown) between the wave activity and the vertical velocities in the region of strong convective activity at 10–15°N (cf. Fig. 11). This is in line with Hsieh and Cook (2005), who found the AEW activity to be more closely related to instabilities induced by convection in the area of vertical motion, than to shear instabilities caused by the AEJ.

Fig. 12

August 1999 mean standard deviation of the 3- to 5-day bandpass-filtered 600 hPa meridional wind (top) for ERA-I and the WRF ensemble mean (ENS) and (bottom) the difference between the parameterization groups and ENS

ERA-I exhibits two distinct tracks of AEW at ~20°N and at the Guinea Coast, with a maximum in the west of West Africa. Our WRF ensemble members show a different pattern: The main wave activity follows a single track and originates in the area of maximum rainfall in the eastern Sudano-Sahel. In comparison to ERA-I, the AEWs are overestimated over the Sahel and Sudano-Sahel by parameterizations that over-predict rainfall in the monsoon rainband with respect to TRMM (cf. Fig. 4). Sylla et al. (2013) also reported stronger AEW activity over the Sahel for several RCMs in comparison to ERA-I and attribute this to the internal representation of convection in the RCMs. Therefore, the different wave patterns we see for WRF with respect to ERA-I could be related to a minor importance of the energy transfer between AEJ and AEWs and a higher sensitivity to vertical velocities and associated convective processes.

Discussion

Our results show that the examined parameterizations can be classified according to their impact on the modeled WAM regime. While the quantitative skill of a certain scheme in comparison to observations might change under different conditions (e.g. time period, driving data, domain size, chosen evaluation criteria), their individual qualitative impact on monsoon dynamics is assumed to be more universal. For overlapping analyses, the model internal tendency to produce more/ less precipitation or to enhance/ weaken the dynamic features with certain parameterizations are in agreement with Flaounas et al. (2011b), which gives us confidence in their robustness.

Microphysics schemes

Our ranking for the MP schemes is in line with the findings of Hong and Lim (2006), who found that the amount of precipitation is correlated with the complexity of the microphysics scheme. While they suggested that at resolutions of about 25 km, a simple ice-scheme should be sufficient to resolve the mesoscale features, we find that the representation of cloud processes has a strong impact and that the simple 3-class scheme WSM3 consistently leads to drier conditions in the model. During the monsoon season essentially all rainfall is associated with deep convection for which ice processes play a major role in the generation of precipitation. LIN and TH separately include cloud ice, snow and graupel, and TH additionally predicts the number concentration for cloud ice. For these two schemes, cloud particles may penetrate deeper above freezing level. According to Hong and Lim (2006), the conversion from clouds to rain is more efficient at producing precipitation than the ice phase alone in the case of WSM3. Furthermore, Hong et al. (2004) found that the interaction between ice clouds and long-wave radiation has a strong impact on the amount of precipitation because of enhanced radiative heating. In their case, precipitation was decreased with more cloud ice and vice versa.

Different from other WRF sensitivity studies that included microphysics schemes in other regions (e.g. Pohl et al. 2011; Crétat et al. 2012; Evans et al. 2012) we found a major importance of the chosen MP scheme for simulated precipitation amounts. For ENS, non-convective precipitation contributes around 40 % during the pre-monsoon phase and up to 60 % after the monsoon onset in July. During the WAM, MCS contribute most to the precipitation and the fraction of stratiform rainfall increases (Schumacher and Houze 2006), which WRF is able to partly resolve explicitly. This is confirmed by Marsham et al. (2013), who compare two model simulations at 12 km horizontal resolution with explicit and parameterized convection during the WAM. Because of the large fraction of organized convection, they report a better performance of the explicit simulation and relate their findings to a better representation of the diurnal cycle and the associated monsoon dynamics. Our results illustrate that even at a medium horizontal resolution (24 km), the impact of different MP formulations is non-negligible in this region and we expect it to increase with increasing horizontal model resolution.

Planetary boundary layer schemes

With respect to the PBL schemes analyzed here, our results may seem to be counterintuitive. Several studies (e.g. Hu et al. 2010; Shin and Hong 2011; Xie et al. 2012) suggest that the mixing rates and surface drag are highest for ACM2 and lowest for MYJ. Enhanced mixing and the associated improved transport of surface fluxes into the atmosphere should lead to a stronger monsoon and inversely. However, we find that this is not the case and that the local, weak mixing in MYJ produces the strongest monsoon winds. Figure 13 reveals that the strong impact of the PBL scheme is due to their influence on the incoming short-wave radiation at the surface, which is lower for ACM2 than for MYJ at the Guinea Coast and in the Sudano-Sahel. At the 700-500 hPa levels, ACM2 produces more mid-level clouds, which reflect the incident short-wave radiation (Fig. 14a). Meanwhile, MYJ produces less low- and mid-level clouds than ACM2 which consequently leads to larger solar irradiation and higher near-surface temperatures (cf. Figure 9). The differences of the vertical moisture profiles of the three PBL schemes in Fig. 14b indeed show very dry conditions for MYJ in the lower troposphere. The moist conditions in the mid-troposphere for ACM2 lead to a rapid saturation of the atmosphere and consequently to a build-up of clouds by the MP scheme. With MYJ and YSU, more moisture is transported into the higher levels above 400 hPa. This is presumably due to the different promotion of convective processes (CU scheme activity) by the PBL schemes, as described in Sect. 3.4. The strong mixing in ACM2 seems to generate unfavorable conditions for releasing instabilities by the CU schemes. ACM2 therefore lacks the efficient drying of the atmosphere through deep convective processes and the associated strong precipitation events, which in turn leads to an excess of moisture in the planetary boundary layer.

Fig. 13

August 1999 incoming short-wave radiation at the surface a for ERA-I, the WRF ensemble mean (ENS) and b the difference between the parameterization groups and ENS

Fig. 14

August 1999 average vertical profile for the region of monsoon rainfall (10°W–10°E, 4°N–15°N) for the PBL groups of a cloud fraction, b water vapor difference

This ultimately attributes the largest spread in monsoon dynamics between the ensemble members to modifications of the incoming radiation, caused by the vertical moisture distribution in the PBL scheme. This is an important result, since the focus often remains on the energy transport via latent heat as main source of monsoon variability. This raises the question whether the inter-annual variation in cloudiness, and especially the amount and prevalence of low-level clouds, are key parameters for the surface energy budget and thus for the monsoon variability, as discussed by Knippertz et al. (2011). Cloud-radiation interactions remain one of the least understood processes and, together with the representation of clouds, are highly difficult to parameterize in atmospheric models with potentially devastating impact on the validity of modeled monsoon dynamics.

Cumulus schemes

The effects of the cumulus parameterizations are difficult to interpret since they are the result of a complex interplay of processes as illustrated in Fig. 6b. This applies especially to the ensemble approach of GF. However, the dampening effect for precipitation and monsoon dynamics of BMJ could be related to it being a sounding adjusting scheme, which will transform any atmospheric profile it starts from into a plausible, but pre-determined post-convection sounding. This might eliminate special and extreme characteristics of the vertical atmospheric structure.

Representation of monsoon dynamics

Our simulations reproduce the dependency of TEJ velocity and AEJ position on the strength of moisture advection from the Atlantic Ocean (westerly monsoon winds) as reported from studies that investigate the different dynamics of wet or dry years (e.g. Sultan and Janicot 2003; Grist and Nicholson 2001; Nicholson and Webster 2008). A drier (wetter) monsoon in the Sahel is often related to a weaker (stronger) TEJ and a southward (northward) displacement of the AEJ, reproduced here by the dry (wet) ensemble members. The identified correlations between these dynamical components are of comparable magnitude as in reanalysis studies. For example, Nicholson and Webster (2008) and Nicholson (2009) use NCEP Reanalysis data for a climatological analysis of the relationship between monsoon wind velocity and sea-level pressure gradient (r² = 0.84), and between the monsoon wind velocity and Sahel rainfall (r² = 0.75), respectively. Since the Sahel rainfall depends on the position of the AEJ, this also implicitly describes the relationship of the monsoon winds and the AEJ position. Table 2 further evaluates this picture, showing GPCC August precipitation in the Sahel of dry and wet year composites from 1979–2010, and related ERA-I dynamics in comparison to the driest and wettest WRF ensemble member for 1999. The maximum precipitation is strongly overestimated by WRF, indicating an artificial origin. Although all WRF ensemble members use the same “wet year forcing”, their spread in the AEJ position and TEJ velocity is comparable to the mean inter-annual range (but with larger absolute values).

Table 2 Comparison of the observed range of a wet/dry year composite for August 1979–2010 for precipitation in the Sahel (Fig. 1), TEJ velocity and latitudinal AEJ position (as in Fig. 10) with the wet/dry WRF ensemble members in 1999

However, compared to ERA-I, stronger monsoon winds and thus an increased moisture supply from the ocean is necessary to reach the same TEJ velocity and AEJ position in WRF. Configurations that show comparable monsoon flows to ERA-I suffer from an equator-ward displaced AEJ (maximum temperature gradient) and from overall dry conditions. The two main sources for moisture during the WAM are the south-westerly monsoon flow and local moisture recycling (Gong and Eltahir 1996; Levermann et al. 2009; Thorncroft et al. 2011). The latter process contributes about 30 % to the precipitation over the West African continent. However, the evaporative fraction (EF) presented in Fig. 15 is much lower for the WRF ensemble than for ERA-I and for NCEP/ NCAR reanalysis data (Levermann et al. 2009). For both reanalysis datasets, the EF in August reaches about 70–90 % south of 15°N, where the rainband passed or still resides. For WRF, the EF only reaches about 60–80 % over a considerable smaller area. Even though the surface fluxes in the reanalysis data sets might be less reliable, this illustrates that local evaporation contributes less to the atmospheric moisture in WRF. This could partly explain the need for stronger monsoon winds as source of moisture to achieve comparable monsoon dynamics.

Fig. 15

August 1999 mean evaporative fraction (EF) for ERA-I and the WRF ensemble mean (ENS). EF is the ratio of the latent heat flux to the sum of latent and sensible heat fluxes

This discrepancy in latent heat flux questions the correct representation of soil moisture, surface runoff and water conservation in the WRF model. As pointed out by several authors (e.g., Sylla et al. 2011; Taylor 2008; Steiner et al. 2009), this potentially has implications on convection and could be one reason for the persistent coastal dry bias. Potential improvements of WAM simulations through the implementation of high-resolution surface information and through coupled hydrological models are a current topic of discussion and should be considered as next steps.

Summary and conclusions

In this study, we employ a WRF physics ensemble to investigate the impact of parameterizations on the West African monsoon (WAM) for the rainy season 1999. We use ERA-Interim as forcing data and focus on parameterization schemes that affect the moisture distribution. Three different cumulus (CU), microphysics (MP) and planetary boundary layer (PBL) parameterizations are combined, resulting in an ensemble of twenty-seven members (cf. Table 1). The ensemble reveals strong parameterization related uncertainties but at the same time provides information on the sensitivity of the WAM system to the local dynamics and hence to the parameterization of the sub-grid processes. We analyze the effects of each parameterization group on precipitation and the representation of dynamical WAM features (monsoon wind, Tropical Easterly Jet, African Easterly Jet) and rank the parameterization schemes accordingly.

We find that the MP and PBL schemes introduce the largest spread in total precipitation over the study region. For the ensemble mean, non-convective precipitation generated by the MP schemes contributes 50–60 % of the total rainfall during the WAM, when mesoscale convective systems prevail. Larger amounts of precipitation are associated with more complex MP schemes, which alter atmospheric dynamics by the release of latent heat. Furthermore, we identify a strong influence of the choice of the PBL scheme on the position of the rainband, especially when comparing ACM2 (southward shift) and MYJ (northward shift). This is due to a larger (smaller) fraction of low- and mid-level clouds for ACM2 (MYJ) that weakens (strengthens) the monsoon because of less (more) incoming solar radiation. The choice of the CU scheme has minor influence on the total amount of precipitation over the study region, but alters the spatial distribution and thus the width of the rainband and the location of intense rainfall events. Moreover, the CU schemes have a strong impact on the representation of the diurnal cycle. We detect a complex and non-linear interaction between the CU and PBL schemes with respect to generating convective precipitation.

Ultimately, the inter-member differences in the strength of the monsoon wind and in the northward transition of the rainband are traced back to the enhancement or weakening of the moist Hadley-type meridional circulation that connects the monsoon winds to the Tropical Easterly Jet. This leads to the following ranking of the parameterization schemes (weak < enhanced):

$$\begin{gathered} {\text{CU: BMJ < KF < GF}} \hfill \\ {\text{MP: WSM3 < LIN < TH}} \hfill \\ {\text{PBL: ACM2 < YSU < MYJ}} \hfill \\ \end{gathered}$$

The produced rainfall amounts are accordingly except that KF (YSU) produces slightly more total precipitation than GF (MYJ) because of respective promotion of convective precipitation, that is not linearly related to the intensity of the dynamics.

The differences between the ensemble members illustrate that the WRF model captures the characteristic interdependencies of monsoon dynamics and rainfall that were also found for years with differing monsoon regime. The spread of the ensemble in Sahel precipitation and associated dynamics during August 1999 is comparable to the observed inter-annual spread (1979–2010) in August between dry and wet years in spite of the same boundary forcing.

Our findings emphasize the strong potential impact of regional moist processes on the monsoon dynamics. They also underline the need for a careful selection of model parameterizations and justify the frequent ensemble applications in that region.