1 Introduction

The response of the climate to greenhouse gas (GHG) forcing is not uniform in space and time but instead exhibits considerable structure in both the spatial patterns and timing of the anthropogenically induced temperature signal. Figure 1 (top), for example, shows the ensemble-average surface temperature change from fifteen models participating in the Coupled Model Intercomparison Project phase 5 (CMIP5; Taylor et al. 2012), 100 years after an abrupt \(\hbox {CO}_{2}\) quadrupling. We see that the northern hemisphere (NH) has warmed up more than the southern hemisphere (SH), the Arctic more than the Antarctic, and there are interesting spatial patterns with North Atlantic warming considerably less than at similar latitudes elsewhere.

Fig. 1
figure 1

Ensemble-average ocean temperature change after \(100\,\hbox {years}\) from 15 CMIP5 models under a quadrupling of \(\hbox {CO}_{2}\): (top) at the sea surface (bottom) in the zonal-average (contoured every degree K). Note the expanded scale in the top 1,500 m. The 15 CMIP5 models used here are: ACCESS1-0, bcc_csm1-1, CanESM2, CCSM4, CSIRO-Mk3-6-0, GFDL-CM3, GFDL-ESM2G, GFDL-ESM2M, GISS-E2-R, IPSL-CM5A-LR, IPSL-CM5B-LR, MIROC5, MPI-ESM-LR, MRI-CGCM3, and NorESM1-M

Full size image

In this study we contribute to the discussion of what sets the patterns and timescale of the transient response of the coupled system to anthropogenically forced climate change, a subject of great importance and interest. We put forward a methodology that focuses specifically on the ocean’s role in setting these patterns and enables us to study competing processes one at a time and in isolation from one-another and from other effects.

It has been argued that the delayed surface warming and sea ice expansion around Antarctica is the result of deep ocean heat uptake, possibly driven by changes in upper ocean stratification (Russell and Rind 1999; Gregory 2000; Zhang 2007; Kirkman and Bitz 2011; Liu and Curry 2010; Bintanja et al. 2013). In contrast, the warming delay in the North Atlantic is often attributed to a weakening of the Atlantic Meridional Overturning Circulation (AMOC) in a warming climate, resulting in a cooling tendency (Russell and Rind 1999; Wood et al. 1999; Weaver et al. 2007; Xie and Vallis 2011; Kim and An 2013; Drijfhout et al. 2012; Rugenstein et al. 2013; Winton et al. 2013). The mechanisms behind Arctic amplification are vigorously debated in the literature and involve a complex interplay of local climate feedbacks and atmospheric and oceanic heat transport (e.g., Holland and Bitz 2003; Serreze and Barry 2011; Hwang et al. 2011; Mahlstein and Knutti 2011; Kay et al. 2012). Our study helps to clarify some of these questions. In particular we find that delayed warming around Antarctica is likely not attributable to local anomalous ocean heat uptake and storage, changes in the strength of the AMOC are a major contributor to delayed warming in the Atlantic sector, and poleward advection of anthropogenic temperature across the Arctic circle may play an important role in Arctic amplification.

In Sect. 2 we present a strategy that involves integration of an ocean-only model in which the anthropogenic temperature signal is forced from the surface by anomalous GHG-induced air–sea heat fluxes and damped at a rate controlled by a ‘climate feedback’ parameter. For simplicity, the GHG-induced surface forcing is prescribed to be geographically uniform, and the climate feedback parameter is held constant in time and space. Moreover, the prescribed annual cycles of surface winds and freshwater forcing are held steady in time, thus isolating the role of the anthropogenic temperature in the surface buoyancy budgetFootnote 1. With these simplifications, we can be sure that any observed structure and timing of the temperature response is wholly attributable to the effects of ocean circulation. In Sect. 3 we study the form of the resulting ‘climate response functions’ (Hansen et al. 2011), both globally and regionally, and the patterns and timing of the SST response. We observe a broad correspondence between the evolution of the anthropogenic temperature signal in our simplified ocean-only model and that of the fully coupled system (Fig. 1), suggesting that many of the mechanisms at work in fully coupled models are captured by our idealized system. In Sect. 4 we discuss the extent to which anthropogenic temperature can be considered to be a ‘passive tracer’, sourced at the ocean surface by downwelling energy fluxes and weakly damped to space at a rate controlled by the ‘climate feedbacks’. In Sect. 5 we conclude with a discussion.

2 Studying climate perturbations in an ‘ocean-only’ model

We begin by spinning an ocean model up to equilibrium (the MITgcm, Marshall et al. 1997a, b) configured with realistic topography at \(1^{\circ }\) resolution with 50 vertical levels, and forced with analyzed fields in a perpetual year. A hybrid latitude-longitude and cubed sphere configuration is used as described in Forget (2013). The eddy diffusivity parameter is set equal to a constant \(850\,\hbox {m}^{2}\,\hbox {s}^{-1}\) and the background diapycnal mixing to \(10^{-5}\,\hbox {m}^{2}\,\hbox {s}^{-1}\). The equilibrium solution is then perturbed with anomalous down-welling flux imagined to come from an atmosphere subject to GHG forcing. Climate feedbacks are parameterized through a damping of sea-surface temperature (SST) at a rate chosen to mimic the global, top-of-the-atmosphere radiative response to surface temperature changes as found in coupled atmosphere-ocean general circulation models. We test the approach by computing ‘climate response functions’ and spatial patterns of warming and comparing them with those from coupled models.

We write the thermodynamic equation for the ocean thus:

$$\begin{aligned} \frac{D_{res}}{Dt}T=Q(\mathcal {H)}+R \end{aligned}$$

where \(\frac{D_{res}}{Dt}\) is advection by the residual-mean circulation, \(R\) (for Redi 1982) is the mixing of temperature (\(T\)) by mesoscale eddies along neutral density surfaces and

$$\begin{aligned} Q(\mathcal {H)}=\frac{1}{\rho c_{w}}\frac{\partial \mathcal {H}}{\partial z} \end{aligned}$$

is the forcing expressed as the vertical divergence of the vertical (\(z\)) heat flux, \(\mathcal {H}\) (in \(\hbox {W}\hbox {m}^{-2}\)), due to small-scale processes, \(\rho\) is the density and \(c_{w}\) the specific heat of water. The air–sea heat flux, \(\mathcal {H}\), is expressed in terms of the air–sea temperature and specific humidity difference and wind speed through bulk formulae. A repeating annual cycle of forcing is used in which \(\mathcal {H}\) is computed every hour using analyzed meteorological fields. To simulate a warming world we modify \(\mathcal {H}\) to represent the perturbed downwelling energy flux associated with GHG forcing.

In detail, our procedure is as follows:

  1. 1.

    Integrate the ocean model out toward equilibrium starting from a climatological ocean state of temperature and salinity, here chosen to be that given by the World Ocean Atlas due to Steele et al. (2001) which includes an Arctic analysis. The CORE1 protocol set out in Griffies et al. (2009) is used. The sea surface salinity is restored on a timescale of 250 days. After 300 years of integration the air–sea fluxes computed from bulk formulae and the SST fields of the control integration are stored as diagnosed ‘data’—we will call them \(\mathcal {H}_{c}\) and \(SST_{c}\) where the subscript ‘c’ is for control. These data are calculated as daily means over a 10-year integration period. It should be noted that fluxes are also diagnosed under the prognostic sea ice model (i.e., at the top of the liquid ocean) and that the seasonal cycle of sea ice is not allowed to change during the subsequent integration even with perturbed forcing. This avoids likely nonlinearities inherent in the vanishing of sea ice.

  2. 2.

    Starting from the equilibrium state at the end of step 1, we carry out the following integration:

    $$\begin{aligned} \frac{D_{res}T}{Dt}=Q\left( \mathcal {H}_{c}\right) +R. \end{aligned}$$
    (1)

    This is our control state: \(T\longrightarrow T_{c}\) and \(SST\longrightarrow SST_{c}\). Note that Eq. (1) does not directly involve the use of bulk formulae since \(\mathcal {H}_{c}\) is read in as data.

  3. 3.

    Again, starting from the equilibrium state, we introduce an instantaneous perturbation to the stored air–sea fluxes in a manner that represents GHG warming thus:

    $$\begin{aligned} \mathcal {H\longrightarrow H}_{c}+\mathcal {H}_{anthro}, \end{aligned}$$

    where \(\mathcal {H}_{anthro}\) is a prescribed downwelling flux. This results in a perturbation, \(T_{anthro}\), of the ocean’s temperature field:

    $$\begin{aligned} T&\longrightarrow T_{c}+T_{anthro} \\ SST&\longrightarrow SST_{c}+SST_{anthro}. \end{aligned}$$

    The temperature field evolves according to

    $$\frac{D_{res}}{Dt}\left( T_{c}+T_{anthro}\right) =Q\left( \mathcal {H}_{c}+ \mathcal {H}_{anthro}\right) -\gamma \left( SST-SST_{c}\right) +R\left( T_{c}+T_{anthro}\right).$$
    (2)

    Here \(\gamma\) is a prescribed parameter which damps \(SST_{anthro}\) at a rate chosen to be proportional to the global radiative feedback within coupled models. This can be seen by writing

    $$\begin{aligned} \gamma =\frac{\lambda }{\rho c_{w}h} \end{aligned}$$

    where \(h\) is the depth over which \(\mathcal {H}\) decays to zero—i.e. the mixed layer depth. We see that \(\lambda\) has units of \(\hbox {W}\hbox {m}^{-2}\,\hbox {K}^{-1}\) and so can be interpreted as a climate feedback parameter.

In the calculations described here we choose \(\mathcal {H}_{anthro}\) and \(\lambda\) to be spatially-uniform over the ocean and constant in time, crudely mimicking enhanced downwelling radiation due to GHG forcing and the large-scale radiative damping of resulting \(SST\) anomalies to space. Over ice we set \(\mathcal {H}_{anthro}=0\). Any patterns in \(T_{anthro}\) that emerge must be a consequence of ocean dynamics and not other (e.g. coupled) processes. Moreover, we will choose parameters so that \(T_{anthro}\) can be thought of as mimicking the evolution of the temperature perturbation due to anthropogenic GHG forcing in coupled climate models.

If we set \(\lambda =1\,\hbox {Wm}^{-2}\,\hbox {K}^{-1}\), typical of the net global radiative feedback found in coupled models (e.g., Bony et al 2006; Andrews et al. 2012) and in observations (e.g. Murphy et al. 2009), then a damping timescale of \(SST_{anthro}\) is implied of \(\frac{\rho c_{w}h}{\lambda }\, \simeq 460\) days if \(h\) is \(10\,\hbox {m}\), the depth of the upper layer of the model. Note that damping timescales yielded by bulk formulae (which typically lead to damping rates of order 10 to \(20\,\hbox {Wm}^{-2}\, \hbox {K}^{-1}\) associated with large-scale SST anomalies—see Marotzke and Pierce 1997) are some 10–20 times shorter than this, a month or so rather than a year or so.

Before going on it should be stated clearly that the approach outlined here is far short of capturing the complexity of the coupled problem. For example, in the true coupled climate system \(\lambda\) is not constant, but instead varies geographically due to Earth’s distinct atmospheric regimes (Armour et al. 2013). Here, however, there is a great conceptual advantage: \(\lambda\) and indeed \(\mathcal {H}_{anthro}\), can be kept constant in space and time. Thus any spatial patterns that we observe in the evolving \(T_{anthro}\) must be controlled by ocean circulation. There is also a considerable computational advantage because Eq. (2) only involves integration of an ocean model forward, rather than the fully coupled system.

3 Transient response to a ‘step-function’ warming perturbation

The control ocean circulation is spun up for a period of 300 years. Key fields from the control simulation are shown in Figs. 2 and 3: SST, sea-ice edge, Atlantic Meridional Overturning Circulation (AMOC) and mixed layer depth. The solution has plausible distributions of these key fields. However, it should be noted that the AMOC is somewhat weak (peaking at 12 Sv) and the mixed layer deepest in the Greenland–Iceland–Norwegian Sea rather than the Labrador Sea.

Fig. 2
figure 2

(Top) annual-mean SST, winter sea-ice extent (white line) and summer sea-ice extent (white shading) (bottom) winter mixed layer depth in m

Full size image
Fig. 3
figure 3

(Top) AMOC after \(100\,\hbox {years}\) in the control solution (in Sv). (Bottom) change in AMOC in the perturbed solution after 100 years, referenced to the control

Full size image

This control solution is then perturbed with a downwelling flux of magnitude \(\mathcal {H}_{anthro}=4\,\hbox {Wm}^{-2}\), approximating the global downwelling longwave radiative forcing from a doubling of atmospheric CO\(_{2}\) (Myhre et al. 1998; Andrews et al. 2012), following the procedure outlined in Sect. 2. The climate feedback parameter is set to \(\lambda =1\,\hbox {Wm}^{-2}\,\hbox {K}^{-1}\). With these parameter values we would expect to have a global-average SST anomaly of \(4\,\hbox {K}\) after a new equilibrium is reached. Let’s see what happens.

3.1 GHG climate response functions

On application of the downwelling radiative flux the ocean warms up—see the time-evolution of the global and regional SST averages shown in Fig. 4. These have the characteristic form of ‘climate response functions’ discussed and reviewed, for example, in Hansen et al. (2011). The global-average response function reaches 80 % or so of its asymptotic value after 100 years, and so is on the faster end of the spectrum of responses discussed in Hansen et al. (2011), but in an acceptable range. Hansen et al. (2011) argue that after 100 years a global-average response of between 60 and 90 % encompasses the real world response, with 90 % considered fast and 60 % slow. These curves can be rather readily fit by analytical Green’s functions obtained from a two-layer model (see, e.g., Geoffroy et al. 2013a, b; Kostov et al. 2014). Their form depends on both \(\lambda\) and the efficiency of ocean heat uptake, as encapsulated in our ocean model. Footnote 2

Fig. 4
figure 4

SST response expressed as a % of the theoretical asymptotic state (here \(4\hbox {K}\)) over a period of \(400\,\hbox {y}\). Each curve corresponds to an average over a large area of the globe–global, NH, SH, NH polewards of \(30^{\circ }\hbox {N}\), SH south of \(30^{\circ }\hbox {S}\), SH between \(50^{\circ }\hbox {S}\) to \(70^{\circ }\hbox {S}\) and tropics defined as between \(30^{\circ }\hbox {S}\) to \(30^{\circ }\hbox {N}\)

Full size image

We immediately note that the regional response is rather different from the global response function. There is delayed warming in the SH relative to the NH—compare, for example, the curve for the NH north of \(30^{\circ }\hbox {N}\) to that from the SH south of \(30{^\circ }\hbox {S}\). Note also that the tropics warms slightly more rapidly than the global-average and that around Antarctica in the \(50{^\circ }\) to \(70{^\circ }\hbox {S}\) band, warming is significantly delayed. We will see below that these separate curves depart significantly from the global-average value of \(4 \hbox {K}\) because of ocean heat transport, being generally lower (by as much as 60 %) in the SH than in the NH.

We note that the magnitude of global sea-surface warming in the ocean-only calculation (Fig. 5, top) depends on the values of the forcing and feedback we have used. The broad agreement in amplitude with the global sea-surface warming of the CMIP5 simulations (Fig. 1, bottom) is largely a coincidence arising from several competing factors: (1) the radiative forcing applied to the ocean-only model (\(4\,\hbox {Wm}^{-2}\)) is smaller than the approximately 6.9 Wm−2 radiative forcing simulated by the ensemble of CMIP5 models under \(4 \times \hbox {CO}_{2}\) (Andrews et al. 2012); (2) the global radiative feedback \(\lambda =1\,\hbox {Wm}^{-2}\,\hbox {K}^{-1}\) chosen for the ocean-only model is slightly smaller (damping more weakly) than the approximately \(1.1\,\hbox {Wm}^{-2}\,\hbox {K}^{-1}\) global radiative feedback found in the ensemble of CMIP5 models (Andrews et al. 2012), and smaller still than the radiative feedbacks over the ocean that tend to damp more strongly than those over the land (Armour et al. 2013); and (3) the efficiency of ocean heat uptake simulated by the ocean-only model is smaller than that of the ensemble of CMIP5 models, as can be seen by the more shallow penetration of heat in Fig. 5 (bottom) than in Fig. 1 (bottom), perhaps due to a somewhat weak and shallow AMOC (Kostov et al. 2014). We thus focus our analysis on the relative patterns of warming that, we argue, are set by ocean dynamics and are largely insensitive to our choice of forcing and feedback.

Fig. 5
figure 5

Temperature perturbation after \(100\,\hbox {years}\) of an ocean-only calculation perturbed by a uniform downwelling flux at the ocean’s surface. (Top) at the sea surface (bottom) in the zonal-average (contoured every degree K)

Full size image

3.2 Regional patterns of warming

Clear evidence of the role of ocean circulation in setting the timing and pattern of warming can be seen in the horizontal SST plots shown after 100 years in Fig. 5 (top) and the zonal-average section Fig. 5 (bottom). This should be compared with Fig. 1 showing the same plots but from an ensemble of CMIP5 models. The striking resemblance between Figs. 5 and 1 demonstrates that, on timescales of decades to centuries, the large-scale structure of warming patterns is largely shaped by ocean circulation and not by atmospheric processes.

The ‘yellow band’ around Antarctica, all the way along and poleward of the Antarctic Circumpolar Current (ACC), clearly shows the influence of the Southern Ocean which is in a distinctly different dynamical regime from the rest of the ocean (see the review by Marshall and Speer 2012 on the Southern Ocean upwelling branch of the global MOC). The SH south of \(30{^\circ }\hbox {S}\) has reached only 60 % of the equilibrium response after 100 years. The NH exhibits a much more rapid rise in SST, reaching 85 % of the equilibrium response after 100 years, with interesting regional variations. The subpolar gyres of the NH (in the Pacific and the Atlantic) have a slightly delayed warming relative to the subtropical gyres.

Figure 5 (bottom) plots the zonal-average perturbation in \(T_{anthro}\) after 100 years to reveal the broad pattern of warming in the meridional plane. The asymmetry between north and south is very apparent with warmth penetrating down in to the interior in the polar regions of the NH, but with little deep accumulation of heat in the SH. Note how we see clear signals of the ‘bowls’ of the subtropical gyres with the surface warmth evidently being pumped and subducted down in to the interior.

The pattern of \(T_{anthro}\) seen in Fig. 5 (bottom) has a marked resemblance to that of the idealized ventilation tracer shown in Fig. 6 whose value is set to unity separately at the ice-free surface (top plot) and below 3.1 km (bottom plot). Note how the bottom tracer is carried upward to the surface around Antarctica. This water has not yet been affected by surface forced climate change yet and will thus ‘quench’ water being warmed at the surface south of \(50{^\circ }\hbox {S}\) or so. North of \(50^{\circ }\hbox {N}\), the reverse is true. Surface waters are evidently being forced down, carrying with them the surface warmth.

Fig. 6
figure 6

Idealized ventilation tracer after \(100\hbox {y}\) whose (top) value at the surface is set to unity (bottom) value below 3,100 m is set to unity

Full size image

3.3 Temperature, air–sea heat fluxes and ocean heat uptake

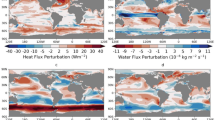
Figure 7 shows the anomalous air–sea heat flux, \(\mathcal {H}_{anthro}-\lambda SST_{anthro}\), after 100 years. Note that there is a dominant flux of energy into the ocean in those regions where the SST rise is delayed—in the Southern Ocean and the northern North Atlantic. The feedback term (plotted at the bottom) largely balances \(\mathcal {H}_{anthro}\) over most of the ocean, but not in the delay regions (see Fig. 5, top) where \(SST_{anthro}\) is far below the value implied at equilibrium: \(\mathcal {H}_{anthro}/\lambda =4\hbox {K}\).

Fig. 7
figure 7

\(\mathcal {H}_{anthro}-\lambda SST_{anthro}\) (in \(\hbox {Wm}^{-2}\)) after 100 years. Red is warming the ocean: blue is cooling the ocean (bottom) contribution from the climate feedback term \(-\lambda SST_{anthro}\). Note that in these experiments the imposed warming is a uniform \(\mathcal {H}_{anthro}=4\,\hbox {Wm}^{-2}\)

Full size image

As a sanity check on the relevance of our calculations to the anthropogenic warming signal in coupled climate models, Fig. 8 shows the (ensemble average) anomalous air–sea heat flux (in \(\hbox {Wm}^{-2}\)) from CMIP5 coupled climate models 100 years after \(\hbox {CO}_{2}\) quadrupling. Patterns which are broadly similar to those in Fig. 7 (top) can be seen with pronounced heating of the ocean in the delay regions. We observe much more structure in the coupled models than in our ocean-only calculation and the magnitudes of the air–sea flux exceed those of our model locally, particularly in high-latitude regions. This is not not unexpected, since we have applied a smaller radiative forcing in our ocean-only calculation than in the CMIP5 models and, importantly, have not accounted for changes in atmospheric heat transport that act to flux more energy poleward under global warming (Hwang et al. 2011). Nonetheless, the broad patterns are consistent with our ocean-only calculations with peaks of air–sea heat flux anomalies into the ocean within the warming delay regions around \(60^{\circ }\hbox {N}\) and \(60^{\circ }\hbox {S}\).

Fig. 8
figure 8

Anomalous air–sea heat flux from an ensemble of 15 CMIP5 experiments after 100 years in \(\hbox {CO}_{2}\) quadrupling experiments

Full size image

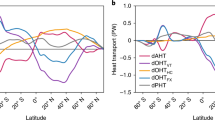
Where does the heat go entering the oceans in the delay regions? Perhaps it is stored at depth. If we assume that anomalous heating in Fig. 9 (top) over the southern ocean between \(50^{\circ }\hbox {S}\) and \(70{^\circ }\hbox {S}\) of order \(4\,\hbox {Wm}^{-2}\) acts for \(100\,\hbox {years}\) and is accumulated in the ocean then we would expect to see \(56\times 10^{22}\,\hbox {J}\) stored there. Instead, integrating under the green curve in the top left panel of Fig. 9, we find only \(8\times 10^{22}\,\hbox {J}\) stored locally, substantially less. This is due in part to reduced surface heat flux driven by a slight surface temperature response in this region. But mainly it is due to an enhanced ocean heat transport (Fig. 9, bottom left)—ocean circulation carries the heat away northward out of the region of delayed warming, rather than storing it locally. If we postulate that the anomalous air–sea flux between \(50{^\circ }\hbox {S}\) and \(70^{\circ }\hbox {S}\) is entirely balanced by anomalous northward heat transport at \(50^{\circ }\hbox {S}\), we require 0.11 PW, only slightly more than is observed in Fig. 9 (bottom, left).

Fig. 9
figure 9

(Left, top) the cumulative heat uptake by the ocean after \(100\hbox {y}\) in our ocean only climate change experiment is plotted in red. The change in ocean heat content after 100 years is plotted in green. (Left, bottom) anomalous meridional heat flux after 100 years (in PW, annual mean). (Right, top) the red and green curves from the top left plot are separated into contributions from changing ocean currents (thin dashed line) and contributions from passive advection of anthropogenic temperature (thick dashed line). (Right, bottom) anomalous heat transport broken in to contributions from changing ocean currents (thin dashed line) and contributions from passive advection of anthropogenic temperature (thick dashed line)

Full size image

Similarly we observe that anomalous meridional ocean heat fluxes carry 0.02 PW more heat out of the North Atlantic (the region between \(40^{\circ }\hbox {N}\) and \(60^{\circ }\hbox {N}\)) than in to it. Consequently the temperature in this region is depressed. This is the ‘warming hole’ seen in coupled models in the subpolar gyre of the North Atlantic (e.g., Drijfhout et al. 2012) and evident in Fig. 1.

The change in the meridional ocean heat flux at \(60^{\circ }\hbox {N}\) is 0.04PW or so and ultimately finds its way up in to the Arctic—see Fig. 5. Some of this heat is stored in the ocean under the north polar cap [see Figs. 5 (bottom), 9 (top, left)] but much of the anomalous poleward flux is lost to the atmosphere. All that is required is a \(1\,\hbox {Wm}^{-2}\) of cooling over the Arctic to balance an influx of heat of 0.04 PW, much as seen in Fig. 7 (top).

In summary we see that the delayed warming in the SH, the delay in the subpolar gyre of the North Atlantic and the amplification seen over the Arctic can be understood as largely a consequence of anomalous meridional energy transport in the ocean. In the next section we explore the processes that set this pattern of anomalous ocean heat transport.

4 Is anthropogenic temperature passive or active?

The correspondence between Figs. 5 (bottom) and 6 suggests that in the calculations presented here at least, the evolution of \(T_{anthro}\) can perhaps be understood in terms of a quasi-passive tracer. Suppose, for example, that \(T_{anthro}\) is small enough that changes in circulation induced by it, \(v_{anthro}\), can be neglected relative to the unperturbed control circulation, \(v_{c}\). In this limit \(\frac{D_{res}}{Dt}\) is the same in both the control and perturbed calculation. Then, on subtracting Eq. (1) from (2), we find that \(T_{anthro}\) evolves according to

$$\begin{aligned} \frac{D_{res}T_{anthro}}{Dt}=Q(\mathcal {H}_{anthro})-\gamma SST_{anthro}+R(T_{anthro}). \end{aligned}$$
(3)

We see that \(T_{anthro}\) evolves as a passive tracer advected and mixed by the unperturbed circulation, forced at the surface by a uniform downwelling flux and damped (weakly) at a rate set by the climate feedbacks. Caution is required, however, because it is the heat flux that matters to the evolving temperature field and so we must compare \(v_{c}T_{anthro}\) to \(v_{anthro}T_{c}\). Because \(T_{c}\) is typically so much larger than \(T_{anthro}\), it is not at all clear that changes in circulation, even if they are small, can really be neglected.

To clarify matters we therefore integrated Eq. (2) forward for a tracer and at the same time integrate \(T\) forward as in the control simulation. We call this a ‘temperature-like’ tracer, \(T_{racer}\), since it has the units of temperature, is initialized with the control temperature distribution, and is subject to the same anomalous surface conditions (flux \(\mathcal {H}_{anthro}\) and feedback \(\lambda\)) as in the perturbation experiment described above. Of course, unlike \(T_{anthro}\), \(T_{racer}\) cannot change the advecting currents or mixing processes. The extent to which the resulting \(T_{racer}\) and \(T_{anthro}\) distributions are similar is a measure of the passiveness, or otherwise, of \(T_{anthro}\). Figure 10 shows \(T_{racer}\) and the difference \(T_{anthro}-T_{racer}\) at the sea surface and Fig. 11 shows the same fields in meridional section after zonally-averaging. Note how \(T_{racer}\) has strong resemblance to the ventilation tracer in Fig. 6 (top). Except for a region in the northern North Atlantic, \(T_{racer}\) captures almost all of the \(T_{anthro}\) signal. In the Atlantic sector, circulation changes associated with the anthropogenic signal induce a weakening and shoaling of the AMOC—see Fig. 3 (bottom)—which also plays an important role.

Fig. 10
figure 10

Contribution to \(SST_{anthro}\) after 100 years from (top) passive \(SST_{racer}\) (compare to Fig. 5) and (bottom) active processes, \(SST_{anthro}-SST_{racer}\)

Full size image
Fig. 11
figure 11

Contribution to the zonal-average \(T_{anthro}\) after 100 years from (top) passive, \(T_{racer}\) and (bottom) active processes, \(T_{anthro}-\) \(T_{racer}\)

Full size image

The right hand side of Fig. 9 separates out the relative contribution of ‘passive’ and ‘active’ components of \(T_{anthro}\) to heat uptake and storage (top) and anomalous meridional energy transport (bottom). We see that the energy transport change is shaped largely by its passive component, but that over the NH low to mid-latitudes, active and passive components compensate one-another. In particular the active heat transport anomaly there is predominantly southward, in large part because of the diminished strength of the AMOC—see Fig. 3. It is important to remember that in fully coupled models undergoing global warming, the winds and freshwater fluxes are perturbed in conjunction with the surface heating signal we have isolated here. Increased net freshwater input into the North Atlantic could further act to weaken the AMOC (Gregory et al. 2005; Weaver et al. 2007) and thus northward heat transport. On the other hand, it has been shown that the main cause of the AMOC slowdown in global change ocean simulations is increased heat fluxes (Mikolajewicz and Voss 2000; Saenko et al. 2002; Kamenkovich et al. 2003).

The above methods and findings on the active versus passive nature of ocean heat uptake can be compared to those of previous studies. Banks and Gregory (2006) and Xie and Vallis (2012) use passive tracer techniques to isolate the redistribution of the existing ocean heat reservoir due to changing ocean circulation (\(v_{anthro}T_{c}\)) within coupled climate change simulations. As described above, our passive tracer, \(T_{racer}\), is initialized, forced/damped at the surface and integrated forward identically to \(T_{anthro}\), absent only changing ocean circulations and mixing processes. This allows us to calculate \(v_{anthro}T_{anthro}\) directly, and thus the difference between \(T_{anthro}\) and \(T_{racer}\) distributions (Figs. 9, 10, 11) represents \(v_{anthro}T_{c}+\) \(v_{anthro}T_{anthro}\), revealing the full impact of changing circulation and mixing on ocean temperatures. Moreover, by allowing surface flux boundary conditions to evolve in response to \(SST_{racer}\) values (Fig. 10), the method allows an assessment of the ‘active’ influence of the anthropogenic temperature signal on surface warming and heat fluxes. This is similar in spirit to Winton et al. (2013), who held ocean circulations fixed within a coupled model (GFDL’s ESM2M) to evaluate their impact on surface climate change. It is important to emphasize that in these previous studies, ocean circulation changes arise, in part, from perturbations in surface winds and freshwater fluxes within coupled model integrations. We have focused here on the ‘active’ nature of heat uptake itself, in isolation from other surface forcings.

Our results show that changes in ocean circulation and mixing processes play a role in setting regional patterns of ocean heat storage (Fig. 11), consistent with the previous studies. Moreover, by allowing SSTs and surface heat fluxes to evolve within our passive tracer simulation, we find that the ‘active’ nature of heat uptake influences the patterns of surface warming and heat fluxes (Fig. 9), particularly within the Atlantic sector where a weakening of AMOC decreases northward heat transport, consistent with Winton et al. (2013). The penetration of the anthropogenic temperature signal is shallower in most regions than the passive tracer (Fig. 11), plausibly due to an increase in upper ocean stratification with warming. One exception is in the high northern latitudes, where increased northward heat transport into the Arctic in the ‘active’ case acts to enhance warming at the surface and at depth (Fig. 11). Nevertheless, the large-scale features of upper ocean heat storage and surface warming are found to be largely captured by the uptake and advection of the passive tracer. This is at odds with the conclusions of Xie and Vallis (2011), which we speculate may be due to differences in methodology, as outlined above, or due to the fact that they perform their analysis within an idealized model of only the Atlantic Ocean, where circulation changes are indeed found to be important. We see only a modest ‘active’ role for heat storage within the Southern Ocean south of the Antarctic Circumpolar Current (c.f., Fig. 11 with Winton et al. 2013). This suggests that within this region anomalous heat fluxes are largely passive and that surface wind and freshwater flux changes may play a more important role than the anthropogenic temperature signal in the redistribution of ocean heat content (Gregory 2000 and Kirkman and Bitz 2011). We propose that the model setup and passive tracer methods outlined here may provide a useful framework within which to further explore how each of these surface perturbations affect ocean circulation, in isolation and together.

5 Discussion and conclusions

In this study we have described how one can use a ‘stand-alone’ ocean model to parse out the role of ocean circulation in setting the timing and spatial response of SST to GHG forcing. A spatially uniform downwelling flux was used to induce surface warming and climate feedbacks parameterized through a simple damping term. The sea surface warms and the warming signal \(T_{anthro}\) is subsequently subducted and shaped by ocean currents and mixing processes. The gross behavior is revealed by the form of the Climate Response Functions as in Fig. 4: regional curves are rather different from the global response with, for example, the Arctic warming much more rapidly than the Antarctic. The close correspondence between the patterns of warming from the ocean-only calculation and that obtained from fully coupled models strongly suggests that delayed warming in the Southern Ocean, delay in the northern North Atlantic and amplification of the global warming signal in the Arctic, are all strongly controlled by ocean circulation rather than processes within the atmosphere.

In some regions \(T_{anthro}\) acts nearly like a passive tracer introduced in to the ocean at the surface, weakly damped by climate feedbacks but advected and mixed by climatological currents. This limit is approached over much of the Southern Ocean, where warming is sufficiently small that changes in ocean circulation are small. Here delayed surface warming leads to enhanced uptake of heat around Antarctica. However, the heat is not stored locally in the Southern Ocean but is instead advected equatorward by (residual-mean) ocean currents.

Changes in ocean circulation induced by \(T_{anthro}\) itself can become important in other regions of the ocean, such as the North Atlantic, where they play a zero-order role in setting SST patterns. Here \(T_{anthro}\) induces a weakening of the AMOC, diminishing poleward heat transport in to the North Atlantic providing a cooling tendency offsetting the warming signal at the surface due to GHGs. Advection of heat in to the Arctic, meanwhile, accelerates warming over the polar cap.

The methodological approach outlined here could have great use in isolating the distinctive role of the ocean in shaping the response of the climate to anthropogenic forcing. For example in Marshall et al. (2014), it is applied to study how interhemispheric asymmetries in the mean ocean circulation, with sinking in the northern North Atlantic and upwelling around Antarctica, strongly influences the SST response to both GHG and ozone hole forcing and suggests reasons why in recent decades the Arctic has been warming with sea ice disappearing but the Southern Ocean around Antarctica has been (mainly) cooling with sea ice extent growing.

Finally we should like to propose that the framework outlined here could be used to compare the ocean component of coupled climate models in a context that is germane to anthropogenic climate change. Because of the simplicity of the approach, which only involves ocean models run in a CORE framework, the cluster of models that contributed to Griffies et al. (2009), could be compared, one against the other, and in the context of the CMIP5 project.