1 Introduction

General circulation models (GCM) are the only predictive tools capable of isolating the drivers of climate change in response to natural and/or anthropogenic forcings. However, while some features are well represented (e.g. global and regional temperature), other fundamental aspects of the climate system are not well understood, are poorly observed and are still uncertain in GCMs. One such aspect of uncertainty is the hydrological cycle. The hydrological cycle is not only important at the global scale, as latent heat release is one of the major drivers of mean circulation, but a change in its characteristics will have profound impacts at the regional scale. It is crucial to evaluate and understand the ability of GCMs to represent the global hydrological cycle, in order to determine how much we can trust GCM predictions of changes in the hydrological cycle in climate change scenarios (e.g. Waliser et al. 2007; Liepert and Previdi 2009; John et al. 2009; Liepert and Previdi 2012; Balan Sarojini et al. 2012). The global hydrological cycle is intimately linked with the global energy budget of the Earth. This link creates some fundamental constraints on the global hydrological cycle mean, variability and changes with future climate (e.g. Held and Soden 2006, and references therein). Studying the hydrological cycle in conjunction with the energy budget is therefore crucial to the understanding of GCM deficiencies (Wild and Liepert 2010).

1.1 Limitations for evaluating the global hydrological cycle in GCMs

1.1.1 Limitations in observations

Making use of observations is essential to support a rigorous evaluation of the energy and water budgets in GCMs, but there are important limitations in these products. The most recent attempts in estimating the Earth’s global hydrological cycle and energy budget, using the best observational datasets available at the time, were performed by Trenberth et al. (2007b, 2009). Such studies provide an essential basis to evaluate the GCMs because they ensure a closure (with uncertainties associated with observations) in the global energy and water budgets, which might not be the case if all variables were calculated independently from different sources (Schlosser and Houser 2007; Sheffield et al. 2009). Some issues, however, remain in terms of the availability and quality of observational products. For example, although estimates of global evaporation are emerging, they are still under development and validation (Fisher et al. 2008; Jung et al. 2009; Jiménez et al. 2011). Such a lack of observations limits us to the use of reanalysis products together with the water balance equations, a method often used to estimate moisture quantities (Oki et al. 1995; Yeh et al. 1998; Seneviratne et al. 2004). This method has the advantage of closing the water budget, but it provides an incomplete description of the Earth’s climate system. Moreover, while many satellite and gauge observations exist to quantify global precipitation, biases persist within precipitation data due to uncertainties in the calibration of instruments and the precision of their measurements (Trenberth et al. 2007a; Schlosser and Houser 2007; Tian et al. 2009), or the sparsity of the observational coverage (e.g. Balan Sarojini et al. 2012). Global precipitation estimates have recently been revised to higher rates than previously estimated (Trenberth et al. 2011) by considering new satellite products (Huffman et al. 2009). For similar reasons, large uncertainties apply to energy quantities, particularly surface heat fluxes and downward surface longwave radiation (Stephens et al. 2012; Wild et al. 2013, and references therein). This highlights that, although observational studies of the global energy and water budgets are an essential aspect of assessing GCMs, their incompleteness and lack of independence and physical consistency prevent an accurate component-level evaluation of the global hydrological cycle in GCMs (Waliser et al. 2007).

1.1.2 Limitations in reanalyses

Additional valuable information that can be used to verify GCM fidelity is provided by reanalysis products. Reanalyses bridge the gap between observations and GCMs. As in GCMs, moisture and energy components are calculated explicitly in reanalyses, and not inferred from the water and energy balance equations. While this internal model consistency provides added value to observations, reanalyses differ in terms of their representation of the water and energy budgets, either due to different data assimilation systems, to different observational data, or to different model formulation (Trenberth et al. 2011). In many reanalyses, the energy and water budgets are also out of balance (e.g. Berrisford et al. 2011; Bosilovich et al. 2011; Robertson et al. 2011); reanalyses are not constrained to conserve mass and to balance radiation at the top of the atmosphere (TOA) as GCMs are. This lack of constraints leads to significant uncertainties in the representation of the global hydrological cycle in reanalyses (Trenberth et al. 2011). This constraint provides stability to GCM simulations and makes GCMs more appropriate tools for understanding the drivers of the hydrological cycle; the internal consistency between radiative forcing and precipitation response in GCMs supports a process-level assessment of climate model behavior and trustworthiness, e.g. by isolating the impact of each process on atmospheric circulation (Allan 2009). However, Liepert and Previdi (2012) have shown that most GCMs have deficiencies in simulating the global atmospheric moisture balance and produce highly uncertain estimates of atmospheric moisture transport from ocean to land. These deficiencies affect the multi-model ensemble mean’s moisture budgets over the globe, ocean and land under current and future climate conditions.

1.2 Towards understanding model uncertainties in the global hydrological cycle

In this study, we aim to contribute to the understanding of model uncertainties in the global hydrological cycle in two ways:

  1. 1.

    By verifying the internal consistency of state-of-the-art GCMs in simulating the hydrological cycle, including its link with radiative forcing;

  2. 2.

    By evaluating an aspect of climate model uncertainties in simulating the hydrological cycle, namely the impact of increasing horizontal resolution.

The significant role of horizontal resolution in GCMs has been verified for many aspects of the simulated climate system. These include improvements in the large-scale atmospheric and oceanic circulation, global and regional precipitation distribution, El Niño Southern Oscillation and its teleconnections (Duffy et al. 2003; Hack et al. 2006; Roberts et al. 2009; Shaffrey et al. 2009; Marti et al. 2010; Delworth et al. 2012; Kinter III et al. 2013, and references therein). Blocking events are also improved in high-horizontal resolution GCMs due to an improvement in the atmospheric mean state and variability (Matsueda and Palmer 2010; Jung et al. 2012), and the better resolved orography (Berckmans et al. 2013). High-resolution GCMs are also able to simulate realistic high-impact precipitation events (Iorio et al. 2004; Kimoto et al. 2005; Kitoh et al. 2011), and to better simulate the structure and variability of tropical and extra-tropical cyclones (Jung et al. 2006; Catto et al. 2010; Manganello et al. 2012; Strachan et al. 2013), responsible for transporting large amounts of water from the ocean to the land.

Here we assess how two atmospheric GCMs (AGCM), developed over a range of horizontal resolutions, are able to simulate the processes that connect and drive each component of the hydrological cycle, with an approach comparable and complementary to that of recent studies based on observations and reanalyses (Trenberth et al. 2007b, 2009, 2011). The use of multi-model analyses is important, as different model formulations may have a different water balance and thus exhibit different sensitivity to resolution. However, the GCMs included in the Coupled Model Intercomparison Projects, CMIP3 or CMIP5, do not span such a wide range of resolutions, and only two studies focus on the systematic impact of resolution on the global hydrological cycle using HadAM3 and ECHAM5 with resolutions up to 90 km (Pope and Stratton 2002; Hagemann et al. 2006). It is also crucial to determine at which resolution the model behavior converges, as such convergence may depend on the climate features considered (for example Strachan et al. 2013 have shown a convergence in the model representation of the average number of tropical cyclones at 135 km, while the convergence is at 60 km for simulating a realistic interannual variability of storms occurrence). Pope and Stratton (2002) and Hagemann et al. (2006) have not found convergence in the representation of the hydrological cycle across the resolutions considered. This is addressed in this study by assessing a hierarchy of similar formulation at multiple resolutions, over a range of 270–25 km.

2 Data and methodology

2.1 Atmosphere-only GCM experiments

We consider AGCMs instead of coupled GCMs, as AGCMs are constrained by observed boundary conditions (sea surface temperature and sea ice cover) that: (1) make their results more comparable to observations and reanalyses, allowing a proper evaluation of the models; (2) allow for comparison between models, providing that the same boundary conditions are applied across the models; (3) simplify the simulated climate system by removing interactions with the ocean. Sea surface temperature and salinity are intimately linked with the hydrological cycle (Trenberth and Shea 2005; O’Gorman and Schneider 2008; Allan 2009; Trenberth et al. 2010), but GCMs still have some major biases in their oceanic mean state representation and in the ocean-atmosphere coupling (e.g. doubled inter-tropical convergence zone; Randall et al. 2007a; Guilyardi et al. 2012). As resolution increases either in the atmosphere, ocean, or both, new feedback processes are generated and can affect the large-scale simulations (Roberts et al. 2009). With such coupled models, it is very difficult to isolate the atmospheric processes responsible for affecting the hydrological cycle in GCMs with various resolutions.

We use two AGCMs developed by the UK Met Office Hadley Centre. The first is the atmospheric component of HadGEM1 with 38 vertical levels extending to over 39 km in height (fully described by Johns et al. 2006; Martin et al. 2006; Ringer et al. 2006). The second is the atmospheric component of HadGEM3 (Hewitt et al. 2011) in the GA3.0 configuration with 85 vertical levels extending to 85 km in height (Walters et al. 2011). The models are based on the same dynamical core, but differ in their parametrization schemes, for instance in the treatment of clouds: HadGEM1 uses a diagnostic cloud scheme, while HadGEM3 uses a prognostic cloud scheme allowing clouds to be advected with the wind even long after the convection has ceased (Hewitt et al. 2011; Walters et al. 2011). These differences allow us to consider HadGEM1 and HadGEM3 as two independent models. Both models use a regular latitude/longitude grid. They were developed at four horizontal resolutions, while retaining their vertical resolution: HadGEM1-A at N48, N96, N144, and N216; HadGEM3-A at N96, N216, N320, and N512 (Table 1). HadGEM1-A and HadGEM3-A describe a non-hydrostatic atmosphere using a semi-Lagrangian, semi-implicit formulation, which allows an increase in horizontal resolution, while keeping a relatively long time step necessary for climate integrations (Davies et al. 2005). Some of the physics parametrization schemes include inherent dependence on the model’s grid-box size, a requirement of the latitude/longitude grid, which automatically allows resolved processes at high resolution to take up the role of physical parametrization at low resolution. This method has the advantage of keeping model formulation as similar as possible while increasing resolution. A special tuning was performed for a single model (out of a total of eight in this study), namely HadGEM1-A at N216, to ensure radiative balance, an important prerequisite in climate modeling, particularly when studying the global hydrological cycle and its link with the energy budget. This model initially suffered from a lack of clouds leading to a net radiation imbalance at TOA of +4 W m−2. To increase cloud cover and bring the radiative budget at TOA closer to zero, the collision/coalescence parameter used for determining the autoconversion rate of cloud water droplets was decreased, a common tuning in high-resolution models (Duffy et al. 2003; Roeckner et al. 2006; Hack et al. 2006; Hourdin et al. 2013; Delworth et al. 2012). For numerical stability reasons, some dynamical settings also needed to be adjusted; these adjustments are common when increasing horizontal resolution in GCMs (Pope and Stratton 2002; Roeckner et al. 2006; Shaffrey et al. 2009; Hourdin et al. 2013). In HadGEM1-A and HadGEM3-A, these include the time step, the magnitude of polar filtering in the advection scheme, the vertical velocity threshold at which the targeted moisture diffusion scheme is triggered to prevent numerical instabilities (Table 1); we find that these dynamical adjustments do not impact the climatology of the simulations. At higher resolutions (N216 in HadGEM1-A; N320 and N512 in HadGEM3-A), the timescale for dissipation of convective available potential energy (CAPE) was also decreased, which justifies the ability of high-resolution models to sustain higher energy and remove it faster than low-resolution models (Table 1). The exception to these limited and uninfluential adjustments is again a single model (out of eight): HadGEM1-A at N216. This model was particularly unstable, requiring limited use of horizontal and vertical diffusions on the horizontal wind components. We found that such treatments, unlike the adaptations applied to the other seven models, had an impact on the hydrological cycle by increasing precipitation and moisture transport over land. Despite these departures from the standard formulation, HadGEM1-A at N216 is included in this study to allow for an extra comparison with HadGEM3-A. The impact of these adaptations when developing high-resolution GCMs on the hydrological cycle are treated in detail in a following manuscript (Demory et al. in prep).

Table 1 Description of the models and simulations used in this study (u, v and w are zonal, meridional and vertical wind components, and θ is potential temperature)
Full size table

The atmospheric components are fully coupled with the UK Met Office Surface Exchange Scheme (MOSES-II; Cox et al. 1999) in HadGEM1, replaced by the Joint UK Land Environment Simulator (JULES), a more developed version of MOSES-II, in HadGEM3 (Walters et al. 2011). MOSES-II is a distributed grid-point model (it resolves processes in the vertical only, there is no horizontal flux) using the same regular grid as the atmosphere, at the same resolution. The land-surface boundary conditions (orography, vegetation and soil cover) come from high-spatial resolution maps that have been interpolated to each resolution grid (as detailed by Shaffrey et al. 2009). The land–sea mask for each atmospheric model resolution includes a land fraction field that is used in a coastal tiling scheme to facilitate flux-conserving coupling to the ocean grid in the HadGEM family coupled models (Essery et al. 2003). As such, the atmosphere mask is derived from the appropriate resolution ocean land-sea mask: 1° for N48 and N96, 1/3° for N144 and N216 (HadGEM1), and 1/4° for N216, N320 and N512 (HadGEM3). Since they are calculated on different grids, the global, land and sea areas are different between low- and high-resolution models, and the land fractions differ by up to 1 % of the global area (Table 1). It was found that these differences in the land fraction have a large impact at regional scales, in particular in areas covered by islands, such as the Maritime Continent (Schiemann et al. 2013).

2.2 Simulations description

Running high-resolution models is expensive in terms of computing cost and data storage. Running HadGEM1-A at various resolutions took approximately 1 year because this model scaled poorly on the Japanese Earth Simulator supercomputer, and was also very unstable at N216. HadGEM3-A is more scalable and more stable than HadGEM1-A but it is also more expensive (mainly because of its higher vertical resolution). Performing 25-year integrations at N512 therefore still required several months depending on the supercomputer maintenance and queuing system (Mizielinski et al. in prep). Considering these costs and timescales, we quantify the robustness of our results using a mini-ensemble of three to five simulations per model resolution (except HadGEM1-A at N144 and HadGEM3-A at N216 and N320, for which one simulation was performed; Table 1). The ensembles were created by perturbing the initial model prognostic field (θ) globally at bit level (in the order of 10−14 K). The spread of the ensembles climatology is very small (as shown in Tables 2, 3) and not included in Figs. 2 and 3.

Fig. 1
figure 1

Monthly-mean time series of weighted average P–E (mm day−1) over the globe (top), land (top middle), ocean (bottom middle), and atmospheric moisture convergence over land (bottom) for HadGEM1-A at N48 (solid black) and N216 (dashed red) resolutions. Each thin line represents an ensemble member; the thick line represents a 12-month running average performed on the ensemble mean

Full size image
Fig. 2
figure 2

The Earth’s global energy budget (W m−2). Background values are based on observations (2000–2004; Trenberth et al. 2009). In the boxes (legend on the lower left corner) are values from HadGEM1-A and HadGEM3-A with various horizontal resolutions (1979–2002, and 1986–2002 at N512), and ERA-I and MERRA reanalyses (2002–2008). Image adapted from Trenberth et al. (2009) © American Meteorological Society. Reprinted with permission

Full size image
Fig. 3
figure 3

Same as Fig. 2 for the Earth’s global hydrological cycle: water reservoirs (103 km3) and flows (103 km3 year−1). Background values are from TR11 (2002–2008). Three values are given for the water vapor transport from ocean to land: (1) atmospheric moisture convergence, (2) E–P from the ocean, and (3) P–E from the land. The area of the globe (0.51), ocean (0.36) and land (0.15) × 1015 m2 must be factored into the units to express them in mm and mm day−1. Image adapted from Trenberth et al. (2007b) © American Meteorological Society. Reprinted with permission

Full size image

Most of the simulations were performed for 24 years (1979–2002) using the monthly Atmospheric Model Intercomparison Project II (AMIP-II) sea surface temperature and sea ice provided on a 1° grid (Taylor et al. 2000), interpolated to daily intervals by the models. HadGEM3-A at N512 uses the new daily Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) available from 1986 on a 1/20° grid (Donlon et al. 2012), which we consider to be a more appropriate product to force such a high-resolution model than AMIP-II. OSTIA has slightly colder climatology than AMIP-II (Mizielinski et al. in prep). Moreover, a climatological annual cycle of present-day (1990s–2000s) greenhouse gas and aerosol emissions is imposed in HadGEM1-A, while observed values from 1970 to present are used in HadGEM3-A. The incoming solar energy is constant in all models but HadGEM3-A at N512, in which the 11-year solar cycle is included. To evaluate the impact of such use in HadGEM3-A at N512 on the global water and energy budgets, we performed ensembles of 17-year (1986–2002) test-simulations with HadGEM3-A at N96 and N216 using the OSTIA forcing dataset and the 11-year solar cycle (refer to Table 1, and compare experiments HG3 N96 ostia and HG3 N216 ostia with the standard versions HG3 N96 and HG3 N216 in Tables 2, 3, respectively). Including the 11-year solar cycle contributes to a slightly larger radiative imbalance at TOA, which presents an equivalent imbalance at the surface without changing the atmospheric energy and water fluxes. Using OSTIA reduces the global upwelling longwave fluxes at the surface by 0.7–0.8 W m−2, which is reflected by a decrease in the surface longwave back radiation, and decreases precipitable water by 0.4 mm.

To evaluate the effect of adjusting the CAPE timescale on the energy and water budgets, we analysed an AMIP-II 20-year test-simulation (1979–1998) with HadGEM3-A at N216 with a CAPE timescale equal to 60 min instead of 90 min in the standard version. Reducing CAPE in HadGEM3-A changes very little the energy and water budgets (refer to experiment HG3 N216 cape in Tables 2, 3). For this reason, HadGEM3-A N216 cape is added in the analyses as an extra member to HadGEM3-A at N216.

2.3 Model output and methodology

The radiation and energy fluxes are calculated at every time step and averaged monthly by the model. The fields are then averaged over the simulation periods. Ground surface heat flux is not output by the model and is therefore calculated from the surface energy balance. Total evaporation rate is calculated from surface latent heat flux by making use of the latent heat of vaporisation. Precipitation, rainfall and snowfall rates are instantaneous values that are averaged monthly over each time step by the model.

The atmospheric moisture convergence is calculated using a central finite difference method, equivalent to that used in the model, from the moisture fluxes vertically integrated at every time step and averaged over the month. The precipitable water is calculated as the difference between atmospheric wet mass and atmospheric dry mass, which includes the contributions from water vapor, cloud liquid water and cloud frozen water.

The models’ energy and moisture quantities are computed globally, over land and over ocean. Weighted averages are computed on each model grid to retain the detail in variable distribution afforded by the high-resolution simulations (e.g. precipitation along coastlines or over orography). However, averaging fields separately over land and ocean using different land-sea masks may impede the comparability between resolutions. To ensure that the fraction of land and ocean remains the same in different grids, the land fraction fields of the high-resolution model (N144 or N216 for HadGEM1-A; N320 or N512 for HadGEM3-A) were regridded to the lower-resolution grids (N48 and N96 for HadGEM1-A; N96 and N216 for HadGEM3-A). Doing so allows comparability within a model with various resolutions, although it does not allow a strict comparison between the two model versions HadGEM1-A and HadGEM3-A, which is not the purpose of this paper. The alternative approach that consists of calculating the weighted average on the native grids using the original land-sea masks has been tested as well: the total amount of water and energy circulating in the simulated system is slightly altered due to the differences in land fractions, but the sensitivity to resolution remains similar.

2.3.1 Moisture conservation in HadGEM1-A and HadGEM3-A

Before performing analyses on the simulated hydrological cycle at global or regional scales, it is essential to verify that the respective GCMs close the moisture budget. Most Intergovernmental Panel on Climate Change (IPCC) GCMs do not necessarily close the moisture budget, which leads to the so-called ‘moisture conservation error’: some GCMs show small conservation errors, while others depict errors that can be larger than the interannual variability of global mean precipitation (Liepert and Previdi 2012). The current generation of Hadley Centre models (from HadGEM1 to HadGEM3) conserve dry mass exactly (Staniforth et al. 2005), but do not close the global moisture budget exactly. Liepert and Previdi (2012) show that the HadGEM1 model is nonetheless amongst the models that best balance atmospheric moisture (5th on 18 CMIP3 models considered). In HadGEM1-A and HadGEM3-A, the moisture budget is preserved with the precision of 0.002 and 0.004 mm day−1 globally respectively (refer to P–E in Table 3). This precision is smaller than most reanalyses (Trenberth et al. 2011), among them ERA-Interim that has a precision of 0.003 ± 0.3 mm day−1 (the ERA-Interim’s value depends on the period considered, here 1989–2008; Berrisford et al. 2011). This level of model precision is larger than the interannual variability of the global moisture budget (approximately 0.001 mm day−1), but far smaller than the interannual variability of global mean precipitation (approximately 0.02 mm day−1; Table 3), and smaller than the positive trend in global precipitation and evaporation (approximately 0.01 mm day−1; not shown) associated with an increase in sea surface temperature over time. This small conservation error therefore does not affect the evolution of the hydrological variables over time: P–E over the globe, land and ocean, as well as moisture convergence over land (that represents the ocean to land moisture transport), are very stable over time (Fig. 1). This stability further confirms a realistic balance of the moisture budget over the climatological period, allowing a thorough study of the hydrological cycle within these models.

There is an additional error to be considered before starting these analyses. P–E over land should be mathematically equal to the ocean to land moisture transport. Over land, P–E differs from moisture convergence by 0.05–0.09 mm day−1 in HadGEM1-A and by 0.05–0.1 mm day−1 in HadGEM3-A, with no systematic sensitivity to resolution. These differences are attributed to computational reasons: they are the result of the finite difference method applied to the moisture fluxes to interpolate them on the right grid before computing moisture divergence. This interpolation results in a noisy field that generates computational errors when averaged over land. These computational errors are larger than the moisture conservation error, and are also larger than the interannual variability of P–E and moisture convergence over land (approximately 0.02–0.04 mm day−1; Table 3). However, they are smaller than the systematic increase in moisture convergence over land with resolution (0.14–0.32 mm day−1 from N48 to N96/N216 in HadGEM1-A, and 0.08–0.13 mm day−1 from N96 to N216/N512 in HadGEM3-A), which is consistent with the systematic increase in P–E over land with resolution (0.14–0.35 mm day−1 from N48 to N96/N216 in HadGEM1-A, and 0.11–0.18 mm day−1 from N96 to N216/N512 in HadGEM3-A; Table 3). At this scale, these random computational errors do not bring into question the outcomes of this study.

2.4 Observational and reanalysis data

As mentioned in Sect. 1.1, it is necessary to validate the simulated energy and water budgets with observational data that ensure the closure of the budgets. This is ensured, as far as possible, by the most recent observational estimates provided by Trenberth et al. (2007b, 2009, 2011), hereafter referred to as TR07, TR09 and TR11 respectively, and those recently provided by Wild et al. (2013). TR07, TR09, TR11 and Wild et al. (2013) present a complete description of the energy and/or water budgets for the periods 1979–2000, 2000–2004, 2002–2008 and 2001–2010, respectively.

We also make use of the estimates provided by TR11 using eight different reanalysis products for the period 2002–2008, with a particular focus on those with the best ability in representing and balancing the global energy and water budgets: the European Centre for Medium-Range Weather Forecasts (ECMWF)’s ERA-Interim (ERA-I; Dee et al. 2011) and the NASA Goddard Center’s MERRA (Rienecker et al. 2011).

At last, we also perform an independent comparison using ERA-Interim reanalyses by making use of the global energy and water budgets presented by Berrisford et al. (2011) for the period 1989–2008. This time period is closer to the model simulation periods of 1979–2002 and 1986–2002 than the period 2002–2008 considered by TR11, which ensures a more consistent validation of model simulations of the global energy and water budgets presented in the following section.

3 Results

3.1 Global energy budget

HadGEM1-A and HadGEM3-A simulate a similar global energy budget (Fig. 2; for detailed values over the globe, land and ocean, refer to Table 2). Radiation at TOA is very close to balance. The net radiation at TOA varies from −0.2 to +0.7 W m−2 in both models with various resolutions, with the exception of HadGEM3-A at N512 that has a larger imbalance of +1.7 W m−2 partly due to the introduction of the 11-year solar cycle (Sect. 2). The slight imbalance is caused by the incomplete forcing imposed to the atmospheric models, particularly HadGEM1-A in which the 1990s greenhouse gas forcing is constant and not in exact balance with the underlying sea surface temperatures that vary year by year. This imbalance remains nevertheless in agreement with the imbalance of 0.9 W m−2 found by TR09 taking into account errors in satellite observations and changes in atmospheric compositions. It is also smaller than most reanalysis products, such as ERA-I and MERRA, and is smaller than the imbalance of +2 to +4 W m−2 common amongst IPCC Fourth Assessment Report (AR4) coupled models (Wild 2008).

Compared to observations, the models overestimate net surface shortwave (SW) radiation by 11 W m−2, explained by too little SW absorbed by the atmosphere and too little reflected by clouds and aerosols. The latter enhances net absorbed SW radiation at TOA (noted ASR on Fig. 2) by 4–5 W m−2, while the former enhances surface insolation by a further 5–7 W m−2 compared to TR09. These biases mainly occur over the land (Table 2). They are common amongst GCMs (Wild and Roeckner 2006; Andrews 2009; Takahashi 2009; Wild et al. 2013) and the reasons are still being debated. In the IPCC AR4 GCMs, these are mostly attributed to clear-sky biases due to inaccurate partitioning of solar absorption between the atmosphere and the surface (Wild 2008). There is also a general lack of clouds in HadGEM1 that further reduces the planetary albedo (Johns et al. 2006; Milton and Earnshaw 2007), while total cloud radiative forcing is mostly right due to a compensation of errors: there is too little high and low thin clouds, and too much high and low thick clouds (Martin et al. 2006). At the surface there is too much reflected SW, mainly from the Saharan region due to the absence of an interactive dust scheme, which slightly reduces the net SW flux at the surface. The models show smaller biases compared to reanalyses. Surface insolation is larger by approximately 8 and 3 W m−2 compared to ERA-I and MERRA respectively (note that ERA-I has an erroneous high incoming solar radiation that might, in part, explain their excess in surface insolation compared to TR09; Berrisford et al. 2011; Dee et al. 2011). However, although their range is large, most reanalyses (5 out of 8 in TR11) produce larger values of surface insolation than observations. These differences are mainly attributed to biases in clouds and aerosols by TR11.

The surface emitted longwave (LW) radiation is higher by approximately 3 W m−2 in the models than TR09’s estimates. However, the models agree well with 6 out of 8 reanalysis estimates calculated by TR11, among them ERA-I, while MERRA has a lower value, closer to TR09. LW back radiation at the surface is higher in the models by 5 W m−2 compared to TR09, but lower than the value estimated by ERA-I and most other reanalyses (5 out of 8 reanalyses used by TR11 estimate the surface back radiation to be between 341 and 344 W m−2). These high values compared to TR09 are also reflected in the outgoing longwave radiation (OLR). The models exceed OLR by 4–5 W m−2 compared to TR09, but are in agreement with 5 out of 8 reanalyses estimates used by TR11, among them ERA-I and MERRA. Uncertainties lie in the estimates of LW radiation variables (Kato et al. 2012; Wild et al. 2013, and references therein). TR09 retrieved the value of 333 W m−2 for surface LW back radiation from the surface energy balance. However, independent studies show that surface back radiation ranges from 338 to 348 W m−2 (Wild 2008; Stephens et al. 2012; Wild et al. 2013). This higher range of observations requires an equivalent adjustment in surface heat fluxes: sensible and latent heat fluxes are estimated between 15–25 and 80–90 W m−2 respectively (Wild et al. 2013). These values are underestimated by TR09, particularly over land (using new observational products of evapotranspiration, Mueller et al. 2011 estimate latent heat over land to be ∼48 ± 5.5 W m−2, while TR09’s estimate is ∼38.5 W m−2). These higher estimates bring GCMs within the range of observational uncertainties (Table 2). Reanalyses are close to this new range of observations. Most reanalyses analysed by TR11 also agree on higher values of latent heat flux than TR09, which would indicate that the models perform better than currently believed. The models exhibit an excess in net surface radiation compared to TR09, which is entirely compensated by latent heat flux in HadGEM1-A. In HadGEM3-A, the excess net radiation is returned as a combination of sensible and latent heat fluxes, bringing HadGEM3-A closer to the new range of observations. The surface energy budget is not fully balanced in the models, as reflected by the residuals (net absorbed at surface), which are nonetheless smaller than in reanalyses assessed by TR11.

3.2 Global water budget

In response to the global energy budget, which causes too much net available energy at the surface, the hydrological cycle in HadGEM1-A and HadGEM3-A is too intense compared to observations (the water fluxes are larger in models than in observations as shown on Fig. 3 and detailed in Table 3), a common error in GCMs (Duffy et al. 2003; Hack et al. 2006; Hagemann et al. 2006; Randall et al. 2007b; Trenberth et al. 2011). HadGEM3-A agrees better with observations than HadGEM1-A, particularly over the ocean, which is a result of the lower latent heat release (Sect. 3.1). The models’ estimates are also higher than most reanalyses, including ERA-I and MERRA, particularly over the ocean. However, the spread in reanalysis products is large and their values uncertain. Over land, the models agree better with observations and reanalyses. Atmospheric moisture transport from ocean to land and continental runoff are generally overestimated by the models compared to TR07 and reanalyses.

3.3 Impact of AGCM horizontal resolution

3.3.1 At global scale

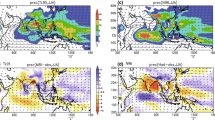
Globally, the energy and water budgets are not sensitive to resolution in both HadGEM1-A and HadGEM3-A (Figs. 2, 3). There is as much global energy, precipitation and evaporation at low as at high resolution. This finding is in line with previous studies (Pope and Stratton 2002; Hack et al. 2006; Hagemann et al. 2006; Duffy et al. 2003 when their models are properly tuned to balance radiation at TOA). Nonetheless, precipitable water increases systematically with resolution in HadGEM1-A, bringing the high-resolution model estimates closer to TR07 and reanalyses. The increase in humidity with resolution occurs globally and is associated with a slightly warmer mid-level troposphere (top and middle left panels of Fig. 4). Global-mean mid-level atmospheric temperature increases by approximately 0.71K in HadGEM1-A from N48 to N216 and atmospheric specific humidity increases by 5.29 %, while global-mean relative humidity remains relatively constant from low to high resolution (increase of 1 % globally). The model therefore follows a temperature-humidity relationship of 7.45 %/K, close to the Clausius–Clapeyron relationship (Held and Soden 2006). As a consequence of the increase in precipitable water, the residence time of moisture in the atmosphere slightly increases in HadGEM1-A with resolution, from 7.5 at N48 to 8 days at N216, again bringing the high-resolution model closer to TR07 and TR11’s observed estimates of about 9 days. In the Tropics, specific humidity increases mainly as a result of increasing relative humidity (middle panels of Fig. 4). This is associated with more high-level clouds and less low- to mid-level clouds at high resolution that increase net surface heating (right panels of Fig. 4). This finding is consistent with previous studies (Pope and Stratton 2002; Roeckner et al. 2006; Hourdin et al. 2013). In the extra-Tropics, changes in relative humidity with resolution follow a similar distribution to cloud cover with a reduction at midlatitude that is consistent with the warmer atmosphere (top left panel of Fig. 4), and an increase at the poles and tropopause. The shift in cloudiness towards the poles is associated with a poleward shift of the jets at high resolution (bottom panel of Fig. 4), a result that is again consistent with previous studies (Roeckner et al. 2006; Hourdin et al. 2013). At the poles, total cloudiness increases, which enhances outgoing LW radiation but also the greenhouse effect that is associated with the increase in air temperature.

Fig. 4
figure 4

Difference in zonal mean annual mean air temperature (top left), cloud amount (top right), relative change in specific humidity (middle left), relative humidity (middle right) and zonal wind (bottom left) between HadGEM1-A at N216 and HadGEM1-A at N48

Full size image

As mentioned in Sect. 2, the use of OSTIA products at N512 decreases precipitable water by 0.4 mm. This effect shows that precipitable water would increase with resolution in HadGEM3-A as well if all simulations were forced with the same products, although to a lesser extent compared to HadGEM1-A (Fig. 3; fully detailed in Table 3). The sensitivity of precipitable water to horizontal resolution was also noticed in HadAM3 (Pope and Stratton 2002) but it was not verified in ECHAM5 (Hagemann et al. 2006), which probably shows that the sensitivity of precipitable water to resolution is formulation dependent. In fact in HadGEM3-A, relative changes in specific humidity with resolution (from N96 to N320) are tightly linked with changes in relative humidity and cloudiness, while air temperature changes very little (Fig. 5). Total cloudiness decreases at midlatitude, which is again associated with a poleward shift of the midlatitude jets. Tropical low- and mid-level cloudiness slightly increases, which increases relative and specific humidity while tropical air temperature decreases slightly. This shows a weaker relationship between the increase in precipitable water and air temperature in HadGEM3-A than in HadGEM1-A, but is nonetheless in agreement with other models (Hourdin et al. 2013). Although the mechanisms appear to be different, the impact of resolution on the vertical structures shown on Figs. 4 and 5 is surprisingly similar between HadGEM1-A and HadGEM3-A (note that we are not comparing the same resolutions but instead we compare two equivalent jumps in resolutions: N216 vs. N48 in HadGEM1-A, and N320 vs. N96 in HadGEM3-A).

Fig. 5
figure 5

Same as Fig. 4 between HadGEM3-A at N320 and HadGEM3-A at N96

Full size image

3.3.2 Contrast between land and ocean

When splitting the analyses over land and ocean, the energy budget varies little with resolution (Table 2; note that the land-sea partitioning of solar incoming radiation at TOA simulated by HadGEM1-A and HadGEM3-A is different from observations, so that the models start with a biased value of incoming SW over land and sea at all resolutions). Over land, there is no systematic change in evapotranspiration with resolution in both models (Fig. 3). Ocean evaporation does not change systematically either, because observed sea surface temperatures are imposed and global mean near-surface humidity and wind speed are mostly insensitive to resolution. Precipitation, however, systematically changes with resolution: it decreases over the ocean, while it increases over the land. This is in line with Pope and Stratton (2002), but not with Hagemann et al. (2006) who found in ECHAM5 an increase in ocean precipitation, due to an increase in radiative cooling with resolution over the ocean. Moreover, land precipitation in HadGEM1-A mainly increases through convective rain, while large-scale rain decreases with resolution (Table 3). This result again opposes previous studies, which found that large-scale precipitation increases with resolution, while convective precipitation decreases (Duffy et al. 2003; Hagemann et al. 2006). There are strong precipitation biases in HadGEM1-A at N48, particularly in the Tropics that could explain the difference in the behaviour of this model compared to others (Fig. 6). Increasing resolution increases precipitation, particularly over the Maritime Continent region, while precipitation decreases over the surrounding oceanic regions of the Maritime Continent, which improves the main biases of the model against observations (Schiemann et al. 2013). In HadGEM3-A, total land precipitation increases both through large-scale and convective rain, a consequence of the prognostic cloud scheme (Wilson et al. 2008).

Fig. 6
figure 6

Differences in annual mean precipitation between HadGEM1-A at N48 and GPCP (top), and HadGEM1-A at N216 and GPCP (bottom)

Full size image

The change in precipitation is particularly large in HadGEM1-A over the whole range of resolutions (Fig. 3). In HadGEM3-A, the change is large from N96 to N216, while the values converge at resolutions higher than N216. These results bring oceanic precipitation in high-resolution models closer to observations, while the wet biases over land increase in high-resolution models compared to current observations and reanalysis estimates. However, if we remove the effect of the global precipitation bias (which we have shown to be caused by excessive net radiation) by computing the ratio of land precipitation to global precipitation, we notice that the land precipitation fraction is systematically closer to the observational and reanalysis ratios in both HadGEM1-A and HadGEM3-A at high resolution (Fig. 7). Moreover, the increase in land precipitation with resolution is larger than the change in land evaporation, which decreases the ratio of evaporation to precipitation over land with resolution (black solid and open circles on Fig. 8; note that all simulations are included in this figure, showing the small effect of using different forcings on the hydrological cycle). The E/P ratio over land is lower in HadGEM1-A than in HadGEM3-A, particularly at N216, but the resolution dependence follows a similar and consistent pattern. This result brings high-resolution models closer to the ratio suggested by TR07, TR11 and older studies’ estimates of different water budgets (black triangles and grey bar on Fig. 8). The land E/P ratio simulated at high resolution is also very similar to the 20-year climatology (1989–2008) of ERA-I, calculated independently from that used by TR11. The other reanalysis estimates provided by TR11 are also included in Fig. 8, revealing a large spread. We have noticed that 4–5 out of 8 reanalysis products seem to show a similar tendency of high land E/P ratio at low resolution and low E/P ratio at high resolution; however, water balance in reanalyses is not well respected, so this finding may be misleading. This tendency of high-resolution models to decrease the E/P ratio over land strongly suggests that high-resolution models are able to reduce the contribution of local moisture sources to precipitation, a process commonly believed to be overestimated in GCMs (e.g. Ruiz-Barradas and Nigam 2005). To provide further evidence for the fact that this model behavior can be attributed to increasingly resolved dynamical processes, we show that the contribution to land precipitation from non-local sources of moisture through atmospheric moisture convergence becomes increasingly important with resolution (red solid and open squares on Fig. 8). Moisture convergence is low at low resolution, while it is increasingly larger at high resolution in both HadGEM1-A and HadGEM3-A. This finding is consistent with an increase with resolution in continental runoff that returns moisture back to the oceans (Fig. 3). HadGEM3-A values of moisture transport reach a plateau around N216–N320 resolution, showing that the model behavior converges around 60-km resolution. It is not possible to determine this convergence with HadGEM1-A over the range of resolutions considered.

Fig. 7
figure 7

Land to global precipitation ratio for each member of HadGEM1-A (solid circles) and HadGEM3-A (open circles; the test-simulations at N216 are included here). ‘REA’ corresponds to ERA-I reanalysis estimates (1989–2008). ‘OBS’ corresponds to observational estimates from TR07, TR11 and GPCP2.1 (1983–2002); the grey bar includes estimates from Peixoto and Kettani (1973), Baumgartner and Reichel (1975), Chahine (1992), Oki et al. (2004), Oki and Kanae (2006), Schlosser and Houser (2007)

Full size image
Fig. 8
figure 8

Evaporation to precipitation ratio (black circles) and moisture convergence to precipitation ratio (red squares) over land for each member of HadGEM1-A (solid) and HadGEM3-A (open; all AMIP-II and OSTIA simulations are included). ‘REA’ corresponds to reanalysis estimates of E/P provided by TR11; ‘ERA-I 20 years’ is calculated independently from ERA-I (1989–2008). ‘OBS’ corresponds to observational estimates of E/P from TR07 and TR11; the grey bar includes estimates from Peixoto and Kettani (1973), Baumgartner and Reichel (1975), Chahine (1992), Oki et al. (2004), Oki and Kanae (2006), Schlosser and Houser (2007)

Full size image

3.4 Impact of AGCM horizontal resolution on the annual cycle of the hydrological cycle over land

At timescales of a month or less, variations in atmospheric moisture are not negligible and become a source of moisture for precipitation. The annual cycle over global land is properly represented in HadGEM1-A compared to TR07, although the fluxes are overestimated, particularly at high resolution (Fig. 9). The models have a good representation of the maximum peak of land precipitation in July, and a decrease during the boreal autumn season, although it is 1 month too early (October instead of November). The minimum in evapotranspiration is well represented in the models, but it peaks too early (June instead of July). As in TR07, the recycling of moisture over land is larger in the summer (Fig. 10).

Fig. 9
figure 9

Annual cycle of moisture budget over land in HadGEM1-A with various resolutions for 1979–2002 (1979–2000 in TR07; dark colors): mean evaporation (blue), convergence of atmospheric moisture (green), change in atmospheric moisture storage (purple) and total precipitation (red). Units are in 103 km3 month−1

Full size image
Fig. 10
figure 10

Annual cycle of E/P over land in HadGEM1-A with various resolutions (grey bars) for 1979–2002 (1979–2000 in TR07; black bars)

Full size image

The impact of resolution on the annual cycle of the water budget over land is similar to that on the climatological mean. All the components of the water budget tend to increase with resolution during each month, which systematically brings the high-resolution model further away from observations. However, atmospheric moisture convergence at N216 is more realistic during the summer season, while it is more comparable to observations at N48 during the winter season. Moreover, E/P ratio over land is systematically improved with resolution for each month. The slope in E/P with resolution is also larger in summer than in winter, resulting in a smaller and more realistic annual cycle of E/P as resolution increases. These high values of recycling at low resolution in summer are associated with low values of atmospheric moisture convergence (approximately half those estimated by TR07), while moisture convergence at N216 is close to TR07 (Fig. 9). HadGEM1-A at N216 is also the only model that simulates a decrease in atmospheric moisture storage that is consistent with observations during the autumn season. This result shows that, although the water budget over land is increasingly overestimated at higher resolution compared to observations, the model at N216 tends to have the right behavior in recycling less moisture than at low resolution and in increasing moisture convergence over land. This finding underlines the excessive reliance on physical parametrization versus model dynamics (local, unresolved processes versus large-scale processes) in coarser HadGEM1 and HadGEM3 GCMs. This behavior is systematically the same, whether we consider the mean hydrological cycle or its annual cycle, and reflects the robust signal of the impact of resolution on the water fluxes over land.

4 Discussion and conclusion

We have assessed the ability of two AGCMs with varying horizontal resolutions, HadGEM1-A and HadGEM3-A, to simulate the processes that connect and drive each component of the global hydrological cycle. The global energy and water budgets were systematically compared to recent observations and reanalysis products. Although improvements are still needed, the models produce a high quality climatology: (1) they simulate small residuals in the energy and water balances, which are smaller than residuals stemming from observational uncertainty and smaller than residuals in most CMIP3 GCMs (Liepert and Previdi 2012); (2) the simulated water and energy budgets in HadGEM1-A and HadGEM3-A are in agreement with most reanalyses and are mostly within the range of observational uncertainty (Wild et al. 2013); (3) the models simulate well the link existing between the global energy budget and the hydrological cycle, with full consistency between atmospheric radiative cooling and precipitation (Allan 2009). The high surface net radiation is consistent with high outgoing longwave radiation and latent heat flux, and leads to an overly intense simulated global hydrological cycle compared to observations and reanalyses. This over-intensity is mainly found in HadGEM1-A, while it is restricted in HadGEM3-A by a compensating sensible heat flux that is closer to recent observations (Wild et al. 2013).

The global energy and water budgets are found to be insensitive to spatial resolution. This finding is in line with Duffy et al. (2003) who showed that when the models are tuned to balance radiation at TOA, the global water budget is insensitive to resolution. HadGEM1-A and HadGEM3-A needed little adjustments (refer to Sect. 2) to satisfy such a balance, possibly due to the scale-dependent formulation of the parametrizations. This ability to simulate nearly identical global budgets at all resolutions allows an attribution of the processes involved in the representation of the hydrological cycle over land and ocean with various resolutions. In fact, although resolution affects the energy budget over land and ocean very little, it affects the hydrological cycle by increasing (decreasing) precipitation over land (ocean). This makes high-resolution model simulations closer to observations over the ocean, but further away over land. Changes in precipitation are compensated by an increase in atmospheric moisture transport from ocean to land with resolution, which affects the partitioning of moisture sources that contribute to precipitation. While the models at N96 resolution, typical of current IPCC-class GCMs, appear to show the closest results to observations over land, the evaporation to precipitation ratio over land is too high, and the moisture convergence to precipitation ratio is too low at this resolution (this is also verified over the annual cycle of the water budget over land). This finding shows that it is not solely the amount of water that needs to be properly represented in GCMs. Each model has its own balance depending on available energy, and it is only by improving the global energy budget that the biases in the global water budget will be diminished. This point also highlights that when model deficiencies arise from its formulation, increasing resolution does not remove the main biases (Iorio et al. 2004; Scaife et al. 2010), but it often improves the trustworthiness of the model, as shown by calculating the water fluxes over land and ocean as a fraction of global precipitation, a method used to remove global biases. Nonetheless, we have shown that the relative contributions of atmospheric processes controlling moisture fluxes also need to be simulated properly. At higher resolution in both HadGEM1-A and HadGEM3-A, the ratio of evaporation to precipitation over land decreases while that of moisture convergence to precipitation increases, giving more weight to the resolved (large-scale dynamics) processes than the unresolved (local physics) processes largely dominant at low resolution. Our finding supports the hypothesis that heterogeneity in model parametrization is one of the underlying causes of model disagreement in the CMIP exercises.

Our results, using HadGEM3-A, appear to converge around 60-km resolution, suggesting that using a 60-km GCM is necessary to simulate such dynamical processes driving the mean global hydrological cycle, while a resolution of 130–300 km is too coarse. Although these results include a small number of ensemble members (running multiple high-resolution simulations is challenging due to computational resources and data storage limitations), these analyses include up to ten members per resolution, together with multi-decadal simulations and many land points. Moreover, despite the differences in model formulation between HadGEM1-A and HadGEM3-A that result in a different global water budget, the two model versions show the same tendency of decreasing E/P over land with increased resolution. This systematic tendency is significant, but analyzing other chains of AGCMs that may become available in the future with such a range of horizontal resolutions would be required to further strengthen our argument. To perform such a comparison and attribute changes in the hydrological cycle with resolution, we emphasize again the requirements for a balanced radiative budget at TOA, for a balanced atmospheric water budget, and for the global energy and water budgets to be insensitive to resolution. The processes associated with the increase in atmospheric moisture transport from ocean to land with resolution are treated in detail, globally and regionally, in a following manuscript (Demory et al. in prep).